Three-dimensional thermomechanical wave propagation analysis of sandwich nanoplate with graphene-reinforced foam core and magneto-electro-elastic face layers using nonlocal strain gradient elasticity theory

Abstract

This article investigates the propagation of bending, longitudinal, and shear waves in a smart sandwich nanoplate with a graphene platelet (GPL)-reinforced foam core and magneto-electro-elastic (MEE) surface layers using sinusoidal higher-order shear deformation theory (SHSDT). The suggested nanoplate is comprised of a Ti–6Al–4V foam core placed between MEE surface layers. The MEE surface layers are composed of a volumetric combination of cobalt-ferrite (CoFe₂O₄) and barium-titanate (BaTiO₃). The foam core and MEE face layers’ material characteristics are temperature dependent. In this study, three different core types are considered: metallic solid core (Type-I), GPL-reinforced solid core (Type-II) and GPL-reinforced foam core (Type-III), as well as three different foam distributions: symmetrical foam I (S-Foam I), symmetrical foam II (S-Foam II) and uniform foam (U-Foam). To derive the nanoplate's equations of motion and determine the system response, Hamilton's principle and Navier's method are employed. The effects of various parameters such as the wave number, nonlocal parameter, foam void coefficient and distribution pattern, GPL volume fraction, and thermal, electric, and magnetic charges, on the phase velocity and wave frequency are investigated via analytical calculations. The findings of the research indicate that the 3-D wave propagation characteristics of the sandwich nanoplate can be considerably modified or tuned with respect to external loads and material parameters. Thus, the proposed sandwich structure is expected to provide important contributions to radar stealth applications, protection of nanoelectromechanical devices from high frequency and temperature environments, advancement of smart nanoelectromechanical sensors characterized by lightweight and temperature sensitivity and wearable health equipment applications.

1 Introduction

Because of their high frequency of propagation, waves have a wide range of potential uses, including nanosized sensors and actuators. Understanding the mechanical characteristics of the structures that allow waves to propagate is crucial. The wave propagation of nanoplates is a complex phenomenon influenced by various factors. The influence of surface effects on the transmission of elastic waves in MEE nanoplates has been demonstrated, with the propagation characteristics being highly influenced by specific surface material variables [1]. Additionally, piezoelectric nanomaterials exhibit size-dependent characteristics and display a specific frequency at which waves are unable to propagate through a piezoelectric surface with nanoscale thickness. This finding offers new possibilities for utilizing these materials in various kinds of engineering disciplines [2]. Numerical illustrations have also been used to study the impact of the circular velocity, temperature rise, nonlocal factors and radius ratio on the vibration modes of nanoannular layers, demonstrating the complicated structure of wave transmission in nanostructures [3]. Based on modified coupled stress theory (MCST), Liu et al. [4] examined the dispersion behavior of Lamb waves in functionally graded (FG) piezoelectric plates. The results provided can be used as a guide for small-scale composite structure design and dynamic behavior evaluation. Using the concept of higher-order nonlocal gradient elasticity theory, Faghidian et al. [5] extensively investigated the propagation attributes of bending waves in FG porous nanoplates. Liu et al. [6] examined the dispersion characteristics of elastic waves in nanoscale FG piezoelectric systems. A study conducted in [7] examined the behavior of flexural wave propagation in a microbeam. This investigation considered the influence of a viscoelastic foundation and size effects, utilizing the concept of nonlocal strain gradient elasticity theory (NSGT). In [8], a more advanced NSGT was developed using variational calculus and thermodynamics concepts to analyze wave propagation in carbon nanotubes (CNTs). This approach incorporated two different size-dependent theories. The study conducted in [9] focused on analyzing the wave dispersion characteristics of a porous foam plate. Using the Gurtin–Murdoch surface elasticity framework, the surface impact was also included in the investigation. Using the state-vector methodology and propagation matrix technique, Chen et al. [10] studied harmonic wave dispersion in a multilayer MEE layer. In summary, the wave propagation of nanoplates is a multifaceted phenomenon influenced by surface effects, size-dependent properties, nonlocal parameters, temperature changes, viscoelasticity, and critical temperatures [11,12,13]. These factors collectively contribute to the complex behavior of nanoplates, making them a rich area for further research and exploration.

The sandwich plate having MEE face layers have been extensively studied in the discipline of science of materials and composite structures. Several studies have focused on examining these constructions considering different factors including material properties that vary with temperature, FG layers, and the effects of surface and interface conditions [14,15,16,17,18]. For instance, Mahesh [19] presented a mathematical model to calculate the deformations of MEE sandwich skew layers with an elasticity-based core and face sheets made of functionally graded carbon nanotube-reinforced MEE surface layers. This study provides important perspectives on the response of sandwich layers when subjected to various loading circumstances. Additionally, the work by Bamdad et al. [20] evaluated the vibration and buckling response of a sandwich Timoshenko porous beam with temperature-dependent material properties, considering MEE aspects. This research sheds light on the dynamic behavior of sandwich structures having MEE layers, particularly in the context of temperature effects. Investigations have extensively examined several characteristics of MEE elements at micro and nanoscale. This includes analyzing wave propagation, studying bending behavior, conducting buckling analysis, and developing precise solutions for diverse combinations [21,22,23]. Moreover, the researchers in [24, 25] have examined the efficiency characteristics of MEE structures and the influence of interface defects on their mechanical characteristics. The extensive body of research on MEE sandwich plates provides valuable knowledge on their mechanical, electrical, and thermal behavior, offering insights that are essential for the development and optimization of these systems in many technical applications.

Sandwich plates with foam core layers have been the subject of extensive research in various fields, including materials science, composite materials, and engineering [26,27,28,29]. The use of foam cores in sandwich plates has been investigated for their response to different types of loading, including impact, blast, and underwater shock waves. Furthermore, the response of sandwich plates with foam cores to different types of loading has been explored. For example, Al-Waily et al. [30] conducted a free vibration analysis of sandwich plates with a polyurethane foam core sandwiched between two aluminum faces. Additionally, Bahei–El–Din and Dvorak [31] investigated the performance of sandwich layers strengthened with polyurethane/polyurea interconnecting layers when subjected to blast loads. They emphasized the defensive function of polyurethane in improving the reaction of the sandwich layers. Moreover, it has been discovered that the structural integrity of foam-cored sandwich layers is influenced by the interaction between mechanical forces, temperature-induced distortions, and a decrease in their mechanical characteristics that occurs as a result of high temperatures [32]. This highlights the importance of considering thermo-mechanical load interactions in the design and analysis of sandwich plates with foam cores. Sandwich structures with smart nanoplates have been the subject of extensive research in recent years. The integration of smart materials and nanoreinforcements has shown excellent outcomes in enhancing the mechanical and functional features of sandwich plates. Ramakrishnan et al. [33] examined the impact behavior of sandwich layers including a nanoreinforced epoxy matrix, demonstrating the potential for improved stiffness and impact resistance. Moradi-Dastjerdi and Behdinan [34] proposed a multifunctional sandwich plate with graphene nanocomposite layers and piezoceramic active faces, highlighting the potential for temperature-sensitive smart materials in sandwich structures. The electromechanical behavior of piezoelectric sandwich nanostructures, providing insights into thermal management and energy harvesting, as examined by Li et al. [35]. Furthermore, smart substances such as magnetorheological fluids and piezoceramics have been explored to improve the stability and vibration response of sandwich plates. Hoseinzadeh and Rezaeepazhand [36] illustrated the improvement in the dynamic durability of multilayer hybrid sandwich layers by employing smart elastomer plates. This suggests the possibility of utilizing active vibration control in sandwich constructions. The integration of smart materials and nanoreinforcements in sandwich plates offers a wide range of functionalities including enhanced mechanical properties, dynamic stability, vibration control, and structural health monitoring. These advancements hold significant promise for the development of next-generation smart nanoreinforced sandwich structures with multifunctional capabilities.

Nonlocal theories have gained significant attention in the study of micro and nanostructures. In the investigation of the mechanical response of nanostructures, small-scale effects cannot be disregarded. Classical theories are scale-free and fail to account for small-scale effects. Traditional theories are unable to effectively estimate the characteristics of nanostructures due to this fact [37, 38]. These theories, such as surface elasticity theory [39,40,41,42], nonlocal elasticity theory (NET) [43, 44], NSGT [8, 45,46,47] and MCST [48,49,50], have been applied to model the static, dynamic, buckling, free vibration and wave propagation response of micro and nanostructures. In addition, nonlocal theories have been employed to create mathematical models for the analysis of bending, buckling, free vibration, wave propagation, and torsional vibration in structures including nanoplates, nanorods, nanoshells, and nanobeams [51,52,53,54]. For example, the longitudinal vibration behavior of FG restrained nanorods with elastic spring boundary conditions was investigated by Yayli [55] via NET. In this study, the effects of the power law index, nonlocal parameters, and elastic spring boundary conditions on the axial frequency of a nanorod structure were investigated. In addition, Yayli [56] studied the torsional vibration behavior of nanorods with elastic torsional boundary conditions using NET. With this study, free torsional vibration analysis of nanorod structures is analyzed for both deformable and nondeformable boundary conditions. The NET has been incorporated into the framework of micro continuum mechanics to derive relationships between angular dispersion and nonlocal parameters, providing a more comprehensive understanding of the behavior of materials such as piezoelectric sensors [57]. Furthermore, nonlocal theories have been applied to investigate the mechanical and vibrational properties of various materials, including graphene and CNTs, demonstrating their extensive applicability in the study of nanoelectromechanical systems and nanotechnology applications [50, 58,59,60,61]. Moreover, the nonlocal stress field theory has been employed to develop nanostructural models, leading to advancements in understanding the dynamic behavior of axially moving nanobeams and the transverse free vibration of nanobeams with intermediate support [62]. These advancements have contributed to addressing the limitations of continuum theory in analyzing nanoscale structures, providing a more accurate and reliable approach for studying size-dependent mechanical properties. Furthermore, the free vibration characteristics of viscoelastic nanodisks based on the MCST have been explored, demonstrating the diverse theoretical frameworks utilized to understand the vibrational behavior of nanoplates [63].

The NSGT is a comprehensive approach that considers both nonlocal and strain gradient effects in the mechanical analysis of size-dependent structures [64]. Unlike classical elasticity theory, NSGT accounts for micro/nanoscale effects, providing a more accurate representation of the mechanical and physical responses of small-scale structures [65]. This theory introduces two length scales into a single framework, capturing higher-order stress gradients and strain gradient nonlocality [66]. Additionally, the NSGT considers the influence of both nonlocal stress and strain gradients on the dynamic behavior of structures, offering a more comprehensive understanding of the mechanical response of size-dependent systems [67]. Furthermore, NSGT has been applied to various structural elements such as nanobeams, nanoplates, and nanoshells, demonstrating its versatility and applicability across different geometries and materials [65, 68, 69]. This theory also provides a basis for the development of solution methods that were previously unavailable in both nonlocal elasticity theory and strain gradient theory, opening up new avenues for analysis and design in the field of structural engineering [70].

As summarized above, the use of advanced materials such as metallic foams and MEEs in the fabrication and design of high-performance composite structures that respond to various environmental conditions is an innovative area that has not yet been widely investigated. MEE structures are preferred in advanced engineering applications such as smart vibration transducers, magnetic field sensors, micro- and nanoelectromechanical systems (M/NEMS), energy harvester devices, structural health monitoring and vibration control instruments thanks to their unique capabilities involving energy conversion, storage, and sensing. Metallic foam structures, on the other hand, are extensively demanded in aerospace, automotive, marine, and civil engineering applications due to their outstanding lightweight, high strength, thermal management, and energy absorption capabilities. Especially in NEMS sensor applications, the sensing and energy conversion performance are significantly affected by high temperature and complex wave environment conditions. Therefore, in such systems, it is essential to perform wave dispersion analysis that takes into account temperature dependent material characteristics. In this research, a sandwich nanoplate structure with a GPL-reinforced metallic foam core and two MEE surface plates, which can be used in MEMS sensor and actuator applications, nanosized health monitoring systems, ultrasonic wave transducers, soft robotics systems, radar wave absorption systems and military applications requiring impact dampening, is presented. A comprehensive literature review revealed that the investigation of 3-D wave propagation in a GPL-reinforced smart sandwich nanoplate structure, which also considers the temperature-dependent material properties of MEE plates, is a novel and original topic that has not yet been studied. In this study, the wave propagation characteristics of the proposed sandwich nanoplate are investigated with parameters such as the wave number, foam void coefficient and distribution pattern, nonlocal parameters, GPL volume fraction, temperature rise, and thermal, magnetic, and electric charges. It is expected that the results obtained with parametric simulations and graphical illustrations will contribute to the literature in the aforementioned fields.

2 Theory and formulation

2.1 Overview of the proposed sandwich nanostructure

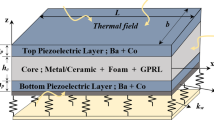
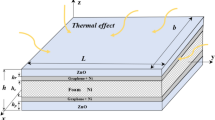
As depicted in Fig. 1, the proposed three-layer nanocomposite structure includes a GPL-reinforced metallic foam core and MEE surface plates. Here, the length, width, and total thickness of the nanoplate are symbolized by $a$, $b$ and $h$, respectively. Furthermore, ${h}_{c}$ and ${h}_{p}$ define the thicknesses of the core layer and MEE layers, while ${h}_{1}$, ${h}_{2}$, ${h}_{3}$ and ${h}_{4}$ denotes the distances from the top and bottom surfaces of the plates to the midpoint of the sandwich plate.

Fig. 1

A foam core sandwich nanoplate composed of MEE face layers

As shown in Fig. 2, the core layer, which has three different types: solid core, GPL-reinforced solid core and GPL-reinforced foam core, is sandwiched between two MEE face plates. The core layers are made of biocompatible Ti–6Al–4V material. It is also considered that the MEE face layers contain homogenous distributions of CoFe₂O₄ and BaTiO₃. Additionally, external electric and magnetic charges are provided along the thickness of the MEE plates. This causes the layers to expand and contract along the $x$ and $y$ axes.

Fig. 2

Type of the sandwich nanoplate

2.2 Foam distribution models

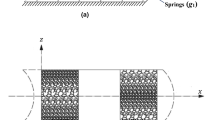
In this research, three types of foam distributions as U-Foam, S-Foam I and S-Foam II are considered as given in Fig. 3. The greatest pores in S-Foam I occur at the core's mid-plane, but in S-Foam II, the greatest pores are found at the upper and lower faces of the foam. The size of the pores remains constant in the U-Foam distribution.

Fig. 3

Foam distribution models

Equations (1–3) can be employed to define the Young’s modulus $E(z)$, Poisson’s ratio $v(z)$, coefficient of thermal expansion $\alpha (z)$, thermal conductivity $\kappa (z)$ and density $\rho (z)$ with respect to the z-axis for S-Foam I, S-Foam II and U-Foam foam dispersion patterns [71].

S-Foam I:

$$ \begin{aligned} & E\left( z \right) = E_{1} \left\{ {1 - \lambda_{0} \chi \left( z \right)} \right\} \\ & \nu \left( z \right) = \nu_{1} \left\{ {1 - \lambda_{0} \chi \left( z \right)} \right\} \\ & \alpha \left( z \right) = \alpha_{1} \left\{ {1 - \lambda_{m} \chi \left( z \right)} \right\} \\ & \kappa \left( z \right) = \kappa_{1} \left\{ {1 - \lambda_{m} \chi \left( z \right)} \right\} \\ & \rho \left( z \right) = \rho_{1} \left\{ {1 - \lambda_{m} \chi \left( z \right)} \right\} \\ \end{aligned} $$

(1)

S-Foam II:

$$ \begin{aligned} & E\left( z \right) = E_{1} \left\{ {1 - \lambda_{0}^{*} \left( {1 - \chi \left( z \right)} \right)} \right\} \\ & \nu \left( z \right) = \nu_{1} \left\{ {1 - \lambda_{0}^{*} \left( {1 - \chi \left( z \right)} \right)} \right\} \\ & \alpha \left( z \right) = \alpha_{1} \left\{ {1 - \lambda_{m}^{*} \left( {1 - \chi \left( z \right)} \right)} \right\} \\ & \kappa \left( z \right) = \kappa_{1} \left\{ {1 - \lambda_{m}^{*} \left( {1 - \chi \left( z \right)} \right)} \right\} \\ & \rho \left( z \right) = \rho_{1} \left\{ {1 - \lambda_{m}^{*} \left( {1 - \chi \left( z \right)} \right)} \right\} \\ \end{aligned} $$

(2)

U-Foam:

$$ \begin{aligned} & E\left( z \right) = E_{1} \left( {1 - {\Omega }} \right) \\ & \nu \left( z \right) = \nu_{1} \left( {1 - {\Omega }} \right) \\ & \alpha \left( z \right) = \alpha_{1} \left( {1 - {\Omega }^{*} } \right) \\ & \kappa \left( z \right) = \kappa_{1} \left( {1 - {\Omega }^{*} } \right) \\ & \rho \left( z \right) = \rho_{1} \left( {1 - {\Omega }^{*} } \right) \\ \end{aligned} $$

(3)

where ${E}_{1}$, ${\nu }_{1}$, ${\alpha }_{1}$, ${\kappa }_{1}$ and ${\rho }_{1}$ are the maximum values of the corresponding material properties, that are equivalent to the quantities of pure Ti–6Al–4V; ${\lambda }_{0}$, ${\lambda }_{0}^{*}$ and $\Omega$ define the foam void coefficients for S-Foam I, S-Foam II and U-Foam, respectively; ${\lambda }_{m}$, ${\lambda }_{m}^{*}$ and ${\Omega }^{*}$ are the corresponding coefficients of thermal expansion, thermal conductivity and density, respectively. $\chi \left(z\right)$ can be written as:

$$\chi \left(z\right)=\text{cos}\left[\frac{\pi z}{h}\right]$$

(4)

Foam parameters are related to mass density parameters in the following manners:

$$ \left\{ {\begin{array}{*{20}c} {\lambda _{m} = \frac{{1 - \sqrt {1 - \lambda _{0} \chi \left( z \right)} }}{{\chi \left( z \right)}}} & {({\text{S}} - {\text{Foam I}})} \\ {\frac{{1 - \sqrt {1 - \lambda _{0}^{*} (1 - \chi \left( z \right))} }}{{1 - \chi \left( z \right)}}} & {({\text{S}} - {\text{Foam II}})} \\ {\Omega ^{*} = 1 - \sqrt {1 - \Omega } } & {({\text{U}} - {\text{Foam}})} \\ \end{array} } \right. $$

(5)

The final material characteristics of the nanocomposite plate can be calculated as follows:

$${P}_{\text{eff}}=\frac{1}{{h}_{p}}\int\limits_{{h}_{1}}^{{h}_{2}}P\left(z\right)\text{d}z+\frac{1}{{h}_{c}}\int\limits_{{h}_{2}}^{{h}_{3}}P\left(z\right)\text{d}z+\frac{1}{{h}_{p}}\int\limits_{{h}_{3}}^{{h}_{4}}P\left(z\right)\text{d}z$$

(6)

in which ${h}_{1}=-{h}_{c}/2-{h}_{P}$, ${h}_{2}=-{h}_{c}/2$, ${h}_{3}={h}_{c}/2$ and ${h}_{4}={h}_{c}/2+{h}_{P}$. P(z) can be determined according to the temperature-dependent material characteristics.

2.3 GPL distribution method

It is required to get the material characteristics of the GPL-reinforced sandwich nano composite structure before carrying out the analysis of the plate. The effective Young’s modulus of the nanostructures can be determined using the Halpin–Tsai (H–T) micromechanical method as [72]:

$${E}_{1}=\frac{3}{8}\left(\frac{{\xi }_{L}{\eta }_{L}{V}_{\text{GPL}}}{1-{\eta }_{L}{V}_{\text{GPL}}}\right){E}_{m}+\frac{5}{8}\left(\frac{1+{\xi }_{w}{\eta }_{w}{V}_{\text{GPL}}}{1-{\eta }_{w}{V}_{\text{GPL}}}\right){E}_{m}$$

(7)

where

$${\xi }_{L}=\frac{2{l}_{\text{GPL}}}{{t}_{\text{GPL}}}$$

(8a)

$${\xi }_{w}=\frac{2{w}_{\text{GPL}}}{{t}_{\text{GPL}}}$$

(8b)

$${\eta }_{L}=\frac{\left({E}_{\text{GPL}}/{E}_{m}\right)-1}{\left({E}_{\text{GPL}}/{E}_{m}\right)+{\xi }_{L}}$$

(8c)

$${\eta }_{w}=\frac{\left({E}_{\text{GPL}}/{E}_{m}\right)-1}{\left({E}_{\text{GPL}}/{E}_{m}\right)+{\xi }_{w}}$$

(8d)

${w}_{\text{GPL}}$, ${l}_{\text{GPL}}$ and ${t}_{\text{GPL}}$ are the width, length, and thickness of the GPLs, respectively. Also, ${V}_{\text{GPL}}$, ${E}_{m}$ and ${E}_{\text{GPL}}$ represent the volume fraction of the GPL, the modulus of elasticity of the matrix and the GPLs, respectively. Poisson’s ratio and the mass density of the GPL-reinforced metal matrix can be calculated with the rule of mixture as [72]:

$$v_1=v_{\rm GPL}V_{\rm GPL}+v_{m}V_{m}$$

(9a)

$${\rho }_{1}={\rho }_{\text{GPL}}{V}_{\text{GPL}}+{\rho }_{m}{V}_{m}$$

(9b)

where

$${V}_{m}=1-{V}_{\text{GPL}}$$

(9c)

in which ${V}_{m}$ represents the volume fraction of the metal matrix. Also, the subscript symbols GPL and m refer to GPLs and metal, respectively.

2.4 Effective material properties of MEE face plates

The surface layers exhibit consistent variations in their mechanical, electrical, thermal, and magnetic characteristics, which are dependent on the volumetric percentage of CoFe₂O₄ and BaTiO₃. The effective material characteristics of MEE surface plates can be specified by employing the rule of mixtures [73]:

$$ \begin{aligned} & P_{{{\text{eff}}}}^{lp} \left( z \right) = C_{{{\text{lp}}}} P_{{{\text{Co}}}} + B_{{{\text{lp}}}} P_{{{\text{Ba}}}} ,\; h_{1} \le z \le h_{2} \\ & P_{{{\text{eff}}}}^{{{\text{up}}}} \left( z \right) = C_{{{\text{up}}}} P_{{{\text{Co}}}} + B_{{{\text{up}}}} P_{{{\text{Ba}}}} ,\; h_{3} \le z \le h_{4} \\ & C_{{{\text{lp}}}} + B_{{{\text{lp}}}} = 1 \\ & C_{{{\text{up}}}} + B_{{{\text{up}}}} = 1 \\ \end{aligned} $$

(10)

where ${P}_{\text{eff}}\left(\text{z}\right)$ denotes the effective material characteristics. $z$ stands for the distance from the neutral axis; ${C}_{\text{lp}}$, ${C}_{\text{up}}$, ${B}_{\text{lp}}$ and ${B}_{\text{up}}$ are the volumetric ratio of the ${\text{CoFe}}_{2}{\text{O}}_{4}$ and ${\text{BaTiO}}_{3}$ for lower and upper MEE face layers, respectively; ${P}_{\text{Co}}$ and ${P}_{\text{Ba}}$ define the properties of ${\text{CoFe}}_{2}{\text{O}}_{4}$ and ${\text{BaTiO}}_{3}$ for the top and bottom surface plates, respectively; and superscripts $\text{up}$ and $\text{lp}$ stand for the top and bottom surface layers, respectively.

The foam core layer and the MEE surface layers exhibit material properties that depend on temperature. These properties may be represented by a nonlinear temperature formula, which involves $E$, $v$, $\kappa$ and $\alpha$ as follows [74,75,76]:

$$P={P}_{0}({P}_{-1}{T}^{-1}+1+{P}_{1}T+{P}_{2}{T}^{2}+{P}_{3}{T}^{3})$$

(11)

in which $T={T}_{0}+\Delta T$ and ${T}_{0}=300$ K. ${P}_{0}$, ${P}_{-1}$, ${P}_{1}$, ${P}_{2}$ and ${P}_{3}$ define the temperature-dependent material constants. In addition, P refers to any material parameter that varies with temperature. The temperature-dependent thermal and mechanical characteristics of CoFe₂O₄ and BaTiO₃ are presented with Table 1. In addition, the thermal and mechanical characteristics of Ti–6Al–4V are given in Table 2. The temperature-dependent material properties provided by Table 1 for CoFe₂O₄ and BaTiO₃ have not been used before for the wave propagation analysis of sandwich structures. These properties were derived from mathematical simulations, as well as from partial experimental investigations reported by [74, 76].

Table 1 Temperature-dependent material coefficients for CoFe₂O₄ and BaTiO₃

Table 2 Temperature-dependent material coefficients of Ti–6Al–4V [74, 76]

2.5 Formulation of the temperature dispersion

The equations required for uniform, linear, and nonlinear temperature increases over the nanoplate are provided in this section. The temperature of a sandwich nanocomposite plate, initially at ${T}_{0}$ = 300 K, is steadily increased to its top temperature $T$ through a uniform temperature increase, as described by the subsequent formulation:

$$\Delta T=T-{T}_{0}$$

(12)

According to reference [77], the temperatures of the bottom and top surfaces of a sandwich nanostructure, denoted as ${T}_{b}$ and ${T}_{t}$, respectively, can be determined by assuming a linear temperature rise:

$$T(z)={T}_{b}+({T}_{t}-{T}_{b})\left(\frac{h+2z}{2h}\right)$$

(13)

When there is a nonlinear rise in temperature along the pattern of thickness of the nanocomposite plates, Eq. (14) can be calculated by imposing particular temperature limitations to identify the values of ${T}_{t}$ and ${T}_{b}$ [78].

$$-\frac{\text{d}}{\text{d}z}\left(\kappa \left(z\right)\frac{\text{d}T}{\text{d}z}\right)=0, T\left(\frac{h}{2}\right)={T}_{t},\hspace{0.33em}\hspace{0.33em} T\left(-\frac{h}{2}\right)={T}_{b}$$

(14)

The temperature of any location through the thickness direction can be computed using the following formula for a specific set of boundary conditions:

$$T(z)={T}_{b}+\frac{({T}_{t}-{T}_{b})}{\int\limits_{-\frac{h}{2}}^{\frac{h}{2}} \frac{1}{\kappa \left(z\right)}d(z)}\int\limits_{-\frac{h}{2}}^{z}\kappa \left(z\right)\text{d}z$$

(15)

2.6 Formulation of NSGT

According to the NSGT, the total stress, which includes both nonlocal and strain gradient stress tensors, can be represented as [8, 39]:

$${{\varvec{\sigma}}}^{{\varvec{t}}}={\varvec{\sigma}}-\nabla {{\varvec{\sigma}}}^{(1)}$$

(16)

where $\nabla$, $\sigma$ and ${\sigma }^{(1)}$ denote the Laplacian operator, the nonlocal classical stress tensor and the higher-order stress tensor, respectively. $\sigma$ and ${\sigma }^{(1)}$ can be calculated as [8]:

$${\varvec{\sigma}}=\int\limits_{V}{\alpha }_{0}({{\varvec{x}}}{^{\prime}},{\varvec{x}},{e}_{0}a){\varvec{C}}\boldsymbol{ }:{{\varvec{\varepsilon}}}{^\prime}({{\varvec{x}}}{^{\prime}})dV$$

(17)

$${{\varvec{\sigma}}}^{(1)}={l}_{m}^{2}\int\limits_{V}{\alpha }_{1}({{\varvec{x}}}{^{\prime}},{\varvec{x}},{e}_{1}a){\varvec{C}}\boldsymbol{ }:\nabla {{\varvec{\varepsilon}}}{^\prime}({{\varvec{x}}}{^{\prime}})dV$$

(18)

where ${\alpha }_{0}\left({{\varvec{x}}}{^{\prime}},{\varvec{x}},{e}_{0}a\right)$ and ${\alpha }_{1}\left({{\varvec{x}}}{^{\prime}},{\varvec{x}},{e}_{1}a\right)$ are nonlocal kernel functions. ${e}_{0}a$ and ${e}_{1}a$ are nonlocal parameters with ${e}_{0}$ and ${e}_{1}$ material constants, ${\varvec{C}}$ is the elastic constant tensor, ${l}_{m}$ is the material length scale parameter, and ${\varvec{\varepsilon}}$, and $\nabla{\varvec{\varepsilon}}$ denote the strain and strain gradient tensors, respectively.

The general constitutive relation can be expressed as follows whenever the two nonlocal kernel functions, ${\alpha }_{0}\left({{\varvec{x}}}{^{\prime}},{\varvec{x}},{e}_{0}a\right)$ and ${\alpha }_{1}\left({{\varvec{x}}}{^{\prime}},{\varvec{x}},{e}_{1}a\right)$, fulfill the constraints formulated by Eringen [79]:

$$ \left[ {1 - (e_{1} a)^{2} \nabla ^{2} } \right]\left[ {1 - (e_{0} a)^{2} \nabla ^{2} } \right]\sigma _{{ij}} = C_{{ijkl}} \left[ {1 - (e_{1} a)^{2} \nabla ^{2} } \right]e_{{kl}} - C_{{ijkl}} l_{m}^{2} \left[ {1 - (e_{0} a)^{2} \nabla ^{2} } \right]\nabla ^{2} e_{{kl}} $$

(19)

Assuming that $e={e}_{0}={ \, e}_{1}$, the nonlocal strain gradient constitutive equation can be represented as follows:

$$ \left[ {1 - \left( {ea} \right)^{2} \nabla ^{2} } \right]\sigma _{{ij}} = C_{{ijkl}} \left[ {1 - l_{m}^{2} \nabla ^{2} } \right]e_{{kl}} $$

(20)

where $ea$ represents the nonlocal parameter. The equations established above can be rearranged for MEE sandwich nanoplates taking into account thermal, electrical and magnetic effects as given below [79]:

$$ \begin{aligned} & {\varvec{\sigma}}\left( {x,y,z} \right)\left( {1 - e_{0} a^{2} \nabla^{2} } \right) = \left( {1 - l_{m}^{2} \nabla^{2} } \right)\left[ {\overline{\user2{C}}\left( z \right){\varvec{\varepsilon}} - \overline{\user2{e}}\left( z \right){\varvec{E}} - \overline{\user2{q}}\left( z \right){\varvec{H}}} \right] - \overline{\user2{C}}\left( z \right)\alpha \left( z \right)\Delta T \\ & {\varvec{D}}\left( {x,y,z} \right)\left( {1 - e_{0} a^{2} \nabla^{2} } \right) = \left( {1 - l_{m}^{2} \nabla^{2} } \right)\left[ {\overline{\user2{e}}^{T} \left( z \right){\varvec{\varepsilon}} + \overline{\user2{\xi }}\left( z \right){\varvec{E}} + {\overline{\mathbf{g}}}\left( z \right){\varvec{H}}} \right] \\ & {\varvec{B}}\left( {x,y,z} \right)\left( {1 - e_{0} a^{2} \nabla^{2} } \right) = \left( {1 - l_{m}^{2} \nabla^{2} } \right)\left[ {\overline{\user2{q}}^{T} \left( z \right){\varvec{\varepsilon}} + {\overline{\mathbf{g}}}\left( z \right){\varvec{E}} + \overline{\user2{\mu }}\left( z \right){\varvec{H}}} \right] \\ \end{aligned} $$

(21)

where $D$, $B$, $E$ and $H$ stand for the electrical displacement, magnetic induction, and electrical and magnetic loads, respectively; $\xi$, $\text{g}$, $q$ $e$, and $\mu$ define the dielectric, magneto-electric, magnetostrictive, piezoelectric and magnetic permeability coefficients, respectively.

2.7 Displacement fields and strains

Through the utilization of SHSDT, the displacement field of the sandwich nanocomposite plate can be defined in the following manner [80]:

$$ \begin{aligned} & u\left( {x,y,z,t} \right) = u_{0} \left( {x,y,t} \right) - z\frac{{\partial w_{b} \left( {x,y,t} \right)}}{\partial x} - f\left( z \right)\frac{{\partial w_{s} \left( {x,y,t} \right)}}{\partial x} \\ & v\left( {x,y,z,t} \right) = v_{0} \left( {x,y,t} \right) - z\frac{{\partial w_{b} \left( {x,y,t} \right)}}{\partial y} - f\left( z \right)\frac{{\partial w_{s} \left( {x,y,t} \right)}}{\partial y} \\ & w\left( {x,y,z,t} \right) = w_{b} \left( {x,y,t} \right) + w_{s} \left( {x,y,t} \right) \\ \end{aligned} $$

(22)

where $u$, $v$, and $w$ are the movements of any point in the $x$, $y$ and $z$ axes. ${w}_{b}$ and ${w}_{s}$ represent the bending and shear, respectively. Also ${u}_{0}$, ${v}_{0}$ and ${w}_{o}$ define the mid-plane displacements. Furthermore, $f\left(z\right)$ has the following expression based on the SSDT [81]:

$$f\left(z\right)=z-\frac{h}{\pi }\text{sin}\frac{\pi z}{h}$$

(23)

The displacement field in Eq. (22) is associated with strain–displacement interactions that can be expressed in a basic manner as described in reference [80]:

$$ \begin{aligned} & \varepsilon_{xx} = \frac{{\partial u_{0} }}{\partial x} - z\frac{{\partial^{2} w_{b} }}{{\partial x^{2} }} - f\left( z \right)\frac{{\partial^{2} w_{s} }}{{\partial x^{2} }} \\ & \varepsilon_{yy} = \frac{{\partial v_{0} }}{\partial y} - z\frac{{\partial^{2} w_{b} }}{{\partial y^{2} }} - f\left( z \right)\frac{{\partial^{2} w_{s} }}{{\partial y^{2} }} \\ & \gamma_{xy} = \frac{{\partial v_{0} }}{\partial x} + \frac{{\partial u_{0} }}{\partial y} - 2z\frac{{\partial^{2} w_{b} }}{\partial x\partial y} - 2f\left( z \right)\frac{{\partial^{2} w_{s} }}{\partial x\partial y} \\ & \gamma_{yz} = g\left( z \right)\frac{{\partial w_{s} }}{\partial y} \\ \end{aligned} $$

(24a)

where

$$g\left(z\right)=1-{f}{^\prime}(z)$$

(24b)

The variables ${\varepsilon }_{ii}$ and ${\gamma }_{ii}$ stand for the normal and shear strain components, respectively. Here, $ii$ represents $xx$ and $yy$, and $ij$ stands for $xy$, $yz$, and $xz$.

2.8 Constitutive equations

In this study, it is considered that foam core ($c$) is sandwiched between MEE face plates ($p$). By applying the principles of NSGT, the constitutive relations of the Ti–6Al–4V foam core plate can be established in the following way [82, 83]:

$$\left({1 }-{\text{( }{ \, e}_{0}a \, \text{)}}^{2} \, {\nabla}^{2}\right){\left\{\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{yz}\\ {\sigma }_{xz}\\ {\sigma }_{xy}\end{array}\right\}}^{c}=\left(1-{l}_{m}^{2} \, {\nabla}^{2}\right){\left[\begin{array}{ccccc}{c}_{11}&\quad {c}_{12}&\quad 0&\quad 0&\quad 0\\ {c}_{21}&\quad {c}_{22}&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad {c}_{44}&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad {c}_{55}&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad {c}_{66}\end{array}\right]}^{c}\left\{\begin{array}{c}{\varepsilon }_{xx}-\alpha T\\ {\varepsilon }_{yy}-\alpha T\\ {\gamma }_{yz}\\ {\gamma }_{xz}\\ {\gamma }_{xy}\end{array}\right\}$$

(25)

In this context, ${c}_{ij}$ denotes the elastic constant and can be computed as follows:

$$ \begin{aligned} & c_{11} = c_{22} = \frac{E\left( z \right)}{{1 - v^{2} }} \\ & c_{12} = c_{21} = \frac{vE\left( z \right)}{{1 - v^{2} }} \\ & c_{44} = c_{55} = c_{66} = \frac{E\left( z \right)}{{2\left[ {1 + v} \right]}} \\ \end{aligned} $$

(26)

The constitutive relations of the MEE face layers, which take into account thermal strains, are determined by through the application of NSGT [82]:

$$\begin{aligned} \left( {{{1 }} - {\text{( }}{\mkern 1mu} e_{0} a{\mkern 1mu} )^{2} {\mkern 1mu} \nabla ^{2} } \right)\left\{ {\begin{array}{*{20}c} {\sigma _{{xx}} } \\ {\sigma _{{yy}} } \\ {\sigma _{{yz}} } \\ {\sigma _{{xz}} } \\ {\sigma _{{xy}} } \\ \end{array} } \right\}^{p} & = \left( {1 - l_{m}^{2} \;\nabla ^{2} } \right)\left[ {\begin{array}{*{20}c} {c_{{11}} } &\quad {c_{{12}} } &\quad {0} &\quad {0} &\quad {0} \\ {c_{{21}} } &\quad {c_{{22}} } &\quad {0} &\quad {0} &\quad {0} \\ 0 &\quad {0} &\quad {c_{{44}} } &\quad {0} &\quad {0} \\ 0 &\quad {0} &\quad {0} &\quad {c_{{55}} } &\quad {0} \\ 0 &\quad {0} &\quad {0} &\quad {0} &\quad {c_{{66}} } \\ \end{array} } \right]^{p} \left\{ {\begin{array}{*{20}c} {\varepsilon _{{xx}} - \alpha T} \\ {\varepsilon _{{yy}} - \alpha T} \\ {\gamma _{{yz}} } \\ {\gamma _{{xz}} } \\ {\gamma _{{xy}} } \\ \end{array} } \right\} \\ &\quad - \left( {1 - l_{m}^{2} {\mkern 1mu} \nabla ^{2} } \right)\left[ {\begin{array}{*{20}c} 0 &\quad {0} &\quad {e_{{31}} } \\ 0 &\quad {0} &\quad {e_{{32}} } \\ 0 &\quad {e_{{24}} } &\quad {0} \\ {e_{{15}} } &\quad {0} &\quad {0} \\ 0 &\quad {0} &\quad {0} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right\}\\ &\quad - \left( {1 - l_{m}^{2} {\mkern 1mu} \nabla ^{2} } \right)\left[ {\begin{array}{*{20}c} 0 &\quad {0} &\quad {q_{{31}} } \\ 0 &\quad {0} &\quad {q_{{32}} } \\ 0 &\quad {q_{{24}} } &\quad {0} \\ {q_{{15}} } &\quad {0} &\quad {0} \\ 0 &\quad {0} &\quad {0} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {H_{x} } \\ {H_{y} } \\ {H_{z} } \\ \end{array} } \right\} \\ \end{aligned}$$

(27)

The MEE layers' magnetic and electric displacements can be expressed as follows:

$$\begin{aligned} \left( {{{1 }} - {\text{( }}{\mkern 1mu} e_{0} a{\mkern 1mu} )^{2} {\mkern 1mu} \nabla ^{2} } \right)\left\{ {\begin{array}{*{20}c} {B_{x} } \\ {B_{y} } \\ {B_{z} } \\ \end{array} } \right\} = & \left( {1 - l_{m}^{2} {\mkern 1mu} \nabla ^{2} } \right)\left[ {\begin{array}{*{20}c} 0 &\quad {0} &\quad {0} &\quad {q_{{15}} } &\quad {0} \\ 0 &\quad {0} &\quad {q_{{24}} } &\quad {0} &\quad {0} \\ {q_{{31}} } &\quad {q_{{32}} } &\quad {0} &\quad {0} &\quad {0} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon _{{xx}} } \\ {\varepsilon _{{yy}} } \\ {\gamma _{{yz}} } \\ {\gamma _{{xz}} } \\ {\gamma _{{xy}} } \\ \end{array} } \right\} \\ + & \left( {1 - l_{m}^{2} {\mkern 1mu} \nabla ^{2} } \right)\left[ {\begin{array}{*{20}c} {g_{{11}} } &\quad {0} &\quad {0} \\ 0 &\quad {g_{{22}} } &\quad {0} \\ 0 &\quad {0} &\quad {g_{{33}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right\} + \left( {1 - l_{m}^{2} {\mkern 1mu} \nabla ^{2} } \right)\left[ {\begin{array}{*{20}c} {\mu _{{11}} } &\quad {0} &\quad {0} \\ 0 &\quad {\mu _{{22}} } &\quad {0} \\ 0 &\quad {0} &\quad {\mu _{{33}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {H_{x} } \\ {H_{y} } \\ {H_{z} } \\ \end{array} } \right\} \\ \end{aligned} $$

(28a)

$$ \begin{aligned} \left( {{{1 }} - {\text{( }}{\mkern 1mu} e_{0} a{\mkern 1mu} )^{2} {\mkern 1mu} \nabla ^{2} } \right)\left\{ {\begin{array}{*{20}c} {D_{x} } \\ {D_{y} } \\ {D_{z} } \\ \end{array} } \right\} = & \left( {1 - l_{m}^{2} {\mkern 1mu} \nabla ^{2} } \right)\left[ {\begin{array}{*{20}c} 0 &\quad {0} &\quad {0} & \quad {e_{{15}} } &\quad {0} \\ 0 &\quad {0} &\quad {e_{{24}} } &\quad {0} &\quad {0} \\ {e_{{31}} } &\quad {e_{{32}} } &\quad {0} &\quad {0} &\quad {0} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon _{{xx}} } \\ {\varepsilon _{{yy}} } \\ {\gamma _{{yz}} } \\ {\gamma _{{xz}} } \\ {\gamma _{{xy}} } \\ \end{array} } \right\} \\ + & \left( {1 - l_{m}^{2} {\mkern 1mu} \nabla ^{2} } \right)\left[ {\begin{array}{*{20}c} {\xi _{{11}} } &\quad {0} &\quad {0} \\ 0 &\quad {\xi _{{22}} } &\quad {0} \\ 0 &\quad {0} &\quad {\xi _{{33}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right\} + \left( {1 - l_{m}^{2} {\mkern 1mu} \nabla ^{2} } \right)\left[ {\begin{array}{*{20}c} {g_{{11}} } &\quad {0} &\quad {0} \\ 0 &\quad {g_{{22}} } &\quad {0} \\ 0 &\quad {0} &\quad {g_{{33}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {H_{x} } \\ {H_{y} } \\ {H_{z} } \\ \end{array} } \right\} \\ \end{aligned} $$

(28b)

In the quasi-static approximation, it is permitted for the distribution of electric and magnetic elements in the path of thickness to change as a mixture of cosine variation and linear fluctuation. This is done in order to satisfy Maxwell's equations. This modification is supported in the manner described below [84, 85]:

$$\Psi \left(x,y,z,t\right)=\frac{2z}{{h}_{p}}{\psi }_{0}-\psi \left(x,y,t\right)\text{cos}\left(\frac{\pi z}{{h}_{p}}\right)$$

(29a)

$$\Phi \left(x,y,z,t\right)=\frac{2z}{{h}_{p}}{\phi }_{0}-\phi \left(x,y,t\right)\text{cos}\left(\frac{\pi z}{{h}_{p}}\right)$$

(29b)

$\Psi \left(x,y,z,t\right)$ and $\Phi \left(x,y,z,t\right)$ represent the spatial variations of the electric and magnetic fields, respectively. In addition, the parameters ${\psi }_{0}$ and ${\phi }_{0}$ are used to symbolize the initial magnetic and electric potentials that are provided to the MEE layers from external sources. Equations (29a) and (29b) enable us to determine the electric and magnetic field elements as follows [84,85,86]:

$$ \begin{aligned} & \left\{ {H_{x} , H_{y} } \right\} = - \left\{ {\frac{{\partial {\Psi }}}{\partial x}, \frac{{\partial {\Psi }}}{\partial y} } \right\} = \left\{ {\frac{\partial \psi }{{\partial x}}, \frac{\partial \psi }{{\partial y}} } \right\}\cos \left( {\frac{\pi z}{{h_{p} }}} \right) \\ & H_{z} = - \frac{{\partial {\Psi }}}{\partial z} = - \frac{2}{{h_{p} }} \psi_{0} - \frac{\pi }{{h_{p} }} \psi \sin \left( {\frac{\pi z}{{h_{p} }}} \right){ } \\ \end{aligned} $$

(30a)

$$ \begin{aligned} & \left\{ {E_{x} , E_{y} } \right\} = - \left\{ {\frac{{\partial {\Phi }}}{\partial x}, \frac{{\partial {\Phi }}}{\partial y} } \right\} = \left\{ {\frac{\partial \phi }{{\partial x}}, \frac{\partial \phi }{{\partial y}} } \right\}\cos \left( {\frac{\pi z}{{h_{p} }}} \right) \\ & E_{z} = - \frac{{\partial {\Phi }}}{\partial z} = - \frac{2}{{h_{p} }} \phi_{0} - \frac{\pi }{{h_{p} }} \phi \sin \left( {\frac{\pi z}{{h_{p} }}} \right) \\ \end{aligned} $$

(30b)

2.9 Motion equations

The application of the virtual displacement methodology [87], which is a variation of Hamilton’s method, is utilized to get the differential equations of the sandwich MEE nanoplate.

$$\int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta U - \delta T - \delta W} \right){\text{d}}t = 0} $$

(31)

Here, the symbols $\delta U$, $\delta T$, and $\delta W$ are used to denote the virtual strain energy, kinetic energy, and virtual work in relation to the external loads that are supplied.

The sandwich nanoplate’s strain energy can be defined as [88]:

$$U=\frac{1}{2}\int\limits_{V}\left({\sigma }_{ij}{\varepsilon }_{ij}-{D}_{i}{E}_{i}-{B}_{i}{H}_{i}\right)\text{d}V$$

(32)

Using the variational formulation, Eq. (32) can be written as:

$$ \delta U=\int\limits_{V}{\left({\sigma }_{ij}{\delta \varepsilon }_{ij}-{D}_{i}{\delta E}_{i}-{B}_{i}{\delta H}_{i}\right)\text{d}V}$$

(33)

Substituting the stress, strain, magnetic displacement, electric displacement, and electric and magnetic field components into Eq. (33), the variational form of $U$ can be derived as follows:

$$\delta U=\int\limits_{A}\int\limits_{-\frac{h}{2}}^{\frac{h}{2}}\left({\sigma }_{xx}{\delta \varepsilon }_{xx}+{\sigma }_{yy}{\delta \varepsilon }_{yy}{+\sigma }_{yz}{\delta \gamma }_{yz}{+\sigma }_{xz}{\delta \gamma }_{xz}{+\sigma }_{xy}{\delta \gamma }_{xy}-{D}_{x}{\delta E}_{x}-{D}_{y}{\delta E}_{y}-{D}_{z}{\delta E}_{z}- {B}_{x}{\delta H}_{x}-{B}_{y}{\delta H}_{y}-{B}_{z}{\delta H}_{z}\right)\text{d}z\text{d}A$$

(34)

Finally, the finalized representation of the strain energy is derived in the following form:

$$ \delta U = \int\limits_{A} {\left[ \begin{gathered} - \left( {\frac{{\partial N_{{xx}} }}{{\partial x}} + \frac{{\partial N_{{xy}} }}{{\partial y}}} \right)\delta u_{0} - \left( {\frac{{\partial N_{{xy}} }}{{\partial x}} + \frac{{\partial N_{{yy}} }}{{\partial y}}} \right)\delta \nu _{0} - \left( {\frac{{\partial ^{2} M_{{xx}}^{b} }}{{\partial x^{2} }} + 2\frac{{\partial ^{2} M_{{xy}}^{b} }}{{\partial x\partial y}} + \frac{{\partial ^{2} M_{{yy}}^{b} }}{{\partial y^{2} }}} \right)\delta w_{b} \hfill \\ - \left( {\frac{{\partial ^{2} M_{{xx}}^{s} }}{{\partial x^{2} }} + 2\frac{{\partial ^{2} M_{{xy}}^{s} }}{{\partial x\partial y}} + \frac{{\partial ^{2} M_{{yy}}^{s} }}{{\partial y^{2} }} + \frac{{\partial S_{{xz}}^{s} }}{{\partial x}} + \frac{{\partial S_{{yz}}^{s} }}{{\partial y}}} \right)\delta w_{s} + \left( {\frac{{\partial \overline{{D_{x} }} }}{{\partial x}} + \frac{{\partial \overline{{D_{y} }} }}{{\partial y}} + \overline{{D_{z} }} } \right)\delta \phi \hfill \\ + \left( {\frac{{\partial \overline{{B_{x} }} }}{{\partial x}} + \frac{{\partial \overline{{B_{y} }} }}{{\partial y}} + \overline{{B_{z} }} } \right)\delta \psi \hfill \\ \end{gathered} \right]} dA A$$

(35a)

in which the resultant forces and moments in Eq. (35a) are expressed as:

$$\left\{{N}_{ij}, {M}_{ij}^{b}, {M}_{ij}^{s}\right\}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}\left\{1, z, f\left(z\right)\right\}{\sigma }_{ij}^{p}\text{d}z+\int\limits_{-\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}}\left\{1, z, f\left(z\right)\right\}{\sigma }_{ij}^{c}\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}\left\{1, z, f\left(z\right)\right\}{\sigma }_{ij}^{p}\text{d}z i,j=x,y$$

(35b)

$${S}_{xz}^{s}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}g\left(z\right){\sigma }_{xz}^{p}\text{d}z+\int\limits_{-\frac{h}{2}}^{\frac{h}{2}}g\left(z\right){\sigma }_{xz}^{c}\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}{g\left(z\right)\sigma }_{xz}^{p}\text{d}z$$

(35c)

$${S}_{yz}^{s}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}g\left(z\right){\sigma }_{yz}^{p}\text{d}z+\int\limits_{-\frac{h}{2}}^{\frac{h}{2}}g\left(z\right){\sigma }_{yz}^{c}\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}{g\left(z\right)\sigma }_{yz}^{p}\text{d}z$$

(35d)

$$\overline{{D }_{x}}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}{D}_{x}\text{cos}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}{D}_{x}\text{cos}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z$$

(35e)

$$\overline{{D }_{y}}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}{D}_{y}\text{cos}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}{D}_{y}\text{cos}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z$$

(35f)

$$\overline{{D }_{z}}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}{\frac{\pi }{{h}_{p}}D}_{z}\text{sin}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}{\frac{\pi }{{h}_{p}}D}_{z}\text{sin}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z$$

(35g)

$$\overline{{B }_{x}}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}{B}_{x}\text{cos}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}{B}_{x}\text{cos}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z$$

(35h)

$$\overline{{B }_{y}}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}{B}_{y}\text{cos}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}{B}_{y}\text{cos}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z$$

(35i)

$$\overline{{B }_{z}}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}{\frac{\pi }{{h}_{p}}B}_{z}\text{sin}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}{\frac{\pi }{{h}_{p}}B}_{z}\text{sin}\left(\frac{\pi \widehat{z}}{{h}_{p}}\right)\text{d}z$$

(35j)

The variable $\widehat{z}$ is established for the purpose of characterizing piezo-electromagnetic face sheets. The top layer is denoted as $\widehat{z}=z-\frac{{h}_{c}}{2}-{h}_{p}$, and the bottom layer, is designated as $\widehat{z}=$ z $+\frac{{h}_{c}}{2}+{h}_{p}$.

The equation representing the kinetic energy of the nanocomposite structure can be expressed as [89]:

$$T=\frac{1}{2}\int\limits_{A}\int\limits_{-\frac{h}{2}}^{\frac{h}{2}}\rho \left(z\right)\left({\left(\frac{\partial u}{\partial t}\right)}^{2}+{\left(\frac{\partial \nu }{\partial t}\right)}^{2}+{\left(\frac{\partial w}{\partial t}\right)}^{2}\right)\text{d}z\text{d}A$$

(36)

By applying a variational formulation and integrating with respect to time, the kinetic energy can be written as:

$$\int\limits_{{t}_{1}}^{{t}_{2}}\delta T\text{d}t=\int\limits_{{t}_{1}}^{{t}_{2}}\int\limits_{A}\int\limits_{-\frac{h}{2}}^{\frac{h}{2}}\rho \left(z\right)\left(\frac{\partial u}{\partial t}\frac{\partial \delta u}{\partial t}+\frac{\partial \nu }{\partial t}\frac{\partial \delta \nu }{\partial t}+\frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t}\right)\text{d}z\text{d}A\text{d}t$$

(37a)

By utilizing Eq. (22), the previous equation for kinetic energy can be expressed as:

$$ \begin{aligned} \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \delta T{\text{d}}t & = \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{A}^{{}} {\int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho \left( z \right)\left[ {\left( {\frac{{\partial u_{0} }}{{\partial t}} - z\frac{{\partial ^{2} w_{b} }}{{\partial x\partial t}} - f\left( z \right)\frac{{\partial ^{2} w_{s} }}{{\partial x\partial t}}} \right)\left( {\frac{{\partial \delta u_{0} }}{{\partial t}} - z\frac{{\partial ^{2} \delta w_{b} }}{{\partial x\partial t}} - f\left( z \right)\frac{{\partial ^{2} \delta w_{s} }}{{\partial x\partial t}}} \right)} \right.} } } \\ & \quad + \left( {\frac{{\partial v_{0} }}{{\partial t}} - z\frac{{\partial ^{2} w_{b} }}{{\partial y\partial t}} - f\left( z \right)\frac{{\partial ^{2} w_{s} }}{{\partial y\partial t}}} \right)\left( {\frac{{\partial \delta v_{0} }}{{\partial t}} - z\frac{{\partial ^{2} \delta w_{b} }}{{\partial y\partial t}} - f\left( z \right)\frac{{\partial ^{2} \delta w_{s} }}{{\partial y\partial t}}} \right) \\ & \left. {\quad + \left( {\frac{{\partial w_{b} }}{{\partial t}} + \frac{{\partial w_{s} }}{{\partial t}}} \right)\left( {\frac{{\partial \delta w_{b} }}{{\partial t}} + \frac{{\partial \delta w_{s} }}{{\partial t}}} \right)} \right]{\text{d}}z{\text{d}}A{\text{d}}t \\ \end{aligned} $$

(37b)

Eventually, the final form of the virtual kinetic energy expression of the presented nanoplate model, which is determined with the mass moments of inertia ${I}_{i} (i=\text{0,1},{2,3},{4,5})$, can be obtained as follows:

$$ \begin{aligned} \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \delta T{\text{d}}t &= \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{A}^{{}} {\left\{ {\left( { - I_{0} \frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }} + I_{1} \frac{{\partial ^{3} w_{b} }}{{\partial x\partial t^{2} }} + I_{2} \frac{{\partial ^{3} w_{s} }}{{\partial x\partial t^{2} }}} \right)\delta u_{0} } \right.} } \hfill \\ &\quad + \left( { - I_{0} \frac{{\partial ^{2} v_{0} }}{{\partial t^{2} }} + I_{1} \frac{{\partial ^{3} w_{b} }}{{\partial x\partial t^{2} }} + I_{2} \frac{{\partial ^{3} w_{s} }}{{\partial x\partial t^{2} }}} \right)\delta v_{0} \hfill \\ &\quad - \left[ {I_{0} \left( {\frac{{\partial ^{2} w_{b} }}{{\partial t^{2} }} + \frac{{\partial ^{2} w_{s} }}{{\partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial ^{3} u_{0} }}{{\partial x\partial t^{2} }} + \frac{{\partial ^{3} v_{0} }}{{\partial y\partial t^{2} }}} \right)} \right. \hfill \\ &\quad \left. { - I_{3} \left( {\frac{{\partial ^{4} w_{b} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial ^{4} w_{b} }}{{\partial y^{2} \partial t^{2} }}} \right) - I_{4} \left( {\frac{{\partial ^{4} w_{s} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial ^{4} w_{s} }}{{\partial y^{2} \partial t^{2} }}} \right)} \right]\delta w_{b} \hfill \\ & \quad - \left[ {I_{0} \left( {\frac{{\partial ^{2} w_{b} }}{{\partial t^{2} }} + \frac{{\partial ^{2} w_{s} }}{{\partial t^{2} }}} \right) + I_{2} \left( {\frac{{\partial ^{3} u_{0} }}{{\partial x\partial t^{2} }} + \frac{{\partial ^{3} v_{0} }}{{\partial y\partial t^{2} }}} \right)} \right. \hfill \\ &\quad \left. { - I_{4} \left( {\frac{{\partial ^{4} w_{b} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial ^{4} w_{b} }}{{\partial y^{2} \partial t^{2} }}} \right) - I_{5} \left( {\frac{{\partial ^{4} w_{s} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial ^{4} w_{s} }}{{\partial y^{2} \partial t^{2} }}} \right)} \right]\left. {\delta w_{s} } \right\}{\text{d}}A{\text{d}}t \hfill \\ \end{aligned}$$

(37c)

in which

$$\left\{{I}_{0}, {I}_{1}, {I}_{3}\right\}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}\left\{1, z, {z}^{2}\right\}{\rho }^{p}\text{d}z+\int\limits_{-\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}}\left\{1, z, {z}^{2}\right\}{\rho }^{c}\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}\left\{1, z, {z}^{2}\right\}{\rho }^{p}\text{d}z,$$

(37d)

$$\left\{{I}_{2}, {I}_{4}, {I}_{5}\right\}=\int\limits_{-\frac{{h}_{c}}{2}-{h}_{p}}^{-\frac{{h}_{c}}{2}}\left\{f\left(z\right),zf\left(z\right), {\left[f\left(z\right)\right]}^{2}\right\}{\rho }^{p}\text{d}z+\int\limits_{-\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}}\left\{f\left(z\right),zf\left(z\right), {\left[f\left(z\right)\right]}^{2}\right\}{\rho }^{c}\text{d}z+\int\limits_{\frac{{h}_{c}}{2}}^{\frac{{h}_{c}}{2}+{h}_{p}}\left\{f\left(z\right),zf\left(z\right), {\left[f\left(z\right)\right]}^{2}\right\}{\rho }^{p}\text{d}z$$

(37e)

There are three components to the external work: the electro-elastic (${N}_{Ex}$, ${N}_{Ey}$), magnetostrictive (${N}_{Hx}$, ${N}_{Hy}$) and thermal (${N}_{Tx}$, ${N}_{Ty}$) components, as well as the axial (${N}_{px}$, ${N}_{py}$) components. Thus, the external work can be stated as:

$$\delta W=\int\limits_{A}\left(-\left({N}_{px}+{N}_{Ex}+{N}_{Hx}+{N}_{Tx}\right)\frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x}-\left({N}_{py}+{N}_{Ey}+{N}_{Hy}+{N}_{Ty}\right)\frac{\partial w}{\partial y}\frac{\partial \delta w}{\partial y}\right)\text{d}A$$

(38)

where ${N}_{px}$ and ${N}_{py}$ define the compressive mechanical loads. The following are the definitions of the external electric forces (${N}_{{E}_{x}},$ ${N}_{{E}_{y}}$) and magnetic forces (${N}_{{H}_{x}},{N}_{{H}_{y}}$) that are caused by electro-elasticity and magneto-strictivity [46]:

$$ \begin{aligned} & N_{{E_{x} }} = - \left[ {\mathop \int \limits_{{ - \frac{{h_{c} }}{2} - h_{p} }}^{{ - \frac{{h_{c} }}{2}}} e_{31} \frac{{2\phi_{0} }}{{h_{p} }}{\text{d}}z + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{p} }} e_{31} \frac{{2\phi_{0} }}{{h_{p} }} {\text{d}}z} \right] \\ & N_{{E_{y} }} = - \left[ {\mathop \int \limits_{{ - \frac{{h_{c} }}{2} - h_{p} }}^{{ - \frac{{h_{c} }}{2}}} e_{32} \frac{{2\phi_{0} }}{{h_{p} }}{\text{d}}z + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{p} }} e_{32} \frac{{2\phi_{0} }}{{h_{p} }}{\text{d}}z} \right] \\ \end{aligned} $$

(39a)

$$ \begin{aligned} & N_{{H_{x} }} = - \left[ {\mathop \int \limits_{{ - \frac{{h_{c} }}{2} - h_{p} }}^{{ - \frac{{h_{c} }}{2}}} q_{31} \frac{{2\psi_{0} }}{{h_{p} }}{\text{d}}z + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{p} }} q_{31} \frac{{2\psi_{0} }}{{h_{p} }} {\text{d}}z} \right] \\ & N_{{H_{y} }} = - \left[ {\mathop \int \limits_{{ - \frac{{h_{c} }}{2} - h_{p} }}^{{ - \frac{{h_{c} }}{2}}} q_{32} \frac{{2\psi_{0} }}{{h_{p} }}{\text{d}}z + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{p} }} q_{32} \frac{{2\psi_{0} }}{{h_{p} }}{\text{d}}z} \right] \\ \end{aligned} $$

(39b)

The thermomechanical forces in the x–y directions, denoted as ${N}_{{T}_{x}}$ and ${N}_{{T}_{y}}$, are determined by the temperature increase as:

$$ \begin{aligned} & N_{{T_{x} }} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2} - h_{p} }}^{{ - \frac{{h_{c} }}{2}}} c_{11}^{p} \alpha_{p} \Delta T{\text{d}}z + \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} c_{11}^{c} \alpha_{c} \Delta T{\text{d}}z + \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{p} }} c_{11}^{p} \alpha_{p} \Delta T{\text{d}}z \\ & N_{{T_{y} }} = \mathop \int \limits_{{ - \frac{{h_{c} }}{2} - h_{p} }}^{{ - \frac{{h_{c} }}{2}}} c_{12}^{p} \alpha_{p} \Delta T{\text{d}}z + \mathop \int \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} c_{12}^{c} \alpha_{c} \Delta T{\text{d}}z \mathop \int \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{p} }} c_{12}^{p} \alpha_{p} \Delta T{\text{d}}z \\ \end{aligned} $$

(40)

Here, ${c}_{11}^{p}$,and ${c}_{11}^{c}$ are the equivalent elastic constants of the face and core layers, respectively. ${\alpha }_{p}$, and ${\alpha }_{c}$ are the equivalent thermal expansion coefficients of the face and core layers, respectively.

By employing the SSDT, the nano sandwich plate's equations of motion can be derived by substituting the virtual energy contributions δ $\mathcal{U}$, $\delta T$, and $\delta W$ into Eq. (31). The final six equations of motion are derived in the following arrangement:

$$\delta u:\frac{{N}_{xx}}{\partial x}+\frac{{N}_{xy}}{\partial y}-{I}_{0}\frac{{\partial }^{2}{u}_{0}}{\partial {t}^{2}}+{I}_{1}\frac{{\partial }^{3}{w}_{b}}{\partial x\partial {t}^{2}}+{I}_{2}\frac{{\partial }^{3}{w}_{s}}{\partial x\partial {t}^{2}}=0$$

(41a)

$$\delta v:\frac{{N}_{xy}}{\partial x}+\frac{{N}_{yy}}{\partial y}-{I}_{0}\frac{{\partial }^{2}{v}_{0}}{\partial {t}^{2}}+{I}_{1}\frac{{\partial }^{3}{w}_{b}}{\partial y\partial {t}^{2}}+{I}_{2}\frac{{\partial }^{3}{w}_{s}}{\partial y\partial {t}^{2}}=0$$

(41b)

$$\delta {w}_{b}:\frac{{\partial }^{2}{M}_{xx}^{b}}{\partial {x}^{2}}+2\frac{{\partial }^{2}{M}_{xy}^{b}}{\partial x\partial y}+\frac{{\partial }^{2}{M}_{yy}^{b}}{\partial {y}^{2}}-{I}_{0}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)-{I}_{1}\left(\frac{{\partial }^{3}{u}_{0}}{\partial x\partial {t}^{2}}+\frac{{\partial }^{3}{v}_{0}}{\partial y\partial {t}^{2}}\right)+{I}_{3}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}{w}_{b}}{\partial {y}^{2}\partial {t}^{2}}\right)+{I}_{4}\left(\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}{w}_{s}}{\partial {y}^{2}\partial {t}^{2}}\right)-\left({N}_{px}+{N}_{Ex}+{N}_{Hx}+{N}_{Tx}\right)\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}\right)-\left({N}_{py}+{N}_{Ey}+{N}_{Hy}+{N}_{Ty}\right)\left(\frac{{\partial }^{2}{w}_{b}}{\partial {y}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}\right)=0$$

(41c)

$$\delta {w}_{s}:\frac{{\partial }^{2}{M}_{xx}^{s}}{\partial {x}^{2}}+2\frac{{\partial }^{2}{M}_{xy}^{s}}{\partial x\partial y}+\frac{{\partial }^{2}{M}_{yy}^{s}}{\partial {y}^{2}}+\frac{\partial {S}_{xz}^{s}}{\partial x}+\frac{\partial {S}_{yz}^{s}}{\partial y}-{I}_{0}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)-{I}_{2}\left(\frac{{\partial }^{3}{u}_{0}}{\partial x\partial {t}^{2}}+\frac{{\partial }^{3}{v}_{0}}{\partial y\partial {t}^{2}}\right)+{I}_{4}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}{w}_{b}}{\partial {y}^{2}\partial {t}^{2}}\right)+{I}_{5}\left(\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}{w}_{s}}{\partial {y}^{2}\partial {t}^{2}}\right)-\left({N}_{px}+{N}_{Ex}+{N}_{Hx}+{N}_{Tx}\right)\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}\right)-\left({N}_{py}+{N}_{Ey}+{N}_{Hy}+{N}_{Ty}\right)\left(\frac{{\partial }^{2}{w}_{b}}{\partial {y}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}\right)=0$$

(41d)

$$\delta \phi :-\frac{\partial \overline{{D }_{x}}}{\partial x}-\frac{\partial \overline{{D }_{y}}}{\partial y}-\overline{{D }_{z}}=0$$

(41e)

$$\delta \psi :-\frac{\partial \overline{{B }_{x}}}{\partial x}-\frac{\partial \overline{{B }_{y}}}{\partial y}-\overline{{B }_{z}}=0$$

(41f)

The final form of the size-dependent governing equations for the MEE sandwich nanocomposite plate established by NSGT can be derived by utilizing Eqs. ((22–28), (35) and (39–41)) in the formats described below:

$$ \begin{aligned} \delta U = & & \delta u:\left( {1 - l_{m}^{2} \frac{{\partial ^{2} }}{{\partial x^{2} }}} \right)\left( \begin{gathered} A_{{11}} \frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \left( {A_{{12}} + A_{{66}} } \right)\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + A_{{66}} \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} - B_{{11}}^{b} \frac{{\partial ^{3} w_{b} }}{{\partial x^{3} }} \hfill \\ - B_{{11}}^{s} \frac{{\partial ^{3} w_{s} }}{{\partial x^{3} }} - \left( {B_{{12}}^{b} + 2B_{{66}}^{b} } \right)\frac{{\partial ^{3} w_{b} }}{{\partial x\partial y^{2} }} - \left( {B_{{12}}^{s} + 2B_{{66}}^{s} } \right)\frac{{\partial ^{3} w_{s} }}{{\partial x\partial y^{2} }} + P_{{11}} \frac{{\partial \phi }}{{\partial x}} + J_{{11}} \frac{{\partial \psi }}{{\partial x}} \hfill \\ \end{gathered} \right) \\ & \quad - \left( {1 - {\text{( }}{\mkern 1mu} e_{0} a{\mkern 1mu} {\text{)}}^{2} \frac{{\partial ^{2} }}{{\partial x^{2} }}} \right)\left( {I_{0} \frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }} - I_{1} \frac{{\partial ^{3} w_{b} }}{{\partial x\partial t^{2} }} - I_{2} \frac{{\partial ^{3} w_{s} }}{{\partial x\partial t^{2} }}} \right) = 0 \\ \end{aligned} $$

(42a)

$$\delta v:\left(1-{l}_{m}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left({A}_{66}\frac{{\partial }^{2}{v}_{0}}{\partial {x}^{2}}+{A}_{22}\frac{{\partial }^{2}{v}_{0}}{\partial {y}^{2}}+\left({A}_{12}+{A}_{66}\right)\frac{{\partial }^{2}{u}_{0}}{\partial x\partial y}-{B}_{22}^{b}\frac{{\partial }^{3}{w}_{b}}{\partial {y}^{3}}-{B}_{22}^{s}\frac{{\partial }^{3}{w}_{s}}{\partial {y}^{3}}-\left({B}_{12}^{b}+2{B}_{66}^{b}\right)\frac{{\partial }^{3}{w}_{b}}{\partial {x}^{2}\partial y}-\left({B}_{12}^{s}+2{B}_{66}^{s}\right)\frac{{\partial }^{3}{w}_{s}}{\partial {x}^{2}\partial y}+{P}_{12}\frac{\partial \phi }{\partial y}+{J}_{12}\frac{\partial \psi }{\partial y}\right)-\left(1-{\text{( }{ \, e}_{0}a \, \text{)}}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left({I}_{0}\frac{{\partial }^{2}{v}_{0}}{\partial {t}^{2}}-{I}_{1}\frac{{\partial }^{3}{w}_{b}}{\partial y\partial {t}^{2}}-{I}_{2}\frac{{\partial }^{3}{w}_{s}}{\partial y\partial {t}^{2}}\right)=0$$

(42b)

$$\begin{aligned}&\delta {w}_{b}:\left(1-{l}_{m}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left({B}_{11}^{b}\frac{{\partial }^{3}{u}_{0}}{\partial {x}^{3}}+\left({B}_{12}^{b}+2{B}_{66}^{b}\right)\left(\frac{{\partial }^{3}{u}_{0}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{3}{v}_{0}}{\partial {x}^{2}\partial y}\right)+{B}_{22}^{b}\frac{{\partial }^{3}{v}_{0}}{\partial {y}^{3}}-{D}_{11}^{b}\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{4}}\right.\\ &\qquad\left.-2\left({D}_{12}^{b}+2{D}_{66}^{b}\right)\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {y}^{2}}-{D}_{22}^{b}\frac{{\partial }^{4}{w}_{b}}{\partial {y}^{4}}-{D}_{11}^{s}\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{4}}-2\left({D}_{12}^{s}+2{D}_{66}^{s}\right)\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{2}\partial {y}^{2}}-{D}_{22}^{b}\frac{{\partial }^{4}{w}_{s}}{\partial {y}^{4}}\right.\\ &\qquad\left. +{P}_{13}\frac{{\partial }^{2}\phi }{\partial {x}^{2}}+{P}_{14}\frac{{\partial }^{2}\phi }{\partial {y}^{2}}+{J}_{13}\frac{{\partial }^{2}\psi }{\partial {x}^{2}}+{J}_{14}\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)-\left(1-{\text{( }{ \, e}_{0}a \, \text{)}}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[{I}_{0}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)\right.\\ &\qquad\left.+{I}_{1}\left(\frac{{\partial }^{3}{u}_{0}}{\partial x\partial {t}^{2}}+\frac{{\partial }^{3}{v}_{0}}{\partial y\partial {t}^{2}}\right)-{I}_{3}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}{w}_{b}}{\partial {y}^{2}\partial {t}^{2}}\right)-{I}_{4}\left(\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}{w}_{s}}{\partial {y}^{2}\partial {t}^{2}}\right)\right.\\ &\qquad\left.+\left({N}_{px}+{N}_{Ex}+{N}_{Hx}+{N}_{Tx}\right)\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}\right)+\left({N}_{py}+{N}_{Ey}+{N}_{Hy}+{N}_{Ty}\right)\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}\right)\right]=0\end{aligned}$$

(42c)

$$\begin{aligned}&\delta {w}_{s}:\left(1-{l}_{m}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left({B}_{11}^{s}\frac{{\partial }^{3}{u}_{0}}{\partial {x}^{3}}+\left({B}_{12}^{s}+2{B}_{66}^{s}\right)\left(\frac{{\partial }^{3}{u}_{0}}{\partial x\partial {y}^{2}}+\frac{{\partial }^{3}{v}_{0}}{\partial {x}^{2}\partial y}\right)+{B}_{22}^{s}\frac{{\partial }^{3}{v}_{0}}{\partial {y}^{3}}-{D}_{11}^{s}\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{4}}\right.\\ &\qquad\left.-2\left({D}_{12}^{s}+2{D}_{66}^{s}\right)\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {y}^{2}}-{D}_{22}^{s}\frac{{\partial }^{4}{w}_{b}}{\partial {y}^{4}}-{H}_{11}^{s}\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{4}}-2\left({H}_{12}^{s}+2{H}_{66}^{s}\right)\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{2}\partial {y}^{2}}-{H}_{22}^{b}\frac{{\partial }^{4}{w}_{s}}{\partial {y}^{4}}\right.\\ &\qquad\left.+{A}_{55}^{s}\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}+{A}_{44}^{s}\frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}+\left({P}_{15}-{P}_{17}\right)\frac{{\partial }^{2}\phi }{\partial {x}^{2}}+\left({P}_{16}-{P}_{18}\right)\frac{{\partial }^{2}\phi }{\partial {y}^{2}}+\left({J}_{15}-{J}_{17}\right)\frac{{\partial }^{2}\psi }{\partial {x}^{2}}+\left({J}_{16}-{J}_{18}\right)\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)\\ &\qquad-\left(1-{\text{( }{ \, e}_{0}a \, \text{)}}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[{-I}_{0}\left(\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)+{I}_{2}\left(\frac{{\partial }^{3}{u}_{0}}{\partial x\partial {t}^{2}}+\frac{{\partial }^{3}{v}_{0}}{\partial y\partial {t}^{2}}\right)-{I}_{4}\left(\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}{w}_{b}}{\partial {y}^{2}\partial {t}^{2}}\right)\right.\\ &\qquad\left.-{I}_{5}\left(\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}{w}_{s}}{\partial {y}^{2}\partial {t}^{2}}\right)+\left({N}_{px}+{N}_{Ex}+{N}_{Hx}+{N}_{Tx}\right)\left(\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}\right)\right.\\ &\qquad\left.+\left({N}_{py}+{N}_{Ey}+{N}_{Hy}+{N}_{Ty}\right)\left(\frac{{\partial }^{2}{w}_{b}}{\partial {y}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}\right)\right]=0\end{aligned}$$

(42d)

$$\delta \phi :\left(1-{l}_{m}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left(-{P}_{11}\frac{\partial {u}_{0}}{\partial x}{-P}_{12}\frac{\partial {v}_{0}}{\partial y}{+P}_{13}\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}{+P}_{14}\frac{{\partial }^{2}{w}_{b}}{\partial {y}^{2}}+\left({P}_{15}-{P}_{17}\right)\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}+\left({P}_{16}-{P}_{18}\right)\frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}-{P}_{20}\frac{{\partial }^{2}\phi }{\partial {x}^{2}}-{P}_{22}\frac{{\partial }^{2}\phi }{\partial {y}^{2}}+{P}_{30}\phi -{J}_{20}\frac{{\partial }^{2}\psi }{\partial {x}^{2}}-{J}_{22}\frac{{\partial }^{2}\psi }{\partial {y}^{2}}+{J}_{30}\psi \right)=0$$

(42e)

$$\delta \psi :\left(1-{l}_{m}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left(-{J}_{11}\frac{\partial {u}_{0}}{\partial x}{-J}_{12}\frac{\partial {v}_{0}}{\partial y}{+J}_{13}\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}{+J}_{14}\frac{{\partial }^{2}{w}_{b}}{\partial {y}^{2}}+\left({J}_{15}-{J}_{17}\right)\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}+\left({J}_{16}-{J}_{18}\right)\frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}-{J}_{20}\frac{{\partial }^{2}\phi }{\partial {x}^{2}}-{J}_{22}\frac{{\partial }^{2}\phi }{\partial {y}^{2}}+{J}_{30}\phi -{S}_{20}\frac{{\partial }^{2}\psi }{\partial {x}^{2}}-{S}_{22}\frac{{\partial }^{2}\psi }{\partial {y}^{2}}+{S}_{30}\psi \right)=0$$

(42f)

The parameters utilized in Eq. (42) are defined in Appendix-A1 section.

2.9.1 Application of the Navier solution method

The Navier approach is applied to obtain the response of the sandwich nanoplate under simply supported boundary conditions. The boundary conditions for the simply supported plate can be found as follows:

$$ \begin{gathered} {\text{at}}\;\;x = 0,\;a:N_{x} = v = w = M_{x} = P_{x} = \phi_{y} = 0 \hfill \\ {\text{at}}\;\;y = 0,\;b:N_{y} = u = w = M_{y} = P_{y} = \phi_{x} = 0 \hfill \\ \end{gathered} $$

(43)

For nonclassical boundary conditions:

$$ \begin{gathered} {\text{at}}\;\;x = 0,\; a:\frac{\partial }{\partial x}\left( {N_{x} ,v,w,M_{x} ,P_{x} ,\phi_{y} } \right) = 0 \hfill \\ {\text{at}}\;\;y = 0,\;b:\frac{\partial }{\partial y}\left( {N_{y} ,u,w,M_{y} ,P_{y} ,\phi_{x} } \right) = 0 \hfill \\ \end{gathered} $$

(44)

Given the simply supported boundary conditions, the displacements can be determined using the Navier approximations as [11, 90]:

$$ \begin{aligned} & u_{0} = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } U_{mn} \cos \left( {k_{1} x} \right)\sin \left( {k_{2} y} \right)e^{{i\omega_{mn} t}} \\ & v_{0} = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } V_{mn} \sin \left( {k_{1} x} \right)\cos \left( {k_{2} y} \right)e^{{i\omega_{mn} t}} \\ & w_{b} = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } W_{bmn} \sin \left( {k_{1} x} \right)\sin \left( {k_{2} y} \right)e^{{i\omega_{mn} t}} \\ & w_{s} = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } W_{smn} \sin \left( {k_{1} x} \right)\sin \left( {k_{2} y} \right)e^{{i\omega_{mn} t}} \\ & \phi = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } {\Phi }_{mn} \sin \left( {k_{1} x} \right)\sin \left( {k_{2} y} \right)e^{{i\omega_{mn} t}} \\ & \psi = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } {\Psi }_{mn} \sin \left( {k_{1} x} \right)\sin \left( {k_{2} y} \right)e^{{i\omega_{mn} t}} \\ \end{aligned} $$

(45)

where ${U}_{mn},$ ${V}_{mn}$, ${W}_{bmn}$, ${W}_{smn}$, ${X}_{mn}$ and ${Y}_{mn}$ define THE unknown maximum amplitudes and $i=\sqrt{-1}$. In addition, ${k}_{1}$ and ${k}_{2}$ are the longitudinal wave numbers along the $x$ and $y$ axes, respectively and ${\omega }_{mn}$ is the circular mode frequency of the mode (m, n). As a result of the process of inserting the suggested solution equations (Eq. (45)) into the final form of the size-dependent governing equations (Eq. (42)), we can obtain the following matrix equation:

$$\left\{\left[K\right]-{\omega }_{mn}^{2}\left[M\right]\right\}\left\{\Delta \right\}=\left\{F\right\}$$

(46)

where $\left[K\right]$, $\left[M\right]$ and $\left\{F\right\}$ define the symmetric stiffness matrix (${K}_{ij}={K}_{ji}$), symmetric mass matrix (${M}_{ij}={M}_{ji}$), and force vector, respectively. The six variables in Eq. (45) can be written in vector form as follows:

$$\left\{\Delta \right\}={\left\{\begin{array}{cccccc}{U}_{mn}&\quad {V}_{mn}&\quad {W}_{bmn}&\quad {W}_{smn}&\quad {X}_{mn}&\quad {Y}_{mn}\end{array}\right\}}^{{\varvec{T}}}$$

(47)

It is possible to modify Eq. (46), as given below, to get the free vibration response:

$$\left\{\left[\begin{array}{cccccc}{K}_{11}&\quad {K}_{12}&\quad {K}_{13}&\quad {K}_{14}&\quad {K}_{15}&\quad {K}_{16}\\ {K}_{21}&\quad {K}_{22}&\quad {K}_{23}&\quad {K}_{24}&\quad {K}_{25}&\quad {K}_{26}\\ {K}_{31}&\quad {K}_{32}&\quad {K}_{33}&\quad {K}_{34}&\quad {K}_{35}&\quad {K}_{36}\\ {K}_{41}&\quad {K}_{42}&\quad {K}_{43}&\quad {K}_{44}&\quad {K}_{45}&\quad {K}_{46}\\ {K}_{51}&\quad {K}_{52}&\quad {K}_{53}&\quad {K}_{54}&\quad {K}_{55}&\quad {K}_{56}\\ {K}_{61}&\quad {K}_{62}&\quad {K}_{63}&\quad {K}_{64}&\quad {K}_{65}&\quad {K}_{66}\end{array}\right]-{\omega }_{mn}^{2}\left[\begin{array}{cccccc}{M}_{11}&\quad {M}_{12}&\quad {M}_{13}&\quad {M}_{14}&\quad {M}_{15}&\quad {M}_{16}\\ {M}_{21}&\quad {M}_{22}&\quad {M}_{23}&\quad {M}_{24}&\quad {M}_{25}&\quad {M}_{26}\\ {M}_{31}&\quad {M}_{32}&\quad {M}_{33}&\quad {M}_{34}&\quad {M}_{35}&\quad {M}_{36}\\ {M}_{41}&\quad {M}_{42}&\quad {M}_{43}&\quad {M}_{44}&\quad {M}_{45}&\quad {M}_{46}\\ {M}_{51}&\quad {M}_{52}&\quad {M}_{53}&\quad {M}_{54}&\quad {M}_{55}&\quad {M}_{56}\\ {M}_{61}&\quad {M}_{62}&\quad {M}_{63}&\quad {M}_{64}&\quad {M}_{65}&\quad {M}_{66}\end{array}\right]\right\}\left\{\begin{array}{c}{U}_{mn}\\ {V}_{mn}\\ {W}_{bmn}\\ {W}_{smn}\\ {X}_{mn}\\ {Y}_{mn}\end{array}\right\}=\left\{0\right\}$$

(48)

The elements of the stiffness and mass matrices are presented in Appendix-A2. The wave frequencies of the proposed MEE sandwich nanoplate, assuming the modes ${M}_{mn}$, can be determined by putting the determinant of $\left\{\left[K\right]-{\omega }_{mn}^{2}\left[M\right]\right\}$ to zero and solving for the frequency ${\omega }_{mn}$. This applies for ${k}_{1}={k}_{2}=k$ and $m = n$.

As a function of wavenumber, circular frequencies can be described as:

$${\omega }_{nn}={M}_{nn}\left({k}_{nn}\right)$$

(49)

For $n=1, {2,3}$ and $4$, Eq. (49) can be written as:

$${\omega }_{1}={M}_{1}\left(k\right), {\omega }_{2}={M}_{2}\left(k\right), {\omega }_{3}={M}_{3}\left(k\right), {\omega }_{4}={M}_{4}\left(k\right)$$

(50)

where ${\omega }_{1}$ stands for the frequencies of bending wave mode ${M}_{1}$, ${\omega }_{2}$ and ${\omega }_{3}$ for longitudinal wave modes ${M}_{2}$ and ${M}_{3}$, and ${\omega }_{4}$ for the shear wave mode ${M}_{4}$. The phase velocity of each wave mode can be calculated by determining the circular frequencies as:

$$c={v}_{nn}=\frac{{\omega }_{nn}}{{k}_{nn}}, n=1, 2, 3, 4$$

(51)

The escape frequency of the proposed structure can be calculated for the wave number k → ∞ as:

$${\widetilde{\omega }}_{nn}=\underset{k\to \infty }{\text{lim}}\frac{{\omega }_{nn}}{2\pi }, n=1, 2, 3, 4$$

(52)

3 Numerical results and discussion

In this section, firstly, validation studies are conducted for the suggested approach. Following this, the established methodology is utilized to examine the behavior of wave propagation in the sandwich nanoplate under electric, magnetic, and thermal loads. Table 3 displays the material properties of CoFe₂O₄ and BaTiO₃ in terms of their mechanical, electrical, magnetic, and thermal characteristics. The foam layer and MEE surface layers employed in the numerical simulations have the following geometric parameters: $a=b=10\text{ nm}$, $h=a/10$, ${h}_{c}=0.8h$ and ${h}_{\text{p}}=0.1h$.

Table 3 Electromechanical material properties of CoFe₂O₄ and BaTiO₃

3.1 Verification of the suggested model

In order to evaluate the validity of the existing approach, a comparison is conducted with two instances of published scientific studies. The preliminary analysis involves comparing the initial five natural frequencies of a composite plate, which is generated utilizing the CUF approach under thermal stresses, with the findings reported in a recent work [91]. The dimensions of the plate are $a=1\text{ m}$, $h=0.01\text{ m}$ and $a/h=100$. The material properties of the plate structure are: ${E}_{1}=144.8$ GPa, ${E}_{2}={E}_{3}=9.65$ GPa, ${v}_{12}=0.3$, ${G}_{12}={G}_{13}=4.14$ GPa, ${G}_{23}=3.45$ GPa, $\rho =1450$ kg/m³, ${\alpha }_{11}=-2.6279\times {10}^{-7}$ °C⁻¹ and ${\alpha }_{12}=30.535\times {10}^{-6}$ °C⁻¹. Table 4 presents the evaluation of the dimensionless frequency data acquired from the current investigation compared to the results obtained from [91]. Based on the data provided in this table, the findings produced from the CUF model, and the current model is in full agreement.

Table 4 Comparison of first five natural frequencies for the CUF and SHSDT

The second validation study investigates the circular wave frequencies of Si₃N₄/SUS304 FG plates under thermal environment. The current approach is validated for the particular case of wave propagation in the FG plate using Table 5. This table presents a comparison between the wave frequencies provided by Sun and Luo [92] and the data obtained from the current approach. The table indicates a strong correlation between the numerical findings obtained from the current research and those from the reference study.

Table 5 Comparison of circular wave frequencies for the FG plates ($h=0.02$ m, $k={k}_{x}={k}_{y}$, ${T}_{t}={T}_{b}=300$ K, ${E}_{t}=322.27$ GPa, ${E}_{b}=207.78$ GPa, ${v}_{t}=0.24$, ${v}_{b}=0.3178$, ${\rho }_{t}=2370$ Kg/m³, ${\rho }_{b}=8166$ Kg/m³)

3.2 Wave propagation analysis of the sandwich nanoplate

This subsection investigates the effect of various parameters such as wave number, foam void coefficient, GPL volume fraction, temperature rise, nonlocal parameter, material size parameter, and electric, magnetic, and thermal loads on the phase velocity and wave frequency of the sandwich nanoplates, taking into account three different foam distributions and three different core layers. Equations (53) and (54) define the input magnetic and electric fields, respectively.

$${H}_{p}=\frac{{H}_{0}}{D}, D= \frac{E{H}^{3}}{12\left(1-{\nu }^{2}\right)}$$

(53)

$${V}_{p}=\frac{{V}_{0}}{D}, D= \frac{E{H}^{3}}{12\left(1-{\nu }^{2}\right)}$$

(54)

3.2.1 Comparison of sandwich nanoplates core types

To examine the effect of the core structure on the phase velocity $(c)$ and wave frequency $(f)$ of the sandwich plate, three distinct core structure types are considered: metallic core (Type I), GPL-reinforced metallic core (Type II), and GPL-reinforced metallic foam core (Type III). The investigations are conducted using the nanoplate’s first 314 natural vibration modes. For Type I, the core layer consists of pure Ti–6Al–4V, for Type II, the GPL volume fraction is considered to be 0.2 and for Type III the GPL volume fraction is considered to be 0.2 and the foam void coefficient ${\lambda }_{0}$ is considered to be 0.3. Figure 4 exhibits the influence of the core type on the wave number against the phase velocity (Fig. 4a) and wave frequency (Fig. 4b) for the bending wave. As shown in Fig. 4a, the maximum phase velocities for all three models are obtained for a wave number of $k= 3.456 \text{x} {10}^{9}$ 1/nm, corresponding to the 11th wave mode $(n=11)$. The highest phase velocity is obtained for Type II while the lowest phase velocity is obtained for Type I. The maximum phase velocities are calculated as 4.82 km/s, 4.61 km/s and 3.62 km/s, respectively. When the effect of the core type on the wave frequency is analyzed from Fig. 4b, it is seen that the highest wave frequency is obtained for Type II, and the lowest wave frequency is obtained for Type I. For $k= 3.456\times {10}^{9}$ 1/nm, the wave frequencies are obtained as 2.65 THz, 2.53 THz, and 1.98 THz from highest to lowest, respectively. For shear waves, the variations in the phase velocity and wave frequency with respect to the core type and wave number are illustrated in Fig. 5. In the shear wave, the highest phase velocity and wave frequency values are obtained with Type II, while the lowest values are obtained with Type I. While the phase velocity remains constant until $k= 3.456\times {10}^{9}$ 1/nm, corresponding to the 11th wave mode, it increases after the 11th mode frequency. The variations in the phase velocity and wave frequency for longitudinal waves according to the wave number and core type are depicted in Fig. 6a, b. As can be seen from the figures, similar to those of the shear wave and bending wave, the highest phase velocity and wave frequency values are obtained with Type II, and the lowest values are obtained with Type I. However, in contrast to the bending wave, while the phase velocity decreases until the 11th wave mode, it remains constant after the 11th mode.

Fig. 4

Variation in the bending phase velocity (a) and wave frequency (b) of the nanoplate depending on the wave number for the Type-I, Type-II and Type-III core models; ${V}_{\text{GPL}}=0.2$; ${\lambda }_{0} =0.3$; ${V}_{p}$ = 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$; ${V}_{\text{Ba}}=0.5$ and $\Delta T=0$

Fig. 5

Variation in the shear wave phase velocity (a) and wave frequency (b) of the nanoplate depending on the wave number for the Type-I, Type-II and Type-III core models; ${V}_{\text{GPL}}=0.2$; ${\lambda }_{0}=0.3$; ${V}_{p}$= 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$; ${V}_{\text{Ba}}=0.5$ and $\Delta T=0$

Fig. 6

Comparison of the longitudinal wave phase velocity (a) and wave frequency (b) of the nanoplate depending on the wave number for the Type-I, Type-II and Type-III core models; ${V}_{\text{GPL}}=0.2$; ${\lambda }_{0} =0.3$; ${V}_{p}$ = 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$; ${V}_{\text{Ba}}=0.5$ and $\Delta T=0$

3.2.2 Comparison of sandwich nanoplates’ foam type

Three alternative foam distributions (U-Foam, S-Foam I, and S-Foam II) are studied to assess the influence of the foam void distribution on the phase velocity and wave frequency of the sandwich plate. Figure 7 demonstrates the impact of foams’ void distributions on wave number against phase velocity (Fig. 7a) and wave frequency (Fig. 7b) for the bending wave. As shown in Fig. 7a, the phase velocity increases with increasing wave number. The maximum phase velocities for all void distribution models are obtained for $k= 3.456\times {10}^{9}$ 1/nm, corresponding to the 11th wave mode. The highest phase velocity is obtained as 4.09 km/s in S-Foam II, while the lowest phase velocity is obtained as 3.83 km/s in U-Foam. When the effect of the core type on the wave frequency is analyzed from Fig. 4b, it is observed that the wave frequency increases with the wave number. The highest wave frequency is obtained in S-Foam II and the lowest wave frequency is obtained in U-Foam. For $k= 3.456\times {10}^{9}$ 1/nm, the wave frequencies are obtained as 2.25 THz, 2.14 THz and 1.92 THz from highest to smallest.

Fig. 7

Variation in the bending wave phase velocity (a) and wave frequency (b) of the nanoplate depending on the wave number for the U-Foam, S-Foam I and S-Foam II distribution models; ${V}_{\text{GPL}}=0.1$; ${\lambda }_{0}=0.5$; ${V}_{p}$ = 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$; ${V}_{\text{Ba}}=0.5$ and $\Delta T=0$

3.2.3 The effect of the GPL volume fraction

For four different GPL volume fractions (${V}_{\text{GPL}}=0, 0.1, 0.2\,\, \text{and}\,\, 0.3$), the influence of the GPL volume fraction of the solid core on the bending wave phase velocity and wave frequency response of the sandwich plate for the U-Foam distribution is illustrated in Fig. 8. From Fig. 8a, it is seen that the highest phase velocity values are obtained in the 11th wave mode for ${V}_{\text{GPL}}=0.3$. For ${V}_{\text{GPL}}$ values of $0, 0.1, 0.2$ and $0.3$, the phase velocities of the sandwich plate are calculated to be 3.61 km/s, 3.91 km/s, 4.22 km/s and 4.56 km/s, respectively. In addition, the wave frequencies for the 11th wave mode are 1.82 THz, 2.02 THz, 2.23 THz, and 2.45 THz, as demonstrated in Fig. 8b. This is because the modulus of elasticity of GPL is greater than that of Ti–6Al–4V.

Fig. 8

Variation in the bending wave phase velocity (a) and wave frequency (b) of the nanoplate depending on the volume fraction of GPL (${V}_{\text{GPL}}=0, 0.1, 0.2\,\, \text{and} \,\,0.3$); ${\lambda }_{0}=0.5$; ${V}_{p}$ = 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$; ${V}_{\text{Ba}}=0.5$ and $\Delta T=0$

3.2.4 The effect of the foam

The effect of the foam void coefficient on the phase velocity and wave frequency of the sandwich plate is investigated for four different void coefficients ($0, 0.25, 0.50, 0.75$) and three different foam distributions (U-Foam, S-Foam I and S-Foam II). As depicted in Fig. 9, the foam void coefficient and distribution type significantly affect the phase velocity. An examination of Fig. 9a–c reveals that the phase velocity decreases with increasing void coefficient in all void distribution models. For the same void coefficient and wave mode, the highest phase velocity is observed in the S-Foam II model. For example, at ${\lambda }_{0}=0.5$ and $k= 3.456\times {10}^{9}$ 1/nm, the phase velocity is 3.83 km/s for U-Foam, 4.01 km/s for S-Foam I and 4.09 km/s for S-Foam II. Considering the decrease in phase velocities for ${\lambda }_{0}=0$ and ${\lambda }_{0}=0.75$, it is determined that the velocity decrease in U-Foam is 13.9%, 6.2% in S-Foam I and 2.9% in S-Foam II. Accordingly, the most affected distribution model by the foam void coefficient is U-Foam, while the least affected model is S-Foam II. In other words, the S-Foam II distribution can be preferred in cases where the phase velocity value in the foam structure is not significantly affected by the void coefficient.

Fig. 9

Comparison of the bending wave phase velocity of the sandwich nanoplate depending on the foam void coefficient (${\lambda }_{0}=0, 0.25, 0.50, 0.75$) for the U-Foam (a), S-Foam I (b) and S-Foam II (c) distribution models; ${V}_{\text{GPL}}=0.1$; ${V}_{p}$ = 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$; ${V}_{\text{Ba}}=0.5$ and $\Delta T=0$

The effects of the foam void coefficient and wave number on the wave frequency of the sandwich nanostructure are presented in Fig. 10. Figure 10a–c clearly demonstrates that as the foam void coefficient grows, the wave frequency decreases in all void distribution models. The S-Foam II model offers the highest wave frequency for the same void coefficient and wave mode. For example, at ${\lambda }_{0}=0.5$ and $k= 11\times {10}^{9}$ 1/nm, the wave frequencies are 21.44 THz for U-Foam, 22.29 THz for S-Foam I and 22.91 THz for S-Foam II. In terms of the wave frequency, the model most affected by the void coefficient is the U-Foam model, while the least affected model is the S-Foam II model. Because, the rate of decrease in the wave number-wave frequency curves is the lowest in the S-Foam II model.

Fig. 10

Comparison of the bending wave frequency of the sandwich nanoplate depending on the foam void coefficient (${\lambda }_{0}=0, 0.25, 0.50, 0.75$) for the U-Foam (a), S-Foam I (b) and S-Foam II (c) distribution models; ${V}_{\text{GPL}}=0.1$; ${V}_{p}$ = 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$; ${V}_{\text{Ba}}=0.5$ and $\Delta T=0$

3.2.5 The effect of temperature

The influence of the temperature rise on the phase velocity and wave frequency is investigated with four distinct temperature rise values as shown in Fig. 11. For the analysis, ${V}_{\text{GPL}}$ and ${\lambda }_{0}$ are taken as 0.1 and 0.5, respectively. As shown in Fig. 11a, b, the phase velocity and wave frequency increase nonlinearly with increasing wave number and decrease with increasing temperature. The maximum wave velocity is 4.11 km/s for $\Delta T=0$ at $k= 3.456\times {10}^{9}$ 1/nm corresponding to the 11th wave mode, while the minimum wave velocity is 3.28 km/s for $\Delta T=900$. In other words, a 25.3% decrease in the wave velocity occurred with the effect of temperature rise. For wave number $k= 3.456\times {10}^{9}$ 1/nm, the wave frequencies are 2.51 THz, 2.31 THz, 1.98 THz and 1.81 THz from highest to smallest. As a result, it is found that the wave frequency of the sandwich plate is significantly affected by the temperature rise.

Fig. 11

Variation in the bending wave phase velocity (a) and wave frequency (b) of the nanoplate depending on the wave number and temperature rise ($\Delta T=0, 300, 600, 900$) for U-Foam distribution model; ${\lambda }_{0}=0.5$; ${V}_{\text{GPL}}=0.1$; ${V}_{p}$ = 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$ and ${V}_{\text{Ba}}=0.5$

3.2.6 The effect of nonlocal elasticity

Figure 12 demonstrates the influence of the nonlocal parameter ${e}_{0}a$ on the phase velocity and wave frequency for four different nonlocal parameters (${e}_{0}a=0, 1, {2,4}$ nm²). According to Fig. 12, both the phase velocity and the wave frequency decrease with increasing nonlocal parameter values. When the effect of the nonlocal parameter on the phase velocity is examined from Fig. 12a, while not much difference is observed until the maximum phase velocity, the difference between the phase velocities becomes significant after the maximum phase velocity. Moreover, while the phase velocity increased for all nonlocal parameters until the maximum phase velocity corresponding to the 11th wave mode, after the 11th mode the wave velocity started to decrease significantly for ${e}_{0}a=1 , 2 \text{and} 4$ nm². As shown Fig. 12b, the effect of the nonlocal parameter is quite small until the wave number $k= 10.99\times {10}^{9}$ 1/nm, which corresponds to the 35th wave mode. After the 35th mode, the effect of ${e}_{0}a$ becomes more pronounced. In addition, while the wave frequency increases parabolically until $k= 32.04\times {10}^{9}$ 1/nm, it starts to follow a horizontal trend after this point for ${e}_{0}a=1, 2 \text{and }4$ nm².

Fig. 12

Variation in the bending wave phase velocity (a) and wave frequency (b) of the sandwich nanoplate depending on the nonlocal parameter (${e}_{0}a=0, 1, {2,4}$ nm²) for the U-Foam distribution model; ${\lambda }_{0}=0.5$;${V}_{\text{GPL}}=0.1$; ${V}_{p}$ = 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$ and ${V}_{\text{Ba}}=0.5$

3.2.7 Effect of the strain gradient elasticity

The impacts of the material size parameter ${l}_{m}$ on the phase velocity and wave frequency are illustrated in Fig. 13 for the U-Foam distribution model. As the material size parameter increase, both the phase velocity and the wave frequency exhibit an upward trend, as depicted in Fig. 13a. In the phase velocity wave number curves, a parabolic increase in the phase velocity is observed until the 11th wave mode, while after the 11th mode, a horizontal trend is observed. However, the parabolic increase continued for ${l}_{m}= 1, 2$ and $4$ nm², while it remained constant for ${l}_{m}=0$. Following $k= 10.99\times {10}^{9}$ 1/nm, a notable augmentation in the impact of the material size parameter becomes apparent. An analysis of the wave frequency curves in Fig. 13b reveals that the wave frequency exhibits a nonlinear increase with both wave number and material size parameter. This augmentation is quite high, especially for high values of $k$.

Fig. 13

Variation in the bending wave phase velocity (a) and wave frequency (b) of the sandwich nanoplate depending on the material size parameter (${l}_{m}=0, 1, 2, 4$ nm²) for the U-Foam distribution model; ${\lambda }_{0}=0.5$; ${V}_{\text{GPL}}=0.1$; ${V}_{p}$ = 0; ${H}_{p}=0$; ${V}_{\text{Co}}=0.5$ and ${V}_{\text{Ba}}=0.5$

3.2.8 The effect of the electric load

The variations in the phase velocity and wave frequency of the composite nanostructure with wave number and electrical load are shown in Fig. 14 for two different BaTiO₃ and CoFe₂O₄ mixing ratios. In the analysis, four different voltage values are applied (${V}_{p}$ = 0, 0.1, 0.2 and 0.3). As shown in Fig. 14a, b, increasing the voltage has a decreasing effect on the phase velocity. For instance, in Fig. 14a, the phase velocity is found to be 4.175 km/s when no voltage is applied (${V}_{p}$ = 0), whereas for ${V}_{p}$ = 0.3, this value is found to be 3.81 km/s. The case in which the MEE face layers are composed completely of BaTiO₃ is examined in Fig. 14b (${V}_{Ba}$ = 1 and ${V}_{Co}$ = 0). It is evident that a higher BaTiO₃ volume fraction causes the phase velocity to further drop. This is due to the piezoelectric behavior of BaTiO₃. Upon analyzing the ${V}_{p}$=0 curves from Fig. 14a, b, it becomes noticeable that Fig. 14b yields lower phase velocity values. The decrease in phase velocity can be attributed to the relatively lower stiffness characteristic of BaTiO₃ in comparison to that of CoFeO₄. The relationship between the electric load and the wave frequency is examined in Fig. 14c, d. As it is clearly seen from the figure, increasing the electric charge has a decreasing effect on the wave frequency. An increase in the BaTiO₃ ratio results in a further decrease in the wave frequency, which can be attributed to the piezoelectric property and modulus of elasticity of BaTiO₃, similar to the phase velocity.

Fig. 14

Variation in the bending wave phase velocity (a, b) and wave frequency (c, d) of the sandwich nanoplate depending on the applied voltage (${V}_{P}=0, 0.1, 0.2, 0.3$) for the U-Foam distribution model; $\Delta T=0$; ${\lambda }_{0}=0.5$;${V}_{GPL}=0.1$; ${H}_{p}=0$; $a=b=10\text{ nm}$, $h=a/10$, ${h}_{c}=0.6h$ and ${h}_{\text{p}}=0.2h$

3.2.9 Effect of the magnetic load

Figure 15 shows the effects of magnetic load on the phase velocity and wave frequency of the sandwich nanoplate for four different magnetic loads. Based on the curves presented in Fig. 15a, b, it can be observed that the phase velocity values rise as the magnetic load intensity increases. The maximum phase velocities for values of magnetic field intensities ${H}_{p}=0, 0.001, 0.002$, and$0.003$ are obtained as 4.43 km/s, 4.62 km/s, 4.92 km/s, and 5.21 km/s, respectively. When the option of MEE layers consisting entirely of CoFe₂O₄ is examined from Fig. 15b, it is determined that the phase velocity increased further due to both the magnetic characteristics of CoFe₂O₄ and its high elastic modulus. As depicted in Fig. 15c, d, the wave frequency increases significantly with the increasing magnetic load and CoFe₂O₄ mixing ratio.

Fig. 15

Variation in the bending wave phase velocity (a, b) and wave frequency (c, d) of the sandwich nanoplate depending on the applied magnetic load for the U-Foam distribution model; $\Delta T = 0$; $V_{p} = 0$; $\lambda_{0} = 0.5$; $V_{{{\text{GPL}}}} = 0.1$; $a = b = 10\;{\text{nm}}$, $h = a/10$, $h_{c} = 0.6h$ and $h_{{\text{p}}} = 0.2h$

4 Conclusion

This study integrates SHSDT and NSGT to examine the 3-D wave propagation behavior of a smart sandwich nanostructure with a GPL-reinforced foam core and MEE face layers. For the core layer of the sandwich nanocomposite structure, three different core types are identified: Ti–6Al–4V metal core, GPLS-reinforced Ti–6Al–4V metal core and GPL-reinforced foam core. This allowed the effect of GPL and THE foam structure to be analyzed separately. In addition, three different foam distribution patterns (U-Foam, S-Foam I and S-Foam II) are used in the foam core, which allows the effect of the foam distribution pattern on the phase velocity and wave frequency to be examined. The remarkable aspect of the proposed study is that the 3-D wave propagation analysis of the MEE smart sandwich nanoplate is carried out under electrical, magnetic and thermal effects, taking into account temperature-dependent material parameters. As a result of detailed analyses with parameters such as the foam distribution pattern, foam void coefficient, GPL volume fraction, electric and magnetic load, temperature rise, and nonlocal parameters, several important findings are reported. When the effect of GPL reinforcement on the wave propagation behavior of the sandwich structure is analyzed, it is found that GPL reinforcement significantly enhances the phase velocity and wave frequency due to the extra stiffness it provides to the structure. This increase is supported by the analytical results because the wave frequency and phase velocity values in the Type II model with a porous structure are greater than those in the Type I model with a nonporous structure. The foam dispersion pattern affects the propagation characteristics of the waves in the nanocomposite structure. This effect develops at various rates according to the type of foam distribution pattern. In symmetric dispersion patterns, higher phase velocities and wave frequencies are achieved compared to uniform dispersion patterns. The enhanced GPL composition of the core layer had a substantial impact on the wave propagation characteristics of the sandwich nanoplate. The phase velocity and wave frequency exhibit a nonlinear growth as the volume fraction of GPL increases. An increase in the foam void coefficient in the core layer leads to a decrease in the phase velocity and wave frequency. The most affected dispersion pattern by the foam void coefficient is U-Foam, while the least affected dispersion is S-Foam II. The temperature rise effect softens the sandwich nanoplate, causing the phase velocity and wave frequency to decrease. Similar to the temperature effect, the nonlocal parameter effect softens the sandwich nanocomposite structure, resulting in a decrease in the phase velocity and wave frequency. Additionally, the material size parameter has a hardening effect on the sandwich nanoplate, similar to GPL reinforcement, causing the phase velocity and wave frequency to increase. Both the phase velocity and the wave frequency exhibit a decreasing trend with increasing electric charge. Additionally, the phase velocity and wave frequency are strongly influenced by the mixing ratio of BaTiO₃ in the MEE face layers. The application of a magnetic load results in an increase in both the phase velocity and wave frequency of the sandwich plate. This increase, particularly in high modes, is caused by the magnetostrictive characteristics of CoFe₂O₄, which stiffen the sandwich plate. In addition, the phase velocity and wave frequency of the plate can be controlled significantly with the mixing ratio of CoFe₂O₄.

With this study, important findings were obtained about the wave propagation behavior of foam core MEE sandwich nanostructures. It is expected that these findings will contribute to the development of smart nanosensor applications, nanosized health monitoring systems, electromagnetic wave absorption applications and ultrasonic wave transducers that can adapt to various environmental conditions.

Appendix A

$$ \begin{aligned} \left\{ {A_{{ij}} ,B_{{ij}}^{b} ,~D_{{ij}}^{b} ,~B_{{ij}}^{s} ,~D_{{ij}}^{s} ,~H_{{ij}}^{s} } \right\}& = \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} c_{{ij}}^{p} \left\{ {1,~z,~z^{2} ,~f\left( z \right),zf\left( z \right),~\left[ {f\left( z \right)} \right]^{2} } \right\}{\text{d}}z\\ & \quad + \mathop \int \nolimits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} c_{{ij}} ^{c} \left\{ {1,~z,~z^{2} ,~f\left( z \right),zf\left( z \right),~\left[ {f\left( z \right)} \right]^{2} } \right\}{\text{d}}z \\ & \quad + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} c_{{ij}}^{p} \left\{ {1,~z,~z^{2} ,~f\left( z \right),zf\left( z \right),~\left[ {f\left( z \right)} \right]^{2} } \right\}{\text{d}}z,\;\;i,j = 1,2,6 \\ A_{{ii}}^{s} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} c_{{ii}}^{p} \left[ {g\left( z \right)} \right]^{2} dz + \mathop \int \nolimits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} c_{{ii}} ^{c} \left[ {g\left( z \right)} \right]^{2} {\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{f} }} c_{{ii}}^{p} \left[ {g\left( z \right)} \right]^{2} {\text{d}}z,\;\;i = 4,5 \\ \left\{ {P_{{11}} ,P_{{13}} ,P_{{15}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} e_{{31}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} e_{{31}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z, \\ \left\{ {P_{{12}} ,P_{{14}} ,P_{{16}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} e_{{32}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} e_{{32}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z, \\ \left\{ {P_{{17}} ,P_{{18}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \cos \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)g\left( z \right)\left\{ {e_{{15}} ,e_{{24}} ~} \right\}dz + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \cos \left( {\frac{{\pi \hat{z}}}{{h_{f} }}} \right)g\left( z \right)\left\{ {e_{{15}} ,e_{{24}} ~} \right\}{\text{d}}z, \\ \left\{ {P_{{20}} ,P_{{22}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {\xi _{{11}} ,\xi _{{22}} ~} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {\xi _{{11}} ,\xi _{{22}} ~} \right\}{\text{d}}z, \\ \left\{ {P_{{30}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{f} }}^{{ - \frac{h}{2}}} \xi _{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \xi _{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z, \\ \left\{ {J_{{11}} ,J_{{13}} ,J_{{15}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} q_{{31}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} q_{{31}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z, \\ \left\{ {J_{{12}} ,J_{{14}} ,J_{{16}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} q_{{32}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} q_{{32}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z, \\ \left\{ {J_{{17}} ,J_{{18}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \cos \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)g\left( z \right)\left\{ {q_{{15}} ,q_{{24}} ~} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \cos \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)g\left( z \right)\left\{ {q_{{15}} ,q_{{24}} ~} \right\}{\text{d}}z, \\ \left\{ {J_{{20}} ,J_{{22}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {g_{{11}} ,g_{{22}} ~} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {g_{{11}} ,g_{{22}} ~} \right\}{\text{d}}z, \\ \left\{ {J_{{30}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} g_{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} g_{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z, \\ \left\{ {S_{{20}} ,S_{{22}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {\mu _{{11}} ,\mu _{{22}} ~} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {\mu _{{11}} ,\mu _{{22}} ~} \right\}{\text{d}}z, \\ \left\{ {S_{{30}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \mu _{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \mu _{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z, \\ \left\{ {J_{{11}} ,J_{{13}} ,J_{{15}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} q_{{31}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} q_{{31}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z, \\ \left\{ {J_{{12}} ,J_{{14}} ,J_{{16}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} q_{{32}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} q_{{32}} \frac{\pi }{{h_{p} }}\sin \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {1,~z,~f\left( z \right)} \right\}{\text{d}}z \\ \left\{ {J_{{17}} ,J_{{18}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \cos \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)g\left( z \right)\left\{ {q_{{15}} ,q_{{24}} ~} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \cos \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)g\left( z \right)\left\{ {q_{{15}} ,q_{{24}} ~} \right\}{\text{d}}z, \\ \left\{ {J_{{20}} ,J_{{22}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {g_{{11}} ,g_{{22}} ~} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {g_{{11}} ,g_{{22}} ~} \right\}{\text{d}}z, \\ \left\{ {J_{{30}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} g_{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} g_{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z, \\ \left\{ {S_{{20}} ,S_{{22}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {\mu _{{11}} ,\mu _{{22}} ~} \right\}{\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \cos ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right)\left\{ {\mu _{{11}} ,\mu _{{22}} ~} \right\}{\text{d}}z, \\ \left\{ {S_{{30}} } \right\} &= \mathop \int \nolimits_{{ - \frac{h}{2} - h_{p} }}^{{ - \frac{h}{2}}} \mu _{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z + \mathop \int \nolimits_{{\frac{h}{2}}}^{{\frac{h}{2} + h_{p} }} \mu _{{33}} \left( {\frac{\pi }{{h_{p} }}} \right)^{2} \sin ^{2} \left( {\frac{{\pi \hat{z}}}{{h_{p} }}} \right){\text{d}}z. \\ \end{aligned} $$

(A1)

$$ \begin{aligned} & k_{1} = \left( {\frac{m\pi }{a}} \right), k_{2} = \left( {\frac{n\pi }{b}} \right) \\ & K_{11} = - k_{1}^{2} A_{11} - k_{2}^{2} A_{66} , \\ & K_{12} = - \left( {k_{1} k_{2} } \right)\left( {A_{12} + A_{66} } \right), \\ & K_{13} = k_{1}^{3} B_{11}^{b} + k_{1} k_{2}^{2} \left( {B_{12}^{b} + 2B_{66}^{b} } \right), \\ & K_{14} = k_{1}^{3} B_{11}^{s} + k_{1} k_{2}^{2} \left( {B_{12}^{s} + 2B_{66}^{s} } \right) \\ & K_{15} = k_{1} P_{11} , \\ & K_{16} = k_{1} J_{11} , \\ & K_{22} = - k_{1}^{2} A_{66} - k_{2}^{2} A_{22} , \\ & K_{23} = k_{1}^{2} k_{2} \left( {B_{12}^{b} + 2B_{66}^{b} } \right) + k_{2}^{3} B_{11}^{b} , \\ & K_{24} = - k_{1}^{2} k_{2} \left( {B_{12}^{s} + 2B_{66}^{s} } \right) + k_{2}^{3} B_{22}^{s} , \\ & K_{25} = k_{2} P_{12} , \\ & K_{26} = k_{2} J_{12} , \\ & K_{33} = K_{34} = - k_{1}^{4} D_{11}^{b} - 2k_{1}^{2} k_{2}^{2} \left( {D_{12}^{b} + 2D_{66}^{b} } \right) - k_{2}^{4} D_{22}^{b} - \left[ {1 - \mu^{2} \pi^{2} \left( {\frac{{m^{2} }}{{a^{2} }} + \frac{{n^{2} }}{{b^{2} }}} \right)} \right]\\ &\quad \left[ {k_{1} - k_{2} \pi \left( {k_{1} + k_{2} } \right) - \left( {N_{px} + N_{Ex} + N_{Hx} + N_{Tx} } \right)k_{1}^{2} - \left( {N_{py} + N_{Ey} + N_{Hy} + N_{Ty} } \right)k_{2}^{2} } \right], \\ & K_{35} = - k_{1}^{2} P_{13} - k_{2}^{2} P_{14} , \\ & K_{36} = - k_{1}^{2} J_{13} - k_{2}^{2} J_{14} , \\ & K_{44} = - k_{1}^{4} H_{11}^{s} - 2k_{1}^{2} k_{2}^{2} \left( {H_{12}^{s} + 2H_{66}^{s} } \right) - \frac{{n^{4} \pi^{4} }}{{b^{4} }}H_{22}^{s} - k_{1}^{2} A_{55}^{s} - k_{2}^{2} A_{44}^{s} - \left[ {1 - \mu^{2} \pi \left( {k_{1} + k_{2} } \right)} \right]\\ &\quad \left[ {k_{1} - k_{2} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right) - \left( {N_{px} + N_{Ex} + N_{Hx} + N_{Tx} } \right)k_{1}^{2} - \left( {N_{py} + N_{Ey} + N_{Hy} + N_{Ty} } \right)k_{2}^{2} } \right], \\ & K_{45} = - k_{1}^{2} \left( {P_{15} - P_{17} } \right) - k_{2}^{2} \left( {P_{16} - P_{18} } \right), \\ & K_{46} = - k_{1}^{2} \left( {J_{15} - J_{17} } \right) - k_{2}^{2} \left( {J_{16} - J_{18} } \right), \\ & K_{55} = K_{66} = k_{1}^{2} P_{20} + k_{2}^{2} P_{22} + P_{30} , \\ & K_{56} = k_{1}^{2} J_{20} + k_{2}^{2} J_{22} + J_{30} , \\ & M_{11} = M_{22} = - I_{0} \left[ {1 + \mu^{2} \pi \left( {k_{1} + k_{2} } \right)} \right], \\ & M_{12} = M_{15} = M_{25} = M_{35} = M_{45} = M_{55} = M_{56} = M_{16} = M_{26} = M_{36} = M_{46} = M_{66} = 0, \\ & M_{13} = I_{1} k_{1} \left[ {1 + \mu^{2} \pi \left( {k_{1} + k_{2} } \right)} \right], \\ & M_{14} = I_{2} k_{1} \left[ {1 + \mu^{2} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right)} \right], \\ & M_{23} = I_{1} k_{2} \left[ {1 + \mu^{2} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right)} \right], \\ & M_{24} = I_{2} k_{2} \left[ {1 + \mu^{2} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right)} \right], \\ & M_{33} = - \left[ {I_{0} + I_{3} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right)} \right]\left[ {1 + \mu^{2} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right)} \right], \\ & M_{34} = - \left[ {I_{0} + I_{4} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right)} \right]\left[ {1 + \mu^{2} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right)} \right], \\ & M_{44} = - \left[ {I_{0} + I_{5} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right)} \right]\left[ {1 + \mu^{2} \pi \left( {k_{1}^{2} + k_{2}^{2} } \right)} \right]. \\ \end{aligned} $$

(A2)