In-plane instability of shallow layered arches with interlayer slip

Abstract

In this paper, a beam theory for predicting limit point buckling and bifurcation buckling of shallow arches composed of two layers flexibly bonded is presented. The flexibility of layer bond results in interlayer slip, which significantly affects the critical transverse loads. The presented theory is based on a layerwise assumption of the Euler–Bernoulli theory and a linear behavior of the interlayer. After establishing the equilibrium equations and boundary conditions, a numerical method for efficient solution of these equations is provided. In a first example, the presented theory is validated by comparative computations with a much more elaborate finite element analysis assuming a plane stress state. In several other examples, the effect of interlayer stiffness, load distribution and boundary conditions on the stable and unstable equilibrium paths of shallow arches with interlayer slip is investigated.

1 Introduction

When the critical transverse load is exceeded, an immovably supported shallow arch with fully constraint out-of-plane displacement is subjected to in-plane buckling. This instability can take the form of limit point buckling (snap-through) or bifurcation buckling. While in a symmetric arch subjected to a symmetric transverse load the buckling shape of the snap-through mode is symmetric, in the bifurcation mode the shape is antisymmetric. The problem of in-plane buckling of shallow arches has been recognized for a long time and, accordingly, the results of numerous comprehensive studies have been published in the past (e.g., Kerr and El-Bayoumy [18], Lo and Conway [22], Virgin et al. [37], Bradford et al. [5], Tsiatas and Babouskos [36]).

The deformation of shallow arches can be substantial even before reaching the stability limit, and thus their response becomes nonlinear. The analysis of the stability and instability behavior of shallow arches should therefore be based on a geometrically nonlinear model [28]. If the shallow arch is elastically supported, the instability behavior may become much more complex (e.g., Pi et al. [27], Pi and Bradford [26], Han et al. [13]). For the estimation of the critical transverse load, it is generally sufficient to perform a static analysis. However, the deflection that occurs with further load increase is a dynamic process; thus, several papers consider the inertia terms to estimate the nonlinear dynamic response (e.g., Öz and Pakdemirli [25], Pi and Bradford [29], Keibolahi et al. [17], Zhong et al. [38]).

In most studies, homogeneous arches are considered, while limit point buckling and bifurcation buckling of layered and inhomogeneous curved structures have less frequently been analyzed so far (e.g., Heuer and Ziegler [16], Schultz et al. [34], Babaei and Eslami [4], Kiss [20], Chan et al. [9]). In particular, Kiss [19] presents a thorough analytical study of shallow arches made of functionally graded materials on the effects of various parameters on the buckling load and stable as well unstable equilibrium paths. However, to the best of the authors’ knowledge, these studies refer solely to members whose layers are perfectly bonded.

In numerous applications, however, a perfect bond between the layers cannot be achieved because the fastener is flexible. In such a case, the longitudinal displacement of the fibers is not continuous over the height of the member, but exhibits a jump at the layer interface due to the flexible bonding, which is referred to as interlayer slip. The mechanical behavior of layered members with interlayer slip (e.g., Girhammar and Gopu [11], Heuer and Adam [15], Girhammar and Pan [12], Lorenzo et al. [23], Gahleitner and Schoeftner [10]) is much more complex than for homogeneous structures. Solutions for the geometric nonlinear behavior (e.g., Ranzi et al. [31], Adam et al. [2]) and buckling of columns with interlayer slip (e.g., KryŽanowski et al. [21], Schnabl and Planinc [32], Challamel and Girhammar [8], Schnabl et al. [33]) exist in the literature. To date, however, limit point buckling and bifurcation buckling of transversely layered shallow arches with interlayer slip subjected to transverse loads have not been investigated.

To fill this research gap, a nonlinear beam theory for shallow arches whose two layers are flexibly bonded is presented below to efficiently predict the stable and unstable deformation branches of these structures. After describing the strategy for numerically solving the differential equilibrium conditions, the effect of the interlayer slip on the snap-through and in-plane bifurcation on the response and the buckling loads is investigated in several application problems. To validate the presented theory, for one example problem the response is additionally determined with finite shell element analyses assuming plane stress and compared to the results of the presented theory.

2 Fundamental equations

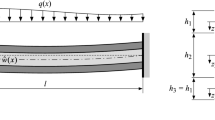
The considered shallow arch shown in Fig. 1 is composed of two elastic homogeneous layers with constant cross-section along the span, which are elastically bonded in circumferential direction. In radial direction the layer connection is rigid. The parameters of the upper layer are identified by the subscript “1”, and those of the lower layer by the subscript “2”. The cross-sectional area is symmetrical in the vertical direction. The member axis corresponds to the line connecting the elastic centers of gravity of the arch with rigidly bonded layers. The member is immovably supported at both ends.

The shallow arch is referenced to the curvilinear coordinate x following the member axis, z is the in-plane coordinate perpendicular to x, and y is the out-of-plane coordinate perpendicular to x and z, see Fig. 1. The origin of the reference coordinate system is located in the member axis at the left support. The member axis is the line connecting the elastic centers of the composite cross section of the beam with rigidly bonded layers, whose distance $d_1$ ($d_2$) from the local centroid of the upper (lower) layer is determined as (see Fig. 1)

$$\begin{aligned} d_1 = \frac{EA_2}{EA_e}d~,~~d_2 = \frac{EA_1}{EA_e}d. \end{aligned}$$

(1)

In these relations, d denotes the distance between both layerwise centroids, $EA_1=E_1 A_1$ is the product of Young’s modulus $E_1$ and cross-sectional area $A_1$ of the upper layer, correspondingly for the lower layer $EA_2=E_2 A_2$, and $EA_e = EA_1 + EA_2$. In addition, the local coordinates $(\zeta _1, \eta _1)$ and $(\zeta _2, \eta _2)$ parallel to the z- and y-coordinates, respectively, are defined for the two layers, whose origins are in the respective local centroid of the considered layer. The variable R(x) represents the radius of principal curvature, which is in the present case of a shallow arch very large compared to the member length, and $k(x)=R^{-1}$ denotes the principal curvature. The member is subjected to the transverse load per unit length p(x), see Fig. 1.

Fig. 1

Shallow arch composed of two flexibly bonded layers

Fig. 2

Displacement field of the shallow arch

Let $u^{(\infty )}(x)$ and w(x) denote the components of the displacement at the member axis in x- and z-direction, and $\Delta u(x)$ the interlayer slip, i.e., the relative displacement in circumferential direction between the layers at the interface. In a shallow arch with non-compressible cross section, it is reasonable to assume that the radial displacement w(x) is the same for each fiber and small compared to the principal radius of curvature R(x). Moreover, the two layers are slender and stiff, and thus, their shear deformation is negligible. Therefore, the validity of the kinematic assumptions of the Euler–Bernoulli theory can be assumed for each layer separately. Consequently, the displacement field of the shallow arch is fully described by the three kinematic variables w, $u^{(\infty )}$ and $\Delta u$. The Euler–Bernoulli theory implies that the cross-sectional rotation $\chi$ is the same for both layers. It is composed of a part due to the tangential displacement and a part due to the radial displacement difference,

$$\begin{aligned} \chi (x) = u^{(\infty )}k - w_{,x} \approx -w_{,x} \end{aligned}$$

(2)

However, in several studies (e.g., Pi et al. [28], Bradford et al. [6]) it has been shown that for immovably supported nonlinear shallow curved arches, the effect of axial deformations $u^{(\infty )}k$ on cross-sectional rotation and curvature is negligible [26]. Assuming that the member axis is in the lower layer, the longitudinal displacements $u_1^{(0)}(x)$ and $u_2^{(0)}(x)$ of the local layer axes can be expressed as a function of the governing kinematic variables w, $u^{(\infty )}$ and $\Delta u$ as follows, see Fig. 2,

$$\begin{aligned}&u_1^{(0)}(x) = u^{(\infty )} - d_1 \chi - \Delta u \approx u^{(\infty )} + d_1 w_{,x} - \Delta u \,,\nonumber \\&u_2^{(0)}(x) = u^{(\infty )} + d_2 \chi \approx u^{(\infty )} - d_2 w_{,x}. \end{aligned}$$

(3)

Then, the longitudinal displacements $u_1(x,\zeta _1)$ ($u_2(x,\zeta _2)$) in the radial distance $\zeta _1$ ($\zeta _2$) from the central axis of the upper (lower) layer follow from

$$\begin{aligned} u_i(x,\zeta _i) = u_i^{(0)} + \zeta _i \chi \approx u_i^{(0)} - \zeta _i w_{,x}~, \qquad i = 1,2. \end{aligned}$$

(4)

Since the instability of shallow arches is associated with moderately large displacements and membrane stresses, the longitudinal strains in the layer-wise central axes need to be formulated nonlinearly. For an arch structure, the full expression for the membrane strains with all nonlinear terms reads [7]

$$\begin{aligned} e_i(x) = u_{i,x}^{(0)} + w k - u_{i,x}^{(0)}w k - w_{,x}u_{i}^{(0)}k + \frac{1}{2} \left( (u_{i,x}^{(0)})^2 + w_{,x}^2 + (u_i^{(0)} k)^2 + \left( w k\right) ^2 \right) ,\, i=1,2. \, \end{aligned}$$

(5)

However, in the case of an immovably supported shallow arch, only the nonlinearity $\frac{1}{2}w_{,x}^2$ is of significant order, while the other nonlinear terms are negligible, and therefore, the membrane strains in the layer axes can be approximated by the following expression (e.g., Heuer [14], Adam [1]):

$$\begin{aligned} e_i(x) \approx u_{i,x}^{(0)} + w k + \frac{1}{2} w_{,x}^2 \, ,\,\, i=1,2, \end{aligned}$$

(6)

and further after inserting Eq. (3),

$$\begin{aligned}&e_1(x) = u^{(\infty )}_{,x} + w k + \frac{1}{2} w_{,x}^2 + d_1 w_{,xx} - {\Delta u}_{,x} \, ,\nonumber \\&e_2(x) = u^{(\infty )}_{,x} + w k + \frac{1}{2} w_{,x}^2 - d_2 w_{,xx}. \, \end{aligned}$$

(7)

The expression for the bending strain at distance $\zeta _i$ from the ith local layer axis can also be simplified (e.g., Pi and Bradford [26]),

$$\begin{aligned} \epsilon _{bi}(x,\zeta _i) = \frac{\zeta _i \chi }{(R+\zeta _i)dx/R} \approx - \zeta _i w_{,xx}\,,\,\, i=1,2, \end{aligned}$$

(8)

because on the one hand the contribution of ${(u^{(\infty )}k)}_{,x}$ to the curvature is negligible and on the other hand $R+\zeta _i\approx R$, since $\zeta _i \ll R$. The total strain at the distance $\zeta _i$ from the ith local layer axis is then

$$\begin{aligned} \epsilon _i(x,\zeta _i) = e_i + \epsilon _{bi} , \quad i=1,2. \, \end{aligned}$$

(9)

Next, the stress resultants are expressed as a function of the governing kinematic variables and their derivatives. Multiplying the strains Eq. (9) by Young’s modulus $E_1$ ($E_2$) gives the normal stresses, which are integrated over the cross-sectional area $A_1$ ($A_2$) to obtain the normal force in the upper (lower) layer,

$$\begin{aligned}&N_1 = EA_1 e_1 = EA_1 \left( u^{(\infty )}_{,x} + w k + \frac{1}{2} w_{,x}^2 + d_1 w_{,xx} - \Delta u_{,x} \right) \,,\nonumber \\&N_2 = EA_2 e_2 = EA_2 \left( u^{(\infty )}_{,x} + w k + \frac{1}{2} w_{,x}^2 - d_2 w_{,xx} \right) . \, \end{aligned}$$

(10)

The sum of the layerwise axial forces yields the overall axial force as

$$\begin{aligned} N = N_1 + N_2 = EA_e \Bigl (u_{,x}^{(\infty )} + w k + \frac{1}{2} w_{,x}^2 \Bigr ) - EA_1 \Delta u_{,x}. \, \end{aligned}$$

(11)

When calculating the layer-wise moments, the normal stresses are multiplied by $\zeta _i$ before layerwise integration with the result (e.g., Ziegler [39])

$$\begin{aligned} M_i = -EJ_i w_{,xx} \, , \qquad i=1,2, \, \end{aligned}$$

(12)

where $EJ_i = E_i J_i$ is the bending stiffness and $J_i$ the area moment of inertia about the $\eta _i$-axis of the ith layer. The overall bending moment M is related to the layerwise stress resultants $M_i$ and $N_i$ and further with Eqs. (12) and (10) to the kinematic variables as

$$\begin{aligned} M = M_1 + M_2 - N_1 d_1 + N_2 d_2 = - EJ_{\infty } w_{,xx} + EA_1 d_1 \Delta u_{,x} \end{aligned}$$

(13)

with $EJ_{\infty }$ denoting the bending stiffness of the member with rigidly bonded layers,

$$\begin{aligned} EJ_{\infty } = EJ_0 + EA_1 d_1^2 + EA_2 d_2^2,~~EJ_0 = EJ_1 + EJ_2, \end{aligned}$$

(14)

where $EJ_0$ is the bending stiffness of the member with unbonded layers. The interlaminar shear traction, i.e., the longitudinal force transferred between the two layers in the interface, is proportional to the interlayer slip $\Delta u$, $K_{s}$ denotes the slip modulus, see, e.g., Girhammar and Pan [12],

$$\begin{aligned} t_{s} = K_{s} \Delta u. \, \end{aligned}$$

(15)

3 Boundary value problem

3.1 Equilibrium equations

The differential equations of nonlinear equilibrium of the shallow arch can be found, for instance, with the minimum total potential energy principle $\delta \Pi = 0$ (e.g., Ziegler [39]). The potential energy of the system reads as

$$\begin{aligned} \Pi = \frac{1}{2}\sum _{i=1}^2 E_i \int _{V_i} \epsilon _i^2 \,\hbox {d}V + \frac{1}{2} K_s \int _{l} {\Delta u}^2 \,\hbox {d}x - \int _{l}p w\,\hbox {d}x. \, \end{aligned}$$

(16)

After inserting the strains Eqs. (9), (7) and (8) and some algebra, the potential energy as a function of the governing kinematic variables is obtained as follows

$$\begin{aligned} \Pi&= \frac{1}{2} \int _{l} \Bigg ( EA_e \left( u_{,x}^{(\infty )} + wk + \frac{1}{2}w_{,x}^2\right) ^2 + EA_1 \left( \Delta u_{,x}^2 - 2 \Delta u_{,x}\left( u_{,x}^{(\infty )} + wk + \frac{1}{2}w_{,x}^2\right) \right) \Bigg . \nonumber \\&\quad \Bigg . + EJ_{\infty } w_{,xx}^2 - 2 EA_1 d_1 w_{,xx} \Delta u_{,x} + K_s {\Delta u}^2 - p w\,\Bigg )\hbox {d}x. \, \end{aligned}$$

(17)

Applying the principles of calculus of variations and partial integration to the potential and using the internal forces, we obtain

$$\begin{aligned} \delta \Pi&= \int _{l} \left( - N_{,x} \delta u^{(\infty )} + ({N_1}_{,x} + K_s \Delta u) \delta \Delta u + \left( - M_{,xx} - {(N w_{,x})}_{,x} + N k - p\right) \delta w \right) \hbox {d}x \nonumber \\&\quad +\left[ N \delta u^{(\infty )} - N_1 \delta \Delta u + (M_{,x} + N w_{,x})\delta w - M {\delta w}_{,x} \right] _0^l = 0. \end{aligned}$$

(18)

By definition, the coefficients $\delta u^{(\infty )}$, $\delta \Delta u$, and $\delta w$ are arbitrary, and therefore Eq. (18) is met only if the following differential equations of equilibrium:

$$\begin{aligned}&N_{,x} = 0 \,, \end{aligned}$$

(19)

$$\begin{aligned}&{N_1}_{,x} + K_s \Delta u = 0 \,, \end{aligned}$$

(20)

$$\begin{aligned}&- M_{,xx} - N w_{,xx} + N k - p = 0, \, \end{aligned}$$

(21)

and the boundary conditions

$$\begin{aligned}&N_b=0~~~\text {or}~~~u^{(\infty )}_b=0 \,,~~~~{(N_1)}_b=0~~~\text {or}~~~{\Delta u}_b=0 \,,\nonumber \\&M_b=0~~~\text {or}~~~{(w_{,x})}_b=0 \,,~~~~{(M_{,x} + N w_{,x})}_b=0~~~\text {or}~~~w_b=0 \end{aligned}$$

(22)

are satisfied. The subscript b denotes a boundary at $x=0$ and $x=l$, respectively. From Eq. (19) it follows that the overall axial force is constant along the arch. Therefore, in Eq. (21) $N w_{,xx}$ is written instead of ${(N w_{,x})}_{,x}$.

Substituting the internal forces into Eqs. (19)–(21) leads to the differential equilibrium conditions in the governing kinematic variables,

$$\begin{aligned}&EA_e \left( u_{,xx}^{(\infty )} + w k_{,x} + w_{,x} k + w_{,x} w_{,xx} \right) - EA_1 \Delta u_{,xx} = 0, \end{aligned}$$

(23)

$$\begin{aligned}&EA_1 \Bigl (u_{,xx}^{(\infty )} + w k_{,x} + w_{,x} k + w_{,x}w_{,xx} + d_{1} w_{,xxx} - \Delta u_{,xx}\Bigr ) + K_{s} \Delta u = 0, \end{aligned}$$

(24)

$$\begin{aligned}&EJ_{\infty } w_{,xxxx} - EA_1 d_1 \Delta u_{,xxx} - N \left( w_{,xx} -k \right) = p. \end{aligned}$$

(25)

Equation (20) (respectively Eq. (24)) implies that the free-body diagram of an infinitesimal element of the upper layer is in equilibrium. Likewise, a free-body diagram of an infinitesimal element of the lower layer must be in equilibrium, i.e., $N_{2,x} - t_{s} = 0$, or expressed in kinematic variables,

$$\begin{aligned} EA_2 \Bigl (u_{,xx}^{(\infty )} + w k_{,x} + w_{,x} k + w_{,x}w_{,xx} - d_{2} w_{,xxx} \Bigr ) - K_{s} \Delta u = 0 \end{aligned}$$

(26)

When Eq. (24) is divided by $EA_1$ and Eq. (26) is divided by $EA_2$, and then the second equation is subtracted from the first equation, we obtain

$$\begin{aligned} \Delta u_{,xx} - \kappa ^2 \Delta u - (d_1+d_2) w_{,xxx} = 0~,~~\kappa =\left( \frac{EA_e K_{s}}{EA_1 EA_2}\right) ^{1/2}. \end{aligned}$$

(27)

In this relation neither the longitudinal displacement $u^{(\infty )}$ nor the nonlinear terms appear. Therefore, in the following, this equilibrium equation is used instead of Eq. (24) to solve the present boundary value problem more efficiently.

3.2 Boundary conditions

As can be seen from Eq. (22), for the solution of the equilibrium Eqs. (27), (23), (25), a total of four boundary conditions per boundary must be defined. Here, shallow arches with three different boundary conditions are examined, i.e., soft-hinged support, hard-hinged support, and clamped support. Common to all of these supports is that the member axis is immovable at these points in all directions, see also Eq. (22), [2],

$$\begin{aligned}&w_b = 0, \end{aligned}$$

(28)

$$\begin{aligned}&u_b^{(\infty )}=0. \end{aligned}$$

(29)

3.2.1 Soft-hinged support

In the case of a soft-hinged support (sh), the beam axis is hinged, i.e., ${(w_{,x})}_b \ne 0$, resulting in zero total bending moment, $M_b=0$, see Eq. (22). Expressed in kinematic variables according to Eq. (13), it follows that [3]

$$\begin{aligned} \Bigl (-EJ_{\infty } w_{,xx} + EA_1 d_1 \Delta u_{,x}\Bigr )_b = 0. \end{aligned}$$

(30)

Since the interlayer slip is not constrained at the support, i.e., $\Delta u \ne 0$, the axial force in the upper layer is therefore zero at this end, $(N_1)_b=0$ (see Eq. (22)) [3], or with the first of Eq. (10)

$$\begin{aligned} \Bigl (u^{(\infty )}_{,x} + w k + \frac{1}{2} w_{,x}^2 + d_1 w_{,xx} - \Delta u_{,x} \Bigr )_b = 0. \end{aligned}$$

(31)

3.2.2 Hard-hinged support

The boundary condition Eq. (30) also applies at a hard hinged support (hh). In this case, however, a rigid plate at the member end prevents the interlayer slip (see, e.g., Adam et al. [2]),

$$\begin{aligned} (\Delta u)_b = 0. \end{aligned}$$

(32)

3.2.3 Clamped support

At a clamped end (cl), the rotation of the cross-section is constrained (see, e.g., Adam et al. [2]),

$$\begin{aligned} (w_{,x})_b = 0 \end{aligned}$$

(33)

and furthermore the interlayer slip is constrained, see Eq. (32).

4 Analysis

The solution of the present boundary value problem is based on the Ritz approach for the deflection [30]

$$\begin{aligned} w(x) \approx w^*(x) = \sum _{i=i_a}^{J} q_i\phi _i(x),~~\phi _i(x) = \left( \frac{x}{l}\right) ^i \left( 1-\frac{x}{l}\right) ^{i_b}, \end{aligned}$$

(34)

where the $J-i_a+1$ shape functions $\phi _i(x)$ are polynomials. The initial value $i_a$ of the summation depends on the geometric boundary conditions in w to be satisfied at $x=0$, and the exponent $i_b$ on the geometric boundary conditions to be satisfied at $x=l$. For the boundary conditions considered here, $i_a$ and $i_b$ are [30]

$$\begin{aligned}&\text {soft-hinged (sh) and}&\nonumber \\&\text {hard-hinged support (hh):}&\text {at}~x=0: i_a=1;&~\text {at}~x=l: i_b=1 \end{aligned}$$

(35)

$$\begin{aligned}&\text {clamped end (cl):}&\text {at}~x=0: i_a=2;&~\text {at}~x=l: i_b=2 \end{aligned}$$

(36)

The Ritz approach is substituted into the two equilibrium conditions Eqs. (23) and (27). These two ordinary differential equations are solved together with the corresponding boundary conditions (Eqs. (29); (31) for sh respectively Eq. (31) for hh and cl) for $\Delta u$ and $u^{(\infty )}$ analytically, which are then also a function of the unknown coefficients $q_i$, denoted as $\Delta u^*$ and $u^{(\infty )*}$.

The coupled $J-i_a+1$ nonlinear equations in the coefficients $q_i$, $i=i_a,...,J$, are found by applying the Galerkin method [39] to the third equilibrium condition Eq. (25). Therefore, Eq. (25) is consecutively multiplied by the $J-i_a+1$ shape functions $\phi _i$ and integrated over l, yielding the following set of equations:

$$\begin{aligned} \int _{0}^{l} \Bigl (EJ_{\infty } w_{,xxxx}^* - EA_1 d_1 \Delta u_{,xxx}^* - N^* \left( w_{,xx}^* - k \right) - p \Bigr ) \phi _i \hbox {d}x - M_b^* (\phi _{i,x})_b = 0, \quad i=i_a,...,{J}. \end{aligned}$$

(37)

$N^*$ is the approximation of the overall axial force obtained by substituting $w^*$, $\Delta u^*$ and $u^{(\infty )*}$ into Eq. (11) and evaluated at any x (for instance at $x=l/2)$. Since the chosen Ritz approach violates the static boundary condition $M_b=0$ in the case of a hinged support, the work of this boundary moment was added in the above expression. Integration of this equation partially twice with respect to x, the order of the derivatives to x is reduced by two. The simultaneously appearing negative work of the boundary moment cancels out with the positive work of the boundary moment, and thus, Eq. (37) becomes

$$\begin{aligned} \int _{0}^{l} \Bigl (\left( EJ_{\infty } w_{,xx}^* - EA_1 d_1 \Delta u_{,x}^*\right) \phi _{i,xx} + N^* \left( w_{,x}^* \phi _{i,x}+k \phi _{i}\right) - p \phi _i\Bigr ) \hbox {d}x = 0,\quad i=i_a,...,{J}. \end{aligned}$$

(38)

The solution of the nonlinear coupled set of $J-i_a+1$ equations for $q_i$, $i=i_a,...,{J}$, resulting from evaluation of this integral is found by numerical standard solvers. The approximation of the deformation of the shallow arch follows by substituting the found coefficients $q_i$ into $w^*(x)$, $\Delta u^*(x)$ and $u^{(\infty )*}(x)$. It should be noted that with increasing number of shape functions not only the deformation but also the static boundary conditions are better approximated.

5 Application

5.1 Shallow arch 1 subjected to distributed load

A first example is a shallow arch (hereafter referred to as shallow arch 1), fixed on both sides and soft-hinged supported (boundary conditions $sh-sh$), and curved in the shape of a sine half-wave against the positive z-direction,

$$\begin{aligned} {\hat{w}}(x) = - {\hat{w}}_0 \sin \frac{\pi x}{l}, \end{aligned}$$

(39)

i.e., $k(x) \equiv -{\hat{w}}_{,xx} = -{\hat{w}}_0 {\pi }^2 / l^2 \sin \frac{\pi x}{l}$. The rise of this structure is 3 cm, i.e., ${\hat{w}}_0 = 0.03$ m. The arch is composed of two elastically bonded layers and has a length $l=1.0$ m. The cross-sectional dimensions of the upper layer with Young’s modulus of $E_1 = 7 \cdot 10^{10}$ N/m$^2$ are $h_1= 4$ mm and $b_1= 0.1$ m. The lower layer with Young’s modulus $E_2=1 \cdot 10^{10}$ N/m$^2$ has the same width as the upper layer, $b_2 = b_1$, and thickness $h_2= 26$ mm. Thus, the section height is 30 mm and is the same as the rise of the arch. The slip modulus of the interlayer is $K_s= 10^9$ N/m$^2$, which corresponds to a composite action parameter [12]

$$\begin{aligned} \alpha l = \left( {K_s\left( \frac{EA_e}{EA_1 EA_2}+\frac{(h_1/2+h_2/2)^2}{EJ_0}\right) }\right) ^{(1/2)}l \end{aligned}$$

(40)

of $\alpha l=14.97$ and thus to a moderate interaction of the two layers [12]. A uniformly distributed transverse load is applied to the shallow arch, i.e., $p(x)=p_0$, which leads to an unstable response above a certain critical load.

For the structural response analysis described in the previous section, the deflection w is approximated by 11 shape functions $\phi _i$, $i=1,...,11$, according to the Ritz approach Eq. (34), which has been shown to be sufficient in a convergence study. Consequently, 11 nonlinear coupled equations in $q_i$, $i=1,...,11$ result from the Galerkin method Eq. (38). Not only the critical loads are of interest, but the entire response path as a function of load $p_0$ in both the stable and unstable branches. Therefore, the load $p_0$ is increased stepwise, and at each load step the real solutions of this system of equations are computed. These computations were performed with the software package Mathematica Mat [24] using the function “FindRoot” to find the real roots of this system of equations.

To validate the presented theory, the response of this shallow arch is additionally analyzed with the finite element (FE) method in the software suite Abaqus [35] assuming a plane stress state. In the corresponding numerical model, the two layers are discretized with the 8-noded quadrilateral plane stress elements of type CPS8R. A Poisson’s ratio of 0.3 is assumed. The intermediate layer is modeled with 4-noded linear cohesive elements of type COH2D4. In the FE model, the interlayer has a certain thickness, which in this case is chosen as 0.002 mm. The stiffness normal to the interlayer, which is infinite in the beam theory, is chosen to be very large, i.e., 10,000 $K_s$. In total, the structure is discretized into 18,500 finite elements, corresponding to 109,132 degrees of freedom, which is a multiple of the 11 degrees of freedom of the beam model. The soft-hinged supports are modeled as kinematic coupling of the outer surface of the lower layer at an additional node. To determine the complete branch of the response, the Riks arc-length algorithm implemented in Abaqus is used to solve the resulting system of equations.

Fig. 3

Shallow arch 1. Left column: non-dimensional load–deformation curves at given location x/l. Right column: distribution of the deformation variables over x/l at discrete load levels. a, b Deflection; c, d interlayer slip

Fig. 4

Shallow arch 1. Left column: non-dimensional load–internal force curves at given location x/l. Right column: distribution of the internal forces over x/l at discrete load levels. a, b Axial forces; c, d bending moments

Figure 3 shows with thick lines the response of this shallow arch in terms of the kinematic variables found with the described beam theory. While the left column shows the non-dimensional external force ${\overline{p}}=p_0 l^3 /EJ_{\infty }$ over the considered non-dimensional response variable at the indicated location of the beam axis, the right column displays the distribution of this response variable over the beam axis x/l at four discrete load levels, denoted A, B, C and D in the left column. The first row contains the normalized deflection w/l and the second row the normalized interlayer slip $\Delta u /l$.

As can be seen from Fig. 3a, in the primary stable deformation branch the slope of the deflection at midspan w(0.5l)/l decreases with increasing load until the critical load ${\overline{p}}_\mathrm{{cr}} = 2.46$ is reached at limit point A, where the deflection snaps through to the remote stable equilibrium path at point B. At load reversal, at the critical load ${\overline{p}}_\mathrm{{cr}}=1.60$ (limit point C), the arch snaps back to the primary stable deformation branch. As observed, the limit points are local extrema on the stable deformation branches. The stable deformation branches are illustrated by solid black lines, the unstable deformation branch between the limit points A and C is depicted by a dashed black line. The solution of the FE plane stress analysis represented by a thin red line with markers is virtually identical to the beam solution, confirming the assumptions of the proposed beam theory. The deflection shape shown in Fig. 3b is similar for the four load levels A, B, C, D given in Fig. 3a. The deflection shape depicted with green color (load level D) is located in the unstable deformation branch of the shallow arch.

The load ${\overline{p}}$ plotted against the interlayer slip $\Delta u(l)/l$ at the right support has the form of a loop, see Fig. 3c. The largest value of the interlayer slip is found in the unstable response branch. When the structure snaps through from A to B, the interlayer slip at the supports becomes smaller in magnitude, but in the interior of the structure it is larger than in the other three discrete load levels B, C, D, as Fig. 3d shows. The interlayer slip from the beam theory and the FE analysis agree well.

To illustrate the importance of considering the interlayer flexibility when estimating the critical loads, Fig. 3a also shows the response of the shallow arch with rigidly bonded layers as thin black lines. As observed, on the primary stable deformation branch, the critical load ${\overline{p}}_\mathrm{{cr}}=3.47$, which is $41\%$ larger than for the arch with elastically bonded layers. The critical load ${\overline{p}}$ on the remote stable deformation branch decreases from 1.60 to 1.12.

The internal forces shown in Fig. 4 also demonstrate the influence of the interlayer slip on the nonlinear stable and unstable response of the shallow arch. The total normal force N divided by $EA_e$ is much larger for the structure with rigid bond than that of the arch with flexibly bonded layers, see Fig. 4a. In Fig. 4b, the layer-wise normal forces $N_1/EA_e$ and $N_2/EA_e$ are plotted as a function of x/l for load levels A, B, C and D in addition to the total normal force $N/EA_e$. It can be seen that at the supports the boundary condition $(N_1)_b=0$ (Eq. 31) is satisfied, while the total axial force is fully transferred to the second layer, i.e., $(N_2)_b=N$. Figure 4c shows ${\overline{p}}$ versus the normalized total moment $Ml/EJ_{\infty }$ at midspan. Next to it, Fig. 4d shows the normalized total moment $Ml/EJ_{\infty }$ as well as the moment of the bottom layer $M_2l/EJ_{\infty }$ plotted over x/l at load levels A, B, C and D. As can be seen, the total moment at the supports is zero, demonstrating that the number of shape functions in the Ritz approach is sufficient to satisfy the boundary condition Eq. (30). The moment in the bottom layer $(M_2)_b$ is nonzero at the boundaries. The moment in the upper layer $M_1$ is small compared to M and $M_2$ and thus not presented.

Fig. 5

Shallow arch 2 subjected to a distributed load. Left column: non-dimensional load–deformation curves at given location x/l. Right column: distribution of the deformation variables over x/l at discrete load levels. a, b Deflection; c, d interlayer slip

Fig. 6

Shallow arch 2 subjected to a distributed load. Left column: non-dimensional load–internal force curves at given location x/l. Right column: distribution of the internal forces over x/l at discrete load levels. a, b Axial forces; c, d bending moments

5.2 Shallow arch 2 subjected to distributed load

After the comparative FE analysis of the first example has confirmed the presented beam theory, the investigations are continued on a second shallow arch where the thickness of the two layers is smaller. The thickness of the upper layer is now $h_1=2$ mm and the thickness of the lower layer $h_2=5$ mm. The total height of the cross-section is therefore 7 mm. The rise of the shallow arch is ${\hat{w}}_0=25$ mm. The slip modulus is reduced by one power of ten and is $K_s=10^8$ N/m$^2$, and thus the composite action parameter according to Eq. (40) becomes $\alpha l = 10.41$. All other parameters as well as the boundary conditions ($sh-sh$) of this structure referred to as shallow arch 2 are the same as in the previous example.

Figure 5 shows the response of this structure in analogy to Fig. 3. The response of the symmetric shallow arch subjected to the symmetric transverse load $p_0$ based on the presented beam theory is shown in the figures of the left column with a thin red line with rectangular markers. Such an analysis can predict limit point buckling, but not bifurcation buckling. Therefore, a second analysis is performed in which the transverse load has a slight perturbation, i.e., the external load is slightly asymmetric in the form

$$\begin{aligned} p(x)=p_0 \left( 0.99 H(x)+0.02 H(x-l/2)\right) \end{aligned}$$

(41)

with H denoting the unit step-function. The total resultant of the transverse load thus remains unchanged, but its application point shifts slightly to the right of midspan. The result of this analysis is shown in the figures of the left column with thick black lines. Comparison of the outcomes of the two computations shows that this very slender shallow arch does indeed become unstable due to bifurcation buckling. As observed, a bifurcation point (point A) is located on the primary stable equilibrium path. At this point, the equilibrium path changes to an orthogonal path on which the total axial force remains constant until bifurcation point C is reached on the remote stable equilibrium path. The actual critical load at bifurcation point A is ${\overline{p}}_\mathrm{{cr}}=3.61$, compared to the critical load in the limit point related to a perfectly symmetrical load of ${\overline{p}}_\mathrm{{cr}}=3.99$ (snap-through). It is noticeable that the response on the stable deformation branches up to the bifurcation point is identical from both computations. The response in the unstable branches is however much more complex for bifurcation buckling than for limit point buckling. In the configuration leading to bifurcation, the unstable branch of the limit point analysis are preserved, but two additional load paths are obtained. This is especially evident in the case of interlayer slip (Fig. 5c). It should be emphasized here that in reality there are always imperfections in the load as well as in the structure, which means that the critical load of a perfect configuration with subsequent limit point bucking is never reached. The response shown in red is therefore purely hypothetical. In reality, however, a bifurcation problem always exists for the considered configuration of shallow arch 2.

Figure 5b shows the distribution of w/l over x/l at the four discrete load levels A, B, C, D (indicated in Fig. 5a) in the case of bifurcation buckling. It can be seen that the deflection becomes asymmetric at the bifurcation point A. In contrast, at the opposite point B on the second stable response branch, far away from an unstable deformation branch, the deflection is virtually symmetrically distributed. At bifurcation point C, the deflection becomes asymmetric again. In the unstable branch at point D, the deflection is also asymmetric. For the interlayer slip (Fig. 5d), a strong deviation from the antimetric response is observed near the bifurcation points.

Figure 6a proves that during bifurcation buckling in the unstable response branches between bifurcation points A and C, the overall normal force N is virtually constant. It can also be seen that, in contrast to shallow arch 1, there is a change from compressive to tensile normal force during the transition from A to B. The asymmetric distribution of the layerwise normal forces $N_1$ and $N_2$ over x/l at the onset of bifurcation buckling is apparent from Fig. 6b. In contrast to shallow arch 1, the plot of the external force ${\overline{p}}$ against the moment $Ml/EJ_{\infty }$ exhibits a loop, as can be seen in Fig. 6c. In addition, Fig. 6d shows that a sign change in the normalized moment $Ml/EJ_{\infty }$ along the beam axis occurs at the onset of bifurcation buckling.

Fig. 7

Modified shallow arch 2 (increased interlayer stiffness). subjected to a distributed load. Non-dimensional load–response curves at given location x/l. a Deflection; b interlayer slip; c overall axial force; d overall bending moment

5.3 Modified shallow arch 2 subjected to distributed load

In a third example (referred to as modified shallow arch 2), the slip modulus is five times larger than in shallow arch 2 (i.e., $K_s = 5 \cdot 10^8$ N/m$^2$ and further $\alpha l=23.28$), otherwise all parameters and the load distribution remain unchanged. Figure 7 shows that also in this structure instability is determined by bifurcation buckling and not by limit point buckling. The critical loads are much larger than for shallow arch 2 (primary stable equilibrium branch: ${\overline{p}}_\mathrm{{cr}} = 5.66$ instead of ${\overline{p}}_\mathrm{{cr}} = 3.61$; remote stable equilibrium branch ${\overline{p}}_\mathrm{{cr}} = -2.23$ instead of ${\overline{p}}_\mathrm{{cr}} = -0.83$). This result again proves that capturing the flexibility of the interlayer is essential for predicting the nonlinear stable and unstable response. Moreover, the response behavior is much more complex than for shallow arch 2, i.e., the number of unstable equilibrium paths increases. The external force ${\overline{p}}$ versus normal force $N/EA_e$ diagram has two loops in this case, as can be seen in Fig. 7c. Instead of two, this structure has four bifurcation points. However, only the two with the smaller critical loads are of practical importance because they indicate the transition from stable to unstable deformation branches. As can be seen, in the associated unstable response branches the normal force is again virtually constant (at $N/EA_e=-1.02 \cdot 10^{-4}$ and $N/EA_e=-2.99 \cdot 10^{-4}$, respectively).

Fig. 8

Shallow arch 2 subjected to a single force. Non-dimensional load–response curves at given location x/l. a Deflection; b interlayer slip; c overall axial force; d overall bending moment

5.4 Shallow arch 2 subjected to single force

In the fourth example, shallow arch 2 is considered again, but this time it is loaded by a single force. In a first computation, this single load is applied exactly in the center,

$$\begin{aligned} p(x)=P_0 \delta (x-l/2), \end{aligned}$$

(42)

where $\delta$ is the Dirac delta function. In a second computation, this force is shifted by 1% to the left,

$$\begin{aligned} p(x)=P_0 \delta (x-0.99 l/2) \end{aligned}$$

(43)

to capture the influence of a small load imperfection. In Fig. 8, the normalized single force ${\overline{p}}=P_0 l^2 /EJ_{\infty }$ is plotted over the response of this structure: in Fig. 8a the normalized deflection w/l at $x/l=0.5$, in Fig. 8b the normalized interlayer slip $\Delta u/l$ at the right support, in Fig. 8c the normalized total normal force $N/EA_e$, and in Fig. 8d the normalized total bending moment $M l / EJ_{\infty }$ at $x/l=0.5$. As observed, also in this example instability is governed by bifurcation buckling. Comparison with Fig. 5 shows that a single force is more critical than a distributed load, since the critical loads are smaller with ${\overline{p}}_\mathrm{{cr}} = 2.29$ and ${\overline{p}}_\mathrm{{cr}} = -0.45$, respectively (compared to ${\overline{p}}_\mathrm{{cr}} = 3.61$ and ${\overline{p}}_\mathrm{{cr}} = -0.83$, respectively, for a distributed load). The response exhibits more unstable deformation branches than for a distributed load. Four bifurcation points are observed as in modified shallow arch 2, as can be seen particularly from Fig. 8c.

Fig. 9

Shallow arch 2. subjected to a distributed load. Variation of boundary conditions. Non-dimensional load–displacement curves at given location x/l. a Deflection; b interlayer slip

5.5 Effect of the boundary conditions

In the next example, the influence of the boundary conditions on the critical loads and the nonlinear response is studied. For this investigation, the support conditions in shallow arch 2 are changed at the left end ($x/l=0)$. In the first case, the left support is hard-hinged ($sh-hh$), in the second case the left support is clamped ($sh-cl$). The right end ($x/l=1)$ remains a soft-hinged support in both cases. The load is uniformly distributed $p(x)=p_0$ over x. Figure 9a shows the normalized external load ${\overline{p}}=p_0l^3/EJ_{\infty }$ versus normalized deflection w/l at $x/l=0.5$ for the two arches with modified support (green line: case 1 $hh-sh$; blue line: case 2 $cl-sh$) and, in addition, the response of the soft-hinged structure on both sides ($sh-sh$) subjected to an imperfectly distributed load already shown in Fig. 5a. As can be seen from this figure, at the end of the primary stable deformation path the critical load is the same for the two arches with modified boundary conditions at the left support, with ${\overline{p}}_\mathrm{{cr}}=3.44$, and slightly smaller than for bifurcation buckling of the symmetrically supported structure (where ${\overline{p}}_\mathrm{{cr}}=3.61$). While the unstable deformation branch of the structure with boundary conditions $hh-sh$ subsequently follows the course of the load–deflection path of case $sh-sh$ (bifurcation buckling), the shallow arch clamped on the left end shows a completely different deformation pattern. This is also reflected in the critical load on the remote stable deformation branch, which is ${\overline{p}}_\mathrm{{cr}}=-0.17$ for the structure with boundary conditions $hh-sh$ and ${\overline{p}}_\mathrm{{cr}}=2.07$ for the boundary conditions $cl-sh$.

In Fig. 9b, ${\overline{p}}$ is plotted versus the normalized interlayer slip $\Delta u/l$ at the right end. In the first response path (loading), the interlayer slip is virtually the same for all three structures with different boundary conditions. The deviations become significant only in the unstable deformation branch. It can be seen that the deformation pattern has only one loop when the left boundary conditions are modified. This loop is much smaller in area for boundary conditions $hh-sh$ than for the other two cases. The largest interlayer slip at the member end $x/l=1$ in a stable branch occurs for the boundary conditions $cl-sh$ immediately before snap-back to the primary stable deformation branch.

Fig. 10

Shallow arch 2, modified shallow arch 2, and shallow arch 2 with rigidly bonded layers. subjected to distributed load. Critical load in the first load path

5.6 Variation of the rise

Finally, the influence of the rise ${\hat{w}}_0$ of the shallow arch in the form of a sinusoidal half-wave on the critical load $p_\mathrm{{cr}}$ in the first load path is investigated. To this end, in Fig. 10 the normalized critical load ${\overline{p}}_\mathrm{{cr}}=p_\mathrm{{0cr}}l^3/EJ_{\infty }$ on the primary stable deformation branch is plotted against the normalized rise ${\hat{w}}_0/l$ in the range from 0 to 0.05 for variations of the shallow arch 2 under uniform load $p_0$ with interlayer stiffness $K_s=10^8$ N/m$^2$ ($\alpha l=10.41$), $K_s = 5 \cdot 10^8$ N/m$^2$ ($\alpha l=23.28$), and with rigidly bonded layers ($\alpha l=\infty$), respectively. The computations were performed with both symmetric loading and imperfectly distributed loading according to Eq. (41). This figure shows that, as expected, the critical load increases with increasing normalized rise ${\hat{w}}_0/l$ as well as with increasing interlayer stiffness. The minimum value of ${\hat{w}}_0/l$ above which a stability problem occurs can also be read. For small values of ${\hat{w}}_0/l$ after this limit, the structure becomes unstable due to limit point buckling. For larger ${\hat{w}}_0/l$ values, instability is governed by bifurcation buckling, which can be seen from the fact that the corresponding critical load is smaller than that for hypothetical limit point buckling. The limit values of ${\hat{w}}_0/l$ at the transition from limit point buckling to bifurcation buckling again depends on the interlayer stiffness.

6 Summary and conclusions

Since in-plane limit point buckling (snap-through) and in-plane bifurcation buckling of shallow arches composed of flexibly bonded layers have not been studied in the literature to date, this paper introduced a beam theory for the stability and instability analysis of shallow arches with interlayer slip. In a first example, a comparative computation on a much more elaborate finite shell element model based on a plane stress state showed that the presented theory is both efficient and suitable to predict both the stable and unstable nonlinear response of slender shallow arches with interlayer slip. In the example problems, deflection, interlayer slip, total and layer-wise normal forces, and total bending moment and layer-wise moments are shown graphically as governing response variables.

In order to detect a possible bifurcation buckling of a symmetric shallow arch in a numerical computation, it is essential to impose a small imperfection (see, e.g. Kiss [19]). In the present examples, this was realized by applying a load with extremely small eccentricity. For the more slender arches considered, it was shown that otherwise limit point buckling instead of the actual unstable behavior (bifurcation buckling) is predicted and consequently the critical load is overestimated. Compared to limit point buckling, bifurcation buckling is accompanied by additional unstable branches in the load–deformation diagrams.

With increasing slenderness of the shallow arch as well as increasing interlayer stiffness, the number of unstable branches in the load–deformation diagrams increases. Likewise, the influence of the load distribution on the response was shown. In several examples, multiple unstable deformation branches were predicted, depending on various parameters such as the stiffness of the interlayer and the loading conditions. Selected examples have demonstrated that neglecting the flexibility of the interlayer leads to a considerable overestimation of the critical load.

The presented theory can be used to perform parametric studies due to its simplicity and numerical efficiency. Thus, a tool is available to comprehensively investigate and better understand the stability problem of transversely loaded shallow arches with interlayer slip. In future studies, inertia terms should be added to the theory in order to investigate the dynamic nature of the snap-through phenomenon.