Moderately large deflection of slightly curved layered beams with interlayer slip

Abstract

This paper presents a beam theory for analyzing the static response of slightly curved three-layer beams with interlayer slip. Since the beams are supposed to be immovably supported, membrane stresses develop even at moderately large deflections and the response becomes geometrically nonlinear. The theory is based on a layerwise application of the Euler–Bernoulli theory and a linear elastic constitutive law for the interlaminar displacements. In three application examples, the accuracy of this theory is shown by comparing the results of this theory with the outcomes of a more complex finite element analysis assuming a plane stress state. These application examples demonstrate the effect of a small initial deflection on the nonlinear response of the considered layered structural members.

1 Introduction

The structural members of many engineered constructions are composed of several layers of different materials to obtain an optimal result in terms of weight, stiffness, strength, cost or appearance, etc. However, depending on the fastener, it is not always possible to achieve a rigid bond between the layers in many of these multi-layer constructions. Due to the flexibility of the connector, a slip occurs in these flexibly bonded structural members under load, which fundamentally changes the load-bearing behavior. For this reason, the classical theories of engineering mechanics can no longer be used to analyze the deformation and internal forces, and different theories have been developed in recent decades in order to be able to compute the static response of such beam components (see, e.g., [8, 11, 22]). A number of papers have extended these theories to include the effect of second-order theory on beams with flexibly bonded layers, such as [7, 10, 16, 21]. It should be mentioned here only briefly that a number of papers also deal with vibrations of beams with interlayer slip (e.g., [9, 12, 18]. In this context, in [5, 25] the damping effect at the interface of the layers on the reduction in vibrations of multilayer beams was analyzed.

If the supports are fully immovable, significant membrane stresses develop even at moderately large deflections and the response of such beams becomes geometrically nonlinear (see, e.g., [14, 20]). The analysis of the geometrically nonlinear response of beams with interlayer slip, on the other hand, is the subject of only a small number of publications (e.g., [6, 15]). Recently, the authors of this paper presented a theory for analyzing the geometrically nonlinear static and dynamic response of beams with interlayer slip, whose supports are fixed [1, 2]. A small initial deflection, intentional or due to an imperfection of the structural element, also changes the response. In particular, if the supports are completely immovable, a slight initial deflection against the load direction results in compressive forces that have a great impact on the load-bearing behavior. For example, the phenomenon of snap-through can occur with such a structure. Consequently, several papers in the past have presented theories for the analysis of slightly curved homogeneous or rigidly bonded composite beams without interlayer slip (e.g., [4, 19]). In many of these studies, a core element is a nonlinear axial strain–displacement relation presented in [19]. However, to the best knowledge of the authors, apart from a preliminary study [17], there is no beam theory to date that analyzes the moderately large static response of slightly curved layered beams with interlayer slip. In the present study, therefore, such a theory is proposed for three-layer beams, where an initial deflection is considered in the underlying nonlinear axial strain–displacement relation [19]. The basis for this theory is a study of the authors for beams with interlayer slip with straight beam axis [1]. The boundaries of the considered members can be either clamped, soft hinged or hard hinged.

This paper is structured as follows. After describing the assumptions and requirements, the differential equations and boundary conditions of the present nonlinear boundary value problem are derived and its solution is briefly discussed. Subsequently, the influence of a small initial deflection on the static response of composite beams with interlayer slip is discussed in three application examples, and the accuracy of the presented theory is demonstrated by the results of a comparative finite element analysis assuming a plane stress state.

2 Fundamental equations

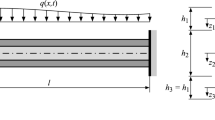
The considered single span beams of length l under in-plane bending about the y-axis are composed of three elastic layers, denoted from top to bottom by 1, 2 and 3, as exemplified in Fig. 1. The top and bottom layers are identical. This implies that both the geometry (layer thickness $h_1=h_3$ and cross-sectional area $A_1=A_3$) and the material parameters (Young’s modulus $E_1=E_3$ and the slip modulus $K \equiv K_{12}=K_{23}$) are the same, and consequently also their bending stiffness $EJ_1=EJ_3$ and axial stiffness $EA_1=EA_3$.

A small initial deflection of the beam axis, ${\hat{w}}(x)$, is a function of the longitudinal (horizontal) coordinate x whose origin is at the left support, see Fig. 1. A lateral coordinate ($z_i, i=1,2,3$) is defined separately for each layer, with the origin $z_i=0$ coinciding with the neutral axis of the respective layer, see also Fig. 1.

Fig. 1

Immovably supported slightly curved three-layer beam with partial layer interaction

The layers are elastically bonded to each other. Therefore, when the beam is loaded by the distributed vertical load q(x), slip occurs between the layers at the interfaces, contrary to the classical theory. The slip between the top layer and the middle layer is referred to as $\varDelta u_{12}$ and between the middle layer and the bottom layer as $\varDelta u_{23}$, see Fig. 2. Vertical separation of the layers is, however, not possible. The load-induced moderately large lateral deflection w(x), which is common to all layers (and fibers) of the beam, is superposed to the initial deflection ${\hat{w}}(x)$.

Since the considered structural members are assumed to be slender, the shear deformation is negligible and the Euler–Bernoulli theory can be applied separately for each layer. Accordingly, the horizontal fiber displacement $u_i$ in the i-th layer at distance $z_i$ from the neutral layer axis can be expressed as a function of the axial displacement $u_i^{(0)}$ at $z_i = 0$ and the deflection w as follows [12]:

$$\begin{aligned} u_i = u_i^{(0)} - z_i w_{,x} \qquad i = 1,2,3 \end{aligned}$$

(1)

$(.)_{,x}$ denotes partial differentiation of (.) with respect to x. From the displacement pattern of the cross-section at x shown in Fig. 2, it follows that the axial displacements of the upper and lower layers, $u_1^{(0)}$ and $u_3^{(0)}$, are related to the central axial displacement $u_2^{(0)}$, the cross-sectional rotation $w_{,x}$ and the interlayer slips $\varDelta u_{12}$, $\varDelta u_{23}$ as follows [13]:

$$\begin{aligned} u_1^{(0)} = u_2^{(0)} + d w_{,x} - \varDelta u_{12} \, , \,\, u_3^{(0)} = u_2^{(0)} - d w_{,x} + \varDelta u_{23} \end{aligned}$$

(2)

The variable d denotes the distance between the curved central axis and the neutral axis of the top/bottom layer. If the cross-section of the outer layers is rectangular, $d = (h_1+h_2)/2$.

Fig. 2

Cross-section at x in its initial and its deformed state

Since the considered beam is immovably supported at both ends, a moderately large lateral deflection w(x) induces a non-negligible stretching of the central axis, resulting in a nonlinear axial strain–displacement relation (see, e.g., [26]). For a slightly curved beam with initial deflection ${\hat{w}}(x)$, this nonlinear relation reads [19]

$$\begin{aligned} e_i = u_{i,x}^{(0)} + \frac{1}{2} w_{,x}^2 + w_{,x} {\hat{w}}_{,x} \, , \qquad i=1,2,3 \end{aligned}$$

(3)

The longitudinal strain of any fiber of the beam is therefore obtained as follows:

$$\begin{aligned} \epsilon _i = e_i - z_i w_{,xx} = u_{i,x}^{(0)} + \frac{1}{2} w_{,x}^2 + w_{,x} {\hat{w}}_{,x} - z_i w_{,xx} \, , \qquad i=1,2,3 \end{aligned}$$

(4)

The composite member is stressed in its elastic deformation range, and thus, Hooke’s law applies. For the following considerations, it is useful to write Hooke’s law in the form of the axial force $N_i$ as well as the bending moment $M_i$ separately for each of the three layers (see, e.g., [26]):

$$\begin{aligned} M_i = -EJ_i w_{,xx} \, , \qquad i=1,2,3 \end{aligned}$$

(5)

$$\begin{aligned} N_i = EA_i e_i = EA_i \left( u_{i,x}^{(0)} + \frac{1}{2} w_{,x}^2 + w_{,x} {\hat{w}}_{,x} \right) \end{aligned}$$

(6)

The interlaminar shear tractions in the interface between the top and the central layer, $t_{s12}$, and in the interface between the middle and the bottom layer, $t_{s23}$, are accordingly proportional to the corresponding interlayer slip. Since the slip modulus K is the same for both interfaces, these quantities read [8]

$$\begin{aligned} t_{s12} = K \varDelta u_{12} \, , \,\, t_{s23} = K \varDelta u_{23} \end{aligned}$$

(7)

The last missing set of fundamental equations are the local equilibrium conditions, which represent the differential relationship between the internal forces. The layerwise equilibrium of the free-body diagram of a beam element shown in Fig. 3 in the longitudinal (x-) direction leads to the relationship between the layerwise axial forces and the interlaminar shear tractions [13]:

$$\begin{aligned} N_{1,x} + t_{s12} = 0 \end{aligned}$$

(8)

$$\begin{aligned} N_{3,x} - t_{s23} = 0 \end{aligned}$$

(9)

$$\begin{aligned} N_{2,x} - t_{s12} + t_{s23} = 0 \end{aligned}$$

(10)

In a common assumption of second order analysis, in these relations the horizontal forces $S_i, i=1,2,3$, have been replaced by the corresponding axial forces $N_i,i=1,2,3$.

The sum of these three equations yields the local equilibrium relation for the overall normal force, $N=N_1+N_2+N_3$,

$$\begin{aligned} N_{,x} = 0 \end{aligned}$$

(11)

which is also obtained directly from the equilibrium of the entire beam element in the x-direction. The overall axial force N results only from the linear and nonlinear axial strains due to moderately large deflection, since no external axial load is applied to the member. Equation (11) shows that N is constant along the entire beam length l.

Equilibrium of this beam element in transverse (z-)direction and about the y-axis yields two more differential equations:

$$\begin{aligned}&T_{,x} = - q \end{aligned}$$

(12)

$$\begin{aligned}&M_{,x} + N \left( w_{,x} + {\hat{w}}_{,x} \right) - T = 0 \end{aligned}$$

(13)

In Eq. (12), T is the transverse cross-sectional force, and in Eq. (13) M, is the overall bending moment, which is composed of the layerwise stress resultants as follows, see Fig. 3 [12],

$$\begin{aligned} M = \sum \limits _{i=1}^3 M_i - (N_1 - N_3) d \end{aligned}$$

(14)

Finally, Eqs. (12) and (13) are combined into one equation by differentiating Eq. (13) with respect to x and then substituting it into Eq. (12):

$$\begin{aligned} M_{,xx} + N \left( w_{,xx} + {\hat{w}}_{,xx} \right) = - q \end{aligned}$$

(15)

Fig. 3

Free-body diagram of a deformed beam element. First order (in red) and second order (in blue) internal forces (modified from [1])

3 Boundary value problem

3.1 Governing differential equations

The deformation of this beam problem is completely described by the four kinematic variables w, $\varDelta u_{12}$, $\varDelta u_{23}$ and $u_2^{(0)}$ and their spatial derivatives. Expressing the four local equilibrium equations Eqs (8)-(10) and Eq. (15) by the the governing kinematic variables, the four solution equations of the slightly curved beam with interlayer slip are obtained. The first three equations are a result from combining Eqs. (8)-(10) with the constitutive relations Eqs (6), (7) and the kinematic relations Eqs (2):

$$\begin{aligned} \varDelta {u_{12,xx}} - \frac{K}{{E{A_1}}}\varDelta {u_{12}} - u_{2,xx}^{(0)} - {w_{,x}}{w_{,xx}} - w_{,x}{\hat{w}}_{,xx} - w_{,xx}{\hat{w}}_{,x} - d{w_{,xxx}} = 0 \end{aligned}$$

(16)

$$\begin{aligned} \varDelta {u_{23,xx}} - \frac{K}{{E{A_1}}}\varDelta {u_{23}} + u_{2,xx}^{(0)} + {w_{,x}}{w_{,xx}} + w_{,x}{\hat{w}}_{,xx} + w_{,xx}{\hat{w}}_{,x} - d{w_{,xxx}} = 0 \end{aligned}$$

(17)

$$\begin{aligned} \frac{K}{E{A_2}}\left( \varDelta {u_{23}} - \varDelta {u_{12}}\right) + {u_{2,xx}^{(0)} + w_{,x} w_{,xx}} + w_{,x}{\hat{w}}_{,xx} + w_{,xx}{\hat{w}}_{,x} = 0 \end{aligned}$$

(18)

Before the fourth governing differential equation can be established, it is necessary to first express the overall bending moment M as a function of the kinematic variables. Inserting Eqs. (5) and (6) into Eq. (14) and then replacing $u_{1,x}^{(0)}$ and $u_{3,x}^{(0)}$ by Eq. (2) differentiated with respect to x yield

$$\begin{aligned} M = - {EJ_\infty }{w_{,xx}} + E{A_1}d\left( {\varDelta {u_{12,x}} + \varDelta {u_{23,x}}} \right) \end{aligned}$$

(19)

where

$$\begin{aligned} EJ_\infty = EJ_0 + 2d^2EA_1 \end{aligned}$$

(20)

is the bending stiffness of the beam with rigidly bonded layers and

$$\begin{aligned} EJ_0 = 2EJ_1 + EJ_2 \end{aligned}$$

(21)

denotes the bending stiffness of the non-composite member, i.e., $K=0$.

Equation (19) is two-times differentiated with respect to x and inserted into Eq. (15). The result is the fourth governing equation:

$$\begin{aligned}&D\{ {w}(x),\varDelta u_{12}(x),\varDelta u_{23}(x),u^{(0)}_2(x) \} \nonumber \\&\quad = - {EJ_\infty }{w_{,xxxx}} + E{A_1}d\left( {\varDelta {u_{12,xxx}} + \varDelta {u_{23,xxx}}} \right) + N \left( w_{,xx} + {\hat{w}}_{,xx} \right) + q = 0 \end{aligned}$$

(22)

The overall axial force N that appears in this equation must also be expressed by the kinematic variables, which is achieved when the axial forces in the layers according to Eq. (6) are totaled, and then, $u_{1,x}^{(0)}$ and $u_{3,x}^{(0)}$ are replaced by the kinematic relations Eq. (2) differentiated by x:

$$\begin{aligned}&N = EA_e\left( u_{2,x}^{(0)}+\frac{1}{2} w_{,x}^2+w_{,x}{\hat{w}}_{,x}\right) +EA_1(\varDelta u_{23,x}-\varDelta u_{12,x}) \end{aligned}$$

(23)

$$\begin{aligned}&\quad EA_e = 2EA_1 + EA_2 \end{aligned}$$

(24)

According to Eq. (11), N is constant over the axis x. Therefore, N can also be written in the form of the following integral expression, which has proved to be advantageous for the analytical solution of the boundary value problem:

$$\begin{aligned} N = \frac{EA_e}{l}\int _0^l\left( u_{2,x}^{(0)}+\frac{1}{2} w_{,x}^2+w_{,x}{\hat{w}}_{,x}\right) dx+\frac{EA_1}{l}\int _0^l(\varDelta u_{23,x}-\varDelta u_{12,x})dx \end{aligned}$$

(25)

As an alternative to one of the three equilibrium conditions Eqs. (16)–(18), the following equilibrium condition can be used:

$$\begin{aligned} EA_e \left( u_{2,xx}^{(0)} + w_{,x} w_{,xx} + w_{,x}{\hat{w}}_{,xx} + w_{,xx}{\hat{w}}_{,x} \right) + EA_1(\varDelta u_{23,xx}-\varDelta u_{12,xx}) = 0 \end{aligned}$$

(26)

which is obtained by substituting Eq. (23) into Eq. (11).

In the computations, it has been found that Eqs. (16) and (17) are unfavorable for solving the boundary value problem, as they couple all four kinematic variables. An alternative equation is obtained by adding Eqs. (16) and (17):

$$\begin{aligned} \varDelta {u_{23,xx}} + \varDelta {u_{12,xx}} - \frac{K}{{E{A_1}}}\left( {\varDelta {u_{23}} + \varDelta {u_{12}}} \right) - 2d{w_{,xxx}} = 0 \end{aligned}$$

(27)

Subtracting Eq. (16) from Eq. (17) and using Eq. (26) to eliminate the terms with $u_{2}^{(0)}$, w and ${\hat{w}}$ yield a second alternative equation:

$$\begin{aligned} \varDelta {u_{23,xx}} - \varDelta {u_{12,xx}} - \frac{K {EA}_e}{{EA}_1{EA}_2} \left( {\varDelta {u_{23}} - \varDelta {u_{12}}} \right) = 0 \end{aligned}$$

(28)

In Eqs. (27) and (28), $u_{2}^{(0)}$ and ${\hat{w}}$ no longer occur. Only the variables $\varDelta {u_{12}}$ and $\varDelta {u_{23}}$ appear in Eq. (28).

3.2 Boundary conditions

To solve the coupled set of governing equations, Eqs. (27), (28), (18) and (22), five boundary conditions at each beam end need to be specified. Three different beam ends are considered, i.e., a hinged support without shear restraints, a hard hinged support and a clamped end. These support conditions have in common that the lateral deflection is zero:

$$\begin{aligned} w_b = 0 \end{aligned}$$

(29)

The subscript b indicates that w at a boundary (i.e., $x = 0$ or $x = l$) is considered.

Additionally, the central axis of the considered composite members is immovably supported at both ends, i.e.,

$$\begin{aligned} \left( u_2^{(0)}\right) _b = 0 \end{aligned}$$

(30)

A free beam end is not discussed because a member with such boundary condition does not develop significant membrane stresses and thus, no overall axial force N at moderately large deflection, making the geometrically nonlinear response and the geometrically linear one virtually identical.

Hinged support without shear restraints (soft hinged support)

A hinged support yields the overall bending moment at the boundary zero, i.e., $M_b = 0$. At a soft hinged support, the slip between the layers is not constrained, and consequently, in the actual symmetric three-layer configuration the layerwise axial force in the upper and lower layer is zero as well, i.e., ${(N_1)}_b = 0$ and ${(N_3)}_b = 0$. With these three boundary conditions, it follows from Eq. (14) that the layerwise bending moments are zero, i.e., ${(M_i)}_b = 0$, $i=1,2,3$, or expressed in terms of the kinematic variable w, compare with Eq. (5),

$$\begin{aligned} (w_{,xx})_b = 0 \end{aligned}$$

(31)

If the difference $(N_1)_b - (N_3)_b$ is formed, which must be zero at the boundary according to the above, $(N_1)_b - (N_3)_b =0$, together with Eqs. (6) (for $i=1$ and 3) and (31), leads to another boundary condition in the kinematic variables:

$$\begin{aligned} {\left( {\varDelta {u_{12,x}} + \varDelta {u_{23,x}}} \right) _b} = 0 \end{aligned}$$

(32)

The third boundary condition in the kinematic variables is obtained from the sum of $(N_1)_b$ and $(N_3)_b$, which is zero at the boundary, $(N_1)_b + (N_3)_b =0$:

$$\begin{aligned} {\left( {\varDelta {u_{23,x}} - \varDelta {u_{12,x}}} \right) _b} + 2{\left( {u_{2,x}^{(0)} + \frac{1}{2}w_{,x}^2} + w_{,x}{\hat{w}}_{,x} \right) _b} = 0 \end{aligned}$$

(33)

As observed, Eq. (33) couples all kinematic variables of the problem. This boundary condition is equivalent to the fact that at the boundaries the total normal force induced by the horizontally immovable supports is fully transferred into the middle layer, i.e., $(N_2)_b = N_b$.

Hard hinged support

A hinged support where the interlayer slips are fully constrained by, for instance, a rigid end plate, i.e.,

$$\begin{aligned} (\varDelta {u_{12}})_b = (\varDelta {u_{23}})_b = 0 \end{aligned}$$

(34)

is referred to as hard hinged support. Consequently, the shear tractions of the interlayers also vanish, ${(t_{s12})}_b = {(t_{s23})}_b = 0$.

Combining $M_b = 0$ with Eq. (19) yields a further boundary condition:

$$\begin{aligned} - {EJ_\infty }\left( {w_{,xx}}\right) _b + E{A_1}d\left( {\varDelta {u_{12,x}} + \varDelta {u_{23,x}}} \right) _b = 0 \end{aligned}$$

(35)

Rigidly clamped end

At a rigidly clamped end, the slope of the lateral deflection is zero:

$$\begin{aligned} (w_{,x})_b = 0 \end{aligned}$$

(36)

Additionally, the interlayer slip at both interfaces vanishes:

$$\begin{aligned} (\varDelta {u_{12}})_b = (\varDelta {u_{23}})_b = 0 \end{aligned}$$

(37)

4 Solution of the governing equations

The boundary value problem at hand is solved using Galerkin’s procedure [26]. The basis is the approximation of the deflection w(x) (denoted as $w^*(x)$) by a finite series in the sense of a Ritz approach [26],

$$\begin{aligned} w(x) \approx w^*(x) = \sum _{i=1}^{n} \gamma _i \varPhi _i\left( x \right) \end{aligned}$$

(38)

where the n shape functions $\varPhi _i(x)$, $i=1,\ldots ,n$, satisfy the boundary conditions in w. For example, the eigenfunctions of the associated geometric linear straight beam (i.e., without initial deflection) with interlayer slip may serve as suitable shape functions. For the three following examples, the choice of the shape functions is discussed in more detail. In this manner, the governing partial differential equations are transformed into a set of n algebraic equations in the unknown weighting coefficients $\gamma _i$.

Equally, it may be advantageous to also express the initial deflection $\hat{w}(x)$ as a series:

$$\begin{aligned} \hat{w}(x) = \sum _{i=1}^{n} \hat{w}_{a}^{(i)} \varPsi _i\left( x \right) \end{aligned}$$

(39)

where the shape functions $\varPsi _i\left( x \right)$ satisfy the boundary conditions of $\hat{w}(x)$. $\varPsi _i\left( x \right)$ can be different or the same as $\varPhi _i\left( x \right)$. However, since $\hat{w}(x)$ (as opposed to w) is a known quantity, the associated weighting coefficients $\hat{w}_{a}^{(i)}$ are known quantities.

In a first step, the series expansions of w and $\hat{w}$, Eqs. (38) and (39), are inserted into the differential equations Eqs. (27), (28) and (18), which are then solved in combination with the current boundary conditions for the three remaining kinematic variables $\varDelta u_{12}$, $\varDelta u_{23}$ and $u_2^{(0)}$ as a function of the unknowns $\gamma _i$, $i=1,\ldots ,n$.

These variables are substituted into the equation for the axial force N, Eq. (25), which thus also becomes a function of $\gamma _i$, $i=1,\ldots ,n$. The resulting expression and Eqs. (38), (39) are now substituted into the fourth solution equation Eq. (22). This equation is then multiplied successively by the n shape functions $\varPhi _i$ and integrated over the beam length l according to Galerkin’s rule [26]:

$$\begin{aligned} \int \limits _l {D\{ {w^*}(x),{\varDelta {u}_{12}^*}(x),{\varDelta {u}_{23}^*}(x),{{u}^{(0)}_2}^*(x) \} {\varPhi _i}(x)dx}=0~,~~i=1,\ldots ,n \end{aligned}$$

(40)

This results in n equations for the unknown coefficients $\gamma _i$, which are nonlinearly coupled due to the effect of the normal force. These equations can then be solved for $\gamma _i$, $i=1,\ldots ,n$, using a standard solver for nonlinear equations.

5 Application examples

5.1 Simply supported beam with half-sine initial deflection subjected to half-sine load

In the first example, a fully restrained simply supported three-layer beam with interlayer slip is considered, which has an initial deflection in the form of a sine half-wave:

$$\begin{aligned} \hat{w}(x) = \hat{w}_{a} \sin \left( \lambda x \right) ~,~~\lambda =\frac{\pi }{l} \end{aligned}$$

(41)

This member shown in Fig. 4 is subjected to the half-sine distributed load

$$\begin{aligned} q(x) = q_{0} \sin \left( \lambda x \right) \end{aligned}$$

(42)

Fig. 4

Example 1: simply supported beam with initial deflection according to a half-sine subjected to a half-sine load

Since the deflection $w_l$ of the corresponding linear straight three-layer beam with interlayer slip due to this load is also sine half-wave distributed [1],

$$\begin{aligned} w_l(x) = \frac{q_{0}}{{\bar{k}}} \sin \left( \lambda x \right) ~,~{\bar{k}}=\lambda ^4\left( \lambda ^2+\alpha ^2\right) \left( \frac{\alpha ^2}{EJ_{\infty }}+\frac{\lambda ^2}{EJ_{0}} \right) ^{-1} \end{aligned}$$

(43)

and furthermore, the small initial deflection $\hat{w}(x)$ also follows a half-sine wave; it is reasonable to assume that the nonlinear deflection w(x) of the beam under consideration can be approximated by a sine half-wave. The series approximation of w(x) according to Eq. (38) thus degenerates to

$$\begin{aligned} {w}^*(x) = \gamma \sin \left( \lambda x \right) \end{aligned}$$

(44)

with the only unknown weighting factor $\gamma$. The parameter $\alpha ^2$ in Eq. (43) [12],

$$\begin{aligned} \alpha =\left( \frac{EJ_{\infty }K}{EA_1 EJ_0}\right) ^{1/2} \end{aligned}$$

(45)

which is proportional to the slip modulus K, defines the degree of bonding in the lateral direction [10].

Equation (44) as well as the initial deflection ${\hat{w}}$ according to Eq. (41) is inserted into the coupled differential equations Eqs. (27), (28) and (18), which are subsequently solved in combination with the six soft hinged boundary conditions Eqs. (30), (32), (33) at $x=0$ and $x=l$, respectively, for $\varDelta u_{12}$, $\varDelta u_{23}$, $u_{2}^{(0)}$,

$$\begin{aligned}&\varDelta u_{12}(x) = \frac{\lambda ^2 \gamma }{4} \left( \frac{4 d \lambda \cos \left( \lambda x \right) }{\lambda ^2 + \frac{K}{EA_1}} - \beta (x) \left( \gamma + 2 \hat{w}_{a} \right) \right) \end{aligned}$$

(46)

$$\begin{aligned}&\varDelta u_{23}(x) = \frac{\lambda ^2 \gamma }{4} \left( \frac{4 d \lambda \cos \left( \lambda x \right) }{\lambda ^2 + \frac{K}{EA_1}} + \beta (x) \left( \gamma + 2 \hat{w}_{a} \right) \right) \end{aligned}$$

(47)

$$\begin{aligned} u_{2}^{(0)}(x) = \frac{\lambda ^2 \gamma }{4} \left( - \frac{1}{2 \lambda } \sin \left( 2 \lambda x \right) + \theta (x) \right) \left( \gamma + 2 \hat{w}_{a} \right) \end{aligned}$$

(48)

with

$$\begin{aligned}&\beta (x) = \frac{EA_e l \sinh \left( \frac{1}{2} \delta \left( l-2 x \right) \right) }{4 EA_1 \sinh \left( \frac{\delta l}{2} \right) + EA_2 \delta l \cosh \left( \frac{\delta l}{2} \right) }~~,~\delta =\left( \frac{EA_e K}{EA_1 EA_2}\right) ^{1/2}~~,~\nonumber \\&\theta (x) = \frac{2 EA_1 \left( \left( l-2 x \right) \sinh \left( \frac{\delta l}{2} \right) - l \sinh \left( \frac{1}{2} \delta \left( l-2 x \right) \right) \right) }{4 EA_1 \sinh \left( \frac{\delta l}{2} \right) + EA_2 \delta l \cosh \left( \frac{\delta l}{2} \right) } \end{aligned}$$

(49)

In the present case, the solution was found with the software suite Mathematica v 12.2 [24]. Substituting these expressions into Eq. (25), the overall normal force is obtained as a function of $\gamma$,

$$\begin{aligned} N = \frac{\lambda ^2 \psi }{4} \gamma \left( \gamma + 2 \hat{w}_{a} \right) \end{aligned}$$

(50)

with

$$\begin{aligned} \psi = \frac{ EA_e EA_2 \delta l \cosh \left( \frac{\delta l}{2} \right) }{4 EA_1 \sinh \left( \frac{\delta l}{2} \right) + EA_2 \delta l \cosh \left( \frac{\delta l}{2} \right) } \end{aligned}$$

(51)

Finally, applying Galerkin’s rule to Eq. (22) yields in combination with Eqs. (41), (42), (44), (46), (47), (50), the following cubic equation for $\gamma$,

$$\begin{aligned} \frac{1}{4} {\psi \lambda ^4 \gamma }^3 + \frac{3}{4} \psi \lambda ^4 {\hat{w}_a} {\gamma }^2 + \frac{1}{2} \psi \lambda ^4 \hat{w}_a^2 {\gamma } + {\bar{k}} {\gamma } = q_0 \end{aligned}$$

(52)

which is solved taking into account the current beam parameters.

In the following, a three-layer beam with a rectangular cross-section is considered, which has the following dimensions: span $l=1.0$ m, layer thickness $h_1 = h_3 = 0.01$ m, $h_2 = 0.0102$ m, width $b = 0.1$ m. The structural member has an upward initial deformation of the beam axis whose amplitude $\hat{w}_a$ is 1% of the span l, i.e., $\hat{w}_a = -0.01$ m. The initial deflection is therefore oriented against the positive z-coordinate and the load direction. The material parameters are given as $E_1 = E_3 = 7.0 \cdot 10^{10}$ N/m$^2$, $E_2 = 1.0 \cdot 10^{10}$ N/m$^2$, $K = 1.0 \cdot 10^{9}$ N/m$^2$. These material parameters together with the dimension of the cross-section yield for the layer interaction parameter $\alpha$ (Eq. (45)) times l the value $\alpha l = 13.3$, which corresponds to a moderate interaction of the layers [10]. A load amplitude of $q_0=1.0 \cdot 10^4$ N/m is chosen. For these parameters, the nonlinear equation Eq. (52) has only one real solution, which is $\gamma =0.010672$. Therefore, no snap-through occurs.

To examine the accuracy of the beam theory presented, its solution is compared with the results of a computationally much more expensive finite element (FE) analysis in the software suite Abaqus [23]. The FE analysis is based on the assumption of a plane stress state. Therefore, it does not include the Euler–Bernoulli hypothesis and is consequently of higher accuracy than the proposed beam theory. In contrast with the beam model, where the thickness of the interlayers is zero, in the FE model the interlayers are represented by very thin cohesive zones with a thickness of 0.1 mm, i.e., $h_1 / 100$. In turn, the thickness of the middle layer is reduced twice by this value (i.e., $h_2 = 0.01$ m), to keep the overall height of the structural member unchanged. The three layers are discretized by quadrilateral plane stress elements with eight nodes per element, while linear cohesive elements with four nodes per element are used for the cohesive zones. The tangential stiffness of the cohesive elements corresponds to the slip modulus K of the beam theory, while 10, 000 times K is set for their normal stiffness, since the normal stiffness is infinite in the beam model. The soft-hinged supports are each realized by a kinematic coupling of the outer surfaces of the central layer at an additional node. In total, the FE model has approximately 48, 000 degrees of freedom, compared to one degree of freedom of the single-term Ritz approximation used to solve the beam equations.

The first result shown in Fig. 5 is the deflection of the slightly curved member along its span, normalized by the midspan deflection $w_{ref}$ of the corresponding linear beam with straight beam axis, where one support can move horizontally. The reference deflection $w_{ref}$ over span l is $w_{ref}/l=0.0106$ [1]. The outcome of the beam theory is illustrated by a black solid line; the black circular markers refer to the solution of the FE model. It can be seen that the nonlinear deflection of both models is virtually identical, with a difference of less than 1%. This result confirms both the proposed beam theory and the chosen Ritz approximation for the deflection with a single shape function for the problem at hand.

Fig. 5

Normalized deflection of a nonlinear slightly curved, a nonlinear straight and a linear straight simply supported beam with interlayer slip subjected to half-sine load

Additionally, this figure also shows the normalized deflection of both the nonlinear beam and linear beam (where one support is horizontally movable) with straight axis, i.e., $\hat{w}_a=0$, by a solid red line and a solid blue line, respectively. The midspan deflection of the nonlinear straight beam is 11% smaller than that of the nonlinear slightly curved one, which shows how important it is to include the very small initial deformation (here 1% of the beam span) in the nonlinear strain–displacement relations when the supports are fully restrained. The response of the linear straight beam is larger than that of the nonlinear straight member and, in the present problem, almost equal to that of the slightly curved nonlinear beam. In order to better understand the latter result, which is surprising at first glance, Fig. 6 represents the midspan deflection w(l/2) divided by $w_{ref}$ as a function of the normalized amplitude of the initial curvature $\hat{w}_a$/l. This graph shows that at $\hat{w}_a/l=-0.01$ the ratio $w(l/2)/w_{ref}$ is one, i.e., the nonlinear and linear deflection are equal. In the range $-0.01< \hat{w}_a / l < -0.005$, the midspan deflection of the curved beam is even slightly larger than that of the linear beam with one horizontally movable support. For $\hat{w}_a/l < -0.01$ and $\hat{w}_a/l > -0.005$ (i.e., also for straight nonlinear beam $\hat{w}_a /l=0$), the deflection of the nonlinear member is smaller than that of the linear one. For instance, if $\hat{w}_a$ is 10% of the span (i.e. $\hat{w}_a / l=\pm 0.1$), the nonlinear midspan deflection is only 4% of the linear one.

Fig. 6

Normalized midspan deflection of a nonlinear slightly curved simply supported beam subjected to half-sine load as a function of the normalized amplitude of the initial deflection

Figure 7 shows the normalized interlayer slips $\varDelta u_{12}$ (solid lines) and $\varDelta u_{23}$ (dashed lines) over x/l for the same cases, (i) slightly curved nonlinear beam (black lines), (ii) nonlinear beam with straight axis (red lines), and (iii) linear beam with straight axis (blue line). For case (i), the solution of the FE plane model is shown with markers. These deformation quantities are normalized with $w_{ref}$. First, the excellent agreement between the solutions for the slightly curved nonlinear member from the proposed beam theory and the FE model is pointed out. Furthermore, the grave effect of geometric nonlinearities on the interlayer slip becomes obvious. While for the linear straight beam the two interlayer slips are equal and have the largest value at the left support, for the nonlinear members (i) and (ii) the deviation between $\varDelta u_{12}$ and $\varDelta u_{23}$ becomes larger toward the supports. At $x/l=0$, $\varDelta u_{12}$ of the slightly curved beam is larger than the linear response, while $\varDelta u_{23}$ is below the linear solution. In contrast, for the straight nonlinear member $\varDelta u_{12}$ is smaller than the linear response, $\varDelta u_{23}$ is above it. The interlayer slips also demonstrates how crucial it is to take the initial curvature into account when calculating the response.

Fig. 7

Normalized interlayer slips of a nonlinear slightly curved, a nonlinear straight and a linear straight simply supported beam subjected to half-sine load

Figure 8 shows the result for the fourth kinematic variable, which is the longitudinal displacement of the central axis $u_2^{(0)}$ divided by $w_{ref}$, as a function of x/l. It can be seen that the shape of $u_2^{(0)}$ over x/l of the nonlinear curved beam (black solid line) is the mirror image of $u_2^{(0)}$ of the straight nonlinear beam (red solid line). This illustrates the effect of the small initial deflection also on this response variable. $u_2^{(0)}$ from the proposed beam theory and from the FE model is again virtually the same. Note that $u_2^{(0)}$ is identically zero for the linear straight member.

Fig. 8

Normalized longitudinal displacement of the central axis of a nonlinear slightly curved, a nonlinear straight and a linear straight simply supported beam with interlayer slip subjected to half-sine load

Figure 9 shows the overall normal force N and the layerwise normal forces $N_1$, $N_2$ and $N_3$ of the slightly curved (black lines) as well as the straight nonlinear beam (red lines). These quantities are normalized to the maximum normal force in the bottom layer of the geometric linear beam, $N_{ref}=N_{3(l)}(x/l=0.5)$. It can be seen that the small initial deflection of $\hat{w}_a /l =-0.01$ changes the sign of the overall normal force N (solid lines). While in the straight beam N is a tensile force, in the curved beam it is a compressive force. Furthermore, it can be seen that at the boundaries the normal force in the middle layer $N_2$ coincides with N according to the corresponding boundary condition Eq. (33), which then decays to almost zero toward the center of the beam. Since in the beam with initial deflection N is a compressive force, the axial force in the upper layer over $N_{ref}$ at midspan is $N_1(x/l=0.5)/N_{ref}<-1$, while in the straight beam the tensile force N causes $N_1(x/l=0.5)/N_{ref}>-1$.

Fig. 9

Overall and layerwise normalized axial forces of a nonlinear slightly curved and a nonlinear straight simply supported beam subjected to half-sine load

The overall bending moment M and the moments in the individual layers $M_1$, $M_2$, $M_3$, shown in Fig. 10 by black lines for the nonlinear curved beam and by red lines for the nonlinear straight beam, are normalized to the maximum overall bending moment of the linear beam, i.e., $M_{ref}=M_{(l)}(x=l/2)$. The most important observation is that due to the small initial curvature $\hat{w}_a/l=-0.01$, the maximum overall moment M becomes slightly larger than in the linear straight beam, while it is 11% smaller in the straight nonlinear beam.

Fig. 10

Overall and layerwise normalized bending moments of a nonlinear slightly curved and a nonlinear straight simply supported beam subjected to half-sine load

Finally, the effect of the interlayer slip on the moderately large response of the slightly curved beam is investigated based on this example. To this end, Fig. 11 compares the deflection ratio of the considered curved member (with $\alpha l=13.3$; black line) with the deflection of the rigidly bonded beam ($\alpha l=\infty$; blue line) and the beam without bond ($\alpha l=0$; red line). As expected, the deflection of the beam without horizontal layer interaction is the largest (i.e., 3.6 times larger than for the flexibly bonded beam), and the beam with full bonding is the smallest (i.e., 1.8 times smaller than for the flexibly bonded beam). Figure 12 displays the normalized interlayer slips $\varDelta u_{12}/w_{ref}$ and $\varDelta u_{23}/w_{ref}$ for $\alpha l =13.3$ and $\alpha l =0$. By definition this quantity is zero for the rigidly bonded beam without slip. Lastly, for the longitudinal displacement of the central axis $u_2^{(0)}/w_{ref}$, the behavior is similar, as Fig. 13 shows.

Fig. 11

Normalized deflection of three nonlinear slightly curved simply supported beams with different interlayer stiffness subjected to half-sine load

Fig. 12

Normalized interlayer slips of three nonlinear slightly curved simply supported beams with different interlayer stiffness subjected to half-sine load

Fig. 13

Normalized longitudinal displacement of the the central axis of three nonlinear slightly curved simply supported beams with different interlayer stiffness subjected to half-sine load

5.2 Slightly curved simply supported beam subjected to non-symmetric load

In the second example, again a simply supported beam is considered, but with an arbitrarily distributed initial deflection and under an arbitrarily distributed load. In this case, the nonlinear response as well as the initial curvature is approximated by a finite series expansion according to Eqs (38) and (39) based on the following shape functions,

$$\begin{aligned} \varPhi _i(x) = \varPsi _i(x) = \sin \left( \lambda _i x \right) ~,~~\lambda _i = \frac{i \pi }{l}~,~~i=1,\ldots ,n \end{aligned}$$

(53)

These shape functions correspond to the eigenfunctions of the linear beam with interlayer slip (see, e.g., [3]) and thus satisfy the boundary conditions in the deflection w. Following the steps explained in detail in the previous example, the series expansions Eqs. (38) and (39) and Eq. (53) are inserted into the governing equations Eqs (27), (28) and (18), which are then solved in combination with the soft-hinged boundary conditions Eqs. (30), (32), (33) at $x=0$ and $x=l$ using the software suite Mathematica v. 12.2 [24]. This yields the following analytical expressions for the interlayer slips $\varDelta u_{12}$ and $\varDelta u_{23}$ and the horizontal displacement $u_{2}^{(0)}$ as a function of the unknown weighting coefficients $\gamma _i$, $i=1,\ldots ,n$,

$$\begin{aligned}&\varDelta u_{12}(x) =\frac{1}{4} \sum _{i=1}^{n} \lambda _i^2 \gamma _i \left( \frac{4 d \lambda _i \cos \left( \lambda _i x \right) }{\lambda _i^2 + \frac{K}{EA_1}} - \beta (x) \left( \gamma _i + 2 \hat{w}_{a}^{(i)} \right) \right) \end{aligned}$$

(54)

$$\begin{aligned}&\varDelta u_{23}(x) =\frac{1}{4} \sum _{i=1}^{n} \lambda _i^2 \gamma _i \left( \frac{4 d \lambda _i \cos \left( \lambda _i x \right) }{\lambda _i^2 + \frac{K}{EA_1}} + \beta (x) \left( \gamma _i + 2 \hat{w}_{a}^{(i)} \right) \right) \end{aligned}$$

(55)

$$\begin{aligned} \begin{aligned} u_{2}^{(0)}(x)&= - \frac{1}{4} \sum _{i=1}^{n} \sum _{j=1}^{n} \lambda _i \lambda _j \left( \frac{1}{\lambda _{j-i} + \delta _{ji}} \sin \left( \lambda _{j-i} x \right) + \frac{1}{\lambda _{i+j}} \sin \left( \lambda _{i+j} x \right) \right) \\&\cdot \left( \gamma _i \gamma _j + \gamma _i \hat{w}_{a}^{(j)} + \gamma _j \hat{w}_{a}^{(i)} \right) + \frac{\theta (x)}{4} \sum _{i=1}^{n} \lambda _i^2 \gamma _i \left( \gamma _i + 2 \hat{w}_{a}^{(i)} \right) \end{aligned} \end{aligned}$$

(56)

Note that $\delta _{ij}$ in Eq. (56) denotes the Kronecker delta introduced to avoid an undetermined expression when $i=j$. Evaluation of Eq. (25) with these expressions leads to the following equation for the overall normal force,

$$\begin{aligned} N = \frac{\psi }{4} \sum _{i=1}^{n} \lambda _i^2 \gamma _i \left( \gamma _i + 2 \hat{w}_{a}^{(i)} \right) \end{aligned}$$

(57)

Applying Galerkin’s rule Eq. (40) then leads to the following set of nonlinear coupled equations for the unknown coefficients $\gamma _i$, $i=1,\ldots ,n$, for the present problem,

$$\begin{aligned} \frac{\psi \lambda _i^4}{4 i^2} \left( \gamma _i + \hat{w}_a^{(i)} \right) \sum _{j=1}^{n} j^2 \left( \gamma _j^{2}+2 \hat{w}_a^{(j)}\gamma _j \right) + {\bar{k}}_i \gamma _i = \frac{2}{l} q_i ~,~~i=1,\ldots ,n \end{aligned}$$

(58)

with

$$\begin{aligned} {\bar{k}}_i=\lambda _i^4\left( \lambda _i^2+\alpha ^2\right) \left( \frac{\alpha ^2}{EJ_{\infty }}+\frac{\lambda _i^2}{EJ_{0}} \right) ^{-1}~,~~q_i = \int \limits _{0}^{l} {q(x) {\varPhi _i}(x)dx} \end{aligned}$$

(59)

In the numerical application, the same beam is considered with the same configuration, geometry and material parameters as in the previous example. The initial deflection is composed of a sine half-wave and a sine wave,

$$\begin{aligned} {\hat{w}}(x)={\hat{w}}_a^{(1)} \sin \left( \lambda _1 x\right) + {\hat{w}}_a^{(2)} \sin \left( \lambda _2 x\right) \end{aligned}$$

(60)

where ${\hat{w}}_a^{(1)}=-0.02$ m and ${\hat{w}}_a^{(2)}=0.005$ m. Thus, the initial deflection in this example is oriented upwards along the entire beam axis against the positive z-coordinate. The member shown in Fig. 14 is subjected to a load equally distributed over the left half of the span,

$$\begin{aligned} q(x)=q_0 \left( H(x)-H(x-l/2)\right) \end{aligned}$$

(61)

with H denoting the Heaviside function and, as in the previous example, the load amplitude is $q_0=1.0 \cdot 10^4$ N/m.

Fig. 14

Example 2: simply supported beam with initial deflection composed a sine half-wave and a sine wave, subjected to a uniformly distributed load on the left half

Figure 15 shows the normalized deflection $w/w_{ref}$ as a function of x/l, with $w_{ref}$ denoting the maximum deflection of the corresponding straight linear beam under the same load, i.e., $w_{ref}(x=0.425l)=0.006868$ m. It can be seen that with $n=3$ series terms the solution of the beam theory (black solid line) is virtually identical to the FE plane stress solution (circular markers). The deflection can also be approximated very well with two series terms ($n=2$), compare with the dashed black line. However, with one series term ($n=1$), the influence of the asymmetric initial deflection and asymmetric loading on the deflection cannot be captured, as the black dotted line illustrates. In addition, this figure shows both the normalized deflection of the nonlinear straight beam (solid red line) and the linear straight beam (solid line), both of which are larger than that of the slightly curved nonlinear beam.

Fig. 15

Normalized deflection of a nonlinear slightly curved, a nonlinear straight and a linear straight simply supported beam with interlayer slip subjected to a load uniformly distributed over the left half of the member

Figure 16 presents the normalized interlayer slips $\varDelta u_{12}/w_{ref}$ (solid lines) and $\varDelta u_{23}/w_{ref}$ (dashed lines) of the slightly curved beam again for $n =1$ (blue lines), $n =2$ (red lines) and $n =3$ (black lines) series terms, respectively, as well as the corresponding results from the FE analysis. This example also shows that the two interlayer slips $\varDelta u_{12}/w_{ref}$ and $\varDelta u_{23}/w_{ref}$, which can be well approximated with two series terms, deviate more and more from each other at the ends of the beam, where they have opposite curvature. The normalized interlayer slips of the straight nonlinear beam (red lines) and the linear beam (blue line), which are depicted in Fig. 17 additionally to the outcome of the slightly curved beam (black lines), demonstrate the influence of the initial deflection on this response variable.

Fig. 16

Normalized interlayer slips of a nonlinear slightly curved simply supported beam with interlayer slip subjected to a load uniformly distributed over the left half of the beam. Variation in the number of series terms. Series solution based different number of terms and FE plane stress solution

Fig. 17

Normalized interlayer slips of a nonlinear slightly curved, a nonlinear straight and a linear straight simply supported beam with interlayer slip subjected to a load uniformly distributed over the left half of the beam

For the representation of the normalized longitudinal displacement of the central axis $u_2^{(0)}/w_{ref}$, at least three series terms are necessary, as Fig. 18 demonstrates (black solid line). The consideration of two series terms (black dashed line) leads to a visible deviation from the FE solution (circular markers). The approximation with one series term (black dotted line) does not lead to a reasonable result. The longitudinal displacement of the nonlinear straight beam, which is also illustrated by a red solid line, shows a completely different pattern than that of the slightly curved beam.

Fig. 18

Normalized longitudinal displacement of the central axis of a nonlinear slightly curved, a nonlinear straight and a linear straight simply supported beam with interlayer slip subjected to a load uniformly distributed over the left half of the beam

5.3 Slightly curved clamped-soft hinged beam subjected to half-sine load

The beam of the third example shown in Fig. 19 is clamped on the left end and soft-hinged supported on the right end, and subjected to a load in the form of a sine half-wave according to Eq. (42). The initial deflection ${\hat{w}}$ is affine to the deflection $w_l$ of the associated linear three-layer beam with flexible bonding,

$$\begin{aligned} {\hat{w}}(x)={\hat{w}}_a \frac{w_l(x)}{\text {max}|w_l(x)|} \end{aligned}$$

(62)

where

$$\begin{aligned} \begin{aligned} w_l(x)=&\frac{q_0}{2{EJ}_0 \lambda ^4 \left( \alpha ^2+\lambda ^2\right) {EJ}_{\infty }} \Biggl (2 \sin (\lambda x)\left( \alpha ^2 {EJ}_0+\lambda ^2{EJ}_{\infty }\right) \Biggr . \\&\left. -\frac{\lambda }{\alpha l \cosh (\alpha l)\left( {EJ}_0 \left( \alpha ^2 l^2-3\right) +3 {EJ}_{\infty }\right) +3 \left( {EJ}_0-{EJ}_{\infty }\right) \sinh (\alpha l)} \right. \\&\left. \biggl (\left( {EJ}_0-\text {EJ}_{\infty }\right) \Bigl (2 l \sinh (\alpha (l-x))\left( 3 \lambda ^2 {EJ}_{\infty }+\alpha ^2 {EJ}_0 \left( \lambda ^2l^2+3\right) \right) \Bigr . \biggr .\right. \\&\left. \left. \Bigl . -(l-x) \sinh (\alpha l) \left( 6 \lambda ^2 {EJ}_{\infty }+\alpha ^2 {EJ}_0 \left( \lambda ^2\left( 2 l^2+2 lx-x^2\right) +6\right) \right) \Bigr ) \right. \right. \\&\Biggl . \biggl . +\alpha ^3 {EJ}_0^2 l x \left( \alpha ^2+\lambda ^2\right) \left( 2 l^2-3 lx+x^2\right) \cosh (\alpha l)\biggr ) \Biggr ) \end{aligned} \end{aligned}$$

(63)

Note that $w_l(x)$ was determined according to the procedure explained in [8].

Fig. 19

Example 3: slightly curved clamped-soft hinged beam subjected to a half-sine load

It is therefore reasonable to assume that the shape of the deflection w(x) of the nonlinear beam is closely affine to the deflection $w_l(x)$ of the linear beam. w(x) is consequently approximated with the following single-term Ritz approach,

$$\begin{aligned} w^*(x)=\gamma w_l(x) \end{aligned}$$

(64)

The geometry and dimensions, as well as the three layers and the material parameters, are chosen the same as in the two previous examples. The load amplitude is $q_0=1.0 \cdot 10^4$ N/m. The amplitude of the initial deflection is negative, i.e. ${\hat{w}}_a=-0.015$ m. The initial deflection is therefore also in this example oriented upwards against the positive z-coordinate and the load direction.

The solutions $u_2^{(0)}(x,\gamma )$, $\varDelta u_{12}(x,\gamma )$ and $\varDelta u_{23}(x,\gamma )$ of this boundary value problem with Eqs. (30), (37) representing the boundary conditions at the left support and Eqs. (30), (32), (33) representing the boundary condition at the right support, is found as described in the previous example. The resulting cubic equation for the weighting coefficient $\gamma$ has one root because the initial deflection is so small that no snap-through can occur. Since the expressions obtained in this way are very lengthy, they cannot be presented here.

Figure 20 shows the normalized deflection $w/w_{ref}$ of the considered slightly curved beam along the beam axis x/l as a result of the presented beam theory (black solid line) as well as from the comparative FE plane stress analysis (circular markers). As in the previous examples, the difference between these two results is negligible. This outcome confirms both the theory presented and the selected shape function according to Eq. (64). Note that also in this example the reference solution $w_{ref}$ is the maximum deflection of the corresponding linear straight clamped-soft hinged beam, $w_{ref}=w_{lin}(x=0.545l)=0.00661$ m. To illustrate the influence of the initial deflection and the geometric nonlinearity, the normalized deflection of the straight nonlinear beam and the straight linear beam (with one horizontally movable support) are also shown. It can be seen that in this example the maximum deflection of the curved beam is 25% smaller than the linear response and 21% smaller than that of the geometrically nonlinear beam with straight axis.

Fig. 20

Normalized deflection of a nonlinear slightly curved, a nonlinear straight and a linear straight clamped-soft hinged beam with interlayer slip subjected to half-sine load

The interlayer slips $\varDelta u_{12}$ and $\varDelta u_{23}$ as well as the longitudinal displacement of the central axis $u_2^{(0)}$ of the slightly curved beam agree very well with those of the FE analysis, as observed in Figs. 21 and 22. The comparison of these quantities with the results of the geometrically nonlinear and the linear beam demonstrates once more the great influence of the initial curvature on the response behavior. For example, the sign of $u_2^{(0)}$ of the curved and the straight nonlinear beam is exactly reversed along the entire beam axis x/l.

Fig. 21

Normalized interlayer slips of a nonlinear slightly curved, a nonlinear straight and a linear straight clamped-soft hinged beam with interlayer slip subjected to half-sine load

Fig. 22

Normalized longitudinal displacement of the central axis of a nonlinear slightly curved, a nonlinear straight and a linear straight clamped-soft hinged beam with interlayer slip subjected to half-sine load

6 Summary and conclusions

This paper addresses the prediction of the static response of slightly curved symmetrically layered members with flexible bond. Since the beams considered are immovably supported, moderately large deflections lead to geometrically nonlinear behavior. Both the geometrically nonlinear effect and the interlayer slips due to the flexible bonded layers are captured by a beam theory presented in this contribution. This theory is based on a layerwise application of the Euler–Bernoulli theory, a linear material law for the interlaminar stresses, and a nonlinear axial strain–displacement relation. In the resulting boundary value problem, the deflection, the longitudinal displacement of the central axis and the two interlayer slips are coupled. The solution of this boundary value problem was found by a Ritz-Galerkin method.

Comparative calculations have shown that for slender beams the presented theory approximates excellently a finite element (FE) solution under the assumption of a plane stress state. The solution based on this theory is very efficient and less time-consuming than an FE analysis and is therefore suitable for finding reference solutions on the one hand and for quickly estimating the response on the other. The application is, however, limited to beams with simple geometry and boundary conditions. In three application examples, it was shown how important it is to take into account even very small initial deflection in the analysis of moderately large deflections of immovably supported beams with interlayer slip.