A higher-order plate theory for the analysis of vibrations of thick orthotropic laminates

Abstract

In this contribution, flexural vibrations of linear elastic laminates composed of thick orthotropic layers, such as cross-laminated timber, are addressed. For efficient computation, an equivalent single-layer plate theory with eight kinematic degrees of freedom is derived, both in terms of equations of motion at the continuum level and in terms of a finite element representation. The validity of the plate theory is demonstrated by comparing natural frequencies of a simply supported plate over a wide frequency range for which an analytical solution is available. Furthermore, the influence of individual material properties on the accuracy of the plate theory is investigated, demonstrating its broad applicability. The influence of material orientation on the accuracy of the plate theory is examined by comparative finite element simulations. It is shown that, for cross-ply laminates, the plate theory is valid for elements oriented at any angle to the material principal axes.

1 Introduction

Many applications in civil, mechanical and aerospace engineering are based on laminated plates, i.e., planar structures composed of several stacked layers. By combining different materials and/or material orientations, a better performance in terms of mass or stiffness can be achieved compared to homogeneous plates. For the mechanical modeling of plates, layer-wise theories [1] or equivalent single-layer theories can be used. Due to their flexibility and efficient numerical implementation possibility, in this paper the latter type of theories are considered. When the layers of the composite plate are thin, classical laminated plate theory can be used to analyze the laminate based on a two-dimensional representation [2]. For thick laminates where shear deformation must be considered, first-order shear deformation theory (FSDT) must be employed, although the solution for thick plates has been traced back to thin-plate solutions in literature [3, 4]. Since the assumption of constant shear stresses in the thickness direction underlying the FSDT contradicts the vanishing of these stresses at the top and bottom plate surfaces, shear correction factors must be used to compensate for this error [5]. However, the FSDT still only captures the layer-wise shear stresses in a mean sense. Consequently, a number of higher-order shear deformation theories (HSDT) have been developed, e.g., [6, 7], where the kinematic hypothesis for the plate deformation is based on higher-order polynomials. In some composites, the individual layers exhibit significantly different shear stiffnesses, which leads to stepped deformation patterns across the thickness under transverse loading. Much attention has been paid to this effect in the development of the so-called zig-zag theories. An accurate representation of the displacement field across the plate is a requirement for failure analysis, as performed for laminated beams in [8]. The review [9] distinguishes three zig-zag theory approaches from literature: (i) The Ambartsumian Multilayered Theory [10] as extension of the classical Reissner-Mindlin theory that applies to homogeneous plates, (ii) theories based on the Reissner mixed variational theorem [11], and (iii) the Lekhnitskii Multilayered Theory [12]. All theories are based on axiomatic assumptions regarding the transverse shear stress field and/or the displacement field. In an effort to unify the plate theories in one framework, the Carrera Unified Formulation [13] was derived.

In the present paper, an approach based on the work of Lekhnitskii [12], originally developed for composite beams, is followed. Lekhnitskii’s theory was extended for the analysis of plates in [14] and further refined in [15], specifically for cross-laminated timber (CLT). In this type of composite, timber panels are stacked perpendicular to each other, corresponding to a cross-ply laminate. In its linear elastic range, timber can be characterized as orthotropic material with principal axes parallel to the annual rings (longitudinal axis L) and radial (R) and tangential (T) to the annual rings, respectively, in a cylindrical coordinate system [16]. Since the material properties in the R- and T-direction are of similar order, no distinction is made between the two in practice. Then, a Cartesian coordinate system can be used to describe the constitutive behavior, with timber represented as a transversely isotropic material, except that shear moduli and Young’s moduli are decoupled. More specifically, the shear moduli $G_{LR}\approx G_{LT}$ and $G_{RT}$ differ by a factor of approximately 15, and the ratio of Young’s modulus to shear modulus $E_L/G_{LR}\approx 17$. Thus, CLT can be characterized as a highly shear-flexible laminate in which the aforementioned zig-zag deformation pattern prevails due to the abruptly changing shear moduli in the layers. The plate theory developed in [15] was extended in [17] for dynamic loading, focusing on the sound-radiating properties of CLT panels. Generally, due to the typically high stiffness-to-mass ratio of composites, vibrations and as a result, sound radiation, can become more relevant than for isotropic plates. In [17], it was shown for a simply supported plate that the proposed plate theory can more accurately capture natural frequencies in a frequency range of 20 to 550 Hz than with FSDT. However, with increasing frequency, i.e., with increasing cross-sectional curvature of the mode shapes, the discrepancies to the 3D elasticity solutions increased. Therefore, in [18], on the one hand, the plate theory was extended to capture the out-of-plane deformation of the plate, which has been neglected until then. On the other hand, insignificant terms were omitted and the kinematic assumptions were reformulated in view of a straight-forward finite element (FE) implementation, avoiding derivatives of kinematic degrees of freedom in the displacement field. The strong and weak formulations, the latter in terms of finite element matrices and load vector, were derived, and both the accuracy and efficiency of the computations were demonstrated for a realistic CLT floor construction. One limitation of the plate theory presented in [18] is that it is only applies to symmetric lay-ups. Furthermore, it was assumed that the material principal axes of the layers correspond to global coordinate axes. Although this is no limitation as long as rectangular CLT panels discretized by regular FE meshes are considered, the plate theory is extended in the present paper for more general setups, i.e., angle-ply composites with non-symmetric lay-ups. The paper is organized as follows: in Sect. 2, the strong and weak formulation of the plate theory is derived. This is followed by numerical simulations in Sect. 3 in which, first, the validity of the plate theory is proved and, second, the range of applicability in terms of material properties and layer setups is investigated. The paper ends with conclusions in Sect. 4.

2 Proposed plate theory

2.1 Kinematics and constitutive behavior

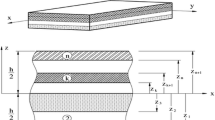
Laminated plates consisting of an arbitrary number n of plies whose mid-planes coincide with a global x-y-plane and normal direction z are considered. For an orthotropic ply k of the laminate with principal axes 1, 2,  and 3 oriented at an arbitrary angle with respect to the global xyz coordinate system (see Fig. 1), the stresses $\varvec{\sigma }^k$ and strains $\varvec{\varepsilon }^k$ in the ply are connected via the constitutive equations

$$\begin{aligned} \begin{Bmatrix} \sigma _{xx}\\ \sigma _{yy} \\ \sigma _{zz} \\ \sigma _{yz} \\ \sigma _{xz} \\ \sigma _{xy} \end{Bmatrix}^k = \begin{bmatrix} Q_{11}^k &{}\quad Q_{12}^k &{}\quad Q_{13}^k &{}\quad 0 &{}\quad 0 &{}\quad Q_{16}^k\\ Q_{12}^k &{}\quad Q_{22}^k &{} \quad Q_{23}^k &{} \quad 0 &{}\quad 0 &{} \quad Q_{26}^k \\ Q_{13}^k &{}\quad Q_{23}^k &{}\quad Q_{33}^k &{}\quad 0 &{}\quad 0 &{}\quad Q_{36}^k \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad Q_{44}^k &{}\quad Q_{45}^k &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad Q_{45}^k &{}\quad Q_{55}^k &{}\quad 0 \\ Q_{16}^k &{}\quad Q_{26}^k &{}\quad Q_{36}^k &{}\quad 0 &{}\quad 0 &{}\quad Q_{66}^k \end{bmatrix} \begin{Bmatrix} \varepsilon _{xx}\\ \varepsilon _{yy} \\ \varepsilon _{zz} \\ 2\varepsilon _{yz} \\ 2\varepsilon _{xz} \\ 2\varepsilon _{xy} \end{Bmatrix}^k, \end{aligned}$$

(1)

where the stiffness coefficients $Q_{ij}^k$ are related to the material properties $E_1$, $E_2$, $E_3$ (Young’s moduli), $G_{12}$, $G_{13}$, $G_{23}$ (shear moduli) and $\nu _{12}$, $\nu _{13}$, $\nu _{23}$ (Poisson ratios) [2]. When the principal material axes are aligned with the global coordinate system, $Q_{16}^k$, $Q_{26}^k$, $Q_{36}^k$ and $Q_{45}^k$ are zero. Following the work presented in [18], the following functions are considered for the displacements in the x-, y- an z-direction in layer k, denoted $u^k,v^k$ and $w^k$:

$$\begin{aligned} u^k\left( x,y,z,t \right)&= u_0\left( x,y,t \right) +z\varphi _x\left( x,y,t \right) + A^k\left( z\right) \psi _x\left( x,y,t \right) , \nonumber \\ v^k\left( x,y,z,t \right)&= v_0\left( x,y,t \right) +z\varphi _y\left( x,y,t \right) + E^k\left( z\right) \psi _y\left( x,y,t \right) , \nonumber \\ w^k\left( x,y,z,t \right)&= w_0\left( x,y,t \right) - \Delta w\left( x,y,t \right) f(z). \end{aligned}$$

(2)

In contrast to [18], in-plane displacements $u_0$ and $v_0$ are taken into account, so that the plate theory is also valid for non-symmetric lay-ups. The further degrees of freedom of the plate theory are the out-of-plane displacement $w_0$ and the correction term $\Delta w$ to capture thickness changes via the function f(z) and the rotations $\varphi _x$, $\varphi _y$, $\psi _x$ and $\psi _y$. The functions $A_k(z)$ and $E_k(z)$ capture the zig-zag deformation pattern across the plate thickness and are defined as

$$\begin{aligned} A^k\left( z\right) = \int \frac{a^k\left( z\right) }{Q_{55}^k}dz + C_a^k \qquad E^k\left( z\right) = \int \frac{e^k\left( z\right) }{Q_{44}^k}dz + C_e^k, \end{aligned}$$

(3)

with the functions

$$\begin{aligned} a^k\left( z\right)&= S_{11}^1\left( \sum \limits _{i=1}^{k-1}\left( h_i^2-h_{i-1}^2 \right) Q_{11}^i+\left( z^2-h_{k-1}^2 \right) Q_{11}^k\right) \nonumber \\&\quad - S_{11}^2\left( \sum \limits _{i=1}^{k-1}\left( h_i-h_{i-1} \right) Q_{11}^i+\left( z-h_{k-1} \right) Q_{11}^k\right) ,\nonumber \\ e^k\left( z\right)&= S_{22}^1\left( \sum \limits _{i=1}^{k-1}\left( h_i^2-h_{i-1}^2 \right) Q_{22}^i+\left( z^2-h_{k-1}^2 \right) Q_{22}^k \right) \nonumber \\&\quad -S_{22}^2\left( \sum \limits _{i=1}^{k-1}\left( h_i-h_{i-1} \right) Q_{22}^i+\left( z-h_{k-1} \right) Q_{22}^k \right) \nonumber \\ \text {with}\,\, S_{ii}^1&= \frac{1}{\bar{Q}}\sum \limits _{i=1}^{n}\left( h_i-h_{i-1} \right) Q_{ii}^i, \nonumber \\ S_{ii}^2&= \frac{1}{\bar{Q}}\sum \limits _{i=1}^{n}\left( h_i^2-h_{i-1}^2 \right) Q_{ii}^i,\,ii=\{11,22\}\quad \text {and}\quad \bar{Q}=Q_m h^3. \end{aligned}$$

(4)

The integration constants $C_a^k$ and $C_e^k$ in Eq. (3) can be determined by application of compatibility conditions at the layer interfaces $h_i,\,i=1\ldots n+1$, and the additional constraint that at $z=0$ the corresponding function (e.g., $A^k\left( z\right)$) is zero [15]. The scaling constant $\bar{Q}$ with $Q_m$ as the mean shear stiffness of the cross section and the plate thickness h is introduced in Eq. (4) to render functions $a^k(z)$ and $e^k(z)$ in units of stress and functions $A^k(z)$ and $E^k(z)$ in units of a length. Note that the functions in Eqs. (3) and (4) are polynomials of order 3 and 2, respectively, so integration along the cross section, as introduced below, is a straightforward task.

Fig. 1

Global (xyz) and local (123) coordinate system in a ply

2.2 Equations of motion

The equations of motions in terms of the eight kinematic degrees of freedom are derived by application of d’Alembert’s principle [19] in the form

$$\begin{aligned} \int \limits _S \int \limits _{-h/2}^{h/2}(\sigma _{xx}\delta \varepsilon _{xx}&+\sigma _{yy}\delta \varepsilon _{yy}+\sigma _{zz}\delta \varepsilon _{zz}+2\sigma _{xy}\delta \varepsilon _{xy}+2\sigma _{yz}\delta \varepsilon _{yz}+2\sigma _{xz}\delta \varepsilon _{xz} -p_z\delta w \nonumber \\&+\rho \ddot{u}\delta u +\rho \ddot{v}\delta v +\rho \ddot{w}\delta w)\,dz\,dS = 0, \end{aligned}$$

(5)

where the superscript k for stresses, strains and displacements has been omitted for the sake of readability. $\rho$ denotes the mass density, S the mid-plane area and $p_z\left( x,y,t \right)$ the transverse loading of the plate. For small strains, $\varepsilon _{ij}=1/2\left( \partial u_i/\partial x_j + \partial u_j/\partial x_i\right)$ with $u_i=\left\{ u,v,w\right\}$ and $x_i=\left\{ x,y,z\right\}$. Substitution of the displacement field Eq. (2) yields the strains and, taking into account Eq. (1), the stresses as a function of the kinematic degrees of freedom and, similarly virtual strains in terms of their variations. Partial integration eliminates the derivations of the variations. Performing integration over the cross section h and setting the variations to zero and one mutually, we obtain after some manipulations a system of eight coupled partial differential equations of the form

$$\begin{aligned} {\textbf {M}} \ddot{{\textbf {q}}} + {\textbf {K}} {\textbf {q}} + {\textbf {K}}_x {\textbf {q}}_{,x} + {\textbf {K}}_y {\textbf {q}}_{,y} + {\textbf {K}}_{xx} {\textbf {q}}_{,xx} + {\textbf {K}}_{xy} {\textbf {q}}_{,xy} + {\textbf {K}}_{yy} {\textbf {q}}_{,yy} = {\textbf {f}}, \end{aligned}$$

(6)

where ${\textbf {q}}(x,y,t) = \left\{ u_0~v_0~w_0~\Delta w~\varphi _x~\varphi _y~\psi _x~\psi _y \right\} ^T$ is the vector of degrees of freedom, and derivations of (.) with respect to x, y and t are denoted by $(.)_{,x}$, $(.)_{,y}$ and $\dot{(.)}$, respectively. The matrices in Eqs. (6) read

$$\begin{aligned}&{\textbf {M}}= \begin{bmatrix} A_{\rho } &{}\quad . &{}\quad . &{}\quad . &{}\quad B_{\rho } &{}\quad . &{}\quad G_{\rho } &{}\quad .\\ . &{}\quad A_{\rho } &{}\quad . &{}\quad . &{}\quad . &{}\quad B_{\rho } &{}\quad . &{}\quad H_{\rho }\\ . &{}\quad . &{}\quad A_{\rho } &{}\quad -E_{\rho } &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad -E_{\rho } &{}\quad F_{\rho } &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ B_{\rho } &{}\quad . &{}\quad . &{}\quad . &{}\quad D_{\rho } &{}\quad . &{}\quad I_{\rho } &{}\quad .\\ . &{}\quad B_{\rho } &{}\quad . &{}\quad . &{}\quad . &{}\quad D_{\rho } &{}\quad . &{}\quad J_{\rho }\\ G_{\rho } &{}\quad . &{}\quad . &{}\quad . &{}\quad I_{\rho } &{}\quad . &{}\quad L_{\rho } &{}\quad .\\ . &{}\quad H_{\rho } &{}\quad . &{}\quad . &{}\quad . &{}\quad J_{\rho } &{}\quad . &{}\quad M_{\rho } \end{bmatrix}, \end{aligned}$$

(7)

$$\begin{aligned}&{\textbf {K}} = \begin{bmatrix} . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad . &{}\quad V_{33} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad . &{}\quad . &{}\quad A_{55} &{}\quad A_{45} &{}\quad a &{}\quad e_{45}\\ . &{}\quad . &{}\quad . &{}\quad . &{}\quad A_{45} &{}\quad A_{44} &{}\quad a_{45} &{}\quad e\\ . &{}\quad . &{}\quad . &{}\quad . &{}\quad a &{}\quad a_{45} &{}\quad aa_{55} &{}\quad ae_{45}\\ . &{}\quad . &{}\quad . &{}\quad . &{}\quad e_{45} &{}\quad e &{}\quad ae_{45} &{}\quad ee_{44} \end{bmatrix}, \end{aligned}$$

(8)

$$\begin{aligned}&{\textbf {K}}_{x}= \begin{bmatrix} . &{}\quad . &{}\quad . &{}\quad R_{13} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad . &{}\quad R_{36} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad . &{}\quad . &{}\quad -A_{55} &{}\quad -A_{45} &{}\quad -a &{}\quad -e_{45}\\ -R_{13} &{}\quad -R_{36} &{}\quad . &{}\quad . &{}\quad E_{55}-S_{13} &{}\quad E_{45}-S_{36} &{}\quad af-T_{13} &{}\quad ef_{45}-U_{36}\\ . &{}\quad . &{}\quad A_{55} &{}\quad S_{13}-E_{55} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad A_{45} &{}\quad S_{36}-E_{45} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad a &{}\quad T_{13}-af &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad e_{45} &{}\quad U_{36}-ef_{45} &{}\quad . &{}\quad . &{}\quad . &{}\quad . \end{bmatrix}, \end{aligned}$$

(9)

$$\begin{aligned}&{\textbf {K}}_{y} = \begin{bmatrix} . &{}\quad . &{}\quad . &{}\quad R_{36} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad . &{}\quad R_{23} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad . &{}\quad . &{}\quad -A_{45} &{}\quad -A_{44} &{}\quad -a_{45} &{}\quad -e\\ -R_{36} &{}\quad -R_{23} &{}\quad . &{}\quad . &{}\quad E_{45}-S_{36} &{}\quad E_{44}-S_{23} &{}\quad af_{45}-T_{36} &{}\quad ef-U_{23}\\ . &{}\quad . &{}\quad A_{45} &{}\quad S_{36}-E_{45} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad A_{44} &{}\quad S_{23}-E_{44} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad a_{45} &{}\quad T_{36}-af_{45} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad e &{}\quad U_{23}-ef &{}\quad . &{}\quad . &{}\quad . &{}\quad . \end{bmatrix}, \end{aligned}$$

(10)

$$\begin{aligned}&{\textbf {K}}_{xx} = - \begin{bmatrix} A_{11} &{}\quad A_{16} &{}\quad . &{}\quad . &{}\quad B_{11} &{}\quad B_{16} &{}\quad G_{11} &{}\quad H_{16}\\ A_{16} &{}\quad A_{66} &{}\quad . &{}\quad . &{}\quad B_{16} &{}\quad B_{66} &{}\quad G_{16} &{}\quad H_{66}\\ . &{}\quad . &{}\quad A_{55} &{}\quad -E_{55} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad -E_{55} &{}\quad F_{55} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ B_{11} &{}\quad B_{16} &{}\quad . &{}\quad . &{}\quad D_{11} &{}\quad D_{16} &{}\quad I_{11} &{}\quad J_{16}\\ B_{16} &{}\quad B_{66} &{}\quad . &{}\quad . &{}\quad D_{16} &{}\quad D_{66} &{}\quad I_{16} &{}\quad J_{66}\\ G_{11} &{}\quad G_{16} &{}\quad . &{}\quad . &{}\quad I_{11} &{}\quad I_{16} &{}\quad L_{11} &{}\quad N_{16}\\ H_{16} &{}\quad H_{66} &{}\quad . &{}\quad . &{}\quad J_{16} &{}\quad J_{66} &{}\quad N_{16} &{}\quad M_{66} \end{bmatrix}, \end{aligned}$$

(11)

$$\begin{aligned}&{\textbf {K}}_{yy} = - \begin{bmatrix} A_{66} &{}\quad A_{26} &{}\quad . &{}\quad . &{}\quad B_{66} &{}\quad B_{26} &{}\quad G_{66} &{}\quad H_{26}\\ A_{26} &{}\quad A_{22} &{}\quad . &{}\quad . &{}\quad B_{26} &{}\quad B_{22} &{}\quad G_{26} &{}\quad H_{22}\\ . &{}\quad . &{}\quad A_{44} &{}\quad -E_{44} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad -E_{44} &{}\quad F_{44} &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ B_{66} &{}\quad B_{26} &{}\quad . &{}\quad . &{}\quad D_{66} &{}\quad D_{26} &{}\quad I_{66} &{}\quad J_{26}\\ B_{26} &{}\quad B_{22} &{}\quad . &{}\quad . &{}\quad D_{26} &{}\quad D_{22} &{}\quad I_{26} &{}\quad J_{22}\\ G_{66} &{}\quad G_{26} &{}\quad . &{}\quad . &{}\quad I_{66} &{}\quad I_{26} &{}\quad L_{66} &{}\quad N_{26}\\ H_{26} &{}\quad H_{22} &{}\quad . &{}\quad . &{}\quad J_{26} &{}\quad J_{22} &{}\quad N_{26} &{}\quad M_{22} \end{bmatrix}, \end{aligned}$$

(12)

$$\begin{aligned}&{\textbf {K}}_{xy} = - \left[ \begin{array}{ccccc} 2A_{16} &{}\quad A_{12}+A_{66} &{}\quad . &{}\quad . &{}\quad 2B_{16} \\ A_{12}+A_{66} &{}\quad 2A_{26} &{}\quad . &{}\quad . &{}\quad B_{12}+B_{66}\\ . &{}\quad . &{}\quad 2A_{45} &{}\quad -2E_{45} &{}\quad . \\ . &{}\quad . &{}\quad -2E_{45} &{}\quad 2F_{45} &{}\quad . \\ 2B_{16} &{}\quad B_{12}+B_{66} &{}\quad . &{}\quad . &{}\quad 2D_{12}\\ B_{12}+B_{66} &{}\quad 2B_{26} &{}\quad . &{}\quad . &{}\quad D_{12}+D_{66} \\ 2G_{16} &{}\quad G_{12}+G_{66} &{}\quad . &{}\quad . &{}\quad 2I_{16} \\ H_{12}+H_{66} &{}\quad 2H_{26} &{}\quad . &{}\quad . &{}\quad J_{12}+J_{66} \end{array} \right. \quad \left. \begin{array}{ccc} B_{12}+B_{66} &{}\quad 2G_{16} &{}\quad H_{12}+H_{66}\\ 2B_{26} &{} G_{12}+G_{66} &{} 2H_{26}\\ . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad .\\ D_{12}+D_{66} &{}\quad 2I_{16} &{}\quad J_{12}-J_{66}\\ 2D_{26} &{}\quad I_{12}+I_{66} &{}\quad 2J_{26}\\ I_{12}+I_{66} &{}\quad 2L_{16} &{}\quad N_{12}+N_{66}\\ 2J_{26} &{}\quad N_{12}+N_{66} &{}\quad 2M_{26} \end{array} \right] ,\nonumber \\ \end{aligned}$$

(13)

while the load vector is

$$\begin{aligned} {\textbf {f}} = \left\{ 0~0~p(x,y,t)~\int \limits _{-h/2}^{h/2}f(z) dz\,p(x,y,t)~0~0~0~0\right\} ^T. \end{aligned}$$

(14)

For better illustration, zeros have been replaced by a dot (.) in the above matrices. The plate stiffness parameters apparent in Eqs. (7)–(13) are defined as

$$\begin{aligned} \left\{ A_{ij},B_{ij},D_{ij},E_{ij} \right\}&= \int \limits _{-h/2}^{h/2}\left\{ 1,z,z^2,f(z)\right\} Q_{ij}(z)\,dz, \quad i,j=1\ldots 6,\nonumber \\ \left\{ F_{ij},G_{ij},H_{ij} \right\}&= \int \limits _{-h/2}^{h/2}\left\{ f(z)^2,A^k(z),E^k(z)\right\} Q_{ij}(z)\,dz,\nonumber \\ \left\{ I_{ij},J_{ij},L_{ij} \right\}&= \int \limits _{-h/2}^{h/2}\left\{ A^k(z)\,z,E^k(z)\,A^k(z)^2,\right\} Q_{ij}(z)\,dz,\nonumber \\ \left\{ M_{ij},N_{ij},R_{ij},S_{ij} \right\}&= \int \limits _{-h/2}^{h/2}\left\{ E^k(z)^2,A^k(z)\,E^k(z),f'(z), f'(z)\,z\right\} Q_{ij}(z)\,dz,\nonumber \\ \left\{ T_{ij},U_{ij},V_{ij} \right\}&= \int \limits _{-h/2}^{h/2}\left\{ A^k(z)\,f'(z),E^k(z)\,f'(z) ,f'(z)^2 \right\} Q_{ij}(z)\,dz,\nonumber \\ \left\{ a,e,af,ef\right\}&= \int \limits _{-h/2}^{h/2}\left\{ a^k(z), e^k(z), a^k(z)\,f(z), e^k(z)\,f(z)\right\} \,dz, \nonumber \\ \left\{ aa_{55},ee_{44}\right\}&= \int \limits _{-h/2}^{h/2}\left\{ \dfrac{a^k(z)^2}{Q_{55}(z)}, \dfrac{e^k(z)^2}{Q_{44}(z)}\right\} \,dz, \nonumber \\ \left\{ a_{45},e_{45},ae_{45} \right\}&= \int \limits _{-h/2}^{h/2}\left\{ a^k(z)\dfrac{Q_{45}(z)}{Q_{55}(z)},e^k(z)\dfrac{Q_{45}(z)}{Q_{44}(z)},a^k(z)\,e^k(z)\dfrac{Q_{45}(z)}{Q_{44}(z)\,Q_{55}(z)} \right\} \,dz,\nonumber \\ \left\{ af_{45},ef_{45} \right\}&= \int \limits _{-h/2}^{h/2}\left\{ a^k(z)\,f(z) \dfrac{Q_{45}(z)}{Q_{55}(z)}, e^k(z)\,f(z) \dfrac{Q_{45}(z)}{Q_{44}(z)} \right\} \,dz, \end{aligned}$$

(15)

and the corresponding plate mass parameters read

$$\begin{aligned} \left\{ A_{\rho },B_{\rho },D_{\rho },E_{\rho },F_{\rho },G_{\rho },H_{\rho }\right\}&= \int \limits _{-h/2}^{h/2}\left\{ 1,z,z^2,f(z),f(z)^2,A^k(z),E^k(z)\right\} \rho (z)\,dz,\nonumber \\ \left\{ I_{\rho },J_{\rho },L_{\rho },M_{\rho },N_{\rho } \right\}&= \int \limits _{-h/2}^{h/2}\left\{ A^k(z)\,z,E^k(z)\,A^k(z)^2,E^k(z)^2,A^k(z)\,E^k(z)\right\} \rho (z)\,dz. \end{aligned}$$

(16)

Since, as mentioned earlier, all functions in the thickness direction z are layer-wise polynomials, the plate stiffness and mass parameters can be computed efficiently, for instance, using the polyint and polyval functions in MATLAB.

2.3 Dispersion relation

Assuming planar bending waves with wave vector ${\textbf {k}}(x,y,z) = \left\{ k_x~k_y~0\right\} ^T$ and angular frequency $\omega$ in the form ${\textbf {q}}(x,y,t) = {\textbf {A}} \exp \left( -\text {j}\left( \omega t + k_x x + k_y y\right) \right)$ with $\text {j}=\sqrt{-1}$, substituting in Eqs. (6), after some manipulations, yields the eigenvalue problem $\left( {\textbf {K}}^d-\omega ^2 {\textbf {M}}\right) {\textbf {A}}={\textbf {0}}$, where ${\textbf {M}}$ is given in Eq. (7) and elements of the complex conjugate stiffness matrix in this dispersion relation ${\textbf {K}}^d$ read

$$\begin{aligned} K^d_{11}&= A_{11} k_x^2 + 2A_{16}k_x\,k_y + A_{66}k_y^2, \\ K^d_{12}&= A_{16} k_x^2 + \left( A_{12}+A_{66}\right) k_x\,k_y + A_{26}k_y^2,\\ K^d_{14}&= -\text {j}\left( R_{13}k_x + R_{36}k_y\right) , \nonumber \\ K^d_{15}&= B_{11} k_x^2 + 2B_{16}k_x\,k_y + B_{66}k_y^2,\\ K^d_{16}&= B_{16} k_x^2 + \left( B_{12}+B_{66}\right) k_x\,k_y + B_{26}k_y^2, \\ K^d_{17}&= G_{11} k_x^2 + 2G_{16}k_x\,k_y + G_{66}k_y^2,\\ K^d_{18}&= H_{16} k_x^2 + \left( H_{12}+H_{66}\right) k_x\,k_y + H_{26}k_y^2, \\ K^d_{22}&= A_{66} k_x^2 + 2A_{26}k_x\,k_y + A_{22}k_y^2,\\ K^d_{24}&= -\text {j}\left( R_{36}k_x + R_{23}k_y\right) , \\ K^d_{25}&= B_{16} k_x^2 + \left( B_{12}+B_{66}\right) k_x\,k_y + B_{26}k_y^2,\\ K^d_{26}&= B_{66} k_x^2 + 2B_{26}k_x\,k_y + B_{22}k_y^2, \\ K^d_{27}&= G_{16} k_x^2 + \left( G_{12}+G_{66}\right) k_x\,k_y + G_{26}k_y^2,\\ K^d_{28}&= H_{66} k_x^2 + 2H_{26}k_x\,k_y + H_{22}k_y^2, \\ K^d_{33}&= A_{55} k_x^2 + 2A_{45}k_x\,k_y + A_{44}k_y^2,\\ K^d_{34}&= -\left( E_{55} k_x^2 + 2E_{45}k_x\,k_y + E_{44}k_y^2\right) , \\ K^d_{35}&= \text {j}\left( A_{55}k_x + A_{45}k_y\right) , \\ K^d_{36}&= \text {j}\left( A_{45}k_x + A_{44}k_y\right) , \\ K^d_{37}&= \text {j}\left( a k_x + a_{45} k_y\right) , \\ K^d_{38}&= \text {j}\left( e_{45} k_x + e k_y\right) , \\ K^d_{44}&= F_{55} k_x^2 + 2F_{45}k_x\,k_y + F_{44}k_y^2 + V_{33},\\ K^d_{45}&= \text {j}\left( \left( S_{13}-E_{55}\right) k_x + \left( S_{36}-E_{45}\right) k_y\right) ,\\ K^d_{46}&= \text {j}\left( \left( S_{36}-E_{45}\right) k_x + \left( S_{23}-E_{44}\right) k_y\right) , \\ K^d_{47}&= \text {j}\left( \left( T_{13}-af\right) k_x + \left( T_{36}-af_{45}\right) k_y\right) , \\ K^d_{48}&= \text {j}\left( \left( U_{36}-ef_{45}\right) k_x + \left( U_{23}-ef\right) k_y\right) , \\ K^d_{55}&= D_{11} k_x^2 + 2D_{16}k_x\,k_y + D_{66}k_y^2 + A_{55}, \\ K^d_{56}&= D_{16} k_x^2 + \left( D_{12}+D_{66}\right) k_x\,k_y + D_{26}k_y^2 + A_{45}, \\ K^d_{57}&= I_{11} k_x^2 + 2I_{16}k_x\,k_y + I_{66}k_y^2 + a, \\ K^d_{58}&= J_{16} k_x^2 + \left( J_{12}+J_{66}\right) k_x\,k_y + J_{26}k_y^2 + e_{45}, \\ K^d_{66}&= D_{66} k_x^2 + 2D_{26}k_x\,k_y + D_{22}k_y^2 + A_{44}, \\ K^d_{67}&= I_{16} k_x^2 + \left( I_{12}+I_{66}\right) k_x\,k_y + I_{26}k_y^2 + a_{45}, \\ K^d_{68}&= J_{66} k_x^2 + 2J_{26}k_x\,k_y + J_{22}k_y^2 + e, \\ K^d_{77}&= L_{11} k_x^2 + 2L_{16}k_x\,k_y + L_{66}k_y^2 + aa_{55}, \\ K^d_{78}&= N_{16} k_x^2 + \left( N_{12}+N_{66}\right) k_x\,k_y + N_{26}k_y^2 + ae_{45}, \\ K^d_{88}&= M_{66} k_x^2 + 2M_{26}k_x\,k_y + M_{22}k_y^2 + ee_{44}. \end{aligned}$$

The dispersion relation can be used to compute the natural frequencies of bounded plates if the wave number components $k_x$ and $k_y$ for the corresponding standing waves are known. For instance, mode shapes of a rectangular, simply supported plate with dimensions $l_x$ and $l_y$ in x- and y- direction, respectively, are characterized by $k_x=m\pi /l_x$ and $k_y=n\pi /l_y$ with integers $m,n=1,2,\ldots$. Solving $\Vert {\textbf {K}}^d-\omega ^2 {\textbf {M}}\Vert =\mathbf {0}$ for $\omega$ and considering the lowest of the eight eigenvalues, we obtain the natural frequency. Solving for the corresponding complex eigenvector ${\textbf {A}}$, we obtain the amplitudes for the kinematic degrees of freedom ${\textbf {q}}$ for this mode.

2.4 Weak formulation of the governing equations

In the finite element implementation of the plate theory, the strains in the k-th layer are expressed as $\varvec{\varepsilon }^k(x,y,z,t)=\mathbf {Z}^k(z)\mathbf {L}(x,y)\mathbf {q}(x,y,z,t)$ with the matrices

$$\begin{aligned} \mathbf {Z}^k(z)&= \left[ \begin{array}{cccccccccc} 1 &{}\quad z &{}\quad A^k(z) &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . \\ . &{} . &{} . &{} 1 &{} z &{} E^k(z) &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . &{} -f'(z) &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} 1 &{} -f(z) &{} \dfrac{e^k(z)}{Q_{44}(z)} \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . \end{array} \right. \nonumber \\&\quad \left. \begin{array}{ccccccc} . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . &{} .\\ 1 &{} -f(z) &{} \dfrac{a^k(z)}{Q_{55}(z)} &{} . &{} . &{} . &{} .\\ . &{}\quad . &{}\quad . &{}\quad 1 &{}\quad z &{}\quad A^k(z) &{}\quad E^k(z) \end{array} \right] \end{aligned}$$

(17)

and

$$\begin{aligned} {\textbf {L}}(x,y)= \begin{bmatrix} \partial /\partial x &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{} . &{} . &{} . &{} \partial /\partial x &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} \partial /\partial x &{} .\\ . &{} \partial /\partial y &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} \partial /\partial y &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} \partial /\partial y \\ . &{} . &{} . &{} 1 &{} . &{} . &{} . &{} .\\ . &{} . &{} \partial /\partial y &{} . &{} . &{} 1 &{} . &{} .\\ . &{} . &{} . &{} \partial /\partial y &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} 1\\ . &{} . &{} \partial /\partial x &{} . &{} 1 &{} . &{} . &{} .\\ . &{} . &{} . &{} \partial /\partial x &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} 1 &{} .\\ \partial /\partial y &{}\quad \partial /\partial x &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad .\\ . &{} . &{} . &{} . &{} \partial /\partial y &{} \partial /\partial x &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} \partial /\partial y &{} .\\ . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad . &{}\quad \partial /\partial x \end{bmatrix} \end{aligned}$$

(18)

With the constitutive equations $\varvec{\sigma } = {\textbf {Q}} \varvec{\varepsilon }$ according to Eqs. (1), the work of the internal forces in d’Alembert’s principle can be written as

$$\begin{aligned} \int \limits _S \int \limits _{-h/2}^{h/2} \delta \varvec{\varepsilon }^T \varvec{\sigma } dz\,dS = \int \limits _S \delta {\textbf {q}}^T {\textbf {L}}(x,y)^T \underbrace{\int \limits _{-h/2}^{h/2} {\textbf {Z}}(z)^T {\textbf {Q}} {\textbf {Z}}(z) dz}_{{\textbf {K}}^{fe}}~{\textbf {L}}(x,y)\,{\textbf {q}}\,dS, \end{aligned}$$

(19)

where

$$\begin{aligned} {\textbf {K}}^{fe} = \begin{bmatrix} {\textbf {K}}_{11}^{fe} &{} {\textbf {0}} &{} {\textbf {K}}_{13}^{fe} \\ {\textbf {0}} &{} {\textbf {K}}_{22}^{fe} &{} {\textbf {0}} \\ \left. {\textbf {K}}_{13}^{fe}\right. ^T &{} {\textbf {0}} &{} {\textbf {K}}_{33}^{fe} \end{bmatrix} \end{aligned}$$

(20)

with the submatrices

$$\begin{aligned} {\textbf {K}}_{11}^{fe}= & {} \begin{bmatrix} A_{11} &{}\quad B_{11} &{}\quad G_{11} &{}\quad A_{12} &{}\quad B_{12} &{}\quad H_{12} &{}\quad -R_{13} \\ &{} D_{11} &{} I_{11} &{} B_{12} &{} D_{12} &{} J_{12} &{} -S_{13} \\ &{} &{} G_{11} &{} A_{12} &{} B_{12} &{} H_{12} &{} -R_{13} \\ &{} &{} &{} A_{22} &{} B_{22} &{} H_{22} &{} -R_{23} \\ &{} &{} &{} &{} D_{22} &{} J_{22} &{} -S_{23} \\ &{} &{} &{} &{} &{} M_{22} &{} -U_{23} \\ \text {symm.} &{} &{} &{} &{} &{} &{} V_{33} \end{bmatrix}, \end{aligned}$$

(21)

$$\begin{aligned} {\textbf {K}}_{13}^{fe}= & {} \begin{bmatrix} A_{16} &{}\quad B_{16} &{}\quad G_{16} &{}\quad H_{16} \\ B_{16} &{} D_{16} &{} I_{16} &{} J_{16} \\ G_{16} &{} I_{16} &{} L_{16} &{} N_{16} \\ A_{26} &{} B_{26} &{} G_{26} &{} H_{26} \\ B_{26} &{} D_{26} &{} I_{26} &{} J_{26} \\ H_{26} &{} J_{26} &{} N_{26} &{} M_{26} \\ -R_{36} &{} -S_{36} &{} -T_{36} &{} -U_{36} \end{bmatrix}, \end{aligned}$$

(22)

$$\begin{aligned} {\textbf {K}}_{22}^{fe}= & {} \begin{bmatrix} A_{44} &{}\quad -E_{44} &{}\quad e &{}\quad A_{45} &{}\quad -E_{45} &{}\quad a_{45} \\ &{} F_{44} &{} -ef &{} -E_{45} &{} F_{45} &{} -af_{45} \\ &{} &{} ee_{44} &{} e_{45} &{} -ef_{45} &{} ae_{45} \\ &{} &{} &{} A_{55} &{} -E_{55} &{} a \\ &{} &{} &{} &{} F_{55} &{} -af \\ \text {symm.}&{} &{} &{} &{} &{} aa_{55} \end{bmatrix}, \end{aligned}$$

(23)

$$\begin{aligned} {\textbf {K}}_{33}^{fe}= & {} \begin{bmatrix} A_{66} &{}\quad B_{66} &{}\quad G_{66} &{}\quad H_{66} \\ &{} D_{66} &{} I_{66} &{} J_{66} \\ &{} &{} L_{66} &{} N_{66} \\ \text {symm.} &{} &{} &{} M_{66} \end{bmatrix}. \end{aligned}$$

(24)

The corresponding mass property matrix ${\textbf {M}}^{fe}$ and load vector ${\textbf {f}}^{fe}$ are the same as defined in Eqs. (7) and (14). Degrees of freedom and geometry are interpolated by isoparametric shape functions [20] in the form ${\textbf {q}}={\textbf {N}}\,{\textbf {q}}_e$ where ${\textbf {q}}_e=\left\{ {\textbf {q}}^{(1)}~{\textbf {q}}^{(2)}~\ldots {\textbf {q}}^{(r)} \right\} ^T$ are the nodal degrees of freedom of the r-noded finite elements and ${\textbf {N}}$ is an $8\times 8r$ shape function matrix. Denoting the derivatives of the shape functions ${\textbf {B}} = {\textbf {L}}{} {\textbf {N}}$, inserting these approximations into d’Alembert’s principle yields for integration over one finite element the elemental mass and stiffness matrix and the elemental load vector according to

$$\begin{aligned} {\textbf {M}}_e&= \int \limits _{-1}^{1} \int \limits _{-1}^{1} {\textbf {N}}^T\,{\textbf {M}}_{fe}\,{\textbf {N}}\,\text {det}\,{\textbf {J}}\,d\xi \, d\eta , \nonumber \\ {\textbf {K}}_e&= \int \limits _{-1}^{1} \int \limits _{-1}^{1} {\textbf {B}}^T\,{\textbf {K}}_{fe}\,{\textbf {B}}\,\text {det}\,{\textbf {J}}\,d\xi \, d\eta , \nonumber \\ {\textbf {f}}_e&= \int \limits _{-1}^{1} \int \limits _{-1}^{1} {\textbf {N}}^T\,{\textbf {f}}_{fe}\,\text {det}\,{\textbf {J}}\,d\xi \, d\eta , \end{aligned}$$

(25)

where ${\textbf {J}}$ is the Jacobian relating global and local coordinates [20]. Integration is performed by Gauss quadrature in the local $\xi ,\eta$ coordinate system.

3 Computations

In the applications presented here, the main focus is on cross-laminated timber. A rectangular CLT panel with dimensions $l_x\times l_y=4\times 5\,\text {m}$ and an antisymmetric lay-up with layer thicknesses $2-4-2-4\,\text {cm}$ is considered. Unless otherwise specified, orthotropic material properties $E_1=12.000\,\text {N/mm}^2$, $E_2=E_3=400\,\text {N/mm}^2$, $G_{12}=G_{13}=800\,\text {N/mm}^2$, $G_{23}=50\,\text {N/mm}^2$ and $\nu _{12}=\nu _{13}=\nu _{23}=0.3$ as well as a density of $\rho =450\,\text {kg/m}^3$ are assigned to all layers. As correction function f(z) for the out-of-plane displacement, a quadratic parabola centered in mid-plane $z=0$ is used, i.e $f(z)=4/h^2\,z^2$.

3.1 Verification of the proposed plate theory

For simply supported laminates consisting of thick orthotropic layers, analytic solutions based on 3D elasticity theory are provided in [21]. Specifically, for free vibration the displacement field is written as

$$\begin{aligned} \begin{Bmatrix} u(x,y,z,t) \\ v(x,y,z,t) \\ w(x,y,z,t) \end{Bmatrix} =\sum \limits _{n=1}^{\infty }\sum \limits _{m=1}^{\infty } \begin{Bmatrix} \Phi (z)\cos \left( \dfrac{m\pi x}{l_x}\right) \sin \left( \dfrac{n\pi y}{l_y}\right) \\ \Psi (z)\sin \left( \dfrac{m\pi x}{l_x}\right) \cos \left( \dfrac{n\pi y}{l_y}\right) \\ \chi (z)\sin \left( \dfrac{m\pi x}{l_x}\right) \sin \left( \dfrac{n\pi y}{l_y}\right) \end{Bmatrix} \cos \left( \omega _{mn} t\right) . \end{aligned}$$

(26)

Computing the relative errors $\epsilon _f$ between the natural angular frequencies $\omega _{mn}$ based on the equations in [21] and their counterparts based on the proposed plate theory, as described in Sect. 2.3, yields for the first $n=1\ldots 6\,\times m=1\ldots 6$ modes the result shown in Fig. 2a. While for lower modes the error is practically negligible, with increasing mode numbers m/n also $\epsilon _f$ increases. However, for all 36 computed natural frequencies the relative error is less than 1 $\%$.

Fig. 2

Relative error for the natural frequencies $\epsilon _f$ of 36 modes of a simply supported plate based on plate theory compared to 3D elasticity. a Visualization over mode number. b Visualization over natural frequency

Alternatively, if one plots the relative errors versus the corresponding natural frequency $f=\omega /2\pi$, one obtains the graph shown in Fig. 2b denoted as “8 DOF”. The increase in relative error with increasing frequency can be clearly seen. In this figure, two more results are depicted: First, the relative errors for the proposed plate theory when degree of freedom $\Delta w$ is neglected, denoted as “7 DOF”. Over the entire frequency range, the relative error is approximately constant at about $1\%$. It can be concluded that taking $\Delta w$ into account in the equations of motions yields more accurate results for the natural frequencies at low frequencies, but also that the employed function for f(z) seems to become more inappropriate with increasing frequency, i.e., increasing cross section rotations and curvatures. Second, in Fig. 2b results for the relative error of the natural frequencies neglecting degrees of freedom $u_0$ and $v_0$ are depicted (“6 DOF”), which follow from the plate theory proposed in [18] and apply for symmetric cross sections. In this case, the errors are an order of magnitude larger (note the logarithmic scale in Fig. 2b), which highlights the importance of the two in-plane displacements for non-symmetric cross sections, even when the boundary conditions are free of in-plane constraints, as in the present problem.

Figure 3 provides a more detailed comparison of the results based on 3D elasticity and the plate theory (denoted here as 2D). For two modes, the cross section functions $\Phi (z)$, $\psi (z)$ and $\chi (z)$ in Eq. (26) are shown, which govern the displacement in x-, y- and z-direction along the cross section. For the mode with $m=2,~n=3$ (Fig. 3a), excellent agreement is obtained for all three functions and the natural frequency by the proposed plate theory, employing the above symmetric quadratic parabola for f(z). On the other hand, at a higher natural frequency corresponding to $m=6,~n=4$, the zig-zag deformation pattern in $\Phi (z)$ and $\psi (z)$ is more pronounced due to the larger cross section rotation and curvature, as visible in Fig. 3b. $\chi (z)$ tends to become more asymmetric; therefore, f(z) approximates less accurately the actual out-of-plane deformation. However, the overall agreement between 3D elasticity and the proposed plate theory is still very good.

The weak formulation of the plate theory presented in Sect. 2.4 was implemented in MATLAB. Discretizing the plate with isoparametric finite elements of size of $0.2\times 0.2$ m and eight nodes each, taking into account quadratic shape functions, yields an FE model with 12,728 degrees of freedom. Performing an eigenvalue analysis for the first 50 natural frequencies takes 6.7 s on a personal computer with six Intel Xeon E5-1650 v4 processors. In Fig. 4, the relative errors $\epsilon _f$ in the computed natural frequencies are depicted in comparison with the analytical outcomes according to [21]. The modes from the numerical simulation were assigned to mode numbers n and m by means of the modal assurance criterion (MAC), defined for the two real mode shape vectors $\varvec{\varphi }_1$ and $\varvec{\varphi }_2$ as [22]

$$\begin{aligned} \text {MAC}(\varvec{\varphi }_1,\varvec{\varphi }_2) = \dfrac{\Vert \varvec{\varphi }_1^T\,\varvec{\varphi }_2 \Vert ^2}{\varvec{\varphi }_1^T\,\varvec{\varphi }_1\,\varvec{\varphi }_2^T\,\varvec{\varphi }_2}. \end{aligned}$$

(27)

Specifically, the component $q_3=w(x,y)$ from the nodal degrees of freedom was compared with the sinusoidal modes shapes given in Eq. (26) to find n and m accordingly.

Fig. 3

Mode shape distributions over the cross section a $m=2,~n=3$ b $m=6,~n=4$

Fig. 4

Relative error for the natural frequencies $\epsilon _f$ of 36 modes of a simply supported plate based on the FE implementation of the plate theory compared to 3D elasticity

The deviation of natural frequencies based on the FE implementation is less than 1 $\%$ for all 36 modes, i.e., it is within the accuracy of the plate theory itself (compare with Fig. 2a). This proves the validity of the FE implementation.

3.2 Applicable material properties

Up to this point, the material properties employed represent typical values for CLT with a ratio of Young’s moduli and shear moduli $E_{2}/E_1=E_{3}/E_1=1/30$, $G_{12}/E_1=G_{13}/E_1=1/15$, $G_{23}/G_{12}=G_{23}/G_{13}=1/16$.

Fig. 5

Relative error for the natural frequencies $\epsilon _f$ of 36 modes of a simply supported plate based on plate theory compared to 3D elasticity. a Variation of $E_{2}/E_1$. b Variation of $G_{12}/E_1$ c Variation of $G_{23}/G_{12}$

To investigate the applicability of the proposed plate theory for a wider range of materials and/or properties, these parameters are varied. To limit the possible variations, the structure of the material properties, i.e., $E_2=E_3$, $G_{12}=G_{13}$ is not changed in the following parametric study. As in the previous section, the results for the first $n \times m = 36$ natural frequencies of a simply supported plate with dimensions described above are compared. The outcomes of the analytically available solution [21] are set in contrast to those of the (strong formulation of the) plate theory and shown as the relative error $\epsilon _f$ in Fig. 5. Increasing Young’s modulus $E_2$ such that it approaches $E_1$ has a minor effect on the accuracy of the plate theory, as shown in Fig. 5a. Up to $E_2/E_1=1/2$, the relative errors in the considered 36 natural frequencies have almost the same appearance. When $G_{12}$ is increased with respect to $E_1$ (Fig. 5b), the errors in the natural frequencies increase. Since $G_{23}$ is not changed, also in this case the ratio $G_{23}/G_{12}$ decreases (for $G_{12}/E_1=1/5$ this would correspond to $G_{23}/G_{12}=1/48$). This is also investigated in the third parametric study, whose results are shown in Fig. 5c. Here $G_{23}/G_{12}$ is changed, while $G_{12}/E_1$ remains the same. From the latter two parametric studies, it can be concluded that as the difference of the shear moduli $G_{23}$ to $G_{12}$ increases, i.e., as the zig-zag deformation pattern becomes increasingly pronounced, the errors in the natural frequencies increase. However, only for relatively unrealistic conditions, when $G_{23}/G_{12}$ is smaller than 1/30, the relative errors in the considered frequency range exceed $1\%$. Therefore, it can be concluded that the plate theory is valid for a wide range of material properties.

3.3 Influence of laminate orientation

In the analytical solution [21], a layer-wise orthotropic stress–strain relation is assumed with $Q_{i6}=0,~i=1,2,3$ and $Q_{45}=0$ in Eq. (1). This means that local axes 1 and 2 are aligned parallel to the global axes x and y (compare with Fig. 1). This is also the underlying assumption of the plate theory originally proposed in [15]. Since the plate theory presented in this paper is formulated for the general case where an angle $0\le \alpha \le 90^{\circ }$ can occur between the two coordinate systems, the influence of this orientation on the accuracy of modal properties (natural frequencies and mode shapes) is compared here. Note that the considered plate is still a cross-ply laminate, but the dimensions and boundaries are no longer oriented parallel to the principal material axes. Since no analytical solution is available for this case, the results of FE simulations conducted in ABAQUS serve as a reference. The considered four-layered laminated plate with the above dimensions and material properties is discretized with 20-noded hexahedral elements with quadratic shape functions. A very fine mesh with 24 elements over the thickness and in-plane dimensions of $0.1\times 0.1$ m is used, yielding a FE model with more than 600.000 degrees of freedom. To minimize the effect of the implementation of the boundary condition, the plate is not considered simply supported in this study, but clamped at all edges, i.e., all available degrees of freedom at the edges are set equal to zero. A modal analysis is performed for the first 40 modes and compared with the outcomes of computations based on the weak formulation of the plate theory in Fig. 6. Mode shapes are compared using MAC values evaluated at 60 nodal positions of the plate on the left hand side of the figure, where “3D FEM” refers to the ABAQUS reference solution and “2D FEM” to the solution obtained by the plate theory. On the right hand side, the corresponding natural frequencies between the two simulations are compared by means of the relative errors $\epsilon _f$.

Fig. 6

MAC matrix (left) and errors in the natural frequencies $\epsilon _f$ (right) comparing the outcomes of the FE implementation of the plate theory with the 3D elasticity FEM solution

When the material axes are aligned in parallel to the global axes ($\alpha =0^{\circ }$) as before, Fig. 6a shows a very close agreement of the modal properties: The MAC values are aligned along the diagonal with values approaching 1, which means that the two sets of modal vectors are fully correlated. The relative error of the natural frequency increases from values slightly below 0–1$\%$ in the frequency range up to 300 Hz. This behavior is consistent with the previous studies; compare, e.g., Fig. 5. On the other hand, if the laminate orientation angle $\alpha$ is increased to 20 and $40^{\circ }$, respectively, the errors in the natural frequencies dramatically increase, as can be seen in Fig. 6b and c. The mode shapes, on the other hand, are not affected as much by the obviously incorrect plate theory, except for individual modes at higher frequencies. In Fig. 7 an explanation for this behavior is provided. The cross section functions $A^k(z)$ and $E^k(z)$ that govern the zig-zag deformation pattern (see Eq. (2)) are depicted for the considered plate for different angles $\alpha$. Obviously, $A^k(z)$ for $\alpha =0^{\circ }$ corresponds to $E^k(z)$ for $\alpha =90^{\circ }$ and vice versa. For $\alpha$ between these two extreme values, $A^k(z)$ and $E^k(z)$ show a rather smooth deformation pattern without the characteristic zig-zag function. Since all the functions in Fig. 7 are commonly scaled to a minimal value of $-1$, the graphs illustrate that for $\alpha \ne 0$ the magnitude of the two functions $A^k(z)$ and $E^k(z)$, i.e., its relative importance in the displacement field Eq. (2) depends strongly on $\alpha$.

Fig. 7

Cross section functions $A^k(z)$ and $E^k(z)$ as a function of the laminate orientation angle $\alpha$

As a remedy, the nodal (x, y)-coordinates of the finite elements can be transformed into a coordinate system oriented in accordance with the principal material axes by means of a rotation matrix

$$\begin{aligned} {\textbf {R}} = \begin{bmatrix} \cos \alpha &{}\quad \sin \alpha \\ -\sin \alpha &{}\quad \cos \alpha \end{bmatrix}. \end{aligned}$$

(28)

In this coordinate system, the constitutive relation for a cross-ply laminate (Eq. 1) simplifies, since $Q_{i6}=0,~i=1,2,3$ and $Q_{45}=0$. Consequently, the entries in ${\textbf {K}}^{fe}$ in Eq. (20) vanish with these indices. Taking into account these local coordinate transformations in the FE simulations yields for $\alpha =20^{\circ }$ and $\alpha =40^{\circ }$ the results depicted in Fig. 8. In comparison with Fig. 6, the relative errors in the natural frequencies $\epsilon _f$ are now of the same order of magnitude as for the case $\alpha =0^{\circ }$, and also the MAC matrix shows the targeted diagonal shape. Thus, it can be concluded for cross-ply laminates that rotating the nodal coordinates by the angle $\alpha$ before computing the element stiffness makes the FE implementation valid for arbitrary orientations of the element with respect to the principal material axes.

Fig. 8

MAC matrix (left) and errors in the natural frequencies $\epsilon _f$ (right) comparing the outcomes of the FE implementation of the plate theory with the 3D elasticity FEM solution with prior the nodal coordinate rotation

4 Conclusions

In this paper, an equivalent single-layer plate theory for thick laminated plates has been presented whose bending deformation is dominated by a zig-zag shape across the thickness, as is the case, for instance, for cross-laminated timber. Based on previous work by the authors, the plate theory is formulated for arbitrary cross sections (i.e., symmetric and asymmetric), considering orthotropic material behavior for the individual layers stacked at a general angle $\alpha$. The deformation is governed by eight kinematic degrees of freedom, two in-plane displacements, two out-of-plane displacements, and four rotations. Equations of motion were derived, from which the dispersion relation governing the propagation of bending waves in unbounded plates was obtained. As special case, the natural frequencies and mode shapes of simply-supported rectangular plates were computed and contrasted with results from literature based on the solution of the 3D elasticity problem, revealing excellent agreement over a wide frequency range. The limiting factor in terms of accuracy was found to be the function for the out-of-plane deformation, which was assumed to be symmetric here. A parametric study with respect to material properties underscored the wide applicability of the plate theory in this sense.

The weak formulation in terms of finite element elemental mass and stiffness matrices and load vector was derived, allowing the investigation of arbitrarily complex geometries. Varying the orientation of the composite plate, it was shown that the plate theory is valid for cross-ply laminates oriented at an arbitrary angle with respect to plate boundaries, if the elemental stiffness matrix is computed in a locally rotated coordinate system. On the other hand, the present study demonstrates that, as expected, the plate theory yields inaccurate results for angle-ply laminates. For these laminates, the assumed displacement field would need be adjusted. As a further extension of the plate theory, nonlinear material behavior could be implemented, e.g., by a damage formulation. Since even in symmetric composite lay-ups the failure of individual plies generally leads to asymmetric stress distributions, the proposed plate theory can be considered as important first step in this direction.