Numerical analysis of the magnetic shape memory effect based on the absolute nodal coordinate formulation

Abstract

In this paper, the absolute nodal coordinate formulation (ANCF) is applied to simulate the magnetic shape memory effect. Using the absolute nodal coordinate formulation makes it possible to describe complicated or large deformation cases. The nonlinear bidirectional coupling terms between the mechanical and magnetic field are taken into account in the analysis of the single-crystalline Ni-Mn-Ga sample. A two-loop iteration procedure with variable steps is implemented to predict the magnetic-field-induced strain (MFIS) in the specimen under a changing external magnetic field and a constant auxiliary compression. In addition, the proposed approach is used to track the superelastic behavior of the magnetic shape memory alloy when subjected to a constant magnetic field. The approach effectively describes the hysteresis and superelastic phenomenon of the shape memory effect. The solution is compared here with solutions obtained using classical linear and quadratic quadrilateral elements. The deviation observed in the solution is discussed, and its cause is further clarified from a two-domain pure magnetostatic analysis of a permanent magnet. It is found that the accurate solution of such problems is associated with discontinuity of the normal component of the magnetic potential gradient across the domain interface. Special measures must be taken to make the absolute nodal coordinate formulation element compatible with the discontinuity. A mixed FEs strategy, which adopts ANCF FE in the displacement field solver and classical FE in the magnetic field solver, is proposed as an alternative option to rectify the problem, which is verified by predicting the MFIS and the dynamic mechanical response of a sample under cyclic compression.

1 Introduction

The magnetic shape memory effect (MSME) refers to the change in the physical shape of a magnetic material in the presence of a moderate magnetic field [28]. A magnetic shape memory alloy (MSMA) is a promising new smart material with certain prominent characteristics that include large magnetic-field-induced strain (MFIS) [23, 25], high fatigue life, and ultra-fast actuation response [24]. Different aspects of the MSMA material have already been studied including transformation temperature [9], saturation magnetization, magnetic anisotropy energy [26], and the structure of magnetic domains [15]. Early experimental studies help reveal the underlying mechanisms behind the MSME phenomenon based on which different modeling methods have been proposed to predict the behavior of the MSMA. Existing modeling methods comprise the constrained theory [7], the statistical approach [9], the phase-field method [17], and others. Many models are constructed based on thermodynamics [11]. Among these, the models that get most attention use the variational principle [14, 30] or the finite element method (FEM) because of their straightforward implementation procedures. In the finite element framework, an iterative numerical method has been proposed to obtain the displacement and magnetization of the specimen [31]. In Wang and Steinmann’s work, several internal state variables are introduced to represent the micro-status of the specimen. Another approach that does not use numerical iteration was inspired by the Karush–Kuhn–Tucker conditions. It treats the internal state variables as an additional set of degrees of freedom and integrates the corresponding evolution laws into the finite-element-based equilibrium equations [1, 5].

The above existing numerical analyses of the magnetic shape memory effect focus mainly on small deformation cases and even ignore the influence of the elastic deformation on the demagnetization field [5, 31]. However, the MSMAs are known for their ability to develop large MFIS (up to 12$\%$ in single-crystalline MSMA with seven-layered orthorhombic martensite structure) [25]. Therefore, studying the behaviors of MSMA undergoing large deformation and with complicated deformation modes is practically important. How the specimen behavior is influenced by these conditions cannot be ignored. Additionally, research works on the numerical dynamic analysis of single-crystalline Ni-Mn-Ga are still rare [29]. Some works ignore the inertial effect to study the dynamic response [10, 16] and do not integrate the equation of motion into the solving procedure. In a very recent paper [8], Fan and Wang pioneered the work on numerical analysis of dynamic mechanical response of a single-crystalline Ni-Mn-Ga sample by solving the equation of motion with the classical FE. Compared with the classical FE, the absolute nodal coordinate formulation (ANCF) offers a promising approach capable of accounting for large deformation and large reference motions and brings its inherent advantages to the future complicated dynamic analysis of MSMA.

Using the components of the deformation gradient as the nodal coordinates, the absolute nodal coordinate formulation imposes no restrictions on the amount of rotation or deformation within the finite element. Due to the simplicity and its consistency with strain and stress measures from general continuum mechanics [4], the absolute nodal coordinate formulation has been widely used in various applications especially for problems with geometrical and material nonlinearities [19, 20, 34, 35]. Additionally, the ANCF has been verified as a powerful tool for multibody dynamic analysis. Since the kinematic description of ANCF is based on the global coordinate system, the ANCF method can act as a straightforward bridge to integrating the MSME simulation into a general multibody dynamic analysis, which is necessary for future different application scenarios of possible slender MSMA actuator/sensor.

The objective of the paper is to develop an approach to simulating the behaviors of the magnetic shape memory alloy subjected to large deformation. To achieve this, a general large-rotation and large-deformation finite element formulation, i.e., the absolute nodal coordinate formulation is employed. Considering the bidirectional coupling effects between the mechanical and magnetic fields, a numerical procedure is presented comprising the mechanical FE solver, the magnetic FE solver, and the internal state variable evolution solver. The approach can qualitatively describe the full generation process of the magnetic-field-induced strain and capture the special features of the magnetic shape memory effect including hysteresis and the superelastic effect. The deviation between the result given by ANCF FE and classical FEs is further analyzed using a pure magnetostatic case. It is found that the gradient discontinuity issue on the interface need be overcome for the ANCF FE in the two-domain MSME simulation to obtain a more accurate solution. To fix the problem, a mixed FEs strategy, which adopts ANCF FE to solve the displacement field and classical FE for the magnetic field, is proposed.

The remainder of the paper is organized as follows: In Sect. 2, the microstate description of the MSMA specimen is briefly introduced. Section 3 constructs the ANCF finite element. The corresponding equilibrium equations based on the variational principle and the equation of motion is established. Subsequently, a numerical analysis framework is established to estimate the behavior of the MSMA based on adopting the newly constructed ANCF element as the approach to solve the displacement and the magnetic field. Section 4 presents several typical examples to verify the method. Meanwhile, the limitations of the ANCF method in MSME analysis are investigated, and a modification of the approach that is free of those limitations is proposed. With the modified approach, the dynamic mechanical response of a sample under cyclic compression is simulated. And finally, Sect. 5 offers the authors’ conclusions.

2 Microstate description of the magnetic shape memory effect

The magnetic shape memory effect (MSME) is caused by martensite variant reorientation and domain transformation at room temperature. Ever since Ullakko et al. [28] revealed the MFIS in 1996, the single-crystalline Ni-Mn-Ga alloy has been extensively studied. In the single-crystalline Ni-Mn-Ga alloys, three martensite structures are observed: five-layered modulated (5M) approximately tetragonal martensite with c/a$<1$ and maximum theoretical strain of about 6%, seven-layered modulated (7M) orthorhombic martensite with maximum theoretical strain of about 12%, and non-modulated (NM) tetragonal martensite with c/a>1 with maximum theoretical strain of about 20%. No considerable magnetic shape memory effect has been reported in the last structure [27, 36]. Compared with a 7M structure specimen, the samples in the 5M structure exist in a border range [36] and demonstrate best performance for practical application [22]. Therefore, a bulk MSMA specimen with 5M structure was studied in this work.

To get an evident MSME process, a compression assist is usually applied. A typical experimental procedure or the stress-assisted magnetic-field-induced strain generation procedure is depicted in Fig. 1a. After “training” under a cyclic and large mechanical stress, a single-crystalline Ni-Mn-Ga specimen in the 5M (5-layer modulated) structure exhibits a single variant state with the magnetic easy axis, i.e., the short c-axis, aligned with the external loading [15]. As shown in Fig. 1a, under the external magnetic field $\mathbf {H}_a$ and the assisted compression $\mathbf {t}_\text {A}$, variant one begins to transform to variant two with the c-axis generally aligning with the magnetic field direction. With increasing the external magnetic field strength, variant two grows at the expense of the stress-favored variant one with simultaneous domain wall movement until the specimen evolves to the single variant and single domain state. Macroscopically, the specimen extends as a result of the internal variant reorientation, the rotation of the magnetization vector, and/or domain wall movement. Consequently, the final maximum induced strain is around $1-c/a\approx 0.06$ [15].

Fig. 1

Experiment process and the microstructure of the magnetic shape memory alloy

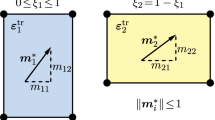
In this study, a simple assumption based on the experiment [15] and adopted by Wang and Steinman [30, 31] is used to describe the generation of MFIS. The corresponding micro-configuration of a two-variant 5M Ni-Mn-Ga sample is shown in Fig. 1b. The variants form distributed bands that are separated by twin interfaces. In each variant region, two kinds of magnetic domains are separated by $180^\circ$ domain walls. In each magnetic domain, the magnetization vector aligns with either the positive or negative direction of the corresponding easy axis with saturation magnitude $M_s$. The external magnetic field will induce the movement of the magnetic domain walls in variant one and the rotation of the magnetization vectors in variant two as shown in Fig. 1b. Correspondingly, internal state variables $\alpha$ and $\theta$ are introduced to represent the magnetic domain volume fraction in variant one and magnetization vector rotation in variant two, respectively. In summary, only three internal state parameters, i.e., the variant two volume fraction $\xi _2$, the magnetization vector rotation $\theta$, and the magnetic domain volume fraction $\alpha$ are capable of fully describing the internal state of the specimen as shown in Fig. 1b. Accordingly, the elastic moduli tensor, the effective magnetization vector, and the total strain are dependent on these three parameters. The elastic moduli tensor can be written as [31]

$$\begin{aligned} \mathbf {C}=\left( 1-\xi _2 \right) {\mathbf {C}^{1}}+\xi _2 {\mathbf {C}^{2}} \end{aligned}$$

(1)

where $\mathbf {C}^1$ and $\mathbf {C}^2$ are the elastic moduli tensor of variant one and variant two, respectively. The tensor can be written in Voigt notation form as

$$\begin{aligned} {{\mathbf {C}}^{1}}=\begin{bmatrix} \kappa _2 &{} \kappa _3 &{} \kappa _3 &{} 0 &{} 0 &{} 0 \\ {} &{} \kappa _1 &{} \kappa _4 &{} 0 &{} 0 &{} 0 \\ {} &{} {} &{} \kappa _1 &{} 0 &{} 0 &{} 0 \\ {} &{} {} &{} {} &{} \kappa _5 &{} 0 &{} 0 \\ {} &{} \text {sym.} &{} {} &{} {} &{} \kappa _6 &{} 0 \\ {} &{} {} &{} {} &{} {} &{} {} &{} \kappa _5 \\ \end{bmatrix}{{\mathbf {C}}^{2}}=\begin{bmatrix} \kappa _1 &{} \kappa _3 &{} \kappa _4 &{} 0 &{} 0 &{} 0 \\ {} &{} \kappa _2 &{} \kappa _3 &{} 0 &{} 0 &{} 0 \\ {} &{} {} &{} \kappa _2 &{} 0 &{} 0 &{} 0 \\ {} &{} {} &{} {} &{} \kappa _5 &{} 0 &{} 0 \\ {} &{} \text {sym.} &{} {} &{} {} &{} \kappa _5 &{} 0 \\ {} &{} {} &{} {} &{} {} &{} {} &{} \kappa _6 \\ \end{bmatrix} \end{aligned}$$

(2)

where $\kappa _i,~i=1,2...6$ are the moduli constants. Driven by the the magnetic domain wall motion, the rotation of the magnetization vector, and variant reorientation, the effective magnetization vector $\bar{\mathbf {M}}$ is expressed using the corresponding three internal state parameters as

$$\begin{aligned} \bar{\mathbf {M}}={{M}_{s}}\left[ \left( 1-\xi _2 \right) \sin \theta +\xi _2 \left( 2\alpha -1 \right) \right] {{\mathbf {e}}_{2}} \end{aligned}$$

(3)

where $\mathbf {e}_2$ is the unit direction vector of the external magnetic field measured in the current configuration. With the transformation from variant one to variant two, the transformation strain $\xi _2{\varepsilon }^\text {tr}$ appears. As a result, the total strain is written as

$$\begin{aligned} \varvec{\upvarepsilon }=\varvec{\upvarepsilon }^\text {el}+\xi _2\varvec{\upvarepsilon }^\text {tr} \end{aligned}$$

(4)

where $\varvec{\upvarepsilon }^\text {el}$ is the Green–Lagrange strain tensor. It is written as follows:

$$\begin{aligned} {\varvec{\upvarepsilon }^\text {el}}=\frac{1}{2}\left( {{\mathbf {F}}^{\text {T}}}\mathbf {F}-\mathbf {I} \right) =\frac{1}{2}\left( \mathbf {r}_{,\mathbf {X}}^{\text {T}}\mathbf {r}_{,\mathbf {X}}-\mathbf {I}\right) \end{aligned}$$

(5)

where $\mathbf {F}=\mathbf {r}_{,\mathbf {X}}$ is the deformation gradient tensor, $\mathbf {r}$ is the position vector in the current deformed configuration, $\mathbf {X}$ is the material coordinate in the initial reference configuration, and the subscript following a comma denotes partial differentiation with respect to that variable. In Eq. (4), the maximum transformation strain tensor ${{\varvec{\varepsilon }}^{\text {tr}}}$ can be written in Voigt notation form as follows:

$$\begin{aligned} \varvec{\upvarepsilon }_v^{\text {tr}}={\left[ -\varepsilon _1 \quad \varepsilon _2 \quad 0 \quad 0 \quad 0 \quad 0 \right] }^{\text {T}} \end{aligned}$$

(6)

where $\varepsilon _1$ and $\varepsilon _2$ represent the maximum transformation strains along the principle axes. According to the microstructure and the lattice dimensions of variant one and two, the induced strain in z direction does not appear during the variant transformation as shown in Fig. 1a. Therefore, it is reasonable to apply the plane strain assumption to simplify the simulation. In the plane strain case, the elastic moduli tensor in Voigt notation $\mathbf {C}^1$ and $\mathbf {C}^2$ degenerates to

$$\begin{aligned} {{\mathbf {C}}^{1}}=\begin{bmatrix} \kappa _2 &{}\quad \kappa _3 &{}\quad 0 \\ {} &{}\quad \kappa _1 &{}\quad 0 \\ \text {sym.} &{} {} &{}\quad \kappa _5 \end{bmatrix},\quad {{\mathbf {C}}^2}=\begin{bmatrix} \kappa _1 &{}\quad \kappa _3 &{}\quad 0 \\ {} &{}\quad \kappa _2 &{}\quad 0 \\ \text {sym.} &{} {} &{}\quad \kappa _5 \end{bmatrix}. \end{aligned}$$

(7)

The elastic and maximum transformation strain in Voigt notation degenerate to

$$\begin{aligned} \left. \begin{array}{l} \varvec{\upvarepsilon }_v^{\text {el}}={\frac{1}{2} \left[ \begin{array}{cccccc} \mathbf {r}^\text {T}_{,X}\mathbf {r}_{,X}-1 &{} ~~ &{} \mathbf {r}^\text {T}_{,Y}\mathbf {r}_{,Y}-1 &{} ~~ &{} 2 \mathbf {r}^\text {T}_{,X}\mathbf {r}_{,Y} \end{array} \right] }^{\text {T}}\\ \varvec{\upvarepsilon }_v^{\text {tr}}={\left[ \begin{array}{ccccc} -\varepsilon _1 &{} &{} \varepsilon _2 &{} &{} 0 \end{array} \right] }^{\text {T}} \end{array} \right\} . \end{aligned}$$

(8)

3 ANCF element construction and numerical analysis method

This Section briefly introduces the variational principle approach for the MSME problem, which leads to the FEM solution of the displacement and magnetic field. Then, the planar ANCF FE employing both the displacement and magnetic field degrees of freedom is constructed. Finally, a modified numerical simulation framework that integrates the ANCF FE solver and the internal state parameter evolution solver [30, 31] is presented.

3.1 Variational principle approach

The governing partial differential equations and the evolution laws of the internal variables can be derived by calculating the variation of the total energy functional. The functional formulation presented in [31] is briefly introduced. The total energy functional of the whole magneto-mechanical system is

$$\begin{aligned} G\left( \mathbf {r},\psi ,\xi _2 ,\theta ,\alpha ; \mathbf {X} \right) =U_\text {el}+U_\text {an}+U_\text {ze}+U_\text {sta}+U_\text {mix}+U_\text {ml}+U_\text {dis} \end{aligned}$$

(9)

where $\psi$ is the scalar magnetic potential, $U_\text {el}$ is the elastic potential energy, $U_\text {an}$ is the magneto-crystalline anisotropy energy, $U_\text {ze}$ is the Zeeman energy, $U_\text {sta}$ is the magnetostatic energy, $U_\text {mix}$ is the mixture energy, $U_\text {ml}$ is the potential energy of the external mechanical load, and $U_\text {dis}$ is the total energy dissipation. All the terms are expressed under the Lagrangian description with respect to the reference configuration. In Eq. (9), the elastic potential energy $U_\text {el}$ can be written as:

$$\begin{aligned} U_\text {el}=\int _{\Omega _r}{\rho _r}\phi \left( \mathbf {X},\xi _2 \right) dV \end{aligned}$$

(10)

where $\Omega _r$ is the specimen region, $\rho _r$ is the mass density in the reference configuration, and $\phi$ is the elastic energy density. The magneto-crystalline anisotropy energy $U_\text {an}$ is written as:

$$\begin{aligned} U_\text {an}=\int _{\Omega _r}{\left( 1-\xi _2 \right) {\rho _r}{K_u}{\sin ^2}\theta dV} \end{aligned}$$

(11)

where $K_u$ is the anisotropy constant. The Zeeman energy, or the external field energy $U_{\text {ze}}$ is:

$$\begin{aligned} U_\text {ze}=\int _{\Omega _r}{-\mu _0}{\rho _r}\bar{\mathbf {M}}\cdot {\mathbf {H}_a}dV \end{aligned}$$

(12)

where $\mu _0$ is the magnetic permeability of free space and $\mathbf {H}_a$ is the external magnetic field. The magnetostatic energy of the demagnetization field $U_\text {sta}$ can be written as:

$$\begin{aligned} U_\text {sta}=\int _{\Omega _r}-{\mu _0}{\rho _r}\bar{\mathbf {M}}\cdot {{\mathbf {H}}_{d}}dV+\int _{\mathbb {R}^3}{-\frac{\mu _0}{2}J{\mathbf {H}}_{d}\cdot {\mathbf {H}}_{d}dV} \end{aligned}$$

(13)

where $\mathbb {R}^3$ is the analyzed whole space including the specimen domain $\Omega _r$ and the surrounding space domain $\Omega _{r}^{'}$, $\mathbf {H}_{d}=-\mathbf {F}^{-\text {T}}\nabla \psi$ is the demagnetization field induced by the magnetization of the MSMA specimen measured in the current configuration, and J=det(F), i.e., the determinant of the deformation gradient tensor. According to the divergence theory and the Gauss’s law for magnetism, the magnetostatic energy can also be written in the following form [30]:

$$\begin{aligned} U_\text {sta}=\int _{\Omega _r}{-\frac{\mu _0}{2}{\rho _r}\bar{\mathbf {M}}\cdot {{\mathbf {H}}_{d}}dV}. \end{aligned}$$

(14)

The mixture energy due to the interactions of different martensite variants and magnetic domains $U_{\text {mix}}$ is written as follows:

$$\begin{aligned} U_\text {mix}=\int _{{{\Omega }_{r}}}{{{\rho }_{r}}{{f}^{\xi }}\left( \xi _2 \right) dV}+\int _{{{\Omega }_{r}}}{{{\rho }_{r}}\left[ \left( 1-\xi _2 \right) {{f}^{\alpha }}\left( \frac{1}{2} \right) +\xi _2 {{f}^{\alpha }}\left( \alpha \right) \right] dV} \end{aligned}$$

(15)

where $f^\xi \left( \xi _2\right)$ and $f^\alpha \left( \alpha \right)$ are the energy densities arising from the mixture of the two variants and the interactions of the different magnetic domains in each variant region. The potential energy of mechanical loading $U_{\text {ml}}$ is:

$$\begin{aligned} U_\text {ml}=-\int _{\partial {\Omega _r}}{{\mathbf {t}_\text {A}}\cdot \mathbf {r}dA} \end{aligned}$$

(16)

where $\mathbf {t}_\text {A}$ is the external compression applied per unit referential area and $\partial \Omega _r$ is the boundary, on which the compression is applied. Besides the above energy quantities, to capture the hysteresis phenomena observed in the experiments, the dissipation effect during the variant transformation process should be considered. The total energy dissipation $U_\text {dis}$ during the forward and reverse transformation processes can be written in the following form:

$$\begin{aligned} U_\text {dis}=\pm \int _{{\Omega _r}}{\int _{{\xi _2^0}}^{\xi _2} {{\rho _r}{D^\pm }\left( \tau \right) d\tau }dV} \end{aligned}$$

(17)

where $\xi _2^0$ and $\xi _2$ are the initial and final volume fractions of variant two in the specimen. Accordingly, $\xi _2^0\le \xi _2$ applies for the forward transformation and $\xi _2^0\ge \xi _2$ for the reverse transformation. $D^{\pm }$ are positive functions called the dissipative resistances (“+” and “−” represent the forward and reverse transformation, respectively). By adding up the energy quantities together, the total energy functional for the magneto-mechanical system is:

$$\begin{aligned} \begin{aligned}&G\left( \mathbf {r},\psi ,\xi _2 ,\alpha ,\theta ; \mathbf {X} \right) =\int _{\Omega _r}\left( 1-\xi _2 \right) {\rho _r}\left[ {K_u}{\sin ^2}\theta +{f^\alpha }\left( \frac{1}{2} \right) \right] dV \\&\quad +\int _{{\Omega _r}}{{\rho _r}\phi \left( \mathbf {X},\xi _2 \right) }dV +\int _{{\Omega _r}}{{\rho _r}{f^{\xi }}\left( \xi _2 \right) dV} +\int _{{\Omega _r}}{{\rho _r}\xi _2 {f^\alpha }\left( \alpha \right) dV} \\&\quad +\int _{{\Omega _r}}{-{\mu _0}{\rho _r}\bar{\mathbf {M}}\cdot {\mathbf {H}_a}dV}+\int _{{\Omega _r}}{-{\mu _0}{\rho _r}\mathbf {M}\cdot {\mathbf {H}_d}dV} \\&\quad +\int _{{\mathbb {R}^3}}{-\frac{{\mu _0}}{2}J{\mathbf {H}_d}\cdot {\mathbf {H}_d}dV} \pm \int _{{\Omega _r}}{\int _{{\xi _2^0}}^{\xi _2}{{\rho _r}{D^\pm }\left( \tau \right) d\tau }dV}-\int _{\partial {\Omega _r}}{{\mathbf {t}_\text {A}}\cdot \mathbf {r}dA}. \end{aligned} \end{aligned}$$

(18)

In the energy functional, the independent variables are the position vector $\mathbf {r}$, the scalar magnetic potential $\psi$, and the three internal state variables $\xi _2$, $\theta$, and $\alpha$. Specifically, in the FEM implementation, $\mathbf {r}$ and $\psi$ are interpolated using the nodal vectors $\mathbf {e}^u$, $\mathbf {e}^\psi$ of the corresponding element, and the internal state variables $\xi _2$, $\theta$, and $\alpha$ are directly calculated on the Gauss integration points of each element.

The governing equations of the system are obtained by calculating the variations of G with respect to the independent variables $\mathbf {r}$, $\psi$, and the internal state variables [30] as shown in the following:

$$\begin{aligned} {{\delta }_{\psi }}G=\int _{{{\Omega }_{r}}}{{{\mu }_{0}}{{\rho }_{r}}\bar{\mathbf {M}}}\cdot \mathbf {F}^{-\text {T}}\nabla \left( \delta \psi \right) dV -\int _{{{\Omega }_{r}+\Omega _{r}^{'}}}{\mu _0}J\nabla \psi (\mathbf {F}^\text {T}\mathbf {F})^{-1} \cdot \nabla \left( \delta \psi \right) dV=0, \end{aligned}$$

(19)

$$\begin{aligned} {{\delta }_{\mathbf {r}}}G=\int _{{{\Omega }_{r}}}{{{\rho }_{r}}\left( \frac{\partial \phi }{\partial \mathbf {r}}\delta \mathbf {r} \right) }dV+\delta _\mathbf {r}U_{\text {sta}}-\int _{\partial {{\Omega }_{r}}}{{{\mathbf {t}}_\text {A}}\cdot \delta \mathbf {r}}dA=0, \end{aligned}$$

(20)

(21)

$$\begin{aligned} {\delta _\theta }G=\int _{{{\Omega }_{r}}}{\left( 1-\xi _2 \right) \left( 2{K_u}\sin \theta -\mu _0{M_s}{H_{\text {tot}}} \right) \delta \left( \sin \theta \right) }dV\ge 0, \end{aligned}$$

(22)

$$\begin{aligned} {\delta _\alpha }G=\int _{\Omega _r}{\xi _2 \left[ \frac{\partial {{f}^{\alpha }}\left( \alpha \right) }{\partial \alpha }-2{{\mu }_{0}}{{M}_{s}}{H_{\text {tot}}} \right] }\delta \alpha dV\ge 0 \end{aligned}$$

(23)

where $H_{\text {tot}}=H_a+H_{dy}$, $H_a=\mathbf {H}_a\cdot \mathbf {e}_2$, and $H_{dy}=\mathbf {H}_d\cdot \mathbf {e}_2$ are the components of the external and the demagnetization field in the external magnetic field direction. The inequalities as shown in Eqs. (21–23) are obtained based on thermodynamics [13]. Magnetostatic energy in the form of Eq. (14) is used in the variation of the total energy functional with respect to $\mathbf {r}$. The governing equations indicate that the magnetic field and the displacement field are implicitly related via the internal state evolution of the MSMA. In addition, the influence of the deformation on the magnetic field explicitly goes into $\mathbf {H}_d=-\mathbf {F}^{-\text {T}}\nabla \psi$ via the deformation gradient tensor $\mathbf {F}$, and the magnetic field influences the deformation via the variation of the magnetostatic energy as shown in Eq. (14). These two explicit coupling terms are ignored in [31] but considered in this work.

The variational principle is a very general approach in formulating the constitutive models of the multi-physics problems such as the piezoelectric effect. Under the framework of variational principle, similar equations can be obtained in the piezoelectric effect [2, 18]. However, there are essential differences between MSME and piezoelectric effect analysis. As shown in Sect. 2, the MSME involves with changes to the micro-crystallographic structure. Correspondingly, several internal variables are introduced to describe the evolution of the micro-structure in the numerical simulation. The state of the MSMA specimen should be determined iteratively via equations obtained from Eqs. (21–23) since the internal variables depend on the current magnetic and displacement field. Thus, there must be an iterative state evolution solver in the MSME analysis procedure. As a result, most MSME simulations in the literature are quasi-static analyses [1, 3, 5, 33]. By contrast, the numerical analysis of the piezoelectric effect is not associated with the micro-crystallographic structure. So there is no additional iterative solver besides the displacement and electric field solver in the piezoelectric effect analysis procedure [18].

3.2 ANCF element construction

As mentioned in Sect. 2, the classical MSME experiment as shown in Fig. 1a can be analyzed as a planar issue since there is no transformation strain along the z axis. For such planar rectangular domain, the planar quadrilateral element is the most appropriate element for the analysis [1, 5]. Therefore, the planar quadrilateral element proposed by Olshevskiy et al. [21] is used in the analysis. For the magnetic field analysis, the scalar magnetic potential $\psi$ is adopted as the basic variable, and the corresponding gradients $\psi _{,x},\psi _{,y}$ are also used as the nodal DOFs under the framework of the ANCF method, where x and y are the element coordinates in the straight configuration. By doing so, the ANCF method is checked in the MSME analysis by directly generalizing the original mechanical-element to a magneto-mechanical element. The schematic diagram of the element is shown in Fig. 2,

As shown in Fig. 2, 12 variables, i.e., $\mathbf {e}_i^\psi =[\psi _i,\psi _{i,x},\psi _{i,y}]^\text {T}$ at node i, i=1,2,3,4, are used for the interpolation of the magnetic potential. Selecting the bases for the 12-term interpolation based on the Pascal triangle, a natural option is the same basis as that used in the displacement field interpolation, i.e., $\{1,x,y,x^2,xy,y^2,x^3,x^2y,xy^2,y^3\}$. Accordingly, the same shape functions $s_i, i=1,2,...,12$ are obtained for the magnetic potential interpolation. The shape function matrix is shown as follows:

$$\begin{aligned} \mathbf {S\left( \xi ,\eta \right) }=\left[ \begin{array}{cccc} s_1\mathbf {I}&s_2\mathbf {I}&...&s_{12}\mathbf {I} \end{array} \right] \end{aligned}$$

(24)

where $\xi =x/l$ and $\eta =y/w$ are the local normalized coordinates in the straight configuration, and $0\le \xi , \eta \le 1$, and l and w are the element length and width in the straight configuration. The detailed expression of the shape functions $s_i, i=1,2,...,12$ is shown in Appendix A. In the shape function matrices of the displacement field and magnetic field element, the identity matrix $\mathbf {I}\in {{\mathbb {R}}_{3\times 3}}$ and $\mathbf {I}\in {{\mathbb {R}}_{1\times 1}}$ in Eq. (24), respectively. The position and magnetic potential at an arbitrary point are interpolated using the nodal vectors as $\mathbf {r}=\mathbf {S}\mathbf {e}^u$ and $\psi =\mathbf {S}\mathbf {e}^\psi$. The corresponding nodal vectors are

$$\begin{aligned} \left. \begin{array}{l} \mathbf {e}^u={\left[ \begin{array}{cccc} \mathbf {e}_{1}^{u\text {T}} &{} \mathbf {e}_{3}^{u\text {T}} &{} \mathbf {e}_{3}^{u\text {T}} &{} \mathbf {e}_{4}^{u\text {T}} \end{array} \right] }^{\text {T}}\\ \mathbf {e}^\psi ={\left[ \begin{array}{cccc} \mathbf {e}_1^{\psi \text {T}} &{} \mathbf {e}_2^{\psi \text {T}} &{} \mathbf {e}_3^{\psi \text {T}} &{} \mathbf {e}_4^{\psi \text {T}} \end{array} \right] }^{\text {T}} \end{array} \right\} \end{aligned}$$

(25)

where $\mathbf {e}_i^u=\left[ \begin{array}{ccc}\mathbf {r}_i^\text {T}&\mathbf {r}_{i,x}^\text {T}&\mathbf {r}_{i,y}^\text {T}\end{array}\right] ^\text {T}$ and $\mathbf {e}_i^\psi =\left[ \psi _i,\ \psi _{i,x},\ \psi _{i,y}\right] ^\text {T},~ i=1,2,3,4$. The deformation gradient with respect to the initial reference configuration is obtained as

$$\begin{aligned} \mathbf {F} = \frac{\partial {\mathbf {r}}}{\partial {\mathbf {x}}}\left( \frac{\partial {\mathbf {X}}}{\partial {\mathbf {x}}}\right) ^{-1} \end{aligned}$$

(26)

where $\mathbf {x}=[x,y]^\text {T}$ are the element coordinates in the straight configuration, and the mapping matrix between the initial reference configuration and the straight configuration is denoted as $\mathbf {J}_0$. Denoting the initial nodal vector of an element as $\mathbf {e}_0^\text {u}$, $\mathbf {J}_0$ at the point with the local normalized coordinates $\xi$ and $\eta$ can be obtained as

$$\begin{aligned} \mathbf {J}_0 =\frac{\partial {\mathbf {X}}}{\partial {\mathbf {x}}}=\left[ \frac{1}{l}\frac{\partial {\mathbf {S}(\xi ,\eta )}}{\partial {\xi }}\mathbf {e}_0^\text {u} \quad \frac{1}{w}\frac{\partial {\mathbf {S}(\xi ,\eta )}}{\partial {\eta }}\mathbf {e}_0^\text {u} \right] . \end{aligned}$$

(27)

Fig. 2

The generalized ANCF planar quadrilateral element

3.2.1 Magnetic FEM equilibrium equation

The scalar potential $\psi$ and its gradients $\psi _{,x},\psi _{,y}$ are used as the nodal degrees of freedom. The demagnetization field is ${\mathbf {H}_d}= -\mathbf {F}^{-\text {T}}\nabla \psi$. Under the framework of FEM, the demagnetic field at an arbitrary point can be obtained as

$$\begin{aligned} {{\mathbf {H}}_{d}}=-\mathbf {F}^{-\text {T}}\left[ \begin{matrix} {{\mathbf {S}}_{,x}} \\ {{\mathbf {S}}_{,y}} \\ \end{matrix} \right] {{\mathbf {e}}^{\psi }}=-\mathbf {F}^{-\text {T}}\mathbf {B}{{\mathbf {e}}^{\psi }} \end{aligned}$$

(28)

where $\mathbf {S}_{,x}$ and $\mathbf {S}_{,y}$ are the derivatives of the shape function matrix $\mathbf {S}$ with respect to the material coordinate. The dimension of the corresponding vectors and matrices is $\mathbf {S},\ {{\mathbf {S}}_{,x}},\ {{\mathbf {S}}_{,y}}\in {{\mathbb {R}}_{1\times n}}$, and $\mathbf {B}\in {{\mathbb {R}}_{2\times n}}$, where n is the number of the nodal coordinates in an element, and for the adopted ANCF element n=12. Substituting Eq. (24) into Eq. (19) results in the following equilibrium equation:

$$\begin{aligned} {{\mathbf {K}}^{\psi }}\mathbf {e}_{\text {sys.}}^{\psi }=\left( \mathbf {K}_{{{\Omega }_{r}}}^{\psi }+\mathbf {K}_{\Omega _{r}^{'}}^{\psi } \right) \mathbf {e}_{\text {sys.}}^{\psi }=\mathbf {Q}_{{{\Omega }_{r}}}^{\psi } \end{aligned}$$

(29)

where $\mathbf {K}^\psi$ is the assembled system stiffness matrix consisting of two corresponding parts in the specimen region $\Omega _{r}$, and the surrounding space region $\Omega _{r}^{'}$, $\mathbf {e}_\text {sys.}^\psi$ is the assembled system nodal vector associated with the magnetic potential, and $\mathbf {Q}_{\Omega _r}^\psi$ is the generalized force vector obtained in the specimen region. The corresponding expressions in an element domain $\Omega _\text {elem}$ are

$$\begin{aligned} \left. \begin{aligned}&\mathbf {K}_{{{\Omega }_{\text {elem}}}}^{\psi }={{\mu }_{0}}\int _{V}{{{J\mathbf {B}}^{\text {T}}}}{{\left( {{\mathbf {F}}^\text {T}}\mathbf {F} \right) }^{-1}}\mathbf {B}dV \\&\mathbf {Q}_{{{\Omega }_{\text {elem}}}}^{\psi }={{\mu }_{0}}{{\rho }_{r}}\int _{V}{{{\mathbf {B}}^{\text {T}}}}{{\mathbf {F}}^{-1}}\bar{\mathbf {M}}dV \\ \end{aligned} \right\} . \end{aligned}$$

(30)

3.2.2 Mechanical FEM equilibrium equation

Similar to the magnetic FE, the position field is interpolated as $\mathbf {r}=\mathbf {S}{{\mathbf {e}}^{u}}$. Recalling that $\varvec{\upvarepsilon }=\varvec{\upvarepsilon }^\text {el}+\xi _2 {\varvec{\upvarepsilon }^{\text {tr}}}$, the equilibrium equation can be written as

$$\begin{aligned} \mathbf {Q}_{\text {sys.}}^{\text {s}}+\mathbf {Q}_{\text {sys.}}^{\text {tr}}+\mathbf {Q}_{\text {sys.}}^{\text {mag}}=\mathbf {Q}_{\text {sys.}}^{\text {ext}} \end{aligned}$$

(31)

where $\mathbf {Q}_{\text {sys.}}^{\text {s}}$ is the assembled system elastic force, $\mathbf {Q}_{\text {sys.}}^{\text {tr}}$ is the assembled system force associated with the martensite variant transformation, $\mathbf {Q}_{\text {sys.}}^{\text {mag}}$ is the assembled magneto-mechanical coupling force derived from the magnetostatic energy $U_{\text {sta}}$ as shown in Eq. (14), and $\mathbf {Q}_{\text {sys.}}^{\text {ext}}$ is the assembled system external generalized force. All the forces are defined in the specimen region, and the expressions of the internal forces on the element level are as follows:

$$\begin{aligned} \left. \begin{aligned}&\mathbf {Q}_{{{\Omega }_{\text {elem}}}}^{\text {s}}={{\rho }_{r}}{{\int _{V}{\left( \frac{\partial \varvec{\upvarepsilon }_{v}^{\text {el}}}{\partial {{\mathbf {e}}^{u}}} \right) }}^{\text {T}}}\mathbf {C\varepsilon }_{v}^{\text {el}}dV \\&\mathbf {Q}_{{{\Omega }_{\text {elem}}}}^{\text {tr}}={{\rho }_{r}}{{\int _{V}{\xi _2\left( \frac{\partial \varvec{\upvarepsilon }_{v}^{\text {el}}}{\partial {{\mathbf {e}}^{u}}} \right) }}^{\text {T}}} \mathbf {C\varepsilon }_{v}^{\text {tr}}dV \\&\mathbf {Q}_{{{\Omega }_{\text {elem}}}}^{\text {mag}}=\frac{1}{2}\rho \mu _0 {\int _{V}\begin{bmatrix} \psi _{,x}\mathbf {S}_d-\psi _{,y}\mathbf {S}_b \\ \psi _{,y}\mathbf {S}_a-\psi _{,x}\mathbf {S}_c \end{bmatrix}^\text {T}\bar{\mathbf {M}}}dV \\ \end{aligned} \right\} \end{aligned}$$

(32)

where the intermediate vectors $\mathbf {S}_a,\ \mathbf {S}_b,\ \mathbf {S}_c$, and $\mathbf {S}_d$ are

$$\begin{aligned} \left. \begin{aligned}&\mathbf {S}_a=\mathbf {S}_{,X}(1,:) \quad \mathbf {S}_b=\mathbf {S}_{,X}(2,:) \\&\mathbf {S}_c=\mathbf {S}_{,Y}(1,:) \quad \mathbf {S}_d=\mathbf {S}_{,Y}(2,:) \end{aligned} \right\} \end{aligned}$$

(33)

where $(i,\ :),\ i=\text {1,2}$ means the i th row of the derivative of the shape function matrix in the reference configuration $\mathbf {S}_{,X}$ or $\mathbf {S}_{,Y}$, which can be obtained by

$$\begin{aligned} \left. \begin{aligned}&\mathbf {S}_{,X}=\left[ \mathbf {J}_0(2,2)\mathbf {S}_{,x}-\mathbf {J}_0(2,1)\mathbf {S}_{,y}\right] /\text {det}(\mathbf {J}_0)\\&\mathbf {S}_{,Y}=\left[ \mathbf {J}_0(1,1)\mathbf {S}_{,y}-\mathbf {J}_0(1,2)\mathbf {S}_{,x}\right] /\text {det}(\mathbf {J}_0) \end{aligned} \right\} \end{aligned}$$

(34)

where $\mathbf {J}_0(i,j)~i,j=1,2$ is the term at the i th row and j th column of the mapping matrix $\mathbf {J}_0$ as shown in Eq. (27). The generalized nodal force of the external pressure on the element level is

$$\begin{aligned} \mathbf {Q}_{{{\Omega }_{\text {elem}}}}^{\text {ext}}=-\int _{A}{{{\mathbf {S}}^{\text {T}}} {{t}_\text {A}}\mathbf {n}_\text {A}dA} \end{aligned}$$

(35)

where $\mathbf {n}_\text {A}$ is the unit outward normal vector of the end specimen surface, on which the compression with magnitude of $t_\text {A}$ is applied. Unlike the equilibrium equation of the magnetic FEM solver as shown in Eq. (29), the counterpart in the mechanical FEM solver Eq. (31) is nonlinear and solved via the Newton–Raphson iteration.

3.2.3 Equation of motion

To predict the dynamic mechanical response of a sample, the equation of motion should be established. Based on the principle of virtual work, the equation of motion on the element level can be written as

$$\begin{aligned} \mathbf {M}_{\Omega _{elem}}\ddot{\mathbf {e}}^u+\mathbf {Q}_{\Omega _{elem}}^\text {s}+\mathbf {Q}_{\Omega _{elem}}^\text {tr}+\mathbf {Q}_{\Omega _{elem}}^\text {mag}=\mathbf {Q}_{\Omega _{elem}}^\text {ext} \end{aligned}$$

(36)

where $\mathbf {M}_{\Omega _{elem}}$ is the element mass matrix, and $\ddot{\mathbf {e}}^u$ is the second time derivative of the nodal vector $\mathbf {e}^u$ associated with the position field. For the ANCF element, the element mass matrix is

$$\begin{aligned} \mathbf {M}_{\Omega _{elem}}=\rho _r\int _V\mathbf {S}^\text {T}\mathbf {S}dV. \end{aligned}$$

(37)

Clearly, the mass matrix remains constant in the integration loop of the equation of motion, which is calculated only once beforehand bringing computational merit. In this work, the equation of motion (37) is solved via an implicit integration generalized-$\alpha$ method [6].

3.3 Framework of numerical solution

Besides the displacement and magnetic field solution obtained from the FEM solver presented in Sect. 3.2, the internal state variables $p=\{\xi _2,\ \theta , \ \alpha \}$ need to be determined as the input variables for the FEM solver. To some extent, the internal state variables act as the bridge that connects displacement and magnetic field. Therefore, the numerical solution procedure must integrate the sub-solver of the internal state variables p into the procedure.

Considering the natural constraint $-1\le \sin \theta \le 1$, the evolution law of $\sin \theta$ can be determined by recalling Eq. (22),

$$\begin{aligned} \sin \theta = {\left\{ \begin{array}{ll} 1 &{} {F_\theta }\left( {H_a},\psi \right) > 1 \\ F_\theta &{} -1\le {{F}_{\theta }}\left( {{H}_{a}},\psi \right) \le 1 \\ -1 &{} {F_\theta }\left( {H_a},\psi \right) < -1 \end{array}\right. }, \end{aligned}$$

(38)

where ${F_\theta }\left( {H_a},\psi \right) =\frac{{\mu _0}{M_s}}{2{K_u}}\left( {H_a}+{H_{dy}} \right)$. Based on the physical interpretation of the domain volume fraction $\alpha$, $0\le \alpha \le 1$. Recalling Eq. (23) and substituting ${{f}^{\alpha }}\left( \alpha \right) =2{{\mu }_{0}}{{M}_{s}}H_{cri}^{\alpha }{{\left( \alpha -1/2 \right) }^{2}}$ [30] results in

$$\begin{aligned} \alpha = {\left\{ \begin{array}{ll} 1 &{} {F_\alpha }> 1 \\ F_\alpha &{} 0 \le {F_{\alpha }} \le 1 \\ 0 &{} {F_\alpha }< 0 \\ \end{array}\right. } \end{aligned}$$

(39)

where ${F_\alpha }=\left[ 1+\left( {H_a}+{H_{dy}} \right) /H_{cri}^{\alpha } \right] /2$, and $H_{cri}^\alpha$ is a critical magnetic field value. Equation (40) can be written based on Eq. (21) and the physical constraint $0\le \xi _2 \le 1$ as

$$\begin{aligned} \xi _2 = {\left\{ \begin{array}{ll} 1 &{} {\xi _2}^{*} > 1 \\ {\xi _2}^{*} &{} \exists {{\xi _2}^{*}}\in \left[ 0,1 \right] {{\left. F_{\xi _2 }^{\pm } \right| }_{\xi _2 ={{\xi _2 }^{*}}}}=0 \\ 0 &{} {\xi _2}^{*} < 0 \end{array}\right. } \end{aligned}$$

(40)

where ${\xi _2}^{*}$ is the solution of $F_{\xi _2 }^{\pm }=\rho _r (\pm {{D}^{\pm }}-{{\pi }^{\xi _2 }})=0$. The dissipative resistances ${{D}^{\pm }}\left( \xi _2 \right)$ and intermediate function ${{\pi }^{\xi }}\left( \mathbf {r},\psi ,\xi _2 ,\theta ,\alpha \right)$ are defined as

$$\begin{aligned} \left. \begin{aligned}&{{\rho }_{r}}{{D}^{+}}\left( \xi _2 \right) ={{A}_{1}}\xi _2 +{{B}_{1}} \quad {{\rho }_{r}}{{D}^{-}}\left( \xi _2 \right) ={{A}_{2}}\xi _2 +{{B}_{2}}{{\rho }_{r}}\\&\rho _r {{f}^{\xi }}\left( \xi _2 \right) =B\xi _2 \left( 1-\xi _2 \right) \quad \rho _r {{f}^{\alpha }}\left( \alpha \right) =2\mu _0 M_s H_{cri}^\alpha \left( \alpha -\frac{1}{2}\right) ^2 \\&\rho _r {{\pi }^{\xi }}=-\left[ \frac{\partial \phi }{\partial \xi _2 }+\frac{\partial {{f}^{\xi }}\left( \xi _2 \right) }{\partial \xi _2 }+{{f}^{\alpha }}\left( \alpha \right) -{{f}^{\alpha }}\left( \frac{1}{2} \right) \right. \\&\quad \left. -{K_u}{{\sin }^{2}}\theta -{{\mu }_{0}}{M_s}\left( {H_a}+{H_{dy}} \right) \left( 2\alpha -1-\sin \theta \right) \right] \\ \end{aligned} \right\} \end{aligned}$$

(41)

where $A_i,B_i,~i=1,2$ and B are constants in the dissipative resistances and mixture energy density. By substituting Eq. (41) into $F_{\xi _2 }^{\pm }=\rho _r\left( \pm {{D}^{\pm }}-{{\pi }^{\xi }}\right)$, it is possible to write $F_{\xi _2 }^{\pm }$ into a quadratic equation,

$$\begin{aligned} F_{\xi _2 }^{\pm }=a^*{{\xi _2 }^{2}}+{{b}^{\pm }}\xi _2 +{{c}^{\pm }}, \end{aligned}$$

(42)

where the coefficients are

$$\begin{aligned} \left. \begin{aligned}&a^*=\frac{3}{2}\varvec{\upvarepsilon }_{v}^{\text {tr}\text {T}}\mathbf {C}^{21}\varvec{\upvarepsilon }_v^{\text {tr}} \\&b^{\pm }=2\varvec{\upvarepsilon }_v^{\text {tr}\text {T}}\mathbf {C}^{21}\varvec{\upvarepsilon }_v^{\text {el}}+\varvec{\upvarepsilon }_{v}^{\text {el}\text {T}}\mathbf {C}^1\varvec{\upvarepsilon }_{v}^{\text {tr}}\pm c_{1}^{\pm } \\&c^{\pm }=\frac{1}{2}\varvec{\upvarepsilon }_{v}^{\text {el}\text {T}}\mathbf {C}^{21}\varvec{\upvarepsilon }_{v}^{\text {el}}+\varvec{\upvarepsilon }_{v}^{\text {tr}\text {T}}{{\mathbf {C}}^{1}}\varvec{\upvarepsilon }_{v}^{\text {el}}\pm c_{2}^{\pm }+c_3 \\ \end{aligned} \right\} \end{aligned}$$

(43)

where $\mathbf {C}^{21}=\mathbf {C}^2-\mathbf {C}^1$, $c_1^\pm$ and $c_2^\pm$ are four constants associated with ${{D}^{\pm }}$, and ${c_3}\left( \psi ,\theta ,\alpha \right)$ is an intermediate variable independent of $\xi _2$. The signs in front of $c_{1}^{\pm }$ and $c_{2}^{\pm }$ are “+” and “-”, respectively, for the forward and reverse transformation process. Their expressions are

$$\begin{aligned} \left. \begin{aligned}&c_{1}^{+}={{A}_{1}}-2B \quad c_{1}^{-}={{A}_{2}}+2B \\&c_{2}^{+}={{B}_{1}}+B \qquad c_{2}^{-}={{B}_{2}}-B \\&{{c}_{3}}=2{{\mu }_{0}}{{M}_{s}}H_{cri}^{\alpha }{{\left( \alpha -1/2 \right) }^{2}}-{{K}_{u}}{{\sin }^{2}}\theta \\&\quad -{{\mu }_{0}}{{M}_{s}}\left( {H_a}+{H_{dy}} \right) \left( 2\alpha -1-\sin \theta \right) \\ \end{aligned} \right\} . \end{aligned}$$

Normally, there are two roots for the quadratic equation (40) evolution law. Here, due to the equality of $\varepsilon _1$ and $\varepsilon _2$, the quadratic equation (42) degenerates to a linear equation by substituting Eqs. (7) and (8) into Eq. (43). As a result, $\xi _2$ can be uniquely determined by Eq. (40).

Figure 3a shows the flow chart of the modified two-loop numerical simulation procedure based on [31, 32]. The procedure comprises three solvers, i.e., the mechanical FE solver, the magnetic FE solver, and the evolution solver of the internal state variables. These solvers solve the corresponding partial differential equations to, respectively, obtain the displacement, the scalar magnetic potential, and the internal state variables of the specimen. Because the convergence speed and the computational cost for each numerical solver is different, the procedure is divided into two loops. Solving the displacement field is set as the outer loop, while the magnetic potential $\psi$ and the internal state variables $p=\left\{ \xi _2\ ,\theta \ ,\alpha \right\}$ are calculated in the internal loop. The iterative procedure keeps calculating and updating the state of the specimen until the residual is smaller than the specified tolerance. In the outer loop, the residual in the axial strain is adopted. To improve efficiency, a linear predictor is adopted to determine the initial value of each step based on the converged values obtained in the previous two steps. Specifically, the initial value of the variables in the next step is predicted as $S_0^{(1)}=(1+\lambda )S^{(0)}-\lambda S^{(-1)}$, where S is the collection of the unknown variables to be determined. The subscript “0” indicates the initial value, the subscript ”1” indicates the value that has been updated after the solution in the corresponding solver, the superscripts “1”, “0” and “-1” denote the next, current, and previous step, and $\lambda$ is the ratio between the current and the previous step. Based on the static analysis, the dynamic analysis flow chart is shown in Fig. 3b. The compression is set as the time-dependent variable to introduce the algorithm. In each time step, the equation of motion is firstly solved, and the position DOFs $\mathbf{r} _1^{(0)}$ are calculated by the integrator loop with the mechanical FE solver. Then, the magnetic field and internal variables are solved associated with $\mathbf{r} _1^{(0)}$. The obtained $\mathbf{r} _1^{(0)},\psi _1^{(0)}$, and $p_1^{(0)}$ are passed to the next outer loop step if the strain difference between the current step and the last step in the inner loop is smaller than the tolerance.

Fig. 3

Flow chart of the numerical procedure to simulate the magnetic shape memory effect

4 Numerical examples

Numerical examples are presented in this Section to assess the performance of the proposed element with respect to the comparison with the classical FE. Firstly, two typical behaviors of the MSMA are simulated: the specimen under a changing magnetic field and the specimen undergoing various compressions. Accordingly, two key features of the MSME, i.e., the memory effect and the superelastic effect, are simulated. Then, a permanent magnet with the surrounding space is analyzed to further check the accuracy of the ANCF element in the pure magnetostatic analysis. Finally, the dynamic mechanical response of the MSMA specimen under a time-dependent compression is simulated.

4.1 Simulation of the magnetic shape memory effect

Figure 1a illustrates the typical experiment that examines magnetic-field-induced strain generation under auxiliary compression. This situation is simulated to verify the new element and the presented numerical procedure. The magnetic field problem is essentially unbounded. To simulate the problem under the framework of the FEM, a simple truncation technique is adopted with a ten-fold larger space surrounding the specimen. As shown in Fig 4a, the scalar magnetic potential on the boundary of the surrounding space is set to zero [31]. With regard to the mechanical constraints, nodes on the middle plane of the specimen are restricted along the x direction, and the position of the center node is fixed such that the rigid motion mode is removed to avoid a singularity in the static displacement analysis. The specimen adopted in [31] is analyzed in this Section. The dimensions of the specimen domain ${{\Omega }_{r}}$ and the surrounding space domain $\Omega _{r}^{'}$ are

$$\begin{aligned}{{\Omega }_{r}}:10\times 5\times 5~\text {mm}\quad \Omega _{r}^{'}:100\times 50\times 50~\text {mm}.\end{aligned}$$

To induce the magnetic shape memory effect, auxiliary compression of magnitude $t_\text {A}$ is applied along the x axis, and an external magnetic field $\mathbf {H}_a$ is applied along the positive y axis direction. Exploiting symmetry, only a quarter model is adopted. Correspondingly, the boundary conditions of the magnetic and displacement field change as shown in Fig. 4b. For the magnetic field, a zero scalar magnetic potential constraint is applied on the horizontal antisymmetric edge. The normal component of the potential gradient is set to zero on the symmetric edge nodes. For the displacement field, an additional constraint is applied at the y position on the horizontal antisymmetric edge nodes.

Fig. 4

Analysis model of the specimen with the surrounding space

The specimen is meshed using the FE with both $\mathbf {e}^u$ and $\mathbf {e}^\psi$ as nodal vectors. The surrounding space is modeled by the FE with only $\mathbf {e}^\psi$ as nodal vectors. Internal state variables are directly calculated on the Gauss integration points of each element. Besides the constructed ANCF FE, classical FEs including the linear and 8-node quadrilateral FE are also adopted to simulate the MSME process.

The single-crystalline Ni-Mn-Ga alloy in the 5M structure martensite state is analyzed, and the constitutive matrix is shown in Eq. (7). The material parameters adopted in the literature [31] are

$$\begin{aligned} \left. \begin{aligned}&{{\kappa }_{1}}=1.70\times {{10}^{11}}~\text {N}/{{\text {m}}^{2}} \qquad ~~~ {{\kappa }_{2}}=1.50\times {{10}^{11}}~\text {N}/{{\text {m}}^{2}} \\&{{\kappa }_{3}}={{\kappa }_{4}}=1.52\times {{10}^{11}}~\text {N}/{{\text {m}}^{2}} \quad {{\kappa }_{5}}={{\kappa }_{6}}=0.43\times {{10}^{11}}~\text {N}/{{\text {m}}^{2}} \\&{{\rho }_{r}}=8.3\times {{10}^{3}}~\text {Kg}/{{\text {m}}^{3}}\qquad ~~~{{\rho }_{r}}{{M}_{s}}=5.64\times {{10}^{5}}~\text {A}/\text {m}\\&{{\rho }_{r}}{{K}_{u}}=1.772\times {{10}^{5}}~\text {Kg/ }\!\![\!\!\text { m}\cdot {{\text {s}}^{\text {2}}}\text { }\!\!]\!\!\text { } \quad {{\varepsilon }_{\text {1}}}={{\varepsilon }_{2}}=0.06 \\ \end{aligned}\right\} . \end{aligned}$$

Other parameters associated with the magnetization, the anisotropy energy, the mixture energy, and the dissipative resistances are [31]

$$\begin{aligned} \left. \begin{aligned}&H_{\text {cri}}^{\alpha }=1.0\times {{10}^{4}}~\text {A}/\text {m} \qquad c_{1}^{+}=3.115\times {{10}^{3}}~\text {N}/{{\text {m}}^{2}} \\&c_{1}^{-}=-1.046\times {{10}^{4}}~\text {N}/{{\text {m}}^{2}} \quad c_{2}^{+}=6.324\times {{10}^{4}}~\text {N}/{{\text {m}}^{2}}\\&c_{2}^{-}=5.070\times {{10}^{4}}~\text {N}/{{\text {m}}^{2}} \\ \end{aligned}\right\} . \end{aligned}$$

The meshing schematic diagram of the specimen and the surrounding space are shown in Fig. 5. The converged results obtained with $n_1=n_3=16$ and $n_2=8$ are presented in the following Sections.

Fig. 5

Schematic diagram of meshing strategy

4.1.1 Magnetic-field-induced strain at a constant compression level

A specimen under a constant compression and various magnetic field strengths is analyzed quasi-statically by gradually increasing or decreasing the applied magnetic field. The external magnetic field ${{\mathbf {H}}_a}=1\times {{10}^{6}}{{\mathbf {e}}_{2}}~\text {A/m}$, and the initial step size is set as $2\times {{10}^{4}}~\text {A/m}$. Both the forward and the reverse process are simulated. Compression $t_\text {A}=1.0$ MPa is applied along the x axis on the specimen. Figure 6 shows the average magnetic-field-induced strain and the effective magnetization magnitude.

Fig. 6

Field-strain and field-magnetization curves under compression $t_\text {A}$=1.0 MPa

The numerical model effectively describes MSME hysteresis behavior. A full forward and reverse martensite variant reorientation process is obtained under the compression $t_\text {A}=1.0\ \text {MPa}$. As shown in Fig. 6, different data points on the ANCF curve marked using arrows are numbered from 1 to 6 for the sake of description. Table 1 lists the internal state parameters and macro-variables in the corresponding configurations.

Table 1 The state of the specimen in the intermediate configurations under compression $t_\text {A}=1~\text {MPa}$

In the initial configuration 1, the specimen exhibits the single variant and domain state. Applying the external field, the specimen is magnetized via the rotation of the magnetization vector. At the beginning, the magnetization is not strong enough to initiate the variant reorientation. With the increase in the external field strength and the subsequent rise in magnetization, variant two appears in configuration 2. After configuration 2, as shown in Fig. 6b, the increase in the magnetization becomes faster due to both magnetization vector rotation and variant reorientation in this stage. Later, the variant two volume fraction reaches nearly 1 in configuration 3. Then, the rotation of the magnetization vector keeps increasing and nearly goes to $90^\circ$ in the final configuration 4. Consequently, the specimen is fully magnetized, and the induced strain nearly reaches its maximum value of 0.06. Then, at the beginning stage of the reverse process, e.g., in configuration 5, the magnetization vector in variant one rotates back towards the compression direction, but the induced strain remains mostly unchanged. After the field decreases to a critical value, strain begins decreasing. In the next configuration 6, variant one recovers to $56\%$ and the effective magnetization becomes 0.44$M_s$ due to the further decrease in the external field strength. With the removal of the external field, variant one almost totally recovers. As a result, the induced strain and the magnetization vanish. The different paths in the forward and reverse process clearly show the hysteresis response of the induced strain and magnetization.

To get a further interpretation on the evolution of the internal state of the specimen, the distribution of the magnitude of the effective magnetization $\bar{M}$ and the variant two under two intermediate magnetic field strengths $H_a=5.0\times 10^5$ and $7.0\times 10^5$ A/m is plotted in Figs. 7 and 8. As shown in Fig. 7, the distribution of magnetization is not uniform. Specifically, the maximum magnitude appears on the edges while the minimum magnetization is found in the center region. This is consistent with the illustration in [31]. Correspondingly, a nonuniform distribution of variant two is also observed in Fig. 8 before variant reorientation is complete. As a result, a non-homogeneous deformation mode appears regardless of the uniform uni-axial loading. In detail, little shrink appears on the vertical edge. This is because the elastic moduli tensor becomes different in various regions of the specimen due to the induced different internal state variables or the internal micro-states in different local regions. However, this non-homogeneous phenomenon disappears with the increase in the magnetic field strength since the internal state variables reach their “saturation” value and are uniform throughout the specimen domain. This intermediate non-homogeneous phenomenon is not observed in the solution given by the linear FE due to its limited ability to describe non-uniform strain in an element.

Fig. 7

Distribution of the effective magnetization magnitude under compression $t_A$=1.0 MPa (ANCF solution)

Fig. 8

Distribution of the variant two volume fraction $\xi _2$ under compression $t_A$=1.0 MPa (ANCF solution)

4.1.2 The superelastic response of the MSMA subjected to a constant magnetic field

In this Section, the stress–strain response of the specimen under a constant external magnetic field is investigated. The superelastic effect under a constant magnetic field is another special feature of the magnetic shape memory alloy. The specimen is studied initially in the single variant two state. Under compression, variant two transforms to variant one. Consequently, the MSMA exhibits a superelastic response, where a small increase in compression induces a significant increase in strain. In contrast to the MFIS simulation in Sect.  4.1.1, the induced strain is negative here. Under the field of $\mu _0 H_a=1.0\;\text {T}$, compression is generally applied from 0 and 5 MPa in a quasi-static process. Figure  9 shows the stress–strain curve. The ANCF element effectively describes the superelastic behavior of the MSMA. However, similar to the comparison in Sect. 4.1.1, the result given by ANCF FE slightly deviates from those given by classical FEs.

Fig. 9

The stress–strain curves of the MSMA sample calculated at $\mu _0 H_a=1.0\;\text {T}$

In summary, the introduced ANCF element is capable of simulating the special behavior of the MSMA and following the full process of the generation of MFIS. However, the ANCF element results do not fully agree with the results obtained from the two classical FEs as shown in Figs. 6 and 9. To explore the cause for this deviation, the new element is examined in a pure magnetostatic analysis in the following Section.

4.2 Magnetostatic analysis of a permanent magnet

A pure magnetostatic analysis as shown in Fig. 10 is performed using the ANCF element in this Section. The magnetic field inside a bulk permanent magnet domain $\Omega _r$ and the surrounding space $\Omega _{r}^{'}$ are analyzed. The dimensions of the $\Omega _r$ and $\Omega _{r}^{'}$ are the same with the model in Sect. 4.1. Magnetization $\mathbf {M}$ is 750 A/m along the positive y axis.

Fig. 10

Permanent magnet model with continuity and boundary conditions

For this magnetostatic problem without free current, the Maxwell equations degenerate to $\nabla \cdot \mathbf {B}=0$ due to the use of the scalar magnetic potential $\psi$ and the relation $\mathbf {H}=-\nabla \psi$, where $\mathbf {B}$ is the magnetic flux density. The constitutive relations in the magnet and surrounding space domain are

$$\begin{aligned} \left. \begin{aligned}&\mathbf {B}=\mu _0(\mathbf {H}+\mathbf {M})&\text {in} \ \Omega _r \\&\mathbf {B}=\mu _0\mathbf {H}&\text {in} \ \Omega _{r}^{'} \end{aligned}\right\} . \end{aligned}$$

(44)

As shown in Fig. 10a, the interface continuity conditions between two domains are

$$\begin{aligned} \left. \begin{aligned}&\llbracket \mathbf {B}\rrbracket \cdot \mathbf {n}_d=0 \\&\llbracket \mathbf {H}\rrbracket \times \mathbf {n}_d=\mathbf {0} \end{aligned}\right\} \end{aligned}$$

(45)

where $\llbracket \cdot \rrbracket$ indicates the jump between the variable value on the two interface sides, and $\mathbf {n}_d$ is the normal vector of the interface directing from $\Omega _r$ to $\Omega _{r}^{'}$. In other words, the normal component of $\mathbf {B}$ and the tangential component of $\mathbf {H}$ are continuous on the interface. In the framework of the variational principle, such interface continuity conditions enter into the FE formulation as the nodal loads on the interface $\Omega _r\cap \Omega _{r}^{'}$ as shown in Eq. (B.6) in the detailed derivation in Appendix B. Besides the interface continuity conditions, the magnetic insulation condition $\mathbf {B}\cdot \mathbf {n}=0$ is applied on the boundaries in this analysis, where $\mathbf {n}$ is the outward normal vector on the boundary $\partial \Omega _{r}^{'}$. As was the case for the analysis in Sect. 4.1, only a quarter model is analyzed as shown in Fig. 10b. All the conditions on the boundaries $\Gamma _3\sim \Gamma _6$ and the interface $\Gamma _1\sim \Gamma _2$ in the specific model are shown in Fig. 10b and Table 2.

Table 2 Boundary conditions (BCs) of the quarter model

Among the whole conditions, all the Neumann conditions automatically hold under the framework of the variational principle method or the finite element method as shown in Appendix B. The equality constraints of the scalar potential and the tangential gradient are automatically satisfied by assigning a unique value on the interface nodes using FEM as shown in Appendix C. The remaining continuity condition $\llbracket \mathbf {B}\rrbracket \cdot \mathbf {n}=0$ leads to the nodal load on the interface $\mathbf {Q}=\int _{\Gamma _d} (-\mathbf {M}\cdot \mathbf {n}_d)\mathbf {S}^\text {T} d\Gamma _d$, where $\Gamma _d$ is the interface. In summary, the only boundary condition that needs to be explicitly applied is the Dirichlet condition on $\Gamma _3$. The model is analyzed using the classical linear quadrilateral element, the classical 8-node quadratic quadrilateral element, and the proposed ANCF magnetic quadrilateral element. The result provided by the commercial software COMSOL is used as the reference. In the element implementation, it is important to notice the difference between ANCF FE and the classical FE. Using magnetic potential gradients as additional nodal degrees of freedom, the ANCF element brings a disadvantage, i.e., extra explicit constraints on the nodal gradients should be applied to be consistent with the Neumann boundary conditions (BCs) on $\Gamma _4\sim \Gamma _6$ in the ANCF element implementation. The distribution of the component of the magnetic field $\mathbf {H}$ along the y axis is shown in Fig. 11. To get a clear look into the interface, the local region $0.02\times 0.01~\text {m}^2$ is presented in Fig. 11. A unique range is employed in all the Figures for the sake of comparison.

Fig. 11

Distribution of $H_y$ in the permanent magnet model

It is clear that the magnetic field calculated by the classical elements agrees well with that obtained by COMSOL, while the ANCF element cannot give a close result. This is because the ANCF element introduces gradients as nodal degrees of freedom, which implies that all the gradient components of $\psi$ on the nodes are manually assigned to be equal on the two interface sides. These explicit equality constraints on the interface nodes largely change the local distribution of the normal gradient on the interface though the ANCF element cannot lead to a continuous normal gradient at the non-node side points (the proof is presented in Appendix C). However, based on the different constitutive relations as shown in Eq. (44) in two domains and the continuity conditions as shown in Eq. (45), in this specific analysis there is a jump in the y axis component of the magnetic field the $\mathbf {H}$ on the horizontal interface $\Gamma _1$. Looking into the value of $H_y$ on interface node A as shown in Fig. 10b, the classical linear and 8-node quadrilateral elements give a jump of 725 A/m and 750.3 A/m on the domain interface, respectively. These are close to the theoretical value 750 A/m. According to the above analysis, the jump in $H_y$ on interface $\Gamma _1$ should be explicitly guaranteed on the nodes in the ANCF analysis. To handle the normal gradient gap issue, two equivalent options are available. For the first option, an extra set of nodes can be introduced on the interface. In the meantime, the constraints setting the magnetic potential and the tangential gradient of the two sets of nodes to be equal are applied. As a result, only the normal magnetic potential gradients of the second set of nodes are independent DOFs. Alternatively, rather than the extra set of nodes, another set of independent normal gradients on the interface nodes can be directly introduced. Either of them will bring a new set of independent gradients to the system. Due to the straightforward implementation, the first procedure is adopted in this paper to release the implicit full equality constraints on the magnetic potential gradients of the interface nodes in the original model. By doing so, the ANCF analysis is expected to be improved. Figure 12 shows the obtained distribution of $H_y$.

Fig. 12

Distribution of $\mathbf {H}_y$ obtained by the ANCF element with additional set of interface nodes

Apparently, the solution is improved, and the jump in $H_y$ on the interface is captured. However, the obtained gap value $\llbracket {H}_y\rrbracket =803$ A/m on point A is still farther from the reference solution than values obtained using classical finite elements. This is because the jump constraint on $H_y$ is not exactly applied at the interface.

In summary, the cause for the deviation of the ANCF element solution is rooted in the direct adoption of magnetic potential gradients as FE nodal coordinates. This brings an added and even more complicated explicit constraint on the gradients to handle the natural BCs and interface gradient discontinuity. By contrast, in the case of the classical FE, such conditions are implicitly satisfied in the framework of variational principle.

In conclusion, both the classical linear and 8-node quadratic quadrilateral element can give a close result to that obtained by COMSOL. Nevertheless, the ANCF formulation is not recommended in the magnetic analysis with two or more different medium domains if no special operations are taken to handle the domain interface continuity conditions. The reasons are as follows. Firstly, an extra set of nodes or additional corresponding gradient DOFs need be introduced to capture the “jump” of the corresponding magnetic field component on the domain interface. Additionally, complicated constraints need to be explicitly applied on the interface nodes to guarantee the continuity conditions on the domain interface. To exactly describe the interface continuity condition, the gap value on the corresponding field component must be obtained in advance, which is virtually impossible in problems without analytical solutions. Therefore, the ANCF FE must be improved for the two-domain MSME analysis. As an alternative, using the ANCF FE for the deformation analysis but the classical FE for the magnetic field analysis can be a good option. From the perspective of interpolation, the displacement is described using the cubic 12-term interpolation while the magnetic potential is interpolated with lower order bases without gradients as interpolation conditions. Figure 13 shows the MSME simulation results obtained using mixed FEs, i.e., ANCF FE and linear FE.

Fig. 13

Field-strain and field-magnetization curves under compression $t_A$=1.0 MPa

Apparently, the mixed FEs strategy works well since it gives very close results to those obtained by the classical FE while keeping all potential benefits of the ANCF approach in the mechanical analysis involving large deformation. Additionally, the simulation time of the mixed FEs strategy is less than half (around $45\%$) that of the original ANCF simulation. The mixed FEs strategy provides an attractive way to integrate the ANCF method in the MSME analysis of the complicated specimen with large deformation.

4.3 Dynamic mechanical response of MSMA specimen

In this Section, the dynamic mechanical response of the MSMA specimen under a constant magnetic field and a high-frequency cyclic compression is simulated via the mixed FEs strategy. The same specimen as employed in Sect. 4.1 is adopted. Referring to [8, 16], a linearly varying compression is used as the mechanical impact. As shown in Fig. 14a, the magnitude of the compression is 5 MPa, and the period is 0.02 s. The magnetic field is $\mu _0H_a=1.0\ \text {T}$, which guarantees a full superelastic loop for the studied sample as shown in Fig. 9. As was the case in Sect. 4.1.2, the specimen is initially in the single variant two state. The generalized-$\alpha$ integrator with a numerical damping is used for the solution of the equation of motion. The mechanical response of the sample is shown in Fig. 14b.

Fig. 14

Dynamic simulation of MSMA sample

As shown in Fig. 14b, the mechanical response of the MSMA sample consists of 6 stages. From A to B, the sample exhibits elastic axial contraction under the effect of compression $t_A$. With the increase in compression, the transformation from variant 2 to variant 1 begins at point B, and the macro-axial strain jumps to the maximum induced strain 0.06 at point C. The increase in compression only leads to a tiny elastic growth in the axial strain. Corresponding to the peak value of 5 MPa at 0.01 s, the axial strain reaches the maximum at point D. Similarly, as compression drops, the sample demonstrates elastic behavior in segment DE and FG and decreases sharply from E to F as a result of the variant transformation. During the simulation, there is vibration on the strain at point C and F due to the inertial effect. This cannot be seen in the quasi-static analysis [10]. As was the case in [8], a switch-like response of the axial strain is obtained. The validity of the proposed approach is verified.

As a summary of the numerical examples Section, a clarification is made as follows. This work tries to check the possibility of applying the ANCF method to the MSME analysis not just to propose a new magneto-mechanical element. As a first step, the ANCF method is implemented for both mechanical and magnetic field via a magneto-mechanical ANCF element. It is demonstrated that the approach can well capture the key behaviors of MSME. Meanwhile, the limitations of this approach are highlighted, which come from the magnetic part of the analysis. As a measure for overcoming those difficulties, a mixed FEs strategy is proposed, in which ANCF is only used in the mechanical part, and the magnetic equations are solved using classical FEs. This approach keeps inherent advantages of ANCF in the mechanical part but is free from the limitations mentioned above in the magnetic part of the analysis. This mixed approach has also an advantage in computational time with respect to the approach when ANCF is used in both mechanical and magnetic parts of the analysis.

5 Conclusions

This paper explores a possible way to simulate the magnetic shape memory effect with large deformation based on the absolute nodal coordinate formulation. The surrounding space is accounted for, and the nonlinear bidirectional coupling terms between the magnetic field and the mechanical field are considered. The newly constructed ANCF magneto-mechanical element is capable of describing the full generation process of the magnetic-field-induced strain and capturing the special features of the magnetic shape memory effect including field-strain/magnetization hysteresis and the superelastic effect. The difference between the results obtained using the ANCF element and the classical element is discussed, and the cause for the deviation is analyzed using a pure two-domain magnetostatic problem. The conclusion is drawn that the ANCF element should be used carefully with appropriate constraints for the two-domain MSME simulation such that the corresponding gradient discontinuity on the interface is suitably satisfied. A mixed FEs strategy, which adopts ANCF FE in the displacement field solver and classical FE in the magnetic field solver, is proposed as an alternative option to fix the problem. The mixed FEs approach shows high agreement with the classical FE on tracking the generation of MFIS in the sample under a varying magnetic field. Additionally, the method predicts the dynamic response of the MSMA sample under a cyclic compression. With relatively low computational cost, the mixed FEs approach can be an attractive way to integrate the ANCF method in the MSME analysis of a complicated specimen with large deformation. Future work will focus on the handling of the gradient jump issues in the two-domain magnetic shape memory effect simulation.

Appendices

Appendix A. Shape functions of the ANCF element

The shape functions $s_i, i=1,2,...,12$ of the ANCF planar quadratic element [21] are

$$\begin{aligned} \left. \begin{array}{l} s_1=(\eta - 1)(\xi - 1)(- 2\eta ^{2} + \eta - 2\xi ^{2} + \xi + 1)\\ s_2=-l\xi (\eta - 1)(\xi - 1)^2\\ s_3=-w\eta (\eta - 1)^2(\xi - 1)\\ s_4=-\xi (\eta - 1)(- 2\eta ^{2} + \eta - 2\xi ^{2} + 3\xi )\\ s_5=-l\xi ^{2}(\eta - 1)(\xi - 1)\\ s_6=w\eta \xi (\eta - 1)^2\\ s_7=-\eta \xi (2\eta ^{2} - 3\eta + 2\xi ^{2} - 3\xi + 1)\\ s_8=l\eta \xi ^{2}(\xi - 1)\\ s_9=w\eta ^{2}\xi (\eta - 1)\\ s_{10}=-\eta (\xi - 1)(- 2\eta ^{2} + 3\eta - 2\xi ^{2} + \xi )\\ s_{11}=l\eta \xi (\xi - 1)^2\\ s_{12}=-w\eta ^{2}(\eta - 1)(\xi - 1)\\ \end{array} \right\} \end{aligned}$$

where $\xi =x/l,~\eta =y/w$ are the local normalized coordinates in the straight configuration, and $0\le \xi , \eta \le 1$, and l and w are the element length and width in the straight configuration.

Appendix B. Variational principle of a general two-domain magnetostatic problem

To get a clear understanding on the boundary conditions and the interface continuity conditions, the variational principle of a general two-domain magnetostatic problem is presented here. The problem is shown in Fig. 15.

Fig. 15

General two-dimensional magnetostatic model

One can assume that $\Omega _1$ is a permanent magnet domain with a constant magnetization $\mathbf {M}$ and $\Omega _2$ is a free space domain. Therefore, the constitutive relations are shown in Eq. (44). Recalling the illustration in Sect. 4.2, the governing differential equation is

$$\begin{aligned} \nabla \cdot \mathbf {B}=\nabla \cdot \mathbf {H}=-\frac{\partial }{\partial {x}}\left( \frac{\partial {\psi }}{\partial {x}}\right) -\frac{\partial }{\partial {y}}\left( \frac{\partial {\psi }}{\partial {y}}\right) =0. \end{aligned}$$

(B.1)

It should be noted that Eq. (B.1) is derived based on the constant magnetization assumption and holds on the whole domain. Without loss of generality, the boundary conditions are

$$\begin{aligned} \left. \begin{aligned}&\psi =p\quad \text {on}\ \Gamma _1 \\&\left( \frac{\partial \psi }{\partial {x}}\hat{\mathbf {x}}+\frac{\partial \psi }{\partial {y}}\hat{\mathbf {y}}\right) \cdot \mathbf {n}+\gamma \psi =q\qquad \text {on}\ \Gamma _2 \end{aligned}\right\} \end{aligned}$$

(B.2)

where $\hat{\mathbf {x}}$ and $\hat{\mathbf {y}}$ are the unit direction vectors of the axes, and $\mathbf {n}$ is the unit outward normal vector on boundary $\Gamma _2$. The first and second term are classified into the Dirichlet BC and the natural BC, respectively. The natural BCs can be implicitly satisfied in the framework of variational principle as shown in the following formulation. Specifically, in the case of $\gamma =0$ and $q=0$, the second term degenerates to the magnetic insulation condition. Besides the BCs as shown in Eq. (B.2), the interface conditions as shown in Eq. (45) should be satisfied. Recalling the constitutive relations Eq. (44), the first term in Eq. (45) is

$$\begin{aligned} \left[ \left( \frac{\partial \psi ^+}{\partial {x}}\hat{\mathbf {x}}+\frac{\partial \psi ^+}{\partial {y}}\hat{\mathbf {y}}\right) -\left( \frac{\partial \psi ^-}{\partial {x}}\hat{\mathbf {x}}+\frac{\partial \psi ^-}{\partial {y}}\hat{\mathbf {y}}\right) \right] \cdot \mathbf {n}_d=\mathbf {M}\cdot \mathbf {n}_d\quad \text {on}\ \Gamma _d \end{aligned}$$

(B.3)

where $\psi ^+$ and $\psi ^-$ are the potentials on the two sides of the interface, and $\mathbf {n}_d$ is the interface normal vector directing from $\Omega _1$ to $\Omega _2$. The second term in Eq. (45) can be satisfied automatically in the framework of FEM. The two-domain magnetostatic problem can be fully described by Eqs. (B.1–B.3). The equivalent variational formulation is

$$\begin{aligned} \left. \begin{aligned}&\delta {F}(\psi )=0 \\&\psi =p\qquad \text {on}\ \Gamma _1 \end{aligned}\right\} \end{aligned}$$

(B.4)

where the functional expression is

$$\begin{aligned} \begin{aligned}&F(\psi )=\frac{1}{2}\iint _\Omega \left[ \left( \frac{\partial \psi }{\partial {x}}\right) ^2+\left( \frac{\partial \psi }{\partial {y}}\right) ^2\right] d\Omega \\&\qquad \qquad +\int _{\Gamma _2}\left( \frac{\gamma }{2}\psi ^2-q\psi \right) d\Gamma +\int _{\Gamma _d}\left( -\mathbf {M}\cdot \mathbf {n}_d\right) {\psi }d\Gamma . \end{aligned} \end{aligned}$$

(B.5)

The FEM equilibrium equation can be obtained based on Eqs. (B.4) and (B.5). In the specific permanent magnet case as shown in Sect. 4.2, $\gamma =q=0$, and the equilibrium equation on the element level is

$$\begin{aligned} \int _{\Omega _{\text {elem}}}{\left( \mathbf {S}_{,x}^\text {T}\mathbf {S}_{,x}+\mathbf {S}_{,y}^\text {T}\mathbf {S}_{,y}\right) }d\Omega {\mathbf {e}^\psi }=\int _{\Gamma _d}{\left( \mathbf {M}\cdot \mathbf {n}_d\right) \mathbf {S}^\text {T}}d\Gamma . \end{aligned}$$

(B.6)

The proof between Eq. (B.4) and the PDE description Eqs. (B.1–B.3) is presented as follows. Taking the first variation of $F(\psi )$ with respect to $\psi$, one obtains

$$\begin{aligned} \begin{aligned}&\delta {F}=\iint _{\Omega _1}\left[ \left( \frac{\partial \psi }{\partial {x}}\right) \left( \frac{\partial {\delta \psi }}{\partial {x}}\right) +\left( \frac{\partial \psi }{\partial {y}}\right) \left( \frac{\partial {\delta \psi }}{\partial {y}}\right) \right] d\Omega \\&\qquad \qquad +\iint _{\Omega _2}\left[ \left( \frac{\partial \psi }{\partial {x}}\right) \left( \frac{\partial {\delta \psi }}{\partial {x}}\right) +\left( \frac{\partial \psi }{\partial {y}}\right) \left( \frac{\partial {\delta \psi }}{\partial {y}}\right) \right] d\Omega \\&\qquad \qquad \int _{\Gamma _2}\left( \gamma \psi -q\right) \delta {\psi }d\Gamma +\int _{\Gamma _d}\left( -\mathbf {M}\cdot \mathbf {n}_d\right) {\delta \psi }d\Gamma . \end{aligned} \end{aligned}$$

(B.7)

Based on the partial integration rules,

$$\begin{aligned}\left. \begin{aligned}&\left( \frac{\partial \psi }{\partial {x}}\right) \left( \frac{\partial {\delta \psi }}{\partial {x}}\right) = \frac{\partial }{\partial {x}}\left( \frac{\partial \psi }{\partial {x}}\delta \psi \right) -\frac{\partial }{\partial {x}}\left( \frac{\partial \psi }{\partial {x}}\right) \delta \psi \\&\left( \frac{\partial \psi }{\partial {y}}\right) \left( \frac{\partial {\delta \psi }}{\partial {y}}\right) = \frac{\partial }{\partial {y}}\left( \frac{\partial \psi }{\partial {y}}\delta \psi \right) -\frac{\partial }{\partial {y}}\left( \frac{\partial \psi }{\partial {y}}\right) \delta \psi \end{aligned}\right\} , \end{aligned}$$

and the divergence theorem,

$$\begin{aligned} \iint _{\Omega }\left( \frac{\partial {U}}{\partial {x}}+\frac{\partial {V}}{\partial {y}}\right) d\Omega =\oint _{\Gamma }\left( U\hat{\mathbf {x}}+V\hat{\mathbf {y}}\right) \cdot \mathbf {n}d\Gamma , \end{aligned}$$

Eq. (B.7) can be written as

$$\begin{aligned} \begin{aligned} \delta {F}&=\iint _{\Omega _1}\left[ -\frac{\partial }{\partial {x}}\left( \frac{\partial {\psi }}{\partial {x}}\right) -\frac{\partial }{\partial {y}}\left( \frac{\partial {\psi }}{\partial {y}}\right) \right] \delta {\psi }d\Omega +\iint _{\Omega _2}\left[ -\frac{\partial }{\partial {x}}\left( \frac{\partial {\psi }}{\partial {x}}\right) -\frac{\partial }{\partial {y}}\left( \frac{\partial {\psi }}{\partial {y}}\right) \right] \delta {\psi }d\Omega \\&\quad +\oint _{\partial \Omega _1}\left[ \left( \frac{\partial \psi }{\partial {x}}\hat{\mathbf {x}}+\frac{\partial \psi }{\partial {y}}\hat{\mathbf {y}}\right) \hat{\mathbf {n}}\right] \delta {\psi }d\Gamma +\oint _{\partial \Omega _2}\left[ \left( \frac{\partial \psi }{\partial {x}}\hat{\mathbf {x}}+\frac{\partial \psi }{\partial {y}}\hat{\mathbf {y}}\right) \hat{\mathbf {n}}\right] \delta {\psi }d\Gamma \\&\quad +\int _{\Gamma _d}\left( -\mathbf {M}\cdot \mathbf {n}_d\right) {\delta \psi }d\Gamma +\int _{\Gamma _2}\left( \gamma \psi -q\right) \delta {\psi }d\Gamma \end{aligned}\end{aligned}$$

(B.8)

where $\partial \Omega _1=\Gamma _1+\Gamma _d^+$ and $\partial \Omega _2=\Gamma _2+\Gamma _d^-$ are the full boundaries of domain $\Omega _1$ and $\Omega _2$. Noting that $\psi$ is constant on $\Gamma _1$, and therefore the spatial gradient vanishes, Eq. (B.8) can be simplified to

$$\begin{aligned} \begin{aligned} \delta {F}&=\iint _{\Omega }\left[ -\frac{\partial }{\partial {x}}\left( \frac{\partial {\psi }}{\partial {x}}\right) -\frac{\partial }{\partial {y}}\left( \frac{\partial {\psi }}{\partial {y}}\right) \right] \delta {\psi }d\Omega \\&\quad +\int _{\Gamma _d}\left[ \left( \frac{\partial \psi ^+}{\partial {x}}\hat{\mathbf {x}}+\frac{\partial \psi ^+}{\partial {y}}\hat{\mathbf {y}}\right) \hat{\mathbf {n}}_d^++\left( \frac{\partial \psi ^-}{\partial {x}}\hat{\mathbf {x}}+\frac{\partial \psi ^-}{\partial {y}}\hat{\mathbf {y}}\right) \hat{\mathbf {n}}_d^--\mathbf {M}\cdot \mathbf {n}_d\right] \delta {\psi }d\Gamma \\&\quad +\int _{\Gamma _2}\left[ \left( \frac{\partial \psi }{\partial {x}}\hat{\mathbf {x}}+\frac{\partial \psi }{\partial {y}}\hat{\mathbf {y}}\right) \hat{\mathbf {n}}+\gamma \psi -q\right] \delta {\psi }d\Gamma \end{aligned}\end{aligned}$$

(B.9)

where $\mathbf {n}_d=\mathbf {n}_d^+$ and $\mathbf {n}_d^-$ are the outward normal vectors of $\Omega _1$ and $\Omega _2$ on the interface. Accounting for $\mathbf {n}_d^+=-\mathbf {n}_d^-$ and the arbitrariness of $\delta {\psi }$, the equivalence between Eq. (B.4) and the PDE description Eqs. (B.1–B.3) is presented.

Appendix C. Tangential gradient continuity proof for the ANCF element

The tangential gradient continuity on the interface between the two adjacent elements is verified as follows. As shown in Fig. 16, four arbitrary points are picked to check their tangential gradient along the corresponding edge. Substituting the normalized coordinates $(\xi ,\eta )$ into the shape function matrix, the corresponding tangential gradients are obtained as Eq. C.1,

$$\begin{aligned} \left. \begin{aligned}&\psi _{,x}^A=f_1(\psi _1-\psi _2)+f_2\psi _{1,x}+f_3\psi _{2,x}\\&\psi _{,y}^B=f_4(\psi _2-\psi _3)+f_5\psi _{2,y}+f_6\psi _{3,y}\\&\psi _{,x}^C=f_1(\psi _4-\psi _3)+f_2\psi _{4,x}+f_3\psi _{3,x}\\&\psi _{,y}^D=f_4(\psi _1-\psi _4)+f_5\psi _{1,y}+f_6\psi _{4,y} \end{aligned}\right\} , \end{aligned}$$

(C.1)

Fig. 16

The generalized ANCF planar quadrilateral element

where the intermediate coefficients are

$$\begin{aligned} \left. \begin{aligned}&f_1=\frac{6\xi (\xi -1)}{l}, ~ f_2=3\xi ^{2}-4\xi +1, ~ f_3 = \xi (3\xi -2) \\&f_4=\frac{6\eta (\eta -1)}{w}, ~ f_5=3\eta ^{2}-4\eta +1, ~ f_6 = \eta (3\eta -2) \end{aligned}\right\} . \end{aligned}$$

Apparently, as shown in the above equations, the tangential gradient on the element edge depends only on the coordinates of the related two nodes. In other words, the tangential gradient is continuous between the two adjacent elements. Therefore, the tangential gradient continuity as shown in the second term of Eq. (45) is proved. This tangential gradient continuity cannot be exactly guaranteed and proved by the classical FEs. However, it turns out that the obtained tangential gradients on the two sides along the element edge are quite close and the influence is small. To clarify the source of the problem in ANCF analysis, the normal gradient continuity is also checked for the ANCF element as Eq. (C.2),

$$\begin{aligned} \left. \begin{aligned}&\psi _{,y}^A=f_7(\psi _2-\psi _1+\psi _4-\psi _3)+(1-\xi )\psi _{1,y}+\xi \psi _{2,y}+f_8\left[ (\xi -1)(\psi _{4,x}-\psi _{1,x})+\xi (\psi _{3,x}-\psi _{2,x})\right] \\&\psi _{,x}^B=f_9(\psi _2-\psi _1+\psi _4-\psi _3)+(1-\eta )\psi _{2,x}+\eta \psi _{3,x}+f_{10}\left[ (\eta -1)(\psi _{2,y}-\psi _{1,y})+\eta (\psi _{3,y}-\psi _{4,y})\right] \\&\psi _{,y}^C=f_7(\psi _2-\psi _1+\psi _4-\psi _3)+(1-\xi )\psi _{4,y}+\xi \psi _{3,y}+f_8\left[ (\xi -1)(\psi _{4,x}-\psi _{1,x})+\xi (\psi _{3,x}-\psi _{2,x})\right] \\&\psi _{,x}^D=f_9(\psi _2-\psi _1+\psi _4-\psi _3)+(1-\eta )\psi _{1,x}+\eta \psi _{4,x}+f_{10}\left[ (\eta -1)(\psi _{2,y}-\psi _{1,y})+\eta (\psi _{3,y}-\psi _{4,y})\right] \end{aligned}\right\} ,\nonumber \\ \end{aligned}$$

(C.2)

where the intermediate functions $f_i,i=7,8,9,10$ are given as follows:

$$\begin{aligned}\left. \begin{aligned}&f_7=\frac{1}{w}\xi (2\xi ^2-3\xi +1), ~ f_8=\frac{l}{w}\xi (\xi -1) \\&f_9=\frac{1}{l}\eta (2\eta ^2-3\eta +1), ~ f_{10}=\frac{w}{l}\eta (\eta -1) \end{aligned}\right\} . \end{aligned}$$

Clearly, the normal gradient of the magnetic potential on the element edge depends not only on the DOFs of the related two nodes but also the DOFs of the other two nodes. In other words, the normal gradient is not continuous between the two adjacent elements by default. Therefore, the element is not a $C^1$-continuous element. As similar statement can also be found in [12]. Since the ANCF element cannot lead to a continuous normal gradient of the magnetic potential at the arbitrary non-node point on the element side, the derivation of the ANCF analysis result essentially comes from the use of gradients as DOFs at the nodes.