Simulation of magnetised microstructure evolution based on a micromagnetics-inspired FE framework: application to magnetic shape memory behaviour

Abstract

Microstructure evolution in magnetic materials is typically a non-local effect, in the sense that the behaviour at a material point depends on the magnetostatic energy stored within the demagnetisation field in the entire domain. To account for this, we propose a finite element framework in which the internal state variables parameterising the magnetic and crystallographic microstructure are treated as global fields, optimising a global potential. Contrary to conventional micromagnetics, however, the microscale is not spatially resolved and exchange energy terms are neglected in this approach. The influence of microstructure evolution is rather incorporated in an effective manner, which allows the computation of meso- and macroscale problems. This approach necessitates the development and implementation of novel mixed finite element formulations. It further requires the enforcement of inequality constraints at the global level. To handle the latter, we employ Fischer–Burmeister complementarity functions and introduce the associated Lagrange multipliers as additional nodal degrees-of-freedom. As a particular application of this general methodology, a recently established energy-relaxation-based model for magnetic shape memory behaviour is implemented and tested. Special cases—including ellipsoidal specimen geometries—are used to verify the magnetisation and field-induced strain responses obtained from finite element simulations by comparison to calculations based on the demagnetisation factor concept.

Appendix

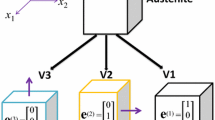
In previous works, see, for example, [34], the magnetic state of the underlying two-dimensional microstructure was parametrised by using the net magnetisations $\eta _i$ of both martensite variants, the deviations of the magnetisation vectors from the magnetic easy axes characterised by angles $\theta _j$ in each of the four magnetic domains, and the martensite volume fractions $\xi _i$. Results of numerical simulations suggested that the deviations of the magnetisation vectors within one martensite variant are not independent, since the optimal deviations were $\theta _2\!=\!-\theta _1$ and $\theta _4\!=\!-\theta _3$. This relation can be shown analytically, allowing a reparametrisation of the underlying microstructure by simultaneously decreasing the number of constraints. In the following derivations, only one variant of martensite is considered, i.e. $\xi _1\!=\!1$. The second martensite variant may be treated analogously.

In the first step, the effective magnetisation of the first martensite variant ${\varvec{m}}^{*}_1$ is defined as

$$\begin{aligned} {\varvec{m}}^{*}_1 = \gamma _1\,[\cos (\theta _1)\,\varvec{e}_1+\sin (\theta _1)\,{\varvec{e}}_2] + [1-\gamma _1]\,[-\cos (\theta _2)\,\varvec{e}_1-\sin (\theta _2)\,{\varvec{e}}_2], \end{aligned}$$

(71)

where $\gamma _i\!=\!0.5\,[\,\eta _i/\xi _i + 1\,]$, with $0 \!\le \!\gamma _i\!\le \! 1$, denote the magnetic domain volume fractions and $-\pi /2\!\le \!\theta _j\!\le \!\pi /2$. Note that here magnetisation vectors are introduced for each domain of one martensite variant, whereas in the modelling framework described in Sect. 3 an effective magnetisation vector for the whole variant is used. This approach is interpretable as the introduction of a plane spanned by the magnetisations of the two domains ${\varvec{m}}_j$, where several combinations of those and the domain volume fraction $\gamma _1$ yield the same effective magnetisation ${\varvec{m}}^{*}_1$. It is assumed that the angle $\theta _2$ minimises the anisotropy energy density. In the following, $\gamma _1\!\ne \!0$ and $\gamma _1\!\ne \!1$ shall hold, i.e. both domains exist, and $\theta _j\!\ne \!\pm \pi /2$. The anisotropy energy density of the first martensite variant ($\xi _1\!=\!1$, $\eta _1$ replaced by $\gamma _1$) $\psi ^{\,\mathrm {an}}_1\!=\!\gamma _1\,\sin ^2(\theta _1) + [\,1-\gamma _1\,]\,\sin ^2(\theta _2)$ is reformulated using (71) via

$$\begin{aligned} \frac{\psi ^{\,\mathrm {an}}_1}{k_1} = \frac{m_{12}^2 + 2\,m_{12}\,[\,1-\gamma _1\,]\,\sin (\theta _2) + [\,1-\gamma _1\,]\,\sin ^2(\theta _2)}{\gamma _1}. \end{aligned}$$

(72)

The partial derivative of (72) w.r.t. $\theta _2$ results in

$$\begin{aligned} \frac{1}{k_1}\,\frac{\partial \psi ^{\,\mathrm {an}}_1}{\partial \theta _2} = \frac{2\,[\,1-\gamma _1\,]}{\gamma _1}\,\cos (\theta _2)\,\left[ \,m_{12} + \sin (\theta _2)\,\right] . \end{aligned}$$

(73)

The necessary condition for a minimum w.r.t. $\theta _2$ states $\partial _{\theta _2} \psi ^{\,\mathrm {an}}_1\!=\!0$, which, under the assumptions mentioned above, is always satisfied for $m_{12}\!=\!-\sin (\theta _2)$ or $\cos (\theta _2)\!=\!0$. The second partial derivative of (72) w.r.t. $\theta _2$, i.e.

$$\begin{aligned} \frac{1}{k_1}\,\frac{\partial ^2 \psi ^{\,\mathrm {an}}_1}{\partial \theta _2^2} = \frac{2\,[\,1-\gamma _1\,]}{\gamma _1}\,\left[ \,\cos ^2(\theta _2) - \sin (\theta _2)\,\left[ \,m_{12} + \sin (\theta _2)\,\right] \,\right] \end{aligned}$$

(74)

is used to check the sufficient condition for a minimum, respectively, maximum. Insertion of $m_{12}\!=\!-\sin (\theta _2)$ into (74) yields

$$\begin{aligned} k_1\,\frac{2\,[\,1-\gamma _1\,]}{\gamma _1}\,\cos ^2(\theta _2) > 0,\quad \text {for}\quad \cos (\theta _2)\ne 0, \end{aligned}$$

(75)

viz. the sufficient condition for a minimum. The insertion of $\cos (\theta _2)\!=\!0$ into (74) yields

$$\begin{aligned} k_1\,\frac{2\,[\,1-\gamma _1\,]}{\gamma _1}\,\left[ \,-\sin ^2(\theta _2) - \sin (\theta _2)\,m_{12}\,\right]< 0,\quad \text {for}\quad -1< m_{12} < 1, \end{aligned}$$

(76)

viz. the sufficient condition for a maximum. Since (71) must be fulfilled, the cases $\cos (\theta _2)\!=\!0, m_{12}\!=\!-1$ and $m_{12}\!=\!1$ yield either $\theta _2\!=\!-\theta _1$ or $\gamma _1\!=\!0$, respectively, $\gamma _1\!=\!1$, which was excluded in the assumptions mentioned above. As a consequence, the anisotropy-related energy density is minimised for a given effective magnetisation ${\varvec{m}}^{*}_1$ with $\theta _2\!=\!-\theta _1$. The derivation for the second martensite variant follows by analogy and yields $\theta _4\!=\!-\theta _3$. Note that the number of state variables can therefore be reduced by two: instead of $[\,\eta _1, \eta _2, \theta _1, \theta _2, \theta _3, \theta _4\,]^{\,\mathrm {t}}$, the new set of variables $[\,m_{11}, m_{12}, m_{21}, m_{22}\,]^{\,\mathrm {t}}$ is used for the FE implementation, where, in addition, the number of inequality constraints is reduced from 14 to four.