1 Introduction

Routh introduced his technique [22] for conservative mechanical systems in the form of a hybrid Lagrangian and Hamiltonian description. The advantage of this Routhian formalism becomes apparent when so-called cyclic coordinates are present in the system. By decoupling the cyclic coordinates and the related hidden motion of the system, Routh’s method gives fewer number of ordinary differential equations, which are also called the equations of essential motion. The reduced model captures the essential dynamics of the given system. The so-called hidden motion, that is, the time evolution of the cyclic coordinates, can be reconstructed based on the essential motion. The model reduction also makes it easier to investigate the dynamical behavior either analytically or numerically. Moreover, the stability of certain steady-state motions can be analyzed by means of Lyapunov functions that are based on the so-called Routh potential [23].

To this day, the Routh reduction is still part of active research. For example, a new application of the Routh reducibility is presented in [20] and novel examples are revisited such as the tipple top on a cylinder’s surface [1]. The Routhian approach served as basis for several generalizations like the new model reduction techniques in [19], or for the extension of the theory like the one for discrete systems in [13].

Controllability is a crucial property of every control system; a system is controllable if any initial state can be transferred to any desired state in a finite length of time by some control action [15,16,17]. Main applications include redundancy/safety checking, optimal control, filter design, computer vision or stabilizing unstable states by feedback [3, 14, 17, 24], to mention a few only.

In the present paper, the Kalman controllability of cyclic mechanical systems is analyzed where external actuation is restricted to the cyclic coordinates, while the essential coordinates serve as the output states. As it is illustrated by several examples, this is a quite common and natural scenario in practice. In Sect. 2, the general methodology is presented for obtaining the reduced mechanical models, and the state-space model of the reduced system is given in closed form. A chain of theorems is presented which provide conditions of Kalman controllability based on reduced size rank conditions. By means of the kinetic energy of the Routh reducible system, one of the theorems present necessary conditions for Kalman controllability without constructing the full mechanical model or the corresponding state-space model.

In Sect. 3, these results are demonstrated on the control of four nonlinear Routh reducible mechanical systems. The first two examples, the well-known Furuta pendulum and the double inverted pendulum highlight the advantages of the extended reduction methodology: compared with the literature (see [5, 18]), reduced size models and reduced rank controllability conditions are obtained. The third example of the Wilson pendulum [11] demonstrates the application of the theorems when uncontrollability is proven in a Routh reducible system. The last example of a rotor model [10] represents the limitation of the reduction methodology when the Kalman controllability condition applied for the full state model cannot be simplified to reduced rank conditions.

2 Routh reducible systems and their control

2.1 Setup

Consider an \(n\ge 2\)-degree-of-freedom (DoF) holonomic mechanical system with external active forces; the equations of motion can be obtained by the Lagrangian equations of the 2nd kind in the form

$$\begin{aligned} \frac{\mathrm d}{\mathrm d t} \frac{\partial L}{\partial \dot{y}_k} - \frac{\partial L}{\partial y_k}&= Q_k\,, \end{aligned}$$
(1)

where L is the Lagrangian function, \(y_k\), \(k=1,\dots ,n\) are the generalized coordinates and \(Q_k\), \(k=1,\dots ,n\) are the generalized forces. The Lagrangian L can be expressed as

$$\begin{aligned} L=T-V, \end{aligned}$$

where the kinetic energy T is a function of the generalized coordinates \(y_k\) and velocities \(\dot{y}_k\), while the potential function V depends on \(y_k\) only. For scleronomic mechanical systems, where only time-independent geometric constraints are present, the general form of the kinetic energy is:

$$\begin{aligned} T=\frac{1}{2}\dot{{\mathbf {y}}}^{\mathsf {T}} {\mathbf {M}}({\mathbf {y}}) \dot{{\mathbf {y}}} \,, \end{aligned}$$
(2)

where \({\mathbf {y}} = \mathrm {col}\begin{bmatrix} y_1&\cdots&y_n \end{bmatrix}= \begin{bmatrix} y_k\\ \end{bmatrix}\) is the vector of generalized coordinates, \(\dot{{\mathbf {y}}}\) is the vector of generalized velocities and \({\mathbf {M}}\) is the positive definite nonlinear mass matrix.

At this point, the usual Einstein summation notation is introduced: a repeated index in a product means the summation along that index. In this particular case, the \(\dot{y}_k M_{kl} (y_l)\, \dot{y}_l\) stands for \(\sum _{k=1}^{n}\sum _{l=1}^{n} \dot{y}_k M_{kl}\, \dot{y}_l\) replacing the matrix products in the vector notation (2).

The Lagrangian can be independent of some of the generalized coordinates, which are called cyclic coordinates. The cyclic coordinates can be eliminated from the equations of motion resulting not only in fewer variables, but also in fewer equations [22].

Assume that the n degree of freedom mechanical system has m essential coordinates \(q_i\), \(i = 1,\dots ,m\) (on which the Lagrangian depends) and \(n-m\) cyclic coordinates \(\varphi _\alpha \), \(\alpha = 1,\dots ,n-m\). This way the generalized coordinates can be split in the form

separating and distinguishing the essential and cyclic coordinates. Similarly, the nonlinear mass matrix can be partitioned as

(3)

where \({\mathbf {A}} = [A_{ij}]\) is related to the essential velocities only, \({\mathbf {D}} = [D_{\alpha \beta }]\) is related to the cyclic velocities only, and \({\mathbf {B}} = [B_{i\alpha }]\) refers to their mixed products in the kinetic energy:

$$\begin{aligned} T =\frac{1}{2} \dot{q}_i A_{ij} \dot{q}_j + \dot{q}_i B_{i\alpha } {\dot{\varphi }}_\alpha + \frac{1}{2} {\dot{\varphi }}_\alpha D_{\alpha \beta }{\dot{\varphi }}_\beta \,. \end{aligned}$$

The generalized forces \(Q_\alpha \) along the cyclic coordinates \(\varphi _\alpha \) only; in this case, the Lagrangian equations of 2nd kind assume the form:

$$\begin{aligned} \frac{\mathrm d}{\mathrm d t} \frac{\partial L}{\partial \dot{q}_i} - \frac{\partial L}{\partial q_i}&= 0\,,\quad&i=1,\ldots ,m, \end{aligned}$$
(4)
$$\begin{aligned} \frac{\mathrm d}{\mathrm d t} \frac{\partial L}{\partial {\dot{\varphi }}_\alpha }&= Q_\alpha \,, \quad&\alpha =1,\dots ,n-m. \end{aligned}$$
(5)

From now on, the convention is applied that Latin subscripts (\(i,j,\ldots \)) run between 1 and m, while Greek subscripts (\(\alpha ,\beta ,\ldots \)) run from 1 to \(n-m\) referring to essential and cyclic coordinates, respectively. Following Routh’s classical method [22], the generalized momenta for the cyclic coordinates are introduced as

$$\begin{aligned} p_\alpha =\frac{\partial L}{\partial \dot{\varphi }_\alpha }\,. \end{aligned}$$
(6)

The cyclic velocities \({\dot{\varphi }}_\alpha \) can be expressed generally as a function of the essential positions \(q_i\) and velocities \(\dot{q}_i\) and all the generalized momenta \(p_\beta \):

$$\begin{aligned} {\dot{\varphi }}_\alpha = {\dot{\varphi }}_\alpha (q_i, \dot{q}_i, p_\beta ) \,. \end{aligned}$$
(7)

However, as opposed to the original derivation [6] of Routh, the generalized momenta are not constant in this case due to the presence of external active forces represented by the generalized forces \(Q_\alpha \). Accordingly, from Eqs. (5) and (6), it follows that

$$\begin{aligned} {\dot{p}}_\alpha = Q_\alpha \,. \end{aligned}$$
(8)

If \(p_\alpha ^0\) denotes the initial value of the generalized momentum which is determined by the initial conditions of the system, we obtain

$$\begin{aligned} p_\alpha = \int _{0}^{t} Q_\alpha (\tau )\mathrm {d}\tau + p_{\alpha }^{0}\,. \end{aligned}$$
(9)

2.2 Nonlinear equations of motions

The notation of partial derivatives with respect to positions is merged with the Einstein summation notation by writing the index after a comma in the subscript: for example, \(\partial \Box / \partial y_k = \Box _{,k}\) and \(\partial \Box _{kl} / \partial y_m = \Box _{kl,m}\).

Theorem 1

The nonlinear equations of motion for Routh reducible systems actuated only at the cyclic coordinates are obtained in the form

$$\begin{aligned}&A_{ij}\, \ddot{q}_j - B_{i\alpha }\, (D^{-1})_{\alpha \beta }\, B_{j\beta }\, \ddot{q}_j + \dot{q}_j\, A_{ij,k}\, \dot{q}_k \nonumber \\&\qquad - \frac{1}{2} \dot{q}_j\, A_{jk,i}\, \dot{q}_k -\dot{q}_j\, (B_{i\alpha }\, (D^{-1})_{\alpha \beta }\, B_{j\beta })_{,k}\, \dot{q}_k \nonumber \\&\qquad +\frac{1}{2} \dot{q}_j \, (B_{j\alpha }\, (D^{-1})_{\alpha \beta }\, B_{k\beta })_{,i} \, \dot{q}_k +((D^{-1})_{\alpha \beta }\, B_{i\beta })_{,j}\, \dot{q}_j\, p_\alpha \nonumber \\&\qquad +\frac{1}{2} p_\alpha \, (D^{-1})_{\alpha \beta ,i}\, p_\beta - ((D^{-1})_{\alpha \beta }B_{j\beta })_{,i}\, \dot{q}_j p_\alpha +V_{,i} \nonumber \\&\quad \;\, =-(D^{-1})_{\alpha \beta }\, B_{i\beta }\, Q_\alpha \,, \end{aligned}$$
(10a)
$$\begin{aligned}&\dot{p}_\alpha = Q_\alpha \,. \end{aligned}$$
(10b)

Proof

The generalized momenta are defined as:

$$\begin{aligned} p_\alpha = \frac{\partial L}{\partial {\dot{\varphi }}_\alpha } = \frac{\partial T}{\partial {\dot{\varphi }}_\alpha } = B_{i\alpha }{\dot{q}}_i + D_{\alpha \beta }{\dot{\varphi }}_\beta \,. \end{aligned}$$

Note that the symmetry property \(D_{\alpha \beta }=D_{\beta \alpha }\) is applied here.

The cyclic velocities in Eq. (7) can be obtained as:

$$\begin{aligned} {\dot{\varphi }}_\alpha = (D^{-1})_{\alpha \beta }p_{\beta } - (D^{-1})_{\alpha \beta } B_{i\beta } \dot{q}_i\,, \end{aligned}$$
(11)

where \([(D^{-1})_{\alpha \beta }]\) refers to the inverse matrix of \([D_{\alpha \beta }]\). This important formula is used for eliminating the cyclic velocities in the Routhian

$$\begin{aligned} R =&(p_\alpha {\dot{\varphi }}_\alpha - L )\big |_{(11)} = -\frac{1}{2} \dot{q}_i A_{ij} \dot{q}_j \nonumber \\&+ \frac{1}{2} \dot{q}_i B_{i\alpha } (D^{-1})_{\alpha \beta } B_{j\beta }\dot{q}_j - p_\alpha (D^{-1})_{\alpha \beta }B_{i\beta } \dot{q}_i \nonumber \\&+ \frac{1}{2} p_\alpha (D^{-1})_{\alpha \beta } p_\beta + V\,. \end{aligned}$$
(12)

The nonlinear equations of motion for the essential coordinates are derived from

$$\begin{aligned} - \frac{\mathrm d}{\mathrm d t} \frac{\partial R}{\partial \dot{q}_i} + \frac{\partial R}{\partial q_i} = 0\,. \end{aligned}$$

Evaluating the substitution of the Routhian (12), we obtain

$$\begin{aligned} A&_{ij}\, \ddot{q}_j - B_{i\alpha }\, (D^{-1})_{\alpha \beta }\, B_{j\beta }\, \ddot{q}_j + \dot{q}_j\, A_{ij,k}\, \dot{q}_k \nonumber \\&- \frac{1}{2} \dot{q}_j\, A_{jk,i}\, \dot{q}_k -\dot{q}_j\, (B_{i\alpha }\, (D^{-1})_{\alpha \beta }\, B_{j\beta })_{,k}\, \dot{q}_k \nonumber \\&+\frac{1}{2} \dot{q}_j \, (B_{j\alpha }\, (D^{-1})_{\alpha \beta }\, B_{k\beta })_{,i} \, \dot{q}_k \nonumber \\&+((D^{-1})_{\alpha \beta }\, B_{i\beta })_{,j}\, \dot{q}_j\, p_\alpha +\frac{1}{2} p_\alpha \, (D^{-1})_{\alpha \beta ,i}\, p_\beta \nonumber \\&- ((D^{-1})_{\alpha \beta }B_{j\beta })_{,i}\, \dot{q}_j p_\alpha +V_{,i} \nonumber \\&+(D^{-1})_{\alpha \beta }\, B_{i\beta }\, \dot{p}_\alpha =0\,, \end{aligned}$$

which is identical to Eq. (10a) in Theorem 1 after some algebraic manipulation and using Eq. (8) for replacing the time derivative of the generalized momenta \({\dot{p}}_\alpha \) with the generalized forces \(Q_\alpha \). \(\square \)

2.3 Reduced linearized equations

In case of \(Q_\alpha \equiv 0\), the steady-state motion of the cyclic mechanical system corresponds to the trivial solution \(q_j(t)\equiv q_{j}^\mathrm {eq}\) of the essential equations of motion (10a). This trivial solution is obtained from Eq. (10a) by substituting \(\dot{q}_j^\mathrm {eq}(t)\equiv 0\) and \(\ddot{q}_j^\mathrm {\,eq}(t)\equiv 0\). Using the so-called Routh potential function

$$\begin{aligned} R_0 = \frac{1}{2} p_\alpha \, (D^{-1})_{\alpha \beta }\, p_\beta +V\,, \end{aligned}$$
(13)

the condition of the existence of the steady-state motion is equivalent to the existence of an extremum of \(R_0\), which leads to the condition

$$\begin{aligned} R_{0,i}\big |_{q_j^\mathrm {eq}}=\left. \left( \frac{1}{2} p_\alpha \, (D^{-1})_{\alpha \beta ,i}\, p_\beta +V_{,i}\right) \right| _{q_j^\mathrm {eq}}=0\,. \end{aligned}$$
(14)

Without the loss of generality, this trivial solution can always be chosen to be zero: \(q_{j}^\mathrm {eq}=0\). Generally, the linearized equations can be obtained by the Taylor series expansion of the nonlinear terms and by neglecting the higher order ones. The quantities coming from the nonlinear mass matrix can depend on the generalized coordinates, so these should also be expanded. For example,

$$\begin{aligned} (D^{-1})_{\alpha \beta ,i}&\approx (D^{-1})_{\alpha \beta ,i}\big |_{q_{l}^\mathrm {eq} = 0} + \left. \frac{\partial (D^{-1})_{\alpha \beta ,i}}{\partial q_k}\right| _{q_{l}^\mathrm {eq} = 0} \,\cdot q_k \,+\mathrm {h.o.t.}\nonumber \\&= (d^{-1})_{\alpha \beta ,i} + (d^{-1})_{\alpha \beta ,ik}\, q_k + \mathrm {h.o.t.}\,, \end{aligned}$$

where a new shorthand notation is applied for the expressions at the equilibrium \(q_{j}^\mathrm {eq}\), that is, \( (d^{-1})_{\alpha \beta ,i} := (D^{-1})_{\alpha \beta ,i}^\mathrm {eq}\) and \( (d^{-1})_{\alpha \beta ,ik} := (D^{-1})_{\alpha \beta ,ik}^\mathrm {eq}\).

Theorem 2

If

$$\begin{aligned} (d^{-1})_{\alpha \beta ,i}=0 \end{aligned}$$
(15)

in a Routh reducible system, then the reduced linearized equations of motion at the equilibrium \(q_{l}^{\mathrm {eq}}=0\) can be obtained as

$$\begin{aligned}&a_{ij}\, \ddot{q}_j - b_{i\alpha }\, (d^{-1})_{\alpha \beta }\, b_{j\beta }\, \ddot{q}_j +((d^{-1})_{\alpha \beta }\, b_{i\beta })_{,j}\, \dot{q}_j\, p^{\mathrm {0}}_\alpha \nonumber \\&\qquad - ((d^{-1})_{\alpha \beta }b_{j\beta })_{,i}\, \dot{q}_j p^{\mathrm {0}}_\alpha +\frac{1}{2} p^{\mathrm {0}}_\alpha \, (d^{-1})_{\alpha \beta ,ij}\, p^{\mathrm {0}}_\beta q_j +v_{,ij} q_j \nonumber \\&\quad =-(d^{-1})_{\alpha \beta }\, b_{i\beta }\, Q_\alpha \,. \end{aligned}$$
(16)

Proof

The nonlinear mass matrix \({\mathbf {M}}\) and the potential function V depend on the essential coordinates \(q_i\), but they do not depend on the essential velocities \(\dot{q}_i\). To linearize the equations of essential motion (10a), the Taylor series expansion of \(A_{ij}, B_{i\alpha }, (D^{-1})_{\alpha \beta }\) and \( V_{,i}\) are needed at the equilibrium \(q_{l}^{\mathrm {eq}}=0\):

$$\begin{aligned} A_{ij}&\approx A_{ij}\big |_{q_{l}^{\mathrm {eq}}=0} + \left. \frac{\partial A_{ij}}{\partial q_k}\right| _{q_{l}^{\mathrm {eq}}=0} \,\cdot {}q_k + \mathrm {h.o.t.} \nonumber \\ {}&= a_{ij} + a_{ij,k}\,q_k + \mathrm {h.o.t.}\,, \\ B_{i\alpha }&\approx B_{i\alpha }\big |_{q_{l}^{\mathrm {eq}}=0} + \left. \frac{\partial B_{i\alpha }}{\partial q_k}\right| _{q_{l}^{\mathrm {eq}}=0} \,\cdot {}q_k + \mathrm {h.o.t.} \nonumber \\ {}&= b_{i\alpha } + b_{i\alpha ,k}\,q_k + \mathrm {h.o.t.}\,,\\ (D^{-1})_{\alpha \beta }&\approx (D^{-1})_{\alpha \beta }\big |_{q_{l}^{\mathrm {eq}}=0} + \left. \frac{\partial (D^{-1})_{\alpha \beta }}{\partial q_k}\right| _{q_{l}^{\mathrm {eq}}=0} \,\cdot {}q_k + \mathrm {h.o.t.} \nonumber \\ {}&= (d^{-1})_{\alpha \beta } + (d^{-1})_{\alpha \beta ,k}\,q_k + \mathrm {h.o.t.}\,, \\ (D^{-1})_{\alpha \beta ,i}&\approx (D^{-1})_{\alpha \beta ,i}\big |_{q_{l}^{\mathrm {eq}}=0} + \left. \frac{\partial (D^{-1})_{\alpha \beta ,i}}{\partial q_k}\right| _{q_{l}^{\mathrm {eq}}=0} \,\cdot {}q_k + \mathrm {h.o.t.} \nonumber \\ {}&= (d^{-1})_{\alpha \beta ,i} + (d^{-1})_{\alpha \beta ,ik}\, q_k + \mathrm {h.o.t.}\,, \\ V_{,i}&\approx V_{,i}\big |_{q_{l}^{\mathrm {eq}}=0} + \left. \frac{\partial V_{,i}}{\partial q_k}\right| _{q_{l}^{\mathrm {eq}}=0} \,\cdot {}q_k + \mathrm {h.o.t.} \nonumber \\ {}&= v_{,i} + v_{,ik}\,q_k + \mathrm {h.o.t.} \,. \end{aligned}$$

After substituting these back into Eq. (10a) and dropping the nonlinear higher-order terms of essential coordinates \(q_i\), velocities \(\dot{q}_i\) and accelerations \(\ddot{q}_i\), one obtains:

$$\begin{aligned}&a_{ij}\, \ddot{q}_j - b_{i\alpha }\, (d^{-1})_{\alpha \beta }\, b_{j\beta }\, \ddot{q}_j +((d^{-1})_{\alpha \beta }\, b_{i\beta })_{,j}\, \dot{q}_j\, p_\alpha - ((d^{-1})_{\alpha \beta }b_{j\beta })_{,i}\, \dot{q}_j p_\alpha \nonumber \\ {}&\qquad +\frac{1}{2} p_\alpha \, (d^{-1})_{\alpha \beta ,i}\, p_\beta +\frac{1}{2} p_\alpha \, (d^{-1})_{\alpha \beta ,ij}\, p_\beta q_j +v_{,i} +v_{,ij} q_j =-(d^{-1})_{\alpha \beta }\, b_{i\beta }\, Q_\alpha \,. \end{aligned}$$
(17)

Note that \(p_\alpha \) should be substituted here according to (9). In case of a control feedback loop, assume that the generalized forces \(Q_\alpha \) depend on the time in an implicit form through the time-dependent essential coordinates and essential velocities only \(Q_\alpha (t) := Q_\alpha (q_j(t), \dot{q}_j(t))\), which is a reasonable condition in the presence of feedback control; this means that further nonlinear terms may appear in the corresponding parts of formula (17). These terms are excluded by the condition \( (d^{-1})_{\alpha \beta ,i}=0\) of Theorem 2.

This can also be interpreted in the following way. The classical Routh reducible systems are conservative [22], which means that there are no external excitations: \(Q_\alpha \equiv 0\). Consequently, the derivative of the Routh potential function \(R_0\) with respect to the essential coordinate \(q_i\) is \(R_{0,i} = (1/2) p_\alpha ^0\, (d^{-1})_{\alpha \beta ,i}\, p_\beta ^0 +v_{,i}\), which must be 0 at \(q_l^\mathrm {eq}\). This is a key step to carry out the Routh reduction. Since \(Q_\alpha \ne 0\) in the presence of feedback control, the corresponding generalized momenta are not constant (see Eq. (9)) and the Routh reduction cannot be carried out at the same steady-state motion as in case of \(Q_\alpha \equiv 0\). However, if the condition of Theorem 2 is fulfilled, namely if \( (d^{-1})_{\alpha \beta ,i}=0\), Eq. (16) follows directly from Eq. (17) with substituting \(p_\alpha = p_\alpha ^0 + \mathrm {h.o.t.}\) and keeping only the linear terms in (17). \(\square \)

2.4 Nonlinear reduced equation for systems with a single essential coordinate

Systems with only \(m=1\) essential coordinate lead to further simplifications, even if the number of cyclic coordinates remains unlimited.

Simplify the notation further by denoting the partial derivatives with respect to the only essential coordinate with prime, for example: \( V':={\partial V}/{\partial q}\,,\ \ V'':= {\partial ^2 V}/{\partial q^2}\,. \)

Theorem 3

The essential nonlinear equation of motion for an n degree of freedom cyclic mechanical system with only \(m=1\) essential coordinate can be simplified as:

$$\begin{aligned}&A\ddot{q} - B_\alpha (D^{-1})_{\alpha \beta }B_\beta \ddot{q} + \frac{1}{2}A'{\dot{q}}^2 -\frac{1}{2}\left( B_\alpha (D^{-1})_{\alpha \beta }B_\beta \right) '\! {\dot{q}}^2 \nonumber \\&\quad + \frac{1}{2}(D^{-1})_{\alpha \beta }'p_\alpha p_\beta +V' = -(D^{-1})_{\alpha \beta }B_\beta Q_\alpha \,, \end{aligned}$$
(18a)
$$\begin{aligned} \dot{p}_\alpha&= Q_\alpha \,. \end{aligned}$$
(18b)

Proof

\(m=1\) implies that all Latin indices i, j, k are just ones or can be omitted in Theorem 1 (Eq. (10a)), which results in Eq. (18a) directly. \(\square \)

2.5 Reduced linearized equation for systems with single essential coordinate

Theorem 4

If \( (d^{-1})_{\alpha \beta }'=0\), then the linearized equation of motion at the equilibrium \(q^{\mathrm {eq}}=0\) for an n degree of freedom cyclic mechanical system with only \(m=1\) essential coordinate can be simplified as:

$$\begin{aligned}&\bigg (a - b_\alpha (d^{-1})_{\alpha \beta }b_\beta \bigg ) \ddot{q} + \bigg (\frac{1}{2}p_\alpha ^{\mathrm {0}} (d^{-1})_{\alpha \beta }'' p_\beta ^{\mathrm {0}} +v''\bigg )q \nonumber \\&\quad = -(d^{-1})_{\alpha \beta }b_\beta Q_\alpha \,. \end{aligned}$$
(19)

Proof

By linearizing equation (18) similarly to the proof of Theorem 2, Eq. (19) is obtained if we use the condition \((d^{-1})_{\alpha \beta }'=0\). \(\square \)

2.6 State-space model of controlled Routh reducible systems

The state-space representation [15, 17] of linear dynamical systems is considered in the form:

$$\begin{aligned} \dot{{\mathbf {X}}}&= \tilde{{\mathbf {F}}} {\mathbf {X}} + \tilde{{\mathbf {G}}} {\mathbf {u}} \,, \end{aligned}$$
(20a)
$$\begin{aligned} {\mathbf {z}}&= \tilde{{\mathbf {H}}}{\mathbf {X}}\,, \end{aligned}$$
(20b)

where \({\mathbf {u}}\) is the control input and \({\mathbf {z}}\) is the output. In the case of a n degree of freedom cyclic mechanical system, the state vector \({\mathbf {X}} \in {\mathbb {R}}^{2n}\) contains all the generalized coordinates and velocities:

and the system matrix \(\tilde{{\mathbf {F}}} \in {\mathbb {R}}^{2n\times 2n}\) describes the dynamics of the linear uncontrolled system. Assume that the output \({\mathbf {z}} \in {\mathbb {R}}^{2m}\) contains the measured essential coordinates \(q_j\) and velocities \(\dot{q}_j\) only:

$$\begin{aligned} {\mathbf {z}}&= \mathrm {col}\left[ \begin{array}{cc} q_j&\ {\dot{q}}_j \end{array}\right] . \end{aligned}$$
(21)

According to (20b), this means that the output matrix \(\tilde{{\mathbf {H}}} \in {\mathbb {R}}^{2m\times 2n}\) has the special structure:

$$\begin{aligned} \tilde{{\mathbf {H}}}&= \begin{bmatrix} {\mathbf {I}}_{m\times m} &{}\ {\mathbf {0}}_{(n-m)\times (n-m)} &{}\ {\mathbf {0}}_{m\times m} &{}\ {\mathbf {0}}_{(n-m)\times (n-m)} \\ {\mathbf {0}}_{m\times m} &{}\ {\mathbf {0}}_{(n-m)\times (n-m)} &{}\ {\mathbf {I}}_{m\times m} &{}\ {\mathbf {0}}_{(n-m)\times (n-m)} \end{bmatrix}. \end{aligned}$$

Assume that the control input \({\mathbf {u}}\in {\mathbb {R}}^{n-m}\) acts at the cyclic coordinates \(\big [\varphi _\alpha \big ]\in {\mathbb {R}}^{n-m} \) only. According to (5), this input vector contains the generalized forces

$$\begin{aligned} {\mathbf {u}} = \big [ Q_\alpha \big ]\in {\mathbb {R}}^{n-m}\,. \end{aligned}$$
(22)

The construction of the conditions of Theorem 2 was already motivated by the assumption that the generalized forces depend linearly on the measured essential coordinates and velocities. This corresponds to the input formula

$$\begin{aligned} {\mathbf {u}}&= \mathbf {Kz}\,, \end{aligned}$$
(23)

where \({\mathbf {K}} \in {\mathbb {R}}^{(n-m)\times 2m}\) includes the feedback gains, and the input matrix \(\tilde{{\mathbf {G}}} \in {\mathbb {R}}^{2n\times (n-m)}\) in (20a) has the structure

$$\begin{aligned} \tilde{{\mathbf {G}}} = \mathrm {col} \left[ \begin{array}{cccc} {\mathbf {0}}_{(n+m)\times (n-m)}&\ \tilde{\varvec{\Gamma }}^{}_{(n-m)\times (n-m)} \end{array}\right] , \end{aligned}$$

where \(\tilde{\varvec{\Gamma }} \in {\mathbb {R}}^{(n-m)\times (n-m)}\).

Consider a Routh reducible cyclic mechanical system which is to be controlled along the cyclic coordinates only with feedback gains applied for the measured essential coordinates and velocities only. This yields the following reduced state-space model:

$$\begin{aligned} \dot{{\mathbf {x}}}&= {\mathbf {F}} {\mathbf {x}} + {\mathbf {G}} {\mathbf {u}} \,, \end{aligned}$$
(24a)
$$\begin{aligned} {\mathbf {z}}&= {\mathbf {H}}{\mathbf {x}}\,, \end{aligned}$$
(24b)
$$\begin{aligned} {\mathbf {u}}&= \mathbf {Kz}\,, \end{aligned}$$
(24c)

where the reduced state vector \({\mathbf {x}} \in {\mathbb {R}}^{2m}\) contains only the essential coordinates and velocities

$$\begin{aligned} {\mathbf {x}} = \mathrm {col} \left[ \begin{array}{cc} q_j&\ {\dot{q}}_j \end{array}\right] , \end{aligned}$$
(25)

and the reduced system matrix \({\mathbf {F}}\in {\mathbb {R}}^{2m\times 2m}\) is obtained from the governing equations of the uncontrolled system after the Routh reduction is carried out. Consider that in a general case the output vector \({\mathbf {z}} \in {\mathbb {R}}^{2m}\) is the same as the input vector \({\mathbf {x}}\), that is, the reduced output matrix \({\mathbf {H}} \in {\mathbb {R}}^{2m\times 2m}\) becomes identity:

$$\begin{aligned} {\mathbf {H}} = {\mathbf {I}}\,, \quad {\mathbf {z}}&= {\mathbf {x}}\,. \end{aligned}$$

This means that the control input \({\mathbf {u}}\in {\mathbb {R}}^{n-m}\) of the feedback system is:

$$\begin{aligned} {\mathbf {u}} = \mathbf {Kx}\, \end{aligned}$$
(26)

as it follows from (24). The input matrix \({\mathbf {G}} \in {\mathbb {R}}^{2m\times (n-m)}\) can also be reduced to the form

$$\begin{aligned} {\mathbf {G}} = \mathrm {col} \left[ \begin{array}{cc} {\mathbf {0}}_{m\times (n-m)}&\ {\mathbf {G}}^{(2)}_{m\times (n-m)} \end{array}\right] , \end{aligned}$$

where \({\mathbf {G}}^{(2)} \in {\mathbb {R}}^{m\times (n-m)}\) can be obtained by means of the Routh reduction procedure of the governing equations.

Compared to the full state-space model (20), the main benefits of the reduced state-space formalism (24) are the smaller model size: the size of the state vector is reduced from 2n (all generalized coordinates and velocities) to 2m (only the essential coordinates and velocities); that is, the cyclic dynamics of the system is eliminated from the governing equations.

Moreover, the reduced model is more general in the sense that the standard state-space model (20) is linearized around a fixed point (a static equilibrium of the mechanical system), but the reduced state-space model (24) is linearized around a more general steady-state motion with constant cyclic velocities, which includes the static equilibrium as a special case when the cyclic velocities are zero.

Theorem 5

If \((d^{-1})_{\alpha \beta ,i}=0\) holds in Eq. (15), then the system matrix \( {\mathbf {F}}\) and input matrix \( {\mathbf {G}}\) of the state-space model (24) of a Routh reducible mechanical system can be obtained as:

$$\begin{aligned} {\mathbf {F}}&= \begin{bmatrix} {\mathbf {0}} &{} {\mathbf {I}} \\ {\mathbf {F}}^{(21)} &{} {\mathbf {F}}^{(22)} \end{bmatrix}, \end{aligned}$$
(27a)
$$\begin{aligned} {\mathbf {G}}&= \begin{bmatrix} {\mathbf {0}}\\ {\mathbf {G}}^{(2)} \end{bmatrix}, \end{aligned}$$
(27b)

with

$$\begin{aligned} {\mathbf {F}}^{(21)} = \left[ F^{(21)}_{kj}\right] =&\left[ -\frac{1}{2}c_{ki} p^{0}_\alpha \, (d^{-1})_{\alpha \beta ,ij}\, p^{0}_\beta -c_{ki} v_{,ij} \right] , \end{aligned}$$
(27c)
$$\begin{aligned} {\mathbf {F}}^{(22)} = \left[ F^{(22)}_{kj}\right] =&\ \Big [c_{ki} ((d^{-1})_{\alpha \beta }b_{j\beta })_{,i}\, p^{0}_\alpha \nonumber \\&\ -c_{ki}((d^{-1})_{\alpha \beta }\, b_{i\beta })_{,j}\, p^{0}_\alpha \Big ], \end{aligned}$$
(27d)
$$\begin{aligned} {\mathbf {G}}^{(2)} = \left[ {G}^{(2)}_{k\alpha }\right] =&\ \Big [-c_{ki}(d^{-1})_{\alpha \beta } b_{i\beta }\Big ], \end{aligned}$$
(27e)

where

$$\begin{aligned} c_{ki} = \left( \left( a_{jl} - b_{j\alpha }\, (d^{-1})_{\alpha \beta }\, b_{l\beta }\, \right) ^{-1}\right) _{ki}. \end{aligned}$$
(27f)

Proof

From Eq. (16) in Theorem 2, the generalized accelerations \(\ddot{q}_k\) can be expressed as

$$\begin{aligned} \ddot{q}_k =&c_{ki} ((d^{-1})_{\alpha \beta }b_{j\beta })_{,i}\, p^{\mathrm {0}}_\alpha \dot{q}_j -c_{ki}((d^{-1})_{\alpha \beta }\, b_{i\beta })_{,j}\, p^{\mathrm {0}}_\alpha \dot{q}_j \nonumber \\ {}&-\frac{1}{2}c_{ki} p^{\mathrm {0}}_\alpha \, (d^{-1})_{\alpha \beta ,ij}\, p^{\mathrm {0}}_\beta q_j -c_{ki} v_{,ij} q_j -c_{ki}(d^{-1})_{\alpha \beta } b_{i\beta } Q_\alpha \,, \end{aligned}$$
(28)

where \(c_{ki}\) is the inverse of the Schur complement [26] of the block \(D_{\alpha \beta }\) of the mass matrix \({\mathbf {M}}\) in the form

$$\begin{aligned} c_{ki} = \left( \left( f_{jl} - g_{j\alpha }\, (d^{-1})_{\alpha \beta }\, g_{l\beta }\, \right) ^{-1}\right) _{ki}. \end{aligned}$$

The system matrix \( {\mathbf {F}}\) and the input matrix \({\mathbf {G}}\) of the state-space model (24) are obtained in the form of (27) after some algebraic manipulation by collecting the coefficients of the state variables \({\mathbf {x}}\) in (25) and inputs \({\mathbf {u}}\) in (22). This proves Theorem 5. \(\square \)

2.7 Necessary condition for controllability of Routh reducible mechanical systems

A system is controllable if any initial state can be transferred to any desired state in a finite length of time by some control action [15,16,17].

Theorem 6

A cyclic mechanical system with \((d^{-1})_{\alpha \beta ,i}=0\) (15) is not controllable by feedback of the essential coordinates and velocities with actuation at the cyclic coordinates if

$$\begin{aligned} c_{ki}(d^{-1})_{\alpha \beta } b_{i\beta }=0. \end{aligned}$$
(29)

Proof

Based on the given structure (27b), (27e) of the input matrix \({\mathbf {G}}\) in controlled Routh reducible systems, \(c_{ki}(d^{-1})_{\alpha \beta } b_{i\beta }=0\) implies \({\mathbf {G}} = {\mathbf {0}}\). The system is not controllable if the input matrix \({\mathbf {G}} \) is a zero matrix since the rank of the controllability matrix becomes zero trivially [16]. This proves Theorem 6. \(\square \)

With Theorem 6, the controllability of some cyclic mechanical systems can be excluded by means of the algebraic form of the kinetic energy only, without deriving the equations of motion or the state-space model. Note that the trivial case of \(b_{i\beta }=0\) makes the condition \(c_{ki}(d^{-1})_{\alpha \beta } b_{i\beta }=0\) true, so the controllability can simply be excluded based on the missing off-diagonal segments of the linearized mass matrix.

In general cases, the condition of Theorem 6 is not fulfilled and the controllability of the system can be decided by applying Kalman’s controllability condition [15,16,17]. The system and input matrices \( {\mathbf {F}}\) and \( {\mathbf {G}}\), respectively, can be calculated as given in Theorem 5, and the controllability matrix \({\mathbf {R}}\) can be constructed as

$$\begin{aligned} {\mathbf {R}} = \begin{bmatrix} {{\mathbf {G}}}&{{\mathbf {F}}}{{\mathbf {G}}}&\dots&({{\mathbf {F}}}^{2m-1}){{\mathbf {G}}} \end{bmatrix}. \end{aligned}$$
(30)

According to Kalman’s controllability condition, the system is controllable if the rank of the controllability matrix \({\mathbf {R}}\) is maximal [16], that is, \(\mathrm {Rank}({\mathbf {R}}) = 2m\).

3 Examples

3.1 Furuta pendulum

Fig. 1
figure 1

Furuta pendulum

Full size image

The Furuta pendulum or rotary pendulum [8, 9] is a \(n=2\) degree of freedom mechanical device shown in Fig. 1. Due to the strongly nonlinear dynamical nature and unique dynamical coupling between the coordinates, the device is often used for testing control strategies for swing-up [2, 6, 25] and balancing around the upward unstable equilibrium. The Furuta pendulum has \(m=1\) essential coordinate (the pendulum angle \(\theta \)) and \(n-m=1\) cyclic coordinate (the arm angle \(\varphi \)): \( {\mathbf {q}} = \big [q_1\big ] = \big [\theta \big ] \) and \( \varvec{\varphi }= \big [\varphi _1\big ] = \big [\varphi \big ] \).

The kinetic energy and the potential function are given as:

$$\begin{aligned} T&= \frac{1}{2}J_\mathrm {p} \dot{\theta }^2 + \frac{1}{2}(J_\mathrm {a} + J_\mathrm {p}\sin ^2\theta ) \dot{\varphi }^2 -m_2rl\cos \theta \,\dot{\varphi }\dot{\theta }\ ,\\ V&= m_2gl\cos \theta \,, \end{aligned}$$

where \(J_\mathrm {a} = m_1l_1^2+J_{1} + m_2r^2\) and \(J_\mathrm {p} = m_2l^2 + J_2\); the parameters m and J refer to mass and mass moment of inertia with subscripts referring to the arm and pendulum, while r denotes the length of the arm, l stands for the length of the pendulum, and \(l_1\) is the distance between the arm center of gravity and its axis of rotation.

The nonlinear mass matrix assumes the form:

Since this system has a single essential coordinate, the nonlinear equation of motion can be derived by using Theorem 3:

$$\begin{aligned}&\left( J_\mathrm {p} - \frac{m_2^2r^2l^2\cos ^2\theta }{J_\mathrm {a} + J_\mathrm {p}\sin ^2\theta }\right) \ddot{\theta }+\frac{1}{2}m_2^2r^2l^2\frac{J_\mathrm {a}+J_\mathrm {p}}{(J_\mathrm {a} + J_\mathrm {p}\sin ^2\theta )^2}\dot{\theta }^2 \nonumber \\&\quad \qquad -\left( \frac{J_\mathrm {p}\cos \theta }{(J_\mathrm {a} + J_\mathrm {p}\sin ^2\theta )^2} p^2 +m_2gl\right) \sin \theta = \frac{m_2rl\cos \theta }{J_\mathrm {a} + J_\mathrm {p}\sin ^2\theta }Q\,,\\&\quad \dot{p} =Q\,, \end{aligned}$$

where the single generalized force is the motor torque \(Q=M_\mathrm t\) (see Fig. 1), which acts along the cyclic coordinate \(\varphi \) as a feedback control based on the essential coordinate \(\theta \) and velocity \({\dot{\theta }}\).

If one is interested only in the linearized equation of motion, Theorem 4 can be used to obtain it directly without deriving the nonlinear equation of motion since the condition of the theorem is fulfilled:

$$\begin{aligned} (d^{-1})'=\left. \frac{-2J_\mathrm {p}\sin \theta \cos \theta }{(J_\mathrm {a}+J_\mathrm {p}\sin ^2\theta )^2}\right| _{\theta ^\mathrm {eq}=0} =0\,. \end{aligned}$$
(31)

Either way, the result is:

$$\begin{aligned} \left( J_\mathrm {p} - \frac{m_2^2r^2l^2}{J_\mathrm {a}}\right) \ddot{\theta }-\left( \frac{J_\mathrm {p}}{J_\mathrm {a}^2} {(p^{0})}^2 + m_2gl\right) \theta = \frac{m_2rl}{J_\mathrm {a}} Q\,. \end{aligned}$$

The motion of the system can be interpreted physically together with the differential equation of the hidden motion (7):

$$\begin{aligned} {\dot{\varphi }}&= \frac{p + m_2 r l \cos \theta {\dot{\theta }}}{J_\mathrm {a}+J_\mathrm {p}\sin ^2\theta }\,, \end{aligned}$$

which governs the time variation of the cyclic coordinate \(\varphi \); the cyclic velocity is expressed from the generalized momentum (6):

$$\begin{aligned} p = (J_\mathrm {a} + J_\mathrm {p} \sin ^2\theta )\dot{\varphi }-(m_2rl\cos \theta )\dot{\theta }\,. \end{aligned}$$

The linearization takes place around the steady-state motion where the arm rotates with constant angular velocity \( \dot{\varphi }^\mathrm {eq} = {p^0}/{J_\mathrm {a}} \)

with the essential coordinate \(\theta (t)\equiv \theta ^\mathrm {eq}=0\) of the pendulum at the upward position. The case \(p^{0}=0\) corresponds to the static equilibrium of the Furuta pendulum, which is the standard case considered in the literature [4, 21].

Regarding the controllability of this system, the necessary condition should be checked in Theorem 6 before deriving the state-space model. Since Eq. (31) holds and (27f) and (29) assume the form

$$\begin{aligned} c&=\frac{1}{J_\mathrm {p} - m_2^2r^2l^2/J_\mathrm {a}}\,,\\ c(d^{-1})b&= -\frac{m_2rl}{J_\mathrm {p}J_\mathrm {a} - m_2^2r^2l^2} \ne 0\,, \end{aligned}$$

this system may be controllable and worth to further investigate the state-space model. This can be carried out without the knowledge of equation of motion based on Theorem 5, because Eq. (31) holds. The formulas (27c), (27d) and (27e) assume the form:

$$\begin{aligned} {{F}}^{(21)}&= -\frac{1}{2} c p^0 \left( -\frac{2J_\mathrm {p}}{J_\mathrm {a}^2}\right) p^0-c(-m_2gl) \nonumber \\&= \frac{J_\mathrm {p}\left( p^0\right) ^2}{J_\mathrm {p} J\mathrm {a}^2 -J_\mathrm {a}m_2^2r^2l^2} +\frac{m_2gl}{J_\mathrm {p} - m_2^2r^2l^2/J_\mathrm {a}}\,,\\ {{F}}^{(22)}&= 0\,,\\ {G}^{(2)}&= -c\frac{1}{J_a} m_2rl = -\frac{m_2rl}{J_\mathrm {a} J_\mathrm {p} - m_2^2r^2l^2}\,, \end{aligned}$$

which provide the elements of the system and input matrices \( {{\mathbf {F}}}\) and \( {{\mathbf {G}}}\) in (27d) and (27e), respectively. The controllability matrix \({\mathbf {R}}\) is obtained in the form

$$\begin{aligned} {\mathbf {R}} = \begin{bmatrix} {{\mathbf {G}}}&\ \ {{\mathbf {F}}}\,{{\mathbf {G}}} \end{bmatrix} = \begin{bmatrix} 0 &{} -\frac{m_2rl}{J_\mathrm {a} J_\mathrm {p} - m_2^2r^2l^2}\\ -\frac{m_2rl}{J_\mathrm {a} J_\mathrm {p} - m_2^2r^2l^2} &{} 0 \end{bmatrix}\,; \end{aligned}$$
(32)

its rank is maximal: \(\mathrm {Rank}({\mathbf {R}}) = 2\). Consequently, the Furuta pendulum is controllable along the cyclic coordinate by sensing the essential coordinate and its time derivative only, so an appropriate linear state feedback control law is able to stabilize the pendulum at the upward position.

Similar result can be found in the literature [5] where full state feedback was considered as opposed to the Routh reducibility approach which is based on the observation of the pendulum angular position and angular velocity only. The advantage of our framework is quite apparent here: the dimension of the controllability matrix is 2 by 2 compared to 4 by 4 in [5].

3.2 Double inverted pendulum on a cart

Fig. 2
figure 2

Double pendulum on a cart

Full size image

The double pendulum on a cart [7, 12] is shown in Fig. 2. The cart can be moved horizontally along a straight line, and the two pendulums can rotate in the vertical plane. The mass of the cart is neglected and, for the sake of simplicity, the two pendulums have the same mass m and length l. Friction and damping are neglected at the bearings and at the horizontal guide.

The double inverted pendulum is an \(n=3\) degree of freedom mechanical device. The cart position is described by the x coordinate along the horizontal axis, and the pendulum positions are given by the angles \(\theta _1\) and \(\theta _2\) measured from the vertical axis. The external force F acts on the cart horizontally, which will be used to control the system based on the pendulum angles and angular velocities. The kinetic energy assumes the form

$$\begin{aligned} T&=m{\dot{x}}^2 + \frac{2}{3}ml^2\dot{\theta }_1^2 + \frac{1}{6}ml^2\dot{\theta }_2^2 \nonumber \\&\quad - \frac{3}{2}ml\cos \theta _1 {\dot{x}}\dot{\theta }_1 - \frac{1}{2}ml\cos \theta _2 {\dot{x}}\dot{\theta }_2 \nonumber \\&\quad + \frac{1}{2}ml^2\cos (\theta _1-\theta _2)\dot{\theta }_1\dot{\theta }_2\, \end{aligned}$$

and the potential function is

$$\begin{aligned} V=\frac{3}{2} mgl \cos \theta _{1} + \frac{1}{2}mgl\cos \theta _{2}\,. \end{aligned}$$

The cart position x is a cyclic coordinate because it is present neither in the kinetic energy T nor in the potential function V. This means that there are \(m=2\) essential coordinates \({\mathbf {q}} = \mathrm {col}[q_1\ \ q_2] = \mathrm {col}[\theta _1\ \ \theta _2]\) and \(n-m=1\) cyclic coordinate \(\varvec{\varphi } = \mathrm {col}[\varphi _1] = \mathrm {col}[x]\), The nonlinear mass matrix can be partitioned as

The reduced linearized equations of motion are obtained using Theorem 2 since condition (15) fulfills:

$$\begin{aligned} (D^{-1})&= \frac{1}{2m}\,, \nonumber \\ (d^{-1})_{,i}&=\left. \left( D^{-1}\right) _{,i}\right| _{\theta _j^\mathrm {eq} =0} = \begin{bmatrix} 0\\ 0 \end{bmatrix}, \end{aligned}$$
(33)

and the linearized equations of motion are:

$$\begin{aligned} \frac{5}{24}ml^2\ddot{\theta }_1 + \frac{1}{8}ml^2\ddot{\theta }_2 -\frac{3}{2}mlg\theta _1&= \frac{3}{4}lF \,, \\ \frac{1}{8}ml^2\ddot{\theta }_1 + \frac{5}{24}ml^2\ddot{\theta }_2 -\frac{1}{2}mgl\theta _2&= \frac{1}{4}lF \,, \end{aligned}$$

where the only generalized force Q is the horizontal force F acting on the cart: \(Q=F\).

We now check the necessary condition of controllability in Theorem 6. Since (33) holds and (23f) assumes the form

$$\begin{aligned} c_{ki}&= \frac{1}{2ml^2}\begin{bmatrix} 15&{}-9\\ -9&{}15 \end{bmatrix}\,, \end{aligned}$$

the condition (29)

$$\begin{aligned} c_{ki}&(d^{-1})_{\alpha \beta } b_{i\beta } = \begin{bmatrix} \frac{9}{2 ml}\\[1ex]- \frac{3}{2 ml} \end{bmatrix} \ne \begin{bmatrix} 0\\ 0 \end{bmatrix}\, \end{aligned}$$

is fulfilled, so it is worth to investigate the controllability further. Theorem 5 leads to the system and input matrices in the form

$$\begin{aligned} { {\mathbf {F}}} = \begin{bmatrix} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ \frac{45 g}{4 l} &{} - \frac{9 g}{4 l} &{} 0 &{} 0\\ - \frac{27 g}{4 l} &{} \frac{15 g}{4 l} &{} 0 &{} 0 \end{bmatrix}, \quad { {\mathbf {G}}} = \begin{bmatrix} 0\\ 0\\ \frac{9}{2 ml}\ \frac{3}{2 ml} \end{bmatrix}. \end{aligned}$$

The controllability matrix is

$$\begin{aligned} {\mathbf {R}} = \begin{bmatrix} 0 &{} \frac{9}{2 ml } &{} 0 &{} \frac{54 g}{ml^{2} }\\ 0 &{} - \frac{3}{2 ml } &{} 0 &{} - \frac{36 g}{ml^{2} }\\ \frac{9}{2 ml } &{} 0 &{} \frac{54 g}{ml^{2} } &{} 0\\ - \frac{3}{2 ml } &{} 0 &{} - \frac{36 g}{ml^{2} } &{} 0 \end{bmatrix}, \end{aligned}$$
(34)

which has maximal rank: \( \mathrm {Rank}({\mathbf {R}}) = 4 \). Thus, the double inverted pendulum is Kalman controllable, which means that it can be stabilized at the upward position by an appropriate linear feedback of the two pendulum angular positions and velocities with actuation only along the cyclic coordinate of the cart.

The controllability of the double inverted pendulum was also shown in [18] where full state feedback was used, which also involves the cart position and velocity. The rank of the corresponding 6 by 6 controllability matrix was checked by means of computer algebra due to the complexity of the calculations, while the rank of the reduced controllability matrix in (34) can be checked analytically.

3.3 Wilson pendulum

Fig. 3
figure 3

Wilson pendulum

Full size image

The Wilson pendulum [11] is a disk placed in two nested frames as shown in Fig. 3. For the sake of simplicity, it is considered that only the disk has mass m and matrix of mass moment of inertia \({\mathbf {J}} = \mathrm {diag}[J_\mathrm {A}\ J_\mathrm {A}\ J_\mathrm {B}]\), while these are negligible at the frames. The internal frame is linked to the external one by means of a spring of stiffness k. Further geometric parameters are shown in Fig. 3. Friction and damping are also neglected at the bearings.

The kinetic energy and potential function are

$$\begin{aligned} T =&\frac{1}{2}ml^2\dot{\alpha }^2 + \frac{1}{2}J_\mathrm {A}(\dot{\alpha }^2 \cos ^2\beta + \dot{\beta }^2) + \frac{1}{2}J_\mathrm {B}(\dot{\varphi } -\dot{\alpha }\sin \beta )^2\,, \\ V =&mgl\cos \alpha + \frac{1}{2}k\left( \sqrt{a^2+r^2 -2ar\cos \beta } - (a-r)\right) , \end{aligned}$$

respectively. Based on the Lagrangian function \(L=T-V\), the Wilson pendulum has \(m=2\) essential coordinates \({\mathbf {q}} = \mathrm {col}[q_1\ \ q_2] = \mathrm {col}[\alpha \ \ \beta ]\)

and \(n-m=1\) cyclic coordinate \(\varvec{\varphi } = \mathrm {col}[\varphi _1] = \mathrm {col}[\varphi ]\), where \(\alpha \) and \(\beta \) are the Euler angles of the frames and \(\varphi \) is the angle of rotation of the disk. From the kinetic energy T, the nonlinear mass matrix \({\mathbf {M}}\) can be obtained as

Because of condition (15)

$$\begin{aligned} (D^{-1})&= \frac{1}{J_\mathrm {B}}\,, \nonumber \\ (d^{-1})_{,i}&= \left. \left( D^{-1}\right) _{,i}\right| _{q_j^\mathrm {eq} =0} = \begin{bmatrix} 0\\ 0 \end{bmatrix} \end{aligned}$$
(35)

holds, the linearized equations around the unstable equilibrium \(\alpha ^\mathrm {eq}=0\), \(\beta ^\mathrm {eq}=0\) are obtained from Theorem 2 in the form of:

$$\begin{aligned} (ml^2 +J_\mathrm {A}) \ddot{\alpha } -p^0 \dot{\beta } -mgl\alpha&=0\,,\end{aligned}$$
(36a)
$$\begin{aligned} J_\mathrm {A}\ddot{\beta } + p^0\dot{\alpha } + 2akr \beta&= 0\,. \end{aligned}$$
(36b)

The motion of the system can be interpreted physically together with the differential equation of the hidden motion (7):

$$\begin{aligned} {\dot{\varphi }}&= \frac{p}{J_\mathrm {B}} + \dot{\alpha }\sin \beta \,, \end{aligned}$$

which governs the time variation of the cyclic coordinate \(\varphi \); the cyclic velocity is expressed from the generalized momentum (6):

$$\begin{aligned} p&= J_\mathrm {B}\big (\dot{\varphi } - \dot{\alpha }\sin \beta \big ). \end{aligned}$$

The linearization takes place around the steady-state motion where the disk rotates with constant angular velocity \( \dot{\varphi }^\mathrm {eq} = {p^0}/{J_\mathrm {B}} \), with the essential coordinates \(\alpha (t)\equiv \alpha ^\mathrm {eq}=0\) and \(\beta (t)\equiv \beta ^\mathrm {eq}=0\) of the frames. The trivial solution is clearly unstable even in the presence of the gyroscopic forces related to \(p^0\), since the stiffness matrix is negative definite.

The necessary condition of controllability can be checked by Theorem 6, since (35) holds. Because

$$\begin{aligned} b_{i\beta }=\begin{bmatrix} -J_\mathrm {B}\sin \beta ^\mathrm {eq}\\ 0 \end{bmatrix} =\begin{bmatrix} 0\\ 0 \end{bmatrix}\,, \end{aligned}$$

the condition (29) in Theorem 6 becomes true, so the Wilson pendulum cannot be controlled by actuating at the cyclic coordinate \(\varphi \) with a control torque \(M_\mathrm t\) (see Fig. 3). The input matrix is \( { {\mathbf {G}}}={\mathbf {0}}\), and the controllability matrix has also zero rank: \(\mathrm {Rank}({\mathbf {R}}) = 0\). Accordingly, the input torque \(M_\mathrm t\) does not appear in the reduced linearized equations (36). This means that there is no linear feedback which can stabilize the linearized system (36).

3.4 Rotor model

Fig. 4
figure 4

3-DoF rotor model

Full size image

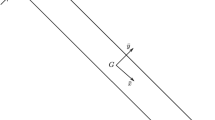
A simple \(n=3\)-DoF rotor model [10] is shown in Fig. 4. The disk has mass m and mass moment of inertia J with respect to the axis normal to the disk at the center of gravity C. The axis of rotation is also perpendicular to the plane of the disk at the point O. The elastic shaft connects the point P of the disk and point O fixed to the environment, and the massless shaft is modeled by a spring of stiffness k. The imbalance of the disk is represented by the eccentricity e, which is the distance of points P and C. The input torque \(M_\mathrm t\) acts at the shaft.

The kinetic energy and potential function assume the form

$$\begin{aligned} T =&\frac{1}{2}m({\dot{r}}^2 +r^2\dot{\varphi }^2) + \frac{1}{2}J(\dot{\varphi } - \dot{\psi })^2\,,\\ V =&\frac{1}{2}k(r^2 +e^2-2re\cos \psi )\,. \end{aligned}$$

Based on the Lagrangian function \(L=T-V\), the generalized coordinates can be divided into \(m=2\) essential coordinates \({\mathbf {q}} = \mathrm {col}[q_1\ \ q_2] = \mathrm {col}[r\ \ \psi ] \), and \(n-m=1\) cyclic coordinate \(\varvec{\varphi } = [\varphi _1] = [\varphi ]\), where r and \(\varphi \) are the polar coordinates of the position of the center C of gravity, and \(\psi \) describes the additional free rotation of the disk (see Fig. 4). The nonlinear mass matrix assumes the form

It was shown in [10] that the steady-state motion above the critical angular velocity \(\dot{\varphi }_0>\dot{\varphi }_\mathrm {crit} = \sqrt{k/m}\) is given by \( r^\mathrm {eq} = \frac{e \dot{\varphi }_\mathrm {crit}}{\dot{\varphi }_0^2 -\dot{\varphi }_\mathrm {crit}^2}\) and \( \psi ^\mathrm {eq} = \pi \). Introduce new coordinates in order to transform the equilibrium position to be zero for a given angular velocity \({\dot{\varphi }}_0\), as required by the theorems.

The nonlinear mass matrix with the new coordinates becomes:

As shown in [10], the linearized equations of motion around the equilibrium have negative definite stiffness matrix for a certain rotational speed range \({\dot{\varphi }}_\mathrm {crit}< {\dot{\varphi }}_0 < {\dot{\varphi }}_{\mathrm {max}}\). Since condition (15) gives

$$\begin{aligned} (d^{-1})_{\alpha \beta ,i} = \left. \left( D^{-1}\right) _{,i}\right| _{q_j^\mathrm {eq} =0} = -\frac{1}{m(r^\mathrm {eq})^2+J}2mr^\mathrm {eq} \ne 0\,, \end{aligned}$$

Theorems 2, 5 and 6 imply that the Routh reduction cannot be carried out, and the equations of motion cannot be reduced to the essential coordinates only, even if the control torque is applied at the cyclic coordinate only. This means that Theorem 6 cannot be used to check controllability. This represents a limitation of the Routh reduction methodology regarding controllability.

4 Conclusion

The concept of controlling Routh reducible mechanical systems is introduced where external forcing is applied at the cyclic coordinates only, while some of the essential coordinates and their derivatives are observed. It is concluded that full state feedback is not necessary for the linear controllability of these reduced systems. The Kalman controllability of steady-state motions can be analyzed with reduced rank matrices. Theorems define the conditions when Routh reducibility can be extended for the Kalman controllability conditions. A necessary condition for controllability is also derived, which relies only on the reduced expression of kinetic energy.

The above described specific scenario of controlling cyclic systems is a quite natural choice as shown by many examples from the simplest Furuta pendulum to more complex gyroscopic control problems. Accordingly, the application of the corresponding theorems is demonstrated on realistic mechanical examples. Two of these, the Furuta pendulum and the double inverted pendulum are proved to be controllable by means of reduced rank controllability matrices as compared to the similar results of the literature using full state description and more complex algebraic conditions. Based on the necessary condition of controllability, the Wilson pendulum is proven not to be controllable. The last example, a rotor model, represents the limitation of this approach: the condition of model reduction does not hold, but it cannot be excluded that the full system is controllable.