Abstract
High-resolution, daily precipitation climate products that realistically represent extremes are critical for evaluating local-scale climate impacts. A popular bias-correction method, empirical quantile mapping (EQM), can generally correct distributional discrepancies between simulated climate variables and observed data but can be highly sensitive to the choice of calibration period and is prone to overfitting. In this study, we propose a hybrid bias-correction method for precipitation, EQM-LIN, which combines the efficacy of EQM for correcting lower quantiles, with a robust linear correction for upper quantiles. We apply both EQM and EQM-LIN to historical daily precipitation data simulated by a regional climate model over a region in the northeastern USA. We validate our results using a five-fold cross-validation and quantify performance of EQM and EQM-LIN using skill score metrics and several climatological indices. As part of a high-resolution downscaling and bias-correction workflow, EQM-LIN significantly outperforms EQM in reducing mean, and especially extreme, daily distributional biases present in raw model output. EQM-LIN performed as good or better than EQM in terms of bias-correcting standard climatological indices (e.g., total annual rainfall, frequency of wet days, total annual extreme rainfall). In addition, our study shows that EQM-LIN is particularly resistant to overfitting at extreme tails and is much less sensitive to calibration data, both of which can reduce the uncertainty of bias-correction at extremes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Climate data is often necessary for social, ecological, and hydrological models and is routinely used in climate impact models and assessments. Model reliability is largely dependent on the quality and resolution of climate data products (Flint and Flint 2012; Holden et al. 2011; Franklin et al. 2013; Field et al. 2014). The representation of extremes, in particular, can have a disproportionately large effect on such models (Lanzante et al. 2021). Increases in the frequency, variability, and magnitude of extreme precipitation over the last several decades, especially in the northeastern USA, are well-documented (Hayhoe et al. 2007; Huang et al. 2017). To study the future impacts of changing extremes at local scales, climate data products must represent extreme events accurately and be available at fine spatial and temporal resolutions (Lanzante et al. 2021). General circulation models (GCMs) provide important information about historical and future larger-scale climate trends, but their resolution is too coarse to investigate localized effects of changes in extreme climate events (Ekström et al. 2015; Lafon et al. 2013). Additionally, raw GCM output is characterized by a non-trivial degree of bias (Lafon et al. 2013), and the ability of GCMs to reproduce extreme tails of climate variables is limited (Leander and Buishand 2007). Therefore, prior to its use in hydrological (Pierce et al. 2015; Shrestha et al. 2017), agricultural (Hoffmann and Rath 2012), or ecological models, GCM output is downscaled to a finer resolution and bias-corrected with respect to observed data (Zia et al. 2016). These post-processing techniques result in climate data that is more realistic at finer spatial scales. Here, we propose a bias-correction method that more accurately captures precipitation extremes. We incorporate it into a high-resolution downscaling and bias-correction workflow for constructing daily, high- resolution data products for use in modeling efforts.
In the process of downscaling, model output is converted from a coarse to finer resolution. In dynamical downscaling, a regional climate model (RCM) is forced with a GCM, resulting in finer-scale output in which regional climate processes, topography, and orography are incorporated (Feser et al. 2011). In statistical downscaling, statistical relationships between coarse-scale climate variables and local, observed data are established, and the effects of fine-scale predictors are integrated into downscaled data (Maraun et al. 2010). Dynamical downscaling is computationally intensive and can introduce additional biases (Caldwell et al. 2009; Leung et al. 2003), but, localized climate processes, including extremes (Gao et al. 2006), are generally better reproduced than in GCMs (Maraun 2016). However, RCMs do not perform well in capturing the most extreme events (Baigorria et al. 2007; Leander and Buishand 2007). Statistical downscaling is efficient, can be applied to a variety of climate variables (Mearns et al. 2003), and is especially effective in topographically complex terrain (Hanssen-Bauer et al. 2005). Climate data products with fine spatial resolutions, which are important for studying localized changes in extreme climate events, can be generated by combining statistical and dynamic downscaling, (Friederichs and Hense 2007). In this study, we combine statistical and dynamical downscaling to produce precipitation data products with a fine spatial resolution.
Downscaling is complemented by bias-correction, a procedure in which climate model output is adjusted such that its statistical properties (e.g., mean, variance, and potentially higher moments) resemble those of observations in a common climatological period (Lafon et al. 2013; Cannon et al. 2020). We note that the terms “downscaling” and “bias-correction” are sometimes used to refer to equivalent processes. However, in this study, downscaling only refers to the process in which coarse, gridded climate data is interpolated to a finer spatial resolution, and bias-correction refers specifically to applying transformations to climate model output such that distributional biases are reduced. Most bias-correction methods assume stationarity of model errors over time (Roberts et al. 2019), which can be problematic for bias-correcting future climate model output over multi-decadal time spans (Cannon et al. 2015; Fowler et al. 2007). In addition, sufficient observational data is necessary to derive robust transfer functions (Fowler et al. 2007). Bias-correction methods for precipitation range from simple approaches such as the “delta change” or “delta factor” method (Teutschbein and Seibert 2012) to more flexible and effective quantile-mapping based methods (Teutschbein and Seibert 2012; Cannon et al. 2015; Wood et al. 2002). In quantile-mapping (QM) based methods, a transfer function (TF) maps quantiles of climate model output to those of observed data. QM methods can be parametric (Piani et al. 2010), non-parametric (Lafon et al. 2013), or a combination of both (Tani and Gobiet 2019). Distribution mapping (DM) is a parametric QM method in which known, parametric distributions are fit to observed and model data. The Gamma distribution is often used to model wet-day precipitation (e.g., (Lafon et al. 2013; Gudmundsson et al. 2012; Luo et al. 2018)) but is generally not adequate for modeling extreme precipitation tails (Heo et al. 2019; Gutjahr and Heinemann 2013). Hybrid DM approaches in which the Gamma distribution is fit to lower quantiles and a heavy-tailed distribution is fit to tail quantiles can improve bias-correction of extreme precipitation (Gutjahr and Heinemann 2013; Um et al. 2016). A non-parametric counterpart to DM, empirical quantile mapping (EQM), is a flexible method in which no distributional assumptions are made. In EQM, the TF represents a mapping from empirical model quantiles to observed quantiles and typically outperforms DM (Jakob Themeßl et al. 2011; Ivanov and Kotlarski 2017). EQM is effective in correcting precipitation variables (Jakob Themeßl et al. 2011; Fang et al. 2015; Jakob Themeßl et al. 2011; Miao et al. 2016; Enayati et al. 2021) and is attractive as a bias-correction method as it corrects the mean, standard deviation, and higher-order distributional moments (Gudmundsson et al. 2012).
A disadvantage of QM methods and EQM in particular, is their propensity to overfit on calibration data, especially at precipitation extremes where data is scarce and highly variable (Lafon et al. 2013; Grillakis et al. 2013; Holthuijzen et al. 2021; Piani et al. 2010; Mamalakis et al. 2017). In EQM, TFs are interpolated using linear interpolation, splines, or other smoothing techniques (Gudmundsson 2016). Flexible methods such as EQM can result in TFs that can correct model data nearly perfectly (overfitting) but may not generalize to out-of-sample or future model data. Overfitting is problematic because it can lead to instability of the TF at higher quantiles (Gobiet et al. 2015; Grillakis et al. 2013; Hnilica et al. 2017). When applied to future projections, EQM has been shown to significantly distort future climate change signals (Grillakis et al. 2017; Maraun et al. 2017) and exaggerate or deflate extreme trends, introducing additional uncertainty into bias-corrected data (Cannon et al. 2015; Tani and Gobiet 2019). Hybrid EQM approaches that combine parametric and non-parametric modeling can reduce the degree of overfitting of the TF at extreme tails (Tani and Gobiet 2019). In a hybrid approach, bias-correction below a specified threshold is achieved via a non-parametric TF (EQM), while bias-correction above the threshold is with DM, based on an extreme distribution, such as the Generalized Pareto distribution (Tani and Gobiet 2019). Hybrid EQM methods combine the flexbility of EQM for correcting lower to middle quantiles with the robustness of parametric distributions for correcting upper quantiles. In particular, the use of extreme or heavy-tailed distributions for modeling extremes can improve bias-correction of tail quantiles (Laflamme et al. 2016; Mamalakis et al. 2017; Yang et al. 2010; Gutjahr and Heinemann 2013; Kim et al. 2018; Yang et al. 2010; Tani and Gobiet 2019). However, the risk of overfitting the TF at distributional tails still exists, as poor fits to heavy-tailed distributions can introduce outliers (Luo et al. 2018; Shin et al. 2019). In addition, selection of the threshold is difficult, as the amount of data beyond the threshold must be sufficiently large to allow for distribution fitting and must approximate a known heavy-tailed distribution (Beirlant et al. 2006; Gutjahr and Heinemann 2013). There is a need for a hybrid EQM method in which bias-correction of extremes can be performed without the risk of overfitting and the introduction of outliers.
We propose and demonstrate a simple, hybrid EQM method for bias-correction that, when used in conjunction with downscaling, results in high-resolution (1km) daily precipitation data in which precipitation extremes are accurately represented. The proposed method, EQM-LIN, combines the effectiveness of EQM for correcting the bulk of the distribution with a robust, linear correction for extremes. As part of a high-resolution, downscaling and bias-correction workflow, we use EQM-LIN to bias-correct historical (1976–2005), daily precipitation data that were dynamically downscaled by a regional climate model (RCM). We also compare the effectiveness of EQM-LIN to EQM for bias-correction, with an emphasis on the ability of the two methods to accurately capture extremes. Because EQM-LIN is computationally cheap, easy to apply, and corrects both mean and extreme bias for precipitation variables, it is an important methodological addition to the body of bias-correction literature.
2 Methods
2.1 Data
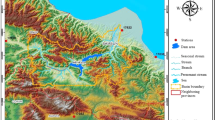
The study area, the Lake Champlain Basin, consists of parts of Vermont, New Hampshire, eastern New York, USA and southern Quebec, Canada (Fig. 1). Eleven watersheds drain into Lake Champlain, and the Green Mountains, Adirondack Mountains, and White Mountains span portions of Vermont, New York, and New Hampshire, respectively (Winter et al. 2016). The study area is approximately 13,251 km2. Elevations range from 30 to 1500 m above mean sea level (MSL). The study area is characterized by a subhumid continental climate with cold and snowy winters. At high elevations, mean annual precipitation can reach 1,000–1,520 mm, while at low elevations, mean annual precipitation ranges between 750–900 mm; locally intense precipitation in the form of thunderstorms is likely during summer months (Stager and Thill 2010).
Simulated historical (1976–2005) precipitation (PRCP) data were generated by the Advanced Weather and Research Forecasting model (WRF) version 3.9.1, an RCM (Skamarock et al. 2019). WRF output was generated at a daily temporal resolution. WRF is a widely used numerical weather prediction system for both research and applied forecasting purposes (Skamarock et al. 2019). Historical simulations (1976–2005) were forced by bias-corrected Community Earth System Model 1 (CESM1), a GCM (Monaghan et al. 2014). CESM1 historical simulations were dynamically downscaled with WRF to a 4-km resolution using three one-way nests (36 km, 12 km, 4 km). The 4-km resolution WRF data were used for this study. Additional WRF model details are included in the Supplementary Materials, and a full description and evaluation of simulations can be found in (Huang et al. 2020).
Historical daily climate station data was obtained from the Global Historical Climate Network (GHCND) (https://www.ncdc.noaa.gov/cdo-web/search?datasetid=GHCND). GHCND data records are adjusted to account for changes in instrumentation and other anomalies (Oceanic and Administration 2018; Peterson and Vose 1997). We retained only those stations with at least 70% complete records over the historical time period 1976–2005 (85 stations). We chose to use station data, rather than gridded data products (e.g., Livneh et al. 2015; Daymet, (Thornton et al. 2012); and PRISM, (Daly et al. 2000)), because interpolation algorithms used to create gridded climate products can introduce bias (Behnke et al. 2016) and additional uncertainty when used for bias-correcting climate model output (Walton and Hall 2018; Tarek et al. 2021). Gridded products can misrepresent extreme tails (Bannister et al. 2019), and (Wootten et al. 2021) showed that Daymet, Livneh, and PRISM precipitation products varied widely in their representation of wet-day occurrences, length of wet and dry periods, and precipitation intensity in the South-Central USA. Station data represent direct climatological measurements and are available throughout the Northeastern USA (Peterson and Vose 1997; Durre et al. 2010). We acknowledge that there is a spatial misalignment between gridded model data and point-based GHCND station data. In the study region, elevation has the most significant impact on precipitation. The WRF model accounts for elevation at a 4-km spatial resolution, which is adequate to capture the main effects of elevation within the study region. In addition, the effect of fine-scale (1 km) elevation is incorporated via topographical downscaling (Winter et al. 2016), adding further value to model data. There are numerous examples in the bias-correction literature in which point-based station and downscaled model data are treated as equivalent (e.g., Rajczak et al. (2016), Heo et al. (2019), and Gutjahr and Heinemann (2013)).
In the proposed workflow, historical WRF simulations (model output) are downscaled to a 1-km grid prior to bias-correction using topographic downscaling, a variation of inverse distance weighting (IDW) that incorporates elevational lapse rates (Winter et al. 2016). Elevation estimates at each 1-km grid cell were derived by interpolating elevation values from a 30-m digital elevation model (DEM) (USGS 2018) via IDW. The 1-km grid cell size was chosen based on resolution requirements for climate impacts modeling efforts over the Lake Champlain Basin (Wang et al. 2012; Winter et al. 2016).
Prior to bias-correction, historical model data were also interpolated to GHCND station locations via topographical downscaling for the purpose of constructing TFs. To generate high-resolution, bias-corrected data products, bias-correction was applied to model data downscaled to the 1-km grid. All performance metrics were calculated using model data topographically downscaled to the 85 GHCND station locations and GHCND station data. Raw WRF model data exhibited a wet bias that was most pronounced during summer months (Fig. 2). This type of seasonal bias in WRF model simulations has also been found in other studies in the northeastern USA (e.g., Huang et al. (2020)).
2.2 Bias-correction methods
The proposed approach, empirical quantile mapping with a linear correction for extremes, EQM-LIN, was compared to empirical quantile mapping (EQM), which is one of the most frequently used and effective methods for bias-correction. In addition, we compared EQM-LIN to DM with the Gamma distribution (DM-GAMMA), a hybrid EQM approach in which lower quantiles were corrected using EQM, and upper quantiles were fit to Generalized Pareto Distributions (GPDs) (EQM-GPD) (Tani and Gobiet 2019), as well as a trend-preserving method, quantile delta mapping (QDM) (Cannon et al. 2015). The results are presented in the Supplementary Material but not evaluated in the main manuscript, since none of the additional methods performed as well as or significantly better than EQM or EQM-LIN.
For both bias-correction methods EQM-LIN and EQM, TFs were constructed by spatially pooling GHCND station and model data downscaled to station locations. The same TF was applied to all model values, regardless of spatial location. We chose to spatially pool data because (1) much of the spatial variation in the data is due to elevation, which is accounted for during the downscaling procedure, and (2) additional interpolation necessary to construct separate TFs based on spatial location would have added uncertainty to bias-corrected data. Spatially explicit bias-correction in general can be a difficult task and involves estimating the TF at every location at which bias-corrected data is desired (Holthuijzen et al. 2021), which is contrary to our desire to develop a bias-correction approach that is simple, efficient, and easily implemented.
For both bias-correction methods, twelve TFs were constructed, one for each month of the year (Jakob Themeßl et al. 2011; Piani et al. 2010) using model data topographically downscaled to GHCND stations and GHCND station data. Daily raw model data downscaled to station locations and raw model data downscaled to the 1-km grid were corrected with the corresponding monthly TF. Because GHCND station gauges are accurate to 0.1 mm (Oceanic and Administration 2018), we defined wet-day precipitation days as days in which daily precipitation was greater than or equal to 0.1 mm. Prior to construction of TFs and bias-correction, daily model values below 0.1 mm were set to 0. All analyses were conducted in R Statistical Language (R Core Team 2018).
Empirical quantile mapping: EQM
The TF used in EQM is expressed by the empirical cumulative distribution function (ecdf) and its inverse (ecdf− 1). Monthly TFs are of the form:
where, xcorr,t is the corrected model precipitation value on day t, \(\text {ecdf}_{obs}^{-1}\) is the inverse ecdf of observed data, ecdfmod is the ecdf of model data, and xmod,t is the raw model precipitation value on day t. Monthly TFs were constructed using 10,000 estimated quantiles, and interpolation of the TF was accomplished with monotone Hermite splines using the qmap package (Gudmundsson 2016) in R. Values exceeding the range of the TF were corrected using the method of constant extrapolation (Boé et al. 2007). The approximate shape of the TF can be examined by plotting estimated quantiles of model and observed data against one another to form a “quantile-quantile-” or “qq-” map (Fig. 3). The shape of the quantile-quantile map can provide insight into the type and magnitude of model bias. For instance, if the TF falls below (rises above) the 1:1 line, model quantiles are too high (low) relative to observed quantiles.
Empirical quantile mapping with a linear correction for extremes: EQM-LIN
In EQM-LIN, the majority of model data are bias-corrected via EQM using Eq. 1, while model data beyond a specified threshold are adjusted with a constant correction via a linear TF (2). All bias-correction by EQM was done with the qmap package (Gudmundsson 2016) in R, and custom code was used to construct the linear TF. The following steps describe the EQM-LIN procedure:
-
1.
Calibration data is divided into two datasets in which model data is less than (CAL-LOW ) and greater than a specified threshold (CAL-HIGH). The threshold, T is a function of the inverse ecdf of model data and is expressed as \(T={ecdf}_{mod}^{-1}(\tau _{LIN})\), where 0 < τLIN < 1. Thus, T is a precipitation value in mm that indicates where both model and observed datasets are divided. The procedures for estimating T and τLIN are thoroughly outlined in Appendix A.
-
2.
Next, the intercept for the linear TF, δ is obtained (details are discussed in Appendix A). The intercept represents the constant correction that will be applied to extreme model values (all model values in CAL-HIGH). The linear TF is expressed as xcorr,t = δ + xmod,t and is applied to model values in CAL-HIGH (2). Model values in CAL-LOW are corrected via EQM. The TF for EQM-LIN is expressed as:
$$ x_{corr, t} = \left\{\begin{array}{l} {\text{ecdf}}_{obs}^{-1}(\text{ecdf}_{mod}(x_{mod, t})) , \quad x_{mod, t} \!<\! T \\ x_{mod, t} + \delta, \quad x_{mod, t} \ge T, \end{array}\right. $$(2)where xcorr,t and xmod,t are as defined in Eq. 1. Thus, the linear portion of the TF (xcorr,t = δ + xmod,t) always has a slope of 1 and intercept δ.
In this study, we only consider linear TFs with a slope of 1 and intercept of δ. Optimizing the slope as well as the threshold would increase the overall complexity of EQM-LIN and could introduce the potential for overfitting on out-of-sample data.
We chose τLIN to be 0.79, based on a grid search over a range of values in a five fold cross-validation approach (details are discussed in Appendix A). We chose the value of τLIN that resulted in the minimization of the mean absolute error of observed and model ecdfs above the 95th percentile (MAE95), (Reiter et al. 2016) (Section 3). MAE95 quantifies the distributional similarity between observed and model data at extremes. Since the focus of this study was on accurately representing distributional extremes, we chose the minimization of MAE95 rather than another metric. However, we found that minimization of MAE95 resulted in improvements in all performance metrics and indices.
The shape of the EQM-LIN TF is identical to that of EQM below T, while above the threshold the TF is linear. Figure 4 shows a quantile-quantile map for model and observed data for the month of August and the associated EQM and EQM-LIN TFs.
The quantile-quantile map and corresponding EQM and EQM-LIN TFs for daily observed and model data during the month of August over the calibration period 1976–2005. (a) quantile-quantile map, constructed using 10,000 quantiles evenly spaced between 0 and 1; (b) EQM TF ; (c) EQM-LIN TF, with the blue line denoting the non-parametric (EQM) portion of the TF and the red line indicating the linear portion; d) enlarged section of EQM-LIN TF in (c) (gray box) to illustrate the transition from EQM portion to the linear portion of the TF. In (c) and (d), the threshold (dashed line), indicates the 79th quantile of model data (6.88 mm)
3 Validation
Performance evaluation of EQM and EQM-LIN was accomplished with a five-fold cross-validation procedure using observed and model data during the calibration period (1976–2005). Cross-validation is commonly used to evaluate the efficacy of bias-correction methods, as out-of-sample data can be considered proxies for future projections (Tani and Gobiet 2019; Gudmundsson et al. 2012; Jakob Themeßl et al. 2011). Test datasets always consisted of consecutive years (for example, if training data consisted of years 1976–2000, test data would contain years 2001–2005).
We chose performance metrics and indices that quantified (1) model skill and (2) the effectiveness of bias-correction methods in capturing overall climatology with an emphasis on extreme tails. All performance metrics were calculated using model data topographically downscaled to GHCND station locations and GHCND station data. Model skill, distributional similarity between model and observed data, was quantified with the mean absolute error (MAE). We chose MAE, rather than other skill metrics, such as the Perkins Skill Score (Perkins et al. 2007), because it is more sensitive to outliers. Since TFs for EQM and EQM-LIN are constructed on a monthly basis, MAE metrics are also calculated by month. MAE was calculated between distributions of daily observed and raw model data as well as between distributions of daily observed and bias-corrected data at GHCND station locations for a given month (Gudmundsson et al. 2012). MAE95 was used to quantify model skill at extreme tails. MAE95 is computed similarly to MAE, but only the upper 5% of daily observed and model distributions are used (Reiter et al. 2016). The number of quantiles estimated in the calculation of MAE95 was equal to the maximum number of 95th quantile values in observed or model distributions. Generally, the number of values greater than the 95th quantile in each data type (model, bias-corrected model, and observed) did not differ appreciably. MAE and MAE95 metrics were calculated by month for each of the five cross-validated data folds for raw and bias-corrected data, and results are reported as the average metrics over the five folds. MAE and MAE95 quantify distributional error between model and observed data; lower values are indicative of better model skill, with an ideal mean absolute error of 0 (no error).
We used a subset of ETCCDI indices (Peterson 2005) to assess how well bias-corrected data captured overall climate characteristics of observed data. ETCCDI indices are standard indices that allow for the comparison of results over varying time periods, geographical regions, and source data, and are recommended by the World Research Climate Program (WRCP) (Karl et al. 1999). ETTCDI indices were computed annually with spatially pooled data. Prior to calculating ETCCDI indices, downscaled raw model, bias-corrected model, and station data were averaged over the 85 station locations for each day in the 30-year calibration period (10950 days). Thirty annual values of each ETCCDI index were calculated for observed, raw model, and bias-corrected model data. The choice of indices was based on the preference of stakeholders.
“D” indices (D90, D95, and D99) are defined as the annual number of days in which mean daily precipitation exceeded the 90th, 95th, or 99th quantiles. “S” metrics (S90, S95, and S99) are defined as the annual sum of mean daily precipitation (mm) for days in which mean daily precipitation exceeded the 90th, 95th, or 99th quantiles. TotalP is the annual sum of mean daily precipitation (mm) on wet days (days for which mean daily precipitation 0.1 mm), WetDays is the annual count of wet days, and the simple precipitation index (SPI) is calculated as TotalP/WetDays (mm/day). SPI is a measure of precipitation intensity. The nine indices characterize the extreme tails, as well as general characteristics, of the 30-year climatology of precipitation. An overview of MAE metrics and ETCCDI indices is given in Table 1.
Performance evaluated by ETCCDI indices or MAE metrics cannot be directly compared, since each provides assessments on different temporal scales. MAE metrics quantify distributional errors of the entire distribution of daily model data compared to observed data. ETCCDI indices quantify how well model data capture 30-year climatology at a temporally coarser (annual) scale using spatially averaged data. In combination, both evaluation metrics give insight in the overall adequacy of the bias-correction method at both aggregated and finer temporal scales.
3.1 Analyses
Bayesian one-way analysis of variance (ANOVA) models were used to determine if MAE and MAE95 differed significantly among raw model, EQM and EQM-LIN data. Separate ANOVA tests were conducted for MAE and MAE95. ANOVA tests were conducted with data from all five cross-validated folds, as MAE and MAE95 values within folds can be considered subsamples. All analyses were conducted with the RJags package (Plummer et al. 2016) in R. The response variables, MAE or MAE95 values, were log-transformed prior to analysis to ensure homogeneity of variances, an assumption of ANOVA models. The predictor variable for both ANOVA models was data type, a variable with three levels: raw model (Mod), EQM-LIN, and EQM. Credible intervals in the form of 95% highest posterior density (HPD) intervals were used to determine if the difference in posterior distributions was significantly different from 0. Credible intervals were constructed for all pairwise differences of posterior distributions of EQM-LIN, EQM, and raw model data. Credible intervals can be interpreted as follows: there is a 95% chance that the true pairwise difference in posterior distributions is contained within the interval, given the data. Therefore, if 0 is contained within the interval, the difference is not significant at the 95% confidence level. Full details on these analyses are provided in the Supplementary Materials.
Distributions of all nine ETCCDI indices calculated from EQM-, EQM-LIN-corrected, and raw model data were compared to those of observed data. Performance of bias-corrected and raw data relative to observed data was formally assessed using Kolmogorov-Smirnov (KS) tests (Smirnov et al. 1948). The two-sample KS test is a non-parametric test that is used to assess the equality of two empirical distributions (see Appendix B). It is sensitive to differences in both location and shape of the two ecdfs being compared and is often used in climatological studies (Cannon et al. 2015; Rosenberg et al. 2010; Tschöke et al. 2017). Here, we applied the KS test three times for each ETCCDI index to determine the similarity of ecdfs between observed and EQM- and EQM-LIN-corrected data and between observed and raw model data. All tests were conducted with the two-sided null hypothesis that the samples being compared belonged to a common distribution. The significance level, α, was set to 0.05; p-values below 0.05 indicate there is evidence that the two samples do not come from a common distribution. However, to control for multiple comparisons, α was adjusted using the Holm-Bonferroni method (Holm 1979) (details are shown in Appendix C). We acknowledge that the KS test has low power for small sample sizes (30 values or less) (Razali et al. 2011). All KS tests in this study are performed on pairs of distributions composed of 30 annual values; thus, we use KS tests, along with visual inspection of boxplots, to guide our interpretation of results.
4 Results
Overall, data bias-corrected with either EQM or EQM-LIN exhibited substantial improvements in both MAE and MAE95 compared to raw model data (Mod), but improvements were more pronounced for EQM-LIN. Both bias- correction methods generally improved ETCCDI indices compared to Mod, and EQM-LIN performed as well as or slightly better than EQM for all indices.
4.1 MAE and MAE95
MAE values of EQM- and EQM-LIN-corrected model data and Mod were 0.704 mm, 0.655 mm, and 1.06 mm respectively (Fig. 5a). MAEs of both bias-corrected datasets were significantly lower than MAE of Mod. Monthly MAE values for EQM-LIN were overall slightly lower than those of EQM. The credible interval for the difference in MAE between EQM and EQM-LIN contained 0, indicating that although MAE of EQM-LIN was lower than that of EQM, the difference was not significant at the 95% confidence level.
MAE95 values of EQM- and EQM-LIN-corrected model data and Mod were 3.45 mm, 1.73 mm, and 7.12 mm, respectively. For EQM-LIN corrected data, MAE95 varied little among months; however, both raw model and EQM-corrected data exhibited substantial increases in MAE95 between months 8 and 11 (Fig. 5b). Similar to results for MAE, MAE95 values of both bias-corrected datasets were significantly lower than MAE95 of Mod. In contrast to results for MAE, 95% credible intervals for the difference in MAE95 of EQM and EQM-LIN indicated that MAE95 of EQM-LIN was significantly lower than MAE95 of EQM at the 95% confidence level (see Supplementary Materials for full details of ANOVA analysis).
4.2 ETCCDI indices
Distributions of ETCCDI indices for both bias-corrected datasets more closely resembled those of observed data compared to Mod, with EQM-LIN performing as good as or slightly better than EQM. Generally, mean and extreme total annual precipitation was overestimated in Mod, but Mod performed adequately in capturing extreme wet day frequency. While bias-correction resulted in the distributions of most ETCCDI indices becoming more similar to those of observed data, it also resulted in an underestimation of wet-day frequency (see Appendix D, Table 3 for selected summary statistics of ETTCDI index distributions for Mod, EQM, and EQM-LIN).
D and S indices
Less extreme “S” indices (S90 and S95) were substantially overestimated in Mod, and distributions of S90 and S95 calculated from Mod were significantly different from observed data (Fig. 6a; Table 2). The distribution of the more extreme S99 index was better represented in Mod and did not differ significantly from observed data. Both bias-correction methods provided minor improvements of the representation of S99 in Mod. For EQM-LIN, distributions of S90 and S95 did not differ significantly from those of observed data (Fig. 6a; Table 2). However, for EQM, the distribution of S95 was significantly different from that of observed data (Table 2). While both bias-correction methods were able to reduce the overestimation of total extreme annual rainfall exhibited in Mod, EQM-LIN slightly outperformed EQM.
Boxplots of (a) D90, D95, and D99 and (b) S90, S95, and S99 for observed (Obs), model (Mod), EQM-, and EQM-LIN-corrected data. Each boxplot represents 30 annual values (ETCCDI indices are calculated annually). Significance of KS-tests of distributional similarity of ETCCDI indices of Mod, EQM, or EQM-LIN compared to Obs are indicated with (*); dots represent outliers. (Statistical significance of KS tests was adjusted using the Holm-Bonferroni method; α = 0.05)
Distributions of “D” indices (D90, D95, and D99) were quite similar for Mod, bias-corrected, and observed data (Fig. 6b). P-values of KS tests for D90, D95, and D99 confirmed that distributions of Mod and bias-corrected data were not significantly different from observed data (Table 2). These results show that the frequency of extreme precipitation days, D90, D95, and D99, are adequately represented in Mod and that bias-correction via either method does not adversely affect the representation of “D” indices.
TotalP, WetDays, and SPI
TotalP was significantly overestimated in Mod (p< 0.0001), but distributions of TotalP calculated using either bias-corrected dataset were not significantly different from observed data (p= 0.81) (Fig. 7; Table 2). Thus, both bias-correction methods were highly effective in correcting total annual precipitation.
Boxplots of TotalP, WetDays, and SPI for observed (Obs), model (Mod), EQM-, and EQM-LIN-corrected data. Each boxplot represents 30 annual values (ETCCDI indices are calculated annually). Significance of KS-tests of distributional similarity of ETCCDI indices of Mod, EQM, or EQM-LIN compared to Obs are indicated with (*); dots represent outliers. (Statistical significance of KS tests was adjusted using the Holm-Bonferroni method; α = 0.05)
The distribution of WetDays derived from Mod did not differ significantly from observed data (p= 0.13) (Table 2). However, WetDay distributions calculated from EQM- and EQM-LIN-corrected data were significantly underestimated relative to observed data (p < 0.0001) (Fig. 7; Table 2). SPI was overestimated by Mod, due to the large overestimation of Total P; SPI was overestimated to a lesser degree, by EQM- and EQM-LIN-corrected data due to the underestimation of WetDays (Fig. 7). Distributions of SPI calculated from EQM, EQM-LIN, and Mod all differed significantly from observed data (Table 2). Although bias-correction via either EQM-LIN or EQM results in underestimating WetDays, annual precipitation totals (TotalP) are effectively corrected. Moreover, while the distribution of WetDays is adequately represented in Mod, Mod contains an excessive number of low-precipitation occurrences relative to observed data (see Supplementary Materials, Section 4). However, despite the underestimation of wet day frequency following bias-correction, precipitation intensity (SPI) is slightly improved compared to raw model data.
5 Discussion
Local-scale modeling efforts in hydrology, ecology, agriculture, and economics, as well as climate impact assessments, require high-resolution climate products. Since climate extremes exert a large influence on humans and the environment, it is crucial that extremes are accurately represented in climate products. An effective way to obtain high-resolution climate products is to statistically downscale and bias-correct dynamically downscaled output from an RCM. Bias-correction of precipitation extremes, in particular, is a difficult task. In this study, we developed a hybrid bias-correction method, EQM-LIN, that combines the efficacy of EQM for bias-correcting the bulk of raw model data, with a robust linear adjustment for correcting distributional tails. We found that EQM-LIN results in the accurate representation of mean and extreme precipitation. EQM-LIN outperformed EQM in terms of model skill (MAE and MAE95) and performed at least as well or better than EQM with respect to most ETCCDI climatological indices. Furthermore, our study indicates that a linear correction, as implemented in EQM-LIN, is resistant to overfitting and results in a more robust TF at higher quantiles, both of which can decrease uncertainty in bias-corrected data.
The substantial difference in performance between EQM-LIN and EQM with respect to model skill is due to the different ways in which TFs are constructed at extreme tails. In EQM, distributional tails are corrected with a flexible TF that closely interpolates the quantile-quantile map of raw and observed data. However, since data at extreme tails is, by definition, scarce and variable, the TF produced by EQM may be unstable and can result in a faulty correction on out-of-sample model data (Cannon et al. 2015; Berg et al. 2012). In our study, MAE95 values of EQM increased markedly between months 8 and 11, reaching a maximum in month 9, while those of EQM-LIN remained near 2.5 mm (Fig. 5b). An inspection of training and testing datasets used during cross-validation reveals that often, the association between raw model and observed quantiles (the quantile-quantile map) was quite different between training and corresponding testing datasets. In such cases, EQM tended to overfit on training data, and consequently, the correction applied to testing data was unsuitable.
Figure 9 depicts such a scenario for month 9, when the difference in MAE95 between the two bias-correction methods was large. In Fig. 9, the EQM TF constructed with training data (black dots) extends non-linearly above the one-to-one line and then increases sharply. The shape of the training TF indicates that, generally, raw model quantiles are too low relative to those of observed data. When the training TF is applied to test data, raw model values in the tails, especially, are increased. For instance, a raw model value of 58.6 mm would be corrected to 81.8 mm (Fig. 9). However, the relationship between raw model and observed quantiles in the test data (blue dots), indicates that raw model quantiles are only slightly too high compared to observed quantiles (Fig. 9). When raw model data in the test set are bias-corrected with the training TF, raw model values are increased too much relative to observed values (Fig. 9). The quantile-quantile map of corrected model quantiles and observed quantiles (which should lie near or on the one-to-one line if the correction was satisfactory) is shifted far to the right of one-to-one line, indicating that corrected model values, especially in the tails, are too high. This example shows that the flexibility of EQM is also what makes it susceptible to overfitting on calibration data and supports other studies showing that EQM is sensitive to the choice of, and can overfit on calibration data (Reiter et al. 2018; Berg et al. 2012; Holthuijzen et al. 2021; Piani et al. 2010; Lafon et al. 2013).
For the same scenario, EQM-LIN produces a linear TF at extreme tails with a slope of 1 and an intercept of δ (the constant correction factor) (Fig. 10). Raw model values are adjusted by a constant, δ. Though this approach is less flexible than that of EQM, it produces more stable TFs and is less sensitive to training data. In Fig. 10, the training TF for EQM-LIN (black dots) is linear and does not exhibit the fluctuations apparent in the training TF of EQM (Fig. 9). The intercept (δ) of the TF in Fig. 10 is slightly less than zero, which means that raw model values will be decreased by δ. The TF for EQM-LIN represents an appropriate correction, as model quantiles in the test dataset are, in fact, too high relative to observed quantiles (Fig. 10, blue dots). For instance, the TF of EQM-LIN corrects a raw model value of 58.6 to 58.1 mm (Fig. 10). Accordingly, the quantile-quantile map of corrected model quantiles and observed quantiles is close to the one-to-one line, indicating a satisfactory correction.
Figures 9 and 10 are representative of scenarios in which the relationship between raw model and observed quantiles differ between training and testing data and highlight differences in bias-correction between EQM and EQM-LIN. In our study area, such scenarios are common in months when precipitation is variable and when extreme precipitation events are more likely (months 6–9). The difference in bias-correction between EQM-LIN and EQM can also be seen visually in downscaled, bias-corrected data over the study region. Figure 8 shows raw, downscaled, and corrected and downscaled precipitation data for one day in which daily mean precipitation exceeded the 95th percentile (September 12, 1986). Note that in Fig. 8, EQM results in an increase of high precipitation values (bright pink regions), while EQM-LIN results in a slight dampening of precipitation in the same regions. In Fig. 8, a model precipitation value of 52.14 mm is transformed to 68.25 mm using EQM and 51.28 mm using EQM-LIN. The increase and dampening of model precipitation by EQM and EQM-LIN, respectively, in Fig. 8 are a result of differences in EQM and EQM-LIN transfer functions.
Raw model, downscaled raw model, and bias-corrected data for one day (September 12, 1986) (a) with corresponding TFs for EQM (b) and EQM-LIN (c). Plot (a) shows raw model (4 km grid), downscaled raw model (1 km grid), and downscaled and bias-corrected precipitation data (mm) for a day in which daily mean precipitation exceeded the 95th quantile (September 12, 1986). Plots (b) and (c) show the corresponding EQM and EQM-LIN TFs, respectively; in (b) and (c), gray lines indicate how EQM and EQM-LIN adjust the maximum model precipitation value for this day (52.14 mm) as an example. This figure visually illustrates the difference between bias-correction via EQM and bias correction with EQM-LIN
Construction of the EQM TF in a train-test scenario; data for this plot reflect one particular train-test fold used during cross-validation for month 9 (September). The TF obtained from training data is shown in black. The quantile-quantile map of model and observed data in the test set is shown in blue. The corrected quantile-quantile map (quantiles of corrected model data versus quantiles of observed data) in the test set are shown in red. xmod,t and xcorr,t denote model and corrected model values, respectively, for day t. Gray arrows indicate how model data in the test set is corrected, based on the TF from training data
Construction of the EQM-LIN TF in a train-test scenario; data for this plot reflect one particular train-test fold used during cross-validation for month 9 (September). The TF obtained from training data is shown in black. The quantile-quantile map of model and observed data in the test set is shown in blue. The corrected quantile-quantile map (quantiles of corrected model data versus quantiles of observed data) in the test set are shown in red. xmod,t and xcorr,t denote raw model and corrected model values, respectively, for day t. Gray arrows indicate how raw model data in the test set is corrected, based on the training-set TF. The threshold (dashed line), indicates the 79th quantile of model data (6.88 mm). For ease of viewing, plot a) (gray box) shows the scenario at selected lower (0–10 mm) precipitation quantiles, and plot b) (gray dotted box) shows the scenario at selected extreme (50–80 mm) precipitation quantiles
Though EQM-LIN significantly outperformed EQM in terms of model skill (MAE and MAE95), results were not as dramatic for climatological (ETCCDI) indices. ETCCDI indices are calculated using spatially averaged, daily data, which reduces variation and may explain the similarity in performance of EQM and EQM-LIN for ETCCDI indices. Bias-correction via both EQM and EQM-LIN resulted in improvements over raw data for most indices. Though both bias-correction methods improved the overestimation of total annual mean precipitation (TotalP) as well as total extreme annual precipitation (Sum90) exhibited in raw model data, EQM-LIN performed slightly better than EQM for moderate extremes (Sum95). Raw model data adequately captured higher extremes (D99, S99); bias-correction provided a slight improvement in the representation of S99.
Interestingly, the distribution of raw model wet day frequency (WetDays) was similar to that of observed data, while bias-correction via either method resulted in considerable underestimation of wet day frequency. The negative impact of bias-correction on wet day frequency is most likely due to the excessive number of low-precipitation occurrences (“drizzle effect”) (Baigorria et al. 2007; Leander and Buishand 2007) in raw model data. EQM, which is used to correct low-valued quantiles in both bias-correction methods, results in the majority of excessive low-precipitation days being set to zero. The underestimation of wet day frequency after bias-correction via EQM is not unusual; similar results were found by (Fowler et al. 2007) and (Martins et al. 2021). Moreover, although wet-day frequency appears to be adequately represented in raw model data, it comes at the expense of substantial overestimation of total annual precipitation (TotalP) and precipitation intensity (SPI). After bias-correction via either method, precipitation intensity is better represented, and the distribution of total annual precipitation is very close to that of observed data. Thus, for most climatological indices, bias-correction via either method provides critical improvements to raw model data, especially with respect to extremes.
6 Conclusion
In this study, we show that a hybrid EQM approach for bias-correction (EQM-LIN), in which the majority of model data is corrected via EQM and extreme tails are corrected by a linear TF, resists overfitting on calibration data, increases overall and model skill, especially at extreme tails, and results in a better representation of climatological indices compared to conventional EQM. Our method is simple, intuitive, and easy to implement, making it a suitable alternative to EQM for bias-correcting historical and future climate simulations. Though we apply the method to precipitation data, we expect it could be applied to other climate variables as well. Future work might include adjusting the slope of the linear correction or using another function to construct the TF at extreme tails.
References
Alexander L, Donat M, Takayama Y, Yang H (2011) The climdex project: creation of long-term global gridded products for the analysis of temperature and precipitation extremes. In: WCRP open science conference, Denver
Baigorria GA, Jones JW, Shin DW, Mishra A, O’Brien JJ (2007) Assessing uncertainties in crop model simulations using daily bias-corrected regional circulation model outputs. Clim Res 34(3):211–222
Bannister D, Orr A, Jain SK, Holman IP, Momblanch A, Phillips T, Adeloye AJ, Snapir B, Waine TW, Hosking JS et al (2019) Bias correction of high-resolution regional climate model precipitation output gives the best estimates of precipitation in himalayan catchments. J Geophys Res Atmos 124 (24):14220–14239
Behnke R, Vavrus S, Allstadt A, Albright T, Thogmartin WE, Radeloff VC (2016) Evaluation of downscaled, gridded climate data for the conterminous United States. Ecol Appl 26(5):1338–1351
Beirlant J, Goegebeur Y, Segers J, Teugels JL (2006) Statistics of extremes: theory and applications. Wiley, New York
Berg P, Feldmann H, Panitz HJ (2012) Bias correction of high resolution regional climate model data. J Hydrol 448:80–92
Boé J, Terray L, Habets F, Martin E (2007) Statistical and dynamical downscaling of the seine basin climate for hydro-meteorological studies. Int J Climatol J R Meteorol Soc 27(12):1643–1655
Caldwell P, Chin HNS, Bader DC, Bala G (2009) Evaluation of a WRF dynamical downscaling simulation over California. Clim Change 95(3-4):499–521
Cannon AJ, Piani C, Sippel S (2020) Bias correction of climate model output for impact models. In: Climate extremes and their implications for impact and risk assessment. Elsevier, pp 77–104
Cannon AJ, Sobie SR, Murdock TQ (2015) Bias correction of gcm precipitation by quantile mapping: how well do methods preserve changes in quantiles and extremes? J Clim 28(17):6938–6959
Daly C, Taylor G, Gibson W, Parzybok T, Johnson G, Pasteris P (2000) High-quality spatial climate data sets for the United States and beyond. Trans ASAE 43(6):1957
Durre I, Menne MJ, Gleason BE, Houston TG, Vose RS (2010) Comprehensive automated quality assurance of daily surface observations. J Appl Meteorol Climatol 49(8):1615–1633
Ekström M, Grose MR, Whetton PH (2015) An appraisal of downscaling methods used in climate change research. Wiley Interdiscip Rev Clim Change 6(3):301–319
Enayati M, Bozorg-Haddad O, Bazrafshan J, Hejabi S, Chu X (2021) Bias correction capabilities of quantile mapping methods for rainfall and temperature variables. J Water Clim Change 12(2):401–419
Fang G, Yang J, Chen Y, Zammit C (2015) Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in china. Hydrol Earth Syst Sci 19(6):2547–2559
Feser F, Rockel B, von Storch H, Winterfeldt J, Zahn M (2011) Regional climate models add value to global model data: a review and selected examples. Bull Am Meteorol Soc 92(9):1181–1192
Field CB, Barros VR, Dokken DJ, Mach KJ, Mastrandrea MD, Bilir TE, Chatterjee M, Ebi KL, Estrada YO, Genova RC et al (2014) Contribution of working group ii to the fifth assessment report of the intergovernmental panel on climate change. Clim Change
Flint LE, Flint AL (2012) Downscaling future climate scenarios to fine scales for hydrologic and ecological modeling and analysis. Ecological Processes 1(1):2
Fowler H, Ekström M, Blenkinsop S, Smith A (2007) Estimating change in extreme european precipitation using a multimodel ensemble. J Geophys Res Atmos 112(D18)
Fowler HJ, Blenkinsop S, Tebaldi C (2007) Linking climate change modelling to impacts studies: recent advances in downscaling techniques for hydrological modelling. Int J Climatol 27(12):1547–1578
Franklin J, Davis FW, Ikegami M, Syphard AD, Flint LE, Flint AL, Hannah L (2013) Modeling plant species distributions under future climates: how fine scale do climate projections need to be? Glob Change Biol 19(2):473–483
Friederichs P, Hense A (2007) Statistical downscaling of extreme precipitation events using censored quantile regression. Mon Weather Rev 135(6):2365–2378
Gao X, Pal JS, Giorgi F (2006) Projected changes in mean and extreme precipitation over the mediterranean region from a high resolution double nested rcm simulation. Geophys Res Lett 33(3)
Gobiet A, Suklitsch M, Heinrich G (2015) The effect of empirical-statistical correction of intensity-dependent model errors on the temperature climate change signal. Hydrol Earth Syst Sci 19(10):4055–4066
Grillakis MG, Koutroulis AG, Daliakopoulos IN, Tsanis IK (2017) A method to preserve trends in quantile mapping bias correction of climate modeled temperature. Earth Syst Dyn 8(3):889
Grillakis MG, Koutroulis AG, Tsanis IK (2013) Multisegment statistical bias correction of daily gcm precipitation output. J Geophys Res Atmos 118(8):3150–3162
Gudmundsson L (2016) qmap: statistical transformations for post-processing climate model output. R package version 1.0-4
Gudmundsson L, Bremnes J, Haugen J, Engen-Skaugen T (2012) Downscaling rcm precipitation to the station scale using statistical transformations–a comparison of methods. Hydrol Earth Syst Sci 16 (9):3383–3390
Gutjahr O, Heinemann G (2013) Comparing precipitation bias correction methods for high-resolution regional climate simulations using cosmo-clm. Theor Appl Climatol 114(3):511–529
Hanssen-Bauer I, Achberger C, Benestad R, Chen D, Førland E (2005) Statistical downscaling of climate scenarios over Scandinavia. Clim Res 29(3):255–268
Hayhoe K, Wake CP, Huntington TG, Luo L, Schwartz MD, Sheffield J, Wood E, Anderson B, Bradbury J, DeGaetano A et al (2007) Past and future changes in climate and hydrological indicators in the us northeast. Clim Dyn 28(4):381–407
Heo JH, Ahn H, Shin JY, Kjeldsen TR, Jeong C (2019) Probability distributions for a quantile mapping technique for a bias correction of precipitation data: a case study to precipitation data under climate change. Water 11(7):1475
Hnilica J, Hanel M, Puš V (2017) Multisite bias correction of precipitation data from regional climate models. Int J Climatol 37(6):2934–2946
Hoffmann H, Rath T (2012) Meteorologically consistent bias correction of climate time series for agricultural models. Theor Appl Climatol 110(1):129–141
Holden ZA, Abatzoglou JT, Luce CH, Baggett LS (2011) Empirical downscaling of daily minimum air temperature at very fine resolutions in complex terrain. Agric For Meteorol 151(8):1066– 1073
Holm S (1979) A simple sequentially rejective multiple test procedure. Scand J Stat:65–70
Holthuijzen MF, Beckage B, Clemins PJ, Higdon D, Winter JM (2021) Constructing high-resolution, bias-corrected climate products: a comparison of methods. J Appl Meteorol Climatol 60(4):455–475
Huang H, Winter JM, Osterberg EC, Hanrahan J, Bruyère CL, Clemins P, Beckage B (2020) Simulating precipitation and temperature in the lake champlain basin using a regional climate model: limitations and uncertainties. Clim Dyn 54(1-2):69–84
Huang H, Winter JM, Osterberg EC, Horton RM, Beckage B (2017) Total and extreme precipitation changes over the Northeastern United States. J Hydrometeorol 18(6):1783–1798
Ivanov MA, Kotlarski S (2017) Assessing distribution-based climate model bias correction methods over an alpine domain: added value and limitations. Int J Climatol 37(5):2633–2653
Jakob Themeßl M, Gobiet A, Leuprecht A (2011) Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int J Climatol 31(10):1530–1544
Karl TR, Nicholls N, Ghazi A (1999) Clivar/gcos/wmo workshop on indices and indicators for climate extremes workshop summary. In: Weather and climate extremes. Springer, pp 3–7
Kim DI, Kwon HH, Han D (2018) Exploring the long-term reanalysis of precipitation and the contribution of bias correction to the reduction of uncertainty over South Korea: a composite gamma-pareto distribution approach to the bias correction. Hydrol Earth Syst Sci Discuss:1–53
Laflamme EM, Linder E, Pan Y (2016) Statistical downscaling of regional climate model output to achieve projections of precipitation extremes. Weather Clim Extremes 12:15–23
Lafon T, Dadson S, Buys G, Prudhomme C (2013) Bias correction of daily precipitation simulated by a regional climate model: a comparison of methods. Int J Climatol 33(6):1367–1381
Lanzante JR, Dixon KW, Adams-Smith D, Nath MJ, Whitlock CE (2021) Evaluation of some distributional downscaling methods as applied to daily precipitation with an eye towards extremes. Int J Climatol 41(5):3186–3202
Leander R, Buishand TA (2007) Resampling of regional climate model output for the simulation of extreme river flows. J Hydrol 332(3-4):487–496
Leung LR, Mearns LO, Giorgi F, Wilby RL (2003) Regional climate research: needs and opportunities. Bull Am Meteorol Soc 84(1):89–95
Livneh B, Bohn TJ, Pierce DW, Munoz-Arriola F, Nijssen B, Vose R, Cayan DR, Brekke L (2015) A spatially comprehensive, hydrometeorological data set for Mexico, the US, and Southern Canada 1950–2013. Sci Data 2(1):1–12
Luo M, Liu T, Meng F, Duan Y, Frankl A, Bao A, De Maeyer P (2018) Comparing bias correction methods used in downscaling precipitation and temperature from regional climate models: a case study from the Kaidu river basin in Western China. Water 10(8):1046
Mamalakis A, Langousis A, Deidda R, Marrocu M (2017) A parametric approach for simultaneous bias correction and high-resolution downscaling of climate model rainfall. Water Resour Res 53(3):2149–2170
Maraun D (2016) Bias correcting climate change simulations-a critical review. Curr Clim Change Rep 2(4):211–220
Maraun D, Shepherd TG, Widmann M, Zappa G, Walton D, Gutierrez JM, Hagemann S, Richter I, Soares PM, Hall A et al (2017) Towards process-informed bias correction of climate change simulations. Nat Clim Chang 7(11):764
Maraun D, Wetterhall F, Ireson A, Chandler R, Kendon E, Widmann M, Brienen S, Rust H, Sauter T, Themeßl M et al (2010) Precipitation downscaling under climate change: recent developments to bridge the gap between dynamical models and the end user. Rev Geophys 48(3)
Martins J, Fraga H, Fonseca A, Santos JA (2021) Climate projections for precipitation and temperature indicators in the douro wine region: the importance of bias correction. Agronomy 11(5): 990
Mearns L, Giorgi F, Whetton P, Pabon D, Hulme M, Lal M (2003) Guidelines for use of climate scenarios developed from regional climate model experiments. Data Distribution Centre of the Intergovernmental Panel on Climate Change
Miao C, Su L, Sun Q, Duan Q (2016) A nonstationary bias-correction technique to remove bias in gcm simulations. J Geophys Res Atmos 121(10):5718–5735
Monaghan A, Steinhoff D, Bruyere C, Yates D (2014) Ncar cesm global bias-corrected cmip5 output to support wrf/mpas research. Research Data Archive National Center Atmospheric Research Computational Information Systems Laboratory, Boulder 10:d6DJ5CN4
Oceanic N, Administration A (2018) Climate data online search. https://www.ncdc.noaa.gov/cdo-web/search?datasetid=GHCND. Accessed: 2017-09-30
Perkins S, Pitman A, Holbrook N, McAneney J (2007) Evaluation of the AR4 climate models’ simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions. J Clim 20(17):4356–4376
Peterson T (2005) Climate change indices. WMO Bull 54(2):83–86
Peterson TC, Vose RS (1997) An overview of the global historical climatology network temperature database. Bull Am Meteorol Soc 78(12):2837–2850
Piani C, Haerter J, Coppola E (2010) Statistical bias correction for daily precipitation in regional climate models over europe. Theor Appl Climatol 99(1-2):187–192
Pierce DW, Cayan DR, Maurer EP, Abatzoglou JT, Hegewisch KC (2015) Improved bias correction techniques for hydrological simulations of climate change. J Hydrometeorol 16(6):2421– 2442
Plummer M, Stukalov A, Denwood M, Plummer MM (2016) Package `rjags’. Vienna, Austria
R Core Team (2018) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
Rajczak J, Kotlarski S, Salzmann N, Schaer C (2016) Robust climate scenarios for sites with sparse observations: a two-step bias correction approach. Int J Climatol 36(3):1226–1243
Razali NM, Wah YB, et al. (2011) Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and anderson-darling tests. J Stat Model Anal 2(1):21–33
Reiter P, Gutjahr O, Schefczyk L, Heinemann G, Casper M (2016) Bias correction of ensembles precipitation data with focus on the effect of the length of the calibration period. Meteorol Z, 85–96
Reiter P, Gutjahr O, Schefczyk L, Heinemann G, Casper M (2018) Does applying quantile mapping to subsamples improve the bias correction of daily precipitation?. Int J Climatol 38(4):1623– 1633
Roberts DR, Wood WH, Marshall SJ (2019) Assessments of downscaled climate data with a high-resolution weather station network reveal consistent but predictable bias. Int J Climatol 39(6):3091–3103
Rosenberg EA, Keys PW, Booth DB, Hartley D, Burkey J, Steinemann AC, Lettenmaier DP (2010) Precipitation extremes and the impacts of climate change on stormwater infrastructure in washington state. Clim Chang 102(1):319–349
Shin JY, Lee T, Park T, Kim S (2019) Bias correction of rcm outputs using mixture distributions under multiple extreme weather influences. Theor Appl Climatol 137(1):201–216
Shrestha M, Acharya SC, Shrestha PK (2017) Bias correction of climate models for hydrological modelling–are simple methods still useful?. Meteorol Appl 24(3):531–539
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Liu Z, Berner J, Huang X (2019) A description of the advanced research wrf model. https://opensky.ucar.edu/islandora/object/opensky:2898. Accessed: 2019-03-04
Smirnov N, et al. (1948) Table for estimating the goodness of fit of empirical distributions. Ann Math Stat 19(2):279–281
Stager C, Thill M (2010) Climate change in the champlain basin: What natural resource managers can expect and do, the nature conservancy adirondack ch. and vt ch. Rep., Keene Valley NY
Tani S, Gobiet A (2019) Quantile mapping for improving precipitation extremes from regional climate models. Journal of Agrometeorology 21(4):434–443
Tarek M, Brissette F, Arsenault R (2021) Uncertainty of gridded precipitation and temperature reference datasets in climate change impact studies. Hydrol Earth Syst Sci 25(6):3331–3350
Teutschbein C, Seibert J (2012) Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J Hydrol 456:12–29
Thornton PE, Thornton MM, Mayer BW, Wilhelmi N, Wei Y, Devarakonda R, Cook R (2012) Daymet: daily surface weather on a 1 km grid for north america, 1980-2008 Oak Ridge National Laboratory (ORNL) Distributed Active Archive Center for Biogeochemical Dynamics (DAAC)
Tschöke GV, Kruk NS, de Queiroz PIB, Chou SC, de Sousa Junior WC (2017) Comparison of two bias correction methods for precipitation simulated with a regional climate model. Theor Appl Climatol 127(3):841–852
Um MJ, Kim H, Heo JH (2016) Hybrid approach in statistical bias correction of projected precipitation for the frequency analysis of extreme events. Adv Water Resour 94:278–290
USGS (2018) The national map. https://viewer.nationalmap.gov/basic/
Walton D, Hall A (2018) An assessment of high-resolution gridded temperature datasets over california. J Clim 31(10):3789–3810
Wang T, Hamann A, Spittlehouse DL, Murdock TQ (2012) Climatewna:high-resolution spatial climate data for western north america. J Appl Meteorol Climatol 51(1):16–29
Winter JM, Beckage B, Bucini G, Horton RM, Clemins PJ (2016) Development and evaluation of high-resolution climate simulations over the mountainous northeastern United States. J Hydrometeorol 17(3):881–896
Wood AW, Maurer EP, Kumar A, Lettenmaier DP (2002) Long-range experimental hydrologic forecasting for the eastern United States. Journal of Geophysical Research: Atmospheres 107(D20) ACL–6
Wootten AM, Dixon KW, Adams-Smith DJ, McPherson RA (2021) Statistically downscaled precipitation sensitivity to gridded observation data and downscaling technique. Int J Climatol 41(2):980–1001
Yang W, Andréasson J, Phil Graham L, Olsson J, Rosberg J, Wetterhall F (2010) Distribution-based scaling to improve usability of regional climate model projections for hydrological climate change impacts studies. Hydrol Res 41(3-4): 211–229
Zia A, Bomblies A, Schroth AW, Koliba C, Isles PD, Tsai Y, Mohammed IN, Bucini G, Clemins PJ, Turnbull S et al (2016) Coupled impacts of climate and land use change across a river–lake continuum: insights from an integrated assessment model of lake champlain’s missisquoi basin, 2000–2040. Environmental Research Letters 11(11):114026
Funding
The development of this manuscript was supported by the National Science Foundation under VT EPSCoR Grant No. NSF OIA 1556770.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethics approval and consent to participate
No animals were involved in this manuscript.
Consent for publication
All authors consent to the publication of this manuscript.
Conflict of interest
The authors declare no competing interests.
Additional information
Author contribution
All authors contributed to the study conception and design. Data was prepared by Jonathan M. Winter. Model development, writing, and analyses were performed by Maike F. Holthuijzen. All authors edited, commented on, and reviewed the manuscript. All authors read and approved the final manuscript.
Data availability
Data will be available upon request.
Code availability
Code will be available in a public Github repository.
Consent to participate
All authors consent to participating in the review process for this manuscript.
Open Access
This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix A: Estimating the threshold T and intercept δ
1.1 A.1 Estimating the threshold, T
The first step for obtaining the threshold T is to estimate τLIN from the data. We chose τLIN to be 0.79, based on a grid search over a range of values in a five fold cross-validation approach. We chose the value of τLIN that resulted in the minimization of the mean absolute error of observed and model ecdfs above the 95th percentile (MAE95), Reiter et al. (2016) (Section 3). It is crucial that τLIN be estimated using cross-validation; our result of τLIN = 0.79 may not generalize to all data.
To obtain T, we must assume a fixed value of τLIN. The next steps involves the construction of ecdfs for observed and model data in the calibration period. Ecdfs are constructed using 10,000 quantiles evenly spaced between 0 and 1. Next, the threshold, T is computed as \(ecdf_{mod}^{-1}(\tau _{LIN})\). Note that, T is the model precipitation value in mm corresponding to the quantile τLIN (whereas 0 ≤ τLIN ≤ 1).
1.2 A.2 Estimating the intercept, δ
To obtain δ, we assume that T has been calculated. Ecdfs of observed and model data are constructed using 10,000 quantiles evenly spaced between 0 and 1. Values in the ecdfs of model and observed data are sorted in increasing order. Note the rank of T within the sorted precipitation values of the model ecdf; the rank value will be denoted as RT. For example, suppose T = 12 mm and the rank of T within the ecdf of model data is 5,000, then RT = 5000.
Next, select the precipitation value from sorted, observed ecdf at rank RT and denote this value as Tobs. The intercept of the linear TF, δ which represents the constant correction, is calculated as the difference Tobs − T. Continuing with the example, suppose Tobs = 9.1 mm; then δ = 9.1 − 12 = − 2.9. This means model extremes (all values ≥ T) will be decreased by 2.9 mm.
The constant correction at extremes, δ, is similar to the constant extrapolation correction used by Boé et al. (2007). However, here, the constant correction is the difference T − Tobs, whereas in Boé et al. (2007), it is \(ecdf_{obs}^{-1}(1.00) - ecdf_{mod}^{-1}(1.00)\) as in Boé et al. (2007).
Appendix B: KS test
The KS test statistic, D is computed as
In Eq. 3, Fn and Gn are the two ecdfs being compared, n denotes the number of independent and identically distributed ordered values used to obtain Fn and Gn, and \(\underset {x}{sup}\) is the supremum of the collection of n distances.
Appendix C: Holm-Bonferroni method for multiple comparisons
When multiple statistical comparisons are made, it is often necessary to adjust the Type I error rate (commonly referred to as the significance level or α). The Type I error rate is the probability of falsely rejecting the null hypotheses when it is, in fact, true (a false positive). In the context of multiple hypothesis testing, it is often desirable to adjust the family-wise error rate (FWER), the probability of rejecting one null hypothesis in m hypothesis tests. The Holm-Bonferroni method is suitable when a less conservative adjustment of the FWER is preferred.
Suppose m hypothesis tests have been conducted, and m p-values have been calculated. The Holm-Bonferroni adjustment for the FWER involves two steps:
-
1.
Order p-values from least to greatest and assign each p-value a rank from 1 to k, \(k=1{\dots } m\)
-
2.
Find the smallest p-value such that \(p_{k} < \frac {\alpha }{m+1-k}\).
If the condition in step 2 is true, the p-value is significant; if the condition in step 2 if false, the p-value is not significant.
Appendix D: Summary results for ETCCDI indices
Table 3 shows the 25th, 50th, and 75th quantiles for each data type (Mod, EQM, and EQM-LIN) and ETCCDI index.
Rights and permissions
This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Holthuijzen, M., Beckage, B., Clemins, P.J. et al. Robust bias-correction of precipitation extremes using a novel hybrid empirical quantile-mapping method. Theor Appl Climatol 149, 863–882 (2022). https://doi.org/10.1007/s00704-022-04035-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-022-04035-2