Abstract
A new approach for rigorous spatial analysis of the downscaling performance of regional climate model (RCM) simulations is introduced. It is based on a multiple comparison of the local tests at the grid cells and is also known as ‘field’ or ‘global’ significance. The block length for the local resampling tests is precisely determined to adequately account for the time series structure. New performance measures for estimating the added value of downscaled data relative to the large-scale forcing fields are developed. The methodology is exemplarily applied to a standard EURO-CORDEX hindcast simulation with the Weather Research and Forecasting (WRF) model coupled with the land surface model NOAH at 0.11 ∘ grid resolution. Daily precipitation climatology for the 1990–2009 period is analysed for Germany for winter and summer in comparison with high-resolution gridded observations from the German Weather Service. The field significance test controls the proportion of falsely rejected local tests in a meaningful way and is robust to spatial dependence. Hence, the spatial patterns of the statistically significant local tests are also meaningful. We interpret them from a process-oriented perspective. While the downscaled precipitation distributions are statistically indistinguishable from the observed ones in most regions in summer, the biases of some distribution characteristics are significant over large areas in winter. WRF-NOAH generates appropriate stationary fine-scale climate features in the daily precipitation field over regions of complex topography in both seasons and appropriate transient fine-scale features almost everywhere in summer. As the added value of global climate model (GCM)-driven simulations cannot be smaller than this perfect-boundary estimate, this work demonstrates in a rigorous manner the clear additional value of dynamical downscaling over global climate simulations. The evaluation methodology has a broad spectrum of applicability as it is distribution-free, robust to spatial dependence, and accounts for time series structure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Climate change not only affects temperature statistics but also the hydrological cycle. It is expected to have a strong influence on ecosystems and human activities (Trenberth et al. 2003; Schär et al. 2004; O’Gorman and Schneider 2009; Hartmann et al. 2013). Therefore, climate projections and their uncertainty estimates need to be characterised and improved. Global climate models (GCMs) are the primary source of climate change information, but have a limited resolution due to computational constraints. At the same time, impact assessment requires information on much finer scales. Downscaling methods serve the purpose of translating the coarse GCM information to regional or local spatial and correspondingly finer temporal scales. Downscaling with nested regional climate models (RCMs) is the computationally most parsimonious physically based approach, which has been shown to perform equally well (Laprise 2008; Rummukainen 2010). RCMs showing skill at regionalising past climate are considered to be applicable also under different climate conditions in the future. Therefore, evaluating hindcast simulations against observation-based products is essential. Systematic biases caused by internal RCM physics or the nesting procedure can only be isolated by reanalysis-driven simulations. These so called perfect-boundary experiments have minimum large-scale biases and hence perform better than GCM-driven simulations (e.g., Christensen et al. 1997; Pan et al. 2001). In this sense, they yield upper bounds for the RCM skill. Particularly relevant is the ability of an RCM to generate appropriate fine-scale climatological features. It is quantified by the relative skill against the large-scale forcing and is known as added value (Laprise 2008; Di Luca et al. 2012). Due to the data assimilation, reanalyses excel GCM runs and hence are harder to outperform. Therefore, perfect-boundary evaluation yields a lower bound of the added value that the same RCM can have in a GCM-driven setting (Prömmel et al. 2010).
Within the recent EU-funded projects PRUDENCE (Christensen and Christensen 2007) and ENSEMBLES (van der Linden and Mitchell 2009), RCMs with grid resolutions of 20–50 km were evaluated for the European region. A systematic evaluation of perfect-boundary RCM simulations driven by the ERA-Interim reanalysis is a priority of the Coordinated Regional climate Downscaling EXperiment (CORDEX) (Giorgi et al. 2009). Its European branch, EURO-CORDEX, focusses on hindcast simulations at horizontal grid resolutions of 0.44 ∘ (∼ 50 km) and 0.11 ∘ (∼12 km) (e.g. Kotlarski et al. 2014; Katragkou et al. 2015).
RCM performance is quantified by statistical measures also known as performance metrics. Relative versions of these metrics allow comparison of RCM skill against that of the large-scale forcing data. Despite being direct objective measures of added value, relative performance metrics are still underapplied. Most previous works estimate the relative skill by comparing domain-aggregated scalar evaluation statistics and/or by visually inspecting the fields of the evaluation statistics for the downscaled and the larger-scale driving data (e.g. Duffy et al. 2006; Feser 2006; Sotillo et al. 2006; Buonomo et al. 2007; Sanchez-Gomez et al. 2009; Prömmel et al. 2010; Di Luca et al. 2012; Kendon et al. 2012; Cardoso et al. 2013; Chan et al. 2013; Pearson et al. 2015 Torma et al. 2015), which affects the fidelity of spatial analysis of added value or wholly precludes it. Winterfeldt and Weisse (2009) and Vautard et al. (2013) apply few relative metrics only for individual locations, and Winterfeldt et al. (2011) and Dosio et al. (2015) on a gridpoint basis.
As performance measures are subject to sampling variability, they should be physically interpreted only after the accompanying sampling uncertainty has been quantified. Within the frequentist approach to statistical inference (Jolliffe 2007), this can be done via confidence intervals, which is the popular approach (e.g. Elmore et al. 2006; Buonomo et al. 2007; Sanchez-Gomez et al. 2009; Kendon et al. 2012; Chan et al. 2013) or more directly via hypothesis testing as in, e.g. Duffy et al. (2006) and Cardoso et al. (2013). Most evaluation studies estimate statistical significance for domain-aggregated scalar measures (e.g. Feser 2006; Sanchez-Gomez et al. 2009; Kendon et al. 2012; Cardoso et al. 2013; Pearson et al. 2015), thus avoiding spatial analysis of the statistical significance. Others estimate statistical significance (grid)point-wise, but take neither multiplicity nor spatial autocorrelation of test statistics into account (e.g. Duffy et al. 2006; Buonomo et al. 2007; Winterfeldt and Weisse 2009; Winterfeldt et al. 2011; Chan et al. 2013; Katragkou et al. 2015).
The purpose of this study is to introduce a new approach for rigorous spatial analysis of downscaling performance and extend the arsenal of relative performance metrics. The methodology is exemplarily applied to a standard EURO-CORDEX run at 0.11 ∘ grid resolution with the WRF-NOAH model system (Warrach-Sagi et al. 2013a) over the territory of Germany, where high-resolution gridded observation data products are available.
More specifically, we employ distribution-based evaluation statistics and their relative versions to quantify the downscaling skill against the driving reanalysis. Our priority is to study in more detail the spatial structure of model performance as represented by the spatial patterns of grid cell statistics. We propose general formulae for deriving relative versions of performance metrics. Many of the relative measures are new or applied for the first time in the context of RCM added value analysis. Following the more direct hypothesis testing approach, at each grid cell we estimate the p value for each test statistic in a Monte Carlo framework. The problem of multiplicity is solved by determining the ‘field’ significance (e.g. Livezey and Chen 1983; Ventura et al. 2004; Wilks 2006a) as implemented by the false discovery rate (FDR) approach of Benjamini and Hochberg (1995). As FDR is generally more powerful and robust to spatial correlations than alternative multiple comparison methods (Wilks 2006a), it provides a more meaningful spatial pattern of local rejections. We refer to the latter as the spatial pattern of statistical significance. It includes the locations at which the values of evaluation statistics are in breach with the null hypothesis, that is, which are highly unlikely to have occurred by chance. The analysis focusses on these patterns rather than on the magnitudes of the evaluation statistics as is conventionally the case. Finally, we suggest a process-oriented interpretation of the spatial and seasonal patterns of model skills and deficiencies. To the best of our knowledge, this is the first application of the concept of field significance in the context of RCM evaluation.
The first part of this paper (Ivanov et al. 2017; henceforth referred to as Part I) analyses monthly temperature fields. It demonstrates that in most cases, the downscaled distributions are statistically indistinguishable from the observed ones and that the fine-scale features generated in the monthly temperature field over regions of complex topography are appropriate. This study is devoted to daily precipitation in essentially the same evaluation set-up. The selection of an appropriate blocklength for the local resampling tests for daily data is nontrivial and based on an exploratory analysis of the observed autocorrelation structure. Also, there are additional evaluation statistics for the distribution of precipitation on wet days. Section 2 reviews the methodology. In Section 3, for the reader’s convenience, we again review the landscape, then discuss the precipitation climate of Germany and finally, introduce the data sets. Results are discussed in Section 4. Section 5 summarises the main findings of the study.
2 Evaluation methodology
We review the evaluation methodology with emphasis on the new aspects for daily precipitation. For more general details, the reader is referred to Part I.
2.1 Evaluation statistics
The overall similarity between the modelled and observed distributions is quantified by the Perkins score (Perkins et al. 2007). As it measures the common area below the two probability density functions (PDFs), its perfect value is 1. The bin width of 2 mm/day is based on the Sturges algorithm (Sturges 1926). Dry days constitute a separate bin, formally 0–1 mm/day.
We consider differences between characteristics of simulated and observed distributions, which we refer to as additive biases. More specifically, these are the bias of the mean seasonal precipitation and biases of characteristics of the wet-day precipitation distribution. The latter are commonly also referred to as measures of conditional precipitation intensities as they are conditional on the occurrence of a wet day. In particular, the mean, 10th, 50th, and 90th percentiles on wet days are used to quantify the conditional intensities of mean, light, moderate, and heavy precipitation, respectively. Conditional intensities depend not only on the respective absolute intensities but also on the frequency of wet days: for fixed absolute intensities, more wet days entail lower conditional intensities and vice versa (Schär et al. 2016). Of course, the perfect value of additive biases is 0.
The frequency bias score for a precipitation intensity category is the ratio between the number of events belonging to the category in the downscaling and in the observations. The thresholds for the categories are defined by observed percentiles of the 1980–2009 wet-day precipitation climatology. In the following, X % stands for the Xth observed climatological percentile. We use the quartiles as thresholds to define the ‘moderate’ (25–75%) category, the median for the ‘stronger-than-moderate’ (>50%) category, and the deciles for the ‘light’ (<10%) and ‘heavy’ (>90%) categories. We also consider a wet-day frequency bias, where the threshold of 1 mm/day separates the ‘dry-day’ from the ‘wet-day’ category. The perfect value of these scores is 1. As the event frequencies are calculated from the whole sample (not just from the wet days), they only depend on the absolute precipitation intensity (Schär et al. 2016). Therefore, when interpreting the spatial patterns on the maps, it is instructive to compare biases of wet-day percentiles to biases of the wet-day frequency and of the corresponding event frequency. The categories of the <10, >50, and >90% events correspond to the 10th, 50th, and 90th wet-day percentile, respectively. If a wet-day intensity bias does not spatially coincide with a favourable wet-day frequency bias, then it cannot be an artefact of misrepresented wet-day frequency, and is hence caused by misrepresented absolute intensities. For example, if the 90th wet-day percentile is overestimated but the wet-day frequency is not underestimated, it can be concluded that the overestimation of the 90th wet-day percentile is due to an increase of the absolute intensity of heavy precipitation. Vice versa, if a wet-day percentile bias does not spatially coincide with a favourable bias of the corresponding event frequency, then it is linked to a misrepresented wet-day frequency. For example, if the 90th wet-day percentile is overestimated, but the frequency of the >90% category is not, then the overestimation of the 90th wet-day percentile should be an artefact of an underestimated wet-day frequency.
For each of these measures of absolute performance (i.e. against the observations), we calculate the corresponding relative performance metric that quantifies the added value against the driving large-scale data. The relative versions of the dimensionless metrics (Perkins score, frequency biases) are defined as follows:
and of the dimensional (the wet-day percentile biases) as
where M rel is the relative measure, M is the value of the measure for the downscaling, M perf is the perfect value of the measure, and M ref is the value for the large-scale driving data. The relative metrics are dimensionless and have a no-skill value of 0; their positive values indicate positive added value and vice versa.
2.2 Estimating statistical significance
Local tests
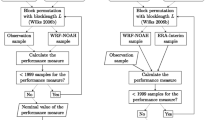
The null distributions of the evaluation statistics are estimated non-parametrically at each grid cell by means of permutation tests that are distinct for the absolute and the relative metrics. The null hypothesis is that two samples are identically distributed: the observations and downscaling for the absolute tests and the downscaling and driving reanalysis for the relative tests. For example, in the case of a relative test, the downscaled and ERA-Interim data are pooled together and two samples are randomly drawn out of the pool without replacement employing the efficient permutation algorithm suggested in Wilks (2006b). One of the synthetic data batches thus drawn is labelled ‘WRF-NOAH sample’ and the other ‘ERA-Interim sample’. From these two samples and the observations, an artificial value for the respective relative test statistic is calculated. The process is repeated 1999 times to generate the null distribution of the statistic. The nominal value of the statistic, which is computed from the original data samples, is compared against its null distribution to obtain the respective p value. For the Perkins score, which can be maximum 1, we test against the one-tailed alternative of smaller values. The rest of the tests are implemented two-tailed using the equal-tail bootstrap p value (e.g. Davidson and MacKinnon 2007).
This would be a complete description of the resampling if the data were independent. As we work with time series, this is not the case. The distribution of statistical estimators based on dependent data heavily depends on the joint distribution of the observations (Léger et al. 1992). In effect, this means that each bootstrap resample of the original data must be a sample from that joint distribution. However, classical bootstrap shuffles the original data and destroys this structure, which can distort the bootstrap distribution of the statistic. The idea of block resampling methods is to shuffle blocks of contiguous data values instead of individual values, so that the dependence structure of the original series is preserved. The problem of selecting the appropriate blocklength L is nontrivial. It must be large enough to ensure that the temporal autocorrelation structure in the original series is retained and also that data values separated by a time period of length L or more are essentially independent. As Léger et al. (1992) point out, the choice ‘requires an educated guess based on studying the data more deeply’. Tests are oversized, i.e. liberal, if the blocklength L is too small, and lose power, i.e. are conservative, if L is too large (Wilks 2006b). In the Appendix, we show that the blocklength of L = 28 days preserves the intraseasonal lag autocorrelations in observed daily precipitation. This choice warrants relatively conservative tests, which is consistent with our leitmotif of only isolating the strongest effects.
Field significance
Assume that each of the local tests is performed at a significance level of α% and that in reality all tests are insignificant. If the map consisted of an infinite number of grid cells, the test results at which were unrelated, then the proportion of tests that would come up as significant by chance would tend to exactly α%. In practice, however, the number of tests is finite and the tests are dependent because of spatial autocorrelations. Each of these effects renders the proportion of local tests erroneously detected as significant substantially larger than α% (Livezey and Chen 1983). As we need interpretable spatial patterns, this is not tolerable. To ensure that no more than α% of the tests are significant by chance, we have to impose a smaller significance level to them. This is known as the problem of multiplicity (e.g. Katz and Brown 1991), which is solved by the so called multiple comparison or field/global significance tests. The null hypothesis of the latter, also called global null hypothesis, is that all local tests are true. Here, we determine field significance after the false discovery rate (FDR) approach of Benjamini and Hochberg (1995), which is one of the most powerful multiple comparison tests. It controls the FDR, which is the expected proportion of the rejected local tests that are actually insignificant. The robustness of this test to spatial dependence (Ventura et al. 2004) renders it directly applicable to spatial fields. The spatial pattern of local rejections it yields is meaningful. We work at the 5% level of global significance.
Subregional analyses
Testing field significance in German subregions (see Section 3.1) is expected to reveal more regional detail. This is because the global test tends to become more permissive when the number of local tests decreases (see Part I). To make the results for the different subregions comparable, we use the same blocklength L = 28 for all of them. This also ensures that the tests are rather conservative. We only mention subregional testing in case it reveals new features and qualitatively modifies results.
3 Climatology of Germany and data sets
3.1 Landscape and climatology of Germany
Landscape
Figure 1 shows a topographical 2′×2′ map of Germany with the major landforms and cities labelled. The landscape of Germany can be divided into three distinct parts, from north to south namely North German Lowlands, Central German Uplands, and South Germany. The terrain in the North German Lowlands is flat and mostly below 100 m above mean sea level. The East and North Frisian Islands as well as Germany’s largest island of Rügen are also part of the Lowlands. The Central German Uplands consist of plateaus and low mountain ranges separated by river valleys. Some of the most conspicuous elevations are the Eifel (747 m), Hunsrück (816 m), Rothaar (843 m), Taunus (879 m), Rhön (950 m), Harz (1142 m), Fichtel (1051 m), and Ore Mountains (1215 m) as well as the Thuringian (982 m), Bavarian (1121 m), and Bohemian (1456 m) Forests. South Germany has complex terrain with middle and high mountain ranges separated by river valleys and plateaus. Here belong the Black Forest (1493 m), the Swabian Jura (1015 m), and the Bavarian Alps (2962 m).
Topographical map of Germany. The 2\(^{\prime }\) gridded relief (ETOPO 2v2g, http://www.ngdc.noaa.gov/mgg/fliers/06mgg01.html) as well as the rivers, shore-, and borderlines (GSHHG: the Global Self-consistent, Hierarchical, High-resolution Geography Database, http://www.ngdc.noaa.gov/mgg/shorelines/shorelines.html) data are available on the web site of the US National Oceanic and Atmospheric Administration. Height in metres above mean sea level is plotted in colour scale; cities are displayed as red dots; rivers, shore-, and borderlines—as blue, black, and red curves, respectively. Some major forms of relief are labelled in black, water bodies in blue, and cities in red. The grey lines define the NW, NE, SW, SE German subregions (see text), which are labelled in white
An idea about the dominant soil types in Germany can be obtained from the right panel of Fig. 2. It displays the most recent soil texture data base for Europe covering all soil textures of WRF based on the Harmonised World Soil Database and the German soil survey for Germany (Milovac et al. 2014); the original 1-km resolving data set was upscaled to the WRF-NOAH grid using the default nearest-neighbour interpolation scheme of the WRF Pre-processing System (WPS). Sandy soils predominate in the North German Lowlands, clays in South Germany along river valleys, and loamy soils in the rest of the country.
Dominant soil category in WRF-NOAH, based on the 5-km resolution FAO data (left panel) and in the most recent 1-km resolving soil texture data base for Europe developed at the Institute of Physics and Meteorology (IPM) of UHOH (right panel). Black contour lines display the WRF-NOAH orography; rivers, shore-, and borderlines are shown as blue, black, and red lines, respectively
Climatology
Precipitation in Germany develops in a predominantly westerly flow, associated with frontal systems in winter and convective processes in summer (Wulfmeyer et al. 2011). The North is subject to marine influence from the North and Baltic Seas. The climatology of mean seasonal precipitation for the 1989–2009 period is shown in Fig. 3. In winter, mean precipitation decreases generally from west (2–3 mm/day) to east (1–2 mm/day); west slopes and tops of mountains are isolated wetter areas (3–6.5 mm/day), while east slopes and river valleys are affected by rain shadows (∼1 mm/day). In summer, precipitation tightly follows the topography, lowlands and river valleys being drier (1.5–2.5 mm/day) and elevated areas wetter (2.5–5 mm/day); particularly strong is the orographic enhancement of precipitation over the Fore-Alps and the west slopes of the Black Forest (5–10.5 mm/day); the North Sea influence makes the North Coast relatively wetter (2.5–3.5 mm/day). As seen, precipitation is larger in summer than in winter. Correspondingly, its temporal variability, as quantified by the spread of the wet-day distribution, is from 1–2 to about 5–6 mm/day larger in summer (not shown).
Subregions
To get into more detail, we divide Germany’s projection on the WRF-NOAH grid into four semi-equal rectangular parts by means of the 4.89 ∘W meridian and 0.55 ∘N parallel, visualised on the geographic projection of Fig. 1 as grey lines. The resulting subregions are labelled north-west (NW), north-east (NE), south-west (SW), and south-east (SE) Germany.
3.2 Data
Observations
The observation-based daily precipitation data are a rasterised product of the German Weather Service (Deutscher Wetterdienst, DWD). They are derived after the REGNIE (REGionalisierung der NIEderschlagshöhen) methodology from data at weather stations (DWD 2009) and have a spatial resolution of approximately 1 km over Germany. The temporal resolution is daily, from 06 to 06 GMT. The climatological (1961–1990) monthly mean undercatch of the German precipitation gauges used in the REGNIE data ranges from 5.6% in July in very protected locations below 1000 m in South Germany up to 33.5% in February below 700 m at non-protected gauges in East Germany (Richter 1995).
Reanalysis
The ERA-Interim reanalysis (Dee et al. 2011) of the European Centre for Medium-Range Weather Forecasts (ECMWF) is used to drive the RCM simulation. For the evaluation, we use 6-hourly total precipitation, projected on a grid of 0.6∘×0.6∘ from the original Gaussian reduced grid.
WRF-NOAH simulation
The object of this study is a standard EURO-CORDEX evaluation simulation with WRF-NOAH, provided by the University of Hohenheim (UHOH) (Warrach-Sagi et al. 2013a). The WRF model version 3.3.1 is run with the land surface model NOAH (Chen and Dudhia 2001a, (Chen and Dudhia 2001b)) for a hindcast evaluation over the period 1987–2009. The model operates one-way nested over the standard EURO-CORDEX domain on a rotated longitude-latitude grid with horizontal resolution of 0.11∘×0.11∘ (EUR-11). The vertical is described by 50 layers up to 20 hPa. The simulation is driven by the 6-hourly ERA-Interim reanalysis at the lateral boundaries and daily sea surface temperature data also from the reanalysis. The relaxation zone around the model domain is 30 grid cells wide and the model time step is 60 s. The physical package includes the Morrison two-moment microphysics scheme (Morrison et al. 2009), the Yonsei University atmospheric boundary layer parameterisation (Hong et al. 2006), the Kain-Fritsch-Eta Model convection scheme (Kain 2004), and the Community Atmosphere Model (CAM) shortwave and longwave radiation schemes (Collins et al. 2004). Soil moisture and temperature profiles were initialised on 1st January 1987 from ERA-Interim after interpolation to the NOAH model. The WPS uses the 30 ″ land-cover data form the Moderate Resolution Spectroradiometer (MODIS), classified according to the International Geosphere-Biosphere Programme (IGBP). The soil textures are from the 5 ′ data of the Food and Agriculture Organization of the United Nations (UN/FAO). To reduce at least some spin-up effects that may distort the model results, the analysis starts in the winter of 1989/1990. We use 3-hourly model output fields of total precipitation. We note that Vautard et al. (2013) and Kotlarski et al. (2014) evaluated this simulation as a part of the EURO-CORDEX RCM ensemble for Europe on a 25-km scale.
3.3 Data processing
The DWD observations and ERA-Interim reanalysis were transformed by quadratic inverse-distance-weighted interpolation to the WRF-NOAH grid with an interpolation radius of 11 and 50 km, respectively. After the spatial regridding, from the WRF-NOAH and ERA-Interim outputs we built data sets for daily precipitation sums, from 06 to 06 GMT on the next day. To ensure equal numbers of years for all seasons and to avoid putting months belonging to the same winter season into different years, we investigate the 20-year period 1st December 1989–30th November 2009. To avoid the drizzling effect, we define days with precipitation below 1 mm/day as dry days, setting the corresponding precipitation values to 0 in all data sets after the interpolation to the WRF-NOAH grid. The 1-mm/day threshold has been shown to remove drizzle discrepancies between observations and models and is standard in climate impact-related research (e.g. Kjellström et al. 2010).
Note that we estimate the added value of the downscaling relative to the large-scale driving reanalysis interpolated on the RCM grid. This preserves the high-resolution climate features, which are our primary interest. The same approach is followed, e.g. in Sotillo et al. (2006) and Winterfeldt et al. (2011).
4 Results and discussion
In the following, we generalise evaluation results as a (systematic) dry/wet bias when most of the considered precipitation intensity and frequency characteristics are under-/overestimated. The terms under-/overprediction refer to the frequency bias. Also, precipitation intensities are meant absolute (rather than conditional) unless stated otherwise. Therefore, biases of conditional precipitation intensities are discussed only if they are indicative of biases of the respective absolute intensities and are not merely an artefact of wet-day frequency biases. For brevity, we only show results for winter (DJF) and summer (JJA). We note that due to the higher local temporal variability of daily precipitation in summer, the bootstrap sampling variability of the test statistics is also larger in summer. Therefore, in summer, the deviation of a statistic from its expected value under the null must be correspondingly larger than in winter to be significant.
4.1 Basic diagnostics
Prior to the spatial analysis, to get an overall impression of the model performance, we pool the gridpoint data together and visually compare the empirical probability density (PDFs) and wet-day cumulative distribution (CDFs) functions of the observations and the model data.
The PDFs are shown in Fig. 4. The probability axes are logarithmic to facilitate the visualisation of the very small probabilities for heavy precipitation events. Results for whole Germany are shown in Fig. 4a. In both seasons, WRF-NOAH is generally closer to reality than ERA-Interim. The Perkins score indicates that while in winter WRF-NOAH has no general skill over ERA-Interim in terms of reproducing the daily precipitation PDFs (both models have a score of 92%), in summer the downscaling excels (99% for WRF-NOAH against 88% for ERA-Interim). However, the Perkins score is not sensitive to heavy precipitation events, because they occur more rarely and contribute less to the PDFs. For this purpose, the logarithmic PDF representation comes in handy: WRF-NOAH clearly better reproduces the probability densities of precipitation events above about 21 mm/day (heavy precipitation) in both seasons. ERA-Interim performs overall better in winter than in summer, whereas the opposite is true for WRF-NOAH. The reanalysis overforecasts wet days and precipitation amounts up to 11 mm/day (light-to-moderate precipitation), more pronounced in summer, and underpredicts heavy precipitation. In winter, WRF-NOAH also overforecasts wet days and light-to-moderate precipitation and underforecasts heavy precipitation. In summer, it closely follows the observations.
Probability density functions and Perkins score S of daily precipitation for Germany (left panel: winter, right panel: summer) (a), the German subregions (see text) for winter and summer, respectively (b) and (c), from the DWD observations (black), ERA-Interim reanalysis (green), and WRF-NOAH simulation (red). Dry days formally fall into the 0–1-mm/day category, the bin size is otherwise 2 mm/day
Similar conclusions can be drawn for the four subregions from their PDFs shown in Fig. 4b, c for winter and summer, respectively. Some new aspects are revealed about WRF-NOAH. In winter, the overprediction of light-to-moderate precipitation amounts is most pronounced in NE Germany, and the underprediction of heavy precipitation in SE Germany. In summer, contrary to the general tendency, wet days are underpredicted in the North, particularly in NW Germany; heavy precipitation tends to be overpredicted in the West, particularly in the SW, and underpredicted in the East.
The corresponding wet-day cumulative distribution functions displayed in Fig. 5 shed light on the overall representation of the conditional precipitation intensity. ERA-Interim strongly underestimates all precipitation quantiles. WRF-NOAH largely solves this problem in summer, but in winter, the improvement is negligible. However, in summer, precipitation quantiles are still underestimated in SE Germany. Because of the underprediction of wet days, the lowermost nonzero absolute percentiles in NW Germany in summer are underestimated; hence, the lowermost conditional percentiles are also underestimated.
Cumulative distribution functions of daily precipitation on wet days for Germany (left panel: winter, right panel: summer) (a), the German subregions (see text) for winter and summer, respectively (b) and (c), from the DWD observations (black), ERA-Interim reanalysis (green), and WRF-NOAH simulation (red). The bin size is 2 mm/day
4.2 Absolute performance
Figure 6a shows the quality of representation of the local PDFs as measured by the Perkins score, Fig. 6b the bias of mean seasonal precipitation, and Fig. 6c the biases of selected characteristics of the wet-day distribution. Figure 7a displays the frequency biases of wet days and Fig. 7b of light, moderate, stronger-than-moderate, and heavy precipitation events. As seen, the significant grid cells are usually a small number and concentrated in specific regions (coastal areas, windward/lee sides, mountain tops, river valleys, kettles, etc). Thus, they form clear spatial patterns, which can be linked to physical processes known to have the same geographic and seasonal fingerprint for the respective distribution characteristic. Generally, the downscaling has a systematic and significant dry bias over tops and lee sides of mountains and hills as well as in the Bavarian Alps, and a wet bias over windward sides, in deep river valleys, some areas in NE Germany, and over the plateau of Upper Swabia. The north coast has a dry summer and wet winter bias.
Selected distribution-based performance measures of daily precipitation simulated by WRF-NOAH in comparison to high-resolution observations from the DWD: Perkins score (left panel: winter, right panel: summer) (a), mean bias (left panel: winter, right panel: summer) (b), and biases of some wet-day distribution characteristics (upper panels: winter, lower panels: summer) (c). A grid cell is plotted only if the respective test is locally significant at the 5% level of field significance. Black contour lines display the WRF-NOAH orography; rivers, shore-, and borderlines are shown as blue, black, and red lines, respectively
Frequency biases of daily precipitation categories defined by observed wet-day percentiles (X% stands for the Xth percentile) for the 1980–2009 climatological period: ‘wet-day’ category (left panel: winter, right panel: summer) (a), and ‘light’, ‘moderate’, ‘stronger-than-moderate’, and ‘heavy’ (from left to right) precipitation categories in winter (upper panels) and summer (lower panels) (b), simulated with WRF-NOAH in comparison to high-resolution observations from the DWD. A grid cell is plotted only if the respective test is locally significant at the 5% level of field significance. Black contour lines display the WRF-NOAH orography; rivers, shore-, and borderlines are shown as blue, black, and red lines, respectively
As noted in Section 2.1, a comparison of the significance patterns of biases of conditional intensities (Fig. 6c) with the frequency bias of the wet-days (Fig. 7a) and of the corresponding precipitation categories (Fig. 7b) should reveal whether biases of conditional intensities are caused by biases of the respective absolute intensities or are an artefact of wet-day frequency biases. In most areas, biases of wet-day percentiles are indeed consistent with biases of the corresponding precipitation categories. Notable exceptions are the underestimated conditional intensities of moderate and heavy precipitation over the Lowlands and the north-east coast in winter (Fig. 6c, third and fourth panel on the upper row), which are caused by the strong overprediction of wet days (Fig. 7a, left panel).
The dominant patterns of local significance are consistent with the analysis of the overall distributions in Section 4.1: in winter the overprediction of wet days (Fig. 7a, left panel) and light (Fig. 7b, first panel on the upper row) at the expense of heavy precipitation (Fig. 7b, fourth panel on the upper row) and the underestimation of conditional precipitation intensities (Fig. 6c, upper panels), in summer the underestimation of lowermost conditional percentiles in NW Germany (Fig. 6c, second panel on the lower row), the overestimation of heavy precipitation characteristics in the West, particularly SW, and underestimation in the East, particularly SE (Figs. 6c and 7b, fourth panel on the lower row). For most evaluation measures, the non-rejecting area is considerably larger in summer than that in winter, which is also consistent with the better overall performance in summer as inferred in Section 4.1. Only for the biases of mean seasonal precipitation (Fig. 6b) and the conditional intensity of light precipitation (Fig. 6c, second column), the non-rejecting area is almost equal in the two seasons.
4.2.1 Discussion
The major spatial and seasonal patterns of absolute downscaling performance are now discussed in detail.
-
(1)
In winter, wet days and light precipitation events are significantly overpredicted over almost whole Germany, while in summer, mainly over regions of complex topography (Fig. 7a and first column of Fig. 7b).
Overprediction of wet days and light precipitation is a common problem of state-of-the-art mesoscale climate models and is known to be more pronounced in winter (Frei et al. 2003; Feldmann et al. 2008; Kjellström et al. 2010; Heikkilä et al. 2011; Warrach-Sagi et al. 2013b; Marteau et al. 2014). In winter, it occurs virtually everywhere, which points to a link to the large-scale scheme. Its significance in summer mainly over complex topography indicates a link to the representation of convection. Indeed, Kendon et al. (2012) compared a very high-resolution (1.5 km) and a state-of-the-art (12 km) RCM simulations over a region of the United Kingdom and showed that the overprediction of wet days and light precipitation is considerably reduced in the 1.5-km simulation. They attributed the issue to the convection parameterisation scheme, but, like Marteau et al. (2014), recognised that the large-scale scheme also has a significant contribution. Over flat areas, in summer, large-scale biases do not leave a significant footprint on the simulated distributions because they should be masked by the larger variability.
-
(2)
Certain areas in NE Germany and the plateau of Upper Swabia tend to have a wet bias. In NE Germany, in winter, overpredicted occurrence of precipitation (Fig. 7a, left panel) and of light, moderate as well as stronger-than-moderate precipitation events (Fig. 7b, first, second, and third panel on the upper row) leads to larger seasonal precipitation amounts (Fig. 6b, left panel) and distorts the PDFs (Fig. 6a, left panel). In summer, the conditional intensity of moderate precipitation is overestimated (Fig. 6c, third panel on the lower row); a more detailed analysis reveals that it is indicative of overestimated absolute intensity, as it spatially coincides with overestimated frequency of wet days and stronger-than-moderate events, both of which are not statistically significant. In Upper Swabia, precipitation occurrence (Fig. 7a) and moderate precipitation events (Fig. 7b, second column) are overpredicted in both seasons; in winter, light (Fig. 7b, first panel on the upper row) and in summer, moderate and stronger-than-moderate precipitation events (Fig. 7b, second and third panels on the lower row) are also overpredicted; the PDFs are distorted in both seasons (Fig. 6a).
Warrach-Sagi et al. (2013b) have documented the wet bias of WRF-NOAH in NE Germany and attribute it to inconsistencies in the FAO soil texture data (Warrach-Sagi et al. 2008). Indeed, the FAO soil texture map, shown in the left panel of Fig. 2, contains loam over a large area, whereas, according to the most recent UHOH soil data base (Fig. 2, right panel), NE Germany is dominated by sandy soils. Likewise, according to the FAO data, the soil texture in Upper Swabia is loam, while the new data indicates sandy loam. Loamy soils imply more soil water availability for evapotranspiration, which is a primary moisture supply source for the atmospheric boundary layer. This in turn could account for the enhanced WRF-NOAH precipitation.
-
(3)
The north coastal areas stand out with specific precipitation biases, which can be summarised as a systematic wet winter bias, most pronounced over the west coast of the Jutland Peninsula and the north coast of the Rügen Island (Figs. 6b and 7a, left panels; Fig. 6c, first panel on the upper row, and Fig. 7b, upper row), and a systematic dry summer bias, most pronounced at the east part of the Jutland Peninsula and the east Frisian islands (Figs. 6b and 7a, right panels; Figs. 6c and 7b, second and third panels on the lower rows). Correspondingly, the PDFs are distorted all over the north coast in winter and over the east part of the Jutland Peninsula and the East Frisian islands in summer (Fig. 6a).
In Part I, we saw that the winters are too warm and summers too cold in these areas. Furthermore, the wet bias in winter, when the zonal circulation is most intense, is the strongest at the windward side of the coast. These consistent patterns point out to potential problems in the representation of atmospheric processes at the sea-land transition zone. For instance, an exaggerated low-level convergence of the westerly flow that impinges on the coast, in summer combined with a too intense sea-breeze circulation, could be the culprits. However, until further research is done, these suggestions remain speculative. Note that in their study of the same simulation, Kotlarski et al. (2014) detect the German north coast as a part of a large area in North Europe with a dry summer bias, which they speculatively attribute to the cloud microphysics scheme. Our objective and conservative analysis methodology spatially confines the significantly biased area only along the coast and thus suggests a link to processes at the sea-land transition.
-
(4)
In both seasons, there is a systematic wet bias over west slopes of mountains and hills, in winter accompanied by a systematic dry bias over east slopes; these biases are most pronounced for characteristics of stronger-than-moderate and heavy precipitation (Figs. 6b, c and 7); the PDFs are correspondingly distorted over windward slopes in winter (Fig. 6a, left panel).
This is the spatial pattern of enhanced orographic forcing, known as the ‘windward-lee effect’, which is a common deficiency of state-of-the-art mesoscale weather and climate models (Feldmann et al. 2008; Schwitalla et al. 2008; Bauer et al. 2011; Wulfmeyer et al. 2011; Marteau et al. 2014). As very high-resolution models that explicitly resolve convection do not have this deficiency, convection schemes should be the cause. Parameterising deep convection leads to misplaced low-level convergence lines and does not account for moving convective cells and advection of hydrometeors. This eventually leads to misplaced location of deep convection and hence of precipitation (Schwitalla et al. 2008; Wulfmeyer et al. 2011; Bauer et al. 2011). Obviously, the drying effect over east slopes does not appropriately scale in summer and is masked by the larger variability.
-
(5)
In summer, there is a systematic dry bias over mountains and hills, most pronounced for characteristics of stronger-than-moderate and heavy precipitation (Figs. 6c and 7b, second, third, and fourth panels on the lower rows), and the PDFs are correspondingly distorted (Fig. 6a, right panel).
The specific spatial pattern of underrepresented heavy precipitation events points to problems with the convection scheme. Note that the ERA-Interim-driven simulations of Chan et al. (2013) and Marteau et al. (2014) document overestimation in summer. The fact that other RCM implementations of similar horizontal resolution (the primary differences between which concern the parameterisation of subgrid processes) show a reverse effect also supports this interpretation. Indeed, convection-permitting simulations (e.g. Schwitalla et al. 2008; Chan et al. 2013; Torma et al. 2015) demonstrate a substantial improvement of heavy and peak precipitation intensities in the summer season.
-
(6)
The Bavarian Alps stand out with a systematic dry, and deep river valleys and kettles with a systematic wet bias in both seasons (Fig. 6b, c; Fig. 7a, b, second, third, and fourth columns). The biases mostly concern characteristics of moderate, stronger-than-moderate, and heavy precipitation. Note that the overprediction of moderate precipitation events in the Bavarian Alps in summer (Fig. 7b, second panel on the lower row) is at the expense of stronger-than-moderate and heavy events (Fig. 7b, third and fourth panels on the lower row). These biases lead to a significant misrepresentation of the PDFs (Fig. 6a).
The elevation of the Bavarian Alps in WRF-NOAH is generally underestimated, while the elevations of deep river valleys and kettles, including such in the Bavarian Alps, are overestimated (see e.g. Fig. 9a in Part I). An underestimated orographic forcing due to the still too coarse spatial resolution of orography might at least partially account for the observed biases in these regions: weaker upslope flows in the Bavarian Alps and weaker rain shadowing in the deep valleys.
-
(7)
The larger non-rejecting area in summer for most measures indicates that the performance of WRF-NOAH is overall better in summer than in winter. The biases of mean seasonal precipitation (Fig. 6b) and the intensity of light precipitation (Fig. 6c, second column) do not exhibit seasonal dependence.
In winter, the daily precipitation field is predominantly determined by synoptic-scale processes, so that the biases over spatially homogeneous regions can only be due to misrepresentation of the large scales. In summer, biases are found exclusively over regions of complex topography, so they are due to misrepresented fine-scale surface forcings; over spatially homogeneous regions, the generated small-scale variability masks potential weak large-scale biases.
The fact that the downscaling performance with respect to mean seasonal precipitation is comparable in winter and summer, despite the large-scale biases in winter, suggests existence of compensating large-scale biases in winter. Which these are, is already clear: too frequent light precipitation events, but with underestimated intensity.
Although the intensity of light precipitation in summer is underestimated only over areas with localised surface forcings, the total significant area is comparable to that in winter, when underestimation is observed over spatially homogeneous regions as well. This indicates more widespread underestimation of light precipitation in regions with localised surface forcings in summer, which suggests a link to the parameterisation of deep convection. The latter is indeed known to produce too widespread precipitation with underestimated intensity (e.g. Schwitalla et al. 2008; Kendon et al. 2012).
The better overall performance of the downscaling in summer is in line with the results for the 10-km GCM-driven simulation of Feldmann et al. (2008) for South-West Gemany. Note that Marteau et al. (2014) draw the opposite conclusion from their 8-km ERA-Interim-driven simulation for a region in East France. However, their analysis focusses on seasonal averages, for which we not find seasonality of the downscaling performance.
-
(8)
The wet winter bias (Fig. 6b, left panel; 6c, first panel on the upper row; Fig. 7a, left panel; and Fig. 7b, upper row) is a well-recognised problem of RCM simulations for Central Europe, the causes of which are still an object of discussion (e.g. Feldmann et al. 2008; Kotlarski et al. 2014 Katragkou et al. 2015).
In these studies, the areas of model biases are large and therefore often not directly interpretable. Kotlarski et al. (2014) and Feldmann et al. (2008) only plot biases exceeding in absolute value 10% of the observed seasonal mean precipitation. Such boundaries alleviate the problem but are still subjective and therefore do not necessarily lead to meaningful spatial patterns. Katragkou et al. (2015) calculate statistical significance locally by means of a t test, implicitly assuming normally distributed independent monthly means. Furthermore, they do not account for test multiplicitly, which entails that an intolerably large proportion of the significant tests could be due to chance and hence not interpretable. In turn, the methodology we demonstrate is distribution-free, accounts for the time series structure and test multiplicity, and is robust to spatial autocorrelations. Thus, it objectively picks out the grid cells to interpret, of which only 5% on average are mistaken. The specific spatial patterns immediately point to issues like processes at the sea-land transition zone, the windward-lee effect, large-scale biases of precipitation occurrence, and misrepresented soil textures behind the wet winter bias.
4.3 Relative performance
Figure 8 shows the relative versions of (a) the Perkins score (1), (b) the mean seasonal precipitation (2), and (c) biases of selected characteristics of the wet-day distribution (2). Figure 9 displays the relative frequency biases of (a) wet days (1) and (b) light, moderate, stronger-than-moderate, and heavy precipitation events (1). These results reveal the spatial patterns of the significant added value with respect to the different distribution characteristics. Again, these patterns comprise specific geographical areas, which allows us to link the added value to the respective improved/deteriorated physical processes that have the same geographic and seasonal fingerprint on the respective distribution characteristic. Generally, in winter, positive added value is concentrated in regions of complex topography, whereas in summer, it is detectable over considerably larger areas, for many performance metrics also over flat terrain. Negative added value with respect to some of the metrics occurs in winter over the west part of the Jutland Peninsula, lee sides of mountains and hills, as well as some areas in NE Germany, and in summer over the north coast, the Bavarian Alps, in deep river valleys, and some areas in NE Germany.
As Fig. 6 but for the respective relative measures, quantifying the added value of WRF-NOAH against ERA-Interim
As Fig. 7 but for the respective relative measures, quantifying the added value of WRF-NOAH against ERA-Interim
Like the absolute biases, in most cases, the relative biases of conditional intensities are predominated by relative biases of the respective absolute intensities (compare Fig. 8c, second, third and fourth columns, against Fig. 9a and b, first, third and fourth columns, respectively). A notable exception is the improved conditional intensity of heavy precipitation over most of the north coast and the Lowlands (without the region to the west of the Lüneburg Heath) in summer (Fig. 8c, fourth panel on the lower row), which is rather caused by the improved wet-day frequency (Fig. 9a, right panel) than absolute precipitation intensity (Fig. 9b, fourth panel on the lower row).
For most measures, the area of significant improvement is larger in summer than in winter, which is in line with the impression from Section 4.1 for a higher relative skill in summer. Notable exceptions are again the mean seasonal precipitation (Fig. 8b) and the conditional intensity of light precipitation (Fig. 8c, second column).
4.3.1 Discussion
Before we turn to a detailed analysis of relative performance, we briefly review the current state of knowledge about the potential and limitations of regional climate modelling with focus on daily precipitation.
As discussed in Part I, an RCM can potentially add value only with respect to physical variables, climate statistics, regions, and seasons, for which there is fine-scale variability. The latter consists of a stationary component, induced by small-scale stationary surface forcings, and a transient component that is physically linked to small-scale transient processes. The stationary component is present only over regions with localised stationary surface forcings, no matter of the season or temporal scale considered. The transient component can potentially be present anywhere in all seasons, but is only detectable at fine temporal scales.
In winter, the control exerted by the driving lateral boundary fields over midlatitude domains like ours is strong because of the intense zonal flow that ‘flushes’ the model domain, sweeping away any internally generated transient processes; precipitation is generated by synoptic-scale processes, and mesoscale phenomena, except over regions with local-scale surface forcings, are also infrequent. Consequently, fine-scale variability in winter is predominantly stationary, and hence, only found over regions with localised surface forcings. Contrariwise, in summer, the slower atmospheric circulation entails a reduced lateral boundary forcing, which means more freedom for the RCM to spontaneously generate transient fine-scale features (e.g. Caya and Biner 2004; Feldmann et al. 2008; Lucas-Picher et al. 2008); daily precipitation is largely generated by small-scale transient processes like convection. Consequently, transient fine-scale variability in summer is considerable, which entails that fine-scale variability exists even over regions without localised surface forcings, that is, virtually everywhere (e.g. Di Luca et al. 2012).
Fine-scale surface forcings for daily precipitation are all factors that directly or indirectly affect moisture sources and vertical velocities in the boundary layer, e.g. complex orography, strong horizontal gradients of surface roughness and of sensible and latent heat fluxes due to sea-land transition or change of land-use type, mountain and sea-breeze circulations in summer.
Now, we can proceed to a detailed discussion of the spatial and seasonal patterns of relative performance.
-
(1)
Over complex orography like mountains and hills as well as deep river valleys and kettles, most precipitation statistics are improved (Fig. 8a, b, left panel, c, first, third and fourth columns, Fig. 9).
Stationary surface forcings for precipitation are localised in such regions, so there is fine-scale variability, and hence, added value can be expected throughout the year. WRF-NOAH obviously develops appropriate fine-scale climatological features in response to such forcings. More detailed analysis (not shown) reveals that the improvement consists mainly in compensating ERA-Interim’s dry bias in convex and wet bias in concave topography forms.
-
(2)
In some areas in NE Germany, there is deterioration in winter with respect to the mean precipitation (Fig. 8b, left panel), the frequency of wet days (Fig. 9a, left panel), and stronger-than-moderate precipitation events (Fig. 9b, third panel on the upper row) as well as the overall PDFs (Fig. 8a, left panel).
A comparison with the spatial patterns of absolute performance reveals that these are the regions with wet bias, which we attributed to misrepresented soil textures. Although evapotranspiration is more intense in summer, the biases related to it are insignificant as they are partly masked by the larger variability.
-
(3)
In winter, over the parts of the north coast exposed to the westerlies (the west coast of the Jutland Peninsula and the north-east coast), most precipitation statistics are deteriorated (Fig. 8a, b, left panels and c, first panel on the upper row; Fig. 9a, left panel and b, third and fourth panels on the upper row); improvement is detectable over the coastal lee regions (Fig. 8c, first, third and fourth panels on the upper row and Fig. 9b, fourth panel on the upper row). In summer, many precipitation statistics are improved nearly everywhere along the north coast (Fig. 8a, right panel, c, first and fourth panels on the lower row, Fig. 9a, right panel and b, second panel on the lower row); still, there is deterioration almost all over the coast with respect to the frequency of stronger-than-moderate events (Fig. 9b, third panel on the lower row), over the east part of the Jutland Peninsula with respect to the mean seasonal precipitation (subregionally significant, not shown), and over the north-west coast with respect to the intensity (Fig. 8c, second panel on the lower row) and frequency (Fig. 9b, first panel on the lower row) of light precipitation.
A more detailed analysis reveals that the added value in both seasons is due to the alleviated ERA-Interim systematic dry bias and reduced overprediction of wet days in the respective areas. The improvement can be explained by the better description of the induced quasi-stationary fine-scale processes. The pattern of negative added value coincides with that of the WRF-NOAH absolute biases. This further emphasises the importance of an improved description of processes at the sea-land transition zone.
-
(4)
In winter, over lee sides of mountains and hills, the downscaling deteriorates characteristics of moderate, stronger-than-moderate, and particularly heavy precipitation (Fig. 8c first, third, and fourth panels on the upper row; Fig. 9b, fourth panel on the upper row). This is obviously related to the windward-lee effect. The latter does not lead to deterioration over windward slopes because there it is weaker than the dry ERA-Interim bias (not shown).
-
(5)
Outside of regions with fine-scale stationary surface forcings, such as flat areas far from coastal zones, added value is present in summer, but not in winter. The improvement is with respect to the overall PDFs (Fig. 8a) and the frequencies of wet days (Fig. 9a), light, moderate, and stronger-than-moderate precipitation (Fig. 9b, first, second, and third columns). The improvement of the 90th wet-day percentile (Fig. 8c, fourth panel on the lower row) was already attributed to improved wet-day frequency rather than intensity of heavy precipitation.
As already discussed, in summer, transient fine-scale variability, respectively potential added value, exists everywhere, inclusively over spatially homogeneous areas. These results indicate that over spatially homogeneous areas the WRF-NOAH downscaling makes a good use of the higher potential to generate consistent fine-scale climatological features in summer.
-
(6)
In summer, the frequencies of wet days (Fig. 9a, right panel), moderate (Fig. 9b, second panel on the lower row), and heavy precipitation events (Fig. 9b, fourth panel on the lower row) as well as the intensity of heavy precipitation (Fig. 8c, fourth panel on the lower row) are deteriorated over the highest parts of the Bavarian Alps; the frequency of heavy precipitation is deteriorated in deep river valleys (Fig. 9b, fourth panel on the lower row); in the Bavarian Alps also the overall PDFs are worsened (Fig. 8a, right panel).
These deficiencies are linked to underestimated orographic forcing, as already discussed.
-
(7)
The area of positive added value is generally larger in summer than in winter, whereas that of negative added value tends to be larger in winter (Figs. 8 and 9).
In summer, as already discussed, there is transient fine-scale variability, which allows for added value even over areas without localised surface forcings. In winter, the deteriorations are due mostly to weak large-scale biases that are easier to detect as the variability is smaller than in summer. Notable exceptions are the mean seasonal precipitation (Fig. 8b), which is locally improved only in winter and only over complex orography, and the intensity (Fig. 8c, second column) of light precipitation, which is deteriorated in summer over the north-west coast. As already discussed in Part I, monthly averaging eliminates the transient variability. Hence, added value with respect to mean seasonal precipitation can be expected in both seasons, but only over regions with localised surface forcings; in summer, the improvement is masked by the larger variability. The amplified underestimation of light precipitation over the north-west coast in summer is attributable to an exaggerated sea-breeze circulation.
-
(8)
The region to the west of the Lüneburg Heath is spatially homogeneous, but stands out with an improved intensity of heavy precipitation in summer (Figs. 8c and 9b, fourth panels on the lower rows).
As discussed in Part I, this is an isolated area of enhanced marine influence. Its specific topography is captured by WRF-NOAH but not by ERA-Interim.
5 Conclusions
A new methodology for rigorous spatial analysis of the downscaling performance of regional climate simulations is introduced. It is based on a multiple comparison of the local test results by means of the false discovery rate (FDR) approach. Controlling the proportion of falsely rejected tests in a meaningful way and being robust to spatial dependence, the FDR method reveals an interpretable spatial pattern of local rejections. The latter is referred to as the spatial pattern of statistical significance. It includes the locations at which the values of evaluation statistics are highly unlikely to have occurred by chance. A novelty of the study is that it focusses on this pattern rather than on the magnitudes of the evaluation statistics. Indeed, high deviations of the values of evaluation statistics from their expected values under the null are not necessarily statistically significant, and small deviations are not necessarily insignificant, because statistical significance depends also on the variability. A small deviation at a location with small variability may be significant, whereas a high deviation at a location with high variability might be insignificant. The sampling uncertainty of the local evaluation statistics is rigorously estimated via a block permutation procedure, which is free of distribution assumptions. The block length is precisely determined so as to adequately account for the time series structure and yield slightly conservative tests that detect only the strongest effects. New quantitative metrics for the added value relative to the driving large-scale field are developed.
The methodology is exemplarily applied to evaluate the winter and summer climatology of daily precipitation for the 1990–2009 period from a standard EURO-CORDEX simulation with WRF-NOAH at 0.11 ∘ grid resolution over Germany. It objectively selects the interpretable grid cells, of which only 5% on average are mistaken. The specific spatial patterns of statistical significance can be hypothetically linked to physical processes known to have the same geographic and seasonal fingerprints for the respective performance measure.
In summer, in most regions, the downscaled distributions are statistically indistinguishable from the observed ones. In winter, there are measures that indicate significant biases in most regions. In particular, the overprediction of wet days and light precipitation events over almost whole Germany in winter is related to the large-scale scheme, while in summer, it occurs mainly over regions of complex topography and is attributable to the convection parameterisation. The systematic wet bias in North-East Germany and the plateau of Upper Swabia is attributable to a misrepresentation of soil textures: loamy instead of sandy soils entail a richer moisture supply source for the atmospheric boundary layer. Over the north coastal areas, biases in winter point to a misrepresentation of the low-level convergence of the westerlies at the sea-land transition zone, in summer possibly superposed on an exaggerated sea-breeze circulation. The windward-lee effect due to the parameterisation of deep convection is found in both seasons. The convection parameterisation in summer leads to underestimated intensity and occurrence of heavy precipitation. Underestimated orographic forcing due to the still too coarse spatial resolution of orography is at least partially responsible for the systematic dry bias over the Bavarian Alps and wet bias in concave orography. Weak large-scale biases are significant over spatially homogeneous regions in winter, but in summer, are masked by the larger variability, which makes the overall performance of WRF-NOAH better in summer. Exceptions are the mean seasonal precipitation, which does not exhibit a seasonal dependence owing to compensating large-scale biases in winter as well as the intensity of light precipitation due to the convection parameterisation in summer.
The general wet bias in winter and the dry bias along the north coast in summer were detected in the analysis of the same simulation in Kotlarski et al. (2014). However, in that study, the areas of model biases are large and therefore often not directly interpretable. Our objective and slightly conservative evaluation methodology spatially confines the significantly biased areas to specific geographic regions, which facilitates their interpretation.
The direct measures for added value, many of which newly developed, reveal the spatial patterns of significant improvement/deterioration with respect to different distribution characteristics. Again, these patterns comprise specific geographic areas, which allows us to link them to the respective improved/deteriorated physical processes. The orographic modification of precipitation is improved in both seasons over regions of complex orography. However, deteriorations are detected in North-East Germany in winter due to the wet bias, probably related to misrepresented soil textures. In coastal areas, there is performance gain from the better description of fine-scale surface forcings, but there are also deteriorations attributable to the misrepresented processes at the sea-land transition zone. The windward-lee effect in winter and the underestimated orographic forcing in summer also lead to negative added value locally. Over spatially homogeneous areas, WRF-NOAH makes a good use of the higher potential to generate consistent fine-scale transient processes in summer. The area of positive added value is larger in summer than in winter, because in summer, there is transient fine-scale variability, which allows for improvements even over areas without localised surface forcings. Exceptions are again mean seasonal precipitation and the characteristics of light precipitation. In summer, the former is not improved even over complex orography because it is masked by the larger variability, and the latter is deteriorated over the north-west coast due to the misrepresented processes at the sea-land transition zone.
This ‘perfect-boundary’ evaluation suggests that the WRF-NOAH downscaling system generates appropriate stationary fine-scale climate features in the daily precipitation field over regions of complex topography in both seasons and appropriate transient fine-scale features virtually everywhere in summer. As the added value in a climate projection context cannot be smaller than this perfect-boundary estimate, our analysis demonstrates in a rigorous manner the clear additional value of dynamical downscaling over global climate simulations. The new evaluation methodology has a broad spectrum of applicability to future climate simulations, including ensemble runs, owing to the fact that it is distribution-free, robust to spatial dependence, and accounts for time series structure.
References
Bauer HS, Weusthoff T, Dorninger M, Wulfmeyer V, Schwitalla T, Gorgas T, Arpagaus M, Warrach-Sagi K (2011) Predictive skill of a subset of models participating in D-PHASE in the COPS region. Q J Roy Meteor Soc 137(S1):287–305. doi:10.1002/qj.715
Benjamini Y, Hochberg Y (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J Roy Stat Soc B Met 57(1):289–300. doi:10.2307/2346101
Buonomo E, Jones R, Huntingford C, Hannaford J (2007) On the robustness of changes in extreme precipitation over Europe from two high resolution climate change simulations. Q J Roy Meteor Soc 133(622):65–81. doi:10.1002/qj.13
Cardoso RM, Soares PMM, Miranda PMA, Belo-Pereira M (2013) WRF high resolution simulation of Iberian mean and extreme precipitation climate. Int J Climatol 33(11):2591–2608. doi:10.1002/joc.3616
Caya D, Biner S (2004) Internal variability of RCM simulations over an annual cycle. Clim Dyn 22(1):33–46. doi:10.1007/s00382-003-0360-2
Chan SC, Kendon EJ, Fowler HJ, Blenkinsop S, Ferro CAT, Stephenson DB (2013) Does increasing the spatial resolution of a regional climate model improve the simulated daily precipitation? Clim Dyn 41 (5-6):1475–1495. doi:10.1007/s00382-012-1568-9
Chen F, Dudhia J (2001a) C oupling an advanced land surface-hydrology model with the Penn state-NCAR MM5 modeling system. Part I: model implementation and sensitivity. Mon Weather Rev 129(4):569–585. doi:10.1175/1520-0493(2001)129%3C0569:CAALSH%3E2.0.CO;2
Chen F, Dudhia J (2001b) Coupling an advanced land surface-hydrology model with the Penn state-NCAR MM5 modeling system. Part II: preliminary model validation. Mon Weather Rev 129(4):587–604. doi:10.1175/1520-0493(2001)129%3C0587:CAALSH%3E2.0.CO;2
Christensen HJ, Machenhauer B, Jones GR, Schär C, Ruti MP, Castro M, Visconti G (1997) Validation of present-day regional climate simulations over Europe: LAM simulations with observed boundary conditions. Clim Dyn 13(7):489–506. doi:10.1007/s003820050178
Christensen JH, Christensen OB (2007) A summary of the PRUDENCE model projections of changes in European climate by the end of this century. Clim Change 81(1):7–30. doi:10.1007/s10584-006-9210-7
Collins WD, Rasch PJ, Boville BA, Hack JJ, McCaa JR, Williamson DL, Kiehl JT, Briegleb B, Bitz C, Lin SJ, Zhang M, Dai Y (2004) Description of the NCAR community atmosphere model (CAM 3.0). NCAR technical note, NCAR/TN-464+STR. http://www.cesm.ucar.edu/models/atm-cam/docs/description
Davidson R, MacKinnon JG (2007) Improving the reliability of bootstrap tests with the fast double bootstrap. Comput Stat Data An 51(7):3259–3281. doi:10.1016/j.csda.2006.04.001
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thépaut JN, Vitart F (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137(656):553–597. doi:10.1002/qj.828
Di Luca A, de Elía R, Laprise R (2012) Potential for added value in precipitation simulated by high-resolution nested regional climate models and observations. Clim Dyn 38 (5-6):1229–1247. doi:10.1007/s00382-011-1068-3
Dosio A, Panitz HJ, Schubert-Frisius M, Lüthi D (2015) Dynamical downscaling of CMIP5 global circulation models over CORDEX-Africa with COSMO-CLM: evaluation over the present climate and analysis of the added value. Clim Dyn 44(9-10):2637–2661. doi:10.1007/s00382-014-2262-x
Duffy PB, Arritt RW, Coquard J, Gutowski W, Han J, Iorio J, Kim J, Leung L R, Roads J, Zeledon E (2006) Simulations of present and future climates in the western United States with four nested regional climate models. J Clim 19(6):873–895. doi:10.1175/JCLI3669.1
DWD (2009) Regionalisierte Niederschlagshöhen. Deutscher Wetterdienst, Abteilung Hydrometeorologie, Postfach 10 04 65, 63004 Offenbach, Germany. http://www.dwd.de/bvbw/generator/DWDWWW/Content/Wasserwirtschaft/en/Unsere_Leistungen_en/Hydromet_Info_en/Hydromet_Rasterwerte_en/REGNIE_Infoblatt_pdf_en,templateId=raw,property=publicationFile.pdf/REGNIE_Infoblatt_pdf_en.pdf
Elmore KL, Baldwin ME, Schultz DM (2006) Field significance revisited: spatial bias errors in forecasts as applied to the Eta model. Mon Weather Rev 134(2):519–531. doi:10.1175/MWR3077.1
Feldmann H, Früh B, Schädler G, Panitz HJ, Keuler K, Jacob D, Lorenz P (2008) Evaluation of the precipitation for South-western Germany from high resolution simulations with regional climate models. Meteorol Z 17(4):455–465. doi:10.1127/0941-2948/2008/0295
Feser F (2006) Enhanced detectability of added value in limited-area model results separated into different spatial scales. Mon Weather Rev 134(8):2180–2190. doi:10.1175/MWR3183.1
Frei C, Christensen JH, Déqué M, Jacob D, Jones RG, Vidale PL (2003) Daily precipitation statistics in regional climate models: evaluation and intercomparison for the European Alps. J Geophys Res: Atmos 108(D3):4124. doi:10.1029/2002JD002287
Giorgi F, Jones C, Asrar GR (2009) Addressing climate information needs at the regional level: the CORDEX framework. WMO Bull 58(3):175–183
Hartmann DL, Klein Tank AMG, Rusticucci M, Alexander LV, Brönnimann S, Charabi Y, Dentener FJ, Dlugokencky EJ, Easterling DR, Kaplan A, Soden BJ, Thorne PW, Wild M, Zhai PM (2013) Observations: aAtmosphere and surface. In: Stocker T F, Qin D, Plattner G K, Tignor M, Allen S K, Boschung J, Nauels A, Xia Y, Bex V, Midgley P M (eds) Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change, vol 2. Cambridge University Press, Cambridge, pp 159– 254
Heikkilä U, Sandvik A, Sorteberg A (2011) Dynamical downscaling of ERA-40 in complex terrain using the WRF regional climate model. Clim Dyn 37(7–8):1551–1564. doi:10.1007/s00382-010-0928-6
Hong SY, Noh Y, Dudhia J (2006) A new vertical diffusion package with an explicit treatment of entrainment processes. Mon Weather Rev 134(9):2318–2341. doi:10.1175/MWR3199.1
Ivanov MA, Warrach-Sagi K, Wulfmeyer V (2017) Field significance of performance measures in the context of regional climate model verification. Part 1: temperature. Submitted to Theor Appl Climatol
Jolliffe IT (2007) Uncertainty and inference for verification measures. Weather Forecast 22(3):637–650. doi:10.1175/WAF989.1
Kain JS (2004) The Kain-Fritsch convective parameterization: an update. J Appl Meteorol 43 (1):170–181. doi:10.1175/1520-0450(2004)043%3C0170:TKCPAU%3E2.0.CO;2
Katragkou E, García-Díez M, Vautard R, Sobolowski S, Zanis P, Alexandri G, Cardoso RM, Colette A, Fernandez J, Gobiet A, Goergen K, Karacostas T, Knist S, Mayer S, Soares PMM, Pytharoulis I, Tegoulias I, Tsikerdekis A, Jacob D (2015) Regional climate hindcast simulations within EURO-CORDEX: evaluation of a WRF multi-physics ensemble. Geosci Model Dev 8(3):603–618. doi:10.5194/gmd-8-603-2015
Katz RW, Brown BG (1991) The problem of multiplicity in research on teleconnections. Int J Climatol 11 (5):505–513. doi:10.1002/joc.3370110504
Kendon EJ, Roberts NM, Senior CA, Roberts MJ (2012) Realism of rainfall in a very high-resolution regional climate model. J Clim 25(17):5791–5806. doi:10.1175/JCLI-D-11-00562.1
Kjellström E, Boberg F, Castro M, Christensen JH, Nikulin G, Sánchez E (2010) Daily and monthly temperature and precipitation statistics as performance indicators for regional climate models. Clim Res 48 (3):RG3003. doi:10.3354/cr00932
Kotlarski S, Keuler K, Christensen OB, Colette A, Déqué M, Gobiet A, Goergen K, Jacob D, Lüthi D, van Meijgaard E, Nikulin G, Schär C, Teichmann C, Vautard R, Warrach-Sagi K, Wulfmeyer V (2014) Regional climate modeling on European scales: a joint standard evaluation of the EURO-CORDEX RCM ensemble. Geosci Model Dev Discuss 7(1):217–293. doi:10.5194/gmdd-7-217-2014
Laprise R (2008) Regional climate modelling. J Comput Phys 227(7):3641–3666. doi:10.1016/j.jcp.2006.10.024
Léger C, Politis DN, Romano JP (1992) Bootstrap technology and applications. Technometrics 34 (4):378–398. doi:10.2307/1268938
Livezey RE, Chen WY (1983) Statistical field significance and its determination by Monte Carlo techniques. Mon Weather Rev 111(1):46–59. doi:10.1175/1520-0493(1983)111%3C0046:SFSAID%3E2.0.CO;2
Lucas-Picher P, Caya D, Biner S, Laprise R (2008) Quantification of the lateral boundary forcing of a regional climate model using an aging tracer. Mon Weather Rev 136 (12):4980–4996. doi:10.1175/2008MWR2448.1
Marteau R, Richard Y, Pohl B, Smith C C, Castel T (2014) High-resolution rainfall variability simulated by the WRF RCM: application to eastern France. Clim Dyn:1–15. doi:10.1007/s00382-014-2125-5
Milovac J, Ingwersen J, Warrach-Sagi K (2014) Top soil texture forcing data for the area of Germany for the Weather Research and Forecasting (WRF) model based on the Bodenübersichtskarte (BUK) at a scale 1:1000000 (BUK1000) and provided by the University of Hohenheim (UHOH). World Data Center for Climate (WDCC). doi:10.1594/WDCC/WRF_NOAH_BUK_Ger_top_SOILTYP
Morrison H, Thompson G, Tatarskii V (2009) Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: comparison of one- and two-moment schemes. Mon Weather Rev 137(3):991–1007. doi:10.1175/2008MWR2556.1
O’Gorman PA, Schneider T (2009) The physical basis for increases in precipitation extremes in simulations of 21st-century climate change. P Natl Acad Sci USA 106(35):14,773–14,777. doi:10.1073/pnas.0907610106
Pan Z, Christensen JH, Arritt RW, Gutowski WJ, Takle ES, Otieno F (2001) Evaluation of uncertainties in regional climate change simulations. J Geophys Res Atmos 106(D16):17,735–17,751. doi:10.1029/2001JD900193
Pearson KJ, Shaffrey LC, Methven J, Hodges KI (2015) Can a climate model reproduce extreme regional precipitation events over England and Wales? Q J R Meteorol Soc 141 (689):1466–1472. doi:10.1002/qj.2428
Perkins SE, Pitman AJ, Holbrook NJ, McAneney J (2007) Evaluation of the AR4 climate models’ simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions. J Climate 20(17):4356–4376. doi:10.1175/JCLI4253.1
Prömmel K, Geyer B, Jones JM, Widmann M (2010) Evaluation of the skill and added value of a reanalysis-driven regional simulation for Alpine temperature. Int J Climatol 30(5):760–773. doi:10.1002/joc.1916
Richter D (1995) Ergebnisse methodischer Untersuchungen zur Korrektur des systematischen Messfehlers des Hellmann-Niederschlagsmessers. Berichte des Deutschen Wetterdienstes, vol 194, Selbstverlag des Deutschen Wetterdienstes. Offenbach am Main, p 93
Rummukainen M (2010) State-of-the-art with regional climate models. Wiley Interdiscip Rev Clim Change 1 (1):82–96. doi:10.1002/wcc.8
Sanchez-Gomez E, Somot S, Déqué M (2009) Ability of an ensemble of regional climate models to reproduce weather regimes over Europe-Atlantic during the period 1961–2000. Clim Dyn 33(5):723–736. doi:10.1007/s00382-008-0502-7
Schär C, Vidale PL, Lüthi D, Frei C, Häberli C, Liniger MA, Appenzeller C (2004) The role of increasing temperature variability in European summer heatwaves. Nature 427(6972):332–336. doi:10.1038/nature02300
Schär C, Ban N, Fischer EM, Rajczak J, Schmidli J, Frei C, Giorgi F, Karl TR, Kendon EJ, Tank AMGK, O’Gorman PA, Sillmann J, Zhang X, Zwiers FW (2016) Percentile indices for assessing changes in heavy precipitation events. Clim Change:1–16. doi:10.1007/s10584-016-1669-2
Schwitalla T, Bauer HS, Wulfmeyer V, Zängl G (2008) Systematic errors of QPF in low-mountain regions as revealed by MM5 simulations. Meteorol Z 17(6):903–919. doi:10.1127/0941-2948/2008/0338
Sotillo M, Martín M, Valero F, Luna M (2006) Validation of a homogeneous 41-year (1961–2001) winter precipitation hindcasted dataset over the Iberian Peninsula: assessment of the regional improvement of global reanalysis. Clim Dyn 27(6):627–645. doi:10.1007/s00382-006-0155-3
Sturges HA (1926) The choice of a class interval. J Am Stat Assoc 21(153):65–66
Torma C, Giorgi F, Coppola E (2015) Added value of regional climate modeling over areas characterized by complex terrain—Precipitation over the Alps. J Geophys Res: Atmos 120(9):3957–3972. doi:10.1002/2014JD022781
Trenberth KE, Dai A, Rasmussen RM, Parsons DB (2003) The changing character of precipitation. Bull Amer Meteor Soc 84(9):1205–1217. doi:10.1175/BAMS-84-9-1205
van der Linden P, Mitchell JFB (2009) ENSEMBLES: climate change and its impacts: summary of research and results from the ENSEMBLES project. Met Office Hadley Centre, FitzRoy Road, Exeter EX1 3PB, UK
Vautard R, Gobiet A, Jacob D, Belda M, Colette A, Déqué M, Fernández J, Garcá-Díez M, Goergen K, Güttler I, Halenka T, Karacostas T, Katragkou E, Keuler K, Kotlarski S, Mayer S, van Meijgaard E, Nikulin G, Patarčić M, Scinocca J, Sobolowski S, Suklitsch M, Teichmann C, Warrach-Sagi K, Wulfmeyer V, Yiou P (2013) The simulation of European heat waves from an ensemble of regional climate models within the EURO-CORDEX project. Clim Dyn 41(9-10):2555–2575. doi:10.1007/s00382-013-1714-z
Ventura V, Paciorek CJ, Risbey JS (2004) Controlling the proportion of falsely rejected hypotheses when conducting multiple tests with climatological data. J Clim 17(22):4343–4356. doi:10.1175/3199.1
Warrach-Sagi K, Wulfmeyer V, Grasselt R, Ament F, Simmer C (2008) Streamflow simulations reveal the impact of the soil parameterization. Meteorol Z 17(6):751–762. doi:10.1127/0941-2948/2008/0343
Warrach-Sagi K, Schwitalla T, Bauer HS, Volker-Wulfmeyer (2013a) A regional climate model simulation for EURO-CORDEX with the WRF model. In: Resch M M, Bez W, Focht E, Kobayashi H, Kovalenko Y (eds) Sustained simulation performance 2013. Springer International Publishing, pp 147–157, DOI 10.1007/978-3-319-01439-5_11
Warrach-Sagi K, Schwitalla T, Wulfmeyer V, Bauer HS (2013b) Evaluation of a climate simulation in Europe based on the WRF-NOAH model system: precipitation in Germany. Clim Dyn 41(3-4):755–774. doi:10.1007/s00382-013-1727-7
Wilks DS (2006a) On “field significance” and the false discovery rate. J Appl Meteorol 45(9):1181–1189. doi:10.1175/JAM2404.1
Wilks DS (2006b) Statistical methods in the atmospheric sciences, International Geophysics Series, vol 91, 2nd edn. Elsevier Academic Press, Cornell University, USA
Winterfeldt J, Weisse R (2009) Assessment of value added for surface marine wind speed obtained from two regional climate models. Mon Weather Rev 137(9):2955–2965. doi:10.1175/2009MWR2704.1
Winterfeldt J, Geyer B, Weisse R (2011) Using QuikSCAT in the added value assessment of dynamically downscaled wind speed. Int J Climatol 31(7):1028–1039. doi:10.1002/joc.2105
Wulfmeyer V, Behrendt A, Kottmeier C, Corsmeier U, Barthlott C, Craig GC, Hagen M, Althausen D, Aoshima F, Arpagaus M, Bauer H S, Bennett L, Blyth A, Brandau C, Champollion C, Crewell S, Dick G, Girolamo PD, Dorninger M, Dufournet Y, Eigenmann R, Engelmann R, Flamant C, Foken T, Gorgas T, Grzeschik M, Handwerker J, Hauck C, Höller H, Junkermann W, Kalthoff N, Kiemle C, Klink S, König M, Krauss L, Long CN, Madonna F, Mobbs S, Neininger B, Pal S, Peters G, Pigeon G, Richard E, Rotach MW, Russchenberg H, Schwitalla T, Smith V, Steinacker R, Trentmann J, Turner DD, van Baelen J, Vogt S, Volkert H, Weckwerth T, Wernli H, Wieser A, Wirth M (2011) The Convective and Orographically-induced Precipitation Study (COPS): the scientific strategy, the field phase, and research highlights. Q J R Meteorol Soc 137(S1):3–30. doi:10.1002/qj.752
Acknowledgments
This work was funded by the Helmholtz Centre for Environmental Research (UFZ) and the Ministry of Science, Research, and Arts Baden-Württemberg. The authors gratefully acknowledge the financial support by the German Research Foundation (DFG) in the frame of the integrated research project PAK 346 ‘Structure and Function of Agricultural Landscapes under Global Climate Change’, which is continued by the Research Unit FOR 1695 ‘Agricultural Landscapes under Global Climate Change Processes and Feedbacks on a Regional Scale’. Martin Ivanov acknowledges the Water and Earth System Science Competence Cluster (WESS) funded by the Federal Ministry of Education and Research (BMBF) and UFZ Leipzig as well as the support by ETH Zürich in the frame of the ELAPSE project (Enhancing Local and Regional Climate Change Projections for Switzerland) funded by the Swiss State Secretariat for Education, Research and Innovation SERI under project number C12.0089.
Author information
Authors and Affiliations
Corresponding author
Appendix: Choice of the blocklength L
Appendix: Choice of the blocklength L
We are only interested in intraseasonal autocorrelations. Assuming that the maximum time lag, at which an intraseasonal autocorrelation can be reliably estimated, is equal to about 20% of the season length, we consider the set \(\mathcal {K}\) of eligible time lags from k = 1 to k = 18 days. What is the minimum blocklength that preserves the 18 lagged autocorrelations over the spatial domain? Figure 10 schematises our implementation of Elmore et al.’s (2006) idea. At each grid cell i∈I and for each time lag \(k \in \mathcal {K}\), we calculate the 95% bootstrap percentile confidence intervals (Wilks 2006b) for increasing values of the bootstrap blocklength l, until the blocklength l m i n(i,k), for which the corresponding bootstrap confidence interval contains the nominal autocorrelation value r o (k). In order to mimic real weather situations, the randomisation at all grid cells must be synchronised. At each blocklength the bootstrap distribution consists of 1999 replications. Tests confirmed that this sample size ensures stable final estimates of L. The permutation blocklength is determined as \(L=\max \limits _{i \in I, k \in \mathcal {K}} lmin(i, k)\). Note that the procedure takes twice the maximum, once over the spatial domain I and once over the eligible autocorrelation lags \(\mathcal {K}\). This choice ensures that at all grid cells the temporal autocorrelation structure represented by the first 18 lag autocorrelations will be maintained by the bootstrap. The resulting tests are rather conservative, so that the possibility of incorrectly rejecting the null hypothesis is minimal. This suits our purpose to isolate only the strongest effects.
We thus determine the permutation blocklength L separately for winter and for summer. Note that the seasonal data series, strictly speaking, are not real time series. Actually, there is a data gap of 9 months between, e.g. the winters of two consecutive years. Still, the seasonal data series have autocorrelation structure that must be accounted for by the bootstrap. In winter, L = 25 days is the minimum blocklength that keeps the autocorrelations at lags of 15, 16, and 18 days, while in summer L = 28 days and is required by the lags of 16 and 18 days. It seems counterintuitive that the blocklength L for summer is larger than that for winter. This is because temporal serial correlations of daily precipitation are known to be generally higher in winter than in summer, and stronger serial dependence entails a larger blocklength that can account for it (e.g. Wilks 2006b). A more detailed analysis reveals that for 88% of the grid cells the blocklength lmin that preserves the first 18 lagged temporal autocorrelations is indeed larger in winter than in summer. There are, however, few locations, mainly at the North-West coast and the Weserbergland, that require larger blocklengths in summer than in winter. Taking the maximum lmin over all grid cells in Germany results in an overall blocklength estimate L that is larger is summer than in winter. Actually, lmin = 28 is required at few grid cells at the North-West coast in summer. A more in-depth investigation why in these cases the required blocklength is so large is beyond the scope of this paper. To enable a direct comparison between the winter and summer results, we use the larger value, i.e. L = 28 days for both seasons, so that the permutation procedures become identical. This is also in consistence with the leitmotif of only isolating the strongest effects, which entails adherence to relatively conservative tests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ivanov, M., Warrach-Sagi, K. & Wulfmeyer, V. Field significance of performance measures in the context of regional climate model evaluation. Part 2: precipitation. Theor Appl Climatol 132, 239–261 (2018). https://doi.org/10.1007/s00704-017-2077-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-017-2077-x