Orbits of N-expansions with a finite set of digits

Abstract

For $N \in {\mathbb {N}}_{\ge 2}$ and $\alpha \in {\mathbb {R}}$ such that $0 < \alpha \le \sqrt{N}-1$, we define $I_\alpha :=[\alpha ,\alpha +1]$ and $I_\alpha ^-:=[\alpha ,\alpha +1)$ and investigate the continued fraction map $T_{\alpha }:I_{\alpha }\rightarrow I_{\alpha }^-$, which is defined as $T_{\alpha }(x):= \frac{N}{x}-d(x),$ where $d: I_{\alpha }\rightarrow {\mathbb {N}}$ is defined by $d(x):=\left\lfloor \frac{N}{x} -\alpha \right\rfloor$. For $N\in {\mathbb {N}}_{\ge 7}$, for certain values of $\alpha$, open intervals $(a,b) \subset I_{\alpha }$ exist such that for almost every $x \in I_{\alpha }$ there is an $n_0 \in {\mathbb {N}}$ for which $T_{\alpha }^n(x)\notin (a,b)$ for all $n\ge n_0$. These gaps (a, b) are investigated using the square $\varUpsilon _\alpha :=I_{\alpha }\times I_{\alpha }^-$, where the orbits $T_{\alpha }^k(x), k=0,1,2,\ldots$ of numbers $x \in I_{\alpha }$ are represented as cobwebs. The squares $\varUpsilon _\alpha$ are the union of fundamental regions, which are related to the cylinder sets of the map $T_{\alpha }$, according to the finitely many values of d in $T_{\alpha }$. In this paper some clear conditions are found under which $I_{\alpha }$ is gapless. If $I_{\alpha }$ consists of at least five cylinder sets, it is always gapless. In the case of four cylinder sets there are usually no gaps, except for the rare cases that there is one, very wide gap. Gaplessness in the case of two or three cylinder sets depends on the position of the endpoints of $I_{\alpha }$ with regard to the fixed points of $I_{\alpha }$ under $T_{\alpha }$.

1 Introduction

In 2008, Edward Burger and his co-authors introduced in [2] new continued fraction expansions, the so-called N-expansions, which are nice variations of the regular continued fraction (RCF) expansion. These N-expansions have been studied in various papers since; see [1, 3, 7]. In [8], a subclass of these N-expansions is introduced, for which the digit set is always finite. These particular N-expanions are defined as follows:

For $N \in {\mathbb {N}}_{\ge 2}$ and $\alpha \in {\mathbb {R}}$ such that $0 < \alpha \le \sqrt{N}-1$, let $I_{\alpha }:=[\alpha ,\alpha +1]$ and $I_{\alpha }^-:=[\alpha ,\alpha +1)$. Hereafter we denote by ${\mathbb {N}}_{\ge k}$ the set of positive integers $n\ge k$, while we write ${\mathbb {N}}$ if $k=1$. We define the N-expansion map $T_{\alpha }:I_{\alpha } \rightarrow I_{\alpha }^-$ (or $I_{\alpha }$) as

$$\begin{aligned} T_{\alpha }(x):=\frac{N}{x}-d(x), \end{aligned}$$

(1)

where $d: I_{\alpha } \rightarrow {\mathbb {N}}$ is defined by

$$\begin{aligned} d(x):=\left\lfloor \frac{N}{x} -\alpha \right\rfloor ,\quad \text {if either}\;x\in (\alpha ,\alpha +1]\;\text {or both}\;x=\alpha \;\text {and}\; \frac{N}{\alpha } - \alpha \not \in {\mathbb {Z}}\end{aligned}$$

and

$$\begin{aligned} d(\alpha ) = \left\lfloor \frac{N}{\alpha } -\alpha \right\rfloor -1, \quad \text {if}\;\frac{N}{\alpha } - \alpha \in {\mathbb {Z}}. \end{aligned}$$

Note that if $\frac{N}{\alpha } -\alpha \in {\mathbb {Z}}$, we have that $T_{\alpha }(\alpha ) = \alpha +1$. This is the only case in which the range of $T_{\alpha }$ is $I_{\alpha }$ and not $I_{\alpha }^-$.

For a fixed $\alpha \in (0,\sqrt{N}-1]$ and $x \in I_{\alpha }$ we define for $n \in {\mathbb {N}}$

$$\begin{aligned} d_n=d_n(x):=d(T_{\alpha }^{n-1}(x)). \end{aligned}$$

Note that for $\alpha \in (0,\sqrt{N}-1]$ fixed, there are only finitely many possibilities for each $d_n$.

Applying (1), we obtain for every $x\in I_{\alpha }$ a continued fraction expansion of the form

$$\begin{aligned} x=T_{\alpha }^0(x)=\frac{N}{d_1+T_{\alpha }(x)}= \frac{N}{d_1+\frac{N}{ d_2+T_{\alpha }^2(x)}}=\dots =\frac{N}{d_1+\frac{N}{d_2+\frac{N}{d_3 + \ddots }}}, \end{aligned}$$

(2)

which we will throughout this paper write as $x=[d_1,d_2,d_3,\ldots ]_{N, \alpha }$ (note that this expansion is infinite for every $x\in I_{\alpha }$, since $0\not \in I_{\alpha }$); we will call the numbers $d_i,\, i \in {\mathbb {N}}$, the partial quotients or digits of this N-continued fraction expansion of x; see [3, 8], where these continued fractions (also with a finite set of digits) were introduced and elementary properties were studied (such as the convergence in reference [3]).

In each cylinder set $\varDelta _i:=\{x \in I_{\alpha }; d(x)=i \}$ of rank 1, with $d_{\min }\le i \le d_{\max }$, where $d_{{\textit{max}}}:=d(\alpha )$ is the largest partial quotient, and $d_{{\textit{min}}}:=d(\alpha + 1)$ the smallest one given N and $\alpha$, the map $T_{\alpha }$ obviously has one fixed point $f_i$ . As of now we will write simply ‘cylinder set’ for ‘cylinder set of rank 1’.

It is easy to see that¹

$$\begin{aligned} f_i=f_i(N)=\dfrac{\sqrt{4N+i^2}-i}{2}, \quad {\text {for}}\quad d_{\min } \le i \le d_{\max }. \end{aligned}$$

(3)

Note that $\frac{N}{\alpha } - \alpha \in {\mathbb {Z}}$ if and only if for some $d \in {\mathbb {N}}_{\ge 2}$ we have that $\alpha =f_{d+1}$, while for any $\alpha _0 \in [f_{d+2},f_{d+1})$ we have that $\varDelta _{d+1}\ne \emptyset$.

Given $N\in {\mathbb {N}}_{\ge 2}$, we let $\alpha _{max}=\sqrt{N}-1$ be the largest value of $\alpha$ we consider. The reason for this is that for larger values of $\alpha$ we would have 0 as a partial quotient as well. Since $T_{\alpha }'(x)=-N/x^2$ and because $0<\alpha \le \sqrt{N}-1$, we have $|T_{\alpha }'(x)|>1$ on $I_{\alpha }^-$. From this it follows that the fixed points act as repellers and that the maps $T_{\alpha }$ are expanding if $0<\alpha \le \sqrt{N}-1$. This is equivalent to the convergence of the N-expansion of all $x\in I_{\alpha }$.

Each pair of consecutive cylinders sets $(\varDelta _i,\varDelta _{i-1})$ is divided by a discontinuity point $p_i(N,\alpha )$ of $T_{\alpha }$, satisfying $\frac{N}{p_i}-i=\alpha$, so $p_i=\frac{N}{\alpha +i}$. A cylinder set $\varDelta _i$ is called full if $T_{\alpha }(\varDelta _i)=I_{\alpha }^-$ (or $I_{\alpha }$). If a cylinder set is not full, it contains either $\alpha$ (in which case $T_{\alpha }(\alpha )<\alpha +1$) or $\alpha +1$ (in which case $T_{\alpha }(\alpha +1)>\alpha$), and is called incomplete. On account of our definition of $T_{\alpha }$, cylinder sets will always be an interval, never consist of one single point.

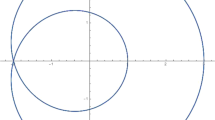
The main object of this paper is the sequence $T_{\alpha }^n(x)$, $n=0,1,2,\ldots$, for $x\in I_{\alpha }$, which is called the orbit of x under $T_{\alpha }$. More specifically, we are interested in subsets of $I_{\alpha }$ that we will call gaps for such orbits. Before we will give a proper definition of ‘gap’, we will give an example of orbits of points in $I_{\alpha }$ for a pair $\{N,\alpha \}$. Note that, since the fixed points are repellent, orbits cannot remain in one cylinder set indefinitely if $x\in I_{\alpha }$ is not a fixed point of $T_{\alpha }$, so any orbit will show an infinite migration between cylinder sets. A naive approach is to compute the orbits of many points of $I_{\alpha }$ and obtain a plot of the asymptotic behaviour of these orbits by omitting the first, say hundred, iterations. Figure 1 shows such a plot for $N=51$ and $\alpha =6$. It appears that there are parts of $I_{\alpha }$ (illustrated by dashed line segments) that are not visited by any orbit after many iterations of $T_{\alpha }$.

Fig. 1

$N=51$, $\alpha =6$

In fact, setting $\ell _i=T_{\alpha }^i(\alpha )$ and $r_i =T_{\alpha }^i(\alpha +1)$, the orbit of any point—apart from the fixed points $f_1$ and $f_2$—after once having left the interval $(r_2,r_1)\subset \varDelta _2$ or $(\ell _1,\ell _2)\subset \varDelta _1$ of Fig. 1, will never return to it.

In order to get a better understanding of the orbits of N-expansions, it is useful to consider the graphs of $T_{\alpha }$, which are drawn in the square $\varUpsilon _{\alpha }(=\varUpsilon _{N,\alpha }):=I_{\alpha } \times I_{\alpha }^-$. This square is divided in rectangular sets of points $\Box _i:=\{(x,y)\in \varUpsilon _\alpha :d(x) =i\}$, which are the two-dimensional fundamental regions associated with the one-dimensional cylinder sets we already use. We will call these regions in short cylinders. Now consider $(x,T_{\alpha }(x)) \in \varUpsilon _{\alpha }$. Then $(x,T_{\alpha }(x))$ goes to $(T_{\alpha }(x),T_{\alpha }^2(x))$ under $T_{\alpha }$. Regarding this, $T_{\alpha }$ has one fixed point $F_i:=(f_i,f_i)$ in each $\Box _i$. We will denote the dividing line between $\Box _i$ and $\Box _{i-1}$ by $l_i$, which is the set $\{p_i\} \times [\alpha ,\alpha +1)$, with $p_i$ the discontinuity point between $\varDelta _i$ and $\varDelta _{i-1}$. In case $T_{\alpha }(\varDelta _i)=I_{\alpha }^-$, we will call the cylinder $\Box _i$ full and the branch of the graph of $T_{\alpha }$ in $\Box _i$ complete; if a cylinder is not full, we will call it and its associated branch of $T_{\alpha }$ incomplete. We will call the collection of $\varUpsilon _{\alpha }$ and its associated branches, fixed points and dividing lines an arrangement of $\varUpsilon _{\alpha }$. If $\varUpsilon _{\alpha }$ is a union of full cylinders, we will call the associated arrangement also full.

Figure 2 is an example of such an arrangement, in which a part of the cobweb is drawn associated with the orbit we investigated previously. The discontinuity point $p_2=\frac{51}{8}$ is now visible as a dividing line between $\varDelta _1$ and $\varDelta _2$.

Fig. 2

$N=51$, $\alpha =6$, $x=6.5$

In [3, 8] the arrangement for $N=4$ and $\alpha =1$ is studied, consisting of two full cylinders $\Box _1$ and $\Box _2$ and not showing any gaps. On the other hand, the demonstration of the interval $(\frac{5}{2},\frac{13}{5})$ being a gap of the interval [2, 3] in the case $(N,\alpha )=(9,2)$ in [8] is done without referring to such an arrangement. In this paper, and even more so in the next paper, we will show that arrangements may considerably support the insight in the occurrence of gaps.

We will now give a formal definition of gaps, which is slightly delicate, since $T_{\alpha }(I_{\alpha }) = I_{\alpha }^-$ (or $I_{\alpha }$ if $\frac{N}{\alpha } - \alpha \in {\mathbb {Z}}$).

Definition 1

A maximal open interval $(a,b) \subset I_{\alpha }$ is called a gap of $I_{\alpha }$ if for almost every $x \in I_{\alpha }$ there is an $n_0 \in {\mathbb {N}}$ for which $T_{\alpha }^n(x)\notin (a,b)$ for all $n\ge n_0$.

There are several papers where ‘gaps’ appear in number theoretic expansions. One of the first important examples is given by the so-called negative $\beta$-expansion, introduced and studied by Shunji Ito and Taizo Sadahiro [5]. For $\beta >1$, let $I_{\beta }:=\Big [ -\frac{\beta }{\beta +1},\frac{1}{\beta +1}\Big )$, and let the $(-\beta )$-transformation $T_{-\beta }:I_{\beta }\rightarrow I_{\beta }$ be defined by

$$\begin{aligned} T_{\beta }(x) = -\beta x -\left\lfloor \frac{\beta }{\beta +1} - \beta x\right\rfloor . \end{aligned}$$

Ito and Sadahiro characterise the admissible sequences of $(-\beta )$-expansions, give a necessary and sufficient condition for the $(-\beta )$-shift to be sofic, and explicitly determine the invariant measure of the $(-\beta )$-transformations. In their Example 18, Ito and Sadahiro also noticed the existence of gaps, as intervals where the density of the invariant measure is zero. In [11], Lingmin Liao and Wolfgang Steiner studied negative $\beta$-expansions defined on [0, 1], which are conjugate to the negative $\beta$-expansions defined by Ito and Sadahiro. In [11] a complete classification of the gaps and of the mixing properties of these negative $\beta$-expansions is given. For maps slightly more general than the negative $\beta$-maps the reader is referred to Franz Hofbauer’s paper [4].

In Theorem 2 we show that there is a unique absolutely continuous invariant probability measure $\mu _{\alpha }$ such that $T_{\alpha }$ is ergodic with respect to $\mu _{\alpha }$. As in [11] (for negative $\beta$-expansions), one also could define a gap as any interval in $I_{\alpha }$ where the density of $\mu _{\alpha }$ is zero.

Remark 1

In the example of Fig. 1 the intervals $(r_2,r_1)$ and $(\ell _1,\ell _2)$ are gaps and for $x\in (r_2,r_1)\cup (\ell _1,\ell _2){\setminus } \{f_1,f_2\}$ there exists an $n_0 = n_0(x)$ such that $T_{\alpha }^n(x)\not \in (r_2,r_1)\cup (\ell _1,\ell _2)$ for $n\in {\mathbb {N}}_{\ge 2}$. The ‘for almost’² formulation in the definition of ‘gap’ is necessary so as to exclude fixed points and pre-images of fixed points, i.e. points that are mapped under $T_{\alpha }$ to a fixed point, which may never leave an gap. In Sect. 5 we even find a class of gaps (a, b) such that for uncountably many $x\in I_{\alpha }$ and all $n\in {\mathbb {N}}\cup \{0\}$ we have $T_{\alpha }^n(x)\in (a,b)$.

Remark 2

Whenever we use the word ‘gap’ in relation to arrangements, we mean the gap of the associated interval $I_{\alpha }$.

In [8] computer simulations were used to get a more general impression of orbits of N-expansions. For a lot of values of $\alpha$, plots such as Fig. 1 were stacked, for $0<\alpha \le \alpha _{\max }$, so as to obtain graphs such as Fig. 3, with the values of $\alpha$ on the vertical axis and at each height the corresponding interval $I_{\alpha }$ drawn. In the same paper, similar graphs are given for $N=9,20,36$ and 100. In all cases it appears that ‘gaps’ such as in Fig. 1 appear for values of $\alpha$ equal to or not much smaller than $\alpha _{\max }$. Since the plots in [8] are based on computer simulations, they do not actually show very small gaps (smaller than pixel size) nor clarify much the connection between the gaps for each N. Still, the suggestion is strong that for $\alpha$ sufficiently small there are no gaps. It also seems that for $\alpha$ large enough several disjoint gaps may occur. In Fig. 3 we see this for $\alpha$ near $\alpha _{\max }=\sqrt{50}-1$.

Fig. 3

A simulation of intervals $I_{\alpha }$ with gaps if existent, for $0<\alpha \le \sqrt{50}-1$ and $N=50$

In this paper we will not only investigate conditions for gaplessness, we will also show that simulations such as Fig. 3 fail to reveal the existence, for certain N and $\alpha$, of one extremely large gap in plots such as Fig. 3below the last visible gap. In a subsequent paper we will go into another very interesting property of orbits of N-expansions that is hardly revealed by simulations such as Fig. 3: the existence of large numbers of gaps for large N and $\alpha$ close to $\alpha _{\max }$. But now we will concentrate on gaplessness.

Remark 3

If no gaps exist with non-empty intersection with a cylinder set, we call the cylinder set gapless.

In Sect. 2 we will consider two classes of arrangements that have no gaps: full arrangements and specific arrangements with more than three cylinders. The gaplessness of the latter class, involving the proof of Theorem 4, for which some preliminary results will be presented shortly, is largely given in Sect. 2, but involve some intricacies for small values of N so as to finish it at the end of this paper. In Sect. 3 we will consider arrangements with two cylinders and in Sect. 4 we will concentrate on arrangements with three cylinders, but will prove a sufficient condition for gaplessness that is valid for arrangements with any number of cylinders larger than 2. Finally, in Sect. 5 we will prove a result on gaps in certain arrangements with four cylinders and we will finish the proof of Theorem 4. After that, it is merely a matter of checking that for $N\in \{2,3,4,5,6\}$ all arrangements are gapless.

Although most results in this paper seem intuitively clear and obvious, our experience with these continued fraction maps is they are surprisingly unruly. The simulations from Fig. 3 may serve as an example that things are not what they always seem to be. From these simulations one might draw the (erroneous) conclusion that the number of gaps is at most 3. In a forthcoming paper we show however that the number of gaps is a function of N and $\alpha$, and is growing larger and larger as N tends to infinity. Although the proofs in this paper are often elementary, they require case distinctions and cumbersome calculations.

2 Full arrangements and arrangements with more than four cylinders

If $I_{\alpha }$ consists of full cylinder sets only, we obviously have no gaps. In this situation the mutual relations between N, $\alpha$ and $d(\alpha )$ show a great coherence, as expressed in the following theorem:

Theorem 1

The interval $I_{\alpha }$ consists of m full cylinder sets, with $m \in {\mathbb {N}}_{\ge 2}$, if and only if there is a positive integer k such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha =k,\\ N=mk(k+1),\\ d(\alpha )=(m-1)(k+1). \end{array}\right. } \end{aligned}$$

(4)

Proof of Theorem 1

Writing $d:=d(\alpha )$, the interval $I_\alpha$ is the union of m full cylinder sets if and only if

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{N}{\alpha } - d = \alpha +1, \\ \frac{N}{\alpha +1}-(d-m+1)=\alpha . \end{array}\right. } \end{aligned}$$

(5)

Note that the first equation in (5) can be written as

$$\begin{aligned} N = \alpha ^2 + (d+1)\alpha , \end{aligned}$$

while the second equation in (5) equals

$$\begin{aligned} N = \alpha ^2 + (d+2-m)\alpha + d + 1 - m. \end{aligned}$$

Subtracting the first of these equations from the last we find

$$\begin{aligned} \alpha = \frac{d+1-m}{m-1}. \end{aligned}$$

(6)

From (5), we have

$$\begin{aligned} \alpha = \frac{-(d+1) + \sqrt{(d+1)^2+4N}}{2}, \end{aligned}$$

(7)

which yields that $\alpha$ is either a quadratic irrational or a rational number. Since (6) implies that $\alpha$ is a rational number we find that the integer $(d+1)^2+4N$ must be a square, i.e. there exists a positive integer s such that $s^2=(d+1)^2+4N$. Note that d is an even integer if and only if $s^2$ is an odd integer if and only if s is an odd integer. Consequently we find that the numerator of $\alpha$ in (7) is always even, and (7) yields that $\alpha$ is a positive integer, say k. From the equations in (5) it follows that not only $\alpha = k$ but also $\alpha +1 = k+1$ is a divisor of N.

From the definition of $T_{\alpha }$ in (1) (especially the case $\frac{N}{\alpha }-\alpha \in {\mathbb {Z}}$) we see that

$$\begin{aligned} d = d(\alpha ) = \frac{N}{k} - (k+1). \end{aligned}$$

(8)

On the other hand (6) yields that, since $\alpha =k$,

$$\begin{aligned} d = (m-1)(k+1), \end{aligned}$$

and from this and (8) we see that

$$\begin{aligned} \frac{N}{k} - (k+1) = (m-1)(k+1), \end{aligned}$$

i.e.$N = mk(k+1)$.

Conversely, let k be a positive integer such that the relations of (4) hold. Then both $N/ \alpha$ and $N/ (\alpha +1)$ are positive integers, implying that all cylinder sets are full. Moreover, since $d=d(\alpha )= d_{\max }$ is given by

$$\begin{aligned} d = \frac{N}{\alpha } - \alpha -1 = \frac{mk(k+1)}{k} - k - 1 = (m-1)(k+1), \end{aligned}$$

and $d_{\min } = d(\alpha +1)$ is given by

$$\begin{aligned} d(\alpha +1) = \left\lfloor \frac{N}{\alpha +1} - \alpha \right\rfloor = mk - k = (m-1)k, \end{aligned}$$

it follows that there are

$$\begin{aligned} d_{\max } - \left( d_{\min } -1\right) = (m-1)(k+1) - (m-1)k +1 = (m-1) + 1 = m \end{aligned}$$

full cylinder sets. $\square$

Theorem 1 serves as a starting point for our investigation of orbits of N-expansions. The first thing we will do is give some preliminary results (in Sect. 2.1) that we need for proving (in Sect. 2.2) Theorem 3 and Theorem 4 on gaplessness of arrangements with at least five cylinders.

2.1 Preliminary results

The first thing to pay attention to is the way N and $\alpha$ and $d(\alpha )$, the value of the largest partial quotient, are interdependent, which is illustrated by the following lemmas:

Lemma 1

Given N and $\alpha$, let $d := d(\alpha )$ be the largest possible digit. Then

$$\begin{aligned} d\ge N-1\,\, {\text {if and only if}}\,\, \alpha <1. \end{aligned}$$

The proof of this lemma is left to the reader.

If $\alpha =\alpha _{\max }=\sqrt{N}-1$, we have

$$\begin{aligned} d(\alpha )={\left\{ \begin{array}{ll} \left\lfloor \frac{2}{\sqrt{2}-1}-(\sqrt{2}-1)\right\rfloor =4&{} {\text {for}}\,\,N=2;\\ \left\lfloor \frac{3}{\sqrt{3}-1}-(\sqrt{3}-1)\right\rfloor =3&{} {\text {for}}\,\,N=3;\\ \left\lfloor \frac{4}{\sqrt{4}-1}-(\sqrt{4}-1)\right\rfloor -1=2&{} {\text {for}}\,\,N=4;\\ \left\lfloor \frac{N}{\sqrt{N}-1}-(\sqrt{N}-1)\right\rfloor =\left\lfloor 2+\frac{\sqrt{N}+1}{N-1}\right\rfloor =2&{} {\text {for}}\,\, N\in {\mathbb {N}}_{\ge 5}.\\ \end{array}\right. } \end{aligned}$$

(9)

On the other hand we have, for $N\in {\mathbb {N}}$, $N\ge 2$ fixed:

$$\begin{aligned} \lim _{\alpha \downarrow 0} d(\alpha )=\lim _{\alpha \downarrow 0} \left\lfloor \frac{N}{\alpha }-\alpha \right\rfloor =\infty . \end{aligned}$$

The following lemma provides for a lower bound for the rate of increase of $d(\alpha )$ compared with the rate of decrease of $\alpha$.

Lemma 2

Let $N\in {\mathbb {N}}_{\ge 2}$ be fixed and $d:=d(\alpha )$. Then d is constant for $\alpha \in [f_{d+1},f_d)$, and d increases overall more than twice as fast as $\alpha$ decreases.

Proof of Lemma 2

Starting from $\alpha _{\max }$, d increases by 1 each time $\alpha$ decreases beyond a fixed point, i.e. if $\frac{N}{\alpha } - \alpha \in {\mathbb {N}}$. For the difference between two successive fixed points $f_{d-1}$ and $f_d$ we have

$$\begin{aligned} f_{d-1}-f_d= & {} \frac{\sqrt{4N+(d-1)^2}-(d-1)}{2}-\frac{\sqrt{4N+d^2}-d}{2}\\= & {} \frac{\sqrt{4N+(d-1)^2}-\sqrt{4N+d^2}+1}{2}<\frac{1}{2}. \end{aligned}$$

This finishes the proof. $\square$

Closely related to the previous lemma is the following one, the proof of which is left to the reader.

Lemma 3

Let $d \in {\mathbb {N}}_{\ge 2}$ and $N\in {\mathbb {N}}_{\ge 2}$ be fixed and let $f_d(N)$ be defined by the equation $N/f_d(N) - d = f_d(N)$ (so $f_d(N)$ is the fixed point of the map $x \mapsto N/x - d$ for $x\in (0,N/d)$). Then

$$\begin{aligned} f_{d-1}(N+1)-f_d(N+1)>f_{d-1}(N)-f_d(N). \end{aligned}$$

So, for d fixed, the distance between two consecutive fixed points increases if N increases. We have, in fact, for d fixed:

$$\begin{aligned} \lim _{N\rightarrow \infty } \left( f_{d-1}(N) - f_d(N)\right) = \tfrac{1}{2}; \end{aligned}$$

cf. the proof of Lemma 2. For N fixed, on the other hand, we have:

$$\begin{aligned} \lim _{d\rightarrow \infty } f_d(N) = 0. \end{aligned}$$

While $d(\alpha )$ is a monotonously non-increasing function of $\alpha$, the number of cylinder sets is not. The reason is obvious: starting from $\alpha =\alpha _{\max }$, the number of cylinder sets changes every time either $\alpha$ or $\alpha +1$ decreases beyond the value of a fixed point; in the first case, the number increases by 1, and in the second case, it decreases by 1. Since $T_{\alpha }'(x)=-N/x^2<0$ and $T_{\alpha }''(x)=2N/x^3>0$ on $I_{\alpha }$, $T_{\alpha }(x)$ is decreasing and convex on $I_{\alpha }$, implying that a net increase of the number of cylinder sets. Still, for N and $\alpha$ large enough, it may take a long time of $\alpha$ decreasing from $\alpha _{\max }$ before the number of cylinder sets stops alternating between two successive numbers $k\in {\mathbb {N}}_{\ge 2}$ and $k+1$, and starts to alternate between the numbers $k+1$ and $k+2$. As an example, we take $N=100$. If $\alpha$ decreases from $\alpha _{\max }$, the interval $I_{\alpha }$ consists of two cylinder sets until $\alpha$ decreases beyond $f_3$ and cylinder set $\varDelta _3$ emerges; then, if $\alpha +1$ decreases beyond $f_1$, cylinder set $\varDelta _1$ disappears and so on, until $\alpha$ decreases beyond $f_8$ and $\varDelta _9$ emerges while $\varDelta _6$ has not yet disappeared.

In order to get a grip on counting the number of cylinder sets, the following arithmetic will be useful: a full cylinder set counts for 1, an incomplete left one counts for $\frac{N}{\alpha }-d_{\max }-\alpha$, and an incomplete right one for $\alpha +1-(\frac{N}{\alpha +1}-d_{\min })$, giving rise to the following definition:

Definition 2

Let $N \in {\mathbb {N}}_{\ge 2}$ and $\alpha \in {\mathbb {R}}$ such that $0 < \alpha \le \sqrt{N}-1$ and $T_{\alpha }$ the N-continued fraction map. The branch number³$b(N,\alpha )$ is defined as

$$\begin{aligned} b(N,\alpha )&:=d_{\max }-d_{\min }-1\,\,{\text {(the number of full cylinder sets save for the outermost ones)}} \\&\quad +\frac{N}{\alpha }-d_{\max } -\alpha \,\,{\text {(the length of the image of the leftmost cylinder set)}} \\&\quad +\alpha +1-\left( \frac{N}{\alpha +1}-d_{\min }\right) \,\,{\text {(the length of the image of the rightmost cylinder set).}} \end{aligned}$$

From this the next lemma follows immediately:

Lemma 4

For $N\in {\mathbb {N}}_{\ge 2}$ and $0<\alpha \le \sqrt{N}-1$ we have

$$\begin{aligned} b(N,\alpha )=\frac{N}{\alpha }-\frac{N}{\alpha +1}=\frac{N}{\alpha (\alpha +1)}. \end{aligned}$$

It follows that for fixed N the branch number $b(N,\alpha )$ is a strictly decreasing function of $\alpha$.

Remark 4

Applying Lemma 4, we find

$$\begin{aligned} b(N,\alpha _{\max })=\frac{N}{(\sqrt{N}-1)\sqrt{N}}=1+\frac{1}{\sqrt{N}-1}. \end{aligned}$$

(10)

It follows that $b(N,\alpha )>1$ for all $N\in {\mathbb {N}}_{\ge 2}$, so the number of cylinder sets is always at least 2. On the other hand, from Lemma 4 it follows that the number of cylinder sets increases to infinity as $\alpha$ decreases from $\alpha _{{\textit{max}}}$ to 0. Actually, we have infinitely many digits only if $\alpha = 0$. In this case the corresponding N-expansion is the greedy N-expansion, studied in [1, 3].

The relation $N/(\alpha (\alpha +1))=b$ yields

$$\begin{aligned} \alpha =\frac{\sqrt{\frac{4N}{b} +1}-1}{2}, \end{aligned}$$

(11)

from which we derive that $d(\alpha ) =d$ (or $d(\alpha )=d-1$ in case $\frac{N}{\alpha } - \alpha \in {\mathbb {Z}}$), where d is given by

$$\begin{aligned} d=\left\lfloor \frac{(b-1)\sqrt{\frac{4N}{b} +1}+b+1}{2}\right\rfloor . \end{aligned}$$

(12)

2.2 Gaplessness if the branch number is large enough

So far, we merely discussed the way $I_{\alpha }$ is divided in cylinder sets, depending on the values of $N, \alpha , d(\alpha )$ and the branch number b. In order to present some first results on sufficient conditions for gaplessness, we will zoom in on some ergodic properties of $T_{\alpha }$.

Lemma 5

If $\mu$ is an absolutely continuous invariant probability measure for $T_{\alpha }$, then there exists a function h of bounded variation such that

$$\begin{aligned} \mu (A) = \int _{A} h\, d \lambda , \,\, \lambda -\text{ a.e. },\,\, \text{ with }\,\lambda \,\text{ the } \text{ Lebesgue } \text{ measure }, \end{aligned}$$

i.e. any absolutely continuous invariant probability measure has a version of its density function of bounded variation.

Proof of Lemma 5

Since $\inf |T_{\alpha }'| > 1$, applying Theorem 1 from [9] immediately yields the assertion. $\square$

Theorem 2

Let $N \in {\mathbb {N}}_{\ge 2}$. Then there is a unique absolutely continuous invariant probability measure $\mu _\alpha$ such that $T_{\alpha }$ is ergodic with respect to $\mu _\alpha$.

Proof⁴of Theorem 2 Let $\mu _\alpha$ be a unique absolutely continuous invariant probability measure for $T_{\alpha }$ and choose its density function h of bounded variation. Then there exists an open interval J such that $h(x) > 0$ for any $x \in J$, since h has at most countably many discontinuity points. Consider $\{T^{n}J : n \ge 0\}$. Since $\inf |T'|>1$, there exists an $n_{0}$ such that $T^{n_0}(J)$ includes a discontinuity point. (If necessary we may choose endpoints of J not in the preimages of discontinuity points of $T_{\alpha }$.) We note that for any measurable subset $A \subset J$ with $\mu _\alpha (A)>0$ equivalently $\lambda (A)>0$, $\mu (T^{n}A)>0$ for any $n \ge 1$. Now $T^{n_{0}+1}(J)$ includes two intervals $J_{\ell }$ and $J_{r}$ attached to $\alpha$ and $\alpha + 1$ respectively. For any measurable subset $B_{0}\subset J_{\ell } \cup J_{r}$ of positive $\lambda$-measure, $\mu (B_{0}) > 0$, since otherwise we have a contradiction; $\mu (B_{0}) = 0$ and $\mu (T^{-(n_{0}+1)}(B_{0}) )> 0$ (since there is a $B_{1} \subset J$ such that $T^{n_{0}+1}(B_{1}) = B_{0}, \mu (B_{1})>0$). This shows that any two absolutely continuous invariant probability measures $\mu _{1}$ and $\mu _{2}$ cannot have disjoint supports (i.e. they cannot be singular to each other), which is equivalent to the uniqueness of the absolutely continuous invariant probability measure and hence its ergodicity. $\square$

The next result follows directly from Theorem 2:

Corollary 1

If iteration of $T_{\alpha }$ maps all open subintervals of $I_{\alpha }$ to the interval $I_{\alpha }^{-}$, then $I_{\alpha }$ contains no gaps.

Proof of Corollary 1

The assumption implies that the absolutely continuous invariant probability measure $\mu _\alpha$ is equivalent to the Lebesgue measure, which implies that for any measurable subset $A \subset I_{\alpha }$, $\mu (A) =0$ if and only if $\lambda (A)=0$. Suppose that there is a gap J. Since J is an open interval, we have $\lambda (J) >0$, thus $\mu (J)>0$. Since $\mu (I_{\alpha })<\infty$ implies a.e. $x \in J$, there exists infinitely many positive integers n such that $T^{n}(x) \in J$ (by the Poincaré recurrence theorem), which contradicts the assumption that there is a gap. $\square$

Before we present the first of two theorems on gaplessness, we note that in the case $N=2$, the condition $|T_{\alpha }'(x)|>2$ for all $x \in I_{\alpha }$ is not satisfied for any $\alpha \in (0,\sqrt{2}-1]$.

Theorem 3

Let $N\in {\mathbb {N}}_{\ge 3}$, and let $0< \alpha \le \sqrt{N}-1$. Let $|T_{\alpha }'(x)|> 2$ for all $x \in I_{\alpha }$. Then $I_{\alpha }$ contains no gaps.

Proof of Theorem 3

The condition implies $N/(\alpha +1)^2>2$, yielding $\alpha < \sqrt{N/2}-1$. From Lemma 4 it follows that

$$\begin{aligned} b(N,\alpha )> \frac{2\sqrt{2N}}{\sqrt{2N}-2}, \end{aligned}$$

which is larger than 2 for all $N \in {\mathbb {N}}_{\ge 3}$. So $I_{\alpha }$ consists of at least three cylinder sets. Since $|T_{\alpha }^{\prime }(x)| > 2$ for all $x\in I_{\alpha }$, there exists an $\varepsilon >0$ such that for any open interval $J_0$ that is contained in a cylinder set of $T_{\alpha }$ we have

$$\begin{aligned} \left| T_{\alpha }(J_0)\right| \ge (2+\varepsilon )|J_0|, \end{aligned}$$

where |J| denotes the length (i.e. Lebesgue measure) of an interval J.

If $T_{\alpha }(J_0)$ contains two consecutive discontinuity points $p_{i+1},p_i$ of $T_{\alpha }$, then

$$\begin{aligned} (p_{i+1},p_i)\subset T_{\alpha }(J_0), \end{aligned}$$

and we immediately have that

$$\begin{aligned} I^O_{\alpha }:=(\alpha ,\alpha +1)=T_{\alpha }(p_{i+1},p_i)\subset T_{\alpha }^2(J_0). \end{aligned}$$

If $T_{\alpha }(J_0)$ contains only one discontinuity point p of $T_{\alpha }$, then $T_{\alpha }(J_0)$ is the disjoint union of two subintervals located in two adjacent cylinder sets:

$$\begin{aligned} T_{\alpha }(J_0)=J_1^{\prime }\cup J_2^{\prime }. \end{aligned}$$

Obviously,

$$\begin{aligned} |T_{\alpha }(J_0)| = |J_1^{\prime }| + |J_2^{\prime }|. \end{aligned}$$

Now select the larger of these two intervals $J_1^{\prime }$, $J_2^{\prime }$, and call this interval $J_1$. Then

$$\begin{aligned} |J_1| \ge (1+\tfrac{\varepsilon }{2})|J_0|. \end{aligned}$$

In case $T_{\alpha }(J_0)$ does not contain any discontinuity point of $T_{\alpha }$, we set $J_1=T_{\alpha }(J_0)$. Induction yields that there exists an $\ell \in {\mathbb {N}}$ such that

$$\begin{aligned} |J_{\ell }| \ge \left( 1 + \frac{\varepsilon }{2}\right) ^{\ell } \left| J_0\right| , \end{aligned}$$

whenever $T_{\alpha }(J_{\ell - 1})$ includes no more than one discontinuity point of $T_{\alpha }$. But then there must exist a $k \in {\mathbb {N}}$ such that $T_{\alpha }(J_k)$ contains two (or more) consecutive discontinuity points of $T_{\alpha }$, and we find that $T_{\alpha }^2(J_k)=I_{\alpha }^O$. Applying Corollary 1, we conclude that there is no gap in $I_{\alpha }$. $\square$

Remark 5

As one of our referees remarked, the result from Theorem 3 is rather folklore. As to one of its first appearances we refer to Keith Wilkinson’s paper [13]; it might be interesting also to consult Gerhard Keller’s paper [6].

The next theorem, which is partly a corollary of the previous one, gives an even more explicit condition for gaplessness.

Theorem 4

Let $I_{\alpha }$ consist of five cylinder sets or more. Then $I_{\alpha }$ has no gaps.

Proof of Theorem 4, part I: Let $I_{\alpha }$ consist of five cylinder sets or more. Then $b(N,\alpha )>3$, implying

$$\begin{aligned} \alpha <\frac{1}{2}\sqrt{\tfrac{4N}{3}+1}-\frac{1}{2}\,\,({\text {cf.}}\,(11)),\,{\text {in which case}}\,\,|T_{\alpha }'(\alpha +1)|>3-\frac{3\sqrt{12N+9}-9}{2N}. \end{aligned}$$

The second inequality yields that for $N \in {\mathbb {N}}_{\ge 18}$ we have $|T_{\alpha }'(\alpha +1)|>2$ and, applying Theorem 3, $I_{\alpha }$ is gapless. Now suppose $N\in \{12,\ldots ,17\}$. Then $b(N,\alpha )=3$ involves arrangements with four cylinders. In each of these cases, the smallest $\alpha$ such that $I_{\alpha }$ has not yet (i.e. decreasing from $\alpha _{\max }$) consisted of five cylinder sets is $f_7$. In all six cases (two of which are illustrated in Fig. 4) we have $|T_{\alpha }'(f_7+1)|>2$, yielding the gaplessness of $I_{\alpha }$ for arrangements with five or more cylinders in case $N\in \{12,\ldots ,17\}$. This finishes the proof of Theorem 4 for $N\in {\mathbb {N}}_{\ge 12}$. For $N\in \{2,\ldots ,11\}$ a similar approach does not work. We will use some ideas that we will introduce and develop in the next sections and will finish the proof of Theorem 4 at the end of Sect. 5.

Fig. 4

Two arrangements illustrating the gaplessness of arrangements with five cylinders or more on account of Theorem 3

In the following we will go into conditions for gaplessness of arrangements consisting of less than five cylinders. We will start with two cylinders and will use the results for arrangements with three and four cylinders.

Remark 6

Since $b(N,\alpha )$ is a strictly decreasing function of $\alpha$ (cf. Lemma 4) and $b(N,\alpha _{\max })=1+1/(\sqrt{N}-1)$, the condition $I_{\alpha }=\varDelta _{d}\cup \varDelta _{d-1}$ is never satisfied in case $N \in \{2,3\}$.

3 Gaplessness if $I_{\alpha }$ consists of two cylinder sets

In general, if the branch number is not much larger than 1 (which is if $\alpha$ is not much smaller than $\alpha _{\max }$), the overall expanding power of $T_{\alpha }$, determined by $T_{\alpha }'$ (or $|T_{\alpha }'|$, which we will often use), is not enough to exclude the existence of gaps; we shall elaborate on this in a subsequent article. However, in the case of two cylinder sets $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}$, there is a very clear condition under which this power suffices:

Theorem 5

Let $I_{\alpha }=\varDelta _{d}\cup \varDelta _{d-1}$. If $T_{\alpha }(\alpha )\ge f_{d-1}$ and $T_{\alpha }(\alpha +1)\le f_{d}$, then $I_{\alpha }$ is gapless.

Although the statement of 5 is intuitively clear, for the proof of Theorem 5 we need several results and lemmas that we will prove first. Then, immediately following Remark 11, we will prove Theorem 5 itself.

Remark 7

In case $I_{\alpha }=\varDelta _{d}\cup \varDelta _{d-1}$ and either $T_{\alpha }(\alpha )<f_{d-1}$ or $T_{\alpha }(\alpha +1) >f_d$, it is easy to see that $(T_{\alpha }(\alpha ),T_{\alpha }^2(\alpha ))$ or $(T_{\alpha }^2(\alpha +1),T_{\alpha }(\alpha +1))$ is a gap, respectively.

Since arrangements under the condition of Theorem 5 play an important role in this section, we introduce the following notations:

Definition 3

Let $N \in {\mathbb {N}}_{\ge 4}$ be fixed. For $d \in {\mathbb {N}}_{\ge 2}$, we define ${\mathcal {F}}(d)$ as the family of all arrangements $\varUpsilon _{N,\alpha }$ such that $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}$, $T_{\alpha }(\alpha )\ge f_{d-1}$ and $T_{\alpha }(\alpha +1) \le f_{d}$. We will write ${\mathcal {F}}^*(d)$ in case $\alpha$ satisfies the equation $T_{\alpha }(\alpha )= f_{d-1}$, the root of which we will henceforth denote by $\alpha (N,d)$.

Remark 8

Note that for each $N\in {\mathbb {N}}_{\ge 4}$ and $d\in {\mathbb {N}}_{\ge 2}$ we have that $\alpha (N,d)$, if it exists, is the only value of $\alpha$ such that ${\mathcal {F}}^*(d)$ is not void.

If the expanding power of $T_{\alpha }$ is large enough to exclude the existence of gaps for the largest $\alpha$ for which an arrangement in ${\mathcal {F}}(d)$ exists, there will not be gaps in any arrangement in ${\mathcal {F}}(d)$. We will now first show how to find these largest $\alpha$, which takes some effort. If we have finished that, we will go into the expanding power of $|T_{\alpha }'|$ in these arrangements with largest $\alpha$.

For $4 \le N \le 8$, with $d=2$, we have $T_{\alpha _{\max }}(\alpha _{\max })>f_1$, while $T_{\alpha _{\max }}(\alpha _{\max }+1)=\alpha _{\max }<f_2$. Hence we see $\varUpsilon _{N,\alpha _{\max }}\in {\mathcal {F}}(2)$ and $\mathcal F(2)\ne \emptyset$. For $N\in {\mathbb {N}}_{\ge 9}$ we have $T_{\alpha _{\max }}(\alpha _{\max })<f_1$. If $d=2$ we can find $\alpha$ such that $\varUpsilon _{N,\alpha }$ in ${\mathcal {F}}^*(2)$ for each $9 \le N \le 17$; see Fig. 5, where ten arrangements in various ${\mathcal {F}}(d)$ are drawn. Underneath each arrangement we have mentioned an approximation of $\sigma (\alpha ):=|T_{\alpha }'(\alpha +1)|$, which we will later return to. This $\sigma$ is important, because it is the expanding power on the rightmost cylinder set that may be too weak to exclude gaps.

If $d=2$ and $N\in {\mathbb {N}}_{\ge 18}$, the condition $T_{\alpha }(\alpha )=f_{d-1}$ yields $T_{\alpha }(\alpha +1)> f_d$, and d has to increase by 1 so as to find an arrangement in ${\mathcal {F}}(3)$. If $d=3$, for $18\le N\le 24$ we find that the largest $\alpha$ is $f_{d-2}-1$, in which case $T_{\alpha }(\alpha +1)=\alpha <f_d$ and $T_{\alpha }(\alpha )>f_{d-1}$ (so in this case the arrangement with the largest $\alpha$ is in ${\mathcal {F}}(3)$ but not in ${\mathcal {F}}^*(3)$); for $25\le N\le 49$, the largest $\alpha$ is such that $T_{\alpha }(\alpha )=f_2$. If $N\in {\mathbb {N}}_{\ge 50}$, the family ${\mathcal {F}}(3)$ is empty and d has to increase further; see Fig. 5 once more. In the proof of Lemma 8 this approach (of exhausting ${\mathcal {F}}(d)$ for successive values of N and going to ${\mathcal {F}}(d+1)$ for larger values of N) will be formalised into a proof by induction. Due to (12) such an increase is always possible, no matter how large d and N become.

Fig. 5

Arrangements in ${\mathcal {F}}(d)$, $d \in \{2,3,4,5\}$, where $\alpha$ is maximal

Note that this inductive approach works since for each d only finitely many N exist such that there are $\alpha$ with $\varUpsilon _{N,\alpha }\in {\mathcal {F}}(d)$. To see why this claim holds, note that for fixed N and d, the smallest $\alpha$ for which $d=d(\alpha )=d_{\mathrm{max}}$ is $\alpha _d$, given by

$$\begin{aligned} \alpha _d=f_{d+1}=\frac{\sqrt{4N+(d+1)^2}-(d+1)}{2}; \end{aligned}$$

cf. (3). For this $\alpha$ it is not necessarily so that $I_{\alpha _d}=\varDelta _d\cup \varDelta _{d-1}$, i.e. that $I_{\alpha _d}$ consists of two cylinder sets (e.g. if $N=2$ and $d=5$, there are five cylinder sets). However, if $b(N,\alpha _d)\le 2$, we know that $I_{\alpha _d}$ exists of two cylinder sets, the left one of which is full. According to Lemma 4, the branch number $b(N,\alpha _d)$ satisfies

$$\begin{aligned} b(N,\alpha _d) = \frac{N}{f_{d+1}(f_{d+1}+1)} = \frac{4N}{4N+(d+1)^2-2d\sqrt{4N+(d+1)^2}+d^2-1}. \end{aligned}$$

Keeping d fixed and letting $N\rightarrow \infty$, we find

$$\begin{aligned} \lim _{N\rightarrow \infty } b(N,\alpha _d) = 1. \end{aligned}$$

In view of this and Lemma 3 (and the results mentioned directly thereafter), we choose N sufficiently large, such that for $\alpha \ge \alpha _d$ we have $b(N,\alpha )< 5/4$ and $f_{d-1}-f_d > 1/4$.

Now suppose that for such a sufficiently large value of N there exists an $\alpha \ge \alpha _d$, such that $\alpha \in {\mathcal {F}}(d)$. Then by Definition 2 of branch number and the assumption that $\alpha \in {\mathcal {F}}(d)$, we have that

$$\begin{aligned} b(N,\alpha ) \ge 1+ f_{d-1} - f_d > \tfrac{5}{4}, \end{aligned}$$

which is impossible since for N sufficiently large, d fixed and $\alpha \ge \alpha _d$ we have

$$\begin{aligned} b(N,\alpha ) \le b(N,\alpha _d) < \tfrac{5}{4}. \end{aligned}$$

It follows that for d fixed and N sufficiently large, ${\mathcal {F}}(d)$ is void.

We will prove (in Lemma 8) that if $N\in {\mathbb {N}}_{\ge 25}$ there exists a minimal $d\in {\mathbb {N}}_{\ge 3}$ such that the arrangement in ${\mathcal {F}}(d)$ with $\alpha$ maximal lies in ${\mathcal {F}}^*(d)$. Before we will prove this, we will explain the relation between d and N for arrangements in ${\mathcal {F}}^*(d)$.

In Fig. 5 we see that for $N\in \{49,99,165\}$ the arrangements in ${\mathcal {F}}^*$ are very similar, and that the arrangement for $N=100$ is more similar to these than the arrangement for $N=50$. Moreover, the last three arrangements look hardly curved. This is easy to understand, considering the following equations, where $b(N,\alpha )=b$ is fixed:

$$\begin{aligned} |T_{\alpha }'(\alpha )|=\frac{b(\sqrt{4bN+b^2}+2N+b)}{2N}\quad {\text {and}}\quad |T_{\alpha }'(\alpha )|-|T_{\alpha }'(\alpha +1)| =\frac{b\sqrt{4bN+b^2}}{N}. \end{aligned}$$

Since $(b\sqrt{4bN+b^2})/N$ is a decreasing function of N, approaching 0 from above as $N \rightarrow \infty$, the second equation implies that for a fixed branch number b the branches become less curved as N increases; i.e., the curves approach linearity as $N \rightarrow \infty$ and b is fixed. Although in ${\mathcal {F}}^*(d)$ the branch number is not so much fixed as bounded between 1 and 2, we have a similar decrease of curviness as N increases. The arrangements for $N \in \{49,99,165\}$ in Fig. 5 suggest that (assuming $T_{\alpha }(\alpha )=f_{d-1}$, i.e. $\alpha = \alpha (N,d)$)) if $N \rightarrow \infty$ (and $d \rightarrow \infty$ and $\alpha \rightarrow \infty$ accordingly), the difference $f_d-T_{\alpha }(\alpha +1)$ tends to 0, yielding a ‘limit graph’ of $T_{\alpha }$ that consists of two parallel line segments (the straightened branch curves of $T_{\alpha }$); see Fig. 6, obtained by translating the graph over $(-\alpha ,-\alpha )$. In this situation we have both $a:=T_{\alpha }(\alpha )\ (\mathrm {mod}\ \alpha )=f_{d-1}\ (\mathrm {mod}\ \alpha )$ and $T_{\alpha }(\alpha +1)=f_d$ (also $\ (\mathrm {mod}\ \alpha )$ in Fig. 6). Because in the limit both parts of the graph are linear with the same slope, we also have that $(0,a+1)$ lies on the prolonged right line segment, from which we derive that the line segments have slope $-1/a$. The line with equation $y=-\frac{x}{a}+a+1$ intersects the line $y=1$ at $(a^2,1)$ (so the dividing line is $x=a^2$) and intersects the line $x=1$ in $\left( 1,-\frac{1}{a}+a+1\right)$, yielding the point $\left( -\frac{1}{a}+a+1,-\frac{1}{a}+a+1\right)$ on the line through (0, a) with equation $y=-\frac{x}{a}+a$ (since $T_{\alpha }(\alpha +1)=f_d)$. From this we derive $2a^2=1$, so $a=\sqrt{1/2}$.

Fig. 6

The ‘limit graph’ of $T_{\alpha }$, translated over $(-\alpha ,-\alpha )$, under the conditions $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}$ and $N/\alpha -d=f_{d-1}$ for $N\rightarrow \infty$ (and $\alpha , d \rightarrow \infty$ accordingly)

From Fig. 6 we almost immediately find that the branch number for the limit case is $\sqrt{2}$ and that the dividing line is at 1/2. We use this heuristic to find a formula describing the relation between N and d for arrangements in ${\mathcal {F}}^*(d)$ very precisely. Note that for arrangements similar to the limit graph we have

$$\begin{aligned} 1 + f_{d-1} - f_d =\frac{\sqrt{4N+(d-1)^2}-\sqrt{4N+d^2}+1}{2}+1\approx b(N,\alpha )\approx \sqrt{2}, \end{aligned}$$

from which we derive

$$\begin{aligned} N\approx (4+3\sqrt{2})(d^2-d)+2\quad {\text {or}}\quad d\approx \frac{1}{2}\left( 1+\sqrt{(6\sqrt{2}-8)(N-2)+1}\right) .\quad \end{aligned}$$

(13)

If, for d fixed, we determine arrangements in ${\mathcal {F}}^*(d)$ such that the difference $f_d-T_{\alpha }(\alpha +1)$ is positive and as small as possible according to our heuristic, the best function seems to be $N=(4+3\sqrt{2})(d^2-d)$, yielding the right N (after rounding off to the nearest integer) for $d \in \{3,\ldots ,500\} {\setminus } \{9,50,52,68,69,80,97,129,$ $167,185,210,231,289,330,416,440,444,479,485\}$, in all of which cases the rounding off should have been up instead of down. For $d=2$ we find $N=\lceil 2(4+3\sqrt{2})\rceil =17$, for $d=3$ we find $N=\lfloor 6(4+3\sqrt{2})\rfloor =49$, for $d=4$ we find $N=\lceil 12(4+3\sqrt{2})\rceil =99$ and or $d=5$ we find $N=\lceil 20(4+3\sqrt{2})\rceil =165$; see Fig. 5 once more.

Although we do not know generally if rounding off to the nearest integer yields the right N, with (13) we can find a very good overall indication of the relation between d and N for arrangements in ${\mathcal {F}}^*(d)$ by looking at the difference between the image of $\alpha (N,d)+1$ and $f_d$; see Definition 3. With some straightforward calculations we find that

$$\begin{aligned} \alpha (N,d)=\frac{N\left( \sqrt{4N+(d-1)^2}-(d+1)\right) }{2(N-d)}. \end{aligned}$$

(14)

Applying (14), we write $f_d(N)-(N/(\alpha (N,d)+1)-(d-1))$ as

$$\begin{aligned} j_d(N):= \frac{(N^2+dN+d)\sqrt{4N+d^2}-N^2\sqrt{4N+(d-1)^2}-(N^2-d(d-4)N-d(d-2))}{2(N^2+dN+d)} \end{aligned}$$

and, more generally, define

$$\begin{aligned} j_d(x):= \frac{(x^2+dx+d)\sqrt{4x+d^2}-x^2\sqrt{4x+(d-1)^2}-(x^2-d(d-4)x-d(d-2))}{2(x^2+dx+d)} \end{aligned}$$

(15)

for $x \in [25,\infty )$.

We note that $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}$ is equivalent to $N/(\alpha +1)-(d-1)\ge \alpha$. In case $\alpha =\alpha (N,d)$, we have

$$\begin{aligned} \frac{N}{\alpha (N,d)+1}-(d-1)=\frac{N^2\sqrt{4N+(d-1)^2}-\left( (d-1)N^2+2d(d-2)N+2d(d-1)\right) }{2(N^2+dN+d)}. \end{aligned}$$

(16)

Applying (16), for the difference $h_d(N) := N/(\alpha (N,d)+1) - (d-1) - \alpha (N,d)$ we write

$$\begin{aligned} h_d(N):=\frac{2N^3+4dN^2+(2d^3-5d^2+3d)N+2d^2(d-1)-dN(2N+1)\sqrt{4N+(d-1)^2}}{2(N-d)(N^2+dN+d)}, \end{aligned}$$

(17)

and, more generally, define

$$\begin{aligned} h_d(x):=\frac{2x^3+4dx^2+(2d^3-5d^2+3d)x+2d^2(d-1)-dx(2x+1)\sqrt{4x+(d-1)^2}}{2(x-d)(x^2+dx+d)}, \end{aligned}$$

(18)

for $x \in [25,\infty )$.

Now we can prove the lemma that is illustrated by the arrangements for $N\in \{17,49,99,165\}$ in Fig. 5. In order to so, we define for fixed $d \in {\mathbb {N}}_{\ge 2}$

$$\begin{aligned} S(d):=\{N\in {\mathbb {N}}_{\ge 4}:I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}, T_{\alpha }(\alpha ) = f_{d-1}(N)\quad {\text {and}}\quad T_{\alpha }(\alpha +1) \le f_{d}(N)\} \end{aligned}$$

and

$$\begin{aligned} M_d:=\max S(d). \end{aligned}$$

Lemma 6

Let $d \in {\mathbb {N}}_{\ge 2}$. Then $M_d\in \{\lfloor (4+3\sqrt{2})(d^2-d)\rfloor , \lceil (4+3\sqrt{2})(d^2-d)\rceil \}$.

Proof of Lemma 6

First we note that for $d=2$, we have that $\lceil (4+3\sqrt{2})(d^2-d)\rceil$ equals 17, which corresponds with what we had already calculated and drawn in Fig. 5. Now let $d\in {\mathbb {N}}_{\ge 3}$. First we have to show that $h_d(M_d)>0$ for $M_d\in \{\lfloor (4+3\sqrt{2})(d^2-d)\rfloor ,\lceil (4+3\sqrt{2})(d^2-d)\rceil \}$, for this assures us that $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}$. We will leave this to the reader; it is merely very cumbersome to show, while technically straightforward.⁵

The only thing left to do is showing that

$$\begin{aligned} {\left\{ \begin{array}{ll} j_d((4+3\sqrt{2})(d^2-d))>0;\\ j_d((4+3\sqrt{2})(d^2-d)+1)<0, \end{array}\right. } \end{aligned}$$

(19)

since the first equation implies that $j_d(\lfloor (4+3\sqrt{2})(d^2-d)\rfloor )>0$, while the second implies that $j_d(\lceil (4+3\sqrt{2})(d^2-d)\rceil +1)<0$. The work to be done is as cumbersome and straightforward as the previous work to be done for this proof and is left to the reader as well. $\square$

Before we will show that for $N\in {\mathbb {N}}_{\ge 25}$ there are a $d\in {\mathbb {N}}_{\ge 3}$ and an $\alpha$ such that $\varUpsilon _{N,\alpha } \in {\mathcal {F}}^*(d)$, we will prove the following lemma:

Lemma 7

Let $d \in {\mathbb {N}}_{\ge 3}$. Let $N \in {\mathbb {N}}_{\ge 25}$ be such that $I_{\alpha (M_d,d)}=\varDelta _d\cup \varDelta _{d-1}$ and $T_{\alpha (M_d,d)}(\alpha (M_d,d))=f_{d-1}$ for $M_d \in \{N,N+1\}$. Then

$$\begin{aligned} T_{\alpha (N+1,d)}(\alpha (N+1,d)+1)-\alpha (N+1,d)>T_{\alpha (N,d)}(\alpha (N,d)+1)-\alpha (N,d), \end{aligned}$$

i.e. $h_d(N+1) > h_d(N)$.

Proof of Lemma 7

We want to show that $h_d(N)$ from (17) is an increasing sequence, and do so by calculating the derivative of with $x \in [25,\infty )$, and then showing that $h_d'(x)>0$ on $[25,\infty )$. Although a little bit intricate, the work is straightforward and is left to the reader. $\square$

Now we can prove the following lemma:

Lemma 8

Let $N \in \{9,\ldots ,17,25,26,\ldots \}$. Then there are $d \in {\mathbb {N}}_{\ge 2}$ and $\alpha \in (0,\sqrt{N}-1)$ such that $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}$, $T_{\alpha }(\alpha ) = f_{d-1}$ and $T_{\alpha }(\alpha +1)\le f_d$ (i.e. $\alpha = \alpha (N,d)$).

Proof of Lemma 8

We will use induction on d. For $N \in \{9,\ldots ,17,25,26,\ldots ,99\}$ and $d \in \{2,3,4\}$ we refer to Fig. 5 and leave the calculations to the reader. Specifically, we have for $50\le N \le 99$ that $\varUpsilon _{N,\alpha (N,4)} \in {\mathcal {F}}^*(4)$. It is easily seen that $\varUpsilon _{99,\alpha (99,5)} \in {\mathcal {F}}^*(5)$ as well. Due to Lemma 6, there is an $N_5>99$ such that $\varUpsilon _{N_5,\alpha (N_5,5)} \in {\mathcal {F}}^*(5)$. Applying Lemma 7, we see that for all $N \in \{99,\ldots ,N_5\}$ we have $\varUpsilon _{N,\alpha (N,5)} \in {\mathcal {F}}^*(5)$. For the induction step, let $d\in {\mathbb {N}}_{\ge 5}$ be such that there is an $\alpha$ for which $\varUpsilon _{N_d,\alpha } \in {\mathcal {F}}^*(d)$, where $N_d$ is the largest such N possible, cf. Lemma 6. If we can show that for this $N_d$ there is an $\alpha '$ such that $\varUpsilon _{N_d,\alpha '} \in {\mathcal {F}}^*(d+1)$, we are finished. This can be done by showing that

$$\begin{aligned} h_{d+1}((4+3\sqrt{2})(d^2-d)-1)>0, \end{aligned}$$

(20)

for this implies $h_{d+1}(N_d)>0$, in which case $\alpha '$ is such that $\frac{N_d}{\alpha '}-(d+1)=f_d$, i.e. $\alpha ^{\prime } = \alpha (N,d+1)$. Although intricate, the calculations are straightforward and are left to the reader. $\square$

Remark 9

Although Lemma 8 is about N in the first place, our approach is actually based on increasing d and then determining all N such that arrangements $\varUpsilon _{N,\alpha } \in {\mathcal {F}}^*(d)$ exist. The proof of Lemma 8 yields the arrangements with the smallest d (and therefore the largest $\alpha$) for which $\varUpsilon _{N,\alpha } \in {\mathcal {F}}^*(d)$, as illustrated by the last five arrangements of Fig. 5.

Example 1

For $d=4$ we have $M_d-1=\lfloor (4+3\sqrt{2})(d^2-d)\rfloor =98$. Then $\varUpsilon _{M_d-1,\alpha (M_d-1,4)} \in {\mathcal {F}}^*(4)$ and $\varUpsilon _{M_d,\alpha (M_d,4)} \in {\mathcal {F}}^*(4)$, while $\varUpsilon _{M_d+1,\alpha (M_d+1,5)} \in {\mathcal {F}}^*(5)$; see Fig. 5. It follows immediately from our construction of $\alpha (M_d+1,5)$ that this is the largest $\alpha$ such that $\varUpsilon _{M_d+1,\alpha } \in {\mathcal {F}}(5)$.

With manual calculations we can quickly calculate the expanding power of $T_{\alpha }$ in $\alpha +1$ for arrangements in ${\mathcal {F}}$ and ${\mathcal {F}}^*$ and N not too large, say $N \in {\mathbb {N}}_{\le 49}$, where the smallest values are found where $\alpha$ is as large as possible. The next proposition gives a lower bound for $|T_{\alpha }'(\alpha +1)|$ for such arrangements for most N.

Proposition 1

Let $N \in \{18\}\cup \{50,51,\ldots \}{\setminus } \{95,\ldots ,99\}$ and $\alpha \in (0, \sqrt{N}-1]$ such that $I_{\alpha }=\varDelta _{d}\cup \varDelta _{d-1}$ for some $d\in {\mathbb {N}}$, $d\in {\mathbb {N}}_{\ge 2}$. Furthermore, suppose that $T_{\alpha }(\alpha )\ge f_{d-1}$ and $T_{\alpha }(\alpha +1) \le f_{d}$. Then $|T_{\alpha }'(\alpha +1)|>\root 3 \of {2}=1.259921\ldots$.

Proof of Proposition 1

Considering Lemma 8, we can confine ourselves to arrangements in ${\mathcal {F}}^*$ with $\alpha$ as large as possible. For $\alpha =\alpha (N,d)$ (cf. (14)) we can write $|T_{\alpha }'(\alpha +1)|=N/(\alpha +1)^2$ as

$$\begin{aligned}&k_d(N)\nonumber \\&\quad =\frac{2N^4+(d-1)^2N^3+2d(d-1)N^2+2d^2N+((d-1)N^3+2dN^2)\sqrt{4N+(d-1)^2}}{2(N^4+2dN^3+d(d+2)N^2+2d^2N+d^2)}.\nonumber \\ \end{aligned}$$

(21)

It is not hard to find that, for d fixed, $k_d$ is a decreasing sequence, with $\lim _{N \rightarrow \infty } k_d(N)=1$. However, from (13) it follows that if $N\rightarrow \infty$ we have that also $d\rightarrow \infty$ in a precise manner. Due to the previous lemmas, for each d we can confine ourselves to considering only $N/(\alpha +1)^2$ for the largest N and $\alpha$ such that $\varUpsilon _{N,\alpha } \in {\mathcal {F}}^*(d)$. Applying Lemma 6, an easy way to check if indeed $|T_{\alpha (N,d)}'(\alpha (N,d)+1)|>\root 3 \of {2}$ is considering $k_d(x)$, with $x \in [100,\infty )$, and then calculating $k_d((4+3\sqrt{2})(d^2-d)+1)$ for $d\in {\mathbb {N}}_{\ge 5}$, which is amply larger than $\root 3 \of {2}=1.2599\cdots$. For the remaining cases $d=3$ and $N=18$ and for $d=4$ and $N \in \{50,51,\ldots ,94\}$ it is easily checked manually that indeed $|T_{\alpha (N,d)}'(\alpha (N,d)+1)|>\root 3 \of {2}$. $\square$

Remark 10

Considering our previous remarks concerning arrangements in ${\mathcal {F}}^*$, it may be clear that $\lim _{N\rightarrow \infty } N/(\alpha (N,d)+1)^2=\sqrt{2}$.

Remark 11

The value $\root 3 \of {2}$ in the proof of Proposition 1 relates to the proof of Theorem 5 and also to the proofs of Proposition 9 and Theorem 3, where the numbers $\sqrt{2}$ and 2 have a similar importance. Considering the proof of Proposition 1, we could actually replace $\root 3 \of {2}$ by the smallest possible value, given by

$$\begin{aligned} \frac{94}{(\alpha (94)+1)^2}=\frac{20480015+320305\sqrt{385}}{21233664}=1.2604\ldots . \end{aligned}$$

Finally we are ready to prove Theorem 5, stating that $I_{\alpha }=\varDelta _{d}\cup \varDelta _{d-1}$, with $d:=d(\alpha )$, is gapless if $T_{\alpha }(\alpha )\ge f_{d-1}$ and $T_{\alpha }(\alpha +1)\le f_{d}$. Considering Remark 11 the value $\root 3 \of {2}$ in Proposition 1 can be replaced by 1.26, the third power of which is 2.000376. We will use this to stress that the gaplessness of Theorem 5 is actually relatively ample and does not require infinitesimal estimations.

Proof of Theorem 5

First we note that the conditions imply $N \in {\mathbb {N}}_{\ge 4}$. Now let $\varUpsilon _{N,\alpha } \in {\mathcal {F}}(d)$ and let $K\subset I_{\alpha }$ be any open interval. Since K expands under $T_{\alpha }$, there is an $n \in {\mathbb {N}}\cup \{0\}$ such that $T_{\alpha }^n(K)$ contains for the first time a fixed point or the discontinuity point $p_d$, in the former case of which we are finished. So we assume that $T_{\alpha }^n(K)\cap \varDelta _d=(b,p_d]=:L$, with $f_d<b < p_d$. Note that $T_{\alpha }(L)=[\alpha ,T_{\alpha }(b))\subset [\alpha ,f_d)$. For $T_{\alpha }^2(L)=(T_{\alpha }^2(b),T_{\alpha }(\alpha )]$, we similarly may assume that $f_{d-1}<T_{\alpha }^2(b)<\alpha +1$ (since otherwise $f_{d-1}\in T_{\alpha }^2(L)$, and again we are done).

Now suppose that $T_{\alpha }^3(L)$ contains $p_d$, excluding $f_d \in T_{\alpha }^3(L)$. Then $T_{\alpha }^3(L) = L_1\cup M_1$, with $L_1 = [T_{\alpha }^2(\alpha ),p_d]$ and $M_1=(p_d,T_{\alpha }^3(b))$. First we confine ourselves to $N \in \{18\}\cup \{50,\ldots \} {\setminus } \{95,\ldots ,99\}$. Since then $|T_{\alpha }^3(L)|>2.000376|L|$ (cf. Remark 11), we have certainly $|L_1|>1.001|L|$ or $|M_1|>1.001|L|$. If we consider the images of $L_1$ and $M_1$ under $T_{\alpha }$, $T_{\alpha }^2$ and $T_{\alpha }^3$ similarly as we did with the images of L, we find that due to expansiveness (see the proof of Theorem 3) there must be an m such that $f_d \in T_{\alpha }^{3m}(L_1)$ or $f_{d-1} \in T_{\alpha }^{3m}(M_1)$ and we are finished. If $T_{\alpha }^3(L)$ does not contain $p_d$, the expansion of L will only go on longer, yielding even larger $L_1'$ and $M_1'$ and the reasoning would only be stronger that no gaps can exist.

For $N \in \{4,\ldots ,17,19,20,\ldots ,49,95,96,\ldots ,99\}$ a similar approach can be taken, but there is no useful general lower bound for $|T_{\alpha }'(x)|$ on $I_{\alpha }$. For these cases, however, the moderate expanding power in $\varDelta _{d-1}$ is easily made up for by a relatively strong expanding power in $\varDelta _d$, and the gaplessness is easily, although tediously, checked by hand (cf. Examples 2 and 3 below). This finishes the proof of Theorem 5. $\square$

Example 2

In case $N=7$, there exist $\alpha \in (0,\sqrt{7}-1]$ for which $I_{\alpha }=\varDelta _2\cup \varDelta _1$. The largest $\alpha$ for which $\varUpsilon _{7,\alpha } \in {\mathcal {F}}(2)$ is $\alpha _{\max }=\sqrt{7}-1$, in which case $|T_{\alpha }'(\alpha +1)|=1$. However, $|T_{\alpha }'(f_2)|=2.0938\cdots >2$, and the approach taken above even works due to the expanding power of $T_{\alpha }$ on $[\alpha ,f_2)$ alone.

Example 3

In case $N=99$, we have $I_{\alpha }=\varDelta _4\cup \varDelta _3$, and $\varUpsilon _{99,\alpha } \in {\mathcal {F}}^*$ for $\alpha =99(\sqrt{405}-5)/190=7.8807\cdots$. Then $|T_{\alpha }'(\alpha +1)|=1.2552\cdots$, $|T_{\alpha }'(f_3)|=1.3503\cdots$ and $|T_{\alpha }'(f_4)|=1.4908\cdots$. So for an interval $(p_4,x)$, with $x \in (p_d,f_3)$, assuming that $f_4\not \in T_{\alpha }^3(p_4,x)$, we have $|T_{\alpha }^3(p_4,x)|> 1.3503\cdots \times 1.2552\cdots \times 1.4908\cdots \times |(p_4,x)|\gg 2|(p_4,x)|$, implying enough expanding power for $T_{\alpha }^3$ to exclude the existence of gaps.

Remark 12

We can also prove that $|T_{\alpha }'(x)|>\sqrt{2}$ on $\varDelta _d$ for all arrangements under the assumptions of Theorem 5, but we cannot do without knowledge about the slope on $\varDelta _{d-1}$.

Next we will make preparations for formulating a sufficient condition for gaplessness in case $I_{\alpha }$ consists of three cylinder sets. Proving it involves more subtleties on the one hand, but will have a lot of similarities with the two-cylinder set case on the other hand. Once we have finished that, not much work remains to be done for gaplessness in case $I_{\alpha }$ consists of four or five cylinder sets.

4 A sufficient condition for gaplessness if $I_{\alpha }$ consists of three or four cylinder sets

If $I_{\alpha }=\varDelta _d\cup \ldots \cup \varDelta _{d-m}$, with $m \in \{2,3\}$, there is a sufficient condition for gaplessness that resembles the condition for gaplessness in case $I_{\alpha }$ consists of two cylinder sets a lot:

Theorem 6

Let $I_{\alpha }=\varDelta _d\cup \ldots \cup \varDelta _{d-m}$, with $m\in \{2,3\}$. Then $I_{\alpha }$ is gapless if

$$\begin{aligned} T_{\alpha }(\alpha )\ge f_{d-1}\quad \mathbf{or }\quad T_{\alpha }(\alpha +1)\le f_{d-m+1}. \end{aligned}$$

We will prove this theorem in parts. In Sect. 4.1 we will prove Theorem 6 for $m=2$; in Sect. 4.2 we will extend the result of Sect. 4.1 to $m=3$; considering Theorem 4, extension to larger m is not useful.

Remark 13

The difference between the ‘and’ of Theorem 5 and the ‘or’ of Theorem 6 has to do with the existence, in the latter case, of at least one full cylinder set.

4.1 Gaplessness if $I_{\alpha }$ consists of three cylinder sets

Since we have $m=2$, the condition $T_{\alpha }(\alpha )\ge f_{d-1}$ can be split in

$$\begin{aligned} {\left\{ \begin{array}{ll} 1.&{} T_{\alpha }(\alpha +1)\le f_{d-1} \le T_{\alpha }(\alpha );\\ 2.&{} f_{d-1}\le T_{\alpha }(\alpha ) \le T_{\alpha }(\alpha +1);\\ 3.&{} f_{d-1}\le T_{\alpha }(\alpha +1) \le T_{\alpha }(\alpha ); \end{array}\right. } \end{aligned}$$

(22)

of course the condition $T_{\alpha }(\alpha +1)\le f_{d-1}$ can be split in a similar way. We will prove Theorem 6 by proving gaplessness according to this distinction in three cases, associated with Lemmas 9, 10 and 11 respectively. The first of these is not very hard to prove:

Lemma 9

Let $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}$. If $T_{\alpha }(\alpha )\ge f_{d-1}$ and $T_{\alpha }(\alpha +1)\le f_{d-1}$, then $I_{\alpha }$ is gapless.

Proof of Lemma 9

The assumptions imply that $b(N,\alpha )>2$, yielding $\sigma (\alpha )=|T_{\alpha }'(\alpha +1)|> \sqrt{2}$ for $N\in {\mathbb {N}}_{\ge 17}$. If $N\in {\mathbb {N}}_{\ge 17}$, we let $K\subset I_{\alpha }$ be any open interval. Since K expands under $T_{\alpha }$, there is an $n\in {\mathbb {N}}\cup \{0\}$) such that $T_{\alpha }^n(K)$ contains a fixed point or a discontinuity point $p_{d-i}$ (with $i\in \{0,1\}$) , in the former case of which we are finished. So we assume that $T_{\alpha }^n(K)\supset L$, where $L=(b,p_{d-i}]$, with $f_{d-i}<b < p_{d-i}$, with $i \in \{0,1\}$. If $T_{\alpha }(L)$ contains a fixed point, we are finished. If $T_{\alpha }(L)$ does not contain a fixed point, then it cannot contain a discontinuity point, and we have that $|T_{\alpha }^2(L)|>2|L|$, implying enough expanding power of $T_{\alpha }$ to ensure gaplessness of at least one cylinder set (which might be non-full). Since both $T_{\alpha }(\alpha )\ge f_{d-1}$ and $T_{\alpha }(\alpha +1)\le f_{d-1}$, it follows that $I_{\alpha }$ is gapless. For $2\le N \le 16$ the slopes on $I_{\alpha }$ may differ considerably: for some N, such as $N=7$ and $N=16$ we also have $\sigma >\sqrt{2}$, but if this is not he case, the steepness left of $f_{d-2}$ is amply larger then $\sqrt{2}$; see Fig. 7 for some examples where $\alpha$ is as large as possible. This finishes the proof of Lemma 9 [cf. case 1 in (22)]. $\square$

Fig. 7

Arrangements with largest $\alpha$ such that there is a d with $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}$ under the condition $T_{\alpha }(\alpha )\ge f_{d-1}$ and $T_{\alpha }(\alpha +1)\le f_{d-1}$

If $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}$ under the condition $T_{\alpha }(\alpha )\ge f_{d-1}$ and $T_{\alpha }(\alpha +1) > f_{d-1}$ or under the condition $T_{\alpha }(\alpha ) < f_{d-1}$ and $T_{\alpha }(\alpha +1) \le f_{d-1}$, $I_{\alpha }$ is gapless as well, but this is much harder to prove. The following definition will be convenient:

Definition 4

Let $I_{\alpha }=\varDelta _d\cup \ldots \cup \varDelta _{d-m}$, and $1\le m\le d-1$. If $T_{\alpha }(\alpha )\le f_{d-1}$ or $T_{\alpha }(\alpha +1)\ge f_{d-m+1}$, the cylinder set $\varDelta _d$ respectively $\varDelta _{d-m}$ is called small.

Taking a similar approach as in the proof of Theorem 5, one can show that the map $T_{\alpha }$ has enough expansive power to ensure that for any open interval $K\subset I_{\alpha }$ there exists a non-negative integer n such that $T_{\alpha }^n(K)$ contains a fixed point. If this fixed point is in a non-small or even full cylinder set, we are done (as in the proofs of Theorem 5 and Lemma 9). However, if this fixed point is from the small cylinder set, then it only follows that every point of the small cylinder set is in the orbit under $T_{\alpha }$ of some point in K. Note this implies that the small cylinder set is gapless. So we may assume that the small cylinder set is gapless. Let us assume that the left cylinder set is small. We define $L:=T_{\alpha }(\varDelta _d){\setminus }\varDelta _d$. Since $\varDelta _d$ is gapless, we have $L=(p_d,T(\alpha )]\subset (p_d,f_{d-1})$, so $T_{\alpha }(L)=[T_{\alpha }^2(\alpha ),\alpha +1)$. If $T_{\alpha }^2(\alpha )\le f_{d-2}$, we are finished, so we assume that $T_{\alpha }^2(\alpha ) > f_{d-2}$. We then have $T_{\alpha }^2(L)=(T_{\alpha }(\alpha +1),T_{\alpha }^3(\alpha )]$. If $T_{\alpha }^3(\alpha )\ge f_{d-1}$ we are finished, since then $f_{d-1} \in T_{\alpha }^2(L)$.

The question arises whether it is possible to keep avoiding fixed points if we go on with letting $T_{\alpha }$ work on L and its images (or similarly, if the right cylinder set is small, some interval $R:=T_{\alpha }(\varDelta _1){\setminus }\varDelta _1$). We will argue that this is not possible in the two most plausible cases for gaps to exist, involving the least expansion.

Fig. 8

Arrangements with one very small cylinder

The first case is illustrated with two arrangements in Fig. 8, one where $N=23$ and one where $N=11$. In both arrangements one outer cylinder is very small while the other one is full or almost full. In the arrangement where $N=23$, we see that L is a very narrow strip between $p_5$ and $T_{\alpha }(\alpha )$, $T_{\alpha }^2(L)$ is not so narrow anymore, and $T_{\alpha }^3(L)$ is definitely wide enough to make clear that avoiding fixed points $f_4$ and $f_3$ is not possible. The middle arrangement, where $N=11$, is an example of the case where $\varDelta _{d-2}$ is small and $\varDelta _d$ is actually full. Here we have that $R:=T_{\alpha }(\varDelta _1){\setminus }\varDelta _1$ is a very narrow strip between $T_{\alpha }(\alpha +1)$ and $p_2$ and that $T_{\alpha }^2(R)$ is only slightly larger than $T_{\alpha }(\varDelta _1)$, whence eventually there will be an $n \in {\mathbb {N}}$ such that $f_3 \in T_{\alpha }^n(R)$ or $f_2 \in T_{\alpha }^n(R)$.

The rightmost arrangement in Fig. 8 is an illustration of the second plausible case for the existence of gaps: here $\varDelta _3$ is small, while $\varDelta _1$ is incomplete but not small. This arrangement illustrates the role $p_d$ might play in avoiding fixed points: in this case, taking $L:=T_{\alpha }(\varDelta _3){\setminus }\varDelta _3$, we have $T_{\alpha }^3(L)=M_1\cup M_2$, with $M_1=[T_{\alpha }^4(\alpha ),p_2]$ and $M_2=(p_2,T_{\alpha }^2(\alpha +1)]$. Since $T_{\alpha }^3(L)$ contains a discontinuity point, the expansion under $T_{\alpha }$ is interrupted. If $T_{\alpha }(M_1)$ would be a subset of $T_{\alpha }(\varDelta _3)$ and $T_{\alpha }(M_2)$ would be a subset of $T_{\alpha }(L)$, the expansion would be finished and we would have three gaps: $(T_{\alpha }(\alpha ),T_{\alpha }(\alpha +1))$, $(T_{\alpha }^3(\alpha ),T_{\alpha }^4(\alpha ))$ and $(T_{\alpha }^2(\alpha +1),T_{\alpha }^2(\alpha ))$—but this is not the case, as we will shortly prove.

Of course arrangements exist such that one of the outer cylinders is small, fixed points are avoided (in the sense we used above) for a long time and it takes more of $T_{\alpha }$ working on L or R before one of the discontinuity points is captured. But in these cases the interruption of the expansion is even weaker than in the cases above. We will first show that arrangements such as the rightmost one of Fig. 8 exclude the existence of gaps (cf. Lemma 10) and will then consider cases such as the first two arrangements of Fig. 8 (cf. Lemma 11).

Lemma 10

Let $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}$.Then $I_{\alpha }$ is gapless if

$$\begin{aligned} f_{d-1}\le T_{\alpha }(\alpha ) \le T_{\alpha }(\alpha +1)\quad {\text {or}}\quad T_{\alpha }(\alpha )\le T_{\alpha }(\alpha +1) \le f_{d-1}. \end{aligned}$$

Fig. 9

Arrangement illustrating Lemma 10

Fig. 10

Two arrangements in which almost $T_{\alpha }^2(\alpha )<p_d<T_{\alpha }^4(\alpha +1)$ (in fact, in both cases $p_d = T_{\alpha }^2(\alpha )$)

Fig. 11

The ‘limit graph’ of $T_{\alpha }$, translated over $(-\alpha ,-\alpha )$, under the conditions $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}$ and $N/(N/\alpha -d)-(d-1)=p_d$ for $N\rightarrow \infty$ (and $\alpha , d \rightarrow \infty$ accordingly). This ‘arrangement’ can be seen as one with three cylinders, where $\varDelta _{d-2}\ (\mathrm {mod}\ \alpha )$, the one on the right, is infinitely small; see also the arrangements in Fig. 10

Fig. 12

Arrangements of $\varUpsilon _{N,\alpha }$ with $b=2$; in each case $\alpha = \frac{\sqrt{2N+1}-1}{2}$

Proof of Lemma 10

We will confine ourselves to the first case of this lemma, that is if $f_{d-1}\le T_{\alpha }(\alpha ) \le T_{\alpha }(\alpha +1)$, since the second one is proved similarly (in fact, this case is slightly harder due to the smaller size of the absolute value of the derivatives). Regarding our observations above, we may assume that the small cylinder set (which in this case is $\varDelta _{d-2}$) is gapless (cf. the remarks after Definition 4). We will show that this implies the gaplessness of the other cylinder sets as well. We define $R:=T_{\alpha }(\varDelta _{d-2}){\setminus }\varDelta _{d-2}$ and try to determine $\alpha$ such that $p_d \in T_{\alpha }^3(R)$ (see the remark immediately preceding this lemma). Necessary conditions for this are $T_{\alpha }^2(\alpha )<p_d<T_{\alpha }^4(\alpha +1)$ (assuming that $f_d\not \in T_{\alpha }(R)$ and $f_{d-1}\not \in T_{\alpha }^2(R)$, since in either case we would be done). If these conditions are satisfied, we write $T_{\alpha }^3(R)=V_1\cup V_2$, with $V_1=[T_{\alpha }^2(\alpha ),p_d]$ and $V_2=(p_d,T_{\alpha }^4(\alpha +1)]$. We will show that we cannot have both $T_{\alpha }(V_1)\subset T_{\alpha }(R)$ and $T_{\alpha }(V_2)\subset T_{\alpha }(\varDelta _{d-2})$, which is necessary for limiting the expansion of R under $T_{\alpha }$ and so not eventually capturing $f_d$ and $f_{d-1}$; see Fig. 9.

We take an approach that is similar to the proof of Theorem 5, for which several lemmas and a proposition where used, partially concerning a relation between N and d in the arrangements involved, partially concerning the slope in $\alpha +1$. In this proof we will not explicitly formulate similar statements as lemmas or propositions, nor do we prove them, since they require similar basic but very intricate calculations that we prefer to omit.

In order to find the relationship between N and d for arrangements with the conditions $T_{\alpha }^2(\alpha )<p_d$ and $T_{\alpha }^4(\alpha +1)>p_d$ mentioned above, we refer to some more relevant arrangements, as shown in Fig. 10. In both cases in Fig. 10, $\alpha$ is such that $T_{\alpha }^2(\alpha )=p_d$, which is a value of $\alpha$ that is only a little larger than the values for which $T_{\alpha }^2(\alpha )<p_d$ and $T_{\alpha }^4(\alpha +1)>p_d$. A ‘limit arrangement’ (where the third, rightmost cylinder is infinitely small), similar to the ‘limit arrangement’ used in the proof of Theorem 5, is shown in Fig. 11. The assumptions yield $a^3+a^2-1=0$, with real root $a=0.75487\cdots =:\gamma$.

Similar to the proof of Theorem 5 we then find that for arrangements as in Fig. 10 we have

$$\begin{aligned} N\approx \frac{(d-1)(d-1+\gamma )(1+\gamma )}{\gamma ^2}. \end{aligned}$$

Using this relationship, we can take a similar approach as in the proof of Proposition 1. We leave out the tedious steps and confine ourselves to observing that the slope of the line segments in Fig. 11 is $-(\gamma +1)=-1.75487\cdots$ and that in arrangements where $T_{\alpha }^2(\alpha )<p_d$ and $T_{\alpha }^4(\alpha +1)>p_d$, we will see that the slope $T_{\alpha }'(\alpha +1)$ approaches $-(\gamma +1)$ as N tends to infinity. However, for our proof the inequality $|T_{\alpha }'(\alpha +1)|>\frac{1}{2}(\sqrt{5}+1)=1.61803\cdots =:G$ suffices, which turns out to hold for $N\in {\mathbb {N}}_{\ge 273}$. We will use this to show that for $N\in {\mathbb {N}}_{\ge 273}$ we have $|T_{\alpha }^3(R)| > |T_{\alpha }(\varDelta _{d-2})|+|T_{\alpha }(R)|$. From this it immediately follows that we cannot have that both $T_{\alpha }(V_1)\subset T_{\alpha }(R)$ and $T_{\alpha }(V_2)\subset T_{\alpha }(\varDelta _{d-2})$, and we are done with the proof of Lemma 11.

Since $|T_{\alpha }'(x)|$ is a decreasing function on $I_{\alpha }$, and writing $\beta :=|\varDelta _{d-2}|$, we have

$$\begin{aligned} |T_{\alpha }(\varDelta _{d-2})|>|T_{\alpha }'(\alpha +1)|\cdot \beta ,\quad {\text {so}}\quad |R|>(|T_{\alpha }'(\alpha +1)|-1)\beta . \end{aligned}$$

It follows that

$$\begin{aligned} |T_{\alpha }(R)|>(|T_{\alpha }'(\alpha +1)|-1)\cdot |T_{\alpha }'(p_{d-1})|\beta , \end{aligned}$$

that

$$\begin{aligned} |T_{\alpha }^2(R)|>(|T_{\alpha }'(\alpha +1)|-1)\cdot |T_{\alpha }'(p_{d-1})|\cdot |T_{\alpha }'(f_d)|\beta , \end{aligned}$$

and finally that

$$\begin{aligned} |T_{\alpha }^3(R)|>(|T_{\alpha }'(\alpha +1)|-1)\cdot |T_{\alpha }'(p_{d-1})|^2\cdot |T_{\alpha }'(f_d)|\beta . \end{aligned}$$

We also have $|T_{\alpha }(\varDelta _{d-2})|<|T_{\alpha }'(p_{d-1})|\beta$, so

$$\begin{aligned} |R|<(|T_{\alpha }'(p_{d-1})|-1)\beta \quad {\text {and}}\quad |T_{\alpha }(R)|<|T_{\alpha }'(f_{d-1})|\cdot (|T_{\alpha }'(p_{d-1})|-1)\beta . \end{aligned}$$

It follows that

$$\begin{aligned} |T_{\alpha }(\varDelta _{d-2})|+|T_{\alpha }(R)|&<(|T_{\alpha }'(p_{d-1})|+|T_{\alpha }'(f_{d-1})|\cdot (|T_{\alpha }'(p_{d-1})|-1))\beta \\&=(|T_{\alpha }'(p_{d-1})|-|T_{\alpha }'(f_{d-1})|+|T_{\alpha }'(f_{d-1})|\cdot |T_{\alpha }'(p_{d-1})|)\beta \\&<|T_{\alpha }'(f_{d-1})|\cdot |T_{\alpha }'(p_{d-1})|\beta . \end{aligned}$$

So, although crudely, we certainly have that $|T_{\alpha }^3(R)| > |T_{\alpha }(\varDelta _{d-2})|+|T_{\alpha }(R)|$ if

$$\begin{aligned} |T_{\alpha }'(f_{d-1})|\cdot |T_{\alpha }'(p_{d-1})|<(|T_{\alpha }'(\alpha +1)|-1)\cdot |T_{\alpha }'(p_{d-1})|^2\cdot |T_{\alpha }'(f_d)|, \end{aligned}$$

that is, if

$$\begin{aligned} 1<(|T_{\alpha }'(\alpha +1)|-1)\cdot |T_{\alpha }'(p_{d-1})|\cdot \frac{|T_{\alpha }'(f_d)|}{|T_{\alpha }'(f_{d-1})|}. \end{aligned}$$

(23)

Since

$$\begin{aligned} (|T_{\alpha }'(\alpha +1)|-1)\cdot |T_{\alpha }'(p_{d-1})|\cdot \frac{|T_{\alpha }'(f_d)|}{|T_{\alpha }'(f_{d-1})|}> & {} (|T_{\alpha }'(\alpha +1)|-1)\cdot |T_{\alpha }'(p_{d-1})|\\> & {} (|T_{\alpha }'(\alpha +1)|-1)\cdot |T_{\alpha }'(\alpha +1)|, \end{aligned}$$

we know that (23) holds for $|T_{\alpha }'(\alpha +1)|>G$, which in turn holds for all $N\in {\mathbb {N}}_{\ge 273}$. We remark that this value is quite a wide upper bound, since we did a rough approximation. Still, checking that we cannot have both $T_{\alpha }(V_1)\subset T_{\alpha }(R)$ and $T_{\alpha }(V_2)\subset T_{\alpha }(\varDelta _{d-2})$ for smaller N is not that hard and is left to the reader. This finishes the proof of Lemma 10 [cf. case 2 in (22)].$\square$

Lemma 10 implies that in case $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}$ and $f_{d-1}\le T_{\alpha }(\alpha ) \le T_{\alpha }(\alpha +1)\,\,{\text {or}}\,\,T_{\alpha }(\alpha )\le T_{\alpha }(\alpha +1) \le f_{d-1}$ the division of an interval containing $p_d$ in two smaller ones cannot prevent an overall expansion that excludes any gaps. The other plausible case with three cylinder sets in which gaps might exist is if one outer cylinder set is very small, while the other one is full or nearly full, such that either $T_{\alpha }^3(\alpha +1)\ge T_{\alpha }(\alpha +1)$ (if $\varDelta _{d-2}$ is the small cylinder set) or $T_{\alpha }^3(\alpha )\le T_{\alpha }(\alpha )$ (if $\varDelta _d$ is the small cylinder set). We will show that this is not possible either:

Lemma 11

Let $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}$. Then $I_{\alpha }$ is gapless if

$$\begin{aligned} f_{d-1}\le T_{\alpha }(\alpha +1)\le T_{\alpha }(\alpha )\quad {\text {or}}\quad T_{\alpha }(\alpha +1)\le T_{\alpha }(\alpha )\le f_{d-1}. \end{aligned}$$

Proof of Lemma 11

Taking into account our observations immediately following Definition 4 and the arrangements of Fig. 8 for $N=23$ and $N=11$, we only have to prove that there are no $\alpha$ such that $T_{\alpha }^3(\alpha )<T_{\alpha }(\alpha )$ is possible if $T_{\alpha }(\alpha +1)\le T_{\alpha }(\alpha )\le f_{d-1}$ (in case $\varDelta _d$ is small) or such that $T_{\alpha }^3(\alpha +1)>T_{\alpha }(\alpha +1)$ is possible if $f_{d-1}\le T_{\alpha }(\alpha +1)\le T_{\alpha }(\alpha )$ (in case $\varDelta _{d-2}$ is small). Note that the conditions $T_{\alpha }^3(\alpha )<T_{\alpha }(\alpha )$ and $T_{\alpha }^3(\alpha +1)>T_{\alpha }(\alpha +1)$ imply that the branch number is slightly larger than 2. Now remember that $I_{\alpha }$ consists of m full cylinder sets if and only if $\alpha =k$, $N=mk(k+1)$ and $d=(m-1)(k+1)$ for some $k \in {\mathbb {N}}$, cf. Theorem 1. Figure 12 shows for increasing values of N a sequence of arrangements where the branch number b is 2, from one full arrangement (here for $N=4$) with two cylinders to the next one (here for $N=12$). Since $|T_{\alpha }'(\alpha )|>|T_{\alpha }'(\alpha +1)|$, the arrangements suggest that in case b is slightly larger than 2, the most favourable arrangement for $T_{\alpha }^3(\alpha +1)= T_{\alpha }(\alpha +1)$ to have real roots is if $N=2k^2+2k-1$, where $k\in {\mathbb {N}}_{\ge 2}$, while for $T_{\alpha }^3(\alpha )= T_{\alpha }(\alpha )$ to have real roots is if $N=2k^2+2k+1$, where $k\in {\mathbb {N}}$. We will confine ourselves to investigating only the possibility of $T_{\alpha }^3(\alpha +1)= T_{\alpha }(\alpha +1)$; the calculations for the other case are similar.

So we will try and find out if for $N=2k^2+2k-1$, $d=k+1$, with $k\in {\mathbb {N}}_{\ge 2}$, the positive root of $T_{\alpha }^3(\alpha +1)= T_{\alpha }(\alpha +1)$ lies in $I_{\alpha }$. To do this, we solve

$$\begin{aligned} \frac{2k^2+2k-1}{\frac{\displaystyle 2k^2+2k-1}{\displaystyle \frac{2k^2+2k-1}{\alpha +1}-(k-1)}-k}-(k+1)=\frac{2k^2+2k-1}{\alpha +1}-(k-1), \end{aligned}$$

which is reducible to

$$\begin{aligned} (2k^3+6k^2-k-1)\alpha ^2+(2k^4+5k^2+k-2)\alpha -(4k^5+6k^4+2k^3-3k^2-k+1)=0, \end{aligned}$$

yielding

$$\begin{aligned} \alpha =\frac{\sqrt{36k^8+144k^7+164k^6-12k^5-95k^4-2k^3+21k^2-4k}-(2k^4+5k^2+k-2)}{2(2k^3+6k^2-k-1)}. \end{aligned}$$

(24)

A straightforward computation shows that this last expression is smaller than $f_{k+2}$, meaning that the root (24) lies outside $I_{\alpha }$ if $I_{\alpha }=\varDelta _{k+1}\cup \varDelta _k\cup \varDelta _{k-1}$. Since $N=2k^2+2k-1$ was the most favourable option for investigation, this finishes our proof [cf. case 3 in (22)].$\square$

Remark 14

The arrangement for $N=11$ in Fig. 8 illustrates that the difference between $T_{\alpha }^3(\alpha +1)$ and $T_{\alpha }(\alpha +1)$ may be very small.

4.2 A sufficient condition for gaplessness in case $I_{\alpha }$ consists of four cylinder sets

In the previous subsection we proved Theorem 6 for $m=2$, by proving Lemmas 9, 10 and 11. In this subsection we will consider $m=3$ and go into the analogons of Lemmas 9, 10 and 11.

If $I_{\alpha }$ consists of four cylinder sets, the analogon of Lemma 9 is that arrangements $I_{\alpha }$ are gapless if $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}\cup \varDelta _{d-3}$ while $T_{\alpha }(\alpha )\ge f_{d-1}$ and $T_{\alpha }(\alpha +1)\le f_{d-2}$. The analogon of Lemma 11 is that arrangements $I_{\alpha }$ are gapless if $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}\cup \varDelta _{d-3}$ while $f_{d-2}\le T_{\alpha }(\alpha +1)\le T_{\alpha }(\alpha )\,\,\mathbf{or }\,\,T_{\alpha }(\alpha +1)\le T_{\alpha }(\alpha )\le f_{d-1}$. In both cases branch numbers larger than 3 are involved, in which case $|T_{\alpha }'(\alpha +1)|>2$ if $N\in {\mathbb {N}}_{\ge 18}$ (and Theorem 3 yields the desired result). The cases $2\le N\le 17$ can be checked manually and are left to the reader; in Fig. 13 the arrangement for $N=11$, associated with Lemma 11, illustrates that gaps are out of the question.

The analogon of Lemma 10 is that arrangements $I_{\alpha }$ are gapless if $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}\cup \varDelta _{d-3}$ while $f_{d-1}\le T_{\alpha }(\alpha ) \le T_{\alpha }(\alpha +1)\,\,\mathbf{or} \,\,T_{\alpha }(\alpha )\le T_{\alpha }(\alpha +1) \le f_{d-2}$. The arrangements for $N=15$, $N=24$ and $N=35$ in Fig. 13 are interesting illustrations of the analogon of Lemma 10 in the case of two full cylinder sets instead of one. We will confine ourselves to the arrangement for $N=15$; the other ones have similar properties.

The arrangement for $N=15$ is the boundary case for the situation where we have four cylinders, the left one of which (that would be $\varDelta _6$ in this example) is extremely small and the right one is such that almost $p_5\in T_{\alpha }^2(T_{\alpha }(\varDelta _6){\setminus }\varDelta _6)$. The interesting thing is that this option would imply a quick interruption of the expansion of $T_{\alpha }(\varDelta _6){\setminus }\varDelta _6$, involving two large gaps. But it is not really an option: the arrangement for $N=15$ in Fig. 13 is exceptional among relatively small N (as well as the arrangements for $N=24$ and $N=35$ are), while for $N>36$ we have $|T_{\alpha }'(\alpha +1)|>2$ if $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\varDelta _{d-2}$ and $N/(\alpha +1)-(d-2)=p_d$ or $N/\alpha -d=p_d$. We derived this in a similar way as in the proof of Lemma 10 (see Fig. 11) or the preparations for Theorem 5 (see Fig. 6). Figure 14 shows the associated ‘limit graph’, from which it is easily found that $a=\frac{1}{2}(3-\sqrt{5})$, yielding branch number $2+g$, with $g=1/G$ the small golden section.

With this, we conclude the proof of Theorem 6. $\square$

In the next section we will prove that if $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}\cup \varDelta _{d-3}$ gaps exist only in very rare cases and if they do, that they are very large. After that, we will finish the proof of Theorem 4, stating that all arrangements with five cylinders are gapless.

Fig. 13

Four arrangements with two full cylinders

Fig. 14

The ‘limit graph’ of $T_{\alpha }$, translated over $(-\alpha ,-\alpha )$, under the conditions $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\varDelta _{d-2}$ and $N/(\alpha +1)-(d-2)=p_d$ for $N\rightarrow \infty$ (and $\alpha , d \rightarrow \infty$ accordingly)

5 Gaplessness in case $I_{\alpha }$ contains two full cylinder sets

If an arrangement contains three cylinders, and two of them are full, the arrangement is gapless according to Theorem 6. In this section we will proof that arrangements of four cylinders generally do not contain a gap either, save for special values of N. The core of this proof rests on values of $\alpha$ satisfying one of the equations

$$\begin{aligned} T_{\alpha }(\alpha )=T_{\alpha }^3(\alpha )\,\,{(\text {with root}\,\alpha _{\ell })}\,\, {\text {and}}\,\, T_{\alpha }(\alpha +1)=T_{\alpha }^3(\alpha +1)\,\,{\text {(with root}\, \alpha _u)}. \end{aligned}$$

We will show that for N such that $\alpha _{\ell }<\alpha _u$ very large gaps exist for $\alpha \in [\alpha _{\ell },\alpha _u]$.

The central theorem of this section is the following:

Theorem 7

Let $N \in {\mathbb {N}}_{\ge 2}$ and $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}\cup \varDelta _{d-3}$. Then there is a gap in $I_{\alpha }$ if and only if $N=2k^2+2k-i$, with $k > 1$ and $i \in \{1,2,3\}$. Moreover, if there is a gap in $I_{\alpha }$, the gap contains $f_{d-1}$ and $f_{d-2}$, while $\varDelta _d$ and $\varDelta _{d-3}$ are gapless.

Proof of Theorem 7

Suppose that there is a gap containing $f_{d-1}$ and $f_{d-2}$ in $I_{\alpha }$ and that $\varDelta _d$ and $\varDelta _{d-3}$ are gapless. Then, as a sub-interval of a gap, the interval $(f_{d-1},f_{d-2})$ is a gap. Since $f_{d-1}<f_{d-2}$, $N/(f_{d-1}+d-1)=f_{d-1}$ and $N/(f_{d-2}+d-2)=f_{d-2}$, we know that

$$\begin{aligned} (f_{d-1},f_{d-2}) \subsetneq \left( \frac{N}{f_{d-2}+d-1},\frac{N}{f_{d-1}+d-2}\right) , \end{aligned}$$

where the larger open interval is a gap as well. What is more, the infinite sequence of intervals

$$\begin{aligned} (f_{d-1},f_{d-2})&\subsetneq&\left( \frac{N}{f_{d-2}+d-1},\frac{N}{f_{d-1}+d-2}\right) \\&\subsetneq&\left( \frac{N}{\frac{N}{f_{d-1}+d-2}+d-1} ,\frac{N}{\frac{N}{f_{d-2}+d-1}+d-2}\right) \subsetneq \cdots \end{aligned}$$

consists of the union of $(f_{d-1},f_{d-2})$ with pre-images of $(f_{d-1},f_{d-2})$ in $\varDelta _{d-1}$ and $\varDelta _{d-2}$ respectively and therefore of gaps containing $f_{d-1}$ and $f_{d-2}$. It is contained in the closed interval [q, r], with

$$\begin{aligned} q=[\overline{d-1,d-2}]_{N,\alpha }\in \varDelta _{d-1} \quad {\text {and}} \quad r=[\overline{d-2,d-1}]_{N,\alpha }\in \varDelta _{d-2}, \end{aligned}$$

yielding

$$\begin{aligned} T_{\alpha }^2(q)=q, \quad T_{\alpha }(q)=r,\quad T_{\alpha }(r)=q\quad {\text {and}}\quad T_{\alpha }^2(r) =r. \end{aligned}$$

(25)

Since $\varDelta _d$ and $\varDelta _{d-3}$ are gapless, $T_{\alpha }(\alpha )$ and $T_{\alpha }(\alpha +1)$ lie outside the interval (q, r), which is to say

$$\begin{aligned} p_d<T_{\alpha }(\alpha )\le q\quad {\text {and}}\quad r\le T_{\alpha }(\alpha +1)<p_{d-2}. \end{aligned}$$

For the images of $\alpha$ under $T_{\alpha }$ this means that either $T_{\alpha }^2(\alpha )\in \varDelta _{d-3}$ or $T_{\alpha }^2(\alpha )\in \varDelta _{d-2}$, in the latter case of which we have, due to the expansiveness of $T_{\alpha }$ and the equalities of (25),

$$\begin{aligned} |T_{\alpha }(\alpha )-q| \le |T_{\alpha }^2(\alpha ) - r|\le |T_{\alpha }^3(\alpha ) - q|, \end{aligned}$$

with equalities only in the case $T_{\alpha }(\alpha )=q$. From this we derive that

$$\begin{aligned} {\text {either}}\,\, T_{\alpha }^2(\alpha )\in \varDelta _{d-3}\quad {\text {or}}\quad T_{\alpha }^2(\alpha )\in \varDelta _{d-2}\wedge T_{\alpha }^3(\alpha ) \le T_{\alpha }(\alpha ) \end{aligned}$$

(26)

and, similarly, that

$$\begin{aligned} {\text {either}}\,\, T_{\alpha }^2(\alpha +1)\in \varDelta _d\quad {\text {or}}\quad T_{\alpha }^2(\alpha +1)\in \varDelta _{d-1}\wedge T_{\alpha }^3(\alpha +1) \ge T_{\alpha }(\alpha +1). \end{aligned}$$

(27)

In the following we will write $\alpha _u(N,m)$ (u for ‘upper’) for the positive root of the equation $T_{\alpha }^3(\alpha +1) = T_{\alpha }(\alpha +1)$ (so $T_{\alpha }(\alpha +1)=r$) and $\alpha _{\ell }(N,m)$ (l for ‘lower’) for the positive root of the equation $T_{\alpha }^3(\alpha ) = T_{\alpha }(\alpha )$ (so $T_{\alpha }(\alpha )=q$), with m the number of full cylinder sets; in the current case we have $m=2$. Recall that $I_{\alpha }$ consists of m full cylinder sets if and only if $\alpha =k$, $N=mk(k+1)$ and $d=(m-1)(k+1)$ for some $k \in {\mathbb {N}}$, cf. Theorem 1, so if $m=2$, we have arrangements consisting of two full arrangements only for $\alpha =k$, $N=2k(k+1)$ and $d=k+1$. If N is $2k(k+1)-n$, with $n \in {\mathbb {N}}$, and $\alpha =k-x$, with $x\in {\mathbb {R}}$, we have

$$\begin{aligned} b(N,\alpha )=\frac{2k^2+2k-n}{(k-x)(k+1-x)}=2+\frac{4xk-n+2x-2x^2}{(k-1)(k+1-x)}>2+\frac{4xk-n}{k^2+x^2}, \end{aligned}$$

which is a little bit larger than 2 provided x and n are relatively small. For these arrangements we have

$$\begin{aligned} d(\alpha )=\left\lfloor \frac{2k^2+2k-n}{k-x}-(k-x)\right\rfloor =\left\lfloor k+2+3x+\frac{2x^2+2x-n}{k-x}\right\rfloor =k+2 \end{aligned}$$

and

$$\begin{aligned} d(\alpha +1)= & {} \left\lfloor \frac{2k^2+2k-n}{k+1-x}-(k+1-x)\right\rfloor =\left\lfloor k-1+3x+\frac{2x^2+2x-n}{k+1-x}\right\rfloor \\= & {} k-1. \end{aligned}$$

So, for x and n relatively small, the arrangements consist of four cylinders, while the branch number is only a little bit larger than 2. We will now use this to finish the forward implication of Theorem 7.

Since $\varDelta _{d-3}$ decreases and $\varDelta _d$ increases as $\alpha$ decreases, we see that the assumption that there is a gap containing $f_{d-1}$ and $f_{d-2}$ in $I_{\alpha }$ implies $\alpha _u(N,2)\ge \alpha _{\ell }(N,2)$. We will shortly show that the only values of N for which $\alpha _u(N,2)\ge \alpha _{\ell }(N,2)$ are $N=2k^2+2k-i$, with $k > 1$ and $i \in \{1,2,3\}$; in all cases $d=k+2$. Although we could keep i as a variable in our calculations, we can limit ourselves to the case $i=3$, since $i=3$ is the least favourable value of i allowing for a gap, as is suggested⁶ in Figs. 12, 15, 16, 17 and 18. We will show that for $i=3$ indeed $\alpha _u(N,2)\ge \alpha _{\ell }(N,2)$. Subsequently we will show that for $4\le i\le 4k$ no gaps exist; the upper bound is 4k, since $2k^2+2k-4k=2(k-1)^2+2(k-1)$, so as to confine the calculations to the group of arrangements where $d=k+2$.

Fig. 15

Arrangement with $N=11,\alpha =1.8719$

Fig. 16

Arrangement with $N=11,\alpha =1.8687$

So, let $N=2k^2+2k-3$ and $d=k+2$. Then $\alpha _{\ell }(N,2) = [k+2,\overline{k+1,k}]$ and $\alpha _u(N,2)+1= [k-1,\overline{k,k+1}]$.⁷ Omitting straightforward calculations, we find that

$$\begin{aligned} \alpha _u(2k^2+2k-3,2)=\frac{(2k^2+2k-3)\sqrt{D}-(2k^4+3k^2+3k-6)}{4k^3+12k^2-6k-6} \end{aligned}$$

and

$$\begin{aligned} \alpha _{\ell }(2k^2+2k-3,2)=\frac{(2k^2+2k-3)(\sqrt{D}-(k^2+5k+4))}{4k^3-18k-8}, \end{aligned}$$

with

$$\begin{aligned} D=9k^4 + 18k^3 -3k^2 - 12k=(3k^2+3k-2)^2-4. \end{aligned}$$

Since we assume that there is a gap containing $f_{d-1}$ and $f_{d-2}$, we have $\alpha _u\ge \alpha _{\ell }$. Omitting the basic calculations, we find that this inequality holds for $k\in {\mathbb {N}}_{\ge 2}$. In the case $k=3$ (and so $N=21$), we have indeed

$$\begin{aligned} \alpha _u(2k^2+2k-3,2)= & {} \frac{\sqrt{508032}-192}{192}=2.7123\cdots >2.7122\cdots \\= & {} \frac{\sqrt{508032}-588}{46}=\alpha _{\ell }(2k^2+2k-3,2); \end{aligned}$$

see Fig. 19.

Some more basic calculations show that the cases $N=2k^2+2k-1$ and $N=2k^2+2k-2$ allow for larger intervals $[\alpha _{\ell },\alpha _u]$ where large gaps exist; see the next examples.

$$\begin{aligned}&\alpha _u(11,2)=\frac{\sqrt{9075}-26}{37}=1.8719\cdots \quad {\text {and}} \quad \alpha _{\ell }(11,2)=\frac{99-\sqrt{9075}}{2}=1.8686\cdots \\&\alpha _u(10,2)=\frac{\sqrt{1725}-12}{17}=1.7372\cdots \quad {\text {and}} \quad \alpha _{\ell }(10,2)=\frac{45-\sqrt{1725}}{2}=1.7334\cdots \\&\alpha _u(9,2)=\frac{\sqrt{5103}-22}{31}=1.5946\cdots \quad {\text {and}} \quad \alpha _{\ell }(9,2)=\frac{27-\sqrt{567}}{2}=1.5941\cdots \\&\alpha _u(8,2)=\frac{\sqrt{228}-5}{7}=1.4428\cdots \quad {\text {and}} \quad \alpha _{\ell }(8,2)=9-\sqrt{57}=1.4501\cdots \end{aligned}$$

We see that the intervals $\alpha _u-\alpha _{\ell }$ decrease as N decreases, until (for $N=8$) the ‘interval’ would have negative length, hence does not exist.

Fig. 17

Arrangement with $N=10,\alpha =1.7372$

Fig. 18

Arrangement with $N=9,\alpha =1.5946$

Now suppose $N=2k^2+2k-4$ (note that voor $k=2$ we have $N=8$). Then

$$\begin{aligned} \alpha _u(2k^2+2k-4,2)=\frac{(k+2)\sqrt{D}-(k^3+k^2+2k+4)}{2(k^2+4k+2)} \end{aligned}$$

and

$$\begin{aligned} \alpha _{\ell }(2k^2+2k-4,2)=\frac{(k-1)\sqrt{D}-(k^3+4k^2-k-4)}{2(k^2-2k-1)}, \end{aligned}$$

with

$$\begin{aligned} D=9k^4+18k^3-7k^2-16k. \end{aligned}$$

There are no gaps provided $\alpha _{\ell }(2k^2+2k-4,2)-\alpha _u(2k^2+2k-4,2)>0$. Once more we omit the calculations, finding that this inequality holds for $k\in {\mathbb {N}}_{\ge 2}$, so we conclude that there are no gaps in case $N=2k^2+2k-4$. If we replace the number 4 in $N=2k^2+2k-4$ by larger integers (if possible), there will not be any gaps either: the length of the ‘interval’ $[\alpha _{\ell },\alpha _u]$ would only become more negative. This concludes the proof that if $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}\cup \varDelta _{d-3}$ and there is a gap containing $f_{d-1}$ and $f_{d-2}$ in $I_{\alpha }$, then $N=2k^2+2k-i$, with $k > 1$ and $i \in \{1,2,3\}$.

Fig. 19

Arrangement with $N=21,\alpha =2.7123$

Fig. 20

Arrangement with $N=20,\alpha =2.6124$

For the converse statement, we assume that $N = 2k^2 + 2k - i$, with $k \in {\mathbb {N}}$ and $i \in \{1, 2, 3\}$. If also $d=k+2$, then earlier in this proof we showed that only then $\alpha _{\ell }(N,2) \le \alpha _u(N,2)$. We will show that for $\alpha$ such that $\alpha _{\ell }(N,2) \le \alpha \le \alpha _u(N,2)$ there is a gap in $I_{\alpha }=\varDelta _d\cup \varDelta _{d-1}\cup \varDelta _{d-2}\cup \varDelta _{d-3}$ containing both $f_{d-1}$ and $f_{d-2}$.

As earlier in this proof, we set

$$\begin{aligned} q = [\overline{d-1,\, d-2} ]_{N,\alpha } \quad \text {and}\quad r = [\overline{d-2,\, d-1}]_{N,\alpha }. \end{aligned}$$

Set $G=(q,r)$, then clearly both $f_{d-1}\in G$ and $f_{d-2}\in G$. Furthermore, by definition of $\alpha _{\ell }(N,2)$ and $\alpha _u(N,2)$ we have that for every $\alpha \in [\alpha _{\ell }(N,2), \, \alpha _u(N,2)]$ that

$$\begin{aligned} T_{\alpha }(\alpha )\le q\quad (\text {and therefore}\; T_{\alpha }^2(\alpha )\ge r) \end{aligned}$$

and that

$$\begin{aligned} T_{\alpha }(\alpha +1)\ge r\quad (\text {and therefore}\; T_{\alpha }^2(\alpha +1)\le q). \end{aligned}$$

Note that $T_{\alpha }((p_d,q))= (r, \alpha +1)$ and that $T_{\alpha }((r,p_{d-2})) = (\alpha , q)$. Then we have that $T_{\alpha }(G^c) = G^c$, where $G^c$ is the complement of G in $I_{\alpha }$. We are left to show that $G=(q,r)$ is a gap; i.e. that for almost all $x\in G$ there exists an $n=n(x)$ such that $T_{\alpha }^n(x)\in G^c$.

To show this, consider the map $T:I_{\alpha }\rightarrow I_{\alpha }$, defined by

$$\begin{aligned} T(x) = {\left\{ \begin{array}{ll} \frac{-x}{p_d-\alpha } + \frac{(\alpha +1)p_d - \alpha ^2}{p_d-\alpha }, &{} \hbox {if}\; x\in \varDelta _{d}; \\ \frac{N}{x} - (d-1), &{} \hbox {if}\; x\in \varDelta _{d-1}; \\ \frac{N}{x} - (d-2), &{} \hbox {if}\; x\in \varDelta _{d-2}; \\ \frac{-x}{\alpha + 1 - p_{d-2}} + \frac{(\alpha +1)^2 - \alpha p_{d-2}}{\alpha +1 - p_{d-2}}, &{} \hbox {if}\; x\in \varDelta _{d-3}. \end{array}\right. } \end{aligned}$$

(28)

So on $\varDelta _d$ and on $\varDelta _{d-3}$ we have that T is a straight line segment with negative slope, through $(\alpha ,\alpha +1)$ and $(p_d,\alpha )$ on $\varDelta _d$, resp. through $(p_{d-2},\alpha +1)$ and $(\alpha +1, \alpha )$ on $\varDelta _{d-3}$. For $x\in \varDelta _{d-1}\cup \varDelta _{d-2}$ we have that $T(x) = T_{\alpha }(x)$. To show that G is a gap, it is enough to show the ergodicity of T. Then the maximality of G follows from the fact that the support of the absolutely continuous invariant measure is $G^c$, since $T_{\alpha }(G^c) = G^c$. The proof of the existence of the absolutely continuous invariant measure for T and its ergodicity is similar to the proof of Theorem 2. Here all branches are complete and the proof is rather simpler. Once we have the ergodicity of T, it is obvious that for a.e. $x \in G$ there exists $n_{0}=n_{0}(x)$ such that $z=T^{n_0}(x) \in G^c$. Then z never returns in G under iterations of $T_{\alpha }$. This finishes the proof of Theorem 7. $\square$

We stress that the in case of $N=2k^2+2k-3$ the intervals $[\alpha _{\ell },\alpha _u]$ on which gaps exist may be very small; see Fig. 19. On the other hand, in case $N=2k^2+2k-4$, the gaplessness may be a very close call; see Fig. 20. Table 1 illustrates how fast these differences between $\alpha _{\ell }$ and $\alpha _u$ decrease as N increases:

Table 1 The thin thread between having a gap or not

Remark 15

While a fixed point $f_i$ is repellent for points within $\varDelta _i$, the fixed points in two adjacent cylinder sets behave mutually contracting for all other points in these cylinder sets. As a consequence, it may take quite some time before the orbit of points in the full cylinders of gap arrangements with four cylinders leave these full cylinders for the first time. As an example we take the gap arrangement for $k=50$ (according to the notations used above). Then $N=2\cdot 50^2+2\cdot 50-3=5097$, $d=52$ and $\alpha \approx \alpha _u\approx \alpha _{\ell }\approx 49.98019737$. Table 2 shows for ten values of x between $\alpha$ and $\alpha +1$ the smallest n such that $T_{\alpha }^n(x)\not \in \varDelta _{51}\cup \varDelta _{50}$. What is more, there are uncountably many x in the gap (a, b) that contains $f_{d-1}$ and $f_{d-2}$ such that $T_{\alpha }^n(x)\in (a,b)$ for all $n\in {\mathbb {N}}\cup \{0\}$. Indeed, for any sequence $(d_1,d_2,\ldots ,d_n,\ldots )$ such that $d_n\in \{d-1,d-2\}$, with $n\in {\mathbb {N}}$, we have that $x=[d_1,d_2,d_3,\ldots ]_{N, \alpha }\in (a,b)$.

Table 2 The difficulty of leaving the gap: with $N=5097$, $\alpha =49.98019737$, for each of ten values of $x \in [\alpha ,\alpha +1]$ the smallest n is given such that $T_{\alpha }^n(x)\not \in \varDelta _{51}\cup \varDelta _{50}$

For the final, second part of the proof of Theorem 4, we will consider one by one all cases left, that is $N \in \{2,\ldots ,11\}$. If $N=11$ and $\alpha \ge f_7$, $I_{\alpha }$ consists of five cylinder sets if and only if $\alpha \in (f_2-1,f_6)$; see the left arrangement of Fig. 21, which we already saw in Fig. 13. Since $\alpha _{\ell }(11,3)>\alpha _u(11,3)$ (cf. page 5), we conclude on similar grounds as in the proof of Theorem 7, that the arrangement is gapless. If $\alpha \in [f_7,f_2-1]$, the interval $I_{\alpha }$ consists of four cylinder sets, implying gaplessness because of Theorem 7. Since $|T_{\alpha }'(f_7+1)|=2.04\cdots$, gaps are also excluded for all $\alpha \le f_7$. A similar approach works for $N=10$ (with $|T_{\alpha }'(f_7+1)|=2.03\cdots$), $N=9$ (with $|T_{\alpha }'(f_7+1)|=2.02\cdots$) and even $N=8$, in which case $f_7=1$, $|T_{\alpha }'(f_7+1)|=2$, and the arrangement with four cylinders is full.

For $N \in \{3,\ldots ,7\}$ we take a different approach, confining ourselves to the case $N=7$; the cases $N \in \{3,\ldots ,6\}$ are done similarly. We will omit most calculations, which are generally quite tedious and do hardly elucidate anything. So let $N=7$. Then $I_{\alpha }$ consists of at least five cylinder sets if and only if $\alpha <f_6$; see the second arrangement of Fig. 21. We have $|T_{\alpha }'(\alpha +1)|=2$ for $\alpha =\frac{1}{2}\sqrt{14}-1$, in which case $d_{\min }=2$; see the third arrangement of Fig. 21. Now suppose $\frac{1}{2}\sqrt{14}-1\le \alpha <f_6=1$. We have $|T_{\alpha }'(f_6+1)|=\frac{7}{4}$ and $|T_{\alpha }'(\alpha )|>7$. Regarding these relatively large values, it is not hard to understand that $\varDelta _2$ is gapless. The part of the orbit of $\alpha +1$ under $T_{\alpha }$ in the third arrangement of Fig. 21 illustrates that even in the case of $\alpha =\frac{1}{2}\sqrt{14}$, the expansion of $[T_{\alpha }(\alpha +1),p_3]$ under $T_{\alpha }$ clearly excludes the existence of gaps.

Fig. 21

Borderline cases for part II of the proof of Theorem 4

Finally, let $N=2$. We have $|T_{\alpha }'(f_1)|=2$, indicating the rapid increase of $|T_{\alpha }'|$ on $I_{\alpha }$ if $\alpha$ decreases. The large expansiveness of $T_{\alpha }$ left of $f_1$ assures the gaplessness of $\varDelta _1$. We will show that for any $\alpha \in (0,\sqrt{2}-1]$ the image of $[T_{\alpha }(\alpha +1),p_2])$ contains most of the fixed points, implying the gaplessness of $I_{\alpha }$; see the last arrangement of Fig. 21 for an illustration of this. If $T_{\alpha }(\alpha +1)\le f_2$ this is quite obvious, so we assume $T_{\alpha }(\alpha +1)> f_2$. Suppose that $T_{\alpha }^2(\alpha +1)=f_s$, for some $s \in {\mathbb {N}}_{\ge 2}$. Then, omitting some basic calculations, we have $\alpha =(s+1-\sqrt{s^2+8})/(2s-7)$, whence

$$\begin{aligned} d=d(\alpha )= & {} \left\lfloor \frac{4s^2-11s+(4s-13)\sqrt{s^2+8}-15}{2s-7}\right\rfloor \\\ge & {} \frac{4s^2-13s+(4s-13)\sqrt{s^2+8}-8}{2s-7}, \end{aligned}$$

from which we derive that $d\ge 4s$.

This finishes the proof of Theorem 4.$\square$

Remark 16

A paper worthwhile to read alongside our paper is [12]. As the title of this paper states, it deals with mixing properties of expanding Lorentz maps. There are many interesting results in [12] that embed the results from our paper in a more general context.