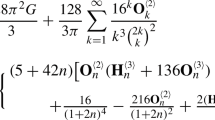Abstract
In the present paper, we introduce and study the limit sets of the almost periodic functions f: \({{\mathbb {R}}}\rightarrow {{\mathbb {C}}}\). It is interesting, that \(r=\inf |f(x)|\) and \(R=\sup |f(x)|\) may be expressed in exact form. In particular, the formula for r coincides with the well known partition problem formula. We show that the ring \(r\le |z|\le R\) is the limit set of the almost periodic function f(x) (under some natural conditions on f). We obtain interesting applications to the partition problem in number theory and to trigonometric series theory. We extend classical results for periodic functions (estimation of Fourier coefficients and Bernstein’s theorem about absolute convergence of trigonometric series) to almost periodic functions. Using our results on almost periodic functions, we propose a new approach to interesting problems of the stability of motion. An application of our function theoretic results to the spectral problems in operator theory is studied as well. The results and corresponding computations are illustrated by several figures.
Similar content being viewed by others
References
Arnold, V.I.: Mathematical Methods of Classical Mechanics, corrected reprint of the, 2nd edn. Springer, New-York (1989)
Bary, N.K.: A treatise on trigonometric series, vol. 2. Pergamon Press, New York (1964)
Besicovitch, A.S.: Almost periodic functions. Cambridge Univ. Press, Cambridge (1932)
Bhatia, R., Davis, C., Koosis, P.: An extremal problem in Fourier analysis with applications to operator theory. J. Funct. Anal. 82, 138–150 (1989)
Boettcher, S., Mertens, S.: Analysis of the Karmarkar differencing algorithm. Eur. Phys. J. B 65, 131–140 (2008)
Bohr, H.: Fastperiodische funktionen. Springer, Berlin (1932)
Böttcher, A.: On the corona theorem for almost periodic functions. Integral Equations Operator Theory 33, 253–272 (1999)
Coddington, E.A., Levinson, N.: Theory of ordinary differential equations. McGraw-Hill Inc., New York (1955)
Diagana, T.: Almost automorphic type and almost periodic type functions in abstract spaces. Springer, New York (2013)
Favorov, SYu.: Holomorphic almost periodic functions in tube domains and their amoebas. Comput. Methods Funct. Theory 1, 403–415 (2001)
Fink, A.M.: Almost periodic differential equations. Springer, Berlin-New York (1974)
Gouéré, J.-B.: Quasicrystals and almost periodicity. Comm. Math. Phys. 255, 655–681 (2005)
Kahane, J.-P., Lemarie-Rieusset, P.G.: Fourier series and wavelets (French), 2nd edn. Cassini, Paris (2016)
Kostić, M.: Almost periodic and almost automorphic solutions to integro-differential equations. de Gruyter, Berlin (2019)
Kostić, M.: Selected topics in almost periodicity. de Gruyter, Berlin (2022)
Kovalyov, M., Pesch, E.: A generic approach to proving NP-hardness of partition type problems. Discrete Appl. Math. 158(17), 1908–1912 (2010)
Kuijlaars, A.: Chebyshev-type quadrature and partial sums of the exponential series. Math. Comp. 64, 251–263 (1995)
Lacey, M., Thiele, C.: \(L^p\) estimates on the Bilinear Hilbert Transform for \(2<p<\infty \). Ann. of Math. 2(146), 693–724 (1997)
Lefschetz, S.: Differential Equations: Geometric Theory, \(2^{nd}\) edition. Interscience Publishers, New York (1963)
Lenz, D., Strungaru, N.: On weakly almost periodic measures. Trans. Amer. Math. Soc. 371, 6843–6881 (2019)
Levitan, B.M.: Some questions of the theory of almost periodic functions. I, Uspehi Matem. Nauk (N.S.) 2, no. 5 (21), 133–192 (1947)
Levitan, B.M.: Almost periodic functions. Gostehizdat, Moscow (1953)
Levitan, B.M., Zhikov, V.V.: Almost periodic functions and differential equations. Cambridge Univ. Press, Cambridge (1982)
Lubinsky, D.S.: A maximal function approach to Christoffel functions and Nevai’s operators. Constr. Approx. 34, 357–369 (2011)
N’Guérékata, G.M.: Almost periodic and almost automorphic functions in abstract spaces, 2nd edn. Springer, Cham (2021)
Sakhnovich, L.A.: Triangular integro-differential operators with difference kernels. Sib. Math. J. 19, 616–626 (1978)
Sakhnovich, L.A.: Integral Equations with Difference Kernels on Finite Intervals, second ed. (revised and extended), Birkhäuser, Cham (2015)
Sakhnovich, L.A.: \((S+N)\)-triangular operators: spectral properties and important examples. Math. Nachr. 289, 1680–1691 (2016)
Sepulcre, J.M., Vidal, T.: A new approach to obtain points of the closure of the real parts of the zeros of the partial sums \(1 + 2^z + \ldots + n^z, \ge 2\). Kybernetes 41, 96–107 (2012)
Sepulcre, J.M., Vidal, T.: A new geometrical perspective on Bohr-equivalence of exponential polynomials. Anal. Math. Phys. 11, Art. 55 (2021)
Sepulcre, J.M., Vidal, T.: A note on spaces of almost periodic functions with values in Banach spaces. Canad. Math. Bull. 65, 953–962 (2022)
Sepulcre, J.M., Vidal, T.: Equivalent almost periodic functions in terms of the new property of almost equality. Quaest. Math 46, 147–160 (2023)
Stamov, G.T.: Almost periodic solutions of impulsive differential equations. Springer, Heidelberg (2012)
Titchmarsh, E.C.: Introduction to the theory of Fourier Integrals. Oxford Univ. Press, Oxford (1937)
Vasilevski, N.: Commutative algebras of Toeplitz operators on the Bergman space. Birkhäuser, Basel (2008)
Weisz, F.: Lebesgue points and summability of higher dimensional Fourier series. Birkhäuser/Springer, Cham (2021)
Acknowledgements
The author is grateful to the referees for their careful reading and very helpful remarks. The author is deeply grateful to I. Tydniouk for fruitful discussions, useful comments, and for essential help in charting and calculations. The author is very grateful to A. Sakhnovich for the important help with the references, for very productive discussion and for improvements in the presentation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andrei Martinez Finkelshtein
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Lev Sakhnovich is retired from Courant Institute.
Appendices
Appendix: Examples and Figures
In the appendix, we consider various almost periodic functions and the corresponding parametric plots.
Example A.1
We begin with the case \(n=2\).
In this case, the function f(x) has the form
Hence f(x) admits the representation \(f(x)=A(x)+iB(x)\), where
Thus (see also (2.22)), we have
Relations (A.2)–(A.4) imply the next proposition.
Proposition A.2
-
(1)
If \(n=2\) and \(x_k=(2k\pi -\alpha _1+\alpha _2)/(\lambda _1-\lambda _2)\), where k is integer, then \(f(x_k)=e^{i(x_{k}\lambda _1+\alpha _1)}(|c_{1}|+|c_{2}|)\) and we obtain
$$\begin{aligned} \sup |f(x)|=|c_{1}|+|c_{2}|. \end{aligned}$$(A.5) -
(2)
If \(n=2\) and \({\tilde{x}}_k=((2k+1)\pi -\alpha _1+\alpha _2)/(\lambda _1-\lambda _2)\), where k is integer, then \(f({\tilde{x}}_k)=e^{i({\tilde{x}}_{k}\lambda _1+\alpha _1)}(|c_{1}|-|c_{2}|)\) and we obtain
$$\begin{aligned} \inf |f(x)|=\big |\, |c_{1}|-|c_{2}|\, \big |. \end{aligned}$$(A.6)
Example A.3
In the special (periodic) case of \(n=2\):
Proposition A.2 yields
The function \(f(x)=\xi +i \eta \) can be represented in the parametric form
The corresponding parametric plot (for \(a=2\), that is, for \(r=1\) and \(R=3\)) is depicted in Fig. 1 (in this appendix). Several figures for the case (A.7) are given in [29, p. 104].
Example A.4
In the special case of \(n=2\), where the numbers \(\lambda _1\) and \(\lambda _2\) are linearly independent over the field of rational numbers:
Proposition A.2 yields
The function \(f(x)=\xi +i\eta \) is again represented in the parametric form
For the illustration of this parametric plot see Fig. 2.
Example A.3
Example A.4
Example A.5
Example A.6
Example A.5
In the case
we have
The function f(x) is represented in the parametric form
This parametric plot is depicted in Fig. 3.
Example A.6
Consider the case \(n=3\), where f(x) is given by
This is an intermediate case because the function f(x) is not periodic, but the system \(\lambda _1=1,\,\lambda _2=2,\,\lambda _3=\sqrt{3}\) is not linearly independent. Here, we have :
The function f(x) has the parametric form
This parametric plot is depicted in Fig. 4.
Stability of Motion
Let us shortly discuss a question of stability which may be modelled without resorting to the Hamiltonian treatment.
We consider the motion along an orbit which belongs to some fixed annulus. This motion is stable if the orbit of the perturbed motion belongs to this annulus too. The possible form of the perturbed orbits is illustrated in the example below.
Our definition of stability differs from the classical ones because we handle the orbits instead of the equations which generated these orbits.
Example B.1
Choose the original orbit \(f(x)=e^{ix}+3e^{ix\lambda }\). Then, we may fix the corresponding annulus (1.3) such that \(R_f=4\), \(r_f=2\). Now, we consider the perturbed orbits of the form \(g(x)=e^{ix}+3e^{ix\mu }\), where \(\mu \ne \lambda \), \(\mu \in {{\mathbb {R}}}\). Clearly, the perturbed orbits belong to the same annulus.
If the number \(\mu \) is irrational, then the corresponding perturbed orbit passes through all the points of the corresponding annulus; we will call such an orbit essential. If the number \(\mu \) is rational, then the corresponding perturbed orbit does not pass through all the points of the corresponding annulus; we will call such an orbit inessential. The essential orbits form an uncountable set (continuum set). The inessential orbits form a countable set. From the physical point of view the inessential orbits may be neglected. The division of the class of orbits into two subclasses (of essential and inessential orbits) is prompted by the KAM theory.
In our example, the motion along the orbit \(f(x)=e^{ix}+3e^{ix\lambda }\) is stable with respect to the perturbed orbits of the form \(g(x)=e^{ix}+3e^{ix\mu }\). It is not required that the perturbations should be small. Indeed, we have \(\sup |f(x)-g(x)|=6\). The results of Sect. 2 enable us to study much more general unperturbed almost periodic orbits than \(f(x)=e^{ix}+3e^{ix\lambda }\) and much more general perturbed cases than \(g(x)=e^{ix}+3e^{ix\mu }\).
The plots are depicted for three cases. Figure 5 (Case I) depicts the unperturbed orbit \(f(x)=e^{ix}+3e^{i\sqrt{2}\,x}\) and perturbed orbit \(g(x)=e^{ix}+3e^{ 2 i x}\) (in red). Figure 6 (Case II) depicts the perturbed orbit \(g(x)=e^{ix}+3e^{ 2 i x}\). Finally, Fig. 7 (Case III) depicts the perturbed orbit \(g(x)=e^{ix}+3e^{i (7/5)x}\).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Sakhnovich, L. Almost Periodic Functions: Their Limit Sets and Various Applications. Comput. Methods Funct. Theory (2023). https://doi.org/10.1007/s40315-023-00515-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40315-023-00515-2
Keywords
- Limit set of an almost periodic function
- Linearly independent numbers
- Fourier series
- Absolute convergence
- Partition problem
- Spectrum
- Triangular operator
- Stability of motion