Abstract
Rock anchors, which can withstand substantial forces and are essential for securing the foundations of the built environment, can fail due to steel tensile failure, bond detachment, or rock mass fracturing through uplift. In this study, uplift failure of the rock mass surrounding rock anchors was simulated using both physical and numerical models. The physical models used a specially designed testing rig with predefined sizes and different joint layouts to simulate rock mass uplift failure. The numerical models were calibrated using the physical models and used to investigate scenarios involving increased complexity and greater depths. This paper presents the load distribution within rock masses with orthogonal joints when exposed to an anchor load. Extensive analysis of the numerical models revealed that symmetrical load arches were induced in rock masses that contained a joint set oriented parallel to the loading direction. However, joints that were obliquely oriented relative to the anchor axis induced asymmetrical load arching. The greatest displacement occurred in the direction parallel to the joint set with the smallest angle to the anchor loading axis. Large-scale models with zero or near-zero in situ horizontal stress revealed that the load capacity in a rock mass with continuous vertical joints was relatively low, especially when compared to rock masses with discontinuous vertical joints. It was observed that the uplift capacity of the rock mass around an anchor decreased if the load arches of adjacent anchors overlapped; consequently, a decrease in anchor spacing was found to correspond to a decrease in uplift capacity.
Highlights
-
Symmetrical load arches are induced within a rock mass if the joint sets are oriented parallel to or close to parallel to the anchor axis.
-
An oblique orientation of the joints relative to the anchor axis results in asymmetrical load arching in the rock mass when the anchor is loaded.
-
Rock masses with continuous vertical joints have a low load capacity, especially compared to rock masses with discontinuous vertical joints.
-
In a row of rock anchors, the rock mass uplift capacity of individual anchors is decreased if the anchor spacing is too low.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Rock anchors are engineered systems designed to withstand large forces and secure the foundations of our built environment and are an important component in stabilizing rock slopes, retaining walls, and large-scale infrastructures. As critical structural elements, the reliability and performance of rock anchors are of extreme importance. However, the complexity of rock masses and the multifaceted nature of their interactions with anchors pose unique challenges in the field of rock mechanics (Brown 2015).
An understanding of the mechanisms responsible for rock anchoring failures is crucial to improving the stability of infrastructure (Tayeh et al. 2019). Anchors, typically composed of multiple strands of cables or solid bars deeply bonded within the rock mass, are susceptible to various modes of failure; this includes tensile failure of the steel, the detachment of the bond between the steel and the grout or between the grout and the rock, and the initiation and propagation of fractures within the rock mass (Littlejohn and Bruce 1977; Brown 2015). The consequences of anchor failure extend far beyond structural concerns, with potential economic ramifications and societal impacts.
The ROCARC (Rock Anchoring for Stabilization of Infrastructures) project is a comprehensive research initiative aimed at advancing the understanding of rock anchoring mechanisms as well as enhancing the design of rock anchors for the improved stabilization of infrastructures. Over a four-year period between August 2020 to July 2024, ROCARC will be financially supported by the Research Council of Norway (RCN) and will encourage collaboration between research institutions and industrial partners. The primary objectives of the project include the investigation of critical aspects of rock anchoring, including load transfer dynamics between anchors and rock masses, failure modes of the rock mass, and the bond strength between the grout and rock. These goals are pursued using a interdisciplinary approach that incorporates tests using physical models, field trials, and numerical modeling techniques. Laboratory tests simulate anchor loads and failure patterns in controlled environments, while field trials examine anchor behavior in actual rock masses. Numerical modeling serves as a crucial tool for parameter studies as well as the development of a comprehensive methodology for rock anchor design, which ultimately underpins the stability and safety of our critical infrastructures.
Previous research has explored the behavior of rock anchors and the intricate mechanisms leading to rock mass uplift failure. Such investigations comprise both laboratory-scale models and field experiments, which shed light on the multitude of factors that influence anchor behavior. Laboratory tests have revealed the complexities of anchor behavior, including the expansion of the failure cone in intact rock samples (García-Wolfrum et al. 2007), block deformation during anchor pullout (Dados 1984), and load arching in blocky models (Grindheim et al. 2022). Here, load arching refers to the path of the most compressed section of the joints (Grindheim et al. 2022). Researchers have also conducted field tests to induce rock mass uplift failure around rock anchors, providing valuable insights into anchor behavior and its dependence on the structure of the rock mass (Bruce 1976; Ismael 1982; Dados 1984; Weerasinghe and Littlejohn 1997; Thomas-Lepine 2012; Grindheim et al. 2023), more details are given in Grindheim et al. (2023). The challenges revealed by laboratory and field experiments led to the adoption of numerical modeling as a compelling alternative. Numerical modeling is a useful tool for assessing the impact of rock mass characteristics on anchor performance; it can potentially improve anchor design and safety by considering variations in jointing, fracture spacing, orientation, and persistence (Panton 2016). A study by Shabanimashcool and Bērziņš (2023) introduced an innovative numerical method for predicting the uplift resistance of a rock mass; in particular, they highlighted the significant impact of joint sets aligned parallel to the anchor axis on uplift resistance. Their method incorporated block rotation and interlocking, leading to the formation of load arches that enhanced load transfer mechanisms.
Current design methods for safeguarding against rock mass uplift failure that assume a conical uplift failure mechanism suffer from notable shortcomings as outlined by Brown (2015). These deficiencies arise from implicit assumptions about stress distribution, the failure mechanism, and uniform strength properties in the rock mass. To accurately predict failure or deformation in rock masses stabilized by anchors, understanding the induced stress distribution is crucial, especially in complex scenarios. Anisotropic properties of the rock mass can further complicate this analysis. The assumption of a failure cone implies constant shear and tensile strengths regardless of depth, which may not hold, especially for deep anchors. The rock mass structure, including bedding, jointing, and discontinuities, can also significantly influence the failure surface. Existing design methods, based on simplistic uplift cone hypotheses and assumed strength parameters, lack the complexity needed to account for real-world variations in strength, local rock mass structure, and progressive failure mechanisms. Consequently, there is a need to improve these approaches to better reflect the real-world complexities involved in rock mass uplift failure (Brown 2015). Numerical simulations with 2D/3D models are thus a promising approach to obtain deeper knowledge on the load distribution and anchor failure in complex rock masses. However, the development of a reliable numerical model necessitates additional effort. This paper presents a study on constructing and calibrating a numerical model based on laboratory scaled tests, where the goal is to enhance our understanding on the load transfer and uplift mechanisms in a rock mass exposed to anchor loading and thereby provide knowledge needed to improve the design methods for rock anchors.
The importance of numerical modeling in the field of rock anchoring for infrastructure stabilization has become evident. The complexities inherent in the interactions between anchors and the host rock mass demand a deeper understanding that often exceeds the limits of physical experimentation. Numerical modeling serves as the bridge between theory and practice, allowing researchers and engineers to explore the intricate interactions of forces, load transfer mechanisms, and failure modes within the safety of a virtual environment. This paper, as part of the broader ROCARC project, seeks to use the power of numerical modeling to address load transfer in rock masses exposed to rock anchor loading. The numerical models are calibrated based on laboratory tests conducted by members of the ROCARC project, utilizing input parameters derived from field and laboratory physical tests. The anticipated outcome of this work is the emergence of new knowledge that will advance our ability to predict anchor behavior, optimize engineering practices, and enhance the stability and longevity of infrastructures.
2 Numerical Model Setup
2.1 Testing Plan
Numerical models were developed to investigate rock mass uplift failure and the arching effect using Universal Distinct Element Code (UDEC) version 5.0 (Itasca 2011). The models were calibrated and geometrically configured based on the results of physical models conducted using a testing rig (Grindheim et al. 2024). The model was then extended to include geometries that were not physically tested but still retained the parameters used in the calibration process. Eight different patterns were simulated, of which five were replicates of the physical models investigated using the testing rig (see Fig. 1) and three were developed for this numerical simulation (see Fig. 2). The calibrated results were also extended to large-scale rock anchoring to investigate the load distribution around a real-sized anchor, and to investigate the interaction between adjacent anchors.
Geometry of the numerical models with varying joint patterns: a Pattern 1—continuous horizontal and vertical joints, b Pattern 2—continuous horizontal and discontinuous vertical joints, c Pattern 3—discontinuous horizontal and continuous vertical joints, d Pattern 4—continuous horizontal and discontinuous vertical joints rotated by 25°, and e Pattern 5—interlocked joints
2.2 Geometry and Boundary Conditions
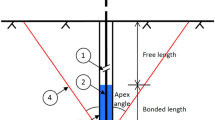
The geometry of the numerical models was based on the physical models investigated using a testing rig; these were composed of concrete pavement blocks cut to dimensions 130 \(\times\) 60 \(\times\) 190 mm and 65 \(\times\) 60 \(\times\) 190 mm (width \(\times\) height \(\times\) depth) as illustrated in Fig. 3. A comprehensive description of the physical testing conducted using the rig is detailed in Grindheim et al. (2024). The working area of the physical testing rig was 1900 \(\times\) 1200 \(\times\) 300 mm, and the concrete blocks used for Patterns 1–4 had the mentioned dimensions, while for pattern 5 the blocks had dimensions of 120 \(\times\) 60 \(\times\) 190 mm and 60 \(\times\) 60 \(\times\) 190 mm. The wall height of the failure tests in the physical rig was 900 mm. During the investigation of pattern 2, an assessment of scale effects was conducted by utilizing enlarged concrete garden wall blocks, which is described in Grindheim et al. (2024). The blocks employed for this test had dimensions of 236 \(\times\) 135 \(\times\) 172 mm.
Several geometries were evaluated using the numerical models. Initial tests involved models comprised of only concrete blocks and an anchor. These models encountered boundary issues: because the blocks were either fixed or slid along a roller boundary, these simulations led to excessively high capacities or large displacements. The second geometry incorporated a steel frame on two sides (the bottom and right vertical side of the rig), with horizontal stress applied directly to the leftmost blocks. This setup encountered difficulties with the applied horizontal stress and failed when the stress exceeded 0.1 MPa. Subsequently, a UDEC model featuring a steel frame on three sides (the bottom and the two vertical sides of the rig) was tested using in situ stress and was found to be most effective (seen in Figs. 1, 2).
The final geometry employed in the numerical models consisted of a steel frame with a thickness of 40 mm on three sides (bottom and two vertical sides), enclosing a working area of 1900 \(\times\) 900 mm (width \(\times\) height). The UDEC models were two-dimensional, i.e., the conventional model depth was set to a unit depth (1 m) within the software. The size of the blocks was identical to those used in the physical models (with the exception of depth). The anchor block was located at the bottom center inside the frame and measured 100 \(\times\) 100 mm. It was divided into four blocks along the diagonal to allow for load application from the center of the block. In the numerical models, a small void with a width of 20 mm was included above the anchor block to prevent direct contact overlap failure when transferring the anchor load directly to the blocks above it. The bond strength between the anchor and concrete blocks was increased to ensure that the model worked correctly; this also made it more similar to a real anchor, in which load is transferred to the rock mass through shear along the contacts between the anchor and the borehole wall rather than compression.
In the physical testing rig, the steel frame was stationary, and horizontal stresses were applied to the concrete blocks using hydraulic cylinders. The valves of the horizontal cylinders were closed, preventing the blocks from moving horizontally and providing a fixed horizontal constraint. In the numerical model, this was replicated by keeping the outer edge of the steel frame fixed in both the x- and y-directions (defined reference system in Fig. 3). In situ stresses were applied that corresponded to the stresses applied by the hydraulic cylinders. The top of the model was a free surface in both physical failure models; consequently, the same conditions were used for the numerical models.
2.3 Material and Joint Properties
The properties of the material used in the physical models were identified using laboratory testing and used in the numerical models. The uni-axial compressive strength (UCS), Young’s modulus, and Poisson’s ratio of the material were determined through UCS tests as described by Bieniawski and Bernede (1979). The tensile strength of the material was determined using Brazil tests as described by ISRM (1978). The friction angle of the joints between the concrete blocks was determined through tilt-tests as described by Alejano et al. (2018), with observed values ranging from 25° to 35°. A calibration process was used to determine the friction angle and the normal stiffness of the concrete joints. The shear stiffness of the joints was found using the normal stiffness as well as the following equations (Itasca 2011).
The rock mass stiffness (\(E_m\)) was determined using the intact rock stiffness (\(E_r\)) and the joint normal stiffness (\(k_n\)) using Eq. (1):
where s is the joint spacing. The shear stiffness (G) of the rock mass and the intact block material was determined using Eq. (2):
where \(\nu\) is the Poisson’s ratio of the intact material. Once the normal and shear stiffness of the intact material and the rock mass were determined, the shear stiffness of the joints could be calculated using Eq. (3):
where \(G_m\) is the shear stiffness of the rock mass and \(G_r\) is the shear stiffness of the intact material. The joint properties can be changed under dynamic cyclic loading (Indraratna et al. 2021; Soomro et al. 2022), but dynamic loading is not the focus of this study, therefore, constant joint properties are used in the modeling. The steel parameters were obtained from Eurocode 2 (Standards Norway 2021) and Eurocode 3 (Standards Norway 2015). To ensure that failure occurred within the concrete blocks rather than the anchor, the joint properties of the connections within the anchor block and between the anchor block and the concrete blocks were deliberately set at artificially high levels. Given the smooth, flat, and clean surfaces of the concrete blocks, the cohesion, dilation angle, and tensile strength of the joints were assigned a value of zero. The material properties utilized in the models are detailed in Table 1, while Table 2 provides a summary of the joint parameters.
2.4 Model Loading
The anchor load was applied at a constant displacement rate of 0.5 mm/s in the physical model. This was replicated in the numerical model by applying a constant velocity of 0.5 mm/s in the y-direction to the anchor block.
2.5 Calibration
The numerical models were calibrated against the failure test of Pattern 2 as shown in Fig. 4. This calibration involved the alignment of the load–displacement and horizontal stress-vertical displacement curves of the numerical model with those of the physical model. The loads measured in the numerical model were proportionally reduced to correspond with those observed in the laboratory, given that the block depth was 19 mm in the laboratory compared to 1 m in the UDEC model. The models were calibrated using the measured laboratory test data to ensure similarities to the physical test models.
In the physical models, small voids existed between the concrete blocks. These voids closed when loaded, a phenomenon that was observed during laboratory testing. The closure of these voids was particularly evident during laboratory testing, where the anchor load was flattening with a force of 20 kN, suggesting frictional movement associated with void closure. This flat section persisted until a displacement of 10.9 mm was reached. The presented results in Fig. 4a have been corrected for the void closure in laboratory test.
In the laboratory test, the horizontal stress remained approximately constant until an anchor displacement of 10.9 mm, suggesting that the voids were continuing to close up to this point. However, because these voids were absent in the numerical model, this behavior was not replicated, and the presented results from the laboratory tests have been offset by 10.9 mm in Fig. 4b.
Once fitted, the load–displacement curve was closely aligned with the curve obtained from the physical model. A good fit was observed from the starting point of the curve to its peak, suggesting that the calibration was successful. Similarly, the horizontal stress curve exhibited a good fit with the laboratory measurements, particularly when the section associated with void closure was excluded.
2.6 Modeling of Larger-Scale Rock Anchoring
UDEC models for large-scale rock anchor tests were developed based on the calibration derived from physical models. The blocks in these models had properties equivalent to those used in the physical models. The models included single 10 m anchors in rock masses with joint patterns identical to those in Patterns 1–4. An additional model was created that featured a group of five anchors, each with a length of 5 m and spacing varying from 1 to 5 m in the rock mass, replicating the joint pattern of Pattern 2.
2.6.1 Single Anchor
The models that featured a single large-scale anchor were initialized with a 64-mm anchor (in width) with a length of 10 m, including a 1-m bonded section at the base. The model had a width of 40 m and a depth of 11 m. The joint spacing in the rock mass was twice that of the physical models, a necessary adjustment for model functionality. Unlike the smaller models, in which the boundaries interacted with the blocks influenced by the anchors, the boundary conditions of these larger models were modified due to their size (i.e., no steel frame). The model size ensured that the boundaries did not interfere with the blocks affected by the anchor loading. The model’s bottom boundary was fixed in both the x- and y-directions, while the vertical boundaries at the sides of the model were only fixed in the x-direction. The top surface was left as a free surface. The in situ stresses were exclusively gravity-induced. The anchor load was applied at a constant velocity of 5 mm/s in the y-direction and maintained for a predetermined duration. Due to the increased size and quantity of blocks in the large-scale models, the running time for these models was increased. To ensure that the simulations were completed within a reasonable time frame, the applied velocity of the models was increased. A single model was run at a displacement rate of 0.5 mm/s to investigate potential differences resulting from an increased displacement rate. Although no significant differences were observed, the anchor stress was slightly lower in the model with the lower displacement rate. These single anchor tests were conducted on rock masses that exhibited joint patterns identical to those presented in Patterns 1–4.
2.6.2 Anchor Groups
A model was developed to simulate the uplift of a group of anchors; this model utilized a joint pattern similar to that of Pattern 2. This anchor group was composed of five anchors, each with a width of 64 mm and a length of 5 m, including a 1-m bonded section at the base. The anchor length was reduced to reduce the model size to improve the running time. The model had a width of 40 m and a depth of 6 m. The joint spacing and boundary conditions were identical to those used in the single large-scale anchor models. Similarly, the in situ stresses were exclusively due to gravity, and the anchor load was applied at a constant velocity of 5 mm/s in the y-direction. Several models were created in which the spacing of anchors was varied, including test spacings of 1 m, 3 m, and 5 m intervals.
3 Results of Simulations and Comparisons with the Physical Model
3.1 Models of the Laboratory Tests
3.1.1 Displacement
This section presents and describes the vertical displacement observed in the numerical simulation of laboratory tests and compares these results with the vertical displacement observed in the physical models corresponding to Patterns 1–5. Cloud images of the vertical displacement were extracted from models that were allowed to run until a 5-mm vertical anchor displacement was achieved; these remained in the elastic stage throughout the simulation. The models corresponding to each pattern are presented individually. Figures 5, 6, 7, 8, 9 and 10 show the vertical displacement cloud images for all numerical models. In all models, the maximum vertical displacement was typically perpendicular to one of the two orthogonal joint sets when a vertical anchor load was applied.
The vertical displacement exhibited by Pattern 1 (continuous horizontal and vertical joints) is depicted in Fig. 5. In the numerical model, the vertical displacement was greatest in the center immediately above the anchor and decreased laterally. The vertical displacement was approximately constant along vertical lines. Some disparities between the numerical and physical models were observed; in the physical model, the vertical displacement was greatest at the bottom and decreased upwards. This difference is likely due to slight variations in block sizes, leading to small voids and open joints in the physical model, which gradually closed from the bottom upwards as the anchor was loaded. The observed discrepancy could also potentially be attributed to the distribution of joint normal stiffness. In the physical model, the joint normal stiffness is non-linearly distributed, with the lower horizontal joints being more ‘closed’ than the upper joints due to the overlying weight. In contrast, the joint normal stiffness is uniformly distributed across all joints in the numerical model. This results in the top blocks experiencing less movement in the physical model, while in the numerical model, perfect contacts between the blocks resulted in simultaneous block displacement across the entire model upon loading. Vertical displacements were similar between the numerical and physical models in the lateral directions.
Figure 6 illustrates the vertical displacement of Pattern 2, featuring continuous horizontal joints and discontinuous vertical joints. Similar to Pattern 1, the model exhibits its greatest displacement above the anchor. The vertical displacement observed in the physical model was less pronounced in the vertical direction compared to the numerical model, possibly due to the same factors described in Pattern 1. The vertical displacement observed in the numerical and physical models was relatively similar in the lateral directions. It should be noted that an increase in model block size appears to slightly reduce displacement in both the vertical and lateral directions, with this effect being more pronounced in the physical model.
Vertical displacement cloud images of Pattern 2 (continuous horizontal and discontinuous vertical joints) after 5 mm of vertical anchor displacement: a numerical model with normal blocks, b physical model with normal blocks, c numerical model with large blocks, and d physical model with large blocks
The vertical displacement of Pattern 3, which is characterized by continuous vertical and discontinuous horizontal joints, is depicted in Fig. 7. In this pattern, the numerical and physical models are much more similar compared to the previous patterns. The most significant vertical displacement still occurs directly above the anchor. Like the previous patterns, the physical model displays slightly less vertical displacement than the numerical model in this direction, likely attributable to the same factors identified in the other patterns.
Figure 8 illustrates the vertical displacements observed in models of Pattern 4, which involve joints tilted at a 25°angle. Both the numerical and physical models produced nearly identical results, with the highest vertical displacement occurring perpendicular to the continuous joints. The physical model exhibited slightly lower displacements, which can be attributed to the closure of small voids during loading and the non-linear distribution of the joint normal stiffness.
The vertical displacements of Pattern 5, which featured interlocked joints, is presented in Fig. 9. Both the numerical and physical models produced similar results, with slightly smaller displacements observed in the physical model, likely due to the same reasons as the previous patterns. The greatest vertical displacement occurred in the central region and decreased laterally.
The preparation of inclined tests in the laboratory proved to be both time-consuming and challenging. Consequently, the decision was made to explore the load capacity and stress distribution in models with varying inclinations through numerical modeling. The tests were conducted to examine the impact of the inclination angle on the vertical displacement of the models and used material properties similar to those employed in the laboratory. Vertical displacements for the inclined patterns (tested exclusively using numerical simulations) are depicted in Fig. 10. The models featured continuous horizontal joints and discontinuous vertical joints at varying rotation angles: 10° for Pattern 4b, 40° for Pattern 4c, and 60° for Pattern 4d. In Pattern 4b, the highest vertical displacement was observed to be perpendicular to the continuous joints, with diminishing displacements observed parallel to this direction, similar to Pattern 4 (Fig. 8). In contrast, for Patterns 4c and 4d—which had larger rotation angles compared to Pattern 4b—the highest vertical displacement occurred parallel to the continuous joints. No movement was detected in the layers beneath those in contact with the anchor block, suggesting the uplift of the overlying layers. In Patterns 4c and 4d, the vertical displacement appeared to be nearly uniform in the layers interacting with the anchor block. This uniformity could potentially indicate shear movement along the continuous joint below the lowest layer in contact with the anchor.
3.1.2 Load Distribution
This section presents and describes the stress distribution in the numerical models used to simulate laboratory tests. The laboratory tests provided valuable insights into the load capacities and displacements of each pattern as well as the horizontal stress on the sides of each model as measured by the hydraulic cylinders. However, these tests could not adequately describe the load distribution within each pattern, a crucial aspect of understanding load arching; this generally aligns with the orientation of the major principal stress. Fortunately, this gap can be addressed through numerical modeling using materials with equivalent properties as determined during the calibration process. The individual results for each pattern after a 5-mm vertical anchor displacement are presented in Figs. 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 21, 22, 23, 24, 25 and 26; these diagrams depict the principal stress tensors and horizontal stress on the sides for each numerical model.
Figure 11 illustrates the principal stress distribution in Pattern 1, which is characterized by continuous horizontal and vertical joints. In this model, the major principal stress manifests as horizontal stress at the bottom of each layer in the middle of the model (Fig. 11b), and at the top of each layer at the sides of the model adjacent to the steel frame (Fig. 11c). The major principal stress forms arches within each layer, and these load arches transfer the vertical anchor load to the steel frame on the sides. This pattern exhibits a prominent arching effect that can be clearly observed in the block model.
The horizontal stress in the blocks along the left wall of Pattern 1 is shown in Fig. 12. These horizontal stresses reveal that the arching effect is present within each layer, peaking every 0.06 m. These measurements indicate that the arching effect is most pronounced in the uppermost layers of the model and least evident in the bottom layers adjacent to the anchor.
The principal stress distribution within Pattern 2, which is characterized by continuous horizontal and discontinuous vertical joints, is illustrated in Fig. 13. In this model, the major principal stress was observed to be horizontal at the bottom of each layer in the middle of the model (Fig. 13b) and at the top of each layer at the sides of the model adjacent to the steel frame (Fig. 13c). The major principal stress trajectories create arches within each layer, facilitating the transfer of the vertical anchor load to the steel frame on the sides. This phenomenon is particularly noticeable in the model with large blocks (Fig. 13d), clearly demonstrating the presence of an arching effect within the block model. When the block size was increased, the load capacity of both the pattern and the arch increased.
The principal stress distribution in Pattern 2 (continuous horizontal and vertical joints) after 5 mm of vertical anchor displacement. The stress distribution of the model with small blocks is shown across a the full model, b the center of the model, and c the sides of the model. In addition, d presents the stress distribution in the full model with large blocks
Pattern 2 exhibits a horizontal stress distribution in the blocks along the left wall as depicted in Fig. 14 that is analogous to that of Pattern 1. These horizontal stresses show that the arching effect is evident within each layer, peaking every 0.06 m in the model with small blocks and every 0.135 m in the model with large blocks. It is clear from the horizontal stresses that the arching effect is more pronounced in the model with larger blocks.
Figure 15 depicts the principal stress distribution in Pattern 3, which features continuous vertical joints and discontinuous horizontal joints. In this model, the highest stress was observed in the center at the bottom of the model as well as near the top of the sides of the model adjacent to the steel frame. The major principal stress distribution is expressed in the form of two arches within the model, transferring the vertical anchor load to the steel frame on the sides, highlighting the prominent arching effect within the block model. The formation of two arches could be attributed to boundary conditions affecting the blocks: a larger model may have resulted in the development of a single arch.
Figure 16 plots the horizontal stress along a vertical line in the blocks adjacent to the left wall of Pattern 3. The horizontal stresses indicate that the primary load transfer occurs at the top of the model, suggesting that the uppermost arch in Fig. 15 bears most of the load. There is also a noticeable load increase at the midpoint of the left wall that aligns closely with the location of the lower arch shown in Fig. 15.
The principal stress distribution in Pattern 4, which features continuous horizontal and discontinuous vertical joints rotated by 25°, is shown in Fig. 17. The anchor load was asymmetrically transferred to the steel frame, forming an arch. On the left side of the anchor, the load was transferred parallel to the continuous joint set and remained within the block layers, while it was transferred across the layers on the right side of the model. The primary load transfer on the left side of the model took place in the two layers that were in direct contact with the anchor. In contrast, the load transfer predominantly occurred above the anchor block on the right side of the model. Overall, this pattern demonstrates a clear arching effect.
The horizontal stress along a vertical line in the blocks adjacent to the left wall of Pattern 4 is depicted in Fig. 18. This diagram reveals that the horizontal stress is zero or near-zero in the layers beneath those in contact with the anchor. In the layers in contact with the anchor as well as in the layers above this point, the distribution of horizontal stress mirrors that of Patterns 1 and 2, i.e., arching occurs within each individual layer. There is a slight decrease in horizontal stress in the upper layers.
Figure 19 presents the principal stress distribution in Pattern 5, which is characterized by interlocked joints. In this model, the highest stress is concentrated at the center of the bottom of the model as well as at the top of the model along its sides. The major principal stress extends from the anchor and follows the vertically oriented blocks, giving rise to multiple load arches along these vertically oriented blocks. These load arches transfer load from the vertical anchor to the top of the steel frame along the side walls, highlighting the presence of an arching effect across the interlocked pattern.
The horizontal stress along a vertical line in the blocks adjacent to the left wall of Pattern 5 is presented in Fig. 20. The horizontal stresses suggest that the main load transfer takes place at the top of the model. The figure also suggests that there are minor local peaks at the top of each vertical block that align with the arching depicted in Fig. 19, especially in sections where the arches primarily vent through the vertical blocks. The horizontal stresses gradually increase toward the top of the model.
The following three Patterns (4b–d) were not tested in the laboratory; their results presented were numerical analysis only. The principal stress distribution of Pattern 4b, which features continuous horizontal and discontinuous vertical joints rotated by 10°, is displayed in Fig. 21. This model primarily exhibits the greatest stress within the layers in direct contact with the steel frame on both sides. Within these layers, the major principal stress is observed to be parallel to the blocks and is located at the bottom layer of the blocks in the center of the model and the top of the blocks near the sides of the model. In addition, some arching was observed in the two layers to the left of the anchor block, with the major principal stress being greatest at the bottom of the blocks near the anchor and at the top of the blocks near the frame. These principal stress patterns show that load arches were induced within the layers adjacent to and above the anchor block; these load arches propagated to the frame on both ends. These arches transferred the vertical anchor load to the steel frame on the sides, demonstrating the presence of an arching effect within this block model.
The horizontal stress distribution along a vertical line in the blocks adjacent to the left wall in Pattern 4b is presented in Fig. 22. The layers beneath those in contact with the anchor exhibit horizontal stress that is zero or near-zero. In contrast, the horizontal stress distribution in the layers in contact with the anchor and above is similar to that observed in Pattern 4, where arching is evident within each individual layer.
The principal stress distribution of Pattern 4c, which is characterized by continuous horizontal and discontinuous vertical joints rotated by 40°, is presented in Fig. 23. In this model, the anchor load is directly transferred to the steel frame via the layers in contact with the anchor on the left side. In contrast, on the right side of the model, the load is transferred toward the steel frame in a direction that is perpendicular to the continuous joints, resulting in an asymmetrical arch. Consequently, the load is predominantly shifted to the left side, as exhibited by the larger stress tensors in that direction.
The horizontal stress distribution along a vertical line in the blocks adjacent to the left wall in Pattern 4c is presented in Fig. 24. The horizontal stress in the layers beneath those in contact with the anchor is either zero or near-zero. However, two peaks in the horizontal stress were observed at the point where the two layers in contact with the anchor meet the left wall. The more significant peak is located in the lower of the two layers. These peaks indicate that the primary load transfer to the side occurs through these two layers, which is consistent with the observations in Fig. 23.
Figure 25 shows the principal stress distribution in Pattern 4d, which features continuous horizontal and discontinuous vertical joints rotated by 60°. This pattern exhibits a mild arching effect, as indicated by small stress tensors. The load arch is asymmetrical: on the left side of the anchor, the load is almost horizontally transferred to the steel frame, while on the right side of the anchor, the load is greatly dispersed in an upward direction from the center of the model toward the steel frame.
Figure 26 shows that the horizontal stress distribution in Pattern 4d along a vertical line in the blocks adjacent to the left wall is relatively distinct from the other patterns. The horizontal stress is highest at the bottom of the model and decreases toward the top, nearing zero at a height of 0.54 m and above. This observation is consistent with the findings presented in Fig. 25, where the load distribution on the left side of the anchor was nearly horizontal.
A study of Patterns 4–4d reveals the impact of inclination angle on load distribution and arching within the models. The model with the lowest angle (Pattern 4b), characterized by nearly horizontal continuous joints, exhibits arching similar to that of Pattern 2 (Fig. 13), in which each layer contains relatively flat arches. However, increasing the inclination angle to 25°alters this arching pattern. In Pattern 4, arching persists within the layers on the left side of the anchor, while the load on the right side is transferred through the layers. Further increases in the inclination angle diminish the arching effect and reduce the load capacity of the block model. Figures 23, 24, 25 and 26 highlight the limited arching observed in these patterns. The angle between the arches and the loading axis of the anchor aligns with the inclination angle: a larger angle results in flatter arches. The asymmetry of the load arch intensifies as the inclination angle increases. All patterns indicate that the load aligns itself either perpendicular or parallel to the joint orientation.
3.1.3 Model Failure
The UDEC models failed to simulate the failure mode of the block models due to the high strength of the blocks. Specifically, the simulation stopped after reaching the peak load due to the contact overlap of the blocks, preventing further failure development. Consequently, the numerical models were unable to show the failure mode of the block models. To accurately model the failure development within the model, it would be beneficial to use a concrete type model, such as the one proposed by Schädlich and Schweiger (2014). However, in the context of this paper, the primary focus is on the load transfer mechanisms during the elastic stage. For this specific aspect, the elastic perfectly plastic Mohr-Coulomb model is deemed sufficiently accurate. Nonetheless, future studies aiming to delve deeper into failure development of the laboratory tests may benefit from considering the use of a concrete type model. This approach could provide a more comprehensive understanding of the failure mechanisms and enhance the predictive capabilities of the numerical modeling.
3.1.4 Sensitivity Analysis
A sensitivity analysis was conducted on the calibrated model (Pattern 2). Model parameters were individually varied by ±10%, and the resultant peak load and horizontal stress were recorded. This analysis provided insights into the impact of the parameters on model outcomes, highlighting the parameters that require precise measurements and mapping to determine the rock mass uplift strength. Table 3 presents the results of the sensitivity analysis, with each parameter categorized into either joint, block, or model groups to describe their influence.
Joint parameters were found to significantly affect uplift capacity and horizontal stress. In contrast, joint shear stiffness had a minimal impact, suggesting the estimation formulas given in Itasca (2011) are adequate. A 10% variation in the joint normal stiffness led to an approximately 5% change in the monitored values. The friction angle substantially influenced model capacity but had negligible impact on horizontal stress.
Block parameters were found to exert a minor influence on uplift capacity and horizontal stress. Block density altered the model capacity by roughly 2%, while horizontal stress was only affected by block cohesion. Other block parameters were found to influence the measured values by less than 0.5%.
Model parameters had a strong influence on uplift capacity and horizontal stress. In situ stress levels only slightly altered peak values, contributing to an approximately 1% change in the horizontal stress. In contrast, changes to the spacing of the joints significantly impacted the models. This is consistent with our expectations: increased spacing implies a more massive rock mass, while decreased spacing indicates a more fractured rock mass. Reductions in joint spacing had a greater effect on the uplift capacity than increases in joint spacing, while horizontal stress was equally influenced by both, altering peak values by around 20%.
4 Numerical Simulation of Deep Rock Anchors
This section presents the results of numerical simulations that were focused on deep anchors in rock masses under gravitational loading. The single anchor models feature a 10 m anchor with a bonded section of 1 m and were used to investigate the effects of block orientation and joint pattern on anchor capacities. A numerical model of Pattern 2 was also used to investigate the interaction of adjacent anchors using 5-m long anchors with a bonded length of 1 m and variable spacings of 1–5 m. As these models do not represent actual rock masses, the focus is on the trends observed in vertical displacement and load distribution in the rock mass from the anchors, rather than the specific values. All models used rock masses with material properties equivalent to those used in laboratory tests as determined through a calibration process using Pattern 2, outlined in Sect. 2.5.
4.1 Displacement
This section describes the vertical displacement observed in numerical models designed to resemble large-scale rock anchoring. Vertical displacement data were derived from models run until a vertical anchor displacement of 50 mm was reached. Four distinct patterns were simulated, each represented by an individual model. Vertical displacement data across all numerical models is depicted in Figs. 27, 28, 29, 30 and 31.
4.1.1 Single Anchor
Figure 27 presents the vertical displacement of a single 10-m anchor pulled 50 mm within a rock mass characterized by continuous horizontal and vertical joints (corresponding to Pattern 1). The primary displacement is observed in the blocks that are directly interacting with the anchor. The anchor’s influence on the rock mass is confined to a narrow region, affecting only blocks that are in direct contact with either side of the anchor. Beyond this contact, the rock mass remains static and unaffected.
The vertical displacement of a 10-m long rock anchor embedded within a rock mass characterized by continuous horizontal and discontinuous vertical joints (Pattern 2) is presented in Fig. 28. The anchor influences the rock mass within 2 m of the base of the anchor, expanding to a radius of 5 m at the surface. It should be noted that the rock mass beneath the horizontal layer in contact with the anchor base remains unaffected. The horizontal layer at the base is elevated due to the anchor’s displacement and can be described as a single unit that measures 2 m in width on either side.
Figure 29 presents the vertical displacement of a 10-m anchor pulled 50 mm within a rock mass that corresponds to Pattern 3, which is characterized by continuous vertical and discontinuous horizontal joints. The displacement primarily impacts the two layers in direct contact with the anchor; these layers were displaced by 50 mm. The rest of the rock mass remained unaffected.
Figure 30 presents the vertical displacement of a 10-m anchor displaced by 25 mm within a rock mass that corresponds to Pattern 4. This model was stopped at 25 mm displacement by UDEC due to contact overlap. This pattern is characterized by continuous horizontal joints and discontinuous vertical joints rotated by 25°. The asymmetry of the joints around the anchor is reflected in the distribution of vertical displacement across the rock mass. The greatest displacement occurs in the direction normal to the continuous joints and extends upwards from the bonded section. Consequently, the rock mass up to 12 m to the right of the anchor experiences uplift, while the rock mass on the left side remains largely unaffected, with the exception of the layers in direct contact with the bonded section, which experience uplift up to 2 m away from the anchor.
4.1.2 Anchor Groups
Figure 31 illustrates the vertical displacement of a rock mass model corresponding to Pattern 2 (characterized by continuous horizontal and discontinuous vertical joints) with embedded anchor groups spaced in a variety of intervals following a 50-mm pull. At anchor spacings of 1 m and 3 m, the uplifted rock mass behaves as a single medium with a flat base (Fig. 31a, b), indicating uniform uplift. However, when the anchors are spaced in 5-m intervals (Fig. 31c), each anchor lifts individual rock mass regions, with minor overlap close to the surface. The behavior of the rock mass beyond the two outer anchors mirrors that of a single 10 m anchor in the same rock mass.
4.2 Load Distribution
This section presents the distribution of principal stress in numerical models that were used to simulate large-scale rock anchoring. The stress distributions were obtained following a vertical anchor displacement of 50 mm. A total of four patterns were simulated; Figs. 32, 33, 34, 35, 36, 37 and 38 illustrate the distribution of principal stress across these numerical models.
4.2.1 Single Anchors
Figure 32 shows the distribution of principal stress surrounding a single 10-m rock anchor embedded in a rock mass with continuous horizontal and vertical joints (Pattern 1). The model indicates that the principal stress is oriented vertically throughout the rock mass due to gravitational forces. The anchor load is transferred within the vertical layers in contact with the anchor while the rest of the rock mass is unaffected. No arching is observed in this pattern when the rock mass is exclusively loaded by gravity.
The principal stress distribution around a single 10-m rock anchor embedded in a rock mass with continuous horizontal and discontinuous vertical joints (Pattern 2) is presented in Fig. 33. The model reveals that the anchor load is distributed horizontally at the base of the anchor along the bonded section (Fig. 33b). The stress forms arches within each layer that interact with the bonded section, effectively transferring the vertical anchor load to the competent rock mass at distance. Above the bonded section, the anchor force is transferred upwards (Fig. 33c), leading to the uplift of the rock mass. This pattern results in a clear arching effect within the rock mass. The flat load arches distribute the anchor load to the rock mass up to a distance of 7 m from the anchor on either side.
The principal stress distribution around a single 10-m long anchor in Pattern 2 (continuous horizontal and discontinuous vertical joints) after 50 mm of vertical anchor displacement. a Full field stress distribution, b a detailed view of the stress distribution along the bonded section, and c a detailed view of the stress distribution immediately above the bonded section
Figure 34 illustrates the principal stress distribution around a single 10-m rock anchor embedded in a discontinuously horizontally jointed and continuously vertically jointed rock mass (Pattern 3). This model indicates that the principal stress is oriented vertically throughout the rock mass due to gravitational forces. The anchor force is transferred to the vertical layers in direct contact with the bonded length, which facilitates the uplift of these specific layers. Like Pattern 1, this pattern does not exhibit load arching.
The principal stress distribution around a single 10-m rock anchor embedded in a rock mass with continuous horizontal and discontinuous vertical joints rotated by 25° (Pattern 4) is presented in Fig. 35. The numerical model reveals that the principal stress is asymmetrically distributed at the base of the anchor within the bonded zone. On the left side of the anchor, load transfer predominantly occurs through layers in direct contact with the bonded section, with the principal stress running parallel to the continuous joints (Fig. 35b). Conversely, on the right of the anchor, the load is directed obliquely upward from the horizontal, with the major principal stress oriented perpendicularly to the continuous joints at small distances (Fig. 35c). Load arches were induced in each layer interacting with the left side of the bonded length, efficiently transferring the vertical anchor load to distant sections of competent rock mass. In contrast, on the right side of the bonded length, the upward-facing principal stress contributes to the elevation of the rock mass as depicted in Fig. 30. These phenomena result in asymmetrical arching within the rock mass. On the left side of the anchor, the flat load arches distribute the anchor load to the rock mass up to a distance of 10 m from the anchor. On the right, the principal load transfer is limited to a mere 2 m from the anchor base.
The principal stress distribution around a single 10-m long anchor in Pattern 4 (continuous horizontal and discontinuous vertical joints rotated by 25°) after 50 mm of vertical anchor displacement. a Full field stress distribution, b a detailed view of the stress distribution along the bonded section on the left of the anchor, and c a detailed view of the stress distribution along the bonded section on the right of the anchor
4.2.2 Anchor Groups
Anchor groups were simulated by situating a group of five anchors spaced at varying intervals within a rock mass model characterized by continuous horizontal and discontinuous vertical joints (Pattern 2). The distribution of principal stresses was similar to that observed in the single anchor scenario. Figures 36, 36 and 38 show that the layers interacting with the bonded section of the anchors exhibited relatively flat load arches, with the major principal stress oriented horizontally. The influence of the outermost anchors extended up to 6 m into the rock mass, consistent with the single anchor model. Within the anchor groups, the highest horizontal stress was observed between two neighboring anchors. The principal stress diagrams clearly demonstrate the interactions between anchors at 1 m (Fig. 36), 3 m (Fig. 37), and 5 m spacings (Fig. 38). This suggests that, in a rock mass with continuous horizontal joints, anchors should be spaced further apart to avoid interaction.
At the ends of the anchor row, the principal stress in the rock mass above the bonded length was found to be oriented upward and outward as shown in Figs. 36c, 37c, and 38d. This pattern mirrors that observed for single anchors embedded in rock masses corresponding to Pattern 2 (Fig. 33c). When the anchor spacing exceeded 3 m, an upward-facing principal stress was detected adjacent to each anchor, albeit with diminished intensity near the central anchors (Fig. 38c).
The principal stress distribution around a group of 5-m long anchors with anchor spacing of 1 m in a rock mass with continuous horizontal and discontinuous vertical joints (Pattern 2) after 50 mm of vertical anchor displacement. a Full field stress distribution, b stress distribution along the bonded length of a side anchor, and c stress distribution above the bonded length of a side anchor
The principal stress distribution around a group of 5-m long anchors with anchor spacing of 3 m in a rock mass with continuous horizontal and discontinuous vertical joints (Pattern 2) after 50 mm of vertical anchor displacement. a Full field stress distribution, b stress distribution along the bonded length of a side anchor, and c stress distribution above the bonded length of a side anchor
The principal stress distribution around a group of 5-m long anchors with anchor spacing of 5 m in a rock mass with continuous horizontal and discontinuous vertical joints (Pattern 2) after 50 mm of vertical anchor displacement. a Full field stress distribution, b stress distribution along the bonded length of a side anchor, and c stress distribution above the bonded length of a side anchor
4.3 Load Capacity
As demonstrated by the models, the anchor capacity in rock masses varies greatly depending on its pattern. Figure 39 presents the anchor stress–displacement curves of the 10-m single anchors as measured from the top of the anchors. The model with continuous horizontal and discontinuous vertical joints rotated by 25°(Pattern 4) exhibited the highest stress of 80 MPa, while models with continuous vertical joints (Patterns 1 and 3) exhibited the lowest amount of stress (2 MPa), where friction was the sole resistance to anchor pullout. The maximum stress observed in Pattern 2 was 38 MPa. These findings suggest that the presence of interlocking blocks enhances the load capacity of the rock mass, particularly under conditions of low or absent in situ stress.
The stresses measured in the anchors can be used to calculate the uplift capacity of the rock mass in these two-dimensional models. The load capacity of the rock mass is the product of the anchor stress and the area of the anchor. Specifically, an anchor stress of 80 MPa corresponds to a load of 5120 kN, an anchor stress of 38 MPa corresponds to a load of 2432 kN, and an anchor stress of 2 MPa corresponds to a load of 128 kN. The bar anchors utilized by Grindheim et al. (2023) had a nominal tensile strength of 1000 MPa, equating to a load capacity of 3217 kN for a 64 mm circular bar. These calculations show that Pattern 4, at a depth of 10 m and a bonded length of 1 m, is the only rock mass with a capacity that exceeds that of the anchor in this two-dimensional, 1-m unit depth model.
Grindheim et al. (2024) used laboratory tests to show that the load capacity of a block model increases with increasing confinement. Shabanimashcool and Bērziņš (2023) further demonstrated that load arching is contingent on the dilation angle using a numerical model, revealing that a dilation angle of only 2° was sufficient to induce load arching in a rock mass. These findings were used to develop three scenarios that were used to examine variations in the load capacity of rock mass around the single 10-m anchors. The scenarios included: (i) 0 MPa horizontal in situ stress, (ii) 0.5 MPa in situ horizontal stress, and (iii) 0 MPa horizontal in situ stress with a 2° dilation angle. The first scenario is identical to the parameters used in the previously presented models, with the capacities of each pattern presented in Fig. 39. The results from each of the three scenarios are presented in Fig. 40. The numerical models revealed that increasing horizontal stress only enhanced the load capacity of models with continuous vertical joints (Patterns 1 and 3), while the load capacity of the other models (Patterns 2 and 4) remained relatively stable. Changes in the dilation angle only increased the capacity of the patterns with continuous vertical joints (Patterns 1 and 3; Fig. 40a, c, respectively), while the capacities of the other patterns were similar to those observed in scenario (i).
The vertical anchor stress as a function of the anchor displacement for 10-m single anchors under three distinct conditions: (i) 0 MPa in situ horizontal stress, (ii) 0.5 MPa in situ horizontal stress, and (iii) 0 MPa in situ horizontal stress with a 2°dilation angle. These results are presented for the following patterns: a Pattern 1, b Pattern 2, c Pattern 3, and d Pattern 4
The load capacity of the rock mass surrounding each individual anchor was found to decrease as the spacing between two adjacent anchors reduced. Figure 41 presents the stress in individual anchors after a 50-mm anchor displacement in models featuring a row of anchors within a rock mass characterized by continuous horizontal and discontinuous vertical joints (Pattern 2). The figure shows that there is a rapid increase in anchor stress as the spacing between the anchors increases. When the spacing is minimal, there is a significant difference between the stress in the central anchors and the two side anchors. This difference diminishes as the spacing increases. In addition, the load capacity of the rock mass surrounding the anchors increases with larger anchor spacing.
4.4 Failure Mode
The failure of the models could not be fully investigated as UDEC halted the models before the development of the failure surface due to block overlap. Despite this, the separation between some blocks at the base of the anchor was observed, indicating the potential initiation of the failure surface. In patterns with continuous horizontal and discontinuous vertical joints, a laminar failure occurred at the base, exhibiting a flat surface following the horizontal joint immediately below the anchor base. This suggests a non-conical failure, consistent with the observations of Shabanimashcool and Bērziņš (2023), who observed a frustum-shaped failure. This was particularly evident in the uplift of the anchor groups with short spacings (1-m and 3-m intervals), where the entire rock mass was lifted with a flat base between the anchors. In the models with continuous vertical joints, failure occurred along the vertical joints, and the blocks in contact with the anchor slid along the joint surface. In the model with rotated joints, a separation surface was observed along the continuous joints at the base of the anchor and along the discontinuous joints on the right of the anchor base. These observed failures suggest that failure initiates along these joints, but their further development within the rock mass remains uncertain.
5 Discussion
A series of uplift tests were conducted in a laboratory using an in-house testing rig. The data obtained from these tests were used to calibrate numerical models that provided insights into the stress distribution within block models during loading. The calibration data was also extrapolated to deep rock anchor models to gain a more realistic understanding of the stress distribution exhibited in these scenarios.
5.1 Influence of Joint Patterns on the Stress Distribution, Load Arching, and Vertical Displacement Within the Rock Mass
Figures 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25 and 26 show the load distribution in numerical models based on the results of laboratory testing. Load arching was observed within the horizontal layers of models with continuous horizontal joints. The arching effect was stronger in the model with larger blocks, as previously described by Shabanimashcool and Bērziņš (2023). The load arching was slightly steeper in Patterns 3 and 5, which featured continuous vertical and discontinuous horizontal joints and interlocked joints, respectively. In models with rotated joints, the orientation of the load arching was found to be aligned with the continuous layers. The arching effect was most pronounced in the flattest models, and decreased at rotation angles between 25° and 40°, consistent with the work conducted by Shabanimashcool and Bērziņš (2023), who observed that the arching effect occurs in rock masses that have at least one joint set parallel or nearly parallel to the anchor axis. In models that had 10° and 25° tilt angles, one of the joint sets was nearly parallel to the anchor axis, resulting in the formation of load arches, while in models with a greater degree of rotation, the angle between the joint sets and the anchor axis was too large to form a strong arch.
The vertical displacement observed in the numerical models of laboratory tests is displayed in Figs. 5, 6, 7, 8, 9 and 10. The vertical displacement was greatest above the anchor block and dissipated laterally. The vertical displacement in the numerical models was slightly greater than that observed in the physical models, likely due to void closure and the non-linear distribution of normal stiffness in the physical models. Specifically, the perfect block contacts and a uniform normal stiffness in the numerical models allowed for the direct transfer of force between the blocks. Due to these differences, there was less vertical displacement above and to the sides of the anchor in the physical models. The numerical and physical models exhibited similar lateral vertical displacement behavior. Models with a small tilt angle (Patterns 4 and 4b) exhibited vertical displacements that were greatest in the direction perpendicular to the continuous layers, indicating that force transfer was normal to the layers. In models with a larger tilt angle (Patterns 4c and 4d), the vertical displacement was greatest parallel to the continuous layers, indicating direct force transfer along the layers, resulting in uplift.
Figures 32, 33, 34, 35, 36, 37 and 38 present the stress distribution in a rock mass in large-scale rock anchor models following anchor pull. These models showed that the anchor load is distributed over a large area, especially when the joints are horizontally continuous. In such cases, the anchor load was distributed through flat load arches over an area with a radius of up to 15 m. This arching was absent when the continuous joints and/or the blocks were vertically oriented. The load arching was observed to be asymmetrical in the model with a 25° tilt angle. The left side of the anchor exhibited a strong arching effect in which the load was directly transferred into the continuous layers up to 10 m away from the anchor, while the load on the right side of the anchor was confined to an area within 4 m of the anchor. When pulling a group of anchors, there was significant overlap between the load arches in models with continuous horizontal joints. This resulted in the underutilization of the load capacity of each anchor and reduced the capacity of the central anchors. In such a rock mass, the anchor spacing should be at least twice the width of the arch to allow for full capacity utilization. Alternatively, the anchors should be installed at different levels to prevent arch overlap. In real-world scenarios, the reduction in capacity due to overlapping arches is likely to be less pronounced than in the two-dimensional models, as real-world applications exhibit three-dimensional effects that would provide restraining influences in both the in-plane and out-of-plane directions.
Figures 27, 28, 29, 30 and 31 show the vertical displacement in the rock mass surrounding large-scale rock anchors. In models with continuous vertical joints, the displacement was confined to blocks in contact with the anchor on either side. However, a larger region was subjected to uplift by the anchors in models with discontinuous vertical joints. These results were consistent with the work of Shabanimashcool and Bērziņš (2023), who observed a flat region that resembled a frustum shape being uplifted at the anchor base if one joint set was parallel to the anchor axis. In the tilted block model, the primary uplift occurred perpendicular to the continuous joints, with the base of the uplifted region following the joints; this corresponded to a frustum rotated by 25°. In models with anchor groups spaced in intervals of 1 m and 3 m, the surrounding rock mass was uplifted as a singular medium with a flat base, suggesting that individual anchor capacity was reduced when the anchor spacing was minimal. This observation is consistent with the work of Ismael et al. (1979), especially with regard to their assumptions of rock mass failure with a flat base between the anchors in a group.
These models suggest that the orientation of the blocks relative to the anchor axis affects the stress distribution and the vertical displacement of the rock mass. Shabanimashcool and Bērziņš (2023) also observed load arching when at least one joint set was parallel to the anchor axis. The continuity of joints also influenced the behavior of the rock mass, with models that featured continuous vertical joints exhibiting uplift in smaller regions compared to models with discontinuous vertical joints. Previous studies by Hobst and Zajíc (1983) and Wyllie (1999) discussed the effect of jointing on the failure shape of rock masses with shallow anchors. Brown (2015) suggested that these influences might not apply to deeper rock anchors and questioned the validity of a 90° uplift cone. The observed vertical displacement around the deep anchors in these models revealed a smaller uplift region compared to the 90° cone, potentially supporting the proposal made by Brown (2015).
5.2 Load Capacities
Figure 39 presents the load capacities of a single 10-m anchor in four distinct block masses with identical block sizes under gravity loading. These models reveal that there is a significant variation in load capacity depending on the orientation and continuity of the joints. Patterns with continuous vertical joints exhibit the lowest capacities, consistent with the suggestions of Hobst and Zajíc (1983) and Wyllie (1999), who proposed that an anchor’s load capacity would be minimized in a rock mass with joints parallel to the anchor axis and maximized when the joints were normal to the anchor axis. Pattern 2, which exhibited vertical interlocking, had the second-highest load capacity. The highest load capacity was observed in the pattern with tilted blocks, which was relatively surprising considering the results of the physical models. This discrepancy could be attributed to the combination of load arches and the absence of clear slip surfaces near the anchor in the pattern. In an actual rock mass, the load capacities would presumably exceed those found in these models, especially considering the utilization of smooth and flat joints in the numerical model, which are unlikely to occur under natural conditions.
In the laboratory tests conducted, concrete blocks with smooth surfaces were used, representing an artificial case that could be seen as a worst-case scenario. This is due to the fact that rock masses in real-world scenarios are unlikely to exhibit such smooth surfaces and a zero dilation angle. Figure 40 demonstrates the influence of minor variations in the in situ horizontal stress and the joint dilation angle on the load capacities of single, large-scale anchors. The models featuring continuous vertical joints exhibit the highest sensitivity to these changes. In these models, a dilation angle of 2° leads to an increased load capacity, consistent with the findings of Shabanimashcool and Bērziņš (2023), who demonstrated the occurrence of load arching in a rock mass with a joint set sub-parallel to the anchor axis contingent on a dilation angle of 2° or more. In contrast, models lacking continuous vertical joints displayed less sensitivity to changes in in situ horizontal stress, consistent with the physical models of Grindheim et al. (2024), which found vertical stress changes to have a more pronounced effect on these patterns.
The load of individual anchors within a group is presented in Fig. 41, which shows a clear reduction in the capacity of individual anchors when installed in close proximity. At a spacing of 5 m, the load distribution was more uniform, albeit slightly lower in the central anchor. To fully utilize the uplift capacity of the rock mass, the anchors should be placed at a distance that prevents them from falling within the load arch of the neighboring anchors. In this rock mass, that distance would be approximately 7 m as indicated by Fig. 33. However, this distance would vary for other patterns depending on the spread of the load arches.
The sensitivity analysis conducted in this study reveals that several joint parameters have a strong effect on uplift capacity in rock masses with laminar joints. Joint spacing was the most critical factor, followed by the friction angle and joint normal stiffness. The prevailing design method, which is considered to be conservative and is based on simplified assumptions, omits joint parameters in uplift capacity calculations (Brown 2015). This sensitivity analysis reveals that the exclusion of joint parameters can lead to imprecise design calculations, as joints can exert a strong control on the uplift capacity. Consequently, designs must remain relatively conservative to ensure the stability of the rock mass.
These numerical models have demonstrated that the rock mass capacity is influenced by factors, such as joint orientation and continuity, in situ stresses, and the dilation angle of the joints. Given these findings, it demonstrates the importance of load testing anchors after installation, especially for critical infrastructure, to ensure that the anchors fulfill their requirements. Individual load testing of anchors is the standard practice (PTI 2004; BSI 2015), this research demonstrates that in certain scenarios, when the joint configuration is likely to induce overlapping load arches, it could be beneficial with simultaneous load testing of neighboring anchors.
5.3 Anchor Spacing
BSI (2015) recommends a minimum center-to-center anchor spacing of four times the fixed anchor diameter to limit interaction between the anchors. However, dam strengthening typically employs a spacing range of 1.5–3.5 m, with instances of 1.0–1.5 m spacing also reported (Xu and Benmokrane 1996). The single 10-m anchor models revealed that the rock volume affected by uplift varies significantly depending on the rock mass. In a rock mass with continuous horizontal joints, the anchor influenced rock within a 7-m radius. In the model with rotated joints, the influence extended 10 m in one direction and 4 m in the other. To avoid anchor interactions in these rock masses, anchor spacings should be at least 14 m and 13 m for Patterns 2 and 4, respectively. These findings suggest that the recommended spacings may be insufficient to prevent interaction between adjacent anchors at the same depth.
Xu and Benmokrane (1996) highlighted issues arising from the installation of a row of anchors in rock masses with sub-horizontal bedding or structural features, as laminar failure could occur in these rock masses. They proposed the installation of staggered vertical anchors to circumvent this problem, an approach employed by Brown (2015) in the context of a dam foundation in igneous rock that exhibited sheet jointing. These models suggest that to avoid interaction between two anchors at the same depth in a rock mass with sub-horizontal jointing, anchor spacing must exceed 5 m, potentially up to a recommended spacing of 15 m.
5.4 Limitations of the Numerical Models
The numerical models presented in this study have several limitations that may account for the discrepancies observed between the physical models and numerical simulations. As discussed in Sect. 4.4, the contacts between the blocks in the physical model contained voids that needed to be closed before load transfer; in addition, some concrete blocks were uneven due to imperfect cutting. In contrast, the numerical models assumed perfect block contacts, resulting in immediate load transfer upon application.
During the testing of high-load physical models, cracking sounds were heard, and it was observed that the corners of some blocks failed slightly. Indeed, it was observed that some of the intact blocks had failed in the tests involving Patterns 3 and 5. However, the numerical models maintained block integrity throughout the simulation. The UDEC’s inability to model intact block failure limited its ability to simulate the post-peak behavior of the physical models. Furthermore, the UDEC models often stopped near peak loading due to block overlap, necessitating an increased focus on the pre-peak load behavior observed during the elastic stage of the tests.
The boundary conditions in the numerical models are also known to influence the results. Load arching was observed to start at the top of the steel frame on both sides (Figs. 15, 16, 17, 18, 19). In Pattern 3, which featured continuous vertical and discontinuous horizontal joints, the boundary conditions resulted in two arches being formed (Fig. 15), potentially increasing the capacity of this pattern.
Potential scale effects may have influenced the smaller models used in this study. Previous research, such as the work by Bidgoli et al. (2013), has investigated the deformability of fractured rocks and found that models smaller than a representative elementary volume (REV) for the rock mass exhibited higher strength, while those larger than the REV showed stable strength. This observation aligns with the findings of Mas Ivars et al. (2008), who also noted higher strength in models below the REV. Given these insights, it is likely that the laboratory models used in this study, which most likely were smaller than the REV size of the rock mass, were able to attain a higher load capacity.
The limitations of the large-scale models are primarily due to their basis in the calibration process used to determine the material properties rather than any real experimental tests conducted on appropriate rock masses and anchoring. The artificial rock masses used are equivalent to soft rock masses rather than hard rock masses, raising questions about the generalizability of these results to hard rock masses. In particular, the modeled rock masses lack intact rock bridges. Furthermore, all numerical models are two-dimensional, consequently ignoring any three-dimensional effects and casting uncertainty on the generalisability of these results to real-world three-dimensional applications.
6 Conclusions
Numerical models were developed and calibrated using physical models to simulate the uplift of rock mass due to a rock anchor. These models examined the load transfer within the rock mass under a concentrated upward anchor load. Each model incorporated two joint sets that varied in terms of the orientation and pattern of the joints.
Key findings from the analysis of these models include (1) the horizontal stress in the rock mass surrounding the rock anchor increased upon the application of the anchor load, especially in models with joint sets oriented parallel or perpendicular to the anchor axis; (2) the greatest displacement in rock masses with orthogonal joint sets occurred in the direction parallel to the joint set with the smallest angle to the loading axis of the anchor.
The distribution of principal stress in the models showed that most of the joint patterns investigated resulted in load arching when exposed to an anchor load. In models with continuous horizontal joints, relatively flat load arches were observed within each layer. Small rotations of these joints resulted in the corresponding rotation of these flat load arches. This arching effect became weaker and more asymmetrical as the rotation angle increased beyond 25°. In a rock mass with continuous vertical joints and discontinuous horizontal joints, upward-facing load arching was observed at a 30° angle from the horizontal. The arching effect was symmetrical when the joint sets were normal and parallel to the anchor loading axis and asymmetrical when the joint sets obliquely intersected with the loading direction.
In large-scale anchor models initialized with material properties equivalent to those used in laboratory tests (as determined using calibration processes) with zero or near-zero in situ horizontal stresses, the load capacity was found to be low in rock masses with continuous vertical joints and higher in rock masses with discontinuous vertical joints.
The uplift capacity of individual anchors in a row of anchors decreased when the load arches of adjacent anchors overlapped, i.e., the closer the spacing between anchors, the lower the uplift capacity of individual anchors. In models with continuous horizontal and discontinuous vertical joints, the simulations showed that the anchor spacing must be larger than the anchor depth to avoid the overlap of the load arches generated by individual anchors. In a rock mass with continuous horizontal joints, laminar failure occurred along one of the joints at the base of the anchors when a row of anchors was installed at the same level; this was particularly evident when the anchor spacing was too small.
This research indicates that the uplift mechanisms and capacity of the rock mass are significantly influenced by both the orientation of joints relative to the anchor and the spacing between anchors. Full-scale uplift tests in varying rock masses are recommended to capture the 3D effects in real rock masses and provide a more comprehensive understanding of the behavior of anchor systems. This includes conducting simultaneous uplift tests on anchors installed in groups or rows to understand how spacing impacts individual anchor capacity across different rock masses. These proposed tests aim to translate our findings into practical design applications.
Data Availability
The datasets generated during the current study are available from the corresponding author upon reasonable request.
Abbreviations
- \(\nu\) :
-
Poisson’s ratio
- \(G_m\) :
-
Shear stiffness of the rock mass
- E :
-
Young’s modulus
- \(G_r\) :
-
Shear stiffness of the intact rock
- \(E_m\) :
-
Young’s modulus of the rock mass
- \(k_n\) :
-
Joint normal stiffness
- \(E_r\) :
-
Young’s modulus of the intact rock
- s :
-
Joint spacing
- G :
-
Shear stiffness
References
Alejano LR, Muralha J, Li CC et al (2018) ISRM suggested method for determining the basic friction angle of planar rock surfaces by means of tilt tests. Rock Mech Rock Eng 51:3853–3859. https://doi.org/10.1007/s00603-018-1627-6
Bidgoli MN, Zhao Z, Jing L (2013) Numerical evaluation of strength and deformability of fractured rocks. J Rock Mech Geotech Eng 5(6):419–430. https://doi.org/10.1016/j.jrmge.2013.09.002
Bieniawski Z, Bernede M (1979) Suggested methods for determining the uniaxial compressive strength and deformability of rock materials. Int J Rock Mech Min Sci Geomech Abstr 16(2):137–140. https://doi.org/10.1016/0148-9062(79)91451-7
Brown ET (2015) Rock engineering design of post-tensioned anchors for dams—a review. J Rock Mech Geotech Eng 7(1):1–13. https://doi.org/10.1016/j.jrmge.2014.08.001
Bruce DA (1976) The design and performance of prestressed rock anchors with particular reference to load transfer mechanisms (as reproduced by ProQuest LLC 2014 (UMI U433767)). Ph.D. thesis, University of Aberdeen, Aberdeen, Scotland
BSI (2015) BS 8081:2015 Code of practice for grouted anchors. British Standards Institution, London
Dados AT (1984) Design of anchors in horizontally jointed rocks. J Geotech Eng 110(11):1637–1647. https://doi.org/10.1061/(ASCE)0733-9410(1984)110:11(1637)
García-Wolfrum S, Serrano A, Olalla C (2007) Model failure tests on rock anchors. In: 11th Congress of the International Society for Rock Mechanics: the second half century of rock mechanics. Taylor & Francis Group, Lisbon, Portugal, ISRM, pp 339–342
Grindheim B, Aasbø KS, Høien AH et al (2022) Small block model tests for the behaviour of a blocky rock mass under a concentrated rock anchor load. Geotech Geol Eng 40:5813–5830. https://doi.org/10.1007/s10706-022-02251-1
Grindheim B, Li CC, Høien AH et al (2024) Behavior of a rock mass in uplift field tests of rock anchors. Rock Mech Rock Eng. 57:2339–2364. https://doi.org/10.1007/s00603-023-03689-2
Grindheim B, Li CC, Høien AH, et al (2024) Laboratory tests of large-scale block models on the load transfer and failure mechanisms of rock masses subjected to anchor loading. Rock Mech Rock Eng (Manuscript under review)
Hobst L, Zajíc J (1983) Anchoring in rock and soil. Elsevier Scientific Publishing Company, New York
Indraratna B, Soomro MHAA, Rujikiatkamjorn C (2021) Semi-empirical analytical modelling of equivalent dynamic shear strength (EDSS) of rock joint. Transp Geotech 29(100):569. https://doi.org/10.1016/j.trgeo.2021.100569
Ismael NF (1982) Design of shallow rock-anchored foundations. Can Geotech J 19(4):46–3471. https://doi.org/10.1139/t82-050
Ismael NF, Radhakrishna HS, Klym TW (1979) Uplift capacity of rock anchor groups. IEEE Trans Power Appar Syst 98(5):1653–1658. https://doi.org/10.1109/TPAS.1979.319483
ISRM (1978) Suggested methods for determining tensile strength of rock materials part 2: suggested method for determining indirect tensile strength by the Brazil test. Int J Rock Mech Min Sci 15:99–103. https://doi.org/10.1016/0148-9062(78)90003-7
Itasca (2011) UDEC 5.0 user manual. Itasca Consulting Group Inc., Minneapolis
Littlejohn GS, Bruce DA (1977) Rock anchors—state of the art. Foundation Publications LTD., Brentwood
Mas Ivars D, Pierce M, DeGagné D et al (2008) Anisotropy and scale dependency in jointed rock-mass strength—a synthetic rock mass study. In: Continuum and distinct element numerical modeling in geo-engineering. Itasca, Minneapolis, USA, 1st International FLAC/DEM Symposium, p 9
Panton B (2016) Numerical modelling of rock anchor pullout and the influence of discrete fracture networks on the capacity of foundation tiedown anchors. Master’s thesis, The University of British Columbia, Vancouver, Canada
PTI (2004) Recommendations for prestressed rock and soil anchors, 4th edn. Post-Tensioning Institute, Farmington Hills
Schädlich B (2014) Schweiger HF (2014) A new constitutive model for shotcrete. In: 8th European conference on numerical methods in geotechnical engineering. Taylor and Francis Group, Delft, The Netherlands, NUMGE, p 6
Shabanimashcool M, Bērziņš A (2023) A simplified approach to estimate anchoring capacity of blocky rock mass with pressure arch theory. Rock Mech Rock Eng. https://doi.org/10.1007/s00603-023-03421-0
Soomro MHAA, Indraratna B, Karekal S (2022) Critical shear strain and sliding potential of rock joint under cyclic loading. Transp Geotech 32(100):708. https://doi.org/10.1016/j.trgeo.2021.100708
Standards Norway (2015) NS-EN 1993-1-1:2005+A1:2014+NA:2015—Eurocode 3: design of steel structures. Part 1-1: general rules and rules for buildings. Standards Norway, Oslo, Norway
Standards Norway (2021) NS-EN 1992-1-1:2004+A1:2014+NA:2021—Eurocode 2: design of concrete structures. Part 1-1: general rules and rules for buildings. Standards Norway, Oslo, Norway
Tayeh BA, El dada ZM, Shihada S et al (2019) Pull-out behavior of post installed rebar connections using chemical adhesives and cement based binders. J King Saud Univ Eng Sci 31(4):332–339. https://doi.org/10.1016/j.jksues.2017.11.005
Thomas-Lepine C (2012) Rock bolts—improved design and possibilities. Master’s thesis, Norwegian University of Science and Technology (NTNU), Trondheim, Norway
Weerasinghe RB, Littlejohn GS (1997) Uplift capacity of shallow anchorages in weak mudstone. In: Ground anchorages and anchored structures: proceedings of the international conference. Thomas Telford Publishing, London, England, pp 23–33
Wyllie DC (1999) Tension foundations. E & FN SPON, London, pp 310–359
Xu H, Benmokrane B (1996) Strengthening of existing concrete dams using post-tensioned anchors: a state-of-the-art review. Can J Civ Eng 23(6):1151–1171. https://doi.org/10.1139/l96-925
Acknowledgements
The authors acknowledge the financial support of the Research Council of Norway through the research project ROCARC (Project number 303448) and of the NPRA, Bergen, Norway, through the Rock Anchoring project (Project number 90503200). Partners of the project include the NTNU, Norwegian Group of Rock Mechanics (NBG), NPRA, SINTEF, NGI, The Arctic University of Norway (UiT), Multiconsult AS, Norconsult AS, and NORSAR.
Funding
Open access funding provided by NTNU Norwegian University of Science and Technology (incl St. Olavs Hospital - Trondheim University Hospital). This work was supported by the Research Council of Norway through the research project ROCARC (Project number 303448) and by the NPRA, Bergen, Norway, through the Rock Anchoring project (Project number 90503200).
Author information
Authors and Affiliations
Contributions
All the authors contributed to the study’s conception and design. The initial model of Pattern 2 was developed by Nghia Trinh. The rest of the models were developed by Bjarte Grindheim. The project leader was Charlie C. Li. Data collection and analysis were performed by Bjarte Grindheim. The first draft of the manuscript was written by Bjarte Grindheim, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grindheim, B., Trinh, N., Li, C.C. et al. Investigating Load Arches and the Uplift Capacity of Rock Anchors: A Numerical Approach. Rock Mech Rock Eng (2024). https://doi.org/10.1007/s00603-024-03930-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00603-024-03930-6