1 Introduction

Rock anchors are post-tensioned high-capacity reinforcement measures. They distinguish themselves from rock bolts, which are smaller in scale and lack post-tensioning. Specifically, rock anchors are sub-structural members that transmit a tensile force from the main structure to the surrounding ground (Hanna 1982). The tensile force is resisted by the shear and/or tensile strength of the surrounding ground and the weight of the overlying mass (Brown 2015), and the anchors are often installed deep to fasten the structure to competent ground (Hanna 1982). Rock anchors are commonly used to support and stabilize large-scale infrastructures, such as dams, the abutments of large masts, cableways and bridges, rock formations and slopes (Xanthakos 1991), wind turbines (Yan et al. 2013; Shabanimashcool et al. 2018), and to reduce the uplift of submerged structures (Mothersille and Littlejohn 2012; Roesen and Trankjær 2021).

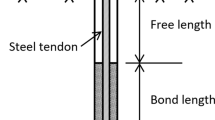
The reliable and cost-effective design of rock anchoring requires knowledge and understanding of their failure modes. According to Tayeh et al. (2019), it is important to understand the failure modes, strength, load displacement, and steel relaxation characteristics for the correct usage of rock anchors. In principle, rock anchors can fail in four ways, as shown in Fig. 1, which are: (1) steel tendon tensile failure; (2) tendon–grout bond or interface failure; (3) grout–rock bond or interface failure; and (4) rock mass uplift failure (Littlejohn and Bruce 1977; Brown 2015). The capacity of the rock-anchoring system is equal to the weakest of the four failure modes (Pease and Kulhawy 1984; Kim and Cho 2012). Failure modes 1 and 2 are well understood and have been laboratory tested in many studies, whereas Failure modes 3 and 4 are more uncertain, and the current standard design approaches to protect against Failure modes 3 and 4 has several deficiencies due to this uncertainty, according to Brown (2015). However, the current design practice ensures that rock anchors are embedded deep enough that Failure modes 1–3 occur before rock mass uplift (Weerasinghe and Adams 1997). The focus of this study was on Failure mode 4—rock mass uplift failure.

Fig. 1
figure 1

Four principal failure modes of a pre-tensioned rock anchor from the literature: (1) steel tendon tensile failure; (2) tendon–grout bond or interface failure; (3) grout–rock bond or interface failure; and (4) rock mass uplift failure

Full size image

The estimation of the uplift capacity is based on crude cone or wedge mechanisms, where the dead weight of the rock cone or wedge is calculated (Xanthakos 1991) and/or the shear resistance of the cone is calculated with presumptive shear-strength values or from back-calculation (Brown 2015). The calculation based on dead weight alone is invariably conservative because the tensile and shear strength of the rock is ignored (Xanthakos 1991). Tests by Bruce (1976) showed that the standard ’weight of rock cone’ method was conservative by at least one order of magnitude. Very few experimental tests have documented rock mass failure around rock anchors (Xanthakos 1991), and those studies in which rock mass uplift failure has been observed were based on short anchors (Brown 2015). Some of the studies that have tested and reported on rock mass uplift failure include Bruce (1976), Ismael et al. (1979), Ismael (1982), Dados (1984), Weerasinghe and Littlejohn (1997), García-Wolfrum et al. (2007), Thomas-Lepine (2012), Thomas-Lepine and Lia (2014).

The apex angle of the cone varies depending on the nature of the anchorage and the properties of the rock mass. It is common to assume an apex angle of 60\(^{\circ }\) or 90\(^{\circ }\), located at the distal end or at the mid-point of the bonded length. In some designs, the apex angle is placed at the proximal end of the anchored zone. An apex angle of 60\(^{\circ }\) is commonly used for soft, heavily fissured, or weathered rock masses and 90\(^{\circ }\) is used for everything else (Brown 2015). The rock mass and structural geology affects the failure surface. Rock mass bedding planes can increase or decrease the apex angle of the failure surface cone. Bedding planes oriented normal to the anchor direction are most favorable, with the least favorable being when the bedding planes are parallel to the anchor (Hobst and Zajíc 1983; Wyllie 1999). Shabanimashcool and Bērziņš (2013) conducted a numerical study that contradicts the hypothesis proposed by Hobst and Zajíc (1983) and Wyllie (1999). Their study revealed that rock masses with discontinuity sets parallel to the anchor exhibited the highest capacity, presenting new insights into the load-bearing behavior of such rock masses.

Bruce (1976) performed full-scale testing of 53 strand anchors in carboniferous strata, in which seven failed through rock mass uplift failure. Rock mass failure was only observed for the short anchorages, whereas for the longer (>1.5 m) anchorages, the failures occurred in the tendon–grout and grout–rock interfaces. Ismael et al. (1979) and Ismael (1982) conducted full-scale uplift tests on several rock types, from shale to sound limestone. The radial cracking and heaving of the rock mass extended to a distance equal to the anchor depth. Dados (1984) performed full-scale uplift tests in a granitic mass. The ground-surface heaving was measured, and it was observed that the maximum radius at the site where the heaving was 10% or more of the maximum heaving was roughly equal to the anchor length. Weerasinghe and Littlejohn (1997) performed uplift of 7-wire strand anchors in weak mudstone. These tests identified ground-surface heaving close to the anchors; it was found that the maximum distance from the anchor with observed heaving stabilized at around 1200–1400 mm when the anchors were installed at depths of 1400 mm or more. They observed a combined mode of rock mass failure on the top 0.5 m of the fixed anchor and grout–rock shear failure on the remaining part of the anchor. García-Wolfrum et al. (2007) performed small-scale uplift tests on intact rock blocks in the laboratory. The failure surfaces of these tests were not conical; instead, they widened toward the surface. Thomas-Lepine (2012), Thomas-Lepine and Lia (2014) tested the uplift of bolts in a limestone quarry. The failure shape of the tests was influenced by the jointing of the rock mass because the tested bolts were small and short. Throughout the literature, failure shape has been reported as being strongly structurally controlled, with rock mass failure only occurring for short embedment depths. For deeper anchors, the failure occurred in one of the grout interfaces.

In a recent numerical investigation conducted by Shabanimashcool and Bērziņš (2013), it was demonstrated that the presence of a discontinuity sub-parallel to the anchor enhances the rock mass capacity through load arching effects. The rock blocks aligned normal to the sub-parallel discontinuities interlock via block rotations, leading to the development of an arch-shaped compressive stress at the block contacts. This arch configuration significantly increased the rock mass’s resistance against the tensile force transmitted by the anchor. The numerical models revealed a distinct failure shape different from the conventional inverted cone; instead, the rock mass exhibited a frustum shape, resembling a cone with its end cut parallel to the ground surface at the anchor base, and its apex located deeper than the anchor base. Furthermore, corroborating these findings, a laboratory study by Grindheim et al. (2022) also observed the occurrence of load arches in a laminar block model subjected to rock anchor loading.

The current design methods to protect against failure mode 4 have several deficiencies, which were listed in a review by Brown (2015). The stress distribution induced by the anchor in the overlying rock mass is not considered, nor is the way the anisotropy of the rock mass affects the stresses and failure. Most tests have been performed on shallow anchors as a necessity, which questions their representativeness for larger and longer anchorages. Plus, the influence of the rock mass structure on the failure shape is ignored. In the literature, it is evident that the rock mass structure affects the failure shape of shallow anchors; whereas for deeper anchors, the near-surface rock mass structure might not have the same controlling influence, and the 90\(^{\circ }\) uplift cone assumption might not be valid. Bruce (1976) also questioned whether rock mass failure occurred for anchors installed deeper than 2 m, where the rock mass is much stronger than the grout, therefore making it the only other failure modes that occurs below a certain depth. Brown (2015) also questioned the usage of presumptive or back-calculated shear or tensile strength values, based on using a ’theoretical’ failure cone, to calculate the rock mass strength that do not consider the variability of the strength parameters in the varying local rock mass structures, or the progressive and complex nature of rock mass failure.

The full-scale testing of rock anchors is important because of the uncertainties and deficiencies of the design methods, with uplift failure being the least satisfactory of them all. The purpose of the field tests introduced in this paper was to investigate the uplift capacity of the rock mass surrounding the rock anchors. The tests, which were highly instrumented and measured, were performed on full-scale anchors in a limestone quarry. The instrumentation included standard measurements, such as anchor load and displacement, and also ground-surface heaving, the vertical displacements at different depths in the rock mass, and changes in the horizontal stress in the rock mass. Geophones were used to localize the fracturing during testing, an optical and an acoustic televiewer were used to localize the fracture planes, both before and after testing, and after the test, the fractured rock was removed so that the failure crater from the tests could be mapped. The objective of this work was to develop a better understanding of the mechanics of the uplift failure of the rock mass around the rock anchors. Through these field tests and the current literature combined with historical data, this may help in the development of a more precise dimensioning method to protect against uplift failure.

2 Method and Procedure

2.1 Testing Plan

The field tests were designed to lifting up the rock mass around four anchors. From theory that an upward load applied at the toe of the anchor would promote uplift failure in the rock mass. Therefore, the anchors used in the tests were designed such that an endplate could be attached to the distal end of the anchor stem, and with the cylindrical surface being smooth (Fig. 2). The anchor was fully encapsulated in the borehole using cementitious grout. The pull load applied at the anchor head was entirely transferred to the endplate. The anchors used were 64 mm in diameter. These were placed in 140-mm boreholes. The endplates of the anchors were planned to be placed at two different depths—1 and 1.5 m. The inner span of the beam supports was 3 m, which was decided based on the anchoring depth and an apex angle of 90\(^{\circ }\) for the failure cone, as recommended in the literature (Littlejohn and Bruce 1977; Brown 2015).

Fig. 2
figure 2

Setup of the field tests with smooth bar anchors with an endplate and the assumed failure surface

Full size image

2.2 Test Site

The selection of the test site was based on specific criteria related to the rock mass. The tests needed a location characterized by moderate rock mass quality with a blocky structure. During the tests, it was wanted that failure occurred both within the intact rock and along existing joints. If the rock quality was excessively high and massive, it would have exceeded the equipment’s capacity to induce failure. Conversely, if the rock was excessively weak, it would resemble a geotechnical test in soil-like material. The location of the field tests was the open-pit quarry of Verdalskalk AS in Tromsdalen, Norway. The test site was located in the top corner of the quarry on an unmined rock surface, which comprised relatively flat and strong limestone, classified as a moderately strong rock mass. The rock at the site was homogeneous, with a uniaxial compressive strength (UCS) of 115 MPa, ranging from 106.7 to 121.4 MPa, and a Young’s modulus of about 71 GPa. The rock mass and rock joints in the test area were mapped and measured. The rock mass was classified using the Q- and rock mass rating (RMR) system, summarized in Table 1, and was found to be of good quality. Three joint sets were found in the rock mass. The dip and dip direction of the joint sets, together with the bench slope nearby, are given in the stereogram in Fig. 3. All the joint sets were planar and rough. The rock mass at the site had signs of blast damage close to the bench crest, therefore as much as possible of the loose material was removed as a safety precaution before the drilling started. Figure 4 shows the rock mass under the test site seen from the bench below. The blast damage was highest closest to the top of the bench.

Table 1 Rock mass classification of the test site using the Q- and RMR-systems
Full size table
Fig. 3
figure 3

Stereogram with legend showing the joint-set mapping in the rock mass and the bench slope at the test site

Full size image
Fig. 4
figure 4

Rock mass at the test site seen from the bench below, with clear signs of blast damage at the top of the bench closest to the test site indicated by red arrows

Full size image

The holes for the rock anchors were drilled to a depth of 1.6 m with a spacing of at least 3 m and a minimum of 3 m to the bench crest. Around two of the anchors, holes 102 mm in diameter were drilled to a depth of 2.5 m for the instrumentation. All the holes were drilled pneumatically.

2.3 Anchor Capacity Estimates Based on Current Knowledge

The anchor capacities of the tests were estimated based on the design methods given by the Norwegian Public Roads Administration (NPRA) (NPRA 2018) and from the back-calculation of historical data. The design method given in NPRA (2018) used the dead weight of the overlying rock mass and presumptive shear-strength values along the failure cone. The presumptive shear strength and apex angle were provided in a table based on the number of joint sets in the rock mass. For a rock mass with three joint sets and random joints, the shear strength was assumed to be 50 kPa and the apex angle 60\(^{\circ }\). The historical data used for the back-calculation came from tests in intact rock (García-Wolfrum et al. 2007), carboniferous strata (Bruce 1976), a very weak shale (Littlejohn and Bruce 1977) and a granitic mass (Dados 1984). The rock mass strength used in the estimates was based on an average from the historical data, rounded to the closest half MPa. The anchor depth was set to 1.4 so that the rock mass capacity would not overcome the capacity of the anchor steel and the bending strength of the beam, which resulted in a safety factor of 1.25. It was also important to make sure that the rock mass was the weakest part of the system and that the anchors could be pulled all the way out. The anchor capacity estimations are presented in Table 2.

Table 2 Anchor capacity estimates based on presumptive values from NPRA (2018) and back-calculation from historical data
Full size table

The back-calculated shear strengths from the historical data are summarized in Table 3. It was assumed that the failure surface was an inverted cone, that the shear strength was uniform in the rock mass, and the apex angle was 90\(^{\circ }\) where nothing different was stated. All calculations were made from the bottom of the embedment depth.

Table 3 Back calculated shear strengths from historical data
Full size table

2.4 Test Preparation

2.4.1 Rock Anchors

The anchors used were modified FatBar 64 anchors from Peikko, Finland. Two lengths were used—2.5 and 3 m. The anchors were smooth cylindrical bars, 64 mm in diameter, with an M68 threaded section of 625 mm at the distal end. A washer, plate and nut were placed at the distal end, acting as an endplate. The endplate was 130 mm in diameter. The anchor steel had a Young’s modulus of 200 GPa, with a nominal tensile strength of 1000 MPa (i.e., 3217 kN for the anchor bar).

The threaded lower section of the anchors was wrapped with adjustable plastic sleeves to de-bond it from the grout in the borehole, as illustrated in Fig. 5. Through this arrangement, the pull load applied on top of the anchor was completely transferred to the endplate at the distal end of the anchor.

Fig. 5
figure 5

Close-up of the endplate of the anchor, with the debonding pipe above for covering the anchor thread, which allowed the anchor stem to be completely debonded from the grout

Full size image

2.4.2 Anchor Installation

To ensure that the steel beam was levelized, two platforms of cast concrete were constructed symmetrically on the sides of each anchor for the beam footings. The dimensions of the platforms were 0.8 \(\times\) 1.0 m, with a distance of 1.4 m to the anchor on each side. The concrete was left to harden for four weeks before the testing commenced.

After the concrete platforms had been cast, installation of the anchors could commence. The water in the boreholes was drained first, and then two boreholes were filled with gravel to a depth of 1.5 m and the other two to 1 m. The anchors were lifted into the boreholes using an excavator, and then grout was pumped into the holes until it appeared at the hole collar. The grout had a water-to-cement ratio (W/C) of 0.42 with an average strength of 56.2 MPa after 28 days.

2.4.3 Instrumentation

The four anchors were instrumented to different degrees. All the anchors were fitted with a pressure gauge that measured the oil pressure coming into the hydraulic jack, which was used to calculate the applied pull load. The total displacements of the anchor and the beam were measured using linear variable differential transformer-type (LVDT) extensometers. Under the steel beam, an aluminum truss with six LVDTs was placed on the ground surface with its end supports situated 2 m from the anchor. The measurement wires of the LVDTs were attached to small bolts fastened onto the ground surface to measure the ground-surface displacement at different distances from the anchor during testing. All the measurements were logged, at a sampling rate of 10 Hz, by a computer.

The two anchors installed at 1.5 m depth, labeled ’A1.5m’ and ’B1.5m’, were highly instrumented. Two observation holes were drilled around these anchors at two distances, and the observation holes were mapped using acoustic and optical televiewers before and after the tests. Load cells were installed in the two boreholes next to the anchors, with three load cells placed in each borehole at three separate depths, giving a total of six load cells used in each of these two tests. All the load cells were continuously logged at 10 Hz by a computer. Six borehole extensometers were installed—four around Anchor A1.5m and two around Anchor B1.5m. The borehole extensometers were placed at two separate distances around each anchor. These measured the vertical displacement at five depths and were connected to a Bluetooth gateway that logged readings once every 5 min. The location of the instrumentation around Anchors A1.5m and B1.5m is shown in Fig. 6.

Fig. 6
figure 6

Location of instrumentation boreholes around (a) Anchor A1.5m and (b) Anchor B1.5m containing load cells (LCs), extensometers (EXs) and observation holes (OBs) for the televiewer

Full size image

Geophones were attached to the ground surface to monitor the seismic signals of the rock mass when it fractured during the tests of Anchors A1.5m, B1.5m and B1m. The P-wave velocity of the limestone was estimated by striking a hammer three times on the ground surface next to each geophone, and then back-calculating the velocity from the measurements, which resulted in a P-wave velocity of 2000 m/s. The test of Anchor B1m was logged at 4000 Hz, but there were holes in the data due to problems with the file creation speed. Therefore, the last two anchors, A1.5m and B1.5m, were logged at a frequency of 2000 Hz. The test setup of Anchor A1.5m showing the instrumentation is illustrated in Fig. 7, Table 4 provides an overview of the instrumentation of the anchors.

Fig. 7
figure 7

Setup for the field tests showing instrumentation around Anchor A1.5m

Full size image
Table 4 Overview of anchor naming, endplate depth and instrumentation
Full size table

2.5 Uplift Test Arrangement and Procedure

The test arrangement is shown in Fig. 2. A steel beam was placed over the anchor on two concrete platforms, with a 3500-kN hydraulic jack placed on top. The beam had the following dimensions: length = 4.04 m; width = 0.79 m; height = 0.83 m; and span = 3.0 m. In the center, where the jack was placed, the beam was reinforced with a 0.05-m-thick steel plate with the dimensions 500 \(\times\) 790 mm. The hydraulic jack was pressurized from a gasoline-driven hydraulic pump. The pressurized oil was sent through a booster unit that increased the maximum pressure provided from 200 to 700 bar, which made it possible to use the full capacity of the jack, when needed.

The anchors were loaded in two ways. The first two, A1m and B1m, were loaded continuously at a load rate of 5\(-\)7.5 kN/s until failure occurred. After peak load, the displacement of the jack was continued until the end of the stroke, then the jack was repositioned and loaded again to the end of the stroke. This was repeated a few times until the load dropped to a low enough level that the anchor could be pulled out by the excavator on the site. The last two anchors, A1.5m and B1.5m, were loaded in a step-wise manner, with each load step held for 5 min. The first two load steps were 900 kN each and all the following were 200 kN. Each load step had an average load rate of around 11.5 kN/s. The load steps were held for 5 min so the borehole extensometers could get one reading per step. All the uplift tests were performed between 15 and 16 June 2022, when the rock mass temperature was approximately 10\(^{\circ }\) C.

3 Test Results and Analysis

3.1 Results

Anchors A1m and B1m were 2.5-m-long anchors installed at a depth of 1 m, which resulted in a grouted section of 0.9 m above the endplate. The last two anchors, A1.5m and B1.5m, were 3-m-long anchors installed 1.5 m deep, which resulted in a grouted section of 1.4 m above the endplate. The maximum load of the anchors was: 2463 kN at 66.7 mm displacement for Anchor A1m, 2310 kN at 59.6 mm displacement for Anchor B1m, 2423 kN at 71.8 mm of displacement for Anchor A1.5m and 1946 kN at 105.7 mm of displacement for Anchor B1.5m. The load–displacement curves are shown in Fig. 8. The ground-surface heaving around the anchors from the LVDT measurements on the surface are shown in Figs. 9, 10, 11 and 12.

Fig. 8
figure 8

Load–vertical displacement curves of all the anchors. The load drops at 220–240 mm displacement marks the end of the jack stroke

Full size image
Fig. 9
figure 9

Surface heaving at a distance from Anchor A1m, where the dotted lines represent extrapolations

Full size image
Fig. 10
figure 10

Surface heaving at a distance from Anchor B1m, where the dotted lines represent extrapolations

Full size image
Fig. 11
figure 11

Surface heaving at a distance from Anchor A1.5m, where the dotted lines represent extrapolations

Full size image
Fig. 12
figure 12

Surface heaving at a distance from Anchor B1.5m, where the dotted lines represent extrapolations

Full size image

Three of the anchors, B1m, A1.5m, and B1.5m, were instrumented with geophones on the ground surface which measured the seismic activity during the tests. The microseismic measurements are presented in Figs. 13, 14 and 15. For Anchor B1m, the seismic measurements fitted well with some of the surface cracks.

Fig. 13
figure 13

Location of the microseismic events around Anchor B1m viewed from the top. The size of the dots represents the relative size of the seismic events. The numbers indicate the locations of the geophones and the red circle marks the anchor. Some of the surface cracks correlated well with the seismic measurements

Full size image
Fig. 14
figure 14

Location of the microseismic events around Anchor A1.5m viewed from the top. The size of the dots represents the relative size of the seismic events. The red triangles indicate the location of the geophones and the red circle represents the anchor

Full size image
Fig. 15
figure 15

Location of the microseismic events around Anchor B1.5m viewed from the top. The size of the dots represents the relative size of the seismic events. The red triangles indicate the location of the geophones and the red circle marks the anchor

Full size image

The longest anchors, A1.5m and B1.5m, were instrumented with horizontal stress measurements, borehole extensometers and mapping with optical televiewer. The horizontal stress measurements were taken at three depths, 0.45 m from the anchors, on each side. These measurements are presented in Figs. 16 and 17. The shallowest load cell on the west side of Anchor A1.5m malfunctioned, therefore there are only two depths shown on that side. Four borehole extensometers were installed around Anchor A1.5m and two were installed around Anchor B1.5m. The measurements from these are shown in Figs. 18 and 19. Before and after the tests, the fracturing in two observation holes next to each anchor was mapped using an optical televiewer. The televiewer footage, the dip azimuth, and the dips of the joints before and after the tests are presented in Figs. 20 and 21.

Fig. 16
figure 16

Horizontal stress measurements in the rock mass for three depths around Anchor A1.5m at (a) 0.44 m west and (b) 0.48 m east

Full size image
Fig. 17
figure 17

Horizontal stress measurements in the rock mass at three depths around Anchor B1.5m at: a 0.41 m west; and b 0.49 m east

Full size image
Fig. 18
figure 18

Borehole extensometer measurements around Anchor A1.5m at different anchor displacements: a from 0.43 m southwest; b from 1.02 m southwest; c displacement increments from all the extensometers at 0.45 m distance; and d displacement increments from all the extensometers at 1.0 m distance. The total lengths of the columns in c and d mark the total vertical displacement, while the individual colors mark the incremental vertical displacement of each load step

Full size image
Fig. 19
figure 19

Borehole extensometer measurements around Anchor B1.5m at different anchor displacements: a displacements toward depth for an extensometer placed 0.44 m southwest; and b vertical displacement increments at the extensometers, where the bright colors are the extensometer at 0.44 m from the anchor and the faded colors are the extensometer placed at 1.0 m distance. The total length of the columns in b mark the total vertical displacement, while the individual colors mark the incremental vertical displacement of each load step

Full size image
Fig. 20
figure 20

Televiewer images, azimuth and dip directions of the joints/fractures in the observation hole 0.55 m south of Anchor A1.5m before and after the test: a optical televiewer images; b joint dip azimuth; and c joint dip

Full size image
Fig. 21
figure 21

Televiewer images, azimuth, and dip directions of the joints in the observation holes 0.45 and 1.05 m south of Anchor B1.5m before and after the test. Optical televiewer images at: a 0.45 m from the anchor; b 1.05 m from the anchor; c the joint dip azimuth; and d the joint dip

Full size image

After the tests were finished, the loose rock material in the rock mass around the anchors was removed, together with the anchors. Then, the surfaces were lidar scanned with an iPad. The scanned failure craters and profiles of the craters are presented in Figs. 22, 23, 24 and 25. The volume of the failure craters was measured from the three-dimensional (3D) scanning and they were 2.3 m\(^3\) for Anchor A1m, 2.3 m\(^3\) for Anchor B1m, 3.6 m\(^3\) for Anchor A1.5m and 3.7 m\(^3\) for Anchor B1.5m.

Fig. 22
figure 22

Profiles along the failure crater of Anchor A1m and the scanned failure surface: a plot of four profiles in the failure crater; and b scanned failure surface showing location of the profile lines, with a red line marking the orientation of the beam

Full size image
Fig. 23
figure 23

Profiles along the failure crater of Anchor B1m and the scanned failure surface: a plot of four profiles in the failure crater; and b scanned failure surface showing the location of the profile lines, with a red line marking the orientation of the beam

Full size image
Fig. 24
figure 24

Profiles along the failure crater of Anchor A1.5m and the scanned failure surface: a plot of four profiles in the failure crater; and b scanned failure surface showing the location of the profile lines, with a red line marking the orientation of the beam

Full size image
Fig. 25
figure 25

Profiles along the failure crater of Anchor B1.5m and the scanned failure surface: a plot of four profiles in the failure crater; and b scanned failure surface showing location of the profile lines, and a red line marking the orientation of the beam

Full size image

3.2 Load Capacity

The load–displacement curves of all the anchors are shown in Fig. 8. The curves are linear until 20–25 mm displacement is reached, then they start to bend. The sudden drops in load at 215–240 mm and at 420 mm displacement marks the end of the jack stroke.

The two shortest anchors, A1m and B1m, were loaded continuously until failure. The peak load of Anchor A1m was 2460 kN and it was reached at 67 mm of displacement. After the peak, the load capacity dropped gradually, with continued displacement, reaching a residual strength of around 200 kN after 300 mm displacement. For Anchor B1m, the peak load of 2310 kN was reached at 60 mm of displacement. After the peak, the load capacity dropped gradually with continued displacement, reaching a residual strength of around 150 kN after 250 mm of displacement.

The longest anchors, A1.5m and B1.5m, were loaded step-wise, load steps close to the peak load reached higher levels than at the end of the last load step, even when the curve was flattening out or in the post-peak stage, which resulted in Anchor B1.5m reaching peak load at a greater displacement than the rest of the anchors. The peak load of Anchor A1.5m was 2420 kN and it was reached at 72 mm of displacement. For Anchor B1.5m, the peak load of 1950 kN was reached at 106 mm of displacement. After the peak, the load capacity of these anchors dropped gradually with continued displacement, and they had a higher load capacity post-peak than the shorter anchors.

3.3 Rock Mass Heaving and Surface Cracking

The ground surface heaving around the anchors is shown in Figs. 9, 10, 11 and 12. The heaving was the greatest closest to the anchors, decreasing outwards, the vertical movement of the anchors were greater than the heaving of the rock mass. The reference points for the measurements were at 2 m distance from the anchor on each side. The ground-surface heaving increased with increasing vertical displacement of the anchors, and the heaving of the anchors were greater than the rock mass heaving.

The heaving of the rock mass around Anchor A1m is shown in Fig. 9, the ground surface heaving relative to the anchor heaving was approximately constant up to 200 mm of displacement. Before 200 mm of anchor displacement, the rock mass heaving closest to the anchor was approximately 10% of the anchor displacement, but after 200 mm of anchor displacement, the rock mass heaving accelerated, which indicates that the rock mass had failed at this point.

Around Anchor B1m, the heaving was asymmetrical on the two sides of the anchor, illustrated in Fig. 10. The rock mass heaving closest to the anchor was around 10% of the anchor displacement up to 100 mm of displacement. After 100 mm of anchor displacement, the heaving increased to around 20% of the anchor displacement, which indicates that the rock mass had failed at this point.

The ground surface heaving around Anchor A1.5m was asymmetrical on the two sides of the anchor, seen in Fig. 11, the greatest heaving being on the south side of the anchor. The heaving on the south side closest to the anchor was around 8% of the anchor displacement up to 150 mm displacement. After 150 mm of anchor displacement, the heaving increased to 13% between 200 and 300 mm of anchor displacement and up to 20% when the anchor displacement was 350 mm and more. These measurements indicate that the rock mass on the south side of the anchor had failed by this point, whereas it was still intact on the measuring points on the north side of the anchor.

The measured heaving around Anchor B1.5m became zero on the north side of the anchor at 1.5 m distance, while on the south side, the heaving spread a little wider, demonstrated in Fig. 12. The rock mass heaving closest to the anchor was approximately 10% of the anchor displacement until 250 mm of displacement. After 250 mm of anchor displacement, the ground heaving increased to around 15% of the anchor displacement for the remaining of the test. This indicates that the rock mass had failed in between 200 and 250 mm of anchor displacement.

The surface cracking around the anchors is shown in Fig. 26. The pre-existing joints in the rock mass tended to open, which is visible in the figure, with discolored rock blocks being lifted onto the ground surface. Observations from the tests showed joints opening up to 2–3 m away from the anchors in the directions parallel with the pre-existing joints in the rock mass, whereas, in the areas with fewer pre-existing joints, the fracturing was limited to a distance equal to the anchor depth or less.

Fig. 26
figure 26

Surface cracking around the anchors after the tests: a Anchor A1m, b Anchor B1m, c Anchor A1.5m and d Anchor B1.5m

Full size image

3.4 Failure Shape and Failure Surface

The failure surface in the rock mass after the tests of all the anchors are illustrated in Figs. 22, 23, 24 and 25. None of the failures have the exact shape of an inverted cone, they are elongated in one direction and asymmetrical with the failure surfaces mostly following the three joint sets in the rock mass. A slight discolouration can be seen on the failure surfaces, which is an indication of weathering, meaning that these surfaces were pre-existing joints in the rock mass. There were some parts of the failure craters that had a lighter color, which is an indication of fracturing of the intact rock. This shows that the failure was a combination of fracturing following the pre-existing joints and of intact rock bridges.

The average apex angle and the measured depth of the failure craters are presented in Table 5. The average apex angles varied from 127\(^{\circ }\) to 141\(^{\circ }\), and they were measured from the profiles taken from the lidar scans in Figs. 22a, 23, 24 and 25a. The depths varied from 0.59 m to 0.83 m. For the shorter anchors, A1m and B1m, the measured depths were slightly less than the grouted depth of 0.9 m, while for the longer anchors, A1.5m and B1.5m, the measured depth were much less than the grouted depths. At the bottom of the failure craters, there were a seemingly intact part of the boreholes remaining, which is shown in Fig. 27 and can be seen in the lidar scans in Figs. 22b, 23, 24 and 25b. In the boreholes, there were only loose pieces of crushed grout, as shown in Fig. 28. The piece with a slick surface is from the upper part of the intact borehole, while the piece exhibiting grooves is from the bottom part where the debonding pipes were (Fig. 28a). The grout pieces were relatively intact on the side facing the rock (Fig. 28b), indicating that the grout experienced a combination of slip and crushing in the bottom part of the borehole. In the rock mass above the intact borehole of Anchor B1.5m, a rock block was stuck to the anchor, and was pulled out together with the anchor; this block is shown in Fig. 29. The grout on this block was intact, which suggests that it was not the grout interfaces that failed at this level.

Fig. 27
figure 27

Intact borehole at the bottom of the failure crater after testing Anchor B1.5m

Full size image
Fig. 28
figure 28

Grout pieces found in the intact borehole after the test on Anchor A1.5m. The piece on the left was found in the upper part of the intact borehole and the piece on the right in the bottom part: a the side of the grout facing the anchor; and b the side of the grout facing the rock

Full size image
Fig. 29
figure 29

Intact grout in a block stuck to Anchor B1.5m when the anchor was lifted out of the ground

Full size image

In Figs. 30, 31 and 32, the microseismic measurements were placed over the lidar scans of Anchors B1m, A1.5m, and B1.5m. All the microseismic measurements were plotted on the surface because the depth measurements were unreliable as all the geophones were placed on the surface. The plots shows that most of the seismic events occurred around the anchors and in the central parts of the failure craters. In the outer area of the craters, there were no, or only small, seismic events, indicating that the rock mass had failed along pre-existing joints in these parts. North and south of Anchor A1.5m, larger seismic events had occurred in a region that was seemingly intact based on the lidar scan. East/northeast of the anchor, there was little seismic activity, which agrees well with the measured surface heaving on this side of the anchor. South of Anchor B1.5m, there was larger seismic events that had occurred in a region that was seemingly intact based on the lidar scan. East of the anchor, there was little seismic activity.

Fig. 30
figure 30

Microseismic measurements placed over the lidar scan of Anchor B1m. The size of the dots represents the relative size of the seismic events

Full size image
Fig. 31
figure 31

Microseismic measurements placed over the lidar scan of Anchor A1.5m. The size of the dots represents the relative size of the seismic events

Full size image
Fig. 32
figure 32

Microseismic measurements placed over the lidar scan of Anchor B1.5m. The size of the dots represents the relative size of the seismic events

Full size image

3.5 Horizontal Stress Development

The horizontal stress development in the rock mass around Anchors A1.5m and B1.5m is presented in Figs. 16 and 17. During the elastic loading of the anchors, the horizontal stress in the rock mass increased only slightly around the anchors, except for on the west side of Anchor B1.5m where it increased considerably (Fig. 17a). The stress measurements in the rock mass became more unstable when the anchor loads entered the plastic and post-peak stage. At this point, fracturing of the rock mass began, which might have affected the measurements.

Around Anchor A1.5m, the drop in load from 0.8 to 1.2 m deep in the post-peak stage (Fig. 16) might indicate that the rock mass had fractured between these two measurement depths and that the rock mass was unloaded within the fracture.

The main increase in horizontal stress around Anchor B1.5m occurred at around 0.8 m deep (Fig. 17), which might indicate a load arch being formed at this level. The loads dropped at 1.2 m deep in the post-peak stage, possibly indicating that a fracture had started to develop above this depth that unloaded the rock mass at this level, while the rock mass was still intact at 0.8 m deep. At 0.4 m deep, large tensile loads were measured on the west side of Anchor B1.5m in the post-peak stage. This might have been associated with the rock block being lifted with the anchor, shown in Fig. 29, close to the load cell, inducing tensile loads in the rock mass.

4 Discussion

4.1 Stress Distribution in the Rock Mass and Load Arching

Brown (2015) listed a few deficiencies in the design method to protect against rock mass failure from a rock mechanics perspective. He stated that ”if failure of, or large deformations in, a rock mass influenced by a single anchor or a system of post-tensioned anchors is to be assumed, knowledge is required of the distribution of stresses induced in the rock mass by the anchor and other means” (p. 7). This statement was addressed by these tests, where the horizontal stresses were measured in the rock mass on two sides of Anchors A1.5m and B1.5m. The stress monitoring showed an increase in the horizontal stress induced by the anchors (Figs. 16 and 17), where the increase was the greatest at 0.8 m deep. These measurements indicate that a load arch was being induced due to the rotation and movement of the blocks in the rock mass, as has been shown to occur in a blocky model under a concentrated anchor load by Grindheim et al. (2022). Shabanimashcool and Bērziņš (2013) demonstrated that load arching is triggered when at least one joint set is sub-parallel to the anchor. In our study, Joint set 2 in the rock mass exhibited nearly vertical orientation, thus facilitating load arching in the direction normal to this joint set, in the east–west direction. This direction aligns with the measurements of increasing horizontal stress, which corresponds well with the model proposed by Shabanimashcool and Bērziņš (2013). The stress measurements were quite low for three of the boreholes with load cells. A possible explanation is that the load cells were installed in the grout in the boreholes and not on the rock surface. It is likely that the load was transferred through the strongest parts of the rock mass, through intact rock bridges and not the weaker grout.

4.2 Apex Angle and Rock Mass Shear Strength

The apex angle of the failure cone is needed to estimate the rock mass shear strength. In these tests, the apex angle was estimated based on the borehole extensometer measurements, the optical televiewer images and the ground surface heaving. It could also be measured from the profiles of the cleaned failure surfaces.

The extensometer measurements from the tests of Anchors A1.5m and B1.5m are shown in Figs. 18 and 19. These figures show that the main cracking occurred between 0.65 and 0.90 m deep at 0.43 m from the anchor, whereas at 1.03 m distance, the main cracking occurred between 0.45 and 0.85 m deep. By assuming the failure surface was a cone with a constant apex angle, these measurements suggests that the apex angle was between 105 and 170\(^{\circ }\), as shown in Fig. 33. These measurements indicate that the failure occurred slightly above the endplate.

The borehole televiewer data is shown in Figs. 20 and 21. In the images, the main fracturing can be seen by comparing the images from before and after the tests. From the test of Anchor A1.5m, it can be seen in Fig. 20a that the main fracture occurred at 1 m deep, 0.55 m from the anchor. Figures 21a and 21b show the that the main fracture around Anchor B1.5m occurred at 1 m deep at 0.45 m distance and at 0.7 m deep at 1.05 m distance. These observations indicate an estimated apex angle of 125\(^{\circ }\), as shown in Fig. 33, which agrees well with the increase in joints with a dip of between 22.5 and 45\(^{\circ }\) in Figs. 20c and 21d. The televiewer measurements also indicated that the failure surface occurred slightly above the endplate.

Fig. 33
figure 33

Plot of the observed (markers and solid lines) and estimated failure surfaces (dotted lines) from the lidar scan, the borehole extensometer data, where failure occurred between the dots, and the optical televiewer measurements

Full size image

In the literature, the ground surface heaving has been used by Dados (1984) to estimate the apex angle. Dados (1984) used the radius around the anchor where the heaving was 10% or more of the maximum heaving as the cutoff limit. Using this criterion on the ground surface heaving measurements, the average apex angle was estimated to be 97\(^{\circ }\) in these tests.

The apex angle of the failure-cone surfaces was measured from the profiles in Figs. 22a, 23, 24 and 25a. The average apex angle of Anchor A1m was 127\(^{\circ }\), Anchor B1m 131\(^{\circ }\), Anchor A1.5m 142\(^{\circ }\) and Anchor B1.5m 129\(^{\circ }\). On average, the apex angle of the rock mass was 132\(^{\circ }\), which agrees with the measurements from the borehole extensometers and the optical televiewer, but not with the estimates based on the ground surface heaving, which indicates that the apex angle in the tests by Dados (1984) was probably wider than the estimates.

The rock mass shear strength was estimated based on the maximum uplift load and the apex angle through back-calculation, with the assumption of failure in the shape of an inverted cone. The rock mass shear strength could also be calculated based on the Mohr–Coulomb failure criterion, which can be used to estimate the anchoring capacity when the apex angle is known. Table 5 gives the estimated shear strength in the rock mass based on the cone area calculated from the measured apex angle and the maximum pull load of the tests. The rock mass shear strength was estimated to be between 1.7 and 4.2 MPa for the rock mass, which is 1.5–4% of the UCS of the intact rock. The UCS of the rock mass estimated based on the RMR and Q classification systems had a wide range, depending on which formula was used. The range of the UCS of the rock mass estimated by the RMR was 23–56 MPa, with an average of 44 MPa (Yudhbir et al. 1983; Ramamurthy et al. 1985; Ramamurthy 1986; Trueman 1988; Asef et al. 2000; Kalamaras and Bieniawski 1993; Sheorey 1997; Aydan and Dalgic 1998; Zhang 2016). The range of the UCS of the rock mass estimated by the Q was 31–54 MPa, with an average of 42 MPa (Bhasin and Grimstad 1996; Singh and Goel 1999; Singh et al. 1997; Barton 2002; Zhang 2016). The ranges and average values of the UCS from the two systems seem to be quite consistent. Taking 42 MPa as the average UCS of the rock mass, then the shear strength was 4–10% of the UCS of the rock mass.

Table 5 Back-calculation of the rock mass shear strength
Full size table

Estimating a uniform shear strength in a heterogeneous rock mass is unrealistic. If the shear strength was uniform, simultaneous failure would have occurred along the inverted cone, resulting in a continuous failure surface. Previous tests conducted by Prudencio and Van Sint Jan (2007) on rock mass failure modes with non-persistent joints revealed multiple failure mechanisms, including planar and stepped failure, and block rotation. Planar failure is associated with higher strengths, brittle behavior and minimal deformation. Stepped failure occurs when sliding takes place on a joint segment, accompanied by stepping between adjacent parallel joints. Block rotation occurs when the joints are closely spaced, and is characterized by low strength, ductile behavior and significant deformation. It is likely that the failure of the rock mass surrounding the anchors involved a combination of the failure modes identified by Prudencio and Van Sint Jan (2007). This challenges the use of uniform shear strength for estimating rock mass strength. Consequently, the uplift capacity of the rock mass should be evaluated based on its specific characteristics, including joint spacing, joint persistence, weathering and overall strength. This necessitates the development of new design criteria, which can be achieved through a deeper understanding of rock mass behavior and the influence of its characteristics on uplift capacity. Such advancements would enable the formulation of more precise design approaches tailored to the individual rock masses in which anchors are installed.

The numerical model developed by Shabanimashcool and Bērziņš (2013) revealed a distinct failure shape compared to the traditional inverted cone. Instead, the models exhibited a failure pattern resembling a frustum, characterized by a conical shape cut by a plane parallel with the ground surface at the anchor base and with the apex located at a depth deeper than the anchor base. In Figs. 22, 23, 24 and 25, the observed failure craters displayed a small flat area in the east–west direction, providing evidence for a frustum-shaped failure rather than the previously assumed inverted cone. Considering these findings in conjunction with the study by Shabanimashcool and Bērziņš (2013), there may be justification for updating the current failure shape used in design. Such an update could lead to revised shear-strength estimates and anchor capacity calculations. The presence of a frustum-shaped failure crater could potentially account for the wider apex angles measured in this study compared to those suggested in the existing literature.

4.3 Rock Mass Capacity

There was a difference between the estimated and measured rock mass capacities (see Tables 2 and 5). The estimates based on the recommendations of NPRA (2018) were one order of magnitude smaller than the measured results. The estimates based on back-calculation were closer in terms of capacity. For the anchors installed 1.4 m deep, the estimates were close to the results, but they underestimated the capacity of the anchors installed 0.9 m deep. The current design method is overly simplified and conservative. The rock mass characteristics are not used in the design. The design method only uses the density of the rock to calculate the weight of the overlying rock and the number of joint sets to estimate the shear strength of the rock mass through a table of presumptive values given by NPRA (2018). The back-calculation of historical tests seems like a better solution to the strength estimation, the problem being that there are very few tests involving rock mass failure, and the shear-strength estimates vary greatly in those used here (see Table 3). Table 3 indicates that the shear strength is greatly influenced by the rock type and the joints in the rock mass. Unfortunately, there are very few reports on full-scale uplift tests where rock mass failure occurred around rock anchors. This was noted by Xanthakos (1991), who wrote ”there is an impressive scarcity of data on anchor failure in rock mass, hence documentation of stability theories is not readily available” (p. 213). Due to this lack of data, the design methods to protect against rock mass failure have erred on the conservative side. This situation could be improved by building a database for depositing all rock-anchor uplift tests in, which could improve the statistical significance of the estimates based on back-calculations.

The shear strengths calculated from these tests (Table 5) are much higher than most of the historical data, except for those from the tests by García-Wolfrum et al. (2007) on intact rock. These high shear-strength values indicate that the failure in these tests occurred in the intact rock as well as along the pre-existing joints. In the back-calculations of the historical data, it was assumed that the failure started at the bottom of the embedment depth, which seems not to have been the case in the present tests. It is likely that the failure of some of the historical cases also occurred above the base of the embedment depth, which would have resulted in higher calculated shear strength values.

In Norway, the rock masses are mostly strong and unweathered consisting of bedrock. These rock masses have high load-carrying capacities, which results in underestimations of the load capacity using current dimensioning methods, as has been shown in these tests in a medium-strong rock mass. The current design methods are supposed to work for all types of rock masses, which means they are designed for weak rock masses. Bruce (1976) noted that the uplift capacity was very sensitive to the degree of weathering and less sensitive to the rock mass structure. Therefore, there is a need to update or re-design the method for areas that have strong and unweathered rock masses. This could reduce the size and number of the anchors needed, which would be more environmentally friendly and more cost effective.

”Existing design approaches using the 90\(^{\circ }\) or 60\(^{\circ }\) uplift cone hypotheses, variously assume shear, cohesive and/or tensile strengths of the rock mass which may be the presumptive values or be back-calculated from the results of pullout tests using a ”theoretical” failure cone. Clearly, these simple approaches do not take into account the variability of the governing strength parameters with depth and with varying local rock mass structure, or the progressive and complex nature of the rock mass failure mechanisms involved” (p. 9) (Brown 2015). This is an important point relating to back-calculations—they rely on some strong assumptions that might be incorrect. The rock mass strength might derive from intact rock bridges, which increase the strength, as opposed to a heavily fractured rock mass where the strength is derived from the shear strength of the joints. The area chosen for these tests had a medium-strength rock mass with an average block size of around 0.2–0.3 m based on the joint mapping. Because the test area was on a bench in an active quarry, the side closest to the bench crest might have been more damaged due to blasting than the side furthest away. This might have resulted in an anisotropic load distribution from the anchor to the rock mass, which might have resulted in an overestimation of the rock mass capacity close to the bench crest and an underestimation of the rock mass capacity farther away, in the more intact rock. According to Shabanimashcool and Bērziņš (2013), critical parameters influencing the rock mass capacity include the orientation of rock joints relative to the anchor, rock block size, intact rock’s tensile and compressive strength, rock mass stiffness, and the behavior of rock discontinuities under shearing. Incorporating these factors into the design process is essential to address the inherent variability of the rock mass.

4.4 Influence of Rock Mass Joint Sets and Test Arrangement on Failure Shape

Brown (2015) stated ”clearly, the structure of the rock mass will influence the shape of the ”failure” surface” (p. 8). This has been proven previously in the literature (Bruce 1976; Dados 1984; Wyllie 1999; Thomas-Lepine 2012) and was also observed in the present tests. Observations from the tests showed joints opening up to 3 m away from the anchor in the directions parallel to the pre-existing joints in the rock mass, whereas in the areas with fewer pre-existing joints, the fracturing was limited to within a distance equal to the anchor depth or less. These observations suggest that the conical failure surface might not be valid because the failure surface follows the joints. The ground surface heaving shown in Figs. 9–12 also indicates an asymmetrical distribution around the anchors.

The joints in the rock mass influenced the failure. In the failure craters, three main joint surfaces were observed, as summarized in Table 6. The orientation of these joints was the same as the joint sets found in the rock mass before the tests (Fig. 3). The failure craters were elongated in the east–west direction. In this direction, Joint sets 1 and 3 formed a wedge that affected the failure shape. The wedge was clearly visible in the failure crater of Anchor B1.5m in Fig. 25b. Further expansion in the east–west direction was stopped by Joint set 2, which can be clearly seen for Anchors A1m and B1.5m. Contrastingly, Joint sets 1 and 3 limited the expansion in the north–south direction.

Shabanimashcool and Bērziņš (2013) demonstrated the significant influence of rock joints on both failure mechanisms and load distribution within the rock mass subjected to anchoring loads. Their model revealed that joints oriented sub-parallel to the anchor led to interlocking in the perpendicular direction, resulting in tensile failure of the rock mass at the anchor base if the load arch exhibited sufficient load-bearing capacity. Conversely, in directions without interlocking, the rock mass experienced shear failure along pre-existing joints, leading to block sliding and uplift. The failure shape in the models became elongated in orientations with interlocking, and the joints constrained the failure in the uplifted directions. These observations can possibly explain the elongated failure shape observed in these uplift tests. The failure craters exhibited elongation in the east–west direction, indicative of interlocking normal to the vertical joints, while uplift and failure along pre-existing joints were observed in the north–south direction. These findings highlight the critical role of joint orientation in influencing failure behavior and spatial distribution in the rock mass under uplift tests.

Table 6 Orientation of joint surfaces found in the failure craters of all the anchors
Full size table

The observed rock mass failure was complex and strongly influenced by the joint sets of the rock mass. It was noted during the tests that the pre-existing joints opened first, as can be seen in Figs. 26a and 26d. The seismic readings correlated well with the opening of the joints on the surface for Anchor B1m, whereas for Anchors A1.5m and B1.5m, the same correlation was not seen. In Figs. 30, 31 and 32, with the lidar scan and seismic events combined, it can be seen that there were few and small seismic events in the peripheral areas of the failure craters. The failure surface in the peripheral areas was slightly discolored, an indication of weathering, which means the rock mass had failed along pre-existing joints in these areas. The failure craters in Figs. 22b, 23, 24 and 25b were slightly elongated in the east–west direction. Joint sets 1 and 3 formed a wedge in this direction, which can be seen in the lidar scans, while Joint set 2 limited the extent of the wedges, which is depicted in the crater left by Anchor B1.5m in Fig. 25b. Most of the surfaces in the craters had the orientation of one of the three joint sets, which shows that the failure mostly followed the pre-existing joints in the rock mass, which has only been assumed formerly in the literature (Hobst and Zajíc 1983; Wyllie 1999; Brown 2015). This shows that the failure was structurally dependent on the rock mass structure.

The average apex angle was measured in the cleaned failure surfaces and found to be between 125 and 140\(^{\circ }\). The depth of the craters varied from 0.59 to 0.83 m. This seemed to be consistent for all tested anchors, even though Anchors A1.5m and B1.5m had 0.5-m deeper embedment depths than Anchors A1m and B1m. These angles are wider than what has been recommended in the literature, which is 60\(^{\circ }\) in weak rock masses and 90\(^{\circ }\) in strong rock masses (Littlejohn and Bruce 1977; Brown 2015). The beam was designed with the assumption of a 90\(^{\circ }\) apex angle placed at the bottom of the grouted section at the endplate. Because the measured angles were wider, the area affected by the tests would be wider than the length of the beam. This resulted in the beam confining the outer area of the affected rock mass, which increased the rock mass strength in those parts. Therefore, a combined failure occurred, where the lower part of the grouted length failed through the grout–rock interface and the upper part in the rock mass, as shown in Fig. 34. At the bottom of the failure craters, the lower parts of the boreholes were found to still be intact (Fig. 27), but the grout had been crushed in this area (Fig. 28). In the rock mass above, a rock block was lifted with the grout still intact in the block (Fig. 29), which further strengthens the evidence of a combined failure.

Fig. 34
figure 34

Possible failure shape of the tested anchors

Full size image

The observations from the televiewer and the borehole extensometers indicated that fracturing occurred in the rock mass at a deeper level than the cleaned failure surfaces indicated, as shown in Fig. 33. There were also indications of this in the seismic measurements for Anchors A1.5m and B1.5m, as indicated in Figs. 31 and 32. The lidar scan of the failure surface combined with the seismic measurements showed that several seismic events occurred outside the cleaned failure surface. The seismic measurements indicated that fracturing had occurred in the rock mass outside the cleaned failure surface. All these observations points to it being likely that additional fracturing developed deeper in the rock mass, but was unable to fully develop due to the reaction force from the beam, or we were not able remove all the failed rock mass with the excavator. It is also possible that the deeper fracturing reduced the confinement on the anchor grout, making it easier for the anchor grout to slip along the borehole wall at the bottom of the borehole, leaving the bottom of the borehole seemingly intact.

Previously, Panton (2016) demonstrated, through Phase 2 models, that the failure volume and apex angle is affected by the setup arrangement of uplift tests. The models showed that the failure volume and apex angle decreased when the test setup provided a reaction force in the area of influence of rock mass dilation. The results from these tests indicated that the failure volume decreased when there was a reaction force in the area of influence of rock mass dilation, while the apex angle remained constant (Fig. 34). Instead, a combined rock mass and grout–rock interface failure occurred, with the grout–rock interface failure occurring at depths where the area of influence became larger than the beam length. At the ground surface, it was observed that the rock mass was intact in the location where the beam stood during the tests, suggesting that the beam affected the extent of the rock mass failure. The reaction force from the beam likely acted as a reinforcement for the rock mass, potentially reducing its vertical uplift. The load from the beam supports on the rock mass may have increased its overall strength and facilitated load arching, leading to a higher rock mass capacity. Consequently, the estimated shear strength in these tests appears to be higher than other similar tests due to the combined effects of reinforcement and load arching within the rock mass.

4.5 Effect of Anchoring Depth

The width and location of the apex angle vary in the literature, having been placed at the base or middle of the bonded section (Littlejohn and Bruce 1977; Brown 2015). The current tests were designed with the assumption of a 90\(^{\circ }\) apex angle placed at the bottom of the grouted section on the endplate. However, the observed locations of the apex varied in depth from 0.59 to 0.83 m below the surface, with none of them occurring at the base of the bonded section. Wyllie (1999) discussed the effect of joints on the shape of the failure cone; horizontal jointing would result in a wider apex angle, whereas vertical jointing would result in a smaller apex angle, but this was for shallow anchors. García-Wolfrum et al. (2007) showed, on small intact rock samples, that the apex angle is not constant, but is the smallest at the bottom and increases toward the surface, like a hyperbolic curve. Shabanimashcool and Bērziņš (2013) proposed a frustum-shaped failure with a plate-like failure surface at the anchor base. Their study highlighted that load arching in the rock mass elevates the strength of the pressurized arch, surpassing the tensile strength of the rock block responsible for transferring the anchor load to the rock mass. All the observed rock mass failures reported in the literature involved shallow anchors (see Table 3).

The failure mode that occurred in the present tests was a combination of rock mass failure and bond failure between the grout and the rock. The grout–rock bond failure occurred in the deepest parts of the grouted section. It is possible that the increased size of the apex angle measured in these tests compared to the estimates resulted in an increased volume of rock affected, which may have resulted in the affected rock mass at depth having greater strength than the grout–rock interface. Therefore, the grout–rock interface failed before the rock mass failed at depth. At shallower depths, the rock mass became the weaker component, resulting in a combined failure mode. Tests in a weak mudstone by Weerasinghe and Littlejohn (1997) similarly revealed a combination of rock mass and bond failure. They suggested that the rock mass failure occurred in the top 0.5 m of the fixed anchor, and that the grout–rock interface failure occurred at depths below this, which could be a reasonable explanation for the present tests if the rock mass failure was assumed to occur at depths down to around 1 m.

Brown (2015) stated in a review that ”most direct observations of the rock mass uplift failure mechanism of which the author is aware, were associated with field pullout tests in which, almost of necessity, the anchor was short in comparison to the lengths of large post-tensioned anchors used in dam construction and rehabilitation projects” (p. 8). This highlights one of the weaknesses with these field tests. Here, the anchor length was short due to the high forces expected for longer lengths, which would have increased the testing cost exponentially due to the increased dimensions of the test equipment that would be needed for testing larger anchors. Therefore, the anchor length had to be adapted to the equipment available and the budget of the project. Consequently, there is still the question of how valid the test results are for anchors with 10\(\times\) the length of those tested here and in earlier tests reported in the literature. Also, Bruce (1976) tested anchors at several depths, and in those tests, rock mass failure did not occur for the deeper anchors (>1.5 m), which might indicate that the rock mass strength is the strongest part of the anchoring system at greater depths.

It is logical to infer that the uplift capacity of a rock mass will exhibit a steeper increase with depth compared to the bond strength of an interface and the tensile strength of steel. This observation is indirectly supported by the existing literature because rock mass failures have rarely been observed below a depth of 1.5 m (see Table 3), with most occurrences reported from shallower depths, as observed in the tests conducted here. This characteristic appears to be independent of the specific rock mass type because shallow failures have been documented in various geological formations, such as carboniferous strata (Bruce 1976), shale (Littlejohn and Bruce 1977), granitic masses (Dados 1984), weak mudstone (Weerasinghe and Littlejohn 1997) and the medium-hard limestone investigated in this study. Furthermore, it has been consistently highlighted in the literature that observed rock mass uplift failures are relatively rare (Littlejohn and Bruce 1977; Xanthakos 1991; Brown 2015), potentially suggesting that the rock mass itself represents the strongest component in the anchoring system. Sabatini et al. (1999) further underscored that, due to the significantly greater strength of rock compared to the bond strength of interfaces (tendon–grout and grout–rock), rock mass uplift failure rarely occurs around rock anchors embedded more than 4.5 m below ground, even in the presence of fractured rock.

5 Conclusions

Rock mass uplift tests involving rock anchors were conducted in a limestone quarry in a medium-strong rock mass to investigate the capacity, load arching and failure mode of the rock mass.

The rock mass capacity was much higher than the capacity estimated using the current design methods recommended in Norway, so the weight of the rock can be neglected in medium-strong or stronger rock masses. Estimations based on the back-calculation of historical tests proved to be more precise. Failure occurred both along the joints in the rock mass and through the intact rock.

The failure mode in the uplift tests occurred through a combination of rock mass uplift and grout–rock bond failure. The apex angle was measured to be between 125 and 140\(^{\circ }\) in the rock mass. This wide apex angle resulted in the test setup limiting the extent of the uplift failure.

The horizontal stress in the rock mass increased when the anchor was pulled. The increase occurred in the elastic stage of loading. An increase in the horizontal stress indicated that a load arch had formed in the rock mass during the loading of a rock anchor.

The failure followed the pre-existing joints in the rock mass. The extent of the failure was also limited by the joint sets. The failure crater was asymmetrical, with the longest axis lying in the direction where two joint sets formed a wedge.

The increase in anchoring depth from 1 to 1.5 m had no influence on the depth of the failure crater in the rock mass. The crater depth was consistent even when the anchoring depth was increased due to the reaction force from the beam and the influence of the increased rock volume affected.