Laboratory Tests of Large-Scale Block Models on the Load Transfer and Failure Mechanisms of Rock Masses Subjected to Anchor Loading

Abstract

This paper presents a laboratory testing rig designed to investigate the failure mechanisms and load transfer of rock masses under rock anchor loading. The study revealed that joint patterns significantly affect the strength and capacity of the rock mass, with existing design approaches based on apex angles of 90$^{\circ }$ or 60$^{\circ }$ found to be potentially overly conservative. Joint orientation and spacing should be included in the anchor design to obtain a more precise design criterion. In all the studied patterns, increasing the horizontal and vertical stress increased the block models’ capacity, and load arching did not occur in the model with an unfavourable joint orientation. This study also revealed that the failure surface followed the joints in all tests and that the block model capacity was significantly higher than estimated with the design principle based on the weight of the overlying rock. The findings of this work have important implications for designing rock anchoring systems in mining and civil engineering demonstrate that joint orientation and block size significantly affect the rock mass capacity. This study confirms the need to consider the influence of in situ stresses on rock mass capacity when designing of rock anchors. Overall, this work guides the development of more precise design criteria for rock anchors, contributing to more efficient and effective rock engineering practices.

Highlights

• The models exhibited increase in horizontal stress upon application of a vertical anchor load to the blocks, indicative of load arching effects.

• The maximum vertical displacement in the blocks was in the normal direction to one of the joint sets under the influence of a vertical anchor load.

• The capacity of the block models was enhanced with an increase in both horizontal and vertical in situ stress.

• Crater-like failures were observed, with separation surfaces aligning with the joint set surfaces.

• Apex angles of the block patterns ranged from 90 to 140$^{\circ }$; symmetrical failures were observed in models with symmetrical jointing around the anchor.

1 Introduction

Rock anchors have been widely used in civil engineering projects for decades to stabilise rock masses and large-scale infrastructures (Xanthakos 1991; Merrifield et al. 2013). These anchors can potentially withstand large loads and can be installed at various angles, making them an effective solution for stabilising a range of slopes, retaining walls, and deep excavations (Xanthakos 1991; Choi et al. 2013). In recent years, there has been increasing interest in the use of high-capacity, post-tensioned rock anchors in infrastructure projects, such as dams, tunnels, and high-rise buildings (Jordan 2007; Aoki 2007; Koca et al. 2011; Mothersille and Littlejohn 2012; Schlotfeldt et al. 2013; Shabanimashcool et al. 2018; Roesen and Trankjær 2021).

The most common failure modes associated with bonded high-capacity rock anchors include tensile failure of the anchor’s steel, anchor shear failure along the anchor’s steel–grout or grout–rock interfaces, and uplift failure of the rock mass (Brown 2015). It is important to note that in the context of this paper, there is a distinction between uplift and pullout. Pullout refers to the anchor being pulled out of the borehole, i.e., failure along one of the interfaces, while uplift refers to the failure of the rock mass around the anchor, which is then uplifted with the anchor. The failure modes are shown in Fig. 1. Tensile failure of the anchor steel occurs when the anchor can no longer resist the tensile forces applied to it, causing it to deform or break. Anchor shear failure occurs when the interfaces are unable to resist the applied shear forces, leading to a loss of support and potential collapse of the structure. Rock mass failure occurs when the surrounding rock mass cannot support the load applied to it (Littlejohn and Bruce 1977; Hanna 1982; Hobst and Zajíc 1983; Xanthakos 1991; Brown 2015). The overall capacity of an anchoring system is defined as equal to the capacity of the weakest failure mode (Kim and Cho 2012).

Fig. 1

The common failure modes of grouted rock anchors: 1 tensile failure of the anchor steel, 2 anchor–grout interface failure, 3 grout–rock interface failure, and 4 rock mass uplift failure

To design effective high-capacity rock anchors, engineers must consider various factors, including the geology and geometry of the rock mass, the loads to be applied to the anchor, and the anticipated failure modes. The design must also consider the properties of the anchor materials, including their strength, corrosion resistance, and ductility. Considering these factors can facilitate the safe design of rock anchors (Brown 2015).

A key challenge associated with the use of high-capacity rock anchors is the potential for rock mass uplift failure, which is the primary focus of this paper. The failure of the rock mass surrounding an anchor can have important implications on the stability of the entire structure (Hanna 1982). Brown (2015) concluded in a review that anchor designs to mitigate rock mass uplift failure are based on simplified assumptions of the stress distribution and volume of rock influenced by the rock anchors: these assumptions have led to an excessively conservative design approach that is considered a poor engineering practice. Due to the limited knowledge of rock mass uplift failure, it was deemed necessary that the rock anchors should be designed conservatively until the rock mass uplift failure mode is fully understood (Hanna 1982). Despite extensive studies and advances in rock mechanics and rock engineering of post-tensioned anchors (Brown 2015), there have been comparatively few studies of rock mass uplift failure due to a lack of available data, and this phenomenon remains poorly understood. Therefore, it is essential to develop an improved understanding of the rock mass uplift failure mode, which can then be used to develop appropriate anchor design criteria to mitigate these risks.

The conventional approach for designing rock anchors to mitigate against rock mass uplift failure is also the least satisfactory. This method is based on the weight of the rock mass in a cone of homogeneous rock, and a shear strength value is assumed along this cone to resist the uplift force generated by the rock anchor (Brown 2015). The cone’s apex angle varies depending on the nature of the anchor and the rock mass properties, with a value of 60$^{\circ }$ commonly used for soft, fissured, or weathered rock masses and 90$^{\circ }$ for all other settings (Littlejohn and Bruce 1977; Brown 2015). Rock anchors in Europe must follow the Eurocode 7 standard (Norwegian Standard 2020), while the Norwegian guidelines recommend an apex angle of 60–90$^{\circ }$ depending on the strength of the rock mass and the number of joint sets (NPRA 2018). However, observations have shown that the apex angle may extend beyond the assumed 90$^{\circ }$ cone surface (Radhakrishna and Klym 1980), and the shear stress is typically concentrated at the proximal end of the grout–rock bond, making the midpoint of the bond the most probable location of the apex (Wyllie 1999). Despite this, current design practices require that rock anchors are embedded sufficiently deeply to prevent rock mass uplift before failure modes 1–3 occur (Weerasinghe and Adams 1997).

Previous experimental studies have been conducted to better understand the behaviour of rock anchors and the mechanisms that can lead to rock mass uplift failure. For example, researchers have used laboratory-scale models to simulate rock anchor behaviour under different loading conditions and investigate the effects of anchor geometry, installation techniques, and anchor materials on the bond strength of the interfaces (Benmokrane et al. 1995; Barley 1997; Jarred and Haberfield 1997; Kim and Lee 2005; Ivanovic and Neilson 2008; Park et al. 2013; Akisanya and Ivanovic 2014; Jia et al. 2019). Overall, these experiments have shown that the behaviour of rock anchors is complex and can be influenced by various factors. Small-scale tests have been performed to simulate rock mass uplift failure; for example, a study by García-Wolfrum et al. (2007) with small anchors (up to 100 mm in length) showed that the failure cone expands towards the ground surface in intact rock samples. Dados (1984) and Grindheim et al. (2022) tested rock mass uplift failure on small block models; these tests showed that the blocks close to the anchor bulged upwards, while the vertical joints tended to open and load arches (i.e., zones of stress concentration within the rock mass) were induced in the layers of a laminar block when pushed upward (Fig. 2).

Shabanimashcool and Bērziņš (2023) proposed a novel method to predict rock mass uplift resistance using numerical modelling. Their study revealed that the presence of a joint set parallel to the anchor axis can significantly enhance the rock mass uplift resistance. This improvement is attributed to block rotation and interlocking along the sub-parallel joint set during anchor pullout, resulting in the formation of a load arch (Fig. 2). The load arch mechanism contributes to increased uplift resistance by promoting block interlocking and enhancing load transfer.

Fig. 2

Load arching due to block rotation and interlocking in a rock mass with sub-parallel joints to the anchor axis

In addition to laboratory-scale experiments, researchers have also conducted field tests to investigate rock mass uplift failure around rock anchors (Bruce 1976; Ismael 1982; Dados 1984; Weerasinghe and Littlejohn 1997; Thomas-Lepine 2012). These experiments involved installing anchors in rock masses and subjecting them to controlled loading conditions to study the anchors’ behaviour and the mechanisms that could lead to rock mass uplift failure. These experiments have provided valuable insights into the behaviour of rock anchors and the challenges associated with their design and installation. These field tests have demonstrated that the shape of the uplift failure crater in the rock mass is controlled by the structure of the rock mass, as illustrated by Hobst and Zajíc (1983) and Wyllie (1999).

Despite the insights from these previous studies, the load transfer and failure mechanisms of rock masses subjected to uplift remain poorly understood. To address this, the present study aims to investigate the behaviour of rock mass uplift failure around rock anchors through laboratory tests. In this experimental work, concrete blocks were set in different configurations and in situ stresses were applied to simulate varying boundary conditions. An anchor block was then pushed upwards to simulate anchor pullout and test the rock mass capacity with different joint patterns and varying boundary conditions, which represents an extension of the work of Grindheim et al. (2022). The results of this study will provide insights into the behaviour of the rock mass around rock anchors and the mechanisms that can lead to rock mass uplift failure. This information can then be used to develop more accurate design criteria for rock anchors and enhance the safety and reliability of rock engineering structures.

2 Test Arrangement and Procedure

2.1 Testing Plan

The laboratory tests in this work were designed to investigate rock mass uplift failure and the load arching effect. A testing scheme involving five different block patterns (Fig. 5) was developed to investigate these phenomena through laboratory uplift tests. The testing followed the schematic shown in Fig. 3 using the testing rig shown in Fig. 4. For each block pattern, four in situ stress levels were applied, three wall heights were used, and two vertical stress levels were applied on the walls with 1.2 m height, which resulted in 20 non-destructive tests for each block pattern. Pattern 2 was tested with two different block sizes. As five block patterns were used, and one pattern was tested with two block sizes, this resulted in a total of 120 planned non-destructive tests. The final test for each block pattern was a failure test in which the block pattern was run to failure, meaning that a total of 126 tests were planned.

Fig. 3

Schematic for the testing of the block patterns

2.2 Test Setups

To study the load distribution and failure pattern of different block models with varying joint patterns, a laboratory rig was specifically constructed, as shown in Fig. 4. The rig, measuring 2230 $\times$ 1530 $\times$ 300 mm (width $\times$ height $\times$ depth), was built with a steel frame and contained 10 hydraulic cylinders fastened to the left inner vertical wall and 16 hydraulic cylinders fastened to the top horizontal beam, which generated the horizontal and vertical stresses, respectively. Each hydraulic cylinder had a capacity of 142 kN, a 100 mm stroke, and was fitted with a 30 mm-thick steel plate on ball mounts facing the test material. Two large pistons were fastened at the bottom centre of the frame with a steel block of dimensions 100 $\times$ 100 $\times$ 250 mm (width $\times$ height $\times$ depth) in between them, representing a rock anchor, from now on referred to as the anchor or anchor block. The two pistons connected to the anchor are located in front and back of the rig frame. They had an individual capacity of 225 kN, resulting in a maximum anchor capacity of 450 kN. The working area inside the hydraulic cylinders on the frame measured 1900 $\times$ 1200 $\times$ 300 mm, with the block material placed inside to represent a rock mass. The hydraulic system of the steel block was servo-controlled and run with a constant displacement rate until either the load limit or the end of the stroke of the cylinders was reached.

Fig. 4

a The testing rig and b a schematic of the testing rig with a section of the concrete blocks on the right

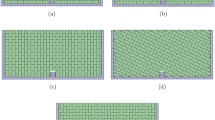
The five block patterns used are shown in Fig. 5. The first block pattern (Fig. 5a) had continuous horizontal and vertical joints. The second block pattern (Fig. 5b) had continuous horizontal joints and discontinuous vertical joints; this block pattern was modelled with two different block sizes. The third block pattern (Fig. 5c) had discontinuous horizontal joints and continuous vertical joints. The fourth joint pattern (Fig. 5d) was the same as block pattern two but rotated by 25$^{\circ }$. The fifth block pattern (Fig. 5e) was an interlocked block pattern in which none of the joints were continuous.

Fig. 5

Sketches of the joint patterns used in the testing rig: a block pattern 1—continuous horizontal and vertical joints, b block pattern 2—continuous horizontal and discontinuous vertical joints, c block pattern 3—discontinuous horizontal and continuous vertical joints, d block pattern 4—25$^{\circ }$ rotation on the horizontal and vertical joints, and e block pattern 5—interlocked joints

2.3 Test Preparations

The materials used in the tests of block patterns 1–5 (Fig. 5) were concrete blocks cut from prefabricated pavement blocks with dimensions of 270 $\times$ 60 $\times$ 200 mm. The blocks used for patterns 1–4 (Fig. 5a–d) were cut to dimensions: 130 $\times$ 60 $\times$ 190 mm; in block pattern 5 (Fig. 5e), the width of the blocks had to be twice the height to avoid gaps; therefore, they were cut into to dimensions of 120 $\times$ 60 $\times$ 190 mm. Along the edges, the blocks were cut to smaller dimensions to fit the patterns, especially for pattern 4 (Fig. 5d). Small errors occurred during the cutting of the blocks, which resulted in uneven width of the layers. This uneven layer width caused varying contact between the horizontal cylinders (Fig. 4) and the blocks; therefore, a cement mortar was applied on the sides of the blocks to fill the gaps and ensure good contact between the layers and horizontal cylinders. The cement mortar had a water–cement ratio (W/C) of 0.28.

Pattern 2 was tested with two block sizes; the larger concrete blocks were prefabricated garden wall blocks with dimensions 270 $\times$ 135 $\times$ 200 mm. The corners of the original blocks were ground down; therefore, the blocks had to be cut to ensure good contact. The new dimensions of the blocks after cutting were 236 $\times$ 135 $\times$ 172 mm.

For block pattern 4 (Fig. 5d), the continuous layers had a tilt angle of 25$^{\circ }$. To maintain this angle, wooden pieces, cut to the precise angle using a saw (which provided greater accuracy than the laboratory’s diamond cutters), were positioned at the base of the frame. It was assumed that the presence of these wooden pieces would not affect the tests as the studied concrete blocks were lifted upwards and away from the wooden pieces during testing.

The tests were monitored using digital image correlation (DIC), which required the blocks to be painted with a non-repetitive 50/50 black-and-white pattern with high contrast. The blocks were first painted white and a black speckle pattern was then applied. The size of the speckles had to be at least 3–4 pixels at the target image resolution to avoid aliasing (Correlated Solutions 2020).

2.3.1 Materials

The material properties of the pavement blocks and garden wall blocks were determined by drilling cores from the blocks and testing them under uniaxial compression, as described in Bieniawski and Bernede (1979). The cores were 49 mm and 60 mm in diameter for the pavement blocks and the garden wall blocks, respectively. The Young’s modulus (E) and Poisson’s ratio ($\nu$) values were calculated from the measured axial stress and axial and radial strain. The average uniaxial compressive strength (UCS) of the pavement blocks was measured as 43 MPa, while Young’s modulus was 23 GPa, Poisson’s ratio was 0.22, and the density was 2272 kg/m$^3$. The garden wall blocks had a UCS of 29 MPa, Young’s modulus of 16 GPa, Poisson’s ratio of 0.23, and a density of 2077 kg/m$^3$.

2.4 Instrumentation

The hydraulic pressure values in the horizontal hydraulic cylinders and anchor pistons were monitored and subsequently used to calculate the horizontal stress and anchor force. The displacement of the anchor pistons was measured using linear variable differential transformer-type (LVDT) extensometers (Fig. 6a), which also assisted with anchor displacement control. To measure the deformation and strain in the blocks, a DIC system was used (Fig. 6b–d). The cameras were positioned in line with the outer edges of the concrete blocks with an angle of 25.5$^{\circ }$ between them (Fig. 6b). These cameras captured five images per second during non-failure tests and ten images per second during failure tests. The software Vic-3D (Correlated Solutions 2020) was used to analyse the images after the tests and calculate the displacements and strains in the model based on using the initial image as a reference.

Fig. 6

Instrumentation of the tests. a LVDT on the front piston (another LVDT is on the back piston), b schematic of DIC setup, c the left camera, and d the right camera

2.5 Test Procedure

A total of 122 tests were conducted out of the 126 planned tests in the test rig, comprising 116 non-destructive tests and six failure tests for five different block patterns (shown in Fig. 5), where Pattern 2 was tested with two different block sizes. The non-destructive tests were stopped when the anchor displacement reached 25 mm (displacement limit) or when the load reached 50 kN (load limit). The wall height and the horizontal and vertical stress applied to the wall were varied for each block pattern as described in Fig. 3. The following procedure was followed for all the tests:

• 1. Place the blocks in the frame with the desired block pattern and height.

• 2. Apply cementitious mortar and a wooden plate to even out the left side of the model and allow the mortar to harden for a week.

• 3. Apply the desired horizontal stress to the blocks from the horizontal cylinders and close the valves to prevent horizontal deformation in the model.

• 4. If a height greater than 1.2 m was selected, apply vertical stress to the blocks from the vertical cylinders and keep the valves open to allow vertical deformation and maintain a constant stress.

• 5. If the tests were not run to failure, set a displacement limit of 25 mm on the system.

• 6. Begin DIC capturing.

• 7. Load the anchor block with a displacement rate of 0.5 mm/s and a load limit of 50 kN for tests not run to failure. For failure tests, continue loading until the end of the piston stroke.

• 8. For tests not run to failure, stop the test if either the load limit of 50 kN or the displacement limit of 25 mm is reached.

• 9. Slowly unload the anchor.

• 10. Stop DIC capturing.

• 11. Remove the confining stresses.

3 Test Results and Analysis

The results and analysis of all the tests are presented for each block pattern in the following sections.

3.1 Block Pattern 1

This section presents the test results obtained for block pattern 1 with continuous horizontal and vertical joints, which correspond to a rock mass with two persistent joint sets.

3.1.1 Non-failure Test Results

• Test results are presented in Table 1.

  • The two columns to the right were tests run with an applied vertical stress to a wall with height 1.2 m.

  • The vertical stress of 0.06 MPa is equivalent to the vertical stress exerted at 2.8 m depth in a rock mass consisting of the concrete blocks.

    • $*$ This corresponds to a depth of 4 m at the anchor (calculated as 1.2 m + 2.8 m).

  • The vertical stress of 0.15 MPa is equivalent to a depth of 6.8 m (i.e., an anchor depth of 8 m).

• Load capacity is lowest at a wall height of 0.6 m with no horizontal stress.

• Load capacity increases with higher wall heights and horizontal stress.

• Block pattern 1 demonstrated rapid load capacity growth with higher wall heights (i.e., increasing vertical stress) and a slower increase with increasing horizontal stress (Table 1).

Table 1 Non-failure test results for block pattern 1, where Italic indicates tests that were stopped at an anchor displacement of 25 mm and Bold Italic indicates tests that were stopped at a load value of 50 kN

3.1.2 Failure Test Results

• Wall height 0.9 m and horizontal stress 0.5 MPa.

• Maximum load 29.7 kN at 28 mm anchor displacement (Fig. 7).

• Load–displacement phases (Fig. 7):

  • Linear increase up to 5 mm displacement,

  • Slight inflexion and less step linear curve beyond 5 mm,

  • Non-linear at 20 mm displacement,

  • Gradual reduction in load with increasing displacement after the peak,

  • Residual load of 10 kN after 60 mm displacement.

• Horizontal stress increased throughout the wall above the 200 mm, indicating load arching at all levels above this height (Fig. 8).

• Maximum horizontal stress measured at the middle of the wall (Fig. 8).

• Failure occurred along the joints with some spalling of block corners, especially along the failure surface (white dashed line) (Fig. 9).

• Apex angle of failure surface was 120$^{\circ }$ (Fig. 9).

Fig. 7

The anchor load–displacement curve for the failure test of block pattern 1. The maximum load of 29.7 kN was reached at 28 mm displacement

Fig. 8

Measured horizontal stress in the model during the failure test of block model 1. Arching is interpreted to occur at the heights where the horizontal stress increased beyond the initial applied horizontal stress

Fig. 9

Failure of block pattern 1 with an apex angle of 120$^{\circ }$. The white lines are the potential failure surface

3.1.3 Horizontal Strain Pattern

• Test conducted with a 1.2 m wall height and an applied horizontal stress of 0.1 MPa (Fig. 10a).

• Vertical joints between the centre blocks tend to exhibit compression (purple) at the bottom and opening (red) at the top.

• On the sides of the model, the vertical joints are compressed at the top and tend to open at the bottom.

• A load arch, which represents the trajectory of the most compressed portion of the joints, is formed in each layer (Fig. 10b). The load arches are constructed by following the most pressed portion of the vertical joints indicated by the horizontal strains.

Fig. 10

a Horizontal strain measurements from the DIC analysis of the test with a wall height of 1.2 m height and 0.1 MPa applied horizontal stress for block pattern 1. In this image, purple represents the highest compressive strain and red the highest tensile (opening) strain. b Interpreted load arches from following the most compressed part of the vertical joints in each layer

3.1.4 Displacement Images

• Figure 11 presents three vertical displacement images obtained from DIC measurements of the tests of block pattern 1. The displacement is presented with a hot-to-cold colour scheme, with red indicating maximum displacement and purple indicating zero displacement. Each image is with a wall height of 1.2 m under different loading conditions.

  • (a) Zero horizontal stress.

  • (b) Horizontal stress of 0.1 MPa.

  • (c) Horizontal stress of 0.1 MPa and vertical stress of 0.15 MPa.

• Maximum displacement (red) occurred above the anchor block.

• Lateral distribution of the displacement expands with increasing horizontal stress (Fig. 11b), whereas an increase in vertical stress concentrates the displacement more centrally (Fig. 11c).

Fig. 11

Vertical displacement images of block pattern 1 with a height of 1.2 m under three loading conditions: a zero horizontal stress, b horizontal stress of 0.1 MPa, and c horizontal stress of 0.1 MPa and vertical stress of 0.15 MPa

3.2 Block Pattern 2

This section presents the test results obtained for block pattern 2 with continuous horizontal and discontinuous vertical joints, which correspond to a rock mass characterised by continuous horizontal joints. Pattern 2 was tested with two block sizes.

3.2.1 Non-failure Test Results

• Test results are presented in Tables 2 and 3, where Table 3 is the model with larger blocks.

• Load capacity is lowest at a wall height of 0.6 m with no horizontal stress.

• Load capacity increases with higher wall heights and horizontal stress.

• The model with larger blocks had the highest capacity, shown by the greater number of cells marked in Bold Italic in Table 3.

• Block pattern 2 demonstrated rapid load capacity growth with higher wall heights and a slower increase with increasing horizontal stress (Tables 2 and 3).

Table 2 Non-failure test results for block pattern 2, where Italic indicates tests that were stopped at an anchor displacement of 25 mm and Bold Italic indicates tests that were stopped at a load value of 50 kN

Table 3 Non-failure test results for block pattern 2 with larger blocks, where Italic indicates tests that were stopped at an anchor displacement of 25 mm and Bold Italic indicates tests that were stopped at a load value of 50 kN

3.2.2 Failure Test Results

• Wall height 0.9 m and horizontal stress 0.5 MPa.

• Maximum loads 33.9 kN and 90.1 kN at 27.9 mm and 38.3 mm anchor displacement (Fig. 12) for the smaller and larger blocks, respectively.

• Load–displacement curves (Fig. 12) had the same phases as described for pattern 1 in Sect. 3.1.2.

• Horizontal stress increased throughout the wall above the 150 mm with both the smaller and larger blocks, indicating load arching at all levels above this height (Fig. 13).

• Maximum horizontal stress measured at the middle of the wall (Fig. 13).

• Failure occurred along the joints with some spalling of block corners, especially along the failure surface (white dashed line) (Fig. 14a).

• Apex angle of failure surface was 120$^{\circ }$ (Fig. 14a) in the model with smaller blocks.

• In the model with larger blocks, the failure (white dashed line) was not fully developed, but the joint pattern implied that the failure apex angle would be 75$^{\circ }$ (Fig. 14b).

Fig. 12

The anchor load–displacement curves for the failure tests of block pattern 2. The maximum load with the smaller blocks was 33.9 kN, reached at 27.9 mm displacement, and the maximum load for the large blocks was 90.1 kN at 38.3 mm displacement

Fig. 13

Measured horizontal stress in the model during the failure tests of block model 2 with a smaller blocks and b larger blocks. Arching is interpreted to occur at the heights where the horizontal stress increased beyond the initial applied horizontal stress

Fig. 14

Failure of block pattern 2 with a smaller blocks and b large blocks. The apex value was measured as 100$^{\circ }$ with the smaller blocks, and it was assumed to be 75$^{\circ }$ based on the joints for the large blocks. The white lines are the potential failure surface

3.2.3 Horizontal Strain Pattern

• Tests conducted with a 1.2 m wall height and an applied horizontal stress of 0.1 MPa (Fig. 15).

• On the sides of the models, the vertical joints are compressed at the top and tend to open at the bottom.

• A load arch is formed in each layer (Fig. 15).

Fig. 15

Horizontal strain measurements from the DIC analysis of the tests with a 1.2 m height and 0.1 MPa applied horizontal stress for block pattern 2: a small blocks and b large blocks

3.2.4 Displacement Images

• Figurs 16 and 17 present three vertical displacement images obtained from DIC measurements of the tests of block pattern 2 with small and large blocks, respectively, under the same conditions as presented for pattern 1 in Sect. 3.1.4.

• Maximum displacement occurred above the anchor block.

• Lateral distribution of the displacement seemingly unaffected by an increase in horizontal stress (Fig. 16b), whereas an increase in vertical stress concentrates the displacement more centrally towards the base of the model (Fig. 16c).

Fig. 16

Vertical displacement images of block pattern 2 with small blocks and a height of 1.2 m under three loading conditions: a zero horizontal stress, b horizontal stress of 0.1 MPa, and c horizontal stress of 0.1 MPa and vertical stress of 0.15 MPa

Fig. 17

Vertical displacement images of block pattern 2 with large blocks and a height of 1.2 m under three loading conditions: a zero horizontal stress, b horizontal stress of 0.1 MPa, and c horizontal stress of 0.1 MPa and vertical stress of 0.15 MPa

3.2.5 Scale Effects

The present study investigated the effect of block size on the load capacity and the behaviour of a staggered block pattern (block pattern 2). The block size was found to have a substantial influence on the model’s load capacity. Remarkably, even though the larger blocks were made of weaker concrete, they exhibited the highest load capacity. This finding indicates that thicker layers lead to stronger arching within the layers. Notably, this observation is consistent with the numerical models proposed by Shabanimashcool and Bērziņš (2023), where an increase in joint spacing, corresponding to an increase in block size, was associated with enhanced anchoring capacity. This phenomenon likely relates to the increased rotational movement of the larger blocks and the steeper arching angle observed in the model with larger blocks.

In contrast to a previous study by Grindheim et al. (2022), in which small square blocks in a staggered pattern were found to have an apex angle of 50$^{\circ }$, the rectangular pavement blocks used in the present study had a width twice their height, resulting in an apex angle of approximately 100$^{\circ }$. The larger studied blocks had a width less than twice their height, which resulted in a measured apex angle of 75$^{\circ }$. These characteristics of block geometry and size significantly influenced both the capacity and failure mode of the rock mass uplift failure, which thus represents a crucial aspect not considered in existing design criteria.

Furthermore, the study shed light on how block size affects load arching and model capacity. Block pattern 2 with larger blocks exhibited the highest capacity and horizontal stress, despite being constructed of weaker block material. This observation indicates that block size plays a pivotal role in the arching effect, with larger blocks displaying a more profound arching effect.

3.3 Block Pattern 3

This section presents the test results obtained for block pattern 3 with discontinuous horizontal and continuous vertical joints, which corresponds to a rock mass with persistent vertical joints.

3.3.1 Non-Failure Test Results

• Test results are presented in Table 4.

• Load capacity is lowest at a wall height of 0.6 m with no horizontal stress.

• Load capacity increases with higher wall heights and horizontal stress.

• Block pattern 3 demonstrated rapid load capacity growth with increasing horizontal stress and a slower increase with higher wall heights (Table 4).

• Slight drop in load capacity when the vertical stress exceeded the horizontal stress (Table 4, row 2, columns 4 and 5).

Table 4 Non-failure test results for block pattern 3, where Italic indicates tests that were stopped at an anchor displacement of 25 mm and Bold Italic indicates tests that were stopped at a load value of 50 kN

3.3.2 Failure Test Results

• Wall height 0.9 m and horizontal stress 0.5 MPa.

• Maximum load 75.2 kN at 33.9 mm anchor displacement (Fig. 18).

• Load–displacement phases (Fig. 18):

  • Linear increase up to 5 mm displacement,

  • Beyond 5 mm displacement, the curve became unstable and numerous small load drops were recorded before the peak load,

  • Gradual reduction with several smaller peaks recorded along the curve after failure,

  • Final load capacity of 30 kN after 100 mm displacement.

• The horizontal stress increased in the upper third, with a notable positive spike in the horizontal stress recorded at a height of 650 mm, indicating load arching at this level (Fig. 19).

• In the bottom half of the model, the horizontal stress decreased with loading (Fig. 19).

• Failure occurred along the joints, with some fracturing of intact blocks observed along the failure surface (white dashed line) and spalling of the block corners (Fig. 20).

• The failure occurred at a 45$^{\circ }$ angle on the right, which is inferred to make an apex angle of 90$^{\circ }$ if the blocks had failed on both sides of the anchor (Fig. 20).

• Failure was observed on the right-hand side only, resulting in an asymmetrical displacement pattern; the observed discrepancy may be attributed to multiple factors:

  • 1. Cement mortar filling the joints causing the left side to function as a single elongated block,

  • 2. Adjustment of the ball mounts on the hydraulic cylinders forming wedges that prevented block release,

  • 3. The cement mortar surface facing the left side of the rig frame being smoother than the concrete blocks, resulting in lower frictional resistance on the left surface in contact with the hydraulic cylinders than the right surface where the concrete blocks had direct contact with the frame. As a result, the cement mortar slid along the hydraulic cylinders and all blocks on the left of the anchor moved together more or less rigidly upward.

Fig. 18

The anchor load–displacement curve for the failure test of block pattern 3. The maximum load of 75.2 kN was reached at 33.9 mm displacement

Fig. 19

Measured horizontal stress in the model during the failure test of block model 3. Arching is interpreted to occur at the heights where the horizontal stress increased beyond the initial applied horizontal stress

Fig. 20

Failure of block pattern 3 with a half apex angle of 45$^{\circ }$ on the right side. The white lines are the potential failure surface

3.3.3 Horizontal Strain Pattern

• Tests conducted with a 1.2 m wall height and an applied horizontal stress of 0.1 MPa (Fig. 21).

• These measurements indicate no distinct pattern in the distribution of compressive and tensile strains that would imply load arching.

Fig. 21

Horizontal strain measurements from the DIC analysis of block pattern 3 tests performed with a 1.2 m height and 0.1 MPa applied horizontal stress

3.3.4 Displacement Images

• Figure 22 presents three vertical displacement images obtained from DIC measurements of the tests of block pattern 3, under the same conditions as presented for pattern 1 in Sect. 3.1.4.

• Maximum displacement occurred above the anchor block.

• In cases (a) (Fig. 22a) and (c) (Fig. 22c), only the blocks above the anchor were lifted.

• In case (b) (Fig. 22b), displacement occurred in a larger portion of the wall.

Fig. 22

Vertical displacement images of block pattern 3 with a height of 1.2 m under three loading conditions: a zero horizontal stress, b horizontal stress of 0.1 MPa, and c horizontal stress of 0.1 MPa and vertical stress of 0.15 MPa

3.4 Block Pattern 4

This section presents the test results obtained for block pattern 4 with continuous horizontal joints and discontinuous vertical joints rotated at an angle of 25$^{\circ }$, which corresponds to a rock mass with persistent inclined horizontal joints.

3.4.1 Non-failure Test Results

• Test results are presented in Table 5.

  • Only 16 non-failure tests were conducted for this block pattern as the model could not withstand the two largest horizontal stresses at the lowest heights.

• Load capacity is lowest at a wall height of 0.6 m with no horizontal stress.

• Load capacity increases with higher wall heights and horizontal stress.

• Block pattern 4 demonstrated rapid load capacity growth with higher wall heights and a slower increase with increasing horizontal stress (Table 5).

Table 5 Non-failure test results for block pattern 4, where Italic indicates tests that were stopped at an anchor displacement of 25 mm, Bold italic indicates tests that were stopped at a load value of 50 kN, and white indicates tests that could not be performed

3.4.2 Failure Test Results

• Wall height 0.9 m and horizontal stress 0.1 MPa.

• Maximum load 19.4 kN at 69.2 mm anchor displacement (Fig. 23).

• Load–displacement phases (Fig. 23):

  • Load increased up to 40 mm displacement,

  • Beyond 40 mm displacement, the load reached a residual load of 18.5 kN with some small variations.

• Highest average horizontal stress measured at the beginning of the test, and it decreased as the test progressed (Fig. 24).

• The horizontal stresses in the hydraulic cylinders increased with an increase in the applied anchor load at the heights from 500 to 650 mm (Fig. 24) which were the locations the continuous joints in contact with the anchor block extended to the left side of the model (Fig. 25), indicating some load arching in these layers.

• The overall reduction in horizontal stress indicates that the arching effect is weaker in this pattern compared to other block patterns (Fig. 24).

• Failure occurred along the joints (white dashed line) (Fig. 25).

• Apex angle of failure surface was 140$^{\circ }$ (Fig. 25).

• The failure of the block model was asymmetrical: on the left side of the anchor, there was a clear and distinct separation between the block layers, whereas, on the right side, the failure occurred stepwise and involved multiple layers of blocks (Fig. 25).

Fig. 23

The anchor load–displacement curve for the failure test of block pattern 4. The maximum load of 19.4 kN was reached at 69.2 mm displacement

Fig. 24

Measured horizontal stress in the model during the failure test of block model 4

Fig. 25

Failure of block pattern 4 with an apex angle of 140$^{\circ }$. The white lines are the potential failure surface

3.4.3 Horizontal Strain Pattern

• Tests conducted with a 1.2 m wall height and an applied horizontal stress of 0.1 MPa (Fig. 26).

• The joints between blocks in the layers show compression on the left side of the anchor and tension on the right side.

• The joints between the layers tend to open on the left side of the anchor and are compressed on the right side.

• These measurements indicate no distinct pattern in the distribution of compressive and tensile strains that would imply load arching.

Fig. 26

Horizontal strain measurements from the DIC analysis of the tests with 1.2 m height and 0.1 MPa applied horizontal stress of block pattern 4

3.4.4 Displacement Images

• Figure 27 presents three vertical displacement images obtained from DIC measurements of the tests of block pattern 4, under the same conditions as presented for pattern 1 in Sect. 3.1.4.

• Maximum displacement is concentrated above the anchor block at the base of the model and propagates upwards normal to the model’s layers (Fig. 27).

• When no vertical stress is applied, a failure surface develops and the block model is lifted (Fig. 27a and b).

• In the presence of an applied vertical stress, the vertical displacement becomes more localised in the centre of the model and tilts slightly clockwise (Fig. 27c).

Fig. 27

Vertical displacement images of block pattern 4 with a height of 1.2 m under three loading conditions: a zero horizontal stress, b horizontal stress of 0.1 MPa, and c horizontal stress of 0.1 MPa and vertical stress of 0.15 MPa

3.5 Block Pattern 5

This section presents the test results obtained for block pattern 4 with interlocking joints, which corresponds to a fractured rock mass without persistent joint sets.

3.5.1 Non-failure Test Results

• Test results are presented in Table 6.

• Load capacity is lowest at a wall height of 0.6 m with no horizontal stress.

• Load capacity increases with higher wall heights and horizontal stress.

• Block pattern 5 demonstrated rapid load capacity growth with higher wall heights and a slower increase with increasing horizontal stress (Table 6).

Table 6 Non-failure test results for block pattern 4, where Italic indicates tests that were stopped at an anchor displacement of 25 mm and Bold Italic indicates tests that were stopped at a load value of 50 kN

3.5.2 Failure Test Results

• Wall height 0.9 m and horizontal stress 0.5 MPa.

• Maximum load 74.5 kN at 35.6 mm anchor displacement (Fig. 28).

• Load–displacement phases (Fig. 28):

  • The load curve remained flat at around 10 kN in the beginning, suggesting that the anchor block was not fully in contact with the concrete blocks,

  • Linear increase in load thereafter until approximately 25 mm displacement,

  • The curve yielded at approximately 25 mm displacement, and after that, it fluctuated with several small load drops before reaching the maximum load,

  • Gradual reduction in load with increasing displacement after the peak,

  • Residual load of 10 kN after 70 mm displacement.

• Horizontal stress increased throughout the wall (Fig. 29).

• Greatest increase in horizontal stress observed at the top of the wall where the curvature would be most pronounced (Fig. 29).

• Failure occurred along the joints with some fracturing of the intact vertical blocks along the failure surface (white dashed line) and some spalling of block corners (Fig. 30).

• Apex angle of failure surface was 90$^{\circ }$ (Fig. 30).

Fig. 28

The anchor load–displacement curve for the failure test of block pattern 5. The maximum load of 74.5 kN was reached at 35.6 mm displacement

Fig. 29

Measured horizontal stress in the model during the failure test of block model 5. Arching is interpreted to occur at the heights where the horizontal stress increased beyond the initial applied horizontal stress

Fig. 30

Failure of block pattern 5 with an apex angle of 90$^{\circ }$. The white lines are the potential failure surface and the white arrows show some previously intact blocks that have fractured

3.5.3 Horizontal Strain Pattern

• Tests conducted with a 1.2 m wall height and an applied horizontal stress of 0.1 MPa (Fig. 31).

• These measurements indicate no distinct pattern in the distribution of compressive and tensile strains that would imply load arching.

Fig. 31

Horizontal strain measurements from the DIC analysis of the tests of block pattern 5 with a 1.2 m height and 0.1 MPa applied horizontal stress

3.5.4 Displacement Images

• Figure 32 presents three vertical displacement images obtained from DIC measurements of the tests of block pattern 5, under the same conditions as presented for pattern 1 in Sect. 3.1.4.

• Maximum displacement occurred above the anchor block.

• Lateral distribution of the displacement expands with increasing horizontal stress (Fig. 32b), whereas an increase in vertical stress concentrates the displacement more centrally (Fig. 32c).

Fig. 32

Vertical displacement images of block pattern 5 with a height of 1.2 m under three loading conditions: a zero horizontal stress, b horizontal stress of 0.1 MPa, and c horizontal stress of 0.1 MPa and vertical stress of 0.15 MPa

4 Discussion

The laboratory tests undertaken in this study were designed to enhance our understanding of the load transfer and failure mechanisms in rock masses under the effect of rock anchor loading. Various block patterns were employed to investigate the impact of different joint patterns on the strength and capacity of the rock mass. Additionally, the models’ boundary conditions were systematically adjusted to examine the influence of in situ stresses on the rock mass capacity. In this section, we discuss the test results and compare them to current dimensioning methods used to mitigate rock mass uplift failure.

4.1 Failure Development

In a study, Høgset et al. (2023) analysed the failure behaviour of a frictional material subjected to an anchoring load. They observed that the load–displacement curve typically exhibited four distinct phases: (1) elastic/linear development, (2) pre-peak yielding, (3) post-peak softening, and (4) a lifting/slipping phase.

In the present study, the load–displacement curves for block patterns 1 and 2 followed this typical pattern (Fig. 33a), albeit with minor variations in failure development. The first phase involved a linear increase in the load without any damage to the blocks. During the second phase, yielding began in the block model, causing the slope of the curve to bend. This phase was characterised by audible cracking sounds and visible fracturing at the block corners and culminated at the peak load value. In the third phase, the load began to decrease due to the opening of the top layer’s central joint, which released the horizontal stress and disrupted the load arch. As the anchor displacement continued, the layers split sequentially from the top of the model to its base, releasing energy and reducing the block model’s load capacity. Once all the layers had split, the block model reached its residual capacity, marking the onset of the fourth phase. During this phase, the uplift body began to develop and was fully formed at approximately 100 mm of displacement.

The behaviour of block pattern 3 was more complex (Fig. 33b), with less clearly distinguishable phases. The model’s initial linear increase phase was clearly developed; however, the subsequent phases were not as readily identifiable, likely due to the absence of horizontal layers that could split in this configuration. Instead, the load arches spanned in blocks across both the vertical and horizontal joints. In the second phase, the intact blocks began to fracture, and the uplift body started to form. Several smaller load drops were recorded in the loading curve before the peak load was reached, corresponding to block fractures. After the peak, the load decreased in the third phase due to slippage between the vertical layers and the separation of the uplift body from the remaining blocks. The fourth phase began once the failure body was fully developed; in this phase, the residual load gradually decreased as blocks slipped off the failure body or fractured at the body’s edge.

In contrast to the above examples, block pattern 4 did not exhibit load arching; thus, there was no load drop after reaching a peak due to joint splitting or block fracturing. The model immediately reached its residual capacity, and the uplift body was lifted along existing joints.

Finally, block pattern 5 exhibited typical load–displacement curve behaviour with distinct loading phases (Fig. 33c). The first phase, characterised by a linear load increase, persisted until the load reached approximately 50 kN. The second phase commenced with the onset of block fracturing and the initial development of the uplift body. Despite some load drops due to additional block fractures, the load continued to increase throughout this phase. After reaching the peak load, the third phase began, during which the uplift body separated from the remaining blocks through a combination of joint opening and block fracturing. This phase was characterised by a steady load decrease with some load drops due to fracturing. The fourth phase started once the uplift body was fully separated from the remaining blocks, during which the uplift body was lifted by the anchor. The residual load remained roughly constant during this stage.

Fig. 33

Load–displacement curves of a block pattern 1, b block pattern 3, and c block pattern 5 illustrating the four loading phases described by Høgset et al. (2023): (1) elastic/linear development, (2) pre-peak yielding, (3) post-peak softening, and (4) lifting/slipping phase

In general, the load–displacement curves for blocky media progress through four distinct phases. In the first phase, characterised by a linear load increase, all the blocks remain undamaged and intact. The second phase commences as the blocks begin to sustain damage due to the increasing anchor load within the block model; at the peak of this phase, the anchor load becomes sufficiently large to disrupt the load arching within the block model. The third phase begins post-peak, when the high anchor load causes the load arches to break, resulting in the onset of block slippage along the joints and joint opening; this phase is also marked by the separation of the uplift body from the remaining blocks. The fourth and final phase starts once the uplift body is fully developed, at which point it is lifted away from the remaining blocks.

Upon full development of the failure bodies in the block models, their internal regions can be classified into two distinct states: neutral and failure, as depicted for block pattern 5 in Fig. 34. In the regions with neutral conditions, the blocks that rotated during load arching become destressed and tend to return to their original positions. In the failure regions, the blocks separate, and some previously intact blocks fail. These failed regions, which affected several blocks in width, were aligned along the joints in the direction where the shear force was anticipated to exceed the strength of the rock mass.

Fig. 34

Illustration showing the neutral and failure states into which the failed block models can be classified. These states are demonstrated using the failure of block pattern 5 as an example

4.2 Influence of Joint Patterns on Failure Shape, Apex Angle, and Load Capacity

The laboratory tests in this study were conducted to investigate the failure behaviour of a rock mass subjected to loading by a rock anchor and to assess the effect of joint patterns on the strength and capacity of the rock mass. The failure shapes of the block tests are shown in Figs. 9, 14, 20, 25, and 30. In all the failure tests, the failure patterns followed the joint patterns in the model. The measured apex angles, as detailed in Table 7, varied from 90–120$^{\circ }$ for the block models with symmetrical joints with respect to the vertical loading direction of the anchor (i.e., models 1, 2, 3, and 5), and the apex angle was 140$^{\circ }$ for the model with asymmetrical joints relative to the loading direction (i.e., model 4). The failure shape appears to be structurally controlled by the joint pattern, as previously noted and illustrated by Hobst and Zajíc (1983) and Wyllie (1999). These researchers suggested that joints perpendicular to the anchor axis produce a wider apex angle, whereas the joints parallel to the anchor would be the least favourable. This trend is consistent with the observed apex angles in this study: the block models with continuous horizontal joints exhibited the widest angles, whereas the model with blocks parallel to the anchor block displacement direction displayed the narrowest apex angle.

Table 7 Load capacity and apex angle of all block patterns measured from the failure tests

The modelling described in this paper is essentially 2D, as it does not account for stresses applied in the in-plane or out-of-plane directions. This simplification results in a very shallow in-plane depth of the models, meaning that they lack the 3D constraints typically present in a real rock mass.

Existing rock anchor design approaches use apex angles of 90$^{\circ }$ or 60$^{\circ }$ when estimating the uplift capacity of the rock mass, with 60$^{\circ }$ used for weak rock masses and 90$^{\circ }$ used for all other rock masses, as described by Brown (2015). However, in most of the studied block patterns, the apex angle was 90$^{\circ }$ or greater, and the uplift capacity was not directly related to the apex angle; for instance, the test of pattern 2 with large blocks had the highest measured capacity but the smallest apex angle (Table 7). Thus, the usage of apex angles to estimate the uplift capacity can be questioned.

A recent study conducted by Høgset et al. (2023) investigated failures in continuous media subjected to ground anchor loads. Their findings indicated that failures predominantly occurred in the lower section of the anchorage, resulting in apex angles ranging from 60 to 80$^{\circ }$ in frictional materials and 100 to 110$^{\circ }$ in low-cohesion materials. These materials were weaker than the weak rock masses for which a 60$^{\circ }$ apex angle is typically recommended in the literature. The results of Høgset et al. (2023) resemble the findings of our study, where the observed apex angles during failure tests generally exceeded the recommendations in the literature, thus suggesting that currently recommended apex angles may be too conservative.

The failure tests revealed variations in the maximum capacities of the block patterns. Block patterns 1–3 and 5 demonstrated capacities ranging from 30 to 90 kN under the same boundary conditions, whereas block pattern 4 exhibited a lower capacity with reduced horizontal stress. Among the first group (block patterns 1–3 and 5), block pattern 1 and the small block variant of block pattern 2, characterised by continuous horizontal joints, displayed the lowest capacities, while the variant of block pattern 2 containing larger blocks showed the highest capacity. Among the block models featuring pavement blocks, block patterns 3 and 5 demonstrated the highest capacity of 75 kN, indicating the absence of persistent discontinuities normal to the anchor loading direction can enhance the load-bearing capacity of the rock mass. These findings underscore the significant influence of block or joint orientation on the rock mass capacity, where threefold load capacity variations may arise based on the block orientation. These observations are consistent with the numerical models of Shabanimashcool and Bērziņš (2023), which found that the presence of joint sets sub-parallel to the anchor axis greatly increased the rock mass uplift capacity. Block model 4, which lacked a joint set sub-parallel to the anchor loading direction, exhibited the lowest overall capacity in the present study.

Interestingly, the highest observed load capacity occurred in the block models with the smallest apex angle (patterns 3 and 5), whereas the lowest load capacity was measured in the block model with the widest apex angle (pattern 4). These results suggest that the apex angle does not significantly control the block models’ load capacity, implying that the apex angle may be less influential than other factors when considering the uplift capacity of a rock mass. Instead, the key factors to consider when evaluating the rock mass uplift capacity are the rock mass orientation and joint spacing, which directly affect the ability of the rock mass to undergo load arching. This observation is consistent with the findings of Shabanimashcool and Bērziņš (2023), who highlighted the importance of parameters such as the rock joint orientation relative to the anchor and rock block size, among others, in determining the rock mass uplift capacity.

4.3 Load Capacity Estimations and Load Arching

The block model capacities were estimated based on current design criteria, which involved calculating the weight of the overlying rock (Brown 2015) and using presumptive shear strength values (NPRA 2018), at all the tested depths. These estimated capacities are given in Table 8. NPRA (2018) recommends using a presumptive shear strength in the range of 50–100 kPa and an apex of 80$^{\circ }$ for a rock mass with two joint sets and strength of 15–50 MPa. For the failure tests with a height of 0.9 m, the estimated capacity was 3.8 kN based on the weight of the overlying rock and 22.3–44.6 kN based on the recommended presumptive shear strength values. The total estimated capacity was 26.1–48.5 kN. The measured capacities in the tests ranged from 19.4 to 90.1 kN, as given in Table 7. The estimate based on the weight of the overlying rock is conservative and is much lower than the measured capacities of the block models. The estimate including the shear strength is closer to the measured values. However, it is difficult to precisely estimate the shear strength of rock mass at present.

Table 8 Estimated block model capacity based on the weight of overlying rock (Brown 2015) and presumptive shear strength value approaches (NPRA 2018)

The average horizontal stress values for all the failure tests are plotted against the anchor block displacement in Fig. 35. The block pattern 1, 2, and 5 tests exhibit similar stress development trends: in these tests, the horizontal stress increased up to a displacement around 35–40 mm and then decreased with further anchor displacement. For block pattern 3, the horizontal stress remained almost constant until 35 mm displacement and then began to gradually drop. The horizontal stress for the tilted block pattern (block pattern 4) initially decreased before reaching a residual horizontal stress level after 10 mm of anchor displacement. These average horizontal stress measurements demonstrate that load arching mainly occurs during the early stages of the tests at displacements less than 40 mm; thereafter, the block models lose their load-bearing capacity and fail with increasing displacement.

Fig. 35

Average horizontal stress for all the block patterns plotted against the anchor block displacement

4.4 Effect of In Situ Stress Changes on Block Model Capacity and Displacement

Figure 36 shows how in situ stress variations change the region of main movement in block pattern 2, a trend also seen in patterns 1, 4, and 5. The main movement occurred above the anchor. Increasing horizontal stress slightly reduced the region in the lateral direction but did not significantly change it in the vertical direction. Increasing the vertical stress, while keeping the horizontal stress constant, concentrated the movement in a small region above the anchor block.

The changes to the region of main movement were also reflected in the capacity of the block models under varying boundary conditions. When the region decreased in size, the capacity of the block model increased. Higher in situ stresses confined the blocks more, reducing the region influenced by the anchor, which demonstrated an increase in block model capacity with increasing in situ stresses.

Block pattern 3 deviated from these observations. When the horizontal stress was greater than the vertical stress, it followed the same trends as the other patterns. However, when the vertical stress was equal to or higher than the horizontal stress, only the blocks above the anchor moved, resulting in a lower capacity.

Fig. 36

The changes in the region of main movement in the blocks under three loading conditions: a zero horizontal stress, b horizontal stress of 0.1 MPa, and c horizontal stress of 0.1 MPa and vertical stress of 0.15 MPa. Demonstrated using block pattern 2 as an example

5 Conclusions

In this study, five block models were tested on a specially constructed laboratory test rig to investigate the models’ failure patterns in response to a concentrated upward load that simulated the loading conditions of a rock anchor. All the models contained two sets of joints; however, the joint patterns varied in the models to simulate a range of different physical scenarios.

The common findings in the model tests were as follows: (1) the failure occurred in the form of a triangle with separation surfaces mostly following the surfaces of the joint sets; (2) in models where the anchor load was applied perpendicular to one of the joint sets (block patterns 1, 2, 3, and 5), the horizontal stress increased with the applied anchor load, indicating a load arching effect, and the vertical displacement was greatest above the anchor; and (3) when the continuous joint set was not perpendicular to the loading direction (pattern 4), the displacement was greatest along a line perpendicular to the continuous joint set that started at the loading point.

The apex angle of the failure cone varied from 90$^{\circ }$ to 120$^{\circ }$ in the models where the joints were distributed symmetrically relative to the vertical loading line of the anchor (block patterns 1, 2, 3 and 5). The apex angle was up to 140$^{\circ }$ in the model of block pattern 4, in which the joints were asymmetrically distributed with respect to the loading direction. The failure surface could potentially be asymmetrical in rock masses containing pervasive oblique joints such as pattern 4.

In the models containing horizontal (patterns 1, 2, and 4) or sub-horizontal continuous joints (pattern 5), the load capacity increased more with increases in the vertical stress than with increases in the horizontal stress. In the model containing vertical continuous joints (pattern 3), the opposite trend occurred, i.e., the load capacity increased more with increases in the horizontal stress than with increases in the vertical stress.

Flat load arches were established within each layer of the blocks in the models containing horizontal continuous joints (patterns 1 and 2). The load arching phenomenon was interpreted in all models except block pattern 4 based on the observed horizontal stress variations. The arching effect appears strongest when the continuous joint set is perpendicular to the anchor loading direction and becomes weaker when the joint set obliquely intersects the loading direction.

The load capacity was lowest in the model containing a continuous joint set that was not perpendicular to the loading direction (pattern 4), moderate in the models containing joint sets that were either perpendicular or parallel to the loading direction (patterns 1 and 2), and highest in the model containing interlocked joint sets (pattern 5). The load capacity increased with increasing block size (patterns 2a and 2b).

The findings from this study regarding the effect of in situ stresses on block model capacities have important practical implications for rock anchor design. In locations where the in situ stresses are moderate or high, the rock mass uplift capacity is enhanced, thus reducing the anchoring length required to prevent rock mass uplift failure. Nonetheless, further full-scale field testing in varying rock masses is essential to gain an improved understanding of the relationship between rock mass uplift capacity, joint orientation, and in situ stresses before these constraints are integrated into design criteria. Thus, continued research in this field will pave the way for more robust and informed rock anchoring design practices.