Two-dimensional Analysis of the Group Interaction Effects Between End-bearing Piles Embedded in a Rock Mass

Abstract

This research is a two-dimensional analysis of the interaction effect in a group of piles socketed in a rock mass when studying the end-bearing capacity of the group. This problem was extensively studied for deep foundations in soils, but very little is published about foundations in rock. The study was conducted in 2D to establish the basis and criteria to analyze the problem, as well as understand the main factors and failure mechanisms involved when several piles work together in a foundation. The factors included in the analysis are, among others: the parameters of the rock mass, the pile embedment, and the pile separation. The research highlights shaft resistance as one of the key factors in the interaction. It proves that neglecting shaft resistance changes the interaction influence and the failure mechanism which may not be on the safe side. The research includes an analysis of the failure modes of different pile configurations using the discontinuity layout optimization (DLO) method, by taking advantage of the method’s ability to show the wedge configuration at the failure. The minimum and maximum efficiencies are characterized in terms of the pile separation values, thereby proposing a procedure to obtain the absolute minimum efficiency of the group. A second procedure is also presented for the approximate prediction of the bearing capacity of the pile tip, for a group with a particular number of piles and properties, by considering the contribution of the corner piles and the intermediate piles.

Highlights

The main contributions of our article to the field of geotechnical engineering are briefly enumerated in the following list:

• 1. First-time evidence of the critical importance of considering the pile shaft resistance to address the bearing capacity of the tip of a pile in rock.

• 2. First-time presentation of a comprehensive analysis of the different parameters influencing the group interaction effect for piles in rock.

• 3. In-deep analysis of the collapse failure mechanisms of an end-bearing pile group embedded in rock using DLO.

• 4. First-time identification of some new failure modes between interacting piles.

• 5. Two simplified equations are proposed to approach the pile-group bearing capacity, including interaction effects.

1 Introduction

Piles are most effective when combined in groups or clusters. Even though they are generally used in groups in practice, most researchers dealt studied single piles instead of analyzing group behavior. Consequently, designers rely on the calculated bearing capacity of single piles to predict the bearing capacity of pile groups.

That is understandable since combining piles in a group makes analysis much more complicated as the behavior changes due to the interactions within the group. The allowable load of a single pile will not be the same when that pile is combined in a cluster or in a group. The bearing capacity of the set is evaluated by a factor multiplying the product of the number of piles (n) by the individual bearing capacity of an isolated pile. This factor is usually known as efficiency (ξ) of the group and, depending on the ground properties, group size, and pile spacing, may be smaller or higher than unity, thus reducing or increasing the average pile individual capacity, respectively.

$${\text{Efficiency }}\xi = \frac{{\text{Bearing capacity of the group}}}{{n * {\text{Bearing capacity of a pile}}}},$$

(1)

Some results were published regarding the behavior of a group of foundations by considering their interaction. Most research dealt with shallow foundations on sand (Stuart 1962). However, some approaches were made to deep foundations, studying the bearing capacity of pile groups in sand from lab tests, such as that by Kezdi (1957), Fleming (1958), Stuart et al. (1960). Stuart and Hanna (1961) adapted Meyerhoff’s analytical formulation (Meyerhoff 1951, 1953) to estimate the pile group efficiency in the sand.

Some empirical equations predict the group efficiency in soil, such as the Converse-Labarre equation (Bolin 1941) and that proposed by the Los Angeles Group Action Method. Others proposed empirical ratios to reduce the efficiency of each pile, taking the neighboring piles into account (Feld 1943). Different approaches were proposed in the form of equations (Seiler and Keeney 1944; Sayed and Bakeer 1992; Das 1999), design charts (Whitaker 1957), and models converting the group into an equivalent pier (Terzaghi and Peck 1967; Poulos and Davis 1980).

There are also some load tests conducted on pile groups in soils, either full-scale, such as those described by Vesić (1969), Garg (1979), Ismael (2001), McCabe and Lehane (2006), and Zhang et al. (2013), or reduced-scale, such as Al-Mhaidib (2006), Al-Omari et al. (2019), Al-Khazaali and Vanapalli (2019), Marwa et al. (2021), and De Sanctis et al. (2021).

Using the Mohr–Coulomb failure criterion in soils, a different approach used numerical models to analyze the behavior of the group through a large number of numerical experiments, such as Chow (1986), Ching et al. (1990), Poulos (1994), Leng et al. (2019).

Unlike the case of pile groups in soil, the common assumption regarding the ultimate bearing capacity of end-bearing pile groups on rock is that group capacity will be essentially equal to the number of piles times the capacity of the isolated pile, considering the group effect negligible (Prakash and Sharma 1991). That might be one of the reasons why so few studies are available on pile groups in rock, while extensive research is done on pile groups in soils.

However, after analyzing data from the actual behavior of piled shafts in rock in a building construction site, Katzenbach et al. (1998) claimed that the group effect should be taken into account and that neglecting it may produce either overestimation or underestimation of the group capacity.

Initial solutions were presented for groups of piles that penetrate a weak upper soil layer to socket into a lower firm bearing stratum of greater stiffness. Poulos and Mattes (1974) presented solutions for pile groups resting on the surface of the rock stratum but without considering the embedment in rock or the specific failure criteria in rock masses. Chow et al. (1990) presented a numerical procedure to predict the settlement of socketed piles in a very firm stratum, defining the efficiency as a stiffness-reduction factor but not addressing the situation of ultimate instability.

Some authors used centrifuge models to experimentally analyze the efficiency of the different piles in the group. Zhang and Wong (2007) investigated the group effect when some defective piles were not founded on the rock (they did not reach the rock stratum) but did not use specific failure criteria for these media. Xing et al. (2014) studied the effect of different bedrock embedments of the piles in the group on soils with the Mohr–Coulomb failure criterion. However, they pointed out that some conservative measures, such as ignoring the shaft resistance associated with the rock-socketed piles, may not be wise for project construction. This aspect then requires some further research.

The efficiency factor in rocks has recently been studied for shallow foundations. Shamloo and Imani (2021) researched the behavior of two closely spaced strip footings on Hoek–Brown rock masses by using the analytical upper bound theorem, which requires the previous assumption of the failure mechanism. Keawsawasvong et al. (2022) applied the advanced upper bound and lower bound finite element limit analysis, which does not require any presumption, thus obtaining numerically the efficiency factors for the shallow foundations.

As previously stated, the group effect of piles in rock was rarely investigated, and it was mainly done using experimental observations beyond the initial numerical solutions oriented to settlement analysis. Therefore, the mutual influence between piles affecting the bearing capacity of the group in rock has not been addressed systematically. The present research should show that this interaction is significant in pile design for rock masses and depends, for a given terrain, not only on the usually considered parameters, such as pile diameter, the separation between piles, and the tip embedment in the rock but also on the pile shaft resistance.

2 Objectives

This research is a numerical investigation regarding the significance of the interaction effects among end-bearing piles in a group founded on the rock. We considered the particular relevance that the assumed shaft resistance on the pile socket has in the group efficiency.

Since usual practice assumes that the group effect produces an end-bearing efficiency (ξ) higher than 1 for piles on rock, the present work will prove that the efficiency highly depends on the shaft resistance of the embedded pile and can reach values lower than 1 in some cases.

A novel numerical procedure, the Discontinuity Layout Optimization (DLO) method (Smith and Gilbert 2007), was used to sustain all the studies, to obtain the bearing capacity and the failure wedges for the different analyzed models. The software’s ability to show the failure mechanisms allows for obtaining invaluable insights regarding the failure behavior of nearby piles.

In the present paper, we will first present the configuration of the problem and the analysis method. Second, a preliminary approach is made to explain the behavior of two nearby piles in a simple medium (soil with Mohr–Coulomb failure criterion) since this will enable comparison with previous research and well-established knowledge. This will lead to a third analysis on the reference case of an infinite row of piles in rock, approaching later a finite number of piles, thus obtaining some initial findings of the model behavior. Finally, a comprehensive set of calculations with different geometric and geomechanical parameters will be presented and analyzed to generalize the previous results.

3 Problem Statement and Numerical Methods of Analysis

3.1 Problem Statement

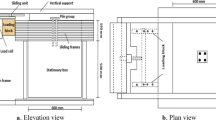
The model considered in the analysis will include the main factors affecting the solution, such as the three parameters characterizing the rock mass: rock type (m₀), uniaxial compressive strength (UCS), geological strength index (GSI), density of the rock (γ_R) and the geometric characterization of the pile group as the pile diameter (B), separation between pile axes (s), and the pile length embedded in the rock stratum (H_R). A non-resistant soil layer (height H_S and density γ_S) is considered over the rock, which is represented only by its weight due to its low resistance in relation to the underlying ground. The piles are rigidly coupled at their tops by an infinitely-rigid pile cap, not in contact with the terrain. All these characteristics are presented in Fig. 1.

Fig. 1

Sketch of the problem and simplified model

Regarding the behavior of the rocks, they are, in general, a heterogeneous, discontinuous, anisotropic material due to the family of planes of weakness crossing the rock mass.

In the present research, are assumed: perfect plasticity, plane strain conditions, associated flow rule, and, common in rock mechanics, the modified Hoek and Brown failure criterion. However, the modified Hoek and Brown failure criterion is only suitable for rock masses whose behavior, despite having discontinuities, can be considered homogeneous and isotropic. The different cases and ability to be represented by the Hoek and Brown criterion are included in Fig. 2. Anisotropic case II generated by a family of planes of weakness and non-isotropic case III produced by two families of discontinuities, as presented in Fig. 2, requires an individualized analysis checking both the criterion of failure along the planes of weakness and the criterion of failure through the rock mass, and therefore they are outside the scope of this research.

Fig. 2

Applicability of the Hoek and Brown yield criterion for group effect in piles which was adapted from Hoek (1983). Red color for cases that are not possible to analyze and green color for possible cases (Color figure online)

Although the problem is three-dimensional by nature, the assumption of plane strain is used to make the problem approachable, maintaining the influence of the main variables affecting the problem without change and, consequently, enabling a simple analysis of this complex problem.

3.2 Failure Criterion of the Rock Mass

Following the latest modification (Hoek et al. 2002), the formulation of the Hoek and Brown failure criterion is now expressed as:

$${\sigma }_{1}^{^{\prime}}={\sigma }_{3}^{^{\prime}}+{\sigma }_{c}\cdot {\left(m\cdot \frac{{\sigma }_{3}^{^{\prime}}}{{\sigma }_{c}}+{s}_{a}\right)}^{a},$$

(2)

where${\sigma }_{1}^{^{\prime}}$ and ${\sigma }_{3}^{^{\prime}}$ are, respectively, the major and minor effective principal stresses at failure,${\sigma }_{c}$ is the uniaxial compressive strength (UCS) of the intact rock,$m$, ${s}_{a}$ and $a$ are material constants, which depend on the rock mass properties and represented by the following expressions:

$$m={m}_{0}\cdot {e}^{\left(\frac{GSI-100}{28-14\cdot D}\right)},$$

(3)

$${s}_{a}={e}^{\left(\frac{GSI-100}{9-3\cdot D}\right)},$$

(4)

$$a=\frac{1}{2}+\frac{1}{6}\cdot \left({e}^{\left(\frac{GSI}{15}\right)}-{e}^{\left(\frac{-20}{3}\right)}\right),$$

(5)

where ${m}_{0}$ is a material constant obtained through triaxial tests data or using the approximate tables given by Hoek et al. (2002),$\mathrm{GSI}$ is the Geological Strength Index, with similar values to $\mathrm{RMR}$ index (Bieniawski 1976),$D$ is a factor that depends on the degree of disturbance to which the rock mass has been subjected by blast damage and stress relaxation (removal of the overburden). The $D$ factor varies from 0 for undisturbed in situ rock masses to 1 for highly disturbed rock masses. In the present study, D is assumed to be 0, which corresponds to conventional execution conditions.

Besides, the following important parameters are also defined (Serrano et al. 2000):

$${\beta }_{n}={A}_{n}{\sigma }_{c},$$

(6)

$${\zeta }_{n}=\frac{{s}_{a}}{{m A}_{n}},$$

(7)

where $A_{n} = m\left( {1 - n} \right)/2^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}}$. The exponent n is a characteristic from the modified criterion and ranges from n = 0.5 to n = 0.65, depending on the degree of rock fracturing. The parameter β_n is called “strength modulus” and will be used to non-dimensionalize the stresses, and the parameter ζ_n is the so-called “rock mass toughness coefficient”. Both parameters will be used extensively in the present research but without a subscript.

3.3 Numerical Solution: Discontinuity Layout Optimization Method

3.3.1 DLO Mathematical Formulation

The discontinuity layout optimization method (DLO) was developed by Smith and Gilbert (2007) and is a powerful solution to address the limit analysis of two-dimensional plastic problems. A detailed explanation of the procedure is beyond the scope of this paper, and we draw the attention of readers to the given references. Only a brief review of the theoretical bases will be included as follows.

The procedure defines a set of nodes over a dominium of study and connects every two nodes with a possible discontinuity. The DLO is used to obtain the minimum-energy compatible configuration of discontinuities among all the possibilities. A linear programming scheme is employed by defining and minimizing an objective function with several conditions.

Considering that the normal and tangential displacements at each discontinuity are the main variables of the problem, a work balance equation (objective function) is written comparing the live and dead load works and the plastic work:

$$\mathrm{min}\lambda\, {{\varvec{f}}}_{{\varvec{L}}}^{{\varvec{T}}}{\varvec{d}}=-{{\varvec{f}}}_{{\varvec{D}}}^{{\varvec{T}}}{\varvec{d}}+{{\varvec{g}}}^{{\varvec{T}}}{\varvec{p}}.$$

(8)

The non-dimensional number λ multiplying the live load is known as the adequacy factor. This number is increased to the limit when the work balance equation reaches its minimum, thus corresponding to a collapse state. The linear programing unknown variables are the displacement and plastic multipliers vectors d and p.

Two vectors of loads are considered: f_D called dead loads and f_L called live loads; those loads are affected by the adequacy factor. The vector of displacements at the discontinuities d^T = {s₁, n₁, s₂, n₂,…,s_m} contains, respectively, the relative shear s_i and normal displacements n_i at each discontinuity i.

The dissipation coefficients at each discontinuity i are contained in vector g^T = {c₁ l₁, c₁ l₁, c₂ l₂, c₂ l₂,…,c_m l_m} each one being the product of the cohesive shear strength c_i by length l_i. The vector p contains plastic multipliers.

The objective function is subject to several conditions:

$${\varvec{B}}{\varvec{d}}=0,$$

(9)

$${\varvec{N}}{\varvec{p}}-{\varvec{d}}=0,$$

(10)

$${{\varvec{f}}}_{{\varvec{L}}}^{{\varvec{T}}}{\varvec{d}}=1,$$

(11)

$${\varvec{p}}\ge 0,$$

(12)

Matrix B includes the direction cosines, and matrix N contains the plasticity flow parameters.

The described DLO formulation only applies to translational failure mechanisms, but extended to consider rotational failure mechanisms by Smith and Gilbert (2013). This research uses the last enhanced formulation for all the calculations.

The representation of the failure mechanism improves with the number of nodes considered, which is a key factor of accuracy. The procedure is an upper-bound solution (Smith et al. 2017), and increasing the number of nodes will approach the numerical solution to the theoretical solution downwards.

As referred to earlier, this method presents clear advantages. First, it identifies the collapse mechanism as the classical limit analysis but without the need for any previous assumption of the mode of failure: this particular advantage will prove critical in this research. Second, it does not usually present numerical problems (Smith et al. 2017) as far as excessive confinement is avoided. Furthermore, the computational cost is relatively small compared to other methods being used. All things considered, this method is highly recommendable to deal with the actual problem considered in this study.

3.3.2 Representation of the Failure Criterion

As shown in the previous section, the DLO procedure uses linear programming and requires a linear failure criterion. The fully non-linear Hoek and Brown failure criterion of the rock should first be linearized to be included in the DLO scheme. An intermediate-secant approach is applied in the linearization to obtain better results (Millan et al. 2021) instead of the most common external tangent approach or internal secant one since it is associated with better accuracy. A representation of the procedure to obtain the linear approximation is shown in Fig. 3.

Fig. 3

Different solutions to linearize the Hoek & Brown failure criterion

The accuracy obviously depends on the number of intervals used to linearize the curve. In this research, a 20-interval approximation is used since the increase in computer load was not significant.

3.3.3 DLO Models

For this research we used the GEO software from LimitState (2020), that was used to implement the previous linearization of the Hoek and Brown criterion.

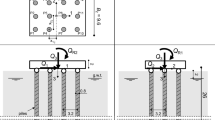
Regarding the modeling, three general cases were considered for the group of piles: (a) an even number of piles, (b) an odd number of piles, and (c) an infinite number of piles. For all of these piles, horizontal symmetry was used to reduce the model size. For the two first cases, the symmetry axis was located at the center of the model, while a double symmetry scheme was used for the third case, to study the model between the axes of two adjacent piles. This approach eliminates the boundary condition of the pile at the edge, thus corresponding to an unlimited number of piles. Figure 4 shows the different cases. The isolated pile was idealized following the type-b model.

Fig. 4

Different cases of pile groups considered in the study and their symmetry: a an even number of piles, b an odd number of piles, and c an infinite number of piles

The rock medium was modeled as a rectangular domain, as shown in Fig. 5a and b for a group of 2 piles and 3 piles, respectively. It includes a free boundary condition at the top, fixed boundary conditions at the bottom and right edges, and symmetry boundary conditions at the left edge; a semi-pile was included at this edge for the 3-pile case. This made it possible to represent only half of the problem. Similar conditions were considered for an infinite row of piles as presented in Fig. 5c, where symmetry boundary conditions were also considered at the left edge (one semi-pile was modeled at each edge).

Fig. 5

Example models of different pile group configurations with separation s/B = 3: a 2-pile group, b 3-pile group, and c infinite row of piles

The piles were connected by an infinitely rigid rod which produces an identical movement in all piles and an identical individual load, assuming only a uniform vertical load on the group of piles. An identical external load was applied on the top of each pile that were increased automatically to reach the collapse state using the adequacy factor explained in the previous section.

Each pile had a fixed diameter $B=0.8\mathrm{ m}$ in this research with an embedment in the rock medium represented by ${H}_{R}$. The overlying soil has a depth ${H}_{S}$ and was only represented by its corresponding pressure.

The extension of the failure mechanism determines the rock domain size for each model. To avoid interferences, the right and bottom edges were placed far from the foundation by trial-and-error for all models.

The accuracy of the results depends on the number of nodes defined in the domain. A convergence study was performed to delimit the minimum number of nodes that should be used in the model. As shown in Fig. 6, a node distribution equivalent to approximately 4 nodes/m was considered enough to obtain good accuracy; variation relative to the higher density lower than 5%. Most models in this research are considerably finer than this limit.

Fig. 6

Convergence analysis relative to the nodal density in the model. Infinite row of piles, separation s/B = 3, embedment H_R = 2.5B, overlying soil H_S = 10 m. Rock with GSI = 5, m₀ = 12, UCS = 50 MPa

4 Key Factors Influencing the Group Effect

4.1 Case of Two Close Piles

Before analyzing the pile group effect on a rock medium, it was considered necessary to start from a simple case that was better studied in the literature, and with some results that can be used as a reference. The key factors can then be analyzed step by step, changing one at a time. The reference case used is the interaction between foundations on granular soil.

This simplified model is directly related to the problem under study, by considering a pile group with null embedment, as presented in Fig. 7a. In this case, the pile tip acts as a shallow foundation without external overload. Then, it is converted progressively into a deep foundation, increasing the plane support depth (Fig. 7b).

Fig. 7

a Modeling of pile tips as close shallow foundations and b Modeling of pile tips as deep close foundations with surface load

The factors studied in this initial problem were the separation between centers s, the surface load -related to the height of the soil stratum H_S-, and the embedment ratio H_R. Three different steps were considered:

• (a) Shallow foundations with different separations and surface loads,

• (b) Foundations with certain embedment, with different separations and surface loads. No shaft resistance.

• (c) Foundations with certain embedment, without surface loads but with shaft resistance.

A general case considering simultaneously an external load and certain embedment was not specifically studied in this section. The objective was to delimit the influence of each factor and, consequently, they were introduced one at a time to identify those that induce variation in the results.

The results of the efficiency with the ratio s/B from step a) are shown in Fig. 8 for the case of a Mohr–Coulomb sand, with friction angle ϕ = 35º. A very good agreement was observed for the shallow foundation results with Kumar and Kouzer (2008) for the case of two close foundations on the surface of the soil with no surface load q_s. The initial line with a positive slope corresponded to the values $\frac{{\left( {2 + d/B} \right)^{2} }}{2}$, with d the distance between foundation edges, and defined by the same authors as the efficiency of the system composed of two foundations working as a unique foundation. When a surface load was applied, the peak value diminished and moved to higher values of s/B (Fig. 8). Two different zones were considered: the increasing slope pre-peak and the posterior downward slope. Each zone corresponds to a different failure mechanism, as shown in Fig. 9 for the case with an external overload of 180 kPa.

Fig. 8

Efficiency of two shallow foundations on sand considering different surface loads q_s

Fig. 9

Failure wedges for the case of shallow foundation on granular soil (φ = 35º) with q_S = 180 kPa. Two different s/B values:1.25 and 3

The increasing slope before the peak in Fig. 8 corresponds to failures where the two foundations perform as a unique foundation, with a common active triangular wedge, as shown in Fig. 9a. After the peak, each foundation has its separate active wedge, and a progressively increasing interaction zone is developed between them (Fig. 9b). For longer separations s/B, each foundation has a separate failure wedge, and the efficiency will be the unity.

For step b), an embedment of H_R = 2.5B was considered, as well as different surface loads, from q_s equal to 0 up to 360 kPa, and null shaft resistance for all cases. The results are presented in Fig. 10.

Fig. 10

Efficiency of two embedded foundations on granular soil (φ = 35º) with the support plane at 2.5B depth and different surface loads qs. No shaft resistance is considered

Figure 10 also shows two different zones around a peak, with a lower efficiency value than shallow foundations. As in the case without embedment as studied previously, the greater the overload, the maximum efficiency of the curves decreases. Most important is to realize that, for high s/B ratios, the efficiency values go below the unity when an embedment in the foundation is considered, either with or without surface load. The corresponding failure modes are presented in Fig. 11 for the case of an embedment of H_R = 2.5B, surface load qs = 180 kN/m², and separations s/B equal to 3 and 8 above and below the value of one of the efficiency.

Fig. 11

Failure wedges for the case of two embedded foundations on granular soil (φ = 35º) with q_S = 180 kPa. Two different s/B values: 3 and 8

This latter behavior was not reported by Stuart and Hanna (1961) in their work on groups of deep foundations, but always showed efficiency over unity for the different depths considered (D/2B = 8, 16, and 20). The reason for this unexpected behavior was the appearance of alternative modes of failure involving lower energy that takes preference over the theoretical modes considered by Stuart & Hanna. These failure modes are analyzed in depth later in this paper.

Finally, for step c) different shaft resistances were introduced to investigate their influence on the system behavior. Since granular soil was considered, the shaft resistance varies from the complete Mohr–Coulomb shear resistance of the soil to a zero value, considering some fractions of the friction angle (50% and 25%) as intermediate values. Results are presented in Fig. 12.

Fig. 12

Efficiency of two embedded foundations on granular soil (φ = 35º) with a 2.5B depth of the support plane, null surface load q_s, and different shaft resistance values

The curves in Fig. 12 have a maximum that, for this case, without overloading and embedment, is located at a certain distance from the theoretical reference curve; in the previous cases, the maximum aligned quite well with that curve. In addition, there is a strong influence of the shaft resistance on the bearing capacity efficiency, always showing values higher than one, but for the null shaft resistance case.

As in b) cases, the difference corresponds to new modes of failure that appear due to the presence of the embedment soil and, simultaneously, to the null shaft resistance. They are shown as an example in Fig. 13.

Fig. 13

Modes of failure for two close embedded foundations on granular soil (φ = 35º) with depth 2.5 B and s/B = 5. a Null shaft resistance; b Shaft resistance 25% of Mohr–Coulomb resistance (φ’ = 35º)

Figure 13 is presented to interpret the evolution of the curves in Fig. 12 based on the failure wedges. As can be seen, there is a significant difference in the failure mode between piles when the shaft resistance is null (Fig. 13a) or not (Fig. 13b). For the first case, the embedment soil does not fail and only moves upward as a rigid block, adapting to the movement of the underneath failure, due to the frictionless contact with the piles. However, since the embedment soil cannot slip along the soil-pile contact for the second case, the embedment soil should fail too, and more energy is needed altogether.

After this first review of the main factors affecting the behavior of two close foundations on soil (separation s/B, external overload, embedment, and shaft resistance), we consider the problem of a group of piles on the rock. We present the problem in two steps before addressing the complete set of cases and calculations, to help better understand the physics of the problem.

4.2 Infinite Row of Piles as a Reference Case

4.2.1 Influence of the Pile Separation

When thinking about the problem of a set of interacting piles, two main zones can immediately be recognized, the inner zone and the edge zone. The inner zone corresponds to piles situated between other piles (called from now on “intermediate piles”), whose behavior is closer to that of the infinite row of piles presented in Fig. 4c. The edge zone corresponds to the piles at the end of the group (called “border piles”), whose behavior is, in part, related to an isolated pile and, also, to the intermediate pile. The behavior of the piles in these two zones is different and may be related to two simple cases used as a reference for their behavior: an isolated pile and an infinite row of interacting piles.

The actual bearing capacity of a group with a finite number of piles can be composed of the contribution of both simple cases, the border piles plus the intermediate piles, and will be studied in the next section.

Since the solution for the isolated pile case is well-established, the following discussion will deal with the infinite-row-of-piles case. This case will be the base case in this research because it reduces the variability of the real case with a finite number of piles only to the separation variable s/B. Although an extensive set of calculations is presented in Sect. 4.1, some previous results relative to this case are introduced next since they were useful to clarify other problems.

The geometry of the problem considered in this section is defined with the pile diameter B = 0.8 m, the soil layer depth ${H}_{S}$ = 10 m, and the embedment of the pile in the rock medium ${H}_{R}$= 2.5B = 2 m. An overload of q_S = 180 kPa was applied to all cases. Two different values of each material parameter were chosen for this set of calculations, combining them in four different cases.

The efficiency of the infinite row of piles on the rock for different separations and considering null shaft resistance is shown in Fig. 14. All of them present a similar behavior to that of the embedded pile on soil shown in the previous section.

Fig. 14

Efficiency of the infinite row of piles for four different cases of study and null shaft resistance

Figure 14 shows an asymptote at s/B = 1, progressing to an infinite efficiency value since, for that separation, the piles would have lateral contact. Then the infinite row of piles corresponds to a unique pile of infinite width and to extreme confinement of the rock, making the general shear failure not possible (infinite bearing capacity).

In addition, Fig. 14 shows that the efficiency coefficient of the infinite row of piles is, for these cases and most of the separations, lower than unity (efficiency related to the isolated pile reference case) and reaches its minimum between s/B = 3 and s/B = 8. The efficiency stays below one, even for high values of s/B when the usual separation for the appearance of two isolated failure wedges is exceeded (approximately s/B = 6, Kumar and Bhattacharya 2013).

Different failure wedges corresponding to some of the cases studied are represented in Fig. 15. As can be seen, no isolated pile wedges are developed before s/B = 15. Consequently, the efficiency will be affected for the studied cases far beyond the usual assumption.

Fig. 15

Failure mechanisms for different values of s/B, case of the infinite row of piles. Double symmetry conditions are used at the edges to model the infinite row of piles. Case 1 from Table 1, with GSI = 5, m₀ = 12, UCS = 50 MPa, H_R = 2B, H_S = 10 m, and q_S = 180 kPa. Null shaft resistance

An example is shown in Fig. 16 where the resulting failure wedge of the row of piles (s/B = 15) is superposed with that of the individual isolated piles. As can be seen, the isolated pile wedges do not interfere, but the final failure is influenced by the interaction. That contradicts the usual assumption in the area for which no interaction is expected beyond a separation higher than s/B = 6.

Fig. 16

Superposition of the failure wedge for the row of piles (grey lines) with s/B = 15 and the individual failure wedges of the isolated piles (white lines). Symmetry conditions are used at the edges to model the infinite row of piles. Same case as in Fig. 14 (Color figure online)

4.2.2 Influence of the Rock Embedment

An in-depth analysis is needed to understand this unexpected behavior that is present in both cases of piles in soil and rock.

From the first analysis performed in Sect. 3, it was clear that the efficiency lower than one is related to a reduced or null shaft strength. It is not that clear why that happens and why a minimum appears beyond the fact that it is due to the apparition of different failure modes than expected.

This behavior seems to be related to the embedment volume of rock placed between piles and how it connects to the piles. Several configurations were studied to clarify this point, changing the embedment rock strength and, as an extreme case, completely removing the rock of the embedment.

The analysis was performed for a particular case of rock (case 1 from Table 1) with characteristics GSI = 5, m₀ = 12, UCS = 50 MPa. The embedment rock resistance varies from the full Hoek and Brown resistance. We reduced the embedment rock resistance down to a fraction of 50% and 25%, which is equivalent to rock obtained by applying that fraction to each friction angle and cohesive strength of the linearization of the Hoek and Brown criterion as explained in Sect. 3.3.2. Finally we reached a null value by suppressing the embedment, but including its weight as an external load.

Table 1 Infinite row of piles case of study

Each of the obtained bearing capacities were normalized by the corresponding isolated pile capacity (P_{h_isolated}) for the same case to obtain efficiency. Both the bearing capacity and the efficiency results are presented in Fig. 17.

Fig. 17

Analysis of the influence of the embedment strength on efficiency. Cases with Hoek and Brown criterion (full case), with a fraction of 50% and 25% of the Hoek and Brown criterion, and with suppressed embedment. a Bearing capacity without normalization; b Efficiency normalized by the corresponding isolated pile results

As observed in Fig. 17a, all cases have the same bearing capacity P_h from s/B = 1 to approximately 8. This means that the rock embedment has a null influence on the P_h over this range of s/B and that all the modes of failure should be similar, not breaking through the embedment. This behavior is demonstrated in Fig. 18, where the failure wedges for the full case and the suppressed embedment case are compared for three different separations s/B equal to 3, 5, and 7.5. It is clear that these wedges are the same (as well as for the other two cases not shown in the figure), and consist of a failure wedge under the embedment base and a vertical displacement of the embedment as a rigid block along the frictionless contact with the piles. From s/B = 8 the failure starts to affect the embedment rock, which causes the P_h results to diverge from one another. The different wedges depending on the embedment resistance are shown in Fig. 19 for s/B = 15 and cases of fractions 50% and 25% of Hoek and Brown, obtaining a combined wedge that goes into the embedment for the first case, and separated, individual wedges for the second one.

Fig. 18

Failure mode comparison between the suppressed-embedment case (upper figure) and the embedded case (lower figure) for different separations. Case 1 from Table 1, with GSI = 5, m₀ = 12, UCS = 50 MPa, H_R = 2B, H_S = 10 m, and q_S = 180 kPa

Fig. 19

Failure mode comparison for reduced resistance of the embedment rock. Cases of fractions a 50% of Hoek and Brown, and b 25% of Hoek and Brown. Separation s/B = 15. Case 1 from Table 1, with GSI = 5, m₀ = 12, UCS = 50 MPa, H_R = 2B, H_S = 10 m, and q_S = 180 kPa

In summary, though the bearing capacity is the same for a wide range of s/B, whatever the embedment properties, Fig. 17b shows that the efficiency is different for all cases. This is due to the fact that the bearing capacity of the isolated pile is affected by the strength of the embedment rock because its failure wedge needs to develop through it, while the failure wedge of the group of piles does not, at least until s/B = 8. The P_{h_isolated} is higher the stronger the strength of the embedment rock, thus the efficiency will be the lowest for the strongest case (GSI = 5, m₀ = 12, and UCS = 50 MPa in Fig. 15b).

4.2.3 Efficiency Minimum

Regarding the minimum value obtained around s/B = 5 in Fig. 17b, it can be explained by comparing the different failure wedges developed by the suppressed-embedment case and the full rock strength (or any of the reduced-strength cases). The comparison is shown in Fig. 18, presenting 3 cases that consider the interaction before the minimum (s/B = 3), around the minimum (s/B = 5), and after the minimum (s/B = 7.5).

As can be observed, the failure wedges for s/B = 3 interact in both cases, superposing themselves, with some complex configurations. However, the failure wedges for s/B = 5 have a configuration coinciding with the simple superposition of two symmetrical wedges of an isolated pile, with the upper passive triangle shared by both wedges. This is the simplest interaction configuration then the minimum efficiency is reached for this separation. For the embedded case, the rock embedment block moves upward as a rigid solid for all three s/B ratios. In short, if the failure wedges intersect in the transition zones, correspond to case a), and if they do so in the passive zones, as in case c). Finally, the minimum occurs when they intersect just at the point of change from the transition to the passive zone, coinciding with case b).

Increasing the separation up to s/B = 7.5, the wedge superposition in the suppressed-embedment case is reduced to a smaller triangle, creating a non-uniform displacement along the rock surface (shown in Fig. 18) without significantly changing the bearing capacity load. The embedded case cannot develop the same pattern of failure since it would need to break the embedment rock, involving more energy. On the contrary, the wedge develops downward with lower energy requirements, maintaining a unique passive triangle that pushes the embedment rock upwards as a block.

This behavior continues while the energy involved is lower than that of the isolated pile failure and, after s/B = 15, changes to independent wedges (for that particular case), as shown in Fig. 15.

Interestingly, the minimum bearing capacity among all cases (Fig. 17a) corresponds to the suppressed-embedment case, having a constant value from s/B = 5 onwards. This value also corresponds to the bearing capacity of the isolated pile without embedment (s/B > 15).

This behavior gives a relevant procedure for estimating the absolute minimum value of the bearing capacity of a group of piles. It can be easily calculated from the isolated shallow foundation corresponding to the group of piles with suppressed-embedment with a high separation between them (high s/B ratio).

4.2.4 Influence of Shaft Resistance

The previous analysis of the infinite row of piles considered a null shaft resistance, as usual in rocks when analyzing the tip-of-the-pile bearing capacity in a group of piles, since the tip resistance is usually much higher than the shaft resistance. In this section, different shaft resistances are introduced to evaluate their influence on the bearing capacity at the tip of the group piles.

The analysis in this section was performed for a particular case of rock (β = 10 MPa; ζ = 0.01) to present the problem. Later, the analysis was extended to a wide range of cases.

Neglecting the shaft resistance, as usually done in practice, will lead to the results represented by the “frictionless” case in Fig. 20, where the efficiency is lower than 1 (as explained in the previous section). Increasing the shaft resistance will obtain progressively higher efficiencies, up to the maximum represented by the full Hoek and Brown failure criterion. The intermediate results considering a shaft resistance of 5%, 15%, and 25% of the Hoek and Brown criterion are also considered to show the trend. Therefore, efficiencies less than one can be obtained by variations of the embedment and the shaft resistance.

Fig. 20

Shaft resistance influence for different separations, infinite row of piles. Rock with β = 10 MPa; ζ = 0.01. H_R = 2B, H_S = 10 m, and q_S = 180 kPa

Figure 19 clearly shows the importance of considering the shaft resistance even when calculating the bearing capacity of the pile tip in a group. In some situations, this shaft resistance may drop to small values and could cause a significant reduction in the pile group efficiency. Some cases correspond to circumstances that can generate instabilities during the excavation of piles, such as the appearance of natural cavities, areas of high surface decompression, or water tables in highly fractured rocks. Some other reasons may be related to the execution system reducing the shaft resistance, for example, when a casing tube is necessary.

Figure 21 shows the failure wedges of three s/B = 5 representative cases from Fig. 20, corresponding to frictionless shaft resistance, for 5% H&B and 15% H&B cases. The growing complexity in the failures associated with a higher shaft resistance requires more energy and produces higher efficiency.

Fig. 21

Failure mode comparison between different cases of shaft resistance. a Frictionless shaft, b 5% H&B, and c 15%H&B. Rock with β = 10 MPa; ζ = 0.01. s/B = 5, H_R = 2B, H_S = 10 m, and q_S = 180 kPa

5 General Results and Discussion

5.1 General Case Calculations with a Finite and Infinite Number of Piles

A complete set of calculations was addressed to explore the influence of the main parameters studied in the previous section on the bearing capacity of the group of piles.

The inputs of the problem will be the main geometric and geotechnical parameters introduced in Sect. 3.1 that are considered variables and are enumerated in Table 2, including their range of variation.

Table 2 List of parameters considered for the set of calculations

To better characterize the problem and simplify the analysis, the rock mass toughness coefficient (ζ) and the strength modulus of the rock (β) were used (described in Sect. 3.2) instead of using the rock type (m₀), uniaxial compressive strength (UCS), and geological strength index (GSI).

The results are presented in the following sections, grouped by different criteria to help the analysis.

5.2 Influence of Rock Parameters

Figure 22 shows the results for the different combinations of rock mass toughness coefficient, ζ, and strength modulus of the rock, β, grouped in independent figures for clarity. Sub-figures (a), (b), and (c) correspond to a shaft resistance using a 5% of the Hoek and Brown criterion (5% H&B) and (d), (e), and (f) of the 15% H&B. Other variables are H_R = 2B, H_S = 10 m, and q_S = 180 kPa.

Fig. 22

Efficiency of an infinite row of piles with respect to pile separation s/B for different normalized parameters β and ζ. a, b, and c Shaft resistance 5% H&B; d, e and f Shaft resistance 15% H&B. H_R = 2B, H_S = 10 m, and q_S = 180 kPa

For the 5%H&B particular case (Fig. 22a, b, and c), the most significant issue is the efficiency reduction obtained for separations larger than s/B = 3. The reason was already explained in Sect. 4.2.3 and is related to a lower energy configuration of the failure wedge that rather elevates the embedment block than fractures it (failure wedges shown in Fig. 18). Increasing β factor, mainly related to the uniaxial compressive stress of the rock, produces an extension of this zone of lower efficiency since the rock strength is higher and fracturing the embedment block gets easier the longer the separation between piles. That is especially evident between β = 1 MPa (Fig. 22a) and the other two cases, β = 10 MPa and β = 25, in Fig. 22b and c, respectively.

The rock mass toughness coefficient (ζ), related to the relative quality and strength of the rock mass, highly influences the efficiency. It is considerably reduced for higher values such as ζ = 0.1 (corresponding to less disturbed rock, difficult to break), and improving showing very similar results for ζ = 0.01 and ζ = 0.001 (disturbed rock, easier to crack by the failure wedge).

The efficiency reduction below one is clearly reduced when the shaft resistance increases, as can be seen in Fig. 22d, e and f, corresponding to a 15% H&B value. This point will be shown in detail in the next section.

5.3 Influence of Shaft Resistance

Figure 23 shows the efficiency for different pile separations and shaft resistance values for four particular cases of rock parameters (cases β = 1 MPa and β = 10 MPa combined with ζ = 0.001 and ζ = 0.1), identifying the different influences and trends. Other variables in this cases are H_R = 2B, H_S = 10 m, and q_S = 180 kPa.

Fig. 23

Efficiency of an infinite row of piles with respect to pile separation s/B for different cases of shaft resistance. Normalized parameters β = 10 MPa and ζ = 0.01. H_R = 2B, H_S = 10 m, and q_S = 180 kPa

The first conclusion that can be derived from Fig. 23 is the strong influence of the shaft resistance on the overall bearing capacity of the pile group and the need to be properly addressed to obtain a reliable prediction of the pile group efficiency.

When the shaft resistance is small (frictionless and 5% H&B cases), it produces efficiencies lower than unity because they allow simpler and less energy-expensive failure wedges, as explained in Sect. 4.2.4 and shown in Fig. 21. For pile separation higher than a minimum s/B (variable for each case), the efficiency tends to 1 when s/B increases, as the group acts more as a set of individual piles: see the evolution of failure wedges with s/B in Fig. 15.

For higher shaft resistances, the efficiency increases, tending to values nearer and over one. Comparing Fig. 23a and b, where only the parameter β changes from 1 to 10 MPa, its effect smoothes the curves, increasing the s/B separation at the minimum value and elevating it. That is coherent with the fact that a higher β implies higher embedment block strength. This effect is more pronounced for the ζ = 0.001 case (very disturbed rock) than for that with ζ = 0.1 (little disturbed rock).

5.4 Influence of the Rock Embedment

The influence of the rock embedment is presented in Fig. 24 for the reference case, the infinite row of piles, and different cases of pile embedment H_R and normalized parameters β and ζ. The adopted shaft resistance is 5%H&B, soil height H_S = 10 m, and surface load q_S = 180 kPa.

Fig. 24

Efficiency of an infinite row of piles with respect to pile separation s/B for different cases of pile embedment H_R and normalized parameters β and ζ. Shaft resistance 5%H&B, H_S = 10 m, and q_S = 180 kPa

The figure mainly shows that the intermediate embedment H_R = 2.5B produces a higher efficiency reduction than the other two cases, by not having the H_R = 5B case any reduction below unity.

The different failure wedges are compared in Fig. 25, where the main difference observed in the failure mechanism, beyond the evident embedment height, is related to the complexity and discontinuity density of the failure shape that increases with H_R. The different efficiencies are related to the fact that, in a row of piles, the energy to break the embedment increases with H_R at a faster rate than the bearing capacity of the isolated pile (Fig. 25d).

Fig. 25

a, b, and c Failure mode comparison between different cases of pile embedment H_R. Normalized parameters β = 1 MPa and ζ = 0.001. Shaft resistance 5%H&B, s/B = 5, H_S = 10, d Comparison between the bearing capacity of the pile row and the isolated pile for the previous cases

For the three cases presented in Fig. 25, the efficiency ratio will be minimum for the intermediate case (H_R = 2.5B).

5.5 Influence of the Soil Height

The influence of the overlaying soil height H_S is presented in Fig. 26 for the reference case (infinite row of piles), shaft resistance equal to 5%H&B, and embedment height H_R = 2.5B m.

Fig. 26

Efficiency of an infinite row of piles with respect to pile separation s/B for different cases of overlying soil height H_S and normalized parameters β and ζ. Shaft resistance 5%H&B, H_R = 2.5B

As could be expected, the soil height influence is relatively small. A higher soil height implies an increased overburden load on the rock surface, producing higher confinement. The pile row and the isolated pile bearing capacity increase in parallel, obtaining a lower efficiency with lower soil height.

5.6 Influence of the Number of Piles

Real-life foundations always have a limited number of piles. The analysis of the infinite row of piles will be affected by the actual number of piles depending on how significant is the effect of the border piles on the intermediate pile behavior. Nevertheless, the general trends and relations previously identified for the infinite row of piles will remain valid.

Three cases were studied, including 2, 3, and 5 piles. The same variables in the infinite row of piles were analyzed to address how their behavior changes. A limited number of results are presented here.

Figure 27 shows results comparing the efficiency factor for the pile row case and the 2, 3, and 5-pile cases. Different s/B separation ratios were considered for some selected cases with normalized parameters β and ζ, and assuming a shaft resistance of 5%H&B, H_R = 2.5B, and H_S = 10 m (surface load q_S = 180 kPa).

When the number of piles in the group increases, the efficiency tends towards the infinite row case. As can be observed, the minimum efficiency occurs around values s/B = 5 for this particular case, coinciding with separations that are usually considered to avoid pile interference.

For small values of s/B, a different behavior appears, showing a positive inclination in the curve that is different from that of the infinite row of piles. For this latter case, a combination of the symmetry condition and little separations lead to over confinement on the model. But without the possibility of developing a failure wedge able to move, this produces an asymptotic response when s/B tends to one. However, when a small number of piles is considered and are situated close together (small s/B ratio), the finite group can develop a global failure aggregating the individual wedges as a unique and broader pile tip, as presented in Fig. 28 a: case s/B=1.5 and 3-pile group, β = 10 MPa and ζ = 0.01, shaft resistance 5%H&B, H_S=10 m. For those later cases, an efficiency higher than one should be expected.

Fig. 27

Efficiency of cases of 2, 3, 5 piles, and an infinite row of piles with respect to pile separation s/B and different normalized parameters β and ζ. Shaft resistance of 5%H&B, H_R = 2.5B, and H_S = 10 m

Fig. 28

Failure mechanisms for a 3-pile group (not at the same scale), separations a s/B = 1,5, b s/B = 2, and c s/B = 3. Normalized parameters β = 10 MPa and ζ = 0.01. Shaft resistance 5%H&B, H_S = 10 m. Symmetry condition is used at the left edge

There is a transition zone where the failure mechanism shows characteristics that belong to both previous simple cases: the case with a unique shared wedge between extreme pairs of piles and the case with separate pile wedges between each pair, as seen in Fig. 28b (case s/B = 2). Figure 28c shows the individual failure development at each pile (not combined with others) with interactions.

5.7 Simplified Equation for Group Bearing Capacity Considering Pile Interaction

As explained in Sect. 4.2.1, the behavior of a finite group of piles can be idealized by adding the intermediate piles (approximated by an infinite row of piles) and the border piles (partially evaluated from an isolated pile). This simplified model helps both to understand the complex behavior of the group and to have a simple tool to predict its bearing capacity.

Figure 29 shows some failure wedges for a particular case with 2, 3, and 5 piles. Although the particular failure depends on the number of piles, similar behavior can be observed among intermediate piles on the one hand, and border piles on the other. The model can reproduce the behavior of a pile group only when it behaves as separate piles interacting (as in Fig. 29), not when it acts as a unique and broader pile due to little separations (as in Fig. 28a and b).

Fig. 29

Failure mechanisms for a different number of piles on the group. s/B = 3 case. Normalized parameters β = 10 MPa and ζ = 0.01. Shaft resistance 5%H&B, H_S = 10 m. Symmetry condition is used at the left edge

Following this point, the proposed simplified model is represented in Fig. 30 for a 3-pile case. Corner piles are assumed to have half of the isolated-pile bearing capacity (P_h,isolated) and half of the pile row. Intermediate piles have approximately the pile-bearing capacity of an infinite row of piles (P_h,row).

Fig. 30

Assumed simplified failure mechanisms for a pile group

Considering the above, the following formulation can be proposed to calculate the joint bearing pressure (P_h,group) for a group of N piles:

$$P_{{{\text{h\_group}}}} = \, P_{{\text{h,isolated}}} + \, \left( {N - 1} \right) \, P_{{\text{h,row}}} ,$$

(13)

$${\text{Error}}_{{}} = \, \left( {P_{{{\text{h\_group}}}} {-} \, P_{{{\text{h\_numerical}}}} } \right)/ \, P_{{{\text{h\_umerical}}}} ,$$

(14)

where P_{h_numerical} represents the numerical method result for the particular group of piles.

The resulting checking test for a particular case, that is normalized parameters β = 10 MPa and ζ = 0.01. Shaft resistance 5%H&B, H_S = 10 m, is presented in Table 3.

Table 3 Test results of the simplified model for the bearing capacity of pile groups (normalized parameters β = 10 MPa and ζ = 0.01. Shaft resistance 5%H&B, H_S = 10 m

6 Preliminary Analysis of a 3D Case

As explained in Sect. 3.1, the pile interference problem in this research is studied using a 2D model because the complexity of the problem needs a previously simplified approach. This 2D model is an approximation to an actual pile case even though it can properly represent the influence of the different parameters and the overall system behavior. To prove this claim, a 3D model of a set of interacting piles is defined using Limit Analysis Finite Element software (Optum CE 2018).

Due to the software limitations, the Hoek and Brown failure criterion is approximated only by two lines, but this limitation is considered acceptable for this preliminary test.

An infinite rectangular array of piles is defined (similar to the infinite row of piles studied in 2D), and it is modeled using double symmetry, as schematically defined in Fig. 31. Normal displacements are constrained along the vertical planes of the model, and null displacements are considered at the base. The equivalent soil load is applied to the upper surface of the rock.

Fig. 31

Infinite array of piles. a 3D full representation; b Double symmetry representation

The finite element mesh used, and shear dissipation results are also presented in Fig. 32, for a case with normalized parameters β = 1 MPa and ζ = 0.001, s/B = 4, HR = B, HS = 10 m, and qS = 180 kPa. The efficiency values are obtained for different s/B ratios and shaft resistances and are shown in Fig. 33. As expected, a similar behavior to that of the 2D case is obtained. The figure shows a sensible reduction of efficiency when the shaft resistance tends to zero, and a contraction towards the origin of the s/B axis if compared to the 2D case, corresponding to lower s/B values for the minimum efficiency. The critical influence of shaft resistance on the efficiency is patent, shifting from values bigger than one to others on the order of 0.6 for this particular case.

Fig. 32

3D model of an infinite array of piles. a 3D finite element mesh (detail); b Shear dissipation results (detail). Normalized parameters β = 1 MPa and ζ = 0.001. s/B = 4, H_R = B, H_S = 10 m, and q_S = 180 kPa

Fig. 33

Shaft resistance influence for different separations, 3D infinite array of piles. Normalized parameters β = 1 MPa and ζ = 0.001. H_R = B, H_S = 10 m, and q_S = 180 kPa

The previous results show that the main findings in this research are valid for the 3D case except for the particular efficiency values that, as expected, change due to the three-dimensional effect. Further research is needed to accurately define the actual values of the efficiency for the 3D cases, once the interaction mechanisms are highlighted and explained by present research.

7 Conclusions

The present research gives some insight into the phenomenon of the interaction within a pile group socketed in rock that affects the end-bearing capacity of the group. The research details the failure mechanisms developed in the rock mass that depend on the rock properties, the separation between piles, the embedment in the rock, and the height of overlaying soil above the rock. Besides, the pile shaft resistance, contrary to the usual assumption of neglecting it, proves to be critical to the final bearing capacity of the tip of the pile.

A 2D model using the novel discontinuity layout optimization method (DLO), based on limit state analysis and optimization, allowed us to study in detail the generation of the pile failure wedges depending on the different parameters, which is an invaluable aid to understanding and explaining the behavior of the foundation at the failure, first exposed in this paper and one of its main achievements.

The main conclusions and achievements of this research are listed below:

• 1.In our opinion, this research addresses a problem that was not studied previously and needed to be considered, since it appears in most pile foundations in rock, such as the problem of the interaction between close piles.

• 2.The main factors influencing the bearing capacity of the group of piles were analyzed. As explained and proved in the present paper, an essential contributing factor was the shaft resistance. This factor has been systematically neglected in rock mechanics, assuming to be on the safe side and considered to be very small. However, our research proves that the non-consideration of the shaft resistance changes the interaction influence and the failure mechanism and may not be on the safe side. This is pointed out for the first time here.

• 3.The different failure mechanisms are presented and explained regarding the pile separation and the pile embedment in the rock. The identification of the different mechanisms was related to the mobilized part of the terrain, considering both sides of the corner piles and the intermediate part between interior piles.

• 4.The minimum and maximum efficiencies are characterized by their respective pile separation values. In particular, efficiencies lower than unity are identified as well as the procedure to obtain the value of s/B leading to the minimum efficiency of the group effect which is important to analyze the safety of the foundation.

• 5.An easy-to-use formulation to calculate the bearing capacity of the group of piles is presented here: Sect. 5.7 Simplified equation for group bearing capacity considering pile interaction. This formulation does not require a numerical model and the associated convergence and stability analysis.

• 6. A preliminary 3D case is studied using a Limit Analysis Finite Element 3D model, showing a coincidence in the overall behavior with that of the 2D model studied in this research, backing their validity as a conceptual explanation of the pile group interaction. Further research is needed to establish specific group efficiency values.