1 Introduction

With the continuous exploitation of conventional resources, oil and gas resources with the characteristics of centralized storage and easy exploitation are decreased sharply, and the exploitation of unconventional oil and gas resources is gradually highlighted. As an important means for oil and gas well stimulation, hydraulic fracturing has been widely used in the exploitation of shale gas and shale oil. The main principle of hydraulic fracturing to increase shale gas production is to create fractures perpendicular to the direction of minimum principal stress in the low-permeability strata and eventually through the production formation. The initiation and propagation of cracks in low-permeability strata are largely dependent on the fracture toughness of shale. Therefore, studying the fracture toughness of shale with different configurations and sizes is of great significance for the efficient exploitation of shale gas. Since rock materials are most prone to failure under tensile stress, mode I (tensile) fractures are the most common failure modes, and mode I inherent fracture toughness (KIc) is the focus of rock fracture mechanics research. Test methods with different configurations have been proposed to measure KIc, which can be roughly divided into two categories: artificially prefabricated notch test methods and non-prefabricated notch test methods. The former methods include the cracked chevron notched Brazilian disc (CCNBD) test (Fowell 1995; Aliha and Ayatollahi 2014), short rod (SR) test, the chevron bend (CB) test (Ouchterlony 1988), and the semi-circular bend (SCB) test (Kuruppu et al. 2014; Tutluoglu et al. 2022) recommended by International Society for Rock Mechanics (ISRM). Besides, non-standard test methods based on artificial prefabricated notches have also been widely used, such as the diametrally compressed ring (DCR) (Aliha et al. 2008), the edge cracked triangular (ECT) (Aliha et al. 2013), the edge-notched disc bend (ENDB) (Aliha and Bahmani, 2017; Bahmani and Nemati 2021), the edge-notched diametrically compressed disc (ENDC) (Aliha et al. 2021a; Bahmani et al. 2021), the single edge crack round bar bending (SECRBB) (Barr and Hasso 1986; Khan and Al-Shayea 2000; Aliha et al. 2018), the chevron notch semi-circular bend (CNSCB) (Kuruppu 1997; Mahdavi et al. 2020), and the cracked straight-through Brazilian disc (CSTBD) (Ayatollahi and Akbardoost 2014; Aliha et al. 2014; Xie et al. 2020). The latter methods include the flattened Brazilian disc (FBD) (Keles and Tutluoglu 2011) and the Brazilian disc test (BDT) (Guo et al. 1993). However, due to the large dispersion of the test data, these methods are not frequently used in fracture testing.

A growing number of studies have shown that the fracture toughness tested by different configurations of specimens varies greatly, even with the standard test methods recommended by ISRM (Aliha et al. 2017; Wei et al. 2017). For example, Aliha et al. (2017) tested the fracture toughness of rock with the SCB configuration, CB configuration, SR configuration, and CCNBD configuration recommended by ISRM, and found that the fracture toughness measured by SR specimens is twice that by CCNBD specimens. Even if the test specimens have the same configuration, the measured fracture toughness is not necessarily the same (Aliha et al. 2010; Ayatollahi and Akbardoost 2014). Aliha et al. (2010) tested the fracture toughness of CSTBD specimens with different sizes, and found that fracture toughness increases with the increase of specimen size. To explain the Ka changing with the size and configuration of the specimen, a series of fracture criteria have been proposed (Erdogan and Sih 1963; Sih 1974; Kong and Schluter, 1995). The maximum tangential stress fracture criterion is the most simple and frequently used criterion (Erdogan and Sih 1963). It is believed that the specimen will fracture when the maximum tangential stress at a certain distance from the crack tip is equal to the tensile strength of the material. The traditional maximum tangential stress (TMTS) fracture criterion ignores the influence of other stress terms on the tangential stress except for the singular terms in Williams stress expansion, and considers that the fracture of specimens with different configurations occurs under the same critical stress intensity factor. Subsequently, a modified maximum tangential stress (MMTS) fracture criterion was proposed (Aliha et al. 2012a), and the first three terms of Williams expansion were considered in determining the tangential stress near the crack tip. The MMTS criterion not only explains the size effect and configuration effect on the measurement of Ka, but also can be used to predict the Ka of the specimen (Aliha et al. 2012a, b; Ayatollahi and Akbardoost 2014; Aliha and Mousavi 2019; Bidadi et al. 2020; Sangsefidi et al. 2020). The determination of the length of the fracture process zone (FPZ) is the key to the prediction of Ka. Some studies have reported that the FPZ length is closely related to the size of the specimen (Bazant et al. 1986; Karihaloo 1999; Ayatollahi and Akbardoost 2014). Ayatollahi and Akbardoost (2014) tested the fracture toughness of CSTBD specimens with different sizes, and obtained the FPZ length by considering different terms of Williams stress expansion. It was found that the FPZ length obtained from the first three terms of Williams stress expansion is significantly larger than that obtained by the singular stress terms, and the FPZ length increases with the increase of specimen size. It indicates that the appropriate fracture criterion and the size effect of FPZ should be jointly considered in predicting the Ka. In above studies, the first three terms of Williams expansion are only considered in both the prediction of Ka and the determination of FPZ length. However, accurate results cannot be effectively obtained by this method in some cases (Wei et al. 2018). Based on the MMTS criterion, Wei et al. (2018) proposed a further maximum tangential stress (FIMTS) fracture criterion. In this criterion, more terms of Williams stress expansion should be considered to accurately describe the stress field around the crack tip.

For specimens with different sizes, the influence of boundary conditions on tangential stress at the front of the crack tip is different, while the prediction difference of the Ka of specimens with different sizes caused by TMTS, MMTS, and FIMTS criteria has never been studied. Moreover, according to the effective crack model (Nallathambi and Karihaloo 1987), the specific difference in predicting the inherent fracture toughness of the material based on the FPZ length determined by different fracture criteria is also not clear. Based on equivalent linear elastic fracture mechanics, Bazant and Planas (1997) established the failure load prediction model of specimens with different configurations from the perspective of energy release rate, namely the size effect law (SEL) model. However, the difference between the prediction results of the maximum tangential stress fracture criterion and the SEL model have not been compared in previous studies on the size effect of fracture toughness (Akbardoost et al. 2014; Akbardoost 2014; Ayatollahi and Akbardoost 2013; Sangsefidi et al. 2021). Therefore, in this paper, fracture tests of shale specimens with CSTBD configuration in different sizes were carried out. The difference between the Ka of shale specimens with different sizes was analyzed through the maximum tangential stress fracture criterion. According to test results of Ka, the TMTS, MMTS, and FIMTS criteria were used to obtain the FPZ length of specimens, and the effective crack model was used to predict the KIc of materials. To efficiently compare the effects of the TMTS, MMTS, FIMTS criteria, and the SEL model on predicting the Ka of specimens, the size effect of FPZ was also considered and three-point bending fracture tests were carried out on shale specimens with NSCB configuration.

2 Experimental Setup

Due to the simple configuration, easy fabrication, and processing and efficient analytical solution for stress intensity factor calculation, the CSTBD configuration has been widely used in tests on rock fracture toughness. In this test, shale specimens with CSTBD configuration were selected to study the size effect of fracture toughness, as shown in Fig. 1. According to linear elastic fracture mechanics (LEFM), the mode I stress intensity factor (KI) of CSTBD specimens can be calculated by Eqs. (1) and (2) (CAA 1981)

$$K_{{\text{I}}} = Y^{ * } \frac{{P\sqrt {\pi a} }}{\pi BR},$$
(1)
$$Y^{ * } = \left[ {1 - \alpha + {6}{\text{.24}}\alpha^{2} - {25}{\text{.44}}\alpha^{3} + 1{61}{\text{.6}}\alpha^{4} - {664}{\text{.96}}\alpha^{5} } \right. + {{\left. {{1288}{\text{.32}}\alpha^{6} - {961}{\text{.28}}\alpha^{7} } \right]} \mathord{\left/ {\vphantom {{\left. {{1288}{\text{.32}}\alpha^{6} - {961}{\text{.28}}\alpha^{7} } \right]} {\sqrt {1 - {2}\alpha } }}} \right. \kern-\nulldelimiterspace} {\sqrt {1 - {2}\alpha } }},$$
(2)
Fig. 1
figure 1

Specimens with the CSTBD configuration

Full size image

where P is the load applied to the specimen, a is half of the crack length, R is the specimen radius, B is the specimen thickness, α (= a/R) is the normalized crack length, and Y* is the dimensionless stress intensity factor, which is only related to α.

Previous experimental studies have shown that the change of loading rate has a significant impact on the fracture toughness of rock (Zhang and Zhao 2013; Xu et al. 2016; Zhou et al. 2018; Ju et al. 2019). At high loading rates, the incubation time of microcracks is short, and the microcracks are mainly formed and propagated in the crystal. At low loading rates, microcracks have enough time to develop, the strength of crystal boundary is far lower than the resistance of crystal fracture, and the cracks prone to propagate along the crystal boundary (Liu et al. 2020). For specimens with prefabricated cracks, force-controlled loading rate, the configuration and dimensions of the specimen jointly determine the time from initial loading to complete failure. For example, when the CSTBD specimens are used under the same force-controlled loading rate, the failure time of specimens with α = 0.993 is taken as reference, and the change of the failure time with the specimen size and the crack length can be obtained. As shown in Fig. 2a, the change of geometric configuration size can lead to the difference of failure time among specimens with different sizes by tens of times. This indicates that even at the same loading rate, the interference of rate effect may exist in measuring the size effect on fracture toughness of rock specimens. Unfortunately, the potential interference of rate effect has been rarely considered in studies. To accurately understand the effect of specimen size change on fracture toughness tests, the potential effect of loading rate should be eliminated, and the configuration size should be appropriately selected. Figure 2b shows the variation trend of dimensionless stress intensity factor Y* with specimen configuration size derived from Eq. (2). The variation Y* trend of CSTBD specimens is gentle (α = 0.15–0.35), which can be regarded as a straight line. According to the KI of CSTBD specimens in Eq. (1), when the \(\sqrt a /R\) of specimens with different sizes are the same and the value of α is between 0.15 and 0.35, the KI change rates of specimens with different sizes are identical under the same force-controlled loading rate, that is, based on LEFM, the specimens with different sizes can fracture at almost the same time. According to the above principles, four sizes of shale specimens were selected for the test. Table 1 shows the detailed parameters of specimen diameter D and crack length 2a of shale specimens.

Fig. 2
figure 2

a Failure time and b dimensionless stress intensity factor Y* variation of CSTBD specimens with different sizes

Full size image
Table 1 Specimen sizes for fracture tests
Full size table

All shale specimens were taken from the same shale rock mass to ensure high geometric integrity and uniformity. First, cores with different diameters were drilled and then cut into discs with a thickness of 30 mm. Second, a water knife was used to cut symmetrical cracks with different lengths from the center of the disc, and the notch tip was further sharpened with steel wire to form the crack tip. Figure 3 shows the processed CSTBD specimens in different sizes. Finally, the prepared specimens were tested by the INSTRON1346 electric servo testing machine. All the specimens were directly loaded by force control through the compression plate at the loading rate of 30 N/s. The force and displacement sensors of the loader collected data automatically every 0.2 s. In addition, according to the rock tensile strength test method recommended by ISRM (1978), the tensile strength of shale was determined to be 7.927 MPa.

Fig. 3
figure 3

The CSTBD specimens manufactured in four different sizes

Full size image

3 Results and Analysis

3.1 The Tested Fracture Toughness of Specimens with Different Sizes

According to the LEFM, when the external load reaches the peak load Pmax, that is, the critical stress intensity factor is equal to the inherent fracture toughness of the material KIc, the crack begins to propagate. However, due to plastic deformation near the crack tip, the tested or apparent fracture toughness Ka is not equal to KIc, and the Ka of the CSTBD specimen can be calculated by the following equation:

$$K_{{\text{I}}} = K_{{\text{a}}} = Y^{ * } \frac{{P_{{{\text{max}}}} \sqrt {\pi a} }}{\pi BR}.$$
(3)

Table 2 shows the failure load and average Ka of CSTBD specimens with different sizes, and Fig. 4 shows more detailed results of the Ka. It can be seen that the Ka is significantly affected by specimen size. As mentioned in Sect. 2.1, the change rate of stress intensity factor for specimens with different sizes is the same under the same force-controlled loading rate. According to the LEFM, specimens with different sizes should be broken at approximately the same time, that is, the Ka of specimens with different sizes is very close in theory. However, there is a discrepancy in test results, and larger specimens need higher loads to be fractured. As discussed in the previous studies (Smith et al. 2010; Ayatollahi and Akbardoost 2014; Wei et al. 2018), such experimental results are understandable when the stress field near the crack tip is determined by considering other terms other than the singular term in Williams stress expansion. Because shale is a kind of quasi-brittle material, there is an inevitable FPZ near the crack tip, which will enlarge the influence of other stress terms on the fracture behavior of specimens. The results of this experiment clearly show the limitations of LEFM and the influence of FPZ on the failure load of specimens.

Table 2 Failure loads and average Ka of CSTBD specimens with different sizes
Full size table
Fig. 4
figure 4

The variation of Ka with specimen size

Full size image

3.2 Comparison of Stress Field Distribution Determined by Different Fracture Criteria

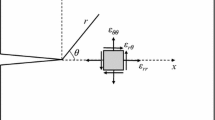
To comprehensively explain the size effect of Ka observed in the test, the maximum tangential stress fracture criterion is used to analyze the test results in detail. According to the well-known Williams stress expansion (Williams 1957), the stress around the crack tip of the plate with cracks under the action of the load in the plane can be described by Eq. (4) in line with the coordinate system in Fig. 5

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ \end{array} } \right\} & = \sum\limits_{n = 1}^{\infty } \frac{n}{2} A_{n} r^{{\left( {\tfrac{n}{2} - 1} \right)}} \left\{ {\begin{array}{*{20}c} {\left( {2 + \frac{n}{2} + \left( { - 1} \right)^{n} } \right)\cos \left( {\frac{n}{2} - 1} \right)\theta - \left( {\frac{n}{2} - 1} \right)\cos \left( {\frac{n}{2} - 3} \right)\theta } \\ {\left( {2 + \frac{n}{2} - \left( { - 1} \right)^{n} } \right)\cos \left( {\frac{n}{2} - 1} \right)\theta + \left( {\frac{n}{2} - 1} \right)\cos \left( {\frac{n}{2} - 3} \right)\theta } \\ {\left( {\frac{n}{2} - 1} \right)\sin \left( {\frac{n}{2} - {3}} \right)\theta - \left( {\frac{n}{2}{ + }\left( { - 1} \right)^{n} } \right)\sin \left( {\frac{n}{2} - 1} \right)\theta } \\ \end{array} } \right\} \\ & \quad - \sum\limits_{n = 1}^{\infty } \frac{n}{2} B_{n} r^{{\left( {\tfrac{n}{2} - 1} \right)}} \left\{ {\begin{array}{*{20}c} {\left( {2 + \frac{n}{2} - \left( { - 1} \right)^{n} } \right)\sin \left( {\frac{n}{2} - 1} \right)\theta - \left( {\frac{n}{2} - 1} \right)\sin \left( {\frac{n}{2} - 3} \right)\theta } \\ {\left( {2 - \frac{n}{2} + \left( { - 1} \right)^{n} } \right)\sin \left( {\frac{n}{2} - 1} \right)\theta + \left( {\frac{n}{2} - 1} \right)\sin \left( {\frac{n}{2} - 3} \right)\theta } \\ { - \left( {\frac{n}{2} - 1} \right)\cos \left( {\frac{n}{2} - {3}} \right)\theta + \left( {\frac{n}{2} - \left( { - 1} \right)^{n} } \right)\cos \left( {\frac{n}{2} - 1} \right)\theta } \\ \end{array} } \right\}, \\ \end{aligned}$$
(4)
Fig. 5
figure 5

Stress components near the crack tip in a rectangular coordinate system; b polar coordinate system

Full size image

where r and θ are polar coordinates, n is the serial number of the term in the infinite series, and the coefficients An and Bn depend on the configuration and geometry of the specimen and the applied load.

The maximum tangential stress fracture criterion proposed that when the maximum tangential stress at a certain distance rc from the crack tip reaches the critical value ft, the specimen will fracture. In this study, rc and ft are considered to be the FPZ length and the tensile strength of the material. For mode I fracture, the maximum tangential stress appears at the front of the crack tip, that is, θ = 0. By substituting θ = 0 into Eq. (4), the tangential stress at the location r away from the crack tip is obtained

$$\begin{aligned} \sigma_{\theta \theta } & = \sigma_{y} \left| {_{\theta = 0} } \right. = \sum\limits_{n = 1}^{\infty } \frac{n}{2} A_{n} r^{{\left( {\tfrac{n}{2} - 1} \right)}} \left( {1 - \left( { - 1} \right)^{n} } \right) \\ & \quad = A_{1} r^{{ - \tfrac{1}{2}}} + 3A_{3} r^{{\tfrac{1}{2}}} + 5A_{5} r^{{\tfrac{3}{2}}} + 7A_{7} r^{{\tfrac{5}{2}}} + 9A_{9} r^{{\tfrac{7}{2}}} + 11A_{11} r^{{\tfrac{9}{2}}} + 13A_{13} r^{{\tfrac{11}{2}}} + \cdot \cdot \cdot , \\ \end{aligned}$$
(5)

where the first term is called singular term, which is also the term of well-known stress intensity factor KI. Therefore, the coefficient A1 can be expressed by KI

$$A_{1} = \frac{{K_{I} }}{{\sqrt {2\pi } }}.$$
(6)

As expressed in Eq. (5), when r is small and infinitely close to 0, two extremes are caused, that is, the first term of Williams stress expansion becomes very large, while other stress terms tend to 0. Compared with the first term, the influence of other stress terms can be completely ignored, and the stress field near the crack tip can be described by the stress intensity factor alone. The TMTS criterion only considers the effect of singular terms on the fracture behavior of the specimen and infers that the Ka obtained in fracture tests is the same. Therefore, the Ka is only related to the properties of the material. However, this is very different from the actual fracture test results. Many studies have shown that the Ka is related to the configuration and size of the specimen (Aliha et al. 2010, 2017; Ayatollahi and Akbardoost 2014). Similar results are also obtained in this test, and the Ka is significantly affected by specimen size.

For quasi-brittle materials (such as rocks, concrete and hard clay), the FPZ length is relatively large, and the influence of other stress terms cannot be directly ignored. If the singular term is only considered to describe the stress field at a certain distance from the crack tip, the mode I fracture behavior of rock specimens cannot be accurately evaluated. To this end, the tangential stress at the crack tip front of the specimen was extracted by the ABAQUS software. Due to the symmetry of loading conditions and specimen configuration, only a quarter of CSTBD specimens is selected for analysis, and a quarter node element is used at the crack tip regions to simulate the stress singularity near the crack tip.

The dimensionless stress intensity factor Y* of the CSTBD specimens with normalized crack length of 0.156, 0.213, 0.252, and 0.303 are 1.037, 1.067, 1.094, and 1.137, respectively. For simplicity, the specimen size and thickness are treated as unknown quantities. According to Eq. (3) in Sect. 3.1, the failure loads of CSTBD specimen with diameters of 64 mm, 94 mm, 119 mm, and 132 mm are \(4.324K_{{\text{a}}} B\sqrt R\), \(3.601K_{{\text{a}}} B\sqrt R\), \({3}{\text{.227}}K_{{\text{a}}} B\sqrt R\), and \({2}{\text{.832}}K_{{\text{a}}} B\sqrt R\), respectively. After applying appropriate boundary conditions and fracture loads in the ABAQUS software, the tangential stress at the crack tip front can be extracted by a simple numerical calculation.

Figure 6 shows the tangential stress distribution at the crack tip front of specimens with different sizes. For comparison, the tangential stress field described by the TMTS criterion (the singular term) is also drawn. In the region near the crack tip, the tangential stress at the front of the crack tip determined by FEM and TMTS criteria is almost the same. However, as the observation point is far away from the crack tip, the gap between them becomes larger and larger. It further shows that the tangential stress of region far away from the crack tip cannot be accurately described through the simple consideration of singular terms. At the same time, for CSTBD specimens, the tangential stress at the crack tip described by the TMTS criterion is always lower than that extracted by FEM. This explains the phenomenon that the Ka determined by some configurations is always lower than the KIc of the materials.

Fig. 6
figure 6

Comparison of tangential stress determined by FEM and TMTS criteria for CSTBD specimens with different sizes: a 64 mm; b 94 mm; c 119 mm; d 132 mm

Full size image

To further compare the influence of higher order stress terms on the tangential stress near the crack tip, the tangential stress extracted by the FEM at the crack tip front of CSTBD specimens with different sizes is plotted together, as shown in Fig. 7. It should be noted that the stress intensity factor of specimens is set as 1 MPa·m0.5 in Fig. 7. There are obvious differences in the tangential stress field of specimens with different sizes. The results show that when the TMTS criterion is used to describe the tangential stress field at the front of crack tip, a large error can be caused in the analysis of material fracture, especially for plastic materials. Besides, the TMTS criterion cannot explain the size effect of fracture toughness in this experiment.

Fig. 7
figure 7

Comparison of tangential stress by FEM at crack tip for CSTBD specimens with different sizes

Full size image

The TMTS criterion is merely suitable for ideal brittle materials, while most of the materials in practical engineering are quasi-brittle materials or plastic materials, and large deviation can be caused by TMTS criterion in the actual situation. Considering the influence of the first three terms of Williams stress expansion on the fracture behavior of specimen, Aliha et al. (2012a) proposed the modified maximum tangential stress (MMTS) fracture criterion based on the TMTS criterion. The MMTS criterion can explain the inconsistency of fracture toughness obtained from specimens with different configurations or sizes. As shown in Fig. 8, the tangential stress distribution determined by MMTS criterion is much closer to that determined by FEM, followed by that determined by TMTS criterion. It shows that the MMTS criterion can more accurately describe the fracture behavior of specimens than the TMTS criterion.

Fig. 8
figure 8

Comparison of tangential stress determined by FEM and MMTS criteria for CSTBD specimens with different size: a 64 mm; b 94 mm; c 119 mm; d 132 mm

Full size image

Although the MMTS criterion modifies the description of the tangential stress field by the TMTS criterion to a certain extent, there are still non-negligible errors for small-size specimens, as shown in Fig. 8a, b. Based on the MMTS criterion, Wei et al. (2018) proposed a further maximum tangential stress (FIMTS) fracture criterion. It is believed that more terms of Williams expansion should be selected to determine the tangential stress field. Using the Levenberg–Marquardt optimization algorithm, the tangential stress of four specimens with different sizes determined by FEM is fitted by nonlinear polynomial by Eq. (5), as shown in Fig. 9. The specific fitting expression is also illustrated in this figure. For specimens with four sizes in this study, the tangential stress can be accurately described by selecting the first seven terms of the Williams stress expansion, and the coefficients of determination can reach 0.999. Therefore, the FIMTS criterion considering the first seven terms of the Williams stress expansion is adopted for subsequent analysis.

Fig. 9
figure 9

The coefficients of Williams expansion obtained by fitting the FEM-determined tangential stresses for CSTBD specimens with different sizes: a 64 mm; b 94 mm; c 119 mm; d 132 mm

Full size image

4 Prediction of Fracture Toughness

4.1 Prediction of K Ic of Shale Specimens

According to the maximum tangential stress fracture criterion, when the maximum tangential stress on the boundary of the FPZ is equal to the tensile strength of the material, the specimen will fracture. Therefore, the conditions for judging specimen fracture by the TMTS criterion can be expressed by Eq. (7)

$$\frac{{K_{{\text{a}}} }}{{\sqrt {{2}\pi } }}r_{{\text{c}}}^{{ - \tfrac{1}{2}}} = f_{{\text{t}}} .$$
(7)

Similarly, the valid conditions for MMTS and FIMTS criteria for judging specimen fracture can be expressed by Eqs. (8) and (9), respectively

$$\frac{{K_{{\text{a}}} }}{{\sqrt {{2}\pi } }}r_{{\text{c}}}^{{ - \tfrac{1}{2}}} + 3A_{{{\text{3c}}}} r_{{\text{c}}}^{{\tfrac{1}{2}}} = f_{{\text{t}}} ,$$
(8)
$$\frac{{K_{{\text{a}}} }}{{\sqrt {{2}\pi } }}r_{{\text{c}}}^{{ - \tfrac{1}{2}}} + 3A_{{{\text{3c}}}} r_{{\text{c}}}^{{\tfrac{1}{2}}} + 5A_{{{\text{5c}}}} r_{{\text{c}}}^{{\tfrac{3}{2}}} + 7A_{{{\text{7c}}}} r_{{\text{c}}}^{{\tfrac{5}{2}}} + 9A_{{{\text{9c}}}} r_{{\text{c}}}^{{\tfrac{7}{2}}} + 11A_{{{\text{11c}}}} r_{{\text{c}}}^{{\tfrac{9}{2}}} + 13A_{{{\text{13c}}}} r_{{\text{c}}}^{{\tfrac{11}{2}}} = f_{{\text{t}}} ,$$
(9)

where Aic (i = 1, 2, 3…) is the critical value of the coefficient of the Williams expansion.

For the Brazilian disc specimen, Aliha (2014) and Aliha et al. (2021b) found that the tensile strength of the tested specimen depends on the thickness/diameter ratio of the specimen. Small tensile strength will make the fracture process zone length determined based on the maximum tangential stress fracture criterion larger. This study used the method recommended by ISRM for determining tensile strength of rock materials to obtain reliable tensile strength, and the tensile strength value has been given in Sect. 2. According to the Ka obtained by fracture tests of CSTBD specimens in Sect. 3.1, the FPZ lengths were obtained by different fracture criteria, as listed in Table 3. It can be found that the FPZ lengths obtained by the FIMTS criterion are the largest, while the FPZ lengths obtained by the TMTS criterion considering only the singular term are the smallest. This is mainly because the tangential stress determined by the TMTS criterion is obviously lower than that determined by the FIMTS criterion. It is worth noting that for small-size specimens, the difference between the FPZ lengths determined by the FIMTS criterion and the TMTS criterion is the largest. With the increase of the specimen size, the difference between the FPZ lengths determined by the three fracture criteria gradually decreases, which indicates that the FPZ lengths of large-size specimens are less affected by the selection of fracture criteria. There is still a certain gap between the FPZ lengths obtained by the MMTS criterion and that obtained by the FIMTS criterion, especially for small-size specimens.

Table 3 The FPZ lengths determined by different fracture criteria
Full size table

According to the effective crack model, the effective crack length aec of the specimen can be calculated by Eq. (10)

$$a_{{{\text{ec}}}} = a + r_{{\text{c}}} .$$
(10)

For CSTBD specimens, the mode I fracture toughness is calculated by Eq. (3), and the ratio of Ka to KIc is obtained as follows:

$$\frac{{K_{{\text{a}}} }}{{K_{{{\text{Ic}}}} }} = \sqrt {\frac{{a_{{{\text{ec}}}} }}{a}} \frac{{Y^{ * } \left( {\alpha_{{{\text{ec}}}} } \right)}}{{Y^{ * } \left( \alpha \right)}},$$
(11)

where αec (= aec/R) is normalized effective crack length. The previously determined FPZ lengths and Ka of shale specimens are substituted into Eq. (11). Figure 10 shows the calculation results of KIc. Regardless of the selection of criterion in determining the FPZ length, the difference of KIc of each size specimen after the correction of the effective crack model is smaller than that between the Ka. Since the KIc of materials is only related to the properties of materials, from this point of view, the fracture toughness obtained by the effective crack model is more reliable. At the same time, the fluctuation of KIc obtained from the FPZ lengths determined by the FIMTS criterion is the smallest, followed by the MMTS criterion and the TMTS criterion, which further shows that the FIMTS criterion is most suitable for describing the fracture behavior of materials. When the effective crack model is used to predict the KIc of materials, the FPZ lengths determined by the FIMTS criterion are preferred. In addition, with the increase of specimen size, the difference between the KIc determined by the three fracture criteria decreases gradually. When the specimen size is 132 mm, the difference between the KIc determined by the TMTS criterion and the FIMTS criterion is only 0.0345 MPa·m1/2. As mentioned in Sect. 3, the tangential stress determined by either fracture criterion is very close to that extracted by FEM for large-size specimens. It shows that the region controlled by the singular term increases with the increase of specimen size. Therefore, when the specimen size increases to a certain extent, the FPZ length is very small or can be ignored compared with the region controlled by the singular term. Besides, the TMTS criterion can be directly used to describe the fracture behavior of materials. This is the essential reason why the larger the specimen size is, the larger the Ka is. When the specimen size tends to infinity, the Ka is the KIc of the material.

Fig. 10
figure 10

The KIc of shale obtained by the effective crack model

Full size image

4.2 Prediction of K a of NSCB Specimens

To compare the prediction effect of the TMTS criterion, MMTS criterion, FIMTS criterion, and SEL model on the Ka of specimens, a three-point bending fracture test on NSCB specimens was carried out. Figure 11 shows the loading diagram of NSCB specimens.

Fig. 11
figure 11

The loading diagram of NSCB specimens

Full size image

According to the fracture toughness test method of NSCB specimens recommended by ISRM (Kuruppu et al. 2014), the parameters of specimens are as follows: a = 20 mm, R = 40 mm, and B = 30 mm. The support frame span 2S = 50 mm. The fracture test was carried out on a biomechanics testing machine with a loading rate of 0.1 mm/min. The Ka of the NSCB specimen is calculated by Eqs. (12) and (13) (Aliha et al. 2017)

$$K_{{\text{a}}} = Y^{ * } \frac{{P_{{{\text{max}}}} \sqrt {\pi a} }}{2RB},$$
(12)
$$Y^{ * } = - 1.297 + 9.516\left( {S/R} \right) - \left( {0.47 + 16.457\left( {S/R} \right)} \right){\kern 1pt} {\kern 1pt} \alpha {\kern 1pt} {\kern 1pt} + \left( {1.071 + 34.401\left( {S/R} \right)} \right)\alpha^{2} .$$
(13)

After three repeated tests, the average failure load of the specimen is 3070 N, and the Ka of shale specimens with the NSCB configuration is 1.5761 MPa·m1/2.

4.2.1 Prediction Results of the Maximum Tangential Stress Fracture Criterion

In contrast to the solution process of FPZ length in Sect. 4.1, the FPZ length is taken as a known quantity and substituted into Eqs. (7), (8) and (9) in the prediction of Ka. Therefore, the determination of FPZ length plays an important role in predicting the results. The TMTS, MMTS, and FIMTS criteria based on the maximum tangential stress fracture criterion are introduced in Sect. 3.2 and will not be repeated here.

Before applying the maximum tangential stress fracture criterion, the distribution of tangential stress at the front of crack tip should be determined first, that is, the values of the coefficients in Williams stress expansion should be obtained. The FEM was also used in the calculation of Williams expansion coefficient of NSCB configuration, which is the same as that of CSTBD specimens before. The tangential stress was extracted after the fracture load of 0.3246KaBR1/2 and appropriate boundary conditions were applied in the finite-element model of NSCB configuration. Figure 12 shows the fitting results of the first seven Williams stress expansion terms to the tangential stress with the determination coefficients reaching 0.999.

Fig. 12
figure 12

The coefficients of Williams expansion obtained by fitting the FEM-determined tangential stresses for NSCB specimens

Full size image

According to the fitting results, the relationship between Ka and the FPZ length based on the TMTS criterion, MMTS criterion, and FIMTS criterion is expressed by Eqs. (14), (15) and (16), respectively

$$K_{{\text{a}}} = f_{{\text{t}}} \sqrt {2\pi r_{{\text{c}}} } ,$$
(14)
$$f_{{\text{t}}} = 0.3989K_{{\text{a}}} r_{{\text{c}}}^{{ - \tfrac{1}{2}}} - {0}{\text{.05196}}K_{{\text{a}}} r_{{\text{c}}}^{{\tfrac{1}{2}}} ,$$
(15)
$$f_{{\text{t}}} = 0.3989K_{{\text{a}}} r_{{\text{c}}}^{{ - \tfrac{1}{2}}} { - 0}{\text{.05196}}K_{{\text{a}}} r_{{\text{c}}}^{{\tfrac{1}{2}}} { + 0}{\text{.0193}}K_{{\text{a}}} r_{{\text{c}}}^{{\tfrac{3}{2}}} - 0.0{1057}K_{{\text{a}}} r_{{\text{c}}}^{{\tfrac{5}{2}}} + 0.00{259}K_{{\text{a}}} r_{{\text{c}}}^{{\tfrac{7}{2}}} - 0.00{0295}K_{{\text{a}}} r_{{\text{c}}}^{{\tfrac{9}{2}}} + 0.0000{126}K_{{\text{a}}} r_{{\text{c}}}^{{\tfrac{11}{2}}} .$$
(16)

To predict the Ka of the specimen, the FPZ length of the specimen with NSCB configuration should be obtained first. In this study, due to the size effect of FPZ, it is considered that the FPZ length of the NSCB specimen with a diameter of 80 mm is the same as that of the CSTBD specimen with a diameter of 94 mm (since the diameter of the NSCB specimen is 80 mm, which is closest to that of the CSTBD specimen with a diameter of 94 mm). Table 4 lists the Ka of NSCB specimens predicted by TMTS, MMTS, and FIMTS criteria by Eqs. (14), (15) and (16). It can be found that the Ka predicted by the FPZ length using the MMTS criterion is closer to the tested fracture toughness, followed by the Ka predicted by the FPZ length using the FIMTS criterion. However, the research of Ayatollahi and Akbardoost (2014) shows that the prediction effect of Ka is the best when the fracture criterion for determining the FPZ length is consistent with the prediction criterion. Considering that the Ka predicted by the two criteria is very close in this study, it may be that the placement error of the specimen during the fracture test affects the test results. Ideally, the experimental results should be consistent with those of Ayatollahi and Akbardoost (2014).

Table 4 The Ka of NSCB specimens predicted by three fracture criteria
Full size table

Comparing the prediction results of each fracture criterion, it can be found that the change of FPZ length has the greatest influence on the Ka predicted by the MMTS criterion. For any FPZ length, the Ka predicted by the MMTS criterion is the largest among the three fracture criteria. Figure 13 shows the tangential stress distribution determined by different fracture criteria under the condition of equal stress intensity factors. In the region of 1.6–3.2 mm away from the crack tip, the tangential stress determined by the MMTS criterion changes most significantly. As a result, the change of FPZ length can easily affect the prediction result using the MMTS criterion. The tangential stress determined by the MMTS fracture criterion is less than that determined by the other two fracture criteria. Under the condition of the same FPZ length, if the tangential stress of the three fracture criteria on the boundary of FPZ is to reach the same value, then the singular term of the MMTS criterion must be larger than that of the other two fracture criteria; thus, the Ka predicted by the MMTS criterion is higher than that predicted by the TMTS and FIMTS criteria.

Fig. 13
figure 13

Tangential stress distribution near the crack tip determined by different fracture criteria for NSCB specimens

Full size image

Reviewing the fracture test results of CSTBD specimens in Sect. 3.1, the fracture toughness tested by NSCB specimens is much larger than that tested by CSTBD specimens. Figure 14 shows the tangential stress distribution near the crack tip of NSCB specimens and CSTBD specimens with a stress intensity factor of 1 MPa·m1/2. It is found that the tangential stress of CSTBD specimens and NSCB specimens in the region close to the crack tip is almost the same. However, as the distance from the crack tip increases, the stress difference between the two configurations also increases, mainly because the higher order term of Williams expansion affects the far-field stress distribution. At the same distance from the crack tip, the tangential stress of CSTBD specimens is always greater than that of NSCB specimens, which indicates that CSTBD specimens are more prone to failure than NSCB specimens with the same material under the same stress intensity factor. As a result, the fracture toughness tested by CSTBD specimens is far less than that of NSCB specimens. It is expected that this phenomenon will be more significant in materials with low tensile strength or plastic materials.

Fig. 14
figure 14

Tangential stress near the crack tip of CSTBD and NSCB specimens under the same stress intensity factor

Full size image

4.2.2 Prediction Results of SEL Model

The above-mentioned maximum tangential stress fracture criteria analyze the fracture behavior of rock materials by different terms of the Williams stress expansion, while the SEL model supports that the crack will propagate subcritical before material fracture without considering the change of stress near the crack tip. In addition, the maximum tangential stress fracture criterion is based on the relationship between the stress and the strength of the material to judge the fracture of the specimen, while the fracture evaluation condition of the SEL model is whether the strain energy released per unit length of crack propagation reaches the fracture energy of the material. In other words, the theoretical basis proposed by the SEL model and the maximum tangential stress fracture criterion is quite different, but both of them believe that the FPZ near the crack tip can affect the strength of the specimen. It can also be understood that the most essential reason for the difference in the Ka determined by different configurations is the existence of the FPZ. According to LEFM, when a structure is subjected to nominal stress σN, the expression of stress intensity factor KI is as follows:

$$K_{{\text{I}}} = \sigma_{{\text{N}}} \sqrt L k\left( \alpha \right),$$
(17)

where L and k(α) denote the characteristic length and dimensionless functions. Therefore, the energy release rate G(α) per unit length of crack propagation can be written as

$$G\left( \alpha \right) = \frac{{K_{{\text{I}}}^{{2}} }}{E} = \frac{{\sigma_{{\text{N}}}^{{2}} L}}{E}g\left( \alpha \right).$$
(18)

Here, g(α) = k(α)2 represents the dimensionless energy release rate, and E represents the elastic modulus of the material. Based on equivalent LEFM, the maximum loads for specimens with various sizes may be assumed to occur when the tip of the equivalent elastic crack is at a certain distance c ahead of the tip of the initial crack. Therefore, the length of c should also be considered in the effective crack length in the calculation of the energy release rate. When the specimen size tends to infinity, the corresponding value of c in the SEL model is denoted as cf., and the following equation can be established:

$$G\left( {\alpha_{0} + c_{{\text{f}}} /L} \right) = \frac{{\sigma_{{{\text{Nu}}}}^{{2}} L}}{E}g\left( {\alpha_{0} + c_{{\text{f}}} /L} \right) = G_{{\text{f}}} ,$$
(19)

where Gf is the fracture energy and belongs to the material constant; σNu is the nominal failure stress of the specimen and α0 is the ratio of the length of the prefabricated crack to the characteristic length of the specimen. By approximating g(α0 + cf/L) with its Taylor series expansion at α0 and retaining only up to the linear term of the expansion, Eq. (20) can be obtained

$$\sigma_{{{\text{Nu}}}} = \sqrt {\frac{{E*G_{{\text{f}}} }}{{Lg\left( {\alpha_{0} } \right) + c_{{\text{f}}} g^{^{\prime}} \left( {\alpha_{0} } \right)}}} .$$
(20)

Equation (20) is replaced with the following simple variables as follows:

$$X = L,\quad Y = \sigma_{{\text{N}}}^{{ - {2}}} ,$$
(21)
$$A = \frac{{g\left( {\alpha_{0} } \right)}}{{E * G_{{\text{f}}} }},\quad C = \frac{{c_{{\text{f}}} g^{^{\prime}} \left( {\alpha_{0} } \right)}}{{E * G_{{\text{f}}} }}.$$
(22)

Then, the relationship between failure stress and specimen size established by the traditional SEL model is as follows:

$$Y = AX + C,$$
(23)

where A and C are constants related to E, Gf, and cf. The values of A and C can be obtained by the linear fitting method with sufficient test data. According to the relationship between failure stress and specimen size, the Ka of specimens in any size can be predicted. The premise of the application of the traditional SEL model is that the ratio of the length of crack to the characteristic length of the specimen with different sizes is equal to a constant. However, it is difficult to ensure the extreme similarity of the specimen geometry in the process of rock specimen manufacturing. Besides, the size of the target configuration that needs to be predicted is also varied, which seriously limits the application of the SEL model. Therefore, the improved SEL model is proposed, in which the configuration parameters of the specimen are put in the independent variables, and the influence of the specimen configuration factors before building the model is considered. Several variables are converted as follows:

$$X = \frac{{g\left( {\alpha_{0} } \right)}}{{g^{^{\prime}} \left( {\alpha_{0} } \right)}}L,\quad Y = \frac{1}{{g^{^{\prime}} \left( {\alpha_{0} } \right)\sigma_{{{\text{Nu}}}}^{{2}} }},$$
(24)
$$A^{^{\prime}} = \frac{1}{{E*G_{{\text{f}}} }},\quad C^{^{\prime}} = \frac{{c_{{\text{f}}} }}{{E*G_{{\text{f}}} }}.$$
(25)

Therefore, Eq. (20) can be written as follows:

$$Y = A^{^{\prime}} X + C^{^{\prime}} .$$
(26)

The application of Eq. (26) has no restrictions on the geometry and size of the test specimen and the predicted specimen, but needs to solve the dimensionless stress intensity factor expression of the test specimen and the predicted specimen in advance.

The expression of stress intensity factor of CSTBD specimens has been given in Sect. 2.1, so it will not be deduced here. According to Eq. (17), some parameters of CSTBD specimens are described as follows:

$$\sigma_{{\text{N}}} = \frac{P}{BR},$$
(27)
$$k\left( \alpha \right) = \sqrt {\frac{a}{R}\frac{1}{\pi }} Y^{ * } .$$
(28)

According to Eqs. (24) and (25), the basic parameters for prediction are obtained, as listed in Table 5. The Ka of CSTBD specimens with diameters of 64 mm, 94 mm and 119 mm were used as test data to predict the Ka of specimens with diameters of 132 mm. According to the data in Table 5 and the relationship between Y and X in Eq. 26, the linear fitting of X and Y was carried out, as shown in Fig. 15. It is found that there is a good linear relationship between Y and X, which indicates that the relationship between failure loads of CSTBD specimens with different sizes can be well described by the SEL model. According to the fitting results, the relationship between Y and X can be expressed as follows:

$$Y = 0.0048 + 5.3893 \times 10^{ - 4} X.$$
(29)
Table 5 Basic parameters of CSTBD specimens for prediction
Full size table
Fig. 15
figure 15

Fitting results based on the test data of CSTBD specimens with diameters of 64 mm, 94 mm, and 119 mm

Full size image

For the CSTBD specimen with a diameter of 132 mm, the X value is 13.432, the predicted value of Y is 0.01204 by Eq. (29), while the Y value obtained by fracture test is 0.01158, the difference between the two is only 0.00046, and the prediction error is only 3.97%. It further shows that the SEL model can be used to predict the failure load of CSTBD specimens. To accurately describe the relationship between failure load and specimen size, the fracture toughness of CSTBD specimens with diameters of 132 mm is also used for fitting. As shown in Fig. 16, there is still a linear relationship between Y and X obtained from the test data of four-size specimens. The relationship between Y and X can be expressed by Eq. (30)

$$Y = {0}{\text{.00507}} + 4.9687 \times {10}^{ - 4} X.$$
(30)
Fig. 16
figure 16

Fitting results based on the test data of CSTBD specimens of all sizes

Full size image

The values of cf and Gf can be obtained from the relationship between the intercept of the fitting line and the slope of the line in Eq. (25). For the NSCB specimens, the value of X is 5.876 by Eqs. (12) and (17), and the value of Y is 0.00798 by substituting it into Eq. (30). According to the definition of Y in Eq. (24), the predicted failure load of NSCB specimen after conversion is 1677.8 N, which is obviously different from that of the test, and the difference is about twice. It is thought that the value of cf in the SEL model can be understood as a reference length. The foundation of the SEL model is that the fracture energy of the material is equal to the energy release rate of the specimen calculated by taking the prefabricated crack length plus the reference length as the final crack length. Since the fracture energy Gf of the material is fixed, the reference length cf determines the prediction result of apparent fracture toughness from Eq. 19. In the actual test process, due to the influence of various factors, the cf fitted by the test data will inevitably deviate from its theoretical value. Because the dimensionless energy release rate g(α) mainly depends on the dimensionless stress intensity factor Y*, and the Y* of predicted configuration not change greatly with α, the change of cf has little impact on the prediction results, even difficult to observe it. On the contrary, the prediction results will be far from the test results. For example, as shown in Fig. 17, the Y*of CSTBD configuration changes gently with α from 0.15 to 0.35, while the Y* of NSCB configuration changes greatly with α greater than 0.5. In previous test results, it has been found that the change of fracture toughness of CSTBD specimens with different sizes conforms to SEL model, while the tested fracture toughness of NSCB specimens is quite different from the predicted value by SEL model base on the test data of CSTBD specimens. This shows that the application of SEL model needs to strictly ensure the accuracy of each set of test data, especially for the configuration in which Y* changes greatly with α.

Fig. 17
figure 17

The dimensionless stress intensity factor of the CSTBD and NSCB specimens at various crack lengths

Full size image

The Ka prediction process in the SEL model is obviously different from that in the maximum tangential stress fracture criterion. In principle, the maximum tangential stress fracture criterion only needs a set of fracture toughness test data of specimens with any sizes to obtain the FPZ length, and then to predict the Ka of the target configuration. However, as analyzed in Sect. 4.2.1, if the size effect of FPZ is not considered, a large prediction error can be caused. Therefore, it is necessary to select specimens with similar size to the predicted target specimens for fracture test, or to carry out fracture test of multiple groups of specimens with different sizes, to obtain the change rule of FPZ length with specimen size. While in the SEL model, it needs to fit the fracture toughness test data of multiple groups of specimens to obtain the equation for prediction. Compared with the maximum tangential stress fracture criterion, SEL model highlights the integrity and maximizes the use of existing test data, but the workload also increases.

Compared with MTS criterion and MMTS criterion, FIMTS criterion considers more high-order terms to obtain accurate results, which is very important for the prediction of fracture load of small-size specimens. For large-size specimens, MMTS criterion can also obtain sufficient accurate results. In addition, for the fracture of specimens with different configurations, the influence of the number of high-order terms on the prediction results needs to be further studied. In practice, most of the pre-existing cracks in rock masses are often subjected to a combination of tensile and shear loading conditions. When the maximum tangential stress fracture criterion is applied to mixed mode loading conditions, it is necessary to determine the crack initiation angle first, and then determine the tangential stress at the front of the crack tip. Therefore, it is very difficult to determine the high-order term by fitting the tangential stress at the crack tip front through Williams stress expansion. Compared with mode I fracture, the calculation of higher order terms of the specimen in mixed mode loading is more complex, which limits the application of FIMTS criterion to some extent. It is worth noting that the fracture process zone length obtained by mode I fracture results is widely used in the prediction of fracture load in the mixed mode loading (Aliha et al. 2013; Ayatollahi and Akbardoost 2013; Sangsefidi et al. 2020). The crack initiation angle under mixed mode loading is related to the fracture process zone length, and the crack initiation angle and the fracture process zone length jointly determine the fracture load of the specimen. It can be seen that the deviation in determining the fracture process zone length will seriously affect the prediction of the fracture load of the specimen. Therefore, based on the mode I fracture test data of the specimen, the fracture process zone length is determined by FIMTS criterion, and then applied to the prediction of the fracture load of the specimen under the mixed mode loading condition may obtain more accurate prediction results.

5 Conclusion

In this study, the fracture toughness of cracked straight-through Brazilian disc (CSTBD) shale specimens with different sizes was tested. The traditional maximum tangential stress (TMTS) criterion, modified maximum tangential stress (MMTS) criterion, and further improved maximum tangential stress (FIMTS) criterion were used to investigate the change of fracture process zone (FPZ) lengths of specimens with different sizes, and the effective crack model was also used to predict the inherent fracture toughness (KIc) of the material. Then, the three-point bending fracture tests of notched semi-circular bend (NSCB) specimens were carried out, and the apparent fracture toughness (Ka) was predicted using the above three fracture criteria and the size effect law (SEL) model. The main conclusions are as follows:

  1. (1)

    With the increase of the specimen size, the Ka and the FPZ lengths obtained by TMTS, MMTS, and FIMTS criteria also increase. For small-size specimens, there is still a large difference between the tangential stress at the front of the crack tip determined by TMTS and MMTS criteria and that determined by finite-element model (FEM). Moreover, with the increase of specimen size, this gap is decreased gradually, and the difference between the FPZ lengths determined by the MMTS, MTS, and FIMTS criteria is also reduced.

  2. (2)

    With the FPZ length determined by the FIMTS criterion, the fluctuation of the KIc predicted by the effective crack model with the specimen size is small, which indicates that the combination of the FIMTS criterion and the effective crack model can better estimate the KIc of materials.

  3. (3)

    In the prediction of the Ka of the NSCB specimens, a large prediction error can be caused without considering the size effect of the FPZ. The Ka predicted by the FIMTS criterion is the closest to that obtained by the test, while the Ka predicted by the TMTS and MMTS criteria is quite different from the tested fracture toughness. It indicates that only considering the singular terms or the first three terms of Williams expansion is not enough to accurately describe the fracture behavior of materials.

  4. (4)

    Based on the failure load of CSTBD specimens with different sizes, the relationship between the configuration size and the failure load is established by the SEL model. However, there is a big deviation when this relationship is used to predict the failure load of NSCB specimens. It shows that the deviation of test data during the establishment of SEL model is easy to affect the prediction results for the configuration in which dimensionless stress intensity factor (Y*) varies greatly with normalized crack length (α).