The Fragmentation Energy-Fan Model in Quarry Blasts

Abstract

This paper investigates fragmentation in an aggregate quarry in the light of the fragmentation-energy fan concept. Six blasts were monitored, located one behind the other in the same quarry area. The rock structure was blocky, the water level and the usage of explosives were variable within and between the blasts; however, the distribution of explosive energy in the blocks was relatively uniform and the performance of both explosives per unit mass appeared to be similar. The powder factor above grade was between 0.28 and 0.44 kg/m³. Fragmentation of the plant feed was measured using an online digital image analysis system and three belt scales in the crushing plant. The oversize material that was not directly fed to the plant after the blast corresponds to 3–9.3% of the total. Data from image analysis was used to build the size distribution in the coarse range (fragments above 120 mm), and the passing fractions at 120 and 25 mm obtained from belt scales data were used in the range 120–25 mm. The non-dimensional percentile sizes between 10 and 90% for each blast are described through power functions of the powder factor above grade; the model coefficients (i.e. nine prefactors and nine exponents) are statistically significant. From them, using the principles of the fragmentation-energy fan and the Swebrec distribution properties, the fragmentation can be expressed in terms of the powder factor by means of five parameters: the fan focus coordinates and the three parameters of a function of the exponents versus the percentage passing. The model shows a good capability to describe fragmentation from 10 to 90 percentile sizes, with an expected error below 6% and a maximum likely error less than 15%.

1 Introduction

Fragmentation is a key factor for optimizing the mining process and minimizing production costs. The size distribution of blasting products can only be measured accurately enough by sieving the muckpile, a complicated, costly and disruptive to production task. Although enhanced 2D technologies (often called 3D though they are not really determining fragmentation of a rock volume) to monitor fragmentation are available, such as LiDAR imaging—laser imaging detection and ranging (McKinnon and Marshall 2014; Oñederra et al. 2015; Thurley 2013; Thurley et al. 2015) or photogrammetry (Noy 2013, 2015; Bamford et al. 2016), 2D image analysis is still the most common tool used. Image analysis systems may show a poor performance at small sizes especially when they have not been calibrated (Sanchidrián et al. 2009) and it is advisable to use additional tools to correct raw data on a blast per blast basis in order to get a good estimation of the actual size distribution (Sanchidrián et al. 2006).

The installation of these systems upstream of the primary crusher allows assessing the influence of blast characteristics on fragmentation. In particular, the influence of powder factor on the fragment sizes (especially the median) was studied since the early 1970s by Soviet researchers (Koshelev et al. 1971; Kuznetsov 1973); these works were years after extended by Cunningham (1983, 1987, 2005) in his Kuz–Ram model, and other models derived from it, such as the crush-zone model (Kanchibotla et al. 1999; Thornton et al. 2001). These models presuppose an underlying size distribution function (the Rosin–Rammler, Rosin and Rammler 1933 for both Kuz–Ram and Crush-zone models), and their goal is then to predict the function parameters (i.e. median size and uniformity index) as a function of rock and blast characteristics. The performance of these models is relatively poor with errors ranging from − 75 to 50% in about half of the cases, when compared with fragmentation obtained by sieving (Sanchidrián and Ouchterlony 2017). One of the reasons for such results is that the Rosin–Rammler function is not a good description of the fragment size distribution from blasting, or it is in a limited range of passing (Ouchterlony 2005, 2009; Sanchidrián et al. 2012a, b, 2014; Sanchidrián 2015).

A natural alternative to this is to focus on determining distribution-independent fragmentation prediction equations for the percentile sizes as functions of powder factor; an early example of this approach was the work by Chung and Katsabanis (2000) that re-analyzed the sieved fragmentation data by Otterness et al. (1991) and obtained equations of the median and the 80-percentile sizes as functions of the powder factor. Fragment sizes obtained by sieving versus powder factor data in production blasts have also been published by Olsson et al. (2003), Ouchterlony et al. (2005) and Ouchterlony et al. (2010, 2015), to name a few. These, and many other half- and small-scale blasts data are analyzed by Ouchterlony et al. (2017). A key conclusion of that work is that the uniformity index of the Rosin–Rammler needs to be variable at different percentiles (i.e. a Rosin–Rammler function with piecewise constant uniformity index) to represent fragmentation at different energy levels—or, in blasting terms, powder factors. This model has been called the fragmentation-energy fan because it derives from the plot of several percentile sizes as function of the powder factor, and the observation that this plot has the form of a set of straight lines in log–log space that converge to a common focal point. This new approach follows the principle that fragmentation should be predicted using distribution-free models that provide fragment sizes for the various percentages passing as a function of rock mass and blast characteristics (Ouchterlony et al. 2017; Sanchidrián and Ouchterlony 2017) without resorting to a particular distribution function. Such fragmentation-energy fan principles are followed in this work to describe fragmentation from blasting in an aggregate quarry.

2 The Site

The experimental work was carried out in the quarry El Aljibe. The quarry is located in central Spain near the town of Almonacid de Toledo and mines mylonite to produce track ballast for high-speed and conventional trains (32/56 mm fraction), for high strength concrete and asphalt mixtures (6/12 mm fraction), and for sub-base and base courses (0/25 mm fraction) in road and rail track construction.

The deposit occurs within the Toledo Shear Zone that separates the Toledo Migmatite Complex unit to the North and the Paleozoic metasediments to the South. Mylonite was produced by ductile deformation of migmatites in amphibolites facies and outcrops in the area in which the quarry is located (Enrile 1991). The mineral composition is similar to a granodiorite or to a tonalitic granite. It has a density of 2710 kg/m³ and an average uniaxial compressive strength of 131 MPa. It is qualitatively described as tough rock with good resistance to abrasion. The rock mass has three sub-vertical joint families and a subhorizontal one, their intersections with the highwall making up a blocky face.

Drilling and blasting is used to mine about 0.5 Mt/yr of run of mine (ROM), this amount depending on the market demand. Generally only one blast is loaded at a time during one working shift. A hydraulic excavator mucks the fragmented rock into 54 t average payload trucks that haul the material to the bin of the primary crusher. Boulders greater than the largest size that can be fed to the primary crusher (about 900 mm) are further fragmented with a hydraulic hammer and hauled to the plant mixed with the rest of material (undersize) coming from the blast. The number of these fragments are recorded in two categories: small, which could be hauled but would likely block the entrance of the crusher, with average size somewhat in excess of 1 m (we have used 1.1 m), and large, that could not be loaded, with average size between 1.5 and 2 m (we have used 1.7 m). The maximum boulder size was about 2 m.

When a truck dumps, the crusher operator monitors the time in the crusher’s log; the ROM mass fed to the plant per day (m _R ) is obtained as the total number of trucks times the average payload.

In the plant, a grizzly feeder is used to scalp the feed of the primary crusher. The grizzly has wedged slots with maximum opening of 109 mm that corresponds to a cut size (i.e. aperture equivalent to a square mesh) of 120 mm (Departamento Técnico de Benito Arnó e Hijos 2005). The aperture (slot) factor of the grizzly (1.10) is in line with data from other works (Colman 1985; Gluck 1965; Gupta and Yan 2006; Ouchterlony et al. 2006, 2015).

The crusher bypass (< 120 mm) is further separated in a vibratory screen with two decks. From top to bottom, these have circular and square openings of cut sizes 80 and 25 mm, respectively. The smallest fraction (< 25 mm) is conveyed to a stockpile, and the coarsest fractions (120/80 and 80/25 mm) are added to the output flow from the crusher (< 170 mm) and conveyed to another stockpile for further handling. An overview of these operations is shown in Fig. 1.

Fig. 1

Flowsheet of the first stage of ROM processing. Fragmentation monitoring systems shown: belt scales (identified as S1, S2, S3) and video camera (identifed as VC); the photograph in the top right corner shows the end part of the feeder grizzly and the bin of the primary crusher with the video camera and lighting system above them

3 The Blasts

The blasts were located one behind the other in the same block at the Northwest part of the pit. This means that the orientation of the natural fractures with respect to the free face is similar in all them. They were made in the normal way of operation of the quarry. Each blast consisted of three rows of blastholes drilled in a staggered pattern. The blastholes were 89 mm of diameter with an inclination from the vertical of 9°. Table 1 shows the main characteristics of the blasts; the mean and standard deviation (following ‘sd’) are given for the parameters measured hole per hole. The volume of the blast and the drilling pattern were measured with a QuarryMan ALS Laser system. The burden of about 30 times the blasthole diameter d is within the range 25d–35d recommended for vertical blastholes loaded with light and heavy explosives, respectively in rocks of medium density, as is the case of El Aljibe (Ash 1963; Hustrulid 1999). The spacing between holes is, however, shorter than the value of 1.2 times suggested for bench blasting (Ash 1963; Hustrulid 1999). A comparison between blasthole length and bench height suggests an excessive subdrill, indicating a poor control of the drill length (Ash 1963; Hustrulid 1999; Langefors and Kihlström 1963).

Table 1 Summary of blast characteristics

The presence of water in the blastholes is described qualitatively in Table 1 as low, medium and high. The charging pattern was adapted to the amount of water in the holes; one or two 60 × 620 mm gelatin cartridges (2.5 kg) were always charged at the bottom of the hole as primers, and smaller gelatin cartridges of 50 × 380 mm (1.042 kg) were loaded up to the water level. ANFO was loaded in the dry part of the hole up to an uncharged length of 2.5 m. Figure 2 shows the distribution of the actual mass of explosives per hole: ANFO (blue boxes), gelatin (small cartridges, magenta boxes and large cartridges, orange boxes), and total (green boxes). It shows the interquartile range that comprises the mass range in half of the holes of the blast that provides a measure of the variability in the charges. This is very limited for gelatin large cartridges since they were used as primers, relatively independent of the level of water in the holes, so their boxes in Fig. 2 appear as dashes. Dispersion is large for ANFO and gelatin (small cartridges), just as the standard deviations are large (see Table 1); an extreme case is blast no. 6 in which 51 out of 72 holes were charged with gelatin only (see the zero median value of ANFO mass in Fig. 2, and the low mean in Table 2). The variability of the total mass of explosive is, however, lower than the individual components. The population of the total explosive energy in each hole is also represented in Fig. 2; the energy of the explosives rated as heat of explosion at full detonation regime is 4090 kJ/kg for gelatin and 3893 kJ/kg for ANFO (Sanchidrián et al. 2007). The distributions of energy across the blast are more uniform than the distributions of masses, which should result in limited variations in the fragmentation within the blast, over which the mean powder factor in each blast prevails, hence the sensitiveness of fragment sizes to it.

Fig. 2

Boxplots of the mass and energy per hole. Blue boxes: mass of ANFO; magenta boxes: mass of small gelatin cartridges; orange boxes: mass of large gelatin cartridges; green boxes: total mass; black boxes: total energy per hole (color figure online)

Table 2 Fragmentation data monitored in mine and plant

The long subdrilling results in a total mass powder factor from 0.47 to 0.61 kg/m³ (see Table 1). These values seem to be excessive for the drilling pattern used, and suggests considering the mass powder factor above grade q (i.e. ratio of explosive mass to rock volume discarding the explosive in the subdrill part of the hole) as a better indicator of the specific charge that contributes to fragmentation. The q powder factors of our blasts are in line with values recommended (e.g. AECI 1986) for rocks with good (0.30 kg/m³) and fair (0.45 kg/m³) blast behavior, respectively.

The low powder factor blasts correspond to more water (i.e. more cartridged product) and the high powder factor to less water (hence more bulk). The reason for this is that cartridges loading (not filling the hole section) puts less explosives than bulk, that fills the holes section, even if the density of cartridged product (gelatin dynamite) is higher than that of bulk (ANFO). Energy per unit mass of both products are not too different (the difference is as small as 5%) so, mass-wise, they are nearly interchangeable.

The different charging schemes resulted in different explosive-to-rock coupling conditions: the bulk explosive (ANFO) was coupled to the borehole wall whereas the gelatin cartridges were coupled through the water annulus. Works by Ash (1973),¹ Smith (1976), Brinkmann (1982) and Bleakney (1984) show that the water coupling is able to transmit a high pressure shock to the rock so that the fragmentation effect does not differ much from when the explosive is fully coupled. Based on that, the action of the water-coupled gelatin on the rock is assumed to be equivalent (only different due to the slightly different specific energy and different mass) to the ANFO directly coupled, filling the hole section. Some shock attenuation must take place in the water annulus for the decoupled charges and, to some degree, the higher detonation pressure of the gelatin (given its higher density and VOD) than the ANFO compensates for that so that the performance of both is not apparently different.

Water saturation of the rock mass may enhance fragmentation by: (1) reducing compressive/tensile strengths; (2) reducing shock wave attenuation; (3) decreasing the cohesion and the frictional properties of joints (Singh and Narendrula 2007; Zhang 2016). The water absorption coefficient of the mylonite was measured at 0.10 ± 0.03% hence the effect of water on shock wave transmission, joints opening and crack propagation was probably limited.

The explosive was bottom initiated with 500 ms non-electric detonators. The blasts were initiated from the center or from the end of the row using an open (B2, B3 and B4 blasts) or closed (B1, B5 and B6 blasts) chevron initiation pattern; a delay of 17 ms was employed within the rows and of 42 ms between rows.

4 Fragmentation Measurements

Three belt scales, identified as S1, S2 and S3, were installed as shown in Fig. 1, which allowed to get two points of the size distribution of the material fed into the plant. Belt scale S1 provides continuous measurements of the bypass mass flow (i.e. fraction < 120 mm), S2 monitors the amount of oversize of the vibrating screen (i.e. fraction 120–25 mm.), and S3 monitors the material running through S2 plus the crusher output. The cumulative mass of the material carried by each belt scale Sk per day is:

$$m_{k} = \mathop \int \limits_{0}^{t} \dot{m}_{k} {\text{d}}t\quad k = 1, \, 2{\text{ and }}3$$

(1)

where t is the daily working time of the plant; numerical integration (trapezoidal rule) of the instantaneous mass flow ṁ _k at each location is carried out.

From the mass balance in the primary crusher circuit, the fractions passing at 120 and 25 mm are:

$$ P_{120} = m_{1} /m_{{pp}}$$

(2)

$$P_{25} = (m_{1} - m_{2} )/m_{{pp}}$$

(3)

where m _pp is the total mass of material processed per day:

$$m_{{pp}} = m_{1} - m_{2} + m_{3}$$

(4)

Note that m _pp includes the oversize that was broken mechanically, since it was also hauled and processed after breakage in the pit. Hence, neglecting the amount of material smaller than 120 mm produced in the breakage of boulders, P₁₂₀ and P₂₅ are mass fractions in the muckpile. To assess the accuracy of mass flow measurements, the ROM mass hauled daily to the plant by the trucks m _R is compared with the mass m _pp from the belt scales, see Fig. 3; m _R values are the basis of the payment to the hauling company so the associated error was expected to be limited; this is why they are taken as baseline to assess the quality of belt scale readings. Ideally they should be related by a linear function through the origin with unit slope. Results from a standard linear regression analysis confirms a significant relationship between m _R and m _pp without constant error (i.e. Y-intercept term is not significant at a 95% confidence level). The slope of the resulting regression line plotted in Fig. 3 is 0.91–0.98 for a 95% coverage. This means that the belt scales overestimate systematically the crusher feed by a factor of 1.02–1.10 with respect to the trucks weight count. Such range of values can be considered acceptable (smaller errors are only possible when the conveyor belts are fully loaded and well maintained, Väyrynen 2013, which is difficult to achieve in practice). Since the observed error is a systematic bias, it affects similarly the numerator and denominator in Eqs. 2 and 3, so that its effect in the passing at 120 and 25 mm is somewhat cancelled. Table 2 summarizes the data monitored in the plant. It also shows the mass of boulders m _B determined from the boulder count of ‘small’ and ‘large’ boulders, and their estimated mean sizes. Table 2 also gives the fraction of blast undersize, P _m  = 1 − m _B /m _pp .

Fig. 3

Perfomance of online mass measurements; m _R is the mass hauled by the trucks to the plant and m _pp is the mass processed by the plant given by the belts scales

Fragmentation monitoring was completed with the online digital image analysis system, Split-Online^®. To get images of the ROM before the crusher, a video camera was installed perpendicularly above the discharge of the crusher feeder at the end part of the grizzly (see Fig. 1). The camera was triggered 20 s after the crusher feeder started working and the mass flow in S1 was greater than 20 t/h. While both conditions were fulfilled, the camera took a photo every 8 s. Each image was sent via wireless to a computer where it was analyzed to get a fragment size distribution curve.

Some examples of the fragments as seen by the camera are shown in Fig. 4. In the images, there are few small fragments or fines because most of the material below 120 mm had passed through the grizzly at the camera location. The image-based fragmentation was thus a measure of the material greater than 120 mm, with a small amount of finer material that, at the point of the images, had not yet passed through the grizzly. Fine and medium fragmentation are described by photos nos. 1 and 2, respectively, while heterogeneous fragmentation with coarse and small fragments is shown in photos nos. 3 and 4. When large fragments are at the edges of the photographed area their sizes are censored, causing an additional error to those typical of digital image analysis. However, this may not be too large compared with other errors in size measurement by image analysis, e.g. segregation and sifting (Rosato et al. 1987, 2002; Möbius et al. 2001; Liffman et al. 2001; Metzger et al. 2011), overlapped fragments (Thurley and Ng 2008; Andersson and Thurley 2008), capturing (Chavez et al. 1996; Thurley 2002), segmentation disintegration and fusion (Eden and Franklin 1996), profiling (Wang 2006), and surface-to-weight conversion (Thurley 2011; Fernlund 1998), to name some of them. The relative ‘undersizing’ of some large fragments due to edges censoring may compensate the trend of large fragments to be in the surface (segregation and sifting error) and their higher probability of being captured (capturing error).

Fig. 4

Samples of raw images taken by the video camera (top) in blast B1 and the resulting auto-delineations (bottom); the image height is equivalent to 896 mm

The bottom (black and white) images in Fig. 4 show the segmented (binary) images corresponding to the upper photographs; areas in white are delineated particles and areas in black correspond to non-delineated material with sizes below a threshold size of 32 mm, below which no reliable delineation is obtained. They show the quality of the automatic analysis; the large fragments splitting and small fragments merging (disintegration and fusion errors) are observed in some of the binary segmented images. Data from delineated particles are considered to form the passing fractions from 32 mm upwards. At this size the passing is calculated from the surface of non-delineated particles corrected by a factor. This factor defines the percentage of non-delineated material that is actually made of fines (Sanchidrián et al. 2009), and was set during the system commissioning to a low value as no significant amount of fines is apparent in the images (since they bypass the crusher feed). Below 32 mm, the system extrapolates fragmentation through an analytical size distribution function which parameters are calculated from two points in the range of sizes in which delineation is reliable (Split Engineering 2010).

Mass measurements and size distribution curves from image analysis are assigned to each blast between the dates in which mucking started and finished. Figure 5 shows as an example the size distributions of the 3161 images taken in blast B1. It illustrates the variability of fragmentation measured by the image analysis system. The 95% coverage band and the mean of the percentage passing at each size are also plotted. The size distributions of the photographs in Fig. 4 are also shown; photos 1 and 4 have a fragmentation near the 95% coverage bounds, while fragmentation in the other two are relatively central.

Fig. 5

Split-measured size distributions in blast B1 (light green lines); 95% coverage (dashed grey lines) and mean of the passing at each size (thick blue line); distributions of photos in Fig. 4 are highlighted: 1 (red), 2 (yellow), 3 (purple), and 4 (green) (color figure online)

5 Processing of Fragmentation Measurements

The global size distribution of blasted material was determined from the belt scale-based points, i.e. (25 mm, P₂₅) and (120 mm, P₁₂₀), and the image analysis-based points for sizes greater than 120 mm.

The size distributions as measured by image analysis on the grizzly are combined into a single distribution by averaging the passing at each size of all the individual distributions of a blast. The maximum size of each blast is the greatest of all measured maxima. However, since boulders had been previously broken this is not the maximum size of the blast; in fact, percentile sizes higher than P _m (90.7–97.0% depending on the blast, see Table 2) cannot be determined. The resulting size distributions for each blast are given in Table 5 in the “Appendix”. The maximum sizes measured are given in the footnote of Table 5; they are in line with the sizes of the largest fragments that are fed into the crusher (about 900 mm).

Passing fractions at 120 and 25 mm from the mass balance Eqs. 2–4 with belt scale data (Table 2) are as expected greater than measurements from image analysis (Table 5), since most of the fines were bypassing the crusher feed and were consequently absent from the photographs. The following procedure is followed for building the size distribution:

• 1. The size range 25 mm ≤ x _j  < 120 mm is interpolated linearly in log–log space from the belt scales data (25 mm, P₂₅) and (120 mm, P₁₂₀) on the same size points used by Split. The size distributions are not extended beyond 25 mm as the fines tail (< 25 mm) of the blasts under analysis was not measured.

• 2. In the range x _j ≥ 120 mm, starting from (x₀, P₀) = (120 mm, P₁₂₀), the successive points (x _j , P_j) are calculated upwards from the image analysis points (x _j , P _j,S ) as follows:

$$\ln \frac{{P_{j + 1} }}{{P_{j} }} = \ln \frac{{P_{j + 1,S} }}{{P_{j,S} }}\frac{{\ln (P_{m} /P_{120} )}}{{\ln (P_{m} /P_{120,S} )}},\quad P_{j + 1} \le P_{m}$$

(5)

where P_120,S is the passing at 120 mm from image analysis and P _m is the undersize passing (Table 2); Fig. 6 shows the Split-measured fragmentation curves on the grizzly and the final curves determined from the procedure above. Note that the grizzly curves have little variation, unlike those in which weighted data are used. Final curves in Fig. 6 have been extrapolated from (x _m , P _m ) to (2000 mm, 100%), albeit no quantitative use is made of that range. The 10–90 percentiles are given in Table 6 in the “Appendix”.

Fig. 6

Size distributions: Split-measured on the grizzly and final ones calculated with belt scale weights. Split measured points are shown with circles; the passing at 120 and 25 mm from belt-scales with squares, and the undersize limits (x _m , P _m ) with astersiks

A Swebrec function (Ouchterlony 2005, 2009) is fitted to the final size distributions in order to assess the quality of the procedure, as this function is generally the best fitting single component distribution to sieved fragmentation data form blasting (Sanchidrián et al. 2012a, b, 2014). The analytical form of the Swebrec cumulative distribution function is:

$$ P = {{100} \mathord{\left/ {\vphantom {{100} {\left\{ {{\kern 1pt} 1 + \left[ {{{\ln ({{x_{{max}} } \mathord{\left/ {\vphantom {{x_{{max}} } x}} \right. \kern-\nulldelimiterspace} x})} \mathord{\left/ {\vphantom {{\ln ({{x_{{max}} } \mathord{\left/ {\vphantom {{x_{{max}} } x}} \right. \kern-\nulldelimiterspace} x})} {\ln ({{x_{{max}} } \mathord{\left/ {\vphantom {{x_{{max}} } x}} \right. \kern-\nulldelimiterspace} x}_{{50}} )}}} \right. \kern-\nulldelimiterspace} {\ln ({{x_{{max}} } \mathord{\left/ {\vphantom {{x_{{max}} } x}} \right. \kern-\nulldelimiterspace} x}_{{50}} )}}} \right]^{{\,b}} } \right\}}}} \right. \kern-\nulldelimiterspace} {\left\{ {{\kern 1pt} 1 + \left[ {{{\ln ({{x_{{max}} } \mathord{\left/ {\vphantom {{x_{{max}} } x}} \right. \kern-\nulldelimiterspace} x})} \mathord{\left/ {\vphantom {{\ln ({{x_{{max}} } \mathord{\left/ {\vphantom {{x_{{max}} } x}} \right. \kern-\nulldelimiterspace} x})} {\ln ({{x_{{max}} } \mathord{\left/ {\vphantom {{x_{{max}} } x}} \right. \kern-\nulldelimiterspace} x}_{{50}} )}}} \right. \kern-\nulldelimiterspace} {\ln ({{x_{{max}} } \mathord{\left/ {\vphantom {{x_{{max}} } x}} \right. \kern-\nulldelimiterspace} x}_{{50}} )}}} \right]^{{\,b}} } \right\}}}\quad {\text{with }}0 < x \le x_{{max}} $$

(6)

where x _max is the maximum size, x₅₀ the median size and b a shape parameter.

The fits have been done on the range P₂₅ to P _m , fixing x _max to 2000 mm. Table 3 summarizes the results of a weighted nonlinear least squares fit with weights equal to 1/P ² _x , which is equivalent to minimizing the sum of relative errors. The fit is good for all blasts as can be seen from the high determination coefficients in Table 3, and visually in Fig. 10 (“Appendix”). This result supports the method used to build the size distributions.

Table 3 Summary of Swebrec fits to final fragmentation data

6 Analysis of Fragmentation

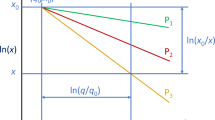
The fragmentation at common powder factors, such as those used in El Aljibe that are neither so low that a dust and boulder fragmentation results, nor so high that other breakage mechanisms like spalling take place, may follow the fragmentation-energy fan pattern described by Ouchterlony et al. (2017). This means that percentile fragment sizes x _P (i.e. a size for which P percent of material passes) plotted versus the powder factor in a log–log scale, form a set of convergent lines towards a focal point (q₀, x₀). Thus, each percentile x _P can be described through a power function of the powder factor, with parameters A _P and α _P variable with the fraction passing P:

$$x_{P} = {{f_{P} (q) = A_{P} } \mathord{\left/ {\vphantom {{f_{P} (q) = A_{P} } q}} \right. \kern-0pt} q}^{{\alpha_{P} }}$$

(7)

As discussed in Sect. 5, percentiles higher than P _m are uncertain so that, since the lower P _m value is 90.7% (see Table 2), we consider valid the fragmentation curves up to P = 90%. Percentiles x _P , P = 10, 20, …, 90 have been chosen, obtained by log–log linear interpolation of the final distribution curves. Equation 7 is fitted in log–log space to this set of x _P sizes using as q the mass powder factor above grade. The coefficients and their main statistics are given in Table 4. The mean determination coefficient is 0.644, and the p-values of the exponents are significant or quasi-significant for the percentiles 80–10% (they are slightly above the 0.05 limit for the percentile 30, and well above for the percentile 90, both marked in italics in Table 4); the x₉₀ line is almost horizontal and its slope is not significant. The values of α _P are monotonically decreasing as P increases. To improve the fits, a non-dimensionalization of the model, x _P /L _c with L _c a characteristic blast size, has been tried following Ouchterlony et al. (2017). The characteristic size chosen has been the one used by Sanchidrián and Ouchterlony (2017):

Table 4 Output of linear least squares fit of x _P in m and x _P /L _c through Eq. 8

$$L_{c} = \sqrt {S \cdot H}$$

(8)

S being holes spacing and H bench height. The percentile formula is then:

$${{x_{P} } \mathord{\left/ {\vphantom {{x_{P} } {L_{c} }}} \right. \kern-0pt} {L_{c} }} = {{A^{\prime}_{P} } \mathord{\left/ {\vphantom {{A^{\prime}_{P} } q}} \right. \kern-0pt} q}^{{\alpha^{\prime}_{P} }}$$

(9)

Results from this new fit are also given in Table 4 and in Fig. 7, where some percentile sizes are plotted versus the powder factor above grade. The parameters of all the fits to percentiles 10–90 are now significant to a 0.05 level, with the p-values of the coefficients generally lower than the dimensional formula ones. The determination coefficient also increases in general and its mean value is 0.804; it is, in the worst case, 0.698 which occurs for a passing of 30%. The fits have been extrapolated towards low powder factors to show that they converge fairly well to a common point according to the fragmentation fan principles. Figure 7 shows that there is a relatively large dispersion around the focal point that does not hide, however, that fragmentation appears to be sensitive to mass powder factors above grade according to the fan principles; we will show that the focus coordinates can be determined with statistical significance.

Fig. 7

Normalized percentile fragment sizes x _P /L _c versus mass powder factor above grade; data in the range of the mass powder factors above grade used in the blasts is magnified in the right graph

A comparison of the fits in Table 4 shows that the fan lines are steeper and have been shifted downwards when x _P is normalized by L _c ; these changes are constant for every percentile: the exponent increases by 0.17 (α _P – $\alpha_{P}^{'}$ ≈ − 0.17), and the prefactor is divided by 7.75 (i.e. A _P /$A_{P}^{'}$ ≈ 7.75).

Significant fits to a 0.05 level for all passing fractions from 10 to 90% are also obtained with the energy powder factor above grade (see Table 1) when an Eq. 9-type formula is used. The variability of the data explained by this model is, however, smaller, and the determination coefficients for all passing below 40% are lower than 0.7. Thus, mass powder factor above grade seems to be the best explosive concentration descriptor in this case.

In order to build an engineering model, analytical functions are derived for the coefficients in Eq. 9. The fan pattern encompasses the following relationship between the slopes α _P ′ and the fraction passing when fragmentation follows a Swebrec distribution (Ouchterlony et al. 2017):

$$\alpha^{\prime}_{P} = a_{1} + a_{2} \,\left( {{1 \mathord{\left/ {\vphantom {1 {P - 1}}} \right. \kern-0pt} {P - 1}}} \right){\kern 1pt}^{{a_{3} }}$$

(10)

where the coefficients a₁, a₂ and a₃ have physical meanings: a₁ = $\alpha_{100}^{'}$, a₂ = $\alpha_{50}^{'}$ − $\alpha_{100}^{'}$ and a₃ = 1/b, b being the Swebrec shape parameter, see Eq. 6. This function has also been found to work successfully to describe fragmentation of a large set of blasts obtained by sieving (Sanchidrián and Ouchterlony 2017). The coefficients a₁, a₂ and a₃ are determined by fitting Eq. 10 to the nine $\alpha_{P}^{'}$ slopes for percentiles P = 10 to 90 (see Table 4). The determination coefficient of the fit is 0.997 and the coefficients a₂ and a₃ are significant at a 95% level, but the interval of a₁ comprises negative values. This means that the slope of the 100% fan line ($\alpha_{100}^{'}$) is almost horizontal, suggesting that the maximum sizes are independent of the powder factor above grade; this result is consistent (it could not be otherwise) with the fact that the maximum size of the blasts was not measured. The coefficient a₁ is thus removed from the fit, i.e. it is made zero. Figure 8 (top graph) shows the function fitted to our data (green line) and the values of the coefficients and their confidence intervals; the agreement between predicted and measured data is good (R² = 0.982). The curve given by Sanchidrián and Ouchterlony (2017), derived from the analysis of 169 blasts, is also plotted (brown line) for comparison. Differences between both lines increase as the percentile does likely due to the zero a₁ coefficient obtained in this work. The similarity is remarkable, despite of the limitations of our data.

Fig. 8

Slope $\alpha_{P}^{'}$ (upper graph) and prefactor $A_{P}^{'}$ (lower graph) of fragmentation energy fan lines in log(x _p /L _c ) − log(q) space versus passing

The fan pattern properties can be used to obtain an expression of the prefactor $A_{P}^{'}$ in terms of the percentage passing. The general equation for the energy fan can be written as follows:

$${{x^{\prime}_{P} } \mathord{\left/ {\vphantom {{x^{\prime}_{P} } {x^{\prime}_{0} }}} \right. \kern-0pt} {x^{\prime}_{0} }} = \left( {{{q_{0} } \mathord{\left/ {\vphantom {{q_{0} } q}} \right. \kern-0pt} q}} \right)^{{\alpha^{\prime}_{P} }}$$

(11)

where $x_{P}^{'}$ refers to x _P /L _c and $x_{0}^{'}$ to x₀/L _c ; Eq. 11 can also be written:

$$x^{\prime}_{P} = x^{\prime}_{0} \left( {{{q_{0} } \mathord{\left/ {\vphantom {{q_{0} } q}} \right. \kern-0pt} q}} \right)^{{\alpha^{\prime}_{P} }}$$

(12)

Comparing Eqs. 9 and 12, it follows:

$$A^{\prime}_{P} = x^{\prime}_{0} {\kern 1pt} \cdot q_{0}^{{\alpha^{\prime}_{P} }}$$

(13)

And:

$$\ln (A^{\prime}_{P} ) = \ln (x^{\prime}_{0} {\kern 1pt} ) + \ln (q_{0} )\alpha^{\prime}_{P}$$

(14)

Equation 14 can be viewed as a function $A_{P}^{'} = f\left( P \right)$, since $\alpha_{P}^{'}$ is itself a function of P. The focus coordinates (q₀, x₀′) can be determined as parameters of the fit of Eq. 14 to the nine pairs ($A_{P}^{'}$,$\alpha_{P}^{'} \left( P \right)$). This way, the set of 18 parameters that define the fan (nine slopes $\alpha_{P}^{'}$ and nine prefactors $A_{P}^{'}$, if nine fan lines are selected) is reduced to five parameters, q₀, x₀′, a₁, a₂ and a₃. Figure 8 (bottom graph) shows the $A_{P}^{'}$ values (blue circles) as function of the passing using a logarithmic scale for the ordinates; the regression line from fitting Eq. 14 using the calibrated expression for $\alpha_{P}^{'}$ in Eq. 10 is also plotted (green line). The determination coefficient of the fit is high, 0.998 and the values of the focal point (q₀, $x_{0}^{'}$) of the fan lines are significant to a 0.05 level; these and their 95% confidence intervals are given in Fig. 8 (bottom graph).

7 Discussion

The fragmentation energy fan concept stems from the observation that the percentile sizes, if represented as function of the powder factor (or, in general, energy concentration) tend to form straight lines when plotted in log–log space. Such lines have decreasing slopes at growing percentage passing so that they form a curve bundle with a relatively well defined common intersection point, or focus; the curve set can be described by the coordinates of that point and the slopes. It further turns out that, if the underlying size distribution is of Swebrec-type (Ouchterlony 2005, 2009), the slopes must follow (see Ouchterlony et al. 2017 for the derivations) a certain functional form of the percentage passing, that simplifies the description of the slopes variation to only three parameters a₁, a₂ and a₃. These, plus the focus coordinates (q₀, $x_{0}^{'}$) are the only parameter set required to define the whole fragmentation spectrum as function of the powder factor, by means of Eqs. 9, 10 and 13. Dimensionless sizes, scaled with a characteristic size, x _P /L _c , also follow the fan pattern as proved by Ouchterlony et al. (2017); they have been used here since they provide better fits to the fan lines.

The procedure followed is (primes are used for the parameters with dimensionless sizes): (1) α _P ′ and A _P ′ are obtained for the P-percentiles from Eq. 9-type fits; (2) Eq. 10 is fitted to the $\alpha_{P}^{'}$, so that a₁, a₂ and a₃ are obtained, and (3) Eq. 14 is fitted to the $A_{P}^{'}$, $\alpha_{P}^{'}$ pairs from (1), from which the focus coordinates q₀, x₀′ are obtained.

The percentiles 10, 20,…, 90, determined from the fan model, are plotted versus the observed ones in Fig. 9. The determination coefficient is 0.992 and the slope of the fitted line has a 95% coverage 0.975–1.002 (the Y-intercept is made zero since it is not significant at a 95% level). Such a result indicates a good performance of the model in the range 10–90% passing.

Fig. 9

Model performance at percentiles between 10 and 90. Measured versus calculated normalized percentile sizes; dashed blue line is the linear regression to the points; red line is observed = calculated values) (color figure online)

To quantify the ability of the model to describe fragmentation, logarithmic errors are calculated at the same passing fractions 10–90%:

$$e_{LP} = \ln ({{x_{{P,{\text{calc}}}} } \mathord{\left/ {\vphantom {{x_{{P,{\text{calc}}}} } {x_{{P,{\text{data}}}} }}} \right. \kern-0pt} {x_{{P,{\text{data}}}} }})$$

(15)

The first and third quartiles of e _LP are − 0.052–0.043, respectively (equivalent to relative errors of − 5.1 and 4.4%). These values show a relatively centered distribution of errors, and are estimates of bounds for errors expected 50% of the times. The maximum likely errors estimated from the 95% percentile of the absolute e _LP values is 0.136, which is roughly equivalent to a relative error of 14.6%. These figures are in the lower bound of the uncertainty range of fragmentation measurements by sieving estimated by Sanchidrián (2015), 8–22%. One of the reasons for such good performance of a simple model with only two P-dependent coefficients, $A_{P}^{'}$ (P) and $\alpha_{P}^{'}$(P)—while nine P-dependent parameters are required in the model developed by Sanchidrián and Ouchterlony (2017)—is that most of the variables with a significant influence on fragmentation (rock strength and rock mass description, bench geometry and delay) have limited variability within our blasts and their effect is well lumped by the factor $A_{P}^{'}$.

The analysis presented assumes that water coupling is able to transmit a high pressure shock to the rock so that the fragmentation effect does not differ much from when the explosive is fully coupled (in line with results by Ash 1973, Smith 1976, Brinkman (1982) and Bleakney 1984). Based on that, the action of the water-coupled gelatin on the rock is assumed to be equivalent to the ANFO directly coupled. The mass of gelatin and ANFO are lumped together to calculate the powder factor, either directly for the mass factor or combined with their specific energies for the energy factor. The fragmentation data are sensitive to the powder-factor so calculated; not surprisingly, they are also, almost equally, sensitive to the energy powder factor.

Water in rock may influence blast fragmentation due to higher wave velocities and less attenuation of the shock wave in water saturated rock, possibly resulting in a better (finer) fragmentation. In this work, blasts with high powder factor correspond to drier rock than blasts with low powder factor. The fragment sizes obtained show an inverse relation with powder factor (hence a direct relation with the water content), so the powder factor influence has probably overridden the water aspect. The low water absorption of the rock, measured at 0.10%, probably makes the water effect on the rock mass negligible.

The variability in the charging pattern (usual in the quarry sector in Spain, where bulk trucks are little used) in blasts where the water content is variable across the block must inevitably bring variability to the data. Still, the results obtained prove, if anything, that the powder factor is the primary controlling variable of fragmentation by blasting.

The data used in this work is given graphically for each of the six blasts in “Appendix”, Fig. 10. In it, red dots: passing fractions at 120 and 25 mm from belt scale mass data (Table 2) and the mass balance (Eqs. 2–4); red dashed lines: undersize level (from boulder mass in Table 2); black lines: image analysis data (orange, extrapolated data below the system resolution, not used); blue lines: size distributions calculated as described in Sect. 5; magenta lines: Swebrec fits to the final distributions, and green dashed lines: size distributions from applying the energy-fan model, Eqs. 9, 10 and 13, to the mass powder factors above grade. These are extrapolated down to percentiles similar to P₂₅, slightly below the minimum 10% passing that was used for deriving the energy fan constants.

Fig. 10

Size distributions. Red points: belt scale measured; red dashed line: undersize level; black line: Split measured (orange: extrapolated); blue line: final distributions; magenta line: Swebrec fit to the final distributions; green dashed line: fragmentation calculated with the fan model. The mass powder factor above grade of each blast, see Table 1, is given in each graph (color figure online)

8 Conclusions

A fragmentation by blasting model is developed for a mylonite quarry with blocky rock structure from the fragmentation-energy fan principles. The data set comprised six production blasts located one behind the other in the same block, so the variability in rock strength and rock mass characteristics was limited. The water level and the usage of explosives (cartridged gelatin water-coupled to rock, and bulk ANFO) were variable within and between the blasts, but the distribution of explosive energy within each block was relatively uniform and the performance of both explosives per unit mass appeared to be similar. Mass powder factor above grade, considered the best descriptor of the specific charge that contributes to fragmentation, ranged from to 0.28–0.44 kg/m³.

Fragmentation has been measured with three belt scales located in the processing plant, from which the fraction passing at two sizes, 120 (cut size of the grizzly) and 25 mm can be calculated, and with an online digital image system installed above the discharge of the grizzly crusher feeder. This prevents to assess the actual size of the boulders, the amount of which was estimated at 3–9.3% of the material. The size distributions of the blasted material are obtained from the image analysis data in the coarse range, where image analysis is more reliable, and from the belt scales data between 25 and 120 mm. The resulting size distributions are well described with the Swebrec function. The size distributions have been interpolated to get the desired percentile sizes in the range where the data are considered to be representative of the muckpile fragmentation, about 10–90% passing.

The percentile fragment sizes of each blast, nondimensionalized by a characteristic length (the geometric mean of the bench height and the hole spacing), form a set of convergent lines when represented as a function of the powder factor above grade in log–log space. The pre-factor and the exponent of the size-to-powder factor power laws has been obtained for nine percentiles, 10–90; the fits are all significant to a 95% level, providing a good description of the data variability with determination coefficients above 0.70. Analytical formulae to calculate fragmentation as function of the mass powder factor above grade have been obtained by deriving expressions for both parameters of the model (pre-factors and exponents) as functions of the fraction passing, based on the principles of Ouchterlony et al.’s (2017) fragmentation energy-fan. The 18 parameters of the nine fan lines (nine exponents and nine prefactors) are this way reduced to five: the fan focus coordinates and three parameters of the function of the slopes with the percentage passing.

The model explains 99% of the variance in the non-dimensional sizes at percentiles between 10 and 90% and it is statistically significant. The expected and maximum errors for sizes in that percentile range are less than 6 and 15%, respectively.

Appendix: Fragmentation Data

See Tables 5 and 6, Fig. 10.

Table 5 Split measured size distributions on the grizzly feeder

Table 6 Reconstructed size distributions built according to Sect. 5