1 Introduction

The N-body problem is a classical problem in physics that involves predicting the motions of N particles under the influence of gravitational forces. This problem has puzzled scientists for centuries due to its mathematical complexity, and it remains an active area of research in physics and astronomy [9, 15, 16, 18, 24]. In this article, we focus on a particular case of the \((N+1)\)-body problem where \(N=3\). This problem has been of interest to physicists for many years due to its simplicity and the fact that it provides a good model for studying the dynamics of planetary rings, such as Saturn’s rings, and the motion of a particle under the interaction of a planet and some co-orbital satellites uniformly distributed on a circumference. One of the earliest works on this problem was done by James Clerk Maxwell in the 1850 s [14]. Maxwell’s analysis showed that the rings of Saturn could not be solid or liquid, but must consist of countless small particles. He also proposed that the particles must be distributed in a thin, flat disk rather than a more three-dimensional structure. Additionally, he demonstrated that the gravitational forces between the particles would keep the rings stable over long periods of time. The work of Maxwell laid the foundation for further investigations into the rings of Saturn and other celestial objects, and his ideas continue to be relevant to current research in planetary science. Since then, many other researchers have studied the N-body problem in the ring configuration using various methods, including numerical simulations and analytical approximations [1, 4, 5, 10,11,12,13, 17, 22, 23, 26, 27]. Some of the key issues that have been addressed include the stability of the ring system, the formation of gaps and clumps, and the role of resonances in the dynamics of the system. Kalvouridis has devoted a great part of his work to deal with this problem. A complete review of the advances he has achieved in this field between the years 1997 and 2008 can be found in [13].

The analysis of the escape from open Hamiltonian systems is one of the most analyzed topics in nonlinear dynamics [2,3,4,5,6,7, 20, 25, 28]. In these kind of systems, there exists a finite energy of escape, \(E_e\), such that if the energy of the particle is smaller than \(E_e\), the equipotential surfaces are closed and the escape from the system is impossible. However, for values of the energy larger than \(E_e\), these surfaces open and several apertures emerge, making possible the escape to infinity.

In this work, we investigate some aspects of the motion of a particle in the gravitational field created by a central body and two identical and co-orbital satellites in syzygy, when the energy of the particle is not high enough to escape the potential well of the system, but is sufficient to leave the region surrounding one of the satellites. The exit from this region is regulated by an unstable periodic orbit, called Lyapunov orbit.

To carry out this study, we have defined a new circular-shaped surface of section centered on the satellite that we want to analyze. Within this section, we have defined a grid of \(512 \times 512\) initial conditions, which we have integrated until the orbit intersects the Lyapunov orbit or until a maximum integration time, for which we have taken different values. In this way, we have calculated the basins of escape on the new surface of section. Additionally, we have determined the stable manifold of the Lyapunov orbit, as well as its projection onto the surface of section, which defines the limiting curve of the basins of escape, in order to analyze their structure and geometry.

2 Analysis of the Results of the Numerical Exploration

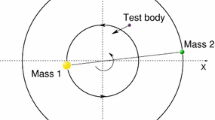
The \((3+1)\)-body ring problem concerns the motion of an infinitesimal particle in the Newtonian field of a system consisting of one central body and two co-orbital primaries with equal masses in syzygy. These primaries rotate at a constant angular velocity around a principal body, of mass \(m_0\) and placed at the center of the circumference. In a barycentric synodic coordinate system Oxyz rotating with the primaries, the equations of motion are [11, 12]

$$\begin{aligned} \ddot{x} - 2\dot{y} = \frac{\partial U}{\partial x},\quad \ddot{y} + 2\dot{x} = \frac{\partial U}{\partial y}, \end{aligned}$$
(1)

where U(x, y) is the potential

$$\begin{aligned} U(x,y) = \frac{1}{2}(x^2+y^2) + \frac{1}{2}\left( \frac{\beta }{r_0} + \frac{1}{r_1} + \frac{1}{r_2}\right) , \end{aligned}$$
(2)

\(\beta = m_0/m\) is the mass ratio between the masses of the central and the peripheral primaries, \(r_0 = \sqrt{x^2+y^2}\), \(r_1 = \sqrt{ (x-x_1^*)^2 + (y-y_1^*)^2 }\), \(r_2 = \sqrt{ (x-x_2^*)^2 + (y-y_2^*)^2 }\), and \((x^*_1,y^*_1)\) and \((x^*_2,y^*_2)\) are the coordinates of the two peripheral primaries.

These equations can model the motion of a particle in a system composed of a planet and a pair of co-orbital satellites. Equation (1) admits a first integral given by

$$\begin{aligned} C = 2U(x, y) - (\dot{x}^2 + \dot{y}^2), \end{aligned}$$
(3)

the so-called Jacobi constant. As \(\dot{x}^2 + \dot{y}^2 = 2U(x, y) - C\), the curves defined by \(C - 2U(x, y)=0\) delimits the boundary of the plane where the motion can take place. There exists a critical value of the Jacobi constant, dependent on the mass ratio and denoted by \(C_{\beta ,e}\), for which the curves of zero velocity open [21]. If the value of the Jacobi constant is not larger than \(C_{\beta ,e}\), particles may leave the system crossing one of the apertures of the potential well.

For values of the Jacobi constant larger than \(C_{\beta ,e}\), the particle cannot leave the potential well of the system, and the curves of zero velocity can take different shapes. For values of the Jacobi constant large enough, the motion of the test particle can only take place around each of the three bodies. For a certain value of the Jacobi constant, the regions surrounding these bodies gets connected, and the particle can freely circulate through the regions surrounding all three bodies. In Fig. 1, we show the curves of zero velocity of the system for \(\beta =2\), \(C=1.6\) (left panel), and \(C=1.5\) (right panel). The black dots show the position of the central body and the peripheral primaries. The region colored in gray corresponds to the domain where the particle can not access.

Fig. 1
figure 1

Curves of zero velocity for \(\beta =2\) and \(C = 1.6\) (left panel) and \(C = 1.5\) (right panel). The region colored in gray corresponds to the domain where the particle can not access

Full size image

In what follows, we set \(\beta =2\) and \(C=1.5\) and focus on studying the motion of a particle in the vicinity of the co-orbital satellite located to the right of the central body. There exists an unstable periodic orbit, known as Lyapunov orbit, which guards the escape from the region near this co-orbital satellite. In the right panel of Fig. 1, we also show the Lyapunov orbit that governs the escape of particles from the region surrounding the satellite located to the right of the central body. The analysis of the basins of escape has been carried out in the configuration space \((\theta ,\alpha )\), with \(0\le \theta ,\alpha \le 2\pi \), on the circular surface of section defined by \(x = x_1^* + r_0\cos \theta \), \(y=r_0\sin \theta \), where \(r_0=0.05\),

$$\begin{aligned} \dot{x}= v \cos \alpha ,\quad \dot{y}=v\sin \alpha , \end{aligned}$$

being v the modulus of the velocity, and \(0\le \alpha \le 2\pi \). In the configuration space defined by the angles \(\theta \) and \(\alpha \), we have considered a grid of \(512 \times 512\) initial conditions. For each value of \(\theta \) and \(\alpha \), we calculate the initial conditions as follows: first, we obtain \(x = x_1^* + r_0\cos \theta \), \(y=r_0\sin \theta \). Next, we determine the magnitude of the velocity,

$$\begin{aligned} v^2 = \dot{x}^2+\dot{y}^2 = 2U(x,y)-C . \end{aligned}$$

Finally, we can calculate the velocity for the given value of \(\alpha \) as \(\dot{x} = v\cos \alpha \), \(\dot{y} = v\sin \alpha \). In the right panel of figure 1, we have depicted, in red, the surface of section where we will analyze the basins of escape.

Each of these initial conditions in the mesh has been integrated for a maximum integration time of \(T_\text {max}=100\) units of time. If, after that time, the corresponding orbit has not intersected the Lyapunov orbit, we consider that the particle has been trapped in the vicinity of the co-orbital satellite on the right. If the orbit intersects the Lyapunov orbit, we consider that the orbit has left the vicinity of the co-orbital satellite that we are analyzing. The time of escape \(t_\text {esc}\) related to an initial condition inside the region surrounding a co-orbital satellite is the time the corresponding orbit requires to cross the Lyapunov orbit guarding this region. Of course, a particle that leaves this region can eventually return to it, but in our study, we have not considered what happens to the orbits once they leave the region we are analyzing. For the numerical integration of the orbit, we have used the recurrent series power method [19].

Fig. 2
figure 2

Number of orbits (\(N_\nu \)) that leave the region surrounding the co-orbital satellite located on the right, with a time of escape \(t_\nu \in (\nu -1,\nu ]\), for any \(\nu =1,\ldots ,100\)

Full size image

In Fig. 2, we show the number of orbits, \(N_\nu \), that leave the region surrounding the co-orbital satellite located on the right, with a time of escape \(t_\nu \in (\nu -1,\nu ]\), for any \(\nu =1,\ldots ,100\). We can observe that most of the orbits that leave the neighborhood of the co-orbital satellite do so with a time of escape smaller than 8 units of time. So, we focus on the study of the geometry of the basins of escape for short times of escape, that is, times of escape smaller than 8 units of time. This fact will also simplify the analysis of the relationship between the basins of escape and the projection of the stable manifold of the Lyapunov orbit onto the Poincaré surface of section.

Fig. 3
figure 3

Basins of escape (red color) considering \(T_\text {max}=2\) (left panel) and \(T_\text {max}=8\) right panel) and projection of the stable manifold to the Lyapunov orbit on the surface of section (in black)

Full size image

In addition, we have accurately determined the orbit of Lyapunov and, following the procedure of Deprit and Henrard [8], we have calculated the stable manifold of this periodic orbit. Next, we have obtained the projection of this manifold onto the surface of section. To do this, we have considered a set of \(10^6\) initial conditions belonging to the initial part of the stable manifold in the vicinity of the periodic orbit. Each of these initial conditions has been integrated backward until it intersects the surface of section. Furthermore, we have continued the numerical integration backward to obtain the sequence of intersections of the stable manifold with the surface of section. Of course, some of these orbits end up leaving the region near the satellite we are analyzing, and in such cases, we stop numerically integrating them.

In Fig. 3, we show the basins of escape (in red) for maximum integration times of 4 and 8 time units (left and right panel, respectively), and the limiting curves of these escape basins, considering 2 (left panel) and 20 (right panel) intersections of the stable manifold with the surface of section. As we can observe in both panels of Fig. 3, the projection of the stable manifold of the periodic orbit onto the surface of section precisely delimits the basins of escape of the region surrounding the satellite on the right. The projection of the stable manifold onto the surface of section is articulated around two main components, which we have labeled as A and B in Fig. 3 (left panel). These two lobular-shaped components correspond to the first (A) and second (B) intersection of the stable manifold with the surface of section. The subsequent intersections can be classified into two types: the first type of structure, which we have named C in Fig. 3, connects A and B. Its ends have an infinite tongue-like shape and tend to A and B infinitely spiraling around them. The second type of structure has an elongated tongue-like shape. We have found six of these structures, which we have named as \(D_1,\ldots ,D_6\). It is important to note that each of these structures (A, B, C, \(D_1,\ldots ,D_6\)) is associated with an infinite sequence of other structures that tend to them, as we can see in Fig. 3 (right panel). As we increase the maximum integration time, these secondary structures become more important since they are associated with larger escape times.

The results we have obtained clearly demonstrate that the limiting curves of the basins of escape are given by the projection of the stable manifold of the Lyapunov orbit onto the surface of section.

3 Conclusions

In this article, we have studied the geometric shape of the curves that limit the escape of a particle from the vicinity of a satellite in a system simulated by using the \((N+1)\)-body ring problem when \(N=3\). We have considered a value of the energy of the particle that does not allow for escape from the potential well but does allow the transit of the particle from the vicinity of one peripheral body to another.

Furthermore, we have shown that the projection of the stable manifold onto the surface of section precisely delimits the escape regions around the co-orbital satellite under investigation. We have described the geometry of these escape regions, classifying the different structures that appear in the projection of the stable manifold onto the surface of section. This study enables a better understanding of the dynamics of the system and can be useful for the design of space missions and the exploration of the environment of the co-orbital system.

Finally, the numerical determination of the basins of escape has allowed us to validate the calculation of the stable manifold of the corresponding Lyapunov orbit.