Investigating the planar circular restricted three-body problem with strong gravitational field

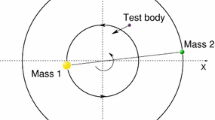
Abstract

The case of the planar circular restricted three-body problem where one of the two primaries has a stronger gravitational field with respect to the classical Newtonian field is investigated. We consider the case where two primaries have the same mass, so as the the only difference between them to be the strength of the gravitational field which is controlled by the power p of the potential. A thorough numerical analysis takes place in several types of two dimensional planes in which we classify initial conditions of orbits into three main categories: (1) bounded, (2) escaping and (3) collision. Our results reveal that the power of the gravitational potential has a huge impact on the nature of orbits. Interpreting the collision motion as leaking in the phase space we related our results to both chaotic scattering and the theory of leaking Hamiltonian systems. We successfully located the escape as well as the collision basins and we managed to correlate them with the corresponding escape and collision time of the orbits. We hope our contribution to be useful for a further understanding of the escape and collision properties of motion in this interesting version of the restricted three-body problem.

Appendix: Existence and stability of circular orbits in the generalized Kepler problem

It is well known that in the classical Newtonian gravitational potential $V = - k/r^n$, where $n = 1$, a circular orbit always exists. When $n \ne 1$ we have the case of the generalized Kepler problem. According to theoretical mechanics a necessary condition for the existence of circular orbits is the central potential to be attractive. In the following we shall demonstrate for which values of n we stable or unstable circular solutions.

The total effective potential $V_{\mathrm{eff}}$ in a central force field is the sum of the central potential $V_C$ and the centrifugal term $V_L$.

$$V_{\mathrm{eff}}(r) = V_C(r) + V_L(r) = - \frac{k}{r^n} + \frac{L^2}{2mr^2},$$

(8)

where $n > 0$, $k > 0$, and $m > 0$. In Fig. 19 we present a plot of $V_{\mathrm{eff}}$, $V_C$, and $V_L$ when $k = m = L = 1$ and $n =3/2$.

Fig. 19

Evolution of $V_{\mathrm{eff}}$ (black), $V_C$ (blue), and $V_L$ (green) as a function of radius r, when $k = m = L = 1$, and $n = 3/2$. The vertical and the horizontal magenta dashed lines indicate the radius $r_0$ and the corresponding energy $E_0$ of the circular orbit, respectively. (Color figure online)

The radius $r_0$ of the circular orbit, if exists, is obtained by setting the first derivative of the total effective potential equal to zero. Therefore we have

$$r_0(n) = \left( \frac{mkn}{L^2}\right) ^{\frac{1}{n-2}} > 0.$$

(9)

For $n = 3/2$ we derive that $r_0 = \frac{4L^2}{9m^2k^2}$. Looking at Eq. (9) it becomes evident that circular solutions are indeed permissible for every value of n except for $n = 2$.

The energy of the circular orbit, $E_0$, can easily be found if we insert the expression (9) of $r_0$ into Eq. (8). After applying elementary calculations we obtain

$$E_0(n) = - k \left( \frac{mkn}{L^2}\right) ^{\frac{n}{2-n}}\left( 1 - \frac{n}{2}\right).$$

(10)

The last term of Eq. (10), that is $\left( 1 - \frac{n}{2}\right)$, suggests that when $0< n <2$ $E_0$ is negative, while for $n > 2$ $E_0$ is positive. In other words, for $0< n <2$ the equilibrium point of $V_{\mathrm{eff}}$ at $r_0$ is a global minimum, while for $n > 2$ it is a global maximum. Here it should be noticed that the sign of the energy at the equilibrium point already implies the stability of the circular orbits.

Our next task is to determine for which values of n the corresponding circular orbit is stable and for which becomes unstable. It is very easy to prove that in a central force field the necessary and also sufficient condition for a circular orbit with radius $r_0$ to be stable is the following

$$S(r_0) = \frac{F'(r_0)}{F(r_0)} + \frac{3}{r_0} > 0,$$

(11)

where of course

$$F(r) = - \frac{dV_C(r)}{dr} = - n \frac{k}{r^{n+1}},$$

(12)

and

$$F'(r) = \frac{dF(r)}{dr} = n\left( n + 1\right) \frac{k}{r^{n+2}}.$$

(13)

Fig. 20

Evolution of S as a function of the power n of the gravitational central potential $V_C$, when $k = m = L = 1$. The horizontal blue dashed line denotes the threshold $S = 0$, which distinguishes between stable and unstable circular orbits. Stable circular orbits exist only in the interval $n \in (0,2)$, while for $n > 2$ circular orbits are permissible however they are all unstable. (Color figure online)

Inserting Eqs. (9), (12), and (13) into (11) we obtain S as a function of n as follows

$$S(n) = - \left( n - 2\right) \left( \frac{mkn}{L^2}\right) ^{\frac{1}{2-n}}.$$

(14)

In Fig. 20 we illustrate the evolution of S(n), when $k = m = L = 1$. It is seen, that in the interval $n \in (0,2)$ $S > 0$ and therefore stable circular orbits exist. On the other hand, for $n > 2$ circular orbits do exist however they are unstable since $S < 0$. In this paper we investigate the nature of orbits in the planar circular restricted three-body problem where one of the primaries has a strong gravitational field. We consider only cases where n varies in the interval (1, 2), where according to Eq. (14) stable Keplerian orbits are indeed permissible.