Abstract
Seismic P- and S-wave velocities of the lower lithosphere and underlying asthenosphere at the SW margin of the East European Craton in northern Poland were obtained with different seismic techniques: seismic refraction, P-residuals of the first arrivals from teleseismic earthquakes, P-wave receiver function, and inversion of the Rayleigh surface wave dispersion curves, the last two using data collected in the passive seismic experiment “13 BB star”. The uniform array consisted of 13 stations deployed in a 120 km in diameter area. Below the depth of 180–220 km a decrease of about 6% of the S-wave velocity is interpreted as a thermal gradient zone corresponding to a lithosphere–asthenosphere transition. The average mantle velocities down to a depth of 300 km beneath the array are relatively high, exceeding values for other Precambrian cratons by 0.1–0.2 km/s, and cannot be modeled by reasonable mantle peridotite compositions in the lithospheric part of the profile. We suggest that significant peridotite anisotropy could explain the misfit between measured and calculated seismic velocities in the lithosphere.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The contact between the East European Craton (EEC) and the Palaeozoic Platform (PP) located to the SW is a major geological boundary in Europe. The contact zone—Trans-European Suture Zone (TESZ)—is mostly located in Poland, where it is hidden beneath the cover of sedimentary rocks of various thicknesses. Nevertheless, its crustal structure is relatively well-known thanks to numerous boreholes and geophysical studies (e.g., Grad et al. 2016). On the other hand, the sub-Moho part of TESZ is poorly recognized. Puziewicz et al. (2017) suggested that its uppermost part is dominated by harzburgites of relatively low Mg/(Mg + Fe) 0.91. The continental-scale seismic studies (Hoernle et al. 1995; Voss et al. 2006) show that the EEC mantle is relatively thin at its SW margin and its thickness increases to the NE. This indicates that the EEC margin close to TESZ is underlain by a non-cratonic lithospheric mantle. The only mantle samples in the SW margin of EEC are xenoliths occurring in the Jurassic lavas of Scania in SW Sweden (Rehfeldt et al. 2007). Their characteristics are typical of Phanerozoic mantle spinel facies.
In this paper, we describe the results of the seismic experiment “13 BB star”. An array of 13 broadband stations was located in the south-western margin of the Fennoscandia, close to the Trans-European Suture Zone (TESZ). Seismic S-wave velocity in the sub-Moho lithosphere is relatively large, 0.1–0.2 km/s higher than for other old Precambrian cratons. First, a S velocity increase was found at a depth of 75–90 km. Second, a high velocity layer at a depth of 180–220 km is underlain by a significant velocity decrease, which corresponds to the asthenosphere.
Our results show that the petrological interpretation of a seismic signal is not possible in the isotropic approach. Therefore, we suggest that the lithospheric mantle underlying the SW margin of East European Craton consists of peridotites which are both seismically and texturally anisotropic.
Methods
To study the lithosphere and asthenosphere in the marginal zone of the EEC, we used different seismic techniques: seismic refraction, P-residuals of the first arrivals from teleseismic earthquakes, P-wave receiver function, and inversion of the Rayleigh surface wave dispersion curves (e.g., Zielhuis and Nolet 1994; Wilde-Piórko et al. 2002, 2010; Geissler et al. 2010; Janutyte et al. 2015; Soomro et al. 2016; Meier et al. 2016; Knapmeyer-Endrun et al. 2017). The nature of the seismic lithosphere–asthenosphere boundary (LAB) is still debated, particularly under “cold” Precambrian shields and platforms. The passive experiment “13 BB star” (Grad et al. 2015) was deployed to study the LAB in the marginal zone of the EEC in northern Poland. The seismic array consisted of 13 stations deployed in the area of ca. 120 km in diameter, equipped with broadband seismometers RefTek 151-120 (“Observer”). The “Observer” is a low noise three-component seismometer with a frequency bandwidth of 0.0083–50 Hz (which corresponds to periods 120–0.02 s), flat to velocity.
The records obtained during a more than 3-year long recording campaign, yielded a detailed image of the lower lithosphere and LAB structure. The array was located in the area of well-known sedimentary cover and crustal structure, so seismic velocities down to a depth of 300 km obtained from the Rayleigh surface wave dispersion curves are not affected by shallow structure uncertainty.
Geological context
The East European Craton is the coherent Precambrian, mainly Archaean and Paleoproterozoic, part of the continental plate and occupies the north-eastern portion of Europe (Bogdanova et al. 2006, 2015). Three independent crustal segments: Fennoscandia, Sarmatia and Volgo-Uralia, collided to form the EEC (Bogdanova et al. 1996). The study area around the “13 BB star” array (Figs. 1, 2a, b) is located in the south-western margin of the Fennoscandia, close to the Trans-European Suture Zone (TESZ). The central station A0 is located about 50 km from the TESZ. The crystalline basement of the EEC is buried beneath a 5–9 km thick cover of sediments, and is interpreted to be the prolongation of the 1.81–1.76 Ga Trans-Scandinavian Igneous Belt (Bogdanova et al. 2015 and references therein). The Polish Basin adjoining the part of EEC discussed in this study is filled with Upper Palaeozoic, Meso- and Cenozoic sedimentary 10–12 km sequences, underlain by a sedimentary “pre-Variscan consolidated crust” reaching the depth of 20 km; Moho is located at ca. 37 km (e.g., Dadlez et al. 2005; Dadlez 2006; Janik et al. 2005).
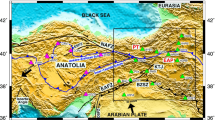
a The tectonic sketch of the pre-Permian Central Europe in the contact of the East European Craton, Variscan and Alpine orogens compiled mainly from Pożaryski and Dembowski (1983), Ziegler (1990), Winchester et al. (2002), Narkiewicz et al. (2011), Cymerman (2007), Skridlaitė et al. (2006), Franke (2014), and Mazur et al. (2015). The gray frame shows the location of the study area. BT Baltic Terrane, EA Eastern Avalonia, FSS Fennoscandia–Sarmatia suture, MLSZ mid-Lithuanian suture zone, PLT Polish–Latvian Terrane, RG Rønne Graben, RFH Ringkobing-Fyn high, STZ Sorgenfrei–Tornquist zone, TTZ Teisseyre–Tornquist zone, VDF Variscan deformation front. The area of Bohemian Massif is highlighted in dark green. The red circle shows the location of the “13 BB star” array in northern Poland (Grad et al. 2015). The P4-dot shows the location of the Vp mantle model from profile P4 (Wilde-Piórko et al. 2010). The orange dotted line shows a profile for which mantle models are shown in Fig. 10. The yellow star shows the location of basanites in Scania (southern Sweden) analyzed by Rehfeldt et al. (2007). b The Moho depth map (Grad et al. 2009, 2016) and c surface heat flow (Majorowicz and Wybraniec 2011) of the study area. The Trans-European Suture Zone separates the thick and cold Precambrian crust from the younger thin and hot crust
Data for the crustal and uppermost mantle investigations of the study area. a Location and arrangement of the “13 BB star” array on the background of the topography map. Red and white circles show the planned regular geometry of the array where broadband seismometers are placed in basic equilateral triangles with side lengths of about 30 km. The navy-blue dots are the final locations of the stations A0, B1–B6 and C1–C6 (Grad et al. 2015). b Heat flow map (Majorowicz and Wybraniec 2011). c Map of the P-wave velocity in the crystalline upper crust. d Thickness of the crystalline upper crust. e Total thickness of the crystalline crust. f Map of the average P-wave velocity in the 5 km thick uppermost mantle. Data c–f were extracted from the high-resolution 3D model of Poland (Grad et al. 2016). Position of the TTZ in Poland after Narkiewicz et al. (2011)
The area of the array (Figs. 1b, c, 2) is characterized by a thick crust with Moho at a depth of 40–45 km, and high Pn velocities (> 8.2 km/s) in the uppermost mantle. Across the TESZ to the southwest the abrupt transition of the crustal thickness to 28–32 km (Fig. 1b) takes place over a short lateral distance of less than 200 km (Grad et al. 2002, 2016). The TESZ is also a border of thermal provinces, separating the “cold” Precambrian craton with a heat flow 30–50 mW/m2 and the “hot” Paleozoic platform with a heat flow 70–80 mW/m2 (Figs. 1c, 2b; Majorowicz et al. 2003; Majorowicz and Wybraniec 2011).
The tomographic seismic cross-sections through the EEC–TESZ contact presented by Hoernle et al. (1995), albeit of low resolution, suggest that the EEC mantle is relatively thin at its SW margin and its thickness increases to the NE, and that the contact zone is underlain by an intermingled sequence of mantle rocks of varying velocities. Voss et al. (2006) present similar data, claiming that the contact between TESZ and EEC is dipping at 30–45° to the NE.
Seismic P- and S-wave velocity models down to 300 km depth
Crustal structure
The crustal structure of the EEC beneath the “13 BB star” array could be extracted from a recently presented high-resolution 3D seismic model for the crust and uppermost mantle down to a depth of 60 km in the area of Poland (Grad et al. 2016). For the whole territory of Poland the sedimentary cover, three-layered crystalline crust and uppermost mantle show great variations both in thickness and P-wave velocity (Fig. 2). The upper crust is about 12 km thick with Vp = 6.1 km/s (Fig. 2c, d). The total thickness of the crystalline crust is about 35 km, and Vp velocity below Moho is about 8.2 km/s (Fig. 2e, f). The seismic P-wave velocity model of the crust beneath the central station A0 in the depth ranges from 160 m a.s.l. down to 60 km is shown in Fig. 3a. In this model, a high velocity layer in sediments at a depth of about 2 km corresponds to Permian rocks.
Seismic P-wave velocity models of the crust (a) and upper mantle (b) of the East European Craton margin in northern Poland. The crustal model beneath the central station A0 of the “13 BB star” array (160 m a.s.l.) was extracted from the 3D seismic model for the area of Poland (Grad et al. 2016). The upper mantle model down to a depth of 300 km was extracted from the 2D model beneath profile P4 (at 412.5 km; Wilde-Piórko et al. 2010). The high velocity layer in sediments at a depth of about 2 km corresponds to the Permian rocks. The low-velocity layer (LVZ) at depths of 60–80 km is a lower lithosphere inhomogeneity, while the decreasing P-wave velocity at about 180–210 km corresponds to the lithosphere–asthenosphere boundary (LAB)
P-wave velocity model
In the Polish part of the EEC the seismic lithosphere thickness is about 200 km, while it is only 90 km south of TESZ in the Paleozoic platform (Wilde-Piórko et al. 2010). Till now, we had no deep seismic data in the area of the “13 BB star” array. So, we used a P-wave velocity model for the P4 profile, which was integrated from deep refraction investigations, receiver function, and P-residuals method. The mantle model down to a depth of 300 km was extracted from the 2D model beneath profile P4 (at 412.5 km; Wilde-Piórko et al. 2010) and is shown in Fig. 3b. The low-velocity layer (LVZ) at depths of 60–80 km is a lower lithosphere inhomogeneity. Similar LVZ were also observed in other areas of the EEC. Beneath Scania in the southern Baltic Shield, a relatively thin low-velocity layer was found 15 km below the Moho (Grad et al. 2014). It can be interpreted as small-scale lithospheric heterogeneity and can be explained by a model with a 16 km thick low-velocity layer with a P-wave velocity drop of 0.33 km/s. Such a velocity contrast is sufficient to explain the strong amplitudes of multiple reflections. Another decrease of the P-wave velocities in the model in Fig. 3b at a depth of about 180–200 km, corresponds to the lithosphere–asthenosphere boundary/zone (LAB).
S-wave velocity models from surface waves
The modeling of the seismic structure of the EEC marginal zone in northern Poland was performed using the data from the “13 BB star” experiment performed during 2013–2016. To calculate dispersion curves from Rayleigh surface waves, the Automated Surface-Wave Measuring System (ASWMS) package was used (Jin and Gaherty 2015). It allows for measuring the phase and amplitude of surface waves from raw seismic waveforms and uses these measurements to calculate phase velocity maps for different wave periods using the Eikonal and Helmholtz equation.
Before performing the phase velocity calculation, all recorded events were created and manually checked for quality. As a result, 135 good quality events were selected for all 13 stations and 478 events were recorded with good quality on over 50% of stations. Finally 5697 station–event pairs were selected as good quality.
For each station–event pair, raw seismic data was converted from daily mini-seed files to single SAC files with embedded event parameters (latitude, longitude, depth and magnitude). SAC data files were then imported to the ASWMS package and used for phase velocity calculations. The primary result of calculations are phase velocity maps for different wave periods. In this case maps were calculated for periods from 10 to 160 s every 5 s. Even though broadband seismometers used in the “13 BB star” experiment had a flat frequency response up to 120 s, they were able to provide frequency data within lower frequencies. Dispersion curves were prepared, with values taken from corresponding grid cells on all the maps. The final dispersion curve was obtained by averaging all the dispersion curves for each period and is shown as blue dots and a blue line in Fig. 4a, with a range based on minimal and maximal velocities. In this figure, numbers above the period values indicate an approximate depth in kilometers of the surface wave penetration.
Modeling of the upper mantle S-wave velocity structure below “13 BB star” array using dispersion curves of Rayleigh surface waves. a Experimental dispersion curve obtained by averaging all dispersion curves for each 5 s periods shown by blue dots; the thin lines show range of dispersion for all array stations. b A set of 20 starting models to explore the whole space of physically plausible solutions within a range of 4–5 km/s. The crustal structure derived from previous studies (Fig. 3a; Grad et al. 2016) is common to all models and partly frozen in inversion. c Results of linearized inversion for all 20 starting models. Colors correspond to the starting models. d Experimental curve (blue) compared to the synthetics computed from all final models (colors correspond to starting models). e A mean model (pink) and its standard deviation (yellow) calculated from the results obtained by inversion for all starting models. f A final (posterior) distribution of models obtained with rjMcMC inversion. The bright color indicates the high probability of Vs at a given depth. A prior distribution of Vs was uniform within a ± 20% range of the reference model consisting of the crust derived from previous studies (Fig. 3a; Grad et al. 2016) and homogeneous mantle (Vs = 4.69 km/s) down to a depth of 300 km. A total number of iterations was 2 × 106, but only the last 106 were considered as posterior. A light blue line is model calculated from the posterior distribution obtained with rjMcMC inversion. g Result of nonlinear Monte Carlo inversion (smooth model). h Model obtained by trial-and-error approach (green line; see text for more explanation). i Experimental curve (blue) compared to the synthetic results (green line) computed for the final model by trial-and-error approach
Four techniques were applied to solve the inverse problem for Rayleigh-wave dispersion: the iterative least-squares optimization of the linear problem, the trans-dimensional Monte Carlo method with unknown data uncertainty, the Monte Carlo Neighborhood Algorithm and the trial-and-error approaches.
-
Linearized damped least-squares inversion was performed with Computer Programs in the Seismology (CPS) package (Herrmann 2013). The minimized difference between model vectors in current and previous iteration was tuned with weighting a damping parameter. The minimized function expresses the trade-off between data misfit and model roughness. The linearized inversion is known for being trapped by local minima and therefore we considered the ensemble of starting models to explore the whole space of physically plausible solutions. In the starting model, the crustal structure was derived from previous studies (Grad et al. 2016). The mantle, in turn, had a different velocity for different models. The lowest and the highest mantle velocity was 4 and 5 km/s, respectively. The rest of the models had mantle velocities evenly spaced between these extreme values (Fig. 4b). The maximum depth was set to 300 km. In the inversion, a weight of 0.5 was assigned to all the crustal layers, and a weight 1.0 to all the mantle layers. In this way, modification of the crust throughout the inversion was inhibited. It is here referred to as a “freezing” of the crust. The optimum value of the weighting parameter, number of iterations (max 20), as well as other elements of inversion strategy were inferred via synthetic tests. The inversion for all 20 starting models was carried out (Fig. 4c) and mean model with standard deviation was calculated and are shown in Fig. 4e (Chrapkiewicz 2017). The corresponding dispersion curves for all 20 models are shown in Fig. 4d.
-
Trans-dimensional Monte Carlo inversion with reversible jump Markov chain Monte Carlo (rjMcMC) code by Bodin et al. (2012) was used to confirm/verify the results of the linearized inversion. It implements the Bayesian approach in case of the unknown dimension of model space and data uncertainty. A prior distribution of Vs was uniform within a ± 20% range of the reference model consisting of the crust derived from previous studies (Grad et al. 2016) and a homogeneous mantle (Vs = 4.69 km/s) down to a depth of 300 km. The convergence to the posterior distribution was investigated for various widths of proposal distributions and chain lengths. A total number of iterations was 2 × 106, but only the last 106 were considered as posterior (Chrapkiewicz 2017, 2018). The results, a mean (light blue) and its standard deviation calculated from the posterior distribution obtained with rjMcMC inversion, are shown in Fig. 4f. It is consistent with the results of linearized inversion (Fig. 4e) within the uncertainties (standard deviations).
-
The Monte Carlo Neighborhood Algorithm (MCNA) inversion described by Sambridge (1999), Mordret et al. (2014) and Lepore et al. (2018) was applied to the starting Rayleigh-wave phase velocity dispersion curve. As a starting model, we chose a layered 1D profile considering the thickness, the S-wave velocity, the density and the Poisson’s ratio as parameters. For each layer, the thickness, density and Poisson’s ratio were fixed. On the contrary, the S-wave velocity was assumed as a combination of gradient and constant trends within 4.7–4.9 km/s down to 300 km. As shown in the literature (Shapiro and Ritzwoller 2002), the starting model was prolonged down to 1000 km using the S-wave velocities from the iasp91 reference model (Kennett and Engdahl 1991). To find the solution of the inversion process, the MCNA involves a nonlinear iterative search technique to seek the global minimum of the error function without being influenced by the chosen starting model. Therefore, the final S-wave velocity models were evaluated by iterative inversions, comparing the dispersion curves with a group of theoretical ones belonging to the same population within a preset confidence limit (Maraschini and Foti 2010). The best model (Fig. 4g) was calculated by a weighted average over the final models, using the inverse of the values assumed by the error function as weighting factors.
-
The trial-and-error approach was employed to improve the best model, putting the Rayleigh-wave velocity variations and the S-wave velocity changes in a more local relation than using the MCNA. To that end, the starting dispersion curve was divided in several intervals whose periods ranged within 15–25 s. Then, the S-wave velocities of the best model were properly corrected at the corresponding depths to obtain the trial-and-error model shown in Fig. 4h. The dispersion curve corresponding to this last model was estimated using the CPS package described by Herrmann (2013). Therefore, the model was imported inside a flat, isotropic, constant velocity model: then, the related eigenfunctions were calculated. The average dispersion curve, shown in Fig. 4i, was evaluated as the product of the eigenfunctions and the relative differential operator.
The models which were obtained using the four techniques indicate similarities in S-wave velocity distribution with depth. The linearized damped least-squares inversion for a broad range of 20 starting models (Fig. 4b) gives a set of models (Fig. 4c) with very similar dispersion curves (Fig. 4d) and a relatively small standard deviation (Fig. 4e). Trans-dimensional Monte Carlo inversion (Fig. 4f, g), which used a huge number of iterations, is consistent with the results of the linearized inversion (Fig. 4e) with slightly larger uncertainties. In both inversions the final models are similar (Fig. 4e, g). The S-wave velocity with depth is changing smoothly, with higher velocities at depth ranges of about 50–100 km and 150–200 km. The experimental dispersion curve fits well in the period ranges of about 20–60 s and 120–160 s (Fig. 4d). However, more complex velocity models are needed to better describe the undulations of the dispersion curve in the period range 60–120 s. The solution is found using two other approaches, i.e., the Monte Carlo Neighborhood Algorithm (Fig. 4g) and the trial-and-error (Fig. 4h, i). In both results, the higher velocities at depth ranges of about 50–100 km and 150–200 km are more distinct. As a common feature in all four models, a S-wave velocity lowering begins in the depth range of 180–220 km, meaning that the low-velocity zone (LVZ) may be interpreted as a transition zone between lithosphere and asthenosphere.
Seismic velocity–density relations
The relationships between density and seismic velocities were investigated using velocity and density measurements under laboratory conditions (e.g., Birch 1961; Krasovsky 1981; Barton 1986; Christensen and Mooney 1995; Schön 1998), as well as in a simultaneous interpretation of seismic experimental data and gravity anomalies (e.g., Kozlovskaya et al. 2001, 2004; Krysiński et al. 2009).
The classical formula of Birch (1961) was obtained in rock samples under laboratory conditions for pressure of up to 10 kilobars:
in which ρ is density in g/cm3, Vp is the P-wave velocity in km/s, and m is the mean atomic weight of rock.
Gardner’s equation (Gardner et al. 1974) is widely used for sedimentary rocks (excluding evaporates and carbonaceous rocks) for the Vp velocity range of 1.5–6.1 km/s:
where ρ is density in g/cm3 and Vp is P-wave velocity in km/s.
The relationships between seismic velocity and density was investigated along a few thousand kilometers long seismic transects with the use of gravity anomalies. The linear relationship the for crystalline Precambrian crust in Central Europe was defined by Krysiński et al. (2009):
where density ρ is in g/cm3, and velocity Vp is in km/s.
A more complex relationship to convert the velocity to density in the crust was Brocher’s empirical formula (Brocher 2005):
where ρ is in g/cm3, and velocity Vp is in km/s.
The most universal density–velocity relations used in the joint seismic-gravity interpretation are the Nafe–Drake curves (Ludwig et al. 1970). Both ρ(Vp) and ρ(Vs) curves together with other relationships are shown in Fig. 5. In this figure, relations ρ(Vp) and ρ(Vs) for the mantle rocks extracted from the model PREM (Dziewonski and Anderson 1981) are also presented.
Relationships between P- and S-wave velocities and density. Empirical Nafe–Drake relation (Nafe and Drake 1963; Ludwig et al. 1970) represented by the solid red line is shown together with other global and regional relations. The green rectangle with green dot shows a range and an average value for the Tertiary and Quaternary sediments (e.g., Dąbrowski and Kaczkowska 1965; Dąbrowski 1971; Hawkins 2003; Harrison 2004). Relationships by Gardner et al. (1974) and Brocher (2005) are representative for sedimentary cover and crust. Crystalline crust of the old (Precambrian) platforms and cratons is well-described by relations of Krasovsky (1981), Sobolev and Babeyko (1994) and Krysiński et al. (2009). As a comparison, the empirical linear relationship known as Birch’s law (for mean atomic weight of rock m = 21 and m = 22) and global data from PREM model are shown (Birch 1961; Dziewonski and Anderson 1981)
The relationships connecting density to both P- and S-wave velocities are very seldom used to integrate seismic and gravity data, because the velocity models from seismic experiments are usually based upon an interpretation of P waves. The linear relationship between Vp, Vs and ρ for lithospheric rocks was presented in the petrophysical handbook for rocks and minerals (Dortman 1992):
These relationships between seismic velocities and density for rocks were tested for seismic data from the area of “13 BB star” and chosen densities are presented in the next chapter.
Constraints on the crust and upper mantle temperature, density and pressure
Temperature
Heat flow Q in the studied area of northern Poland is low (Fig. 1c). It is characteristic for the “thick crust” of the EEC as evident from the map of Q corrected for the paleoclimatic effect for the European continent by Majorowicz and Wybraniec (2011). The value of Q representative for the study was calculated within the 30 km radius circle for which an average value is Q = 46.3 mW/m2 (Fig. 2b). It is about two times lower than Q in the “thin crust” of the Variscan foreland area in SW Poland (Fig. 1c) supposedly caused by a higher mantle contribution (Majorowicz 2004). Previous estimates of the geotherms and thermal LAB depth revealed the depth of the thermal lithosphere (peridotite solidus) of about 100 km under the Variscan foreland part of the Paleozoic Platform, and more than 200 km below the East European Craton (Majorowicz et al. 2003). In the Inner Variscan zone Puziewicz et al.’s (2012) study of geotherms constrained by the petrological studies of mantle xenoliths in the region of the amphibolite Niedźwiedź Massif (Fore-Sudetic Block in NE Bohemian Massif), suggested a lithospheric thickness of about 80 km.
Temperature-depth curves of the EEC for the study area were calculated for the average heat flow Q = 46.3 mW/m2 and for two models of heat generation. To calculate Geotherm 1, we take an average heat generation of A = 1.12 µW/m3 from data of radiogenic heat production from measured U235 (ppm), Th232 (ppm) and K40 (%) contents in 22 core samples from deep wells penetrating depths below the Precambrian basement in the N-NE Poland—these can be found in Table 1 in Majorowicz (1984). Both the average Q = 46.3 mW/m2 and the average A = 1.12 µW/m3 are below the corresponding continental averages from the relationship between Q vs. age, and A vs. age (Fig. 6; compilation from Jessop et al. 1976; Majorowicz and Jessop 1981; Majorowicz 1984). The model of radiogenic heat production with depth A(h) and calculated heat flow Q(h) are shown in Fig. 7 (left panel and middle panel, respectively).
A comparison of average values of the continental heat flow Q (a) and average rates of the radiogenic heat A (b) for tectonic units of different ages. Gray ellipses and black dots with numbers show the ranges and values of the heat flow (Jessop et al. 1976; Majorowicz and Jessop 1981). Yellow boxes indicate the heat flow data averaged in groups according to radiometric crustal age, and the mean heat flow values in each group are plotted as yellow crosses (Morgan 1984). For the heat generation: CM Cenozoic–Mesozoic orogenic areas, H Hercynian areas, C Caledonian areas, LPr Late Precambrian platforms, NEP Precambrian platform of NE Poland, EPr Early Precambrian platforms, Ar Archean areas (Majorowicz 1984). Averaged values of Q and A applied in this paper for the area of “13 BB star” array are shown by big blue dots with lines of age range (Majorowicz 1984)
Thermal characteristic of the East European Craton: heat generation A, heat flow Q and temperature-depth curves. Heat generation is representative for the EEC in northern Poland (Majorowicz 1984). The short green line measures the temperature in the Prabuty IG-1 well (Majorowicz et al. 2003). The Geotherm 1 and Geotherm 2 lines are calculated for the area of “13 BB star” array (compare Fig. 2b). For the comparison, gray lines show worldwide continental geotherms for Q = 30, 40, 50 and 60 mW/m2 (Pollack and Chapman 1977). The dark blue line is geotherm for the Baltic Shield (Maj 1991). The orange line shows enriched peridotite solidus (MacKenzie and Canil 1999; Hirschmann 2000)
We also construct Geotherm 2 assuming the same average Q and different model of A(h). We assume higher A in the granitic upper crystalline crust. Granitic rock for which A was determined are from measured radiogenic elements from 6 cores in NE Poland (Majorowicz 2004). Heat generation A varies in the range 1.3–3.9 µW/m3 with an average 2.3 µW/m3. In comparison to that, heat generation A in the sediments, middle crust and lower crust were reduced to a lower range of A values (Hyndman and Lewis 1999; Hyndman et al. 2009). Mantle A = 0.02 µW/m3 (Rudnick et al. 1998) are assumed for both models. Assumed upper crustal thermal conductivity k = 2.7 W/mK is for ambient conditions. We account for the dependence of k on pressure and temperature. We have used a depth (pressure)–temperature correction by Chapman and Furlong (1992). Mantle k is 2.8 W/mK from Hyndman and Lewis (1999). The mantle adiabat adopted here (Fig. 7) from MacKenzie and Canil (1999) determines the depth to the thermal LAB which varies from 180 km for Geotherm 1 to 230–240 km for Geotherm 2 (Fig. 7, right panel). As a comparison, we show (Fig. 7) the worldwide continental geotherms (Pollack and Chapman 1977) which are based on the relationship between the continental heat flow Q and reduced heat flow Qr, i.e., the heat flow below the high radiogenic upper crust; Qr is about 60% of the surface heat flow Q. We also show the geotherm for the Baltic Shield calculated by Maj (1991), which is also consistent with the data of Kukkonen and Peltonen (1999) obtained from xenolith-controlled geotherm for the central Fennoscandian Shield. Our Geotherms 1 and 2 are well within these bounds. Compared with mantle adiabat (MacKenzie and Canil 1999; Hirschmann 2000) Geotherm 1 estimates LAB close to 180 km, while Geotherm 2 shows that LAB is close to 220 km.
Density
The density distribution with depth is needed for the determination of pressure change with depth. For the crust, from the topography down to the Moho, the density could be determined from the known Vp velocity model (Grad et al. 2016), using the relationship between velocity and density. For the central station A0, the seismic model is shown in Fig. 3a, and the thickness of Tertiary and Quaternary sediments is here only 260 m with velocities 1.8–1.9 km/s, so we used a constant density of ρTQ = 1.9 g/cm3. This density was found as an average for the Polish part of the EEC (Dąbrowski and Kaczkowska 1965; Dąbrowski 1971), as well as in other areas (e.g., Hawkins 2003; Harrison 2004). For the sediments down to a depth of 6 km, we used Gardner’s formula (2) which is widely accepted as being representative for sedimentary cover (Gardner et al. 1974; Sheriff and Geldart 1995). For the Precambrian crystalline crust we used a linear relationship (3) defined for Central Europe (Krysiński et al. 2009). This relationship describes well the crustal density and is very close to other relations for the old cratons (Fig. 5; see e.g., Krasovsky 1981; Sobolev and Babeyko 1994), and fits to the classical Birch’s law for mean atomic weight of rock m = 21–22 (Birch 1961).
We calculated the mantle densities in two ways: (a) using the velocity–density relationships, and (b) from the local geotherm using an independent technique according to Poudjom Djomani et al. (2001). The results are shown in Fig. 8.
Compiled geophysical data at the SW margin of the East European Craton. a Density–depth relations for described approaches for the area of the “13 BB star” and P4 profile. b Average density with standard deviation ± 3σ. c Pressure–depth relationships calculated as a hydrostatic pressure for the crustal and upper mantle rock densities. d Relative pressure compared to pressure calculated for the model with constant density 3.3 g/cm3. e The average relative pressure with standard deviation ± 3σ. f Geotherm 1 and Geotherm 2 (Fig. 7) and average geotherm with ± 100 °C. g Model of the Vp velocity (see Fig. 3b) with assumed ± 0.15 km/s tolerance band. h S-wave velocities obtained by linear inversion technique, the trans-dimensional Monte Carlo method, and trial-and-error approaches (see Fig. 4e, g, h). i The average Vs velocity with standard deviation ± 3σ. See also legend for details description. ND Nafe–Drake
-
(a)
Initial data were P-wave velocity compiled for the mantle from deep seismic refraction, P-residuals, and receiver function (Wilde-Piórko et al. 2010). The P-wave velocity model is shown in Fig. 3b. For conversion to density we used the ρ(Vp) Nafe–Drake relation (Fig. 5). For the average Vs models from surface waves (Fig. 4) we used the ρ(Vs) Nafe–Drake relation. Finally, both Vp and Vs velocities were used in formula (5) for density determination.
-
(b)
The Mantle densities were also calculated from the average local geotherm (Fig. 7) according to the method used by Poudjom Djomani et al. (2001). The reference density at the temperature of 20 °C depends on age. For the Proterozoic mantle the density is 3.35 ± 0.02 g/cm3. The change of density with temperature is described by the formula:
$${\rho _T}={\rho _{{\text{2}}0}} - ({\rho _{{\text{2}}0}}T\alpha ),$$(6)where ρT is density at temperature T, ρ20 is reference density at the temperature of 20 °C, and α is defined as:
$$\alpha ={\alpha _0}+{\alpha _{\text{1}}}T+{\alpha _{\text{2}}}{T^{ - {\text{2}}}}.$$(7)
The constant values for the Proterozoic mantle are: α0 = 0.27014 × 10−4, α1 = 1.05945 × 10−8, and α2 = − 0.1243 (see Table 2 in Poudjom Djomani et al. 2001). The densities determined from formulas (6) and (7) it should be corrected for pressure by the linear formula:
where δρ is density correction, β = 1/k parameter (for Proterozoic k = 130), and P is pressure in GPa. The final formula for density is:
Density–depth relations for the approaches described above are compiled in Fig. 8a.
Pressure
Apart from temperature, in the depth range of a few hundred kilometers, the pressure effect for seismic velocity and density should be taken into consideration. For the investigated area we applied pressure–depth relationships calculated as a hydrostatic pressure for the crust and upper mantle density curves (Fig. 8c–e), using an average value of gravity force 9.81 m/s2. Density profiles described in “Density” were used to calculate pressure with a depth starting with 101,325 Pa at the topography level (160 m a.s.l in this case).
Geophysical data set
Density and pressure are necessary for estimation of mineral rock composition. They are an input to the Hacker and Abers (2004) spreadsheet. Summary of physical conditions, seismic velocities and mineral compositions for the upper mantle of the East European Craton margin beneath “13 BB star” array is compiled in Table 1. All geophysical data with expected tolerance/accuracy are compiled in Fig. 8.
The density–depth relations at the SW margin of East European Craton (Fig. 8a) were determined using Nafe–Drake relations. For the area of the P4 profile, the density was determined from the P-wave velocity model (see Fig. 1a for location and Fig. 3b for the model). This area is located about 200 km from the “13 BB star” array, it gives independent information about the Vp seismic structure of the upper mantle. For the average Vs model from surface waves (Fig. 4e, g, h) another density profile from the Nafe–Drake relation was determined. The third density profile was determined from both P- and S-wave models using formula (5). The change of density with temperature was calculated from formulas (6–9). All four curves are compared with model PREM (Dziewonski and Anderson 1981) and their average with standard deviation ± 3σ is shown in Fig. 8b.
The pressure–depth relationships were calculated in a hydrostatic approach based on crustal and mantle relationships between the density and seismic velocities (Fig. 8c). The pressure increases with depth approximately linearly to about 10 GPa at a depth of 300 km. In this scale, the pressure differentiation for different density–depth models is not visible, and all plotted lines are in practice within the line thickness. Therefore, in Fig. 8d we plotted relative pressure showing deflection from the model with a density of 3.3 g/cm3. The average relative pressure with standard deviation ± 3σ is shown in Fig. 8e.
The average geotherm (from Geotherm 1 and Geotherm 2; Fig. 7) for the area of “13 BB star” array is plotted with a ± 100 °C band (Fig. 8f). At a depth of 300 km the average temperature is about 1750 °C, and “cold” and “warm” geotherms are just in ± 100 °C band.
The seismic model of the P-wave velocity (Fig. 3b) was taken from profile P4 located about 200 km SE from the “13 BB star” array, and is shown in Fig. 8f with an assumed tolerance band of ± 0.15 km/s. Three S-wave velocity models for the study area around the A0 station, obtained using three different inversion approaches (Fig. 4e, g, h), are represented in Fig. 8h. The S-wave average velocity from the three models with standard deviation ± σ is shown in Fig. 8i. We observed that all the three S-wave velocity models fall within one standard deviation of the average velocity, meaning that the models are generally consistent, even though dissimilar local trends are present. The average velocity is around 4.7 km/s just under the Moho, which then increases up to 4.8 km/s between ~ 60 and ~ 90 km, with a further increase up to 4.9 km/s between ~ 170 and ~ 200 km. The mean depth of the LAB can be identified at ~ 200 km. The final LAB depth is the average of the LAB depth from the pink S-wave velocity model (~ 180 km), the LAB depth from the red model (~ 220 km), and the LAB depth from the green model (~ 200 km). The S velocity decreases from 4.9 to 4.75 km/s at the LAB depth.
Discussion
Various rocks have similar seismic velocities, which is a major problem in the geological interpretation of seismic data. The range of potential rocks can be restricted, however, if the tectonic context is properly defined, because this implies the scheme of geological evolution of the discussed site and in consequence the rocks which occur at various structural levels.
Our model refers to the SW margin of the Proterozoic East European Craton adjoining the Trans-European Suture Zone (Fig. 1), and the sampled depth profile was chosen beneath the central station of the seismic array “13 BB star”. The seismic Vs data (Fig. 8i) show the occurrence of mantle region with Vs velocity increasing from Moho to a ca. 90 km depth, underlain by a layer of small, steady velocity increase 90–180 km. Beneath, at a depth between 180 and 200 km, Vs velocity increases significantly. At a depth greater than 200 km the zone of steady velocity decrease occurs. The latter corresponds to asthenosphere, which is suggested by an intersection of proposed geotherms with the mantle adiabat (Fig. 7).
The geotherm calculated for the “13 BB star” region is located between those typical of the Proterozoic and Phanerozoic regions (see e.g., Glebovitsky et al. 2004). The eastern margin of EEC in the northern part of Poland and adjoining part of the Baltic Sea and Scania is characterized by the LAB dipping steeply to the NE from about 120 km to around 200 km (Wilde-Piórko et al. 2010; Plomerová and Babuška 2010). The Phanerozoic nature of the lithospheric mantle beneath Scania is demonstrated by xenoliths occurring in Jurassic (177 Ma; Tappe et al. 2016) basanites. Rehfeldt et al. (2007) describe the mantle xenolith suite, which is characteristic for Phanerozoic and suggests metasomatic rejuvenation. Since the Scania lavas probably come from asthenosphere at 90–120 km depths (Tappe et al. 2016), the Scania xenoliths show that the lithospheric mantle was only in the spinel facies of mantle peridotites in the time of volcanism. The spinel Cr# of 0.1–0.2 (Rehfeldt et al. 2007) thus suggests that the LAB was located at 70–85 km (assuming a temperature of 1000–1100 °C; Klemme and O’Neill 2000, and compilation of Xiong et al. 2015). This LAB depth is significantly shallower from that indicated by our seismic data. This can be explained by the location of our observational point which is more to the NE on the LAB slope of EEC. Alternatively, the asthenosphere adjoining the craton was cooled from Jurassic to recent temperatures, and the Vs maximum at ca. 90–120 km is the fossil LAB zone from the times of Jurassic rifting.
We have tried to fit the seismic velocities at temperatures indicated by the proposed geotherm and possible mantle peridotite compositions, using the spreadsheet proposed by Hacker and Abers (2004). However, the reasonable fit for Vs was obtained only for the uppermost mantle (down to ca. 25 km below Moho). Immediately below Moho the harzburgite layer was proposed by Puziewicz et al. (2017). Below that (Fig. 9) the geologically reasonable rock compositions yield too slow seismic velocities. Our calculations show that temperature variations within ± 100 °C of the proposed geotherm have little effect on seismic velocities. The example of rock composition used for modeling (relatively rich in the garnet one, to increase the velocities) is shown in Fig. 9. We suggest that the misfit between observed Vs values and the reasonable rocks compositions is the result of the isotropic approach to the problem. Both the Scania mantle xenoliths descriptions of Rehfeldt et al. (2007) and large-scale models of Plomerová and Babuška (2010) show the anisotropy of mantle peridotites, which supposedly affects significantly our seismic velocity measurements.
Summary of composition modeling. Diagrams show density, Vp velocity, Vs velocity, and an example of lithospheric mantle compositions used for model calculation by Hacker and Abers (2004) spreadsheet. The primitive mantle after Johnson et al. (1990) assumed to contain no melt. The calculated density, Vp velocity and Vs velocity are shown by thick green lines, together with dashed lines for temperature − 100 °C (blue) and temperature + 100 °C (red). Below LAB density, Vp velocity, Vs velocity shown by green broken lines are calculated for the peridotite solidus temperature. Observations under “13 BB star” are gray
In the continental scale, the area of the “13 BB star” array is located between the large Proterozoic and Phanerozoic regions. A large differentiation of the seismic structure in the mantle was shown by Hoernle et al. (1995). This model is consistent with recent models (Fig. 10) of relative dVs/Vs anomalies compared to the PREM reference model (Dziewonski and Anderson 1981). Model S2.9EA (Kustowski et al. 2008) is a global model parametrized laterally using spherical splines with about 11.5° spacing and with a higher resolution in the upper mantle beneath Eurasia, with a spacing of about 2.9°. Model SAW642ANb (Panning and Romanowicz 2006) is a global radially anisotropic shear velocity model. For the EEC margin all models show high Vs velocities (3–4%) down to a depth of 200 km.
Previous regional models of the Vs velocity in the mantle down to a depth of 400 km for the transition across the SW margin of the East European Craton—for location see orange dotted line in Fig. 1a. Models are compared to PREM reference model (Dziewonski and Anderson 1981). Relative anomalies of dVs/Vs are shown for a model S2.9EA (Kustowski et al. 2008) and for b model SAW642ANb (Panning and Romanowicz 2006). Moho depth was extracted from the Moho depth map of the European plate (Grad et al. 2009)
Conclusions
Compilation of available geophysical data in the SW margin of the East European Craton gives a characteristic of the lower lithosphere and asthenosphere down to a depth of 300 km. The seismic P- and S-wave velocities were obtained using different seismic techniques: P-residuals of first arrivals from teleseismic earthquakes, P-wave receiver function and Rayleigh surface wave dispersion curves. Together with geotherms, density and pressure change with depth, they create a geophysical data set necessary for estimating the composition of mineral rock (Fig. 8). For that we used the Hacker and Abers (2004) spreadsheet. The reasonable fit for S velocities was obtained only for the uppermost mantle, down to ca. 25 km below Moho. Below this, the geologically reasonable rock compositions yield seismic velocities that are too slow (Fig. 9). The test of temperature effect for petrological modeling shows that temperature variations in the relatively large range ± 100 °C are not significant, which indicates that rock compositions have a dominant effect on modeling results.
Beneath the “13 BB star” area, the Vs velocities area is high, which is typical for mantle velocities beneath the old Precambrian cratons. However, here they are even 0.1–0.2 km/s higher. Our petrological interpretation shows that the isotropic approach is not sufficient as an explanation and that the seismic structure beneath the “13 BB star” array should be investigated in detail using the anisotropic approach.
References
Barton PJ (1986) The relationship between seismic velocity and density in the continental crust—a useful constraint? Geophys J R Astron Soc 87:195–208
Birch F (1961) The velocity of compressional waves in rocks to 10 kilobars. Part 2. J Geophys Res 66(7):2199–2224
Bodin T, Sambridge M, Tkalčić H, Arroucau P, Gallagher K, Rawlinson N (2012) Transdimensional inversion of receiver functions and surface wave dispersion. J Geophys Res 117:1–24
Bogdanova SV, Pashkevich IK, Gorbatschev R, Orlyuk MI (1996) Riphean rifting and major Palaeoproterozoic boundaries in the East European Craton: geology and geophysics. Tectonophysics 268:1–21
Bogdanova S, Gorbatschev R, Grad M, Janik T, Guterch A, Kozlovskaya E, Motuza G, Skridlaite G, Starostenko V, Taran L, EUROBRIDGE and POLONAISE Working Groups (2006) EUROBRIDGE: new insight into the geodynamic evolution of the East European Craton. In: Gee DG, Stephenson RA (eds) European lithosphere dynamics, Memoirs, vol 32. Geological Society, London, pp 599–625
Bogdanova S, Gorbatschev R, Skridlaite G, Soesoo A, Taran L, Kurlovich D (2015) Trans-Baltic Palaeoproterozoic correlations towards the reconstruction of supercontinent Columbia/Nuna. Prec Res 259:5–33
Brocher TM (2005) Empirical relations between elastic wavespeeds and density in the Earth’s crust. Bull Seismol Soc Am 95(6):2081–2092
Chapman DS, Furlong KP (1992) Thermal state of the continental lower crust. In: Fountain DM, Arculus R, Kay KW (eds) Continental lower crust. Elsevier, Amsterdam, pp 179–199
Chrapkiewicz K (2017) Joint inversion of receiver function and dispersion curves. Master Thesis at Faculty of Physics, University of Warsaw (in Polish with English abstract)
Chrapkiewicz K, Wilde-Piórko M, Polkowski M, Grad M (2018) Resolution analysis of joint inversion of seismic receiver function and surface wave dispersion curves in the “13 BB Star” experiment. Solid Earth (submitted)
Christensen NI, Mooney WD (1995) Seismic velocity structure and composition of the continental crust: a global view. J Geophys Res 100(B6):9761–9788. https://doi.org/10.1029/95JB00259
Cymerman Z (2007) Does the Mazury dextral shear zone exist? Prz Geol 55:157–167 (in Polish with English abstract)
Dąbrowski A (1971) Physical features of rocks in the Podlasie Depression. Geol Q 15(2):442–464 (in Polish with English abstract)
Dąbrowski A, Kaczkowska Z (1965) Map of mean stratal densities of the formations occurring in Poland above sea level. Geol Q 9(1):203–215 (in Polish with English abstract)
Dadlez R (2006) The Polish Basin-relationship between the crystalline, consolidated and sedimentary crust. Geol Q 50(1):43–58
Dadlez R, Grad M, Guterch A (2005) Crustal structure below the Polish Basin: is it composed of proximal terranes derived from Baltica? Tectonophysics 411:111–128. https://doi.org/10.1016/j.tecto.2005.09.004
Dortman NB (ed) (1992) Petrophysics. A handbook. Book 1: rocks and minerals. Nedra, Moscow (in Russian)
Dziewonski A, Anderson D (1981) Preliminary reference Earth model. Phys Earth Planet Inter 25:297–356
Franke W (2014) Topography of the Variscan orogen in Europe: failed-not collapsed. Int J Earth Sci 103:1471–1499
Gardner GHF, Gardner LW, Gregory AR (1974) Formation velocity and density—the diagnostic basics for stratigraphic traps. Geophysics 39:770–780
Geissler WH, Sodoudi F, Kind R (2010) Thickness of the central and eastern European lithosphere as seen by S receiver functions. Geophys J Int 181(2):604–634
Glebovitsky VA, Nikitina LP, Khiltova VY, Ovchinnikov NO (2004) The thermal regimes of the upper mantle beneath Precambrian and Phanerozoic structures up to the thermobarometry data of mantle xenoliths. Lithos 74:1–20. https://doi.org/10.1016/j.lithos.2003.03.001
Grad M, Keller GR, Thybo H, Guterch A, POLONAISE Working Group (2002) Lower lithospheric structure beneath the Trans-European Suture Zone from POLONAISE ‘97 seismic profiles. Tectonophysics 360:153–168
Grad M, Tiira T, ESC Working Group (2009) The Moho depth map of the European plate. Geophys J Int 176:279–292. https://doi.org/10.1111/j.1365-246X.2008.03919.x
Grad M, Tiira T, Olsson S, Komminaho K (2014) Seismic lithosphere–asthenosphere boundary beneath the Baltic Shield. GFF 136:581–598
Grad M, Polkowski M, Wilde-Piórko M, Suchcicki J, Arant T (2015) Passive seismic experiment “13 BB star” in the margin of the East European Craton, Northern Poland. Acta Geophys 63:352–373
Grad M, Polkowski M, Ostaficzuk SR (2016) High-resolution 3D seismic model of the crustal and uppermost mantle structure in Poland. Tectonophysics 666:188–210. https://doi.org/10.1016/j.tecto.2015.10.022
Hacker BR, Abers GA (2004) Subduction Factory 3: an excel worksheet and macro for calculating the densities, seismic wave speeds, and H2O contents of minerals and rocks at pressure and temperature. Geochem Geophys Geosyst 5(1):Q01005
Harrison N (2004) Gravity, radar and seismic investigations to help determine geologic, hydrologic, and biologic relations in the Nyack Valley, Northwestern Montana, Master’s thesis at University of Montana
Hawkins C (2003) Imaging the shallow subsurface using ground penetrating radar at the Nyack Floodplain, Montana. Master’s thesis at University of Montana
Herrmann RB (2013) Computer programs in seismology: An evolving tool for instruction and research. Seismol Res Lett 84:1081–1088
Hirschmann MM (2000) Mantle solidus: experimental constraints and the effects of peridotite composition. Geochem Geophys Geosyst 1:2000GC000070
Hoernle K, Zhang YS, Graham D (1995) Seismic and geochemical evidence for large-scale mantle upwelling beneath the eastern Atlantic and western and central Europe. Nature 374:34–39. https://doi.org/10.1038/374034a0
Hyndman R, Lewis TJ (1999) Geophysical consequences of the Cordillera-Craton thermal transition in southwestern Canada. Tectonophysics 306:397–422
Hyndman RD, Currie CA, Mazzotti S, Frederiksen A (2009) Temperature control of continental lithosphere elastic thickness, Te vs. Vs. Earth Planet Sci Lett 277:539–548
Janik T, Grad M, Guterch A, Dadlez R, Yliniemi J, Tiira T, Gaczyński E, CELEBRATION 2000 Working Group (2005) Lithospheric structure of the Trans-European Suture Zone along the TTZ and CEL03 seismic profiles (from NW to SE Poland). Tectonophysics 411:129–155
Janutyte I, Majdanski M, Voss PH, Kozlovskaya E, PASSEQ Working Group (2015) Upper mantle structure around the Trans-European Suture Zone obtained by teleseismic tomography. Solid Earth 6:73–91. https://doi.org/10.5194/se-6-73-2015
Jessop AM, Habart MA, Sclater JG (1976) The world heat flow data collection 1975. Geotherm Serv Can Geotherm Ser 50:55–77
Jin G, Gaherty JB (2015) Surface wave phase-velocity tomography based on multichannel cross-correlation. Geophys J Int 201(3):1383–1398. https://doi.org/10.1093/gji/ggv079
Johnson KTM, Dick HJB, Shimizu N (1990) Melting in the oceanic upper mantle: an ion microprobe study of diopsides in abyssal peridotites. J Geophys Res 95(B3):2661–2678
Kennett BLN, Engdahl ER (1991) Travel times for global earthquake location and phase identification. Geophys J Int 105:429–465
Klemme S, O’Neill HSC (2000) The near-solidus transition from garnet lherzolite to spinel lherzolite. Contrib Miner Pet 138:237–248
Knapmeyer-Endrun B, Krueger F, Geissler WH, PASSEQ Working Group (2017) Upper mantle structure across the Trans-European Suture Zone imaged by S-receiver function. Earth Planet Sci Lett 458:429–441
Kozlovskaya E, Karatayev G, Yliniemi J (2001) Lithosphere structure along the northern part of EUROBRIDGE in Lithuania; results from integrated interpretation of DSS and gravity data. Tectonophysics 339:177–191
Kozlovskaya E, Janik T, Yliniemi J, Karatayev G, Grad M (2004) Density–velocity relationship in the upper lithosphere obtained from P- and S-wave velocity models along the EUROBRIDGE’97 seismic profile and gravity data. Acta Geophys Pol 52:397–424
Krasovsky SS (1981) Reflection of continental-type crustal dynamics in the gravity field. Naukova Dumka, Kiev (in Russian)
Krysiński L, Grad M, Wybraniec S (2009) Searching for regional crustal velocity–density relations with the use of 2-D gravity modelling—Central Europe case. Pure Appl Geophys 166:1913–1936. https://doi.org/10.1007/s00024-009-0526-x
Kukkonen IT, Peltonen P (1999) Xenolith-controlled geotherm for the central Fennoscandian Shield: implications for lithosphere–asthenosphere relations. Tectonophysics 304:301–315
Kustowski B, Ekström G, Dziewoński AM (2008) The shear-wave velocity structure in the upper mantle beneath Eurasia. Geophys J Int 174:978–992. https://doi.org/10.1111/j.1365-246X.2008.03865.x
Lepore S, Polkowski M, Grad M (2018) Crustal S wave velocity below the East European Craton in northern Poland from the inversion of ambient noise. Int J Earth Sci. https://doi.org/10.1007/s00531-018-1587-9
Ludwig JF, Nafe JE, Drake CL (1970) Seismic refraction. In: Maxwell AE (ed) The sea, vol 4. Wiley Inc, New York, pp 53–84
MacKenzie JM, Canil D (1999) Composition and thermal evolution of cratonic mantle beneath the central Archean Slave Province, NWT, Canada. Contrib Miner Pet 134:313–324. https://doi.org/10.1007/s004100050487
Maj S (1991) Geothermal gradients in the Baltic Shield lithosphere. Acta Geophys Pol 47(4):411–422
Majorowicz J (1984) Problems of tectonic interpretation of geothermal field distribution in the platform areas of Poland. Publ Inst Geophys Polish Acad Sci A 13(160):149–166
Majorowicz JA (2004) Thermal lithosphere across the Trans-European suture zone in Poland. Geol Q 48(1):1–14
Majorowicz J, Jessop A (1981) Regional heat flow patterns in the Western Canadian Sedimentary Basin. Tectonophysics 74(3–4):209–238
Majorowicz J, Wybraniec S (2011) New terrestrial heat flow map of Europe after regional paleoclimatic correction application. Int J Earth Sci 100(4):881–887
Majorowicz J, Čermak V, Šafanda J, Krzywiec P, Wróblewska M, Guterch A, Grad M (2003) Heat flow models across the Trans-European suture zone in the area of the POLONAISE’97 seismic experiment. Phys Chem Earth 28:375–391
Maraschini M, Foti S (2010) A Monte Carlo multimodal inversion of surface waves. Geophys J Int 182:1557–1566. https://doi.org/10.1111/j.1365-246X.2010.04703.x
Mazur S, Mikołajczak M, Krzywiec P, Malinowski M, Buffenmyer V, Lewandowski M (2015) Is the Teisseyre–Tornquist Zone an ancient plate boundary of Baltica? Tectonics 34:2465–2477
Meier T, Soomro RA, Viereck L, Lebedev S, Behrmann JH, Weidle C, Cristiano L, Hanemann R (2016) Mesozoic and Cenozoic evolution of the Central European lithosphere. Tectonophysics 692:58–73
Mordret A, Landès M, Shapiro NM, Singh SC, Roux P (2014) Ambient noise surface wave tomography to determine the shallow shear velocity structure at Valhall: depth inversion with a neighbourhood algorithm. Geophys J Int 198:1514–1525
Morgan P (1984) The thermal structure and thermal evolution of the continental lithosphere. In: Pollack HN, Murphy VR (eds) Structure and evolution of the continental lithosphere. Physics and chemistry of the Earth, vol 15. Pergamon Press, Oxford, pp 107–193
Nafe JE, Drake CL (1963) Physical properties of marine sediments. In: Hill MN (ed) The sea, vol 3. Interscience Publishers, New York, pp 794–815
Narkiewicz M, Grad M, Guterch A, Janik T (2011) Crustal seismic velocity structure of southern Poland: preserved memory of a pre-Devonian terrane accretion at the East European Platform margin. Geol Mag 148:191–210. https://doi.org/10.1017/S001675681000049X
Panning MP, Romanowicz BA (2006) A three dimensional radially anisotropic model of shear velocity in the whole mantle. Geophys J Int 167:361–379. https://doi.org/10.17611/DP/10131202
Plomerová J, Babuška V (2010) Long memory of mantle lithosphere fabric—European LAB constrained from seismic anisotropy. Lithos 120:131–143. https://doi.org/10.1016/j.lithos.2010.01.008
Pollack HN, Chapman DS (1977) Mantle heat flow. Earth Planet Sci Lett 34:174–184
Poudjom Djomani YH, O’Reilly SY, Griffin WL, Morgan P (2001) The density structure of subcontinental lithosphere through. Earth Planet Sci Lett 184:605–621
Pożaryski W, Dembowski Z (1983) Geological map of Poland and neighboring countries without Cenozoic, Mesozoic and Permian deposits (1:1 000 000). Geological Institute, Warsaw
Puziewicz J, Czechowski L, Krysiński L, Majorowicz J, Matusiak-Małek M, Wróblewska M (2012) Lithospheric thermal structure at the eastern margin of the Bohemian Massif: a case petrological and geophysical study of the Niedźwiedź amphibolite massif (SW Poland). Int J Earth Sci 101:1211–1228
Puziewicz J, Polkowski M, Grad M (2017) Geophysical and petrological modeling of the lower crust and uppermost mantle in the Variscan and Proterozoic surroundings of the Trans-European Suture Zone in Central Europe. Lithos 276:3–14. https://doi.org/10.1016/j.lithos.2016.06.013
Rehfeldt T, Obst K, Johansson L (2007) Petrogenesis of ultramafic and mafic xenoliths from Mesozoic basanites in southern Sweden: constraints from mineral chemistry. Int J Earth Sci 96:433–450
Rudnick RI, McDonough WF, O’Conell RJ (1998) Thermal structure, thickness and composition of continental lithosphere. Chem Geol 145:399–415
Sambridge M (1999) Geophysical inversion with a neighbourhood algorithm—I. Searching a parameter space. Geophys J Int 138:479–494
Schön JH (1998) Physical properties of rocks: fundamentals and principles of petrophysics. Pergamon, The Netherlands
Shapiro NM, Ritzwoller MH (2002) Monte-Carlo inversion for a global shear-velocity model of the crust and upper mantle. Geophys J Int 151:88–105
Sheriff RE, Geldart LP (1995) Exploration seismology, 2nd edn. Cambridge University Press, Cambridge
Skridlaitė G, Bogdanova S, Page L (2006) Mesoproterozoic events in eastern and central Lithuania as recorded by 40Ar/39Ar ages. Baltica 19:91–98
Sobolev SV, Babeyko AY (1994) Modelling of mineralogical composition, density and elastic wave velocities in anhydrous magmatic rocks. Surv Geophys 15:515–544
Soomro RA, Weidle C, Cristiano L, Lebedev S, Meier T, PASSEQ Working Group (2016) Phase velocities of Rayleigh and Love waves in central and northern Europe from automated, broad-band, interstation measurements. Geophys J Int 204:517–534. https://doi.org/10.1093/gji/ggv462
Tappe S, Smart KA, Stracke A, Romer RL, Prelević D, van den Bogaard P (2016) Melt evolution beneath a rifted craton edge: 40Ar/39Ar geochronology and Sr–Nd–Hf–Pb isotope systematics of primitive alkaline basalts and lamprophyres from the SW Baltic Shield. Geochim Cosmochim Acta 173:1–36
Voss P, Mosegaard K, Gregersen S, Working Group TOR (2006) The Tornquist Zone, a north east inclining lithospheric transition at the south western margin of the Baltic Shield: revealed through a nonlinear teleseismic tomographic inversion. Tectonophysics 416:151–166
Wessel P, Smith WHF (1991) Free software helps map and display data. EOS Trans Am Geophys Union 72(41):445–446
Wessel P, Smith WHF (1998) New, improved version of Generic Mapping Tools released. EOS Trans Am Geophys Union 79(47):579
Wilde-Piórko M, Grad M, TOR Working Group (2002) Crustal structure variation from the Precambrian to Palaeozoic platforms in Europe imaged by the inversion of teleseismic receiver functions—project TOR. Geophys J Int 150:261–270
Wilde-Piórko M, Świeczak M, Grad M, Majdański M (2010) Integrated seismic model of the crust and upper mantle of the Trans-European Suture zone between the Precambrian craton and Phanerozoic terranes in Central Europe. Tectonophysics 481:108–115. https://doi.org/10.1016/j.tecto.2009.05.002
Winchester JA, PACE TMR Network Team ((2002) Palaeozoic amalgamation of Central Europe: new results from recent geological and geophysical investigations. Tectonophysics 360:5–21
Xiong Q, Griffin WL, Zheng J-P, O’Reilly SY, Pearson N (2015) Episodic refertilization and metasomatism of Archean mantle: evidence from an orogenic peridotite in North Qaidam (NE Tibet, China). Contrib Miner Pet 169:31–51
Ziegler PA (1990) Geological atlas of western and central Europe, 2nd edn. Shell Internationale Petroleum Maatschappij BV, Den Haag
Zielhuis A, Nolet G (1994) The deep seismic expression of an ancient plate boundary in Europe. Science 265:79–81
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Grad, M., Puziewicz, J., Majorowicz, J. et al. The geophysical characteristic of the lower lithosphere and asthenosphere in the marginal zone of the East European Craton. Int J Earth Sci (Geol Rundsch) 107, 2711–2726 (2018). https://doi.org/10.1007/s00531-018-1621-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00531-018-1621-y