Energy scaling laws for microstructures: from helimagnets to martensites

Abstract

We consider scalar-valued variational models for pattern formation in helimagnetic compounds and in shape memory alloys. Precisely, we consider a non-convex multi-well bulk energy term on the unit square, which favors four gradients $({\pm }\,\alpha ,{\pm }\,\beta )$, regularized by a singular perturbation in terms of the total variation of the second derivative. We derive scaling laws for the minimal energy in the case of incompatible affine boundary conditions in terms of the singular perturbation parameter as well as the ratio $\alpha /\beta$ and the incompatibility of the boundary condition. We discuss how well-studied models for martensitic microstructures in shape-memory alloys arise as a limiting case, and relations between the different models in terms of scaling laws. In particular, we show that scaling regimes arise in which an interpolation between the rather different branching-type constructions in the spirit of Kohn and Müller (Commun Pure Appl Math 47(4):405–435, 1994) and Ginster and Zwicknagl (J Nonlinear Sci 33:20, 2023), respectively, occurs. A particular technical difficulty in the lower bounds arises from the fact that the energy scalings involve various logarithmic terms that we capture in matching upper and lower scaling bounds.

1 Introduction

We explore relations between certain scalar-valued variational models for microstructures in shape-memory alloys and in helimagnetic compounds, respectively. In these models, the formation of microstructures is induced by a lack of convexity. More precisely, the energy functionals favor functions whose gradients lie in discrete sets consisting of two (for martensites) or four (for helimagnets) vectors, respectively. To introduce a length scale to the problem, these non-convex terms are typically complemented by a higher-order regularization term which is interpreted as a surface energy term and in particular penalizes changes between regions of preferred gradients (see e.g. [1] and the discussion in [2]). There are only very few special cases in which minimizers for the resulting variational problems are known (see [3] and the references given there), or qualitative properties of them are proven (see [4, 5] and the references given there). Therefore, starting with the work by Kohn and Müller on martensitic microstructures (see [6, 7] and also below for a more detailed description), it has often proven useful to understand the scaling behaviour of the minimal energy in terms of the problem parameters in order to explain pattern formation in materials. More precisely, such results often indicate that in certain parameter regimes, optimal configurations are rather uniform while in other regimes, complex branching patterns are predicted. Similar results have been obtained for a variety of models for very different phenomena, including among many others, various models for the classes of materials considered here, that is, martensitic microstructures (see e.g. [6,7,8,9,10,11,12,13,14,15,16,17,18] and the references therein) and microstructures in micromagnetics (see e.g. [19,20,21,22,23,24,25,26,27] and the references therein).

1.1 The model and related results

Throughout the text, we consider a generic square domain $(0,1)^2$. For recent related results addressing the domain dependence we refer to [28]. Pattern formation in helimagnets is often described in terms of (discrete) frustrated spin systems (see e.g. [29]). We continue here a study of two-dimensional $J_1-J_3$-type models on a square lattices. It has been found (see [30,31,32]) that zooming into the helimagnetic/ferromagnetic transition point and simultaneously taking the continuum limit as the lattice spacing vanishes, such discrete models from statistical mechanics (if properly rescaled) converge in the sense of $\Gamma -$convergence to singularly perturbed continuum functionals. More precisely, the latter are closely related to functionals of the form

$$\begin{aligned} J(u):= \int \limits _{{\Omega }} {\text {dist}}^2(\nabla u,{\mathcal {P}}_{\alpha ,\beta }) \, dx {\, dy}+ \sigma \mid D^2 u\mid (\Omega ), \end{aligned}$$

(1)

see [30,31,32] for precise results and [27] for a discussion of the simplifications we make here. In (1), $\Omega {=(0,1)^2}\subset \mathbb {R}^2$ denotes the domain occupied by the magnetic body, and the set of preferred gradients ${\mathcal {P}}_{\alpha ,\beta }\subset \mathbb {R}^2$ contains four vectors. The latter can be seen as order parameters and correspond to chiralities of the discrete spin fields. More precisely, it has been found that in the parameter regime we consider here, optimal spin field configurations correspond to helical spins field, where the spin vectors rotate between nearest neighbors by a fixed angle (clockwise or counterclockwise) horizontally and by a fixed angle vertically. The preferred gradients ${\mathcal {P}}_{\alpha ,\beta }=\left\{ ({\pm } \alpha ,{\pm }\beta )\right\}$ with $\alpha , \beta >0$ correspond to appropriately rescaled versions of these optimal rotation angles, horizontally ($\alpha$) and vertically ($\beta$). The actual angles are determined by the parameters of the $J_1-J_3-$model (see [30, 31]). We note that in [27, 31] the case $\alpha =\beta =1$ has been considered. The more general case considered here corresponds to the additional freedom in the discrete spin systems that the ratio between nearest neighbor and next to nearest neighbor interactions may be different (details will be discussed in [32]).

We consider the case of incompatible affine Dirichlet boundary conditions, i.e.,

$$\begin{aligned} u(0,y)=(1-2\theta )\beta y \end{aligned}$$

(2)

with a parameter $\theta \in (0,1/2)$ that measures the incompatibility between the rigid field on the boundary and the preferred gradients inside the sample: If $\theta =0$, the boundary condition is compatible with the preferred gradients in $\Omega$ and the minimal energy vanishes, but the larger $\theta \in (0,1/2)$ gets, the more incompatible are the boundary conditions, and we expect a larger minimal energy.

Let us briefly explain the relation to variational problems from the literature: The case $\alpha =\beta =1$ has been studied in [27]. The main result there is a scaling law for the minimal energy which takes the form

$$\begin{aligned} \min J(u)\sim \min \left\{ \theta ^2,\ \sigma \left( \frac{|\log \sigma |}{|\log \theta |}+1\right) \right\} . \end{aligned}$$

(3)

Here and in the following, we use the notation $G\sim H$ for functions G, H depending on the problem parameters, to indicate that there are constants $c,C>0$ such that for all admissible choices of the problem parameters there holds $cH\le G\le CH$. The first scaling in (3) is achieved by an affine function, while the second scaling corresponds to a branching-type construction, which (up to an interpolation layer close to the interface $\{x=0\}$) uses only the preferred gradients in ${\mathcal {P}}_{\alpha ,\beta }$.

On the other hand, if we set $\alpha =0$ and $\beta =1$, then the functional given in (1) reduces to a variant of the Kohn-Müller model for martensitic microstructures. It is well-known that the scaling law for the minimal energy in this case reads (see e.g. [33, 34])

$$\begin{aligned} \min J(u)\sim \min \left\{ \theta ^2,\ \sigma ^{2/3}\theta ^{2/3}\right\} . \end{aligned}$$

(4)

Again, the first regime corresponds to an affine function, while minimizers in the second regime are expected to show almost self-similar behaviour (see [4, 5] for rigorous results for a simplified model). However, in contrast to the situation above, (almost) minimizers in this regime only satisfy (up to an interpolation layer) $\partial _2 u \in \{{\pm } \beta \}$ but not $\partial _1 u \in \{{\pm } \alpha \}$.

1.2 Main results

We shall prove scaling laws for the minimal energies (1) under the boundary conditions (2). As discussed above, this can be seen as generalizations of results on Kohn-Müller-type models (see e.g. [2, 7, 33, 34]) and of the analysis in [27]. In particular, we show how this "transition" from two-gradient models to four-gradient models takes place in terms of "interpolating" scaling regimes of the minimal energy. A particular technical difficulty in the analysis lies in the fact that the scaling law contains various logarithmic terms that we capture precisely in the upper and lower bounds.

We restrict ourselves to a generic domain $(0,1)^2$ to keep notation simple, but we expect that more general rectangles can be treated along the lines of [27, Section 4.4]. We treat the cases $\alpha \le \beta$ and $\alpha \ge \beta$ separately in Sects. 2 and 3, respectively. As the absolute values $\alpha$ and $\beta$ can be adjusted by the rescaling chosen for the spin model (see [31, 32]), we set the larger of the two values to one and call the smaller one $\gamma \in (0,1]$, see Remarks 2 und 3 for details. Our main results concern the complete characterization of the scaling laws of the minimal energies, which we will outline in the sequel. We treat the cases of small preferred y- und small preferred x-derivatives separately.

1.2.1 The case of small y-derivative

For $\sigma > 0$, $\theta \in (0,1/2]$, and $\gamma \in (0,1]$ we set

$$\begin{aligned} {\mathcal {A}}_{\theta ,\gamma }:=\left\{ u\in W^{1,2}((0,1)^2):\ \nabla u\in BV((0,1)^2),\ u(0,y)=(1-2\theta )\gamma y\right\} . \end{aligned}$$

We note that any function in ${\mathcal {A}}_{\theta ,\gamma }$ has a continuous representative up to the boundary (see e.g. [35, Lemma 9]). In the following, we always refer to this representative without further mentioning. We consider the functional $E_{\sigma ,\gamma ,\theta }:{\mathcal {A}}_{\theta ,\gamma }\rightarrow [0,\infty )$ defined by

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u):= \int \limits _{(0,1)^2} {\text {dist}}^2(\nabla u,{\mathcal {K}}_\gamma ) \, dx {\, dy}+ \sigma \mid D^2 u\mid (\Omega ) \end{aligned}$$

where

$$\begin{aligned} {\mathcal {K}}_\gamma :=\left\{ ({\pm } 1,{\pm } \gamma )\right\} . \end{aligned}$$

While for $\gamma \rightarrow 1$, we end up with the four-gradient problem studied in [27], we shall also exploit the above-mentioned relation to two-gradient problems for martensitic microstructure formation. Precisely, we make use of the following relation.

Remark 1

For $u \in {\mathcal {A}}_{\theta ,\gamma }$ consider $v(x,y):= \frac{u(x,y)-x}{\gamma }$. Then

$$\begin{aligned}&E_{\sigma ,\gamma ,\theta }(u) \\&\quad \le \int \limits _{(0,1)^2} |\partial _1 u - 1|^2 + \min \left\{ |\partial _2 u - \gamma |, |\partial _2 u + \gamma | \right\} ^2 \, dx\, dy + \sigma |D^2 u|((0,1)^2) \\&\quad = \gamma ^2 \left( \int \limits _{(0,1)^2} |\partial _1 v|^2 + \min \left\{ |\partial _2 v - 1|, |\partial _2 v + 1| \right\} ^2 \, dx\, dy + \sigma \gamma ^{-1} |D^2 v |((0,1)^2) \right) . \end{aligned}$$

In this way, the upper bound for the Kohn-Müller-type functional (see (4)) immediately yield bounds for our problem which in some parameter regimes turn out to be sharp, in others not. This will be explored more specifically in the proof of Proposition 3.

It turns out that the scaling law for the minimal energy $E_{\sigma ,\gamma ,\theta }$ shows a transition between the scaling behaviour of the Kohn-Müller-type two-gradient energies and the ones derived in [27] for the four preferred gradients $({\pm } 1,{\pm } 1)$. Precisely, compared to the setting of [27], besides uniform phases and branching-type structures involving all four preferred gradients, also a Kohn-Müller type branching construction is relevant for the scaling behaviour of the minimal energy. We note that in the Kohn-Müller model there are only two preferred gradients, and the construction uses (up to a boundary layer) only the preferred values for the $y-$derivative. However, in contrast to the branching-type construction using four gradients, the refinement is done in an anisotropic way so that the x-derivatives become very large (and therefore get far away from the preferred value) after only a few refinement steps. Our main result is the following scaling law of the minimal energy. Note that we prove matching upper and lower bounds.

Theorem 1

There are constants $c,C>0$ such that for all $\theta \in (0,1/2]$, all $\gamma \in (0,1]$, and all $\sigma >0$, there holds

$$\begin{aligned} {c\, s(\gamma ,\theta ,\sigma ) \le \min _{{\mathcal {A}}_{\theta ,\gamma }} E_{\sigma ,\gamma ,\theta }\le C \, s(\gamma ,\theta ,\sigma ),} \end{aligned}$$

where $s(\gamma ,\theta ,\sigma ) = \min \left\{ \gamma ^2\theta ^2, \ \sigma ^{2/3}\gamma ^{4/3} \theta ^{2/3}, \sigma \left( \frac{|\log \sigma |}{|\log (\gamma ^2 \theta )|} + 1 \right) \right\}$.

Proof

The upper bound is proven in Proposition 3, the lower bound in Proposition 4. $\square$

Remark 2

The case of arbitrary preferred gradients $({\pm } \alpha ,{\pm }\beta )$ with $0<\beta \le \alpha$ can be reduced to the setting considered here by rescaling. Precisely, for a function $u\in {\mathcal {A}}_{\theta ,\beta /\alpha }$, the function $u_\alpha :=\alpha u$ satisfies $u_\alpha (0,y)=\alpha (1-2\theta ) y$, and

$$\begin{aligned} \int \limits _{(0,1)^2}{\text {dist}}^2\left( \nabla u_\alpha ,{\mathcal {P}}_{\alpha ,\beta }\right) \,dx\,dy+ \sigma \left| D^2u_\alpha \right| ((0,1)^2)=\alpha ^2 E_{\sigma /\alpha ,\beta /\alpha ,\theta }(u). \end{aligned}$$

1.2.2 The case of small x-derivative

For $\sigma > 0$, $\theta \in (0,1/2]$, and $\gamma \in (0,1]$ we also consider on

$$\begin{aligned} {\mathcal {B}}_{\theta }:=\left\{ u\in W^{1,2}((0,1)^2):\ \nabla u\in BV((0,1)^2),\ u(0,y)=(1-2\theta )y\right\} \end{aligned}$$

the functional

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u) = \int \limits _{(0,1)^2} {\text {dist}}^2(\nabla u,{\mathcal {M}}_\gamma ) \, dx{\, dy} + \sigma \mid D^2 u\mid (\Omega ) \end{aligned}$$

where

$$\begin{aligned} {\mathcal {M}}_\gamma :=\left\{ ({\pm } \gamma ,{\pm } 1)\right\} . \end{aligned}$$

Also in this case, we consider for any function in ${\mathcal {B}}_{\theta }$ always its continuous representative (see e.g. [35, Lemma 9]). Again, for $\gamma \rightarrow 1$, the problem turns into the four-gradient problem studied in [27], while for $\gamma \rightarrow 0$, this problem turns into a Kohn-Müller-type model. Our main result is the following scaling law for the minimal energy. Note that we a prove matching upper and lower bound in all parameter regimes.

Theorem 2

There are constants $c_i,C_i>0$, $i=1,2,3$ such that for all $\theta \in (0,1/2]$, all $\gamma \in (0,1]$, and all $\sigma >0$, the following statements hold:

• 1. If $0<\gamma \le \theta /8$ then

  $$\begin{aligned} { c_1 \, s_1(\gamma ,\theta ,\sigma ) \le \min _{{\mathcal {B}}_{\theta }} F_{\sigma ,\gamma ,\theta }\le C_1 \, s_1(\gamma ,\theta ,\sigma ), } \end{aligned}$$

  where $s_1(\gamma ,\theta ,\sigma ) = \min \left\{ \theta ^2, \sigma ^{2/3}\theta ^{2/3}, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma \theta }{\gamma ^3} \right| + 1\right) \right\}$.

• 2. If $0< \gamma ^2/2 \le \theta /8 < \gamma$ then

  $$\begin{aligned} { c_2 \, s_2(\gamma ,\theta ,\sigma ) \le \min _{{\mathcal {B}}_{\theta }} F_{\sigma ,\gamma ,\theta }\le C_2 \, s_2(\gamma ,\theta ,\sigma ), } \end{aligned}$$

  where $s_2(\gamma ,\theta ,\sigma ) = \min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma }{\theta ^2} \right| +1\right) \right\}$.

• 3. If $0< \theta /8 < \gamma ^2/2$ then

  $$\begin{aligned} {c_3 \, s_3(\gamma ,\theta ,\sigma ) \le \min _{{\mathcal {B}}_{\theta }} F_{\sigma ,\gamma ,\theta }\le C_3 \, s_3(\gamma ,\theta ,\sigma ),} \end{aligned}$$

  where $s_3(\gamma ,\theta ,\sigma ) = \min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \sigma \gamma \left( \frac{|\log \sigma \gamma ^2 / \theta ^3|}{|\log \gamma ^2 / \theta |} + 1 \right) \right\}$.

Proof

The upper bounds follow from Corollary 1, the lower bounds from Proposition 6. $\square$

Remark 3

By rescaling, one can obtain similar results also for the case of general preferred gradients of the form $({\pm } \alpha ,{\pm }\beta )$ with $0<\alpha \le \beta$. For a function $u\in {\mathcal {B}}_{\theta }$ consider $u_\beta :=\beta u$. Then $u_\beta (0,y)=\beta (1-2\theta )y$ and

$$\begin{aligned} \int \limits _{(0,1)^2}{\text {dist}}^2(\nabla u_\beta ,{\mathcal {P}}_{\alpha ,\beta })\,dx\,dy+ \sigma \left| D^2 u_\beta \right| ((0,1)^2)=\beta ^2 F_{\sigma /\beta ,\theta ,\alpha /\beta }(u). \end{aligned}$$

Let us briefly discuss how the above mentioned relations to the well-known scaling laws are reflected in this result.

Remark 4

Suppose that $\sigma >0$ and $\theta \in (0,1/2]$ are fixed.

• 1. If $\gamma \rightarrow 0$ for $\theta >0$ fixed, we are in case (1) and we recover the well-known scaling law for Kohn-Müller type models (see (4)).

• 2. Consider now the case $\gamma \rightarrow 1$. Note that then we are necessarily in case (3) since for (2) there holds $\gamma ^2/2 \le \theta /8 \le 1/16$. If we are in case (3) then we have

  $$\begin{aligned} \min _{{\mathcal {B}}_{\theta }} F_{\sigma ,\gamma ,\theta }\sim & {} \min \left\{ \theta ^2, \sigma + \theta ^3, \sigma \left( \frac{|\log \sigma / \theta ^3|}{|\log \theta |} + 1 \right) \right\} \\\sim & {} \min \left\{ \theta ^2,\ \sigma +\theta ^3,\ \sigma \left( \frac{|\log \sigma |}{|\log \theta |}+1\right) \right\} \\\sim & {} \min \left\{ \theta ^2,\ \sigma \left( \frac{|\log \sigma |}{|\log \theta |}+1\right) \right\} , \end{aligned}$$

  which is the scaling law from [27, Theorem 1] (see (3)).

Throughout the text, we denote by c and C generic constants that may change from expression to expression and do not depend on the problem parameters. In the absence of ambiguities, we will not distinguish between row and column vectors. For $B \subseteq \mathbb {R}^2$ open and $u\in W^{1,2}(B)$ with $\nabla u\in BV(B)$, we use the notation $E_{\sigma ,\gamma ,\theta }(u;B)$ and $F_{\sigma ,\gamma ,\theta }(u;B)$ for the energy on B, i.e.,

$$\begin{aligned}&E_{\sigma ,\gamma ,\theta }(u;B) := \int \limits _{B} {\text {dist}}^2(\nabla u,{\mathcal {K}}_\gamma ) \, dx{\, dy} + \sigma | D^2 u| (B) \nonumber \\ \text { and }&F_{\sigma ,\gamma ,\theta }(u;B):=\int \limits _{B} {\text {dist}}^2(\nabla u,{\mathcal {M}}_\gamma ) \, dx{\, dy} + \sigma | D^2 u| (B). \end{aligned}$$

(5)

In addition for $x \in (0,1)$ and $I\subseteq (0,1)$ Lebesgue-measurable, we write for $u \in {\mathcal {A}}_{\theta ,\gamma }$

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u;\{x\} \times I):= \int \limits _{I} {\text {dist}}^2(\nabla u(x,y), {\mathcal {K}}_\gamma ) \, dy + |\partial _1 \nabla u(x,\cdot )|(I). \end{aligned}$$

Note that since $\nabla u \in BV((0,1)^2)$ this formula makes sense for almost every $x \in (0,1)$ in the sense of slicing of BV-functions, see [36]. Similarly, we write for $y \in (0,1)$ and $u \in {\mathcal {A}}_{\theta ,\gamma }$

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u;I \times \{y\}):= \int \limits _{I} {\text {dist}}^2(\nabla u(x,y), {\mathcal {K}}_\gamma ) \, dx + |\partial _2 \nabla u(\cdot ,y)|(I). \end{aligned}$$

We use analogous notation for $F_{\sigma ,\gamma ,\theta }$.

2 Proof of Theorem 1

2.1 Upper bound

We start with the proof of the upper bound in Theorem 1. Before we present the precise constructions, let us start with a brief heuristic explanation. Essentially, the boundary conditions can be met in two ways, namely the y-derivative being approximately $(1-2\theta ) \gamma$ and fast oscillations close to $x=0$ between y-derivatives $+\gamma$ and $-\gamma$ with volume fraction $1-\theta$ and $\theta$, respectively. The first case is penalized by the first term in $E_{\sigma ,\gamma ,\theta }$, whereas the second case introduces a certain energy through the second term of $E_{\sigma ,\gamma ,\theta }$. If $\sigma > 0$ is large, uniform structures should be energetically favorable. For small $\sigma > 0$, we present two constructions in which oscillations in the y-derivative refine in a self-similar way towards $x=0$. If $\gamma > 0$ is rather small then the set ${\mathcal {K}}_\gamma = {\left\{ (1,{\pm }\gamma ) \right\} \cup \left\{ (-1,{\pm } \gamma )\right\} }$ is the disjoint union of two rather far apart sets of two preferred gradients with a small distance. Hence, it is energetically favorable to use only two of the four vectors in ${\mathcal {K}}_\gamma$, i.e. we restrict ourselves to the setting of only two preferred gradients. By a simple change of variables, in this scenario the construction from [7] can be invoked. The second construction uses all four preferred gradients and isotropically rescaled building blocks, cf. Fig. 4 and [27]. Assuming that $\nabla u \in {\mathcal {K}}_\gamma$, we find that $|u(x,y)-(1-2\theta )\gamma y| \le x$. It then follows, again assuming that $\nabla u \in {\mathcal {K}}_\gamma$, that the number of jumps of the y-derivative is of order $\frac{\theta \gamma }{x}$. The presented construction realizes this as the number of jumps of the y-derivatives grows from approximately $(\theta \gamma ^2)^{-i}$ to approximately $(\theta \gamma ^2)^{-i-1}$ between $x_i \approx \theta \gamma (\theta \gamma ^2)^i$ and $x_{i+1} \approx \theta \gamma (\theta \gamma ^2)^{i+1}$. Moreover, $|\partial _2 \partial _2 u|((x_{i+1},x_i) \times (0,1)) \approx \gamma (x_i - x_{i+1}) (\theta \gamma ^2)^{-i} \approx 1$ which balances the energy contributions from $|\partial _1 \partial _1 u|$ per refinement step. The lower bound indicates that this is necessary. Eventually, we note that instead of the described refinement step (purely creating surface energy), we could alternatively interpolate to the boundary conditions using gradients that are not in ${\mathcal {K}}_\gamma$, see Fig. 4 (middle). This creates an energy contribution through the first part of the energy. By scaling this contribution becomes smaller as the number of refinement steps taken before increases. The use of refinement steps in the construction then terminates once this interpolation is energetically favorable.

Precisely, we have the following result.

Proposition 3

There is a constant $C>0$ such that for all $\theta \in (0,1/2]$, all $\gamma \in (0,1]$ and all $\sigma >0$, there is a function $u\in {\mathcal {A}}_{\theta ,\gamma }$ with

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u)\le C\min \left\{ \gamma ^2\theta ^2, \ \sigma ^{2/3} \gamma ^{4/3} \theta ^{2/3}, \sigma \left( \frac{|\log \sigma |}{|\log (\gamma ^2 \theta )|} + 1 \right) \right\} . \end{aligned}$$

Proof

We use the labels from Fig. 1 to indicate in which parameter regime which test function is used. The first two scaling regimes arise from the scaling regimes of the Kohn-Müller-type models (see Remark 1, with constructions along the lines of [2, 7, 33, 34]) (Fig. 2).

Fig. 1

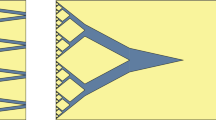
Left: Sketch of the set of preferred gradients with small y-derivative ${\mathcal {K}}_\gamma$. Right: Sketch of the appearing regimes for small y-derivatives in Theorem 1 for fixed $\theta$ in the $\sigma$-$\gamma$-plane: the uniform configuration (UC), the Kohn-Müller type branching using two gradients (TG), and the isotropically rescaled branching using all four preferred gradients (FG). For the corresponding upper bound constructions see Sect. 2.1

1. Uniform configuration (UC). The first scaling, $\gamma ^2\theta ^2$, corresponds to a uniform test function ${u_{\text {UC}}}(x,y)=(1-2\theta )\gamma y+x$, which has energy $E({u_{\text {UC}}})=4\gamma ^2\theta ^2$.

Fig. 2

Left: Sketch of the set of preferred gradients with small x-derivative ${\mathcal {M}}_\gamma$. Right: Sketch of the appearing regimes for small x-derivatives in Theorem 2 for fixed $\theta$ in the $\sigma$-$\gamma$-plane: the uniform configuration (UC), the Kohn-Müller type branching using two gradients (TG), the interpolation between the Kohn-Müller type branching and the isotropically rescaled branching using four gradients (IB), the isotropically rescaled branching using all four preferred gradients (FG), and the rotated interphase configuration (RI). For the corresponding upper bound constructions see Sect. 3.1

Fig. 3

Sketch of the Kohn-Müller-type branching construction. The areas of $\partial _2 u = 1$ and $\partial _2 u = -1$ are colored in green and red, respectively. The parameter $\alpha$ can be chosen in the interval (1/4, 1/2)

2. Kohn-Müller-type two-gradient branching (TG). The second energy scaling, $\sigma ^{2/3}\gamma ^{4/3} \theta ^{2/3}$, can be achieved by a Kohn-Müller type branching construction, which involves only two of the four preferred gradients, see Fig. 3. A similar construction is also given in detail in Proposition 5 (b) below, cf. also the upper bound constructions in [34, 37]. Precisely, it is shown in [34] that there is a constant $C>0$ such that for all $\varepsilon \in (0,\infty )$ and all $\theta \in (0,1/2]$ with $\varepsilon \le \theta ^2$, there is a function $v:=v_{\varepsilon ,\theta }:(0,1)^2\rightarrow \mathbb {R}$ with $v(0,y)=0$ for all $y\in (0,1)$ such that

$$\begin{aligned} \int \limits _{(0,1)^2}{(}\left( \partial _1 v\right) ^2+\min \left\{ \left( \partial _2 v+1-\theta \right) ^2,\ \left( \partial _2 v-\theta \right) ^2\right\} {)}\,dx\, dy+\varepsilon |D^2v|((0,1)^2)\le C\varepsilon ^{2/3}\theta ^{2/3}. \end{aligned}$$

Suppose now $\sigma \le \gamma \theta ^2$ (otherwise $\gamma ^2\theta ^2\le \sigma ^{2/3} \gamma ^{4/3}\theta ^{2/3}$, and the second energy scaling is not relevant). We then set $\varepsilon :=\sigma \gamma ^{-1}\le \theta ^2$, and define ${u_{\text {TG}}}:(0,1)^2\rightarrow \mathbb {R}$ by

$$\begin{aligned} {u_{\text {TG}}}(x,y):=\gamma \left( 2v(x,y)+(1-2\theta )y\right) +x. \end{aligned}$$

This yields ${u_{\text {TG}}}\in {\mathcal {A}}_{\theta ,\gamma }$, and by (4)

$$\begin{aligned}&E_{\sigma ,\gamma ,\theta }({u_{\text {TG}}}) \\&\quad \le \int \limits _{(0,1)^2} |\partial _1 {u_{\text {TG}}} - 1|^2 + \min \{|\partial _2 {u_{\text {TG}}} - \gamma |, |\partial _2 {u_{\text {TG}}}+ \gamma | \}^2 \, dx\, dy + \sigma |D^2 {u_{\text {TG}}}|((0,1)^2) \\&\quad = \gamma ^2 \left( \int \limits _{(0,1)^2} 4|\partial _1 v|^2 +4 \min \{|\partial _2 v - \theta |, |\partial _2 v + 1-\theta | \}^2 \, dx\, dy + 2\sigma \gamma ^{-1} |D^2 v |((0,1)^2) \right) \\&\quad \le 4C\gamma ^2 \varepsilon ^{2/3}\theta ^{2/3}=4C\sigma ^{2/3}\gamma ^{4/3}\theta ^{2/3}. \end{aligned}$$

3. Four-gradient branching (FG). We now turn to the third and last scaling regime, $\sigma \left( \frac{|\log \sigma |}{|\log (\gamma ^2 \theta )|} + 1 \right)$. We may assume that $\sigma \le \gamma ^4 \theta ^2$ (otherwise $\sigma \ge \sigma ^{2/3}\gamma ^{4/3} \theta ^{2/3}$, and the last energy scaling is not relevant). Here, we use a branching-type construction (see Fig. 4), which is a variant of the construction that has been introduced in [27] for the special case $\gamma =1$. We introduce some auxiliary notation and set

where $\lfloor x\rfloor :=\max \{\ell \in \mathbb {N}: \ell \le x\}$ and $\lceil x\rceil :=\min \{\ell \in \mathbb {N}: \ell \ge x\}$. Then

Step 1: Construction of the building block.

The building block is sketched in Fig. 4, left panel. We define $V: [\gamma \theta ^2,\gamma \theta ] \times \mathbb {R}\rightarrow \mathbb {R}^2$ as the function which is 1-periodic in y-direction and satisfies the following:

• (i) If $(x,y) \in [ \gamma \theta ^2,\gamma \theta ] \times [1-l \delta ,1-(l-1)\delta )$ for $1 \le l \le n$ then

  $$\begin{aligned} V(x,y) = {\left\{ \begin{array}{ll} (1, -\gamma ) &{}\text {if } x \le \gamma \theta - \delta \gamma (1-\theta ) (n-{l} +1) {\ \text {and }}\\ &{} y \ge 1- ({l}-1) \delta - \theta \delta , \\ (1,\gamma ) &{} \text {if } x \le \gamma \theta - \delta \gamma (1-\theta ) (n-{l}),\\ &{}y \le 1 - ({l} -1) \delta -\theta \delta , {\ \text { and } }\\ &{} y \le 1-l \delta - \gamma ^{-1} (x - \gamma \theta - \gamma \delta (1-\theta ) (n-{l}) ) , \\ ( -1, -\gamma ) &{}\text {else}.\end{array}\right. } \end{aligned}$$

• (ii) If $(x,y) \in [\gamma \theta ^2, \gamma \theta ] \times [1-(n+1)\delta ,1-n\delta )$ then

  $$\begin{aligned} V(x,y) = {\left\{ \begin{array}{ll} ( 1 , -\gamma ) &{}\text { if } y\ge \max \{ 1 - (n + \theta ) \delta , 1 - \theta + \gamma ^{-1} ( x - \gamma \theta ) \}, \\ ( 1 , \gamma ) &{}\text { if } y \le 1-(n+\theta ) \delta \text { and } x\le 2\gamma \theta -(n+\theta ) \gamma \delta , \\ ( -1 , \gamma ) &{}\text { else.} \end{array}\right. } \end{aligned}$$

• (iii) If $(x,y) \in [\gamma ^2\theta ,\gamma \theta ] \times [1 - \ell \delta ,1 - (\ell -1) \delta )$ for $n+1 < \ell \le m$ then

  $$\begin{aligned} V(x,y) = {\left\{ \begin{array}{ll}(1 ,-\gamma ) &{}\text {if } y\ge 1 -\ell \delta +(1-\theta )\delta \text { and } \\ &{}y \ge 1-(\ell -1) \delta + \gamma ^{-1} (x- 2\gamma \theta + (n+\theta ) \gamma \delta + (\ell -n-2) \theta \gamma \delta ) , \\ ( 1 , \gamma ) &{}\text {if } y \le 1 - \ell \delta + (1 -\theta )\delta \ \text { and }\ \\ &{}x \le 2\gamma \theta - (n +\theta ) \gamma \delta - (\ell -n-3) \gamma \theta \delta , \\ ( -1 , \gamma )&{}\text {else,} \end{array}\right. } \end{aligned}$$

It can be seen that V is ${\text {curl}}$-free as it is piecewise constant and $\nu \parallel (V^{-}-V^+)$ on its jump set $J_{V}$, where $\nu$ is the measure-theoretic normal to $J_{V}$. Consequently, V is a gradient field on $(\gamma ^2\theta ,\gamma \theta )\times \mathbb {R}$, and additionally, $V(x,y) \in K$ for almost all (x, y), and

$$\begin{aligned} \mid DV\mid ((\gamma ^2\theta , \gamma \theta ) \times (0,1)) \le C ( \delta \gamma (1-\gamma ) \gamma m + 1) \le C. \end{aligned}$$

We will use in the next step that for the second component $V_{2}$ of V, we have

$$\begin{aligned} V_2(\theta \gamma ,y)=V_{2}(\theta ^2\gamma ,\delta y)\qquad \text { for all}\ y\in \mathbb {R}. \end{aligned}$$

(6)

Additionally, consider the function $V_{bd}: (0,\gamma \theta (1-\theta )) \times \mathbb {R}\rightarrow \mathbb {R}^2$ which is 1-periodic in the y-component and for $(x,y) \in (0, \gamma \theta (1-\theta )) \times (0,1)$ defined as (see Fig. 4)

$$\begin{aligned} V_{bd}(x,y) = {\left\{ \begin{array}{ll} (-1,-\gamma ) &{}\text { if } y \ge 1- \frac{1}{\gamma (1-\theta )} x, \\ (-1,\gamma ) &{}\text { if } y \le \frac{x}{\gamma \theta } \\ (1,\gamma (1-2\theta )) &{}\text { else. } \end{array}\right. } \end{aligned}$$

Again, we note that also $V_{bd}$ is ${\text {curl }}$-free and $|D^2 V_{bd}|((0, \theta \gamma (1-\theta )) \times (0,1)) \le C$.

Fig. 4

Left: Sketch of the building block. Middle: Sketch of the function $V_{bd}$. Right: Sketch of the branching construction for small y-derivatives

Step 2: Branching construction.

The branching-type construction is sketched in Fig. 4, right panel.

We now set $V_N: ( 0,1)^2 \rightarrow \mathbb {R}^2$ for fixed $N\in \mathbb {N}$ as

$$\begin{aligned} V_N(x,y) = {\left\{ \begin{array}{ll} ( 1 , -\gamma )&{}\text { if } x \ge \gamma \theta \frac{1-\theta }{1-\delta } \text { and } y\ge 1-\theta , \\ (1, \gamma ) &{}\text { if } x \ge \gamma \theta \frac{1-\theta }{1-\delta } \text { and } y\le 1-\theta , \\ V(\delta ^{-k+1}x + \frac{\theta -\delta }{1-\delta },\delta ^{-k+1}y) &{}\text { if } x \in [\delta ^k \gamma \theta \frac{1-\theta }{1-\delta },\delta ^{k-1}\gamma \theta \frac{1-\theta }{1-\delta }) \\ &{}\text { with } 1 \le k \le N, \\ V_{bd}(\delta ^{-N} (x-\delta ^{N+1} \gamma \theta \frac{1-\theta }{1-\delta }),\delta ^{-N}y) &{}\text { if } x \in ( \delta ^{N+1} \gamma \theta \frac{1-\theta }{1-\delta } , \delta ^N \gamma \theta \frac{1-\theta }{1-\delta }), \\ (1,(1-2\theta )\gamma ) &{}\text { if } x \in (0,\delta ^{N+1}\gamma \theta \frac{1-\theta }{1-\delta }). \end{array}\right. } \end{aligned}$$

We note that $V_N$ is ${\text {curl}}$-free as $\nu \parallel (V_N^- - V_N^+)$ on $J_{V_N}$, where $\nu$ is the measure theoretic normal to $J_{V_N}$, see also (6). Moreover, $V_N(x,y) \in {\mathcal {K}}_\gamma$ for almost all $(x,y) \in (\frac{\gamma \theta (1-\theta )}{1-\delta } \delta ^N,1)\times (0,1)$, and

$$\begin{aligned} \mid DV_N\mid \left( (0,1)^2\right) \le C N + 2\gamma \le CN. \end{aligned}$$

(7)

Let $u_N: ( \frac{\gamma \theta (1-\theta )}{1-\delta } \delta ^N, 1 ) \times (0,1) \rightarrow \mathbb {R}$ be a corresponding primitive, i.e., $\nabla u_N=V_N$, such that $u_N(0,0) = 0$.

Step 3: Estimate for the energy.

We have

$$\begin{aligned} \int \limits _{(0,1)^2} {\text {dist}}(\nabla u_N,{\mathcal {K}}_\gamma )^2 \, dx \,dy \le 4 \gamma ^2 \theta ^2 \gamma \theta \frac{1-\theta }{1-\delta } \delta ^N \le C (\gamma ^2 \theta )^{N}. \end{aligned}$$

(8)

Moreover, by (7)

$$\begin{aligned} \mid D^2 u_N\mid ((0,1)^2) \le CN. \end{aligned}$$

(9)

Now fix

and set $u_{\text {FG}}:=u_{N_0}$. Then combining (8) and (9), we obtain

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }({u_{\text {FG}}}) \le C (\gamma ^2 \theta )^{{N_0}} + C \sigma {N_0} \le C \sigma \left( 1+ \frac{\log \sigma }{\log (\gamma ^2 \theta )} \right) = C \sigma \left( \frac{|\log \sigma |}{|\log (\gamma ^2 \theta )|} + 1 \right) . \end{aligned}$$

$\square$

2.2 Lower bound

We now turn to the proof of the lower bound in Theorem 1. Precisely, we show the following result.

Proposition 4

There is a constant $c>0$ such that for all $\theta \in (0,1/2]$, all $\gamma \in (0,1]$, and all $\sigma >0$, there holds

$$\begin{aligned} \min _{{\mathcal {A}}_{\theta ,\gamma }}E_{\sigma ,\gamma ,\theta }\ge c\min \left\{ \gamma ^2\theta ^2, \sigma ^{2/3}\gamma ^{4/3} \theta ^{2/3}, \sigma \left( \frac{|\log \sigma |}{|\log (\gamma ^2 \theta )|} + 1 \right) \right\} . \end{aligned}$$

Proof

The proof is structured in a similar way as the proof of [27, Theorem 1] and is split in several parts that we prove as separate lemmas below. We briefly outline the main steps and how they yield the claimed lower bound.

First, in Lemma 1, we prove a (weaker) lower bound without the logarithmic term in the third regime, i.e.,

$$\begin{aligned} \min _{{\mathcal {A}}_{\theta ,\gamma }}E_{\sigma ,\gamma ,\theta }\ge c \min \{ \gamma ^2 \theta ^2, \sigma ^{2/3} \gamma ^{4/3} \theta ^{2/3}, \sigma \}. \end{aligned}$$

This concludes the proof of the lower bound in the first two regimes, in particular if $\sigma \ge \gamma ^4\theta ^2$ (since in this case, $\gamma ^{4/3}\sigma ^{2/3}\theta ^{2/3}\le \sigma$, and the last regime is not relevant).

Let us now consider the remaining case $\sigma \le \gamma ^4\theta ^2$.

• If $(\gamma ^2\theta )^{34}\le \sigma \le (\gamma ^2\theta )^2$ then $|\log \sigma |/|\log (\gamma ^2\theta )|\sim 1$, and the lower bound is also concluded by Lemma 1 described above.

• If $\sigma \le (\gamma ^2\theta )^{34}$ and $\alpha _0\le \gamma ^2\theta$ with some fixed constant $\alpha \in (0,1)$, we have $|\log (\gamma ^2\theta )|\sim 1$ (recall that always $\gamma ^2\theta \le 1/2$), and we prove in Lemma 3 below that

  $$\begin{aligned} \min _{{\mathcal {A}}_{\theta ,\gamma }}E_{\sigma ,\gamma ,\theta }\ge c\sigma (|\log \sigma |+1), \end{aligned}$$

  which concludes the proof of the lower bound in this case.

• Finally, consider the case $\sigma < (\gamma ^2\theta )^{34}$ and $\gamma ^2\theta \le \alpha _0$ with some fixed constant $\alpha _0 \in (0,1)$. Then there exists some $k\ge 32$ such that $\gamma ^4\theta ^2(\gamma ^2\theta )^{k+1}\le \sigma <\gamma ^4\theta ^2(\gamma ^2\theta )^{k}$, and we prove in Lemma 2 below that

  $$\begin{aligned} \min _{{\mathcal {A}}_{\theta ,\gamma }} E_{\sigma ,\gamma ,\theta }\ge ck\sigma \ge c\sigma \frac{|\log \sigma |}{|\log (\gamma ^2\theta )|}\ge c\sigma \left( \frac{|\log \sigma |}{|\log (\gamma ^2\theta )|}+1\right) \end{aligned}$$

  where in the last estimate we used that $\sigma <(\gamma ^2\theta )^2$. This concludes the proof of the lower bound in this parameter regime.

$\square$

We first prove a weaker lower bound without the logarithmic term.

Lemma 1

There exists $c> 0$ such that for all $u\in {\mathcal {A}}_{\theta ,\gamma }$ there holds

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u) \ge c \min \{ \gamma ^2 \theta ^2, \sigma ^{2/3}\gamma ^{4/3} \theta ^{2/3}, \sigma \}. \end{aligned}$$

Proof

Assume that there exists $u\in {\mathcal {A}}_{\theta ,\gamma }$ such that $E_{\sigma ,\gamma ,\theta }(u) \le \frac{1}{32^2} \min \{\gamma ^2 \theta ^2, \sigma ^{1/2} \gamma ^{3/2} \theta , \sigma \}$. We define

$$\begin{aligned} N := 8 {\left\{ \begin{array}{ll} 1 &{}\text { if } \gamma ^2 \theta ^2 = \min \{\gamma ^2 \theta ^2, \sigma ^{2/3} \gamma ^{4/3} \theta ^{2/3}, \sigma \} ,\\ \sigma ^{-1/3}\gamma ^{1/3} \theta ^{2/3} &{}\text { if } \sigma ^{2/3}\gamma ^{4/3} \theta ^{2/3} = \min \{\gamma ^2 \theta ^2, \sigma ^{2/3}\gamma ^{4/3} \theta ^{2/3}, \sigma \}, \\ \gamma ^{-1} &{}\text { if } \sigma = \min \{\gamma ^2 \theta ^2, \sigma ^{2/3} \gamma ^{4/3} \theta ^{2/3}, \sigma \}. \end{array}\right. } \end{aligned}$$

Note that $N\ge 8$. First find ${\bar{y}} \in (0,1-\frac{2}{N})$ such that

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }\left( u;(0,1) \times ({\bar{y}},{\bar{y}} + \frac{2}{N})\right) \le \frac{4}{N} E_{\sigma ,\gamma ,\theta }(u). \end{aligned}$$

Then by a Fubini-type argument find ${\bar{x}} \in (0,1)$ such that

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }\left( u; \{{\bar{x}}\} \times ({\bar{y}},{\bar{y}}+\frac{2}{N}) \right) \le \frac{4}{N} E_{\sigma ,\gamma ,\theta }(u). \end{aligned}$$

Lastly, again by a Fubini-type argument, we find $y_1,y_2 \in ({\bar{y}},{\bar{y}} + \frac{2}{N})$ such that $y_2-y_1 = \frac{1}{N}$ and

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }\left( u ; (0,1) \times \{y_1\} \right) + E_{\sigma ,\gamma ,\theta }\left( u ; (0,1) \times \{y_2\} \right) \le 4 E_{\sigma ,\gamma ,\theta }(u). \end{aligned}$$

First note that $\int \limits _0^1 \min \{|\partial _1 u(x,y_1) - 1|, |\partial _1 u (x,y_1)+1|\}^2 \, dx \le \frac{4}{32^2} \gamma ^2 \theta ^2$. Hence, there exists $t \in (0,1)$ such that $\min \{|\partial _1 u(t,y_1)-1|, |\partial _1 u (t,y_1)+1|\} \le \frac{1}{16} \gamma \theta < \frac{1}{2}$. Without loss of generality we assume that $|\partial _1 u(t,y_1)-1| < \frac{1}{2}$, i.e. $\partial _1 u(t,y_1) \ge \frac{1}{2}$. Moreover, it holds that

$$\begin{aligned} |\partial _1 \nabla u(\cdot ,y_1)| ((0,1)) + |\partial _1 \nabla u(\cdot ,y_2)| ((0,1)) + |\partial _2 \nabla u|( \{{\bar{x}}\} \times (y_1,y_2) )&\le \sigma ^{-1} 8 E_{\sigma ,\gamma ,\theta }(u) \\&\le \frac{8}{32^2} < \frac{1}{2}. \end{aligned}$$

Hence, $\partial _1 u (s,y_i) \ge 0$ for $i=1,2$ and almost all $s \in (0,1)$, i.e.,

$$\left| \partial _1 u (s,y_i) - 1\right| = \min \left\{ |\partial _1 u (s,y_i) - 1|, |\partial _1 u (s,y_i) + 1| \right\} . $$

Then we estimate

$$\begin{aligned}&\left| u({\bar{x}},y_2) - u({\bar{x}},y_1) - (1-2\theta )\gamma (y_2-y_1) \right| \nonumber \\&\quad =\left| \int \limits _0^{{\bar{x}}} \partial _1 u (t,y_2) - 1 - \partial _1 u(t,y_1) + 1\, dt \right| \nonumber \\&\quad \le {\bar{x}}^{\frac{1}{2}} \left( E(u;(0,1)\times \{y_1\})^{1/2}) + E_{\sigma ,\gamma ,\theta }(u;(0,1)\times \{y_2\})^{1/2} \right) \nonumber \\&\quad \le \frac{1}{8} \min \{\gamma \theta , \sigma ^{1/3}\gamma ^{2/3} \theta ^{1/3}, \sigma ^{1/2} \} \nonumber \\&\quad \le \gamma \theta \frac{1}{N} = \gamma \theta (y_2-y_1). \end{aligned}$$

(10)

Here, we used that $\sigma \le \gamma ^4 \theta ^2$ if $\sigma = \min \{ \gamma ^2 \theta ^2, \sigma ^{2/3} \gamma ^{4/3} \theta ^{2/3}, \sigma \}$. Next, we note that

$$\begin{aligned} | \partial _2 \partial _2 u( {\bar{x}},\cdot )| ((y_1,y_2)) \le \sigma ^{-1} \frac{4}{32^2N} \min \{ \gamma ^2 \theta ^2, \gamma ^{4/3} \sigma ^{2/3} \theta ^{2/3}, \sigma \} \le \frac{1}{2 \cdot 32^2} \gamma <\gamma /2. \end{aligned}$$

By a similar argument as before, we may assume that it holds for almost all $y \in (y_1,y_2)$ that $|\partial _2 u({\bar{x}},y) - \gamma | = \min \{|\partial _2 u({\bar{x}},y) - \gamma |, |\partial _2 u({\bar{x}},y) - \gamma |\}$. Then we estimate

$$\begin{aligned} \left| \int \limits _{y_1}^{y_2} \left( \partial _2 u({\bar{x}},y) - \gamma \right) \, dy \right| ^2&\le (y_2-y_1) \int \limits _{y_1}^{y_2} |\partial _2u({\bar{x}},y) - \gamma |^2 \, dy \nonumber \\&\le (y_2-y_1) \, E_{\sigma ,\gamma ,\theta }(u; \{{\bar{x}}\} \times (y_1,y_2)) \le \frac{4}{N^2} E_{\sigma ,\gamma ,\theta }(u). \end{aligned}$$

(11)

On the other hand, we have by (10)

$$\begin{aligned} \left| \int \limits _{y_1}^{y_2} \left( \partial _2 u({\bar{x}},y) - \gamma \right) \, dy\right| ^2&=\left| u({\bar{x}},y_2)-u({\bar{x}},y_1)-\gamma (y_2-y_1)\right| ^2 \nonumber \\&\ge \big |2\theta \gamma (y_2-y_1)-\left| u({\bar{x}},y_2)-u({\bar{x}},y_1)-(1-2\theta )\gamma (y_2-y_1)\right| \big |^2 \nonumber \\&\ge \gamma ^2 \theta ^2 (y_2-y_1)^2 = \gamma ^2 \theta ^2 \frac{1}{N^2}. \end{aligned}$$

(12)

Combining (11) and (12) yields

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u) \ge \frac{1}{4} \gamma ^2 \theta ^2 \ge \frac{1}{4} \min \{ \gamma ^2 \theta ^2, \sigma ^{2/3}\gamma ^{4/3} \theta ^{2/3}, \sigma \}. \end{aligned}$$

This concludes the proof. $\square$

The next lemma is along the lines of [27, Lemma 6] and its proof, with the necessary careful amendments to deal with the additional parameter $\gamma$.

Lemma 2

There exist $\alpha _0>0$ and $c>0$ such that for all $k \ge k_0=32$, all $\gamma \in (0,1]$, all $\theta \in (0,\alpha _0/\gamma ^2]$, and all

$$\sigma \in \left[ \gamma ^4 \theta ^2 (\gamma ^2 \theta )^{k+1},\gamma ^4 \theta ^2 (\gamma ^2 \theta )^{k}\right) $$

there holds

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u) \ge c k \sigma . \end{aligned}$$

(13)

Proof

Set $k_0:=32$ and $0<\alpha _0<1/(63)^2$ such that $2\cdot 64\cdot 21^2k\alpha _0^{k/4}\le 1$ for all $k\ge k_0$. Let $k\ge k_0$, $\gamma$, $\theta$ and $\sigma$ be as in the lemma and assume that $E_{\sigma ,\gamma ,\theta }(u) \le k \sigma$.

For $i = 1,\dots , k$, there are by a Fubini-type argument $x_i \in \left( \gamma \theta (\gamma ^2\theta )^{i}, \frac{3}{2} \gamma \theta (\gamma ^2\theta )^{i} \right)$ such that (cf. Fig. 5)

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1) ) \le 2(\gamma \theta )^{-1} (\gamma ^2\theta )^{-i} E_{\sigma ,\gamma ,\theta }\left( u; \left( \gamma \theta (\gamma ^2\theta )^{i}, \frac{3}{2} \gamma \theta (\gamma ^2\theta )^{i} \right) \times (0,1) \right) . \end{aligned}$$

Fig. 5

Sketch of the important quantities in the proof of Lemma 2

Claim: There exists a constant $c>0$ such that for all $i\le k/2$ it holds

$$\begin{aligned} \gamma \theta (\gamma ^2\theta )^{i} E_{\sigma ,\gamma ,\theta }(u,\{x_i\} \times (0,1)) + E_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \times (0,1))\ge c \sigma . \end{aligned}$$

Note that once we prove the claim, the lower bound (13) follows via

$$\begin{aligned}&2E_{\sigma ,\gamma ,\theta }(u) \\&\quad \ge \sum _{i=1}^{\lfloor k/2\rfloor } \left[ E_{\sigma ,\gamma ,\theta }\left( u; \left( \gamma \theta (\gamma ^2\theta )^{i}, \frac{3}{2} \gamma \theta (\gamma ^2\theta )^{i} \right) \!\times \! (0,1) \right) \!+\! E_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \!\times \! (0,1))\right] \\&\quad \ge \frac{1}{2}\sum _{i=1}^{\lfloor k/2\rfloor }\left[ \gamma \theta (\gamma ^2\theta )^{i} E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1) ) + E_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \times (0,1))\right] \\&\quad \ge \lfloor k/2\rfloor \, c \sigma \ge \frac{ck}{4} \sigma . \end{aligned}$$

Hence, it remains to prove the claim. From now on fix $i\le k/2$. We define the set

$$\begin{aligned} N_i = \left\{ s \in (0,1): \left| \partial _2 u (x_i,s) + \gamma \right| \le 3 \left| \partial _2 u(x_i,s) - \gamma \right| \right\} \end{aligned}$$

and claim that ${\mathcal {L}}^1(N_i) \le 2/3$, where we denote by ${\mathcal {L}}^1$ the 1-dimensional Lebesgue-measure. For a contradiction, assume that ${\mathcal {L}}^1(N_i) > 2/3$. There are $y_1,y_2 \in (0,1)$ such that $y_2-y_1 \ge 1 - \frac{1}{12}$ and

$$\begin{aligned} \int \limits _0^1 \min \{\mid \partial _1 u(x,y_j)-1\mid , \mid \partial _1 u(x,y_j)+1\mid \}^2 \, dx \le 24 E_{\sigma ,\gamma ,\theta }(u) \text { for } j =1,2. \end{aligned}$$

This yields for $j=1,2$

$$\begin{aligned} |u(x_i,y_j) - (1-2\theta ) \gamma y_j|&\le x_i + x_i^{1/2} \left( 24 E_{\sigma ,\gamma ,\theta }(u ) \right) ^{1/2} \le 2 x_i, \end{aligned}$$

and hence

$$\begin{aligned} u(x_i,y_2) - u(x_i,y_1) \ge (1-2\theta ) \gamma (y_2-y_1) - 4x_i. \end{aligned}$$

This leads to

$$\begin{aligned}&\int \limits _{ (y_1,y_2) \cap \{\partial _2 u (x_i,\cdot ) \ge \gamma /2\}} \partial _2 u(x_i,s) \, ds \nonumber \\&\quad = u(x_i,y_2) - u(x_i,y_1) - \int \limits _{ (y_1,y_2) \cap \{\partial _2 u (x_i,\cdot ) < \gamma /2\}} \partial _2 u(x_i,s) + \gamma - \gamma \, ds \nonumber \\&\quad \ge (1-2\theta ) \gamma (1-\frac{1}{12}) - 4x_i + (2/3 - 1/12) \gamma - 3 E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1))^{1/2} \nonumber \\&\quad \ge \frac{1}{2} \gamma , \end{aligned}$$

(14)

where we used that $4x_i \le 6 \gamma \theta (\gamma ^2\theta ) \le \frac{1}{24} \gamma$ and $E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1)) \le 2 \gamma ^{-1}\theta ^{-1} (\gamma ^2 \theta )^{-i} k \sigma \le \frac{\gamma ^2}{9 \cdot 24^2}$.

On the other hand, we estimate

$$\begin{aligned} \int \limits _{ (y_1,y_2) \cap \{\partial _2 u (x_i,\cdot ) \ge \gamma /2\}} \partial _2 u (x_i,s) \, ds \le \frac{1}{3} \gamma + E_{\sigma ,\gamma ,\theta }(\{x_i\} \times (0,1))^{1/2} < \frac{1}{2} \gamma . \end{aligned}$$

This contradicts (14). Hence, it holds ${\mathcal {L}}^1(N_i) \le 2/3$.

Now, let $t:= 120 (\theta \gamma ^2)^{i+1}$. Then there is a point $y \in (0,1)$ such that the interval $(y,y+t) \subseteq (0,1)$ is not completely contained in $N_i$,

$$\begin{aligned}&E_{\sigma ,\gamma ,\theta }(u; (0,1) \times (y,y+t)) \le 48 t E_{\sigma ,\gamma ,\theta }(u), \\&E_{\sigma ,\gamma ,\theta }(u: (x_{i+1},x_i) \times (y,y+t)) \le 48 t E_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \times (0,1)), \\&E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (y,y+t)) \le 48 t E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1)), \text { and } \\&E_{\sigma ,\gamma ,\theta }(u; \{x_{i+1}\} \times (y,y+t)) \le 48 t E_{\sigma ,\gamma ,\theta }(u; \{x_{i+1}\} \times (0,1)). \end{aligned}$$

Then one of the following statements (1), (2), or (3) holds in $\{x_i\} \times (y,y+t)$, where

• 1. $|\partial _2 \partial _2 u(x_i,\cdot )|((y,y+t)) \ge \frac{1}{2} \gamma$,

• 2. $|\partial _2 u(x_i,\cdot ) - \gamma | \le 3 |\partial _2 u(x_i, \cdot ) + \gamma |$, or

• 3. $|\partial _2 u(x_i,\cdot ) + \gamma | \le 3 |\partial _2 u(x_i, \cdot ) - \gamma |$.

As the interval $(y,y+t)$ is not a subset of $N_i$, assertion (3) cannot be true. Hence, it suffices to consider the cases (1) and (2).

${{Suppose\ that\ estimate\ (1)\ holds:}}$ Then

$$\begin{aligned} \frac{\sigma }{ 2} = \frac{\sigma \gamma }{2\gamma } \le \gamma ^{-1} E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (y,y+t))&\le 48 t \gamma ^{-1} E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1)) \\&= 48 \cdot 120 (\gamma ^2 \theta )^{i} \gamma \theta E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1)) \end{aligned}$$

and thus the claim follows.

${{Suppose\ that\ estimate\ (2)\ holds:}}$ Note that by the triangle inequality

$$\begin{aligned} \frac{1}{2} \gamma \theta t^2&\le \Vert u(x_i,s+t/2) - u(x_i,s) - \gamma t/2 \Vert _{L^1(y,y+t/2)} \\&\quad + \Vert u(x_i,s+t/2) - u(x_i,s) - (1-2\theta ) \gamma t/2 \Vert _{L^1(y,y+t/2)}. \end{aligned}$$

Next, we use that $E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1)) \le 2 \gamma ^{-1}\theta ^{-1} (\gamma ^2\theta )^{-i} k \sigma \le \frac{1}{21^2 \cdot 64} \gamma ^2 \theta ^2$ and estimate

$$\begin{aligned}&\left| \int \limits _y^{y+t/2} u(x_i,s+t/2) - u(x_i,s) - \gamma t/2 \, ds \right| \\&\quad \le \int \limits _y^{y+t/2} \int \limits _{s}^{s+ t/2} |\partial _2 u(x_i,r) - \gamma | \, dr \, ds \\&\quad \le t^{1/2} \int \limits _{y}^{y+t/2} \left( \int \limits _{y}^{y+t} |\partial _2 u(x_i,r) -\gamma |^2 \, dr \right) ^{1/2} \, ds \\&\quad \le 21 t^2 E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1))^{1/2} \le \frac{1}{8} t^2 \gamma \theta . \end{aligned}$$

Then, by (2) and Poincaré ’s inequality we have using the notation $a:= \frac{2}{t}\int \limits _y^{y+t/2} (u(x_i,s+t/2) - u(x_i,s) - \gamma t/2) \, ds$

$$\begin{aligned}&\Vert u(x_i,s+t/2) - u(x_i,s) - \gamma t/2 - a \Vert _{L^1(y,y+t/2)} \\&\quad \le t \Vert \partial _2 u(x_i,s+t/2) - \partial _2 u(x_i,s) \Vert _{L^1(y,y+t/2)} \\&\quad \le t \Vert \partial _2 u(x_i,s) - \gamma \Vert _{L^1(y,y+t)} \\&\quad \le 3 t^{3/2} E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (y,y+t))^{1/2} \\&\quad \le 21 t^2 E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1))^{1/2}. \end{aligned}$$

Consequently, if $\Vert u(x_i + t/2,s) - u(x_i,s) - \gamma t/2 \Vert _{L^1(y,y+t/2)} \ge \frac{1}{4} \gamma \theta t^2$ it follows that

$$\begin{aligned} 21^2t^4 E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1))&\ge \left( \frac{1}{4} \theta \gamma t^2 - \frac{t}{2}|a| \right) ^2 \ge \frac{t^4}{64} \gamma ^2\theta ^2 \ge \frac{t^4}{64} \gamma ^3\theta (\gamma ^2\theta )^{k-i} \nonumber \\&\ge \frac{t^4}{64} \frac{\sigma }{\gamma \theta (\gamma ^2\theta )^{i}}, \end{aligned}$$

(15)

which yields the claim.

Hence, from now on we will assume that $\Vert u(x_i,s) - u(x_i, s + t/2) - (1-2\theta ) \gamma t/2 \Vert _{L^1(y,y+t/2)} \ge \frac{1}{4} \gamma \theta t^2$. First, observe that it holds for all $s \in (y,y+t/2)$

$$\begin{aligned} |u(x_i,s+t/2) - u(x_i,s) - (1-2\theta )\gamma t/2| \le \gamma \theta t + 21 t E_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1))^{1/2} \le 2\gamma \theta t. \end{aligned}$$

(16)

Moreover, define

$$\begin{aligned} A_i = \left\{ s \in (y,y+t): E_{\sigma ,\gamma ,\theta }(u; (0,1) \times \{s\}) \le \frac{80}{ \theta t} E_{\sigma ,\gamma ,\theta }(u; (0,1) \times (y,y+t)) \right\} , \end{aligned}$$

and note that ${\mathcal {L}}^1(A_i) \ge \left( 1-\frac{\theta }{80} \right) t$. For $s \in A_i$ we estimate

$$\begin{aligned} | u(x_{i+1},s) - (1-2\theta ) \gamma s |&\le x_{i+1} + x_{i+1}^{1/2} E_{\sigma ,\gamma ,\theta }(u; (0,1) \times \{s\})^{1/2} \\&\le x_{i+1} + x_{i+1}^{1/2} \left( \frac{80}{\theta t} E_{\sigma ,\gamma ,\theta }(u; (0,1) \times (y,y+t))\right) ^{1/2} \\&\le x_{i+1} + 63 \cdot x_{i+1}^{1/2} \theta ^{-1/2} E_{\sigma ,\gamma ,\theta }(u)^{1/2} \\&\le 2 x_{i+1} \\&\le \frac{1}{40} \gamma \theta t, \end{aligned}$$

where for the second to last inequality we used that for i small enough versus k (recall that $i\le k/2$) we have $k \sigma \le k \gamma ^4\theta ^2 (\gamma ^2\theta )^k \le \gamma \theta (\gamma ^2\theta )^{i+3} \le \frac{1}{63^2} \theta x_{i+1}$. For $s \in (y,y+t)$ we find ${\bar{s}} \in A_i$ such that $|s-{\bar{s}}| \le \frac{\theta }{80} t$. Then we obtain

$$\begin{aligned}&| u(x_{i+1},s) - (1-2\theta ) \gamma s | \\&\quad \le | u(x_{i+1},s) - u(x_{i+1},{\bar{s}})| + | u(x_{i+1},{\bar{s}}) - (1-2\theta ) \gamma {\bar{s}} | + \gamma |s - {\bar{s}}| \\&\quad \le 2 \gamma |s-{\bar{s}}| + |s-{\bar{s}}|^{1/2} E_{\sigma ,\gamma ,\theta }(u; \{x_{i+1}\} \times (y,y+t))^{1/2} + \frac{1}{40} \gamma \theta t \\&\quad \le \frac{1}{16} \gamma \theta t, \end{aligned}$$

where we used similarly to above that for $i \le k/2$ it holds $E_{\sigma ,\gamma ,\theta }(u; \{x_{i+1}\} \times (y,y+t)\} \le \frac{1}{80} \gamma ^2 \theta t$. In particular, using (16) we obtain for almost all $s \in (y,y+t/2)$ that

$$\begin{aligned}&|u(x_{i},s) - u(x_{i},s+t/2) - u(x_{i+1},s) + u(x_{i+1},s+t/2)| \nonumber \\&\quad \le |u(x_{i},s) - u(x_{i},s+t/2) - (1-2\theta ) \gamma t/2| + |u(x_{i+1},s) - (1-2\theta ) \gamma s| \nonumber \\&\quad \quad + |u(x_{i+1},s+t/2) - (1-2\theta ) \gamma (s+ t/2)| \nonumber \\&\quad \le 3 \gamma \theta t. \end{aligned}$$

(17)

On the other hand, it holds by our assumption that

$$\begin{aligned}&\Vert u(x_{i},s) - u(x_{i},s+t/2) - u(x_{i+1},s) + u(x_{i+1},s+t/2) \Vert _{L^1(y,y+t/2)} \nonumber \\&\quad \ge \Vert u(x_{i},s) - u(x_{i},s+t/2) - (1-2\theta )\gamma t/2\Vert _{L^1(y,y+t/2)} \nonumber \\&\quad \quad - \Vert u(x_{i+1},s) - (1-2\theta ) \gamma s\Vert _{L^1(y,y+t/2)} - \Vert u(x_{i+1},s+t/2) - (1-2\theta )\gamma \Vert _{L^1(y,y+t/2)} \nonumber \\&\quad \ge \frac{1}{4} \gamma \theta t^2 - \frac{1}{8} \gamma \theta t^2 \nonumber \\&\quad = \frac{1}{8} \gamma \theta t^2. \end{aligned}$$

(18)

Now, consider the set

$$\begin{aligned} {\mathcal {S}}:=\bigg \{ s \in (y,y+t/2): \frac{1}{8} \gamma \theta t \le v(s) \le 3 \gamma \theta t \bigg \}, \end{aligned}$$

where $v(s)=|u(x_{i},s) - u(x_{i},s+t/2) - u(x_{i+1},s) + u(x_{i+1},s+t/2)|$. We denote by ${\mathcal {L}}^1({\mathcal {S}})$ its $1-$ dimensional Lebesgue measure, and find with (17) and (18)

$$\begin{aligned} \frac{1}{8}\gamma \theta t^2\le {\mathcal {L}}^1({\mathcal {S}})\cdot 3\gamma \theta t+{\mathcal {L}}^1((y,y+t/2) \setminus {\mathcal {S}})\cdot \frac{1}{8}\gamma \theta t\le {\mathcal {L}}^1({\mathcal {S}})\cdot 3\gamma \theta t+\frac{t}{2}\cdot \frac{1}{8}\gamma \theta t, \end{aligned}$$

which implies

$$\begin{aligned} {\mathcal {L}}^1\left( {\mathcal {S}}\right) \ge \frac{t}{48}. \end{aligned}$$

Using that $\frac{1}{4} \gamma \theta (\gamma ^2\theta )^i \le x_i - x_{i+1} \le \frac{3}{2} \gamma \theta (\gamma ^2\theta )^i$ this means that for a subset $(y,y+t/2)$ of size at least $\frac{t}{48}$ it holds

$$\begin{aligned} 10 \, \gamma ^2\theta \le \left| \frac{u(x_{i},s) - u(x_{i+1},s)}{x_i - x_{i+1}} - \frac{u(x_{i},s+t/2) - u(x_{i+1},s+t/2)}{x_i - x_{i+1}}\right| \le 12\cdot 120 \, \gamma ^2\theta . \end{aligned}$$

Therefore there exists a universal constant $c>0$ such that it holds for all s from a subset of $(y,y+t)$ whose measure is at least $\frac{t}{48}$ that

$$\begin{aligned} \left| \left| \frac{u(x_i,s) - u(x_{i+1},s)}{x_i - x_{i+1}}\right| - 1 \right| \ge c \gamma ^2\theta . \end{aligned}$$

Now one can argue as in Step 4 of the proof of [27, Lemma 6] to conclude. We recall the argument in our setting for the convenience of the reader. We assume that for a point s as above there holds $|\partial _{11}u(\cdot ,s)|((x_{i+1},x_{i}))<\frac{1}{2}$. Without loss of generality, this implies for almost all $t\in (x_{i+1},x_{i})$,

$$\begin{aligned} |\partial _1u(t,s)-1|\le 3\min \left\{ |\partial _1u(t,s)-1|, |\partial _1u(t,s)+1|\right\} . \end{aligned}$$

Then

$$\begin{aligned}&\int \limits _{x_{i+1}}^{x_i}\min \left\{ |\partial _1u(t,s)-1|,|\partial _1u(t,s)+1|\right\} ^2\,dt \\&\quad \ge \frac{1}{9}\int \limits _{x_{i+1}}^{x_i}|\partial _1u(t,s)-1|^2\,dt \\&\quad \ge \frac{1}{9(x_i-x_{i+1})}\left( \ \ \int \limits _{x_{i+1}}^{x_i}(\partial _1u(t,s)-1)dt\right) ^2 \\&\quad =\frac{1}{9}(x_i-x_{i+1})\left( \frac{u(x_i,s)-u(x_{i+1},s)}{x_i-x_{i+1}}-1\right) ^2\\&\quad \ge \frac{1}{9}\cdot \frac{1}{4}\gamma \theta (\gamma ^2\theta )^{i}\cdot c^2\gamma ^4\theta ^2\ge \frac{c^2}{36}(\gamma ^2\theta )^{i+3}\ge \frac{c^2}{36}\sigma \end{aligned}$$

since $i+3<k$ and $\sigma <\gamma ^4\theta ^2 (\gamma ^2 \theta )^{k}$.

Hence, it follows $E_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \times (y,y+t)) \ge \frac{t}{48} \min \{\frac{c^2}{36},\frac{1}{2}\} \sigma$, which implies the claim. This concludes the proof of Lemma 2. $\square$

Finally, we consider the parameter regime, in which branching is expected but $|\log (\gamma ^2\theta )|$ is of order 1 and does therefore not appear in the energy scaling, c.f. [27, Lemma 4].

Lemma 3

Let $\alpha _0 \in (0,1)$. Then there exists $c>0$ such that for all $\gamma ^2 \theta \ge \alpha _0$ and $\sigma \le (\gamma ^2 \theta )^{14}$ it holds

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u) \ge c \sigma \left( | \log \sigma | + 1 \right) . \end{aligned}$$

Proof

Assume that $E_{\sigma ,\gamma ,\theta }(u) \le \frac{1}{2} \sigma \left( | \log \sigma | + 1 \right)$ (otherwise there is nothing to show). Let $x \in (0,\gamma \theta /4)$ and $t: = \frac{4x}{\gamma \theta } \le 1$. Let $I_t \subseteq (0,1)$ be an interval of length t such that $E_{\sigma ,\gamma ,\theta }(u; \{x\} \times I_t) \le C t E_{\sigma ,\gamma ,\theta }(u; \{x\} \times (0,1))$ and $E_{\sigma ,\gamma ,\theta }(u; (0,1) \times I_t) \le C t E_{\sigma ,\gamma ,\theta }(u)$. Then one of the following statements is true on $I_t$:

• (a) $|\partial _2 \nabla u (x,\cdot )|(I_t) \ge \gamma / 2$,

• (b) $\min \{|\partial _2 u (x,y) - \gamma |^2,|\partial _2 u (x,y) + \gamma |^2 \} \ge \gamma ^2/4$ for almost every $y \in I_t$,

• (c) $|\partial _2 u (x,y) - \gamma | \le |\partial _2 u (x,y) + \gamma |$ for almost every $y \in I_t$, or

• (d) $|\partial _2 u (x,y) + \gamma | \le |\partial _2 u (x,y) - \gamma |$ for almost every $y \in I_t$.

If (a) or (b) is true then $E_{\sigma ,\gamma ,\theta }(u; \{ x \} \times (0,1)) \ge c \min \{ \sigma \gamma / t, \gamma ^2\theta ^2 \}$. Assume now that (c) is true. Then it follows from the triangle inequality that

$$\begin{aligned} \frac{1}{2} \gamma \theta t^2&\le \min _{a \in \mathbb {R}} \Vert u(x,y) - \gamma y - a \Vert _{L^1(I_t)} + \Vert u(x,y) - (1-2\theta ) \gamma y \Vert _{L^1(I_t)} \\&\le t \Vert \partial _2u(x,\cdot ) - \gamma \Vert _{L^1(I_t)} + \Vert u(x,\cdot ) - u(0,\cdot ) \Vert _{L^1(I_t)}\\&\le t^{3/2} E_{\sigma ,\gamma ,\theta }(u;\{x\} \times I_t)^{1/2} + tx + \Vert \min \{ |\partial _1 u - 1|,|\partial _1 u +1|\} \Vert _{L^1((0,x) \times I_t)}\\&\le C t^2 E_{\sigma ,\gamma ,\theta }(u; \{x\} \times (0,1))^{1/2} + t x + t x^{1/2} E_{\sigma ,\gamma ,\theta }(u)^{1/2}. \end{aligned}$$

Hence,

$$\begin{aligned} \frac{1}{4} \gamma \theta t^2 = \frac{1}{2} \gamma \theta t^2 - t x \le C t^2 E_{\sigma ,\gamma ,\theta }(u; \{x\} \times (0,1))^{1/2} + t x^{1/2} E_{\sigma ,\gamma ,\theta }(u)^{1/2}. \end{aligned}$$

If $\frac{1}{4} \gamma \theta t^2 \le 2C t^2 E_{\sigma ,\gamma ,\theta }(u; \{x\} \times (0,1))^{1/2}$ then $E_{\sigma ,\gamma ,\theta }(u;\{x\} \times (0,1)) \ge c \gamma ^2 \theta ^2$. On the other hand, if $\frac{1}{4} \gamma \theta t^2 \le 2 t x^{1/2} E_{\sigma ,\gamma ,\theta }(u)^{1/2}$ then $x \le 4E_{\sigma ,\gamma ,\theta }(u) \le 2 \sigma ( |\log \sigma | + 1)$.

Hence, we have for all $x \in (2\sigma (|\log \sigma | + 1), \frac{\gamma \theta }{4})$ that $E_{\sigma ,\gamma ,\theta }(u;\{x\} \times (0,1)) \ge c \min \{ \sigma \gamma ^2 \theta / (4x), \gamma ^2\theta ^2 \}$. Next, we note that $\sigma \gamma ^2 \theta / (4x) \le \gamma ^2 \theta ^2$ if and only if $x \ge \sigma /(4 \theta )$. Moreover, observe that $2 \sigma \left( | \log \sigma | + 1 \right) \le \frac{ \sigma }{\theta } \left( | \log \sigma | + 1 \right)$. Thus,

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u)&\ge c \int \limits _{\frac{\sigma }{\theta } \left( | \log \sigma | + 1 \right) }^{\gamma \theta /4} \frac{\sigma \gamma ^2 \theta }{4x} \, dx \\&\ge c \int \limits _{\frac{\sigma }{\theta } \left( | \log \sigma | + 1 \right) }^{\gamma \theta /4} \frac{\sigma }{x} \, dx \\&\ge c \sigma \left( - \log ( \frac{4\sigma }{\gamma \theta ^2} (|\log \sigma | + 1) \right) . \end{aligned}$$

Note that by assumption we have $\theta \le 1/2$ and $\sigma \le \sigma ^{1/2}(\gamma ^2 \theta )^{7} \le \sigma ^{1/2}(\gamma \theta )^2 \frac{1}{32}$. Thus,

$$\begin{aligned} \frac{4 \sigma }{\gamma \theta ^2} (|\log \sigma | + 1) \le \frac{\sigma ^{1/2}}{8} (4|\log \sigma ^{1/4}| + 1) \le \frac{\sigma ^{1/2}}{8} (4\sigma ^{-1/4} + 1) \le \sigma ^{1/4}. \end{aligned}$$

Consequently,

$$\begin{aligned} E_{\sigma ,\gamma ,\theta }(u) \ge \frac{c}{4} \sigma |\log \sigma | \ge \frac{c}{8} \sigma (|\log \sigma | + 1), \end{aligned}$$

since $|\log \sigma | \ge 14 \cdot |\log \theta | \ge 14 \cdot \log 2 \ge 1$. This concludes the proof of Lemma 3. $\square$

3 Proof of Theorem 2

We now turn to the case of small x-derivatives and prove the scaling laws in Theorem 2.

3.1 Upper bound

To prove the upper bound, we first present all constructions used in the proof and show afterwards in Remark 1 how this result implies the upper bound stated in Theorem 2. Some test functions show similarities in structure with those used in [7, 16, 27, 34].

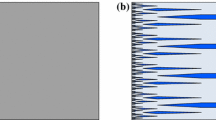
Before we present the precise statement, let us briefly discuss the heuristics for the upper bound constructions. As in the heuristics in the setting of a small y-derivative, the main ways to meet the boundary conditions are y-derivative $(1-2\theta )$ or quick oscillations of y-derivative $+1$ and $-1$ with volume fractions $1-\theta$ and $\theta$, respectively, close to $x=0$. Again, the first option is penalized by the first term of the energy $F_{\sigma ,\gamma ,\theta }$, whereas the second term penalizes oscillations of the y-derivative. Hence, again for $\sigma > 0$ relatively large uniform structures such as $u(x,y) = \gamma x + (1-2\theta ) y$ are energetically favorable, see construction (a) below. Moreover, if $\theta$ is much smaller than $\gamma$ the gradient $\left( \gamma , 1-2\theta \right)$ is rank-1 connected to the gradient ${\left( -\gamma , 1 \right) } \in {\mathcal {M}}_\gamma$ over an almost vertical interface, see Fig. 9 and construction (d) below, giving rise to another competitor with y-derivative $1-2\theta$ close to $x=0$ which turns out to be energetically favorable for moderate values of $\sigma >0$. The remaining constructions will exploit oscillations close to $x=0$ and yield low energies for small values of $\sigma > 0$. Formally, as $\gamma$ approaches 0, the set ${\mathcal {M}}_\gamma$ of four preferred gradients collapses to a set with only two preferred gradients. Consequently, it is to be expected that a version of the optimal (in the sense of scaling) constructions for two preferred gradients from [7, 34] play a role in a regime where $\gamma >0$ is small, see Fig. 6. This construction uses anisotropic rescalings of the building block sketched in Fig. 7 to increase the number of oscillations of the y-derivative towards $x=0$. In this construction it does not hold $\nabla u \in {\mathcal {M}}_\gamma$, essentially balancing the two terms in $F_{\sigma ,\gamma ,\theta }$. On the other hand, isotropic rescalings of the building block lead to $\nabla u \in {\mathcal {M}}_\gamma$ and hence lower the energy contribution from the first term in $F_{\sigma ,\gamma ,\theta }$ while increasing the contribution from the second term of $F_{\sigma ,\gamma ,\theta }$ per refinement step. The construction (c) below exploits that in the way that it starts with refinements through isotropic rescaling of the building block and switches to the anisotropic rescaling of the building block when this is energetically preferable, cf. the energy estimates (22) and (23) and the comment below. A sketch of this construction can be found in Fig. 8. In particular, depending on the parameters this construction transitions either into the Kohn-Müller like construction in (b) or into a construction which mainly uses $\nabla u \in {\mathcal {M}}_\gamma$, which is closer to the construction from [27]. In parameter regimes where $\gamma >0$ is larger than $\theta >0$ it turns out that the anisotropic rescaling of the building block will not play a role leading to branching constructions which essentially satisfy $\nabla u \in {\mathcal {M}}_\gamma$. Similarly to the heuristics for a small y-derivative it follows that the number of jumps of the y-derivative should be of order $\frac{\theta }{\gamma x}$. This will be satisfied at the end of the construction steps in constructions (e) and (f). The main difference between the remaining constructions (e) and (f) is the following: Glueing different construction steps leads to a contribution from the term $|\partial _1 \partial _1 u|$ of order $\gamma$, cf. Fig. 10 (left). On the other hand, the energy contribution of $|\partial _2 \partial _2 u |$ is of order $\frac{\theta }{\gamma }$, cf. Fig. 7. Hence, as long as $\theta \ge \gamma ^2$ the energy contribution from $|\partial _2\partial _2 u|$ necessarily dominates. This leads to construction (e). If $\theta \le \gamma ^2$, we modify the building block in order to balance the energy contributions from $|\partial _1 \partial _1 u|$ and $|\partial _2 \partial _2 u|$ to obtain construction (f), see Fig. 10 (right). Again, the proof of the lower bound suggests that this is necessary.

The following proposition collects the test functions used to prove the upper bound. We label the test functions according to the scaling regimes in Fig. 2. Even if they have the same names, the functions are different from the ones in Proposition 5.

Proposition 5

Let $c_0>0$. Then there is a constant $C>0$ with the following property: For all $\theta \in (0,1/2]$, $\gamma \in (0,1]$, and $\sigma >0$ the following holds:

• (a) There is a function ${u_{\text {UC}}}\in {\mathcal {B}}_{\theta }$ such that $F_{\sigma ,\gamma ,\theta }({u_{\text {UC}}})\le C\theta ^2$.

• (b) If $\sigma \le \theta ^2$ and $\gamma \le c_0 (\sigma \theta )^{1/3}$ then there is a function $u_{{\text {TG}}}\in {\mathcal {B}}_{\theta }$ such that $F_{\sigma ,\gamma ,\theta }(u_{{\text {TG}}})\le C\sigma ^{2/3}\theta ^{2/3}$.

• (c) If $\sigma \theta \le \gamma ^3\le \theta ^3$ then there is a function $u_{\text {IB}}\in {\mathcal {B}}_{\theta }$ such that $F_{\sigma ,\gamma ,\theta }(u_{\text {IB}})\le C\frac{\sigma \theta }{\gamma }\left( \log \frac{\gamma ^3}{\sigma \theta }+1\right)$.

• (d) If $\theta \le \gamma$ then there is a function $u_{\text {RI}}\in {\mathcal {B}}_{\theta }$ such that $F_{\sigma ,\gamma ,\theta }(u_{\text {RI}})\le C\left( \sigma \gamma +\frac{\theta ^3}{\gamma }\right) .$

• (e) If $\sigma \le \theta ^2$ and $\gamma \le \frac{\theta }{\gamma }$ then there is a function $u_{{\text {FG1}}}\in {\mathcal {B}}_{\theta }$ such that $F_{\sigma ,\gamma ,\theta }(u_{{\text {FG1}}})\le C\frac{\sigma \theta }{\gamma }\left( \log \frac{\theta ^2}{\sigma }+1\right) .$

• (f) If $\theta \le \gamma ^2/2$ and $\sigma \le 2\theta ^3/\gamma ^2$ then there is a function $u_{{\text {FG2}}}\in {\mathcal {B}}_{\theta }$ such that ${F_{\sigma ,\gamma ,\theta }}(u_{{\text {FG2}}})\le C\sigma \gamma \left( \frac{|\log (\sigma \gamma ^2/\theta ^3)|}{|\log (\gamma ^2/\theta )|}+1\right) .$

Fig. 6

Sketch of the Kohn–Müller like branching construction used in (b)

Proof

(a) Uniform configuration (UC). Define ${u_{\text {UC}}}: (0,1)^2 \rightarrow \mathbb {R}$ as ${u_{\text {UC}}}(x,y) = (1-2\theta ) y + \gamma x$. Then ${u_{\text {UC}}}\in {\mathcal {B}}_{\theta }$ and

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }({u_{\text {UC}}}) \le 4 \theta ^2. \end{aligned}$$

(b) Kohn-Müller-type two-gradient branching (TG).

We assume $\sigma \le \theta ^2$. Let $\delta = \sigma ^{1/3} \theta ^{-2/3}$, $\alpha = 2^{-3/2}$ and . Note that $2\theta ^{1/3} \sigma ^{-2/3} \ge 2^{N} \ge \theta ^{1/3} \sigma ^{-2/3}$ since $\theta ^{1/3} \sigma ^{-2/3} \ge \theta ^{-1} \ge 2$. Consider the function $W:=(W_1,W_2)^T: (\alpha ,1] \times \mathbb {R}\rightarrow \mathbb {R}^2$ defined as

$$\begin{aligned} W(x,y) = {\left\{ \begin{array}{ll} \begin{pmatrix} - \frac{\delta \theta }{2(1-\alpha )} \\ 1 \end{pmatrix} &{}\text { if } 0\le y \le \frac{\delta }{2}+(x-1)\frac{\delta \theta }{2(1-\alpha )} \\ \begin{pmatrix} \frac{\delta \theta }{2(1-\alpha )} \\ -1 \end{pmatrix} &{}\text { if } \frac{\delta }{2}+(x-1)\frac{\delta \theta }{2(1-\alpha )} \le y \le \frac{\delta }{2} \\ \begin{pmatrix} \frac{\delta \theta }{2(1-\alpha )} \\ 1 \end{pmatrix} &{}\text { if } \frac{\delta }{2} \le y \le \delta (1-\theta )-(x-1)\frac{\delta \theta }{2(1-\alpha )} \\ \begin{pmatrix} - \frac{\delta \theta }{2(1-\alpha )} \\ -1 \end{pmatrix}&\text { if } \delta (1-\theta )-(x-1)\frac{\delta \theta }{2(1-\alpha )}\le y \le \delta , \end{array}\right. } \end{aligned}$$

and extended periodically to $\mathbb {R}$ in the y-component. Then $W_2(\alpha ,y)=W_2(1,2y)$ for all $y\in \mathbb {R}$. We define $U: (\alpha ^N,1)\times (0,1) \rightarrow \mathbb {R}^2$ as

$$\begin{aligned} U(x,y) = \begin{pmatrix} 2^{-k}\alpha ^{-k} W_1(\alpha ^{-k}x, 2^k y) \\ W_2(\alpha ^{-k} x, 2^{k} y) \end{pmatrix} \qquad \text { if }\ x\in (\alpha ^{k+1},\alpha ^k]. \end{aligned}$$

Then U is a gradient field, and we and denote by ${\tilde{u}}: (\alpha ^N,1) \times (0,1) \rightarrow \mathbb {R}$ the corresponding primitive with ${\tilde{u}}(\alpha ^N,0) = 0$. Eventually define $u_{{\text {TG}}}: (0,1)^2 \rightarrow \mathbb {R}$ as

$$\begin{aligned} u_{{\text {TG}}}(x,y) = {\left\{ \begin{array}{ll} {\tilde{u}}(x,y) &{}\text { if } x\ge \alpha ^N,\\ \left( x - \alpha ^N \right) \alpha ^{-N} (1-2\theta )y - x \alpha ^{-N} {\tilde{u}}\left( \alpha ^N,y\right) &{}\text { else. } \end{array}\right. } \end{aligned}$$

We remark that it holds $|{\tilde{u}}(\alpha ^N,y) - (1-2\theta ) y| \le \theta \delta 2^{-N}$. Consequently, we find for $x \le \alpha ^N$

$$\begin{aligned} |\partial _1 u_{{\text {TG}}} (x,y)| \le \frac{\theta \delta }{2^N\alpha ^N}\le 2^{N/2} \theta \delta \le 2 \theta ^{1/6} \sigma ^{-1/3} \theta \delta = 2 \theta ^{1/2} . \end{aligned}$$

(19)

Additionally, we estimate for $1\le k \le N$, using $(2\alpha )^k=2^{-k/2}$ and $\gamma \le c_0 (\sigma \theta )^{1/3}$

$$\begin{aligned}&\int \limits _{\alpha ^k}^{\alpha ^{k-1}} \int \limits _0^1 {\text {dist }}^2(\nabla u_{{\text {TG}}},{\mathcal {M}}_\gamma ) \, dx\, dy + \sigma |D^2 u_{{\text {TG}}}|([\alpha ^k,\alpha ^{k-1}] \times (0,1)) \\&\quad \le \int \limits _{\alpha ^k}^{\alpha ^{k-1}} \int \limits _0^1 {\text {dist }}^2(\nabla u_{{\text {TG}}},{\mathcal {M}}_\gamma ) \, dx\, dy \\&\quad \quad + C\sigma \left( |\partial _{12}u_{{\text {TG}}}|+|\partial _{11}u_{{\text {TG}}}|+|\partial _{22}u_{{\text {TG}}}|\right) ([\alpha ^k,\alpha ^{k-1}] \times (0,1))\\&\quad \le \int \limits _{\alpha ^k}^{\alpha ^{k-1}} \int \limits _0^1 |U_1(x,y) {\pm } \gamma |^2 \, dx \,dy + C \sigma \left( \theta + 2^{k/2} \delta \theta + (1-\alpha ) \alpha ^{k-1} 2^k \delta ^{-1} \right) \\&\quad \le (1-\alpha ) \alpha ^{k-1} \gamma ^2 \left( 2^{k/2}\frac{\delta \theta }{2 \gamma }(1-\alpha ) - 1 \right) ^2 + C \sigma \left( \theta + 2^{k/2} \sigma ^{1/3} \theta ^{1/3} + 2^{-k/2} \sigma ^{-1/3}\theta ^{2/3} \right) \\&\quad \le C \left( 2^{-k/2} \sigma ^{2/3} \theta ^{2/3} + 2^{k/2} \sigma ^{4/3} \theta ^{1/3} +\sigma \theta \right) \\&\quad \le C 2^{-k/2} \sigma ^{2/3} \theta ^{2/3}, \end{aligned}$$

where we used in the last step that by the definition of N, we have $2^{k/2}\le 2^{-k/2}2^N\le 2 \cdot 2^{-k/2}\theta ^{1/3}\sigma ^{-2/3}$, and $2^{-k/2}\sigma ^{2/3}\theta ^{2/3}\ge 2^{-N/2}\sigma ^{2/3}\theta ^{2/3}\ge \sigma \theta ^{1/2} / 2 \ge \sigma \theta / 2$. Hence, we obtain, using the definitions of N, $\alpha$ and $\delta$, as well as the estimates $\gamma \le c_0(\sigma \theta )^{1/3}\le c_0\theta \le c_0\theta ^{1/2}$ and $\sigma \le \theta ^2$, and (19)

$$\begin{aligned}&E_{\sigma ,\gamma ,\theta }(u_{{\text {TG}}}) \\&\quad \le C \sum _{k=1}^N 2^{-k/2} \sigma ^{2/3} \theta ^{2/3} + \int \limits _0^1\int \limits _0^{\alpha ^N} {\text {dist }}(\nabla u_{{\text {TG}}},{\mathcal {M}}_\gamma )^2 \, dx\, dy \\&\quad \quad + \sigma |D^2u_{{\text {TG}}}|((0,\alpha ^N] \times (0, 1)) \\&\quad \le C \sum _{k=1}^N 2^{-k/2} \sigma ^{2/3} \theta ^{2/3} + 2\int \limits _0^1\int \limits _0^{\alpha ^N}|\partial _1u_{{\text {TG}}}|^2+\gamma ^2+\min \left\{ |\partial _2u_{{\text {TG}}}{\pm } 1|^2\right\} \,dx\,dy \\&\quad \quad + \sigma |D^2u_{{\text {TG}}}|((0,\alpha ^N] \times (0, 1)) \\&\quad \le C \sigma ^{2/3} \theta ^{2/3}+ C\alpha ^N\theta +C\alpha ^N\gamma ^2+C\alpha ^N\theta ^2+C\alpha ^N\theta \\&\quad \quad + C\sigma \left( 1+2^{N/2} \delta \theta + \alpha ^N 2^N +C\alpha ^N\theta ^{1/2}\right) \\&\quad \le C \sigma ^{2/3} \theta ^{2/3} + C\theta (2^N)^{-3/2}+C \sigma \\&\quad \le C \sigma ^{2/3} \theta ^{2/3}. \end{aligned}$$

Fig. 7

Sketch of the building block in construction (c) an (e)

Fig. 8

Left: Sketch of the branching construction in the intermediate regime: The regions of the four preferred gradients in the isotropically rescaled building blocks are colored in blue, pink, yellow and beige. In the anisotropically rescaled building blocks, $\partial _1 u \ne {\pm } \gamma$ but $\partial _2 u = 1$ (dark red) or $\partial _2 u = -1$ (light green). Right: Same construction: $\partial _2 u = 1$ (dark red) and $\partial _2 u = -1$ (light green)

(c)  Intermediate Branching (IB).

We assume now that $\sigma \theta \le \gamma ^3\le \theta ^3$, and define a branching construction as follows.

Step 1: Definition of the building block

Consider the function $V: [\frac{\theta }{2\gamma },\frac{\theta }{\gamma }] \times \mathbb {R}\rightarrow \mathbb {R}^2$ defined for $(x,y) \in [\frac{\theta }{2\gamma },\frac{\theta }{\gamma }] \times (0,1)$ as (see Fig. 7)

$$\begin{aligned} V(x,y) = {\left\{ \begin{array}{ll} \begin{pmatrix} -\gamma \\ -1 \end{pmatrix} &{}\text { if } y \ge 1-\theta /2 - \gamma (x - \frac{\theta }{2\gamma } ), \\ \begin{pmatrix} \gamma \\ 1 \end{pmatrix} &{}\text { if } 1-\theta /2 - \gamma (x - \frac{\theta }{2\gamma } ) \ge y \ge 1/2,\\ \begin{pmatrix} \gamma \\ -1 \end{pmatrix} &{}\text { if } 1/2 \ge y \ge 1/2 - \theta /2 + \gamma (x - \frac{\theta }{2\gamma }), \\ \begin{pmatrix} -\gamma \\ 1 \end{pmatrix} &{}\text { if } y \le 1/2 - \theta /2 + \gamma (x-\frac{\theta }{2\gamma }).\\ \end{array}\right. } \end{aligned}$$

(20)

and extended periodically in the y-component. Then V is a gradient field and it holds for the second component $V_2$ that $V_{2}(\theta /(2\gamma ),y)=V_{2}(\theta /\gamma ,2y)$ for all $y\in \mathbb {R}$.

Step 2: Definition branching gradient Let and . Note that $\frac{\gamma ^3}{\sigma \theta } \le 2^{N_0} \le 2 \frac{\gamma ^3}{\sigma \theta }$ and $\frac{\theta }{\gamma ^2} \le 2^{N_1 - N_0} \le 2 \frac{\theta }{\gamma ^2}$. In addition, set $\alpha = 2^{-3/2}$ as in (b). Then we define the function $U: \left( \alpha ^{N_1-N_0} 2^{-N_0},1 \right) \times \mathbb {R}\rightarrow \mathbb {R}^2$ as follows, see Fig. 8. If $x \in (2^{-N_0},1)$ we set

$$\begin{aligned} U(x,y) = V(2^{N} \theta \gamma ^{-1} x, 2^N \theta \gamma ^{-1} y) \text { if } x \in (2^{-N-1},2^{-N}]. \end{aligned}$$

Moreover, for $N_1 > N \ge N_0$ we define for $x \in \left( 2^{-N_0}\alpha ^{N-N_0+1}, 2^{-N_0}\alpha ^{N-N_0}\right)$

$$\begin{aligned} U(x,y) = \begin{pmatrix} \alpha ^{-N+N_0}2^{-N+N_0}V_1\left( \alpha ^{-N+N_0}2^{N_0}\frac{\theta }{\gamma }x,2^{N-N_0}\frac{\theta }{\gamma }y\right) \\ V_2\left( \alpha ^{N-N_0}2^{N_0}\frac{\theta }{\gamma }x,2^{N-N_0}\frac{\theta }{\gamma }y\right) \end{pmatrix}. \end{aligned}$$

Note that for $2^{-N_0}\alpha ^{N-N_0+1}\le x \le 2^{-N_0}\alpha ^{N-N_0}$ we have

$$\begin{aligned} U_1(x,y) = {\pm } 2^{\frac{N-N_0}{2}} \gamma . \end{aligned}$$

(21)

In addition we always have that $U_2(x,y) \in \{{\pm } 1\}$. Moreover, note that U is a gradient.

Step 3: Definition of the branching:

Let ${\tilde{u}}: \left( 2^{-N_0}\alpha ^{N_1-N_0}, 1\right) \times (0,1) \rightarrow \mathbb {R}$ be a corresponding primitive such that ${\tilde{u}}(2^{-N_0}\alpha ^{N_1-N_0},0) = 0$. Note that $2^{-N_0}\alpha ^{N_1-N_0}\gtrsim \sigma /(2^{5/2}\theta ^{1/2})\ge \sigma /8$. Eventually, we define $u_{\text {IB}}: (0,1)^2 \rightarrow \mathbb {R}$ as

$$\begin{aligned} u_{\text {IB}}(x,y) = {\left\{ \begin{array}{ll} {\tilde{u}}(x,y) &{}\text { if } x \ge 2^{-N_0}\alpha ^{N_1-N_0} , \\ \left( x -\sigma \right) \frac{1}{\sigma } (1-2\theta )y - \frac{x}{\sigma } {\tilde{u}}\left( 2^{-N_0}\alpha ^{N_1-N_0},y\right) &{}\text { if } x \le 2^{-N_0}\alpha ^{N_1-N_0}. \end{array}\right. } \end{aligned}$$

Step 4: Energy estimates:

For $N_0\ge N$, we note that $\nabla u_{\text {IB}}\in {\mathcal {K}}_\gamma$ a.e. in $[2^{-N},2^{-N+1}] \times (0,1)$, and thus

$$\begin{aligned}&\int \limits _{2^{-N}}^{2^{-N+1}} \int \limits _0^1 {\text {dist }}(\nabla u_{\text {IB}}, {\mathcal {M}}_\gamma )^2 \, dy\, dx + \sigma |D^2 u_{\text {IB}}|([2^{-N},2^{-N+1}] \times (0,1)) \nonumber \\&\quad \le C \left( |\partial _{11}u_{\text {IB}}|+|\partial _{12}u_{\text {IB}}|+|\partial _{22}u_{\text {IB}}|\right) ([2^{-N},2^{-N+1}] \times (0,1)) \nonumber \\&\quad \le C\sigma \left( \gamma +\theta +\frac{\theta }{\gamma } \right) \nonumber \\&\quad \le C \frac{\sigma \theta }{\gamma }. \end{aligned}$$

(22)

For $N_0 < N \le N_1$ we compute using (21) and $\gamma \le \theta$

$$\begin{aligned}&\int \limits _{2^{-N_0}\alpha ^{N-N_0}} ^{2^{-N_0}\alpha ^{N-N_0-1}} \int \limits _0^1 {\text {dist }}(\nabla u_{\text {IB}}, {\mathcal {M}}_\gamma )^2 \, dy \, dx \nonumber \\&\quad \quad + \sigma |D^2 u_{\text {IB}}|\left( \left[ 2^{-N_0}\alpha ^{N-N_0},2^{-N_0}\alpha ^{N-N_0-1} \right] \times (0,1)\right) \nonumber \\&\quad \le 2^{-N_0}\alpha ^{N-N_0}(1-\alpha )2^{N-N_0}\gamma ^2+C\sigma \left( (2\alpha )^{-N+N_0}\gamma + \theta +2^{-N_0}\alpha ^{N-N_0}(1-\alpha )2^N\frac{\theta }{\gamma }\right) \nonumber \\&\quad \le C(2\alpha )^{N-N_0}\frac{\sigma \theta }{\gamma }+C\sigma \theta , \end{aligned}$$

(23)

where we used that $(2\alpha )^{-N+N_0} \gamma \le (2\alpha )^{-N_1 + N_0} \gamma \le C \frac{\gamma ^2}{\theta ^{1/2}} \le \theta$. Comparing (22) and (23) we note that for $N > N_0$ the anisotropic rescaling of the building block yields a smaller energy per refinement step than the isotropic rescaling.

Next, note that $|u_{\text {IB}}(2^{-N_0}\alpha ^{N_1-N_0},y) - (1-2\theta )y| \le 2\cdot 2^{-N_1} \frac{\gamma }{\theta } \theta$. Consequently, we have for $x \in (0,2^{-N_0}\alpha ^{N_1-N_0})$ the bounds

$$\begin{aligned} |\partial _1 u_{\text {IB}} (x,y)| \le \frac{2\cdot 2^{-N_1} \gamma }{2^{-N_0}\alpha ^{N_1-N_0}}=2\cdot (2\alpha )^{N_0-N_1}\gamma . \end{aligned}$$

Hence, since $2\cdot (2\alpha )^{N_0-N_1}\gamma \ge \gamma$,

$$\begin{aligned}&\int \limits _0^{2^{-N_0}\alpha ^{N_1-N_0}}\int \limits _0^1 {\text {dist }}(\nabla u_{\text {IB}},{\mathcal {M}}_\gamma )^2 \, dy \,dx + \sigma |D^2u_{\text {IB}}|((0,2^{-N_0}\alpha ^{N_1-N_0})) \\&\quad \le \left( (2\cdot (2\alpha )^{N_0-N_1}\gamma )^2+4\theta ^2(1-\theta )+2\theta \right) (2^{-N_0}\alpha ^{N_1-N_0}) \\&\quad \quad +C\sigma \left( \theta +2^{-N_0}\alpha ^{N_1-N_0}2^{N_1}\frac{\theta }{\gamma }\right) \\&\quad \le C\sigma \theta ^{1/2} \le C \frac{\sigma \theta }{\gamma }. \end{aligned}$$

Combining the various estimates we obtain

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u_{\text {IB}})&\le C \left( N_0 \frac{\sigma \theta }{\gamma } + \frac{\sigma \theta }{\gamma } \sum _{N = N_0+1}^{N_1} 2^{(-N+N_0)/2} + (N_1-N_0)\sigma \theta \right) \\&\le C \frac{\sigma \theta }{\gamma } \left( \log \frac{\gamma ^3}{\sigma \theta } + 1\right) , \end{aligned}$$

where we used that $N_1-N_0\le C 2^{(N_1-N_0)/2}\le C\frac{\theta ^{1/2}}{\gamma }\le C/\gamma .$

Fig. 9

Sketch of the construction with a rotated interface used in (d)

(d): Rotated interface (RI). We assume $\theta \le \gamma$, and use the construction sketched in Fig. 9. Precisely, we set

$$\begin{aligned} u_{\text {RI}}(x,y) = {\left\{ \begin{array}{ll} \gamma x + (1-2\theta ) y &{}\text { if } \theta y \ge \gamma x, \\ -\gamma x + y &{}\text { if } \theta y \le \gamma x. \end{array}\right. } \end{aligned}$$

Then

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u_{\text {RI}}) \le 2\frac{\theta ^3}{\gamma } + C\sigma \left( \gamma + \theta + \frac{\theta ^2}{\gamma } \right) \le C\left( \frac{\theta ^3}{\gamma } + \sigma \gamma \right) , \end{aligned}$$

where we used that $\theta \le \gamma$.

Fig. 10

Sketch of the branching construction as described in (e) and sketch of the building block as described in (f)

(e): Four-gradient branching without linear interpolation (FG1). We assume that $\sigma \le \theta ^2$. We use a branching construction and a variant of the construction in (d) instead of interpolation, see Fig. 10. Precisely, we consider the functions $V: (\frac{\theta }{2\gamma },\frac{\theta }{\gamma }) \times \mathbb {R}\rightarrow \mathbb {R}^2$ as defined in (20). Additionally, consider $W: (0,\frac{\theta }{\gamma })\times \mathbb {R}\rightarrow \mathbb {R}^2$ defined as

$$\begin{aligned} W(x,y) = {\left\{ \begin{array}{ll} \begin{pmatrix} -\gamma \\ -1 \end{pmatrix} &{}\text { if } y \ge 1-\gamma x, \\ \begin{pmatrix} -\gamma \\ 1 \end{pmatrix} &{}\text { if } y \le (1-\theta ) \frac{\gamma x}{\theta }, \\ \begin{pmatrix} (1-2\theta ) \gamma \\ 1-2\theta \end{pmatrix}&\text { else,} \end{array}\right. } \end{aligned}$$

(24)

and extend W periodically to $\mathbb {R}$ in the y-variable. Note that W is a gradient field.

For $N \in \mathbb {N}$ define $U_N: (0, 1)^2 \rightarrow \mathbb {R}^2$ as

$$\begin{aligned} U_N(x,y) = {\left\{ \begin{array}{ll} W(2^N x,2^{N} y) &{}\text { if } x\le 2^{-N} \frac{\theta }{\gamma } \\ V(2^k x, 2^k y) &{}\text { if } x \in \left( 2^{-k-1} \frac{\theta }{\gamma }, 2^{-k} \frac{\theta }{\gamma } \right) , 0 \le k \le N-1 \\ \begin{pmatrix} \gamma \\ -1 \end{pmatrix} &{}\text { if } x \ge \frac{\theta }{\gamma }, y \ge 1-\theta + \gamma \left( x - \frac{\theta }{\gamma }\right) , \\ \begin{pmatrix} -\gamma \\ 1 \end{pmatrix}&\text { if } x \ge \frac{\theta }{\gamma }, y \le 1-\theta + \gamma \left( x - \frac{\theta }{\gamma }\right) . \end{array}\right. } \end{aligned}$$

Note that also $U_N$ is a gradient field. Let $u_{{\text {FG1}}}: (0,1)^2 \rightarrow \mathbb {R}$ be a corresponding primitive such that $u_{{\text {FG1}}}(0,0) = 0$. Then $u_{{\text {FG1}}} \in {\mathcal {B}}_{\theta }$ and, using $\gamma \le \theta$,

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u_{{\text {FG1}}}) \le C2^{-N} \left( \frac{\theta ^3}{\gamma } + \frac{\gamma ^2 \theta ^3}{\gamma } \right) + C \sigma N \left( \gamma + \theta + \frac{\theta }{\gamma } \right) \le C \left( 2^{-N} \frac{\theta ^3}{\gamma } + \frac{\sigma \theta }{\gamma } N\right) . \end{aligned}$$

Choosing leads to $F_{\sigma ,\gamma ,\theta }(u_{{\text {FG1}}}) \le C\frac{\sigma \theta }{\gamma } \left( \log \frac{\theta ^2}{\sigma } + 1 \right)$.

(f) Variant of four-gradient branching (FG2). We assume that $\theta \le \gamma ^2/2$ and $\sigma \le \theta ^3/(2\gamma ^2)$. Let . Similarly to the branching construction in Proposition 3, one can construct a function $V: (\theta ^2 / \gamma ,\theta / \gamma ) \times \mathbb {R}\rightarrow \mathbb {R}^2$ such that (see Fig. 10)

• 1. V is 1-periodic in the second variable,

• 2. V is a gradient field,

• 3. $V(x,y) \in {\mathcal {K}}_\gamma$ for a.e. $(x,y) \in (\theta ^2 / \gamma , \theta / \gamma ) \times \mathbb {R}$,

• 4. $|D^2 V|( (\theta ^2 / \gamma ,\theta / \gamma ) \times (0,1)) \le C\gamma$,

• 5. $V(\frac{\theta }{\gamma },y) = \chi _{\{ 0\le y \le 1-\theta \}}(y) - \chi _{\{ 1-\theta \le y \le 1\}}(y)$ for $y\in (0,1)$, and

• 1. $V_{2}(\theta ^2 / \gamma ,y) = V_{2}(\theta / \gamma ,\delta ^{-1}y)$ for all $y \in \mathbb {R}$.

Then we define for $N \in \mathbb {N}$ the function $V_N: (0,1)^2 \rightarrow \mathbb {R}^2$ as

$$\begin{aligned} {V_N(x,y) = {\left\{ \begin{array}{ll} \begin{pmatrix} (1-2\theta )\gamma \\ 1-2\theta \end{pmatrix} &{}\text { if } x \in (0, \delta ^N \frac{\theta }{\gamma }\frac{\delta -\theta }{1-\delta }),\\ W( \delta ^{-N}x - \frac{\theta }{\gamma } \frac{\delta - \theta }{1-\delta },\delta ^{-N}y) &{}\text { if } x \in \left( \delta ^N \frac{\theta }{\gamma }\frac{\delta -\theta }{1-\delta }, \delta ^N \frac{\theta (1-\theta )}{\gamma (1-\delta ))}\right) , \\ V( \delta ^{-k+1} x - \frac{\theta }{\gamma } \frac{\delta - \theta }{1-\delta }, \delta ^{-k+1} y ) &{}\text { if } x \in \left( \delta ^k \frac{\theta (1-\theta )}{\gamma (1-\delta )}, \delta ^{k-1} \frac{\theta (1-\theta )}{\gamma (1-\delta )} \right) \\ &{} \text { for } 1\le k \le N, \\ \begin{pmatrix} \gamma \\ -1 \end{pmatrix} &{}\text { if } x\ge \frac{\theta (1-\theta )}{\gamma (1-\delta )} \text { and } y \ge 1-\theta , \\ \begin{pmatrix} \gamma \\ 1 \end{pmatrix}&\text { if } x\ge \frac{\theta (1-\theta )}{\gamma (1-\delta )} \text { and } y \le 1-\theta , \end{array}\right. } } \end{aligned}$$

where the function W is defined in (24). As before note that $V_N$ is a gradient field. Then let $u_{{\text {FG2}}}: (0,1)^2 \rightarrow \mathbb {R}$ be a corresponding primitive with $u_{{\text {FG2}}}(0,0) = 0$. Note that $u_N \in {\mathcal {B}}_{\theta }$. Moreover, we estimate the corresponding energy

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u_{{\text {FG2}}}) \le C \theta ^2 \delta ^N \frac{\theta (1-\theta )}{\gamma (1-\delta )} + C \sigma \left( \gamma N + \frac{\theta }{\gamma } + \theta \right) \le C \left( \frac{\theta ^3}{\gamma } \delta ^N + \gamma \sigma N \right) . \end{aligned}$$

Choosing yields the estimate

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u_{{\text {FG2}}}) \le C \gamma \sigma \left( \frac{|\log \sigma \gamma ^2 / \theta ^3|}{|\log \gamma ^2/\theta |} + 1\right) . \end{aligned}$$

$\square$

We are now in the position to prove the upper bound in Theorem 2.

Corollary 1

There is a constant $C>0$ such that the following assertions hold:

• 1. If $\gamma \le \theta /8$ then

  $$\begin{aligned} \min _{{\mathcal {B}}_{\theta }} F_{\sigma ,\gamma ,\theta }\le C \min \left\{ \theta ^2, \sigma ^{2/3}\theta ^{2/3}, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma \theta }{\gamma ^3} \right| + 1\right) \right\} . \end{aligned}$$

• 2. If $0< \gamma ^2/2 \le \theta /8 \le \gamma$ then

  $$\begin{aligned} \min _{{\mathcal {B}}_{\theta }} F_{\sigma ,\gamma ,\theta }\le C \min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma }{\theta ^2} \right| +1\right) \right\} . \end{aligned}$$

• 3. If $0 < \theta /8 \le \gamma ^2/2$ then

  $$\begin{aligned} \min _{{\mathcal {B}}_{\theta }} F_{\sigma ,\gamma ,\theta }\le C \min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \sigma \gamma \left( \frac{|\log \sigma \gamma ^2 / \theta ^3|}{|\log \gamma ^2 / \theta |} + 1 \right) \right\} . \end{aligned}$$

Proof

 

• 1. Consider $\gamma \le \theta /8$.

  • If $\min \left\{ \theta ^2, \sigma ^{2/3}\theta ^{2/3}, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma \theta }{\gamma ^3} \right| + 1\right) \right\} =\theta ^2$, then the assertion follows from Proposition 5(a).

  • If $\min \left\{ \theta ^2, \sigma ^{2/3}\theta ^{2/3}, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma \theta }{\gamma ^3} \right| + 1\right) \right\} =\sigma ^{2/3}\theta ^{2/3}$ then $\sigma \le \theta ^2$ (since $\sigma ^{2/3}\theta ^{2/3}\le \theta ^2$) and $\gamma ^3\le \sigma \theta$ (since $\sigma ^{2/3}\theta ^{2/3}\le \frac{\sigma \theta }{\gamma }\left( |\log \frac{\sigma \theta }{\gamma ^3}|+1\right)$ implies that $\frac{\sigma \theta }{\gamma ^3}\left( |\log \frac{\sigma \theta }{\gamma ^3}|+1\right) ^3\ge 1$). Hence, the assertion follows from Proposition 5(b).

  • If $\min \left\{ \theta ^2, \sigma ^{2/3}\theta ^{2/3}, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma \theta }{\gamma ^3} \right| + 1\right) \right\} =\frac{\sigma \theta }{\gamma }\left( |\log \frac{\sigma \theta }{\gamma ^3}|+1\right)$ then $\sigma \theta \le \gamma ^3$ (since $\frac{\sigma \theta }{\gamma }\left( |\log \frac{\sigma \theta }{\gamma ^3}|+1\right) \le \sigma ^{2/3}\theta ^{2/3}$) and $\gamma \le \theta /8\le \theta$, and hence the assertion follows from Proposition 5(c).

• 2. Consider $\gamma ^2/2<\theta /8\le \gamma$.

  • If $\min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma }{\theta ^2} \right| +1\right) \right\} =\theta ^2$, the assertion follows from Proposition 5(a).

  • If $\min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma }{\theta ^2} \right| +1\right) \right\} =\sigma \gamma +\theta ^3/\gamma$ then $\theta \le \gamma$ (since $\theta ^3/\gamma \le \theta ^2$), and the assertion follows from Proposition 5(d).

  • If $\min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma }{\theta ^2} \right| +1\right) \right\} =\frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma }{\theta ^2} \right| +1\right)$ then $\sigma \le 2\theta ^2$ (since $\frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma }{\theta ^2} \right| +1\right) \le \sigma \gamma +\theta ^3/\gamma$ implies that $\frac{1}{2}\frac{\sigma \theta }{\gamma }\le \theta ^3/\gamma$). If $\sigma \le \theta ^2$ then the assertion follows from Proposition 5(e). If $\theta ^2\le \sigma \le 2\theta ^2$ and $\theta \le \gamma$ then the assertion follows from Proposition 5(d) since $\sigma \gamma + \frac{\theta ^3}{\gamma } \le 2\frac{\sigma \theta }{\gamma }$. Eventually, if $\theta ^2 \le \sigma \le 2\theta ^2$ and $\gamma \le \theta$ then the assertion follows from 5(a) since $\theta ^2 \le \frac{\sigma \theta }{\gamma }$.

• 3. Consider $\theta /8<\gamma ^2/2$.

  • If $\min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \sigma \gamma \left( \frac{|\log \sigma \gamma ^2 / \theta ^3|}{|\log \gamma ^2 / \theta |} + 1 \right) \right\} =\theta ^2$ then the assertion follows from Proposition 5(a).

  • If $\min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \sigma \gamma \left( \frac{|\log \sigma \gamma ^2 / \theta ^3|}{|\log \gamma ^2 / \theta |} + 1 \right) \right\} =\sigma \gamma + \frac{\theta ^3}{\gamma }$ then $\theta \le \gamma$ (since $\theta ^3/\gamma \le \theta ^2$) and the assertion follows from Proposition 5(d).

  • If $\min \left\{ \theta ^2, \sigma \gamma + \frac{\theta ^3}{\gamma }, \sigma \gamma \left( \frac{|\log \sigma \gamma ^2 / \theta ^3|}{|\log \gamma ^2 / \theta |} + 1 \right) \right\} =\sigma \gamma \left( \frac{|\log \sigma \gamma ^2 / \theta ^3|}{|\log \gamma ^2 / \theta |} + 1 \right)$ then $\sigma \le \theta ^3/\gamma ^2$ (since $\sigma \gamma \le \theta ^3/\gamma )$. If $\sigma \le \theta ^3/(2\gamma ^2)$ and $\theta \le \gamma ^2/2$ then the assertion follows from Proposition 5(f). Note that the assumption $\theta \le 4\gamma ^2$ always implies that $\theta \le \gamma$ (if $4\gamma ^2\ge \gamma$ then $\gamma \ge 1/2\ge \theta$). Therefore, if $\theta ^3/(2\gamma ^2)\le \sigma \le \theta ^3/\gamma ^2$ then the assertion follows from Proposition 5(d).

$\square$

3.2 Lower bound

The proof of the lower bound is again split in several steps. In the following proposition, we outline how they imply the assertion in all parameter regimes.

Proposition 6

There is a constant $c>0$ such that for all $\sigma \in (0,\infty )$, all $\gamma \in (0,1)$, and $\theta \in (0,1/2]$, the following statements hold:

• 1. If $\gamma \le \theta /8$, then

  $$\begin{aligned} \min _{{\mathcal {B}}_{\theta }}F_{\sigma ,\gamma ,\theta }\ge c\min \left\{ \theta ^2,\,\sigma ^{2/3}\theta ^{2/3},\,\frac{\sigma \theta }{\gamma }\left( \left| \log \frac{\sigma \theta }{\gamma ^3}\right| +1\right) \right\} . \end{aligned}$$

• 2. If $\gamma ^2/2\le \theta /8<\gamma$, then

  $$\begin{aligned} \min _{{\mathcal {B}}_{\theta }}F_{\sigma ,\gamma ,\theta }\ge c\min \left\{ \theta ^2,\,\sigma \gamma +\frac{\theta ^3}{\gamma },\,\frac{\sigma \theta }{\gamma }\left( \left| \log \frac{\sigma }{\theta ^2}\right| +1\right) \right\} . \end{aligned}$$

• 3. If $\theta /8<\gamma ^2/2$, then

  $$\begin{aligned} \min _{{\mathcal {B}}_{\theta }}F_{\sigma ,\gamma ,\theta }\ge c\min \left\{ \theta ^2,\,\sigma \gamma +\frac{\theta ^3}{\gamma },\,\sigma \gamma \left( \frac{\left| \log (\sigma \gamma ^2/\theta ^3)\right| }{\left| \log (\gamma ^2/\theta )\right| }+1\right) \right\} . \end{aligned}$$

Proof

 

• 1. The first statement is proven in Lemma 5(1).

• 2. For the second statement, we consider the cases $\sigma \le \theta ^2/\gamma$ and $\sigma >\theta ^2/\gamma$ separately. If $\sigma \le \theta ^2/\gamma$ then $\sigma \gamma +\theta ^3/\gamma \le 9\theta ^2$, and the assertion follows from the estimate proven in Lemma 5(2), namely

  $$\begin{aligned} \min _{{\mathcal {B}}_{\theta }}F_{\sigma ,\gamma ,\theta }\ge c \min \left\{ \sigma \gamma +\frac{\theta ^3}{\gamma },\,\frac{\sigma \theta }{\gamma }\left( \left| \log \frac{\sigma }{\theta ^2}\right| +1\right) \right\} . \end{aligned}$$

  If $\sigma \ge \theta ^2/\gamma$, then $\theta ^2\le \sigma \gamma \le \sigma \gamma +\theta ^3/\gamma$, and $\sigma \theta /\gamma \ge \frac{\theta ^2}{\gamma }\frac{\theta }{\gamma }\ge (\gamma \theta )\frac{\theta }{\gamma }=\theta ^2$. Hence, the assertion follows from the lower bound in Lemma 4, namely

  $$\begin{aligned} \min _{{\mathcal {B}}_{\theta }}F_{\sigma ,\gamma ,\theta }\ge c\min \left\{ \theta ^2,\,\sigma \gamma \right\} =c\theta ^2. \end{aligned}$$

• 3. For the third statement, we consider three cases separately, depending on the size of $\sigma$.

  • If $\sigma < (\theta ^3/\gamma ^2)(\theta /\gamma ^2)^{32}$ then there exists $k\in \mathbb {N}$, $k\ge k_0=32$ such that

    $$\begin{aligned} \sigma \in \left[ \frac{\theta ^3}{\gamma ^2} \left( \frac{\theta }{\gamma ^2} \right) ^{k+1}, \frac{\theta ^3}{\gamma ^2} \left( \frac{\theta }{\gamma ^2} \right) ^{k} \right) . \end{aligned}$$

    By Lemma 6, we obtain the lower bound $\min _{{\mathcal {B}}_{\theta }}F_{\sigma ,\gamma ,\theta }\ge ck\sigma \gamma$, which yields the claimed lower bound, observing that $2k>k+2\ge \log (\sigma \gamma ^2/\theta ^3)/\log (\theta /\gamma ^2) + 1$.

  • If $(\theta ^3/\gamma ^2)(\theta /\gamma ^2)^{32}\le \sigma <\theta ^3/\gamma ^2$ then we have by Lemma 4 the lower bound $\min _{{\mathcal {B}}_{\theta }}F_{\sigma ,\gamma ,\theta }\ge c\min \left\{ \theta ^2,\,\sigma \gamma \right\} =c\sigma \gamma$. This concludes the proof in this case since

    $$\begin{aligned}{} & {} \min \left\{ \theta ^2,\,\sigma \gamma +\frac{\theta ^3}{\gamma },\,\sigma \gamma \left( \frac{\left| \log (\sigma \gamma ^2/\theta ^3)\right| }{\left| \log (\gamma ^2/\theta )\right| }+1\right) \right\} \le \sigma \gamma \left( \frac{\left| \log (\sigma \gamma ^2/\theta ^3)\right| }{\left| \log (\gamma ^2/\theta )\right| }+1\right) \\{} & {} \quad \le \sigma \gamma \left( \frac{32|\log (\gamma ^2/\theta )|)}{|\log (\gamma ^2/\theta )|}+1\right) \le 33\sigma \gamma . \end{aligned}$$

  • Consider finally the case $\theta ^3/\gamma ^2\le \sigma$. If $\sigma \gamma \ge \theta ^2$ then the assertion follows from 4, using that $\min _{{\mathcal {B}}_{\theta }}\ge c\min \{\theta ^2,\sigma \gamma \}=c\theta ^2.$ On the other hand, if $\sigma \gamma <\theta ^2$ then we obtain by Lemma 4 that $\min _{{\mathcal {B}}_{\theta }}F_{\sigma ,\gamma ,\theta }\ge c\min \{\sigma \gamma ,\theta ^2\}=c\sigma \gamma$ which concludes the proof since

    $$\begin{aligned} \min \left\{ \theta ^2,\,\sigma \gamma +\frac{\theta ^3}{\gamma },\,\sigma \gamma \left( \frac{\left| \log (\sigma \gamma ^2/\theta ^3)\right| }{\left| \log (\gamma ^2/\theta )\right| }+1\right) \right\} \le \sigma \gamma +\theta ^3/\gamma \le 2\sigma \gamma . \end{aligned}$$

$\square$

Similarly to Sect. 2, we start with a rough lower bound without the logarithmic terms. The following can be seen as an analogue to Lemma 1.

Lemma 4

There exists a constant $c>0$ such that for all $\gamma \ge \theta /8$ it holds

$$\begin{aligned} \min F_{\sigma ,\gamma ,\theta }(u) \ge c \min \{ \theta ^2, \sigma \gamma \}. \end{aligned}$$

Proof

Let $u \in {\mathcal {B}}_{\theta }$ and assume that $F_{\sigma ,\gamma ,\theta }(u) \le \frac{1}{256} \min \{ \theta ^2, \sigma \gamma \}$. Then there exist $y_1,y_2 \in (0,1)$ such that $y_2 - y_1 \ge \frac{1}{2}$ and $F_{\sigma ,\gamma ,\theta }(u; (0,1) \times \{y_i\}) \le 4 F_{\sigma ,\gamma ,\theta }(u)$. Additionally, there exists ${\bar{x}} \in (0,1)$ such that $F_{\sigma ,\gamma ,\theta }(u;\{{\bar{x}}\} \times (0,1)) \le F_{\sigma ,\gamma ,\theta }(u)$. Then there exists ${\bar{y}} \in (0,1)$ such that ${\text {dist}}^2(\nabla u ({\bar{x}},{\bar{y}}),{\mathcal {M}}_{\gamma }) \le \frac{1}{256} \theta ^2$. In particular, there exists $M \in {\mathcal {M}}_{\gamma }$ with $|\nabla u ({\bar{x}},{\bar{y}}) - M|^2 \le \frac{1}{256} \theta ^2$. Then we obtain for almost every $y \in (0,1)$

$$\begin{aligned}{} & {} |\nabla u({\bar{x}},y) - M| \le |\nabla u({\bar{x}},{\bar{y}})-M|+|\nabla u({\bar{x}},{\bar{y}})-\nabla u({\bar{x}},y)| \\{} & {} \quad \le \frac{1}{16}\theta +|\partial _{2}\nabla u({\bar{x}},\cdot )|((0,1)) \\{} & {} \quad \le \frac{1}{16}\theta +\frac{1}{256}\gamma \le \frac{\gamma }{2}+\frac{1}{64}\gamma \end{aligned}$$

for almost all $y \in (0,1)$, and hence $|\nabla u(x,y_i) - M| \le \frac{1}{2}\gamma + \frac{1}{256} \gamma +\frac{4}{256}\gamma \le \gamma$ for almost all $x \in (0,1)$ and $i=1,2$. Since the points in ${\mathcal {M}}_\gamma$ have a distance of at least $2 \gamma$, we obtain

$$\begin{aligned} |u({\bar{x}},y_2) - u({\bar{x}},y_1) - M_2 (y_2 - y_1)|^2 \le&\int \limits _{y_1}^{y_2} |\partial _2 u ({\bar{x}},y) - M_2|^2 \, dy \\ \le&\int \limits _{y_1}^{y_2} {\text {dist}}(\nabla u({\bar{x}},y),{\mathcal {M}}_\gamma )^2 \, dy \\ \le&F_{\sigma ,\gamma ,\theta }(u;\{{\bar{x}}\} \times (0,1)) \le F_{\sigma ,\gamma ,\theta }(u). \end{aligned}$$

On the other hand, we estimate

$$\begin{aligned}&|u({\bar{x}},y_2) - u({\bar{x}},y_1) - M_2 (y_2 - y_1)| \\&\quad \ge |(1-2\theta - M_2)(y_2-y_1)| - |u({\bar{x}},y_2) - u({\bar{x}},y_1) - (1-2\theta )(y_2-y_1)| \\&\quad \ge \theta - \sum _{i=1}^2 \int \limits _0^{{\bar{x}}} |\partial _1 u(x,y_i) - M_1| \, dx \\&\quad = \theta - \sum _{i=1}^2 \int \limits _0^{{\bar{x}}} {\text {dist}}(\nabla u(x,y_i),{\mathcal {M}}_{\gamma }) \, dx \\&\quad \ge \theta - \sum _{i=1}^2 \left( \int \limits _0^{{\bar{x}}} {\text {dist}}(\nabla u(x,y_i),{\mathcal {M}}_\gamma )^2 \, dx\right) ^{1/2} \\&\quad \ge \theta - 4 F_{\sigma ,\gamma ,\theta }(u)^{1/2} \ge \frac{1}{2} \theta . \end{aligned}$$

Hence, combining the two estimates, we obtain

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u) \ge \frac{1}{4} \theta ^2. \end{aligned}$$

$\square$

We now turn to the treatment of the remaining logarithmic terms.

Lemma 5

There exists $c>0$ such that the following lower bounds hold:

• 1. If $\gamma \le \theta /8$ then

  $$\begin{aligned} \min F_{\sigma ,\gamma ,\theta }\ge c \min \left\{ \theta ^2, \sigma ^{2/3} \theta ^{2/3}, \frac{\sigma \theta }{\gamma } \left( |\log \frac{\sigma \theta }{\gamma ^3} | + 1\right) \right\} . \end{aligned}$$

• 2. If $\gamma \ge \theta /8$ and $\theta ^2 /\gamma \ge \sigma$ then

  $$\begin{aligned} \min F_{\sigma ,\gamma ,\theta }\ge c \min \left\{ \sigma \gamma + \frac{\theta ^3}{\gamma }, \frac{\sigma \theta }{\gamma } \left( |\log \frac{\sigma }{\theta ^2}| + 1 \right) \right\} . \end{aligned}$$

Proof

We first introduce a slicing argument that is close to the argument in the proof of Lemma 3 which is needed for both statements.

Step 1. Preparations.

Let ${\bar{x}} \in (0,1)$. Let $t \in (0,1)$ and consider the intervals $I_l = (l t, (l+1) t)$ for $l=0,\dots ,\lfloor 1/t \rfloor$.

Choose an interval $I_l$ such that

$$\begin{aligned}F_{\sigma ,\gamma ,\theta }(u; (0,1) \times I_l) \le 4 |I_l| F_{\sigma ,\gamma ,\theta }(u)\text { and } F_{\sigma ,\gamma ,\theta }(u; \{{\bar{x}}\} \times I_l) \le 4 |I_l| F_{\sigma ,\gamma ,\theta }(u; \{{\bar{x}}\} \times (0,1)).\end{aligned}$$

Then one of the following statements is true on $I_l$:

• (a) $|\partial _2 \partial _2 u({\bar{x}},\cdot )|(I_l) \ge \frac{1}{2}$,

• (b) $\min \{ |\partial _2 u({\bar{x}},y) + 1|,|\partial _2 u({\bar{x}},y) - 1|\}^2 \ge \frac{1}{4}$ for almost all $y \in I_l$,

• (c) $|\partial _2 u({\bar{x}},y) - 1| \le |\partial _2 u({\bar{x}},y) + 1|$ for almost all $y \in I_l$,

• (d) $|\partial _2 u({\bar{x}},y) + 1| \le |\partial _2 u({\bar{x}},y) - 1|$ for almost all $y \in I_l$.

We consider the cases separately.

If (a) is true then $F_{\sigma ,\gamma ,\theta }(u;\{{\bar{x}}\} \times (0,1)) \ge \frac{1}{8t} \sigma$.

If (b) is true then $F_{\sigma ,\gamma ,\theta }(u;\{{\bar{x}}\} \times (0,1)) \ge \frac{1}{16}$.

If (c) is true then by the triangle inequality

$$\begin{aligned} \frac{1}{2} \theta t^2&\le \min _{a \in \mathbb {R}} \Vert u({\bar{x}},y) - y - a\Vert _{L^1(I_l)} + \Vert u({\bar{x}},y) - (1-2\theta ) y\Vert _{L^1(I_l)} \\&\le t \Vert \partial _2 u({\bar{x}},\cdot ) - 1\Vert _{L^1(I_l)} + \Vert u({\bar{x}},\cdot ) - u(0,\cdot ) \Vert _{L^1(I_l)} \\&\le t^{3/2} F_{\sigma ,\gamma ,\theta }(u; \{{\bar{x}}\} \times I_l) + \gamma {\bar{x}} t + t^{1/2} {\bar{x}}^{1/2} F_{\sigma ,\gamma ,\theta }(u; (0,1) \times I_l)^{1/2} \\&\le 2 t^{2} F_{\sigma ,\gamma ,\theta }(u; \{{\bar{x}}\} \times (0,1))^{1/2} + \gamma {\bar{x}} t + 2 t {\bar{x}}^{\frac{1}{2}} F_{\sigma ,\gamma ,\theta }(u)^{1/2} \end{aligned}$$

Hence, it follows $64 F_{\sigma ,\gamma ,\theta }(u; \{{\bar{x}}\} \times (0,1)) \ge \theta ^2$ or $\frac{1}{4} t \theta -\gamma {\bar{x}} \le 2{\bar{x}}^{1/2} F_{\sigma ,\gamma ,\theta }(u)^{1/2}$.

If (d) is true the same conclusion follows from the stronger estimate

$$\begin{aligned} \frac{1}{2} t^2 \le \min _{a \in \mathbb {R}} \Vert u({\bar{x}},y) + y - a\Vert _{L^1(I_l)} + \Vert u({\bar{x}},y) - (1-2\theta ) y\Vert _{L^1(I_l)}. \end{aligned}$$

Consequently, we obtain from (a) - (d) that

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u;\{{\bar{x}}\} \times (0,1)) \ge c \min \{ \sigma / t, \theta ^2 \} \qquad \text { or }\qquad \frac{1}{4} t \theta - \gamma {\bar{x}} \le 2{\bar{x}}^{1/2} F_{\sigma ,\gamma ,\theta }(u)^{1/2}. \end{aligned}$$

(25)

Step 2. Proof of (1): The regime: $\gamma \le \frac{1}{8} \theta .$

Kohn-M$\ddot{u}$ller regime: Let us first assume that $\gamma \le \frac{\theta }{8}$ and $\gamma \le \frac{1}{8} \sigma ^{1/3}\theta ^{1/3}$. Then $\sigma \theta /\gamma \ge 8\sigma ^{2/3}\theta ^{2/3}$. In this case we choose $t: = \min \{1, \sigma ^{-1/3}\theta ^{2/3} \}$. If $t = 1$ then $\frac{1}{4} t \theta -\gamma \ge \frac{1}{8} t \theta$. If $t = \theta ^{2/3} \sigma ^{-1/3}$ then $\sigma \le \theta ^2$. It follows that

$$\begin{aligned} \frac{1}{4} t \theta - \gamma {\bar{x}} \ge \frac{1}{4} \sigma ^{-1/3}\theta ^{5/3} - \frac{1}{8} \sigma ^{1/3}\theta ^{1/3} \ge \frac{1}{8} \sigma ^{-1/3}\theta ^{5/3} = \frac{1}{8} t \theta . \end{aligned}$$

Hence, we conclude from (25) that

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u) \ge c \int \limits _{1/2}^1 \min \{ \sigma / t, \theta ^2\} \, dx= \frac{c}{2} \min \{ \sigma / t, \theta ^2\} \qquad \text { or }\qquad \frac{t^2}{64} \theta ^2 \le 4F_{\sigma ,\gamma ,\theta }(u). \end{aligned}$$

In the first case, we obtain $F_{\sigma ,\gamma ,\theta }(u) \ge \frac{c}{2} \min \{ \sigma ^{2/3} \theta ^{2/3},\theta ^2 \}$. In the latter case, there are two possibilities: If $t=1$ then $F_{\sigma ,\gamma ,\theta }(u) \ge c\theta ^2$, and if $t = \sigma ^{-1/3}\theta ^{2/3}$ (i.e., if $\sigma \le \theta ^2$) then $F_{\sigma ,\gamma ,\theta }(u) \ge c \sigma ^{-2/3}\theta ^{10/3} \ge c\sigma ^{2/3}\theta ^{2/3}$. Putting things together, we obtain

$$\begin{aligned} \min F_{\sigma ,\gamma ,\theta }\ge c\min \left\{ \theta ^2,\,\sigma ^{2/3}\theta ^{2/3}\right\} , \end{aligned}$$

which concludes the proof in this case.

${{\textit{Intermediate\ regime}:}}$ Let us now assume that $\gamma \le \frac{\theta }{8}$ and $\gamma \ge \frac{1}{8} \sigma ^{1/3}\theta ^{1/3}$. In addition, we may assume that $F_{\sigma ,\gamma ,\theta }(u) \le c_1 \frac{\sigma \theta }{\gamma } \left( |\log \frac{\sigma \theta }{\gamma ^3} | + 1 \right)$ for $c_1>0$ to be chosen later. Choose ${\bar{x}}\in (0,1/16)$ and $t:=\frac{8\gamma {\bar{x}}}{\theta }$. Then

$$\begin{aligned} \frac{1}{4} t \theta - \gamma {\bar{x}} = 2 \gamma {\bar{x}} - \gamma {\bar{x}} = \gamma {\bar{x}}. \end{aligned}$$

Hence, we obtain from (25) that

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u; \{{\bar{x}}\} \times (0,1)) \ge c\min \left\{ \frac{\sigma \theta }{\gamma {\bar{x}}}, \theta ^2\right\} \text { or } {\bar{x}} \le \frac{4}{\gamma ^2} F_{\sigma ,\gamma ,\theta }(u) \le 4c_1 \frac{\sigma \theta }{\gamma ^3} \left( \left| \log \frac{\sigma \theta }{\gamma ^3} \right| + 1 \right) . \end{aligned}$$

In particular, we have

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u) \ge c\int \limits _{c_1\frac{\sigma \theta }{\gamma ^3} \left( |\log \frac{\sigma \theta }{\gamma ^3} | + 1 \right) }^{1/16} \min \left\{ \frac{\sigma \theta }{\gamma x}, \theta ^2 \right\} \, dx. \end{aligned}$$

Note that $c_1 \frac{\sigma \theta }{\gamma x} \le \theta ^2$ if $x \ge c_1 \frac{\sigma }{\theta \gamma }$. Since $\gamma \le \theta$ it holds $c_1 \frac{\sigma }{\theta \gamma } \le c_1 \frac{\sigma \theta }{\gamma ^3} \le c_1 \frac{\sigma \theta }{\gamma ^3} \left( \left| \log \frac{\sigma \theta }{\gamma ^3} \right| + 1 \right)$. Hence,

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u)&\ge c c_1 \int \limits _{c_1\frac{\sigma \theta }{\gamma ^3} \left( |\log \frac{\sigma \theta }{\gamma ^3} | + 1 \right) }^{1/16} \frac{\sigma \theta }{\gamma x} \, dx \\&= cc_1 \frac{\sigma \theta }{\gamma } \left( \log 1/16 - \log \frac{\sigma \theta }{\gamma ^3} - \log \left( \left| \log \frac{\sigma \theta }{\gamma ^3} \right| + 1 \right) -\log c_1 \right) \\&\ge cc_1 \frac{\sigma \theta }{\gamma } \left( \left| \log \frac{\sigma \theta }{\gamma ^3}\right| + 1 \right) \end{aligned}$$

if the universal constant $c_1 > 0$ is chosen small enough. This concludes the proof of the lower bound in this case, and hence the proof of (1).

${{ { \textit{Step 3. Proof of (2): The regime}:} \ \gamma > \frac{1}{8} \theta \ { and} \ \sigma \le \theta ^2/\gamma .}}$ Let ${\bar{x}} \in (0,\frac{\theta }{16 \gamma })$ and $t:= 4\frac{\gamma {\bar{x}}}{\theta }$. Then

$$\begin{aligned} \frac{1}{2} t \theta - \gamma {\bar{x}} = \gamma {\bar{x}} = \frac{1}{4} t \theta . \end{aligned}$$

Hence we obtain again from (25) that

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u;\{{\bar{x}}\} \times (0,1)) \ge c \min \left\{ \frac{\sigma \theta }{\gamma {\bar{x}}}, \theta ^2\right\} \qquad \text { or }\qquad {\bar{x}} \le \frac{4}{\gamma ^2} F_{\sigma ,\gamma ,\theta }(u). \end{aligned}$$

In particular,

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u) \ge c \int ^{\theta /(16\gamma )}_{\frac{4}{\gamma ^2}F_{\sigma ,\gamma ,\theta }(u)} \min \left\{ \frac{\sigma \theta }{\gamma x}, \theta ^2\right\} \, dx. \end{aligned}$$

We consider the two possibilities $\sigma \le \theta ^2$ and $\sigma >\theta ^2$ separately.

• Consider first the case $\sigma \le \theta ^2$. We assume that $F_{\sigma ,\gamma ,\theta }(u) \le c_2 \frac{\sigma \theta }{\gamma } \left( |\log \frac{\sigma }{\theta ^2}| +1 \right)$ for some $c_2 > 0$ fixed below (otherwise we are done.). We observe that $c_2 \frac{\sigma }{\theta \gamma } \left( |\log \sigma /\theta ^2| + 1\right) \ge c_2 \frac{\sigma \theta }{64 \gamma ^3} \left( |\log \sigma /\theta ^2| + 1\right)$. Additionally, we note that $c_2 \frac{\sigma \theta }{\gamma {\bar{x}}} \le \theta ^2$ if and only if ${\bar{x}} \ge c_2 \frac{\sigma }{\theta \gamma }$ and $c_2 \frac{\sigma }{\theta \gamma } \left( |\log \sigma /\theta ^2| + 1\right) \le c_2 \frac{\theta }{\gamma } \le \theta /(16 \gamma )$ if $c_2 \le 1/16$. Consequently,

  $$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u)&\ge c c_2 \int ^{\theta /(16\gamma )}_{c_2 \frac{\sigma }{\theta \gamma } \left( |\log \sigma /\theta ^2| + 1\right) } \frac{\sigma \theta }{\gamma x} \, dx \\&= cc_2 \frac{\sigma \theta }{\gamma } \left( \log \theta /\gamma - \log 16 - \log \sigma /(\gamma \theta ) - \log c_2 - \log \left( |\log \sigma /\theta ^2| + 1 \right) \right) \\&= cc_2 \frac{\sigma \theta }{\gamma } \left( \log \theta ^2/\sigma - \log 16 c_2 - \log \left( |\log \sigma /\theta ^2| +1 \right) \right) \\&\ge cc_2 \frac{\sigma \theta }{\gamma } \left( |\log \sigma /\theta ^2| + 1\right) \end{aligned}$$

  for $c_2 > 0$ small enough. This shows the lower bound in this case.

• Consider now the case $\sigma >\theta ^2$. We assume that $F_{\sigma ,\gamma ,\theta }(u) \le c_3 \left( \frac{\theta ^3}{\gamma } + \gamma \sigma \right)$ for $c_3 = 1/256$ (otherwise we are done.). Note that by Lemma 4 we already know that $F_{\sigma ,\gamma ,\theta }(u) \ge c\min \{\theta ^2,\,\sigma \gamma \}=c \sigma \gamma$. In particular, if $\sigma \le \theta ^3/\gamma ^2$ then $F_{\sigma ,\gamma ,\theta }(u) \ge \frac{c}{2} ( \sigma \gamma + \frac{\theta ^3}{\gamma })$, and we are done. Hence, we may assume $\sigma \le \frac{\theta ^3}{\gamma ^2}$. Since we consider the regime $\sigma <\theta ^2$, we have $\frac{\sigma }{\theta \gamma } \ge \frac{\theta }{\gamma }$, which implies that $\min \left\{ \frac{\sigma \theta }{\gamma x}, \theta ^2\right\} = \theta ^2$ for all $x \le \frac{\theta }{16\gamma }$. Consequently, we obtain

  $$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u)&\ge c \int \limits _{c_3( \gamma \sigma + \theta ^3/\gamma )}^{\theta /(16\gamma )} \theta ^2 \, dx \\&= c\theta ^3/(16\gamma )- c_3c (\theta ^5/\gamma ^3 + \sigma \theta ^2 /\gamma ) \ge \frac{c}{16} \left( \frac{\theta ^3}{ \gamma } - \frac{\theta ^3}{4\gamma } - \frac{1}{4} \sigma \gamma \right) \\&\ge \frac{c\theta ^3}{32\gamma } \ge \frac{c}{64} \left( \frac{\theta ^3}{\gamma } + \sigma \gamma \right) . \end{aligned}$$

This concludes the proof in the regime $\gamma \ge \theta /8$ and $\sigma \le \theta ^2/\gamma$. $\square$

We finally turn to the parameter regime in which the logarithmic terms in the third regime occur. We proceed similarly to Lemma 2.

Lemma 6

There exist $\alpha _0 >0$ and $c>0$ such that for all $k \ge k_0 = 32$, all $\gamma \in (0,1)$, all $\theta \in (0,\alpha _0\gamma ^2]$ and all

$$\begin{aligned} \sigma \in \left[ \frac{\theta ^3}{\gamma ^2} \left( \frac{\theta }{\gamma ^2} \right) ^{k+1}, \frac{\theta ^3}{\gamma ^2} \left( \frac{\theta }{\gamma ^2} \right) ^{k} \right) \end{aligned}$$

there holds

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u) \ge c k \sigma \gamma . \end{aligned}$$

Proof

Similarly to the proof of Lemma 2 we set $k_0:=32$, $0<\alpha _0<1/(63)^2$ such that $2\cdot 64\cdot 21^2k\alpha _0^{k/4}\le 1$ for all $k\ge k_0$. We assume $F_{\sigma ,\gamma ,\theta }(u) \le k \sigma$ and that $k \ge k_0$.

Let $\sigma \in \left( \frac{\theta ^3}{\gamma ^2} \left( \frac{\theta }{\gamma ^2} \right) ^{k+1}, \frac{\theta ^3}{\gamma ^2} \left( \frac{\theta }{\gamma ^2} \right) ^{k} \right)$. Then find $x_i \in \left( \frac{1}{2} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i, \frac{3}{2} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i \right)$ such that

$$\begin{aligned} F_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1) ) \le \frac{\gamma }{\theta } \left( \frac{\gamma ^2}{\theta } \right) ^i F_{\sigma ,\gamma ,\theta }\left( u; \left( \frac{1}{2} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i, \frac{3}{2} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i \right) \times (0,1) \right) . \end{aligned}$$

for $i = 1,\dots , k$.

Claim:  There exists a constant $c>0$ such that for all $i=1, \dots , \lfloor k/2 \rfloor$ it holds

$$\begin{aligned} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^{i} F_{\sigma ,\gamma ,\theta }(u,\{x_i\} \times (0,1)) + F_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \times (0,1))\ge c \sigma \gamma . \end{aligned}$$

We first show how to derive the lower bound from the claim. We have

$$\begin{aligned}&2F_{\sigma ,\gamma ,\theta }(u) \\&\quad \ge \sum _{i=1}^{\lfloor k/2 \rfloor } F_{\sigma ,\gamma ,\theta }\left( u; \left( \frac{1}{2} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i, \frac{3}{2} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i \right) \!\times \! (0,1) \right) \!+\! F_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \!\times \! (0,1)) \\&\quad \ge \sum _{i=1}^{\lfloor k/2 \rfloor } \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i F_{\sigma ,\gamma ,\theta }(u; \{x_i\} \!\times \! (0,1) ) \!+\! F_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \!\times \! (0,1)) \\&\quad \ge c \frac{k}{4} \gamma \sigma . \end{aligned}$$

Proof of claim: The claim can be obtained following the arguments in the proof of Proposition 2. We sketch it here for the sake of completeness.

First, define $N_i:= \left\{ s \in (0,1): |\partial _2 u(x_i,s) + 1 | \le 3 |\partial _2 u(x_i,s) - 1| \right\}$ and assume for a contradiction that ${\mathcal {L}}^1(N_i) > 2/3$. Then one can show with the analogous definitions of $y_1,y_2 \in (0,1)$ along the lines of the proof of Lemma 2 that

$$\begin{aligned} \int \limits _{(y_1,y_2) \cap \{ \partial _2 u \ge 1/2\}} \partial _2 u(x_i,s) \, ds \le \frac{1}{3} + F_{\sigma ,\gamma ,\theta }(u;\{x_i\} \times (0,1))^{1/2} < 1/2 \end{aligned}$$

and

$$\begin{aligned}&\int \limits _{(y_1,y_2) \cap \{ \partial _2 u \ge 1/2\}} \partial _2 u(x_i,s) \, ds \\&\quad \ge (1-2\theta ) (y_2-y_1) - 4 \gamma x_i - 3 F_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1) )^{1/2} + \frac{2}{3} - \frac{1}{12} \ge \frac{1}{2}. \end{aligned}$$

This shows that ${\mathcal {L}}^1(N_i) \le 2/3$.

Next, let $t = 120 \left( \frac{\theta }{\gamma ^2} \right) ^{i+1}$. Again, we find $(y,y+t) \subseteq (0,1)$ such that $(y,y+t) \cap N_i^c \ne \emptyset$ and

$$\begin{aligned}&F_{\sigma ,\gamma ,\theta }(u; (0,1) \times (y,y+t) ) \le 48 t \, F_{\sigma ,\gamma ,\theta }(u),\\&F_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \times (y,y+t) ) \le 48 t \, F_{\sigma ,\gamma ,\theta }(u;(x_{i+1},x_i) \times (0,1)),\\&F_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (y,y+t) ) \le 48 t \, F_{\sigma ,\gamma ,\theta }(u; \{x_i\} \times (0,1)),\\&F_{\sigma ,\gamma ,\theta }(u; \{x_{i+1}\} \times (y,y+t) ) \le 48 t \, F_{\sigma ,\gamma ,\theta }(u; \{x_{i+1}\} \times (0,1)). \end{aligned}$$

Moreover, we observe that on $(y,y+t)$ one of the following three assertions has to hold

• 1. $|\partial _2 \partial _2 u(x_i,\cdot )|(y,y+t) \ge 1/2$,

• 2. $|\partial _2 u(x_i,s) - 1| \le |\partial _2 u(x_i,s) + 1|$ for almost all $s \in (y,y+t)$,

• 3. $|\partial _2 u(x_i,s) + 1| \le 3 |\partial _2 u(x_i,s) - 1|$ for almost all $s \in (y,y+t)$.

If (1) is true then the estimate follows immediately. Moreover, (3) cannot be true by our choice of $(y,y+t)$. Hence, from now on, we assume that (2) is true. By the triangle inequality, it holds

$$\begin{aligned} \frac{1}{2} \theta t^2&\le \Vert u(x_i,\cdot + t /2)- u(x_i,\cdot ) - t/2\Vert _{L^1(y,y+t/2}) \\&\quad + \Vert u(x_i,\cdot + t/2) - u(x_i,\cdot ) - (1-2\theta ) t/2 \Vert _{L^1(y,y+t/2)}. \end{aligned}$$

First we assume that $\frac{1}{4} \theta t^2 \le \Vert u(x_i,\cdot + t /2)- u(x_i,\cdot ) - t/2\Vert _{L^1(y,y+t/2)}$ and define $a = \int \limits _{y}^{y+t/2} (u(x_i,s+t/s) - u(x_i,s) - t/2) \, ds$. Then one shows as in the proof of Lemma 2 that

$$\begin{aligned} |a| \le 21 t^2 F_{\sigma ,\gamma ,\theta }(u;\{x_i\} \times (0,1))^{1/2} \le \frac{1}{8} t^2 \theta , \end{aligned}$$

where we used that $\frac{\theta }{\gamma } \left( \frac{\gamma ^2}{\theta } \right) ^i k \sigma \le \theta ^2 k \left( \frac{\theta }{\gamma ^2} \right) ^{k-i} \le \frac{1}{21^2 \cdot 64} \theta ^2$. Then it follows similarly to (15)

$$\begin{aligned} 21 t^4 F_{\sigma ,\gamma ,\theta }(u;\{x_i\} \times (0,1)) \ge \left( \frac{1}{4} \theta t^2 - \frac{t}{2} |a| \right) ^2 \ge \frac{t^4}{64} \theta ^2&\ge \frac{t^4}{64} \gamma \frac{\theta ^3}{\gamma ^2} \left( \frac{\theta }{\gamma ^2} \right) ^k \frac{\gamma }{\theta } \left( \frac{\gamma ^2}{\theta }\right) ^i \\&\ge \frac{t^4}{64} \sigma \gamma \frac{\gamma }{\theta } \left( \frac{\gamma ^2}{\theta }\right) ^i, \end{aligned}$$

which yields the claim.

Next, assume that $\frac{1}{4} \theta t^2 \le \Vert u(x_i,\cdot + t/2) - u(x_i,\cdot ) - (1-2\theta ) t/2 \Vert _{L^1(y,y+t)}$. Along the lines of the proof of Lemma 2 one shows for

$$\begin{aligned} {\mathcal {S}}:= \left\{ s \in (y,y+t/2): \frac{1}{8} \theta t \le w(s) \le 3 \theta t \right\} , \end{aligned}$$

where $w(s)=|u(x_i,s) - u(x_i,s+t/2) - u(x_{i+1},s) + u(x_{i+1},s+t/2)|$, that ${\mathcal {L}}^1({\mathcal {S}}) \ge \frac{t}{48}$. Since $\frac{1}{4} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i \le x_i - x_{i+1} \le \frac{3}{2} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i$, we find for $s \in {\mathcal {S}}$

$$\begin{aligned} 10 \frac{\theta }{\gamma } \le \left| \frac{u(x_i,s) - u(x_i,s+t/2) - u(x_{i+1},s) + u(x_{i+1},s+t/2)}{x_{i} - x{i+1}} \right| \le 12\cdot 120 \frac{\theta }{\gamma }, \end{aligned}$$

which implies since $\frac{\theta }{\gamma } \le \alpha _0 \gamma \le (12 \cdot 120)^{-1} \gamma$ that there exists a subset of $(y,y+t)$ whose measure is at least $\frac{t}{48}$ such that

$$\begin{aligned} \left| \left| \frac{u(x_i,s) - u(x_{i+1},s)}{x_{i} - x_{i+1}} \right| - \gamma \right| \ge c \frac{\theta }{\gamma }. \end{aligned}$$

Fix $s \in (y,y+t)$ with the above property and assume that $| \partial _ 1\partial _1 u(\cdot ,s)|((x_{i+1},x_i)) < \gamma /2$. Moreover, we may assume without loss of generality that $|\partial _1 u (t,s) - \gamma | \le 3 |\partial _1 u (t,s) + \gamma |$ for almost all $t \in (x_{i+1},x_i)$. Then it follows similarly to the proof of Lemma 2 that

$$\begin{aligned}&\int \limits _{x_{i+1}}^{x_i} \min \left\{ |\partial _1 u (t,s) + \gamma |, |\partial _1 u (t,s) - \gamma | \right\} ^2 \, dt \\&\quad \ge \frac{1}{9} (x_i - x_{i+1}) \left( \frac{u(x_i,s) - u(x_{i+1},s)}{x_i - x_{i+1}} - \gamma \right) ^2 \\&\quad \ge \frac{1}{36} \frac{\theta }{\gamma } \left( \frac{\theta }{\gamma ^2} \right) ^i c^2 \frac{\theta ^2}{\gamma ^2} \\&\quad \ge \frac{c^2}{36} \gamma \frac{\theta ^3}{\gamma ^2} \left( \frac{\theta }{\gamma ^2} \right) ^{i+1} \ge \frac{c^2}{36} \gamma \sigma . \end{aligned}$$

Consequently, we find

$$\begin{aligned} 48t \, F_{\sigma ,\gamma ,\theta }(u;(x_{i+1},x_i) \times (0,1) ) \ge F_{\sigma ,\gamma ,\theta }(u; (x_{i+1},x_i) \times (y,y+t)) \ge \min \left\{ \frac{1}{2}, \frac{c^2}{36} \right\} \frac{t}{48} \gamma \sigma . \end{aligned}$$

Dividing by t on both sides of the inequality, this concludes the proof. $\square$