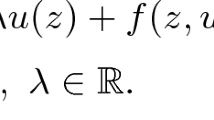Abstract
In this article we derive an (almost) optimal scaling law for a singular perturbation problem associated with the Tartar square. As in Winter (Eur J Appl Math 8(2):185–207, 1997), Chipot (Numer Math 83(3):325–352, 1999), our upper bound quantifies the well-known construction which is used in the literature to prove the flexibility of the Tartar square in the sense of the flexibility of approximate solutions to the differential inclusion. The main novelty of our article is the derivation of an (up to logarithmic powers matching) ansatz free lower bound which relies on a bootstrap argument in Fourier space and is related to a quantification of the interaction of a nonlinearity and a negative Sobolev space in the form of “a chain rule in a negative Sobolev space”. Both the lower and the upper bound arguments give evidence of the involved “infinite order of lamination”.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this article we study a singularly perturbed variational problem for a differential inclusion associated with the Tartar square. The Tartar square, \(T_4\), and more generally its siblings the \(T_N\)-structures, are well-known sets in matrix space with important ramifications in the calculus of variations and the theoretical study of differential inclusions [12, 28, 32, 48,49,50, 62], the theory of partial differential equations, in particular as building blocks for convex integration schemes, ranging from elliptic and parabolic equations [46, 47, 63] to equations of fluid dynamics [21, 24, 61], and with various consequences for applications, for instance for the analysis of certain phase transformations [10, 60] and related differential inclusions [43, 52]. For further applications and implications we refer to the lecture notes and survey articles [32, 33, 45, 53].
1.1 The Tartar square and the “stress-free” setting
Let us recall the “stress-free” set-up and some properties of our problem. The Tartar square—which was introduced in several places in the literature [1, 7, 51, 59, 64] (see also the survey articles from above)—is the following set \({\mathcal {K}}\subset {\mathbb {R}}^{2\times 2}\):
It displays a striking dichotomy between rigidity and flexibility for the associated differential inclusion. On the one hand, it is easily shown (for convenience, a proof is recalled in Section 3) that any solution \(u\in W^{1,\infty }(\Omega )\) to the differential inclusion
is rigid in the sense that any solution to (2) is an affine function whose gradient is equal to one of the four matrices \(A_1,\dots ,A_4\). On the other hand, the Tartar square is flexible on the level of approximate solutions: Indeed, it is possible to find sequences \((u_j)_{j\in {\mathbb {N}}}\in W^{1,\infty }(\Omega )\) such that \({{\,\mathrm{dist}\,}}(\nabla u_j, {\mathcal {K}}) \rightarrow 0\) in measure and such that no subsequence of \((\nabla u_j)_{j\in {\mathbb {N}}}\) converges in measure (to a constant gradient in \({\mathcal {K}}\); see Section 2 as well as [45, Chapter 2.5] and [11, 65] for qualitative and quantitative versions of this construction). Moreover, it is known that arbitrarily small perturbations of the Tartar square enjoy even stronger flexibility in the sense that if \({\mathcal {K}}_{\delta }\subset {\mathbb {R}}^{2\times 2}\) is an arbitrarily small, open neighbourhood of \({\mathcal {K}}\) in \({\mathbb {R}}^{2\times 2}\), then there are infinitely many, non-affine solutions to the differential inclusion \(\nabla u \in {\mathcal {K}}_{\delta }\) which can be obtained by the method of convex integration [48]. These rigidity and flexibility aspects are mirrored in the algebraic properties of the set \({\mathcal {K}}\): On the one hand, the set \({\mathcal {K}}\) does not have any rank-one connections, i.e. for any \(i,j \in \{1,\dots ,4\}\) with \(i \ne j\) it holds that \(rk(A_i-A_j)=2>1\). This excludes “trivial solutions” to (2) such as simple laminates. It furthermore directly implies that the lamination convex hull \({\mathcal {K}}^{lc}\) of \({\mathcal {K}}\) is trivial. On the other hand, however, the rank-one convex hull is non-trivial:
where \(\text {conv}(\cdot )\) denotes the convex hull and
The set \({\mathcal {K}}^{rc} = {\mathcal {K}}^{qc}\) is obtained by laminates of infinite order. Thus, the outlined properties make the Tartar square a prototypical model problem for studying more detailed properties of the dichotomy between rigidity and flexibility.
1.2 The singularly perturbed problem and a scaling law
Motivated by the long-term goal of understanding the described dichotomy and related dichotomies in the study of shape-memory alloys more precisely and quantitatively [16, 22, 23, 25,26,27, 31, 48, 54, 57, 58], and inspired by the observation in [56] that the scaling behaviour of associated singularly perturbed problems give certain upper bounds on possible regularities of wild convex integration solutions, we here study the minimal energy scaling of a singularly perturbed Tartar square. Let us emphasize that in this context upper bound constructions are well-known and had earlier been quantified in [65] and also in [11]. We repeat these estimates in Section 2 for completeness. The main novelty of our work consists in proving (essentially) matching lower scaling bounds.
Let us outline the setting of this. We begin by noting that the differential inclusion (2) for the Tartar square can be rewritten in terms of characteristic functions indicating the “phase” the gradient is in
where
Using this formulation and motivated by Hooke’s law, we consider the following elastic energy:
Here \(u:[0,1]^2 \rightarrow {\mathbb {R}}^2\) is the “deformation” and the functions \(\chi _j\) are subject to the constraints from (4). Moreover, on the left hand side of (5) (and also in the following arguments) we have used the abbreviation
The elastic energy thus measures the deviation of a given deformation from being a solution to the differential inclusion (2). We emphasize that due to the flexibility of approximate solutions, the vanishing of the elastic energy along some sequence \((u_j)_{j\in {\mathbb {N}}}\) does however not entail that along a subsequence the gradients \((\nabla u_j)_{j\in {\mathbb {N}}}\) converge in measure against a constant map (in \({\mathcal {K}}\)).
Heading towards a scaling result for the Tartar square, for \(F\in {\mathcal {K}}^{qc}\) arbitrary but fixed, we set

Associated with this definition we consider two natural choices for the possible classes of deformations among which we minimize: Fixing the mean value of \(\nabla u\) we consider
In this case we always (for instance, for the elastic energy (5)) identify \([0,1]^2\) with the torus \({\mathbb {T}}^2\) of side length one and in addition also assume that the phase indicators \(\chi _j\) are one-periodic functions. As an alternative, we fix affine boundary conditions for u and study for \(F\in {\mathcal {K}}^{qc}\) and \(b\in {\mathbb {R}}^2\)
In order to regain some rigidity, we add a singular perturbation. More precisely, modelling the “surface energy” by
for every sufficiently small parameter \(\epsilon >0\), we consider the total energy

The surface energy, being a higher order term, regularizes the problem by penalizing fine oscillations of the phase indicators and hence provides some compactness in the problem (for fixed \(\epsilon >0\)). We emphasize that there are various possible choices in the surface energy penalization ranging from diffuse interface models as in [18, 19, 39], to sharp interface models as in [9] directly penalizing the oscillation of u, or, closer to our choice, penalizations based on the phase indicator functions \(\chi \) as in [5, 6, 34, 35, 55] and in [4, Chapter 12]. While in principle also other types of surface energies, e.g. on other Besov scales, could be considered, if correspondingly rescaled, they are expected to yield analogous results (see for instance [56] where explicitly different Sobolev scales are compared) but possibly require different tools (such as Littlewood-Paley arguments instead of direct Fourier tools). On the one hand, driven by the modelling point of view that the given choice of surface energy can be viewed as a quantitative form of a “physical surface energy penalization” and, on the other hand, in order to prevent additional layers of difficulties and to highlight our main ideas in a model setting, we here focus on the \(L^2\) based, phase indicator model described above.
Seeking to study quantitatively “how rigid” or “how flexible” the Tartar square is, we are interested in deriving a scaling law for the minimal (total) energy as \(\epsilon \rightarrow 0\). As our main result, we obtain the following (up to exponents of logarithms) matching upper and lower scaling bounds:
Theorem 1
Let \(\chi _j\) for \(j=1,\dots ,4\) be as in (4) and let  be defined as in (11). For every \(\epsilon >0\) and \(\nu \in (0,1)\) let
be defined as in (11). For every \(\epsilon >0\) and \(\nu \in (0,1)\) let
where \(c=c_{\nu }>0\) depends on \(\nu >0\) and \(C>0\) is a universal constant. Let  be either given by
be either given by
Assume that \(F \in {\mathcal {K}}^{qc}\setminus {\mathcal {K}}\) and define

Then, there exists an \(\epsilon _0 \in (0,e^{-1})\) such that for every \(\nu \in (0,1)\) and for any \(\epsilon \in (0,\epsilon _0)\) it holds that

Here the constants \(0<C_1\le C_2\) are independent of \(\epsilon \) but may depend on the choice of F and \(0<\epsilon _0<e^{-1}\).
Let us comment on this result. In contrast to other phase transition problems, our scaling law is not polynomial in the small parameter \(\epsilon >0\) but of an order which is converging more slowly as \(\epsilon \rightarrow 0\) than any polynomial in \(\epsilon >0\). This is due to the fact that we are dealing with infinite order laminates. While any finite order laminate is expected to have a polynomial in \(\epsilon \) scaling, our problem becomes degenerate in that an infinite order laminate requires strictly more oscillation than any finite order laminate. In this sense, Theorem 1 captures and quantifies the infinite order of lamination in our problem and thus distinguishes it from many other scaling laws in the literature on phase transformations.
The infinite order of lamination is also directly reflected in our proof of Theorem 1. On the one hand, it directly enters in the (well-known, here quantified) upper bound construction, however it also enters in a more subtle way in the main novelty of our article: the lower bound for which we use a bootstrap iteration argument. Although the lower bound necessitates an ansatz-free argument, it is still strongly reminiscent of the upper bound construction and also the staircase laminate argument from [17]. Seeking to mimic the rigidity argument for the “stress-free” differential inclusion (2) in which one uses that—by the absence of rank-one connections in the set \({\mathcal {K}}\)—the \(\partial _1 u_1\) and the \(\partial _2 u_2\) components of any solution to (2) “determine” each other, we are lead to an interesting Fourier space “chain rule problem” in negative-order Sobolev spaces. More precisely, due to the diagonal structure of the matrices in \({\mathcal {K}}\), the elastic energy yields quantitative control on the partial Riesz transforms \(R_2 \chi _{1,1}\) and \(R_1 \chi _{2,2}\), where the Riesz transform is defined as \(R_j := \partial _j (-\Delta )^{-1}\), \(j\in \{1,2\}\), with \((-\Delta )\) denoting the Laplacian on periodic functions. Since only partial Riesz transforms of the respective functions are controlled, a priori the control of \(R_2 \chi _{1,1}\) and \(R_1 \chi _{2,2} \) does not suffice to conclude direct \(L^2\) bounds on the functions \(\chi _{1,1}\), \(\chi _{2,2}\) but only allows to localize them in conical domains around the coordinate axes in Fourier space. As in the exact differential inclusion, the two functions are however not independent: due to the absence of rank-one connections in \({\mathcal {K}}\) they are functions of each other, i.e. there is a polynomial g such that \(\chi _{1,1} = g(\chi _{2,2})\) and vice versa. Hence, one may hope to deduce information on the Riesz transform \(R_1\chi _{1,1}\) by the information on \(R_1\chi _{2,2} = R_1 g(\chi _{1,1})\) and vice versa. We view this as a (quantitative) “type of chain rule in a negative Sobolev space”. The quantification of this “chain rule type argument in a negative Sobolev space” (see Lemma 4) thus provides the central step in our argument. Careful quantitative bootstrap type estimates of this then allow us to close the estimates for the lower bound.
All in all, our result (and model) thus serves as an extreme case compared to other scaling laws for differential inclusions in phase transformations in that it is an “extremely expensive” construction in which the energy scaling law is no longer algebraic.
1.3 Relation to the literature
Our result should be viewed in the context of scaling laws in the calculus of variations in general and more specifically in the modelling of shape-memory alloys and related phase transformation problems (see [37] and [45] for surveys on this). In the context of the modelling of shape-memory alloys, scaling laws, providing some insights on the possible behaviour of energy minimizers, have been deduced in various settings [3, 5, 6, 8, 9, 14, 15, 20, 34,35,36, 38,39,40,41,42, 55]. For certain models, in subsequent steps, even finer properties (such as for instance almost periodicity results) have been derived [13]. While these methods have provided important insight into many physically relevant problems, none of the known scaling bounds deal with problems in which a dichotomy between rigidity and flexibility is known. Our problem thus addresses a weak form of this dichotomy for the first time in a model case. Moreover, we emphasize that while our result does not directly model a martensitic phase transformation, it is strongly motivated by the commonly used differential inclusions and the arising microstructures as, for instance, used in describing these problems in the stress-free setting [2, 4]. We emphasize that, for instance, in the (geometrically linearized) cubic-to-monoclinic phase transformation, it was shown that closely related \(T_3\)-structures appear [10, 60], for whose more quantitative analysis our investigation seems to be a natural preliminary step.
1.4 Outline of the article
The remainder of the article is structured as follows: in Section 2 we first provide a quantitative version of the (well-known) upper bound construction for the flexibility of the Tartar square. In Section 4, after briefly recalling the (well-known) rigidity argument for the Tartar square and auxiliary properties of the associated elastic energy in Section 3, as the main novelty of our article, we complement the scaling of the upper bound construction with a (nearly) matching lower bound.
1.5 Notation
Throughout the article, when writing \(a\sim b\) we mean that \(c^{-1}b\le a\le c b\) where c is a fixed constant which is independent of \(\epsilon >0\). Analogously, \(a\lesssim b\) and \(a\gtrsim b\) stand for \(a\le c b\) and \(a \ge c b\).
Given \(d, m, n\in {\mathbb {N}}\) and a summable function \(f:\Omega \subset {\mathbb {R}}^d\rightarrow {\mathbb {R}}^{m\times n}\), we denote the average of f on \(\Omega \) by
For every \({\mathbb {T}}^2\)-periodic function \(f:{\mathbb {T}}^2\rightarrow {\mathbb {R}}\) we denote by
its Fourier transform. We will denote with x the space variable and with k the frequency variable. If there is no ambiguity, we will also use the notation \({{\hat{f}}}={{\,\mathrm{{\mathcal {F}}}\,}}(f)\).
2 An Upper Bound Construction
In this section we quantify the total energy of the well-known construction of infinite orders of laminations which is used in the literature to prove flexibility of the Tartar square (see, for instance, [45, Section 2.5]). We stress that this quantitative construction had first been quantified in the literature in [11, 65] (for closely related continuum and finite element models) and that we recall it for completeness here. This construction is an example of a sequence with vanishing elastic energy which is not strongly compact. Balancing the elastic and the surface energy terms through a parameter optimization, as in [11, 65], we obtain an upper bound (in terms of scaling) of our perturbed problem both for the affine and the periodic settings.
2.1 Quantification of the total energy of the infinite-order laminate
In what follows we take into account zero boundary conditions, that is we will define \(u_\epsilon \in {\mathcal {A}}^\mathrm{aff}_0\) and \(\chi _\epsilon \in {\mathcal {X}}^\mathrm{aff}\) for every \(\epsilon >0\) and quantify
The argument is completely analogous for any other affine boundary datum \(Fx +b\) with \(F\in {\mathcal {K}}^{qc}\setminus {\mathcal {K}}\), \(b\in {\mathbb {R}}^2\). Further the construction directly provides the upper-bound estimate of Theorem 1 for both \(E^\mathrm{aff}_\epsilon \) and \(E^\mathrm{per}_\epsilon \) by taking the \({\mathbb {T}}^2\)-periodic extension of \(u_\epsilon \) and \(\chi _\epsilon \).
Since \({\mathcal {K}}\) does not have rank-one connections we make use of some auxiliary matrices (in particular the matrices from (3)) to build laminates of higher and higher order, reducing the volume fraction of the region in which the gradients differ from elements of \({\mathcal {K}}\) but increasing the surface energy.
First-order laminate. Let \(0<r_1<\frac{1}{2}\) be an arbitrarily small parameter to be determined such that \(\frac{1}{r_1}\) is integer. We resolve the boundary datum as a laminate (and a cut-off layer) with gradients
Any other rank-1-convex combination of elements of \({\mathcal {K}}^{qc}\) would lead to an analogous construction. Thanks to the rank-1-connection between \(B_2\) and \(B_1\), we define the continuous function \(v^{(1)}\) such that
and consider, without relabeling, its \(r_1\)-periodic (in the \(x_1\) variable) extension on \([0,1]^2\). We then use a cut-off argument to attain zero boundary conditions on the whole \(\partial [0,1]^2\) by setting \(u^{(1)}\in W^{1,\infty }_0([0,1]^2;{\mathbb {R}}^2)\) as
where \(\varphi (t)=\max (0,\min (2t,1))\). We also set \(\chi ^{(1)}\in BV([0,1]^2;{\mathcal {K}})\) as the pointwise projection of \(\nabla u^{(1)}\) on \({\mathcal {K}}\), see Fig. 1.
It is convenient to view the elastic energy as the sum of two different terms. One corresponds to the volume-fraction of the auxiliary states \(B_1\) and \(B_2\) and it is proportional to the area of \(\{x\in [0,1]^2\,:\,\nabla u^{(1)}(x)\not \in {\mathcal {K}}\}\). The other contribution is given by the cut-off and it is proportional to the area of \([0,1]\times [0,\frac{r_1}{2}]\). Hence, letting \(C=\max \{|M_1-M_2|^2 \,:\, M_1,M_2\in {\mathcal {K}}^{qc}\}\), we have
The surface energy is proportional to the sum of the perimeters of \([(k-1)\frac{r_1}{2},k\frac{r_1}{2}]\times [0,1]\) for \(k=1,\dots ,\frac{2}{r_1}\), that is
Second-order laminate. Let \(0<r_2<\frac{r_1}{2}\) be an arbitrary parameter such that \(\frac{r_1}{r_2}\) is integer. From the fact that
in each rectangle in which \(\nabla u^{(1)}=B_1,B_2\), we replace \(u^{(1)}\) with a simple laminate (up to cut-off) having gradients \(A_1,P_1\) and \(A_3,P_3\) respectively, attaining boundary conditions \(u^{(1)}\). Namely, we take \(v^{(2)}\) to be continuous and such that
We consider its \(r_2\)-periodic (in the \(x_2\) variable) extension on \([0,\frac{r_1}{2}]\times [\frac{r_1}{2},1-\frac{r_1}{2}]\) and put \(v^{(2)}=u^{(1)}\) on \([0,\frac{r_1}{2}]\times \big ([0,\frac{r_1}{2}]\cup [1-\frac{r_1}{2},1]\big )\). We obtain \(u^{(2)}\in W^{1,\infty }_0([0,1]^2;{\mathbb {R}}^2)\) after a cut-off argument in \(\big ([0,\frac{r_2}{2}]\cup [\frac{r_1}{2}-\frac{r_2}{2}]\big )\times [\frac{r_1}{2},1-\frac{r_1}{2}]\) and repeating this analogous construction in all the other parts of the rectangle in which \(\nabla u^{(1)}=B_1,B_2\), using the rank-1-connection between \(A_3\) and \(P_3\) where \(\nabla u^{(1)}=B_2\). Set \(\chi ^{(2)}\in BV([0,1]^2;{\mathcal {K}})\) the projection of \(\nabla u^{(2)}\) on \({\mathcal {K}}\), see Fig. 2.
The elastic energy is given by the sum of two terms; one is proportional to the area of \(\big \{x\in [0,1]^2\,:\,\nabla u^{(2)}(x)=P_1,P_3\big \}\) and the the other is given by the cut-off. The energy of the cut-off of the current step gives a contributions of order \(r_2\) for every rectangle in which \(\nabla u^{(1)}=B_1,B_2\) that are \(\frac{2}{r_1}\) many; namely,
The surface energy is controlled by the perimeters of the rectangles in which \(\nabla u^{(2)}\) is constant; indeed the rank-1-convexity of the cut-off process yields that, connecting \(\nabla u^{(2)}\) to the boundary data (i.e., \(B_1\) and \(B_2\)), the projection of \(\nabla u^{(2)}\) changes at most once. There are \(\frac{4}{r_1 r_2}\) such rectangles each of perimeter smaller than \(2r_1\). Hence,
m-th-order laminate. We define \(u^{(m)}\in W^{1,\infty }_0([0,1]^2;{\mathbb {R}}^2)\) through an iterative procedure starting from \(u^{(2)}\). Thanks to the relation
we replace \(u^{(m-1)}\), in the rectangles in which \(\nabla u^{(m-1)}=P_{j'}\), with \(r_m\)-periodic laminate of gradients \(A_j\) and \(P_j\) obtaining \(u^{(m)}\in W^{1,\infty }_0([0,1]^2;{\mathbb {R}}^2)\) after a cut-off argument to attain \(u^{(m-1)}\) at the boundary of each rectangle. Here \(r_m\) is an arbitrarily small parameter with \(0<r_m<\frac{r_{m-1}}{2}\) and \(\frac{r_{m-1}}{r_m}\) integer. We then set \(\chi ^{(m)}\in BV([0,1]^2;{\mathcal {K}})\) the projection of \(\nabla u^{(m)}\) on \({\mathcal {K}}\).
For every \(m\ge 3\) we have that
The volume fraction of the cut-off regions of the m-th step is \(2\frac{r_m}{r_{m-1}}\). Thus its contribution in the elastic energy is \(2\frac{r_m}{r_{m-1}}\big |\{x\in [0,1]^2\,:\,\nabla u^{(m-1)}(x)=P_1,\dots ,P_4\}\big |\). Hence
The surface energy of the m-th step is proportional to the sum of the perimeters of the rectangles in which \(\nabla u^{(m)}=P_1,\dots ,P_4\). Denoting with \(R_m\in {\mathbb {N}}\) the number of such rectangles, we have
Since the perimeter of each rectangle is \(r_{m-1}\) we get
The total energy of the construction above is therefore
and it depends on \(\{r_j\}_{j=1}^m\). In order to obtain a good upper bound, we determine the optimal choice of such parameters in terms of \(r_1\).
Comparing the terms \(r_1\) and \(\frac{r_2}{r_1}\) we get \(r_2\le r_1^2\). Since the energy depends on \(r_2\) in only another term, that is \(\frac{r_3}{r_2}\), the choice \(r_2\sim r_1^2\) is optimal. Working inductively, we get \(r_j\sim r_1^j\). Thus, we denote with \(u_{m,r}\) and \(\chi _{m,r}\) the functions \(u^{(m)}\) and \(\chi ^{(m)}\) defined as above, corresponding to \(r_j=r^j\), where \(r>0\) is a small parameter. Hence, we have
2.2 Determination of the length scale
From the analysis performed above we obtain the following result, which provides an upper (scaling) bound for Theorem 1.
Proposition 1
Let \(E_\epsilon \) and \(r(\epsilon )\) be defined as in (13) and (12) respectively. For every \(\epsilon >0\) small enough and every \(F\in {\mathcal {K}}^{qc}\setminus {\mathcal {K}}\), there exist  and
and  such that
such that
where \(C>0\) is a constant depending on F.
Proof
As already noticed, it is sufficient to consider affine boundary conditions. The result comes from a parameter optimization in terms of \(\epsilon \) for the constructions \(u_{m,r}\) and \(\chi _{m,r}\) defined in Section 2.1. Determine first the optimal length scale r for the m-th iteration by comparing the terms r and \(\epsilon r^{-m}\) in (15), obtaining \(r\sim \epsilon ^\frac{1}{m+1}\). We now look for the optimal order of iterations \(m_\epsilon \). From \(2^{-m}\sim \epsilon ^\frac{1}{m+1}\) we get \(m_\epsilon \sim |\log (\epsilon )|^\frac{1}{2}\). This gives
for some \(c>0\), which yields the result for \(F=0\) by (15) by taking \(u_\epsilon =u_{m_\epsilon ,r_\epsilon }\) and \(\chi _\epsilon =\chi _{m_\epsilon ,r_\epsilon }\).
The construction corresponding to a non-zero boundary datum differs from \(u^{(m)}\) and \(\chi ^{(m)}\) only in the first step, i.e. \(m=1\), being then completely analogous. Thus it does not affect the scaling of \(E_\epsilon \), i.e. the constant c can be chosen independently of F. Hence the result is proved. \(\square \)
Remark 1
We note that \(r(\epsilon )\) is smaller than any logarithmic scale and greater than any power of \(\epsilon \). Indeed, given \(0<\alpha \le 1\) we get
and
Hence,
Remark 2
We do not claim that our constant \(c>0\) is optimal. It is expected that this depends on the finer properties of the upper bound construction, e.g. on using branched constructions instead of direct laminations. Since the value of the constant \(c>0\) is not the main emphasis of our scaling result, we do not pursue this further in this article.
3 A Qualitative Rigidity Argument and Some Auxiliary Results for the Elastic Energy
In this section, we recall an argument for the exactly stress-free rigidity of the Tartar square which will serve as our guideline for the lower bound estimate. Additionally, we will recall the expression of the elastic energy in Fourier space for different affine boundary conditions which will become a central ingredient in our quantitative lower bound arguments.
3.1 A qualitative rigidity argument
We recall a qualitative rigidity argument which we will mimic in our lower bound estimate.
Proposition 2
Let \(u\in W^{1,\infty }_{loc}({\mathbb {R}}^2;{\mathbb {R}}^2)\) be a solution of the differential inclusion
then \(\nabla u\) is a constant matrix. In particular \(u(x)=A_i x +b\) for some \(i=1,\dots ,4\) and \(b\in {\mathbb {R}}^2\).
Proof
We follow the approach used in [45, proof of Theorem 2.5]. From the fact that the elements of \({\mathcal {K}}\) are diagonal matrices we deduce
thus
for some \(f_1,f_2:{\mathbb {R}}\rightarrow {\mathbb {R}}\). Hence, we obtain
We note that every matrix of \({\mathcal {K}}\) is completely identified by any of its diagonal entries, thus \(-\chi _1 +\chi _3 - 3 \chi _2 + 3 \chi _4\) changes if and only if \(-3 \chi _1 +3\chi _3 + \chi _2-\chi _4 \) does. By (16) this however implies that \(-\chi _1 +\chi _3 - 3 \chi _2 + 3 \chi _4\) is both a function of \(x_1\) only and of \(x_2\) only. Thus, it must be constant. \(\square \)
Note that this is a particular case of the general fact that any Lipschitz solution of \(\nabla u\in {\mathcal {K}}'\) with \({\mathcal {K}}'\subset {\mathbb {R}}^{n\times m}\) of cardinality 4 whose elements are not rank-1-connected is trivial (see [12, Theorem 7]). We also refer to the discussion in [64] (and in particular the section “on the consequences of separate convexity”) for conditions on \(T_4\) structures in diagonal matrices.
Remark 3
We remark that for the exact differential inclusion from Proposition 2, the differential inclusion directly implies that any solution \(u\in W^{1,1}_{loc}({\mathbb {R}}^2,{\mathbb {R}}^2)\) automatically also satisfies \(u \in W^{1,\infty }_{loc}({\mathbb {R}}^2,{\mathbb {R}}^2)\) since \({\mathcal {K}}\subset {\mathbb {R}}^{2\times 2}\) is compact. This explains the restriction to \(u \in W^{1,\infty }_{loc}({\mathbb {R}}^2,{\mathbb {R}}^2)\) in Proposition 2 compared to the natural choice of \(u\in W^{1,1}_{loc}({\mathbb {R}}^2,{\mathbb {R}}^2)\) for the minimization problem from Theorem 1 as a large set in which the energies are defined.
3.2 Elastic energy in Fourier space
We give the expression of the elastic energy \(E_{el}^{\text {per}}\) defined in (7) in Fourier space with periodic boundary conditions, following a standard approach in the literature [5, 35]. It will be useful in the sequel to rewrite \(E_{el}\) in terms of the diagonal entries of \(\chi \), that is,
Lemma 1
Let \(E_{el}^\mathrm{per}\) be defined in (7) and \(\{\chi _j\}\) be as in (4) and \({\mathbb {T}}^2\)-periodic. Then for every \(F\in {\mathbb {R}}^{2\times 2}_{\mathrm{sym}}\) and \(\chi \in {\mathcal {X}}^\mathrm{per}\) it holds that
Proof
We first notice that
We can thus rewrite \(E_{el}^\mathrm{per}(\chi ,F)\) in Fourier space as follows
By minimizing (17) in \({{\hat{v}}}\), we obtain
for every test function \(w\in L^2({\mathbb {T}}^2;{\mathbb {R}}^2)\), which implies that
This is solved by
Substituting these values into (17) we get the result. \(\square \)
In view of the lower-bound estimate which is formulated in Theorem 2 (see the proof in Section 4.5), it is worth noting that from the characterization given in Lemma 1 we have
Remark 4
We highlight that, phrased in different words, the elastic energy controls the partial Riesz transforms
where \(R_j = \partial _j (-\Delta )^{-1}\), \(j\in \{1,2\}\). Related directional derivative control can also be found in [5, 6, 35, 41]. As stressed in [5, Section 3.2], such an only partial control however is related to hyperbolic type equations and cannot be transferred to full \(L^2\) control in general. In order to deduce the desired scaling law, these bounds thus need to be complemented with the structural conditions on the wells. Here the crucial argument consists in the respective “determinedness” of the two functions \(\chi _{1,1}\) and \(\chi _{2,2}\) which is captured quantitatively in Proposition 3 (and originates from the absence of rank-one connections in \({\mathcal {K}}\)).
We further remark that also in more qualitative arguments related to compensated compactness and Morrey’s conjecture, strong, optimal bounds on Riesz transforms have played a major role; see [44] and also [30].
4 A Bootstrap Argument and a Proof of the Lower Bound
In this section, we turn to the proof of the lower bound of Theorem 1. To this end, we will make use of a bootstrap argument which again highlights the infinite order of lamination in our solutions.
In the following Sections, 4.1–4.4 and 4.5, we first consider the case of periodic data and prove a lower bound for \(E^{\text {per}}_{\epsilon }\). Noting that \(E^{\text {per}}_{\epsilon } \lesssim E^{\text {aff}}_{\epsilon }\) then also leads to the desired lower bound result of Theorem 1 in the case of affine boundary conditions (see Section 4.5 for the details).
4.1 A chain rule argument in \(H^{-1}\)
In this section, we prove the following main result which will be used to prove the lower bound of Theorem 1 in Section 4.5:
Proposition 3
Let \(f_1, f_2\in L^\infty ({\mathbb {T}}^2)\cap BV({\mathbb {T}}^2)\) and let \(g, h:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be nonlinear polynomials with \(g(0)=0=h(0)\) such that \(f_2=g(f_1)\) and \(f_1=h(f_2)\). If
then there exists \(0<\epsilon _0<e^{-1}\) depending on d such that for any \(\epsilon \in (0,\epsilon _0)\) and \(\nu >0\) there exists \(C_\nu >0\) with
Throughout this section, all the norms are restricted to \({\mathbb {T}}^2\). Also, for the sake of simplicity, we assume g and h to be polynomials of the same degree \(d\in {\mathbb {N}}\), \(d\ge 2\). Without loss of generality, we may further assume that \(f_1 \ne 0 \ne f_2\) since else the statement follows directly.
We will use that the first inequality in (18) can be phrased in the following two equivalent formulations
This will yield intermediate bounds on the sets where the \(L^2\)-mass of \({{\hat{f}}}_1\) and \({{\hat{f}}}_2\) concentrate which will lead to (19) thanks to a bootstrap argument.
Remark 5
In our application to the singularly perturbed Tartar square, we will apply Proposition 3 with \(f_2=\chi _{1,1}\) and \(f_1=\chi _{2,2}\) (see Section 4.5). In this case, due to the lack of rank-one directions in \({\mathcal {K}}\), it is possible to find corresponding polynomials g and h for which the relations \(f_2=g(f_1)\) and \(f_1=h(f_2)\) hold. These can be chosen via interpolation, e.g.
Such choices of g and h work both in the Dirichlet and in the periodic settings since from the symmetry of Tartar’s square \(h(0)=g(0)=0\). We emphasize that in the setting of the Tartar square the choice of the functions g, h is extremely non-unique.
We refer to Section 4.5 for the details of the application of Proposition 3 to the Tatar square.
4.2 Preliminary considerations
Given two parameters \(\mu ,\mu _2>0\), we define the following compact cones in frequency space (see Fig. 3)
and let \(\chi _{1,\mu ,\mu _2}\), \(\chi _{2,\mu ,\mu _2}\) be smoothed out characteristic functions of \(C_{1,\mu ,\mu _2}\), \(C_{2,\mu ,\mu _2}\), respectively. More precisely, we may, for instance, choose \(\chi _{j,\mu ,\mu _2}\) as smooth functions which on the cones \(C_{j,\mu ,\mu _2}\) are there equal to one and vanish outside \(C_{j,2\mu ,2\mu _2}\). An example of such a choice is given by \(\chi _{j,\mu ,\mu _2}(k)=\varphi (\frac{k_j}{\mu |k|})\varphi (\frac{|k|}{\mu _2})\), where \(\varphi \) is a \(C^{\infty }({\mathbb {R}})\) function supported on \([-2,2]\) which equals 1 on \([-1,1]\) and such that \(\Vert \varphi \Vert _{C^2}\le C\). With the notation \(\chi _{1,\mu ,\mu _2}(D)\), \(\chi _{2,\mu ,\mu _2}(D)\) we will denote the corresponding Fourier multipliers; i.e.,
for every \(f\in L^2({\mathbb {T}}^2)\).
We begin our bootstrap argument, which eventually leads to the proof of Proposition 3, by observing that the functions \(f_1\) and \(f_2\) concentrate their mass in the cones \(C_{1,\mu ,\mu _2}\) and \(C_{2,\mu ,\mu _2}\), respectively.
Since the statements in this subsection are always symmetric between \(f_1\) and \(f_2\) (with only g replaced by h), in this subsection we only state the results for \(f_1\) but emphasize that they are also valid for \(f_2\). The symmetry is first broken in Section 4.3 in which we will then state and use both the bounds for \(f_1\) and \(f_2\).
Lemma 2
Let \(f_1, f_2\) and g be as in the statement of Proposition 3. Then, for every \(\mu , \mu _2>0\) there hold
where \(C>0\) is a constant depending on \(\Vert f_1\Vert _{L^\infty }\) and g. A symmetric statement holds for \(f_2\) and h.
Proof
We divide the proof into three steps, for which the first two steps are general results on arbitrary functions and where only in the last step these results are applied to the specific function \(f_1\).
Step 1. Following the argument in [35, proof of Lemma 4.3], we first show that for a general function \(f: {\mathbb {T}}^2 \rightarrow {\mathbb {R}}\) with \(\Vert f\Vert _{L^{\infty }}<\infty \) and any \({\tilde{\mu }}>0\) it holds that
Indeed, arguing as in [35, proof of Lemma 4.3], for every \(c\in {\mathbb {R}}^2\) we have that
for every \(L>0\). Integrating over \(\partial B_L\) with \(|c|=L\), we deduce that
Choosing \(L={\tilde{\mu }}^{-1}\), we infer the claim.
Step 2. Next we show that for a general function \(f: {\mathbb {T}}^2 \rightarrow {\mathbb {R}}\) with the notation from above, for \(\mu , \mu _2>0\) as above and for \(j\in \{1,2\}\)
Indeed, without loss of generality, we may consider \(j=1\). Passing to the frequency space, we obtain
Step 3. Finally, we conclude the desired result by applying the bounds from Steps 1 and 2 to \(f=f_1\) and \({\tilde{\mu }} = \mu _2\) and recalling the bounds from (20). \(\square \)
Next, we seek to improve the control on the Fourier supports of \(f_1\) and \(f_2\) iteratively. To this end, as a crucial observation, we use that the Fourier support of \(f_2\) is essentially obtained through a nonlinear function interacting with \(f_1\). If \(f_1\) were such that \(\chi _{1,\mu ,\mu _2}(D) f_1\in L^\infty ({\mathbb {T}}^2)\), and with \(M:= \max \{\Vert f_1\Vert _{L^{\infty }}, \Vert \chi _{1,\mu ,\mu _2}(D) f_1\Vert _{L^{\infty }}\}\), this would be a consequence of the local Lipschitz continuity of g: Indeed, by (20), the fact that \(f_2 = g(f_1)\) and the triangle inequality, we would obtain
The same estimate would follow if g was globally a Lipschitz function, without requiring any further assumptions on \(f_1\).
In our application we work with nonlinear functions g which are only locally Lipschitz (cubic polynomials) and we do not a priori know that \({{\hat{f}}}_1\in L^\infty ({\mathbb {T}}^2)\). Hence, even though \(f_1 \in L^{\infty }\), in our setting, we cannot directly proceed as in (21), since Fourier multipliers are in general not bounded as maps from \(L^{\infty }\) to \(L^{\infty }\). Yet we can still control the left-hand-side of (21) in a similar way, obtaining a (small) loss (see Corollary 1).
More precisely, in order to remedy the lack of \(L^{\infty }\) bounds for \(\chi _{1,\mu ,\mu _2}(D)f_1\) and hence the lack of direct Lipschitz continuity arguments, we make use of Calderón-Zygmund estimates in \(L^p\) spaces with \(p\in (1,\infty )\) and interpolation. While this gives rise to a small loss, it will provide our replacement of (21) in Corollary 1.
Lemma 3
Let \(f_1\) and g be as in the statement of Proposition 3. Let \(d\ge 1\) denote the degree of the polynomials g, h. Then for every \(\mu ,\mu '>0\) and any \(\gamma \in (0,1) \) there hold
with \(C'>0\) being a constant depending on \(\Vert f_1\Vert _{L^\infty }\), g and d. A symmetric statement holds for \(f_2\) and h.
Proof
It is sufficient to prove the statement for \(g(t)=t^d\) for some \(d\in {\mathbb {N}}\), \(d\ge 2\). Using the fact that \(a^d-b^d=(a-b)G(a,b)\) where \(G(a,b)=\sum \limits _{j=0}^{d-1} a^{d-1-j}b^{j}\) is \((d-1)\)-homogeneous, by Hölder’s inequality we obtain
for any \(\gamma \in (0,1)\). By means of \(L^p\) interpolation (see for instance [29, Proposition 1.1.14]) we get
Invoking Hölder’s inequality and the explicit form of G(a, b), we further infer that
In order to bound the \(L^p\) norms for \(p\in \{\frac{2+2\gamma }{\gamma }, \frac{(2+2\gamma )(d-1)}{\gamma }\}\) involving the multiplier contributions in the above expressions, we invoke the quantitative \(L^p\)-\(L^p\) boundedness of Fourier multipliers by means of (a version of) the Marcinkiewicz multiplier theorem (see [29, Corollary 6.2.5]) in combination with the transference principle (see, for instance, [29, Theorem 4.3.7]): Indeed, all our multipliers m(D) are of the form \(\chi _{1,\mu ,\mu _2}(D)\) and \(1-\chi _{1,\mu ,\mu _2}(D)\) and hence satisfy for \(j \in \{1,2\}\) and all \(k \in {\mathbb {R}}^2 \setminus \{(0,0)\}\) the quantitative bounds
with a uniformly (in \(\epsilon >0\)) bounded constant \(A>0\). This thus implies that for each \(j\in \{0,\dots ,d-1\}\)
Here \(1<C(\gamma ,d)\le C(\frac{d}{\gamma })^{12}\) (which follows from [29, Theorem 6.2.4 and Corollary 6.2.5]) and is, in particular, independent of \(\mu \) and \(\mu _2\). Combining the previous inequalities we obtain (22) with \(C'=(Cd)^{12(d+1)}\Vert f_1\Vert ^{d-1+\gamma }_{L^{\infty }}\). \(\square \)
As a direct generalization of the previous result, we state an immediate corollary (our replacement of the estimate (21)) which we will use in the next subsection.
Corollary 1
Let \(f_1, f_2, g\) and h be as in the statement of Proposition 3. Let \(d\ge 1\) denote the degree of the polynomials g, h. Then for every \(\mu ,\mu _2>0\) and any \(\gamma \in (0,1) \) there hold
with \(C_0>0\) being a constant depending on \(\Vert f_1\Vert _{L^\infty }\), g, h and d. A symmetric statement holds for \(f_2\) and h.
Proof
Thanks to the triangle inequality, (20) and (22) we have
and therefore (23). \(\square \)
We stress that the constant \(C_0\) introduced in Corollary 1 is the same as that of Proposition 3 and it is chosen to be greater than \(2C+2C'^2+2\), where C and \(C'\) are the constants of Lemmas 2 and 3 , respectively.
4.3 A bootstrap argument
In this section, we carry out our main bootstrap argument. Let us informally explain the strategy of this, before formulating the precise results in the following lemmas. It consists of three main steps:
Step 1: The starting point. As our starting point, we note that Lemma 2 contains the information that the \(L^2\)-mass of the states \(f_1\) and \(f_2\) concentrate (in the frequency space) on the truncated cones \(C_{1,\mu ,\mu _2}\) and \(C_{2,\mu ,\mu _2}\), respectively (Fig. 3). It allows us to control the mass of \(f_1\), \(f_2\) outside of these cones. This information is a direct consequence of the inequalities in (18), which correspond to elastic energy and surface energy controls.
Step 2: Exploiting the “determinedness” of \(f_2\) in terms of \(f_1\) in the form of the estimate (21). As a next step, we seek to improve the bounds on the mass concentration of \(f_1\) and \(f_2\) and to iteratively also control the mass of \(f_1\) and \(f_2\) inside of the cones except for possible concentrations at the origin: To this end, we use that the estimates (20) and its symmetric version for \(f_2\) can be improved by noting that \(f_2=g(f_1)\) and \(f_1=h(f_2)\) with g and h two polynomials of degree \(d\ge 1\). Here, an estimate of the type (21) is crucial, since it allows us to compare the Fourier supports of \(f_1\) and \(f_2 = g(f_1)\) by viewing (21) as
In particular, this implies that the Fourier support of \(f_2\) in the cone \(C_{2,\mu ,\mu _2}\) is determined by the interaction of the nonlinearity g and the Fourier support of \( f_1\) in the cone \(C_{1,\mu , \mu _2}\).
More precisely, assuming that g is a polynomial of degree \(d\ge 1\) and recalling that multiplication in real space turns into convolution in Fourier space, we obtain that the support of \({{\,\mathrm{{\mathcal {F}}}\,}}(g(\chi _{1,\mu ,\mu _2}(D)f_1))\) is contained in the d-fold Minkowski sum of the support of \({{\,\mathrm{{\mathcal {F}}}\,}}(\chi _{1,\mu ,\mu _2}(D)f_1)\):
where \(S_d(M):=\{\sum _{j=1}^d a_j \,:\, (a_1,\dots ,a_d)\in M^d\}\) denotes the d-fold Minkowski sum of \(M\subset {\mathbb {R}}^2\) with itself. Now since
we hence infer that
(see Fig. 4). Combining this with (24), hence implies that the support of \({{\,\mathrm{{\mathcal {F}}}\,}}f_2\) in \(C_{2,\mu ,\mu _2}\setminus C_{2,\mu , \mu _3}\) is quantitatively controlled in terms of the elastic and surface energies and thus that in a quantitative sense \({{\,\mathrm{{\mathcal {F}}}\,}}f_2\) is essentially supported in the smaller cone \(C_{2,\mu , \mu _3}\). These observations are made precise and quantified in Lemma 4 below. Technically, this step involves slight losses in the estimates due to the fact that our nonlinearities are not globally Lipschitz continuous and Calderón-Zygmund type arguments as in Lemma 3 are required.
Step 3: Iteration. Due to the symmetry of the properties of \(f_1\) and \(f_2\) it is then possible to obtain a new estimate of the type (21), now with reversed roles for \(f_1\) and \(f_2\) and for \(f_2\) localized to the smaller cone \(C_{2,\mu , \mu _3}\)
Repeating the Fourier support argument from above with reversed roles for \(f_1\) and \(f_2\), then also implies that the mass of \(f_1\) must concentrate on a smaller cone \(C_{1,\mu ,\mu _4}\) with \(0<\mu _4<\mu _3\) (Fig. 5).
Illustration of the argument in Step 2 of our bootstrap scheme. The red and blue hashed regions depict \(C_{2,\mu ,\mu _3}\) and \(C_{1,\mu ,\mu _2}\), respectively, whereas the hashed light-red region on the left depicts \(C_{2,\mu ,\mu _2}\). The shaded light-blue region on the left represents the Minkowski sum of \(C_{1,\mu ,\mu _2}\) with itself (obtained as a bound on the mass of the convolution). This implies that the mass inside \(C_{2,\mu ,\mu _2}\) actually concentrates in the smaller red cone \(C_{2,\mu ,\mu _3}\) instead of the original cone \(C_{2,\mu ,\mu _2}\) (colour figure online)
Illustration of Step 3 of our bootstrap scheme. The red and blue hashed regions depict \(C_{2,\mu ,\mu _3}\) and \(C_{1,\mu ,\mu _4}\), respectively. The hashed light-blue region on the left depicts \(C_{1,\mu ,\mu _2}\). The shaded light-red region represents the Minkowski sum of \(C_{2,\mu ,\mu _3}\) with itself (colour figure online)
Finally, iterating this process, we obtain that the states \(f_1\) and \(f_2\) concentrate in smaller and smaller cones in frequency space with corresponding \(L^2\)-errors which are controlled by elastic and surface energies, see the induction argument in Lemma 5.
In the following, we make this heuristic argument precise. To this end, from now on, for some \(\alpha \in (0,\frac{1}{4})\) arbitrary but fixed, we define
Such a choice of the parameters will be clear at the final stage of the argument and will allow us to rewrite the right-hand-side of (19) with a multiple of the total energy.
Lemma 4
Let \(f_1\), g be as in the statement of Proposition 3 and let \(d\ge 1\) be the degree of g. Let \(C_0>0\) and \(\gamma >0\) be the constants from Lemma 3 and let \(\alpha \in (0,\frac{1}{4})\) be as above. Then it holds that
where \(\mu _3:=4\sqrt{2}d\epsilon ^{-1+3\alpha }\).
Proof
By the choice of the parameters \(\mu \) and \(\mu _2\) we get
By the properties of Fourier transform and convolution, from the fact that g is polynomial of degree d and from (27) we have that
Now we define \(\chi _{1,\epsilon }\) to be the characteristic function of \(\{k\in {\mathbb {R}}^2 \,:\, |k_1|>4d\epsilon ^{-1+3\alpha }\}\). From (28) and (23) we infer that
This, together with the fact that \(|\chi _{2,\mu ,\mu _2}-\chi _{2,\mu ,\mu _3}|\le \chi _{1,\epsilon }\chi _{2,\mu ,\mu _2}\), yields
Thus, the triangle inequality, (20) and (29) give the result:
using that \(C_0\ge C\). \(\square \)
Next, we iterate this and thus obtain that \(f_1\) and \(f_2\) can always be approximated by functions with smaller and smaller support in Fourier space (see Fig. 5).
Lemma 5
Let \(f_1,f_2,g, h\) be as in the statement of Proposition 3, let \(d\ge 1\) be the degree of g, h and let
for some universal constant \(M>1\). Let \(C_0>0\) and \(\gamma >0\) be the constants from Lemma 3 and let \(\alpha \in (0,\frac{1}{4})\) be as above. Then, for every \(m\in {\mathbb {N}}\) there holds
where \(m_e=2\big \lfloor \frac{m+2}{2}\big \rfloor \) and \(m_o=2\big \lfloor \frac{m+1}{2}\big \rfloor +1\) are respectively the lower even and odd parts of \(m+2\).
Proof
We reason by induction. The induction basis is provided by Lemma 4.
Without loss of generality we may assume \(m\in 2{\mathbb {N}}\), thus \(m_e=m+2\), \(m_o=m+1\) and also \((m-1)_e=m\), \((m-1)_o=m+1\). Assume the inductive hypothesis
to hold true. We now show that the statement remains valid for \((m-1) \rightsquigarrow m \).
Step 1. Here, by the triangle inequality, the fact that \(f_1 =h (f_2)\) and (32) we get
Step 2. We now reason as similarly as in the proof of Lemma 4. From
we infer
Let \(\chi _{2,\epsilon }\) denote the characteristic function of \(\{k\in {\mathbb {R}}^2 : |k_2|>4\mu _{m+1}\mu \}\). Thus, from the fact that \(|\chi _{1,\mu ,\mu _m}-\chi _{1,\mu ,\mu _{m+2}}|\le \chi _{2,\epsilon }\chi _{1,\mu ,\mu _m}\) and recalling (34), we obtain
Thus, by the triangle inequality
We control the first term on the right-hand-side above by means of the inductive hypothesis (32) and the second by the statement of Lemma 3 (applied to \(f_2\) and h) and again (32), that is
Hence, recalling that \(C_0\ge 2+2C'^2\), we infer
which combined with (33) gives the result. \(\square \)
4.4 Proof of Proposition 3
In this section, we conclude the proof of Proposition 3 by combining all the bounds from Sections 4.2–4.3.
Proof of Proposition 3
Step 1: Choices of parameters in the bootstrap iteration. Consider \(m\in 2{\mathbb {N}}\). From Lemma 5 we deduce
We first identify the number of iterations m such that \(\mu _{m+2}<1\), so that the left-hand-side of (3536) reduces to
The condition \(\mu _{m+2}<1\) corresponds to
For (37) to hold for some \(m\in {\mathbb {N}}\) a necessary condition is that \(\alpha \) satisfies \(\alpha |\log (\epsilon )|>\log (Md)\). Under this assumption on \(\alpha \) (which will be satisfied by our choice of \(\alpha \) in terms of \(\epsilon \), see below), (37) is satisfied for \(m>\frac{1}{\alpha }-2\). In particular, a possible choice for m thus is given by \(m=2\big \lfloor \frac{1}{2\alpha }\big \rfloor \). For such a choice of m we arrive at
We now take \(\gamma =\alpha ^2\). Since \(\alpha \) is a small parameter (to be determined) \(\frac{1}{2}<(1-\alpha ^2)^\frac{1}{\alpha }<1\). Thus, recalling the definition of \(\mu = \epsilon ^{\alpha }\) and \(\mu _2 = \epsilon ^{-1+2\alpha }\), we get
Step 2: Optimization. We can further improve the right-hand-side of (38) by noticing that for every \(\nu >0\) and for some constant \(c>0\) depending on d and \(\nu >0\)
which gives
Optimizing in \(\alpha \), we choose \((4C_0e^c)^{\alpha ^{-1-\nu }}\sim \epsilon ^{-2\alpha }\), that is
Notice that taking for instance \(\alpha =|\log (\epsilon )|^{-\frac{1}{2+\nu }}\) the conditions on \(\alpha \) are satisfied for every \(\epsilon \in (0,\epsilon _0)\), where \(0<\epsilon _0<e^{-1}\) depends only on d. We eventually obtain, for every \(\nu '>0\),
\(\square \)
Remark 6
We emphasize that there is no particular reason to choose the exponent \(\frac{1}{2}\) in the exponent of the right hand side of (38). It would have been possible to produce any power in (0, 1). As this does not play a major role in our estimates below, we have simply chosen this power for convenience.
4.5 Application to Tartar’s square and proof of the lower bound from Theorem 1
We now consider the case \(f_1=\chi _{2,2}\) and \(f_2=\chi _{1,1}\), where the phase indicators \(\chi _j\) are defined as in (4). Using the lower bound from Proposition 3 we derive the following lower bound for the elastic energy, which, in particular, yields the proof of the lower bound in Theorem 1 for the periodic setting. We refer to the argument below, which allows us to then also transfer this to the case of affine boundary conditions.
Theorem 2
Let \(E_\epsilon \) be as in (11) and \(r_\nu (\epsilon )\) as in (12). Let \(F\in {\mathcal {K}}^{qc}\). Assume that \(E_{\epsilon }^{\text {per}}(\chi ,F) \le 1\). Then, for every \(\nu \in (0,1)\) and for every \(\chi _j\) for \(j=1,\dots ,4\) as in (4) it holds that,
for every \(\epsilon \in (0,\epsilon _0)\).
Proof
From Lemma 1 and the definition of surface energy (10), the inequalities in (18) hold true with
We set \(r_\nu (\epsilon ):=\exp (-C|\log (\epsilon )|^{\frac{1}{2}+\nu })\). By Proposition 3 we infer
for every \(\nu \in (0,1)\), where \({\bar{\chi }}\) is the mean of \(\chi \).
In order to conclude the argument, we seek to provide a bound on \({{\,\mathrm{dist}\,}}({\overline{\chi }}, F)\). To this end, we invoke the boundary conditions and make use of Jensen’s inequality applied to the elastic energy: For instance, for every \(u\in {\mathcal {A}}^\text {per}_F\),
and taking then the infimum over u we obtain
Now, invoking the triangle inequality in conjunction with (40), (41) and the observation that \(\Vert \chi -F\Vert _{L^2}^2 \ge |{\mathbb {T}}^2|{{\,\mathrm{dist}\,}}^2(F,{\mathcal {K}})\), it follows that for any boundary datum \(F \in {\mathcal {K}}^{qc} \subset {\mathbb {R}}^{2\times 2}\), we have
Multiplying this inequality with \(r_{\nu }(\epsilon )\) and noting that for \(\epsilon \in (0,1)\) and \(E_{\epsilon }^{\text {per}}(\chi ,F)\le 1\) there holds \(r_{\nu }(\epsilon )E_{el}^{\text {per}}(\chi ,F) \le E_\epsilon ^{\text {per}}(\chi ,F)^\frac{1}{2}\), this implies the desired claim. \(\square \)
It is worth remarking that the lower bound of Theorem 2 trivially holds in the case \(F\not \in {\mathcal {K}}^{qc}\) since in this case from relaxation theory one has \(E_{el}^\text {per}(\chi ,F)\ge c>0\) for some constant c depending on F. It should also be noted that, when \(F\in {\mathcal {K}}^{qc}\), the condition \(E_\epsilon (\chi ,F)\le 1\) is not restrictive in the application of this lower bound in that of Theorem 1 due to the upper bound from Proposition 1.
Theorem 2 combined with Proposition 1 proves the main result of this paper, Theorem 1, in the periodic setting.
Last but not least, we now also transfer the lower bound estimate to the case of affine boundary data:
Proof of the lower bound of Theorem 1 in the case of affine boundary conditions
We first note that \({\mathcal {A}}^{\text {aff}}_{F} \subset {\mathcal {A}}^{\text {per}}_{F}\). Since \((L^{\infty }\cap BV)({\mathbb {T}}^2) \subset (L^{\infty }\cap BV)((0,1)^2)\), this implies that for each \(\chi \in (L^{\infty }\cap BV)({\mathbb {T}}^2)\), it holds that
Recalling the trace theorem for BV functions, we further note that any function in \((L^{\infty }\cap BV)((0,1)^2)\) can also be viewed as a function in \((L^{\infty }\cap BV)({\mathbb {T}}^2)\) by periodic extension. Hence, (42) yields that
Here we have used that \(E_{el}^{\text {per}}(\chi ,F){=}E_{el}^{\text {aff}}(\chi ,F)\) and \(E_{surf}^{\text {per}}(\chi ,F){\le } 40E_{surf}^{\text {aff}}(\chi ,F)\), since the periodic extension of the discrete function \(\chi \) may lead to an additional (discrete) jump when interpreting \((0,1)^2 \subset {\mathbb {T}}^2\) with jump amplitude smaller then 10. Combining this with Theorem 2 then also concludes the proof of the lower bound estimate in Theorem 1 in the case of affine boundary conditions. \(\square \)
References
Aumann, R.J., Hart, S.: Bi-convexity and bi-martingales. Israel J. Math. 54(2), 159–180, 1986
Ball, J.M., James, R.D.: Fine phase mixtures as minimizers of energy. Analysis and Continuum Mechanics, pp. 647–686. Springer, 1989
Bella, P., Goldman, M.: Nucleation barriers at corners for a cubic-to-tetragonal phase transformation. Proc. R. Soc. Edinb. Sect. A 145(4), 715–724, 2015
Bhattacharya, K.: Microstructure of Martensite: Why it Forms and How It Gives Rise to the Shape-Memory Effect. Oxford University Press, Oxford Series on Materials Modeling, 2003
Capella, A., Otto, F.: A rigidity result for a perturbation of the geometrically linear three-well problem. Commun. Pure Appl. Math. 62(12), 1632–1669, 2009
Capella, A., Otto, F.: A quantitative rigidity result for the cubic-to-tetragonal phase transition in the geometrically linear theory with interfacial energy. Proc. R. Soc. Edinb. Sect. A 142(2), 273–327, 2012. https://doi.org/10.1017/S0308210510000478.
Casadio-Tarabusi, E.: An algebraic characterization of quasi-convex functions. Ric. Mat. 42(1), 11–24, 1993
Chan, A., Conti, S.: Energy scaling and domain branching in solid-solid phase transitions. Singular Phenomena and Scaling in Mathematical Models, pp. 243–260. Springer, 2014
Chan, A., Conti, S.: Energy scaling and branched microstructures in a model for shape-memory alloys with \(SO(2)\) invariance. Math. Models Methods Appl. Sci. 25(06), 1091–1124, 2015
Chenchiah, I.V., Schlömerkemper, A.: Non-laminate microstructures in monoclinic-I martensite. Arch. Ration. Mech. Anal. 207(1), 39–74, 2013
Chipot, M.: The appearance of microstructures in problems with incompatible wells and their numerical approach. Numer. Math. 83(3), 325–352, 1999. https://doi.org/10.1007/s002110050452.
Chlebík, M., Kirchheim, B.: Rigidity for the four gradient problem. J. Reine Angew Math. 2002(551), 1–9, 2006. https://doi.org/10.1515/crll.2002.082.
Conti, S.: Branched microstructures: scaling and asymptotic self-similarity. Commun. Pure Appl. Math. 53(11), 1448–1474, 2000
Conti, S., Diermeier, J., Melching, D., Zwicknagl, B.: Energy scaling laws for geometrically linear elasticity models for microstructures in shape memory alloys. ESAIM: Control Optim. Calc. Var. 26, 115, 2020
Conti, S., Diermeier, J., Zwicknagl, B.: Deformation concentration for martensitic microstructures in the limit of low volume fraction. Calc. Var. Partial Differ. Equ. 56(1), 16, 2017
Conti, S., Dolzmann, G., Kirchheim, B.: Existence of Lipschitz minimizers for the three-well problem in solid-solid phase transitions. Ann. Inst. H. Poincaré Anal. Non Linéaire 24(6), 953–962, 2007. https://doi.org/10.1016/j.anihpc.2006.10.002
Conti, S., Faraco, D., Maggi, F.: A new approach to counterexamples to \({L}^1\) estimates: Korn’s inequality, geometric rigidity, and regularity for gradients of separately convex functions. Arch. Ration. Mech. Anal. 175(2), 287–300, 2005
Conti, S., Schweizer, B.: Gamma convergence for phase transitions in impenetrable elastic materials. Multi scale problems and asymptotic analysis, GAKUTO Internat. Ser. Math. Sci. Appl., vol. 24, pp. 105–118. Gakkotosho, Tokyo, 2006
Conti, S., Schweizer, B.: Rigidity and gamma convergence for solid-solid phase transitions with so (2) invariance. Commun. Pure Appl. Math.: J. Issued Courant Inst. Math. Sci. 59(6), 830–868, 2006
Conti, S., Zwicknagl, B.: Low volume-fraction microstructures in martensites and crystal plasticity. Math. Models Methods Appl. Sci. 26(07), 1319–1355, 2016
Cordoba, D., Faraco, D., Gancedo, F.: Lack of uniqueness for weak solutions of the incompressible porous media equation. Arch. Ration. Mech. Anal. 200(3), 725–746, 2011
Dacorogna, B.: Direct Methods in the Calculus of Variations, Applied Mathematical Sciences, vol. 78. Springer, 2007
Dacorogna, B., Marcellini, P., Paolini, E.: Origami and partial differential equations. Notices Am. Math. Soc. 57(5), 598–606, 2010
De Lellis, C., Székelyhidi, L., Jr.: The Euler equations as a differential inclusion. Ann. Math. 2, 1417–1436, 2009
Della Porta, F., Rüland, A.: Convex integration solutions for the geometrically nonlinear two-well problem with higher Sobolev regularity. Math. Models Methods Appl. Sci. 30(03), 611–651, 2020
Dolzmann, G., Müller, S.: The influence of surface energy on stress-free microstructures in shape memory alloys. Meccanica 30, 527–539, 1995. https://doi.org/10.1007/BF01557083.
Dolzmann, G., Müller, S.: Microstructures with finite surface energy: the two-well problem. Arch. Ration. Mech. Anal. 132, 101–141, 1995. https://doi.org/10.1007/BF00380505.
Faraco, D., Székelyhidi, L.: Tartar’s conjecture and localization of the quasiconvex hull in \(\mathbb{R}^{2\times 2}\). Acta Math. 200(2), 279–305, 2008
Grafakos, L.: Classical Fourier analysis, Graduate Texts in Mathematics, vol. 250, 2 edn. Springer, 2014
Harris, T.L., Kirchheim, B., Lin, C.C.: Two-by-two upper triangular matrices and morrey’s conjecture. Calculus of Variations and Partial Differential Equations 57(3), 1–12, 2018
Kirchheim, B.: Lipschitz minimizers of the 3-well problem having gradients of bounded variation. MPI preprint, 1998
Kirchheim, B.: Rigidity and geometry of microstructures. MPI-MIS Lecture Notes, 2003
Kirchheim, B., Müller, S., Šverák, V.: Studying nonlinear PDE by geometry in matrix space. Geometric Analysis and Nonlinear Partial Differential Equations, pp. 347–395. Springer, 2003
Knüpfer, H., Kohn, R.V.: Minimal energy for elastic inclusions. Proc. Math. Phys. Eng. Sci. 467(2127), 695–717, 2011
Knüpfer, H., Kohn, R.V., Otto, F.: Nucleation barriers for the cubic-to-tetragonal phase transformation. Commun. Pure Appl. Math. 66(6), 867–904, 2013
Knüpfer, H., Otto, F.: Nucleation barriers for the cubic-to-tetragonal phase transformation in the absence of self-accommodation. ZAMM Z. Angew. Math. Mech. 99(2), e201800179, 2019
Kohn, R.V.: Energy-driven pattern formation. International Congress of Mathematicians, vol. 1, pp. 359–383. European Mathematical Society Zürich, 2007
Kohn, R.V., Müller, S.: Branching of twins near an austenite-twinned-martensite interface. Philos. Mag. A 66(5), 697–715, 1992
Kohn, R.V., Müller, S.: Surface energy and microstructure in coherent phase transitions. Commun. Pure Appl. Math. 47(4), 405–435, 1994
Kohn, R.V., Wirth, B.: Optimal fine-scale structures in compliance minimization for a uniaxial load. Proc. Math. Phys. Eng. Sci. 470(2170), 20140432, 2014
Kohn, R.V., Wirth, B.: Optimal fine-scale structures in compliance minimization for a shear load. Commun. Pure Appl. Math. 69(8), 1572–1610, 2016
Lorent, A.: An optimal scaling law for finite element approximations of a variational problem with non-trivial microstructure. ESAIM: Math. Model. Numer. Anal. 35(5), 921–934, 2001
Matoušek, J., Plecháč, P.: On functional separately convex hulls. Discrete Comput. Geom. 19(1), 105–130, 1998
Müller, S.: Rank-one convexity implies quasiconvexity on diagonal matrices. Int. Math. Res. Notices 1999(20), 1087–1095, 1999
Müller, S.: Variational models for microstructure and phase transitions. Calculus of Variations and Geometric Evolution Problems, pp. 85–210. Springer, 1999
Müller, S., Rieger, M.O., Šverák, V.: Parabolic systems with nowhere smooth solutions. Arch. Ration. Mech. Anal. 177(1), 1–20, 2005
Müller, S., Šverák, V.: Unexpected solutions of first and second order partial differential equations. MPI MIS preprint (1998)
Müller, S., Šverák, V.: Convex integration with constraints and applications to phase transitions and partial differential equations. J. Eur. Math. Soc. 1, 393–422, 1999. https://doi.org/10.1007/s100970050012.
Müller, S., Šverák, V.: Convex integration for Lipschitz mappings and counterexamples to regularity. Ann. Math. (2) 157(3), 715–742, 2003
Müller, S., Sychev, M.A.: Optimal existence theorems for nonhomogeneous differential inclusions. J. Funct. Anal. 181(2), 447–475, 2001
Nesi, V., Milton, G.W.: Polycrystalline configurations that maximize electrical resistivity. J. Mech. Phys. Solids 39(4), 525–542, 1991
Pompe, W.: The quasiconvex hull for the five-gradient problem. Calc. Var. Partial Differ. Equ. 37(3), 461–473, 2010
Rindler, F.: Calculus of Variations. Springer, 2018
Rüland, A.: The cubic-to-orthorhombic phase transition: rigidity and non-rigidity properties in the linear theory of elasticity. Arch. Ration. Mech. Anal. 221(1), 23–106, 2016. https://doi.org/10.1007/s00205-016-0971-5.
Rüland, A.: A rigidity result for a reduced model of a cubic-to-orthorhombic phase transition in the geometrically linear theory of elasticity. J. Elasticity 123(2), 137–177, 2016
Rüland, A., Taylor, J.M., Zillinger, C.: Convex integration arising in the modelling of shape-memory alloys: some remarks on rigidity, flexibility and some numerical implementations. J. Nonlinear Sci. 29, 2137–2184, 2019
Rüland, A., Zillinger, C., Zwicknagl, B.: Higher Sobolev regularity of convex integration solutions in elasticity: the Dirichlet problem with affine data in int(\(K^{lc}\)). SIAM J. Math. Anal. 50(4), 3791–3841, 2018
Rüland, A., Zillinger, C., Zwicknagl, B.: Higher Sobolev regularity of convex integration solutions in elasticity: the planar geometrically linearized hexagonal-to-rhombic phase transformation. J. Elasticity 138, 1–76, 2019. https://doi.org/10.1007/s10659-018-09719-3.
Scheffer, V.: Regularity and Irregularity of Solutions to Nonlinear Second-order Elliptic Systems of Partial Differential-equations and Inequalities, 1974
Schlömerkemper, A., Chenchiah, I.V., Fechte-Heinen, R., Wachsmuth, D.: Upper and lower bounds on the set of recoverable strains and on effective energies in cubic-to-monoclinic martensitic phase transformations. MATEC Web of Conferences, vol. 33, p. 02011. EDP Sciences, 2015
Shvydkoy, R.: Convex integration for a class of active scalar equations. J. Am. Math. Soc. 24(4), 1159–1174, 2011
Šverák, V.: On Tartar’s conjecture. Annales de l’IHP Analyse non linéaire, vol. 10, pp. 405–412, 1993
Székelyhidi, L., Jr.: Counterexamples to elliptic regularity and convex integration. Contemp. Math. 424, 227–246, 2007
Tartar, L.: Some remarks on separately convex functions. Microstructure and Phase Transition, pp. 191–204. Springer, 1993
Winter, M.: An example of microstructure with multiple scales. Eur. J. Appl. Math. 8(2), 185–207, 1997. https://doi.org/10.1017/S0956792597003021.
Acknowledgements
Both authors would like to thank John Ball for bringing the articles [11, 65] to our attention.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open Access funding enabled and organized by Projekt DEAL. Both authors gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through SPP 2256, project ID 441068247. A.R. is a member of the Heidelberg STRUCTURES Excellence Cluster, which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2181/1 - 390900948.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Communicated by I. Fonseca.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rüland, A., Tribuzio, A. On the Energy Scaling Behaviour of a Singularly Perturbed Tartar Square. Arch Rational Mech Anal 243, 401–431 (2022). https://doi.org/10.1007/s00205-021-01729-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-021-01729-1