Abstract
We establish partial regularity for the \(\omega \)-minimizers of quasiconvex functionals of power growth. A first-order partial regularity result of BV \(\omega \)-minimizers is obtained in the linear growth case under a Dini-type condition on \(\omega \). Only assuming the smallness of \(\omega \) near the origin, we show partial Hölder continuity in the subquadratic case by considering a normalised excess.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We investigate the local regularity of maps \(u:\Omega \rightarrow {\mathbb {R}}^N\) that almost minimize a variational functional \({\mathscr {F}}\), which is given by
on \(W^{1,p}(\Omega ,{\mathbb {R}}^N)\), where the integrand \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) is assumed to be strongly quasiconvex (in Morrey’s sense [54]) and of p-growth. See Sect. 2 for any undefined notation.
When the integrand F is of p-growth for \(p\in [1,\infty )\), the functional \({\mathscr {F}}\) is obviously well-defined for \(u\in W^{1,p}(\Omega ,{\mathbb {R}}^N)\). Now assume that \(\Omega \) is a bounded Lipschitz domain. In the case \(p>1\), one can apply the direct method to obtain the existence of a minimizer in the Dirichlet class \(W^{1,p}_g(\Omega ,{\mathbb {R}}^N)\) for some boundary datum \(g\in W^{1,p}(\Omega ,{\mathbb {R}}^N)\). Considering the compactness issue for \(p=1\), we study a suitably relaxed problem in BV instead of working with \(W^{1,1}\) maps. To extend the integral to maps of bounded variation, we follow Lebesgue [48], Serrin [59] and Marcellini [52], and define
An integral expression of \({\mathscr {F}}_g(u,\Omega )\) was found in [46] based on the work by Ambrosio and Dal Maso [4], and Fonseca and Müller [29]. When F is quasiconvex, of linear growth and \(L^1\) mean coercive, we have
where \(\nu _{\Omega }\) is the outward unit normal on \(\partial \Omega \). The third term is present as the trace operator is not continuous with respect to the \(\hbox {weak}^{*}\) topology in BV. We abbreviate the first two terms by
This expression coincides with the extension by area-strict continuity of (1.1) from \(W^{1,1}\) to BV (see [46], Theorem 4).
Our focus in this work is on \(\omega \)-minimizers, which are also called almost minimizers. This concept is closely connected to the elliptic parametric variational problems studied in geometric measure theory (see [3, 12, 23]), where the analogues are called \((F,\varepsilon ,\delta )\)-sets or almost-minimal currents. See [27] for more comments on the connection between the variational problems in our setting and geometric measure theory. It was Anzellotti [6] that first studied \(\omega \)-minimizers in non-parametric problems, and some later work can be found in [21, 24, 25, 58]. The solutions to multiple problems (for instance, minimizers subject to some constraints) are \(\omega \)-minimizers of some suitable functionals. The introduction of this notion, therefore, allows us to unify the study of those problems. We refer to [6, 24, 38] for more background information and some examples.
Definition 1.1
Suppose that \(F:\, {\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) is of p-growth, and \({\mathscr {F}}\) and \({\bar{{\mathscr {F}}}}\) are defined as in (1.1) and (1.4), respectively.
-
(a)
When \(p>1\), a map \(u\in W^{1,p}_{loc}(\Omega ,{\mathbb {R}}^N)\) is said to be an \(\omega \)-minimizer or almost minimizer of \({\mathscr {F}}\) with constant \(R_0>0\), if for any ball
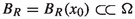 with \(R<R_0\) and any \(v \in W^{1,p}_u(B_R,{\mathbb {R}}^N)\), we have $$\begin{aligned} {\mathscr {F}}(u,B_R) \le {\mathscr {F}}(v,B_R) +\omega (R)\int _{B_R}(1+|\nabla v|^p)\,\mathrm {d}x. \end{aligned}$$(1.5)
with \(R<R_0\) and any \(v \in W^{1,p}_u(B_R,{\mathbb {R}}^N)\), we have $$\begin{aligned} {\mathscr {F}}(u,B_R) \le {\mathscr {F}}(v,B_R) +\omega (R)\int _{B_R}(1+|\nabla v|^p)\,\mathrm {d}x. \end{aligned}$$(1.5) -
(b)
When \(p=1\), a map \(u\in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is said to be an \(\omega \)-minimizer or almost minimizer of \({\bar{{\mathscr {F}}}}\) with constant \(R_0>0\), if for any ball
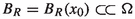 with \(R<R_0\) and any \(v \in BV_u(B_R,{\mathbb {R}}^N)\), we have $$\begin{aligned} {\bar{{\mathscr {F}}}}(u,B_R) \le {\bar{{\mathscr {F}}}}(v,B_R) +\omega (R)\int _{B_R}(1+|Dv|). \end{aligned}$$(1.6)
with \(R<R_0\) and any \(v \in BV_u(B_R,{\mathbb {R}}^N)\), we have $$\begin{aligned} {\bar{{\mathscr {F}}}}(u,B_R) \le {\bar{{\mathscr {F}}}}(v,B_R) +\omega (R)\int _{B_R}(1+|Dv|). \end{aligned}$$(1.6)
Alternatively, we can replace the \(\omega \)-related term by \(\omega (R)\int _{B_R}(1+|\nabla u|^p+|\nabla u-\nabla v|^p)\,\mathrm {d}x\) (\(\omega (R)\int _{B_R}(1+|D u|+|D u-Dv|)\) for \(p=1\)). This definition is more general and appears in some examples. See [24], § 2 for details. We remark that our results (Theorem 1.2 and 1.3) also hold true in this case with only slight modification to the proofs.
Here, the function \(\omega \) is defined on \([0,\infty )\) and is nonnegative. Typically, it is assumed to be small enough near the origin, which explains the word “almost” in the definition above. To be more precise, we assume
-
(\(\varvec{\omega }\) 1) \(\omega :\, [0,\infty )\rightarrow [0,1]\) is nondecreasing, and \(\omega (0) = \lim _{t\rightarrow 0}\omega (t)=0\).
For our first result, the first-order partial regularity, the following properties are furthermore required:
-
(\(\varvec{\omega }\) 2) There exists \(\beta \in (0,1)\) such that \(t\mapsto \frac{\omega (t)}{t^{2\beta }}\) is non-increasing in \((0,\infty )\);
-
(\(\varvec{\omega }\) 3) The Dini-type condition: for any \(\rho >0\), \(\Xi _{\frac{1}{4}}(\rho )<\infty \), where
$$\begin{aligned} \Xi _{\alpha }(\rho ) :=\int _0^{\rho } \frac{\omega ^{\alpha }(t)}{t} \,\mathrm {d}t. \end{aligned}$$
Sometimes, a more specific control of \(\omega \) is assumed:
-
(\(\varvec{\omega }\) 4) \(\omega (t)\le At^{2\beta ^{\prime }}\) for some \(\beta ^{\prime } \in (0,1)\).
In this case, condition (\(\varvec{\omega }\) 3) is satisfied, while (\(\varvec{\omega }\) 2) might not hold anymore. The condition (\(\varvec{\omega }\) 4) can significantly simplify the discussion about \(\omega \).
To state the first result, we also specify the assumptions on F. See (2.3) for the definition of \(E_p\).
-
(H1) \(|F(z)|\le L(1+|z|^p)\) for any \(z\in {\mathbb {R}}^{N\times n}\) with \(L>0\);
-
(H2) F is strongly quasiconvex in the sense that \(F-\ell E_p\) is quasiconvex for some \(\ell >0\);
-
(H3) F is in \(C^{2,1}_{loc}({\mathbb {R}}^{N\times n})\).
Our first result is the partial regularity for the derivatives of \(\omega \)-minimizers:
Theorem 1.2
Suppose that the function F satisfies (H1)-(H3) with \(p=1\), and \(\omega \) satisfies (\(\varvec{\omega }\) 1)-(\(\varvec{\omega }\) 3). If \(u\in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\bar{{\mathscr {F}}}}\), then it is partially regular in the following sense: there exists a relatively closed \({\mathscr {L}}^n\)-null set \(S_u \subset \Omega \) such that u is \(C^1\) on \(\Omega \setminus S_u\). Furthermore, the gradient Du has a local modulus of continuity \(\rho \mapsto \rho ^{\alpha }+\Xi _{\frac{1}{2}}(\rho )\) on \(\Omega \setminus S_u\) for any \(\alpha \in (0,1)\).
In particular, if (\(\varvec{\omega }\) 4) holds, we have \(u \in C^{1,\beta ^{\prime }}_{loc}(\Omega \setminus S_u,{\mathbb {R}}^N)\).
Partial regularity for \(\omega \)-minimizers under the Dini-type condition (like (\(\varvec{\omega }\) 3)) has been done in the super-linear case (see [21, 24, 25]), and the result above gives the counterpart for the end point case (\(p=1\)).
An excess decay estimate plays an important role in our proof of Theorem 1.2. In particular, we need to estimate the series \(\sum _{j=0}^{\infty } \omega ^{\alpha }(\tau ^j R)\) for some \(\alpha , \tau \in (0,1)\) when iterating this process. Such an estimate is essential to control \((Du)_{x_0,R}\) as \(R\rightarrow 0\), and is guaranteed by (\(\varvec{\omega }\) 2) and (\(\varvec{\omega }\) 3). Then it is natural to ask what happens if we only assume the smallness of \(\omega \) near the origin (\(\varvec{\omega }\) 1). In this case, the regularity of Du as above is no longer expected, but it is still possible to get the partial Hölder continuity of u in the subquadratic case (cf. [25]). See Subsec. 4.5 for details. For the second result, a more precise characterisation of the second derivatives of F is required and we replace (H3) by the following with \(L>0\):
-
(H3\(_1\)) F is \(C^2\) with \(|F^{\prime \prime }(z)|\le L(1+\left|z \right|)^{p-2}\) for any \(z\in {\mathbb {R}}^{N\times n}\);
-
(H3\(_2\)) \(F^{\prime \prime }\) is Lipschitz and satisfies
$$\begin{aligned} |F^{\prime \prime }(z_1)-F^{\prime \prime }(z_2)|\le \frac{L|z_1-z_2|}{(1+\left|z_1 \right|+\left|z_2 \right|)^{3-p}}, \quad \text{ for } \text{ any } z_1,z_2 \in {\mathbb {R}}^{N\times n}. \end{aligned}$$
Theorem 1.3
Suppose that the function F satisfies (H1), (H2), (H3\(_{\mathrm{1}}\)) and (H3\(_{\mathrm{2}}\)) with \(1<p<2\), and \(\omega \) satisfies (\(\varvec{\omega }\) 1). If \(u\in W^{1,p}_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\mathscr {F}}\), then it is partially regular in the following sense: there exists a relatively closed \({\mathscr {L}}^n\)-null set \(S^{\prime }_u\subset \Omega \) such that \(u \in C^{0,\alpha }_{loc}(\Omega \setminus S^{\prime }_u,{\mathbb {R}}^N)\) for any \(\alpha \in (0,1)\).
The strategy used for most partial regularity results, which is also followed by us, dates back to De Giorgi and Almgren, who worked on minimal surfaces in the context of geometric measure theory. This method was later adapted by Giusti and Miranda [39] to prove the partial regularity for minimizers in some variational problems, and by Morrey [56] for the solutions to certain elliptic systems. It was Evans [27] that showed the first partial regularity result in the quasiconvex setting. Shortly afterwards, Fusco and Hutchinson [33], and Giaquinta and Modica [35] extended the result to functionals with general integrands \(F(x,u,\nabla u)\), and Acerbi and Fusco [1] dealt with integrands of p-growth with \(p\ge 2\). Carozza, Fusco and Mingione [16] first studied the subquadratic case (\(1<p<2\)), and there are various results afterwards, including [2, 15, 20, 22]. As to the linear growth case (\(p=1\)), there are only limited references. Anzellotti and Giaquinta [7] showed a partial regularity result in the convex case, and some later references for convex functionals include [9,10,11, 36, 58]. Some recent progress in the quasiconvex case is given by Gmeineder and Kristensen [42].
The literature on regularity in quasiconvex settings is extensive, and the list above is far from complete. We refer to [42] and the monograph by Giusti [38] for a thorough review. The question about the size of singular sets in partial regularity results remains open, but see [43,44,45] for some estimates of the Hausdorff dimensions of singular sets in different set-ups.
The key step in our proof is to establish the aforementioned excess decay estimate, which is similar to the one for linear homogeneous elliptic systems with constant coefficients (see, for example, [34], § III.2 ). With a harmonic approximation process and a Caccioppoli-type inequality, one can transfer the estimate for solutions to elliptic systems to (\(\omega \)-)minimizers.
The proofs of the two theorems (Theorem 1.2 and 1.3) are in the same spirit and there are several difficulties especially in our situation. One difficulty appears in the harmonic approximation, where it is impossible to work in the natural space \(W^{1,2}\) for a linear elliptic system. This is due to the lack of integrability in the case \(1\le p<2\). We also emphasize that in the linear-growth case, a weak reverse Hölder inequality is unavailable. Thus, one cannot apply Gehring’s lemma to obtain a higher integrability, which is usually helpful in showing the excess decay estimate. The approximation process in Subsec. 4.3 is adapted from an approach by Gmeineder and Kristensen ([42], § 4.3), and in that process they used a Fubini type property of BV maps and truncation to construct an explicit test map. The difference between minimizers and \(\omega \)-minimizers also leads to an issue, as for the latter there are no Euler-Lagrange equations holding true. However, thanks to the almost-minimality, we are able to establish an Euler-Lagrange type inequality with the help of Ekeland’s variational principle.
Another obstacle turns up in the proof of Theorem 1.3. Since the continuity of \(\nabla u\) does not hold anymore, the excess decay estimate cannot be carried out as in Theorem 1.2. Instead of estimating the typical excess, we normalise it by \(1+|(\nabla u)_{x_0,R}|\) and then try to control the oscillation of \(\nabla u\) on that scale. This method is inspired by [30], where the authors studied elliptic systems (variational functionals) with coefficients a(x, u, Du) (integrands F(x, u, Du)) only continuous in (x, u) in the case \(p\ge 2\). The solutions (minimizers) in this case may be considered as almost minimisers of a family of functionals (see [24], § 2). However, the subquadratic counterpart does not directly follow from the approach in [30] due to the inhomogeneity of our excess integrand \(E_p\). Thus, to switch among different normalising factors, we need to control the ratios between them. A zero-order regularity result for \(\omega \)-minimizers is done in [21] under similar assumptions for the quadratic case (\(p=2\)), and there are similar results in the scalar case in [18, 49, 50, 53].
We believe that the approach used to prove Theorem 1.2 also applies to \(\omega \)-minimizers in the super-linear case (\(p>1\)), which were studied in [21, 24, 25]. In the subquadratic case, an Euler-Lagrange type inequality was also obtained in [25] (Lemma 5), with which the harmonic approximation was carried out indirectly. This method can also be adapted into our case (see Subsec. 4.7 and Remark 5.5).
It is worth mentioning that some variational problems originated from, for example, plasticity, are posed in the space of maps of bounded deformation, where symmetric gradients \(Eu := \frac{1}{2}(Du+Du^{t})\) are considered instead of gradients Du. Two recent pieces of work by Gmeineder [40, 41] present the Sobolev and partial \(C^{1,\alpha }\) regularity theory for BD minimizers. We refer to them and the references therein for the background and existing results in this direction. Moreover, one can consider general elliptic operators and the corresponding variational problems. The trace theorem and the existence of minimizers are established in [14] for functionals defined with \({\mathbb {C}}\)-elliptic operators. Franceschini [31] studied the case of \({\mathbb {R}}\)-elliptic operators and proved the corresponding partial regularity result.
The organisation of this paper is as follows. Section 2 contains some preliminaries, which include the basics of functionals defined on measures and BV maps. Subsection 2.4 presents some background results on elliptic systems, which will be used in the harmonic approximation step. In Sect. 3 we state some auxiliary results about and properties of the integrands involved. The proof of Theorem 1.2 is given in Sect. 4, and is split into six steps. The first goal is to obtain a Hölder-type continuity result of Du, after which we further utilise the boundedness to show regularity to the full extent. At the end we also sketch how to approach our result with an indirect argument. Section 5 is devoted to Theorem 1.3, and some details are omitted since the main steps are similar with those in Sect. 4.
2 Preliminaries
2.1 Basic notation
This subsection is for clarifying the notations used throughout the paper.
The n-dimensional Euclidean space \({\mathbb {R}}^n\) is equipped with the Lebesgue measure \({\mathscr {L}}^n\). Throughout the paper, the symbol \(\Omega \) indicates a bounded open set in \({\mathbb {R}}^n\) with \(n\ge 2\) if not specified. For any measurable set \(S\subset {\mathbb {R}}^n\), if \(0<{\mathscr {L}}^n(S)<\infty \), the average of \(f\in L^1(S,{\mathbb {H}})\) is denoted by

The space \({\mathbb {H}}\) here and in the following is a finite dimensional Hilbert space, and we denote its norm by \(|\cdot |\). For a ball \(B(x,R) \subset {\mathbb {R}}^n\), we may use \(f_{x,R}\) or \(f_R\) to represent \(f_{B(x,R)}\). If \(\mu \) is an \({\mathbb {H}}\)-valued Radon measure on \(\Omega \) and  is a Borel set, the average of \(\mu \) on S is similarly denoted by \(\mu _A(:= \mu (A)/{\mathscr {L}}^n(A))\).
is a Borel set, the average of \(\mu \) on S is similarly denoted by \(\mu _A(:= \mu (A)/{\mathscr {L}}^n(A))\).
When considering a locally integrable function or map, we intend the precise representative of it. For any \(u\in L^1_{loc}(\Omega ,{\mathbb {H}})\), it has an approximate limit \({\tilde{u}}(x)\) \({\mathscr {L}}^n\)-almost everywhere, i.e., for \({\mathscr {L}}^n\)-almost every \(x\in \Omega \) there exists \({\tilde{u}}(x)\in {\mathbb {H}}\) such that

Then \({\tilde{u}}\) is defined on \(\Omega \) except for an \({\mathscr {L}}^n\)-null set and is called the precise representative of u. The meaning of \(u\vert _{\partial B}\) with B being a ball in \(\Omega \) is clear when u has proper regularity, and it is considered as both the trace of \(u: B\rightarrow {\mathbb {H}}\) (when defined) and the pointwise restriction of \({\tilde{u}}\).
The Sobolev spaces \(W^{k,p}(\Omega ,{\mathbb {R}}^N)\) are defined as usual, and see Subsec. 2.3 for the space of maps of bounded variation. For u in \(W^{1,p}(\Omega ,{\mathbb {R}}^N), p\ge 1\) and \(BV(\Omega ,{\mathbb {R}}^N)\), we have the Dirichlet classes
respectively. The map \(w_{u,v}\) above is defined as \(u-v\) in \(\Omega \) and is extended to \({\mathbb {R}}^n\setminus \Omega \) by 0. Notice that we can define \(W^{1,1}_u(\Omega ,{\mathbb {R}}^N)\) with \(u\in BV(\Omega ,{\mathbb {R}}^N)\) for a Lipschitz domain \(\Omega \), as the trace of u exists in \(L^1(\partial \Omega ,{\mathbb {R}}^N)\) and can be considered as that of a map in \(W^{1,1}(\Omega ,{\mathbb {R}}^N)\) (see [37], Chap. 18).
The space of \(N\times n\) matrices with real entries is denoted by \({\mathbb {R}}^{N\times n}\) and equipped with the inner product \(z\cdot w = \text{ tr }(z^{t}w)\) for any \(z,w \in {\mathbb {R}}^{N\times n}\) and the induced norm \(|\cdot |\). Let \(\bigodot ^2({\mathbb {R}}^{N\times n})\) be the space of symmetric and real bilinear forms on \({\mathbb {R}}^{N\times n}\), that is, the space \(\bigodot ^2({\mathbb {R}}^{N\times n})\) consists of maps \({\mathbb {A}}:{\mathbb {R}}^{N\times n}\times {\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}\) such that
for any \(z,z_1,z_2,w \in {\mathbb {R}}^{N\times n}\) and \(a\in {\mathbb {R}}\). The operator norm of \({\mathbb {A}}\in \bigodot ^2({\mathbb {R}}^{N\times n})\) is \(|{\mathbb {A}}|=\sup \{{\mathbb {A}}[z,w]:|z|,|w|\le 1\}\).
Consider an integrand \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\). It is said to be of p-growth (\(p\ge 1\)), if there exists \(L>0\) such that
In particular, the function is of linear growth if \(p=1\). We say the integrand is
-
quasiconvex if for any \(z\in {\mathbb {R}}^{N\times n}\) and any \(\varphi \in C_c^{\infty }((0,1)^n,{\mathbb {R}}^N)\) we have
$$\begin{aligned} \int _{(0,1)^n} F(z+\nabla \varphi )\,\mathrm {d}x \ge F(z); \end{aligned}$$(2.2) -
rank-one convex if \(F(z+t\xi )\) is convex in \(t\in {\mathbb {R}}\) for any \(z,\xi \in {\mathbb {R}}^{N\times n}\) with \(\text{ rank }(\xi )\le 1\) (i.e., \(\xi = a\otimes b\) for some \(a\in {\mathbb {R}}^N, b\in {\mathbb {R}}^n\)).
We refer to [19] for a thorough discussion about different convexity notions. In particular, we will use the fact that quasiconvexity implies rank-one convexity (see [19], Theorem 5.3). When F has sufficient differentiability at a fixed point \(z\in {\mathbb {R}}^{N\times n}\), we consider \(F^{\prime }(z)\) as an \(N\times n\) matrix and \(F^{\prime \prime }(z)\) as a symmetric bilinear form in \(\bigodot ^2({\mathbb {R}}^{N\times n})\).
The reference integrand in the following is a function defined on any finite dimensional Hilbert space (the space is not emphasized in the notation):
In particular, we denote \(E_1\) by E for convenience. More generally, for any \(\mu \ge 0\) define
It is obvious that
Given any \(A\in {\mathbb {R}}^{N\times n}\), set \(E_p^{A}:=E_p^{|A|}\).
The constants c and C throughout this paper may vary from one line to another, and the factors they depend on will be specified when necessary.
2.2 Functionals defined on measures
In this subsection, we recall some background results about functionals defined on measures, that is, functionals with measures instead of only maps as arguments.
Let \(\mu \) be an \({\mathbb {H}}\)-valued Radon measure on an open set \(\Omega \subset {\mathbb {R}}^n\). Then the total variation \(|\mu |\) of it is a real-valued Radon measure on \(\Omega \). \(\mu \) is said to be a bounded Radon measure if \(|\mu |(\Omega )<\infty \). By the Lebesgue-Radon-Nikodym decomposition, \(\mu \) can be decomposed as
Let \(f:{\mathbb {H}}\rightarrow {\mathbb {R}}\) be a Borel function of linear growth. Its recession function is defined by
Hence, the recession function \(f^{\infty }\) is also Borel and positively 1-homogeneous, and satisfies \(|f^{\infty }(z)|\le C|z|\). Now we can define the signed Radon measure \(f(\mu )\): for any Borel set A compactly contained in \(\Omega \), set
For any \(z\in {\mathbb {H}}\), we write \(f(\mu -z)\) as a short-hand of \(f(\mu -z{\mathscr {L}}^n)\). If \(\mu \) is bounded, the definition above can be extended to all Borel subsets of \(\Omega \) and \(f(\mu )\) is a bounded Radon measure on \(\Omega \). If f is in addition assumed to be continuous and the limit superior in the definition of \(f^{\infty }\) is a limit which exists locally uniformly in z, then we say that f admits a regular recession function. The collection of continuous functions with recession functions is denoted by \({\mathbf {E}}_1({\mathbb {H}})\). It is clear that the functions in \({\mathbf {E}}_1({\mathbb {H}})\) are of linear growth.
We now recall the convergence of Radon measures with respect to some particular function f.
Definition 2.1
Suppose that \(\{\mu _j\}\) and \(\mu \) are Radon measures defined on \(\Omega \) such that  in \({\mathcal {M}}(\Omega ,{\mathbb {H}})\) and \(f(\mu _j)(\Omega )\rightarrow f(\mu )(\Omega )\).
in \({\mathcal {M}}(\Omega ,{\mathbb {H}})\) and \(f(\mu _j)(\Omega )\rightarrow f(\mu )(\Omega )\).
-
(a)
\(\mu _j\) is said to converge to \(\mu \) strictly if \(f =|\cdot |\);
-
(b)
\(\mu _j\) is said to converge to \(\mu \) area-strictly if \(f =E\).
Lemma 2.2
Any Radon measure \(\mu \) on \(\Omega \) can be locally area-strictly approximated by smooth maps. If \(\mu \) is bounded on \(\Omega \), the approximation is global.
This can be done by mollification with the help of Theorem 2.2 and 2.34 in [5].
A generalisation of a result by Reshetnyak (see [57] and the appendix of [46]) states that if \(f:{\mathbb {H}}\rightarrow {\mathbb {R}}\) is in \({\mathbf {E}}_1({\mathbb {H}})\), then
for \(\mu _j \rightarrow \mu \) in the area-strict sense. An immediate corollary is that convergence in the area-strict sense implies that in the strict sense.
2.3 Maps of bounded variation
For maps of bounded variation and the relevant results, we refer to [5]. Some definitions and results are stated here for later use.
Consider a bounded open set \(\Omega \subset {\mathbb {R}}^n\). A map \(u :\Omega \rightarrow {\mathbb {R}}^N\) is said to be of bounded variation if it is in \(L^1(\Omega ,{\mathbb {R}}^N)\) and its distributional derivative can be represented by a bounded \({\mathbb {R}}^{N\times n}\)-valued Radon measure, i.e.,
The space of maps of bounded variation is a Banach space under the norm \(\Vert u\Vert _{BV(\Omega )}:= \Vert u\Vert _{L^1(\Omega )}+|Du|(\Omega )\).
Convergence with respect to the BV norm is rather strong and rarely used. Instead, we consider two other forms of convergence: Suppose that \(\{u_j\} \subset BV(\Omega ,{\mathbb {R}}^N)\), \(u\in BV(\Omega ,{\mathbb {R}}^N)\) and \(u_j \rightarrow u\) in \(L^1(\Omega ,{\mathbb {R}}^n)\). We say that \(\{u_j\}\) converges to u in the BV (area-)strict sense if \(\{Du_j\}\) converges to Du in the (area-)strict sense as in Definition 2.1.
It is well-known that smooth maps are dense in \(BV(\Omega ,{\mathbb {R}}^N)\) in the BV area-strict sense:
Lemma 2.3
Let \(\Omega \subset {\mathbb {R}}^n\) be a bounded open set without any additional regularity assumptions on \(\partial \Omega \). If \(u \in BV(\Omega ,{\mathbb {R}}^N)\), there exists a sequence \(\{u_j\} \subset W^{1,1}_u\cap C^{\infty }(\Omega ,{\mathbb {R}}^N)\) such that \(u_j \rightarrow u\) in the BV area-strict sense. If \(u \in W^{1,1}(\Omega ,{\mathbb {R}}^N)\), we can further require strong convergence in \(W^{1,1}(\Omega ,{\mathbb {R}}^N)\).
See [47], Lemma 1 for a proof. The following lemma allows us to approximate a map of bounded variation in energy and is helpful in various cases. See Theorem 4 in [46] for details.
Lemma 2.4
Suppose that \(G:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) is rank-one convex and of linear growth. If \(\Omega \subset {\mathbb {R}}^n\) is a bounded Lipschitz domain, \(u_j,u\in BV(\Omega ,{\mathbb {R}}^N)\) and \(u_j \rightarrow u\) in the BV area-strict sense, then
The two lemmas above give a direct corollary:
Lemma 2.5
Suppose that \(\Omega \subset {\mathbb {R}}^n\) is a bounded Lipschitz domain. For any \(u\in BV(\Omega ,{\mathbb {R}}^N)\), there exists a sequence \(\{u_j\}\subset W^{1,1}_u\cap C^{\infty }(\Omega ,{\mathbb {R}}^N)\) such that \(u_j\rightarrow u\) in the BV area strict sense. Furthermore, for any function \(G:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) that is rank-one convex and of linear growth, we have
Remark 2.6
Notice that \(E(\cdot -z_0)\) for any \(z_0\in {\mathbb {R}}^{N\times n}\) is convex by (3.3), and thus rank-one convex. Obviously it is of linear growth and then Lemma 2.5 applies to \(E(\cdot -z_0)\). The lemma also holds for functions satisfying (H2) with \(p=1\) as quasiconvexity implies rank-one convexity.
The next result is a Fubini-type property for BV maps. It involves BV maps on submanifolds of \({\mathbb {R}}^n\), which are well-defined by local charts and partitions of unity. In our case, we only consider \((n-1)\)-spheres, which can be covered by two local charts that correspond to the stereographic projections from two antipodal points. The two charts are taken to be such that they both correspond to a bounded open subset of \({\mathbb {R}}^{n-1}\), over which the induced metric is comparable to the natural one on \({\mathbb {R}}^{n-1}\). Thus, we can apply various results for maps defined on (open subsets of) \({\mathbb {R}}^{n-1}\). For a BV map \(u :\partial B \rightarrow {\mathbb {R}}^N\), we denote its tangential approximate gradient by \(\nabla _{\tau }u\), which exists \({\mathcal {H}}^{n-1}\)-almost everywhere on \(\partial B\). Its tangential distributional derivative is denoted by \(D_{\tau }u\). Indeed, the former is the absolutely continuous part of the latter with respect to  , and the two coincide when \(u \in W^{1,p}(\partial B,{\mathbb {R}}^N)\) with \(p\ge 1\).
, and the two coincide when \(u \in W^{1,p}(\partial B,{\mathbb {R}}^N)\) with \(p\ge 1\).
Lemma 2.7
Let \(B_R\) denote a ball \(B(x_0,R) \subset {\mathbb {R}}^n\) and u be a map in \(BV(B_R,{\mathbb {R}}^N)\). Then for \({\mathscr {L}}^1\)-almost every \(\rho \in (0,R)\), the pointwise restriction \(u\vert _{\partial B_{\rho }}\) coincides with the traces of u from \(B_{\rho }\) and \(B\setminus {\bar{B}}_{\rho }\), and is in \(BV(\partial B_{\rho },{\mathbb {R}}^N)\). For any two radii \(r_1, r_2\) with \(0<r_1<r_2<R\), we can find \(\rho \in (r_1,r_2)\) such that the above holds and the total variation of \(u\vert _{\partial B_{\rho }}\) on \(\partial B_{\rho }\) is bounded by that of u:
This lemma is Lemma 2.3 in [42] and allows us to work on those balls over the boundary of which a BV map has nice properties. To see this, we recall the definition of fractional Sobolev spaces. Let X be an embedded d-submanifold (\(d\le n\)) of \({\mathbb {R}}^n\) and \(s\in (0,1)\), \(r\in (1,\infty )\). The space \(W^{s,r}(X,{\mathbb {R}}^N)\) consists of maps \(u :X\rightarrow {\mathbb {R}}^N\) of which the Gagliardo norm
is finite. The semi-norm is defined by
Lemma 2.8
Let B be a ball \(B(x_0,R) \subset {\mathbb {R}}^n\) and \(v \in BV(\partial B,{\mathbb {R}}^N)\). Then we have \(v\in W^{1-\frac{1}{r},r}(\partial B,{\mathbb {R}}^N)\) and

where \(C=C(n,N,r)>0\). The range of r depends on the dimension:
This lemma is a corollary of several embedding results. See [13], Lemma D.1 for \(n\ge 3\), and [61], Lemma 38.1 and [62], §3.3.1 for \(n=2\). There is also a discussion after Lemma 2.4 in [42].
2.4 Estimates for elliptic systems
We will need some results on Legendre-Hadamard elliptic systems. A bilinear form \({\mathbb {A}}\in \bigodot ^2({\mathbb {R}}^{N\times n})\) is said to satisfy the strong Legendre-Hadamard condition if there exists \(\lambda , \Lambda >0\) such that
We say that u is \({\mathbb {A}}\)-harmonic in some open set \(\Omega \) if it satisfies
in the distributional sense in \(\Omega \).
Lemma 2.9
Suppose that \({\mathbb {A}}\in \bigodot ^2({\mathbb {R}}^{N\times n})\) satisfies (2.11) with some \(\Lambda , \lambda >0\). If \(h \in W^{1,1}(B_R,{\mathbb {R}}^N)\) is \({\mathbb {A}}\)-harmonic in the ball \(B_R=B(x_0,R) \subset {\mathbb {R}}^n\), then h is in \(C^{\infty }(B_R,{\mathbb {R}}^N)\), and for any \(z\in {\mathbb {R}}^{N\times n}\) and some \(c_a=c_a(n,N,\frac{\Lambda }{\lambda })>0\) we have

This lemma is classical and obtained with, for example, the results in [34], § III.2 and [38], § 7.2. The next result is also classical, and see Proposition 2.11 in [42] and the references therein for a proof.
Lemma 2.10
Suppose that \({\mathbb {A}}\in \bigodot ^2({\mathbb {R}}^{N\times n})\) satisfies (2.11) with some \(\Lambda , \lambda >0\). Let \(r\in (1,\infty )\), \(q\in [2,\infty )\) and B be the unit ball in \({\mathbb {R}}^n\).
-
(a)
For any \(g\in W^{1-\frac{1}{r},r}(\partial B,{\mathbb {R}}^N)\), the elliptic system
$$\begin{aligned} \left\{ \begin{aligned}&-\mathrm {div}({\mathbb {A}}\nabla h)=0,&\mathrm {in }\ B\\&h\vert _{\partial B}=g,&\mathrm {on }\ \partial B \end{aligned} \right. \end{aligned}$$(2.14)admits a unique solution \(h\in W^{1,r}(B,{\mathbb {R}}^N)\), and there exists \(C=C(n,N,r, \frac{\Lambda }{\lambda })>0\) such that
$$\begin{aligned} \Vert h\Vert _{W^{1,r}(B,\,{\mathbb {R}}^N)} \le C \left\Vert g \right\Vert _{W^{1-\frac{1}{r},r}(\partial B,\,{\mathbb {R}}^N)}. \end{aligned}$$ -
(b)
For any \(f\in L^q(B,{\mathbb {R}}^N)\), the elliptic system
$$\begin{aligned} \left\{ \begin{aligned}&-\mathrm {div}({\mathbb {A}}\nabla w)=f,&\mathrm {in }\ B\\&w\vert _{\partial B}=0,&\mathrm {on }\ \partial B \end{aligned} \right. \end{aligned}$$(2.15)admits a unique solution \(w\in W^{2,q}\cap W^{1,q}_0(B,{\mathbb {R}}^N)\), and there exists \(C=C(n,N,q, \frac{\Lambda }{\lambda })>0\) such that
$$\begin{aligned} \Vert w\Vert _{W^{2,q}(B,\,{\mathbb {R}}^N)} \le C \Vert f\Vert _{L^q(B,\,{\mathbb {R}}^N)}. \end{aligned}$$
Remark 2.11
If we only consider the gradient \(\nabla h\) above, it is enough to control \(\left\Vert \nabla h \right\Vert _{W^{1,r}(B,{\mathbb {R}}^N)}\) by \([g]_{W^{1-\frac{1}{r},r}(\partial B,\,{\mathbb {R}}^N)}\) with considering \(g-(g)_{\partial B}\). In particular, if \(g\in W^{1,r}(B,{\mathbb {R}}^N)\), its trace \({{\,\mathrm{tr}\,}}_{B}g\) exists in \(W^{1-\frac{1}{r},r}(B,{\mathbb {R}}^N)\) (see [37], Sect. 18.4). The estimate of \(\left\Vert h \right\Vert _{W^{1,r}(B,{\mathbb {R}}^N)}\) in (a) can be then replaced by \(\left\Vert g \right\Vert _{W^{1,r}(B,{\mathbb {R}}^N)}\).
3 Auxiliary results for the integrands
The first two subsections are devoted for estimates of the integrands involved in our proof. Some proofs are omitted and we refer to [42] for details. Two corollaries of the quasiconvexity of F are given in the third subsection.
3.1 Estimates for the reference integrand
We show some properties for the reference integrand \(E_p\) that will be useful later. In the following, only the case \(p\in [1,2)\) is considered.
Obviously, we have that \(E_p(z)\) is \(C^2\), and an elementary calculation gives
Considering the two cases \(p\in (1,2)\) and \(p=1\) separately, we have
Thus, the function \(E_p\) is a convex function. In the following, we only consider \(E_p\) with \(1\le p<2\). By the definition and convexity of \(E_p\), it is easy to get the following:
Lemma 3.1
Suppose that \(1\le p<2\) and set \(a_1 = \sqrt{2}-1, a_2 =1\). Then the following holds
for any \(a>0\) and any \(z,w \in {\mathbb {H}}\).
A corollary of (3.4) is
Lemma 3.2
Let \(1\le p<2\), \(B \subset {\mathbb {R}}^n\) be an open ball and \(u \in L^p(B,{\mathbb {H}})\). Then for any \(z\in {\mathbb {H}}\) we have
When \(p=1\), the function u can be replaced by a bounded \({\mathbb {H}}\)-valued Radon measure, and the inequality holds in the relaxed sense as in (2.6).
It is easy to show this lemma for \(L^p\) maps with (3.5) and Jensen’s inequality, and the estimate for Radon measures follows by mollification.
Lemma 3.3
Let \(1\le p<2\), \(B \subset {\mathbb {R}}^n\) be an open ball and \(f\in L^p(B,{\mathbb {H}})\). Set  , then we have
, then we have

When \({\mathcal {E}}\le a\), it is obvious that the right-hand side can be replaced by \(\sqrt{(2+a){\mathcal {E}}}\). When \(p=1\), we have the analogue holds for bounded \({\mathbb {H}}\)-valued Radon measures.
The above lemma gives the estimate of  in terms of
in terms of  , and can be shown by Jensen’s inequality and taking the inverse of E.
, and can be shown by Jensen’s inequality and taking the inverse of E.
By definition, we know that for \(E_p^A, A\in {\mathbb {R}}^{N\times n}\), the analogues of Lemma 3.1 and 3.2 hold. Moreover, for any \(p\in [1,2)\) there exists \(c=c(p)>0\) such that
3.2 Estimates for the shifted integrand
Given any \(C^2\) function \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\), we define for any \(w \in {\mathbb {R}}^{N\times n}\) the corresponding shifted integrand
Lemma 3.4
Suppose that \(F:{\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}\) is \(C^2\) and satisfies (H2). When \(p\in (1,2)\), there holds, with \(c=c(p)>0\),
for any ball \(B\subset {\mathbb {R}}^n\), \(w\in {\mathbb {R}}^{N\times n}\), \(\varphi \in W^{1,p}_0(B,{\mathbb {R}}^N)\), \(\eta \in {\mathbb {R}}^N\) and \(\xi \in {\mathbb {R}}^n\). For \(p=1\), the corresponding estimates are, with \(C>0\),
The first estimate (3.11) can be showed with the quasiconvexity condition (H2), [16], Lemma 2.1 and (3.9). See [42], Lemma 4.1 for (3.13). The Legendre-Hadamard estimates (3.12) and (3.14) follow from the convexity of \(E_p\) and [28], 5.1.10.
Lemma 3.5
Suppose that \(F:{\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}\) satisfies (H2),(H3) with \(p\in [1,2)\). Then for any \(m>0\) and any \(w\in {\mathbb {R}}^{N\times n}\) satisfying \(|w|\le m\), we have
hold for \(C=C(m,n,N,L,p)>0\). If we assume (H3\(_{\mathrm{1}}\)) alternatively with \(p\in (1,2)\), the estimate becomes
with \(C=C(L,p)>0\).
Proof
The estimate (3.15) can be obtained with direct calculation and Lemma 3.7 by considering the cases \(|z|\le 1\) and \(|z|>1\) separately.
For (3.16), by definition, Taylor’s theorem and (H3\(_1\)), we have the estimate
Lemma 2.1 in [16] implies that the integral in the last line is controlled by \(C(p)(1+\left|w \right|+\left|z \right|)^{p-2}\). The estimate (3.9) then gives the desired result. \(\square \)
Lemma 3.6
Suppose that \(F:{\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}\) satisfies (H2),(H3) with \(p\in [1,2)\). Then for any \(m>0\) and any \(w\in {\mathbb {R}}^{N\times n}\) with \(|w|\le m\), there exists a constant \(C=C(m,n,N,L,p)>0\) such that
Alternatively, with (H3\(_{\mathrm{1}}\)), (H3\(_{\mathrm{2}}\)) and no bound for w, we have
with \(C=C(n,N,L,p)>0\).
Proof
The estimate (3.17) can be easily obtained by considering the two cases separately. When \(|z|\le 1\), there holds
where the last line is from (H3) and that \(w+tz,w\in B(0,m+1)\). In the other case, we estimate the three terms directly with Lemma 3.7:
For (3.18), the proof is in a similar manner. When \(\left|z \right|\le 1+\left|w \right|\), the condition (H3\(_2\)) implies
When \(\left|z \right|>1+\left|w \right|\), the estimate can be obtained in a way similar to (3.19) with Lemma 3.7. \(\square \)
3.3 Local lipschitz continuity and mean coercivity
In this subsection, we state two corollaries of the quasiconvexity of F. One is the local Lipschitz continuity of F and the other is its \(L^p\) mean coercivity.
It is well-known that separately convex functions are locally Lipschitz (see [55], p.112, and [32, 51]). Lemma 2.2 in [8] gives a better estimate constant. As a corollary of the above results, the following lemma gives the growth of the derivative of a quasiconvex integrand.
Lemma 3.7
Suppose that \(G:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) is a real-valued function and of p-growth with \(p\in [1,\infty )\), i.e.,
for some \(L>0\) and any \(z\in {\mathbb {R}}^{N\times n}\). If G is furthermore quasiconvex, then there exists a constant \(C=C(n,N,p)>0\) such that
In particular, G is Lipschitz when \(p=1\).
The next result is the \(L^p\) mean coercivity of F, which helps us control the \(L^p\)-integral of \(|\nabla v|\) for \(v\in W^{1,p}\) by \(\int F(\nabla v)\,\mathrm {d}x\). For a thorough discussion of the connection between coercivity and quasiconvexity, see [17].
Lemma 3.8
Suppose that \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) satisfies (H1) and (H2) with \(p\in [1,2)\). Fix a ball \(B_R=B(x_0,R)\subset {\mathbb {R}}^n\) and \(u\in W^{1,p}(B_R,{\mathbb {R}}^N)\), then there exist \(a_3=a_3(p,\ell ), a_4=a_4(n,N,L,\ell ,p,F) \in {\mathbb {R}}, a_5 = a_5(n,N,L,\ell ,p)>0\) such that

for any \(v\in W^{1,p}_u(B_R,{\mathbb {R}}^N)\).
Proof
First, with the triangle inequality and (3.6) we have

Notice that \(v-u \in W^{1,p}_0(B_R,{\mathbb {R}}^N)\), then (H2) implies

To estimate the integral on the right-hand side, we apply Lemma 3.7 to get

where the \(\sigma \) is to be determined. Combining (3.22)-(3.24), we know that

where \(c_1=c_1(n,N,p,L,\ell )>0, c_2=c_2(p,\ell )>0\). Take \(\sigma = \frac{1}{2c_1}\), then (3.21) follows. \(\square \)
Remark 3.9
The convexity of \(|\cdot |\) together with Remark 2.6 tells us that (3.21) can be extended to maps in \(BV_u(B_R,{\mathbb {R}}^N)\) if \(p=1\).
4 Partial regularity for Du
This section is for the proof of Theorem 1.2. The function F is assumed to grow linearly near \(\infty \) (i.e., \(p=1\)) and we consider BV \(\omega \)-minimizers.
4.1 Caccioppoli-type inequality
We now give a Caccioppoli-type inequality of the second kind, which is a modified version of Proposition 4.3 in [42].
Proposition 4.1
Suppose that \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) satisfies (H1)-(H3) with \(p=1\), and \(u \in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\bar{{\mathscr {F}}}}\) with constant \(R_0>0\), where \(\omega \) satisfies (\(\varvec{\omega }\) 1). Then for any \(m>0\), there exists \(c=c(m,n,N,L, \ell )\ge 1\) such that the following holds: for any  with \(R<R_0\) and any affine map \(a:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) satisfying \(|\nabla a|\le m\), we have
with \(R<R_0\) and any affine map \(a:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) satisfying \(|\nabla a|\le m\), we have
Proof
Let \({\tilde{F}}=F_{\nabla a}\), \({\tilde{u}}=u-a\). Then \({\tilde{u}}\) is an \(\omega \)-minimizer of the relaxed functional corresponding to \({\tilde{F}}\). Fix \(\frac{R}{2}<t<s<R\). Take a smooth cut-off function \(\rho \) between \(B_t\) and \(B_s\) with \(\rho \in C_c^{\infty }(B_s)\) and \(|\nabla \rho |\le \frac{2}{s-t}\), and set \(\varphi = \rho {\tilde{u}}, \psi = (1-\rho ){\tilde{u}}\). Let \(\{\phi _{\varepsilon }\}\) be the standard mollifiers and \(\varphi _{\varepsilon } = \varphi *\phi _{\varepsilon }\), then \(\varphi _{\varepsilon } \in W^{1,1}_0(B_s,{\mathbb {R}}^N)\) when \(\varepsilon <\text{ dist }(\text{ supp }(\rho ),\partial B_s)\).
The strong quasiconvexity of F gives, as in (3.13),
Take \(\varepsilon \rightarrow 0\), then
We can further proceed as follows:
The second term can be estimated by the triangle inequality and (3.6):
Inserting this into the estimate of \(C\int _{B_t}E(D{\tilde{u}})\), we obtain
Now we can apply the hole-filling trick, adding \(C\int _{B_t}E(D{\tilde{u}})\) to both sides, and divide the inequality by \(C+1\). Finally, by the following iteration lemma we have the desired inequality. \(\square \)
Lemma 4.2
Suppose that \(\theta \in (0,1), R>0\) and the two functions \(\Phi , \Psi :(0,R]\rightarrow {\mathbb {R}}\) are positive. \(\Phi \) is bounded, and \(\Psi \) is decreasing with \(\Psi (\sigma \rho ) \le \sigma ^{-2}\Psi (\rho )\) for any \(\rho \in (0,R], \sigma \in (0,1]\). If for any \(\frac{R}{2}\le t<s \le R\) there holds
for some \(B>0\), then we have, for some \(C=C(\theta )>0\),
This lemma is widely used in the proofs of Caccioppoli-type inequalities and can be shown by modifying Lemma 6.1 in [38].
4.2 Euler–lagrange inequality
The minimizers of regular functionals satisfy the corresponding Euler-Lagrange equations. In the case of \(\omega \)-minimizers, we do not have such equations hold anymore, while a corresponding inequality can be obtained instead with the help of Ekeland’s variational principle(see [26] and [38], Theorem 5.6).
Lemma 4.3
(Ekeland variational principle) Suppose that (X, d) is a complete metric space and \({\mathcal {F}}:X \rightarrow {\mathbb {R}}\cup \{\infty \}\) is a lower-semicontinuous function with respect to d, not identically \(\infty \) and has a lower bound. If for some \(u\in X\) and \(\varepsilon >0\) we have
then there exists a \(w\in X\) satisfying the following:
-
(a)
\(d(u,w) \le \sqrt{\varepsilon }\);
-
(b)
\({\mathcal {F}}(w) \le {\mathcal {F}}(u)\);
-
(c)
\({\mathcal {F}}(w) \le {\mathcal {F}}(v)+\sqrt{\varepsilon }d(v,w)\) for any \(v\in X\).
Suppose that \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) satisfies (H1)-(H3) with \(p=1\), \(\omega \) satisfies (\(\varvec{\omega }\) 1) and \(u\in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\bar{{\mathscr {F}}}}\) with constant \(R_0>0\). Take  such that \(R<R_0\), \(|Du|(\partial B_R)=0\) and \(u\vert _{\partial B_R}\in BV(\partial B_R,{\mathbb {R}}^N)\), which is possible by Lemma 2.7. For any \(\delta >0\), Remark 2.6 implies that there exists \(u_{\delta }\in W^{1,1}_u({\mathbb {B}}_R,{\mathbb {R}}^N)\) such that
such that \(R<R_0\), \(|Du|(\partial B_R)=0\) and \(u\vert _{\partial B_R}\in BV(\partial B_R,{\mathbb {R}}^N)\), which is possible by Lemma 2.7. For any \(\delta >0\), Remark 2.6 implies that there exists \(u_{\delta }\in W^{1,1}_u({\mathbb {B}}_R,{\mathbb {R}}^N)\) such that


By the \(\omega \)-minimality of u we know
for any \(v \in BV_u(B_R,{\mathbb {R}}^N)\).
Again from Remark 2.6, we know that
and there exists \(\{v_j\}\subset W^{1,1}_u(B_R,{\mathbb {R}}^N)\) such that \({\mathscr {F}}(v_j,B_R)\rightarrow I\). The mean coercivity of F (Lemma 3.8) implies

where \(\delta _j := {\mathscr {F}}(v_j,B_R)- I \rightarrow 0\) as \(j\rightarrow \infty \), and \(a_6=1+\frac{L-a_4}{a_3}\), \(a_7 =\frac{a_5+L}{a_3}\). Take v to be \(v_j\) in (4.6) and let \(j\rightarrow \infty \), then we have
Set  . From the above estimate of \(\int (1+|Dv_j|)\,\mathrm {d}x\) we can see \(\varepsilon >0\). Then by (4.5) we have
. From the above estimate of \(\int (1+|Dv_j|)\,\mathrm {d}x\) we can see \(\varepsilon >0\). Then by (4.5) we have
where \(\omega _n = {\mathscr {L}}^n(B(0,1))\) is the Lebesgue measure of the unit ball in \({\mathbb {R}}^n\). Consider the complete metric space \(X = W^{1,1}_u(B_R,{\mathbb {R}}^N)\) with  . To apply the Ekeland variational principle Lemma 4.3, we take
. To apply the Ekeland variational principle Lemma 4.3, we take  and replace \(\varepsilon \) by \(\varepsilon +\delta \). Then there is \(w \in W^{1,1}_u(B_R,{\mathbb {R}}^N)\) such that
and replace \(\varepsilon \) by \(\varepsilon +\delta \). Then there is \(w \in W^{1,1}_u(B_R,{\mathbb {R}}^N)\) such that
-
(a)
\(d(u_{\delta },w) \le \sqrt{\varepsilon +\delta }\);
-
(b)
\({\mathcal {F}}(w) \le {\mathcal {F}}(u_{\delta })\);
-
(c)
\({\mathcal {F}}(w) \le {\mathcal {F}}(v) + \sqrt{\varepsilon +\delta }\,d(w,v)\), for any \(v \in X=W^{1,1}_u(B_R,{\mathbb {R}}^N)\).
For any \(\varphi \in W^{1,1}_0(B_R,{\mathbb {R}}^N)\), we take \(v=w+t\varphi \) and insert it into (c) to obtain

Differentiate with respect to t, then we have an Euler-Lagrange inequality

4.3 Harmonic approximation
Now we compare u with a harmonic map h which coincides with it on the boundary of a certain ball. With the estimate of \(u-h\), we are able to transfer some regularity of h to u.
Proposition 4.4
Suppose that the function \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) satisfies (H1)-(H3) with \(p=1\), \(\omega \) satisfies (\(\varvec{\omega }\) 1) and \(u\in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\bar{{\mathscr {F}}}}\) with constant \(R_0>0\). Let \(m>0\) be a fixed constant, \(a:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^N\) be affine with \(\left|\nabla a \right|\le m\) and \({\tilde{F}}:=F_{\nabla a}\). Assume that  is a ball such that \(|Du|(\partial B_R)=0\) and \(u\vert _{\partial B_R} \in BV(\partial B_R,{\mathbb {R}}^N)\). Then the system
is a ball such that \(|Du|(\partial B_R)=0\) and \(u\vert _{\partial B_R} \in BV(\partial B_R,{\mathbb {R}}^N)\). Then the system
admits a unique solution \(h \in W^{1,r}(B_R,{\mathbb {R}}^N)\) such that

The exponent r is as in Lemma 2.8 and \(C=C(m,n,N,\frac{L}{\ell },r)>0\). Furthermore, for any \(q\in (1,\frac{n}{n-1})\), there exists a constant \(C=C(m,n,N,L,\ell ,q)>0\) such that

where  is as in last subsection.
is as in last subsection.
Proof
From (H3) and (3.14) we have that \(|{\tilde{F}}^{\prime \prime }(0)|\le C(m)\) and satisfies the Legendre-Hadamard condition. By Lemma 2.8 we know that \(u\vert _{\partial B_R} \in W^{1-\frac{1}{r},r}(\partial B_R,{\mathbb {R}}^N)\) for a proper r and

Lemma 2.10 implies the existence of a unique solution \(h\in W^{1,r}(B_R,{\mathbb {R}}^N)\) to (4.9). By replacing u by \({\tilde{u}}\), we have the estimate (4.10).
Let \(\delta , u_{\delta }\) and w be as in last subsection. Take an arbitrary \(\varphi \in C_c^{\infty }(B_R,{\mathbb {R}}^N)\), then we have

where \({\tilde{w}}=w-a\) and the last line is obtained with Lemma 3.6 and (4.8). By approximation, \(\varphi \) can be taken in \(W^{1,\infty }_0\cap C^1(B_R,{\mathbb {R}}^N)\). To obtain the desired estimate, we need to find a proper test map \(\varphi \), before which we scale to the unit ball \(B(0,1) (=:B)\).
Define \(\psi :=w-h\), and set
Consider the system, with \({\mathbb {A}}:= {\tilde{F}}^{\prime \prime }(0)\),
where
As \(T(\Psi ) \in L^{\infty }(B_R,{\mathbb {R}}^N)\), the solution \(\Phi \) exists and lies in \(W^{1,s}_0\cap W^{2,s}(B_R,{\mathbb {R}}^N)\) for any \(s>1\). We take \(s>n\) so that by Morrey’s inequality

Thus, the following can be deduced from (4.12)

Setting \(q=s^{\prime }=\frac{s}{s-1}\), we can obtain

Back to \(B_R\), the above inequality becomes

To compare u and h, we decompose \(u-h\) as \((u-u_{\delta })+(u_{\delta }-w)+(w-h)\):

where the third line comes from (4.4) and Poincaré’s inequality, and the fourth the difference between \(u_{\delta }\) and w (see (a)) and (4.17). The term concerning \(w-a\) can be controlled in terms of \(u-a\):

where \(C(\delta )\) is a \(\delta \)-related constant and goes to 0 as \(\delta \rightarrow 0\) (see Remark 2.6). Combining the estimates above and taking \(\delta \rightarrow 0\), we have (4.11) hold. \(\square \)
4.4 Excess decay estimate
For any ball  , define the excess of u as
, define the excess of u as

Proposition 4.5
Suppose that \(F:{\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}\) satisfies (H1)-(H3) with \(p=1\) and \(\omega :[0,\infty ) \rightarrow [0,\infty )\) satisfies (\(\varvec{\omega }\) 1)-(\(\varvec{\omega }\) 3). The map \(u\in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\upomega \)-minimizer of \({\bar{{\mathscr {F}}}}\) with constant \(R_0>0\). If the ball  with \(R<R_0\) is such that
with \(R<R_0\) is such that

for some \(m>0\), then we have
holds for any \(\sigma \in (0,1)\) and any \(q\in (1,\frac{n}{n-1})\) with some \(c=c(m,n,N,L,\ell ,q)>0\).
Proof
When \(\sigma \ge \frac{1}{5}\), (4.19) is easy to show, and thus we only consider the case \(\sigma \in (0,\frac{1}{5})\). Set \(a(x) = u_{B_R} +(Du)_{B_R}(x-x_0)\), \({\tilde{u}}=u-a\) and \({\tilde{F}}=F_{\nabla a}\). Take \(\rho \in (\frac{9}{10}R,R)\) such that \(|D{\tilde{u}}|(\partial B_{\rho })=0\) and \({\tilde{u}}\vert _{\partial B_{\rho }}\in BV(\partial B_{\rho },{\mathbb {R}}^N)\), then by Lemma 2.8 and 2.7, we have \({\tilde{u}}\vert _{\partial B_{\rho }} \in W^{1-\frac{1}{r},r}(\partial B_{\rho },{\mathbb {R}}^N)\) (\(r=\frac{n}{n-1}\) if \(n\ge 3\), \(r\in (1,2)\) if \(n=2\)), and
Let h be the harmonic map determined by (4.9) with R replaced by \({\rho }\). We moreover define
Then Lemma 2.9, Remark 2.11 and (4.20) imply

Then by assumption, it is possible to control \(\left|\nabla a_0 \right|\) as follows

For any \(\sigma \in (0,\frac{1}{5})\), we have \(2\sigma R<\frac{\rho }{2}\). Lemma 3.2 gives

and inequality (4.1) implies

By Lemma 2.9 we have, for \(x\in B_{2\sigma R}\),

The assumption implies  , then Lemma 3.3 can be used to get the last line. Thus, the integral involving \({\tilde{h}}-a_1\) is controlled by the following
, then Lemma 3.3 can be used to get the last line. Thus, the integral involving \({\tilde{h}}-a_1\) is controlled by the following

The term concerning \({\tilde{u}}-{\tilde{h}}\) can be estimated with (4.11):

where  . Considering \(|Du|\le |Du-(Du)_{B_R}|+|(Du)_{B_R}|\), we obtain by assumption that \(\varepsilon \le C\omega (\rho )\). The above estimates (4.21)-(4.24) and the estimate for \(\varepsilon \) together give
. Considering \(|Du|\le |Du-(Du)_{B_R}|+|(Du)_{B_R}|\), we obtain by assumption that \(\varepsilon \le C\omega (\rho )\). The above estimates (4.21)-(4.24) and the estimate for \(\varepsilon \) together give

which is exactly (4.19). \(\square \)
4.5 Iteration
Now it is the time to do iteration with (4.19) and get a first regularity result of u. Before that we present a lemma concerning the summability of \(\omega \) to some power.
Lemma 4.6
For any fixed \(r>0\), \(\alpha \in [\frac{1}{4},1)\) and \(\tau \in (0,1)\), we have
where \(\beta \) is as in (\(\varvec{\omega }\) 2). In particular,
Proof
The idea is to transform the sum on the left-hand side into that of a series of integrals on many subintervals of [0, r]. Indeed, by (\(\varvec{\omega }\) 2)
Summing over j we obtain
\(\square \)
Proposition 4.7
Suppose that \(F:{\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}\) satisfies (H1)-(H3) with \(p=1\), \(\omega :[0,\infty ) \rightarrow [0,\infty )\) satisfies (\(\varvec{\omega }\) 1)-(\(\varvec{\omega }\) 3) and \(u\in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\bar{{\mathscr {F}}}}\) with constant \(R_0>0\). For any \(\alpha \in (\frac{\beta }{2},1)\) and \(m>0\), there exist \(C = C(m,n,N,L,\ell ,\alpha ,\beta )>0,\varepsilon _m>0\) and \(R_1>0\) such that the following holds: if  is such that
is such that
then for any \(0<\rho <R\),
Proof
By Lemma 3.3, we have

if \({\mathscr {E}}(R)\le 1\). Then set \(\varepsilon _m<\frac{1}{3}\) so that  . Meanwhile, we take \(R_1\) such that \(\omega (R_1)<1\). The assumptions of Proposition 4.5 are satisfied and then, for some fixed \(q\in (1,\frac{n}{n-1})\),
. Meanwhile, we take \(R_1\) such that \(\omega (R_1)<1\). The assumptions of Proposition 4.5 are satisfied and then, for some fixed \(q\in (1,\frac{n}{n-1})\),
where \(c=c(m,n,N,L,\ell ,q)\). Set \(C_{m+1}=c(m+1,n,N,L,\ell ,q))\). Take \(\sigma \in (0,\frac{1}{5})\) and then \(\varepsilon _m \in (0,\frac{1}{3})\) such that
In this case, with \(c_1:=C_{m+1}\sigma ^{-(n+2)}\), (4.30) becomes
To do the iteration, we consider the following
-
(\(\mathbf{I }_j\)) \(|(Du)_{B_{\sigma ^jR}}|\le m+1\),
-
(\(\mathbf{II }_j\)) \({\mathscr {E}}(\sigma ^jR) \le \sigma ^{2j\alpha } {\mathscr {E}}(R) +c_2\sqrt{\omega (\sigma ^jR)}\),
-
(\(\mathbf{III }_j\)) \({\mathscr {E}}(\sigma ^j R)\le \varepsilon _m\),
where \(c_2=\frac{c_1}{\sigma ^{\beta }-\sigma ^{2\alpha }}\). The three hold for \(j=0\). Assume that they hold for \(j=0,1,\dots ,k-1\) with \(k\ge 1\) and do induction. Then (\(\mathbf{III }_j\)) together with \(\varepsilon _m<\frac{1}{3}\) implies  . Combining this with (\(\mathbf{I }_j\)) we have, by Proposition 4.5 and the choice of \(\sigma , \varepsilon _m\),
. Combining this with (\(\mathbf{I }_j\)) we have, by Proposition 4.5 and the choice of \(\sigma , \varepsilon _m\),
which actually gives (\(\mathbf{II} _k\)). Take \(\sigma \) and \(R_1\) small enough such that \(\sigma ^{2\alpha }<\frac{1}{2}, c_2\sqrt{\omega (R_1)}<\frac{\varepsilon _m}{2}\), and we furthermore have (\(\mathbf{III} _k\)). Finally, to get (\(\mathbf{I} _k\)) we use the triangle inequality
For any \(j\in \{0,1,\dots ,k-1\}\), by Lemma 3.3, (\(\mathbf{III }_j\)) and (\(\mathbf{II }_j\)) we have

Sum up the above from 0 to \(k-1\) with the help of Lemma 4.6 to obtain
We require
which can be satisfied when \(\varepsilon _m\ll 1, R_1 \ll 1\). Then (\(\hbox {I}_k\)) also holds true. Notice that in the above we have chosen \(\sigma , \varepsilon _m,R_1\) in order such that \(|(Du)_{B_R}|<m, {\mathscr {E}}(R)<\frac{\varepsilon _m}{2}\) and \(R<R_1\) imply (\(\mathbf{I }_j\))-(\(\mathbf{III }_j\)) for any \(j\in {\mathbb {N}}\). Given any \(\rho \in (0,R)\), we can take \(\sigma ^{k+1}R <\rho \le \sigma ^kR\) and get the desired estimate for \({\mathscr {E}}(\rho )\) by controlling it with \({\mathscr {E}}(\sigma ^kR)\). \(\square \)
We claim that there exists a relatively closed null set \(S_u\subset \Omega \) such that \(u \in C_{loc}^1(\Omega \setminus S_u,{\mathbb {R}}^N)\) and Du locally has the modulus of continuity \(\rho \mapsto \rho ^{\alpha }+\Xi _{\frac{1}{4}}(\rho )\) on \(\Omega \setminus S_u\). Actually, for any \(x_0\in \Omega \) such that

one can show that \(Du =\nabla u {\mathscr {L}}^n\) and \(\nabla u\) has the desired modulus of continuity in a neighbourhood of \(x_0\) by Proposition 4.9 in [42] and mollifying the proof of Theorem 2.9 in [38]. Thus, the set \(S_u \subset \Omega \) is relatively closed and null with respect to the Lebesgue measure.
4.6 Improvement of regularity
With the regularity proved above, it is possible to further show that the local modulus of continuity of Du is \(\rho \mapsto \rho ^{\alpha }+\Xi _{\frac{1}{2}}(\rho )\) for any \(\alpha \in (0,1)\). For any open set  , we assume \(\Vert u\Vert _{C^1(\Omega ^{\prime })} \le M(\Omega ^{\prime })<\infty \). Then it is sufficient to perform the procedure in the quadratic case as in [38], § 9.4. For completeness, we sketch the process here.
, we assume \(\Vert u\Vert _{C^1(\Omega ^{\prime })} \le M(\Omega ^{\prime })<\infty \). Then it is sufficient to perform the procedure in the quadratic case as in [38], § 9.4. For completeness, we sketch the process here.
Proposition 4.8
Suppose that \(F:{\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}\) satisfies (H1)-(H3) with \(p=1\), \(\omega :[0,\infty ) \rightarrow [0,\infty )\) satisfies (\(\varvec{\omega }\) 1)-(\(\varvec{\omega }\) 3) and \(u\in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\bar{{\mathscr {F}}}}\) with constant \(R_0>0\). Let \(S_u\) be the relatively closed singular set as in last subsection. Take  and \(M=M(\Omega ^{\prime })>0\) as above. For any ball
and \(M=M(\Omega ^{\prime })>0\) as above. For any ball  with \(R<R_0\), if \(a:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) is an affine map with \(|\nabla a|\le m\) for some \(m>0\), then there exists \(C=C(m,n,N,L,\ell ,M)>0\) such that
with \(R<R_0\), if \(a:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) is an affine map with \(|\nabla a|\le m\) for some \(m>0\), then there exists \(C=C(m,n,N,L,\ell ,M)>0\) such that

Proof
In Proposition 4.1 we have already obtained a Caccioppoli-type inequality with respect to E. By (3.4), we have \(E(\frac{u-a}{R})\le a_2 \frac{|u-a|^2}{R^2}\). To deal with the left-hand side, notice that \(|\nabla (u-a)|\le |\nabla u|+|\nabla a|\le M+m\) and then \(E(\nabla (u-a))\ge C_{M+m} |\nabla (u-a)|^2\). \(\square \)
Proposition 4.9
Suppose that \(F,\omega ,u, S_u, \Omega ^{\prime }\) and \(M(\Omega ^{\prime })\) are as in Proposition 4.8 and \(z_0\in {\mathbb {R}}^{N\times n}\) satisfies \(|z_0|\le m\). There exists \(q>1\) depending on \(m,n,N,L,\ell ,M\) and \(C=C(m,n,N,L,\ell ,M,q)\ge 1\), such that \(|\nabla u-z_0|\in L^{2q}_{loc}(\Omega ^{\prime })\), and for any ball  we have
we have

Proof
Pick \(B_{\rho }=B(x_0,\rho )\subset B(y_0,R)\) with \(\rho <R_0\) and \(a(x)=u_{B_{\rho }}+z_0(x-x_0)\). The average of \(u-a\) on \(B_{\rho }\) vanishes by the definition of a, and then the Sobolev-Poincaré inequality implies

where \(2_{*}=\frac{2n}{n+2}<2\). Combining Proposition 4.8 we have the weak reverse Hölder inequality

The above estimate holds for any ball \(B_{\rho } \subset B(y_0,R)\) with \(\rho <R_0\) and we can replace the \(\omega (\rho )\) on the right-hand side by \(\omega (R)\). By the generalised Gehring lemma (see [34], Chap.V or [60], § 2.3), we know that there is an \(q_0>1\) such that \(|\nabla u-z_0|\in L^{2q}(B(y_0,R))\) for any \(q\in (1,q_0)\) with (4.33) holding true. \(\square \)
To get the regularity of u, we compare it with a harmonic map again, which is now taken as the minimizer of a quadratic functional. Take a ball \(B_R=B(x_0,R)\) with \(R<R_0\) and  and consider
and consider
where \({\mathbb {A}}={\tilde{F}}^{\prime \prime }(0)\) with \({\tilde{F}}=F_{\nabla a}\) and \(a(x)=u_{B_R}+(\nabla u)_{B_{2R}}(x-x_0)\). It is obvious that h is the minimizer of
Lemma 4.10
Let \(F,\omega ,u, S_u,\Omega ^{\prime }, M(\Omega ^{\prime })\) be as in Proposition 4.8, \({\tilde{F}},a, B_R\) and h be as above, and q be the exponent obtained in Proposition 4.9. Then for some \(C=C(n,N,L,\ell ,M,q)>0\) we have

Proof
As \(u\in C^1({\bar{B}}_R,{\mathbb {R}}^N)\), we have \(|\nabla (u-h)|\in L^2(B_R)\) and by (3.14)
The \(\omega \)-minimality of u, Hölder’s inequality and the \(L^2\)-estimate of (4.35) (see [38], §10.4) give
By the \(C^1\) boundedness of u, we have \(|\nabla (u-a)|\le 2M\) and then I can be estimated as follows

The q can be taken smaller than 2 and thus \(|\nabla (u-a)|^{q^{\prime }} \le (2M)^{q^{\prime }-2}|\nabla (u-a)|^2\). The estimate of III is similar with the help of the \(L^p\)-estimate of (4.35) (see [38], Sect. 10.4). Summing up the estimates for I, II and III gives the desired inequality. \(\square \)
Proposition 4.11
Suppose that \(F,\omega ,u, S_u, \Omega ^{\prime }, M(\Omega ^{\prime })\) and q are as in Proposition 4.9. Take a ball \(B(x_0,R)\) such that \(R<R_0\) and  . For any \(\sigma ,\gamma \in (0,1)\) we have
. For any \(\sigma ,\gamma \in (0,1)\) we have
for any \(\gamma \in (0,1)\) with \(C=C(n,N,L,\ell ,M,q,\gamma )>0\), where \({\mathscr {E}}_1\) is the \(L^2\)-excess

Proof
Suppose that h is as in Lemma 4.10. For any \(\rho <R\), the harmonic function h satisfies, by §III.2 in [34],

Then the excess of \(\nabla u\) can be estimated by comparing \(\nabla u\) and \(\nabla h\). With the help of (4.36), we can obtain (4.37). \(\square \)
Replace 2R by R and then the excess estimate is
It indeed holds for \(\sigma \in (0,1)\) as the case \(\sigma \in (\frac{1}{2},1)\) is obvious. Given \(\alpha \in (0,1)\), we take \(\gamma >\alpha \) and do iteration as in Subsec. 4.5. The final statement is as follows: There exist \(\varepsilon _0>0\) and \(R_2\in (0,R_0)\) such that if  satisfies
satisfies
we have
for any \(\rho \in (0,R)\) with some \(C=C(n,N,L,\ell ,M, \alpha )>0\). It is routine to get that \(\nabla u\) has the local modulus of continuity \(\rho \mapsto \rho ^{\alpha }+\Xi _{\frac{1}{2}}(\rho )\). From the discussion at the end of last subsection, it is not hard to see that \(S_u \subset \Sigma _1 \cup \Sigma _2\), where

4.7 Indirect argument
In [25] the authors showed the partial regularity for \(\omega \)-minimizers in the subquadratic case (\(1<p<2\)), where the harmonic approximation is done via an indirect argument. That method can be adapted to the linear growth case in this paper, and a sketch of the proof is in the following. We remark that with this method, only \(C^2\) regularity of F is needed, in other words, we replace (H3) by
-
(H3)\(^{\prime }\) F is \(C^2\) and
$$\begin{aligned} \left|F^{\prime \prime }(z_1)-F^{\prime \prime }(z_2) \right| \le \nu _M(\left|z_1-z_2 \right|)\end{aligned}$$for any \(z_1,z_2 \in B(0,M+1)\), where \(\nu _M\) is concave and non-decreasing on \([0,\infty )\) with \(\nu _M(0)=\lim _{t\rightarrow 0}\nu _M(t)=0\).
The Dini type condition of \(\omega \) can also be relaxed to \(\Xi _{\frac{1}{2}}(\rho )<\infty \) for any \(\rho >0\), as the desired exponent of \(\omega (R)\) is obtained with one attempt in the excess decay estimate.
For this argument, most of the steps in [25] remain the same. The difference is twofold: the Sobolev-Poincaré inequality and the harmonic approximation.
Define two maps V, W on finite dimensional Hilbert spaces (not specified here):
Then we can see that \(|W(\xi )|\le |V(\xi )|\le 2^{\frac{1}{4}}|W(\xi )|\) and \(|W(\cdot )|^2\) is convex.
Theorem 4.12
Let \(B_{R} = B(x_0,R)\subset {\mathbb {R}}^n\) be a ball with \(n\ge 2\). Then for any \(u\in BV(B_{R},{\mathbb {R}}^N)\) there holds

where the constant \(c_s\) depends on n, N. It also holds with W replaced by V.
Proof
Notice that \(|W|^2\) is convex and thus \(\int |W|^2\) is continuous with respect to convergence in the area-strict sense in BV. Thus, we only need to consider maps in \(W^{1,1}\cap C^{\infty }(B_{R},{\mathbb {R}}^N)\), and the general case follows by approximation. For \(x,y \in B_{R}\), it is easy to see \(|x-y|<2R\). Then fix an \(x\in B_{R}\), by Theorem 2 in [25] we have
Integrating with respect to x in \(B_{R}\), we get

To get a higher order integrability of \(W(|u-u_{R}|/R)\), we need the classical Sobolev inequality. Consider \(g = (u-u_{R})/R\) and \(U = W^2(|g|)\). Notice that \(W^2(|\cdot |)\) is Lipschitz, and then \(U \in W^{1,1}(B_{R})\) with
The Sobolev embedding for \(W^{1,1}\) gives

When \(|Du(x)|\ge 1\), from the expression of DU we have
When \(0<|Du(x)|<1\), apply Young’s inequality and then
Thus, the first term on the right-hand side of (4.43) is controlled by

Combining (4.42) we have the desired inequality. \(\square \)
We have obtained a Caccioppoli-type inequality in Proposition 4.1. It is easy to see that \(V^2(t) \sim E(t)\), so we have the Caccioppoli-type inequality with respect to \(V^2\).
Lemma 4.13
Suppose that \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) satisfies (H1),(H2) and (H3)\(^{\prime }\) with \(p=1\), \(\omega \) satisfies (\(\varvec{\omega }\) 1) with constant \(R_0>0\), and \(u \in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\bar{{\mathscr {F}}}}\). Fix \(m>0\), then there exists \(c_c=c_c(m,n,N,L,\ell )\) such that for any  with \(R <R_0\) and affine map \(a: {\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) with \(|\nabla a|\le m\), there holds
with \(R <R_0\) and affine map \(a: {\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) with \(|\nabla a|\le m\), there holds

The \(\omega \)-minimality of u implies that it is almost an \({\mathbb {A}}\)-harmonic map with a proper \({\mathbb {A}}\), to present which we define the excess for u with \(A \in {\mathbb {R}}^{N\times n}\):

When \(x_0\) (and R) and A are fixed, we abbreviate the quantity as \({\mathscr {E}}_2(R) ({\mathscr {E}}_2)\). The following can be showed with the proof of Lemma 4 in [25] by considering \(\nabla u\) and \(D^su\) separately.
Lemma 4.14
(Approximate harmonicity) Suppose that \(F, \omega \) and u are as in Lemma 4.13. For any \(m>0\), there exists \(c_e>0\) depending on mn, N, L such that for any ball  with \(R<R_0\) and any \(A \in {\mathbb {R}}^{N\times n}\) with \(|A|\le m\), we have
with \(R<R_0\) and any \(A \in {\mathbb {R}}^{N\times n}\) with \(|A|\le m\), we have

for any \(\varphi \in C_0^1(B_{R},{\mathbb {R}}^N)\).
With this result, we are able to approximate u by an \({\mathbb {A}}\)-harmonic map by the following lemma:
Lemma 4.15
For any \(\varepsilon >0\), there exists \(\delta = \delta (n,N,\Lambda ,\lambda ,\varepsilon ) \in (0,1]\) such that for any \({\mathbb {A}}\in \bigodot ^2({\mathbb {R}}^{N\times n})\) that satisfies (2.11), any ball \(B_R=B(x_0,R)\subset {\mathbb {R}}^n\) and any \(v\in BV(B_{R},{\mathbb {R}}^n)\) with


there exists an \({\mathbb {A}}\)-harmonic map h satisfying

The proof of this lemma is by contradiction, see Lemma 6 in [25]. The integrals concerning \(\nabla u\) and \(D^su\) need to be considered separately when necessary. Notice that the scaling between \(B_{R}\) and B(0, 1) for BV maps does not hold straightforward but can proved by approximation with \(W^{1,1}\cap C^{\infty }\) maps.
The excess decay estimate can be done with the same procedure as that in [25], Lemma 7. At some points we need to consider the singular part of the integral of a BV map separately, which will not make an essential difference.
Then if a ball  is such that \(|(Du)_R|\le m\), and \({\mathscr {E}}_2(R)\) and R are taken to be small enough, we will have
is such that \(|(Du)_R|\le m\), and \({\mathscr {E}}_2(R)\) and R are taken to be small enough, we will have
The desired partial regularity hence follows.
5 Partial regularity for u
This section is for the proof of Theorem 1.3, which gives the partial Hölder regularity of \(\omega \)-minimizers in the subquadratic case without the Dini-type condition (\(\varvec{\omega }\) 3). The main steps are similar with those in last section, so we omit some details and only present an outline with the difference.
5.1 Caccioppoli-type inequality
To show Theorem 1.3, we need to consider a normalised excess (see (5.12)). Correspondingly, the Caccioppoli-type inequality in this case also contains a normalising factor \((1+|A|)\).
Proposition 5.1
Suppose that \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) satisfies (H1), (H2), (H3\(_1\)) and (H3\(_2\)) with \(p\in (1,2)\), and \(\omega \) satisfies (\(\varvec{\omega }\) 1). The map \(u\in BV_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\mathscr {F}}\) with constant \(R_0>0\). Then for any ball  with \(R<R_0\) and any affine map \(a:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) with \(\nabla a =A\in R^{N\times n}\), there exists a constant \(c=c(n,N,L,\ell ,p)\) independent of a such that
with \(R<R_0\) and any affine map \(a:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) with \(\nabla a =A\in R^{N\times n}\), there exists a constant \(c=c(n,N,L,\ell ,p)\) independent of a such that
Proof
Set \({\tilde{F}}:= F_A\), \({\tilde{u}}=u-a\), and fix \(\frac{R}{2}<t<s<R\). Take a smooth cut-off function between \(B_t\) and \(B_s\) with \(\rho \in C_c^{\infty }(B_s)\) and \(|\nabla \rho |\le \frac{2}{s-t}\), and set \(\varphi = \rho {\tilde{u}}, \psi = (1-\rho ){\tilde{u}}\). Then \(\varphi \in W^{1,p}_0(B_s,{\mathbb {R}}^N)\), and the quasiconvex condition (H2) with (3.11) gives
The rest part can be carried out as in Proposition 4.1 with E replaced by \(E_p^A\). We estimate the term with \(\omega (s)\) as follows
The inequality obtained from above with Lemma 4.2 is
and then (5.1) follows by (2.4). \(\square \)
5.2 Harmonic approximation
The result in this subsection can be obtained by modifying the process in Subsec. 4.2 and 4.3, so we will omit the repetitive part and only give the difference.
Suppose that \(F,\omega \) and u are as in Theorem 1.3, where \(p\in (1,2)\). Take  with \(R<R_0\), and fix \(A \in {\mathbb {R}}^{N\times n}\). Similar with Subsec. 4.2, we have
with \(R<R_0\), and fix \(A \in {\mathbb {R}}^{N\times n}\). Similar with Subsec. 4.2, we have
where  . Consider the complete metric space \(X = W^{1,p}_u(B_R,{\mathbb {R}}^N)\) with
. Consider the complete metric space \(X = W^{1,p}_u(B_R,{\mathbb {R}}^N)\) with

The Ekeland variational principle (Lemma 4.3) then implies the existence of \(w \in W^{1,p}_u(B_R,{\mathbb {R}}^N)\) such that, with  ,
,
-
(a)
\(d(u,w) \le \sqrt{\varepsilon }\);
-
(b)
\({\mathcal {F}}(w) \le {\mathcal {F}}(u)\);
-
(c)
\({\mathcal {F}}(w) \le {\mathcal {F}}(v) + \sqrt{\varepsilon }\,d(w,v)\), for any \(v \in X=W^{1,p}_u(B_R,{\mathbb {R}}^N)\).
Subsequently, we have the Euler-Lagrange inequality: for any \(\varphi \in W^{1,p}_0(B_R,{\mathbb {R}}^N)\) there holds

Proposition 5.2
Suppose that \(F:\, {\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) satisfies (H1), (H2), (H3\(_1\)) and (H3\(_2\)) with \(p\in (1,2)\), and \(\omega \) satisfies (\(\varvec{\omega }\) 1). The map \(u\in W^{1,p}_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\mathscr {F}}\) with constant \(R_0>0\). For any ball  and any affine map \(a:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) with \(\nabla a = A\in {\mathbb {R}}^{N\times n}\), the system
and any affine map \(a:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^N\) with \(\nabla a = A\in {\mathbb {R}}^{N\times n}\), the system
admits a unique solution \(h \in W_u^{1,p}(B_R,{\mathbb {R}}^N)\) such that

where \(C=C(n,N,\frac{L}{\ell },p)>0\). Furthermore, set

and denote \(\frac{r^{\prime }}{p} = \min \{\frac{2}{p},\frac{n}{n-p}\}\) by s, then there exists a constant \(C=C(n,N,L,\ell ,p)>0\) such that

Proof
Define \({\mathbb {A}}:= F^{\prime \prime }(A)(1+\left|A \right|)^{2-p}\). Then from (H3\(_1\)) and Lemma 3.4 we know that \(\left|{\mathbb {A}} \right|\le L\) and the operator satisfies the Legendre-Hadamard condition. Lemma 2.9 and the comment after it indicate that there exists a unique solution \(h\in W^{1,p}_u(B_R,{\mathbb {R}}^N)\) to (5.5) satisfying (5.6).
Set \({\tilde{F}}=F_A, {\tilde{u}}=u-a\) and \({\tilde{w}}=w-a\). As in (4.12), we have, by Lemma 3.6, (5.4), Hölder’s inequality and the fact \(E(z)^p \le c(p)E_p(z)\),

for any \(\varphi \in W^{1,\infty }_0\cap C^1(B_R,{\mathbb {R}}^n)\). To find a proper test map \(\varphi \), we again scale to the unit ball \(B=B(0,1)\), define \(\Phi , \Psi \) and \({\tilde{W}}\) as Proposition 4.4 and consider
where for any \(y\in {\mathbb {R}}^N\)
Then we have \(T_p(\frac{\Psi }{1+\left|A \right|})\in L^{p^{\prime }}(B,{\mathbb {R}}^N)\) and that (5.9) has a unique solution \(\Psi \in W^{1,p^{\prime }}_0\cap W^{2,p^{\prime }}(B,{\mathbb {R}}^N)\) satisfying
Take \(r = \max \{2,\frac{np^{\prime }}{n+p^{\prime }}\}\), which is smaller than \(p^{\prime }\), then \(\left\Vert \nabla \Phi \right\Vert _{L^{p^{\prime }}}\) can be controlled in the following way with the Sobolev embedding
When \(\left|y \right|\le 1\), it is easy to see that \(\left|T_p(y) \right|^r \le \left|y \right|^2 \le \frac{1}{a_1}E_p(y)\). If \(\left|y \right|>1\), we consider two cases:
-
\(\frac{2n}{n+2}\le p <2\), i.e., \(\frac{np^{\prime }}{n+p^{\prime }}\le 2\) and \(r=2\): \((p-1)r =2(p-1)\le p\) as \(p<2\);
-
\(1<p<\frac{2n}{n+2}\), i.e., \(\frac{np^{\prime }}{n+p^{\prime }}>2\) and \(r= \frac{np^{\prime }}{n+p^{\prime }}\): \((p-1)r = \frac{np(p-1)}{n(p-1)+p}<p\).
In both cases, we have \(\left|T_p(y) \right|^r =\left|y \right|^{p-1}r \le \left|y \right|^p\le CE_p(y)\). Thus, with (5.8), (5.11) and the difference between u and w (see (a)), the estimate (5.7) can be obtained as in Proposition 4.4. \(\square \)
5.3 Excess decay estimate
For a ball  , we define the excess
, we define the excess

When the centre \(x_0\) is fixed, we will abbreviate the excess as \({\mathcal {E}}(R)\).
Proposition 5.3
Suppose that \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) satisfies (H1), (H2), (H3\(_1\)) and (H3\(_2\)) with \(p\in (1,2)\), and \(\omega \) satisfies (\(\varvec{\omega }\) 1). The map \(u\in W^{1,p}_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\mathscr {F}}\) with \(R_0>0\). For any \(\sigma \in (0,1)\), there exists \(\varepsilon _1>0\) such that if
for some ball  , then we have
, then we have
where s is as in Proposition 5.2 and \(c_i=c_i(n,N,L,\ell ,p)>0\), \(i=1,2,3\).
Proof
We only consider \(\sigma \in (0,\frac{1}{4})\) as it is obvious when \(\sigma \in [\frac{1}{4},1)\). As in Proposition 4.5, we define \(a(x) = u_{B_R} +(\nabla u)_{B_R}(x-x_0)\), \({\tilde{u}}=u-a\) and \({\tilde{F}}=F_{\nabla a}\). Let h be the harmonic map determined by (5.5) and set
With (2.13) we have

In each step, a different normalising factor is needed, and we now give the comparison of them. The first one is as follows:

where the last line is from Lemma 3.3 if we take \(\varepsilon _1<1\). We further require \(\sigma ^{-n}(3\varepsilon _1)^{\frac{1}{2p}}<\frac{1}{2}\), i.e., \(\varepsilon _1 < \frac{\sigma ^{2np}}{3\cdot 4^p}\), then the above estimate gives
For \(1+|\nabla h(x_0)|\) and \(1+|(\nabla u)_{\sigma R}|\), we have

where the last line follows from (5.17), Hölder’s inequality and Lemma 3.3. Taking \(2(c_4+\sigma ^{-n})(3\varepsilon _1)^{\frac{1}{2p}}<\frac{1}{2}\), i.e., \(\varepsilon _1 < \frac{1}{3\cdot 16^p}(c_4+\sigma ^{-n})^{-2p}\), we have
The comparison between \(1+\left|(\nabla u)_R \right|\) and \(1+\left|\nabla h(x_0) \right|\) is similar:
which implies
Now we estimate \({\mathcal {E}}(\sigma R)\): by (3.5) and (5.18) there holds

The right-hand side can be estimated by the Caccioppoli-type inequality (5.1)

The term involving \(u-a_0\) can be estimated, like in Proposition 4.5, by decomposing \(u-a_0\) into \({\tilde{u}}-{\tilde{h}}\) and \({\tilde{h}}-a_1\). Applying (5.7) and (5.19), we have

The estimate of \(|\nabla ^2 h(x_0) |\) in Lemma 2.9 and (5.19) implies

where we used (3.5) and Jensen’s inequality. Notice that the term \(\varepsilon _{A,p}\) can be estimated with the triangle inequality and Lemma 3.3, and we obtain

Thus, combining (5.20)-(5.23) we have the desired estimate (5.14) of \({\mathcal {E}}(\sigma R)\) under the condition \(\varepsilon _1 < \frac{1}{3}\min \{\frac{\sigma ^{2np}}{4^p}, \frac{1}{16^p}(c_4+\sigma ^{-n})^{-2p}\}\). \(\square \)
5.4 Final conclusion
In this subsection, we use the excess decay estimate above to further obtain a Morrey’s type estimate for \(\nabla u\), which then implies the Hölder regularity of u.
For any \(\alpha \in (0,1)\), we take \(\gamma =p(\alpha -1)+n \in (n-p,n)\).
Proposition 5.4
Suppose that \(F:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}\) satisfies (H1), (H2), (H3\(_1\)) and (H3\(_2\)) with \(p\in (1,2)\), and \(\omega \) satisfies (\(\varvec{\omega }\) 1). The map \(u\in W^{1,p}_{loc}(\Omega ,{\mathbb {R}}^N)\) is an \(\omega \)-minimizer of \({\mathscr {F}}\) with \(R_0>0\). There exist \(R_1 \in (0,R_0), \varepsilon _2 \in (0,1)\) such that for any ball  with
with
we have
for some \(c_5=c_5(n,N,L,\ell ,p,\gamma )>0\), where \(\gamma \in (n-p,n)\) is defined as above.
Proof
Fix the constants \(\sigma , \varepsilon _2\) and \(R_1\) in order:
where r is as in Proposition 5.2, and \(\varepsilon _1\) and \(c_i, i=1,2,3\), are as in Proposition 5.3.
Suppose that for the ball  with some \(R\in (0,R_1)\) there holds
with some \(R\in (0,R_1)\) there holds
We will show that

holds for any \(k\ge 0\) by induction. Obviously, it holds for \(k=0\), and we assume that (A1) holds for some \(k \ge 0\). With our choice of \(\varepsilon _2\), Proposition 5.3 implies
where \(s=\frac{r^{\prime }}{p}\). By (5.25)-(5.27), we know
which thus gives (I\(_{k+1}\)). Therefore, we have (A1) holds for any \(k\in {\mathbb {N}}\).
With (A1) and Lemma 3.3 we have
From the choice of \(\varepsilon _2, \sigma \), it is easy to see
Set \(\lambda (\rho ) := \int _{B_{\rho }}|\nabla u|^p \,\mathrm {d}x\), then the above gives
for any integer \(k\ge 0\). With Lemma 7.3 in [38] we can further obtain
where \(c_5=c_5(n,\gamma , \sigma )\). \(\square \)
Then by a discussion similar to that at the end of Subsec. 4.5, there exists a relatively closed null set \(S^{\prime }_u \subset \Omega \) such that \(|\nabla u|\) is in the Morrey space \(L^{p,\gamma }_{loc}(\Omega \setminus S^{\prime }_u)\). The Sobolev embedding implies that u lies in the Campanato space \({\mathcal {L}}^{p,\gamma +p}_{loc}(\Omega \setminus S^{\prime }_u,{\mathbb {R}}^N)\), which is actually \(C^{0,\alpha }_{loc}(\Omega \setminus S^{\prime }_u,{\mathbb {R}}^N)\) as \(\gamma =p(\alpha -1)+n\). The proof of Theorem 1.3 is then complete.
Remark 5.5
Theorem 1.3 can also be approached by an indirect argument, similar to that in [25] or [30], by choosing normalising factors carefully. For such an argument, the Lipschitz continuity of \(F^{\prime \prime }\) can be relaxed to
-
(H3\(_2\))\(^{\prime }\) For any \(z_1,z_2 \in {\mathbb {R}}^{N\times n}\) we have
$$\begin{aligned} |F^{\prime \prime }(z_1)-F^{\prime \prime }(z_2)|\le \nu \left( \frac{|z_1-z_2|}{1+|z_1|+|z_2|}\right) \frac{1}{(1+|z_1|+|z_2|)^{2-p}}, \end{aligned}$$where \(\nu \) is a concave, non-decreasing function on \([0,\infty )\) with \(\nu (0)=\lim _{t\rightarrow 0}\nu (t)=0\) and \(\nu \le 1\).
Data Availability
Not applicable.
References
Acerbi, E., Fusco, N.: A regularity theorem for minimizers of quasiconvex integrals. Arch. Rational Mech. Anal. 99(3), 261–281 (1987). https://doi.org/10.1007/BF00284509
Acerbi, E., Fusco, N.: Regularity for minimizers of nonquadratic functionals: the case \(1<p<2\). J. Math. Anal. Appl. 140(1), 115–135 (1989). https://doi.org/10.1016/0022-247X(89)90098-X
Almgren, J.F.J.: Existence and regularity almost everywhere of solutions to elliptic variational problems with constraints. Mem. Amer. Math. Soc. 4(165), 1–199 (1976). https://doi.org/10.1090/memo/0165
Ambrosio, L., Dal Maso, G.: On the relaxation in \(BV(\Omega; \mathbb{R}^m)\) of quasi-convex integrals. J. Funct. Anal. 109(1), 76–97 (1992). https://doi.org/10.1016/0022-1236(92)90012-8
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (2000)
Anzellotti, G.: On the \(C^{1,\alpha }\)-regularity of \(\omega \)-minima of quadratic functionals. Boll. Un. Mat. Ital. C (6) 2(1), 196–212 (1983)
Anzellotti, G., Giaquinta, M.: Convex functionals and partial regularity. Arch. Rational Mech. Anal. 102(3), 243–272 (1988). https://doi.org/10.1007/BF00281349
Ball, J.M., Kirchheim, B., Kristensen, J.: Regularity of quasiconvex envelopes. Calc. Var. Partial Differential Equations 11(4), 333–359 (2000). https://doi.org/10.1007/s005260000041
Beck, L., Schmidt, T.: On the dirichlet problem for variational integrals in \(BV\). J. Reine Angew. Math. 674, 113–194 (2013). https://doi.org/10.1515/CRELLE.2011.188
Bildhauer, M.: Convex Variational Problems. Lecture notes in Mathematics, vol. 1818. Nearly Linear and Anisotropic Growth Conditions. Springer, Berlin, Linear (2003). https://doi.org/10.1007/b12308
Bildhauer, M., Fuchs, M.: On a class of variational integrals with linear growth satisfying the condition of \(\mu \)-ellipticity. Rend. Mat. Appl. 7(22), 249–274 (2002)
Bombieri, E.: Regularity theory for almost minimal currents. Arch. Rational Mech. Anal. 78(2), 99–130 (1982). https://doi.org/10.1007/BF00250836
Bourgain, J., Brezis, H., Mironescu, P.: \(H^{\frac{1}{2}}\) maps with values into the circle: minimal connections, lifting, and the ginzburg-landau equation. Publ. Math. Inst. Hautes Études Sci. 99, 1–115 (2004). https://doi.org/10.1007/s10240-004-0019-5
Breit, D., Diening, L., Gmeineder, F.: On the trace operator for functions of bounded \(\mathbb{A}\)-variation. Anal. PDE 13(2), 559–594 (2020). https://doi.org/10.2140/apde.2020.13.559
Carozza, M., Passarelli di Napoli, A.: A regularity theorem for minimisers for quasiconvex integrals: the case \(1<p<2\). Proc. Roy. Soc. Edinburgh Sect. A 126(6), 1181–1199 (1996). https://doi.org/10.1017/S0308210500023350
Carozza, M., Fusco, N., Mingione, G.: Partial regularity of minimizers of quasiconvex integrals with subquadratic growth. Ann. Mat. Pura Appl. 4(175), 141–164 (1998). https://doi.org/10.1007/BF01783679
Chen, C.-Y., Kristensen, J.: On coercive variational integrals. Nonlinear analysis 153, 213–229 (2017). https://doi.org/10.1016/j.na.2016.09.011
Cupini, G., Fusco, N., Petti, R.: Hölder continuity of local minimizers. J. Math. Anal. Appl. 235(2), 578–597 (1999). https://doi.org/10.1006/jmaa.1999.6410
Dacorogna, B.: Direct methods in the calculus of variations 78 (2008). https://doi.org/10.1007/978-0-387-55249-1
Diening, L., Lengeler, D., Stroffolini, B., Verde, A.: Partial regularity for minimizers of quasi-convex functionals with general growth. SIAM J. Math. Anal. 44(5), 3594–3616 (2012). https://doi.org/10.1137/120870554
Duzaar, F., Kronz, M.: Regularity of \(\omega \)-minimizers of quasi-convex variational integrals with polynomial growth. Differential Geom. Appl. 17(2–3), 139–152 (2002). https://doi.org/10.1016/S0926-2245(02)00104-3
Duzaar, F., Mingione, G.: Regularity for degenerate elliptic problems. Ann. Inst. H. Poincaré Anal. Non Linéaire 21(5), 735–766 (2004). https://doi.org/10.1016/J.ANIHPC.2003.09.003
Duzaar, F., Steffen, K.: Optimal interior and boundary regularity for almost minimizers to elliptic variational integrals. J. Reine Angew. Math. 546, 73–138 (2002). https://doi.org/10.1515/crll.2002.046
Duzaar, F., Gastel, A., Grotowski, J.F.: Partial regularity for almost minimizers of quasi-convex integrals. SIAM J. Math. Anal. 32(3), 665–687 (2000). https://doi.org/10.1137/S0036141099374536
Duzaar, F., Grotowski, J.F., Kronz, M.: Regularity of almost minimizers of quasi-convex variational integrals with subquadratic growth. Ann. Mat. Pura Appl. (4) 184(4), 421–448 (2005). https://doi.org/10.1007/s10231-004-0117-5
Ekeland, I.: On the variational principle. J. Math. Anal. Appl. 47, 324–353 (1974). https://doi.org/10.1016/0022-247X(74)90025-0
Evans, L.C.: Quasiconvexity and partial regularity in the calculus of variations. Arch. Rational Mech. Anal. 95(3), 227–252 (1986). https://doi.org/10.1007/BF00251360
Federer, H.: Geometric Measure Theory. Die Grundlehren der mathematischen Wissenschaften, Band 153. Springer, New York (1969). https://doi.org/10.1007/978-3-642-62010-2
Fonseca, I., Müller, S.: Relaxation of quasiconvex functionals in \(BV(\Omega, \mathbb{R}^p)\) for integrands \(f(x, u,\nabla u)\). Arch. Rational Mech. Anal. 123(1), 1–49 (1993). https://doi.org/10.1007/BF00386367
Foss, M., Mingione, G.: Partial continuity for elliptic problems. Ann. Inst. H. Poincaré Anal. Non Linéaire 25(3), 471–503 (2008). https://doi.org/10.1016/J.ANIHPC.2007.02.003
Franceschini, F.: Partial regularity for \(BV^{\mathscr {B}}\) local minimizers. Master’s thesis, Università degli Studi di Pisa (2019). https://etd.adm.unipi.it/theses/available/etd-06242019-103617/
Fusco, N.: Quasiconvexity and semicontinuity for higher-order multiple integrals. Ricerche mat. 29(2), 307–323 (1980)
Fusco, N., Hutchinson, J.: \(C^{1,\alpha }\) partial regularity of functions minimising quasiconvex integrals. Manuscripta Math. 54(1–2), 121–143 (1985). https://doi.org/10.1007/BF01171703
Giaquinta, M.: Multiple Integrals in the Calculus of Variations and Nonlinear Elliptic Systems. Annals of Mathematics Studies, vol. 105. Princeton University Press, Princeton, NJ (1983)
Giaquinta, M., Modica, G.: Partial regularity of minimizers of quasiconvex integrals. Ann. Inst. H.Poincaré Anal. Non Linéaire 3(3), 185–208 (1986)
Giaquinta, M., Modica, G., Souček, J.: Functionals with linear growth in the calculus of variations. i, ii. Comment. Math. Univ. Carolin. 20(1), 143–156157172 (1979)
Giovanni, L.: A First Course in Sobolev Spaces, Graduate Studies in mathematics, vol. 181, 2nd edn. American Mathematical Society, Providence, RI (2017)
Giusti, E.: Direct Methods in the Calculus of Variations. World Scientific, River Edge, NJ (2003). https://doi.org/10.1142/5002
Giusti, E., Miranda, M.: Sulla regolarità delle soluzioni deboli di una classe di sistemi ellittici quasi-lineari. Arch. Rational Mech. Anal. 31, 173–184 (1968). https://doi.org/10.1007/BF00282679
Gmeineder, F.: The regularity of minima for the Dirichlet problem on BD. Arch. Rational Mech. Anal. 237, 1099–1171 (2020). https://doi.org/10.1007/s00205-020-01507-5
Gmeineder, F.: Partial regularity for symmetric quasiconvex functionals on BD. J. Math. Pures Appl. 145, 83–129 (2021). https://doi.org/10.1016/j.matpur.2020.09.005
Gmeineder, F., Kristensen, J.: Partial regularity for BV minimizers. Arch. Rational Mech. Anal. 232, 1429–1473 (2019). https://doi.org/10.1007/s00205-018-01346-5
Kristensen, J., Mingione, G.: The singular set of \(\omega \)-minima. Arch. Ration. Mech. Anal. 177(1), 93–114 (2005). https://doi.org/10.1007/s00205-005-0361-x
Kristensen, J., Mingione, G.: The singular set of minima of integral functionals. Arch. Ration. Mech. Anal. 180(3), 331–398 (2006). https://doi.org/10.1007/s00205-005-0402-5
Kristensen, J., Mingione, G.: The singular set of Lipschitzian minima of multiple integrals. Arch. Ration. Mech. Anal. 184(2), 341–369 (2007). https://doi.org/10.1007/s00205-006-0036-2
Kristensen, J., Rindler, F.: Relaxation of signed integral functionals in \(BV\). Calc. Var. Partial Differential Equations 37(1–2), 29–62 (2010). https://doi.org/10.1007/s00526-009-0250-5
Kristensen, J., Rindler, F.: Characterization of generalized gradient young measures generated by sequences in \(W^{1,1}\) and \(BV\). Arch. Ration. Mech. Anal. 197(2), 539–598 (2010). https://doi.org/10.1007/s00205-009-0287-9
Lebesgue, H.: Intégrale, longueur, aire. Ann. Mat. Pura Appl. 7, 231–359 (1902). https://doi.org/10.1007/BF02420592
Manfredi, J.J.: Regualrity of the gradient for a class of nonlinear possibly degenerate elliptic equations. PhD thesis, Washington University, St. Louis (1986)
Manfredi, J.J.: Regularity for minima of functionals with \(p\)-growth. J. Differential Equations 76(2), 203–212 (1988). https://doi.org/10.1016/0022-0396(88)90070-8
Marcellini, P.: Approximation of quasiconvex functions, and lower semicontinuity of multiple integrals. Manuscripta Math. 51(1–3), 1–28 (1985). https://doi.org/10.1007/BF01168345
Marcellini, P.: On the definition and the lower semicontinuity of certain quasiconvex integrals. Ann. Inst. H. Poincaré Anal. Non Linéaire 3(5), 391–409 (1986)
Mingione, G.: Regularity of minima: an invitation to the dark side of the calculus of variations. Appl. Math. 51(4), 355–426 (2006). https://doi.org/10.1007/s10778-006-0110-3
Morrey, J.C.B.: Quasi-convexity and the lower semicontinuity of multiple integrals. Pacific J. Math 2, 25–53 (1952). https://doi.org/10.2140/pjm.1952.2.25
Morrey, C.B.J.: Multiple Integrals in the Calculus of Variations. Springer, New York (1966). https://doi.org/10.1007/978-3-540-69952-1
Morrey, J.C.B.: Partial regularity results for non-linear elliptic systems. J. Math. Mech. 17, 649–670 (1967)
Reshetnyak, Y.G.: The weak convergence of completely additive vector-valued set functions. Sibirsk. Mat. Z 9, 1386–1394 (1968). https://doi.org/10.1007/BF02196453
Schmidt, T.: Partial regularity for degenerate variational problems and image restoration models in \(BV\). Indiana Univ. Math. J. 63(1), 213–279 (2014). https://doi.org/10.1512/iumj.2014.63.5174
Serrin, J.: On the definition and propertie of certain variational integrals. Trans. Amer. Math. Soc. 101, 139–167 (1961). https://doi.org/10.1090/S0002-9947-1961-0138018-9
Stredulinsky, E.W.: Weighted Inequalities and Degenerate Elliptic Partial Differential Equations. Lecture Notes in Mathematics, vol. 1074. Springer, Berlin (1984)
Tartar, L.: An Introduction to Sobolev Spaces and Interpolation Spaces. Lecture Notes of the Unione Matematica Italiana, vol. 3. Springer, Berlin, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71483-
Triebel, H.: Theory of Functions Spaces. Monographs in Mathematics, vol. 78. Birkhäuser Verlag, Basel (1983). https://doi.org/10.1007/978-3-0346-0416-1
Acknowledgements
The author would like to thank Jan Kristensen for his guidance throughout the project and Franz Gmeineder for helpful discussions and suggestions. Part of the work was done during a visit at the School of Mathematical Sciences at Peking University, and the hospitality and financial support from the institution is appreciated. The author is funded by the Engineering and Physical Sciences Research Council [EP/L015811/1].
Funding
The author is funded by the Engineering and Physical Sciences Research Council [EP/L015811/1].
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
There are no competing interests.
Additional information
Communicated by L. Szekelyhidi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.



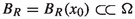 with
with 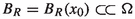 with
with