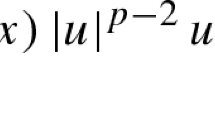Abstract
We study a nonlinear Schrödinger–Poisson system which reduces to the nonlinear and nonlocal PDE
where \(\omega = (N-2)|{\mathbb {S}}^{N-1} |,\) \(\lambda >0,\) \(q\in (1,2^{*} -1),\) \(\rho :{{\mathbb {R}}}^N \rightarrow {{\mathbb {R}}}\) is nonnegative, locally bounded, and possibly non-radial, \(N=3,4,5\) and \(2^*=2N/(N-2)\) is the critical Sobolev exponent. In our setting \(\rho \) is allowed as particular scenarios, to either (1) vanish on a region and be finite at infinity, or (2) be large at infinity. We find least energy solutions in both cases, studying the vanishing case by means of a priori integral bounds on the Palais–Smale sequences and highlighting the role of certain positive universal constants for these bounds to hold. Within the Ljusternik–Schnirelman theory we show the existence of infinitely many distinct pairs of high energy solutions, having a min–max characterisation given by means of the Krasnoselskii genus. Our results cover a range of cases where major loss of compactness phenomena may occur, due to the possible unboundedness of the Palais–Smale sequences, and to the action of the group of translations.
Similar content being viewed by others
Data Availibility Statement
On behalf of all authors, the corresponding author states that there are no data associated to our manuscripts.
Notes
In fact this bound holds in dimensions \(N= 3,4,5\) and every \(q\in (2,2^*-1].\)
References
Ambrosetti, A.: On Schrödinger-Poisson systems. Milan J. Math. 76, 257–274 (2008)
Ambrosetti, A., Malchiodi, A.: Perturbation methods and semilinear elliptic problems on \({\mathbb{R}}^n\). In: Progress in Mathematics, 240. Birkhäuser Verlag, Basel (2006)
Ambrosetti, A., Malchiodi, A.: Nonlinear analysis and semilinear elliptic problems. Cambridge University Press (2007)
Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and its applications. J. Funct. Anal. 14, 349–381 (1973)
Ambrosetti, A., Ruiz, D.: Multiple bound states for the Schrödinger-Poisson problem. Commun. Contemp. Math 10, 391–404 (2008)
Bartsch, T., Wang, Z.-Q.: Existence and multiplicity results for some superlinear elliptic problems on \({\mathbb{R}}^N\). Commun. Partial Differ. Equ. 20(9 & 10), 1725–1741 (1995)
Bellazzini, J., Frank, R., Visciglia, N.: Maximizers for Gagliardo-Nirenberg inequalities and related non-local problems. Mat. Ann. 360(3–4), 653–673 (2014)
Bellazzini, J., Ghimenti, M., Mercuri, C., Moroz, V., Van Schaftingen, J.: Sharp Gagliardo-Nirenberg inequalities in fractional Coulomb-Sobolev spaces. Trans. AMS 370(11), 8285–8310 (2018)
Bao, W., Mauser, N.J., Stimming, H.P.: Effective one particle quantum dynamics of electrons: a numerical study of the Schrödinger-Poisson-\(X\alpha \) model. Commun. Math. Sci 1(4), 809–828 (2003)
Benci, V., Cerami, G.: Positive solutions of some nonlinear elliptic problems in exterior domains. Arch. Rat. Mech. Anal. 99, 283–300 (1987)
Benci, V., Fortunato, D.: Variational methods in nonlinear field equations. Solitary waves, hylomorphic solitons and vortices. Springer Monographs in Mathematics. Springer, Cham (2014)
Benedek, A., Panzone, R.: The space \(L^p\) with mixed norm. Duke Math. J. 28, 301–324 (1961)
Berestycki, H., Lions, P.L.: Nonlinear scalar field equations, I and II. Arch. Rational Mech. Anal. 82, 313–375 (1983)
Boas Jr., R.P.: Some uniformly convex spaces. Bull. Am. Math. Soc. 46, 304–311 (1940)
Bokanowski, O., López, J.L., Soler, J.: On an exchange interaction model for quantum transport: the Schrödinger-Poisson-Slater system. Math. Models Methods Appl. Sci. 13(10), 1397–1412 (2003)
Bonheure, D., Di Cosmo, J., Mercuri, C.: Concentration on circles for nonlinear Schrödinger-Poisson systems with unbounded potentials vanishing at infinity. Commun. Contemp. Math. 14(2) (2012)
Bonheure, D., Mercuri, C.: Embedding theorems and existence results for nonlinear Schrödinger-Poisson systems with unbounded and vanishing potentials. J. Differ. Equ. 251, 1056–1085 (2011)
Brezis, H., Lieb, E.: A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88(3), 486–490 (1983)
Brezis, H.: Functional analysis. In: Sobolev Spaces and Partial Differential Equations. Springer (2011)
Catto, I., Dolbeault, J., Sanchez, O., Soler, J.: Existence of steady states for the Maxwell-Schrödinger-Poisson system: exploring the applicability of the concentration-compactness principle. Math. Models Methods Appl. Sci. 23(10), 1915–1938 (2013)
Cerami, G., Molle, R.: Positive bound state solutions for some Schrödinger-Poisson systems. Nonlinearity 29, 3103–3119 (2016)
Cerami, G., Molle, R.: Multiple positive bound states for critical Schrödinger–Poisson systems. ESAIM Control Optim. Calc. Var. 25 pp. 73, 29 pp (2019)
Cerami, G., Vaira, G.: Positive solutions for some non-autonomous Schrödinger-Poisson systems. J. Differ. Equ. 248, 521–543 (2010)
Costa, D.G.: An Invitation to Variational Methods in Differential Equations. Birkhäuser, Boston (2007)
D’Aprile, T., Mugnai, D.: Non-existence results for the coupled Klein-Gordon-Maxwell equations. Adv. Nonlinear Stud. 4(3), 307–322 (2004)
Floer, A., Weinstein, A.: Nonspreading wave packets for the cubic Schrödinger equation with a bounded potential. J. Funct. Anal. 69(3), 397–408 (1986)
Gel’fand, M., Shilov, G.E.: Properties and Operations. In: Generalized Functions, vol. I. Academic Press, New York and London (1964)
Gilbarg, D., Trudinger, N.: Elliptic Partial Differential Equations of Second Order, 2nd edn. Springer, New York (1983)
Hájek, P., Santalucía, V.M., Vanderwerff, J., Zizler, V.: Biorthogonal Systems in Banach Spaces. Springer, New York (2008)
Jeanjean, L.: On the existence of bounded Palais-Smale sequences and applications to a Landesman-Lazer type problem set on \({\mathbb{R}}^N\). Proc. Roy. Soc. Edinb. 129, 787–809 (1999)
Jeanjean, L., Tanaka, K.: A positive solution for a nonlinear Schrödinger equation on \({\mathbb{R}}^N\). Indiana Univ. Math. J. 54(2), 443–464 (2005)
Kwong, M.: Uniqueness of positive solutions of \(\Delta u-u+u^p=0\) in \({\mathbb{R}}^n\). Arch. Rat. Mech. Anal. 105, 243–266 (1989)
Lieb, E.H., Loss, M.: Analysis, 2nd edn. American Mathematical Society, Rhode Island (2001)
Lions, P.L.: Some remarks on Hartree equation. Nonlinear Anal. 5(11), 1245–1256 (1981)
Lions, P.L.: The concentration-compactness principle in the calculus of variations. The locally compact case. Ann. Inst. H. Poincairé Anal. Non Linéaire 1, pp. 109–145 and 223–283 (1984)
Lions, P.L.: Solutions of Hartree-Fock equations for Coulomb systems. Commun. Math. Phys. 109(1), 33–97 (1987)
Mauser, N.J.: The Schrödinger-Poisson-\(X\alpha \) equation. Appl. Math. Lett. 14(6), 759–763 (2001)
Mercuri, C.: Positive solutions of nonlinear Schrödinger-Poisson systems with radial potentials vanishing at infinity. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 19(3), 211–227 (2008)
Mercuri, C., Moroz, V., Van Schaftingen, J.: Groundstates and radial solutions to nonlinear Schrödinger-Poisson-Slater equations at the critical frequency. Calc. Var. Partial Differ. Equ. 55(6), 1–58 (2016)
Mercuri, C., Tyler, T.M.: On a class of nonlinear Schrödinger-Poisson systems involving a nonradial charge density. Rev. Mat. Iberoam. 36(4), 1021–1070 (2020)
Mercuri, C., Willem, M.: A global compactness result for the p-Laplacian involving critical nonlinearities. Discrete Contin. Dyn. Syst. 28(2), 469–493 (2010)
Montenegro, M.: Strong maximum principles for supersolutions of quasilinear elliptic equations. Nonlinear Anal. 37(4), 431–448 (1999)
Opick, L., Kufner, A., John, O., Fučík, S.: Function Spaces, vol. 1, 2nd edn. De Gruyter, Berlin/Boston (2012)
Rabinowitz, P.: On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43(2), 229–266 (1992)
Ruiz, D.: The Schrödinger-Poisson equation under the effect of a nonlinear local term. J. Funct. Anal. 237, 655–674 (2006)
Ruiz, D.: On the Schrödinger-Poisson-Slater system: behavior of minimizers, radial and nonradial cases. Arch. Rat. Mech. Anal. 198, 349–368 (2010)
Slater, J.: A simplification of the Hartree-Fock Method. Phys. Rev. 81, 385–390 (1951)
Strauss, W.: Existence of solitary waves in higher dimensions. Commun. Math. Phys. 55(2), 149–162 (1977)
Struwe, M.: On the evolution of harmonic mappings of Riemannian surfaces. Comment. Math. Helvetici 60, 558–581 (1985)
Struwe, M.: Variational Methods: Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, 4th edn. Springer, Berlin (2008)
Sun, J., Wu, T., Feng, Z.: Non-autonomous Schrödinger-Poisson System in \({\mathbb{R}}^3\). Discrete Contin. Dyn. Syst. 38(4), 1889–1933 (2018)
Szulkin, A.: Ljusternik-Schnirelmann theory on \(C^1\)-manifolds. Ann. Inst. Henri Poincaré 5(2), 119–139 (1988)
Willem, M.: Minimax Theorems. Birkhäuser, Boston (1996)
Acknowledgements
The authors would like to thank the anonymous referees for the valuable and constructive comments, and thank them in particular for suggesting a simple proof of Lemma 2.6.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest/Competing interests
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Communicated by Y. Giga.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Proof of the Pohozaev-type condition
Appendix A: Proof of the Pohozaev-type condition
Proof of Lemma 2.4
With the regularity remarks of Proposition 1 in place, we now multiply the first equation in (2.3) by \((x, \nabla u)\) and integrate on \(B_R(0)\) for some \(R>0\). We will compute each integral separately. We first note that
Fixing \(i =1,\dots , N\), integrating by parts and using the divergence theorem, we then see that,
So, summing over i, we get
Again, fixing \(i =1,\dots , N\), integrating by parts and using the divergence theorem, we find that,
Thus, summing over i, we get
Finally, once more fixing \(i=1,\dots , N\), integrating by parts and using the divergence theorem, we find that,
and so, summing over i, we see that
Putting (5.20), (5.21), (5.22) and (5.23) together, we see that
We now multiply the second equation in (2.3) by \((x, \nabla \phi _u)\) and integrate on \(B_R(0)\) for some \(R>0\). By a simple calculation we see that
Substituting this into (5.24) and rearranging, we get
where we have used the assumption \(k\rho (x)\le (x,\nabla \rho )\) for some \(k\in {{\mathbb {R}}}\) to obtain the first inequality. We now call the right hand side of (5.25) \(I_R\), namely
We note that \(|(x,\nabla u)|\le R|\nabla u |\) and \(|(x,\nabla \phi _u)|\le R|\nabla \phi _u |\) on \(\partial B_R\), so it holds that
Now, since \(|\nabla u|^2\), \(u^2 \in L^1({{\mathbb {R}}}^N)\) as \(u\in E ({{\mathbb {R}}}^N)\subseteq H^1({{\mathbb {R}}}^N)\), \( \rho \phi _u u^2\), \(|\nabla \phi _u|^2 \in L^1({{\mathbb {R}}}^N)\) because \(\int _{{{\mathbb {R}}}^N}\rho \phi _u u^2\,\mathrm {d}x=\int _{{{\mathbb {R}}}^N}|\nabla \phi _u|^2\,\mathrm {d}x\) and \(\phi _u \in D^{1,2}({{\mathbb {R}}}^N)\), and \(|u|^{q+1} \in L^1({{\mathbb {R}}}^N)\) because \(E({{\mathbb {R}}}^N) \hookrightarrow L^s({{\mathbb {R}}}^N)\) for all \(s \in [2,2^{*}]\), then it holds that \(I_{R_n} \rightarrow 0\) as \(n\rightarrow +\infty \) for a suitable sequence \(R_n \rightarrow +\infty .\) Moreover, since (5.25) holds for any \(R>0\), it follows that
and so, we obtain
using the fact that \(\int _{{{\mathbb {R}}}^N}|\nabla \phi _u|^2\,\mathrm {d}x=\int _{{{\mathbb {R}}}^N}\rho \phi _u u^2\,\mathrm {d}x \). This completes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Dutko, T., Mercuri, C. & Tyler, T.M. Groundstates and infinitely many high energy solutions to a class of nonlinear Schrödinger–Poisson systems. Calc. Var. 60, 174 (2021). https://doi.org/10.1007/s00526-021-02045-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-021-02045-y
Keywords
- Nonlinear Schrödinger–Poisson system
- Weighted Sobolev spaces
- Palais–Smale sequences
- Compactness
- Multiple solutions
- Nonexistence