Orlicz–Minkowski flows

Abstract

We study the long-time existence and behavior for a class of anisotropic non-homogeneous Gauss curvature flows whose stationary solutions, if they exist, solve the regular Orlicz–Minkowski problems. As an application, we obtain old and new existence results for the regular even Orlicz–Minkowski problems; the corresponding $L_p$ version is the even $L_p$-Minkowski problem for $p>-n-1$. Moreover, employing a parabolic approximation method, we give new proofs of some of the existence results for the general Orlicz–Minkowski problems; the $L_p$ versions are the even $L_p$-Minkowski problem for $p>0$ and the $L_p$-Minkowski problem for $p>1$. In the final section, we use a curvature flow with no global term to solve a class of $L_p$-Christoffel–Minkowski type problems.

1 Introduction

A convex body in Euclidean space is a compact convex set with non-empty interior. Write $\mathrm {K}$ for set of convex bodies, and $\mathrm {K}_o$ for the set of convex bodies containing the origin o. The support function of a convex body K is defined by

$$\begin{aligned}h_K(u)=\sup _{v\in K}\langle u,v \rangle \quad \hbox {for}~u\in {\mathbb {R}}^{n+1}.\end{aligned}$$

For any u on the boundary of K,  let $\nu _K(u)$ be the set of all unit exterior normal vectors at u. The surface area measure of K, $S_K$, is a Borel measure on the unit sphere defined by

$$\begin{aligned}S_K(\omega )={\mathcal {H}}^n(\nu _K^{-1}(\omega ))~\hbox {for all Borel sets }~\omega \subset {\mathbb {S}}^n.\end{aligned}$$

Here ${\mathcal {H}}^n$ denotes the n-dimensional Hausdorff measure. When the boundary of K, $\partial K$, is a $C^2$ smooth, strictly convex hypersurface, then $dS_K=\sigma _nd\theta ,$ where $\sigma _n$ is the product of the principal radii of curvature and $d\theta$ is the standard spherical Lebesgue measure. In this case, $h_K$, as a function on the unit sphere, is given by

$$\begin{aligned}h_K(u)=\langle u,\nu _K^{-1}(u)\rangle .\end{aligned}$$

The Minkowski problem is one of the cornerstones of the classical Brunn–Minkowski theory. It asks what are the necessary and sufficient conditions on a Borel measure $\mu$ on ${\mathbb {S}}^n$ in order for it to be the surface area measure of a convex body. The complete solution to this problem was found by Minkowski, Aleksandrov and Fenchel–Jessen (see [54]): A Borel measure $\mu$ whose support is not contained in a closed hemisphere is the surface area measure of a convex body if and only if

$$\begin{aligned} \int _{{\mathbb {S}}^n} ud\mu (u)=o. \end{aligned}$$

Moreover, the solution is unique up to translations.

Let $\varphi :(0,\infty )\rightarrow (0,\infty )$ be a continuous function. The general Orlicz–Minkowski problem asks what are the necessary and sufficient conditions on a Borel measure $\mu$ on ${\mathbb {S}}^n$, such that there exists a convex body $K\in \mathrm {K}_o$ so that

$$\begin{aligned} \varphi (h_K)dS_K=\gamma d\mu \quad \hbox {for some constant}~\gamma >0. \end{aligned}$$

(1.1)

This problem is a generalization of the $L_p$-Minkowski problem (i.e., $\varphi (s)=s^{1-p}$) which itself was put forward by Lutwak [47] almost a century after Minkowski’s original work and stems from the $L_p$ linear combination of convex bodies. We refer the reader to [5,6,7, 10, 12, 15, 19, 39, 41, 46, 56] regarding the $L_p$-Minkowski problem and to [14, 48] for applications.

A natural generalization of $L_p$ spaces are Orlicz spaces, motivating the Orlicz linear combination of convex bodies and leading to the Orlicz–Minkowski problem. We keep the discussion brief here and the reader may consult [4, 25,26,27, 32] as well as [49, 54, 60, 62] for the origin of the Orlicz–Brunn–Minkowski theory and related concepts.

The regular Orlicz–Minkowski problem asks what are the necessary and sufficient conditions on the smooth function $f:{\mathbb {S}}^n\rightarrow (0,\infty )$ such that there exists a convex hypersurface with support function h (as a function on the unit sphere) satisfying

$$\begin{aligned} f \varphi (h)\sigma _n(h_{ij}+\delta _{ij}h)=\gamma \quad \hbox {for some constant}~\gamma >0. \end{aligned}$$

(1.2)

The subscripts of h denote covariant derivatives with respect to a local orthonormal frame field on ${\mathbb {S}}^n$. Our approach to solving this problem is via the flow method in the regular case (1.2) and by parabolic approximation in the general case (1.1).

2 Results

2.1 Curvature flows

Let

$$\begin{aligned}x_0:M^n\rightarrow {\mathbb {R}}^{n+1}\end{aligned}$$

be a smooth parametrization of a closed, strictly convex hypersurface $M_0$ with the origin of ${\mathbb {R}}^{n+1}$ in its interior. One of the flows that we are interested in is the family of hypersurfaces $\{M_t\}$ given by the smooth map

$$\begin{aligned}x:M^n\times [0,T)\rightarrow {\mathbb {R}}^{n+1}\end{aligned}$$

satisfying the initial value problem

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _tx= f (\nu )\langle x,\nu \rangle \frac{\varphi (\langle x,\nu \rangle )}{{\mathcal {K}}}\nu -\zeta (t) x; \\ x(\cdot ,0)=x_0(\cdot ), \end{array} \right. \end{aligned}$$

(2.1)

where ${\mathcal {K}}(\cdot ,t)$ and $\nu (\cdot ,t)$ are respectively the Gauss curvature and the outer unit normal vector of $M_t:=x(M^n,t)$, $f:{\mathbb {S}}^n\rightarrow (0,\infty )$ and $\varphi :(0,\infty )\rightarrow (0,\infty )$ are smooth functions and

$$\begin{aligned}\zeta (t):=\frac{\int \langle x,\nu \rangle d\mu _{M_{t}}}{\int \frac{\langle x,\nu \rangle {\mathcal {K}}}{ f (\nu )\varphi (\langle x,\nu \rangle )} d\mu _{M_t}}.\end{aligned}$$

To explain our interest in studying this flow, we need some definitions and notation.

By a direct calculation, along the flow (2.1) the support functions

$$\begin{aligned}h:{\mathbb {S}}^n\times [0,T)\rightarrow {\mathbb {R}}\end{aligned}$$

of the $M_t$ (as long as they are strictly convex) satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _th= f h\varphi (h)\sigma _n-\zeta h;\\ h(u,0)=h_{M_0}. \end{array} \right. \end{aligned}$$

(2.2)

Stationary solutions of (2.2), whenever they exist, are exactly the solutions of the regular Orlicz–Minkowski problem and thus the limits of the flow hypersurfaces are solutions of (1.2).

For some choices of f and $\varphi (s)=s^{1-p}$, the flow (2.1) becomes homogeneous and was considered in [3, 8, 16, 24, 34,35,36,37,38, 44, 53, 55, 57]. However, when it comes to non-homogeneous flows, the literature on geometric flows is not very rich and there are few works in this direction; e.g., [11, 16,17,18, 42, 45, 50]. Since the Orlicz-Minkowski problem admits solutions in the non-homogeneous case, it is desirable to remove the homogeneity assumption in the flow. The conditions we place on $f,\varphi$ are similar to those used previously in the literature on the Orlicz–Minkowski problem mentioned in the introduction while some are new (Remark 2.2 and Remark 2.4 below).

Theorem 2.1

Suppose

• (1) $f:{\mathbb {S}}^n\rightarrow (0,\infty )$ is smooth and even, $f(u)=f(-u)\quad \forall u\in {\mathbb {S}}^n$,

• (2) $\varphi :(0,\infty )\rightarrow (0,\infty )$ is smooth,

• (3) either

a:

$\phi (s)=\int _0^s\frac{1}{\varphi (t)}dt$ exists for all $s>0,$ and $\lim \limits _{s\rightarrow \infty }\phi (s)=\infty ,$

b:

or $\phi (s)=\int _1^s\frac{1}{\varphi (t)}dt$ satisfies $\lim \limits _{s\rightarrow \infty }\phi (s)=\infty ,$ and for some ${\hat{C}}_1>0,$ we have

$$\begin{aligned}\int _{{\mathbb {S}}^n}\frac{\phi (|\langle u,\theta \rangle |)}{f}d\theta \ge -{\hat{C}}_1\quad \forall u\in {\mathbb {S}}^n,\end{aligned}$$

c:

or $\phi (s)=\int _s^{\infty }\frac{1}{\varphi (t)}dt$ exists for all $s>0,$ and for some $q\in (-n-1,0)$, we have

$$\begin{aligned}\limsup _{s\rightarrow 0^+}\frac{\phi (s)}{s^q}<\infty ,\end{aligned}$$

d:

or $\phi (s)=\int _s^{\infty }\frac{1}{\varphi (t)}dt$ exists for all $s>0,$ $\lim \limits _{s\rightarrow 0^+}\phi (s)=\infty ,$ and for some ${\hat{C}}_2>0,$ we have

$$\begin{aligned}\int _{{\mathbb {S}}^n}\frac{\phi (|\langle u,\theta \rangle |)}{f}d\theta \le {\hat{C}}_2\quad \forall u\in {\mathbb {S}}^n.\end{aligned}$$

In the cases, (3-a), (3-b), and (3-c), let $M_0$ be o-symmetric. In the case (3-d), we choose an o-symmetric $M_0$ such that

$$\begin{aligned}\int _{{\mathbb {S}}^n}\frac{\phi (h_{M_0})}{f}d\theta >{\hat{C}}_2.\end{aligned}$$

Then there exists a smooth, strictly convex solution $M_t$ to (2.1) and it subconverges in $C^{\infty }$ to an o-symmetric, smooth, strictly convex solution of the regular even Orlicz–Minkowski problem.

Remark 2.2

 

• (1) When $\varphi (s)=s^{1-\ell },$ assumptions (3-a), (3-b), (3-c), (3-d) are satisfied, in order, for $\ell >0$, $\ell =0$, $\ell \in (-n-1,0)$, $-1<\ell <0$. To see this, note that

  $$\begin{aligned}&\int _{{\mathbb {S}}^n} \log |x_i|d\theta >-\infty ,\\&\int _{{\mathbb {S}}^n}\frac{1}{|x_i|^\ell }d\theta<\infty \quad \text{ for }\quad 0<\ell <1, \end{aligned}$$

  where $(x_1,\ldots ,x_{n+1})$ denotes the Euclidean coordinates. Hence, Theorem 2.1 generalizes [8, Thm. 1] to the Orlicz setting.

• (2) Since $\phi$ as defined in (3-a) is increasing, we have

  $$\begin{aligned}\int _{{\mathbb {S}}^n}\frac{\phi (|\langle u,\theta \rangle |)}{f}d\theta <\infty \quad \forall u\in {\mathbb {S}}^n.\end{aligned}$$

  Therefore, the integral conditions in (3-b) and (3-d) compared to the condition (3-a) are not more restrictive.

• (3) The cases (3-b) and (3-d) yield new existence results for the regular even Orlicz–Minkowski problem, while the existence results corresponding to (3-a) and (3-c) can be deduced from [4, 32].

• (4) Due to the presence of $\varphi$ (possibly non-homogeneous) and $\zeta$ in the speed of the flow (2.1), we could not employ the method of [2] to promote subconvergence to full convergence.

We slightly modify the flow (2.1) to treat a class of regular Orlicz–Minkowski problems without the assumption that f is even, i.e., we no longer assume

$$\begin{aligned}f(u)=f(-u)\quad \forall u\in {\mathbb {S}}^n.\end{aligned}$$

In order to serve this purpose, we consider the flow

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _tx= f (\nu )\langle x,\nu \rangle \frac{\varphi (\langle x,\nu \rangle )}{{\mathcal {K}}}\nu - x; \\ x(\cdot ,0)=x_0(\cdot ), \end{array} \right. \end{aligned}$$

(2.3)

where again $x_0:M^n\rightarrow {\mathbb {R}}^{n+1}$ is a smooth parametrization of a closed, strictly convex hypersurface $M_0$ with the origin of ${\mathbb {R}}^{n+1}$ in its interior. Here compared to (2.1), we dropped the $\zeta$-factor. In the final section, we will use another curvature flow without a global term (5.1) to treat a class of $L_p$-Minkowski-Christoffel type problems. See also [9, 20,21,22,23] for flows without global terms.

Theorem 2.3

Suppose

• (1) $\varphi :(0,\infty )\rightarrow (0,\infty )$ is smooth,

• (2) $\limsup \limits _{s\rightarrow \infty }s^n\varphi (s)<\frac{1}{f}<\liminf \limits _{s\rightarrow 0^+} s^n\varphi (s).$

Then there exists a smooth, strictly convex solution $M_t$ of (2.3) and it converges in $C^{\infty }$ to a smooth, strictly convex solution of (1.2) with positive support function and constant $\gamma =1.$

Remark 2.4

 

• (1) In the case special case $\varphi (s)=s^{1-p}$, Theorem 2.3 finds the solutions of the regular $L_p$-Minkowski problems for $p>n+1$.

• (2) In [18, p. 42], using a logarithmic curvature flow, an existence result was obtained under the assumption (2) and that $\varphi$ is non-increasing. See also [45], where a similar result was recently obtained.

2.2 General measures

Definition 2.5

A Borel measure $\mu$ on ${\mathbb {S}}^n$ is said to be even if it assumes the same values on antipodal Borel sets. We say $\mu$ is invariant under a subgroup G of the orthogonal group $O(n+1)$ if $\mu (g\omega )=\mu (\omega )$ for all Borel sets $\omega \subseteq {\mathbb {S}}^n$ and $g\in G$.

Theorem 2.6

Suppose

• (1) $\varphi :(0,\infty )\rightarrow (0,\infty )$ is a continuous function,

• (2) $\phi (s)=\int _0^s\frac{1}{\varphi (t)}dt$ exists for all $s>0$ and $\lim \limits _{s\rightarrow \infty }\phi (s)=\infty .$

Let $\mu$ be a finite even Borel measure on ${\mathbb {S}}^n$ whose support is not contained on a great subsphere. Then there exists an o-symmetric convex body such that

$$\begin{aligned} \varphi (h_K)dS_K=\gamma d\mu \quad \hbox {for some constant}~\gamma >0. \end{aligned}$$

This theorem was first proved in [32, Thm. 2] and contains the general even $L_p$-Minkowski problem for $p>0$. The method used there is a variational argument that finds a minimizing body of a suitable functional in a certain class of origin-symmetric (o-symmetric) convex bodies. We treated the regular version of this theorem by using the curvature flow in Theorem 2.1. The general case will be treated by a simple parabolic approximation, cf. Sect. 4.2.

In the next theorem, the assumption that the measure $\mu$ is even is dropped. To prove this theorem, we use the flow (2.1) and a version of Chou–Wang’s approximation argument [18] adapted to the parabolic setting [13] for treating the general $L_p$-Minkowski problem.

Theorem 2.7

Suppose

• (1) $\varphi :(0,\infty )\rightarrow (0,\infty )$ is continuous and $\lim \limits _{s\rightarrow 0^+}\varphi (s)=\infty ,$

• (2) $\phi (s)=\int _0^s\frac{1}{\varphi (t)}dt$ exists for all $s>0$ and $\lim \limits _{s\rightarrow \infty }\phi (s)=\infty .$

Let $\mu$ be a finite Borel measure on ${\mathbb {S}}^n$ whose support is not contained in a closed hemisphere. Then there exist $K\in \mathrm {K}_o$ and a constant $\gamma >0$ such that

$$\begin{aligned} dS_K= \frac{\gamma }{\varphi (h_K)}d\mu . \end{aligned}$$

Moreover, if $\mu$ is invariant under a closed group $G\subset O(n+1),$ then K is invariant under G.

This theorem first appeared in [31] and for the special case $\varphi (s)=s^{1-p}$, it includes the $L_p$-Minkowski problem for $p>1$. In [31], the problem is first solved for discrete measures and then by approximating the general measure by discrete measures. We solve it first in the regular case and then by approximating the general measures by the regular case; cf. Sect. 4.2 for the sketch and the full details. See also Wu–Xi–Leng [58, 59] for the discrete case of the Orlicz–Minkowski problem, and [40] for an existence result of solutions to general Orlicz–Minkowski problem which contains the $L_p$-Minkowski problem for $0<p<1.$ Note that the role of the constant $\gamma$ is essential in general; see [61] for a non-existence result when $\gamma$ is dropped.

3 Flow hypersurfaces

3.1 Regularity estimates

In the sequel, ${\bar{g}}$ and ${\bar{\nabla }}$ denote respectively the standard round metric and the Levi-Civita connection of ${\mathbb {S}}^n$. The principal radii of curvature are the eigenvalues of the matrix

$$\begin{aligned} r_{ij}:={\bar{\nabla }}_i{\bar{\nabla }}_j h+{\bar{g}}_{ij}h \end{aligned}$$

(3.1)

with respect to ${\bar{g}}$. For convenience, we put

$$\begin{aligned}\eta (t)&=\left\{ \begin{array}{ll} \zeta (t) &{} \hbox {flow}~(2.1),\\ 1 &{} \hbox {flow}~(2.3), \end{array} \right. \\ \Theta&= f h\varphi (h),\quad {\mathcal {L}}=\partial _t-\Theta \sigma _n^{ij}{\bar{\nabla }}_i{\bar{\nabla }}_j, \quad \rho =\sqrt{h^2+|{\bar{\nabla }}h|^2}. \end{aligned}$$

Lemma 3.1

The following evolution equations hold along the flows.

$$\begin{aligned} {\mathcal {L}}h&=(1-n)\Theta \sigma _n+\Theta h\sigma _n^{ij}{\bar{g}}_{ij}-\eta h,\\ {\mathcal {L}}\frac{\rho ^2}{2}&= (n+1)h\Theta \sigma _n+\sigma _n{\bar{g}}^{ij}{\bar{\nabla }}_ih{\bar{\nabla }}_j\Theta -\Theta \sigma _n^{ij}r_i^kr_{jk}-\eta \rho ^2,\\ {\mathcal {L}}(\Theta \sigma _n)&=\left( \frac{1}{h}+\frac{\varphi '(h)}{\varphi (h)}\right) (\Theta \sigma _n)^2 +\Theta ^2\sigma _n\sigma _n^{ij}{\bar{g}}_{ij}\\&\quad -\eta \left( n+1+\frac{h\varphi '(h)}{\varphi (h)}\right) \Theta \sigma _n. \end{aligned}$$

Proof

We have $\partial _{t}h=\Theta \sigma _{n}-\eta h$ and hence the first equation follows from the n-homogeneity and (3.1). For the second equation, in an orthonormal frame that diagonalizes $r_{ij},$

$$\begin{aligned} {\bar{\nabla }}_a{\bar{\nabla }}_b\frac{\rho ^2}{2}&=h{\bar{\nabla }}_a{\bar{\nabla }}_bh+{\bar{\nabla }}_ah{\bar{\nabla }}_bh\\&\quad +{\bar{\nabla }}^mh{\bar{\nabla }}_a{\bar{\nabla }}_b{\bar{\nabla }}_mh+{\bar{\nabla }}_a{\bar{\nabla }}^mh{\bar{\nabla }}_b{\bar{\nabla }}_mh\\&= h(r_{ab}-{\bar{g}}_{ab}h)+{\bar{\nabla }}_ah{\bar{\nabla }}_bh\\&\quad +{\bar{\nabla }}^mh{\bar{\nabla }}_a(r_{bm}-{\bar{g}}_{bm}h)\\&\quad +(r_{a}^m-\delta _{a}^mh)(r_{bm}-{\bar{g}}_{bm}h). \end{aligned}$$

Tracing with respect to $\sigma _n^{ab}$ gives

$$\begin{aligned} \sigma _n^{ab}{\bar{\nabla }}_a{\bar{\nabla }}_b\frac{\rho ^2}{2}&=h(n\sigma _n-\sigma _n^{ab}{\bar{g}}_{ab}h)+\sigma _n^{ab}{\bar{\nabla }}_ah{\bar{\nabla }}_bh\\&\quad +{\bar{\nabla }}^mh{\bar{\nabla }}_m\sigma _n-\sigma _n^{ab}{\bar{\nabla }}_ah{\bar{\nabla }}_bh\\&\quad +\sigma _n^{ab}r_{a}^mr_{bm}+\sigma _n^{ab}{\bar{g}}_{ab}h^2-2nh\sigma _n\\&=-nh\sigma _n+{\bar{\nabla }}^mh{\bar{\nabla }}_m\sigma _n+\sigma _n^{ab}r_{a}^mr_{bm}. \end{aligned}$$

Now the second evolution equation follows from

$$\begin{aligned} \partial _t\frac{\rho ^2}{2}&=h\Theta \sigma _n-\eta \rho ^2+{\bar{g}}^{ij}\sigma _n{\bar{\nabla }}_ih{\bar{\nabla }}_j\Theta +{\bar{g}}^{ij}\Theta {\bar{\nabla }}_ih{\bar{\nabla }}_j\sigma _n. \end{aligned}$$

Finally there holds

$$\begin{aligned} \begin{aligned} \partial _{t}(\Theta \sigma _{n})&=f\varphi \sigma _{n}\partial _{t}h+fh\varphi ' \sigma _{n}\partial _{t}h+\Theta \sigma _{n}^{ij}({\bar{\nabla }}_{i}{\bar{\nabla }}_{j}\partial _{t}h+{\bar{g}}_{ij}\partial _{t}h)\\&=f\varphi \sigma _{n}(\Theta \sigma _{n}-\eta h)+fh\varphi ' \sigma _{n}(\Theta \sigma _{n}-\eta h)\\&\quad +\Theta \sigma _{n}^{ij}({\bar{\nabla }}_{i}{\bar{\nabla }}_{j}(\Theta \sigma _{n}-\eta h)+{\bar{g}}_{ij}(\Theta \sigma _{n}-\eta h))\\&=\Theta \sigma _{n}^{ij}{\bar{\nabla }}_{i}{\bar{\nabla }}_{j}(\Theta \sigma _{n})+f\varphi \sigma _{n}(\Theta \sigma _{n}-\eta h)\\&\quad +fh\varphi '\sigma _{n} (\Theta \sigma _{n}-\eta h)+\Theta ^2\sigma _{n}^{ij}{{\bar{g}}}_{ij} \sigma _{n}\\&\quad -\eta \Theta \sigma _{n}^{ij}({\bar{\nabla }}_{i}{\bar{\nabla }}_{j}h+{\bar{g}}_{ij}h). \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(\Theta \sigma _{n})&=\frac{1}{h}\Theta ^{2}\sigma _{n}^{2} +\frac{\varphi '}{\varphi }\Theta ^{2}\sigma _{n}^{2}+\sigma _{n}^{ij}{\bar{g}}_{ij}\Theta ^{2}\sigma _{n}\\&\quad -n\eta \Theta \sigma _{n}-\eta \Theta \sigma _{n}-\eta \frac{\varphi '}{\varphi }\Theta h\sigma _{n}\\&=\left( \frac{1}{h}+\frac{\varphi '}{\varphi }\right) \Theta ^{2}\sigma _{n}^{2}+\sigma _{n}^{ij}{\bar{g}}_{ij}\Theta ^{2}\sigma _{n}\\&\quad -\left( 1+n+\frac{\varphi '}{\varphi }h\right) \eta \Theta \sigma _{n}. \end{aligned}\end{aligned}$$

(3.2)

$\square$

Define

$$\begin{aligned} {\mathcal {E}}[h]=\int _{{\mathbb {S}}^n} \frac{\phi (h)}{ f }d\theta ,\quad {\mathcal {E}}(t)={\mathcal {E}}[h_{M_t}]. \end{aligned}$$

Lemma 3.2

Along the flow (2.1) we have

$$\begin{aligned} \frac{d}{dt}V\ge 0,\quad \frac{d}{dt}{\mathcal {E}}=0. \end{aligned}$$

Along the flow (2.3) we have

$$\begin{aligned} \frac{d}{dt}(V-{\mathcal {E}})\ge 0. \end{aligned}$$

Here V denotes the enclosed volume of $M_t$. In both cases, the monotonicity is strict unless the solution is stationary.

Proof

For the flow (2.1), recalling that

$$\begin{aligned}\zeta (t):=\frac{\int _{{\mathbb {S}}^n}h\sigma _nd\theta }{\int _{{\mathbb {S}}^n}\frac{h}{f\varphi (h)}d\theta },\end{aligned}$$

we obtain

$$\begin{aligned} \frac{d}{d t}{\mathcal {E}}(t)&=\pm \int _{{\mathbb {S}}^n}\left( f h\varphi (h)\sigma _n-\frac{\int _{{\mathbb {S}}^n} h \sigma _nd\theta }{\int _{{\mathbb {S}}^n}\frac{h}{ f \varphi (h)}d\theta }h\right) \frac{1}{f \varphi (h)}d\theta =0. \end{aligned}$$

(3.3)

Here $+$ is for the cases (3-a) and (3-b), and − is for the cases (3-c) and (3-d). Using

$$\begin{aligned}V = \frac{1}{n+1} \int _{{\mathbb {S}}^n} h \sigma _n d\theta ,\end{aligned}$$

the divergence theorem, the n-homogeneity of $\sigma _n$, and that ${\bar{\nabla }}_i\sigma _n^{ij}=0$ (cf. [1, Lem. 2-12]), we obtain

$$\begin{aligned} \frac{1}{n+1}\frac{d}{d t}\int _{{\mathbb {S}}^n}h\sigma _nd\theta&=\int _{{\mathbb {S}}^n}\sigma _n\partial _thd\theta \nonumber \\&=\int _{{\mathbb {S}}^n}\left( \sigma _n-\zeta (t)\frac{1}{f\varphi (h)}\right) \partial _thd\theta \nonumber \\&=\int _{{\mathbb {S}}^n}\frac{(\partial _th)^2}{fh\varphi (h)}d\theta \ge 0. \end{aligned}$$

(3.4)

Equality holds precisely when h solves (1.2).

For the flow (2.3), note that

$$\begin{aligned} \frac{d}{dt}(V-{\mathcal {E}})&=\int _{{\mathbb {S}}^n}\left( \sigma _n-\frac{1}{f\varphi (h)}\right) \partial _thd\theta \nonumber \\&=\int _{{\mathbb {S}}^n}\frac{(\partial _th)^2}{fh\varphi (h)}d\theta \ge 0. \end{aligned}$$

(3.5)

The equality holds precisely when h solves (1.2) with $\gamma =1.$ $\square$

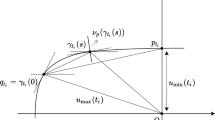
We write $w_-$ and $w_+$ respectively for the minimum width and the maximum width of a closed, convex hypersurface (or a convex body) with support function h. They are defined as

$$\begin{aligned}w_+=\max _{u\in {\mathbb {S}}^n}(h(u)+h(-u)),\quad w_-=\min _{u\in {\mathbb {S}}^n}(h(u)+h(-u)).\end{aligned}$$

Lemma 3.3

Under either flow (2.1) and (2.3) and the corresponding assumptions, there are constants a, b such that $a\le h(\cdot ,t)\le b.$ Moreover, $\eta (t)$ is uniformly bounded above, and below away from zero.

Proof

Suppose $R:=\max h_{M_t}$ is attained at the north pole $e_{n+1}$.

Theorem 2.1, case (3-a): Due to convexity,

$$\begin{aligned} h_{M_t}(x)\ge Rx_{n+1}\quad ~\text{ on }~\{x_{n+1}>0\}\cap {\mathbb {S}}^n. \end{aligned}$$

Since $\phi \ge 0$ is non-decreasing and ${\mathcal {E}}(t)$ constant in time, we obtain

$$\begin{aligned} \phi (\tfrac{1}{2}R)\int _{\{x_{n+1}>\frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{1}{f}d\theta \le {\mathcal {E}}(t)= {\mathcal {E}}(0). \end{aligned}$$

(3.6)

Due to $\lim _{s\rightarrow \infty }\phi (s)=\infty$, we see that $h(\cdot ,t)$ is uniformly bounded above. Let $V(M_t)$ denote the volume of the enclosed region by $M_t.$ To prove the uniform lower bound of h, note that

$$\begin{aligned}V(M_t)\le w_{-}(M_t)w_+(M_t)^n.\end{aligned}$$

Since $M_t$ is o-symmetric, $w_+=2\max h$ and $w_-=2\min h.$ The lower bound of h now follows since $V(M_t)$ is non-decreasing along the flow. The lower and upper bounds on h imply bounds on $\eta .$

Theorem 2.1, case (3-b): Suppose $R>2$. Due to convexity,

$$\begin{aligned}h_{M_t}\ge R|x_{n+1}|.\end{aligned}$$

Moreover, $\phi$ is non-decreasing,

$$\begin{aligned}\left\{ \begin{array}{ll} \phi (s)\ge 0 &{}\quad s\ge 1 \\ \phi (s)\le 0 &{}\quad 0<s\le 1, \end{array} \right. \end{aligned}$$

and ${\mathcal {E}}(t)$ constant in time. Hence,

$$\begin{aligned} {\mathcal {E}}(0)&\ge \int _{{\mathbb {S}}^n}\frac{\phi (R|x_{n+1}|)}{f}d\theta \\&\ge \phi (\tfrac{1}{2}R)\int _{\{|x_{n+1}|>\frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{1}{f}d\theta + \int _{\{|x_{n+1}|\le \frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{\phi (R|x_{n+1}|)}{f}d\theta \\&\ge \phi (\tfrac{1}{2}R)\int _{\{|x_{n+1}|>\frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{1}{f}d\theta + \int _{\{|x_{n+1}|\le \frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{\phi (|x_{n+1}|)}{f}d\theta \\&\ge \phi (\tfrac{1}{2}R)\int _{\{|x_{n+1}|>\frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{1}{f}d\theta + \int _{{\mathbb {S}}^n}\frac{\phi (|x_{n+1}|)}{f}d\theta \\&\ge \phi (\tfrac{1}{2}R)\int _{\{|x_{n+1}|>\frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{1}{f}d\theta - {\hat{C}}_1. \end{aligned}$$

Since $\lim _{s\rightarrow \infty }\phi (s)=\infty$, R remains uniformly bounded above. This in turn implies the lower and upper bounds on support functions and $\eta .$

Theorem 2.1, case (3-c): Since $M_t$ is o-symmetric body and the volume is non-decreasing, the lower and upper bound on the support functions and $\eta$ follow from the proof of [4, Lem. 4.3].

Theorem 2.1, case (3-d): Suppose $R>1$. Since $\phi \ge 0$ is non-increasing and ${\mathcal {E}}(t)={\mathcal {E}}(0)$,

$$\begin{aligned} {\mathcal {E}}(0)&\le \int _{{\mathbb {S}}^n}\frac{\phi (R|x_{n+1}|)}{f}d\theta \\&\le \phi (\tfrac{1}{2}R)\int _{\{|x_{n+1}|>\frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{1}{f}d\theta + \int _{\{|x_{n+1}|\le \frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{\phi (R|x_{n+1}|)}{f}d\theta \\&\le \phi (\tfrac{1}{2}R)\int _{\{|x_{n+1}|>\frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{1}{f}d\theta + \int _{\{|x_{n+1}|\le \frac{1}{2}\}\cap {\mathbb {S}}^n}\frac{\phi (|x_{n+1}|)}{f}d\theta \\&\le \phi (\tfrac{1}{2}R)\int _{{\mathbb {S}}^n}\frac{1}{f}d\theta + \int _{{\mathbb {S}}^n}\frac{\phi (|x_{n+1}|)}{f}d\theta . \end{aligned}$$

Note that as $R\rightarrow \infty$, due to $\lim _{s\rightarrow \infty }\phi (s)=0,$ we obtain

$$\begin{aligned}{\mathcal {E}}(0)\le {\hat{C}}_2.\end{aligned}$$

By our choice of $M_0$, this last inequality is violated.

Theorem 2.3: To get a uniform upper bound on h, note that at a maximum of h we have

$$\begin{aligned} \partial _th_{\max }\le h_{\max }(f_{\max }\varphi (h_{\max })h_{\max }^{n}-1). \end{aligned}$$

The right-hand side will be negative if $h_{\max }\rightarrow \infty .$ To get a lower bound on h away from zero, we can argue similarly. $\square$

In the following two lemmas, we will use two auxiliary functions from [38, 43] to find uniform lower and upper bounds on the Gauss curvature.

Lemma 3.4

We have $\sigma _n\ge c$ for some positive constant.

Proof

The evolution equation of $\chi :=\log (\Theta \sigma _n)-A\frac{\rho ^2}{2}$ is given by

$$\begin{aligned} {\mathcal {L}}\chi&=\Theta \sigma _n^{ij}{\bar{\nabla }}_i\log (\Theta \sigma _n){\bar{\nabla }}_j\log (\Theta \sigma _n)\\&\quad +\left( \frac{1}{h}+\frac{\varphi '(h)}{\varphi (h)}\right) \Theta \sigma _n+\Theta \sigma _n^{ij}{\bar{g}}_{ij}\\&\quad -\eta \left( n+1+\frac{h\varphi '(h)}{\varphi (h)}\right) \\&\quad -(n+1)A h\Theta \sigma _n-A\sigma _n{\bar{g}}^{ij}{\bar{\nabla }}_ih{\bar{\nabla }}_j\Theta \\&\quad +A\Theta \sigma _n^{ij}r_i^kr_{jk}+A\eta \rho ^2. \end{aligned}$$

Dropping some positive terms gives

$$\begin{aligned} {\mathcal {L}}\chi&\ge \left( \frac{1}{h}+\frac{\varphi '(h)}{\varphi (h)}\right) \Theta \sigma _n-\eta \left( n+1+\frac{h\varphi '(h)}{\varphi (h)}\right) \\&\quad +\frac{A}{2}\eta \rho ^2-(n+1)A h\Theta \sigma _n-A\sigma _n{\bar{g}}^{ij}{\bar{\nabla }}_ih{\bar{\nabla }}_j\Theta . \end{aligned}$$

By the $C_0$-estimate, Lemma 3.3, if A is chosen large enough, the right-hand side of the above equation is strictly positive provided $\min \sigma _n\rightarrow 0$. Thus $\sigma _n$ is uniformly bounded below away from zero. $\square$

Lemma 3.5

There is a constant d such that $\sigma _n\le d.$

Proof

For $\varepsilon >0$ sufficiently small, consider the auxiliary function

$$\begin{aligned}\chi :=\frac{f\varphi \sigma _n}{1-\varepsilon \frac{\rho ^2}{2}}.\end{aligned}$$

We have

$$\begin{aligned} {\mathcal {L}}\frac{\Theta \sigma _n}{h}&=2\Theta \sigma _n^{ij}{\bar{\nabla }}_i\log h{\bar{\nabla }}_j\left( \frac{\Theta \sigma _n}{h}\right) \nonumber \\&\quad +\left( n+\frac{h\varphi '(h)}{\varphi (h)}\right) \left( \frac{\Theta \sigma _n}{h}\right) \left( \frac{\Theta \sigma _n}{h}-\eta \right) . \end{aligned}$$

(3.7)

Therefore, by Lemma 3.1 and (3.7), at any point with $t>0$ where $\chi$ attains a maximum,

$$\begin{aligned} \partial _t\chi&\le \frac{1}{1-\varepsilon \frac{\rho ^2}{2}}\Biggl (2\Theta \sigma _n^{ij}{\bar{\nabla }}_i\log h{\bar{\nabla }}_j\left( \frac{\Theta \sigma _n}{h}\right) \\&\quad +\left( n+\frac{h\varphi '(h)}{\varphi (h)}\right) \left( \frac{\Theta \sigma _n}{h}\right) \left( \frac{\Theta \sigma _n}{h}-\eta \right) \Biggr )\\&\quad +\frac{\varepsilon f\varphi (h)\sigma _n}{(1-\varepsilon \frac{\rho ^2}{2})^2}\left( (n+1)h\Theta \sigma _n+\sigma _n{\bar{g}}^{ij}{\bar{\nabla }}_ih{\bar{\nabla }}_j\Theta -\Theta \sigma _n^{ij}r_i^kr_{jk}-\eta \rho ^2\right) . \end{aligned}$$

Using ${\bar{\nabla }}\chi =0$ we have

$$\begin{aligned}{\bar{\nabla }}_j\log \left( \tfrac{\Theta \sigma _n}{h}\right) = {\bar{\nabla }}_j \log \left( \tfrac{1}{1-\varepsilon ^2\rho ^2/2}\right) .\end{aligned}$$

Substituting in

$$\begin{aligned} {\bar{\nabla }}_j \frac{\rho ^2}{2} = h{\bar{\nabla }}_j h + {\bar{g}}^{kl}{\bar{\nabla }}_j {\bar{\nabla }}_k h {\bar{\nabla }}_l h = {\bar{g}}^{kl} r_{jl} {\bar{\nabla }}_k h. \end{aligned}$$

and from the convexity of the hypersurface, we then see that the term $\sigma _n^{ij}{\bar{\nabla }}_i\log h{\bar{\nabla }}_j\left( \frac{\Theta \sigma _n}{h}\right)$ is non-positive. Thus due to AM-GM inequality,

$$\begin{aligned}\sigma _n^{ij}r^k_i r_{jk}\ge c\sigma _n^{1+\tfrac{1}{n}},\end{aligned}$$

and the $C_0$-estimate, we obtain

$$\begin{aligned}\partial _{t} \chi \le c_1\chi +c_2\chi ^2-c_3\chi ^{2+\frac{1}{n}}\end{aligned}$$

for some positive constants $c_1,c_2,c_3$. Here we identified $\chi$ with $\max \chi$. From this the claim follows. $\square$

Lemma 3.6

The principal curvatures are uniformly bounded above, and below away from zero.

Proof

To obtain the lower and upper curvature bounds, we can argue exactly as in the proof of [8, Lem. 8] where we applied the maximum principle to the evolution equation of $\chi :=\log ( \Vert W\Vert / h^{\alpha })$. Here $\Vert W\Vert ^2$ is the sum of squares of the principal curvatures and $\alpha >0$ is a suitable constant. A different argument is also given in the proof of [13, Lem. 8.2]. $\square$

3.2 Convergence

In the previous section, the $C^2$-estimates were obtained for either flow under their corresponding assumptions. Now the higher order regularity estimates follow from the theory of parabolic differential equations; see for details [51, 52]. Therefore, the maximal time interval is unbounded.

Due to Lemma 3.2, subconvergence for the flows (2.1) and (2.3) to stationary solutions is standard: by the upper bound on the support functions, there is a constant C, depending only on $M_0,$ such that

$$\begin{aligned}\int _{{\mathbb {S}}^n} h\sigma _nd\theta \le C.\end{aligned}$$

In view of (3.4) and (3.5), this implies that

$$\begin{aligned}\liminf _{t\rightarrow \infty } \int _{{\mathbb {S}}^n}(\partial _t h)^2=0.\end{aligned}$$

Hence, the flow hypersurfaces subconverge to a stationary solution.

To obtain full convergence for the flow (2.3), let us put

$$\begin{aligned}{\mathcal {F}}=V-\int \frac{\phi (h)}{f}d\theta .\end{aligned}$$

Recall from (3.5) that

$$\begin{aligned} \frac{d}{dt}{\mathcal {F}}=\int _{{\mathbb {S}}^n}\frac{(\partial _th)^2}{fh\varphi (h)}d\theta . \end{aligned}$$

Note that

$$\begin{aligned} \nabla ^{L^2({\mathbb {S}}^n)} {\mathcal {F}}=\sigma _n-\frac{1}{f\varphi (h)}=\frac{\partial _th}{fh\varphi (h)}. \end{aligned}$$

Hence due to our $C_0$-estimates,

$$\begin{aligned} \frac{d}{dt}{\mathcal {F}}\ge c_0\Vert \nabla ^{L^2({\mathbb {S}}^n)}{\mathcal {F}}\Vert _{L^2({\mathbb {S}}^n)}\Vert \partial _th\Vert _{L^2({\mathbb {S}}^n)}. \end{aligned}$$

Now we can argue as in [2, 29] to promote subconvergence to full convergence.

4 General measures

4.1 Notions and notation

Let $\phi : [0,\infty )\rightarrow [0,\infty )$ be an increasing function, continuously differentiable on $(0,\infty )$ with positive derivative, and satisfying $\lim _{s\rightarrow \infty }\phi (s)=\infty .$ For a finite non-zero Borel measure $\mu$ and a continuous, nonnegative function f on ${\mathbb {S}}^n$, the Orlicz norm $\Vert f\Vert _{\phi ,\mu }$ is defined by

$$\begin{aligned} \Vert f\Vert _{\phi ,\mu }=\inf \left\{ \lambda >0: \frac{1}{|\mu |}\int _{{\mathbb {S}}^n}\phi \left( \frac{f}{\lambda }\right) d\mu \le \phi (1)\right\} . \end{aligned}$$

Here $|\mu |=\mu ({\mathbb {S}}^n).$

Note that in general the Orlicz norm does not satisfy a triangle inequality and the case $\phi (t)=t^p$ gives the normalized $L^p$ norm. The Orlicz norm satisfies the following properties:

$$\begin{aligned} \Vert cf\Vert _{\phi ,\mu }&=c\Vert f\Vert _{\phi ,\mu }\quad \forall c\in (0,\infty ),\nonumber \\ f\le g&\Rightarrow \Vert f\Vert _{\phi ,\mu }\le \Vert g\Vert _{\phi ,\mu }. \end{aligned}$$

(4.1)

Definition 4.1

 

• (1) The Hausdorff distance of two convex sets K, L is defined by

  $$\begin{aligned}d_{{\mathcal {H}}}(K,L)=\max _{u\in {\mathbb {S}}^n}|h_K(u)-h_L(u)|.\end{aligned}$$

• (2) A sequence $\{K_i\}_{i\in {\mathbb {N}}}\subset \mathrm {K}$ converges to a convex body K if

  $$\begin{aligned}\lim _{i\rightarrow \infty }d_{{\mathcal {H}}}(K_i,K)=0.\end{aligned}$$

• (3) For $v\in {\mathbb {S}}^n$, define

  $$\begin{aligned}h_{{\hat{v}}}(u)=\langle u,v\rangle _+=\max \{0,\langle u,v\rangle \}\quad \forall u\in {\mathbb {S}}^n.\end{aligned}$$

• (4) Given a function $f:{\mathbb {S}}^n\rightarrow (0,\infty )$, we define the measure

  $$\begin{aligned}d\mu _f=\frac{1}{f}d\theta .\end{aligned}$$

4.2 Parabolic approximation

We begin this section by sketching the proof of Theorem 2.7. Assume $\varphi$ is smooth.

Step 1: We perturb $\varphi$ to $\varphi _{\varepsilon }$ such that

$$\begin{aligned}\varphi _{\varepsilon }(s)=s^{-n-\varepsilon }, \quad \forall s\in (0,\varepsilon ].\end{aligned}$$

Step 2: Suppose $0<f\in C^{\infty }({\mathbb {S}}^n).$ Using a suitable curvature flow, we find a smooth, strictly convex hypersurface $M_{\varepsilon }$ with positive support function such that

$$\begin{aligned} f\varphi _{\varepsilon }(h)\sigma _n=\frac{\int _{{\mathbb {S}}^n} h\sigma _nd\theta }{\int _{{\mathbb {S}}^n}\frac{h}{\varphi _{\varepsilon }(h)}d\mu _f}. \end{aligned}$$

Step 3: Take $\varepsilon =1/i$ and set $\varphi _i=\varphi _{\varepsilon }.$ Applying Step 2 to f and $\varphi _i,$ we find $K_i$ (with the origin in its interior) such that

$$\begin{aligned} dS_{K_i}= \frac{\gamma _i}{\varphi _i(h_{K_i})}d\mu _{f}\quad \text{ for } \text{ a } \text{ constant }~\gamma _i>0. \end{aligned}$$

Moreover, we show that the minimum and maximum width of $K_i$ as well as $\gamma _i$ are uniformly bounded above and below away from zero, such that these bounds, for i sufficiently large, depend only on $\varphi$ and $\mu _f$. Thus, letting $i\rightarrow \infty ,$ we can find a convex body $K\in \mathrm {K}_o$ such that

$$\begin{aligned} dS_K= \frac{\gamma }{\varphi (h_K)}d\mu _f\quad \text{ for } \text{ a } \text{ constant }~\gamma >0. \end{aligned}$$

Step 4: Choose $0<f_i\in C^{\infty }({\mathbb {S}}^n)$ such that $\mu _{f_i}\rightarrow \mu$ weakly as $i\rightarrow \infty$. By the conclusion of Step 3, we find $K_i\in \mathrm {K}_o$ such that

$$\begin{aligned} dS_{K_i}= \frac{\gamma _i}{\varphi (h_{K_i})}d\mu _{f_i}\quad \text{ for } \text{ a } \text{ constant }~\gamma _i>0. \end{aligned}$$

Moreover, $w_{\pm }(K_i)$ and $\gamma _i$ are uniformly bounded above and below away from zero, and these bounds, for i sufficiently large, depend only on $\varphi$ and $\mu$. Thus, letting $i\rightarrow \infty ,$ we find $K\in \mathrm {K}_o$ solving

$$\begin{aligned} dS_K= \frac{\gamma }{\varphi (h_K)}d\mu \quad \text{ for } \text{ a } \text{ constant }~\gamma >0. \end{aligned}$$

A further approximation allows us to assume $\varphi$ is continuous. Now we proceed with the details of this outline.

Assumption 4.1

Suppose

• (1) $\varphi :(0,\infty )\rightarrow (0,\infty )$ is continuous and $\lim \limits _{s\rightarrow 0^+}\varphi (s)=\infty ,$

• (2) $\phi (s)=\int _0^s\frac{1}{\varphi (t)}dt$ exists for all $s>0$ and $\lim \limits _{s\rightarrow \infty }\phi (s)=\infty .$

Suppose $\omega :{\mathbb {R}}\rightarrow [0,1]$ is a smooth function such that

$$\begin{aligned} \omega (s)=\left\{ \begin{array}{ll} 1, &{} s\ge 2\varepsilon , \\ 0, &{} s\le \varepsilon . \end{array} \right. \end{aligned}$$

Let $\varphi _{\varepsilon },\phi _{\varepsilon }:(0,\infty )\rightarrow (0,\infty )$ be defined by

$$\begin{aligned} \varphi _{\varepsilon }(s)=(1-\omega (s))s^{-n-\varepsilon }+\omega (s)\varphi (s) \end{aligned}$$

(4.2)

and

$$\begin{aligned} \phi _{\varepsilon }(s)=\int _0^s\frac{1}{\varphi _{\varepsilon }(t)}dt+\phi (2\varepsilon ). \end{aligned}$$

(4.3)

Due to the convexity of $x\mapsto x^{-1}$,

$$\begin{aligned} \frac{1}{\varphi _{\varepsilon }(s)}\le \frac{1}{\varphi (s)}+s^{n+\varepsilon }\quad \forall s\in [0,2\varepsilon ]. \end{aligned}$$

(4.4)

Moreover, we have

$$\begin{aligned} \phi _{\varepsilon }(s)\ge \phi (s) \end{aligned}$$

(4.5)

since by (4.3) we have

$$\begin{aligned} \phi _{\varepsilon }(s)&\ge \phi (2\varepsilon )\ge \phi (s)\quad \quad ~\text{ for }~ s\le 2\varepsilon ,\\ \phi _{\varepsilon }(s)&=\phi (s)+\int _0^{2\varepsilon }\frac{1}{\varphi _{\varepsilon }(t)}dt\ge \phi (s)\quad \quad ~\text{ for }~ s\ge 2\varepsilon . \end{aligned}$$

This last inequality also shows that $\lim _{s\rightarrow \infty }\phi _{\varepsilon }(s)=\infty .$

Remark 4.2

Note that

$$\begin{aligned} \phi (0)=0\quad \text{ and }\quad \phi _{\varepsilon }(0)=\phi (2\varepsilon ). \end{aligned}$$

Lemma 4.3

The functions $\phi _{\varepsilon }$, $1/\varphi _{\varepsilon }$, and $s/\varphi _{\varepsilon }(s)$ converge uniformly in $[0,\infty )$ to $\phi$, $1/\varphi (s)$, and $s/\varphi (s)$ as $\varepsilon \rightarrow 0,$ respectively.

Proof

The claims follow from (4.2), (4.4), (4.5) and

$$\begin{aligned} 0\le \phi _{\varepsilon }(s)-\phi (s)&\le (2\varepsilon )^{n+1+\varepsilon }+\phi (2\varepsilon )-\phi (\varepsilon ), \end{aligned}$$

(4.6)

$$\begin{aligned} \Big |\frac{1}{\varphi _{\varepsilon }(s)}-\frac{1}{\varphi (s)}\Big |&\le \max _{[0,2\varepsilon ]}\left( s^{n+\varepsilon }+\frac{2}{\varphi (s)}\right) , \end{aligned}$$

(4.7)

$$\begin{aligned} \Big |\frac{s}{\varphi _{\varepsilon }(s)}-\frac{s}{\varphi (s)}\Big |&\le \max _{[0,2\varepsilon ]}\left( s^{n+1+\varepsilon }+\frac{2s}{\varphi (s)}\right) . \end{aligned}$$

(4.8)

To verify (4.6), note that

$$\begin{aligned} \phi _{\varepsilon }(s)-\phi (s)-\phi (2\varepsilon )=&\int _0^{s}\frac{1}{\varphi _{\varepsilon }(t)}dt-\int _0^{s}\frac{1}{\varphi (t)}dt\\ =&\int _0^{2\varepsilon }\frac{1}{\varphi _{\varepsilon }(t)}dt-\int _0^{2\varepsilon }\frac{1}{\varphi (t)}dt\\ \le&\int _0^{\varepsilon }t^{n+\varepsilon }dt+\int _{\varepsilon }^{2\varepsilon }\frac{1}{\varphi (t)}+t^{n+\varepsilon }dt-\int _0^{2\varepsilon }\frac{1}{\varphi (t)}dt\\ =&\int _0^{2\varepsilon }t^{n+\varepsilon }dt-\int _0^{\varepsilon }\frac{1}{\varphi (t)}dt. \end{aligned}$$

$\square$

Lemma 4.4

Let $\mu$ be a finite Borel measure whose support is not contained in a hemisphere. Then for $\varepsilon$ sufficiently small we have

$$\begin{aligned} \min _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi _{\varepsilon },\mu }\ge \frac{1}{2}\min _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu }. \end{aligned}$$

Proof

By [31, Lem. 3.6], the values

$$\begin{aligned} c=\min _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu }~ \text{ and }~ c_{\varepsilon }=\min _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi _{\varepsilon },\mu }~\text{ are } \text{ positive. } \end{aligned}$$

In view of [32, Lem. 3], for each $\varepsilon$ there exists $v_{\varepsilon }\in {\mathbb {S}}^n$ such that

$$\begin{aligned} \phi _{\varepsilon }(1)=\frac{1}{|\mu |}\int _{{\mathbb {S}}^n}\phi _{\varepsilon }\left( \frac{h_{{\hat{v}}_{\varepsilon }}}{c_{\varepsilon }}\right) d\mu . \end{aligned}$$

Due to (4.5), $\phi _{\varepsilon }\ge \phi$. Therefore, we have

$$\begin{aligned} \phi _{\varepsilon }(1)\ge \frac{1}{|\mu |}\int _{{\mathbb {S}}^n}\phi \left( \frac{h_{{\hat{v}}_{\varepsilon }}}{c_{\varepsilon }}\right) d\mu . \end{aligned}$$

Since $\phi$ is increasing, if $c_{\varepsilon _i}\le \frac{c}{2}$ for a subsequence of $\{\varepsilon _i\}\rightarrow 0$, then

$$\begin{aligned} \phi _{\varepsilon _i}(1)&\ge \frac{1}{|\mu |}\int _{{\mathbb {S}}^n}\phi \left( \frac{2h_{{\hat{v}}_{\varepsilon _i}}}{c}\right) d\mu . \end{aligned}$$

Suppose $\lim \limits _{i\rightarrow \infty }v_{\varepsilon _i}=w.$ In view of (4.6), letting $i\rightarrow \infty$ gives

$$\begin{aligned} \phi (1)&\ge \frac{1}{|\mu |}\int _{{\mathbb {S}}^n}\phi \left( \frac{2h_{{\hat{w}}}}{c}\right) d\mu . \end{aligned}$$

Hence, we arrived at the contradiction $0<c\le \Vert h_{{\hat{w}}}\Vert _{\phi ,\mu }\le c/2$. $\square$

Lemma 4.5

Let a, b be two positive constants, $\varphi ,\varphi _{\varepsilon }$ be defined as above, and

$$\begin{aligned} \hat{\mathrm {K}}_o:=\{K\in \mathrm {K}_o: w_-(K)\ge a,~ h_K\le b \}. \end{aligned}$$

Suppose $\mu ,\{\mu _i\}_{i\in {\mathbb {N}}}$ are finite Borel measures on ${\mathbb {S}}^n$ such that $\mu _i\rightarrow \mu$ weakly and the support of $\mu$ is not contained in a closed hemisphere. Then there exist positive constants $\lambda ,\Lambda$ depending on $a,b,\varphi ,\mu$ such that for all $K\in \hat{\mathrm {K}}_o$, i sufficiently large and $\varepsilon$ small enough,

$$\begin{aligned} \lambda \le \int _{{\mathbb {S}}^n}\frac{h_K}{\varphi (h_K)}d\mu _i\le \Lambda ,\quad \lambda \le \int _{{\mathbb {S}}^n}\frac{h_K}{\varphi _{\varepsilon }(h_K)}d\mu _i\le \Lambda . \end{aligned}$$

Proof

Recall that $s/\varphi (s)$ is uniformly continuous on [0, b].

First, we show each $\mu _i$ satisfies

$$\begin{aligned}\int _{{\mathbb {S}}^n}\frac{h_K}{\varphi (h_K)}d\mu _i\ge c_i\quad \forall K\in \hat{\mathrm {K}}_o,\end{aligned}$$

for some constant $c_i>0.$ If the lower bound was zero, then by the Blaschke selection theorem we could find a sequence of convex bodies converging to a convex body ${\hat{K}}\in \hat{\mathrm {K}}_o$ with $\int _{{\mathbb {S}}^n}\frac{h_{{\hat{K}}}}{\varphi (h_{{\hat{K}}})}d\mu _i=0$. Thus, we would have $\mu _i(\{h_{{\hat{K}}}>0\})=0$. But the set $\{h_{{\hat{K}}}>0\}$ contains an open hemisphere, and for large i, $\mu _i(\Sigma )>0$ for any open hemisphere $\Sigma$.

Second, we show that $\{c_i\}$ is uniformly bounded below away from zero. Otherwise, we can find a sequence $\{K_i\}\subset \hat{\mathrm {K}}_o$ such that

$$\begin{aligned}\int _{{\mathbb {S}}^n}\frac{h_{K_i}}{\varphi (h_{K_i})}d\mu _i\rightarrow 0\quad \hbox {as}~i\rightarrow \infty .\end{aligned}$$

Suppose $K_i\rightarrow K\in \hat{\mathrm {K}}_o$ as $i\rightarrow \infty$. We have

$$\begin{aligned} \int _{{\mathbb {S}}^n}\frac{h_{K_i}}{\varphi (h_{K_i})}d\mu _i-\int _{{\mathbb {S}}^n}\frac{h_{K}}{\varphi (h_{K})}d\mu&=\int _{{\mathbb {S}}^n}\left( \frac{h_{K_i}}{\varphi (h_{K_i})}- \frac{h_{K}}{\varphi (h_{K})}\right) d\mu _i\\&\quad +\int _{{\mathbb {S}}^n}\frac{h_{K}}{\varphi (h_{K})}d\mu _i-\int _{{\mathbb {S}}^n}\frac{h_{K}}{\varphi (h_{K})}d\mu . \end{aligned}$$

In view of (4.8) and Definition 4.1, each line of the right-hand side goes to zero thus yielding a contradiction.

Finally, due to (4.8), for every $\delta >0$, there exist $\varepsilon _0,N$, such that for all $\varepsilon \le \varepsilon _0$, $i\ge N$ and $K\in \hat{\mathrm {K}}_o,$ we have

$$\begin{aligned} \int _{{\mathbb {S}}^n}\frac{h_K}{\varphi _{\varepsilon }(h_K)}d\mu _i&=\int _{{\mathbb {S}}^n}\frac{h_K}{\varphi (h_K)}d\mu _i +\int _{{\mathbb {S}}^n}\left( \frac{h_K}{\varphi _{\varepsilon }(h_K)}-\frac{h_K}{\varphi (h_K)}\right) d\mu _i\\&\ge \int _{{\mathbb {S}}^n}\frac{h_K}{\varphi (h_K)}d\mu _i-\delta |\mu |\\&\ge c_i-\delta |\mu |. \end{aligned}$$

Therefore, the uniform lower bound follows by taking $\delta$ small enough.

Now we prove the upper bounds. For i sufficiently large, we have

$$\begin{aligned} \int _{{\mathbb {S}}^n}\frac{h_K}{\varphi (h_K)}d\mu _i\le |\mu _i|\max _{s\in [0,b]}\frac{s}{\varphi (s)}\le 2|\mu |\max _{s\in [0,b]}\frac{s}{\varphi (s)}. \end{aligned}$$

Moreover, due to (4.8), there exist $\varepsilon _0,N$, such that for all $\varepsilon \le \varepsilon _0$, $i\ge N$ and $K\in \hat{\mathrm {K}}_o,$ we have

$$\begin{aligned} \int _{{\mathbb {S}}^n}\frac{h_K}{\varphi _{\varepsilon }(h_K)}d\mu _i\le&\int _{{\mathbb {S}}^n}\frac{h_K}{\varphi (h_K)}d\mu _i+|\mu |. \end{aligned}$$

$\square$

Proposition 4.6

Suppose $\varphi :(0,\infty )\rightarrow (0,\infty )$ is a smooth such that Assumption 4.1 is satisfied. Let $f:{\mathbb {S}}^n\rightarrow (0,\infty )$ be smooth and $\varepsilon$ be sufficiently small. There exists a closed, smooth, strictly convex hypersurface $M_{\varepsilon }$ with positive support function such that

$$\begin{aligned} f\varphi _{\varepsilon }(h)\sigma _n=\gamma _{\varepsilon },\quad \hbox {where}\quad \gamma _{\varepsilon }=\frac{\int _{{\mathbb {S}}^n} h\sigma _nd\theta }{\int _{{\mathbb {S}}^n}\frac{h}{\varphi _{\varepsilon }(h)}d\mu _f}. \end{aligned}$$

(4.9)

In addition, we have

$$\begin{aligned}w_+(M_{\varepsilon })\le \frac{4}{\min \limits _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu _f}},\quad w_-(M_{\varepsilon })\ge \left( \frac{\min \limits _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu _f}}{4}\right) ^nV({\mathbb {S}}^n).\end{aligned}$$

Moreover, for some positive constants $\lambda ,\Lambda$ depending on $\varphi ,\mu _f$,

$$\begin{aligned}\lambda \le \gamma _{\varepsilon }\le \Lambda .\end{aligned}$$

Also, if f is invariant under a closed group $G\subset O(n+1),$ then $M_{\varepsilon }$ is G-invariant.

Proof

Let $M_0$ be the unit sphere. We seek a family of smooth, strictly convex hypersurfaces $\{M_{t,\varepsilon }\}$ whose support functions satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _th= f h\varphi _{\varepsilon }(h)\sigma _n-\frac{\int _{{\mathbb {S}}^n} h\sigma _nd\theta }{\int _{{\mathbb {S}}^n}\frac{h}{\varphi _{\varepsilon }(h)}d\mu _f} h;\\ h(\cdot ,0)\equiv 1. \end{array} \right. \end{aligned}$$

(4.10)

We prove the flow hypersurfaces subconverge smoothly to a solution of (4.9) with the desired properties. To do this, all we need is to obtain $C_0$-estimates; the higher order regularity estimates and convergence follow as in Sects. 3 and 3.2. Moreover, the statement regarding G-invariance follows, since the flow hypersurfaces are G-invariant.

Suppose $T_{\star }$ is the maximal time that the flow hypersurfaces are smooth, strictly convex and contain the origin in their interiors. First, we obtain a uniform upper bound for support functions on $[0,T_{\star })$ independent of $T_{\star }$. Then using this bound, we establish a uniform positive lower bound on the support functions on $[0,T_{\star })$ independent of $T_{\star }$. Thus the flow hypersurfaces will always contain the origin in their interiors as long as they are smooth and strictly convex.

Let us put $h_{t,\varepsilon }=h_{M_{t,\varepsilon }}$ and define

$$\begin{aligned}{\mathcal {E}}(t)=\frac{1}{|\mu _f|}\int _{{\mathbb {S}}^n}\phi _{\varepsilon }(h_{t,\varepsilon })d\mu _f.\end{aligned}$$

Since $\frac{d}{dt}{\mathcal {E}}(t)=0,$ we have ${\mathcal {E}}(t)={\mathcal {E}}(0)=\phi _{\varepsilon }(1).$ Thus from the definition of the Orlicz norm it follows that

$$\begin{aligned} \Vert h_{t,\varepsilon }\Vert _{\phi _{\varepsilon },\mu _f}\le 1. \end{aligned}$$

Choose $v\in {\mathbb {S}}^n$ and $R>0$, such that $Rv\in M_{t,\varepsilon }$ and |Rv| is maximal. The line segment joining the origin and Rv is the largest such line segment contained in the enclosed region by $M_{t,\varepsilon }$ and its support function is $Rh_{{{\hat{v}}}}$. Therefore, by this inclusion $h_{t,\varepsilon }\ge Rh_{{{\hat{v}}}}.$ Due to (4.1),

$$\begin{aligned} R\min _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi _{\varepsilon },\mu _f}\le R\Vert h_{{\hat{v}}}\Vert _{\phi _{\varepsilon },\mu _f}\le \Vert h_{t,\varepsilon }\Vert _{\phi _{\varepsilon },\mu _f}\le 1. \end{aligned}$$

(4.11)

By Lemma 4.4, for $\varepsilon$ sufficiently small, we have

$$\begin{aligned}\min _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi _{\varepsilon },\mu _f}\ge \frac{1}{2}\min _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu _f}.\end{aligned}$$

Together with (4.11), this last inequality yields an upper bound on $R=\max h_{t,\varepsilon }$ and the maximum width:

$$\begin{aligned}w_+(M_{t,\varepsilon })\le 2R\le \frac{4}{\min \limits _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu _f}}.\end{aligned}$$

Moreover, since the volume is non-decreasing along the flow, the lower bound on the minimum width follows as well:

$$\begin{aligned} V({\mathbb {S}}^n)&\le V(M_{t,\varepsilon })\le w_-(M_{t,\varepsilon })w_+(M_{t,\varepsilon })^{n}\\&\le \left( \frac{4}{\min \limits _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu _f}}\right) ^nw_-(M_{t,\varepsilon }). \end{aligned}$$

Thus by a special case of Lemma 4.5 ($\mu =\mu _i=d\mu _f$) we obtain

$$\begin{aligned}\lambda \le \frac{\int _{{\mathbb {S}}^n} h\sigma _nd\theta }{\int _{{\mathbb {S}}^n} \frac{h}{\varphi _{\varepsilon }(h)}d\mu _f}\le \Lambda \end{aligned}$$

for some positive constants. Therefore, as soon as $h_{\min }\le \varepsilon$,

$$\begin{aligned} \partial _t\log h_{\min }&\ge \varphi _{\varepsilon }(h_{\min })h_{\min }^nf_{\min }-\Lambda \\&=h_{\min }^{-\varepsilon }f_{\min }-\Lambda . \end{aligned}$$

Thus for each $\varepsilon$, $h_{t,\varepsilon }$ is uniformly bounded below away from zero. $\square$

Corollary 4.7

Suppose $\varphi :(0,\infty )\rightarrow (0,\infty )$ is a smooth function such that Assumption 4.1 is satisfied. Let $f:{\mathbb {S}}^n\rightarrow (0,\infty )$ be smooth. Then there exists a convex body $K\in \mathrm {K}_o$ such that

$$\begin{aligned} dS_K= \frac{\gamma }{\varphi (h_K)}d\mu _f\quad \text{ for } \text{ a } \text{ constant }~\gamma >0. \end{aligned}$$

In addition, we have

$$\begin{aligned}w_+(K)\le \frac{4}{\min \limits _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu _f}},\quad w_-(K)\ge \left( \frac{\min \limits _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu _f}}{4}\right) ^nV({\mathbb {S}}^n),\end{aligned}$$

and for some positive constants depending only on $\varphi ,\mu _f$,

$$\begin{aligned} \lambda \le \gamma \le \Lambda . \end{aligned}$$

Moreover, if f is invariant under a closed group $G\subset O(n+1),$ then K is invariant under G.

Proof

Let $\varepsilon =\frac{1}{i}$ in Proposition 4.6 and $\varphi _i=\varphi _{\varepsilon }$. For each i, we have a solution $K_i$ containing the origin in its interior such that

$$\begin{aligned} dS_{K_i}=\frac{\gamma _i}{\varphi _{i}(h_{K_i})}d\mu _f. \end{aligned}$$

Moreover, $\{h_{K_i}\}$ is uniformly bounded above, we have a uniform positive lower bound on $w_-(K_i)$, and $\gamma _i\in [\lambda ,\Lambda ]$. Thus by the Blaschke selection theorem, we may find a subsequence of $\{K_i\}$ converging to a limit $K\in \mathrm {K}_o$ while $\gamma _i\rightarrow \gamma \in [\lambda ,\Lambda ]$. Note that if f is invariant under G, then all $K_i$ and thus K is invariant under G.

Suppose $\psi \in C({\mathbb {S}}^n)$. Note that

$$\begin{aligned} \int _{{\mathbb {S}}^n}\psi \left( \frac{1}{\varphi _{i}(h_{K_i})}-\frac{1}{\varphi (h_{K})}\right) d\mu _f&=\int _{{\mathbb {S}}^n}\psi \left( \frac{1}{\varphi _{i}(h_{K_i})}-\frac{1}{\varphi (h_{K_i})}\right) d\mu _f\\&\quad +\int _{{\mathbb {S}}^n}\psi \left( \frac{1}{\varphi (h_{K_i})}-\frac{1}{\varphi (h_{K})}\right) d\mu _f, \end{aligned}$$

In view of (4.7), the first line on the right-hand side tends to zero as $i\rightarrow \infty .$ Since $1/\varphi$ is continuous and $h_{K_i}$ converges to $h_{K}$ uniformly, the term on the second line converges to zero as well. Since $S_{K_i}\rightarrow S_K$ weakly (cf. [54]), K satisfies

$$\begin{aligned} \int _{{\mathbb {S}}^n}\psi dS_{K}=\gamma \int _{{\mathbb {S}}^n}\frac{\psi }{\varphi (h_{K})}d\mu _f\quad \forall \psi \in C({\mathbb {S}}^n). \end{aligned}$$

$\square$

4.3 Proofs

Proof of Theorem 2.7

For the moment, we suppose $\varphi$ is smooth and Assumption 4.1 is satisfied. Using approximation by discrete measures [54, Thm. 8.2.2] and then bump functions in turn [13, Lem. 3.7], there exists a family of positive functions $\{f_i\}\subset C^{\infty }({\mathbb {S}}^n)$ such that $\mu _{f_i}\rightarrow \mu$ weakly as $i\rightarrow \infty .$ We can choose $\{f_i\}$ to be invariant under G when $\mu$ is G invariant. Since the support of $\mu$ is not contained in a closed hemisphere, by [31, Cor. 3.7] we obtain

$$\begin{aligned} \min _{v\in {\mathbb {S}}^n}\Vert h_{{\hat{v}}}\Vert _{\phi ,\mu _{f_i}}\ge \delta >0. \end{aligned}$$

(4.12)

Suppose $K_i$ is a solution corresponding to the measure $\mu _{f_i}$ given by Corollary 4.7. By (4.12), we have uniform lower and upper bounds on $w_-(K_i)$ and $w_+(K_i).$ Thus a subsequence of $\{K_i\}$ converges to a convex body $K\in \mathrm {K}_o$.

Since $\mu _{f_i}\rightarrow \mu$ weakly, by Lemma 4.5 the constants $\lambda ,\Lambda$ of Corollary 4.7 depend only on $w_-,w_+,\varphi ,\mu .$ Hence, K is the desired solution. A further approximation allows us to assume $\varphi$ is merely continuous. $\square$

Proof of Theorem 2.6

We only mention the necessary changes in the argument leading to Theorem 2.7. Suppose $\{f_i\}\subset C^{\infty }({\mathbb {S}}^n)$ is a family of positive even functions such that $\mu _{f_i}\rightarrow \mu$ weakly as $i\rightarrow \infty .$ We consider the flow of smooth, strictly convex hypersurfaces $\{M_{t,i}\}$ whose support functions satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _th= f_i h\varphi (h)\sigma _n-\frac{\int _{{\mathbb {S}}^n} h\sigma _nd\theta }{\int _{{\mathbb {S}}^n}\frac{h}{\varphi (h)}d\mu _{f_i}} h;\\ h(\cdot ,0)\equiv 1. \end{array} \right. \end{aligned}$$

Note for each i, the flow hypersurfaces $\{M_{t,i}\}$ remain o-symmetric and converge smoothly to a strictly convex hypersurface $M_{i}$, enclosing the region $K_i$, which solves

$$\begin{aligned} \varphi (h_{K_i})dS_{K_i}=\frac{(n+1)V(M_i)}{\int _{{\mathbb {S}}^n}\frac{h_{K_i}}{\varphi (h_{K_i})}d\mu _{f_i}}d\mu _{f_i}. \end{aligned}$$

For i sufficiently large, the uniform upper bound for $\{h_{K_i}\}$ follows from the following argument. For $v\in {\mathbb {S}}^n$, let $h_{{\bar{v}}}$ be the support function of the line segment joining $\pm v$. Then we have $\min _{v\in {\mathbb {S}}^n}\Vert h_{{\bar{v}}}\Vert _{\phi ,\mu _{f_i}}>0.$ Now for any v and R such that $\pm Rv\in M_{i}$ with maximal distance from the origin, we have $Rh_{{\bar{v}}}\le h_{K_i}$. Therefore, arguing similarly as in (4.11), we deduce

$$\begin{aligned}R\min _{v\in {\mathbb {S}}^n}\Vert h_{{\bar{v}}}\Vert _{\phi ,\mu _{f_i}}\le 1.\end{aligned}$$

Since $\mu$ is a finite even Borel measure which is not concentrated on a great subsphere, by [31, Cor. 3.7] we have

$$\begin{aligned} \min _{v\in {\mathbb {S}}^n}\Vert h_{{\bar{v}}}\Vert _{\phi ,\mu _{f_i}}\ge \delta >0 \quad \text{ for } i \text{ large } \text{ enough }. \end{aligned}$$

Hence due to $V(M_i)\ge V({\mathbb {S}}^n),$ we find constants a, b such that

$$\begin{aligned} a\le h_{K_i}\le b. \end{aligned}$$

This yields $\lambda , \Lambda$, depending only on a, b, such that

$$\begin{aligned} \lambda \le \int _{{\mathbb {S}}^n}\frac{h_{K_i}}{\varphi (h_{K_i})}d\mu _{f_i}\le \Lambda \quad \text{ for } i \text{ sufficiently } \text{ large }. \end{aligned}$$

Therefore, a subsequence of $\{K_i\}$ converges to a solution of (1.1). $\square$

Remark 4.8

Note that in Theorem 2.6, the condition $\lim _{s\downarrow 0}\varphi (s)=\infty$ is relaxed. In this case, the lower bound on the support function follows easily as is explained in the proof of Theorem 2.6. While to prove Theorem 2.7, we use an approximation argument in which it is essential that the right-hand side of (4.7) converges to zero; cf. Corollary 4.7.

5 Christoffel–Minkowski type problems

Given a smooth, positive function f defined on the unit sphere, the $L_p$-Christoffel–Minkowski problem asks for a smooth, strictly convex hypersurface with positive support function h that satisfies

$$\begin{aligned} fh^{1-p}\sigma _k=\gamma , \quad \text{ for } \text{ some } \text{ constant }~\gamma >0. \end{aligned}$$

Here $p\in {\mathbb {R}}$, $\sigma _k$ is the k-th elementary symmetric polynomial

$$\begin{aligned} \sigma _{k}(\lambda )=\sum _{1\le i_{1}<\dots <i_{k}\le n}\lambda _{i_{1}}\cdots \lambda _{i_{k}}, \end{aligned}$$

and $\lambda _i$ are the principal radii of curvature. The reader may consult [28, 30, 33] and references therein regarding this problem.

In this section, we solve a class of $L_p$-Christoffel–Minkowski type problems, allowing a broader class of curvature functions in place of $\sigma _k,$ which can be considered as a complement of [9, Thm. 3.13]. Our proof remains brief and only the necessary modifications of the proof in [38] are highlighted. Define

$$\begin{aligned} \Gamma _+=\{(\lambda _i)=(\lambda _1,\dots ,\lambda _n)\in {\mathbb {R}}^n; \lambda _i>0\}. \end{aligned}$$

Assumption 5.1

Suppose $F\in C^{\infty }(\Gamma _+)$ is positive, 1-homogeneous, strictly monotone, $F(1,\dots ,1)=1,$ inverse concave, i.e.,

$$\begin{aligned}F_{*}(\lambda _i):=\frac{1}{F(\lambda _i^{-1})}\quad \text{ is } \text{ concave, }\end{aligned}$$

and $F_{*}|_{\partial \Gamma _+}=0$.

By [22, Lem. 2.2.11], $\sigma _k^{\frac{1}{k}}$ satisfies Assumption 5.1.

Theorem 5.1

Let $k\in {\mathbb {N}},$ $p>k+1$ and $0<f\in C^{\infty }({\mathbb {S}}^n)$ satisfy

$$\begin{aligned} {\bar{\nabla }}_i{\bar{\nabla }}_jf^{\frac{1}{p+k-1}}+{\bar{g}}_{ij}f^{\frac{1}{p+k-1}}>0. \end{aligned}$$

Suppose F is a function of the principal radii of curvature and satisfies Assumption 5.1. Then there exists a closed, smooth, strictly convex hypersurface with positive support function that solves

$$\begin{aligned}fh^{1-p}F^k=1.\end{aligned}$$

To prove this theorem, we use a curvature flow similar to (2.3). For a suitable smooth, strictly convex hypersurface $M_0$ parameterized by

$$\begin{aligned}x_0: M\rightarrow {\mathbb {R}}^{n+1},\end{aligned}$$

we seek smooth, strictly convex hypersurfaces $M_t$ satisfying

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _tx= f (\nu )\frac{\langle x,\nu \rangle ^{2-p}}{F_{*}^k}\nu - x; \\ x(\cdot ,0)=x_0(\cdot ). \end{array} \right. \end{aligned}$$

(5.1)

Therefore, the support functions of the $M_t$ satisfy

$$\begin{aligned} \partial _th=fh^{2-p}F^k-h. \end{aligned}$$

(5.2)

Compared to the flow [38, (1.4)], here we do not have the global term $\eta$. Moreover, since in general the problem $fh^{1-p}F^k=1$ does not have any variational structure, we cannot expect the convergence of solutions for all initial hypersurfaces. Therefore, we follow the approach of [9, 22] to obtain the regularity estimates.

Step 1: Choose $M_0$ to be a sufficiently small origin-centered sphere such that

$$\begin{aligned} fh^{1-p}F^k|_{M_0}>1. \end{aligned}$$

This is possible due to $p>k+1.$

Step 2: We obtain uniform lower and upper bounds on the support function as in the proof of Lemma 3.3 here (the case of Theorem 2.3).

Step 3: Let us put

$$\begin{aligned} G=F^k,\quad \Theta =f h^{2-p},\quad {\mathcal {L}}=\partial _t-fh^{2-p}G^{ij}{\bar{\nabla }}_i{\bar{\nabla }}_j. \end{aligned}$$

We have

$$\begin{aligned} {\mathcal {L}}\left( \frac{\Theta G}{h}-1\right)&=2\Theta G^{ij}{\bar{\nabla }}_i\log h{\bar{\nabla }}_j\left( \frac{\Theta G}{h}\right) \nonumber \\&\quad +\left( 1+k-p\right) \left( \frac{\Theta G}{h}\right) \left( \frac{\Theta G}{h}-1\right) . \end{aligned}$$

(5.3)

Thus, $fh^{1-p}F^k$ is uniformly bounded above and below. By Step 2, we obtain uniform lower and upper bounds on F.

Step 4: Let $r^{ij}$ denote the inverse of principal radii of curvature. Since F is inverse concave, as in [38, Lem. 2.7], we can apply the maximum principle to the auxiliary function

$$\begin{aligned}\frac{r^{ij}}{h}\end{aligned}$$

to obtain a uniform lower bound on the principal radii of curvature.

Step 5: Let us arrange the principal radii of curvature as

$$\begin{aligned} \lambda _1\le \cdots \le \lambda _n. \end{aligned}$$

Due to Steps 3 and 4,

$$\begin{aligned} C\ge \frac{F}{\lambda _1}=F(1,\ldots ,\frac{\lambda _n}{\lambda _1})=\frac{1}{F_{*}(\frac{\lambda _1}{\lambda _n},\ldots ,1)}, \end{aligned}$$

for some constant C. Hence, by Assumption 5.1, we get a uniform upper bound on the principal radii of curvature.

Step 6: Now that we have uniform $C^2$-estimates, higher order regularity estimates follow as well and the flow smoothly exists on $[0,\infty ).$

Step 7: By (5.3), we have

$$\begin{aligned} \partial _th=fh^{2-p}F^k-h>0\quad \text{ for } \text{ all }~t\ge 0. \end{aligned}$$

Moreover, due to Step 2,

$$\begin{aligned} 0<h(u,t)-h(u,0)=\int _0^t (fh^{2-p}F^k-h)(u,s)ds<\infty . \end{aligned}$$

Therefore, in view of the monotonicity of h, the limit

$$\begin{aligned} {\tilde{h}}(u):=\lim _{t\rightarrow \infty }h(u,t) \end{aligned}$$

exists and is positive, smooth and ${\bar{\nabla }}^2{\tilde{h}}+{\bar{g}}{\tilde{h}}>0$. Thus the hypersurface with support function ${\tilde{h}}$ is our desired solution to

$$\begin{aligned} fh^{1-p}F^k=1. \end{aligned}$$