1 Introduction

There is a close relationship between neural networks and optimization; conventionally, training a neural network (NN) relies on minimizing an objective function that represents the difference between several samples of the network output and samples of the desired output according to the input (supervised learning); a classic example is Backpropagation [34], where it is shown the construction of an objective function and how to use the derivative of the objective function to build an algorithm to solve an optimization problem, transforming the neural network training into an optimization problem.

In the opposite direction, using neural networks to solve optimization problems have been explored, works as Cybenko [9] and Hornik et al. [13] show that a neural network can be used as an approximation of a function, using neural networks replacing functions in optimization problems can be seen in Villarrubia et al. [31], where an objective function is replaced by a neural network when the use of numerical algorithms based on Lagrange multipliers or the Kuhn–Tucker [17] conditions is not possible.

Previous works such as [23] propose a method to map an optimization problem into a neural network to avoid local minimums; similarly, some techniques use a neural network’s structure and convergence capabilities to solve optimization problems faster. In [33], neural networks are used to increase convergence speed in genetic algorithms used in solving optimization problems. In [7], a way to build a neural network similar to an array of operational amplifiers that, in the steady state, converge to a solution of an optimization problem. In [19], Authors use one-layer recurrent neural networks to provide an always descending direction of its states for solving nonsmooth pseudoconvex optimization problems. From another perspective, in [35], a method to transform a convex optimization problem into a system of ordinary differential equations (ODE) based on neural networks is proposed; the main characteristics are the convergence to the solution, which is more time efficient and less sensitive to initial conditions than other algorithms.

References [7] and [35] show ways to solve optimization problems faster than non-neural networks’ numerical algorithms, which are necessary for applications that require online solutions, such as optimal control [10], mobile applications electronics [24], and autonomous decision-making [29], among others.

In this paper, we present sufficient conditions under which a neural network can replace a numerical algorithm that solves a family of optimization problems. To this end, first, we present a family of optimization problems and a vector of parameters on which the solution depends; then, based on the Karush–Kuhn–Tucker (KKT) first-order conditions, we propose a function that maps the solutions to the KKT conditions and the presented parameters vector. Finally, we find conditions under which the inverse of the proposed function exists and can be replaced by a neural network. In contrast with the previously mentioned works, we do not attempt to solve one particular optimization problem; we develop a way to know if a neural network, trained with solutions to several examples of the family of problems, can substitute a numerical optimization algorithm for solving the problem for different values of the parameter vector; the input to the network is the parameter vector (which is known in the formulation of the optimization problem), and the output is the minimizer.

The primary motivation for substituting an optimization algorithm with a trained neural network is the advantage of the neural network over a numerical algorithm in terms of portability since it can be formulated with only sigmoidal functions [9] in contrast with some algorithms that need gradients calculations and matrix inversions; another advantage of the neural network is its execution time, which takes a known number of operations. Meanwhile, a numerical algorithm converges to a solution in an initial point-dependent number of iterations, also nowadays specialized hardware for running neural networks has been developed, such as [20], making it advantageous to replace optimization algorithms in online applications, for example, in [2] an analysis of different architectures of microprocessor performance on MPC implementation with ACADO [14] as a numerical algorithm is presented, showing that the Atmel ARM Architecture cannot be used when the optimal control problem has more than two states due to a memory overflow; in this work, a three-state MPC implementation is performed with a neural network in substitution of the same numerical algorithm.

This paper is organized as follows. In Sect. 2, we recall the preliminary results and definitions that will be used throughout the paper. In Sect. 3, we establish the family of optimization problems and a parameter vector that will be useful in Sect. 4, where we present the sufficient condition for an optimization problem solution to be found by a neural network replacing a numerical algorithm. In Sect. 5, we present one analytical and numerical example and one control experiment to illustrate our proposal’s effectiveness. In Sects. 6 and 7, discussion and conclusions are presented, respectively.

2 Theoretical preliminaries

Our main result relies on two works, one from functional analysis, Theorem 1 in [8], and one from neural networks, Theorem 2.5 in [13].

Definition 1

Let \(f:R^n \rightarrow R^n\) be a Lipschitz function, the generalized Jacobian of f around \(x_0\), denoted \(\partial f(x_0)\) is the convex hull of all matrices M of the form:

$$\begin{aligned} M= \lim _{x_i \rightarrow x_0}Jf(x_i) \end{aligned}$$

Where Jf(x) is a \(n \times n\) Jacobian of partial derivatives.

Theorem 1 in [8] holds; if \(\partial f(x_0)\) is of maximal rank, then, there exist a neighborhood U and V of \(x_0\) and \(f(x_0)\), respectively, and a Lipschitzian function \(g:V \rightarrow R^n\) such that:

  1. 1.

    \(g(f(u))=u\) for every \(u\in U\)

  2. 2.

    \(f(g(v))=v\) for every \(v\in V\)

Definition 2

A function \(\Psi :R \rightarrow [0,1]\) is a squashing functions if is not-decreasing, \(\lim _{x\rightarrow \infty }\Psi (x)=1\) and \(\lim _{x\rightarrow -\infty }\Psi (x)=0\).

Theorem 2.5 in [13] holds that a multi-output feedforward network whose activation functions are any squashing functions can approximate, to a desired degree of accuracy, any continuous or measurable function from \(R^r \rightarrow R^s\) with \(s,r\in Z^+\).

3 Family of optimization problems

In this section, we describe the family \(P_1\) of optimization problems that are analyzed in this work; we define it as follows:

$$\begin{aligned} \begin{array}{c} min\\ x\in \mathbb {R}^n \end{array} \ f(x,D) \end{aligned}$$
(1)

Subject to:

$$\begin{aligned} g_i(x,D) \le 0: \ i=1,2,3,.....,m \end{aligned}$$
(2)

With \(D \in \mathbb {R}^{n_d}\), \(m_b<n\) and \(m_b \le m\), being \(m_b\) the number of active constraints.

The objective function f(x, D) is a map \(\mathbb {R}^{n+n_d} \rightarrow \mathbb {R}\), at least, twice differentiable w.r.t D and x, \(g_i(x,D)\) is the i-th inequality constraint, at least twice differentiable, w.r.t. D and x, \(\mathbb {R}^{n+n_d} \rightarrow \mathbb {R}\). Functions f(x, D) and \(g_i(x,D)\) are at least once differentiable by x and then once differentiable by D. The term D can have any real value, and each generates a different problem, that’s why \(P_1\) is a family of problems.

Assumption 1

\(P_1\) has at least one solution \(x^*\) that fulfills the KKT first-order conditions:

$$\begin{aligned}{} & {} \nabla _x f(x^*,D)+ \sum _{i=1}^{m}\lambda _i^* \nabla _x g_i(x^*,D)=0 \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \lambda _i^* g_i(x^*,D)=0 \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \lambda _i^* \ge 0 \end{aligned}$$
(5)
$$\begin{aligned}{} & {} g_i(x^*,D) \le 0 \end{aligned}$$
(6)

with \(i=1,2,3,...,m\), where \(\lambda _i\) is the Lagrangian multiplier and \(\lambda _i^*\) is the local optimal Lagrangian multiplier associated with the i-th constraint.

Vector D is denoted as parameter vector on which the solution depends, but it is not an optimization variable; the following example, problem \(P_2\), shows how D is related to the problem statement and solution.

Example 1

$$\begin{aligned} \begin{array}{c} min\\ x_1,x_2 \end{array} \ (x_1-d_1)^2+(x_2-d_2)^2 \end{aligned}$$
(7)

Subject to:

$$\begin{aligned}{} & {} x_1-d_3 \le 0 \end{aligned}$$
(8)
$$\begin{aligned}{} & {} d_3,d_2,d_1 \ge 0 \end{aligned}$$
(9)

With \(D=[d_1,d_2,d_3]^T\).

The solution to problem \(P_2\) is a function of D, being \(x^*\) the minimizer, if we analytically solve \(P_2\), we can express it as \(x^*=f_{opt}(D)\); in this example, there are two possibilities for \(f_{opt}(D)\), showed below, which depend on the relationship between \(d_1\) and \(d_3\).

-Constraint (8) is not active and \(d_3>d_1\):

$$\begin{aligned} x^*=f_{opt}(D)=\begin{bmatrix} d_1 \\ d_2 \end{bmatrix} \end{aligned}$$
(10)

-Constraint (8) is active and \(d_3 \le d_1\):

$$\begin{aligned} x^*=f_{opt}(D)=\begin{bmatrix} d_3 \\ d_2 \end{bmatrix} \end{aligned}$$
(11)

3.1 On defined optimization problems family

The Family defined at the beginning of this section belongs to the subset of a general nonlinear continuous optimization problem (shown in Theorem 4.3.1 and 4.4.2 in [4]) in which x is a KKT point (fulfills Assumption 1), and the condition of being a minimum can be verified by their KKT second-order conditions, and the following gradients are defined.

$$\begin{aligned}{} & {} \nabla _D g_i(x,D)\\{} & {} \nabla _{D}\nabla _{x} g_i(x,D)\\{} & {} \nabla _{D}\nabla _{x} f(x,D) \end{aligned}$$

With \(i=1,2,...,m\).

There are no special structures in this family that restrict f(x, D) and \(g_i(x,D)\) of \(P_1\) to any form; for example, any quadratic objective function with linear constraints could be a member of this family; however, the MPC example in Sect. 5 has another form and is still part of the \(P_1\) family.

4 Sufficient condition for a neural network as an approximator of an optimization problem solver

Definition 3

The verification function denoted \(C(\lambda ,x,D)\) is a mapping \(\mathbb {R}^{m+n+n_d} \rightarrow \mathbb {R}^{m+n+n_d}\) where:

$$\begin{aligned} C(\lambda ,x,D)=\left[ \begin{array}{l} {G(x,D) \lambda } \\ {\nabla _x f(x,D)+\sum _{i=1}^{m}\lambda _i \nabla _x g_i(x,D)}\\ {D} \end{array}\right] \end{aligned}$$
(12)

Where G(x, D) and \(\lambda\) are the constraints in matrix representation and the Lagrange multipliers in a vector array, respectively (13), \(\nabla _k f\) is the gradient of f with respect to vector k; also, to shorten the notation, we state the Lagrangian function in (14).

$$\begin{gathered} G(x,\;D) = \left[ {\begin{array}{*{20}c} {g_{1} (x,D)} & 0 & 0 & {....} & 0 \\ 0 & {g_{2} (x,D)} & 0 & {....} & 0 \\ 0 & 0 & {g_{3} (x,D)} & {....} & 0 \\ 0 & 0 & 0 & {....} & {g_{m} (x,D)} \\ \end{array} } \right], \hfill \\ \lambda = \left[ {\begin{array}{*{20}c} {\lambda _{1} } \\ {\lambda _{2} } \\ . \\ . \\ . \\ {\lambda _{m} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(13)
$$\begin{aligned}{} & {} L(x,D, \lambda )= f(x,D)+\sum _{i=1}^{m}\lambda _i g_i(x,D) \end{aligned}$$
(14)

We can rewrite equation (12) as follows:

$$\begin{aligned} C(\lambda ,x,D)=\begin{bmatrix} G(x,D) \lambda \\ \nabla _x L(x,D, \lambda )\\ D \end{bmatrix} \end{aligned}$$
(15)

Theorem 1

For a problem \(P_1\), the Jacobian \(\partial C(\lambda ^*,x^*,D)\) exists, and if it is of maximal rank, then, exists a Lipschitz function \(H:\mathbb {R}^{m+n+nd}\rightarrow R^{m+n+n_d}\) such that \(H(0_{1 \times (m+n) },D)=[\lambda ^*,x^*,D]^T\).

Proof

We define \(x'=[\lambda , x, D]^T\) and then, calculate the Jacobian \(\frac{\partial C}{\partial x'}\)

$$\begin{aligned} \frac{\partial C}{\partial x'}= \left[ \begin{array}{lll} G(x,D) &{} \left[ \begin{array}{l} \lambda _1 \nabla _x g_1(x,D)^T \\ \lambda _2 \nabla _x g_2(x,D)^T \\ . \\ . \\ . \\ \lambda _m \nabla _x g_m(x,D)^T \end{array}\right] &{}\left[ \begin{array}{l} \lambda _1 \nabla _D g_1(x,D)^T \\ \lambda _2 \nabla _D g_2(x)^T \\ . \\ . \\ . \\ \lambda _m \nabla _D g_m(x,D)^T \end{array}\right] \\ \left[ \begin{array}{lll}\nabla _x g_1(x,D) &{}...&{} \nabla _x g_m(x,D)\end{array}\right] &{} \nabla _{xx}^2 L(x,\lambda ,D) &{} \nabla _{xD}^2L(x,\lambda ,D) \\ 0 &{} 0 &{} I_{n_d \times n_d} \end{array}\right] \end{aligned}$$
(16)

According to problem definition \(P_1\), which includes Assumption 1 in Sect. 3 (has a solution that fulfills the first KKT sufficient conditions), it is possible to say that (16) exists and is defined in \(x'^*:=\begin{bmatrix} \lambda ^* \\ x^*\\ D \end{bmatrix}\), which includes an extreme point of \(P_1\), then, we can say that \(C(x'^*)\) is differentiable and, as a consequence, continuous. Moreover, based on definitions of continuity (for example, [16]), it is also Lipschitz in \(x'^*\).

If (16) has maximal rank and choose \(u=x'^*\) and \(f(u)=v=\begin{bmatrix} 0_{1 \times m} \\ 0_{1 \times n }\\ D \end{bmatrix}\) to express \(C(\lambda *,x^*,D)\) as f in Definition 1, then, H fulfills the conditions shown in [8] (recalled on Sect. 2), proving Theorem 1, making (17) true.

$$\begin{aligned} H(0_{1 \times m+n },D) = g(f(u))=\begin{bmatrix} \lambda ^* \\ x^*\\ D \end{bmatrix} \end{aligned}$$
(17)

Remark 1

The function H can be expressed as \(C^{-1}\), the inverse of C; nevertheless, we do not intend to find an explicit form of \(C^{-1}\). Theorem 1 provides the condition under which \(C^{-1}\) exists.

Theorem 2

For optimization problems in the family \(P_1\), a feedforward neural network approximates a map, to a desired degree of accuracy, from \(\begin{bmatrix} 0_{1 \times m}, 0_{1 \times n }, D \end{bmatrix}^T\) to \(x'^*\) if the Jacobian \(\partial C(\lambda ^*,x^*,D)\) is of maximal rank.

Proof

By Theorem 1, we know that if the Jacobian \(\partial C(\lambda ^*,x^*,D)\) is of maximal rank, then, there is a function H that maps \(\mathbb {R}^{m+n+nd}\rightarrow \mathbb {R}^{m+n+nd}\), and by Theorem 2.5 in [13], we also know that a feedforward network can approximate any continuous function from \(\mathbb {R}^r \rightarrow \mathbb {R}^s\) if we consider \(s=r=m+n+n_d\), then, Theorem 2 is proven.

5 Examples of application in numerical optimization problems

This section shows two examples of theoretical analysis and application; in the first one, a Sequential Quadratic Programming (SQP) algorithm is used to solve a numerical optimization problem. The subproblem, in each algorithm step, is approximated by a neural network making the precision of the approximated solution essential to solve the main problem; this will show the equivalence of using a numerical algorithm solver and a neural network in terms of achieving the same solution in a numerical experiment; in the second example, we show a model predictive control application, which main component is the solution of an optimal control problem that can be formulated as an optimization problem. That control proposal has been implemented in recent years in works such as [3] where it is presented an experimental implementation around a neighborhood of the unstable equilibrium point of a system without making a theoretical analysis of using an NN instead of a numerical algorithm; another similar applications is shown in [15]; they make an analysis of the effects of replacing the numerical algorithm by a neural network in MPC with linear dynamics; the implementation of that result has been applied in works such as [1]; in this way, we test the effectiveness of the application of neural networks in different scenarios, including an application where online solutions are necessary, and then, we show how using this method; we can use a low-capacity microprocessor (which, due to memory size, cannot support the numerical algorithm solver as shown in [2]) to deploy the neural network and substitute an on-board computer.

5.1 Example 1: numerical experiment

In this example, we use an algorithm that converts a main problem into a series of subproblems; in this case, we use sequential quadratic programming (SQP) similar to the one shown in [5], where the approximation of the solution of the subproblems needs to be precise to find the solution to the main problem, this precision requirement helps to show, in a numerical example that the NN is able to approximate a solution of the subproblem well enough [13] to be used in an SQP algorithm and solve of the main problem.

This algorithm is proposed for problems of the following form \(P_3\):

$$\begin{aligned} \begin{array}{c} min\\ x\in \mathbb {R}^n \end{array} \ f(x) \end{aligned}$$
(18)

Subject to:

$$\begin{aligned} g_i(x) \le 0: \ i=1,2,3,.....,m \end{aligned}$$

With \(m_b< n\), \(m_b\) is the number of active constraints, \(f(x):\mathbb {R}^n \rightarrow \mathbb {R}\) is at least twice differentiable, and \(g_i(x):\mathbb {R}^n \rightarrow \mathbb {R}\) is the i-th constraint which needs to be at least twice differentiable w.r.t x.

Then, we define L as follows:

$$\begin{aligned} L=f(x)+\sum _{i=1}^{m}\lambda _ig(i) \end{aligned}$$
(19)

Algorithm 5.1:

  1. 1.

    Define a termination constant \(\epsilon \approx 0\), choose \(x_k\) and \(\lambda _k\) (the subscript \(k=0\) is referred to the number of iterations) that satisfies the constraints and \(\nabla _{xx}L>0\).

  2. 2.

    While \(|\nabla _xL|_2>\epsilon\) do:

    • Solve subproblem \(P_4\) for \(\delta _k^*,\lambda _k^{QP*}\), which are the minimizer and Lagrange multipliers, respectively, associated with the solution of \(P_4\):

      $$\begin{aligned} \begin{array}{c} min\\ \delta \in \mathbb {R}^n \end{array} \ \frac{1}{2} \delta ^T \nabla _{xx}L(x_k,\lambda _k) \delta +\nabla _x f(x_k)\delta \end{aligned}$$

      Subject to:

      $$\begin{aligned} g(x_k)+\nabla _x g(x_k)\delta \le 0_{1 \times m} \end{aligned}$$

    • Make \(x_{k+1}=x_k+\delta _k^*\) and \(\lambda _{k+1}=\lambda _k^{QP*}\).

    • Make \(k=k+1\) and calculate \(\nabla _{xx}L(x_k,\lambda _k)\), \(g(x_k)\) and \(\nabla _x f(x_k)\).

    end

  3. 3.

    \(x^*=x_k\) is the minimizer of the main problem.

We define the numerical example \(P_5\) as follows:

$$\begin{aligned} \begin{array}{c} min\\ x\in \mathbb {R}^2 \end{array} \ (x_1-5)^4+(x_2-3)^2 \end{aligned}$$
(20)

Subject to:

$$\begin{aligned} 3x_1-x_2^2+2\le 0 \end{aligned}$$

Which, according to algorithm 5.1, has a quadratic subproblem \(P_{6}\)

$$\begin{aligned} \begin{array}{c} min\\ \delta \in \mathbb {R}^2 \end{array} \ 6\delta _1^2(x_1-5)^2+(1-\lambda )\delta _2^2+4\delta _1(x_1-5)^3+2\delta _2(x_2-3) \end{aligned}$$
(21)

Subject to:

$$\begin{aligned} 3x_1-x_2^2+2+3\delta _1-2x_2\delta _2\le 0 \end{aligned}$$

5.1.1 Analysis of \(P_6\)

In this example, vector D contains \(x_1,x_2\) and \(\lambda\) which, in the first iteration, \(k=0\) are selected and in further iterations are calculated, as shown in Algorithm 5.1, which means \(D=[x_1,x_2, \lambda ]^T\), then, \(x'\) is defined as follows:

$$\begin{aligned} x'(\lambda ^{QP}, \delta , D)=\begin{bmatrix} \lambda ^{QP} \\ \delta _1 \\ \delta _2 \\ x_1 \\ x_2\\ \lambda \end{bmatrix} \end{aligned}$$
(22)

Where \(\lambda ^{QP}\) is the Lagrange multiplier related to the constraint in the solution to problem \(P_{6}\). The verification function is shown in (23):

$$\begin{aligned} C(\lambda ^{QP}, \delta , D)=\begin{bmatrix} \lambda ^{QP}(3x_1-x_2^2+2+3\delta _1-2x_2\delta _2) \\ 12\delta _1(x_1-5)^2+4(x_1-5)^3+3\lambda ^{QP} \\ (2-2\lambda )\delta _2+2(x_2-3)-2x_2\lambda ^{QP} \\ x_1 \\ x_2\\ \lambda \end{bmatrix} \end{aligned}$$
(23)

The Jacobian takes the form (24).

$$\begin{aligned} \partial C(\lambda ^{QP}, \delta , D)= \begin{bmatrix} g_{qp} &{} 2\lambda ^{QP} &{} 3x_2\lambda ^{QP} &{} 0 &{} 0 &{} 0 \\ 3 &{} 12(x_1-5)^2 &{} 0 &{} C_{24} &{} 0 &{}0 \\ 2x_2 &{} 0 &{}2-2\lambda &{} 0 &{}2-2\lambda ^{QP} &{}-2\delta _2 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$
(24)

With \(g_{qp}=3x_1-x_2^2+2+3\delta _1^*-2x_2\delta _2^*\) and \(C_{24}=24(x_1-5)\delta _1^*+12(x_1-5^2)\).

When there is only one constraint, the analysis is divided into two cases:

  1. 1.

    \(g_{qp}<0\) y \(\lambda ^{QP*}=0\).

  2. 2.

    \(g_{qp}=0\) y \(\lambda ^{QP*}>0\).

In the first case, it is easy to transform (24) by column and row operations to an equivalent matrix (25).

$$\begin{aligned} \begin{bmatrix} g_{qp} &{}0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 3 &{} 12(x_1-5)^2 &{} 0 &{} 0 &{} 0 &{}0 \\ 2x_2 &{} 0 &{}2-2\lambda &{} 0 &{}0 &{}0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$
(25)

Then, to implement, an SQP algorithm is necessary that (26) to be definite positive, which means (25) has a triangular form and, according to [12] and [11], is of maximal rank while using Algorithm 5.1.

$$\begin{aligned} \begin{bmatrix} 12(x_1-5)^2 &{} 0 \\ 0 &{} 2-2\lambda \end{bmatrix} \end{aligned}$$
(26)

The equivalent matrix, using row operations, of the second case Jacobian is shown in (27), by the same analysis of case 1, and with \(\lambda ^{QP*}\) not negative (condition for case 2) and (28) being a condition to use SQP then (24) is of maximal rank for both cases if \(3-\frac{4x_2^2}{2-2\lambda }\lambda ^{QP*} \ne 0\) which, according to \(P_6\) KKT second-order conditions, the following condition should be true in a minimum \(3-\frac{4x_2^2}{2-2\lambda }\lambda ^{QP*} > 0\).

$$\begin{aligned} \begin{bmatrix} 3\lambda ^{QP*} &{}0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 12(x_1-5)^2 &{} 3-\frac{4x_2^2}{2-2\lambda }\lambda ^{QP*} &{} 0 &{} 0 &{} 0 &{}0 \\ 0 &{} 2x_2 &{}2-2\lambda &{} 0 &{}0 &{}0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$
(27)
$$\begin{aligned} 2-2\lambda > 0 \end{aligned}$$
(28)

According to Theorems 1 and 2, the neural network will approximate the solution of \(P_{6}\). Perhaps, a valid thought that comes out is, why do not approximate the solution of \(P_5\) directly? Of course, it is possible to perform that analysis; nevertheless, this numerical example is done to show that, in practice, a neural network is precise enough to solve subproblem \(P_6\) and lead to the same solution of \(P_5\) using other algorithms.

5.1.2 Numerical implementation

The procedure to train the neural network is the following, first, solve the optimization problem \(P_6\) for different values of D using MatLab [22] function fmincon as a solver; 1990000 examples were collected, each example form a pair of data \(y'\) and \(x'\), as shown in (29), being the input and output of the NN, respectively. Where \(x'\) is the solution of \(P_6\) found using fmincon with \(y'\) as an input, each input is selected to make (26) definite positive and every input–output combination fulfills \(3-\frac{4x_2^2}{2-2\lambda }\lambda ^{QP*} \ne 0\), this data are available in the repository referenced in this work.

$$\begin{aligned} y'=\begin{bmatrix} x_1\\ x_2\\ \lambda \end{bmatrix}, x'=\begin{bmatrix} \lambda ^{QP}\\ \delta _1^* \\ \delta _2^* \end{bmatrix} \end{aligned}$$
(29)

This data where used as training data in supervised training on Tensorflow [21].

To make a more efficient training and network design, the inputs and outputs shown in (29) are different from \(y'=[0, \ 0, \ 0, \ D^T]^T\) and (22) used in the theoretical analysis, the reasons and justifications for these differences are listed below.

  • The absence of explicit zeros in \(y'\) is because, in common activation functions, such as the sigmoid shown in (30), that input will not have any effect while increasing the input size.

  • Vector D is missing in \(x'\) as in the implementation, replicating the input in the output is not necessary since it is already known and can be misleading in the training process because the training error will decrease without not necessarily approximating the unknown output, \(\lambda ^*\) and \(x^*\).

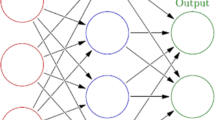
In this example, we use a feedforward neural network whose architecture is shown in Fig. 1, where \(N_j\) is the j-th neuron in the hidden layer and the output neuron \({N_i}^o\), with \(i=1,2,3\), is associated with the desired output, the activation function of the only hidden layer is the sigmoid function (30), and the output layer has a linear activation function (31).

$$\begin{aligned} \sigma _j=\frac{1}{1+\exp {(-(W_{1j}y'+b_{1j}))}} \end{aligned}$$
(30)

with \(j=1,2,...,650\). Where \(W_{1j}=[w^1_{j_{1}}, w^1_{j_{2}},...,w^1_{j_{m+n+n_d}}]\) are the weights for every input and \(b_{1j}\) is the bias for the j-th neuron.

$$\begin{aligned} s_i=b_{2i}+\sum _{j=1}^{350} w_{2j} \sigma _j \end{aligned}$$
(31)

With \(i=1,2,3\). Where \(w_{2j}\) is the j-th weight associated with \(\sigma _j\) as an input to the \(s_i\) neuron and \(b_{2i}\) is the bias associated with the output neuron \(s_i\).

In the next example, we skipped the mathematical description of the NN since the architecture is not the objective of this paper as long as a feedforward network is selected.

A mean squared error is used as an objective function with a training error of \(e_{P}=1.06\times 10^{-4}\), the optimizer used is RMSProp, sigmoid as hidden layer activation function, linear activation function in the output layer, 90% of the 1048575 examples with the form of (29), while fulfilling (26) and (28), as data training and 10% as validation with a mean squared error of \(e_{P}=7.22\times 10^{-5}\). The mean squared error is defined as follows:

$$\begin{aligned} e_{P}=\frac{1}{n_e}\sum _{m_u=1}^{n_e}(|S_{m_u}-x'_{m_u}|_2) \end{aligned}$$
(32)

Where \(S_{m_u}\) is the output of the neural network; with \(S_{m_u}=[s_1,s_2.s_3]\), \(n_e\) is the number of examples, and \(x'_{m_u}\) is the output of the training sample \(m_u\).

The data are available as supplementary information and is generated by a combination of \(x_1 \in [-2.95,7]\) in 0.05 intervals, \(x_2\) a randomly chosen in \((-4,1.5)\) and \(0<\lambda <1\) fulfilling (28); any combination that makes (26) not positive definite or \(3-\frac{4x_2^2}{2-2\lambda }\lambda ^{QP*} = 0\) is discarded.

The data generated is scaled, as suggested in works [30] and [26], by the normalization (33).

$$\begin{aligned} V_n=\frac{V_o-M_V}{S_V} \end{aligned}$$
(33)

Where \(V_n\) is the normalized value, \(V_o\) is the original value, and \(M_V\) and \(S_V\) are the mean and standard deviation of the set of values \(V_o\), respectively.

The data are generated without noise, and at the end of the training, there was not overfit; therefore, any other data preparation was avoided. A Jupyter notebook with the program used for training the NN shown in Fig. 1 can be found in the supplementary information.

Fig. 1
figure 1

Neural network for numerical example 3

Full size image

Main problem \(P_5\) is solved according to algorithm 5.1, the subproblem \(P_{6}\) is solved by MatLab fmincon, Scipy [32] and approximated by the neural network Hardcoded in MatLab and Python, those results are shown in Table 1, and the algorithm initial conditions are \(x=[0 \ 3.5]\), \(\lambda =0.5\) and \(\epsilon =0.003\).

Table 1 Comparative chart for problem \(P_5\)
Full size table

The number of iterations is too small to use them as a valid set for statistic computing time. To have a bigger set, we solved 1000 examples of subproblem \(P_{6}\) with random values of the training data set, and those results are presented in Table 2. Experiments were done on a Personal Computer with an Intel Core i3-10110U CPU @ 2.10GHz, 12 GB ram memory, running on Windows 10.

Table 2 Time statistics of 1000 executions
Full size table

Table 1 shows that the neural network is adequate for solving the main problem \(P_5\). Two of the main motivations for using an NN instead of a numerical algorithm in online implementations are the speed and consistency of the execution time; both can be seen in Table 2 where the neural network is faster and with less standard deviation than the numerical algorithms. The lower standard deviation can be explained by the way a neural network works since its output is obtained by a known quantity of operations of the input through the hidden layer until the output layer while most of the numerical algorithms use initial points and tolerance-dependent iterative processes where only a convergence rate is known and not an exact number of iterations. On the other hand, the speed advantage of the NN in this work could be because the NN is composed of functions as (30), and sums as (31) in contrast with gradient calculations and inverse matrix approximation used in some fminunc/Scipy subprocesses which take more computing time than the used in NN; nevertheless, this is a hypothesis with Table 2 as support, and it cannot be affirmed for every algorithm-NN comparison; however, proving a general statement is out of the scope of this paper.

Remark 2

Regarding Table 2, neither Python nor MatLab language were implemented on real-time platforms there are variations in the execution time of the neural network, even when every execution takes the same number of operations, nevertheless, in terms of computing time, we can see that the neural network is better in every statistic used as a performance measure. In Sect. 5.2.6, a soft real-time example is shown.

5.2 Example 2. Model predictive control.

Model predictive control (MPC) is an ample range of control methods that explicitly use the model of a process to obtain the control signal that minimizes an objective function [6]. In this example, we use the scheme shown in Fig. 2, based on a constant time horizon N and a discretization of the nonlinear model of the process.

Fig. 2
figure 2

Control scheme used in MPC

Full size image

The general optimal control problem \(P_{7}\) in this experiment, shown in Fig. 2, is formulated as follows:

$$\begin{aligned} \begin{array}{c} min\\ U\in \mathbb {R}^N \end{array} \ H(x,\hat{x},U) \end{aligned}$$
(34)

Subject to:

$$\begin{aligned}{} & {} \hat{x}(t+1) =f_i(\hat{x},U(t)); \hat{x}(0)=x(t) \end{aligned}$$
(35)
$$\begin{aligned}{} & {} U\le U_{max}; -U\le U_{min} \end{aligned}$$
(36)

Where H is the objective functional designed to achieve the desired output at the discrete-time N, minimize the control magnitude, and/or avoid an increase in the states magnitude. Expression (35) represents the discretized model of the process at the initial condition x(t); x represents the actual states of the process, while \(\hat{x}\) is the discretized predicted states, and U is a N-dimension vector whose entries are the control inputs for the predicted process (35), bounded by the upper and lower bounds \(U_{max}\) and \(U_{min}\), respectively.

The MPC applied in this example follows Algorithm 5.2.

Algorithm 5.2:

  1. 1.

    Define a constant integer time horizon N, which is the number of control samples and future states calculated at time t in each iteration.

  2. 2.

    To measure the states x(t) of the process at time t.

  3. 3.

    To solve the optimal control problem \(P_{7}\) and obtain a piecewise-constant signal control in form of a \(m \times N\)-dimension matrix \(U^*\). Where m is the number of control inputs, in this example \(m=1\).

  4. 4.

    To apply the first calculated control value in vector \(U^*\), \(U^*(1)\), to the process and go to step 1.

In an MPC implementation, the optimal control problem in step 2 is solved with a numerical algorithm; in this example, we compare that type of implementation versus approximating the solution of \(P_{7}\) with a neural network. In this example, we show a neural network in an MPC implementation of a one-degree-of-freedom inertial wheel-driven pendulum, the main difference with [3], is that we will use the complete range of movement of the pendulum, which has a nonlinear dynamic, making it also different to the analysis in [15], then we substitute the on-board computer (necessary to run the implemented numerical algorithm solver) by a microprocessor using less flash memory than the one available in the ARM microprocessor shown in [2], which was not able to run the algorithm, achieving the same results as both, the neural network and the optimization numerical algorithm in an on-board computer implementation, while showing that less expensive components can be used with the same results.

This proposal is different from the current use of Neural Networks on MPCs mainly on the function that is approximated by the NN, as shown in the survey [27], most of these MPCs control applications use NN to approximate uncertainties on the plant model when it makes not reliable to solve the optimization problem on time in online applications. In both cases, the proposal presented in this work could be implemented, because the NN (in those applications) will approximate equations (34), and the problem could still be analyzed with our proposal; nevertheless, our proposal could be used instead of the second case since in our proposal the entire solution of the optimization problem is approximated (if it fulfills Theorems 1 and 2), while the first principles approximation only approximates a part of the problem and a numerical algorithm is still necessary to solve the problem.

Other uses of neural networks in control have been reported in the literature outside the MPC field, recent works are more focused on control systems with uncertainties based on existing control schemes, for example, [18]. As these schemes are based on classical control methods, it is difficult to compare against our proposal but analysis as [28] shows a benchmark of MPC versus classical popular high-performance control methods in electrical machines with a favorable result on MPC.

The main reason to show an MPC example in this work is to show a physical experiment when an online precise solution is necessary to accomplish the control objective, and how our proposal has an advantage of computational time, and less computational power is required against the state of the art numerical algorithms for solving optimization problems in online applications.

5.2.1 Problem statement for example 2

An MPC control of an inertial wheel-actuated pendulum, with the parameters shown in Fig. 3, with the control objective of moving the pendulum from the stable equilibrium \(\Theta =0\) to the unstable equilibrium \(\Theta =\pi\) is considered.

Fig. 3
figure 3

Inertial wheel-actuated pendulum

Full size image

The dynamics of the system described in Fig. 3 is shown below.

$$\begin{aligned}{} & {} \ddot{\Theta }=-\left(\frac{1}{ml^2}\right)\left(mgl \sin (\Theta )+k\dot{\Theta }+\tau -k_1\dot{\Psi }\right) \end{aligned}$$
(37)
$$\begin{aligned}{} & {} \ddot{\Psi }=\left(\frac{1}{j_d}\right)\left(\tau -k_1\dot{\Psi }\right) \end{aligned}$$
(38)

Where m and k are the mass and friction constant related to the pendulum, respectively, g is the gravitational constant, \(k_1\) and \(j_d\) are the friction constant and the inertial moment related to the inertial wheel respectively, and \(\tau\) is the torque applied to the wheel.

5.2.2 MPC solution for example 2

To formulate the optimization problem, the dynamic Eqs. (37) and (38) are expressed in space state variables as follows, with \(x_1:=\Theta\), \(x_2:=\dot{\Theta }\), \(x_3:=\dot{\Psi }\) and \(\tau :=u\):

$$\begin{aligned} \dot{x}_1= \,\,& {} x_2 \end{aligned}$$
(39)
$$\begin{aligned} \dot{x}_2= & {} -(\frac{1}{ml^2})(mgl \sin (x_1)+kx_2+u -k_1x_3) \end{aligned}$$
(40)
$$\begin{aligned} \dot{x}_3= & {} (\frac{1}{j_d})(u-k_1x_3) \end{aligned}$$
(41)

To implement algorithm 5.2, the following problem \(P_{8}\) is formulated with a sample time \(h=0.0075s\), prediction horizon \(N=2\), and Euler numerical integration.

$$\begin{aligned} \begin{array}{c} min \\ u(1),u(2) \end{array} \ p_1(x_1(3)-r_1(k))^2+p_2(x_2(3)-r_2(k))^2+p_3(x_1(3)-r_3(k))^2 \end{aligned}$$
(42)

Subject to:

$$\begin{aligned} &x_1(1) =\Theta _{m}\\ &x_2(1) =\dot{\Theta }_{m}\\ &x_3(1) =\dot{\Psi }_{m}\\ &x_1(2) =x_1(1)+hx_2(1)\\ &x_2(2) =x_2(1)-(\frac{h}{ml^2})(mgl \sin (x_1(1))+kx_2(1)+u(1) -k_1x_3(1))\\ &x_3(2) =x_3(1)+(\frac{h}{j_d})(u(1)-k_1x_3(1))\\ &x_1(3) =x_1(2)+hx_2(2)\\ &x_2(3) =x_2(2)-(\frac{h}{ml^2})(mgl \sin (x_1(2))+kx_2(2)+u(2) -k_1x_3(2))\\ &x_3(3) =x_3(2)+(\frac{h}{j_d})(u(2)-k_1x_3(2))\end{aligned}$$
(43)
$$\begin{aligned}{} & {} {\begin{matrix} u_{min} \le u(1) \le u_{max}\\ u_{min} \le u(2) \le u_{max} \end{matrix}} \end{aligned}$$
(44)

Where \(\Theta _m\), \(\dot{\Theta }_m\) and \(\dot{\Psi }_m\) are the measured states, the terms \(p_1\), \(p_2\) and \(p_3\) are weights that work as penalization in the objective function when the terminal states \(x_1(3)\), \(x_2(3)\) and \(x_3(3)\) are different to \(r_1(k)\), \(r_2(k)\) and \(r_3(k)\), respectively; in this case, \(r_2(k)=r_3(k)=0\) are selected, \(r_1(k)\) is the desired angle \(\Theta _d\) at sample time k; this is a traditional way to construct an objective function [6].

Problem \(P_{8}\) can be formulated in the form of \(P_1\) as follows:

$$\begin{aligned} \begin{array}{c} min \\ u(1),u(2) \end{array} f(x_1(1),x_2(1),x_3(1),u(1),u(2),r_1(k),r_2(k),r_3(k)) \end{aligned}$$
(45)

Subject to:

$$\begin{aligned} {\begin{matrix} g_1= u(1)- u_{max} \le 0\\ g_2= -u(1)+ u_{min} \le 0\\ g_3= u(2)- u_{max} \le 0\\ g_4= -u(2)+ u_{min} \le 0 \end{matrix}} \end{aligned}$$
(46)

Where function f is the result of substituting the equality constraints (discretized system dynamic) (43) into (42).

5.2.3 Analysis of \(P_{8}\)

As mentioned before, \(r_1(k)\), \(r_2(k)\) and \(r_3(k)\) are the desired output, set-pint; according to Fig. 2, then, vectors \(r=[r_1(k), r_2(k), r_3(k)]^T\) and \(x(1)=[x_1(1), x_2(1),x_3(1)]\) are useful to be chosen as D; then, we can express \(x'\) as (47):

$$\begin{aligned} x'(\lambda , u,)=[\lambda _1, \lambda _2, \lambda _3, \lambda _4, u(1), u(2), r_1(k), r_2(k),r_3(k),x_1(1),x_2(1),x_3(1)]^T \end{aligned}$$
(47)

With a verification function (48).

$$\begin{aligned} C(x')=\left[ \begin{array}{l} {G(u) \lambda }\\ {\nabla _u f(u,D)+\sum _{i=1}^{m}\lambda _i \nabla _u g_i(u)}\\ {D} \end{array}\right] \end{aligned}$$
(48)

Where:

$$\begin{aligned} u=\begin{bmatrix} u(1)\\ u(2)\end{bmatrix},\lambda =\begin{bmatrix} \lambda _1 \\ \lambda _2\\ \lambda _3\\ \lambda _4\end{bmatrix}, D=\begin{bmatrix} r_1 \\ r_2\\ r_3\\ x_1(1)\\ x_2(1)\\ x_3(1)\\ \end{bmatrix}, G(u)=\begin{bmatrix}g_1 &{}0 &{}0 &{}0\\ 0 &{}g_2 &{}0 &{}0\\ 0 &{}0 &{}g_3 &{}0 \\ 0 &{}0&{}0 &{}g_4 \end{bmatrix} \end{aligned}$$

The Jacobian of (48) is (49).

$$\begin{aligned} \partial C(x'^*)=\left[ \begin{array}{llllllllllll} g_1 &{}0 &{}0 &{}0&{}\lambda _1 &{}0&{}0&{}0&{}0 &{}0&{}0&{}0\\ 0 &{}g_2 &{}0 &{}0&{}-\lambda _2&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0 &{}0 &{}g_3 &{}0&{}0&{}\lambda _3 &{}0&{}0&{}0 &{}0&{}0&{}0 \\ 0 &{}0&{}0 &{}g_4 &{}0 &{} -\lambda _4&{}0&{}0&{}0 &{}0&{}0&{}0 \\ 1&{}-1&{}0&{}0&{}R_1&{}R_2&{}C_1&{} C_2 &{} C_3&{}C_4&{} C_5 &{} C_6 \\ 0&{}0&{}1 &{}-1 &{}R_3&{}R_4 &{} C_7 &{}C_8 &{} C_9&{}C_{10}&{} C_{11} &{} C_{12}\\ 0&{}0&{}0&{}0 &{}0&{}0 &{}1&{}0&{}0 &{}0&{}0&{}0\\ 0&{}0&{}0&{}0 &{}0&{}0 &{}0&{}1&{}0 &{}0&{}0&{}0\\ 0&{}0&{}0&{}0 &{}0&{}0 &{}0&{}0&{}1 &{}0&{}0&{}0 \\ 0&{}0&{}0&{}0 &{}0&{}0 &{}0&{}0&{}0 &{}1&{}0&{}0\\ 0&{}0&{}0&{}0 &{}0&{}0 &{}0&{}0&{}0 &{}0&{}1&{}0\\ 0&{}0&{}0&{}0 &{}0&{}0 &{}0&{}0&{}0 &{}0&{}0&{}1 \end{array}\right] \end{aligned}$$
(49)

Using an analysis like the previous example and since constraints \(g_1\) and \(g_2\) cannot be active at the same time (same case with \(g_3\) and \(g_4\)), there are 5 cases generated by the constraints. Values \(C_i\) (i=1,2,...,12), \(R_1\), \(R_2\), and \(R_3\) are derived from the calculation of the Jacobian and are not presented in order to maintain clean writing, and we directly present the requirements for (49) to have maximal rank in all the cases:

$$\begin{aligned}{} & {} R_4=\frac{2p_2h^2}{(ml^2)^2}+ \frac{2p_3h^2}{j_d^2} \ne 0 \end{aligned}$$
(50)
$$\begin{aligned}{} & {} R_1-\frac{R_3R_2}{R_4}=\frac{2h^4(p_1p_2j_d^2 + p_1p_3(ml^2)^2 + p_2 p_3k^2))}{(ml^2)^2(p_2j_d^2 + p_3(ml^2)^2)}\ne 0 \end{aligned}$$
(51)

For control purposes, the weight related to \(x_1\) must be \(p_1>0\); the analysis made for problem \(P_8\) shows that \(p_2\) or \(p_3\) needs to be different to 0; in this case, we used that information to define those values on equation (42); to fulfill expression (50) and (51), we selected \(p_1=100000\), \(p_2=0.1\) and \(p_3=0.001\); as a conclusion for this analysis, the Jacobian (49) is of maximal rank. The choice of \(p_2\) and \(p_3\) based on our proposal shows how this analysis could help in the definition of the optimization problem, in order to guarantee that the solution could be approximated by a Neural Network, in this case, our analysis led us to complement the initial cost function (42).

5.2.4 MPC implementation for example 2

A block diagram of the inertial wheel-driven pendulum implementation is shown in Fig. 4, and a picture of the real system is shown in Fig. 5.

Fig. 4
figure 4

Block diagram of pendulum implementation

Full size image
Fig. 5
figure 5

Frontal and lateral view of the experimental setup

Full size image

The experimental setup selected to implement algorithm 5.2 is described as follows: ACADO toolbox [14] is used to solve the problem \(P_{8}\) at each sample time in order to achieve a sampling time \(h=0.0075s\); Robot Operating System (ROS) [25] is installed into a Raspberry Pi 4 and used as a programming environment.

An offline trajectory is programmed as a desired output, which in each optimal control problem is a constant value equal to the value of the trajectory in that sampling time.

Figure 6 shows the pendulum’s behavior using the numerical algorithm ACADO as a numerical algorithm solver in the MPC.

Fig. 6
figure 6

Desired and actual angle with ACADO as a solver in MPC

Full size image

In this example, the performance of the MPC with ACADO as an optimization solver is considered adequate because it achieves the control objective, which, in this example, is to achieve the unstable equilibrium at \(\Theta =\pi\) (since this work is not specifically about control, states \(x_2\) and \(x_3\) are not shown); Fig. 6 shows oscillations around the desired angle, this is due to the reduction in the Gearmotor that causes sudden stops when there the PWM is bellow \(20 \%\); nevertheless, the objective is considered achieved.

5.2.5 MPC implementation of example 2 with a neural network

Following the same process as the previous example, the architecture of the network is shown in Fig. 7; in (52), the input \(y'\) and output \(x'\) are shown.

$$\begin{aligned} y'=\begin{bmatrix} r_1 \\ r_2\\ r_3\\ x_1(1)\\ x_2(1)\\ x_3(1)\\ \end{bmatrix}, x'=u_1^* \end{aligned}$$
(52)

In this example, every value of \(x'\) in the training data is obtained by running experiments with the control scheme of the previous subsection, where \(r_1\) was the desired output (striped line in Fig. 6), \(r_2=r_3=0\) and x the states measured at each sample time.

Fig. 7
figure 7

Neural network for example 4: MPC

Full size image

A mean squared error is used as an objective function with a training error of \(e_{P}=3.67\times 10^{-3}\), the optimizer used is RMSProp, ReLu is used as hidden layer activation function, a linear activation function is used in the output layer, 90% of the 5500 examples according to (52) where used as data training and 10% as validation data with a mean squared error of \(e_{P}=1.72\times 10^{-3}\). The data set was gathered by running 5 times the experiment presented in Sect. 5.2.4 and prepared using the same procedure as the data set in Example 1, such data set is available in the supplementary information.

The performance of this MPC with the neural network shown in Fig. 7, as an approximator for the solution of problem \(P_{8}\) with the same block diagram of Fig. 4 is shown in Fig. 8.

Fig. 8
figure 8

Desired and actual angle with a neural network as an approximator for the optimal problem solution in MPC

Full size image

The performance of the MPC with ACADO and the neural network was almost the same in terms of achieving the control objective. The trajectory-following mean squared error of the MPC with ACADO is 0.0036 rad, and for the MPC with neural network is 0.0033 rad.

The time performance after 1000 executions of each optimal control solver (ACADO and Neural network) is shown in Table 3; the time performance of the NN was better in each statistic. One remarkable difference in this example is that the implementation of optimal control solvers such as ACADO to solve MPC implementations requires a microprocessor with more ROM memory, dynamic memory, and/or RAM than a general-use microcontroller, in contrast, the implementation of a neural network does not need that computational power, making it more suitable for projects where the computational power is a limitation, that’s why in the following subsection we perform the substitution of the on-board computer (Raspberry pi 4) for an ARM architecture microprocessor.

Table 3 Time statistics of 1000 executions
Full size table

5.2.6 MPC implementation on a microcontroller

In Adhau et al. [2], they test the performance of an MPC implementation using ACADO to generate an embedded software on ARM Cortex M3 microprocessor, PYNQ FPGA, and Raspberry Pi. They show that the ARM software was not able to run the optimization algorithm due to a memory overflow. In the experiment presented below, we implemented the trained network in the last subsection on a Tensilica Xtensa LX6 32-bit-based microcontroller which has similar uses as the ARM. This comparison could be seen as unfair since the microprocessor used has more RAM and SRAM than the ARM. Nevertheless, this implementation uses only 271kB of RAM and 42kB of SRAM, and the ARM shown in [2] has a RAM of 512KB and 96kB of SRAM.

Even when the selected microcontroller can read both encoders, we decided to have almost the same experimental implementation as the one used with the Raspberry Pi, Fig. 9 shows the block diagram.

Fig. 9
figure 9

Block diagram of pendulum implementation

Full size image

Similar to the Raspberry Pi MPC implementation, the NN was hardcoded in the microcontroller implementation, which makes it almost identical to the performance shown in Fig. 10.

Fig. 10
figure 10

Desired and actual angle with a neural network as an approximator for the optimal problem solution in microprocessor MPC implementation

Full size image

On behalf of the time performance, the way we measure the time of execution was by using the micros() function provided by the Arduino IDE, which shows the number of microseconds elapsed since the microprocessor was turned on, after 1000 executions, the time that it takes to calculate the output of the neural network is (always) \(1.5\times 10^{-4}\) seconds, this differs to the results in Table 3 due to the use of a microcontroller instead of a microprocessor with an operative system on which each execution time can vary because of the internal process that the microprocessor could prioritize, while the microcontroller is used dedicated entirely on running the network.

6 Discussion

The examples presented in this work illustrate the precision of the neural network approximation in solving the optimization problem, Example 2 shows how to use the analysis using Theorems 1 and 2 to help in complementing the cost function, nevertheless, it is also shown how the Jacobian \(\frac{\partial C}{\partial x'}\) grows as the dimension of D, x and/or \(\lambda\) grow, and in consequence, it is more difficult to demonstrate that \(\frac{\partial C}{\partial x'}\) is of maximal rank, there is not a general way to avoid this problem but we can observe that particular modifications to the optimization problem can help, for instance, on Example 2, we can work on optimal solutions that always fulfills the KKT condition (4) with \(\lambda =0\) and the KKT second-order condition \(\nabla _{xx}^2 L(x,\lambda ,D)\) is definite positive, then the Jacobian can always be of maximal rank with the form of (53), even when this can be seen as a solution for MPC implementation, it will also reduce the family of application on which it can be implemented. Finding a family of optimization problems where this analysis could be used once for all the family could be a starting point for future work.

$$\begin{aligned} \frac{\partial C}{\partial x'}= \begin{bmatrix} G(x,D) &{} 0 &{}0 \\ \begin{bmatrix}\nabla _x g_1(x,D) &{}...&{} \nabla _x g_m(x,D)\end{bmatrix}&{} \nabla _{xx}^2 L(x,\lambda ,D) &{} 0 \\ 0 &{} 0 &{} I_{n_d \times n_d} \end{bmatrix} \end{aligned}$$
(53)

7 Conclusions

We have considered a family of optimization problems in which we can find the necessary conditions for a neural network to approximate the solution for a given parameter vector. In the examples shown in this work, Theorems 1 and 2, sufficient conditions can lead to the use of the Jacobian as design criteria when using neural networks as solution approximators replacing numerical algorithms.

In example two, an online application of our results has been tested with positive results; moreover, the condition for the Jacobian to be of maximal rank leads to criteria for choosing weights in the objective function, ensuring trustworthy substitution of the numerical algorithm by an NN.

Time consumption and computational power saving can be improved using an NN instead of a numerical algorithm for problems where the network can be trained offline.

The work presented has shown that neural networks can replace numerical algorithms to solve optimization problems of the family presented; the replacement can be an improvement in applications in which the computing time is important, as well as having the minimum standard deviation possible; one example is real-time applications.

Analysis similar to example one can lead to defining families of optimization problems where individual testing of the conditions of the theorems would not be necessary since the Jacobian is of maximal rank in every scenario.