Eddy current losses in permanent magnets of surface mounted permanent magnet synchronous machines—Analytical calculation and high order finite element analyses

Abstract

Permanent magnet exited synchronous machines always show three significant portions of their losses: Iron losses within the magnetic circuit, power losses within the stator winding and finally eddy current losses within the permanent magnets. In particular, surface mounted magnets are directly exposed to asynchronous components of the air-gap field caused by either higher harmonic waves or higher time harmonics. Analytical calculation of the eddy current losses within the permanent magnets for both linear as well as cylindrical arrangements describe fundamental characteristics in dependence on only few significant parameters. These results serve as reference results for detailed numerical calculations using the finite element method, too. The finite element analyses with various formulations of the shape functions show the significant influence of the higher order elements on the accuracy of the eddy current losses. Additionally, the effects of a various pole coverage can be obtained from the results of the numerical calculations. Therefore, a clear summary of the significant parameters influencing the eddy current losses within the permanent magnets for both linear as well as cylindrical arrangements will be established.

Zusammenfassung

Synchronmaschinen mit Permanentmagneterregung besitzen drei wesentliche Verlustanteile: Eisenverluste im magnetischen Kreis, Stromwärmeverluste in der Statorwicklung und Wirbelstromverluste in den Permanentmagneten. Insbesondere Oberflächenmagnete sind direkt den asynchronen Anteilen im Luftspaltfeld, welche einerseits als Oberwellen und anderseits als Oberschwingungen dargestellt werden können, ausgesetzt. Analytische Berechnungen der Wirbelstromverluste in den Permanentmagneten für eine lineare als auch eine zylindrische Geometrie des Luftspalts zeigen die grundsätzlichen Zusammenhänge zu den bestimmenden Parametern auf. Diese Ergebnisse dienen auch als Referenzlösungen für umfangreiche numerische Analysen mit der Methode der Finiten Elemente. Die Analysen mit unterschiedlichen Ansätzen für die Formfunktionen zeigen den deutlichen Einfluss auf die Genauigkeit der Ergebnisse. Die numerischen Ergebnisse dienen auch zur Darstellung des Einflusses der Polbedeckung der Permanentmagnete. Somit entsteht für lineare und zylindrische Luftspaltgeometrien eine klare Übersicht der wesentlichen Einflussparameter auf die Wirbelstromverluste in den Permanentmagneten.

1 Introduction

A rated apparent power of permanent magnet excited electrical machines in the range up to 50 MVA is considered as a realisable trend of development. Due to sub- and superharmonics of the air-gap field, the eddy current losses generated in the permanent magnets of such machines may always lead to an excessive heating [1–5]. In particular with surface mounted permanent magnets, this can cause the magnets to get partially or even fully demagnetised [6–9]. Thus, the precalculation of these eddy current losses caused by the harmonics of the air-gap field is an important matter of interest with the design process of such electrical machines. On one hand by using very fast evaluation methods for the standard design procedures, on the other hand by using highly accurate calculation methods for reference purposes [10–12].

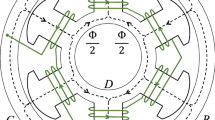
As depicted in Fig. 1 and Fig. 2, both linear as well as cylindrical arrangements are considered. Both arrangements are described with few parameters, such as air-gap $\delta$, ratio of pole pitch and air-gap $\tau_{p}/\delta$, ratio of magnet height and air-gap $h_{M}/\delta$ as well as the pole coverage as ratio of magnet width and pole pitch $b_{M}/\tau_{p}$. With the same parameters and an increasing ordinal number of the harmonic waves in circumferential direction, it is expected that the difference between both arrangements will disappear more and more.

Fig. 1.

Simplified geometry of a pole pitch with a linear arrangement

Fig. 2.

Simplified geometry of a pole pitch with a cylindrical arrangement

First, analytical calculations will be performed with the intent to discuss the significant parameters influencing the eddy currents in the magnets. It is expected, that there is a different behaviour of the eddy current losses in dependence of frequency and wave length of the excitation [13]. The analytically obtained results are used as reference results for the detailed numerical analyses by using the finite element method, too. In order to analyse the accuracy of the numerically obtained results, various approximation orders of the finite element interpolation schemes are concerned. In addition, various pole coverages with their effects on the eddy current losses are discussed by these numerical analyses.

Both calculation methods use an excitation with a surface current sheet along the circumferential direction at the inner stator boundary which can cover for any harmonic order generated from either PWM modulated stator currents, the slotting as well as the saturation. This surface current flow in axial direction $K_{z}(x,t)$ perpendicular to the cross section of the conducting region can be expressed by a travelling wave as

$$\begin{aligned} K_{z}(x,t) =& \hat{K}_{z}\,\operatorname{Re}\Bigl(\mathrm{e}^{j\omega t}\,\mathrm{e}^{-j\nu\pi x/\tau _{p}}\Bigr) \end{aligned}$$

(1)

where $\omega \!=\!2\pi f$ denotes the exciting circular frequency with respect to the moving region, $\nu$ the harmonic order and $-1\!\le\!x/\tau_{p}\!\le\!1$ being the region of two pole pitches along the circumferential direction, respectively. Referring to the total eddy current losses, there is no interaction between waves with different harmonic orders as well as different frequencies. Consequently, each travelling wave can be discussed separately.

2 Analytical calculation

The analytical calculation is based on Laplacian and Helmholtz equations of a magnetic vector potential within the respective regions and uses a pole coverage of $b_{M}/\tau_{p}=1$, which occurs practically with Halbach arrays.

2.1 Analytical approach

The magnetic vector potential $A_{z}(\omega )$ is obtained from the Laplacian equation

$$\begin{aligned} -\Delta A_{z}(\omega ) =& 0 \end{aligned}$$

(2)

in the non-conducting regions of air-gap and rotor and the Helmholtz equation

$$\begin{aligned} \Bigl(-\Delta+\frac{2j}{d^{2}}\Bigr)A_{z}(\omega ) =& 0 \end{aligned}$$

(3)

in the conducting region of the permanent magnets, where

$$\begin{aligned} d =& \sqrt{\frac{2}{\omega \,\mu_{M}\,\sigma _{M}}} \end{aligned}$$

(4)

denotes the skin depth of the eddy currents [13]. Respective interface conditions of the magnetic field between these regions ensure a unique solution of these equations.

The total eddy current losses within the conducting areas are evaluated by using the Poynting theorem. Thereby, the apparent power per length $S'(\omega )$ is obtained from the boundary $\partial\Gamma_{M}$ along the permanent magnets as

$$S^{\prime }(\omega )=\frac{j\omega }{2{\mu }_M}\underset{\partial {\mathrm{\Gamma }}_M}{\oint }{A}_z(\omega )\frac{\partial A_z^{\ast }(\omega )}{\partial n}ds.$$

(5)

Consequently, the total eddy current losses are always proportional to the square of the magnitude $\hat{K}_{z}$ of each travelling wave.

2.2 Analytical results

Figures 3 and 4 depict the power losses of one NdFeB magnet in dependence on exciting frequency and ordinal number of the harmonics for a constant current sheet excitation of $\hat{K}_{z}\!=\!10^{4}\,\mbox{A/m}$. Both arrangements show the data of air-gap $\delta\!=\!2\,\mbox{mm}$, ratio of pole pitch and air-gap $\tau_{p}/\delta\!=\!60$, ratio of magnet height and air-gap $h_{M}/\delta\!=\!3$. Figure 5 shows the respective ratio of the power losses between cylindrical and linear arrangements modified in accordance to the different cross sections of the conducting areas within both arrangements.

Fig. 3.

Power losses of various harmonics versus frequency, linear arrangement, analytical results, pole coverage 1

Fig. 4.

Power losses of various harmonics versus frequency, cylindrical arrangement, analytical results, pole coverage 1

Fig. 5.

Ratio of power losses between cylindrical and linear arrangement, analytical results, pole coverage 1

Obviously, the total eddy current losses are quite similar between both arrangements with a deviation in the range ±5% only. As mentioned in [13], there are different regions in dependence on both frequency $f$ and wave length $2\tau_{p}/\nu$ of the excitation. With a ratio of wave length to skin depth $(2\tau_{p})/(\nu\,d)\!\ll\!1$, the power losses versus frequency increase with a power of 2. On the other hand with a ratio of wave length to skin depth $(2\tau_{p})/(\nu\, d)\!\gg\!1$, the power losses versus frequency increase with a power of 0.5 only. However with very low ordinal numbers, there is a transitional region where the power losses are rather constant.

For more detailed results, in particular about the influence of the permeability of the rotor on the eddy current losses, see [14].

3 Finite element analysis

The finite element analyses deal with a pole coverage of $b_{M}/\tau_{p}=1$ for the direct comparison of the analytical results with those from the numerical analyses. Further, the finite element analyses can examine very easily pole coverages within the practical range of $b_{M}/\tau_{p} \approx 2/3\ldots5/6$.

The finite element analyses carried out with various higher order approx imation functions utilise an identical discretisation with the minimum skin depth as approximately the half of the mesh size in radial direction and the minimum wave length as approximately 7.5 times the mesh size in circumferential direction.

3.1 Higher order finite elements

In the finite element context, any analytical function $u(\xi)$ gets approximated by a finite dimensional subset of interpolation functions defined on a finite element mesh. In local element coordinates, this reads as

$$\begin{aligned} u(\xi) \approx u^{h}(\xi) = \sum_{i=1}^{n_{eq}} u_{i}\,N_{i}(\xi) , \end{aligned}$$

(6)

where $u^{h}(\xi)$ is the approximated function, with $N_{i}(\xi)$ being the shape functions, $u_{i}$ the related coefficients and $n_{eq}$ the number of unknown coefficients, respectively.

In the case of standard Lagrangian elements, the functions $N_{i}$ are defined by the corner coordinates and $u_{i}$ are the related values of the function $u^{h}(\xi)$ on these nodes. The shape functions of first order on the unit domain $\Omega\;[-1,1]$ are defined as

$$\begin{aligned} N_{1}(\xi) = \frac{1-\xi}{2} ,\qquad N_{2}(\xi) = \frac{1+\xi}{2} . \end{aligned}$$

(7)

However, one disadvantage of the Lagrangian basis is that for each polynomial degree $p\ge2$, a new set of shape functions as shown in Fig. 6 (left) is required, which prevents the efficient usage of different approximation orders within one finite element mesh.

Fig. 6.

Lagrange (left) and Legendre (right) based shape functions up to order $p=4$

In contrast, a set of hierarchic shape functions is defined in such a way that every basis of order $p$ is fully contained in the basis of order $p+1$ as shown in Fig. 6 (right). In this work, we make use of the Legendre based interpolation functions as

$$\begin{aligned} N_{k}(\xi) = l_{k-1}(\xi) ,\quad k=3,4,\dots,p+1 , \end{aligned}$$

(8)

where $l_{k}(\xi)$, $k\ge2$, denotes the integrated Legendre polynomials [16, 17]

$$\begin{aligned} l_{k}(\xi) = \sqrt{\frac{2k-1}{2}}\,L_{k}(\xi) , \qquad L_{k}(\xi) = \!\intop_{-1}^{\xi}\! P_{k-1}(x)\,dx . \end{aligned}$$

(9)

Therein, $P_{k}$ are the regular Legendre polynomials [15]

$$\begin{aligned} P_{k}(x) = \frac{1}{2^{k}\,k!}\,\frac{d^{k}}{dx^{k}}\bigl(x^{2}-1\bigr)^{k} , \end{aligned}$$

(10)

the scaling factor arises from their orthogonality

$$\begin{aligned} \intop_{-1}^{+1} P_{k}(x)\,P_{m}(x)\,dx = \frac{2}{2k+1}\,\delta_{km} . \end{aligned}$$

(11)

Using the recursive formula of the regular Legendre polynomials ($k\ge1$)

$$\begin{aligned} (k+1)\,P_{k+1}(x) = (2k+1)\,x\,P_{k}(x) - k\,P_{k-1}(x) \end{aligned}$$

(12)

yields the integrated Legendre polynomials

$$\begin{aligned} L_{k}(x) =& \frac{P_{k}(x)-P_{k-2}(x)}{2k-1} ,\quad k\ge2 , \end{aligned}$$

(13)

and their recursive formula ($k\ge2$)

$$\begin{aligned} (k+1)\,L_{k+1}(x) = (2k-1)\,x\,L_{k}(x) - (k-2)\,L_{k-1}(x) . \end{aligned}$$

(14)

Due to the orthogonality of the Legendre polynomials $P_{k}$ along the unit interval $[-1,1]$, only the first two functions $N_{1}$, $N_{2}$ contribute to the value at the ends of the unit interval $[-1,1]$. All other functions $N_{k}$ of higher order $k>2$ give only a non-zero value within the interval. Therefore, they are also called internal modes or bubble modes. With regard to the given recursive formulas, particularly a mapping of results between different orders will be straight forward and very easy.

On the other hand, the integrated Legendre polynomials $L_{k}$ fulfil the orthogonality

$$\begin{aligned} \intop_{-1}^{+1} L_{k}(x)\,L_{m}(x)\,dx = 0 ,\quad |k-m|>2 . \end{aligned}$$

(15)

Consequently, the sparsity of the matrices decreases only slightly with higher orders of these approximation functions.

Having this knowledge in mind, we can easily construct basis functions up to any order for both quadrilateral and hexahedral elements by applying a tensor product. The other element shapes can be constructed via the Duffy transformation [17].

3.2 Numerical results

3.2.1 General results

Figures 7 and 8 depict the power losses of one NdFeB magnet in dependence on exciting frequency and ordinal number of the harmonics for a constant current sheet excitation of $\hat{K}_{z}\!=\!10^{4}\,\mbox{A/m}$. Both arrangements show the geometry data as already given above with the analytical analyses. Figure 9 shows the respective ratio of the power losses between cylindrical and linear arrangements modified in accordance to the different cross sections of the conducting areas within both arrangements.

Fig. 7.

Power losses of various harmonics versus frequency, linear arrangement, numerical results, order $p=2$, pole coverage 1

Fig. 8.

Power losses of various harmonics versus frequency, cylindrical arrangement, numerical results, order $p=2$, pole coverage 1

Fig. 9.

Ratio of power losses between cylindrical and linear arrangement, numerical results, order $p=2$, pole coverage 1

Obviously, the numerically obtained results are quite similar to the analytically obtained results. Therefore, only ratios between numerical and analytical results as well as ratios between linear and cylindrical arrangements are shown further.

3.2.2 Accuracy of the results

As mentioned above, the differences between linear and cylindrical arrangements are rather small. Thus, only the linear arrangement is discussed in more detail herein.

The relative error

$$\begin{aligned} \epsilon =& P_{FEA}/P_{ana}-1 \end{aligned}$$

(16)

between the power losses of finite element and analytical analyses with different approximation orders is shown in Figs. 10, 11, 12, 13. In addition, Figs. 14 and 15 depict this relative error for $1{\mathrm{st}}$ and $2{\mathrm{nd}}$ orders with the half mesh size in both directions. Tables 1 and 2 list the respective data of these numerical analyses.

Fig. 10.

Relative error of power losses, linear arrangement, pole coverage 1, numerical analyses, order $p=1$

Fig. 11.

Relative error of power losses, linear arrangement, pole coverage 1, numerical analyses, order $p=2$

Fig. 12.

Relative error of power losses, linear arrangement, pole coverage 1, numerical analyses, order $p=3$

Fig. 13.

Relative error of power losses, linear arrangement, pole coverage 1, numerical analyses, order $p=4$

Fig. 14.

Relative error of power losses, linear arrangement, pole coverage 1, numerical analyses with half mesh size, order $p=1$

Fig. 15.

Relative error of power losses, linear arrangement, pole coverage 1, numerical analyses with half mesh size, order $p=2$.

Table 1. Matrix data in dependence on the order, default mesh size

Table 2. Matrix data in dependence on the order, half mesh size

As expected, $1{\mathrm{st}}$ order elements cannot encounter both for small skin depths as well as short wave lengths. $2{\mathrm{nd}}$ order elements are better with an exception of short wave lengths and very high frequencies. $3{\mathrm{rd}}$ and $4{\mathrm{th}}$ order elements give the same results with a relative error less than 0.5% which means convergence with respect to the higher orders.

In comparison of the default mesh with the half size mesh, of course the results of $1{\mathrm{st}}$ and $2{\mathrm{nd}}$ order elements are better with the dense mesh. However, the results of $2{\mathrm{nd}}$ order elements with the dense mesh are still less accurate than the results of in particular $3{\mathrm {rd}}$ order elements with the default mesh. On the other hand, the latter have approximately only the half number of unknowns.

Consequently, the usage of $3{\mathrm{rd}}$ or even higher order elements will be strongly suggested by evaluating eddy current losses. In particular with 3D meshes, the possibility of generating a relatively coarse mesh within the conducting regions shows explicit advantages against a dense mesh with $2{\mathrm{nd}}$ order elements.

3.2.3 Influence of the pole coverage

The finite element calculations very easily allow to encounter for the influence of various pole coverages on the eddy current losses, too. With regard to a practical point of view with linear and cylindrical arrangements, the pole coverages as of $5/6$, $3/4$ and $2/3$ are concerned in more detail.

Figures 16, 17, 18 depict the respective ratio of the power losses between cylindrical and linear arrangements modified in accordance to the different cross sections of the conducting areas within both arrangements. Figures 19, 20, 21 depict the ratio of the power losses with the above mentioned pole coverages in comparison to a full coverage.

Fig. 16.

Ratio of power losses between cylindrical and linear arrangement, numerical analyses, order $p=2$, pole coverage $5/6$

Fig. 17.

Ratio of power losses between cylindrical and linear arrangement, numerical analyses, order $p=2$, pole coverage $3/4$

Fig. 18.

Ratio of power losses between cylindrical and linear arrangement, numerical analyses, order $p=2$, pole coverage $2/3$

Fig. 19.

Ratio of power losses between pole coverages $5/6$ and 1, linear arrangement, numerical analyses, order $p=2$

Fig. 20.

Ratio of power losses between pole coverages $3/4$ and 1, linear arrangement, numerical analyses, order $p=2$

Fig. 21.

Ratio of power losses between pole coverages $2/3$ and 1, linear arrangement, numerical analyses, order $p=2$

Obviously, the pole coverage only affects the power losses of the lower harmonics while the power losses of the higher harmonics are rather constant and directly proportional to the value of the pole coverage.

In order to study the effects of various pole coverages with different approximation orders, the ratio of the respective power losses is shown in Fig. 22. Obviously, the approximation order affects the total value of the losses only but has a negligible effect on ratios of the losses between different arrangements deduced from the same approximation order.

Fig. 22.

Ratio of power losses between pole coverages $2/3$ and 1, linear arrangement, numerical analyses, order $p=4$

4 Conclusion

The paper discusses both analytical and numerical calculation methods of eddy current losses in permanent magnets of electrical machines. Therein, the finite element analyses utilise different approximation orders with hierarchic shape functions in order to validate modelling of wave length as well as skin depth. Obviously, higher order elements with $p\ge3$ can handle these parameters very well.

Further, linear and cylindrical arrangements are compared against their results by using identical geometry parameters and various pole coverages. With all harmonic orders along the entire frequency range, there is a deviation only in the range ±5% between these two arrangements. It is shown that the pole coverage influences only the power losses of the lower harmonic waves while higher harmonic waves have approximately constant power losses directly proportional to the value of the pole coverage.