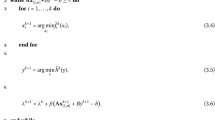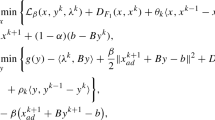Abstract
The alternating direction method of multipliers (ADMM) is an effective algorithm for solving optimization problems with separable structures. Recently, inertial technique has been widely used in various algorithms to accelerate its convergence speed and enhance the numerical performance. There are a lot of convergence analyses for solving the convex optimization problems by combining inertial technique with ADMM, while the research on the nonconvex cases is still in its infancy. In this paper, we propose an algorithm framework of inertial regularized ADMM (iRADMM) for a class of two-block nonconvex optimization problems. Under some assumptions, we establish the subsequential and global convergence of the proposed method. Furthermore, we apply the iRADMM to solve the signal recovery, image reconstruction and SCAD penalty problem. The numerical results demonstrate the efficiency of the iRADMM algorithm and also illustrate the effectiveness of the introduced inertial term.







Similar content being viewed by others
Data availability
Enquiries about data availability should be directed to the authors.
References
Alvarez F (2004) Weak convergence of a relaxed and inertial hybrid projection-proximal point algorithm for maximal monotone operators in hilbert space. SIAM J Opt 14(3):773–782
Alvarez F, Attouch H (2001) An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set Valued Anal 9(1–2):3–11
Attouch H, Bolte J, Redont P, Soubeyran A (2010) Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the kurdyka-lojasiewicz inequality. Math Oper Res 35(2):438–457
Attouch H, Bolte J, Svaiter BF (2013) Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized gauss-seidel methods. Math Prog 137(1–2):91–129
Bolte J, Sabach S, Teboulle M (2014) Proximal alternating linearized minimization for nonconvex and nonsmooth problem. Math Prog 146(1–2):459–494
Bot RI, Cestnek ER (2014) An inertial alternating direction method of multipliers. Minimax Theory Appl 1(1):29–49
Bot RI, Cestnek ER (2015) An inertial tseng’s type proximal algorithm for nonsmooth and nonconvex optimization problems. J Opt Theory Appl 171(2):600–616
Bot RI, Csetnek ER, Hendrich C (2015) Inertial douglas-rachford splitting for monotone inclusion problems. Appl Math Comput 256:472–487
Boyd S, Parikh N, Chu E, Peleato B, Eckstein J (2011) Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn 3(1):1–122
Chao MT, Zhang Y, Jian JB (2020) An inertial proximal alternating direction method of multipliers for nonconvex optimization. Int J Comput Math. https://doi.org/10.1080/00207160.2020.1812585
Chen CH, Chan RH, Ma SQ, Yang JF (2015) Inertial proximal admm for linearly constrained separable convex optimization. SIAM J Imag Sci 8(4):2239–2267
Chen CH, Ma SQ, Yang JF (2015) A general inertial proximal point algorithm for mixed variational inequality problem. SIAM J Opt 25(4):2120–2142
Donoho DL (2006) Compressed sensing. IEEE Trans Inform Theory 52(4):1289–1306
Fan JQ, Li RZ (2001) Variable selection via nonconcave penalized likelihood and its oracle properties. J Am Stat Assoc 96(456):1348–1360
Gabay D, Mercier B (1976) A dual algorithm for the solution of nonlinear variational problems via finite element approximations. Comput Math Appl 2:17–40
Gao X, Cai XJ, Han DR (2019) A Gauss-Seidel type inertial proximal alternating linearized minimization for a class of nonconvex optimization problems. J Glob Opt 76(4):863–887
Glowinski R, Marrocco A (1975) Sur l’approximation, par\(\acute{e}\)l\(\acute{e}\)ments finis d’ordre un, et la r\(\acute{e}\)solution, par p\(\acute{e}\)nalisation-dualit\(\acute{e}\) dune classe de probl\(\grave{e}\)mes de dirichlet non lin\(\acute{e}\)aires. Revue Fr Autom. inform. rech op\(\acute{e}\)r. Anal Num\(\acute{e}\)r 2:41-76
Goncalves MLN, Melo JG, Monteiro RDC (2017) Convergence rate bounds for a proximal admm with over-relaxation stepsize parameter for solving nonconvex linearly constrained problems. Pac J Opt 15(3):379–398
Guo K, Han DR, Wu TT (2017) Convergence of alternating direction dethod for minimizing sum of two nonconvex functions with linear constraints. Int J Comput Math 94(8):1653–1669
He BS, Tao M, Yuan XM (2012) Alternating direction method with Gaussian back substitution for separable convex programming. SIAM J Opt 22(2):313–340
Hong MY, Luo ZQ, Razaviyayn M (2016) Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems. SIAM J Opt 26(1):337–364
Jian JB, Liu PJ, Jiang XZ (2020) A partially symmetric regularized alternating direction method of multipliers for nonconvex multi-block optimization. Acta Math Sin Chin Ser. https://kns.cnki.net/kcms/detail/11.2038.o1.20201127.1522.014.html
Li GY, Pong TK (2015) Global convergence of splitting methods for nonconvex composite optimization. SIAM J Opt 25(4):2434–2460
Li M, Sun DF, Toh CK (2015) A convergent 3-block semiproximal ADMM for convex minimization problems with one strongly convex block. Asia Pac J Oper Res. https://doi.org/10.1142/S0217595915500244
Liu J, Chen JH, Ye JP (2009) Large-scale sparse logistic regression. In: 15th ACM SIGKDD international conference on knowledge discovery and data mining, pp 547–555
Liu J, Yuan Y, Ye JP (2006) Dictionary lasso: guaranteed sparse recovery under linear transformation. arXiv:1305.0047v2
Mordukhovich B (2006) Variational analysis and generalized differentiation i: basic theory. Springer, Berlin
Moudafi A, Elizabeth E (2003) Approximate inertial proximal methods using the enlargement of maximal monotone operators. Int J Pure Appl Math 5(3):283–299
Nesterov Y (2004) Introductory lectures on convex optimization: a basic course. Kluwer Academic Publishing, Cambridge
Ochs P, Brox T, Pock T, (2015) iPiano: Inertial proximal algorithm for strongly convex optimization. J Math Imaging Vis 53(2):171–181
Ochs P, Chen YJ, Brox T, Pock T (2014) iPiano: Inertial proximal algorithm for nonconvex optimization. SIAM J Imag Sci 7(2):1388–1419
Polyak BT (1964) Some methods of speeding up the convergence of iteration methods. USSR Comput Math Math Phys 4(5):1–17
Rockafellar RT, Wets RJB (2009) Variational analysis. Springer, Berlin
Sun T, Barrio R, Rodriguez M, Jiang H (2019) Inertial nonconvex alternating minimizations for the image deblurring. IEEE Trans Image Process 28:6211–6224
Wang FH, Xu ZB, Xu HK (2014) Convergence of alternating direction method with multipliers for nonconvex composite problems. arXiv:1410.8625
Wu ZM, Li M (2019) General inertial regularized gradient method for a class of nonconvex nonsmooth optimization problems. Comput Opt Appl 73(1):129–158
Xu ZB, Chang XY, Xu FM, Zhang H (2012) \(L_{1/2}\) regularization: a thresholding representation theory and a fast solver. IEEE Trans Neur Netw Lear 23(7):1013–1027
Xu JW, Chao MT (2021) An inertial Bregman generalized alternating direction method of multipliers for nonconvex optimization. J Appl Math Comput. https://doi.org/10.1007/s12190-021-01590-1
Yang JF (2017) An algorithmic review for total variation regularized data fitting problems in image processing. Oper Res Trans 21(4):69–83
Zeng JS, Lin SB, Wang Y, Xu ZB (2013) \(L_{1/2}\) regularization: convergence of iterative half thresholding algorithm. IEEE Trans Signal Process 62(9):2317–2329
Zhang R, Kwok JT (2014) Asynchronous distributed admm for consensus optimization. In: Proceedings of the 31st international conference on machine learning, pp 1701–1709
Acknowledgements
This work was supported by the Natural Science Foundation of China (12061013, 11601095, 71861002), Natural Science Foundation of Guangxi Province (2016GXNSFBA380185), Training Plan of Thousands of Young and Middle-aged Backbone Teachers in Colleges and Universities of Guangxi, Special Foundation for Guangxi Ba Gui Scholars, and Guangxi Middle and Young University Teachers’ Basic Research Ability Improvement Project (2022KY1135).
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Contributions
[MC, YG, YZ] conceptualized the study; [MC, YZ] helped in formal analysis and investigation, writing—review and editing, and supervision.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was not required as no humans or animals were involved.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
6 Appendix A.
6 Appendix A.
1.1 A.1 Proof of Lemma 5
Proof
From the definition of the augmented Lagrangian function \({\mathcal {L}}_{\beta }(\cdot )\), it follows that
It is obvious that
From the optimality condition of y-subproblem, which implies that
Since \(\nabla g\) is Lipschitz continuous with modulus \(L>0\), it follows from Lemma 2 and (25) obtain
By substituting (26) into (24), we obtain
and \(p^{k+1}=p^{k}-\beta (Ax^{k+1}+By^{k+1}-b),\) we have
Furthermore, \(Ax^{k+1}+B\bar{y}^{k}-b=Ax^{k+1}+By^{k+1}-b+B(\bar{y}^{k}-y^{k+1}),\) thus
By substituting (28),(29) into (27), we have
Since \(x^{k+1}\) is the minimum value of x-subproblem for iterative scheme (7), we have
On the other hand
By the same reason we can obtain
It is easy to verify that
Furthermore, we know
where the inequality using of \((a+b)^{2}\le 2(a^{2}+b^{2}).\) By substitution (33)–(35) into (32)
Summing up (23),(30), (31), and (36), we obtain
Assumption 1(v) and (7) imply that \(p^{k+1}-p^{k}\in Im B.\) It follows from Lemma 3 and (25) that
Since \(\Vert y^{k+1}-y^{k}\Vert ^{2}\le 2(\Vert y^{k+1}-\bar{y}^{k}\Vert ^{2}+\Vert \bar{y}^{k}-y^{k}\Vert ^{2}),\) we have
Combining to \(\bar{x}^{k+1}=x^{k+1}+\theta (x^{k+1}-\bar{x}^{k})\), \(\bar{y}^{k+1}=y^{k+1}+\eta (y^{k+1}-\bar{y}^{k})\), and (37), it can be obtained through simplification and arrangement
where \(\delta =\beta \lambda _{B^{\top }}+\frac{L}{2}+\frac{3L^{2}}{\beta \mu _{B^{\top }}},M_{0}=\frac{\beta \mu _{B^{\top }}-L}{2}-\frac{3L^{2}}{\beta \mu _{B^{\top }}}.\) Let \(\hat{{\mathcal {L}}}_{\beta }(\hat{w}^{k})={\mathcal {L}}_{\beta }(w^{k})+\frac{1}{2\beta }\Vert p^{k-1}-p^{k}\Vert ^{2}+\delta \Vert y^{k}-\bar{y}^{k}\Vert ^{2}+\frac{1}{2}\Vert x^{k}-\bar{x}^{k}\Vert ^{2}_{S}.\) Thus, we have
where \(M=M_{0}-\eta ^2\delta ,\) from Assumption 1(iv), we know \(M>0.\) This completes the proof. \(\square \)
1.2 A.2 Proof of Lemma 6
Proof
Since \(\{w^{k}\}\) is bounded, \(\{\hat{w}^{k}\}\) is bounded, which has at least one cluster point. Let \(\hat{w}^{*}\) be a cluster point of \(\{\hat{w}^{k}\}\), then the subsequence \(\{\hat{w}^{k_{j}}\}\) to converge it, i.e., \(\lim \limits _{j\rightarrow +\infty }\hat{w}^{k_{j}}=\hat{w}^{*}\). Since f is the lower semicontinuous and g is the continuous, then \(\hat{{\mathcal {L}}}_{\beta }(\cdot )\) is the lower semicontinuous, and hence
Consequently, \(\{\hat{{\mathcal {L}}}_{\beta }(\hat{w}^{k_{j}})\}\) is bounded from below, which, together with the fact that \(\{\hat{{\mathcal {L}}}_{\beta }(\hat{w}^{k})\}\) is nonincreasing, means that \(\{\hat{{\mathcal {L}}}_{\beta }(\hat{w}^{k_{j}})\}\) is convergent. Moreover, \(\{\hat{{\mathcal {L}}}_{\beta }(\hat{w}^{k})\}\) is convergent and \(\hat{{\mathcal {L}}}_{\beta }(\hat{w}^{k})\ge \hat{{\mathcal {L}}}_{\beta }(\hat{w}^{*})\). Rearranging terms of (9), summing up for \(k=0,\cdot \cdot \cdot n\), we have
Since \(\theta \in [0,1),M>0\), we have \(\sum \limits _{k=0}^{+\infty }\Vert x^{k+1}-\bar{x}^{k}\Vert ^{2}_{S}<+\infty \), \(\sum \limits _{k=0}^{+\infty }\Vert y^{k+1}-\bar{y}^{k}\Vert ^{2}<+\infty \). It is apparent from the inequality property that
From (41) and (42), we have \(\sum \limits _{k=0}^{+\infty }\Vert x^{k+1}-x^{k}\Vert ^{2}<+\infty ,\) \(\sum \limits _{k=0}^{+\infty }\Vert y^{k+1}-y^{k}\Vert ^{2}<+\infty \), it follows from (38) that \(\sum \limits _{k=0}^{+\infty }\Vert p^{k+1}-p^{k}\Vert ^{2}<+\infty .\) Therefore, we obtain \(\sum \limits _{k=0}^{+\infty }\Vert w^{k+1}-w^{k}\Vert ^{2}<+\infty .\) \(\square \)
1.3 A.4 Proof of Lemma 7
Proof
From the definition of the augment Lagrangian function \({\mathcal {L}}_{\beta }(\cdot ),\) it follows
This together with optimality condition (8) yields
From Lemma 1, we obtain \((\varepsilon _{1}^{k+1},\varepsilon _{2}^{k+1},\varepsilon _{3}^{k+1},\varepsilon _{4}^{k+1},\varepsilon _{5}^{k+1},\varepsilon _{6}^{k+1})^{\top }\in \partial \hat{{\mathcal {L}}}_{\beta }(\hat{w}^{k+1})\). Furthermore, from (43), there exists a real number \(\zeta _{0}\) such that
It follows from (39) that there exists \(\zeta _{1}>0\) such that
Thus, combining (44) and (45), there exists \(\zeta >0\) such that
This completes the proof. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chao, M., Geng, Y. & Zhao, Y. A Method of Inertial Regularized ADMM for Separable Nonconvex Optimization Problems. Soft Comput 27, 16741–16757 (2023). https://doi.org/10.1007/s00500-023-09017-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-023-09017-8