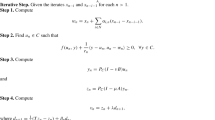Inertial alternating direction method of multipliers for non-convex non-smooth optimization

Abstract

In this paper, we propose an algorithmic framework, dubbed inertial alternating direction methods of multipliers (iADMM), for solving a class of nonconvex nonsmooth multiblock composite optimization problems with linear constraints. Our framework employs the general minimization-majorization (MM) principle to update each block of variables so as to not only unify the convergence analysis of previous ADMM that use specific surrogate functions in the MM step, but also lead to new efficient ADMM schemes. To the best of our knowledge, in the nonconvex nonsmooth setting, ADMM used in combination with the MM principle to update each block of variables, and ADMM combined with inertial terms for the primal variables have not been studied in the literature. Under standard assumptions, we prove the subsequential convergence and global convergence for the generated sequence of iterates. We illustrate the effectiveness of iADMM on a class of nonconvex low-rank representation problems.

Appendices

Appendix 1: Preliminaries of non-convex non-smooth optimization

In this appendix, we recall some basic definitions and results, namely directional derivative and subdifferentials in Definition 3, critical point in Definition 4, the subdifferential of a sum of function in Proposition 6, and KŁ functions in Definition 6.

Let $g: {\mathbb {E}}\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be a proper lower semicontinuous function.

Definition 3

[48, Definition 8.3]

• (i) For any $x\in \mathrm{dom}\,g,$ and $d\in {\mathbb {E}}$, we denote the directional derivative of g at x in the direction d by

  $$\begin{aligned}g'\left( x;d\right) =\liminf _{\tau \downarrow 0}\frac{g(x+\tau d)-g(x)}{\tau }. \end{aligned}$$

• (ii) For each $x\in \mathrm{dom}\,g,$ we denote ${\hat{\partial }}g(x)$ as the Frechet subdifferential of g at x which contains vectors $v\in \mathbb {E}$ satisfying

  $$\begin{aligned} \liminf _{y\ne x,y\rightarrow x}\frac{1}{\left\| y-x\right\| }\left( g(y)-g(x)-\left\langle v,y-x\right\rangle \right) \ge 0. \end{aligned}$$

  If $x\not \in \mathrm{dom}\,g,$ then we set ${\hat{\partial }}g(x)=\emptyset .$

• (iii) The limiting-subdifferential $\partial g(x)$ of g at $x\in \mathrm{dom}\,g$ is defined as follows:

  $$\begin{aligned} \partial g(x) := \left\{ v\in \mathbb {E}:\exists x^{(k)}\rightarrow x,\,g\left( x^{(k)}\right) \rightarrow g(x),\,v^{(k)}\in {\hat{\partial }}g\left( x^{(k)}\right) ,\,v^{(k)}\rightarrow v\right\} . \end{aligned}$$

• (iv) The horizon subdifferential $\partial ^{\infty } g(x)$ of g at x is defined as follows:

  $$\begin{aligned} \partial ^{\infty } g(x)&:= \Big \{ v\in \mathbb {E}:\exists \lambda ^{(k)}\rightarrow 0, \lambda ^{(k)}\ge 0, \lambda ^{(k)} x^{(k)}\rightarrow x,\,g(x^{(k)})\rightarrow g(x),\\&\qquad \,v^{(k)}\in {\hat{\partial }}g(x^{(k)}),\,v^{(k)}\rightarrow v\Big \} . \end{aligned}$$

Definition 4

We call $x^{*}\in \mathrm {dom}\,F$ a critical point of F if $0\in \partial F\left( x^{*}\right) .$

Definition 5

[48, Definition 7.5] A function $f:{\mathbb {R}}^{{\mathbf {n}}} \rightarrow {\mathbb {R}} \cup \{+\infty \}$ is called subdifferentially regular at ${{\bar{x}}}$ if $f({{\bar{x}}})$ is finite and the epigraph of f is Clarke regular at $({{\bar{x}}}, f({{\bar{x}}}))$ as a subset of ${\mathbb {R}}^{{\mathbf {n}}} \times {\mathbb {R}}$ (see [48, Definition 6.4] for the definition of Clarke regularity of a set at a point).

Proposition 6

[48, Corollary 10.9] Suppose $f=f_1 +\cdot + f_m$ for proper lower semi-continuous function $f_i:{\mathbb {R}}^{{\mathbf {n}}}\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and let ${{\bar{x}}} \in \mathrm{dom} f$. Suppose each function $f_i$ is subdifferential regular at ${{\bar{x}}}$, and the condition that the only combination of vector $\nu _i \in \partial ^{\infty } f_i({{\bar{x}}})$ with $\nu _1 + \ldots \nu _m=0$ is $\nu _i=0$ for $i\in [m]$. Then we have

$$\begin{aligned} \partial f({{\bar{x}}}) = \partial f_1({{\bar{x}}}) + \ldots \partial f_m({{\bar{x}}}). \end{aligned}$$

To obtain a global convergence, we need the following Kurdyka-Łojasiewicz (KŁ) property for $F(x) + h(y)$.

Definition 6

A function $\phi (\cdot )$ is said to have the KŁ property at $\bar{{\mathbf {x}}}\in \mathrm{dom}\,\partial \, \phi$ if there exists $\varsigma \in (0,+\infty ]$, a neighborhood U of $\bar{{\mathbf {x}}}$ and a concave function $\varUpsilon :[0,\varsigma )\rightarrow \mathbb {R}_{+}$ that is continuously differentiable on $(0,\varsigma )$, continuous at 0, $\varUpsilon (0)=0$, and $\varUpsilon '(t)>0$ for all $t\in (0,\eta ),$ such that for all ${\mathbf {x}}\in U\cap [\phi (\bar{{\mathbf {x}}})<\phi ({\mathbf {x}})<\phi (\bar{{\mathbf {x}}})+\varsigma ],$ we have

$$\begin{aligned} \varUpsilon '\left( \phi ({\mathbf {x}})-\phi (\bar{{\mathbf {x}}})\right) \, {{\,\mathrm{dist}\,}}\left( 0,\partial \phi ({\mathbf {x}})\right) \ge 1, \end{aligned}$$

(25)

where ${{\,\mathrm{dist}\,}}\left( 0,\partial \phi ({\mathbf {x}})\right) =\min \left\{ \Vert {\mathbf {z}}\Vert :{\mathbf {z}}\in \partial \phi ({\mathbf {x}})\right\}$. If $\phi ({\mathbf {x}})$ has the KŁ property at each point of $\mathrm{dom}\, \partial \phi$ then $\phi$ is a KŁ function.

When $\varUpsilon (t) = c t^{1-{\mathbf {a}}}$, where c is a constant, we call ${\mathbf {a}}$ the KŁ coefficient.

Many non-convex non-smooth functions in practical applications belong to the class of KŁ functions, for examples, real analytic functions, semi-algebraic functions, and locally strongly convex functions, see for example [6, 7].

Appendix 2: Proofs

In this appendix, we provide the proofs of all propositions and theorems of our paper. Before that, let us give some preliminary results. We use x, z to denote vectors in ${\mathbb {R}}^n$.

Lemma 1

[21, Lemma 2.8] If the function $x_i\mapsto \varTheta (x_i,z)$ is $\rho$-strongly convex, differentiable at $z_i$, and $\nabla _{x_i} \varTheta (z_i,z)=0$ then we have

$$\begin{aligned} \varTheta (x_i,z) \ge \frac{\rho }{2}\Vert x_i-z_i\Vert ^2. \end{aligned}$$

We recall the notation $(x_i,z_{\ne i}) = (z_1,\ldots ,z_{i-1},x_i,z_{i+1},\ldots ,z_s)$. Suppose we are trying to solve

$$\begin{aligned} \min _x \varPsi (x):=\varPhi (x) + \sum _{i=1}^s g_i(x_i). \end{aligned}$$

Proposition 7

[21, Theorem 2.7] Suppose ${\mathcal {G}}^k_i: {\mathbb {R}}^{{\mathbf {n}}_i} \times {\mathbb {R}}^{{\mathbf {n}}_i} \rightarrow {\mathbb {R}}^{{\mathbf {n}}_i}$ be some extrapolation operator that satisfies ${\mathcal {G}}^k_i(x^{k}_i, x^{k-1}_i)\le a_i^k\Vert x^{k}_i - x^{k-1}_i\Vert$. Let $u_i(x_i,z)$ is a block surrogate function of $\varPhi (x)$. We assume one of the following conditions holds:

• $x_i\mapsto u_i(x_i,z) + g_i(x_i)$ is $\rho _i$-strongly convex,

• the approximation error $\varTheta (x_i,z):=u_i(x_i,z)-\varPhi (x_i,z_{\ne i})$ satisfying $\varTheta (x_i,z)\ge \frac{\rho _i}{2} \Vert x_i-z_i\Vert ^2$ for all $x_i$.

Note that $\rho _i$ may depend on z. Let

$$\begin{aligned} x_i^{k+1}={{\,\mathrm{argmin}\,}}_{x_i} u_i(x_i,x^{k,i-1}) + g_i(x_i)- \langle {\mathcal {G}}^k_i(x^{k}_i, x^{k-1}_i),x_i\rangle . \end{aligned}$$

Then we have

$$\begin{aligned} \varPsi (x^{k,i-1}) + \gamma _i^k \Vert x_i^k-x_i^{k-1} \Vert ^2 \ge \varPsi (x^{k,i}) + \eta _i^k \Vert x_i^{k+1}-x_i^{k} \Vert ^2, \end{aligned}$$

(26)

where

$$\begin{aligned} \begin{array}{ll} \gamma ^{k}_i=\frac{(a^k_i)^2}{2\nu \rho _i } , \qquad \eta ^{k}_i = \frac{(1-\nu )\rho _i}{2}, \end{array} \end{aligned}$$

and $0<\nu <1$ is a constant. If we do not apply extrapolation, that is $a_i^k=0$, then (26) is satisfied with $\gamma _i^k=0$ and $\eta _i^k = \rho _i/2$.

The following proposition is derived from [20, Remark 3] and [62, Lemma 2.1].

Proposition 8

Suppose $x_i\mapsto \varPhi (x)$ is a $L_i$-smooth convex function and $g_i(x_i)$ is convex. Define ${{\bar{x}}}^{k,i-1}=(x^{k+1}_1,\ldots ,x^{k+1}_{i-1},{{\bar{x}}}^{k}_i, x^{k}_{i+1},\ldots ,x^k_s)$, ${\hat{x}}_i^k=x_i^k + \alpha _i^k (x_i^k-x_i^{k-1})$ and ${{\bar{x}}}_i^k=x_i^k + \beta _i^k (x_i^k-x_i^{k-1})$. Let $x_i^{k+1}={{\,\mathrm{argmin}\,}}_{x_i} \langle \nabla \varPhi ({{\bar{x}}}^{k,i-1}),x_i\rangle + g_i(x_i)+ \frac{L_i}{2}\Vert x_i -{\hat{x}}_i^k\Vert ^2.$ Then we have Inequality (26) is satisfied with

$$\begin{aligned} \gamma ^{k}_i=\frac{L_i}{2} \big ((\beta _i^k)^2 + \frac{(\gamma _i^k-\alpha _i^k)^2}{\nu } \big ), \qquad \eta ^{k}_i = \frac{(1-\nu )L_i}{2 }. \end{aligned}$$

If $\alpha _i^k=\beta _i^k$ then we have Inequality (26) is satisfied with

$$\begin{aligned} \gamma ^{k}_i=\frac{L_i}{2} (\beta _i^k)^2 , \qquad \eta ^{k}_i = \frac{L_i}{2 }. \end{aligned}$$

1.1 Proof of Proposition 1

(i) Suppose we are updating $x_i^k$. Let us recall that

$$\begin{aligned} {\mathcal {L}}(x, y, \omega ):= f(x)+\sum _{i=1}^s g_i(x_i) + h(y)+ \varphi (x, y, \omega ), \end{aligned}$$

where

$$\begin{aligned} \varphi (x, y, \omega )=\frac{\beta }{2}\Vert {\mathcal {A}} x + \mathcal By -b \Vert ^2 + \langle \omega ,{\mathcal {A}} x + \mathcal By -b \rangle . \end{aligned}$$

(27)

Denote ${\mathbf {u}}_i(x_i,z,y,\omega )= u_i(x_i,z)+ h(y) + {{\hat{\varphi }}}_i(x_i,z,y,\omega ),$ where

$$\begin{aligned} {{\hat{\varphi }}}_i(x_i,z,y,\omega ) = \varphi (z, y, \omega ) + \langle {\mathcal {A}}_i^*\big ( \omega +\beta ({\mathcal {A}} z + \mathcal By-b) \big ),x_i-z_i\rangle +\frac{\kappa _i\beta }{2}\Vert x_i-z_i\Vert ^2. \end{aligned}$$

We see that ${{\hat{\varphi }}}_i(x_i,z,y,\omega )$ is a block surrogate function of $x\mapsto \varphi (x, y, \omega )$ with respect to block $x_i$, and ${\mathbf {u}}_i(x_i,z,y,\omega )$ is a block surrogate function of $x\mapsto f(x) + h(y) + \varphi (x, y, \omega )$ with respect to block $x_i$. The update in (8) can be rewritten as follows.

$$\begin{aligned} x_i^{k+1}={{\,\mathrm{argmin}\,}}_{x_i} {\mathbf {u}}_i(x_i,x^{k,i-1},y^k,\omega ^k) + g_i(x_i) - \langle {\mathcal {G}}^k_i(x^{k}_i, x^{k-1}_i),x_i\rangle , \end{aligned}$$

(28)

where

$$\begin{aligned} \begin{aligned} {\mathcal {G}}^k_i(x^{k}_i, x^{k-1}_i)&= \beta {\mathcal {A}}_i^* {\mathcal {A}} \big (x^{k,i-1} - {{\bar{x}}}^{k,i-1})\big ) + \kappa _i \beta \zeta _i^k (x_i^k - x_i^{k-1}). \end{aligned} \end{aligned}$$

(29)

The block approximation error function between ${\mathbf {u}}_i(x_i,z,y,\omega )$ and $x\mapsto f(x) + h(y) + \varphi (x, y, \omega )$ is defined as

$$\begin{aligned} \begin{aligned}&{\mathbf {e}}_i(x_i,z,y,\omega )={\mathbf {u}}_i(x_i,z,y,\omega )-\big (f(x_i,z_{\ne i}) + h(y) + \varphi ((x_i,z_{\ne i}), y, \omega )\big )\\&\quad =u_i(x_i,z) - f(x_i,z_{\ne i}) + {{\hat{\varphi }}}_i(x_i,z,y,\omega ) - \varphi ((x_i,z_{\ne i}), y, \omega )\\&\quad \ge \theta _i(x_i,z,y,\omega ) \\&\quad :=\varphi (z, y, \omega ) - \varphi ((x_i,z_{\ne i}), y, \omega ) + \langle {\mathcal {A}}_i^*\big ( \omega +\beta ({\mathcal {A}} z + \mathcal By-b) \big ),x_i-z_i\rangle +\frac{\kappa _i\beta }{2}\Vert x_i-z_i\Vert ^2. \end{aligned} \end{aligned}$$

(30)

We have $\nabla _{x_i}\theta _i(x_i,z,y,\omega )=\kappa _i\beta (x_i - z_i) +\nabla _{x_i} \varphi (z, y, \omega ) - \nabla _{x_i} \varphi ((x_i,z_{\ne i}), y, \omega )$. So $\nabla _{x_i}\theta _i(z_i,z,y,w)=0$. On the other hand, note that $x_i \mapsto \varphi ((x_i,z_{\ne i}), y^k, \omega ^k)$ is $\beta \Vert {\mathcal {A}}_i^* {\mathcal {A}}_i\Vert$ - smooth. So, $x_i\mapsto \theta _i(x_i,z,y,\omega )$ is a $\beta (\kappa _i - \Vert {\mathcal {A}}_i^* {\mathcal {A}}_i\Vert )$ - strongly convex function. From Lemma 1 we have $\theta _i(x_i,z,y,w)\ge \frac{ \beta (\kappa _i - \Vert {\mathcal {A}}_i^* {\mathcal {A}}_i\Vert ) }{2} \Vert x_i-z_i\Vert ^2$. The result follows from (28), (30) and Proposition (7).

(ii) When $x_i\mapsto u_i(x_i,z)+g_i(x_i)$ is convex and we apply the update as in (8), it follows from Proposition 8 (see also [21, Remark 4.1]) that

$$\begin{aligned} \begin{aligned}&u_i(x_i^{k},x^{k,i-1}) + g_i(x_i^k)+\varphi (x^{k,i-1},y^k,\omega ^k)+ \frac{\beta \Vert {\mathcal {A}}_i^* {\mathcal {A}}_i\Vert }{2} (\zeta _i^k)^2\Vert x_i^{k}-x^{k-1}_i\Vert ^2 \\&\quad \ge u_i(x_i^{k+1},x^{k,i-1}) + g_i(x_i^{k+1})+ \varphi (x^{k,i},y^k,\omega ^k) + \frac{\beta \Vert {\mathcal {A}}_i^* {\mathcal {A}}_i\Vert }{2}\Vert x_i^{k+1}-x^k_i\Vert ^2. \end{aligned} \end{aligned}$$

(31)

On the other hand, note that $u_i(x_i^{k},x^{k,i-1}) = f(x^{k,i-1})$ and $u_i(x_i^{k+1},x^{k,i-1})\ge f(x^{k,i})$. The result follows then.

1.2 Proof of Proposition 2

Denote

$$\begin{aligned} {\hat{h}}(y,y') = h(y') + \langle \omega , \mathcal Ax+ {\mathcal {B}} y'-b\rangle + \langle {\mathcal {B}}^*\omega + \nabla h(y'), y-y'\rangle + \frac{L_h}{2} \Vert y-y'\Vert ^2. \end{aligned}$$

Then we have ${\hat{h}}(y,y') +\frac{\beta }{2}\Vert {\mathcal {A}} x +\mathcal By -b \Vert ^2$ is a surrogate function of $y\mapsto h(y) + \varphi (x,y,\omega )$. Note that the function $y\mapsto {\hat{h}}(y,y') +\frac{\beta }{2}\Vert {\mathcal {A}} x +\mathcal By -b \Vert ^2$ is $(L_h + \beta \lambda _{\min }({\mathcal {B}}^*{\mathcal {B}}))$-strongly convex. The result follows from Proposition 7 (see also [21, Section 4.2.1]).

Suppose h(y) is convex. We note that $y\mapsto \frac{\beta }{2}\Vert {\mathcal {A}} x + \mathcal By -b \Vert ^2$ is also convex and plays the role of $g_i$ in Proposition 8. The result follows from Proposition 8.

1.3 Proof of Proposition 3

Note that

$$\begin{aligned} {\mathcal {L}}(x^{k+1},y^{k+1},\omega ^{k+1})= {\mathcal {L}}(x^{k+1},y^{k+1},\omega ^k) + \frac{1}{\alpha \beta }\langle \omega ^{k+1}-\omega ^k, \omega ^{k+1}-\omega ^k \rangle \end{aligned}$$

(32)

From the optimality condition of (9) we have

$$\begin{aligned} \nabla h({\hat{y}}^k) + L_h(y^{k+1}-{\hat{y}}^k) + {\mathcal {B}}^*\omega ^k+\beta {\mathcal {B}}^*({\mathcal {A}} x^{k+1} + {\mathcal {B}} y^{k+1}-b)=0. \end{aligned}$$

Together with (10) we obtain

$$\begin{aligned} \nabla h({\hat{y}}^k) + L_h (\varDelta y^{k+1} -\delta _k \varDelta y^{k} )+ {\mathcal {B}}^*\omega ^{k}+\frac{1}{\alpha }{\mathcal {B}}^*(w^{k+1}-w^k)=0. \end{aligned}$$

(33)

Hence,

$$\begin{aligned} {\mathcal {B}}^*w^{k+1}=(1-\alpha ){\mathcal {B}}^* \omega ^{k}- \alpha (\nabla h({\hat{y}}^k) + L_h (\varDelta y^{k+1} -\delta _k \varDelta y^{k} ) ), \end{aligned}$$

(34)

which implies that

$$\begin{aligned} {\mathcal {B}}^*\varDelta w^{k+1} = (1-\alpha ){\mathcal {B}}^* \varDelta w^{k} - \alpha \varDelta z^{k+1}, \end{aligned}$$

(35)

where $\varDelta z^{k+1} = z^{k+1} - z^k$ and $z^{k+1}= \nabla h({\hat{y}}^k) + L_h (\varDelta y^{k+1} -\delta _k \varDelta y^{k} )$. We now consider 2 cases.

Case 1: $0<\alpha \le 1$. From the convexity of $\Vert \cdot \Vert$ we have

$$\begin{aligned} \Vert {\mathcal {B}}^*\varDelta w^{k+1}\Vert ^2 \le (1-\alpha ) \Vert {\mathcal {B}}^* \varDelta w^{k} \Vert ^2 + \alpha \Vert \varDelta z^{k+1}\Vert ^2 \end{aligned}$$

(36)

Case 2: $1<\alpha < 2$. We rewrite (35) as ${\mathcal {B}}^*\varDelta w^{k+1} = - (\alpha -1) {\mathcal {B}}^* \varDelta w^{k} - \frac{\alpha }{2-\alpha } (2-\alpha )\varDelta z^{k+1}.$ Hence

$$\begin{aligned} \Vert {\mathcal {B}}^*\varDelta w^{k+1} \Vert ^2 \le (\alpha -1)\Vert {\mathcal {B}}^* \varDelta w^{k}\Vert ^2+ \frac{\alpha ^2}{(2-\alpha )} \Vert \varDelta z^{k+1}\Vert ^2 \end{aligned}$$

(37)

Combine (36) and (37) we obtain

$$\begin{aligned} \Vert {\mathcal {B}}^*\varDelta w^{k+1}\Vert ^2 \le |1-\alpha |\Vert {\mathcal {B}}^* \varDelta w^{k}\Vert ^2+ \frac{\alpha ^2}{1-|1-\alpha |} \Vert \varDelta z^{k+1}\Vert ^2, \end{aligned}$$

(38)

which implies

$$\begin{aligned} (1-|1-\alpha |)\Vert {\mathcal {B}}^*\varDelta w^{k+1} \Vert ^2 \le |1-\alpha |(\Vert {\mathcal {B}}^* \varDelta w^{k}\Vert ^2- \Vert {\mathcal {B}}^* \varDelta w^{k+1} \Vert ^2)+ \frac{\alpha ^2}{1-|1-\alpha |} \Vert \varDelta z^{k+1}\Vert ^2. \end{aligned}$$

(39)

On the other hand, when we use extrapolation for the update of y we have

$$\begin{aligned} \begin{aligned} \Vert \varDelta z^{k+1}\Vert ^2&=\Vert \nabla h({\hat{y}}^k) - \nabla h({\hat{y}}^{k-1})+ L_h (\varDelta y^{k+1} -\delta _k \varDelta y^{k} ) - L_h (\varDelta y^{k} -\delta _{k-1} \varDelta y^{k-1} ) \Vert ^2\\&\le 3 L_h^2 \Vert {\hat{y}}^k -{\hat{y}}^{k-1}\Vert ^2 + 3 L^2_h \Vert \varDelta y^{k+1}\Vert ^2 + 3 \Vert (1+\delta _k) L_h\varDelta y^{k}-L_h\delta _{k-1} \varDelta y^{k-1}\Vert ^2 \\&\le 6 L_h^2 \big [ (1+\delta _k)^2\Vert \varDelta y^{k}\Vert ^2 + \delta _{k-1}^2 \Vert \varDelta y^{k-1} \Vert ^2\big ]+ 3 L^2_h \Vert \varDelta y^{k+1}\Vert ^2 \\&\quad + 6(1+\delta _k)^2 L_h^2 \Vert \varDelta y^{k}\Vert ^2 + 6 L_h^2 \delta _{k-1}^2\Vert \varDelta y^{k-1}\Vert ^2\\&=3 L^2_h\Vert \varDelta y^{k+1}\Vert ^2 + 12(1+\delta _k)^2 L_h^2 \Vert \varDelta y^{k}\Vert ^2 + 12 L^2_h \delta _{k-1}^2\Vert \varDelta y^{k-1}\Vert ^2. \end{aligned} \end{aligned}$$

(40)

If we do not use extrapolation for y then we have

$$\begin{aligned} \begin{aligned}&\Vert \varDelta z^{k+1}\Vert ^2 =\Vert \nabla h(y^k) - \nabla h(y^{k-1}) + L_h \varDelta y^{k+1} - L_h\varDelta y^{k}\Vert ^2\\&\quad \le 3 L_h^2 \Vert \varDelta y^{k}\Vert ^2 + 3 L^2_h \Vert \varDelta y^{k+1}\Vert ^2 + 3 L_h^2 \Vert \varDelta y^{k}\Vert ^2= 6 L_h^2 \Vert \varDelta y^{k}\Vert ^2+ 3 L^2_h \Vert \varDelta y^{k+1}\Vert ^2. \end{aligned} \end{aligned}$$

(41)

Furthermore, note that $\sigma _{{\mathcal {B}}}\Vert \varDelta w^{k+1}\Vert ^2 \le \Vert {\mathcal {B}}^* \varDelta w^{k+1}\Vert ^2$. Therefore, it follows from (39) that

$$\begin{aligned} \begin{aligned} \Vert \varDelta w^{k+1}\Vert ^2&\le \frac{|1-\alpha |}{\sigma _{{\mathcal {B}}}(1-|1-\alpha |)} (\Vert {\mathcal {B}}^* \varDelta w^{k}\Vert ^2- \Vert {\mathcal {B}}^* \varDelta w^{k+1} \Vert ^2) \\&\quad + \frac{\alpha ^2 3 L^2_h}{\sigma _{{\mathcal {B}}}(1-|1-\alpha |)^2}( \Vert \varDelta y^{k+1}\Vert ^2 + {\bar{\delta }}_k \Vert \varDelta y^{k}\Vert ^2 + 4\delta _{k-1}^2\Vert \varDelta y^{k-1}\Vert ^2). \end{aligned} \end{aligned}$$

(42)

The result is obtained from (42), (32) and Proposition 1.

1.4 Proof of Proposition 4

(i) From Inequality (17) and the conditions in (18),

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}^{k+1} + \mu \Vert \varDelta y^{k+1}\Vert ^2 +\sum _{i=1}^s\eta _i \Vert \varDelta x^{k+1}_i \Vert ^2 + \frac{\alpha _1}{\beta } \Vert {\mathcal {B}}^* \varDelta w^{k+1}\Vert ^2 \\&\quad \le {\mathcal {L}}^{k}+ C_1\mu \Vert \varDelta y^{k}\Vert ^2 + C_2\mu \Vert \varDelta y^{k-1}\Vert ^2+ C_x\sum _{i=1}^s\eta _i \Vert \varDelta x^{k}_i\Vert ^2 + \frac{\alpha _1}{ \beta } \Vert {\mathcal {B}}^* \varDelta w^{k}\Vert ^2. \end{aligned} \end{aligned}$$

(43)

By summing from $k=1$ to K Inequality (43) and noting that $C_1+C_2=C_y$ we obtain (20).

(ii) Let us prove $\{\varDelta y^k\}$ and $\{\varDelta x_i^k \}$ converge to 0. Let us first prove the second situation, that is we use extrapolation for the update of y and Inequality (19) is satisfied. From (34) we have $\alpha {\mathcal {B}}^*w^{k+1}=-(1-\alpha ) {\mathcal {B}}^* \varDelta \omega ^{k+1}- \alpha z^{k+1} ,$ where $z^{k+1}= \nabla h({\hat{y}}^k) + L_h (\varDelta y^{k+1} -\delta _k \varDelta y^{k} )$. Using the same technique that derives Inequality (38), we obtain the following

$$\begin{aligned} \alpha \sigma _{{\mathcal {B}}}\Vert w^{k+1}\Vert ^2 \le \alpha \Vert {\mathcal {B}}^*w^{k+1}\Vert ^2 \le |1-\alpha | \Vert {\mathcal {B}}^* \varDelta \omega ^{k+1}\Vert ^2 + \frac{\alpha ^2}{1-|1-\alpha |} \Vert z^{k+1}\Vert ^2. \end{aligned}$$

(44)

On the other hand, we have

$$\begin{aligned} {\mathcal {L}}^{k}&=F(x^{k}) +h(y^{k}) +\frac{\beta }{2}\Vert \mathcal Ax^{k}+\mathcal By^{k}-b+\frac{\omega ^{k}}{\beta }\Vert ^2 -\frac{1}{2\beta } \Vert \omega ^{k}\Vert ^2\ge F(x^{k}) +h(y^{k}) -\frac{1}{2\beta } \Vert \omega ^{k}\Vert ^2. \end{aligned}$$

Together with (44) and

$$\begin{aligned} \Vert z^{k}\Vert ^2&= \Vert \nabla h({\hat{y}}^{k-1})- \nabla h(y^{k})+\nabla h(y^{k}) + L_h (\varDelta y^{k} -\delta _{k-1}\varDelta y^{k-1} ) \Vert ^2 \\&\le 4 \Vert \nabla h({\hat{y}}^{k-1})- \nabla h(y^{k}) \Vert ^2 + 4 \Vert \nabla h(y^{k}) \Vert ^2 + 4L_h^2\Vert \varDelta y^{k}\Vert ^2 + 4 L_h^2\delta _{k-1}^2 \Vert \varDelta y^{k-1}\Vert ^2 \\&\le 12L_h^2 \Vert \varDelta y^{k}\Vert ^2 + 12\delta _{k-1}^2 \Vert \varDelta y^{k-1}\Vert ^2 + 4 \Vert \nabla h(y^{k})\Vert ^2. \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned} {\mathcal {L}}^{k}&\ge F(x^{k}) +h(y^{k}) - \frac{1}{2\alpha \beta \sigma _{{\mathcal {B}}}}\big ( |1-\alpha | \Vert B^* \varDelta \omega ^{k}\Vert ^2 + \frac{\alpha ^2}{1-|1-\alpha |} \Vert z^{k}\Vert ^2 \big ) \\&\ge F(x^{k}) +h(y^{k}) - \frac{|1-\alpha |}{2\alpha \beta \sigma _{{\mathcal {B}}}} \Vert B^* \varDelta \omega ^{k}\Vert ^2\\&\qquad - \frac{\alpha }{2\beta \sigma _{{\mathcal {B}}}(1-|1-\alpha |)} \big (12L_h^2 \Vert \varDelta y^{k}\Vert ^2 + 12\delta _{k-1}^2 \Vert \varDelta y^{k-1}\Vert ^2 + 4 \Vert \nabla h(y^{k})\Vert ^2\big ) \end{aligned} \end{aligned}$$

(45)

Since h(y) is $L_h$-smooth, for all $y\in {\mathbb {R}}^q$ and $\alpha _L>0$ we have, (see [39])

$$\begin{aligned} h(y-\alpha _L \nabla f(y)) \le h(y) - \alpha _L(1-\frac{L_h \alpha _L}{2}) \Vert \nabla h(y)\Vert ^2. \end{aligned}$$

Let us choose $\alpha _L$ such that $\alpha _L(1-\frac{L_h \alpha _L}{2})=\frac{4\alpha }{2\beta \sigma _{{\mathcal {B}}}(1-|1-\alpha |)}$. Note that this equation always has a positive solution when $\beta \ge \frac{4L_h \alpha }{\sigma _{\mathcal { B}} (1-|1-\alpha | )}$. Then we have

$$\begin{aligned} h(y^{k}) - \frac{4\alpha }{2\beta \sigma _{{\mathcal {B}}}(1-|1-\alpha |)} \Vert \nabla h(y^{k})\Vert ^2 \ge h(y^k-\alpha _L \nabla f(y^k)). \end{aligned}$$

Together with (45) we get

$$\begin{aligned} \begin{aligned} {\mathcal {L}}^{k}&\ge F(x^{k}) + h(y^k-\alpha _L \nabla f(y^k)) - \frac{|1-\alpha |}{2\alpha \beta \sigma _{{\mathcal {B}}}} \Vert B^* \varDelta \omega ^{k}\Vert ^2 \\&\quad - \frac{\alpha }{2\beta \sigma _{{\mathcal {B}}}(1-|1-\alpha |)} ( 12L_h^2 \Vert \varDelta y^{k} \Vert ^2+ 12\delta _{k-1}^2 \Vert \varDelta y^{k-1}\Vert ^2). \end{aligned} \end{aligned}$$

(46)

So from $\frac{\alpha _1}{\beta }\ge \frac{|1-\alpha |}{2\alpha \beta \sigma _{{\mathcal {B}}}}$, $\mu \ge \frac{\alpha 12L_h^2}{2\beta \sigma _{{\mathcal {B}}}(1-|1-\alpha |)}$, $(1-C_1)\mu \ge \frac{\alpha 12L_h^2 12\delta _{k}^2}{2\beta \sigma _{{\mathcal {B}}}(1-|1-\alpha |)}$ we have

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}^{K+1} + \mu \Vert \varDelta y^{K+1} \Vert ^2 + \frac{\alpha _1}{ \beta } \Vert B^* \varDelta w^{K+1}\Vert ^2 + (1-C_1)\mu \Vert \varDelta y^{K}\Vert ^2 \\&\quad \ge F(x^{K+1}) + h(y^{K+1}-\alpha _L \nabla f(y^{K+1})). \end{aligned} \end{aligned}$$

(47)

Hence ${\mathcal {L}}^{K+1} + \mu \Vert \varDelta y^{K+1} \Vert ^2 + \frac{\alpha _1}{ \beta } \Vert B^* \varDelta w^{K+1}\Vert ^2 + (1-C_1)\mu \Vert \varDelta y^{K}\Vert ^2$ is lower bounded.

Furthermore, since $\eta _i$ and $\mu$ are positive numbers we derive from Inequality (20) that $\sum _{k=1}^\infty \Vert \varDelta y^k \Vert ^2<+\infty$ and $\sum _{k=1}^\infty \Vert \varDelta x_i^k\Vert ^2 <+\infty$. Therefore, $\{\varDelta y^k\}$ and $\{\varDelta x_i^k \}$ converge to 0.

Let us now consider the first situation when $\delta _k=0$ for all k.

From Inequality (17) and the conditions in (18) we have

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}^{k+1} + \mu \Vert \varDelta y^{k+1}\Vert ^2 +\sum _{i=1}^s\eta _i \Vert \varDelta x^{k+1}_i \Vert ^2 + \frac{\alpha _1}{\beta } \Vert B^* \varDelta w^{k+1}\Vert ^2 \\&\quad \le {\mathcal {L}}^{k}+ C_y\mu \Vert \varDelta y^{k}\Vert ^2 + C_x\sum _{i=1}^s\eta _i \Vert \varDelta x^{k}_i\Vert ^2 + \frac{\alpha _1}{ \beta } \Vert B^* \varDelta w^{k}\Vert ^2. \end{aligned} \end{aligned}$$

(48)

By summing Inequality (48) from $k=1$ to K we obtain

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}^{K+1} + C_y \mu \Vert \varDelta y^{K+1} \Vert ^2 + C_x\sum _{i=1}^s\eta _i \Vert \varDelta x^{K+1}_i \Vert ^2 + \frac{\alpha _1}{ \beta } \Vert B^* \varDelta w^{K+1}\Vert ^2 \\&+ \sum _{k=1}^{K}\big [(1-C_y)\mu \Vert \varDelta y^{k+1}\Vert ^2 + (1-C_x)\sum _{i=1}^s\eta _i \Vert \varDelta x^{k+1}_i\Vert ^2 \big ] \\&\quad \le {\mathcal {L}}^1+ \frac{\alpha _1}{\beta } \Vert B^* \varDelta \omega ^{1}\Vert ^2 +\sum _{i=1}^s \eta _i^0 \Vert \varDelta x^{1}_i\Vert ^2 +C\mu \Vert \varDelta y^{1}\Vert ^2. \end{aligned} \end{aligned}$$

(49)

Denote the value of the right side of Inequality (48) by ${{\hat{{\mathcal {L}}}}}^k$. Note that $0<C_x,C_y<1$, then from (48) we have the sequence $\{{{\hat{{\mathcal {L}}}}}^{k}\}$ is non-increasing. It follows from [38, Lemma 2.9] that ${{\hat{{\mathcal {L}}}}}^k\ge \vartheta$ for all k, where $\vartheta$ is is the lower bound of $F(x^{k}) +h(y^{k})$. For completeness, let us provide the proof in the following. We have

$$\begin{aligned} \begin{aligned} {{\hat{{\mathcal {L}}}}}^k&\ge {\mathcal {L}}^k =F(x^{k}) +h(y^{k}) +\frac{\beta }{2}\Vert Ax^{k}+By^{k}-b\Vert ^2 +\frac{1}{\alpha \beta }\langle \omega ^k, \omega ^{k}-\omega ^{k-1}\rangle \\&\ge \vartheta + \frac{1}{2\alpha \beta }(\Vert \omega ^k\Vert ^2-\Vert \omega ^{k-1}\Vert ^2+\Vert \varDelta \omega ^k\Vert ^2)\ge \vartheta + \frac{1}{2\alpha \beta }(\Vert \omega ^k\Vert ^2-\Vert \omega ^{k-1}\Vert ^2), \end{aligned} \end{aligned}$$

(50)

Assume that there exists $k_0$ such that ${{\hat{{\mathcal {L}}}}}^k < \vartheta$ for all $k\ge k_0$. As ${{\hat{{\mathcal {L}}}}}^k$ is non-increasing we have

$$\begin{aligned} \sum _{k=1}^K ({{\hat{{\mathcal {L}}}}}^k - \vartheta ) \le \sum _{k=1}^{k_0} ({{\hat{{\mathcal {L}}}}}^k -\vartheta ) + (K-k_0) ({{\hat{{\mathcal {L}}}}}^k -\vartheta ) \end{aligned}$$

Hence $\sum _{k=1}^\infty ({{\hat{{\mathcal {L}}}}}^k - \vartheta )= -\infty$. However, from (50) we have

$$\begin{aligned} \sum _{k=1}^K ({{\hat{{\mathcal {L}}}}}^k - \vartheta ) \ge \sum _{k=1}^K\frac{1}{2\alpha \beta }\Vert \omega ^k\Vert ^2 - \frac{1}{2\alpha \beta }\Vert \omega ^{k-1}\Vert ^2\ge \frac{1}{2\alpha \beta }(-\Vert \omega ^{0}\Vert ^2), \end{aligned}$$

which gives a contradiction.

Since ${{\hat{{\mathcal {L}}}}}^K\ge \vartheta$ and $\eta _i$ and $\mu$ are positive numbers we derive from Inequality (20) that $\sum _{k=1}^\infty \Vert \varDelta y^k \Vert ^2<+\infty$ and $\sum _{k=1}^\infty \Vert \varDelta x_i^k\Vert ^2 <+\infty$. Therefore, $\{\varDelta y^k\}$ and $\{\varDelta x_i^k \}$ converge to 0.

Now we prove $\{\varDelta \omega ^k\}$ goes to 0. Since $\sum _{k=1}^\infty \Vert \varDelta y^k \Vert ^2<+\infty$, we derive from (40) that $\sum _{k=1}^\infty \Vert \varDelta z^k \Vert ^2<+\infty$. Summing up Equality (38) from $k=1$ to K we have

$$\begin{aligned} (1-|1-\alpha |) \sum _{k=1}^K \Vert {\mathcal {B}}^*\varDelta \omega ^k \Vert ^2 + \Vert {\mathcal {B}}^*\varDelta \omega ^{K+1} \Vert ^2 \le \Vert {\mathcal {B}}^*\varDelta \omega ^1 \Vert ^2 + \frac{\alpha ^2}{1-|1-\alpha |} \sum _{k=1}^K \Vert \varDelta z^{k+1} \Vert ^2, \end{aligned}$$

which implies that $\sum _{k=1}^\infty \Vert {\mathcal {B}}^*\varDelta \omega ^k \Vert ^2 <+\infty$. Hence, $\Vert {\mathcal {B}}^*\varDelta \omega ^k \Vert ^2\rightarrow 0$. Since $\sigma _{{\mathcal {B}}}>0$ we have $\{\varDelta \omega ^k\}$ goes to 0.

1.5 Proof of Proposition 5

We remark that we use the idea in the proof of [58, Lemma 6] to prove the proposition. However, our proof is more complicated since in our framework $\alpha \in (0,2)$, the function h is linearized and we use extrapolation for y.

Note that as $\sigma _{{\mathcal {B}}}>0$ we have ${\mathcal {B}}$ is a surjective. Together with the assumption $b+ Im({\mathcal {A}}) \subseteq Im({\mathcal {B}})$ we have there exist ${{\bar{y}}}^k$ such that $\mathcal Ax^k+{\mathcal {B}}{{\bar{y}}}^k-b =0$.

Now we have

$$\begin{aligned} \begin{aligned} {\mathcal {L}}^k&=F(x^{k})+ h(y^{k}) +\frac{\beta }{2}\Vert \mathcal Ax^{k}+\mathcal By^{k}-b\Vert ^2 +\langle \omega ^k,\mathcal Ax^{k}+\mathcal By^{k}-b\rangle \\&=F(x^{k}) + h(y^{k}) +\frac{\beta }{2}\Vert Ax^{k}+\mathcal By^{k}-b\Vert ^2 + \langle {\mathcal {B}}^*\omega ^k,y^{k}-{{\bar{y}}}^k\rangle \end{aligned} \end{aligned}$$

(51)

From (33) we have

$$\begin{aligned} \langle {\mathcal {B}}^*\omega ^k,y^{k}-{{\bar{y}}}^k\rangle&=\big \langle \nabla h({\hat{y}}^k) + L_h (\varDelta y^{k+1} -\delta _k \varDelta y^{k} )+ \frac{1}{\alpha }{\mathcal {B}}^*(w^{k+1}-w^k), {{\bar{y}}}^k-y^{k}\big \rangle \\&\ge \langle \nabla h(y^k) , {{\bar{y}}}^k-y^{k}\rangle -\big (\Vert \nabla h(y^k)-\nabla h({\hat{y}}^k)\Vert + L_h \Vert \varDelta y^{k+1}\Vert + L_h \delta _k \Vert \varDelta y^{k}\Vert \\&\quad + \frac{1}{\alpha }\Vert {\mathcal {B}}^*\varDelta \omega ^{k+1}\Vert \big ) \Vert {{\bar{y}}}^k-y^{k}\Vert . \end{aligned}$$

Therefore, it follows from (51) and $L_h$-smooth property of h that

$$\begin{aligned} {\mathcal {L}}^k \ge F(x^{k}) + h({{\bar{y}}}^k) - \frac{L_h}{2}\Vert y^k-{{\bar{y}}}^k\Vert ^2- \big (2L_h\delta _{k}\Vert \varDelta y^k\Vert + L_h \Vert \varDelta y^{k+1}\Vert + \frac{1}{\alpha }\Vert {\mathcal {B}}^* \varDelta \omega ^{k+1}\Vert \big ) \Vert {{\bar{y}}}^k-y^{k}\Vert . \end{aligned}$$

(52)

On the other hand, we have

$$\begin{aligned} \Vert {{\bar{y}}}^k-y^{k}\Vert ^2 \le \frac{1}{\lambda _{\min }({\mathcal {B}}^*{\mathcal {B}})} \Vert {\mathcal {B}}({{\bar{y}}}^k-y^{k})\Vert ^2= \frac{1}{\lambda _{\min }({\mathcal {B}}^*{\mathcal {B}})}\Vert {\mathcal {A}} x^k + \mathcal By^{k} -b\Vert ^2 =\frac{1}{\lambda _{\min }({\mathcal {B}}^*{\mathcal {B}})} \big \Vert \frac{1}{\alpha \beta } \varDelta \omega ^k\big \Vert ^2. \end{aligned}$$

(53)

We have proved in Proposition 4 that $\Vert \varDelta \omega ^k\Vert$, $\Vert \varDelta x^k\Vert$ and $\Vert \varDelta y^k\Vert$ converge to 0. Furthermore, from Proposition 4 we have ${\mathcal {L}}^k$ is upper bounded. Therefore, from (52), (53) and (20) we have $F(x^{k}) + h({{\bar{y}}}^k)$ is upper bounded. So $\{x^k\}$ is bounded. Consequently, $\mathcal Ax^k$ is bounded.

Furthermore, we have

$$\begin{aligned} \Vert y^k\Vert ^2\le \frac{1}{\lambda _{\min }({\mathcal {B}}^*{\mathcal {B}})} \Vert \mathcal By^k\Vert ^2 = \frac{1}{\lambda _{\min }({\mathcal {B}}^*{\mathcal {B}})}\big \Vert \frac{1}{\alpha \beta } \varDelta \omega ^k-\mathcal Ax^k -b \big \Vert ^2. \end{aligned}$$

Therefore, $\{y^k\}$ is bounded, which implies that $\Vert \nabla h({\hat{y}}^k)\Vert$ is also bounded. Finally, from  (33) and the assumption $\lambda _{\min }({\mathcal {B}}{\mathcal {B}}^*)>0$ we also have $\{\omega ^k\}$ is bounded.

1.6 Proof of Theorem 1

Suppose $(x^{k_n},y^{k_n},\omega ^{k_n})$ converges to $(x^*,y^*,\omega ^*)$. Since $\varDelta x_i^k$ goes to 0, we have $x_i^{k_n+1}$ and $x_i^{k_n-1}$ also converge to $x_i^*$ for all $i\in [s]$. From (28), for all $x_i$,

$$\begin{aligned} {\mathbf {u}}_i(x_i^{k+1},x^{k,i-1},y^k,\omega ^k)+ g_i(x_i^{k+1}) \le {\mathbf {u}}_i(x_i,x^{k,i-1},y^k,\omega ^k) + g_i(x_i) - \langle {\mathcal {G}}^k_i(x^{k}_i, x^{k-1}_i),x_i-x^{k+1}_i\rangle . \end{aligned}$$

(54)

Choosing $x_i=x_i^*$ and $k=k_n-1$ in (54) and noting that ${\mathbf {u}}_i(x_i,z)$ is continuous by Assumption 2 (i), we have $\limsup _{n\rightarrow \infty } {\mathbf {u}}_i(x_i^*,x^*,y^*,\omega ^*) + g_i(x_i^{k_n}) \le {\mathbf {u}}_i(x_i^*,x^*,y^*,\omega ^*)+ g_i(x_i^*).$ On the other hand, as $g_i(x_i)$ is lower semi-continuous. Hence, $g_i(x_i^{k_n})$ converges to $g_i(x_i^*)$. Now we choose $k=k_n\rightarrow \infty$ in (54) for all $x_i$ we obtain

$$\begin{aligned} \begin{aligned} L_0(x^*,y^*,\omega ^*) + g_i(x_i^*)&\le {\mathbf {u}}_i(x_i,x^*,y^*,\omega ^*) +g_i(x_i)\\&= L_0(x_i,x^*_{\ne i},y^*,\omega ^*) + {\mathbf {e}}_i(x_i,x^*,y^*,\omega ^*) + g_i(x_i), \end{aligned} \end{aligned}$$

(55)

where $L_0(x,y,\omega )=f(x) + h(y) + \varphi (x, y, \omega )$ and ${\mathbf {e}}_i$ is the approximation error defined in (30). We have

$$\begin{aligned} {\mathbf {e}}_i(x_i,x^*,y^*,\omega ^*)&= u_i(x_i,x^*) - f(x_i,x^*_{\ne i}) + {{\hat{\varphi }}}_i(x_i,x^*,y^*,\omega ^*) - \varphi ((x_i,x^*_{\ne i}), y^*, \omega ^*)\\&\le {{\bar{e}}}_i(x_i,x^*) + {{\hat{\varphi }}}_i(x_i,x^*,y^*,\omega ^*) - \varphi ((x_i,x^*_{\ne i}), y^*, \omega ^*). \end{aligned}$$

Note that ${{\bar{e}}}_i(x^*_i,x^*)=0$ by Assumption 2. From (55) we have $x_i^*$ is a solution of

$$\begin{aligned} \min _{x_i} L(x_i,x^*_{\ne i},y^*,\omega ^*)+ {{\bar{e}}}_i(x_i,x^*) + {{\hat{\varphi }}}_i(x_i,x^*,y^*,\omega ^*) - \varphi ((x_i,x^*_{\ne i}), y^*, \omega ^*). \end{aligned}$$

Writing the optimality condition for this problem we obtain $0 \in \partial _{x_i} {\mathcal {L}}(x^*,y^*,\omega ^*)$. Totally similarly we can prove that $0 \in \partial _{y} {\mathcal {L}}(x^*,y^*,\omega ^*)$. On the other hand, we have

$$\begin{aligned} \varDelta \omega ^k= \omega ^{k} - \omega ^{k-1}= \alpha \beta ({\mathcal {A}} x^k + {\mathcal {B}} y^k -b)\rightarrow 0. \end{aligned}$$

Hence, $\partial _\omega {\mathcal {L}}(x^*,y^*,\omega ^*) = {\mathcal {A}} x^* + {\mathcal {B}} y^* -b=0.$

As we assume $\partial F(x)=\partial _{x_1} F(x) \times \cdots \times \partial _{x_s} F(x)$, we have

$$\begin{aligned} \partial {\mathcal {L}}(x,y,\omega )&= \partial F(x)+ \nabla \Big (h(y) + \langle \omega ,{\mathcal {A}} x +\mathcal By-b \rangle + \frac{\beta }{2} \Vert {\mathcal {A}} x + \mathcal By-b\Vert ^2\Big )\\&=\partial _{x_1} {\mathcal {L}}(x,y,\omega ) \times \cdots \times \partial _{x_s} {\mathcal {L}}(x,y,\omega ) \times \partial _{y} {\mathcal {L}}(x,y,\omega )\times \partial _{\omega } {\mathcal {L}}(x,y,\omega ). \end{aligned}$$

So $0\in \partial {\mathcal {L}}(x^*,y^*,\omega ^*)$.

1.7 Proof of Theorem 2

Note that we assume the generated sequence of Algorithm 1 is bounded. The following analysis is considered in the bounded set that contains the generated sequence of Algorithm 1. We first prove some preliminary results.

(A) The optimality condition of (28) gives us

$$\begin{aligned} \begin{aligned}&{\mathcal {G}}_i^k(x_i^k - x_i^{k-1}) - {\mathcal {A}}_i^*\big (\omega ^k+\beta ({\mathcal {A}} x^{k,i-1} + \mathcal By^k-b) \big ) -\kappa _i\beta (x^{k+1}_i-x_i^k) \\&\qquad \in \partial _{x_i} \big (u_i(x_i^{k+1},x^{k,i-1}) + g_i(x_i^{k+1})\big ). \end{aligned} \end{aligned}$$

(56)

As (22) holds, there exists ${\mathbf {s}}_i^{k+1}\in \partial u_i(x_i^{k+1},x^{k,i-1})$ and ${\mathbf {t}}_i^{k+1}\in \partial g_i(x_i^{k+1})$ such that

$$\begin{aligned} {\mathcal {G}}_i^k(x_i^k - x_i^{k-1}) - {\mathcal {A}}_i^*\big (\omega ^k+\beta ({\mathcal {A}} x^{k,i-1} + \mathcal By^k-b) \big ) -\kappa _i\beta (x^{k+1}_i-x_i^k) = {\mathbf {s}}_i^{k+1} + {\mathbf {t}}_i^{k+1} \end{aligned}$$

(57)

As (23) holds, there exists $\xi _i^{k+1}\in \partial _{x_i} f(x^{k+1})$ such that

$$\begin{aligned} \Vert \xi _i^{k+1} - {\mathbf {s}}_i^{k+1}\Vert \le L_i\Vert x^{k+1} - x^{k,i-1}\Vert . \end{aligned}$$

(58)

Denote $\tau ^{k+1}_i:= \xi _i^{k+1} + {\mathbf {t}}_i^{k+1} \in \partial _{x_i} F(x^{k+1})$ (as (22) holds). Then, from (57) we have

$$\begin{aligned} \tau ^{k+1}_i= \xi _i^{k+1} + {\mathcal {G}}_i^k(x_i^k - x_i^{k-1}) - {\mathcal {A}}_i^*\big (\omega ^k+\beta ({\mathcal {A}} x^{k,i-1} + \mathcal By^k-b) \big ) -\kappa _i\beta (x^{k+1}_i-x_i^k) - {\mathbf {s}}_i^{k+1}. \end{aligned}$$

(59)

On the other hand, we note that

$$\begin{aligned} \partial _{x_i} {\mathcal {L}}(x^{k+1},y^{k+1},\omega ^{k+1})= \partial _{x_i} F(x^{k+1} ) + {\mathcal {A}}_i^*\big (\omega ^{k+1} + \beta ({\mathcal {A}} x^{k+1} +\mathcal By^{k+1}-b) \big ). \end{aligned}$$

(60)

Let $d_i^{k+1}:= \tau _i^{k+1}+ {\mathcal {A}}_i^*\big (\omega ^{k+1} + \beta ({\mathcal {A}} x^{k+1} + \mathcal By^{k+1}-b) \big ) \in \partial _{x_i} {\mathcal {L}}(x^{k+1},y^{k+1},\omega ^{k+1})$. From (59),

$$\begin{aligned} \begin{aligned} \Vert d_i^{k+1}\Vert&= \Big \Vert \xi _i^{k+1} + {\mathcal {G}}_i^k(x_i^k - x_i^{k-1}) - {\mathcal {A}}_i^*\big (\omega ^k+\beta ({\mathcal {A}} x^{k,i-1} + \mathcal By^k-b) \big ) -\kappa _i\beta (x^{k+1}_i-x_i^k) \\&\qquad \qquad - {\mathbf {s}}_i^{k+1}+ {\mathcal {A}}_i^*\big (\omega ^{k+1} + \beta ({\mathcal {A}} x^{k+1} + \mathcal By^{k+1}-b) \big ) \Big \Vert \end{aligned} \end{aligned}$$

(61)

Together with (58) we obtain

$$\begin{aligned} \begin{aligned} \Vert d_i^{k+1}\Vert&\le a^k_i\Vert \varDelta x_i^k\Vert + \beta \Vert {\mathcal {A}}_i^* A\Vert \Vert x^{k+1}-x^{k,i-1}\Vert + \beta \Vert {\mathcal {A}}_i^*{\mathcal {B}}\Vert \Vert \varDelta y^{k+1}\Vert + \Vert {\mathcal {A}}_i^*\Vert \Vert \varDelta \omega ^{k+1}\Vert \\&\qquad \qquad + \kappa _i \beta \Vert \varDelta x_i^{k+1}\Vert + L_i\Vert x^{k+1} - x^{k,i-1}\Vert . \end{aligned} \end{aligned}$$

(62)

It follows from (9) that

$$\begin{aligned} {\mathcal {B}}^*\omega ^k + \nabla h({\hat{y}}^k) + \beta {\mathcal {B}}^* ({\mathcal {A}} x^{k+1} +{\mathcal {B}} y^{k+1} -b) + L_h (y^{k+1} - {\hat{y}}^k) = 0. \end{aligned}$$

Let $d_y^{k+1}:=\nabla h(y^{k+1}) +{\mathcal {B}}^*\big (\omega ^{k+1} +\beta ({\mathcal {A}} x^{k+1} + {\mathcal {B}} y^{k+1} -b )\big ).$ Then $d_y^{k+1}\in \partial _y {\mathcal {L}}(x^{k+1},y^{k+1},\omega ^{k+1})$ and

$$\begin{aligned}&\Vert d_y^{k+1}\Vert =\Vert \nabla h(y^{k+1}) - \nabla h({\hat{y}}^{k}) +{\mathcal {B}}^*(\omega ^{k+1} - \omega ^k) - L_h (y^{k+1} - {\hat{y}}^k)\Vert \\&\quad \le 2L_h \Vert y^{k+1} - {\hat{y}}^{k}\Vert + \Vert {\mathcal {B}}^*\Vert \Vert \varDelta \omega ^{k+1} \Vert \le 2 L_h (\Vert \varDelta y^{k+1}\Vert + \delta _k \Vert \varDelta y^{k}\Vert ) + \Vert {\mathcal {B}}^*\Vert \Vert \varDelta \omega ^{k+1} \Vert . \end{aligned}$$

Let $d_\omega ^{k+1}:={\mathcal {A}} x^{k+1} + {\mathcal {B}}^{k+1} -b$. We have $d_\omega ^{k+1}\in \partial _\omega {\mathcal {L}}(x^{k+1},y^{k+1},\omega ^{k+1})$ and

$$\begin{aligned} d_\omega ^{k+1}=(\omega ^{k+1} - \omega ^k)/(\alpha \beta ) = \varDelta \omega ^{k+1}/(\alpha \beta ). \end{aligned}$$

(B) Let us now prove $F(x^{k_n})$ converges to $F(x^*)$. This implies ${\mathcal {L}}(x^{k_n},y^{k_n},\omega ^{k_n})$ converges to ${\mathcal {L}}(x^*,y^*,\omega ^*)$ since ${\mathcal {L}}$ is differentiable in y and $\omega$. We have

$$\begin{aligned} F(x^{k_n})= f(x^{k_n})+\sum _{i=1}^s g_i(x_i^{k_n}) =u_s(x_s^{k_n},x^{k_n}) +\sum _{i=1}^s g_i(x_i^{k_n}). \end{aligned}$$

So $F(x^{k_n})$ converges to $u_s(x_i^*,x^*) +\sum _{i=1}^s g_i(x_i^*)=F(x^*)$.

We now proceed to prove the global convergence. Denote ${\mathbf {z}}= (x,y,\omega )$, $\tilde{\mathbf {z}}= ({{\tilde{x}}}, {{\tilde{y}}}, {{\tilde{\omega }}})$, and ${\mathbf {z}}^k= (x^k,y^k,\omega ^k)$. We consider the following auxiliary function

$$\begin{aligned} {\bar{{\mathcal {L}}}}({\mathbf {z}}, \tilde{\mathbf {z}})={\mathcal {L}}(x,y,\omega ) + \sum _{i=1}^s \frac{\eta _i + C_x \eta _i}{2}\Vert x_i - {{\tilde{x}}}_i \Vert ^2 + \frac{(1+C_y) \mu }{2} \Vert y-{{\tilde{y}}}\Vert ^2 + \frac{\alpha _1}{\beta } \Vert B^* (\omega - {{\tilde{\omega }}})\Vert ^2. \end{aligned}$$

The auxiliary sequence ${\bar{{\mathcal {L}}}} ({\mathbf {z}}^k, {\mathbf {z}}^{k-1})$ has the following properties.

• 1. Sufficient decreasing property From (48) we have

  $$\begin{aligned}&{\bar{{\mathcal {L}}}} ({\mathbf {z}}^{k+1}, {\mathbf {z}}^{k}) + \sum _{i=1}^s \frac{\eta _i- C_x \eta _i}{2}\big ( \Vert x_i^{k+1} -x_i^k \Vert ^2 + \Vert x_i^{k} -x_i^{k-1} \Vert ^2\big ) \\&\quad + \frac{(1-C_y)\mu }{2} \big ( \Vert y^{k+1} -y^k \Vert ^2 + \Vert y^{k} -y^{k-1} \Vert ^2\big )\le {\bar{{\mathcal {L}}}} ({\mathbf {z}}^k, {\mathbf {z}}^{k-1}). \end{aligned}$$

• 2. Boundedness of subgradient In the proof (A) above, we have proved that

  $$\begin{aligned} \Vert d^{k+1}\Vert \le a_1 (\Vert x^{k+1}-x^k\Vert +\Vert x^k-x^{k-1}\Vert + \Vert y^{k+1}-y^k\Vert + \Vert \omega ^{k+1}-\omega ^k\Vert ) \end{aligned}$$

  for some constant $a_1$ and $d^{k+1} \in \partial {\mathcal {L}}({\mathbf {z}}^{k+1})$. On the other hand, as we use $\alpha =1$, from (35) we obtain

  $$\begin{aligned} \begin{aligned}&\sqrt{\sigma _{{\mathcal {B}}}}\Vert \omega ^{k+1}-\omega ^k\Vert \le \Vert B^*(\omega ^{k+1}-\omega ^k)\Vert = \Vert \varDelta z^{k+1}\Vert \\&\quad =\Vert \nabla h(y^{k}) - \nabla h(y^{k-1}) + L_h(\varDelta y^{k+1} - \varDelta y^k) \Vert \le 2L_h\Vert y^{k}-y^{k-1}\Vert + L_h\Vert y^{k+1}-y^{k}\Vert . \end{aligned} \end{aligned}$$

  (63)

  Hence,

  $$\begin{aligned} \Vert d^{k+1}\Vert \le a_2 (\Vert x^{k+1}-x^k\Vert +\Vert x^k-x^{k-1}\Vert + \Vert y^{k+1}-y^k\Vert + \Vert y^{k}-y^{k-1}\Vert ) \end{aligned}$$

  for some constant $a_2$. Note that

  $$\begin{aligned} \partial {\bar{{\mathcal {L}}}}({\mathbf {z}}, \tilde{\mathbf {z}})=\partial {\mathcal {L}}({\mathbf {z}}, \tilde{\mathbf {z}}) + \partial \Big (\sum _{i=1}^s \frac{\eta _i + C_x \eta _i}{2}\Vert x_i - {{\tilde{x}}}_i \Vert ^2 + \frac{(1+C_y) \mu }{2} \Vert y-{{\tilde{y}}}\Vert ^2 + \frac{\alpha _1}{\beta } \Vert B^* (\omega - {{\tilde{\omega }}})\Vert ^2 \Big ). \end{aligned}$$

  Hence, it is not difficult to show that

  $$\begin{aligned} \Vert {\mathbf {d}}^{k+1}\Vert \le a_3 (\Vert x^{k+1}-x^k\Vert +\Vert x^k-x^{k-1}\Vert + \Vert y^{k+1}-y^k\Vert + \Vert y^{k}-y^{k-1}\Vert ) \end{aligned}$$

  for some constant $a_3$ and ${\mathbf {d}}^{k+1} \in \partial {\bar{{\mathcal {L}}}}({\mathbf {z}}^{k+1},{\mathbf {z}}^{k})$.

• 3. KL property Since $F(x) + h(y)$ has KL property, then ${\bar{{\mathcal {L}}}}({\mathbf {z}}, \tilde{\mathbf {z}})$ also has KŁ property.

• 4. A continuity condition Suppose ${\mathbf {z}}^{k_n}$ converges to $(x^*,y^*,\omega ^*)$. In the proof (B) above, we have proved that ${\mathcal {L}}({\mathbf {z}}^{k_n})$ converges to ${\mathcal {L}}(x^*,y^*,\omega ^*)$. Furthermore, from Proposition 4 we proved that $\Vert {\mathbf {z}}^{k+1}-{\mathbf {z}}^{k} \Vert$ goes to 0. Hence we have ${\mathbf {z}}^{k_n-1}$ converges to $(x^*,y^*,\omega ^*)$. So, ${\bar{{\mathcal {L}}}} ({\mathbf {z}}^{k+1}, {\mathbf {z}}^{k})$ converges to ${\bar{{\mathcal {L}}}} ({\mathbf {z}}^*, {\mathbf {z}}^*)$.

Using the same technique as in [7, Theorem 1], see also [20, 40], we can prove that

$$\begin{aligned} \sum _{k=1}^\infty \big (\Vert x^{k+1}-x^k\Vert +\Vert x^k-x^{k-1}\Vert + \Vert y^{k+1}-y^k\Vert + \Vert y^{k}-y^{k-1}\Vert \big )<\infty . \end{aligned}$$

which implies $\{(x^k,y^k)\}$ converges to $(x^*,y^*)$. From (63) we obtain

$$\begin{aligned} \sum _{k=1}^\infty \Vert \omega ^{k+1}-\omega ^k\Vert \le \sum _{k=1}^\infty \big ( \Vert y^{k+1}-y^k\Vert + \Vert y^{k}-y^{k-1}\Vert \big )<\infty . \end{aligned}$$

Hence, $\{\omega ^k\}$ also converges to $\omega ^*$.

Appendix 3: Additional experiment for different values of $\alpha$

In this experiment, we rerun the experiments from Sect. 3 with other values for $\alpha$, namely 0.5, 1.4 and 1.8; see Figs. 2, 3 and 4 (on pages 31-33). The penalty parameter $\beta$ is computed by $\beta = 2(2 + C_y)\alpha _2/C_y$, where $C_y = 1 - 10^{-6}$ and $\alpha _2=\frac{3\alpha }{(1-|1-\alpha |)^2}$. Although the segmentation errors and objective function values differ for different values of $\alpha$, we observe that, in all cases, iADMM-mm outperforms ADMM-mm which outperforms linearizedADMM. This confirms our observations from Sect. 3. On the other hand, we observe that the performances of ADMM-mm and linearizedADMM are similar for different values of $\alpha$; however, the performances of iADMM-mm (that is, ADMM-mm with inertial terms) for $\alpha = 0.5$ and $\alpha = 1.4$ are slightly worse than for $\alpha =1$, and the value $\alpha = 1.8$ leads to significantly worse performances for iADMM-mm. It is known that, in the convex setting, the ADMM variants often perform better for $\alpha > 1$. However, in our experiments, $\alpha =1$ provides the best performance for iADMM-mm. A possible reason is that the global convergence of iADMM-mm has been established only for the case $\alpha =1$ (see Theorem 2) while $\alpha \in (0,2)$ only guarantees a subsequential convergence (see Theorem 1).

Appendix 4: Additional experiments for a regularized nonnegative matrix factorization problem

In the previous example, the function $f(X,Y) = \lambda _1 \Vert X\Vert _* + r_2(Y )$ was separable while our framework allows non-separable functions; see (1) and the discussion that follows. To illustrate the use and effectiveness of iADMM on a non-separable case, let us consider the following regularized nonnegative matrix factorization (NMF) problem

$$\begin{aligned} \min _{W \in {\mathbb {R}}^{n\times r}_+ ,H \in {\mathbb {R}}^{r\times m}_+} \nicefrac {1}{2} \Vert X-WH\Vert ^2 + c_1 \Vert W\Vert _F^2 + c_2 \Vert H\Vert _F^2, \end{aligned}$$

(64)

where $X\in {\mathbb {R}}^{n\times m}$ is a given nonnegative matrix, and $c_1>0$ and $c_2>0$ are regularized parameters. Problem (64) can be rewritten in the form of (1) as follows:

$$\begin{aligned} \begin{aligned} \min _{W \in {\mathbb {R}}^{n\times r}_+ ,H \in {\mathbb {R}}^{r\times m}_+}&\nicefrac {1}{2} \Vert X-W H\Vert ^2 + c_1 \Vert W\Vert _F^2 + c_2 \Vert Y\Vert _F^2, \\&\mathrm{{such \,that}}\quad H -Y = 0. \end{aligned} \end{aligned}$$

(65)

In this case, $x_1=W$, $x_2=H$, $y=Y$, $f(W,H)=\frac{1}{2} \Vert X-W H\Vert ^2 + \beta \Vert W\Vert _F^2$, $g_1(W)$ and $g_2(H)$ are indicator functions of ${\mathbb {R}}^{n\times r}_+$ and ${\mathbb {R}}^{r\times m}_+$ respectively, $h(Y)=c_2 \Vert Y\Vert _F^2$, ${\mathcal {A}}_1=0$, ${\mathcal {A}}_2={\mathcal {I}}$, $\mathcal {B}= -{\mathcal {I}}$ (where ${\mathcal {I}}$ is identity operator), and $b=0$. As $W\mapsto f(W,H)$ is $L_W$-Lipschitz smooth and $H\mapsto f(W,H)$ is $L_H$-Lipschitz smooth, where $L_W=\Vert H H^\top \Vert +2 c_1$ and $L_H=\Vert W^\top W\Vert$, we use the Lipschitz gradient surrogate for block W and H as in (12), and apply the inertial term as in the footnote 3 (that is, we apply inertial terms that also lead to the extrapolation for the block surrogate of f). The augmented Lagrangian for (65) is

$$\begin{aligned} {\mathcal {L}}(W,H,Y,\omega )=f(W,H)+h(Y)+\langle H-Y,\omega \rangle +\frac{\beta }{2}\Vert H-Y\Vert ^2. \end{aligned}$$

Applying iADMM for solving (65), the update of W is

$$\begin{aligned} \begin{aligned} W^{k+1}&\in \arg \min _{W\in {\mathbb {R}}^{n\times r}_+} \langle -(X-{{\bar{W}}}^k H^k)(H^k)^\top +2 c_1 {{\bar{W}}}^k,W\rangle + \frac{L_W(H^k)}{2}\Vert W-{{\bar{W}}}^k\Vert ^2 \\&=\max \Big \{{{\bar{W}}}^k -\frac{1}{L_W(H^k)}\big (-(X-{{\bar{W}}}^k H^k)(H^k)^\top +2 c_1 {{\bar{W}}}^k\big ),0\Big \}, \end{aligned} \end{aligned}$$

(66)

where ${{\bar{W}}}^k=W^k + \zeta _1^k (W^k-W^{k-1})$. Note that we have used extrapolation for the surrogate of $W\mapsto f(W,H)$. The update of H is

$$\begin{aligned} \begin{aligned} H^{k+1}&\in \arg \min _{H\in {\mathbb {R}}^{r\times m}_+} \langle -(W^{k+1})^\top (X- W^{k+1} {{\bar{H}}}^k)+\omega ^k+\beta ({{\bar{H}}}^k - Y^k),H\rangle \\&\quad + \frac{\beta +L_H(W^{k+1})}{2}\Vert H-{{\bar{H}}}^k\Vert ^2 \\&=\max \Big \{{{\bar{H}}}^k-\frac{1}{\beta +L_H(W^{k+1})}\big (-(W^{k+1})^\top (X- W^{k+1} {{\bar{H}}}^k)+\omega ^k+\beta ({{\bar{H}}}^k - Y^k)\big ) ,0\Big \}, \end{aligned} \end{aligned}$$

(67)

where ${{\bar{H}}}^k=H^k + \zeta _2^k (H^k-H^{k-1})$. We do not use extrapolation for Y (that is, $\delta _k=0$), and simply choose $\alpha =1$. The update of Y is

$$\begin{aligned} \begin{aligned} Y^{k+1}&\in \arg \min _Y \langle -\omega ^k+ 2 c_2 Y^k,Y\rangle + \frac{\beta }{2} \Vert Y-H^{k+1}\Vert ^2 + c_2 \Vert Y-Y^k\Vert ^2 \\&= \frac{1}{\beta + 2 c_2}(\beta H^{k+1} + \omega ^k ), \end{aligned} \end{aligned}$$

(68)

while the update of $\omega$ is

$$\begin{aligned} \omega ^{k+1}= \omega ^k + \beta (H^{k+1}-Y^{k+1}). \end{aligned}$$

Choosing parameters By Proposition 8, the update of W in (66) implies that Inequality (14) is satisfied:

$$\begin{aligned} {\mathcal {L}}(W^{k+1},H^k,Y^k,\omega ^k)+\eta ^k_1 \Vert W^{k+1}-W^k\Vert ^2 \le {\mathcal {L}}(W^{k},H^k,Y^k,\omega ^k)+\gamma ^k_1 \Vert W^{k}-W^{k-1}\Vert ^2, \end{aligned}$$

where

$$\begin{aligned} \eta ^k_1=\frac{L_W(H^k)}{2}, \quad \gamma _1^k= \frac{L_W(H^k)}{2} (\zeta _1^k)^2. \end{aligned}$$

Note that we use $\eta ^k_1$ instead of $\eta _1$ as this value varies along with the update of H (because we used the extrapolation for the surrogate of $W\mapsto f(W,H)$). Similarly, the update of H in (67) implies that Inequality (14) is satisfied:

$$\begin{aligned} {\mathcal {L}}(W^{k+1},H^{k+1},Y^k,\omega ^k)+\eta ^k_2 \Vert H^{k+1}-H^k\Vert ^2 \le {\mathcal {L}}(W^{k+1},H^k,Y^k,\omega ^k)+\gamma ^k_2 \Vert H^{k}-H^{k-1}\Vert ^2, \end{aligned}$$

where

$$\begin{aligned} \eta _2^k=\frac{L_H(W^{k+1})+\beta }{2}, \gamma _2^k=\frac{L_H(W^{k+1})+\beta }{2} (\zeta _2^k)^2. \end{aligned}$$

Because of the update of Y in (68), the inequality in Proposition (2) is satisfied:

$$\begin{aligned} {\mathcal {L}}(W^{k+1},H^{k+1},Y^{k+1},\omega ^k)+\eta _y \Vert Y^{k+1}-Y^k\Vert ^2 \le {\mathcal {L}}(W^{k+1},H^{k+1},Y^k,\omega ^k)+\gamma ^k_y \Vert Y^{k}-Y^{k-1}\Vert ^2, \end{aligned}$$

where $\eta _y=c_2$ and $\gamma _y^k=0$. Following the same rationale that leads to Theorem 1, we obtain, as in (18),

$$\begin{aligned} \gamma _i^k \le C_x \eta _i^{k-1}, \frac{2\alpha _2(2c_2)^2}{\beta } \le C_y (\eta _y-\frac{\alpha _2 (2c_2)^2}{\beta }), \end{aligned}$$

where $\alpha _2=\frac{3\alpha }{\sigma _{{\mathcal {B}}}(1-|1-\alpha |)^2}=3$ and $0<C_x, C_y<1$. In our experiments, we choose

$$\begin{aligned} \zeta _1^k=\min \Big \{\frac{a_{k-1}-1}{a_k},\sqrt{C_x\frac{L_W(H^{k-1})}{L_W(H^k)}} \Big \}, \zeta _2^k=\min \Big \{\frac{a_{k-1}-1}{a_k},\sqrt{C_x\frac{L_H(W^{k+1})+\beta }{L_H(W^k)+\beta }} \Big \}, \end{aligned}$$

where $a_0=1$, $a_k=\frac{1}{2}(1+\sqrt{1+4a_{k-1}^2})$, and $\beta \ge 4 c_2 \frac{(6+3C_y)}{C_y}$.

Experiments We will compare iADMM with (i) ADMM (that is iADMM without using the inertial terms: $\zeta _1^k=\zeta _2^k=0$), and (ii) TITAN - the inertial block majorization minimization proposed in [21] that directly solves Problem (64) and competes favorably with the state of the art on the NMF problem (see [20] which is a special case of TITAN). In our implementation, we use Lipschitz gradient surrogate for W and H and use default parameter setting for TITAN.

In the following experiments, we set the parameters $c_1$ and $c_2$ of Problem (64) to be $c_1=0.001$ and $c_2=0.01$.

In the first experiment, we generate 2 synthetic low-rank data sets X with $(n,m,r)=(500,200,20)$ and $(n,m,r)=(500,500,20)$: we generate U and V by using the MATLAB command rand(n,r) and rand(r,m) respectively, and then let X=U*V. For each data set, we run each algorithm with the same 30 random initial points $W_0$=rand(n,r), $H_0$=rand(r,m) (for iADMM and ADMM we let $Y_0$=$H_0$ and $\omega _0$=zeros(r,m)), and for each initial point we run each algorithm for 15 s. We report the evolution of the average objective function values of Problem (64) with respect to time in Fig. 5 and the mean ± std of the final objective function values in Table 2. We observe that iADMM outperforms ADMM which illustrates the acceleration effect. Among the algorithms, TITAN converges the fastest, but only slightly faster than iADMM. However, iADMM provides the best final objective function values on average.

In the second experiment, we test the algorithms on 4 image data sets CBCL⁴ (2429 images of dimension $19 \times 19$), ORL⁵ (400 images of dimension $92 \times 112$), Frey⁶(1965 images of dimension $28 \times 20$), and Umist⁷ (565 images of dimension $92 \times 112$). For each data set, we run each algorithm with the same 20 random initial points. We run each algorithm 100 s for the data sets Umist and ORL and 30 s for the data sets CBCL and Frey. We draw the evolution of the average objective functions values with respect to time in Fig. 6 and the mean ± std of the final objective function values in Table 3.

Once again we observe that although iADMM converges slighly slower than TITAN, iADMM always produces the best objective function values among the three algorithms. On the other hand, ADMM also outperforms TITAN in term of the final objective function values. This means that, for some reason, ADMM and iADMM are able to avoid spurious local minima more effectively than TITAN.

Fig. 2

Evolution of the average value of the segmentation error rate and the objective function value with respect to time on Hopkins155

Fig. 3

Evolution of the segmentation error rate and the objective function value with respect to time on Umist10

Fig. 4

Evolution of the segmentation error rate and the objective function value with respect to time on Yaleb10

Table 2 Mean and standard deviation of the objective function value over 30 random initializations on the synthetic data sets

Table 3 Mean and standard deviation of the objective function value over 20 random initializations on the image data sets

Fig. 5

Evolution of the average value of the objective function value of Problem (64) with respect to time on synthetic data sets with $(n,m,r)= (500,200,20)$ (left) and $(n,m,r)= (500,500,20)$ (right)

Fig. 6

Evolution of the average value of the objective function value of Problem (64) with respect to time on the image data sets CBCL (top left), ORL (top right), Frey (bottom left) and Umist (bottom right)