1 Introduction

Over the past decade, there has been a considerable surge in the popularity and usage of evolutionary algorithms (EAs). These algorithms have proven to be effective in solving a wide range of real-world optimization problems in engineering and scientific research fields. Among the notable meta-heuristic approaches, the genetic algorithm (GA) stands out as the pioneering stochastic algorithm initially introduced by John Holland in 1960 (Holland 1975). Another important algorithm is simulated annealing (SA), which was proposed by Kirkpatrick et al. (1983). In 1995, Kennedy and Eberhart introduced the particle swarm optimization (PSO) algorithm (Kennedy and Eberhart 1995). Additionally, numerous other approaches have been developed subsequently, such as ant bee colony (ABC) (Karaboga and Basturk 2007), Chernobyl disaster optimizer (CDO) (Shehadeh 2023), biology migration algorithm (BMA) (Zhang et al. 2019), RIME algorithm (RIME) (Su et al. 2023), spider wasp optimization (SWO) (Abdel-Basset et al. 2023), Siberian tiger optimization (STO) (Trojovský et al. 2022), predator–prey optimization (PPO) (Mohammad Hasani Zade and Mansouri 2022), Kepler optimization algorithm (KOA) (Abdel-Basset et al. 2023), leader-advocate-believer-based optimization (LAB) (Reddy et al. 2023), past present future (PPF) (Naik and Satapathy 2021), artificial neural networks (ANNs) (D’Angelo et al. 2022), genetic programming (GP) (D’Angelo et al. 2023), and so on. Although these intelligent algorithms offer benefits, they require enhancements to accommodate the diverse characteristics of complex real-world applications. This implies that no single approach is capable of adequately solving the wide range of optimization problems. Real-world issues often exhibit various challenging features, such as uncertainty, dynamicity, combinatorial complexity, multiple objectives, and constraints. In line with this, the no-free lunch (NFL) theorem (Wolpert and Macready 1997) confirms that no optimization approach can effectively address all types of problems. Alongside the development of novel algorithms, certain researchers have explored general improvement strategies to enhance the performance of meta-heuristic algorithms. Examples of these general improvement strategies include Lévy flight (Viswanathan et al. 1996), quantum behavior (Feynman 1986), chaotic behavior (Kaplan 1979), opposition-based learning (Tizhoosh 2005), Gaussian mutation (Liu 2012), and so on. Driven by the researchers’ statements and the principles of the no-free-lunch theorem, in this paper, the quantum behavior was adopted in order to enhance the performance of the marine predators algorithm. This novel modification enhances the marine predators algorithm to effectively explore and exploit the search space and empowers the capability to balance between exploration and exploitation. Many optimization approaches typically encountered are single-objective in nature and do not adequately address the diverse features of complex real-world applications, specifically the ability to optimize many objectives simultaneously (Andersson 2000; Coello et al. 2002). This includes the challenge of optimizing multiple objectives simultaneously, which is the second principle focus of this paper. In fact, multi-objective evolutionary algorithms (MOEAs) have gained significant attention from researchers in engineering fields. These algorithms have been continually developed and improved. However, solving multi-objective optimization problems (MOPs) remains a difficult and challenging task. Among the influenced multi-objective algorithms: multi-objective particle swarm optimization (MOPSO) (Coello et al. 2004), multi-objective evolutionary algorithm based on decomposition (MOEA/D) (Zhang and Li 2007), non-dominated sorting genetic algorithm (NSGA) (Srinivas and Deb 1994), and strength Pareto evolutionary algorithm (SPEA) (Zitzler and Thiele 1999).

The classification of MOEAs can be divided into three different classes: a priori (Kim and de Weck 2005), posterior (Branke et al. 2001), and interactive (Shin and Ravindran 1991). The priori technique combines the objectives into a single one using a set of weights by aggregation and requires a decision-maker that furnishes some preferences according to how important the objectives are. For a posteriori technique, the Pareto optimal set is determined in just one run antithesis the priori method that should be run multiple times. Besides, this method benefits from maintaining the multi-objective formulation, finding out all kinds of Pareto front, and the decision-maker is required after the optimization process. In the third class, the interactive technique maintains the multi-objective formulation and considers the decision maker during the optimization procedure, thus, this method necessitates a higher execution time and computational cost to obtain accurate Pareto optimal solutions. Along these lines, this work focuses on the algorithms-based posteriori method, and most existing multi-objective evolutionary algorithms follow this technique. Many researchers have been recently reported various multi-objective approaches, for instance: multi-objective slime mould algorithm (MOSMA) (Premkumar et al. 2021), non-sorted harris hawks optimizer (NSHHO) (Jangir et al. 2021), multi-objective bonobo optimizer-based decomposition (MOBO) (Das et al. 2020), multi-objective forensic-based investigation (MOFBI) (Chou and Truong 2022), multi-objective thermal exchange optimization (MOTEO) (Kumar et al. 2022), multi-objective ant lion optimizer (MOALO) (Mirjalili et al. 2017), non-dominated sorting manta ray foraging optimization (NSMRFO) (Daqaq et al. 2022), multi-objective multi-verse optimization (MOMVO) (Mirjalili et al. 2017), multi-objective adaptive guided differential evolution (MOAGDE) (Duman et al. 2021), multi-objective backtracking search algorithm (MOBSA) (Daqaq et al. 2021), and so on. However, the main contribution of this paper could be summarized as:

  • Introduction of MOIMPA: a multi-objective variant of the marine predators algorithm (MPA) that incorporates concepts from Quantum theory is presented.

  • Enhancing exploration and exploitation: MOIMPA aims to improve the MPA’s ability to balance between exploration and exploitation by using a modified Schrödinger wave function to determine particle positions in the search space.

  • Incorporation of Pareto dominance mechanism: MOIMPA includes a repository to store non-dominated Pareto optimal solutions and utilizes a roulette wheel strategy for solutions selected based on coverage.

  • Evaluation of benchmark functions: MOIMPA is tested on benchmark functions such as ZDT and DTLZ, as well as the CEC’09 test suite, to assess its effectiveness and efficiency.

  • Comparison with other optimization methods: A comparison is made between MOIMPA and other evolutionary optimization methods like MOMPA, MOALO, and MOMVO.

  • Statistical results: Statistical metrics such as inverted generational distance (IGD), generalized distance (GD), spacing, and delta are used to demonstrate the robustness of MOIMPA.

  • Accurate approximations of Pareto front: Qualitative experimental results confirm that MOIMPA provides highly accurate approximations of the true Pareto front.

The study is structured as follows: Sect. 2 reviews previous research conducted by other researchers on the marine predators approach. Section 3 presents the mathematical formulations and definitions related to multi-objective optimization, along with the basic MPA approach and the proposed MO version, MOIMPA. Section 4 presents the findings, analysis, and discussions. Lastly, Sect. 5 concludes the paper and outlines potential avenues for future research.

2 Related works

As aforementioned, a new multi-objective version of the marine predators approach (MPA) is suggested in this work to address multi-objective problems. MPA was primarily initiated by Faramarzi et al. (2020), and existing literature demonstrates that MPA has successfully tackled various problems and outperformed several established approaches. Hence, researchers have followed the No Free Lunch theorem (NFL) and improved MPA based on the complexity and nature of their specific problems, and several studies have investigated the effectiveness of their improved approach. Among the research studies that investigate its effectiveness: Aydemir and Onay improved MPA by integrating and combining the elite natural evolution, elite random mutation, and Gaussian mutation strategies Aydemir and Kutlu Onay (2023). In Ferahtia et al. (2022) utilized the MPA approach to minimize the operating costs of the energy management strategy for the microgrid. In another work (Dinh 2022), the standard MPA was applied for medical image fusion and a better MPA performance is proven. According to Al-qaness et al. (2022) the MPAmu as a new variant of MPA was introduced using additional mutation operators for the purpose of improving its premature convergence, this algorithm was used to introduce an effective prediction tool to estimate wind power employing time-series datasets. A hybrid MPA was invented by Abdel-Basset et al. (2022), the authors suggest a novel image segmentation algorithm according to the HMPA, in which the approach was enhanced using the linearly increased worst solutions improvement strategy (LIS). Further, to find out the optimum multilevel threshold image segmentation, the authors in Abualigah et al. (2022) hybridized the marine predators and salp swarm algorithms in view of improving the standard MPA. In an effort to resolve the optimal reactive power dispatch issue integrating the uncertainties of solar and wind energy, an improved MPA is suggested in Habib Khan et al. (2022), the IMPA is based on enhancing the exploitation stage. Moreover, (Sun and Gao 2021) presented three concepts that were introduced to enhance the performance of MPA. The first concept was to construct the initial population utilizing the cubic mapping in order to enhance the diversity, the second was to adapt the estimation distribution algorithm for modifying the evolutionary direction and improving the convergence performance, whereas the last was to avoid stagnation in local optima applying the Gaussian random walk strategy. The experiments resulted in Abd Elaziz et al. (2022) indicating that the sine-cosine algorithm improved the MPA in terms of the search ability which works as a local search of the MPA. In another study (Houssein et al. 2021), a grey wolf optimizer with an opposition-based learning strategy was integrated into MPA with the aim of obtaining a faster convergence rate and avoiding being trapped in local solutions. Furthermore, a new MPA-based multi-group mechanism was proposed to optimize the economic load dispatch problem (Pan et al. 2022).

However, few scholars investigate its performance on multi-objective problems. On this basis, multi-objective MPA (MOMPA) based on crowding distance and elitist non-dominated sorting mechanisms was presented by Jangir et al. in (2023), this approach was run on some constrained, unconstrained benchmark problems and engineering design applications. (Wang et al. 2023) introduced the concept of quantity into the deep learning model to examine a wind speed integrated probability predictive approach, utilizing a multi-objective marine predators algorithm. Additionally, according to (Hassan et al. 2022), a modified version of MPA including a comprehensive learning approach was investigated to handle the multiobjective combined economic emission dispatch (CEED) optimization problem. Finally, according to the recent study (Yousri et al. 2022), another enhanced MPA named MOEMPA was suggested to manage the sharing energy in an interconnected micro-grid with a utility network in India by optimizing the emission and operating cost. Along these lines, the significant powerful features of MPA and its borrowed evolutionary algorithms mentioned above, motivated us to improve a novel multi-objective variant of marine predators algorithm in this study, named multi-objective improved marine predators algorithm (MOIMPA). The outstanding search mechanism in MPA is kept similar to the MOIMPA approach.

3 Background

This section presents a comprehensive introduction to optimization (MO) and its essential mathematical definitions, which is a foundational problem-solving technique utilized to discover the optimal solutions from a range of alternatives. In the context of multi-objective optimization, the primary aim is to concurrently optimize multiple objectives that often conflict with one another, a common occurrence in real-world decision-making situations. To gain a deeper understanding of the concepts and methods employed in this field, it is crucial to explore the marine predators approach and its multi-objective counterpart. Inspired by the efficient foraging strategies of marine predators like sharks and dolphins, the marine predators approach adopts a population-based search algorithm that emulates the movement and behavior of these creatures to solve optimization problems. By modeling the search process based on the natural behavior of marine predators, this approach seeks to enhance the efficiency and effectiveness of the optimization process. Additionally, this study also incorporates the multi-objective variant of the marine predators approach. Multi-objective optimization expands upon the traditional optimization framework by incorporating multiple conflicting objectives. The goal of the multi-objective variant is to explore and identify a set of solutions that represent trade-offs between these objectives, rather than finding a single optimal solution. This approach empowers decision-makers to gain insights into the trade-offs involved and make well-informed decisions based on the available options. First, we’ll outline key mathematical definitions in the field of optimization (MO) before discussing and reviewing the marine predators approach and its multi-objective variant.

3.1 Multi-objective optimization

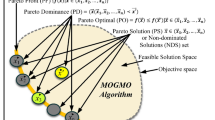
As its name signifies, multi-objective optimization is the subject of addressing various conflicting objectives concurrently. Thus, the arithmetic relational operators are not efficacious in comparing different solutions. Therefore, the Pareto optimal dominance concept is utilized to determine which solution is better than another.

The MOPs mathematical formulation as a minimization problem is given as follows:

$$\begin{aligned} \text{ Optimize: } \quad&O(\vec {x})=\left\{ o_{1}(\vec {x}), o_{2}(\vec {x}), \ldots , o_{N_\textrm{obj}}(\vec {x})\right\} \nonumber \\ \text{ Subject } \text{ to: } \quad&g_{j}(\vec {x}) \ge 0, \quad \quad j=1,2, \ldots , m \nonumber \\&h_{j}(\vec {x})=0, \quad \quad j=1,2, \ldots , p \nonumber \\&X^\textrm{min}_{j} \le x_{j} \le X^\textrm{max}_{j}, \quad j=1,2, \ldots , n \end{aligned}$$
(1)

where \(O(\vec {x})\) is the objective function to be minimized. \(h_{j}(\vec {x})\) and \(g_{j}(\vec {x})\) are the equality and inequality constraints. \(N_\textrm{obj}\), n, m, and p are the numbers of objective functions, variables, inequality, and equality constraints. \(X^\textrm{min}_{j}\) and \(X^\textrm{max}_{j}\) are the boundaries of the jth variable.

The essential relationships that are able to take into account all objectives concurrently are defined as follows (Pareto 1964; Coello Coello 2009):

Let us take two vectors \(\vec {x}=\left( x_{1}, x_{2}, \ldots , x_{n}\right) \) and \(\vec {y}=\left( y_{1}, y_{2}, \ldots , y_{n}\right) \)

Definition 1

(Pareto dominance) \(\vec {x}\) is said to dominate \(\vec {y}\) if and only if \(\vec {x}\) is partially less than \(\vec {y}\) (i.e., \(\vec {x} \le \vec {y}\)):

$$\begin{aligned}{} & {} \forall i \in \{1,2, \ldots , N_\textrm{obj}\}: f_{i}(\vec {x}) \le f_{i}(\vec {y}) \wedge \exists i\nonumber \\{} & {} \in \{1,2, \ldots , N_\textrm{obj}\}\nonumber \\{} & {} \qquad : f_{i}(\vec {x})<f_{i}(\vec {y}) \end{aligned}$$
(2)

Definition 2

(Pareto optimality) \(\vec {x} \in X\) is called a Pareto optimal solution iff:

$$\begin{aligned} \not \exists \vec {y} \in X \mid F(\vec {y}) < F(\vec {x}) \end{aligned}$$
(3)

Definition 3

(Pareto optimal set) The Pareto optimal set is a set that comprises all Pareto optimal solutions (neither \(\vec {x}\) dominates \(\vec {y}\) nor \(\vec {y}\) dominates \(\vec {x}\)):

$$\begin{aligned} P_{s}:=\{x, y \in X \mid \exists F(\vec {y}) > F(\vec {x})\} \end{aligned}$$
(4)

Definition 4

(Pareto optimal front) The Pareto optimal front is defined as:

$$\begin{aligned} P_{f}:=\left\{ F(\vec {x}) \mid \vec {x} \in P_{s}\right\} \end{aligned}$$
(5)

The optimal non-dominated outputs set, which represents the set of solutions for each multi-objective optimization problem, plays a significant role in evaluating and comparing different solution options. Figure 1 provides a visual representation of this concept, illustrating the relationship between the objective space and the corresponding Pareto optimal front. As depicted in Fig. 1, the red shapes represent the solutions in the objective space, while their projection onto the objective space is known as the Pareto optimal front. The Pareto optimal front consists of solutions that are not dominated by any other solution in terms of all the objectives under consideration. In other words, these solutions represent the best possible trade-offs between conflicting objectives, where improving one objective would result in a deterioration of at least one other objective. By examining the solutions depicted in both spaces, it becomes evident that the star shape in Fig. 1 dominates all the other shapes. Domination refers to a solution being superior to another solution in terms of at least one objective, without being worse in any other objective. In this case, the star shape outperforms all other shapes across all objectives, making it the most desirable solution within the given optimization problem. The visualization provided by Fig. 1 highlights the importance of identifying the Pareto optimal front and understanding the dominant relationship between solutions. This knowledge enables decision-makers to make informed choices by considering the trade-offs associated with different solutions and selecting the most appropriate one based on their preferences and constraints.

Fig. 1
figure 1

Search and objective spaces

Full size image

3.2 Marine predators algorithm

The principle phases of the MPA approach are introduced in the following subsection.

3.2.1 Description of MPA

MPA is a population-based approach, inspired by the widespread foraging in ocean predators, and the optimal encounter rate in biological interaction between predator and prey, by Faramarzi et al. (2020). Like other meta-heuristics, in which the initial solution \(X_{0}\) is uniformly distributed throughout the search area as:

$$\begin{aligned} X_{0}=X_{\min }+{\text {rand}}\left( X_{\max }-X_{\min }\right) \end{aligned}$$
(6)

where \(X_\textrm{min}\) is the lower bound, \(X_\textrm{max}\) is the upper bound for variables, and rand is a uniform random vector in the range of 0–1.

According to the survival of the fittest theory, top predators in nature are better at hunting. As a result, the fittest solution is designated as a top predator to form a matrix known as the Elite. This matrix arrays looking for and locating prey depending on information about the prey’s location.

$$\begin{aligned} \textrm{Elite}=\left[ \begin{array}{lll} X_{1,1}^{t} &{}\quad \cdots &{}\quad X_{1,d}^{t} \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ X_{n,1}^{t} &{}\quad \cdots &{}\quad X_{n,d}^{t} \end{array}\right] \end{aligned}$$
(7)

where \(\overrightarrow{X^t}\) denotes the top predator vector, which is copied n times to create the Elite matrix. n denotes the number of search agents, whereas d denotes the number of dimensions. Prey is another matrix with the same dimension as Elite, and it is used by predators to update their locations.

$$\begin{aligned} \textrm{Prey}=\left[ \begin{array}{lll} X_{1,1} &{}\quad \cdots &{}\quad X_{1,d} \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ X_{n,1} &{}\quad \cdots &{}\quad X_{n,d} \end{array}\right] \end{aligned}$$
(8)

The MPA optimization method is separated into three primary phases, each of which takes into account a particular velocity ratio while simulating the whole life of a predator and prey as follows:

3.2.2 High velocity ratio

This situation occurs when the prey moves faster than the predator, or during the early stages of optimization, when exploration is important. In a high-velocity ratio (v 10) situation, the optimum predator tactic is to stay still. This rule’s mathematical model is as follows:

$$\begin{aligned}{} & {} \textrm{iter}<\frac{1}{3} \textrm{iter}_{\max } \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \overrightarrow{\textrm{step}_{i}}=\overrightarrow{R_{B}} \otimes \left( \overrightarrow{\textrm{Elite}_{i}}-\overrightarrow{R_{B}} \otimes \overrightarrow{\textrm{Prey}_{i}}\right) \quad i=1, \ldots , n \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \overrightarrow{\textrm{Prey} _{i}}=\overrightarrow{\textrm{Prey}_{i}}+P \cdot \overrightarrow{R} \otimes \overrightarrow{step_{i}} \end{aligned}$$
(11)

where \(R_B\) is a vector of random integers from the Normal distribution that reflect Brownian motion. The notation \(\otimes \) depicts entry-by-entry multiplications. Prey movement is simulated by multiplying \(R_B\) by Prey. \(P = 0.5\) is a constant, and R is a vector of uniform random values in the range [0,1]. This situation occurs during the first third of iterations when the step size or velocity of movement is large, indicating a high level of exploratory ability. iter is the current iteration while \(iter_\textrm{max}\) is the maximum one.

3.2.3 Unit velocity ratio

When both the predator and the prey are running at about the same speed, it suggests that both are seeking their prey. This portion happens during the intermediate phase of optimization when exploration attempts to be transiently transformed into exploitation. Exploration and exploitation are important at this stage. As a result, half of the population is earmarked for exploration and the other half for exploitation. During this stage, the prey is in charge of exploitation while the predator is in charge of exploration. As a result, if prey travels in Lévy, the best predator tactic is Brownian.

$$\begin{aligned} \frac{1}{3} \textrm{iter}_{max}< \textrm{iter} < \frac{2}{3} \textrm{iter}_\textrm{max} \end{aligned}$$
(12)

For the first half of the population

$$\begin{aligned}{} & {} \overrightarrow{\textrm{step}_{i}}=\overrightarrow{R_{L}} \otimes \left( \overrightarrow{\textrm{Elite}_{i}}-\overrightarrow{R_{L}} \otimes \overrightarrow{\textrm{Prey}_{i}}\right) \quad i=1, \ldots , n / 2\nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \overrightarrow{\textrm{Prey}_{i}}=\overrightarrow{\textrm{Prey}_{i}}+ P \cdot \vec {R} \otimes \overrightarrow{\textrm{step}_{i}}\nonumber \\ \end{aligned}$$
(14)

The second half of the population

$$\begin{aligned}{} & {} \overrightarrow{\textrm{step}_{i}}=\overrightarrow{R_{B}} \otimes \left( \overrightarrow{R_{B}} \otimes \overrightarrow{\textrm{Elite}_{i}} - \overrightarrow{\textrm{Prey}_{i}}\right) ~~~~~~i=n / 2, \ldots , n \nonumber \\ \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \overrightarrow{{\textrm{Prey}}_{i}}=\overrightarrow{\textrm{Elite}_{i}}+P \cdot CF \otimes \overrightarrow{{\textrm{step}}_{\imath }} \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \textrm{CF}=\left( 1-\frac{\textrm{iter}}{\textrm{iter}_{\max }}\right) ^{\left( 2 \frac{\textrm{iter}}{\textrm{iter}_{\max }}\right) }\nonumber \\ \end{aligned}$$
(17)

where CF is an adjustable parameter that is used to track the step size.

3.2.4 Low velocity ratio

During this particular phase, a low-velocity ratio occurs when the predator’s speed surpasses that of the prey. This situation occurs near the end of the optimization process, which is typically associated with high exploitation capability. Lévy is the best predator approach for low-velocity ratios \((v = 0.1)\). This stage is depicted as:

$$\begin{aligned}{} & {} \textrm{iter} >\frac{2}{3} \textrm{iter}_\textrm{max} \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \overrightarrow{\textrm{step}_{i}}=\overrightarrow{R_{L}} \otimes \left( \overrightarrow{R_{L}} \otimes \overrightarrow{\textrm{Elite}_{i}} - \overrightarrow{\textrm{Prey}_{i}}\right) \quad i=1, \ldots , n \nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \overrightarrow{Prey_{i}}=\overrightarrow{\textrm{Elite}_{i}} + P \cdot \textrm{CF} \otimes \overrightarrow{\textrm{step}_{\imath }} \end{aligned}$$
(20)

In the Lévy method, multiplying \(R_L\) and Elite mimics predator movement, whereas adding the step size to Elite position simulates predator movement to aid in the updating of prey location.

Fig. 2
figure 2

The flowchart of the original Marine Predators Algorithm (MPA)

Full size image

The additional feature of MPA is that it simulates predator behavior, increasing the chances of escape from local optima. This advantage stems from the fact that factors such as eddy formation and fish aggregating devices (FADs) can influence predator behavior. As a consequence, the predators would jump into other locations with abundant prey \(20\%\) of the time, while searching for their prey in the local area the rest of the time. FADs can be made in the following way:

$$\begin{aligned}{} & {} \overrightarrow{\textrm{Prey}_{i}}=\nonumber \\{} & {} \left\{ \begin{array}{cl} \overrightarrow{\textrm{Prey}_{i}}+ CF\left[ \overrightarrow{X_{\min }}+\overrightarrow{R} \otimes \left( \overrightarrow{X_{\max }}-\overrightarrow{X_{\min }}\right) \right] \otimes \vec {U}, &{} r \le \textrm{FADs} \\ \overrightarrow{\textrm{Prey}_{l}}+[(1-r) \textrm{FADs} +r]\left( \overrightarrow{\textrm{Prey}_{r_1}}-\overrightarrow{\textrm{Prey}_{r_2}}\right) , &{} r > \textrm{FADs} \end{array}\right. \end{aligned}$$
(21)

where FADs = 0.2 denotes the probability of FADs influencing the optimization process. U is a binary vector containing arrays of zero and one and built by creating a random vector in the range [0, 1] and setting its array to zero if it is less than 0.2 and one if it is larger than 0.2. r is the uniform random number in the range [0,1]. The subscripts \(r_{1}\) and \(r_{2}\) are random prey matrix indexes.

Fig. 3
figure 3

The flowchart of the proposed Improved Marine Predators Algorithm (IMPA)

Full size image

The main steps followed in MPA are demonstrated in Fig. 2. This flow chart depicted in Fig. 2 illustrates the step-by-step process of the MPA algorithm employed in this study. The algorithm presents a clear and structured approach to solving the optimization problem at hand. The flow chart provides a visual representation of the algorithm’s structure and the sequence of operations involved. It serves as a valuable tool for understanding the algorithm’s inner workings and aids in analyzing its efficiency and effectiveness in solving complex optimization problems.

4 The proposed algorithm

In this subsection, quantum mechanics is used to develop the original MPA technique. This quantum model of the MPA technique is named the IMPA algorithm. Quantum algorithm (QA) was first proposed in Benioff (1980). It was declared that QA could solve many difficulties based on the concepts and principles of quantum theory, including the superposition of quantum states, entanglement, and intervention. Quantum-Inspired Evolutionary Algorithm (QEA) is one of the developing algorithms which was inspired by the concept of quantum computing (Han and Kim 2002). This algorithm was successfully applied to solve several combinational optimization problems. The good performance of the QEA algorithm for finding a global best solution in a short time has attracted the attention of researchers to use quantum computing to develop algorithms such as quantum genetic algorithm (QGA) (Vlachogiannis and Østergaard 2009), multiscale quantum harmonic oscillator algorithm (MQHOA) (Wang et al. 2018), quantum Runge Kutta algorithm (QRUN) (Abd El-Sattar et al. 2022), quantum salp swarm algorithm (QSSA) (Niazy et al. 2020), quantum chaos game optimizer (QCGO) (Elkasem et al. 2022), Quantum marine predators algorithm (QMPA) (Abd Elaziz et al. 2021), and Quantum Henry gas solubility optimization algorithm (QHGSO) (Mohammadi et al. 2021). Quantum mechanics were employed to improve the PSO algorithm in dos Santos Coelho (2008). In the quantum model, by employing the Monte Carlo method, the solution \(\textrm{Prey }_{i}\) is calculated as follows:

$$\begin{aligned}{} & {} {p}=\frac{c_1\times w\times \overrightarrow{ \text{ Prey } _{l}}+c_2\times (1-w)\times x_{\textrm{best}}}{\mathrm {c_1+c_2}} \end{aligned}$$
(22)
$$\begin{aligned}{} & {} \overrightarrow{\textrm{Prey}_{i}}=\left\{ \begin{array}{cl}{p}+\alpha \times |M_{\textrm{best}_i}-\overrightarrow{\textrm{Prey}_{i}}|\times \ln {\left( \frac{1}{\textrm{u}}\right) }, &{}\textrm{if}\,\,\, h\ge 0.5\\ {p}-\alpha \times |M_{\textrm{best}_i}-\overrightarrow{\textrm{Prey}_{i}}|\times \ln {\left( \frac{1}{\textrm{u}}\right) }, &{}\textrm{if}\,\,\, h< 0.5 \end{array}\right. \nonumber \\ \end{aligned}$$
(23)

Where \(x_\textrm{best}\) denotes the best solution, \(\alpha \) is a design parameter, u and w represent uniform probability distribution in the range [0,1], h is the random value ranging from 0 to 1. Mbest is the mean best of the population and it is defined as the mean of the \(x_\textrm{best}\) positions and it is calculated as follows:

$$\begin{aligned} {M_\textrm{best}}=\frac{1}{\textrm{N}}\sum _{i=1}^N x_\textrm{best} \end{aligned}$$
(24)

The flow chart of the proposed IMPA technique is shown in Fig. 3, which showcases the flow chart depicting the revised steps and procedures implemented to enhance the optimization process. This modified approach aims to overcome the limitations or shortcomings of the original algorithm, offering improved performance, convergence, and solution quality. The flow chart serves as a valuable reference to analyze and evaluate the efficacy of the modified algorithm in solving multi-objective optimization problems.

Table 1 Descriptions of the considered benchmark functions
Full size table
Table 2 Parameter of the tested approaches
Full size table

4.1 Description of the proposed algorithm MOIMPA

Based on the mathematical emulation explained above, the swarm behaviors of preys can be simulated clearly. When dealing with multi-objective problems, two issues need to be adjusted for the IMPA algorithm. First, the MOIMPA needs to store multiple solutions as the optimal solutions for a multi-objective problem. Second, in each iteration, IMPA updates the preys source with the best solution, but in the multi-objective problem, single best solutions do not exist. In MOIMPA, the first issue is settled by equipping the IMPA technique with a repository of preys sources. The repository can store a limited number of non-dominated solutions. In the process of optimization, each prey is compared with all the residents in the repository using the Pareto dominance operators. If a prey dominates only one solution in the repository, it will be swapped. If a prey dominates a set of solutions in the repository, they all should be removed from the repository and the prey should be added to the repository. If at least one of the repository residents dominates prey in the new population, it should be discarded straight away. If the prey is non-dominated in comparison with all repository residents, it has to be added to the archive. If the repository becomes full, we need to remove one of the similar non-dominated solutions in the repository. For the second issue, an appropriate way is to select it from a set of non-dominated solutions with the least crowded neighborhood. This can be done using the same ranking process and roulette wheel selection employed in the repository maintenance operator. The pseudo-code of the MOIMPA algorithm is shown in Algorithm 1: The included Algorithm 1 provides a step-by-step framework for the MOIMPA algorithm. Step 1: In this step, the prey positions are updated based on Equ (11). This equation defines the update rule for the prey in the first phase of the algorithm, which occurs during the initial one-third of the maximum iterations.

Step 2 and Step 3: During the second phase of the algorithm (between one-third and two-thirds of the maximum iterations), the prey positions are updated differently for the first half and the other half of the population. Step 2 involves updating the positions of the prey in the first half of the population using Equation (14). Similarly, Step 3 updates the positions of the prey in the other half of the population using Equ (16).

Step 4: In the final phase of the algorithm (when the iteration count exceeds two-thirds of the maximum iterations), the prey positions are updated using Equ (20). This equation defines the update rule for the prey during this phase.

Step 5: Applying the effect of eddy formation and fish aggregation devices (FADs) on the prey positions is done in this step. The positions of the prey are adjusted according to Equ (21), which incorporates the influence of FADs.

Step 6: The prey positions are updated further using Equ (23). This equation specifies the position update rule for the prey, enhancing their exploration and exploitation capabilities.

Step 7: The fitness of the new solution is calculated in this step. The fitness represents the quality or objective value associated with the current solution.

Step 8: Finally, the non-dominated solutions obtained are updated in the archive, ensuring the preservation of the best solutions throughout the iterations.

These step-by-step explanations provide a clear understanding of the work performed and the variables involved at each stage of the MOIMPA algorithm presented in Algorithm 1.

figure a

4.2 Performance metrics

With a view to affirm the effectiveness of such a multiobjective algorithm, three main principles must be proved: convergence, distribution, and coverage. On this basis, to compare the MOIMPA reliability and efficiency with other competitive algorithms, four performance indicators were considered such as generation distance (GD) (Van Veldhuizen and Lamont 1998), inverse generation distance (IGD) (Sierra and Coello 2005), spacing (SP) (Schott 1995), and the delta metrics. The IGD and GD indicators are employed to evaluate the approximations to the Pareto front in relation to diversity and convergence. The spacing indicator evaluates the space between the non-dominated solutions (coverage). It is worth noting that the smaller the metric output, the higher the quality of obtained solutions. The mathematical formulations of these metrics are described as follows:

$$\begin{aligned} \textrm{GD}=\frac{\sqrt{\sum _{{i}=1}^{{n_\textrm{pf}}} {d}_{{i}}^{2}}}{{n_\textrm{pf}}} \end{aligned}$$
(25)

where \(d_{i}\) is the Euclidean distance between the \(i^{th}\) Pareto optimal solution attained and the true Pareto optimal solution in the reference set. \(n_\textrm{pf}\) indicates the obtained Pareto optimal solutions number.

$$\begin{aligned} \textrm{IGD}=\frac{\sqrt{\sum _{i=1}^{n_\textrm{tpf}}\left( d_{i}^{\prime }\right) ^{2}}}{n_\textrm{tpf}} \end{aligned}$$
(26)

where \(d_{i}^{\prime }\) is the Euclidean distance between the \(i^\textrm{th}\) true Pareto optimal solution and the Pareto optimal solution obtained in the reference set. \(n_\textrm{tpf}\) indicates the number of true Pareto optimal solutions.

$$\begin{aligned} \textrm{SP}=\sqrt{\frac{1}{n_\textrm{pf}-1} \sum _{i=1}^{n_\textrm{pf}}\left( {\bar{d}}-d_{i}\right) ^{2}} \end{aligned}$$
(27)

where \({\bar{d}}\) is the average of all \(d_{i}\).

5 Experimental results and analysis

To validate the efficiency of the suggested algorithm MOIMPA, a set of test functions with diverse characteristics (various forms of Pareto front) were investigated notably five bi-objective ZDT Zitzler et al. (2000), six three-objective DTLZ (Deb et al. 2002) functions, and the CEC’09 (Zhang et al. 2008) multi-objective problem that contains ten UF functions with bi- and three-objective functions, in addition to the weld beam issue, which is listed in Table 1. Thus, four popular indicator metrics were considered namely: generation distance (GD), spacing (SP), inverse generation distance (IGD), spacing (SP), and the delta metrics as presented in the "Performance Metrics" section. On the other hand, three significant multi-objective optimization algorithms were re-implemented for comparison with a view to affirming the effectiveness of the MOIMPA approach called multiobjective marine predator algorithm (MOMPA) (Jangir et al. 2023), multiobjective ant lion optimization (MOALO) (Mirjalili et al. 2017), and multiobjective multi-verse optimization (MOMVO) (Mirjalili et al. 2017), their control parameters are listed in Table 2. However, these selected parameters are the best in most of the cases in their original papers and are kept as suggested. Thus, for ensuring fair comparison, all multi-objective approaches were executed 20 times and the maximum number of iterations is 300. The detailed settings of the system utilized in this article are presented in Table 3. The outcomes are illustrated qualitatively and quantitatively.

Table 3 The detailed settings of the utilized system
Full size table
Table 4 Performance metrics comparison based on ZDT test suites
Full size table
Table 5 Performance metrics comparison based on UF test suites
Full size table
Table 6 Performance metrics comparison based on DTLZ test suites
Full size table
Table 7 Performance metrics comparison based on weld beam problem
Full size table

The experimental findings based on the average and standard deviation of the 20 runs are listed in Tables 4, 5, 6 and 7. It is worth noting here that the better approach is the one with the lower metric value, and the optimized solutions were highlighted in boldface. Further, the best Pareto optimal fronts attained were depicted in Figs. 4, 5, 6 and 7. On all twenty benchmark test suites under consideration, the MOIMPA reaches statistically significant values in most case studies. Hence, this proposed approach outstrip all five ZDT test problem, in which, four functions on IGD, three on GD, three on SP, and four on delta out of five functions in total. Besides, the MOIMPA also ranks first in the DTLZ problem on four functions out of five on each IGD, GD, SP, and delta metrics. According to the MOMVO algorithm, it outperforms the MOIMPA on UF benchmark test suites in all indicator metrics except the Spacing one, but it does not show any accuracy in terms of std performance compared to MOIMPA. However, the MOALO and the MOMPA obtained the lowest performance. Additionally, it can be seen from Figs. 4, 5, 6 and 7 that the MOIMPA yields better coverage, convergence, and well spread through the true Pareto front for all case studies. The MOMPA approach also provides a good Pareto front on ZDT except for the ZDT6 function. By contrast, the MOMVO and MOALO competitor approaches show the worst Pareto front. To sum up, the suggested optimizer MOIMPA managed to significantly outperform the competitors even on its multi-objective variant MOMPA, which means that the MOIMPA diversity and convergence are improved. The lowest values of all metrics were obtained by MOIMPA optimizer in almost case studies, it outstrips on 11 cases for IGD, 10 for GD, 13 for SP, and 11 for delta metrics out of 20. These comparison results reveal that both the convergence and coverage of the achieved outcomes by MOIMPA toward the true PF are higher than those obtained by its competing approaches and that the MOIMPA has significant stability.

Fig. 4
figure 4

Comparison of obtained Pareto fronts on ZDT functions

Full size image
Fig. 5
figure 5figure 5

Comparison of obtained Pareto fronts on UF functions

Full size image
Fig. 6
figure 6

Comparison of obtained Pareto fronts on DTLZ functions

Full size image
Fig. 7
figure 7

Comparison of obtained Pareto fronts on weld beam function

Full size image

6 Conclusion

This study has presented a modified version of the marine predators approach (MPA) that incorporates quantum optimization techniques and a multi-objective strategy. While the basic MPA is effective in solving various global and engineering problems, it has certain limitations that affect its optimization process and compromises the balance between exploitation and exploration phases, as well as the convergence towards the global solution. To overcome these limitations, quantum mechanics has been integrated into the MPA. The performance of the NSMRFO approach has been evaluated using various test functions, including ZDT, DTLZ, CEC’09 (Completions on Evolutionary Computation 2009), and several engineering problems, providing a comprehensive assessment from different perspectives. The proposed approach has undergone quantitative evaluation using four performance indicators: inverted generational distance (IGD), spacing metric (SP), generational distance (GD), and delta metric. The evaluation was conducted over 20 runs. Comparative analysis was carried out by comparing the results of the MOIMPA optimizer with other algorithms such as MOMPA, MOALO, and MOMVO. Additionally, various engineering design problems were examined to assess the efficiency of MOIMPA. The results demonstrate that the developed optimizer is more efficient based on the outcomes of the evaluation. In our future work, we plan to extend the application of the proposed algorithm to solve more multi-objective engineering problems. This includes optimizing power flow and economic emission dispatch while considering renewable energy resources. By testing the algorithm on these real-world engineering problems, we aim to validate its effectiveness and practicality in solving complex optimization challenges.