Abstract
The multi-tier Covariance Matrix Adaptation Pareto Archived Evolution Strategy (m-CMA-PAES) is an evolutionary multi-objective optimisation (EMO) algorithm for real-valued optimisation problems. It combines a non-elitist adaptive grid based selection scheme with the efficient strategy parameter adaptation of the elitist Covariance Matrix Adaptation Evolution Strategy (CMA-ES). In the original CMA-PAES, a solution is selected as a parent for the next population using an elitist adaptive grid archiving (AGA) scheme derived from the Pareto Archived Evolution Strategy (PAES). In contrast, a multi-tiered AGA scheme to populate the archive using an adaptive grid for each level of non-dominated solutions in the considered candidate population is proposed. The new selection scheme improves the performance of the CMA-PAES as shown using benchmark functions from the ZDT, CEC09, and DTLZ test suite in a comparison against the \((\mu + \lambda )\) Multi-Objective Covariance Matrix Adaptation Evolution Strategy (MO-CMA-ES). In comparison with MO-CMA-ES, the experimental results show that the proposed algorithm offers up to a 69 % performance increase according to the Inverse Generational Distance (IGD) metric.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The quality of the set of candidate solutions to a multi-objective optimisation problem can be assessed using three criteria: proximity to the true Pareto front (i.e. how close the set of candidate solutions is to the true global solution set), diversity (i.e. how well distributed the set of candidate solutions is over the true Pareto optimal front) and pertinency (i.e. how relevant the set of candidate solutions is to a decision maker). An ideal approximation set should be uniformly spread across the true Pareto optimal front (Deb 2001), or—in real-world problems at least–that part of it that represents a useful subset of solutions to the problemFootnote 1 (Purshouse and Fleming 2007).
The vast majority of the current state-of-the-art Evolutionary Multi-objective Optimisation (EMO) algorithms employ elitism to enhance convergence to the true Pareto optimal front. Elitism ensures some or all of the fittest individuals in a population at generation g are inserted into generation \(g+1\). Using this method, it is possible to prevent the loss of the fittest individuals which are considered to have some of the most valuable chromosomes in the population. However, in many multi-objective optimisation problems, solutions exist which may not be considered elite due to their objective value in regard to the population, but may contain useful genetic information. This genetic information can be utilised later in the search to move into unexplored areas of the objective space, but due to elitism and non-dominated sorting schemes it may be abandoned in the early stages of the search.
The aim of this study is to counter the potential negative effects resulting from elitist approaches to selection (for example, the bounded Pareto archive used in the Covariance Matrix Adaption—Pareto Archived Evolution Strategy (CMA-PAES)) by not only preserving elite solutions but also focusing part of the function evaluation budget on non-elitist solutions that have the potential to contribute useful genetic information in the future. To achieve this, a novel multi-tier adaptive grid selection scheme is developed and combined with the existing CMA-PAES algorithm, in a new augmented algorithm named the Multi-tier Covariance Matrix Adaptation Pareto Archived Evolution Strategy. This novel algorithm sacrifices a portion of the function evaluation budget in favour of producing diverse approximation sets consisting of solutions from areas of the objective space which are difficult or impossible to obtain with an elitism approach. With this feature, the final approximation set offers a better representation of the trade-off surface, therefore allowing the decision maker to make a more informed selection. The performance of this new algorithm is then evaluated on several benchmarking test suites from the literature.
The paper is organised as follows: Sect. 2 introduces the field of evolutionary multi-objective optimisation and its performance characteristics, Sect. 3 introduces the CMA-PAES algorithm and novel multi-tier adaptive grid algorithm, Sect. 4 contains the experimental set-up and methods of performance assessment, Sect. 5 presents and discusses the results, and Sect. 6 draws some conclusions as well as suggesting future research direction.
2 Background
2.1 Evolutionary algorithms
Evolutionary algorithms (EAs) are an optimisation technique inspired by some of the concepts behind natural selection and population genetics and are capable of iteratively evolving a population of candidate solutions to a problem (Goldberg 1989). They both explore the solution space of a problem (by using variation operators such as mutation and recombination) and exploit valuable information present in the previous generation of candidate solutions (by using a selection operator which gives preference to the best solutions in the population when creating the next generation of solutions to be evaluated).
One of the main reasons evolutionary algorithms are applicable across many different problem domains (including those where conventional optimisation techniques struggle) is their direct use of evaluation function information, rather than derivative information or other auxiliary knowledge. Derivative information (for example) can be extremely difficult to calculate in many real-world problems because the evaluation of candidate solutions can be expensive. Evolutionary algorithms are also robust to noisy solution spaces because of their population-based nature. This means that each generation contains more information about the shape of the fitness landscape than would be available to conventional, non-population-based optimisation methods (Michalewicz and Fogel 2000).
Evolutionary algorithms have also been used in combination with other approaches to optimisation to form hybrid algorithms which have been applied successfully to real-world problems (Sfrent and Pop 2015). Hyperheuristics are a methodology in search and optimisation which are concerned with choosing an appropriate heuristic or algorithm in any given optimisation context (Burke et al. 2003), and can operate on meta-heuristics. Hybrid algorithms indicate the benefits of using an approach which aim to combine existing algorithms and heuristics such that a more general approach can be taken to optimisation.
2.2 Evolutionary multi-objective optimisation
Many real-world optimisation problems involve the satisfaction of several objectives which, in a general form, can be described by a vector of objective functions f and a corresponding set of decision variables v, as illustrated in Eq. 1.
In many problems, conflicts occur between objectives such that it is not possible to find a single ideal solution to the problem. In this case, the solution consists of a set of Pareto optimal points—where any improvement in one objective will lead to a deterioration in one or more of the other objectives.
The quality of the set of non-dominated solutions (known as the approximation set) can be characterised by considering three main measures (Purshouse 2003):
-
The proximity of the approximation set to the true Pareto front.
-
The diversity of the distribution of solutions in the approximation set.
-
The pertinence of the solutions in the approximation set to the decision maker.
These concepts are illustrated graphically in Fig. 1, where a single-objective value is defined as \(x_m\) and an objective vector of M objectives can be defined as \(\mathrm {X} = \left\langle x_{1}, x_{2}, \dots , x_{M} \right\rangle \). A preference vector can be defined as \(\mathrm {P} = \left\langle \rho _1, \rho _2, \dots , \rho _M \right\rangle \), where every entry \(\rho _m\) refers to the goal which the corresponding objective values \(x_m\) must satisfy.
An ideal approximation set should contain solutions that are as close as possible to the true Pareto front (i.e. having good proximity) and provide a uniform spread of solutions across the region of interest of the decision maker (i.e. having a diverse set of candidate solutions that are pertinent to the decision maker).
Conventional multi-objective optimisation methods often fail to satisfy all these requirements, with methods such as the weighted sum method (Hwang and Masud 1979) and the goal attainment method (Gembicki 1974) only capable of finding a single point from the approximation set rather than a diverse distribution of potential solutions. This means that such algorithms do not fully capture the shape of the trade-off space without running the optimisation routine many times. In contrast, evolutionary algorithms (EAs) iteratively evolve a population of candidate solutions to a problem in parallel and are thus capable of finding multiple non-dominated solutions. This results in a diverse set of potential solutions to choose from, rather than a single solution that may not meet the required performance criteria.
2.3 Obtaining good proximity
The primary goal in evolutionary multi-objective optimisation is finding an approximation set that has good proximity to the Pareto front. This ensures that the candidate solutions in this approximation set represent optimal trade-offs between objectives. The early approaches to evolutionary multi-objective optimisation were primarily concerned with guiding the search towards the Pareto front, reflecting the importance of this goal.
Convergence to the Pareto front is mainly driven by selection for variation, where the best candidate solutions are assigned the highest fitness (and thus have the best chance of contributing to the next generation). Several techniques have been proposed to solve the problem of assigning scalar fitness values to individuals in the presence of multiple objectives—with Pareto-based methods generally being considered the best. Several variants of Pareto-based fitness assignment methods exist (see Zitzler et al. 2004 for more information), but the general procedure is to rank individuals in the approximation set according to some dominance criterion, and then map fitness values to these ranks (often via a linear transformation). Mating selection then proceeds using these fitness values.
The proximity of the approximation set to the true Pareto front can be enhanced by the use of elitism. Elitism aims to address the problem of losing good solutions during the optimisation process (Zitzler et al. 2004), either by maintaining an external population of non-dominated solutions (commonly referred to as an archive), or by using a \((\mu + \lambda )\) type environmental selection mechanism. Studies have shown that elitist MOEAs perform favourably when compared to their non-elitist counterparts (Zitzler and Thiele 1999; Zitzler et al. 2000a). Elitism has also been shown to be a theoretical requirement to guarantee convergence of an MOEA in the limit condition (Rudolph and Agapie 2000).
In archive-based elitism, the archive can be used either just to store good solutions generated by the MOEA or can be integrated into the algorithm with individuals from the archive participating in the selection process. Some mechanism is often needed to control the number of non-dominated solutions in the archive, since the archive is usually a finite size and the number of non-dominated individuals can potentially be infinite. Density-based measures to preserve diversity are commonly used in this archive reduction—for example, the Pareto Archived Evolution Strategy (Knowles and Corne 2000a) uses an adaptive crowding procedure to preserve diversity (see later).
An alternative elitist strategy is the \((\mu + \lambda )\) population reduction scheme, where the parent population and the child population compete against each other for selection. This scheme originated in Evolution Strategies and forms the basis of the environmental selection scheme used in algorithms such as NSGA-II (Deb et al. 2002a) and, more recently, the Multi-Objective Covariance Matrix Adaptation Evolutionary Strategy (MO-CMA-ES) (Igel et al. 2007). In both these algorithms, a two level sorting process is used, with Pareto dominance as the primary sorting criteria and population density as a secondary sorting criteria (used as a tiebreaker amongst individuals having the same level of non-dominance).
MO-CMA-ES is a state-of-the-art elitist multi-objective evolutionary optimisation technique that builds upon the powerful covariance matrix adaptation evolution strategy (CMA-ES) real-valued single-objective optimiser (Hansen and Ostermeier 2001; Hansen et al. 2003). The key features of CMA-ES are that it is invariant against linear transformations of the search space, performs extremely well across a broad spectrum of problems in the continuous domain (Auger and Hansen 2005), and is robust to the initial choice of parameters (due to its advanced self-adaptation strategy). These make the CMA-ES algorithm an excellent choice to base a multi-objective evolutionary optimisation on.
Two variants of MO-CMA-ES exist in the literature: the s-MO-CMA-ES which achieves diversity using the contributing hypervolume measure (or s-metric) introduced by (Zitzler and Thiele 1998), and the c-MO-CMA-ES which achieves diversity using the crowding-distance measure introduced in NSGA-II. Whilst initial results have shown that MO-CMA-ES is extremely promising, it is as yet mostly untested on real-world engineering problems. Some results show that MO-CMA-ES struggles to converge to good solutions on problems with many deceptive locally Pareto optimal fronts—a feature that can be common in real-world problems (Voß et al. 2010).
In the original MO-CMA-ES, a mutated offspring solution is considered to be successful if it dominates its parent. In contrast, (Voß et al. 2010) introduces a new MO-CMA-ES variant which considers a solution successful if it is selected to be in the next parent population, introduces a new update rule for the self-adaptive strategy, and conducts a comparison of MO-CMA-ES variants on synthetic test functions consisting of up to three objectives. MO-CMA-ES with the improved update rule is shown to perform substantially better than the original algorithm and thus is used for comparison in Sect. 5 of this paper.
2.4 Obtaining good diversity
Most EMO algorithms use density information in the selection process to maintain diversity in the approximation set. However, diversity preservation has often been seen as a secondary consideration (after obtaining good proximity to the Pareto front). This is because, as Bosman and Thierens (2003) state:
“...since the goal is to preserve diversity along an approximation set that is as close as possible to the Pareto optimal front, rather than to preserve diversity in general, the exploitation of diversity should not precede the exploitation of proximity”.
Goldberg (1989) initially suggested the use of a niching strategy in EMO to maintain diversity, with most of the first generation of Pareto-based EMO algorithms using the concept of fitness sharing from single-objective EA theory (Fonseca and Fleming 1993; Horn et al. 1994; Srinivas and Deb 1994). However, the success of fitness sharing is strongly dependent on the choice of an appropriate niche size parameter, \(\sigma _\mathrm{share}\). Whilst several authors proposed guidelines for choosing \(\sigma _\mathrm{share}\) (Deb and Goldberg 1989; Fonseca and Fleming 1993), Fonseca and Fleming (1995) were the first to note the similarity between fitness sharing and kernel density estimation in statistics which then provided the EMO community with a set of established techniques for automatically selecting the niche size parameter, such as the Epanechnikov estimator (Silverman 1986).
A large number of the second generation of Pareto-based MOEAs include advanced methods of estimating the population density, inspired by statistical density estimation techniques. These can be mainly classified into histogram techniques (such as that used in PAES (Knowles and Corne 2000a)) or nearest neighbour density estimators (such as that used in SPEA2 (Zitzler et al. 2001) and NSGA-II (Deb et al. 2002a)). Other approaches to diversity preservation include the use of hybrid algorithms, such as the Hybrid Immune Genetic Algorithm (HIGA) Istin et al. (2011), which uses an immune component to continuously evolve new solutions and then inject them back into the population of an EA. These estimates of population density can be used in both mating selection and environmental selection. In mating selection, these density estimates are commonly used to discriminate between individuals of the same rank. Individuals from a less dense part of the population are assigned higher fitness and thus have a higher chance of contributing to the next generation.
Density estimation in environmental selection is commonly used when there exists more locally non-dominated solutions than can be retained in the population. For example, in archive-based elitism, density-based clustering methods are often used to reduce the archive to the required size. Non-dominated solutions from sparser regions of the search space are again preferred over those from regions with higher population densities, with the aim being to ensure that the external population contains a diverse set of candidate solutions in close proximity to the Pareto front.
The Pareto Archived Evolution Strategy (Knowles and Corne 2000a) uses an adaptive crowding procedure to preserve diversity that recursively divides up the objective space into grid segments. This bounded Pareto archiving technique then uses this adaptive grid to keep track of the density of solutions within sections of the objective space (Knowles and Corne 1999). Since it is adaptive, this crowding procedure does not require the critical setting of a niche size parameter which was a common problem with traditional kernel-based methods of diversity preservation. This adaptive grid archiving (AGA) scheme uses a grid with a preconfigured number of divisions to divide the objective space, and when a solution is generated, its grid location is identified and associated with it. Each grid location is considered to contain its own sub-population, and information on how many solutions in the archive are located within a certain grid location is available during the optimisation process. Figure 2 illustrates this grid archiving scheme in two dimensions; in this example, it can be observed that the sub-population at grid location 91 holds a single solution, whereas the sub-population at grid location 62 contains many more. With this additional information, it is possible to discard a solution from one of the more densely populated sub-populations in favour of a candidate solution which will be located in a sparsely populated sub-population, e.g., the one located at grid location 91.
When an archive has reached capacity and a new candidate solution is to be archived, the information tracked by the AGA is used to replace a solution in the grid location containing the highest number of solutions. When a candidate solution is non-dominated in regard to the current solution and the archive, the grid information is used to select the solution from the least populated grid location as the current (and parent) solution.
The AGA concept used in PAES later inspired several researchers and was altered and deployed in multiple EMO algorithms such as the Pareto Envelope-based Selection Algorithm (PESA) (a population-based version of PAES) (Corne et al. 2000), the Micro Genetic Algorithm (Coello Coello and Pulido 2001), and the Domination Based Multi-Objective Evolutionary Algorithm (\(\epsilon \)-MOEA) (Deb et al. 2005).
2.5 Issues with elitism
Whilst elitism has been almost universally adopted in the current state of the art for evolutionary multi-objective optimisers, in many multi-objective optimisation problems solutions may exist which are not considered elite due to their objective value in regard to the population but may still contain useful genetic information. This genetic information can be utilised later in the search to move into unexplored areas of the objective space but, due to elitism and non-dominated sorting schemes, it may be abandoned in the early stages of the search.
The consequences of elitism and non-dominated sorting can be seen in Fig. 3, where an elitist EMO algorithm has produced an approximation set for the CEC09 UF1 (Zhang et al. 2008b) test function with a budget of 300,000 function evaluations (in compliance with the CEC09 competition rules).
By observing this two-objective plot of the approximation set, it can be seen that the elitist EMO algorithm has converged to an approximation set which is missing three distinct areas containing solutions in comparison with the true Pareto optimal front plotted in Fig. 4. The genetic information which would have potentially found these missing areas was discarded by the algorithm during the search process due to the use of elitism and non-dominated sorting. This is a difficulty that occurs in the CEC09 UF1 test problem because of its complicated Pareto optimal set, which has some regions that are easier to reach. In these cases, elitist EMO algorithms will focus selection on these more dominant solutions and converge further into that area of the Pareto optimal set, discarding individuals which may have been only a few generations away from producing non-dominated solutions in unexplored areas of the objective space.
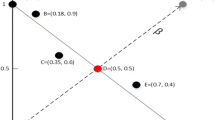
Figure 5 illustrates an example of elitist and non- dominated selection discarding an individual that may contain valuable genetic information, which could have been exploited to produce a better quality approximation set. In this example, a Pareto AGA selection scheme has been used to select parent individuals for the next generation. Because of the scheme’s elitist nature, the individual between 0.6 and 0.7 on the x-axis has not been selected for reproduction, and therefore, the scheme has discarded genetic information which may have ultimately produced solutions towards the missing area of the approximation set. This behaviour over many generations can lead to convergence to incomplete approximation sets.
3 CMA-PAES
The Covariance Matrix Adaptation Pareto Archived Evolution Strategy is an extensible EMO algorithm framework (Rostami and Shenfield 2012) inspired by the simplicity of PAES (Knowles and Corne 2000b). As a result, the execution life cycle of the optimisation process does not have a high computational cost in regard to algorithm overhead. The modular structure of the algorithm has allowed for the Covariance Matrix Adaptation (CMA) operator to be easily incorporated in order to achieve fast convergence through the powerful variation of population solutions. To manage these populations at each generational iteration, an Adaptive Grid Algorithm (AGA) approach is used in conjunction with bounded Pareto archiving with the aim of diversity preservation.
The algorithm execution life cycle for CMA-PAES has been illustrated in Fig. 6. CMA-PAES begins by initialising the algorithm variables and parameters; these include the number of grid divisions used in the AGA, the archive for storing Pareto optimal solutions, the parent vector Y, and the covariance matrix. An initial current solution is then generated at random, which is evaluated and then the first to be archived (without being subjected to the PAES archiving procedure). The generational loop then begins, and the square root of the covariance matrix is resolved using Cholsky decomposition (as recommended by Beyer and Sendhoff 2008) which offers a less computationally demanding alternative to spectral decomposition. The \(\lambda \) candidate solutions are then generated using copies of the current solution and the CMA-ES procedure for mutation before being evaluated. The archive is then merged with the newly generated offspring and subjected to Pareto ranking, and this assigns a rank of zero to all non-dominated solutions, and a rank reflecting the number of solutions that dominate the inferior solutions. The population is then purged of the inferior solutions so that only non-dominated solutions remain before being fed into the PAES archiving procedure. After the candidate solutions have been subjected to the archiving procedure and the grid has been adapted to the new solution coverage of objective space, the archive is scanned to identify the grid location with the smallest population, this is considered the lowest density grid population (ldgp). The solutions from the lowest density grid population are then spliced onto the end of the first \(\mu -ldgp\) of the Pareto rank-ordered population to be included in the adaptation of the covariance matrix, with the aim to improve the diversity of the next generation by encouraging movement into the least dense area of the grid. After the covariance matrix is updated, the generational loop continues onto its next iteration until the termination criteria is satisfied (maximum number of generations).
CMA-PAES has been benchmarked against NSGA-II and PAES in Rostami and Shenfield (2012) on the ZDT synthetic test suite. Two performance metrics were used to compare the performance in terms of proximity (using the generational distance metric) and diversity (using the spread metric). CMA-PAES displayed superior performance (the significance of which was supported with randomisation testing) in returning an approximation set close to or on the true Pareto optimal front as well as maintaining diversity amongst solutions in the set.
CMA-PAES has also been benchmarked against the MO-CMA-ES algorithm in Rostami (2014), using the hypervolume indicator as a measure of performance. In this study, both the algorithms considered demonstrated comparable performance across multiple test problems. The significance of which was supported by the use of nonparametric testing.
3.1 A novel multi-tier adaptive grid algorithm
The new multi-tier AGA aims to prevent a population from prematurely converging as a result of following only the dominant (i.e. elite) solutions which may be discovered early in the optimisation process. This common optimisation scenario often results in genetic drift and consequently a final approximation set with solutions clustered around these elite solutions. This prevention is achieved by dividing an optimisation function evaluation budget and investing a percentage of this budget in to non-elite solutions. These solutions which appear non-elite early on in the optimisation process may potentially contain genetic information that would contribute to finding undiscovered areas of the objective space later in the search.
The algorithm pseudo-code for this new multi-tier approach is listed in Algorithm 1, which is executed from line 14 of the Multi-tier Covariance Matrix Adaptation Pareto Archived Evolution Strategy (m-CMA-PAES) execution life cycle presented in Algorithm 2. This new optimisation algorithm which builds upon the algorithmic components (AGA and CMA) outlined in Fig. 6 is referred to as the m-CMA-PAES. First, the candidate population is divided into sub-populations based on their non-dominated rank using NSGA-II’s fast non-dominated sort. If the size of any sub-population exceeds \(\mu \), then the standard AGA scheme is applied to it with a maximum archive capacity of \(\mu \), resulting in a number of rank-ordered archives each with a maximum capacity of \(\mu \). Then, a single population of size \(\mu \) plus the budget for non-elite individuals \(\beta \) is produced, for example, if \(\beta \) is set as 10 % for a \(\mu \) population of 100, then a population of size \(100 \times 1.10\) is to be produced. Next, the multi-tier archives containing the first \(\mu \times \beta \) solutions are merged with no size restriction (meaning the merged archive size can be greater than \(\mu \times \beta \)). This merged archive is then subjected to a non-elite AGA (ensuring non-elite solutions are not instantly discarded) with an archive capacity of \(\mu \), producing a population of individuals to be selected as parents for the next generation.
The configuration of \(\beta \) is important to the convergence of the algorithm—if it is too high (for example, if it is greater than half of \(\mu \)), then the majority of the function evaluation budget is spent on solutions which are dominated and the search does not progress in a positive direction, and may instead move away from the Pareto optimal front. However, if \(\beta \) is too small, the benefits of investing in non-elite solutions are not exploited to an extent which will significantly impact the performance of the optimisation process. The result of this new grid selection scheme has been illustrated in Fig. 7, where the solution which may potentially contain valuable genetic information is selected, in contrast to it being discarded in Fig. 5.

In m-CMA-PAES, a population of candidate solution individuals \({a_i}^{(g)}\) are initialised as the structure \(\left[ {x_{i}}^{(g)},\bar{p}^{(g)}_{succ,i},\right. \left. {\sigma _i}^{(g)}, {p}^{(g)}_{i,c},{\mathbf {C}}^{(g)}_i \right] \), where each individual is assigned a randomly generated problem variable \({x_{i}}^{(g)} \in \mathrm {R}^n\) between the lower (\(x^{(L)}\)) and upper (\(x^{(U)}\)) variable boundaries, \(\bar{p}^{(g)}_{succ,i} \in [0,1]\) is the smoothed success probability, \({\sigma _i}^{(g)} \in \mathrm {R}_0^{+}\) is the global step size, \({p}^{(g)}_{i,c} \in \mathrm {R}^n\) is the cumulative evolution path, and \({\mathbf {C}}^{(g)}_i \in \mathrm {R}^{n\times {n}}\) is the covariance matrix of the search distribution.

4 Experimental design and performance assessment
4.1 Experimental set-up
In order to evaluate the performance of m-CMA-PAES on multi-objective test problems, a pairwise comparison between m-CMA-PAES and MO-CMA-ES on selected benchmark problems from the literature (consisting of upto 3 objectives) has been conducted. MO-CMA-ES (as outlined in Sect. 2.3) is a state-of-the-art algorithm which uses the CMA operator for variance much like m-CMA-PAES.
Both m-CMA-PAES and MO-CMA-ES have been configured with a budget of 300, 000 function evaluations per algorithm execution and were executed 30 times per test function as per the CEC2009 competition guidelines. The algorithm configurations are presented in Table 1, and the finer configurations for the CMA operator and MO-CMA-ES have been taken from Voß et al. (2010), where the version of MO-CMA-ES used incorporates the improved step-size adaptation.
The ZDT, DTLZ and CEC2009 test suites have been selected for the benchmarking and comparison of m-CMA-PAES and MO-CMA-ES (see Sect. 4.2). These test suites will pose both MOEAs with difficulties which are likely to be encountered in many real-world multi-objective optimisation problems, in both two-dimensional and three-dimensional objective spaces (allowing for feasible comparison with MO-CMA-ES which relies on the hypervolume indicator for secondary sorting and is thus computationally expensive in high-dimensional search spaces).
The metric used for performance assessment is the popular Inverted Generational Distance (IGD) indicator described in Sect. 4.3. The IGD indicator will be used at each generation in order to assess performance and compare both algorithms on not just the IGD quality of the final approximation set, but also the IGD quality over time. In order to comply with the CEC2009 competition rules (as described in Zhang et al. 2008b), both m-CMA-PAES and MO-CMA-ES have been executed 30 times on each test function to reduce stochastic noise. This sample size is seen as sufficient because of the limited benefit of producing more than 25 samples (discussed in Sect. 4.1.1).
4.1.1 Sample size sufficiency
Selecting a sufficient number of samples when comparing optimisers is critical. The sample size of 25, in order to reduce stochastic noise, is reoccurring in the evolutionary computation literature (e.g. Yang et al. 2008; Zamuda et al. 2007; Falco et al. 2012; García et al. 2009; Wang et al. 2011). To prove the sufficiency of this sample size, a large number of hypervolume indicator value samples have been produced by executing m-CMA-PAES 200 times on the DTLZ1 synthetic test problem.
These 200 samples were then used to identify the relationship between the standard error of the mean (SEM) and the sample size using:
This relationship has been illustrated in Fig. 8, which shows the limited benefit of more than 25 independent executions of the algorithm on the synthetic test problem.
sizes, evolution paths and covariance matrices of the successful solutions are updated.
4.2 Multi-objective test suites
The performance of the novel m-CMA-PAES algorithm is compared to MO-CMA-ES across three different real-valued, synthetic, test suites: the widely used ZDT bi-objective test suite proposed in Zitzler et al. (2000b), the scalable DTLZ multi-objective test suite proposed in Deb et al. (2002b) and the unconstrained functions from the CEC2009 multi-objective competition test suite proposed in Zhang et al. (2008b). The configurations used for these test problems and some of their salient features are shown in Table 2
Each of these test suites incorporates a different balance of features that MOEAs may find difficult to overcome during the optimisation process (for example, multi-modal search landscapes, deceptive local Pareto-fronts, non-convex Pareto-fronts). The ZDT and DTLZ test suites provide well-defined Pareto optimal fronts that have been widely used in the literature—thus allowing easy comparison with previous work. The CEC2009 multi-objective optimisation competition test suite is more recent and is predominantly made up of problems with solution sets that consist of complex curves through decision variable space. These test problems contain variable linkages and present many difficulties for multi-objective optimisation routines.
4.3 Performance assessment
As the EMO process is stochastic by nature, each algorithm was executed 30 times against each test function, in an effort to minimise stochastic noise and increase the integrity of the comparison between the algorithms (see Sect. 4.1.1). The performance of each algorithm execution was then measured using the inverted generational distance (IGD) performance metric to assess the quality of the approximation set, in terms of proximity to the true Pareto optimal front and the diversity of solutions in the population.
The IGD metric measures how well the obtained approximation set represents the true Pareto optimal front which is provided as a large reference set. This is calculated by finding the minimum Euclidean distance of each point of the approximation set to points in the reference set. Lower IGD values indicate a better quality approximation set with IGD values of 0, indicating all the solutions in the approximation set are in the reference set and cover all the Pareto front.
The IGD was introduced in Coello Coello and Cortés (2005) as an enhancement to the generational distance metric, measuring the proximity of the approximation set to the true Pareto optimal front in objective space. The IGD can be defined as:
where \(n'\) is the number of solutions in the reference set and d is the Euclidean distance (in objective space) between each solution in the reference set and the nearest solution in the approximation set. A GD value equal to zero indicates that all members of the approximation set are on the true Pareto optimal front, and any other value indicates the magnitude of the deviation of the approximation set from the true Pareto optimal front. This implementation of the GD solves an issue in its predecessor so that it will not rate an approximation set with a single solution on the reference set as better than an approximation set which has more non-dominated solutions that are close in proximity to the reference set.
Much like the GD measure, knowledge regarding the true Pareto optimal front is required in order to form a reference set. The selection of solutions for the reference set will have an impact on the results obtained from the IGD, and therefore, the reference set must be diverse. The calculation of the IGD can be computational expensive when working with large reference sets or a high number of objectives.
The IGD measure has been employed in the performance assessment of algorithms in much of the multi-objective optimisation and evolutionary computation literature (e.g. Zhang et al. 2008a, 2010; Tiwari et al. 2009; Chen et al. 2009; Nasir et al. 2011).
4.4 Statistical comparison of stochastic optimisers
Statistical comparison of the performance of the algorithms was conducted by computing the t values Footnote 2 of the IGD metric produced by both the algorithms. However, when analysing stochastic systems (such as EAs), the initial conditions that ensure the reliability of parametric tests cannot be satisfied (Li et al. 2012)—therefore a nonparametric test (encouraged by Derrac et al. 2011; Epitropakis et al. 2012) for pairwise statistical comparison must be used to evaluate the significance of results. The Wilcoxon signed-ranks (Wilcoxon 1945) nonparametric test (counterpart of the paired t test) can be used with the statistical significance value (\(\alpha = 0.05\)) to rank the difference in performance between two algorithms over each approximation set.
Nonparametric testing is becoming more commonly used in the literature to statistically contrast the performance of evolutionary algorithms in many experiments (García et al. 2010; Derrac et al. 2012; Li et al. 2012; Epitropakis et al. 2012; Hatamlou 2013; Civicioglu 2013).
5 Results
The results from the experiments described in Sect. 4 have been produced and presented in a number of formats in order to allow for a better assessment of each algorithms performance.
The worst, mean and best IGD indicator results for the final approximation set of each algorithm are presented in Table 3 for the two-objective test functions and in Table 4 for the three-objective test functions. Tables 3 and 4 also present information regarding the p value resolved by the Wilcoxon signed-ranks nonparametric test for the final approximation sets of the considered synthetic test problems, and a symbol indicating the observation of the null hypothesis. A ‘\(+\)’ symbol indicates that the null hypothesis was rejected, and m-CMA-PAES displayed statistically superior performance at the 95 % significance level (\(\alpha \) = 0.05) on the considered synthetic test function. A ‘−’ symbol indicates that the null hypothesis was rejected, and m-CMA-PAES displayed statistically inferior performance. An ‘\(=\)’ symbol indicates that there was no statistically significant difference between both of the considered algorithms on the synthetic test problem. The table column ‘%IGD’ indicates the difference in performance between m-CMA-PAES and MO-CMA-ES using m-CMA-PAES as the benchmark. This percentage can be calculated by finding the normalised mean performance of each algorithm:
where \(mean_{a}\) is the mean performance for m-CMA-PAES \(mean_{b}\) is the mean performance for MO-CMA-ES, worst is the highest IGD achieved by either algorithm, and best is the lowest IGD achieved by either algorithm. A positive %IGD indicates the percentage of which m-CMA-PAES outperformed MO-CMA-ES, whereas a negative %IGD indicates the percentage of which m-CMA-PAES was outperformed by MO-CMA-ES.
Overall, m-CMA-PAES outperformed MO-CMA-ES on all but 3 (ZDT3, UF6 and UF9) of the 22 test functions, producing better performing worst, mean and best approximation sets.
The mean of the IGD metric at each generation has been plotted and presented in Figs. 9 and 10 for the two-objective test functions and Figs. 11 and 12 for the three-objective test functions. These plots illustrate the rate of IGD convergence from the initial population to the final population.
m-CMA-PAES significantly outperforms the MO-CMA-ES on most of the test functions used in this comparison. However, as a consequence of investing a percentage of the maximum number of function evaluations in non-elite solutions, it can be observed in Figs. 9, 10, 11, 12 that the convergence of the algorithm is slower in most cases (more so in the two-objective test functions). This suggests that in experiments where the number of function evaluations is not constrained to a low number, the m-CMA-PAES will outperform MO-CMA-ES.
It can be observed in Figs. 9, 10, 11, 12 that the mean IGD for MO-CMA-ES oscillates or rises on some test functions over time. This issue is most visible on UF4 (where the mean IGD for MO-CMA-ES can be seen to oscillate over time) and on DTLZ3 (where the mean IGD for MO-CMA-ES can be seen to improve in performance until 200 generations and then worsen gradually until termination). This issue is due to MO-CMA-ES being dependent on the hypervolume indicator entirely for diversity preservation which, when paired with its elitism scheme, ends up gradually reducing the IGD quality of an approximation set once a difficult area of the search space is encountered.
The results presented in Tables 3 and 4, as well as the box plots presented in Figs. 13 and 14, show that on 18 of the 22 considered test functions m-CMA-PAES significantly outperformed MO-CMA-ES in regard to the achieved mean and median IGD. The box plots show that the interquartile ranges for the m-CMA-PAES results are significantly better than the interquartile ranges for the MO-CMA-ES results. Across all test functions m-CMA-PAES produces fewer outliers—indicating a more reliable and robust algorithm than MO-CMA-ES on the considered test functions.
On the UF3 test function, it can be observed (in Fig. 13) that, although the MO-CMA-ES median IGD outperforms m-CMA-PAES, m-CMA-PAES achieved a better interquartile range and a far better total range—achieving the best approximation set for that test function. A similar result can be seen in the performance on UF6 where m-CMA-PAES also achieves the best approximation set but is outperformed by MO-CMA-ES on the median values of the IGD results.
The MO-CMA-ES significantly outperforms the m-CMA-PAES on UF9. This function (as well as ZDT3 and UF6) consists of disjoint true Pareto optimal fronts as shown in Fig. 15. The comparison in performance on these problems shows that the m-CMA-PAES has performance issues on some problems consisting of multiple parts in their Pareto optimal fronts.
6 Conclusion
In this paper, a multi-tier AGA scheme has been introduced and incorporated into the CMA-PAES algorithm to create m-CMA-PAES. m-CMA-PAES improves the quality of the produced final approximation set by investing a percentage of the allowed function evaluation budget in non-elite but potentially successfully solutions. With this approach, m-CMA-PAES is able to find portions of the Pareto optimal front which remain unexplored by elitist approaches. Experiments and statistical analysis presented in this study show that with CEC09 competition compliant benchmarking configurations, m-CMA-PAES significantly outperforms MO-CMA-ES on all but 4 of the 22 considered synthetic test problems, and out of these 4, MO-CMA-ES only performs statistically significantly better on 2 test functions.
When observing the IGD values at each generation, it can be seen that in some cases the IGD of the final population is higher than some of the generations before it, this is due to the non-elite solutions invested in at each generation being a factor right to the end of the algorithm. This suggests that in further work the algorithm may benefit from either an offline archive which the algorithm selects from at the end of the optimisation process or a final approximation set selection scheme which uses the last two generations of the optimisation process, including non-dominated solutions only.
The results indicate a clear trade-off between m-CMA-PAES and MO-CMA-ES. In the majority of the benchmarks, MO-CMA-ES appears to offer a faster rate of convergence. However, this comes at the cost of premature convergence very early in the optimisation process. In contrast, m-CMA-PAEs offer a slower rate of convergence throughout the entire optimisation process, with steady improvement until the end of the function evaluation budget. Unlike MO-CMA-ES, m-CMA-PAES does not subject the entire non-dominated population to the contributing hypervolume indicator. By not doing so, m-CMA-PAES remains computationally lightweight, unlike MO-CMA-ES which becomes computationally infeasible as the number of problem objectives increase. By investing a portion of the function evaluation budget in non-elite solutions, areas of the Pareto optimal front which are difficult to obtain can be discovered later on in the optimisation process. This results in improved diversity and coverage in the produced approximation sets.
Future works will further investigate the possibility for self-adaptation of the m-CMA-PAES algorithm parameter which defines the budget for non-elite individuals (\(\beta \)). A current limitation of m-CMA-PAES requires the manual configuration of the \(\beta \) parameter, which may result in inefficient usage of the function evaluation budget when parameters such as the population size and the number of problem objectives change.
Notes
For example, in the design of automotive engines, there is typically a trade-off between torque generated and emissions produced. Designs at the extreme ends of this trade-off surface (i.e. with good emissions but poor torque—or vice versa) are usually not very useful for production automobiles.
The t value is the difference between the means of the datasets divided by the standard error.
References
Auger A, Hansen N (2005) A restart CMA evolution strategy with increasing population size. In: The 2005 IEEE congress on evolutionary computation, 2005, IEEE, vol 2, pp 1769–1776
Beyer H, Sendhoff B (2008) Covariance matrix adaptation revisited–the cmsa evolution strategy. In: Parallel problem solving from nature–PPSN X. Springer, Berlin, pp 123–132
Bosman PAN, Thierens D (2003) The balance between proximity and diversity in multiobjective evolutionary algorithms. IEEE Trans Evol Comput 7(2):174–188
Burke E, Kendall G, Newall J, Hart E, Ross P, Schulenburg S (2003) Hyper-heuristics: An emerging direction in modern search technology. In: International series in operations research and management science, pp 457–474
Chen CM, Chen YP, Zhang Q, (2009) Enhancing moea, d with guided mutation and priority update for multi-objective optimization. In: IEEE congress on evolutionary computation, (2009) CEC’09, IEEE, pp 209–216
Civicioglu P (2013) Backtracking search optimization algorithm for numerical optimization problems. Appl Math Comput 219(15):8121–8144
Coello Coello CA, Cortés NC (2005) Solving multiobjective optimization problems using an artificial immune system. Genet Program Evol Mach 6(2):163–190
Coello Coello CA, Pulido GT (2001) A micro-genetic algorithm for multiobjective optimization. In: Evolutionary multi-criterion optimization. Springer, Berlin, pp 126–140
Corne DW, Knowles JD, Oates MJ (2000) The Pareto envelope-based selection algorithm for multiobjective optimization. In: Parallel problem solving from nature PPSN VI. Springer, Berlin, pp 839–848
De Falco I, Della Cioppa A, Maisto D, Scafuri U, Tarantino E (2012) Biological invasion-inspired migration in distributed evolutionary algorithms. Inf Sci 207:50–65
Deb K (2001) Multi-objective optimization. Multi-objective optimization using evolutionary algorithms, pp 13–46
Deb K, Pratap A, Agarwel S, Meyarivan T (2002a) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197
Deb K, Mohan M, Mishra S (2005) Evaluating the \(\varepsilon \)-domination based multi-objective evolutionary algorithm for a quick computation of Pareto-optimal solutions. Evol Comput 13(4):501–525
Deb K, Goldberg DE (1989) An investigation of niche and species formation in genetic function optimization. In: Schaffer JD (ed) Proceedings of the third international conference on genetic algorithms, Morgan Kaufmann, New York, pp 42–50
Deb K, Thiele L, Laumanns M, Zitzler E (2002b) Scalable multi-objective optimization test problems. In: Proceedings of the congress on evolutionary computation (CEC-2002), Honolulu, pp 825–830
Derrac J, García S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1(1):3–18
Derrac J, Cornelis C, García S, Herrera F (2012) Enhancing evolutionary instance selection algorithms by means of fuzzy rough set based feature selection. Inf Sci 186(1):73–92
Epitropakis M, Plagianakos V, Vrahatis M (2012) Evolving cognitive and social experience in particle swarm optimization through differential evolution: A hybrid approach. Inf Sci Int J 216:50–92
Fonseca CM, Fleming PJ (1993) Genetic algorithms for multi-objective optimization: Formulation, discussion and generalization. In: Forrest S (ed) Proceedings of the fifth international conference on genetic algorithms. Morgan Kaufmann, New York, pp 416–423
Fonseca CM, Fleming PJ (1995) Multiobjective genetic algorithms made easy: Selection, sharing, and mating restriction. In: Zalzala AMS (ed) Proceedings of the first international conference on genetic algorithms in engineering systems: innovations and applications (GALESIA), pp 42–52
García S, Molina D, Lozano M, Herrera F (2009) A study on the use of non-parametric tests for analyzing the evolutionary algorithms behaviour: a case study on the cec2005 special session on real parameter optimization. J Heuristics 15(6):617–644
García S, Fernández A, Luengo J, Herrera F (2010) Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf Sci 180(10):2044–2064
Gembicki FW (1974) Vector optimization for control with performance and parameter sensitive indices. PhD thesis, Case Western Reserve University, Cleveland
Goldberg DE (1989) Genetic algorithms in search, optimization and machine learning. Addison-Wesley, Reading
Hansen N, Müller SD, Koumoutsakos P (2003) Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (cma-es). Evol Comput 11(1):1–18
Hansen N, Ostermeier A (2001) Completely derandomized self-adaptation in evolution strategies. Evol Comput 9(2):159–195
Hatamlou A (2013) Black hole: a new heuristic optimization approach for data clustering. Inf Sci 222:175–184
Horn J, Nafpliotis N, Goldberg DE (1994) A niched Pareto genetic algorithm for multiobjective optimization. In: Proceedings of the congress on evolutionary computation (CEC) 1994. IEEE Press, New York, pp 82–87
Hwang CL, Masud ASM (1979) Multiple objective decision making—methods and applications, vol 164, Lecture notes in economics and mathematical systems. Springer, Berlin
Igel C, Hansen N, Roth S (2007) Covariance matrix adaptation for multi-objective optimization. Evol Comput 15(1):1–28
Istin M, Pop F, Cristea V (2011) Higa: Hybrid immune-genetic algorithm for dependent task scheduling in large scale distributed systems. In: 10th international symposium on parallel and distributed computing (ISPDC), 2011, IEEE, pp 282–287
Knowles J, Corne D (1999) The pareto archived evolution strategy: A new baseline algorithm for pareto multiobjective optimisation. In: Proceedings of the 1999 congress on evolutionary computation, 1999, CEC 99, IEEE, vol 1
Knowles JD, Corne DW (2000a) Approximating the nondominated front using the Pareto archived evolution strategy. Evol Comput 8(2):149–172
Knowles JD, Corne DW (2000b) Approximating the nondominated front using the Pareto archived evolution strategy. Evol Comput 8(2):149–172
Li K, Kwong S, Cao J, Li M, Zheng J, Shen R (2012) Achieving balance between proximity and diversity in multi-objective evolutionary algorithm. Inf Sci 182(1):220–242
Michalewicz Z, Fogel DB (2000) How to solve it: modern heuristics. Springer, Berlin
Nasir M, Mondal AK, Sengupta S, Das S, Abraham A (2011) An improved multiobjective evolutionary algorithm based on decomposition with fuzzy dominance. In: IEEE congress on evolutionary computation (CEC), 2011, IEEE, pp 765–772
Purshouse RC (2003) On the evolutionary optimisation of many objectives. PhD thesis, Department of Automatic Control and Systems Engineering, University of Sheffield, Sheffield, UK, S1 3JD
Purshouse RC, Fleming PJ (2007) On the evolutionary optimization of many conflicting objectives. IEEE Trans Evol Comput 11(6):770–784
Rostami S (2014) Preference focussed many-objective evolutionary computation. PhD thesis, Manchester Metropolitan University, Manchester
Rostami S, Shenfield A (2012) Cma-paes: Pareto archived evolution strategy using covariance matrix adaptation for multi-objective optimisation. In: Computational intelligence (UKCI), 2012, IEEE, pp 1–8
Rudolph G, Agapie A (2000) Convergence properties of some multi-objective evolutionary algorithms. In: Proceedings of the congress on evolutionary computation (CEC) 2000, IEEE Press, pp 1010–1016
Sfrent A, Pop F (2015) Asymptotic scheduling for many task computing in big data platforms. Inf Sci 319:71–91
Silverman BW (1986) Density estimation for statistics and data analysis. Chapman and Hall, London
Srinivas N, Deb K (1994) Multiobjective optimization using nondominated sorting in genetic algorithms. Evol Comput 2(3):221–248
Tiwari S, Fadel G, Koch P, Deb K (2009) Performance assessment of the hybrid archive-based micro genetic algorithm (amga) on the cec09 test problems. In: IEEE congress on evolutionary computation (2009) CEC’09, IEEE, pp 1935–1942
Voß T, Hansen N, Igel C (2010) Improved step size adaptation for the mo-cma-es. In: Proceedings of the 12th annual conference on genetic and evolutionary computation. ACM, New York, pp 487–494
Wang Y, Cai Z, Zhang Q (2011) Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans Evol Comput 15(1):55–66
Wilcoxon F (1945) Individual comparisons by ranking methods. Biometrics Bull 1(6):80–83
Yang Z, Tang K, Yao X (2008) Large scale evolutionary optimization using cooperative coevolution. Inf Sci 178(15):2985–2999
Zamuda A, Brest J, Boskovic B, Zumer V (2007) Differential evolution for multiobjective optimization with self adaptation. In: IEEE congress on evolutionary computation, pp 3617–3624
Zhang Q, Zhou A, Jin Y (2008a) Rm-meda: a regularity model-based multiobjective estimation of distribution algorithm. IEEE Trans Evol Comput 12(1):41–63
Zhang Q, Liu W, Tsang E, Virginas B (2010) Expensive multiobjective optimization by moea/d with Gaussian process model. IEEE Trans Evol Comput 14(3):456–474
Zhang Q, Zhou A, Zhao S, Suganthan PN, Liu W, Tiwari S (2008b) Multiobjective optimization test instances for the CEC 2009 special session and competition. University of Essex, Colchester, UK and Nanyang Technological University, Singapore, Special Session on Performance Assessment of Multi-Objective Optimization Algorithms, Technical Report
Zitzler E, Deb K, Thiele L (2000a) Comparison of multiobjective evolutionary algorithms: empirical results. Evol Comput 8(2):173–195
Zitzler E, Deb K, Thiele L (2000b) Comparison of multiobjective evolutionary algorithms: empirical results. Evol Comput 8(2):173–195
Zitzler E, Laumanns M, Bleuler S (2004) A tutorial on evolutionary multiobjective optimization. In: Gandibleux X, Sevaux M, Sörensen K, T’Kindt V (eds) Metaheuristics for multiobjective optimisation. Lecture Notes in Economics and Mathematical Systems, vol 535. Springer, Berlin
Zitzler E, Laumanns M, Thiele L (2001) SPEA2: improving the strength Pareto evolutionary algorithm. TIK Report 103, TIK Institut fur Technische Informatik und Kommunikationsnetze, Computer Engineering and Networks Laboratory, ETH, Swiss Federal Institute of Technology, Gloriastrasse 35, 8092 Zurich
Zitzler E, Thiele L (1998) An evolutionary algorithm for multiobjective optimization: the strength pareto approach. Citeseer
Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput 3(4):257–271
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by A. Di Nola.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rostami, S., Shenfield, A. A multi-tier adaptive grid algorithm for the evolutionary multi-objective optimisation of complex problems. Soft Comput 21, 4963–4979 (2017). https://doi.org/10.1007/s00500-016-2227-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-016-2227-6