1 Introduction

Demographics, particularly age, are key factors in predicting mortality risk during public health emergencies, such as the current COVID-19 pandemic. According to early estimates, the COVID-19 pandemic would be responsible for at least 3 million deaths globally in 2020, which is 1.2 million more deaths than were officially registered (Wang et al. 2022). Authorities throughout the globe reacted to the issue by establishing a variety of steps to limit the spread of the disease. Measures include of fast diagnostic testing of suspected cases, contact tracking and isolation of people, social distance, face mask use in public, and a community-wide lockdown; see for example Torres-Signes et al. (2021), Eikenberry et al. (2020) and the references therein.

The effects of these actions led in unthinkable disruptions to the economic and social well-being of communities around the globe (United Nations Development Programme 2020). For instance, according to the U.S. Bureau of Labor Statistics, the United States (US) unemployment rate rose by \(10.3\%\) to a record \(14.7\%\) in April 2020 as a result of these mitigating efforts (Fairlie et al. 2020). This was the highest rate and most substantial over-the-month increase in history. According to the data, the number of jobless climbed by 15.9 million to around 23.1 million in April 2020. Furthermore, data obtained earlier during the pandemic revealed that COVID-19 disease caused more severe sickness and mortality among older people and those with commodities (Wenjun et al. 2020; Chen 2023). The probability of death from COVID-19 illness grows with age, according to a report from a rigorous examination of the disease’s effects on persons of various ages (Mallapaty 2020).

In addition, the pandemic has had a more severe effect on the health outcomes of those who are older than those who are younger. This is particularly true for elderly adults. According to the findings of a recent study, the COVID-19 mortality rate is much higher among persons over the age of 65 than it is among younger age groups (Christopher et al. 2020). This is due to a number of reasons, including age-related changes in the immune system as well as the presence of underlying health disorders, all of which can raise the risk of severe disease and death as a result of the virus. To establish efficient treatment and prevention strategies to manage the outbreak, it is of the utmost importance to determine the effect of age on mortality risk (Bonanad et al. 2020; Behrooz et al. 2022). Traditional experimental clinical research, on the other hand, may not be the most effective strategy for identifying important risk factors for emerging diseases. These studies frequently depend on limited samples of patients and put their attention solely on confirming a small number of possible risk variables. A lack of generalization may also be present, as well as an inability to evaluate the identified risk variables in terms of the impact they have on patients.

Pandemic-related restrictions and lockdowns have made it much more difficult for older folks to receive medical care, despite the fact that access to healthcare is already difficult for many older adults owing to mobility concerns or lack of transportation. This can result in a delayed diagnosis and treatment, which further exacerbates the health problems experienced by older persons. Moreover, due to the rapid increase in COVID-19 incidence and mortality rates reported in Europe, the United States, and Latin American countries in the weeks following the initial outbreak (O’Driscoll et al. 2021), as well as COVID-19-related deaths and deaths from other diseases that were found to increase with age, which were higher in men 60 years of age and older compared to women (Bilinski and Emanuel 2020; Banerjee et al. 2020), this study addresses the limitations of pandemic mortality risk analysis by developing an age-stratified compartmental model that considers the age-dependent progression of pandemics. Our model employs a comprehensive multi-category model framework to classify the population into several age groups and study potential risk variables linked with pandemic deaths from a dynamic standpoint.

As a proof of concept for our proposed paradigm, using actual data from the U.S. states of Connecticut, North Dakota, and South Dakota, we evaluated the performance of our age-segregated model using widely accepted numerical measures. Our research provides valuable insights for healthcare administrations looking to better comprehend and manage the mortality risk associated with COVID-19. By constructing an age-stratified model that takes into account the complicated interaction between age and pandemic, we provide a more complete method for assessing mortality risk that is easily understood and applicable in intervention.

The following sections of our study explain in detail our suggested age-stratified model as well as the computational methods we employed to tackle the fitting optimization problem. Section 2 reviews related studies from the literature. In Sect. 3, we describe the design of the model and the methodology used to divide the population into several age groups. We also describe the methods used to look into possible risk factors linked to COVID-19 deaths. Section 4 displays the simulation results achieved by using our proposed methodology. We present a detailed analysis of these findings and provide insights into the factors influencing the observed patterns. In the last sect. (Sect. 5), we provide an in-depth discussion of our findings, draw conclusions based on the results of our analysis, and suggest directions for future research.

2 Background

The COVID-19 pandemic has underlined the role of demographic factors in determining mortality risk. As a result of the pandemic, researchers have focused on identifying risk factors and developing treatment protocols. Age, gender, and race play a significant role in determining the mortality risk associated with COVID-19. Particularly, older adults have been shown to be at a greater risk of severe illness and death from the virus, while certain racial and ethnic groups have been disproportionately impacted (Bonanad et al. 2020). For this reason, several theoretical and experimental research on Covid-19 disease outbreak has been carried out to better understand the mechanisms of transmission and control, as well as to assess the effect of mitigation measures and the mortality risk posed by the COVID-19 disease; see Lai et al. (2021), MK and Antoni (2022). However, many of these studies have limitations that do not adequately account for the complexity of the interaction of multiple health factors on the severity of the outcome, especially for vulnerable populations.

Contributing to the advancement of public health policy and comprehension, mathematical modeling has been essential in advancing our knowledge of the transmission mechanisms and burden of the COVID-19 disease. The majority of mathematical models of the COVID-19 pandemic can be broadly classified as population-based, SIR (Kermack-McKendrick)-type models driven by (potentially stochastic) differential equations (Hamam et al. 2022; Raza et al. 2022), or agent-based models, in which individuals typically interact on a network structure and exchange infection stochastically (Calatayud et al. 2022; Raza et al. 2022). For example, Ahmed et al. (2021) recently extended an SEIR model to account for nonlinear incidence rates and the effects of random movement of individuals from different compartments in their environments, resulting in a novel reaction-diffusion model for the spread of COVID-19. The observed dynamic and steady-state stability of virus spread is found to be substantially influenced by individuals’ random motions.

Risk factors for COVID-19 associated mortality and mental health issues have been studied; see, for example, Aritz et al. (2022), Ziyadidegan et al. (2022). In Zhou et al. (2020) published a retrospective cohort analysis that revealed many risk factors for mortality among hospitalized COVID-19 patients in Wuhan. The research found older age, a high Sequential Organ Failure Assessment (SOFA) score, and d-dimer levels over one \(\mu\)g/mL as possible risk indicators that might assist doctors in identifying patients with a poor prognosis. Fadoua and Dirk (2020) developed an age-stratified discrete-time model of the COVID-19 outbreak that examined the effect of easing lockdown measures and forecasted the overall history of the number of infected, hospitalized, and died people in Switzerland. Their data indicate an average infection mortality rate of \(0.4\%\), with a striking maximum of \(9.5\%\) among those aged 80 and older (Fadoua and Dirk 2020). Using K-means clustering and classification techniques, Ziyadidegan et al. (2022) present a comprehensive list of factors that influence the risk level of COVID-19 across all United States counties. These variables were found to influence the risk level. It was discovered that among the most significant characteristics are the percentage of elderly individuals, the percentage of uninsured individuals, the number of intensive care unit beds per 10,000 individuals, and the percentage of smokers. Aritz et al. (2022) identified regions with high mortality risks for COVID-19 in small English areas during the first wave of the epidemic in the first half of 2020 by evaluating various statistical models. Ethnic isolation, air quality, and area morbidity were identified as covariates with a significant and comparable impact on COVID-19 mortality, whereas nursing home location appears to be marginally less significant.

Table 1 Reported odd ratio with 95% CI for excess death rates stratified by age for men and women in Peru in 2020 (Ramírez-Soto et al. 2022)
Full size table

Furthermore, Ramírez-Soto et al. (2022) used weekly death data extracted from 25 Peruvian regions to conduct a meta-analysis study, which revealed a continuous age-dependent increase in the number of excess deaths in men and women, as shown in Table 1. Men and women had 2.08 (95% CI 1.59–2.73) and 1.67 (95% CI 1.41 to 1.96) times higher odds of excess mortality when compared to expected mortality, respectively. Men aged 40–79 had a twofold increase in the risk of premature death. Men aged 60–69 had 3.23 (95% CI 3.15\(-\)3.31) times the odds of excess mortality, while women had 2.23 (95% CI 2.16\(-\)2.29) times the odds.

Since the studies mentioned above either relied on clinical data and were conducted in a clinical setting or were restricted to the use of a basic dynamical model, there is currently no well-established and intuitive model accepted and used in determining age-based mortality. In addition, most of these models are based on complex calculations and parameters that can be difficult for the healthcare administration to comprehend. Table 2 provided some statistical data from early clinical studies on the effect of age on mortality in COVID-19 patients; see David Yanez et al. (2020) for more information. It reported the total number of COVID-19 deaths and COVID-19 mortality rates (per week per million) for the six age and gender groups.

Table 2 Total deaths and weekly death rates per million, stratified by age and gender (David Yanez et al. 2020)
Full size table

We utilize these previously established model frameworks for transmission dynamics to explore the potential risk factors associated with fatalities from a dynamic point of view using real data from the United States. In particular, we propose to investigate a generalized multi-category model grouped by age that stratifies the whole population into different age group. There are three key contributions made by this study: First, we develop an age-stratified model of the COVID-19 illness for the United States that considers the age-dependent course of COVID-19 in order to better analyze the influence of age on mortality and determine the number of cases and deaths. Second, we evaluate the performance of the age-stratified model by solving the fitting optimization problem using the Levenberg-Marquardt method; and then we compare the outcome to the comparable model without age stratification. Using commonly accepted numerical measures, we evaluate the age-dependent model using real-world COVID-19 data from the U.S. states of Connecticut, North Dakota, and South Dakota.

Fig. 1
figure 1

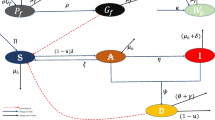
Flow diagram of the non age-stratified ODE model (2.1), indicating the transition of individuals from susceptible state to the recovered or death states through symptomatic and asymptomatic states

Full size image

3 Materials and methods

3.1 Data collection

The Center for Systems Science and Engineering at Johns Hopkins University and the Connecticut Health and Human Services Department compiled the data for this study (Ensheng et al. 2022; Connecticut Health and Human services Department 2021). Beginning on April 12, 2020 and ending on November 16, 2020, North and South Dakota state-level time series data were collected. After the initial surge of COVID-19 cases across the two states and through the summer of that year, when the two Dakotas experienced a massive second wave of the pandemic, these dates are considered to represent when the U.S. government partially lifted its lockdown measures. It consists of 219 observations and populations for each state, in addition to their reported cumulative cases of confirmed infection, recovery, and death. While data were collected for the state of Connecticut between October 5, 2020 and January 19, 2021. It includes the cumulative confirmed infection, the probable confirmed infection, the cumulative death, the probable death, and the total daily death, all stratified by age group.

3.2 Model with no age stratification

Firstly, we present the non-age-stratified model, which is based on the model in Eikenberry et al. (2020), with some modifications. The current model divides the entire human population at time t, denoted by N(t), into six distinct categories. These categories include S(t), E(t), I(t), A(t), R(t), and D(t). Hence,

$$\begin{aligned} N(t) = S(t)+E(t)+I(t)+A(t)+R(t)+D(t) \end{aligned}$$

.

The resulting model (as depicted in Fig. (1) and the variables as described in Table 3 with model parameters in Table 4 is represented by the following nonlinear systems of deterministic ordinary differential equations (ODE) below,

$$\begin{aligned} \begin{aligned} \frac{\text {d}S}{\text {d}t}&=-\beta \left( I+\eta A\right) \frac{S}{N},\\ \frac{\text {d}E}{\text {d}t}&=\beta \left( I + \eta A\right) \frac{S}{N}-\sigma E,\\ \frac{\text {d}I}{\text {d}t}&=\alpha \sigma E-(\gamma ^I+\delta ) I,\\ \frac{\text {d}A}{\text {d}t}&=(1-\alpha )\sigma E - \gamma ^A A,\\ \frac{\text {d}R}{\text {d}t}&=\gamma ^I I + \gamma ^A A,\\ \frac{\text {d}D}{\text {d}t}&=\delta I. \end{aligned} \end{aligned}$$
(2.1)

The transmission rate, represented by the parameter, \(\beta\), is the rate at which susceptible individuals transition into the exposed state. \(\gamma ^I\) and \(\gamma ^A\) represent, respectively, the rates at which symptomatic (infected with symptoms) and asymptomatic (infected with mild or no symptoms) individuals recover from the disease. The parameter \(\sigma\) represents the disease’s incubation period, which is the rate at which an exposed individual transitions into an infectious state. The parameter \(\eta\) represents the relative infectiousness of asymptomatic individuals relative to symptomatic individuals, while \(\alpha\) represents the proportion of symptomatic cases. Approximately \(40\%\)–\(45\%\) of reported cases of SARS-Cov-2 infection involve asymptomatic individuals (Oran and Topol 2020), who are equally capable of transmitting the disease as symptomatic cases (Kimball et al. 2020; Zou et al. 2020). In Tables 3, 4, and 5, detailed descriptions of the model’s state variables and parameters, as well as their likely ranges based on numerous modeling and clinical studies, are provided.

Table 3 Description of the state variables for models (2.1) and (2.2)
Full size table
Table 4 Description of parameters for models (2.1) and (2.2)
Full size table
Fig. 2
figure 2

Flow diagram of the age-stratified ODE model (2.2), indicating the transition of individuals between the different states. Each sub-diagram corresponds to an age group k. The dashed lines indicate that the susceptible state of an age group \(S_k\) might be contaminated by symptomatic and asymptomatic cases belonging to all the age groups

Full size image

3.3 Age-stratified model

According to early data on COVID-19 infection reported by early studies, such as citepbonanad2020effect,deutschbein2022age, and the Centers for Disease Control and Prevention (CDC), hospitalization and mortality rates among SARS-CoV-2 infected people are strongly correlated with age. Infected people aged 50–64, according to the report, are four times more likely to be hospitalized and thirty times more likely to die from the disease than those aged 18–29. For these reasons, we propose a dynamical model that categorizes the entire population based on age groups, based on the models investigated previously in Eikenberry et al. (2020), Fadoua and Dirk (2020). Figure 2 depicts the proposed detailed model that stratifies the population based on age groups and describes the dynamics of the SARS-CoV-2 disease:

$$\begin{aligned} \begin{aligned} \frac{\text {d}S_k}{\text {d}t}&=-\beta _k\left( \sum _{j=1}^K I_j+\eta A_j\right) \frac{S_k}{N},\quad \text { for all k},\\ \frac{\text {d}E_k}{\text {d}t}&=\beta _k\left( \sum _{j=1}^K I_j+\eta A_j\right) \frac{S_k}{N}-\sigma _k E_k, \quad \text { for all k},\\ \frac{\text {d}I_k}{\text {d}t}&=\alpha _k\sigma _k E_k-(\gamma ^I_k+\delta _k) I_k,\quad \text { for all k},\\ \frac{\text {d}A_k}{\text {d}t}&=(1-\alpha _k)\sigma _k E_k - \gamma ^A_k A_k,\quad \text { for all k},\\ \frac{\text {d}R_k}{\text {d}t}&=\gamma ^I_k I_k + \gamma ^A_k A_k,\quad \text { for all k},\\ \frac{\text {d}D_k}{\text {d}t}&=\delta _k I_k,\quad \text { for all k}, \end{aligned} \end{aligned}$$
(2.2)

where \(k = 1,2,3,\ldots , K\), and K is the number of different classes of age groups. Figure 2 depicts the flow diagram of the model with age groups. The parameters \(\gamma ^I_k\) and \(\gamma ^A_k\) are the rates at which symptomatic and asymptomatic individuals recovers associated to age group k, respectively. The parameter \(\eta\) in this case, is the relative infectiousness of asymptomatic persons (in comparison to symptomatic persons) for the age group k, while \(\alpha _k\) is the fraction of cases that are symptomatic for the age group k under considerations. Finally, the parameter \(\delta _k\) is the associated death rates for the age group k.

Observe that each age group is defined with its own parameters and rates because, in practice, the evolution of the COVID-19 differs between individuals and age groups. Also note that, as depicted in Fig. 2, each age group can contaminate the others in the model. In fact, any member of age group k can be infected by a symptomatic or asymptomatic member of the same age group k or a different age group \(k'\ne k\). Therefore, the transmission rate \(\beta _k\) of an age group k is multiplied by \(\left( \sum _{k=1}^K I_k+\eta A_k\right)\). This is expected to improve the evaluation of the COVID-19 evolution and its forecast, as detailed in the section on simulation results.

3.4 Curve fitting optimization problem

This section describes the optimization problem that our curve-fitting model attempts to solve. The Levenberg-Marquard algorithm is used to solve the optimization problem numerically. To fit the model curve to the observed data, we minimize a utility function that includes the mean squared error (MSE) between the observed and estimated data at each day, denoted by j. J represents the number of training days for the model that fits curves. As a result, the optimization problem can be expressed as follows:

$$\begin{aligned} (P) \quad&\widehat{\varvec{X}} = \mathop { }\limits _{\varvec{X}} \sum _{j=1}^{J}\sum _{k=1}^{K} \big (({\widehat{I}}_{k}(j,\varvec{X})-I_k(j))^{2}\nonumber \\&\quad +({\widehat{D}}_k(j,\varvec{X})-D_{k}(j))^{2} \big ),\nonumber \\ \text {subject to: }&\nonumber \\ \text {ODE model in: }&Eq.~(2.2),\nonumber \\ \text {Initialization: }&S_k(0)=S_0^k, \nonumber \\&E_k(0)=E_0^k, \nonumber \\&I_k(0)=I_0^k, \nonumber \\&A_k(0)=A_0^k, \nonumber \\&R_k(0)=R_0^k, \nonumber \\&D_k(0)=D_0^k, \end{aligned}$$
(1)

where \(\chi _k\) represents the initialization value of the observed state \(\chi\) for the age group k with \(\chi \in \{S, E, I, A, R, D\}\). Note that when K is set to 1, (P) is converted to a curve fitting problem for the non age-stratified model. The element \(\hat{I_k}(j,\varvec{X})\) and \(\hat{D_k(j,\varvec{X})}\) denote the estimated values of the state \(I_k\) and \(D_k\) for the age group k at day j given the optimized vector \(\hat{\varvec{X}}\) that includes the list of the target parameters of the ODE model as follows:

$$\begin{aligned}&\widehat{\varvec{X}}=\{\widehat{\varvec{X}}_1,\dots ,\widehat{\varvec{X}}_K\} \end{aligned}$$
(2)
$$\begin{aligned}&\text {where } \widehat{\varvec{X}}_k=\{{\hat{\beta }}_k,{\hat{\sigma }}_k,{\hat{\alpha }}_k,{\hat{\gamma }}_k^I,{\hat{\gamma }}_k^A,{\hat{\delta }}_k\}, \quad \text {for all k}. \end{aligned}$$
(3)

The above optimization problem is formulated as a Non-Linear Least Square (NLLS) problem that cannot be analytically and optimally solved. The problem is solved using the Levenberg-Marquard (LM) (Ramos-Llorden et al. 2018; Lourakis 2005) algorithm, which is one of the most popular NLLS optimization algorithms. In practice, we employed the "lmfit" function in Python.

Table 5 Estimates of the model parameters used in the simulation
Full size table

4 Results

In this section, we compare the fitting and forecasting results for the age-dependent and independent models to assess their efficacy and highlighted the significance of the design that was utilized in the present study. Firstly, we start by fitting the two models to the observed data using the Levenberg-Marquardt algorithm and simulate the North and South Dakota data in order to determine the viability of the traditional model (2.1) before using real data to assess our suggested age-stratified model (2.2). Then, we demonstrated the superiority of the proposed approach by comparing our results with other recently established age-dependent COVID-19 studies.

Fig. 3
figure 3

Fitting and forecasting results for (cumulative) infectious, recovered, and death tolls for the States of North and South Dakota, using the non age-stratified model

Full size image

In Fig. 3, we illustrate the results of fitting and forecasting of the cumulative infectious, recovered, and death rates for the states of North and South Dakota using the previously introduced traditional non-age-stratified model (2.1). Our initial assessment of the non-age model demonstrated that when the model parameters are optimized on real data during the training process, it produces good simulation results. In addition, the predicted results for the next 45 days are displayed without any prior knowledge of the actual data. The purple vertical line marks the distinction between fitting and forecasting. These graphical results for the states of North and South Dakota, as shown in Fig. 3, validate the accuracy of the fitting for the traditional non-age-dependent model. Furthermore, the model correctly fits the actual data during the training phase and follows the virus’s evolution trend during the forecasting phase. In the following section, we show how the proposed age-dependent model approach outperforms other recently established studies by fitting age-stratified real data from the state of Connecticut in the United States and providing different comparison scenarios.

4.1 Comparison of the proposed age dependent/independent models: the case of Connecticut

This section examines the situation in Connecticut due to the availability of data for various age groups. We evaluate the efficacy of curve fitting for the proposed age-stratified SEIARD model (2.2) and compare its results (predictions) to those of the traditional model (2.1), which does not include age groups. But first, we use the traditional model to simulate the data to determine its viability. According to the original data obtained from the Connecticut health and human services department, the population is assumed to be divided into eight distinct age groups indexed by (1) the first band representing 0–39 years and (2) the second representing 10-year age bands (40’−49’, 50’−59’, 60’−69’, 70’−79’, and 80+). Recent studies have also used age stratification to estimate contact rates and excess all-cause deaths of the COVID-19 pandemic; see, for example, Pooley et al. (2022), Ramírez-Soto et al. (2022). Ramírez-Soto et al. (2022), in particular, designed a cross-sectional study for twenty-five Peruvian regions that included mortality data and estimated excess all-cause deaths and excess death rates during the COVID-19 pandemic. In their study, the P-score was used as the primary outcome measure to estimate excess deaths and excess death rates (observed vs. expected deaths) in 2020 by gender and age (0–29, 30–39, 40–49, 50–59, 60–69, 70–79, and 80+ years). Men were found to have higher age-stratified excess death rates than women, with approximately 100,000 excess all-cause deaths occurring in Peru in 2020. However, given the complexity of the pandemic, a novel dynamic compartmental model that enables efficient inference for different age-structured multiple data sources (demographic, operational, and survey data) arising from the COVID-19 epidemic is required to fill this gap. Motivated by the above previously mention studies and for the sake of readability and clarity, we divided the population into two sub-age groups based on Fig. 2 as follows:

  • First Age Group (AG1): this group contains people aged between 0 and 39.

  • Second Age Group (AG2): this group contains people aged 40 and more.

Figure 4a, b show the fitting (between October 1, 2020 and February 28, 2021) and forecasting (between February 28, 2021 and April 14, 2021) results for the state of Connecticut using the traditional, non-age-dependent model. It represents both the total number of infected people and deaths. Indeed, these graphs show that the traditional model is capable of fitting actual data (blue curve), learning the trend of actual data (red curve), and producing accurate forecasts. In Fig. 4c–f we present the fitting and forecasting results for age group 1 (with an age range of 0–39 years) and age group 2 (with an age range of 40 and more) for the State of Connecticut. The graphical results show that, after fitting its parameters to the real data, the proposed model forecasts the data with reasonable accuracy. Notable is the fact that our results for both AG1 and AG2 indicated a near-perfect match with Connecticut cases reported. Due to the success of our age-stratified model in modeling the complex dynamics of the COVID-19 epidemic, this extends the work of Fields et al. (2021), in which three different age groups were considered but their age-stratified model did not fit the data.

Fig. 4
figure 4

Prediction results for (cumulative) infectious and death tolls for the state of Connecticut, using the age-stratified model

Full size image

To validate the effectiveness of including age groups in our analysis, we compare the results obtained by the traditional non-age-stratified (non AG) and proposed age-stratified (AG) models. These results are shown in Fig. 5. In fact, Fig. 5a, b represent the fitting and forecasting results for the state of Connecticut by analyzing the cumulative number of infected and deaths, respectively. The red line represents the observed data in the graph, while the blue and green lines represent the predicted data for the non AG and AG models, respectively. The blue curve in both Fig. 5a, b closely follows the red curve, indicating that the AG model performs similarly to the traditional model (non-AG) with a slight improvement during the forecasting phase.

Fig. 5
figure 5

Comparison of the fitting and forecasting results for the cumulative number of infected and deaths for AG and non AG models for the state of Connecticut

Full size image

In the subsequent paragraph, we intend to validate the graphical results using the numerical metrics provided in Tables 6 and 7. In fact, the tables contain three distinct types of metrics, each of which investigates a distinct aspect of the model’s performance. The tables evaluate both ODE models for these metrics to determine their fitting and forecasting effectiveness. We defined the metrics as follows:

  1. (a)

    Normalized Root Mean Squared Error (NRMSE): This metric provides insights about the difference between the predicted (denoted by \({\hat{y}}\)) and the measured values denoted by y, see for example Mahmoud et al. (2020). It is expressed as follows:

    $$\begin{aligned} \text {NRMSE} = \frac{\sqrt{\frac{1}{M}\sum \limits _{\begin{array}{c} m=1 \end{array}}^{M}{(y_m -{\hat{y}}_m)^2}}}{\max (y_m)-\min (y_m)}, \end{aligned}$$
    (4)

    where M is the total number of observed realizations.

  2. (b)

    Mean Symmetric Absolute Percent Error (MSAPE): This metric provides insights about the percentage of the difference between the approximated and observed values, see, for example, Seo et al. (2018). It is expressed as follows:

    $$\begin{aligned} MSAPE = \frac{1}{M} \sum \limits _{\begin{array}{c} m=1 \end{array}}^{M}{\frac{|y_m - {\hat{y}}_m|}{\left( \frac{y_m + {\hat{y}}_m}{2}\right) }}, \end{aligned}$$
    (5)
  3. (c)

    \(R^2\): This metric provides insights about the error with regards to its real observed values, see, for example, Sardar et al. (2022). It is expressed as follows:

    $$\begin{aligned} R^2 = 1-\frac{\sum \limits _{\begin{array}{c} m=1 \end{array}}^{M} (y_m - {\hat{y}}_m)^2}{\sum \limits _{\begin{array}{c} m=1 \end{array}}^{M}(y_m-{\bar{y}})^2}, \end{aligned}$$
    (6)

    where \({\bar{y}}\) is the mean value of the observed data.

The metrics in the two Tables 6 and 7 indicate that the proposed AG model outperforms the non-AG model in both the fitting and forecasting scenarios. As indicated by the R2 metric, the forecasting results have improved significantly. For instance, the R2 metric associated with the infected cases increases from approximately 0.672 to approximately 0.892 when the age-stratified model is utilized instead of the traditional non-AG model. Similar observations can be made about the cumulative number of deaths, although the difference in this case is minimal. Therefore, by separating the data into distinct age groups, the model is able to better fit the curve and provide accurate forecasts for each age group because it is executed on homogeneous categories with very similar characteristics, unlike the traditional non-AG model.

Table 6 Numerical validation of the fitting results
Full size table
Table 7 Numerical validation of the forecasting results
Full size table

5 Discussion and conclusions

This paper proposes a generalized age-stratified Kermack-Mckendrick epidemic model for the transmission dynamics of COVID-19 to more precisely assess the effect of age on mortality in North Dakota, South Dakota, and Connecticut. Six states comprise the model: susceptible, exposed, infectious with symptoms, infectious without symptoms, recovered, and death. The model consists of deterministic nonlinear differential equation systems. This model was used to investigate the potential risk factors associated with COVID-19 spread and mortality using data from the Johns Hopkins University Center for Systems Science and Engineering and the Connecticut Health and Human Services Department. In particular, we evaluated the performance of the age-segregated model by solving the fitting optimization problem with the Levenberg-Marquardt algorithm, and then comparing the results to those of the model without age stratification.

In addition to concerns about the different COVID-19 variants and influenza viruses that typically circulate during the fall and winter seasons, numerous questions have been raised about their potential effects on various age groups. According to the United States Center for Disease Control and Prevention (CDC), COVID-19 is more likely to cause severe illness in elderly people. These individuals require hospitalization, intensive care, or a respirator due to severe illness. According to the CDC, the death rate for 30–39-year-olds is four times that of 18–29-year-olds, 35 times that of 50–64-year-olds, and 610 times that of those 85 or older (Hosseini-Motlagh et al. 2023; Taylor and Taylor 2023).

In summary, our findings indicate that by age-stratifying the COVID-19 model describing the spread of the illness, a more accurate evaluation and prediction of the disease’s progression may be produced compared to those derived from the non-age stratified model. Based on the findings of our study, the age group most likely to be affected by the COVID-19 epidemic in the United States (or elsewhere) was the senior population. It provides age-dependent models that are based on real-time epidemiological data from the different states in the United States. When policymakers make decisions on how to curb outbreaks of similar infectious diseases while reducing pressures on the healthcare system in the future, their choices can be tailored to account for population demographics and specifically consider the prevalence of people age 65 or older by utilizing our age-dependent compartmentalization model in the population in specific regions or communities where nursing homes are located (David Yanez et al. 2020). Our findings lend credence to the usefulness of the proposed model; we can see that it provides an accurate representation of the training data and that it tracks the progression of the virus over the course of the forecasting period. According to our research, an older population is not only more likely to become infected but also more likely to exhibit clinical symptoms.

The age-stratified model forecasts have implications for the anticipated global burden of COVID-19. These differences in demographics are the reason for these implications. It is possible that areas with older populations will experience a disproportionate number of deaths if appropriate control measures are not implemented. These real-time estimates may help regional public health officials make decisions, and they highlight the importance of implementing holistic models that take into consideration age as well as other demographics such as gender, ethnicity, and other similar factors. Future research could be conducted to create a dynamical model that analyzes factors that, aside from age, make the elderly population particularly susceptible and vulnerable to a serious infection with complications and a higher mortality rate. Lastly, our method can be applied to a variety of domains, including stochastic gonorrhea epidemic models (see, for example, Raza et al. 2019), and nonlinear stochastic Nipah virus epidemic models (see, for example, Raza et al. 2021), and can be augmented with additional epidemic data.