1 Introduction

Infectious diseases are the main cause of health hazards in the world and are responsible for deaths of millions of people around the world (WHO 2019). Various outbreaks of infectious diseases have occurred throughout human history, and indeed there is currently a global health pandemic caused by the novel Coronavirus disease (COVID-19). More than 90 million people have been infected and more than 2 million people have lost their lives since January 2021 due to COVID-19 (Wu et al. 2020; Worldometer 2020). To contain the spread of this virus, various regulations such as social distancing measures, travel restrictions, and city or nation-wide lockdowns have been put in place by policy makers around the world. These regulations, although effective in containing the spread of the disease, have also impacted the daily lives of people, social behavior and the global supply chain (Jones et al. 2008). The transmission of general infectious diseases (e.g. COVID-19) exhibits spatio-temporal patterns and can be predicted based on ecological, environmental and socio-economic factors (Anno et al. 2019; Yang et al. 2020). Prediction of these infections is important for government and health workers to plan for effective mitigation by prioritizing the actions of prevention and control measures (Remuzzi and Remuzzi 2020).

Human movement typically stimulates the introduction of infectious diseases into a new region. There are various evidences that due to human movement, a region-specific disease is introduced to a new region (Nunes et al. 2014; Stoddard and [Steven T], Morrison A. C., Vazquez-Prokopec G. M., Soldan V. P., Kochel T. J., Kitron U, Scott T. W. 2009) and spreads locally (Stoddard and [Steven T.], Forshey B. M., Morrison A. C., Paz-Soldan V. A., Vazquez-Prokopec G. M., Astete H, Scott T. W. 2013; Gross et al. 2020). Indeed, a number of recent studies have incorporated human movement factors into the modeling strategy (Massaro et al. 2019; Mukhtar et al. 2020; Kraemer et al. 2020). For example, the increased human mobility in western Africa had a high impact in making the Ebola virus catastrophic (Farrar and Piot 2014). Bogoch et al. (2015) studied the air transport data of flights going out of the Ebola virus affected countries, finding air transport also one of the reasons for the transmission. In the case of COVID-19, it is also seen that the measures related to human movements, such as travel restrictions and social distancing, have been effective in containing the diseases (Kraemer et al. 2019; Fang et al. 2020). It is a fact that the introduction of human mobility in epidemiological studies has been more accessible due to technological advancements in locational services and availability of movement data (Guinness 2016; Sedlar et al. 2019). In this context, availability of technologies such as WiFi or cell phone tower positioning systems and global navigation satellite systems have made the analysis of mobility much easier (Gonzalez et al. 2008; Toch et al. 2019).

The spread of infectious diseases in space and their outbreak in time constitute a complex spatio-temporal problem, which is an effect of complex dynamics of human behavior, environment, and their interactions. Furthermore, as reported in Pan et al. (2020), during pandemics the human mobility pattern changes compared to that of other times which makes the problem more complex and difficult to analyze. Deep learning methods have proven to be suitable for modeling such complex problems (Mosavi et al. 2020). Indeed, some researchers have used neural networks, and some of them with human mobility data, to model the spread of infectious diseases (Ak et al. 2018; Titus Muurlink et al. 2018; Anno et al. 2019; Akhtar et al. 2019; Wieczorek et al. 2020; Kapoor et al. 2020). Similarly, studies on the development of geographically weighted artificial neural networks (Hagenauer and Helbich 2021), and on geographically and temporally neural network weighted regression (Wu et al. 2021) based on geographically weighted regression have inspired the way of developing neural networks to model spatio-temporal non-stationary relationships. Neural network-based methods rely on a hidden stage to learn from the data and are unable to explicitly account for the spatial and spatio-temporal random effects. However, although these methods have performed well, they are unable to provide uncertainties in the predictions, which we believe are essential in statistical inference and probabilistic forecasting. We argue that predictions accompanied with uncertainties provide further confidence on the results (Beale and Lennon 2012). To incorporate uncertainties in neural networks, Bayesian neural networks have been developed (Kononenko 1989; Dhamodharavadhani et al. 2020) and applied over various spatio-temporal problems (McDermott and Wikle 2019). However, in the field of modeling and understanding the dynamics of COVID-19, the use of neural networks in combination with Bayesian inference is limited. Cabras (2020) presented a method of combining neural networks with Bayesian inference having a focus on COVID-19 infections in Spain. However, mobility and its influences were not considered. As spatio-temporal predictions help in understanding the spread of the disease to further identify the regions of high risk, a large number of papers can be found in the field of spatio-temporal modeling of diseases. Among them, generalized linear models (GLM) with the addition of spatial effects of nearby places and/or temporal effects from past events are found to be often used and proven to be useful in prediction (Cabrera and Taylor 2019; Giuliani et al. 2020; Guo et al. 2017). For example, Giuliani et al. (2020) have used GLM to predict COVID-19 infections in regions of Italy, and found the spatial interactions of nearby places to have a high influence on modeling; this shows the importance of accounting for the spatial effects explicitly. In a parallel vein, Bayesian modeling methods have also been used in this epidemiological context (Aswi et al. 2019; Song et al. 2019; Torres-Signes et al. 2020; Gelman et al. 2013).

The main objective of this paper is to use deep learning methods (using a Long Short Term Memory-LSTM) informing a Poisson regression model in a Bayesian framework to model and predict the spread and outbreak of COVID-19 with uncertainties. In particular, human mobility data along with socio-demographic variables are incorporated in the combined model to predict the dynamics of COVID-19. In doing so, we highlight the importance of human mobility in modeling the dynamics of infectious diseases.

The plan of the paper is as follows. Section 2 presents the data along with all covariates considered in the model to motivate the proposed statistical model. We also consider some spatial weights built from the movement data. Section 3 presents the statistical model, and the results come in Sect. 4. The paper ends with some conclusions and a discussion in Sect. 5.

2 Study area and data

Daily COVID-19 infections aggregated per 245Footnote 1 health zones in the community of Castilla-Leon (Spain) were used in this paper. The temporal range goes from March 1, 2020 to February 5, 2021. Castilla-Leon is the largest community in Spain by area located in the northwest part of Spain. This region has a population of around 2.5 million and is ranked third among the communities in offering social services to the citizens.

Figure 1 shows the location map of Castilla-Leon and the status of the COVID-19 spread in the health zones of the Community. The cumulative cases in the health zones are until 2021-02-05. The health zones with most cases are represented in darker red color. We note that COVID-19 has spread throughout the study area with clusters around major urban areas.

Fig. 1
figure 1

a location of Spain; b location of Castilla-Leon in Spain; c Cumulative numbers of COVID-19 cases per 10000 inhabitants and health zones; d Histogram showing number of health zones of Castilla-Leon by cumulative cases per 10000 inhabitants

Full size image

Figure 1c represents some of the health zones with highest cumulative cases of COVID-19 per 10000 inhabitants, such as Guijuelo (2330), Sacramenia (2290), Sepulveda (2211) and San Ildefonso (2194). For the purpose of this study, we have depicted the temporal distribution of the following four selected health zones Avila Estacion, Casa del Barco, Las Heulgas and Ponferrada II, because the number of COVID-19 infected cases in these health zones is distributed throughout the study period and there is a particular variability in the number of cases. The locations of these selected health zones are highlighted in the map.

COVID-19 cases data were retrieved from the open data portal of Castilla-LeonFootnote 2. Similarly, the socio-demograhic datasets and the health zone boundary, in shapefile form, were downloaded from the open data platform of Instituto Nacional de EstadísticaFootnote 3. The human mobility data for the study area was acquired from Barcelona Supercomputing Center flowmap dashboardFootnote 4. A brief description and source of the datasets used in the current paper are reported in Table 1.

Table 1 Summary of data used and their sources
Full size table

Figure 2 shows the daily number of COVID-19 cases per 10000 inhabitants. The highlighted red line represents the daily mean number of cases per 10000 inhabitants. The cases increased in March and April 2020 (defining the first wave), and then started to decrease until August 2020 due to the imposed lockdown measures. However, due to a certain relaxation towards the summer period, the cases started to increase late August to end up with a second wave in October and November 2020. A third wave of infection is noted in January and February 2021, and started to decrease again due to some partial restrictions and the onset of the vaccination program. Similarly, weekly trends in the number of cases is visible with a drop of cases on weekends, due to the reduced number of tests done over the weekends.

Fig. 2
figure 2

Temporal trend of COVID-19 cases in the study area. The orange line represents the daily mean number of cases in all health zones per 10000 inhabitants

Full size image

The mobility data acquired from the data portal of Barcelona Supercomputing Center was prepared by the Ministry of Transport, Mobility, and Urban Agenda. The data was preprocessed to guarantee anonymized records from mobile phones. These recorded events contain both active events also known as Call Detail Records (CDR) and passive events with a periodic update of device position, change of coverage area, etc. The location information is at the level of the coverage area of each antenna, which is merged to create origin-destination matrices at municipality, districts and provinces level. Along with these records from the cell phones, landuse data, population data, transport network data such as train lines, and location of airports have been used to create the merged matrices (Ministry of Transport and Agenda 2020). The available daily mobility data was at the municipality level; those municipalities with population less than 1000 were combined to form aggregated zones. As all other available data were at the health zones level, these aggregations were converted to the health zone level by applying spatial overlay functions and dividing the movement data in proportion to the area. The socio-demographic covariates considered in this paper were the following: total population per health zone, number of people demanding for employment, number of unemployed people, number of commercial units, office units, and industrial units in the urban areas of each health zone (see a description in Table 2). Additionally, we also considered some built-in variables (see Table 3). In particular, we computed the average number of cases and average number of deaths in the direct neighborhood. The cumulative cases of COVID-19 for the last 14 days were also computed to consider the aggregated impact for a short time frame.

Table 2 Summary of socio-demographic variables
Full size table
Table 3 Summary of built-in variables
Full size table

Last, but not least, we introduce new spatial weights based on the movement data that represent the associated movement-based risk. These weights are computed per health zone and day. We add a temporal lag to handle past-term movement data and the daily data are weighted depending on the temporal distance.

These spatial weights take into account the mobility from all other regions j into region i, and the weights are interpreted as the chance of a moving person to import the infection of the disease into region i from all the other regions. This spatial weight for a region i and day t, \(W_{i, t}\), can be computed as

$$\begin{aligned} {W}_{i, t}= \sum _{j=1}^{n} \left[ \sum _{t' = t-1}^{t - \varDelta t} m_{ji, t'} * w'_{t'} \right] * \frac{I_{j, t}}{P_{j}} \end{aligned}$$
(1)

where n is total number of regions, \(m_{ji,t}\) is the mobility from all regions j to i on day t, \(I_{j, t}\) is the number of infected cases at region j at time t, \(P_j\) is the total population of the region j and \(w_t'\) is the weight given to the mobility data on day t.

A time lag \(\varDelta t\) is added to the computation of the spatial weights as the spread of a disease on the region is dependent on the mobility and infections on past days in all other regions of the study area. We used a 7-day lag as infection is assumed to act a week before first symptoms. We assigned the following weights: given t, we give \(t-1\) and \(t-2\) only a weight of 5%, this weight increases up to 10% for \(t-3\) and \(t-4\), then goes up to 20% for \(t-5\) and \(t-6\), and finally the weight is 30% for \(t-7\).

Figure 3 shows the temporal series of the spatial weights for the four selected health zones along with the daily number of COVID-19 cases for the study period. It is evident that increasing weights correspond to increased COVID-19 cases. Similarly, Fig. 4 shows the flowmap of the median mobility for the week 2021-01-30 till 2021-02-05, prepared with the flowmapblue R packageFootnote 5, and the spatial distribution of the spatial weights for the same period.

Fig. 3
figure 3

Spatial weights and COVID-19 cases for the selected health zones

Full size image
Fig. 4
figure 4

For the last week of study period 2021-01-30 till 2021-02-05: a Flowmap of the study area with the median mobility; b Spatial distribution of median values of spatial weights

Full size image

Summarizing, our model is feeded by COVID-19 covariates, socio-demographic covariates and human movement-related covariates. COVID-19 covariates include cumulative cases, average number of cases in neighboring health zones, deaths and average number of deaths in neighboring health zones, and spatial weights computed from the daily mobility matrices and infection. A temporal covariate, day of the week, was computed as a factor from the date.

3 A Bayesian LSTM method

We use here the term Bayesian LSTM method, to indicate that we use a statistical model within a Bayesian framework informed by the output of a Long Short Term Memory (LSTM) neural network method. We aim to model the number of infections on an areal unit, in our case health zones, based on spatial covariates, temporal trends, and mobility matrices. Thus our combined model considers temporal and spatial dependence structures, and provides predictions in space and time of the number of infections.

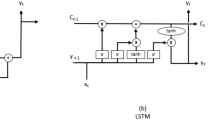
Figure 5 shows a graphical overview of the proposed model which contains two major components: (a) a deep learning method (LSTM), and (b) a Bayesian spatial Poisson regression model. The input to the LSTM method are the temporal series of the cases of infections. The LSTM method learns from these temporal series and predicts the number of cases in the future. Predictions from the LSTM method are embedded into the Poisson regression as an expected value. The spatial correlation structure is modeled using a stochastic partial differential equation (SPDE) method through the Integrated Nested Laplace Approximation (INLA) approach.

Fig. 5
figure 5

Graphical overview of the Bayesian LSTM method

Full size image

3.1 LSTM method

Artificial neural networks are a class of machine learning methods inspired by the functioning of human brain and work on the principle of parallel processing. They consist of layers of interconnected processors known as neurons, which have a vector of weights associated with them. Artificial neural networks models consist of input data also known as input layer, layers of interconnected neurons also known as hidden states, and the output layer which is the output of the model. Fitting an artificial neural network involves estimating the optimal value of these weights which are able to accurately reproduce and mimic some training data. The optimization of these weights is done through the gradient descent method, and the weights assigned to each layer are adjusted proportionally to the derivatives (Bengio et al. 1994).

Among many types of artificial neural networks, recurrent neural networks are arguably the most useful ones for sequential data (as time series) as they have a stack of non-linear units that can learn even long-term dependencies of time series data (Bengio et al. 1994). Recurrent neural networks are built from one or more feedback loops of artificial neurons which are recurrent over time, so they do not only flow forward but in cycles. These cycles represent the influence of the present value of a variable on its own value at a future time step (Goodfellow et al. 2016). In recurrent neural networks, the configuration of hidden states acts as the network memory and the hidden layer state at a time is dependent on its previous state which enables to learn from past data, thus handling long-term dependencies (Mikolov et al. 2014). This makes recurrent neural network an excellent choice for learning and predicting time-dependent data. However, despite having these advantages, as the recurrent neural networks perform the gradient descent method with each timestamp of the data, they are likely to fall into the gradient vanishing problem. Due to this problem, as the recurrent neural network loops through the networks recurrent connections, the effect of a given input on hidden layers, and consequently on the output, either decays or explodes exponentially (Hochreiter 1991). One alternative approach to tackle this problem comes from using a LSTM method (Hochreiter and Schmidhuber 1997), that solves the gradient vanishing problem by introducing LSTM memory cells instead of the hidden units. These LSTM cells consist of input, output and forget gates; the input and output gates are used for the control of the flow of memory cell input and output into the rest of the model, whereas the forget gates are responsible for learning the weights that control the rate at which the value stored in the memory cell decays. With the addition of these gates, the LSTM is able to bypass the vanishing gradient problem while also learning from the long term dependencies in the data (Salehinejad et al. 2018). A dataset with multiple samples, each containing multiple features, comes into LSTM through the input layers one sample at a time. The input data and memory of a hidden layer from the previous time step (t-1), is passed through the three gates, computing the output of each LSTM cell of the time step t, and that is used in the next time step (t+1), and so on for all the time steps of the study period. The LSTM model is fitted with the use of a training dataset which learns all the weights of the cells that connect the input data with the hidden and output layers. The model is finally applied to a new dataset generating the prediction for such data.

In our case, the LSTM method accounts for the temporal trend of the COVID-19 spread, learning from the temporal trend of the infected cases on individual health zones separately, rather than considering the spatial cross-correlation amongst the regions. Note that although, as commented in the Introduction, LSTM methods are lately adapted to also account for spatial structure, in this paper we make use of LSTM to learn only from the temporal trend of infections at individual health zones, leaving the spatial relationships amongst health zones to be accounted for in the Bayesian regression model.

3.1.1 Architecture

We used a four layered LSTM, for which the first layer is the input layer given by the daily time series of COVID-19. In order to create a supervised learning problem, the temporal series of infected cases were converted to an input-output pair which is performed by shifting the data (Brownlee 2017). Thus, for every time step t of the time series, one day ahead shifting is done in the data to create a shifted prediction at \(t+1\). The second layer of the model consists of the 128 LSTM memory cells; similarly, the third and fourth layers consist of 64 and 32 memory cells, respectively. This number of memory cells in each layer comes from experimentation and also motivated by previous works (Shahid et al. 2020). With this configuration, the model has 131489 parameters consisting of three stacked LSTM layers which are recurrently used for the time period T (equal to the total number of days under study). Finally, a dense layer connects all the recurrent layers and connects them to the output layer. The dense layer has the linear activation function. The architecture of the LSTM method is shown in Fig. 6. Additional parameters and hyper-parameters that define the LSTM method are shown in more detail in Appendix B (Table 5).

Fig. 6
figure 6

Architecture of the LSTM method

Full size image

3.2 Spatio-temporal Poisson regression and Bayesian inference

To deal with uncertainty, we consider in a second stage a spatio-temporal stochastic model for the counts of COVID-19 infected cases, which is informed by the output of LSTM run at a first stage.

Let \(Y_{it}\) and \(E_{it}\) be the number of observed and expected cases in the i-th area (health zone) and the t-th period (day), \(t=1,\ldots ,T\). We assume that conditional on the relative risk, \(\rho _{it}\), the number of observed cases follows a Poisson distribution

$$\begin{aligned} Y_{it} | \rho _{it} \thicksim {Po}(\lambda _{it} = E_{it}\rho _{it}) \end{aligned}$$

where \(E_{it}\) are the predicted values from the LSTM model, and the log-risk is modeled as

$$\begin{aligned} log(\rho _{it}) = \beta _0 + Z_{it}^T\beta _{it} + S(x_i) \end{aligned}$$
(2)

with S(.) a spatially structured random effect, and the \(Z_{it}\) stand for the covariates (as mentioned in Sect. 2). We assigned a vague prior to the vector of coefficients \(\beta =(\beta _0, \ldots ,\beta _p)\) which is a zero mean Gaussian distribution with precision 0.001. Finally, all parameters associated to log-precisions are assigned inverse Gamma distributions with parameters equal to 1 and 0.00005.

To compute the joint posterior distribution of model parameters, Bayesian inference has traditionally relied upon Markov Chain Monte Carlo (MCMC) (Gilks 1996; Brooks 2011). This distribution is often in a high dimensional space and thus it is computationally very expensive. As an alternative computationally faster solution, Rue et al. (2009) developed a new approximation to the posterior marginal distributions of model parameters based on a Laplace approximation, and named it as integrated nested Laplace approximation (INLA). INLA focuses on models that can be expressed as latent Gaussian Markov random fields (GMRF). In particular, we use a stochastic partial differential equation (SPDE) method, as introduced by (Lindgren et al. 2011). SPDE consists in representing a continuous spatial process like a Gaussian field (GF) using a discretely indexed spatial random process such as a Gaussian Markov random field (GMRF). Note that conditional autoregressive (CAR) models lead to some counterintuitive or impractical results when irregular lattices are used and/or the ‘cells’ are very different in area (Wall 2004). According to (Bakka et al. 2018) any parameterization of the CAR model must give positive definite precision matrices. Also, setting priors on the CAR parameters needs dealing with the boundaries between proper and intrinsic models (Bakka et al. 2018). The SPDE approach, on the other hand, generates precision matrices with the good computational properties of CAR models and is applicable to any set of observation locations. So, we have used SPDE technique that effectively allows INLA to efficiently compute the spatial autocorrelation structure of the dataset at the mesh vertices.

In particular, the spatial random process S(.) follows a zero-mean Gaussian process with Matérn covariance function represented as

$$\begin{aligned} Cov(S(x_i), S(x_j)) = \frac{\sigma ^2}{2^{\nu - 1} \varGamma (\nu )} (\kappa || x_i - x_j||)^\nu K_\nu (\kappa || x_i - x_j||) \end{aligned}$$
(3)

where \(K_\nu (.)\) is the modified Bessel function of second order, and \(\nu > 0\) and \(\kappa > 0\) are the smoothness and scaling parameters, respectively. INLA approach constructs a Matérn SPDE model, with spatial range r and standard deviation parameter \(\sigma\). The model parameterization is expressed as

$$\begin{aligned} (\kappa ^2-\varDelta )^{(\alpha /2)} (\tau S(x)) = W(x) \end{aligned}$$

where \(\kappa =\sqrt{8\nu }/r\) is the scale parameter, \(\varDelta =\sum _{i=1}^{d} \frac{\partial ^2}{\partial x^2_i}\) is the Laplacian operator, \(\alpha =(\nu +d/2)\) is the smoothness parameter, \(\tau\) is inversely proportional to \(\sigma\) and W(x) is a spatial white noise (Blangiardo and Cameletti 2015). Note that we have \(d=2\) for a two-dimensional process, and we fix \(\nu =1\), so that \(\alpha =2\) in our case.

Fig. 7
figure 7

SPDE triangulation for the study area of Castilla-Leon

Full size image

We use the centroids of each health zone as the target locations over which we build the mesh. The mesh is formed by smaller triangles within the region of interest, and by larger ones outside the region. The constrained refined Delaunay triangulation is illustrated in Fig. 7. The blue line highlights the outline boundary of the study area, with the red dots indicating the centroids of the individual health zones. Note that some few regions show sort of clusters due to the close proximity of health zones. We generate the projection matrix to project the spatially continuous Gaussian random field from the observations to the mesh nodes. Centroids of individual health zones and the triangulations in the mesh are used to generate the projection matrix. We fixed \(r = 0.1\) and \(\sigma ^2 = 1\). Parameters \(\tau\) and \(\kappa\) are renamed as \(\theta _1 = log(\tau )\) and \(\theta _2 = log(\kappa )\), and we assign them zero mean vague Gaussian independent priors with precisions equal to 0.1. In the current study, we have chosen to provide default prior distributions for all parameters in R-INLA, as these have been chosen partly based on priors commonly used in the literature (Martins et al. 2013; Blangiardo and Cameletti 2015; Rue et al. 2016; Moraga 2020). Our results our robust against other alternative similar and justified priors, as we run several cases with different priors obtaining the same results.

4 Results

We fitted our Bayesian neural network approach (named as LSTM-INLA throughout this section) and compared it with two other baseline models, one which is only using a LSTM method (named as LSTM) and the other one that only fits a spatial Poisson regression with INLA and no LSTM (named as INLA). We fitted the models for all the temporal range except for the last week, and used these last 7 days for prediction. The models were evaluated using the averaged Root Mean Squared Error (RMSE) from all health zones. Additionally, we also considered the Bayesian metrics Watanabe Akaike information criterion (WAIC) (Watanabe 2010), deviance information criterion (DIC) (Spiegelhalter et al. 2002) and conditional predictive ordinate (CPO) (Pettit 1990).

Table 4 shows the corresponding metrics, with RMSE evaluated over the training period (RMSE Training) and over only the prediction period (from 2021-01-30 to 2021-02-05, RMSE Prediction).

Table 4 Metrics for model evaluations
Full size table

The RMSE for the LSTM-INLA model is lower than the INLA and LSTM methods for both the training and prediction periods. We note that although the RMSE for the training set is quite as good as for the other two methods, the RMSE for the prediction set for INLA and LSTM is far larger. This suggests that inclusion of LSTM as an expected value for the spatial Poisson regression plays an important role. Similarly, the comparison of INLA and LSTM-INLA models with DIC, WAIC and CPO metrics, shows that the LSTM-INLA combination provides the best fit. The correlation between the observed values and the predicted ones for the prediction period (recall this is the last week of the overall temporal range) is largest when using the combined LSTM-INLA model (0.80) compared to models using only INLA (0.77), and only LSTM (0.75), reinforcing the goodness-of-fit of our proposal.

Figure 8 depicts the observed cumulative cases of COVID-19 at three selected weeks within the overall temporal range and chosen at different phases of the pandemic. We also show the corresponding predictions from the LSTM method and the combined LSTM-INLA model. In particular, first row of Fig. 8 represents the cumulative number of cases on the initial week of COVID-19 spread in Spain, 2020-03-22 to 2020-03-28, second row is for the week 2020-10-18 to 2020-10-24, and third row stands for the 7-days prediction ahead period, from 2021-01-30 to 2021-02-05. A map depicting the prediction from the LSTM-INLA model and observed cases for the final week of the study period is published in an R-Shiny app, which can be accessed through the linkFootnote 6. A sample view of the shiny app is presented in Fig. 11 in Appendix A.

Fig. 8
figure 8

Spatial distribution of the observed cases (left column) of COVID-19 for three selected weeks. Prediction from the LSTM method (central column) and from LSTM-INLA model (right column)

Full size image

To visualize the temporal trends, Fig. 9 shows the observed cases together with the predicted ones for four selected health zones (Avila Estacion, Las Huelgas, Casa del Barco and Ponferrada-II). In particular, we note that we can draw, together with the predictions under LSTM-INLA, the corresponding \(95\%\) credible interval, providing a measure of the uncertainty associated to the prediction, thing that we can not obtain under LSTM alone. Comparing the prediction from the LSTM method (green lines), the LSTM-INLA prediction with 95% credible interval (blue lines) with the observed cases (red lines), we note the better prediction results when using LSTM-INLA. Figure 12 in Appendix D shows the corresponding residual plots. They suggest the better behavior of the LSTM-INLA model as they are lower in magnitude and symmetrically distributed around the zero line. This is also true to the prediction ahead case.

Fig. 9
figure 9

Temporal trend plots of the observed and predicted cases with LSTM and LSTM-INLA models for four selected health zones. The grey band stands for the \(95\%\) credible interval under the LSTM-INLA model

Full size image

Having in mind the model described in Eq. 2, we now put in place some information related to the posterior distribution of fixed and random effects. In particular, Fig. 10 depicts the marginal posterior mean and 95% credible intervals of spatial random effect S(.). ID in the X-axis of Fig. 10 represents 799 triangulation nodes of the SPDE mesh used in the model. A stronger and significative spatial effect is observed basically on the nodes of smaller triangles within the region of interest (as shown in Fig. 7). The nodes outside the region show no spatial effect.

Fig. 10
figure 10

Marginal posterior mean of the spatial random effect \(S(\cdot )\)

Full size image

Additionally, Table 6 in Appendix C and Fig. 13 in Appendix E depict the marginal posterior distributions of all fixed effects including the intercept (\(\beta _0\)) and the other covariates. We note that four covariates, namely number of people demanding for employment, number of commercial offices, number of industrial units and number of office units in the urban areas, have no influence in our model. The positive mean values for covariates such as average cases in neighbouring health zones, cumulative cases, or deaths indicate positive influence in the model. The covariate “Average cases in neighboring health zones” has a positive relationship with the average number of infected cases for a specific health zone. Because COVID-19 is highly infectious, incoming mobility of infected people from neighboring health zones can have a direct impact on the number of infected cases in other health zones. However, increased mortality results in tighter lockdown, limiting mobility between neighboring health zones (dos Santos Siqueira et al. 2020; Alfonso Viguria and Casamitjana 2021). With the decrease in incoming mobility from neighbouring zones the chance of getting infected has lowered. This leads to the decrease in infected cases when there is a rise in mortality level in neighboring zones. Thus, there exists a negative association for covariate “Average deaths in neighbouring health zones”. On the other hand, the covariate associated to daily movement (spatial weight) has the highest positive mean value which indicates strong positive influence of human mobility on the model. Note that we additionally experimented with other spatial weights that affect mobility. For example, we introduced socio-demographic variables to incorporate social behavior of the regions under study while computing the spatial weights, but the outcome of the model was not satisfactory. Similarly, other modifications on the spatial weights were done to check the influence on the prediction, but the chosen spatial weight was found to be the optimal one in terms of prediction.

Finally, Fig. 14 in Appendix E shows the marginal posterior Gaussian distributions of the two hyperparameters for the spatial random field \(\theta _1, \theta _2\). Mean and variance for the two hyperparameters are \(\theta _1=(-3.10, 0.142)\), and \(\theta _2=(3.35, 0.099)\).

5 Conclusions

For modeling the spread and outbreak of infectious diseases, a model comprising the combination of neural network and Bayesian inference for a spatio-temporal Poisson regression has been proposed. This model is able to provide good predictions of further cases of COVID-19 while handling uncertainties. In particular, our model has two components, a LSTM neural network, which learns from the temporal patterns, and a spatial Poisson regression with expected values the predictions coming from the LSTM. The spatio-temporal Poisson regression considers various spatial and temporal covariates. It is noteworthy that we consider daily matrices of population movement that are transformed into spatial weights and act as additional covariates in the model.

The proposed model was evaluated with COVID-19 daily infected cases in Castilla-Leon (Spain), consisting of 245 health zones, and within a temporal range running from March 1, 2020 to February 5, 2021. The combined model was able to predict the number of daily infections in each health zone, outperforming two other cases, one with only a neural network method and the other with only a spatio-temporal Poisson regression. A key and novel aspect is the introduction as a spatial weight of the population movement, being highly influential in the overall fit. However, we note that sudden increasing peaks or abrupt decreasing magnitudes can not be finely fitted by our model. We believe this is due to typos, errors or under-reporting actions, and they clearly mean a challenge for modeling purposes of this sort of data.

6 Discussion

Clearly, the accuracy of prediction may be improved by the addition of other variables relevant to the disease of study which may include the weather conditions and preventive measures. The phenomenon of infectious disease spread has a lot of complexities and is dependent on numerous factors. These factors include the organism causing the disease, the mode of transmission, human behaviors, environmental conditions, and most importantly, some potential preventive measures applied. All of these factors are not quantifiable but a maximum number of these factors are to be considered while modeling the diseases. In this study, one of the most relevant considered factors is human mobility. Some socio-demographic variables were considered but we believe more variables associated with the socio-demography and climatic conditions can be introduced. Similarly, the variables related to human behavior and preventive measures such as social distancing and personal hygiene should be incorporated in future works.

The focus of this work is on the combination of neural networks and Poisson regression within a Bayesian framework. The predictions from neural networks were used as expected values for the Poisson regression which can be improved by transferring the predictions to a prior distribution and use them as prior information in the Bayesian inference. Here we followed a two-stage procedure, but ideally it would be better a joint solution such as spatio-temporal recurrent neural networks able to predict results with uncertainties. Finally, the proposed method is applied only in one scenario of COVID-19 infection for a short period. Thus, data with a longer period and different spatial scales should be used to test the versatility of the model.

The model is believed to be useful for the governments in monitoring any infectious diseases. The results from the model can be used in formulating health-related policies such as the application of preventive measures or vaccination. The contribution of this work is that it is able to take advantage of the neural network methods in learning complex dependencies from the data, as well as from a Bayesian paradigm to associate the uncertainties in the predictions. In conclusion, this work is able to present a model that can provide accurate predictions of infectious diseases and help in a way to mitigate the impacts.