Impact of geostatistical reconstruction approaches on model calibration for flow in highly heterogeneous aquifers

Abstract

Our study is aimed at assessing the extent at which relying on differing geostatistical approaches may affect characterization of the connectivity of geomaterials (or facies) and, in turn, model calibration outputs in highly heterogeneous aquifers. We set our study within a probabilistic framework, by relying on a numerical Monte Carlo (MC) approach. The reconstruction of the spatial distribution of geomaterials and flow simulations are patterned after a field scenario corresponding to the aquifer system serving the city of Bologna (Northern Italy). Two collections of MC realizations of facies distributions, conditional on available lithological data, are generated through two alternative geostatistically-based techniques, i.e., Sequential Indicator and Transition-Probability simulation. Hydraulic conductivity values of the least- and most-conductive facies are estimated within each MC simulation in the context of a Maximum Likelihood (ML) approach by considering available piezometric data. We provide evidence that the choice of the facies reconstruction technique (1) impacts the degree of connectivity of facies whose proportions are close to the percolation threshold while (2) is not sensibly affecting the connectivity associated with facies whose proportions are much larger than the percolation threshold. By relying on the unique (lithological and hydrological) data-set at our disposal, we also explore the performance of ML-based model identification criteria to (1) discriminate amongst competitive facies reconstruction geostatistical models and (2) quantify the (posterior probabilistic) weight associated with each model. We then show that ML-based model averaging provides estimates of hydraulic heads which are slightly more in agreement with available data when compared to the best-performing realization in the T-PROGS set than considering its counterpart associated with the SISIM-based collection.

1 Introduction

Probabilistic reconstruction of complex aquifer systems is nowadays considered a common practice to account for uncertainty resulting from our lack of knowledge of highly-heterogeneous subsurface structures and spatial distribution of attributes of aquifer systems. In a stochastic framework, aquifer heterogeneity can be conceptualized by considering system attributes, such as hydraulic conductivity, as random functions. Widely employed geostatistical methods (e.g., Sequential Gaussian Simulation; Deutsch and Journel 1998) describe hydraulic properties as multivariate Gaussian random fields and quantify the degree of aquifer heterogeneity upon relying on a covariance (or variogram) structure that can be inferred from available data. In the presence of sharp interfaces between high and low-conductivity regions, a composite media approach, considering the system as composed by diverse lithological units (or facies), is typically adopted (Guadagnini et al. 2003; Winter et al. 2006). Categorical rather than continuous random fields can be considered in order to represent the distributions of facies. For this purpose, Sequential Indicator Simulation (SISIM; Goovaerts 1997; Deutsch and Journel 1998), which relies on indicator variograms (inferred, e.g., from borehole lithological data), is one of the most extensively applied methods (Deutsch 2006; Felletti et al. 2006; Marini et al. 2019). While being characterized by ease of implementation, this method may not honor volumetric proportions of facies, as inferred from available data, because it tends to underestimate less-prevalent facies (Emery 2004; He et al. 2009), and/or may not fully capture patterns of facies connectivity (Gomez-Hernandez and Wen 1998; Kerrou et al. 2008), an issue which is particularly noticeable in three-dimensional systems (Dell’Arciprete et al. 2012, 2014). An alternative approach has been embedded in the Transition Probability Geostatistical Simulation approach, T-PROGS (Carle and Fogg 1996, 1997). The latter makes use of available lithological/sedimentological data to evaluate transition probabilities between facies, which are then interpreted through Markov-chain modeling techniques. This approach, as well as other Markov-chain based methods (e.g., Elfeki and Dekking 2001; Li 2007; Langousis et al. 2018), also (1) enables one to include information on spatial juxtapositional tendencies and soft conditioning data and (2) is deemed as more accurate than its covariance-based counterparts to represent volumetric proportions, mean lengths, and connectivity patterns driven by facies distributions (Weissmann et al. 1999; He et al. 2014, 2015; Koch et al. 2014).

Characterization of connectivity is key to quantify the degree of flow heterogeneity and the ensuing early (or late) breakthrough of dissolved chemicals at critical targets (Cvetkovic et al. 2014; Henri et al. 2015; Zinn and Harvey 2003), with direct implications in several contexts, including, e.g., remediation of contaminated sites and environmental risk assessment. Increasing efforts have been devoted to investigate the effects of various geostatistical approaches on connectivity metrics (Bakshevskaia and Pozdniakov 2016; Dell’Arciprete et al. 2012, 2014; Lee et al. 2007; Mohammadi et al. 2020; Sharifzadehlari et al. 2018; Vassena et al. 2010). Other studies addressed the impact different geostatistical methods on the accuracy of estimated facies distribution (He et al. 2009, Kessler et al. 2013; Marini et al. 2019; Park et al. 2007), hydraulic head and flux fields (Lee et al. 2007; Bianchi et al. 2015), or spreading of dissolved chemicals migrating in aquifer systems (Maghrebi et al. 2015; Siirila-Woodburn and Maxwell 2015).

Here, we investigate the extent at which the degree of connectivity resulting from a selected reconstruction method may alter the outcomes of a model calibration process. In this context, we rely on suites of numerical simulations of groundwater flow in the aquifer system serving the city Bologna (Northern Italy), whose internal architecture (in terms of spatial arrangement of geomaterials, or facies) is modeled within a probabilistic Monte Carlo (MC) framework. In this context, we rely on generating collections of equally-probable realizations of spatial distributions of facies conditional on a unique and extensive dataset of lithological information. We rest on the approaches associated with SISIM and T-PROGS and generate two collections (or ensembles) of MC realizations. We then evaluate (1) the variability of connectivity within each of the two sets of facies distributions (hereafter termed intra-ensemble variability), and (2) the extent at which the generation method affects facies connectivity (i.e., the inter-ensemble variability). A groundwater flow model is then calibrated for each MC realization by making use of available piezometric data. Ensuing estimates of hydraulic conductivity, K, are obtained through a Maximum Likelihood (ML) inverse modeling approach (Carrera and Neuman 1986). Our primary goal is to assess whether intra- or inter-ensemble variability of connectivity may have an effect on estimated values of K and their uncertainty. We rely on the ML framework to evaluate the model identification criterion proposed by Kashyap (1982) to (1) rank realizations within each ensemble according to their relative skill to interpret available data and (2) compute the likelihood associated with each realization which is then used for the implementation of a multi-model approach. The latter scheme relies on viewing each of the alternative MC realizations as a candidate hydrogeological model of the investigated site.

An additional goal of our study is the identification of effects that the adopted geostatistical reconstruction method might have on (1) the uncertainty associated with a desired modeling goal and (2) on the predictive performance of the outcomes of a Maximum Likelihood Bayesian Model Averaging (MLBMA; Ye et al. 2004; Neuman 2003), a framework of analysis that has been increasingly adopted to cope with the high degree of uncertainty related to field-scale flow and transport models (see, e.g., Lu et al. 2015; Samani et al. 2018). In essence, MLBMA enables the joint use of multiple candidate models by considering a weighted average of their predictions of the target modeling goal and making use of the ML-based posterior probability of each model. While such an approach might improve our predictive capability, with a more robust assessment of prediction uncertainty with respect to the output of a single model (Ye et al. 2004), it has also been observed (Winter and Nychka 2010) that the average of an ensemble of models can actually provide predictions of higher quality than those associated with best performing single model only if the individual models in the ensemble give rise to a wide range of outcomes.

2 Materials and methods

2.1 Site description

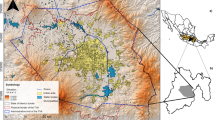
The study area lies between the Apennines margin and the alluvial plain surrounding the city of Bologna, in the Emilia Romagna Region, Northern Italy (Fig. 1a). The area is part of the Po River Basin, which is a syntectonic sedimentary wedge forming the infill of the Pliocene–Pleistocene foredeep (Ricci Lucchi 1984).

Fig. 1

a Location of the investigated domain (Emilia Romagna, Northern Italy); b Three-dimensional representation of the aquifer-group bases within the investigated domain

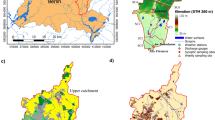
As shown schematically in Fig. 1b, the basin is structured into three main groundwater bodies: Group A (with elevations ranging between 10 m a.s.l. and 150–200 m a.s.l.; which is, in turn, composed by four sub-units, namely A1, A2, A3 and A4); Group B (from 150–200 m to 300–450 m a.s.l.); and Group C (below 450 m a.s.l.). A recent classification (Regione Emilia-Romagna 2010), in compliance with Directive 2000/60/CE, considers the exposure to anthropogenic impacts and the paleo-geographical signatures of the diverse groups and identifies (1) an upper confined aquifer, formed by A1 and A2; and (2) a lower confined unit, which includes A3, A4, B and C. These aquifers are separated by discontinuous aquitards of variable thickness and composed by diverse lithological units (see also Guadagnini et al. 2004; Short et al. 2010; Molinari et al. 2012).

The domain investigated here extends across a surface of 20 × 23 km² in the horizontal plane and from − 450 m to 100 m a.s.l. along the vertical direction. Lithostratigraphic information are available at about 1300 boreholes, whose planar location is displayed in Fig. 2a. Borehole depths range between 10 and 600 m (see Fig. 2b). These data allowed identifying four main lithofacies within the area. These correspond to clay, gravel, silt, and sand, whose volumetric proportion (p_k, with k = c, g, si, sa, for clay, gravel, silt and sand, respectively) are p_c = 52.3%, p_g = 28.1%, p_si = 13.3%, and p_sa = 6.3%. The least- (clay) and the most- (gravel) permeable facies are associated with the two largest p_k values, encompassing (in total) about 80% of the aquifer. The area is characterized by an intense anthropic activity, water supplies being drawn mainly from the underlying aquifer. The intense exploitation of groundwater resources has led to the formation of a massive cone of depression superimposed to the mean natural subsurface flow, which is aligned (on average) along a South-West (i.e. from the Apennines) - North-East (i.e., towards the alluvial plain of the Po River) direction.

Fig. 2

Horizontal (a) and vertical (b) projections of the lithostratigrafic data available along the boreholes; c Location of pumping (black symbols) and monitoring (red symbols) wells within the domain of simulation (H1, H2 and H3 being those selected for validation in Sect. 3); d–e Boundary conditions of the groundwater flow model (grey areas indicate model inactive cells); f Contour map of surface recharge, R, computed according to Eq. (2)

The location of the three major well fields assisting urban water supply (i.e., Borgo Panigale, San Vitale and Tiro a Segno) is illustrated in Fig. 2c together with all pumping wells exploited for industrial/agricultural needs. The total volume of water withdrawn is estimated as 4.3 × 10⁷ m³/year and encompasses civil (78%), industrial (18%) and agricultural (4%) uses. Figure 2c also includes 20 monitoring wells, at which hydraulic head measurements are available and are employed for groundwater flow inverse modeling (see Sect. 2.4).

2.2 Geostatistical reconstruction

The geological structure of the aquifer has been reconstructed by relying on lithostratigraphic data available at 1300 boreholes (see Fig. 2a) and by making use of two geostatistically-based methods, corresponding to (1) a Sequential Indicator simulation (SISIM; e.g., Goovaerts 1997; Remy et al. 2009) and (2) a Transition Probability simulation (T-PROGS; e.g., Carle and Fogg 1996, 1997) approach. These techniques have been extensively used to reconstruct spatial distributions of a correlated categorical variable, $Z = \left\{ {1, \ldots ,n_{facies} } \right\}$ ($n_{facies}$ being the number of facies/categories in the system). Here we summarize for each method the key steps of the generation procedure.

2.2.1 SISIM

• 1. We define Z(x) = {1, 2, 3, 4} as the discrete variable indicating the facies that can be found at location x and the indicator function, $I_{k} \left( {\mathbf{x}} \right)$ (k = 1, …, 4), such that $I_{k} \left( {\mathbf{x}} \right) = 1$ if Z(${\mathbf{x}}$) = k, and $I_{k} \left( {\mathbf{x}} \right) = 0$ otherwise.

• 2. For each facies, we compute the sample directional variogram, $\gamma_{{_{k,\alpha } }} (s_{\alpha } )$, where $s_{\alpha }$ is the separation distance along direction α (with α = x, y, z).

• 3. The variogram $\gamma_{{_{k,\alpha } }} (s_{\alpha } )$ is interpreted via a Maximum Likelihood (ML) approach with an exponential model (see Eq. 6).

• 4. Three-dimensional conditional Monte Carlo realizations of the spatial distribution of the four identified facies are obtained by making use of (1) the conditioning data available at 1300 boreholes included in the investigated domain (see Fig. 2a) and (2) the directional variogram model selected at step (3) via a sequential simulation approach (see, e.g., Remy et al. 2009).

2.2.2 T-PROGS

• 1. We define the transition probability matrix, ${\mathbf{T}}({\mathbf{s}})$, with entries $t_{jk} ({\mathbf{s}}) = \Pr \left\{ {Z({\mathbf{x}} + {\mathbf{s}}) = k\left| {Z({\mathbf{x}}) = j} \right.} \right\}$, representing the probability for facies k to be found at (x + s) conditioned by the presence of facies j at x.

• 2. Sample transiograms, representing the variation of $t_{jk} ({\mathbf{s}})$ with s, are evaluated for all possible pairs of categories $(j,k)$ on the basis of all available lithological data.

• 3. Sample transiograms are interpreted by a Markov-chain model as ${\mathbf{T}}({\mathbf{s}}) = \exp \left( {{\mathbf{Rs}}} \right)$, R being the transition rate matrix. Elements r_jk of R are inferred from sample transiograms as $\left. {r_{jk} = {{\partial t_{jk} } \mathord{\left/ {\vphantom {{\partial t_{jk} } {\partial s}}} \right. \kern-0pt} {\partial s}}} \right|_{s \to 0}$.

• 4. A sequential procedure is applied to assign a category in each unsampled point (see, e.g., Weissmann et al. 1999).

• 5. Facies distribution resulting after the sequential procedure is adjusted by a simulated quenching algorithm (Carle 1997) to minimize the discrepancy between the resulting experimental transiograms and the theoretical Markov-chain model inferred from the data.

For each geostatistical reconstruction technique, we generate a collection of n = 100 Monte Carlo (MC) realizations of facies distributions. We then investigate the impact of the type of geostatistical simulation approach on the degree of facies connectivity through the set of metrics defined in the following section.

2.3 Connectivity metrics

Let $\varOmega$ be a three-dimensional domain which is discretized by $n_{tot}$ (grid) cells and $\varOmega_{k}$ be the subset of n_k cells associated with the k-th facies. Two cells of $\varOmega_{k}$, identified by the coordinates of their centroid (here denoted as ${\mathbf{x}}_{A}$ and ${\mathbf{x}}_{B}$, respectively) are defined as connected if there is a sequence of neighboring cells (from ${\mathbf{x}}_{A}$ to ${\mathbf{x}}_{B}$) completely included in $\varOmega_{k}$. A group of connected cells within $\varOmega_{k}$ is denoted as a cluster. Connectivity indicators that are commonly used (e.g., Lee et al. 2007; Hovadik and Larue 2007; Renard and Allard 2013) for the characterization of three-dimensional subsurface systems include: (1) the total number of clusters composing $\varOmega_{k}$, here denoted as $N_{C,k}$; (2) $\varTheta_{k} { = }{{C_{\hbox{max} ,k}^{{}} } \mathord{\left/ {\vphantom {{C_{\hbox{max} ,k}^{{}} } {n_{tot} }}} \right. \kern-0pt} {n_{tot} }}$, where $C_{\hbox{max} ,k}^{{}}$ is the number of cells in the largest cluster of facies k; and (3) $N_{I,k}$, corresponding to the number of isolated cells of facies k. Clearly, the connectivity of facies k increases as $\varTheta_{k}$ increases and as $N_{C,k}$ and $N_{I,k}$ decrease.

Additional insights on facies connectivity can be offered by the analysis of the connectivity function (Renard and Allard 2013; Western et al. 2001), $\tau_{k,\alpha }^{{}} \left( {s_{\alpha } } \right)$. The latter represents the probability for two cells of category/facies k separated by a distance s_α along direction α to be connected, i.e.,

$$ \tau_{k,\alpha }^{{}} \left( {s_{\alpha } } \right) = \frac{{N\left( {\left. {{\mathbf{x}}_{A} \leftrightarrow {\mathbf{x}}_{B} } \right|{\mathbf{x}}_{A} \in \varOmega_{k} ,{\mathbf{x}}_{B} \in \varOmega_{k} ,{\mathbf{x}}_{A} - {\mathbf{x}}_{B} = s_{\alpha } {\mathbf{e}}_{\alpha } } \right)}}{{N\left( {{\mathbf{x}}_{A} \in \varOmega_{k} ,{\mathbf{x}}_{B} \in \varOmega_{k} ,{\mathbf{x}}_{A} - {\mathbf{x}}_{B} = s_{\alpha } {\mathbf{e}}_{\alpha } } \right)}}\quad with\;\;\alpha = \left\{ {x,y,z} \right\} $$

(1)

where ${\mathbf{e}}_{\alpha }$ is the unit vector along direction α, $N\left( {{\mathbf{x}}_{A} \in \varOmega_{k} ,{\mathbf{x}}_{B} \in \varOmega_{k} ,{\mathbf{x}}_{A} - {\mathbf{x}}_{B} = s_{\alpha } {\mathbf{e}}_{\alpha } } \right)$ indicates the number of pairs of cells, $\left( {{\mathbf{x}}_{A} ,{\mathbf{x}}_{B} } \right)$, belonging to category k that are separated by distance s_α along direction α and $N\left( {\left. {{\mathbf{x}}_{A} \leftrightarrow {\mathbf{x}}_{B} } \right|{\mathbf{x}}_{A} \in \varOmega_{k} ,{\mathbf{x}}_{B} \in \varOmega_{k} ,{\mathbf{x}}_{A} - {\mathbf{x}}_{B} = s_{\alpha } {\mathbf{e}}_{\alpha } } \right)$ is the number of such pairs which also belong to the same cluster (this condition being expressed by ${\mathbf{x}}_{A} \leftrightarrow {\mathbf{x}}_{B}$).

The behavior of the connectivity function, as well as of the other indicators mentioned above, can be interpreted in the framework of percolation theory. The latter was originally formulated for uncorrelated Bernoulli random fields defined on infinite domains (e.g., Stauffer and Aharony 1992 and references therein) and considers a system composed by two phases (e.g., a solid and a void phase) in which, at any node of the grid, the field can be either 1 (void phase) or 0 (solid phase) with probability p and (1 − p), respectively. A realization of such a system would hence be formed by $\varOmega_{1}$, i.e., the set of grid cells where the field is equal to 1, and its complementary set, $\varOmega_{0}$. The basic principle of percolation theory is that there is a critical value of p, termed percolation threshold (p_t), such that the probability P for $\varOmega_{1}$ to form a unique percolating cluster is equal to 1 if $p \ge p_{t}$ and P = 0 if $p < p_{t}$. As highlighted by Stauffer and Aharony (1992), the value of p_t decreases as (1) the grid dimension and (2) the number of neighbors of a grid cell increase. For a three-dimensional cubic grid with six neighbors, $p_{t} = 31\%$.

The application of percolation theory to geological settings is not straightforward, since facies distributions (1) are defined on a finite domain and (2) are spatially correlated. As a consequence, the probability of occurrence of a unique percolating cluster of facies k would not be a step function (i.e., P = 0 if $p_{k} < p_{t}$ and P = 1 if $p_{k} \ge p_{t}$), and would rather increase gradually from 0 to 1 over a range of p_k values. As illustrated by Harter (2005) and Hovadik and Larue (2007), this range widens as the analyzed set-up departs from the theoretical conditions, i.e., as the number of grid cells decreases and as the facies correlation length increases. Moreover, spatial correlation enhances connectivity, resulting in a decrease of the value of p_k at which percolation may occur. As highlighted by Renard and Allard (2013), percolation theory can also assist characterizing the behavior of the connectivity function on finite grids. For example one can note that (1) when $p_{k} < p_{t}$ then $\tau_{k,j}^{{}}$ will rapidly decrease to 0 as the separation distance s increases; and (2) when $p_{k} \ge p_{t}$, $\tau_{k,j}^{{}}$ will tend asymptotically to $\tau_{k}^{\infty } = \left( {{{C_{\hbox{max} ,k}^{{}} } \mathord{\left/ {\vphantom {{C_{\hbox{max} ,k}^{{}} } {n_{k} }}} \right. \kern-0pt} {n_{k} }}} \right)^{2}$. All of these aspects are investigated in Sect. 3.

2.4 Groundwater flow model and model calibration

We evaluate three-dimensional steady state groundwater flow for each MC realization of facies distribution upon relying on the numerical code MODFLOW-2005 (Harbaugh 2005). On the basis of the available lithostratigraphic information, the system is discretized into n_tot = 40 × 46 × 110 cells of uniform size $\Delta x\; = \;\Delta y\; =$ 500 m (along the horizontal) and $\Delta z =$ 5 m (along the vertical). Figure 2d–e illustrate the simulation domain together with the adopted boundary conditions, where no-flow is imposed along the south-west boundary (i.e., corresponding to the Apennines margin) and along the bottom boundary, which coincides with the base of unit B (see Fig. 1b). Values of prescribed hydraulic head, h, are set along the remaining lateral boundaries (see Fig. 2d), as inferred from available piezometric data. Recharge, R, at the top of the domain is modeled as

$$ R = P - Q - E + L $$

(2)

where P is rainfall, Q is surface runoff (land-use dependent, evaluated on the basis of the classical Curve Number method), E represents evapotranspiration (evaluated according to a modified Hargreaves method based on temperature data; Hargreaves and Allen 2003), and L quantifies water-pipe losses in the urban areas. The spatial distribution of R employed in the model is depicted in Fig. 2f.

A preliminary sensitivity analysis (details not shown) highlights that spatial distribution of hydraulic head is not significantly affected by conductivity values associated with silt, K_si, and sand, K_sa (the two categories with the smallest volumetric fraction, see Sect. 2.1). Therefore, we set K_si = 10⁻⁶ m/s and K_sa = 10⁻⁵ m/s (corresponding to intermediate values of conductivity for these geomaterials) and calibrate hydraulic conductivities of clay, K_c, and gravel, K_g, for each MC realization of geomaterial distribution on the basis of hydraulic head data, ${\mathbf{h}}^{ * }$, available at $N_{h} = 20$ monitoring wells (see Sect. 2.1 and Fig. 2c).

Let ${\mathbf{Y}}_{i}^{M} = \left( {Y_{c,i}^{M} ,Y_{g,i}^{M} } \right)$ be the vector collecting log-conductivities of clay, $Y_{c,i}^{M} = \ln K_{c,i}^{M}$, and gravel, $Y_{g,i}^{M} = \ln K_{g,i}^{M}$, of the ith realization (with i = 1,…n) belonging to the ensemble M = S, T (for the approach based on SISIM and T-PROGS, respectively). Maximum Likelihood (ML) estimates, ${\hat{\mathbf{Y}}}_{i}^{M}$, of ${\mathbf{Y}}_{i}^{M}$ are obtained by minimizing the Negative Log Likelihood criterion, NLL (Carrera and Neuman 1986). Minimization is performed through an iterative Levenberg–Marquardt algorithm embedded in PEST (Doherty 2002). In addition to yielding an estimate ${\hat{\mathbf{Y}}}_{i}^{M}$ of the (unknown) true vector ${\mathbf{Y}}_{i}^{M}$, the ML approach also provides (a Cramer-Rao lower bound approximation for) the covariance matrix, ${\mathbf{Q}}_{i}^{M}$, of the corresponding estimation errors.

We view the diverse MC realizations as a set of alternative/competing hydrogeological models of the investigated site. Model selection (or quality, information, discrimination) criteria have been proposed and compared to rank alternative models (e.g., Ye et al. 2008; Lu et al. 2011; Riva et al. 2011 and references therein). Among these, we focus on the KIC model identification criterion (Kashyap 1982). Upon dropping constant terms, the latter can be evaluated as

$$ {\text{KIC}}_{i}^{M} = N_{h} \ln \frac{{J_{i}^{M} }}{{N_{h} }} - N_{P} \ln \left( {2\pi } \right) - \ln \left| {{\mathbf{Q}}_{i}^{M} } \right| $$

(3)

where N_P is the number of model parameters (here, N_P = 2) and $J_{i}^{M}$ is the sum of squared residuals for realization i of ensemble M, $J_{i}^{M} = \left( {{\mathbf{h}}^{ * } - \;{\hat{\mathbf{h}}}_{i}^{M} } \right)^{t} \left( {{\mathbf{h}}^{ * } - \;{\hat{\mathbf{h}}}_{i}^{M} } \right)$, where superscript t denotes transpose and ${\hat{\mathbf{h}}}_{i}^{M}$ is the vector of flow-model outputs (i.e., hydraulic head values evaluated at observation points) obtained using the ML-estimates ${\hat{\mathbf{Y}}}_{i}^{M}$. As compared against other model discrimination criteria, KIC has the unique advantage of enabling one to select a model by balancing (1) parsimony (via N_P), (2) model skill to reproduce observations (via $J_{i}^{M}$), and (3) (expected) information content per observation (via $\left| {{\mathbf{Q}}_{i}^{M} } \right|$) (Ye et al. 2008).

Making use of Eq. (3), one can (1) rank the alternative models and possibly select the one characterized by the minimum value of ${\text{KIC}}_{i}^{M}$ as best, and/or (2) evaluate the posterior weight (or probability), $p\left( {\left. {M_{i} } \right|{\mathbf{h}}^{ * } } \right)$, of model i (within set M), as (see, e.g., Ye et al. 2004)

$$ p\left( {\left. {M_{i} } \right|{\mathbf{h}}^{ * } } \right) = \frac{{\exp \left( { - \frac{1}{2}\left( {\text{KIC}_{i}^{M} - \text{KIC}_{\hbox{min} }^{M} } \right)} \right)p\left( {M_{i} } \right)}}{{\sum\nolimits_{\ell = 1}^{n} {\left[ {\exp \left( { - \frac{1}{2}\left( {\text{KIC}_{\ell }^{M} - \text{KIC}_{\hbox{min} }^{M} } \right)} \right)p\left( {M_{\ell } } \right)} \right]} }} $$

(4)

where $\text{KIC}_{\hbox{min} }^{M}$ is the minimum value of $\text{KIC}_{i}^{M}$ across all n models, and $p\left( {M_{i} } \right)$ is the prior probability of $M_{i}$. Here, we set $p\left( {M_{i} } \right) = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}$, as all realizations of set M are equally likely. Equation (4) allows evaluating the posterior estimate of hydraulic heads at observation wells as

$$ {\mathbf{h}}_{{{\mathbf{POST}}}} = E\left[ {{\hat{\mathbf{h}}}_{{}}^{M} } \right] = \sum\limits_{i = 1}^{n} {} {\hat{\mathbf{h}}}_{i}^{M} p\left( {\left. {M_{i} } \right|{\mathbf{h}}^{ * } } \right) . $$

(5)

In a similar way, it is also possible to evaluate the posterior probability $p\left( {\left. {S_{i} ,T_{i} } \right|{\mathbf{h}}^{ * } } \right)$ of model i upon jointly considering both ensembles (i.e., T-PROGS and SISIM) while setting $\text{KIC}_{\hbox{min} }^{M}$ in Eq. (4) as the minimum between $\text{KIC}_{\hbox{min} }^{S}$ and $\text{KIC}_{\hbox{min} }^{T}$ and replacing n with 2n.

3 Results and discussion

A preliminary analysis of the generated fields has been performed by evaluating the mean value, $\mu_{k}^{M}$, and standard deviation, $\sigma_{k}^{M}$, (with k = c, g, si, sa) of facies volumetric proportions within each ensemble M (with M = S, T). The results of this analysis are listed in Table 1. Both ensembles render values of $\mu_{k}^{M}$ close to those inferred from the conditioning data, i.e., p_k. While T-PROGS realizations provide $\mu_{k}^{T}$ values that almost coincide with p_k, SISIM results slightly overestimate clay (percentage error ~ 3%) and underestimate gravel (percentage error ~ 5%) proportions. The SISIM ensemble is also characterized by a considerably larger variability (among the realizations, i.e., the intra-ensemble variability) of the facies volumetric proportions as compared to the T-PROGS counterpart, $\sigma_{k}^{T}$ being two orders of magnitude smaller than $\sigma_{k}^{S}$.

Table 1 Facies proportions, p_k with k = c, g, si, sa, within the conditioning dataset. Mean, $\mu_{k}^{M}$, and standard deviation, $\sigma_{k}^{M}$, of p_k evaluated over all MC realizations in the M ensemble (M = S, T) are also reported

Figure 3a, b depict facies distributions across a vertical cross-section in a sample realization generated with SISIM and T-PROGS, respectively. A qualitative comparison of these results reveals that the SISIM simulation is characterized by more fragmented lithological units than what can be observed within its T-PROGS counterpart. We assess quantitatively this aspect by computing the connectivity metrics introduced in Sect. 2.3 for both ensembles. We do so by focusing only on clay and gravel because (1) these two categories constitute about 80% of the aquifer system and (2) the connectivity of facies characterized by the largest/smallest conductivity values has been shown to play a major role in driving field-scale flow and transport processes (Wen and Gomez-Hernandez 1998 and references therein).

Fig. 3

Facies distribution along a vertical cross section in one realization generated with a SISIM and b T-PROGS

Figure 4a collects boxplots of $N_{C,k}^{M}$ values and highlights that both facies are considerably more fragmented (i.e., formed by a larger number of clusters) across the SISIM than the T-PROGS realizations. This feature is particularly evident for gravel, values of $N_{C,g}^{S}$ being almost one order of magnitude larger than those of $N_{C,g}^{T}$. Boxplots of $\varTheta_{k}^{M}$ (rescaled by $\mu_{k}^{M}$) are collected in Fig. 4b to provide a depiction of the relative size of the largest cluster with respect to $\varOmega_{k}$. Values of ${{\varTheta_{c}^{M} } \mathord{\left/ {\vphantom {{\varTheta_{c}^{M} } {\mu_{c}^{M} }}} \right. \kern-0pt} {\mu_{c}^{M} }} = {{C_{max,c}^{M} } \mathord{\left/ {\vphantom {{C_{max,c}^{M} } {\left\langle {n_{c}^{M} } \right\rangle }}} \right. \kern-0pt} {\left\langle {n_{c}^{M} } \right\rangle }}$ (brackets representing ensemble average) are close to one, suggesting that clay is essentially formed by a single cluster in all realizations for both generation methods. Otherwise, there is a non-negligible portion of cells associated with gravel that are not connected to the largest cluster (note that ${{\varTheta_{g}^{M} } \mathord{\left/ {\vphantom {{\varTheta_{g}^{M} } {\mu_{g}^{M} }}} \right. \kern-0pt} {\mu_{g}^{M} }}$ < 1, in particular considering the SISIM set where ${{\varTheta_{g}^{S} } \mathord{\left/ {\vphantom {{\varTheta_{g}^{S} } {\mu_{g}^{S} }}} \right. \kern-0pt} {\mu_{g}^{S} }}$ ranges between 0.53 and 0.75). Moreover, Fig. 4c evidences that gravel can be found in a considerably larger number of isolated cells in the SISIM set, as compared to the T-PROGS ensemble. The SISIM set is characterized by a variability of all connectivity metrics that is slightly larger than that associated with the T-PROGS collection. This result is related to the different degree of variability of facies proportions across the realizations of the two ensembles, and resulting in $\sigma_{k}^{S} \gg \sigma_{k}^{T}$ (see Table 1).

Fig. 4

Boxplots of the connectivity indices a $N_{C,k}^{M}$b ${{\varTheta_{k}^{M} } \mathord{\left/ {\vphantom {{\varTheta_{k}^{M} } {\mu_{k}^{M} }}} \right. \kern-0pt} {\mu_{k}^{M} }}$ and c $N_{I,k}$ computed for clay and gravel units over all 100 realizations generated with SISIM (black and red symbols) and T-PROGS (blue and cyan symbols)

In summary, all indicators inferred from the analysis of clusters document quantitatively that facies distributions generated upon relying on SISIM are characterized by a lower degree of connectivity than their T-PROGS counterparts. Values of ${{\varTheta_{k}^{M} } \mathord{\left/ {\vphantom {{\varTheta_{k}^{M} } {\mu_{k}^{M} }}} \right. \kern-0pt} {\mu_{k}^{M} }}$ for both ensembles indicate that clay is characterized by a higher degree of connectivity then gravel. These results are consistent with elements from percolation theory, as: (1) a standard variography analysis (see “Appendix”) suggests that clay and gravel exhibit horizontal and vertical spatial correlation lengths which are larger for the T-PROGS than for the SISIM set; (2) clay has a high probability to form a unique percolating cluster, its volumetric fraction ($p_{c}$ = 52.3%) being significantly larger than the (theoretical) percolation threshold ($p_{t}$ = 31%, see Sect. 2.3). The spatial correlation of gravel contributes to yield a volumetric proportion ($p_{g}$ = 28.1% < $p_{t}$) which is large enough for a percolating cluster to occur. However, consistent with the observation that $p_{g}$ is close to (albeit smaller than) $p_{t}$, one can note a high variability of the connectivity of gravel from one realizations to the other (i.e., intra-ensemble variability). This issue has been further investigated by evaluating the connectivity function defined in Eq. (1). Figure 5 depicts $\tau_{k,\alpha }^{M}$ versus the (dimensionless) lag evaluated, within each realization (dotted curves), for clay and gravel along direction α = x, y, z and for both generated sets (i.e.,. M = S, T). Each plot in the figure also includes (1) the ensemble-averaged connectivity function (solid curves) and (2) the asymptotic sills (dashed horizontal lines) computed as $\overline{{\tau_{k}^{\infty } }} = \left\langle {\left( {{{C_{\hbox{max} ,k}^{{}} } \mathord{\left/ {\vphantom {{C_{\hbox{max} ,k}^{{}} } {n_{k} }}} \right. \kern-0pt} {n_{k} }}} \right)^{2} } \right\rangle$, according to percolation theory. As expected, the connectivity function of clay is larger than the one of gravel regardless the generation approach. Considering clay, values attained by $\tau_{c,\alpha }^{S}$ and $\tau_{c,\alpha }^{T}$ along all directions are quite similar. The curves slightly deviate from the asymptotic value, $\overline{{\tau_{c}^{\infty } }}$, for large separation distances, an effect which is arguably related to the finite extent of the domain. On the other hand, values of $\tau_{g,\alpha }^{T}$ (Fig. 5b–d–f) for gravel are considerably larger than their $\tau_{g,\alpha }^{S}$ counterparts (Fig. 5a–c–e). This observation is consistent with the results depicted in Fig. 4 and provides additional evidence that gravel is less connected (more fragmented) in SISIM than in T-PROGS realizations. Figure 5 also suggests that gravel connectivity is characterized by a remarkably wider variability than what can be observed for clay for both generation methods, resulting also in a more pronounced deviation of the results from $\overline{{\tau_{g}^{\infty } }}$. We quantitatively assess this feature by evaluating the integral connectivity scale (Western et al. 2001), defined as $\varGamma_{{\tau_{k,\alpha }^{{}} }} = \int\limits_{0}^{{N_{\alpha } \Delta \alpha }} {\tau_{k,\alpha }^{{}} } \left( {s_{\alpha } } \right)ds_{\alpha }$, for each realization of the two sets. The variability of $\varGamma_{{\tau_{k,\alpha }^{{}} }}$ within each ensemble is quantified by its coefficient of variation, $CV\left( {\varGamma_{{\tau_{k,\alpha }^{{}} }} } \right)$. For both ensembles and both facies analyzed, we find that $CV\left( {\varGamma_{{\tau_{k,\alpha }^{{}} }} } \right)$ is (almost) independent of direction (i.e., isotropic) and equal to 0.4% (SISIM) or 0.7% (T-PROGS) for clay and 10.5% (SISIM) or 4.5% (T-PROGS) for gravel.

Fig. 5

Connectivity functions (dotted lines) computed in each single realization generated with SISIM (a–c–e) and T-PROGS (b–d–f) versus (dimensionless) separation distance along x (a–b), y (c–d) and z (e–f) axes, evaluated for clay and gravel. Ensemble-averaged connectivity functions (solid curves) and (mean) asymptotic values predicted by percolation theory (red dashed lines) are also reported

Figure 6 collects estimates of clay, $\hat{K}_{c,i}^{M} = \exp \left( {\hat{Y}_{c,i}^{M} } \right)$, and gravel, $\hat{K}_{g,i}^{M} = \exp \left( {\hat{Y}_{g,i}^{M} } \right)$ conductivities obtained in each realization i of ensemble M, where $\hat{Y}_{c,i}$ and $\hat{Y}_{g,i}$ have been evaluated through the ML approach described in Sect. 2.4. The 95% confidence intervals (CIs) associated with each estimate (quantified by means of the diagonal terms of the covariance matrix Q) and the ensemble mean values, $\left\langle {\hat{K}_{c}^{M} } \right\rangle$ and $\left\langle {\hat{K}_{g}^{M} } \right\rangle$, are also depicted. Figure 6a suggests that the two ensembles are characterized by almost identical mean values of clay conductivity estimates (~ $4.6 \times 10^{ - 8}$ m/s) even as SISIM estimates are generally characterized by larger estimation errors (i.e., wider 95% CIs) than their T-PROGS counterparts. Considering gravel (Fig. 6b), $\hat{K}_{g,i}^{S}$ is (generally) larger than $\hat{K}_{g,i}^{T}$, mean values being equal to $1.3 \times 10^{ - 3}$ m/s and $6.4 \times 10^{ - 4}$ m/s, respectively. Results embedded in Fig. 6 are strictly related to the degree of facies connectivity observed for the two ensembles (as clarified by Figs. 4 and 5). Clay is characterized by similar connectivity as well as by similar values of hydraulic conductivity estimates in the two ensembles. Gravel exhibits a considerably smaller degree of connectivity in SISIM than in T-PROGS realizations. Consistently, conductivity estimates, $\hat{K}_{g,i}^{S}$, are significantly larger than $\hat{K}_{g,i}^{T}$. Conductivity estimates exhibit a larger intra-ensemble variability in the SISIM than they do in the T-PROGS set. This aspect is particularly evident for clay, the coefficients of variation $CV\left( {\hat{K}_{c}^{S} } \right)$ and $CV\left( {\hat{K}_{c}^{T} } \right)$ being equal to 80% and 54%, respectively. The intra-ensemble variability of gravel estimates is smaller, values of CV for both ensembles being about 50%. We observe that the intra-ensemble variability of conductivity is not related to the intra-ensemble variability of connectivity: for both sets, we obtain $CV\left( {\hat{K}_{c}^{M} } \right) > CV\left( {\hat{K}_{g}^{M} } \right)$ while $CV\left( {\varGamma_{{\tau_{c,\alpha }^{{}} }} } \right) < CV\left( {\varGamma_{{\tau_{g,\alpha }^{{}} }} } \right)$. This latter result is further supported by inspection of Fig. 7, where estimates $\hat{K}_{k,i}^{M}$ are plotted versus the integral connectivity scale evaluated along the mean flow direction, $\varGamma_{{\tau_{k,y}^{{}} }}$. Results of similar quality (not shown) have been obtained by plotting $\hat{K}_{k,i}^{M}$ versus $\varGamma_{{\tau_{k,x}^{{}} }}$ and $\varGamma_{{\tau_{k,z}^{{}} }}$. The effect of variability of connectivity between the two ensembles (inter-ensemble variability) can be inferred by comparing the pattern of the points associated with the SISIM and T-PROGS realizations in Fig. 7: when considering clay (Fig. 7a), the results of the analysis yield two clouds of points which are practically overlapped, whereas the results for gravel (Fig. 7b) related to SISIM are characterized by values of $\varGamma_{{\tau_{g,y}^{{}} }}$ and $\left\langle {\hat{K}_{g}^{M} } \right\rangle$ which are respectively lower and higher than the corresponding T-PROGS results. When analyzing intra-ensemble effects, one can see that the results of Fig. 7 do not provide a clear indication of correlation between connectivity and hydraulic conductivity within each ensemble. Table 2 summarizes the calibration results by listing the values of J, NLL and KIC obtained in the best realizations (i.e., with $\text{KIC}_{i}^{M} = \text{KIC}_{\hbox{min} }^{M}$) within each of the two ensembles. All criteria appear to favor the best T-PROGS realization over its SISIM counterpart. Figure 8 illustrates the posterior probability, $p\left( {\left. {M_{i} } \right|{\mathbf{h}}^{ * } } \right)$, evaluated for both ensembles according to Eq. 4. It can be observed that the range of variability of $p\left( {\left. {M_{i} } \right|{\mathbf{h}}^{ * } } \right)$ is narrower for the SISIM than for the T-PROGS set, suggesting that the performance of diverse realizations associated with the former approach is more uniform than in the latter case. The best model in the T-PROGS set is associated with a larger posterior probability (34%) than its SISIM counterpart (28%). Figure 9a, b depict the hydraulic heads evaluated at all observation wells using the ML estimates of model parameters, ${\hat{\mathbf{h}}}_{i}^{M}$ (with i = 1, …n), versus observed values, ${\mathbf{h}}^{ * }$, for the SISIM and T-PROGS set, respectively. These figures also include (1) the posterior estimates, ${\mathbf{h}}_{{{\mathbf{POST}}}}$, evaluated according to Eq. (5), (2) the prior estimates, ${\mathbf{h}}_{{{\mathbf{PRIOR}}}}$, evaluated by replacing $p\left( {\left. {M_{i} } \right|{\mathbf{h}}^{ * } } \right)$ in Eq. (5) with the (uniform) prior probability $p\left( {M_{i} } \right)$, and (3) the sum of squared residuals computed with ${\mathbf{h}}_{{{\mathbf{POST}}}}$ and ${\mathbf{h}}_{{{\mathbf{PRIOR}}}}$ (here denoted as $J_{POST}^{M}$ and $J_{PRIOR}^{M}$, respectively). Figure 9c provides a depiction of the results obtained by evaluating the posterior probability $p\left( {\left. {S_{i} ,T_{i} } \right|{\mathbf{h}}^{ * } } \right)$ of model i upon jointly considering T-PROGS and SISIM collections of realizations (see Sect. 2.4). These analyses clearly document that (1) results obtained through ML-based posterior model probabilities are more accurate than those evaluated with their prior counterparts independent of the ensemble considered (note that $J_{POST}^{M} \ll J_{PRIOR}^{M}$); and (2) the T-PROGS set yields smaller values of J than SISIM. The model-averaged results (i.e., ${\mathbf{h}}_{{{\mathbf{POST}}}}$; see Eq. (5)) obtained by analyzing jointly the two ensembles (Fig. 9c) are very similar to those obtained upon relying solely on the T-PROGS set.

Fig. 6

Clay (a) and gravel (b) hydraulic conductivity estimates obtained for all realizations of SISIM and T-PROGS sets; 95% confidence intervals (shaded zones) and mean values (solid lines) are also reported

Fig. 7

Clay (a) and gravel (b) hydraulic conductivity estimates versus integral connectivity scales along the y axis obtained for SISIM and T-PROGS sets

Table 2 Values of J, NLL and KIC obtained in the best realization (i.e., with $\text{KIC}_{i}^{M} = \text{KIC}_{\hbox{min} }^{M}$) in the two ensembles

Fig. 8

Values of KIC-based posterior probabilities, $p\left( {\left. {M_{i} } \right|{\mathbf{h}}^{ * } } \right)$, evaluated within each ensemble of MC realizations

Fig. 9

Prior, ${\mathbf{h}}_{{{\mathbf{P}}{\mathbf{RIOR}}}}$, and posterior, ${\mathbf{h}}_{{{\mathbf{POST}}}}$, hydraulic head estimates versus observed hydraulic heads. Results are obtained from a SISIM set, b T-PROGS set and c evaluating the posterior probability of model i upon jointly considering T-PROGS and SISIM (see Sect. 2.4). The estimates obtained in each realization are also reported

Figure 10 allows comparing (in terms of J) the predictive skill of ${\mathbf{h}}_{{{\mathbf{POST}}}}$ against results of single SISIM (Fig. 10a) and T-PROGS (Fig. 10b) realizations. Posterior model averaging provides slightly more/less accurate predictions than the best-performing single realization in the T-PROGS/SISIM set. This result is related to the observation that, as inferred from Fig. 8, the performance of diverse models in the SISIM ensemble is more uniform that what can be observed with reference to the T-PROGS set. As such, our results provide further documentation that when individual models provide results which are very similar, the performance of model-averaged results is worse than the one of the most skillful single model, whose effectiveness is essentially dampened in the averaging process (see also Winter and Nychka, 2010). The predictive capability in terms of flow-model outputs associated with the two aquifer reconstruction approaches is also tested through a validation procedure, as described in the following. Hydraulic head measurements at three monitoring wells have been taken out (one at a time) from the calibration dataset to compare the local estimate, h_MOD, resulting from the numerical model with the value (${\mathbf{h}}^{ * }$) observed at these locations. The selection of the monitoring wells to be used for validation is aimed at encompassing different regions of the aquifer. In this sense, we consider the data associated with locations which are close to the major well fields (see Fig. 2c) and corresponding to the shallowest (H1, with z = − 21.1 m) and the deepest (H2, with z = − 191.7 m) locations and one, farther from the well fields, at an intermediate depth (H3, with z = − 104 m). We repeat the process of model calibration considering the resulting data-sets on a subset of 30 realizations from each ensemble. Figure 11 depicts, in the form of box plots, the results obtained at these three selected locations across all realizations of the selected SISIM and T-PROGS subsets. It can be observed that T-PROGS clearly outperforms SISIM for the prediction of head at the H1 monitoring well and slightly outperforms SISIM in the estimation of head at H2. The two methods provide results of similar quality in predicting heads at H3.

Fig. 10

Sum of squared residuals, J, obtained for single realizations of SISIM (a) and T-PROGS (b) ensembles. Values obtained for the averaged models with prior (dashed lines) and posterior (straight lines) weights are also reported

Fig. 11

Validation results: box plots of h_MOD obtained at a H1, b H2, c H3 (see Fig. 2c) for the SISIM (black) and T-PROGS (blue) subsets, the green line corresponding to the measured value, h*

4 Conclusions

We explore the extent at which the geostatistical reconstruction method may affect the calibration of hydraulic parameters and the predictive capability of a groundwater flow model. For this purpose, we perform flow simulations on a domain patterned after the Bologna aquifer system by relying on two Monte Carlo ensembles of equally-likely realizations of facies distributions, respectively obtained on the basis of (1) indicator variograms (SISIM) and (2) transition probabilities (T-PROGS) inferred from lithological data. The latter reveal a high degree of heterogeneity in the aquifer, in which the least- (clay) and the most- (gravel) conductive facies represent almost 80% of the total aquifer. We take advantage of a Maximum Likelihood, ML, framework and of model discrimination criteria to (1) calibrate clay and gravel hydraulic conductivities in each realization of the two ensembles, on the basis of available piezometric data; (2) compute the posterior probability associated to each model and (3) evaluate the performance of ML-based model averaging approaches. Our results can be summarized as follows:

• 1. Clay, whose degree of connectivity is similar between the two ensembles, is also characterized by similar results in terms of calibrated conductivities.

• 2. Gravel exhibits an appreciably lower degree of connectivity in SISIM realizations compared to T-PROGS ones. As a consequence, hydraulic conductivity estimates of gravel obtained in the SISIM realizations are generally larger than their T-PROGS counterparts.

• 3. The degree of variability exhibited by connectivity indicators among realizations of the same ensemble seems not to be directly related with the variability of conductivity estimates.

• 4. The variability of the performance (in terms of sum of squared residuals) of alternative models in the SISIM set is smaller than in the T-PROGS set. This results in smaller variability of the posterior probability of models belonging to the SISIM ensemble respect to T-PROGS one.

• 5. The best individual model (as identified by model discrimination criteria) as well as the ML-based average model in the T-PROGS set are more skillful (in reproducing hydraulic head data) than their counterparts obtained for the SISIM set.

The findings of this study form the basis upon which one can obtained enhanced understanding of complex flow and transport dynamics. These elements are currently under study and will be the subject of future works.

5 Appendix

Correlation lengths of clay and gravel have been evaluated in SISIM and T-PROGS sets by means of a three-dimensional variographic analysis. Figure 12 collects ensemble directional indicator variograms, $\gamma_{k,\alpha }^{{}}$ (with α = x, y, z), of clay and gravel computed over all MC realizations in each set along the x ($\gamma_{k,x}$, Fig. 12a), y ($\gamma_{k,y}$, Fig. 12b), and z ($\gamma_{k,z}$, Fig. 12c) axes. All indicator variograms can be interpreted by exponential models, defined as

Fig. 12

Ensemble indicator variograms, γ_k,α, of clay and gravel versus (dimensionless) separation distance along a x, b y, and c z axes computed over all MC realizations in each set. Interpreted models evaluated according to a ML-fit of Eq. 6 are also depicted (dashed lines)

$$ \gamma_{k,\alpha } (s_{\alpha } ) = \sigma_{k}^{2} \left( {1 - \exp \left( { - \frac{{3s_{\alpha } }}{{r_{\alpha } }}} \right)} \right), $$

(6)

where $\sigma_{k}^{2}$ is the sill of facies k, which is very close to $\mu_{k}^{M}$ (1-$\mu_{k}^{M}$), being $\mu_{k}^{M}$ the mean proportion of facies k in ensemble M (see Table 1); s_α and r_α respectively are lag and range along direction α. Results in Fig. 12 and in Table 3 highlight that clay and gravel exhibit horizontal and vertical correlation lengths which are larger for the T-PROGS than for the SISIM set.

Table 3 ML-estimates of horizontal and vertical ranges