An ARFIMA-based model for daily precipitation amounts with direct access to fluctuations

Abstract

Correlations in models for daily precipitation are often generated by elaborate numerics that employ a high number of hidden parameters. We propose a parsimonious and parametric stochastic model for European mid-latitude daily precipitation amounts with focus on the influence of correlations on the statistics. Our method is meta-Gaussian by applying a truncated-Gaussian-power (tGp) transformation to a Gaussian ARFIMA model. The speciality of this approach is that ARFIMA(1, d, 0) processes provide synthetic time series with long- (LRC), meaning the sum of all autocorrelations is infinite, and short-range (SRC) correlations by only one parameter each. Our model requires the fit of only five parameters overall that have a clear interpretation. For model time series of finite length we deduce an effective sample size for the sample mean, whose variance is increased due to correlations. For example the statistical uncertainty of the mean daily amount of 103 years of daily records at the Fichtelberg mountain in Germany equals the one of about 14 years of independent daily data. Our effective sample size approach also yields theoretical confidence intervals for annual total amounts and allows for proper model validation in terms of the empirical mean and fluctuations of annual totals. We evaluate probability plots for the daily amounts, confidence intervals based on the effective sample size for the daily mean and annual totals, and the Mahalanobis distance for the annual maxima distribution. For reproducing annual maxima the way of fitting the marginal distribution is more crucial than the presence of correlations, which is the other way round for annual totals. Our alternative to rainfall simulation proves capable of modeling daily precipitation amounts as the statistics of a random selection of 20 data sets is well reproduced.

1 Introduction

For simulations and forecasts numerical weather generators require amongst others precipitation data as an input. The occurrence and intensity of precipitation is affected by a multitude of atmospheric processes, which evolve on many different temporal and spatial scales. Stochastic precipitation generators are, hence, convenient to capture the outcome of such highly complex physical dynamics.

Two essential aspects of the statistics of precipitation amounts are their distribution and temporal correlations. There is ongoing discussion on the most appropriate choice of a model distribution for daily precipitation amounts. In particular, their tail behavior is crucial for the estimation of large precipitation events. Most global studies with focus on the large amounts find tails heavier than exponential (Nerantzaki and Papalexiou 2019; Papalexiou et al. 2013; Serinaldi and Kilsby 2014). By arguments from atmospheric physics, Wilson and Toumi (2005) deduced a stretched exponential tail with a universal shape parameter as an approximation for the extreme regime. The geographic location and the climatic zone might have strong influence on which distribution is most realistic. Case specific suggestions range from the light-tailed exponential, mixed-exponential or gamma distribution (Richardson 1981; Li et al. 2013) and the heavy-tailed generalized gamma (Papalexiou and Koutsoyiannis 2016) or log-normal (Liu et al. 2011) distribution to fat-tailed Burr-type distributions (Papalexiou and Koutsoyiannis 2012) and q-exponentials (Yalcin et al. 2016). As a remark, since none of the aforementioned distributions is stable under convolution with itself, it is also evident that the distribution will change if the period of accumulation is changed, i. e., hourly data will follow a different distribution than daily data. In most studies the distribution is fitted by maximum likelihood or method of moments approaches. As the tail is naturally represented only poorly in empirical data, this may lead to an underestimation of extremal events (Bennett et al. 2018). Such an effect was addressed by for example entropy based parameter estimation (Papalexiou and Koutsoyiannis 2012).

In terms of correlations one differentiates between essentially two kinds. Short-range correlations typically decay exponentially with effects on short time scales only. Long-range correlations, however, asymptotically vanish such slowly that the sum of all autocorrelations becomes infinite as for example for power-law decay with small exponent. Note that in real-world data the temporal horizon is always finite, such that it is impossible to decide about the origin of persistent empirical correlations. It may lie in strong short-range correlations or long-range dependencies that will survive beyond. Nevertheless, the concept of long-range correlations helps modeling the fluctuations in a system. For example in the presence of long-range correlations statistical quantities like the sample mean show noticeable slower convergence, so that larger sampling errors may occur. Long-range correlations have been observed for precipitation amounts accumulated over time windows of different lengths, such as minutes (Peters et al. 2001; Matsoukas et al. 2000), months (Montanari et al. 1996) and years (Hamed 2007; Pelletier and Turcotte 1997; Bǎrbulescu et al. 2010). This kind of dependency in the data is stronger and more prominent for smaller periods of accumulation and looses intensity for larger ones. Due to the abundance of data on daily precipitation amounts, we concentrate here on time series of 24h accumulated amounts (Bennett et al. 2018).

A classical approach to modeling daily precipitation statistics are two-part models, in which the occurrence or absence of precipitation and its positive amounts are generated independently (Wilks and Wilby 1999; Liu et al. 2011; Li et al. 2013). Correlations between different occurrences are commonly introduced by a Markov chain of first or second order. Recent studies explicitly address correlations between different precipitation amounts by modified Markov chain approaches (Chowdhury et al. 2017; Oriani et al. 2018).

To include dependencies between precipitation amounts as well transformed Gaussian processes, so-called meta-Gaussian processes, have been applied (Bardossy and Plate 1992; Bárdossy and Pegram 2009) (and references below). A prescribed distribution can for example be generated by inverse sampling based on the probability integral transform by applying the quantile function and the cumulative distribution function of a desired marginal distribution to a Gaussian process. The intermittency that precipitation time series naturally exhibit is automatically incorporated into such a model by applying truncated, so-called mixed-type, distributions, that generate a point mass at zero (or a specific threshold). Correlations can directly be defined by the underlying Gaussian process, which is then transformed adequately to obtain a certain distribution. Recent studies include also physical knowledge in the sense that the underlying (spatio-temporally correlated) Gaussian process describes atmospheric dynamics, which are then transformed appropriately. On that account, truncated-Gaussian-power transformations of short-range correlated Gaussian processes have been used to model the distribution of precipitation amounts and their dynamics (Sanso and Guenni 1999; Ailliot et al. 2009; Sigrist et al. 2012). Without explicitly pointing out the property of long-range correlations, Baxevani and Lennartsson (2015) use an underlying Gaussian process with a temporally hyperbolically (and spatially exponentially) decaying spatio-temporal autocorrelation function. Transforming a process, however, does not preserve its temporal correlations, so that additional adjustments of the correlations are necessary to attain prescribed correlations.

One approach to directly estimating the autocorrelations of the underlying Gaussian process is expanding the transformation in Hermite polynomials. A historical note on Hermite series in precipitation modeling is given in Papalexiou and Serinaldi (2020). Guillot (1999) applies this method to the spatial behavior of rainfall events with an exponentially decaying autocorrelation function and a truncated gamma distribution for the rainfall amounts. Alternatively, Papalexiou (2018) fits a function that maps the autocorrelations of the transformed to the autocorrelations of the underlying Gaussian process. Depending on the shape of the mapping between the two a proper functional form has to be chosen.

Major algorithmic effort arises for the synthesis of meta-Gaussian model time series with desired correlations. Serinaldi and Lombardo (2017) generate surrogate data by Davies and Harte’s algorithm based on spectral properties. In Papalexiou (2018), the Yule–Walker equations or an approximation by a finite sum of first-order autoregressive processes are proposed. Introducing long-term correlations into synthetic time series of large sample size is also possible by specifying correlations on the a larger time scale, e. g. annual, and then disaggregating the data to the smaller (daily) time scale (Papalexiou et al. 2018) or by a copula-based method (Papalexiou and Serinaldi 2020). Hosseini et al. (2017) give an approach to explicitly accounting for temporal dependencies on an annual basis between different daily rainfall amounts by considering a high number of previous amounts. By conditional probabilities for gamma distributed amounts they insert temporal correlations directly without the implicit correlations of a transformed Gaussian. The model process essentially represents a Markov process of high order. All the aforementioned methods for the numerical generation of long-range correlated non-Gaussian or, in particular, meta-Gaussian sample data require sophisticated algorithms with a high number of hidden parameters.

An appropriate data model for daily precipitation time series should cover both the non-Gaussianity of the data and their short- and long-range temporal correlations. With this goal, as the references mentioned above but with very different methodology for generating prescribed correlations, we present here a general and parsimonious meta-Gaussian framework for modeling daily precipitation with long-range correlations. We generate Gaussian long-term correlated data by synthesizing samples from a Gaussian ARFIMA(p, d, 0) model. These autoregressive fractionally-integrated moving average processes provide direct access to short- and long-range correlations. Only one parameter d is needed to determine the long-term correlations of the system and $p \in {\mathbb {N}}$ (we apply $p = 1$) parameters control the short-term correlations. For determining how the long-term behavior of the correlations change under transforming the process we apply the Hermite approach, whereas the autoregressive parameter we fit by conditional probabilities. The resulting model is parametric, which means that its overall five parameters have a well defined meaning within the model and can be easily interpreted.

The article is organized as follows. In Sect. 2, we recall the notion of long-range temporal correlations along with the properties of the ARFIMA model. We further summarize how to verify and quantify the presence of long-range correlations in observed data. Then we discuss how analytical control about the asymptotics of the correlations of a nonlinearly transformed Gaussian long-range correlated process is retained by the Hermite polynomial approach. In the last part of this section, we elaborate the theory of effective sample sizes and how the presence of long-range correlations influence the estimates of statistical quantities. Section 3 is devoted to formulating our model and its scope of daily precipitation time series. In particular, we include a discussion of how to match the short-term correlations of data with the auto-regressive part of the ARFIMA model by the usage of conditional probabilities, which is a way to cope with the non-Gaussian statistics of our data. The methodology is completed by the formulation of step-by-step procedure for the application of our model approach. In Sect. 4, we apply our model to 20 stations and depict three of them in detail. We thoroughly validate our findings that the marginal distribution of the empirical data sets in terms of daily mean, annual totals and maxima, the short- and long-term correlations and the waiting-time distribution of the empirical data is well modeled by a truncated-Gaussian-power of a long-range correlated ARFIMA process. Along with that we demonstrate the influence of the chosen method for fitting the marginal distribution on the statistics of annual total and extreme precipitation amounts.

Throughout our article, we use the notation $X_t$ to contextually refer to either a stochastic processes $\mathrm {X}:=(X_t)_{t \in {\mathbb {N}}_{\ge {0}}}$ or its components. Properties of the process like the mean will be indexed by ${\mathrm {X}}$.

2 Long-range temporal correlations

Long-range dependence in time series was established by Hurst in 1951 in his seminal work on water-runoffs of the river Nile (Hurst 1951, 1956). More recently, such memory-like behavior has been found in data from various fields of research, not only in geophysics but also in biology and chemistry, e. g. , for DNA sequences (Peng et al. 1994), neural oscillations (Hardstone et al. 2012) and molecular orientation (Shelton 2014), in atmospheric physics for wind speeds (Kavasseri and Seetharaman 2009) and air pollution (Kai et al. 2008) and even in computer science (Leland et al. 1993; Scherrer et al. 2007), economics (Baillie 1996) and finance (Feng and Zhou 2015; Sánchez Granero et al. 2008).

A time-discrete and (second-order) stationary stochastic process $X_t$ is said to have long memory (LM) or, more precisely, to exhibit (temporal) long-range correlations (LRC) if its autocorrelation function (ACF)

$$\begin{aligned} \varrho _{\mathrm {X}}(k) :=\frac{{\mathrm {Cov}}(X_{t},X_{t+k})}{\sigma ^2} \end{aligned}$$

(1)

with $\sigma ^2 = {\mathrm {Var}}(X_t)$, is not absolutely summable as

$$\begin{aligned} \tau :=\sum _{k = 0}^{\infty } \left| \varrho _{\mathrm {X}}(k) \right| = \infty . \end{aligned}$$

(2)

Note that for stationary processes the ACF (1) depends on the time lag k only and not on the particular point t in time. If the sum in definition (2) is finite though, then the time series is said to have short memory (SM) or to exhibit short-range correlations (SRC). The sum in (2) is the time-discrete analogue of the correlation time of a time-continuous stochastic process. For LM processes a mean correlation time, thus, a typical temporal scale, does not exist.

A conventional behavior of the ACF leading to divergent correlation times is a power law

$$\begin{aligned} \varrho _{\mathrm {X}}(k) \propto k^{- \gamma } \quad (k \rightarrow \infty ) \end{aligned}$$

(3)

with an exponent $0<\gamma \le {1}$. An ACF that decays to zero more rapidly (e. g. exponentially) or is constantly zero (uncorrelated), so that a correlation time exists in definition (2), yields a SM process. If the ACF does follow a power law but with an exponent $\gamma > 1$ in (3), it is summable and is called to have intermediate memory (IM). As we discuss in Sect. 2.3, a Gaussian process with long memory can become a process with intermediate memory by a transformation of the process, since the ACF is not invariant under coordinate transform.

2.1 The ARFIMA process

Hosking (1981) and Granger and Joyeux (1980) generalized SM autoregressive-integrated-moving-average (ARIMA) models (Box et al. 2008) to autoregressive-fractionally-integrated-moving-average (ARFIMA) models to get hands on time-discrete stationary Gaussian LM processes. We use the ARFIMA(1, d, 0) process to model the ACF of empirical daily precipitation data without pronounced seasonality.

The ARFIMA(0, d, 0) process is a time discrete version of fractional Gaussian noise (fGn), which was introduced by Mandelbrot and Van Ness (1968) as the increments of fractional Brownian motion. Both the ARFIMA(0, d, 0) and the fGn process exhibit temporal LRC. The asymptotic power-law decay

$$\begin{aligned} \varrho _{\mathrm {X}}(k) \propto k^{2d-1} \quad (k \rightarrow \infty ) \end{aligned}$$

(4)

of the ACF $\varrho _{\mathrm {X}}$ of an ARFIMA process $X_t$ is controlled by the parameter d as described below.

ARFIMA processes are Gaussian stochastic processes. This means that the joint distribution of any finite ensemble $(X_{t_1},\ldots ,X_{t_s})$, $s\in {\mathbb {N}}$, $t_i\in {\mathbb {N}}_{\ge 0}$, $i=1,\ldots ,s$, of points in time is a multivariate Gaussian distribution. Stationary Gaussian processes are uniquely determined by their first moment ${\mathbb {E}}[X_t]$ and their ACF ${\mathrm {Cov}}(X_t,X_{t+s})/\sigma ^2$ which does not depend on a specific point t in time. Therefore, the modeling of arbitrary types of temporal correlations by Gaussian processes is straightforward (Graves et al. 2017). Another advantage of Gaussian processes stems from the stability of the Gaussianity of their marginal distribution under convolution among different points of the process. On that account, Gaussian processes can be easily defined through iterative schemes driven by Gaussian noise, which itself is chosen as an un- (white) or correlated (colored) Gaussian process, yielding time series models which are easy to handle.

An ARFIMA(0, d, 0) process has the infinite moving-average representation

$$\begin{aligned} X_t = \sum _{j = 0}^{\infty } \psi _j \varepsilon _{t-j} \quad \text {with} \quad \psi _j :=\frac{\varGamma (d+j)}{\varGamma (1+j)\varGamma (d)}, \end{aligned}$$

(5)

where $\varepsilon _t$ is a zero-mean Gaussian white-noise process with variance $\sigma _\varepsilon ^2$. The ARFIMA(1, d, 0) process can be understood as an AR(1) process driven by ARFIMA(0, d, 0) perturbations (Hosking 1981). Hence, its auto-regressive part explicitly specifies short-range correlations by a single additional parameter. The time series model of the ARFIMA (1, d, 0) process reads

$$\begin{aligned} X_t = \varphi X_{t-1} + {\tilde{X}}_t \end{aligned}$$

(6)

with an ARFIMA(0, d, 0) process ${\tilde{X}}_t$ and $|\varphi |<1$. The AR parameter $\varphi$ accounts for SM effects that decay exponentially while the LM parameter d describes the asymptotic power-law decay (4) of the ACF $\varrho _{\mathrm {X}}$. For every $d\in {(0,\nicefrac{1}{2})}$ the ARFIMA process is stationary, causal and invertible (if ${|\varphi |<1}$) and obeys positive LRC. Due to $0<\gamma = 1-2d<1$, it is a LM process in the sense of definition (2).

The ACF $\varrho _{\tilde{\mathrm {X}}}$ of an ARFIMA(0, d, 0) process ${\tilde{X}}_t$ and $\varrho _{\mathrm {X}}$ of an ARFIMA(1, d, 0) process $X_t$ are analytically known and read (Hosking 1981)

$$\begin{aligned} \varrho _{\tilde{\mathrm {X}}}(k)= & {} { \dfrac{\varGamma (1-d)}{\varGamma (d)} \cdot \dfrac{\varGamma (k+d)}{\varGamma (k-d+1)} \text { and} }\nonumber \\ \varrho _{\mathrm {X}}(k)= & {} { \dfrac{\varrho _{\tilde{\mathrm {X}}}(k) }{ (1-\varphi ){_2F_1}(1,1+d,1-d;\varphi )}} \nonumber \\&{\cdot } \Big ( {_2F_1}(1,d+k,1-d+k;\varphi ) \nonumber \\&+ {_2F_1}(1,d-k,1-d-k;\varphi ) -1 ). \end{aligned}$$

(7)

Therein, the function $_2F_1$ is the hypergeometric function. We apply these formulae for the calculation of effective sample sizes in Sect. 2.4 and conditional probabilities in Sect. 3.4.

2.2 Quantifying long-range correlations and the estimation of d

When analysing dependencies in time series, temporal correlations can be taken into consideration but have to be estimated. For the particular case of a power-law decaying ACF, several methods have been proposed (Taqqu et al. 1995), among them the rescaled-range or $\nicefrac{R}{S}$statistics (Hurst 1951), the detrended fluctuation analysis (DFA) (Peng et al. 1994), and wavelet transforms (Abry and Veitch 1998). These methods can estimate LRC much more robustly than a direct estimation of the power-law decay in a double-logarithmic plot of the ACF. Fluctuations of the ACF around zero, in particular, logarithms of negative values, impede reliable inferences about the rate of the decrease of the ACF.

For comparison we employ all three methods, $\nicefrac{R}{S}$-statistics, DFA and wavelet analysis, to our empirical precipitation data. Since there are only very weak non-stationarities in most of the data sets, the detrending of DFA and the one implicitly contained in the wavelet analysis do not alter much the results obtained by $\nicefrac{R}{S}$ statistics. Also the spread of the estimates when later quantifying the long-range correlations for ensembles of model data are very similar, so that in the current setting all three methods appear to be equivalent. Indeed, as it was argued in Höll and Kantz (2015), Løvsletten (2017), wavelet transform and DFA can both be re-written as kernel transforms of the ACF. The algorithmic implementation of DFA and wavelet analysis are described in detail in Kantelhardt et al. (2001), Taqqu et al. (1995), Abry and Veitch (1998); Abry et al. (2003) and many other publications, and an algorithm for the $\nicefrac{R}{S}$ statistics is described in Beran et al. (2013), so we do not repeat these here.

Given a time series of length N, all three methods select time scales $s<N$, and perform an estimate of the strength ${\mathcal {F}}(s)$ of fluctuations in this time scale. The resprective quantities, i. e., the fluctuation function (DFA), the rescaled ranges ($\nicefrac{R}{S}$ statistics), and the wavelet coefficients (wavelet analysis), are time averages over all disjoint intervals of length s contained in the data set, whereas the methods differ in the way how the strength of fluctuations is measured. When representing the strength ${\mathcal {F}}(s)$ of the fluctuations versus the time scale s in a double-logarithmic plot, the asymptotic scaling of

$$\begin{aligned} {\mathcal {F}}(s) \propto s^{\alpha } \quad (s \rightarrow \infty ) \end{aligned}$$

(8)

identifies the correlation structure of the process. The exponent $\alpha$ is commonly referred to as the Hurst exponent. If the process has a finite correlation time in definition (2), then $\alpha =\nicefrac{1}{2}$, while $\alpha =1-\nicefrac{\gamma}{2}$ for LRC processes with $0<\gamma <1$ in the power law (3). This is true independently of the marginal distribution of the data and in particular even if the distribution has power-law tails (Taqqu et al. 1995). For ARFIMA processes one can show (Taqqu et al. 1995; Mielniczuk and Wojdyłło 2007) that $\alpha =d+\nicefrac{1}{2}$.

Note that possible bias in the estimation of the Hurst parameter $\alpha$ has several origins. First, non-Gaussianity and non-stationarity may influence the estimate, which we take account of by comparing results from different methods. Second, the estimate of LRC in finite size data confines to the empirical horizon. The source of observed LRC may lie in strong SRC throughout the observed time window and does not transfer beyond automatically. Nevertheless, involving LRC in finite time modeling serves for reproducing certain statistics directly, as we do in Sect. 2.4. We discuss the results of such analyses on daily precipitation time series and the fit of the parameter d in Sects. 3.2 and 4.1.

2.3 Correlations under transformation

We aim at modeling the distribution of daily precipitation along with LRC in the data by applying a nonlinear transformation to a Gaussian LM process. How the ACF of the original process changes under the transformation can be determined by an Hermite polynomial approach (Beran et al. 2013; Samorodnitsky 2016).

Let $X_t$ be a time-discrete (second-order) stationary and zero-mean Gaussian process with ACF $\varrho _{\mathrm {X}}$ and stationary probability density function (PDF)

$$\begin{aligned} f_{\mathrm {X}}(x) :=\frac{1}{\sqrt{2 \pi \sigma ^2}}\exp \left( -\frac{x^2}{2 \sigma ^2}\right) . \end{aligned}$$

By a nonlinear transformation $g:{\mathbb {R}}\longrightarrow {\mathbb {R}}$ of the process $X_t$, we obtain a stochastic process $Y_t:={g}(X_t)$. Some authors refer to such pointwise transformations as memoryless.

Every transformation g which keeps the second moment ${\mathbb {E}}[g(X_t)^2]$ of the stationary marginal distribution of the process $X_t$ finite can be expanded to an Hermite series. For $\sigma =1$ and $j\in {\mathbb {N}}_{\ge {0}}$ the Hermite polynomials are defined as

$$\begin{aligned} H_j(x) :=(-1)^j \frac{\mathrm {d}^j}{\mathrm {d}x^j} \! \left( {\mathrm {e}}^{-\frac{x^2}{2}}\right) {\mathrm {e}}^{\frac{x^2}{2}} \end{aligned}$$

(9)

and generalized to $H_j^{\sigma ^2}(x):=\sigma ^j{H}_j(\nicefrac{x}{\sigma})$, $j\in {\mathbb {N}}_{\ge 0}$, for arbitrary variances $\sigma ^2$. The Hermite polynomials are orthogonal in the ${\mathcal {L}}^2$-Hilbert space equipped with the Gaussian PDF $f_{\mathrm {X}}$. Hence, with respect to the generalized Hermite polynomials $H_j^{\sigma ^2}$ the transformation g can be represented uniquely by

$$\begin{aligned} \begin{aligned} g&= \sum _{j = 0}^\infty \frac{\alpha _j}{\sigma ^{2j} j!} H^{\sigma ^2}_j \;\; \text {with} \;\; \\ \alpha _j&:={\int _{\mathbb {R}}} g(x) H_j^{\sigma ^2}(x) f_{\mathrm {X}}(x) {\,{\mathrm {d}}{x}}. \end{aligned} \end{aligned}$$

(10)

The smallest index $J>0$, for which the Hermite coefficient $\alpha _J\ne {0}$ is non-vanishing, is called the Hermite rank of the transformation g. This number J determines the asymptotic behavior of the ACF $\varrho _{\mathrm {Y}}$ of the transformed process as follows. Using Mehler‘s formula, it can be shown that

$$\begin{aligned} \varrho _{\mathrm {Y}}(k) = \frac{1}{ {\mathrm {Var}}(Y_t) } \sum _{j=1}^\infty \frac{\alpha _j^2}{\sigma ^{2j} j!} \varrho _{\mathrm {X}}(k)^j. \end{aligned}$$

(11)

Note that $\alpha _0={\mathbb {E}}[g(X_t)]$. As $\varrho _{\mathrm {X}}(k)\rightarrow {0}$$(k\rightarrow \infty )$, by Eq. (11), we obtain $\varrho _{\mathrm {Y}}(k)\propto \varrho _{\mathrm {X}}(k)^J\rightarrow {0}$$(k\rightarrow \infty )$. Hence, the transformed process $Y_t$ of a Gaussian LM process in the sense of definition (3), has a power-law ACF that in leading order decreases as

$$\begin{aligned} \varrho _{\mathrm {Y}}(k) \propto k^{-\gamma J} \quad (k\rightarrow \infty ). \end{aligned}$$

(12)

If the exponent $\gamma$ of the underlying LM process $X_t$ satisfies $\gamma \in (0,\nicefrac{1}{J}]$, then the transformed process $Y_t$ obeys LM as well. Otherwise, if $\gamma {\in }(\nicefrac {1}{J},1]$, we find IM. In the language of ARFIMA, processes with $d\in [\nicefrac{1}{2}-\nicefrac{1}{2J},\nicefrac{1}{2})$ maintain LM but map to IM for $d\in (0,\nicefrac{1}{2}-\nicefrac{1}{2J})$. The higher the Hermite rank of a transformation is, the larger is the range of LM processes that become IM processes. As a remark, since $\alpha _1=\int \nolimits _{\mathbb {R}}g(x)xf_X(x)\,{\mathrm {d}}{x}$, every transformation g, that is not even, obeys the Hermite rank $J=1$. Therefore, without further symmetry assumptions on g the transformation does not change the asymptotic memory behavior of a Gaussian LM process. For example, the square has Hermite rank two, while the exponential function has Hermite rank one.

2.4 Effective sample size and variance

The presence of correlations in data affects the rate of convergence of statistical quantities. The distribution of the sample mean $S_N :=\nicefrac{1}{N}\sum \nolimits _{t=1}^N Y_t$ of $N\in {\mathbb {N}}$ independent and identically distributed (i. i. d.) samples $Y_1,\ldots ,Y_N$ with finite variance $\sigma _{\mathrm {Y}}^2 < \infty$ for large N is approximately Gaussian with mean ${\mathbb {E}}[Y_i]$ and variance $\sigma _{S_N}^2 = \nicefrac{\sigma _{\mathrm {Y}}^2}{N}$ by the central limit theorem. For stationary processes $Y_t$ with ACF $\varrho _{\mathrm {Y}}$, however, we have (von Storch and Zwiers 1984)

$$\begin{aligned} \sigma _{S_N}^2&= \frac{\sigma _{\mathrm{Y}}^2}{N} \tau _{\mathrm {D}}(N) \quad \text {with} \end{aligned}$$

(13)

$$\begin{aligned} \tau _{\mathrm {D}}(N)&= 1 + 2 \sum _{k=1}^{N-1} \left( 1-\frac{k}{N} \right) \varrho _{\mathrm {Y}}(k) \quad > 1. \end{aligned}$$

(14)

By (13), we observe an effective sample size

$$\begin{aligned} N_{\mathrm {eff}} :=\frac{N}{\tau _{\mathrm {D}}}, \quad \text {such that} \quad \sigma _{S_N}^2&= \frac{\sigma _{\mathrm{Y}}^2}{N_{\mathrm {eff}}}, \end{aligned}$$

(15)

which emphasises that the statistics of the sample mean of N correlated data points behaves like the one of $N_{\mathrm {eff}}$ i. i. d. samples does. We may call $\sigma _{S_N}^2$ the effective variance and $\tau _{\mathrm {D}} :=\lim \nolimits _{N \rightarrow \infty } \nicefrac {N}{N_{\mathrm {eff}}}$ the decorrelation time. Note that $N_{\mathrm {eff}} \le N$ by inequality (14). For SM processes $\tau _{\mathrm {D}}$ is finite, so that $N_{\mathrm {eff}}$ increases proportional to N ($\tau _D = \nicefrac {1+\varphi }{1-\varphi }$ for AR(1)). In case of LM, $\tau _D = \infty$, and by Eq. (3), the asymptotic behavior of the effective sample size reads

$$\begin{aligned} N_{\mathrm {eff}} \sim \alpha N^{\gamma } \quad (N \rightarrow \infty ). \end{aligned}$$

(16)

Fig. 1

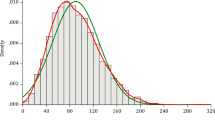
Asymptotic normal distributions with theoretical ($\sigma _{S_N}^2$ by (15)) and fitted (${\overline{\sigma }}_{S_N}^2$) variance of the sample mean $S_N$ of $N = 1000$ i. i. d., AR(1) ($\varphi = 0.3$) and ARFIMA(1, 0.2, 0) standard Gaussian distributed samples

For transformations $Y_i = g(X_i)$ of Gaussian LRC processes $X_i$ the decorrelation time $\tau _D$ and the prefactor $\alpha$ in (16) can be calculated by applying (7) and (11) to (14). Moreover, the Hermite rank J of the transformation g determines the limit distribution of the sample mean, which is Gaussian in case $J = 1$ (Beran et al. 2013). As a remark, for $J >1$ we have non-Gaussian limits such as the Rosenblatt distribution for $J = 2$. In Fig. 1, we visualize the effective sample sizes and asymptotic Gaussian distributions of the sample mean for SM and LM examples.

In Sect. 4, we apply the effective sample size approach to the distribution of the sample mean and annual sums of daily precipitation.

3 Semi-analytical parametric modeling of measured daily precipitation data

The model we present for station measurements of daily precipitation is intended to reproduce both the marginal distribution and the temporal correlations of observed data. In the following subsection we formulate and explain the model and give a sketch of the algorithm for the estimation of the model parameters.

3.1 Fundamentals of the model choice

Long-range correlations in hydrological time series have been discussed intensively before. In particular for daily precipitation time series they could be explained by storage and evaporation effects in the ground, that might cause previous precipitation events affecting later occurrences and amounts of precipitation on larger time scales (Feder 1988, p. 161). By applying $\nicefrac{R}{S}$ statistics, DFA, and wavelet transforms, we consistently observe LRC in our precipitation data sets with Hurst exponents larger than $\nicefrac{1}{2}$ and smaller than 1 (Fig. 2 and Table 4), with very good agreement of the values obtained by the different methods. Some earlier studies (Rybski et al. 2011; Kantelhardt et al. 2006) have found LRC in daily precipitation as well, and point out that in general this memory is rather weak but still significant (Kantelhardt et al. 2003). We tested the significance of our finding by repeating the analysis for several randomly shuffled versions of the time series. For these data sets with removed correlations we obtain Hurst exponents close to $\nicefrac{1}{2}$ in compliance with their expected SM. We conclude that LRC can be prominent in daily precipitation time series on the observed time horizons and apply this property in our model for respective locations.

Unlike for example temperature measurements with their clear positive trends, most European mid-latitude daily precipitation records do exhibit only a moderate annual cycle and essentially no trend over the years. We therefore formulate a stationary model.

We combine reproducing daily precipitation amounts by powers of truncated Gaussian distributions and generating correlations by a LM ARFIMA process (Sect. 3.2). The truncated-Gaussian-power (tGp) transformation has Hermite rank 1, i.e., the estimated exponent $\gamma$ of LRC in the empirical data can be used directly to model LRC by the ARFIMA model. What remains is the adjustment of SRC through the AR(1) part (6) of the ARFIMA model (Sect. 3.4).

3.2 The truncated-Gaussian-power model with long-range correlations

Let $X_t$ be a stationary ARFIMA(1, d, 0) process with AR parameter $|\varphi |<1$ and Gaussian marginal distribution $\mathrm {N}(0,\sigma ^2)$ as defined in (6). From this we obtain a process $Y_t :=g(X_t)$ that has a tGp marginal distribution by the transformation

$$\begin{aligned} g(x) :=\left( x + \nu \right) _+^n, \end{aligned}$$

(17)

where $x_+:=\max (x,0)$ projects onto the positive part. Note that by the transformation (17) the zero-mean ARFIMA process $X_t$ is shifted to a mean $\nu >0$ before its negative part is mapped to zero. In that way, a point mass in zero is created that accounts for the probability of the absence of precipitation. These zero values in time series of this model are crucial for the reproduction of intermittency and the study of correlations. Overall, the model employs five parameters, n, $\nu$ and $\sigma$ for the distribution and d and $\varphi$ for the long and short memory, respectively.

Let $f_{\mathrm {X}}$ and $F_{\mathrm {X}}$ denote the Gaussian PDF and CDF, respectively, of the marginal distribution of the underlying Gaussian process $X_t$. By a coordinate transform the PDF $f_{\mathrm {Y}}$ and CDF $F_{\mathrm {Y}}$ of the stationary marginal distribution of the transformed process $Y_t$ read

$$\begin{aligned} f_{\mathrm {Y}}(y)&= \delta (y) F_{\mathrm {X}}(-\nu ) + \frac{f_{\mathrm {X}}(\root n \of {y} - \nu )}{n y^{\frac{n-1}{n}}} \, {\mathrm {I}}_{(0,\infty )}(y) \; \nonumber \\ F_Y(y)&= F_{\mathrm {X}}(\root n \of {y}-\nu ) \, {\mathrm {I}}_{[0,\infty )}(y), \end{aligned}$$

(18)

where $\delta (.)$ is the Dirac delta function and ${\mathrm {I}}_A$ denotes the indicator function that equals 1 on A and 0 outside. From this we can directly conclude that the tail of the PDF of the tGp transformed process in leading order decreases as

$$\begin{aligned} f_{\mathrm {Y}}(y) \propto {\mathrm {e}}^{-\frac{y^{\nicefrac{2}{n}}}{2\sigma ^2}} y^{\frac{1-n}{n}} \quad (y\rightarrow \infty ), \end{aligned}$$

(19)

so that the stretched exponential part quickly dominates the shape. For $n>2$ the tail of the model PDF behaves like a stretched exponential function and, hence, decays slower than exponentially but faster than every power law. It is a heavy-tailed distribution in the sense of Embrechts et al. (1997) since the moment generating function ${\mathbb {E}}[\mathrm {e}^{sY_t}]$ is infinite for all $s>0$, $t\in {\mathbb {N}}_{\ge {0}}$, but not fat-tailed since all moments of $Y_t$ are finite.

Note that the parameter $\nu$ and the underlying variance $\sigma ^2$ do not only determine the probability of the absence of precipitation but also influence the location and shape of the tail of the model PDF (18), respectively. The power ${n\in {\mathbb {R}}}$, however, adjusts the tail of the distribution only.

Since the tGp transformation has Hermite rank 1, by subordinate (4) and resulting (12) power law, we have

$$\begin{aligned} \varrho _\mathrm {Y}(k) \propto k^{-\gamma } = k^{2d-1} \quad (k\rightarrow \infty ). \end{aligned}$$

(20)

By the relation (20), we estimate the LM parameter d of the ARFIMA(1, d, 0) $X_t$, so that

$$\begin{aligned} d=\alpha -\nicefrac{1}{2} \end{aligned}$$

(21)

provides the fit of the LM parameter d based on the estimated Hurst exponent $\alpha$ of the data by the methods described in Sect. 2.3.

3.3 Model estimation: distribution

Precipitation amounts span several magnitudes, which cannot be expected all to be modeled equally well by a single tGp. We aim at properly reproducing the mean precipitation amount, the correct fraction of days with very little precipitation along with the durations of such periods, and the extremal events as these quantities are of particular importance for risk assessment.

Since classical rain gauges allow for measurements with a precision of 0.1 mm, historical records in the range of one millimeter and below have to be treated with care, due to measurement errors. Mainly evaporation strongly affects measurements of this magnitude. Modern measurement instruments increase the accuracy by applying laser detection. As a remark, rainfall of single-digit millimeter amounts per hour represents drizzling rain or only weak showers.

Accepting that our model might be slightly less accurate for very small amounts, our approach is dedicated to modeling accurately precipitation that exceeds about 4 mm a day. Please, see Sect. 4.2 for comments on the choice of this threshold. For mid-latitude daily precipitation, however, about 75 to 85 percent of the daily records are smaller than 4 mm (cp. Table 1), so that we face the issue of modeling statistics while allowing for deviations in the probabilities for the majority of the measurements. Inspired by a generalized Kolmogorov-Smirnov test (Mason and Schuenemeyer 1983) we determine the parameters n, $\nu$ and $\sigma$ for the tGp distribution (18) by a least square fit of the model survival function $1-F_\mathrm {Y}$ to the empirical survival function in semi-logarithmic scaling. In doing so, high probabilities for small amounts are discriminated and low probabilities for large amounts in the tails are highlighted. As a result, deviations might occur in the estimated probability of non-zero precipiation. Fitting an additional parameter to this quantitity could eliminate such modeling errors. As we argue, however, in Sects. 3.3 and 4.3 , these errors are neglectable, so that we abstain from another parameter for the sake of parismony. Besides maximum likelihood techniques, a very common approach for the fit of distributions is the method of moments (Bennett et al. 2018). Such a fit aims at matching the mean and variance of the empirical data along with the exact probability of non-zero precipitation. Hence, the very small amounts are emphasized with the cost of a worse representation of the tail of the distribution, so that typically, high-frequency amounts are represented well with deviations in low-frequency amounts.

We apply the fit by the survival function and compare the results to those one gets by the method of moments in Sect. 4.2.

3.4 Model estimation: short-range correlations

The presence of additional short-range correlations can be inferred from the violation of the long-term scaling of the strength ${\mathcal {F}}(s)$ of fluctuations (cp. Sect. 2.2) for small s, as shown, e. g. , in Höll and Kantz (2015). Identifying the AR parameter for the ARFIMA(1, d, 0) model from the data is not straightforward though. There is no closed form of the transformed ACF (11), in particular, it cannot be inverted easily for small time lags k.

For the identification and estimation of Gaussian ARIMA models based on the ACF and partial autocorrelations Box and Jenkins established a method in their seminal work on time series analysis (Box et al. 2008). Our data and the corresponding model, however, have a non-Gaussian, strongly asymmetric marginal distribution, so that we formulate a different approach to the estimation of the AR parameter $\varphi$ in Eq. (6).

We gain insight into the short-range dependencies in our daily precipitation data by exploring empirical conditional probabilities as follows. Let $D_0,\ldots ,D_{N-1}$, $N{\in }{\mathbb {N}}$, be the recorded daily precipitation time series. We define the empirical conditional probability $p_\mathrm {D}^c(k)$ of the occurrence of a day with an accumulated precipitation amount of more than $c\in {\mathbb {R}}_{>0}$ millimeters k days after a day of the same kind by

$$\begin{aligned} p_D^c(k) :=\mathrm {P}(D_t> c \mid D_{t-k} > c). \end{aligned}$$

(22)

Also for a tGp transformed ARFIMA process $Y_t$ we consider the conditional probabilities

$$\begin{aligned} p_\mathrm {Y}^c(k) :=\mathrm {P} ( Y_t> c \mid Y_{t-k} > c). \end{aligned}$$

(23)

We estimate $\varphi$ by equating the empirical conditional probability (22) and the respective conditional probability (23) of the model for time lag $k=1$. For that purpose we numerically solve the equation

$$\begin{aligned} p_\mathrm {D}^c(1) - p_\mathrm {Y}^c(1) = 0 \end{aligned}$$

(24)

for $\varphi$ by applying an optimization algorithm to obtain as much agreement in the conditional probabilities as possible. As the process $Y_t$ is obtained by the transformation of a Gaussian process, $p_\mathrm {Y}^c(k)$ is analytically known for $k{\in }{\mathbb {N}}_{\ge 0}$ as

$$\begin{aligned} p_\mathrm {Y}^c(k) = \frac{\iint_{\root n \of {c} -\nu }^\infty f_{(X_t,X_{t-k})}(x,y) \, \mathrm {d}{(x,y)}}{ \int _{\root n \of {c} -\nu }^\infty f_\mathrm {X}(x) \, \mathrm {d}{x}}, \end{aligned}$$

(25)

where $f_{(X_t,X_{t-k})}$ denotes the joint PDF of the two variates $X_t$ and $X_{t-k}$, which follow a zero-mean bivariate Gaussian distribution $\mathrm {N}\left(\left( {\begin{array}{c}0\\ 0\end{array}}\right) ,\Sigma \right)$ with covariance matrix

$$\begin{aligned} \Sigma = \sigma ^2 \begin{pmatrix} 1 &{} \varrho _\mathrm {X}(1) \\ \varrho _\mathrm {X}(1) &{} 1 \end{pmatrix} \end{aligned}$$

(26)

and Hosking (1981)

$$\begin{aligned} \varrho _\mathrm {X}(1) = \frac{(1+\varphi ^2) \cdot {_2F_1}(1,d,1-d;\varphi ) -1 }{ \varphi \left( _2F_1(1,d,1-d;\varphi ) -1 \right) } \end{aligned}$$

(27)

for unity time lag. Since for fixed parameters $n,\nu ,\sigma$ and d by the covariance matrix (26) the joint probability (25) depends on the AR parameter $\varphi$ only, the solution to Eq. (24) serves as an estimator of $\varphi$.

3.5 Step-by-step modeling procedure

Before applying our method to empirical data sets, we assemble a ready-to-use procedure. Details on the several fits and the results for real data we show in Sect. 4. Our algorithm for modeling mid-latitude daily precipitation reads:

• 1. Estimation of the parameters n, $\nu$ and $\sigma$ of the tGp distribution in virtue of the distribution (18) by a least square fit of the model survival function to the empirical survival function

• 2. Estimation of the LM parameter $d = \alpha - \nicefrac {1}{2}$ with Hurst exponent $\alpha$ in the asymptotics of the fluctuation function (8) by applying $\nicefrac{R}{S}$ analysis, DFA or a wavelet analysis to the empirical data

• 3. Estimation of the short-memory parameter $\varphi$ in Eq. (6) by the conditional probabilities in Eq. (24) under usage of the estimated values of n, $\nu$, $\sigma$ and d

• 4. Synthesis of model time series by the generation of an ARFIMA(1, d, 0) time series with variance $\sigma ^2$ and AR parameter $\varphi$ and transformation of this series by the tGp transformation (17) with parameters n and $\nu$

For synthesizing model time series for specific values of the parameters we follow the algorithm formulated in Hosking (1984). The ARFIMA(1, d, 0) time series $X_t$, $t\in {\mathbb {N}}_{>0}$, is generated directly by relation (6) under omission of $L\in {\mathbb {N}}$ with $|\varphi |^L{\le }0.001$ transients ${X_{-L},\ldots ,X_{-1}}$ to eliminate the influence of the initialization. For modeling of precipitation data of about 70 to 100 years 25, 000 to 36, 000 time steps are required. The asymptotic LM structure in synthetic time series of such lengths is reliably generated by applying the moving average (5). By using 2N values as the input $\mathrm {N}(0,\sigma _\varepsilon ^2)$ white noise sequence $(\varepsilon _t)_{-N}^{N-1}$ and omitting N transients ${\tilde{X}}_{-N},\ldots ,{\tilde{X}}_{-1}$, we obtain the ARFIMA(0, d, 0) process $\tilde{\mathrm {X}}$. More sophisticated methods for the generation of ARFIMA processes are presented in Tschernig (1994). For an FFT-based synthetization of long-memory processes see Crouse and Baraniuk (1999). The variance $\sigma _\varepsilon ^2$ of the input white noise can be calculated by the identity (Hosking 1981)

$$\begin{aligned} \frac{\sigma ^2}{\sigma _\varepsilon ^2} = \frac{\varGamma (1-2d)}{\varGamma (1-d)^2} \cdot \frac{_2F_1(1,1+d,1-d;\varphi )}{1+\varphi } \end{aligned}$$

(28)

with the fitted values $\sigma ^2$, d and $\varphi$. The right hand side of Eq. (28) equals the variance $\varrho _\mathrm {X}(0)$ for $\sigma _\varepsilon ^2=1$. Note that for an ARFIMA(0, d, 0) process $({\varphi =0})$ the equality (28) reduces to $\nicefrac{\sigma ^2}{\sigma _\varepsilon ^2}=\nicefrac{\varGamma (1-2d)}{\varGamma (1-d)^2}$.

4 Results

We have tested our modeling approach for daily precipitation records (Klein Tank et al. 2002) of land-based stations in Europe and give the results for 20 stations. The criterion for choosing these data sets was the fact that their recordings should cover more than 70 years without significant gaps and that they represent different geographic locations in Europe. We exemplify our fitted model for three of the data sets we present in the appendix, namely for the (a) Fichtelberg, 1916–2018, in Germany (Deutscher Wetterdienst (DWD) 2018), the (b) Bordeaux, 1946–2018, in France (European Climate Assessment and Dataset 2018) and the (c) Central England, 1931–2018, (Met Office Hadley Centre 2018) data set. Graphical visualizations of the results are very similar for all stations in Table 2, so that based on Table 3 any of the stations would illustrate well our modeling approach and so do the three chosen ones.

4.1 Reproducing long-range correlations

For the estimation of memory in our precipitation time series we applied $\nicefrac{R}{S}$ analysis, DFA and the wavelet transform (cp. Sect. 2.2). The three related quantifications of the strength ${\mathcal {F}}$ of fluctuations for the three selected stations are shown in Fig. 2. It turns out that the Hurst exponents obtained by the different methods for the same data set are very similar, while there are variations from data set to data set. The LM parameter d we fit by the relation (21) based on the exponent $\alpha$ we obtain by DFA(3).

The gray shadow in Fig. 2 shows each ${\mathcal {F}}$ evaluated for 25 synthetic time series obtained by our fitted models establishing two facts: first, the spread which reflects the statistical error is rather small. Second, the observed data are well within the spread of the synthetic data, which validates that our model is able to reproduce the temporal correlations of the observed data very well.

Fig. 2

Estimation of the Hurst exponent: straight line with slope $\nicefrac{1}{2}$ (thick line) for comparison. The grey shadow visualizes the results for 25 model time series, each synthesized by the fitted models according to Table 1

4.2 The marginal distribution

Fig. 3

Fitted models and parameter values for the stations a Fichtelberg, 1916–2018 (Germany), b Bordeaux, 1946–2018 (France), and c Central England, 1931–2018; empirical (dots) and model (solid lines) survival functions (second row), PDFs (third row), and CDFs (bottom row). The vertical lines (tagged by $\perp$) in the survival functions mark the 95%-quantiles of the empirical (upper) and model (lower) distributions. The larger circles and the crosses in the PDFs mark the probability of the absence of precipitation in the data and in the model, respectively

The fitted survival functions and the values of the fitted parameters for the three chosen data sets are depicted in Fig. 3. Comparing the statistics of the empirical data and our fitted model, we see great agreement in the daily mean, the daily variance and the probability of our benchmark of 4 mm (Table 1) and also in the empirical and model PDFs and CDFs (Fig. 3). We point out that the smallest quantile for which the deviation between the empirical and the model CDF is smaller than a certain prescribed error, can be determined precisely as apparent from Fig. 3. We do not elaborate on this further and keep the treshold of 4 mm for simplicity.

Table 1 Comparison of main statistical quantities of the empirical data and the fitted models according to Fig. 3; in the bottom part the probabilities of the absence of precipitation in the data and in the model and of an amount less or equal to 4 mm each are collected

A q-q plot for the comparison of the quantiles of the model and the data shows the high coincidence of the tails of the distributions (Fig. 4), which is one of the essential purposes of our model. By the good representation of the data by our model we substantiate the appropriateness of the tGp distribution for daily precipitation amounts, in agreement with heavy-tailed (Liu et al. 2011; Papalexiou and Koutsoyiannis 2016) and contrary to light-tailed (Li et al. 2013) and fat-tailed (Papalexiou and Koutsoyiannis 2012; Yalcin et al. 2016) models. We point out that the power n, which determines the asymptotic decay of the tail of the tGp distribution, depends on the particular station (cp. Fig. 3 and Table 2). Wilson and Toumi (2005) physically reasoned a universal approximate stretched exponential tail behavior of daily rainfall amounts with a shape parameter $c \approx \nicefrac {2}{3}$. Into our fit, however, we include not only the large but the entire range of the samples. By (18), the parameter n controls the shape of the PDF for the power-law part for small events along with the stretched exponential tail of the tGp. Hence, specific geographical properties enter more into the fit. Nevertheless, we mainly observe powers n in the limited range of roughly 2.1 to 7 maximally, which accords with shape parameters $c = \nicefrac{2}{n}$ in the range of 0.28 to 0.95 in agreement with Wilson and Toumi (2005).

Fig. 4

Left: q-q plots for comparison of the tails of the fitted model and empirical distribution according to Fig. 3 along with 95% confidence intervals Right: p-p plots for a comparison of the fitted model and empirical CDF according to Fig. 3 for small amounts; model values less than 0.1 are mapped to 0; staircase shape arises due to accuracy of 0.1 of empirical data. The vertical and horizontal lines mark the 95%-quantile (left) and the probabilities of the amount of 4 mm (right) of the model and the data, respectively

A closer look at the probabilities of small amounts by a p-p plot (Fig. 4) reveals the difference for their probabilities between the data and the model more than comparing the PDF and CDF only. Depending on the data set, the probability for the absence of precipitation in the model (${Y_t=0}$) can highly differ from the one in the data (Table 1). Note that the deviations in the CDF are particularly highlighted by a p-p plot for very small amounts. Due to the low precision of the empirical data of 0.1 mm compared to the steepness of the model CDF for small values, roughly 50 percent of the entire probability mass are accompanied by only about ten empirical data points. Therefore, the deviations in the p-p plot could be decreased by discretizing the model distribution to the same precision of 0.1. We exemplify how the p-p plot then changes by considering all model values less than 0.1 as no precipitation and rounding them to zero (Fig. 4).

Fig. 5

left: Comparison of the standard deviation of the sample mean of model time series to the empirical sample mean for both the model fitted by the empirical survival function and the method of moments for all 20 stations.    mid: Histogram of annual totals for the Fichtelberg data set (a) together with histogram and PDF for annual totals of 100 model time series fitted by the survival function.    right: Comparison of the standard deviation of annual totals of model time series to the empirical for both fit methods. For comparison standard deviations of i. i. d. model time series are depicted

Since most of the probability mass sits at small values, a maximum likelihood fit of the model to the data would generated highly accurate p-p plots but poor q-q plots. The same occurs when fitting by the method of moments. The tail of a distribution is naturally only rarely sampled with low impact on such fits. To emphasize the tail more than the small values of high probability we applied a different procedure by fitting the model survival function to the empirical one. To fit the tail also certain quantiles ${\tilde{q}}$ with probability ${\tilde{p}}$ can be fixed by $\nu =\root n \of {{\tilde{q}}}-F_X^{-1}({\tilde{p}})$ due to the equality ${\tilde{p}}=F_Y({\tilde{q}})=F_X(\root n \of {{\tilde{q}}}-\nu )$. If the parameters are estimated by fixing such specific quantities, then the fit depends on the existence of parameters such that the chosen equalities are satisfied.

4.3 Annual totals and annual extremes

A more detailed impression of the effects of correlations and the fit method on the statistics can be gained by considering specific quantities, such as annual total and maximal precipitation (Bennett et al. 2018). By the effective sample size (Sect. 2.4), we analytically determine the variance of both the daily sample mean and the annual totals of the model. In Table 2 we state for all stations the effective sample sizes with respect to the sample mean. In Fig. 5 (left panel) we show that for about half of the 20 stations the empirical mean lies inside one standard deviation of the model sample mean. For all stations, the relative distance, defined by $100 \cdot \nicefrac {({\overline{\sigma }} - \sigma _\mathrm {Y})}{{\overline{\sigma }}}$, between the empirical ${\overline{\sigma }}$ and model $\sigma _\mathrm {Y}$ daily standard deviation is less than 5%.

By favoring the tail of the distribution of daily amounts we lack exact reproduction of the empirical daily mean but the deviation is in the range of the data precision of 0.1 mm for all but three of the example stations (Fichtelberg, Karlsruhe, Schwerin, Table 3). The tendency of our model towards an underestimation of the probability of zero daily rainfall translates to a possible positive bias in the annual totals. In Fig. 5 (mid panel), we show the strongest bias we see amongst our examples. In general, deviations of the daily and annual mean above measurement precision are possible, since we do not explicitly fit these quantities.

For annual totals let $K = 365$, so that $A :=\sum \nolimits _{t=1}^K Y_k$ denotes the annual sum of model time series $Y_t$. We shall assume A approximately Gaussian $\mathrm {N}(\mu _A,\sigma _A^2)$ with $\mu _A = K \mu _\mathrm {Y}$. By definition (15), we calculate the variance of the annual sum A as

$$\begin{aligned} \sigma _A^2 = K \sigma _\mathrm {Y}^2 \tau _D(K) \end{aligned}$$

(29)

with the model variance $\sigma _\mathrm {Y}^2$ of daily amounts. In Fig. 5 (right panel), we find coincidence between the standard deviation of the empirical and model annual totals, while their skewness might be slightly underestimated as seen in Fig. 5 (mid panel). For all stations, the empirical mean of the annual totals lies within one standard deviation of the respective model mean with little differences between the two fit methods. We point out, that due the precision of 0.1 mm of the daily data, the precision of the annual sum is limited to 36.5 mm, so that values that differ at this magnitude are practically indistinguishable. Further, the sample variance is known for the tendency to underestimate the true variance in the presence of LRC (Beran et al. 2013), which could explain that the empirical standard deviations slightly fall below model standard deviations. Elaborating the same procedure for our model with a marginal fitted by the method of moments, we find very small differences in the representation of the statistics of the annual totals.

For comparison we also show the standard deviations of the annual totals for an i. i. d. model with fitted tGp marginal distribution. Here, we observe clear underestimation of the empirical standard deviation of annual totals.

Besides annual total amounts another statistical quantity of great interest is the annual maximum precipitation. For evaluating their representation by the model we apply the Mahalanobis distance (Alodah and Seidou 2019). Let $X = (x_i)$, $Y = (y_i) \in {\mathbb {R}}^s$. Then a bivariate Gaussian distribution $\mathrm {N}(\mu ,\Sigma )$ with mean $(\mu _X,\mu _Y)$ and covariance matrix $\Sigma = \mathrm {Cov}(X,Y) \in \mathrm {R}^{2 \times 2}$ can be fitted to the points $(x_i,y_i)_{i=1}^s$, where $\mu _X$ and $\mu _Y$ denote the sample mean of the elements of X and Y and $\Sigma$ contains the sample (co-)variances.

Fig. 6

left: 3D Mahalanobis distance $d_M$ between the mean and the standard deviation of the empirical Fichtelberg data set (a) (solid dot) and of 100 model time series annual maxima (empty dark marks). The solid ellipses mark one standard deviation with respect to $d_M$, the dashed ellipses mark the 95% probabality limit. right: 3D Mahalanobis distance between the mean, the standard deviation and the 100-year return level for all stations; For comparison $d_M$ is depicted for model time series fitted by both the survival function (circles) and the method of moments (diamonds and triangles) along with i. i. d. model time series (light grey). The dashed lines mark one, two and three standard deviations and the solid lines the 5%, 10%, 90% and 95% probability limits

Then the Mahalanobis distance $d_M(x,y)$ between two points $x,y \in {\mathbb {R}}^2$ ist defined by

$$\begin{aligned} d_M(x,y) :=\left( (x-y)^\mathrm {T} \Sigma ^{-1} (x-y) \right) ^{\nicefrac{1}{2}}. \end{aligned}$$

A generalization of the Mahalonobis distance to more than two dimensions is straightforward. By applying this distance measure in a multidimensional event space, it is possible to include the distribution of multiple properties to an evaluation at once. If points are close in the $d_M$ distance then they are also near by in the single marginal spaces. Points of equal distance with respect to $d_M$ form ellipses or multidimensonal ellipsoids, respectively, and serve as probability limits with respect to the parent multivariate Gaussian $N(\mu ,\Sigma )$. A powerful feature of the Mahalanobis distance is that the value $d_M(x,y)$ directly translates to distances in terms of standard deviations of $N(\mu ,\Sigma )$, as which the ellipsoids with distance $d_M(x,y)$ shall be considered.

As a visualization, in Fig. 6 (left panel) for the Fichtelberg data set (a) we show the two-dimensional distribution defined by pairs consisting of the mean and the standard deviation of the annual maxima of time series of our model. Probability limits are plotted based on the bivariate Gaussian fitted to the pairs of 100 model times series. For comparison we involve model time series with and without correlations and fitted by the survival function and by the method of moments. For the first method the point pairing the mean and variance of the empirical annual maxima lies within one standard deviation with respect to $d_M$, whereas even outside the 95% limit for the latter. We conclude that the mean of the annual maxima is underestimated by the method of moments. To allow for a parallel assessment of several properties for all stations, we apply a three-dimensional Mahalanobis distance between triples constisting of the mean, the standard deviation and the 100-year return level of annual maxima. The latter is estimated by the 99%-quantile of a GEV distribution fitted to the annual maxima of the empirical and synthetic time series.

We find (Fig. 6, right panel) that in the Mahalanobis distance the distribution of the annual maxima measured as described above lies within two and predominantly close to one standard deviation from the respective mean of the model time series. When fitted by the method of moments, we observe larger errors for more stations. Furthermore, the effect of the correlations is conceivable compared to the i. i. d. modeling but the effect of properly fitting the tail has more influence on how well the statistics of annual maxima are modeled.

4.4 Reproducing short-range correlations

For the fit of the short-memory parameter $\varphi$ by conditional probabilities we employ the procedure described in Sect. 3.4. We solve expresssion (24) for the aforementioned treshold of $c=4$ mm involving the fitted values for the parameters n, $\nu$, $\sigma$ and d.

In Fig. 7 the conditional probability $p_\mathrm {D}^c(1)$ of a day with precipitation amount larger than $4~\mathrm {mm}$ right after a day suchlike is noticeably raised compared to the unconditioned probability of a single day with precipitation amount larger than $4~\mathrm {mm}$ and relaxes slowly to the unconditioned value. For Fichtelberg data set (a), we already see a good agreement in the conditional probabilities also for larger time lags $k\ge {1}$. For the two other examples, Bordeaux (b) and Central England (c), discrepancies occur for time lags $k\ge {2}$ already. An improved representation of the conditional probabilities for larger time lags than $k=1$ can be obtained by increasing the number p of AR components and applying an ARFIMA(p, d, 0) process as the underlying Gaussian process for our model.

Fig. 7

Visualization of the conditional probabilities $p_\mathrm {D}^c(k)$ (22) and $p_\mathrm {Y}^c(k)$ (23) (left) and of their decay rates by the difference ${|p_{(\,{.}\,)}^c(0)-p_{(\,{.}\,)}^c(k)|}$ (right) for time lags ${k=0,\ldots ,25}$ each with fitted models according to Fig. 3. The depicted values are analytically known for the tGp transformed ARFIMA(1, d, 0) (empty circles) and ARFIMA(0, d, 0) (crosses) processes and approximated numerically for the empirical time series (dark solid circles) and the same 25 synthetic time series as used in Fig. 2 (grey shadow of solid circles). The solid line has slope ${2d-1}$ for comparison

For comparison in Fig. 7 we also visualize the conditional probabilities (23) of a tGp-transformed ARFIMA(0, d, 0) process $\mathrm {Y}$ with parameters n, $\nu$, $\sigma$ and d estimated by the aforementioned methods. Even though short-range correlations are still inherent to such a process, the short-range dependence we see in the data is not entirely captured by fractional differencing only. For $c=4$ and small time lags the conditional probabilities of such a model $\mathrm {Y}$ evidently fall below the empirical values.

We can also take a closer look on the long-term behavior of the conditional probabilities (22) and (23) in Fig. 7. The covariance matrix (26) is the key ingredient of the representation (25) of the conditional probabilities. Therefore, we have $p_\mathrm {Y}^c(k){\rightarrow }p_\mathrm {Y}^c(0)$ as $k\rightarrow \infty$ for the model since the correlations $\varrho _\mathrm {Y}(k)$ asymptotically vanish, which is why the joint probability in (25) asymptotically factorizes. For the data we observe the same approach of $p_\mathrm {D}^c(k)$ to $p_\mathrm {D}^c(0)$ for large time lags k by $|p_\mathrm {D}^c(k)-p_\mathrm {D}^c(0)|$ decreasing to zero. Moreover, the decay of the conditional probabilities $p_\mathrm {Y}^c(k)$ to the probability $p_\mathrm {Y}^c(0)$ of the model follows a power law alike the model ACF $\varrho _\mathrm {Y}$. The conditional probabilities in the empirical data sets show the same scaling behavior, although, we only implicitly consider their correlations. Instead, we numerically determine the conditional probabilities directly from the data by dividing the number of pairs $(D_t,D_{t-1})$ with both entries larger than $4~\mathrm {mm}$ by the overall number of days with an accumulated amount larger than $4~\mathrm {mm}$ following the definition of conditional probabilities.

As a remark, we point out that the values $\varphi$ we obtain do not correspond to a typical correlation time other than in AR or ARMA models with a finite sum in (2). The effect of the auto-regression in (6) on the correlations decays exponentially, though, the sum in (2) remains infinite, due to the LRC in the model.

4.5 Waiting time distribution

Another noticeable statistical effect of LRC in time series is a change in the distribution of waiting times (Bunde et al. 2005). For white noise or only short-range correlated data the waiting times between events of a specifically tagged type is exponentially distributed. In the presence of LRC stretched exponential tails of the waiting time distribution occur (Altmann and Kantz 2005).

Waiting times between two days with an accumulated precipitation amount of $c > 0$ mm shall be interpreted as periods of daily amounts $\le c$. For $c = 0$ they describe dry spells. Due to our fit with focus on the tail, however, we do not precisely reproduce the probability of zero daily precipitation that we find in the empirical data. Thus, a study of dry and wet spells based on the strict treshold of $c = 0$ is not appropriate. In Fig. 8 we give a visual impression of the effect of LRC on the waiting times for the more practicable value of $c = 4$ (cp. Sect. 4.2). Further detailed investigation of dry and wet spells is required. For such an analysis we propose considering waiting times with respect to small values of $c>0$ as a measure of the duration of dry periods in terms of applications.

For comparison we depict the waiting times of both a tGp transformed ARFIMA(1, d, 0) and AR(1) process with the marginal distribution and AR parameter of the latter fitted as described in the Sects. 4.2 and 3.4 .

For $c = 0$ both models underestimate the distribution of dry spells for all the three stations because our model tends to underestimate the probability of a dry day (see Table 3).

Also for $c = 4$ the AR(1) based process fails to reproduce the distribution of long dry spells in the sense that periods longer than about 45 days are visually (way viewer green bars) much more unlikely than in the empirical data (light blue bars). Our LM tGp model, however, is capable of reproducing a higher number (of red bars) of such long dry periods in accordance with the statistics of the waiting times in the original data of the three example stations. We do not test the significance of a stretched exponential decay of the waiting time densities here. Nevertheless, Fig. 8 illustrates that introducing LRC in our data model is a promising approach to modeling the tails of the waiting time distributions of daily precipitation time series.

As remark, for both depicted values of c in Fig. 8 the waiting time distribution of a randomly shuffled version of the originally observed time series clearly differs from the one of the original data. As expected for uncorrelated data (correlations are destroyed by the shuffling) the density of its waiting times decays exponentially and visibly significantly faster than the original waiting times.

Fig. 8

Comparison between empirical waiting time distributions of the original time series and different synthetic time series

5 Summary

We present a complete statistical model for daily precipitation amounts at single mid-latitude European locations without pronounced annual cycle. For 20 randomly chosen data sets (three of them discussed and depicted in detail) we carefully validate that the truncated-power transformation of a Gaussian ARFIMA process yields an accurate model for such data.

The basis of our model selection and estimation is twofold: first, we validate the presence and significance of long-range correlations in daily precipitation time series. Along with that we investigate the stationarity of the data in terms of weak annual cyclicity. Second, we substantiate in statistical detail the application of the previously used truncated-Gaussian-power transformations for the generation of an appropriate distribution for daily amounts. This implies that the tails of such data decay faster than a power law, but slower than exponentially.

Due to the very strong non-Gaussianity of the empirical precipitation data, maximum likelihood estimators might be subject to considerable bias. Therefore, we implemented new methods for parameter fits at two instances, namely the marginal distribution and the auto-regressive parameter of the underlying ARFIMA process.

The three parameters for the distribution we fit by matching survival functions on logarithmic scale to discriminate smaller and emphasize larger precipitation amounts. In doing so, in particular, the statistics of large precipitation events are reproduced more reliably. The relation between the model and empirical annual maxima distribution we measure in the Mahalanobis distance based on synthetic time series to define probability limits. We find that for all stations the triple of mean, variance and 100-year return level of annual maxima lies within two standard deviations of the model with respect to the three-dimensional Mahalanobis distance, and even within about one standard deviation for half of them. Additionally, we conclude that the distribution of the annual maxima is highly sensitive to the fitting method for the marginal distribution by comparing our fit by the survival function to a fit by the methods of moments.

Our model combines daily precipitation amounts with their empirical short- and long-range dependencies in a parsimonious way by requiring only two parameters for fitting the correlations. For the adjustment of the auto-regressive parameter of the ARFIMA model we apply conditional probabilities. In the model these conditional probabilities adopt the power-law decay of its autocorrelation function and we find the same behavior for the empirical conditional probabilities of the data. Moreover, long-range correlations in the synthetic model time series are present up to all relevant orders in time with only small numerical effort.

Due to including correlations, we appropriately reproduce, in particular, the statistics of annual total and annual maximal precipitation amounts. By determining an effective sample size for correlated data, we obtain analytical confidence intervals for the daily mean and annual sum based on the variance of the sample mean. The possible lack of exactly reproducing smaller amounts leads to deviations in the mean of daily and annual total amounts, which are covered by the variance of the data and the model anyway or smaller than the precision of the empirical data. For all stations the relative distance between the sample mean and the model mean is less than 5%, and about half of them lie within on standard deviation.

We also properly reproduce the asymptotic power-law deacy of the autocorrelations as becomes visible by detrended fluctuation analysis, rescaled-range statistics and wavelet transforms. Finally, we introduce visually the capability of long-range correlations in the model for an adequate statistical description of the waiting times in precipitation data, in particular, when modeling the duration of droughts, however, a more detailed study is still necessary.

The application of our model altogether requires the fit of only five parameters, which can be robustly done with multi-decadal data sets. The model will be useful for simulating rainfall, but also to detect changes due to climate change, when fitted to disjoint periods of two or three decades of data.

Overall, we present a parametric stochastic data model for mid-latitude daily precipitation together with a complete fit procedure and its implementation.

6 Appendix

In Table 2 we provide the fitted parameter values of our model to observed time series from 20 different mid-latitude European stations. These data sets are a random selection of the databases (Deutscher Wetterdienst (DWD) 2018; European Climate Assessment and Dataset 2018) by Klein Tank et al. (2002) and (Met Office Hadley Centre 2018) chosen such that the observed period spans more than 70 years, the data sets are nearly complete and the assumption of weak seasonality is satisfied. Prominent annual cyclicity can be evaluated by deviations of the scaling of, e. g., the DFA fluctuation function from linearity (Meyer and Kantz 2019). For an automatized estimation of the stationarity we employed the regression values of the linear fit of the fluctuations quantifying functions. Table 3 compares the statistics of the empirical data and the fitted model. Table 4 collects the estimated Hurst exponents for all stations along with their validation by regression values.

Table 2 Fitted model parameter values for 20 mid-latitude European locations and effective sample sizes by (15)

Table 3 Comparison between the statistics of the empirical data of the stations in Table 2 and the respective fitted models

Table 4 Fitted Hurst exponents for the empirical data of the stations in Table 2 obtained by DFA, $\nicefrac {R}{S}$ and wavelet analysis, respectively. Regression values close to one assess the linearity of the growth of the related fluctuation function, rescaled range and wavelet coefficients in double-logarithmic scaling