Abstract
The risk from natural catastrophes is typically estimated using complex simulation models involving multiple stochastic components in a nested structure. This risk is principally assessed via the mean annual loss, and selected quantiles of the annual loss. Determining an appropriate simulation strategy is important in order to achieve satisfactory convergence of these statistics, without excessive computation time and data storage requirements. This necessitates an understanding of the relative contribution of each of the stochastic components to the total variance of the statistics. A simple framework using random effects models and analysis of variance is used to partition the variance of the annual loss, which permits calculation of the variance of the mean annual loss with varying numbers of samples of each of the components. An extension to quantiles is developed using the empirical distribution function in combination with bootstrapping. The methods are applied to a European flood model, where the primary stochastic component relates to the frequency and severity of flood events, and three secondary components relate to defence levels, exposure locations and building vulnerability. As expected, it is found that the uncertainty due to the secondary components increases as the size of the portfolio of exposures decreases, and is higher for industrial and commercial business, compared with residential for all statistics of interest. In addition, interesting insights are gained as to the impact of flood defences on convergence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The ability to estimate the risk from natural catastrophes, such as hurricanes and floods, is important for disaster risk mitigation and essential for the existence of insurance cover. Natural catastrophe models vary in scope and complexity, depending on their purpose. At the simpler end of the spectrum, models may just involve extrapolation of historic data at a single site using extreme value theory. For example, this type of approach may be used by engineers when setting wind or flood design criteria (Castillo 1988). Extensions to the basic model address issues such as seasonality and other non-stationarities, and application to the spatial domain [e.g. Fawcett and Walshaw (2016), Randell et al. (2016)].
Often, however, the historical data is insufficient in both quantity and quality to make meaningful extrapolations, particularly when these are required over large spatial areas, or when non-stationarity is significant and multidimensional. For example changes in land-use, and the introduction of risk mitigation measures such as flood defences affect past and future risk. These and other such shortcomings are addressed by more complex models, which typically comprise multiple linked components, involving both physical and statistical modules. The latter often use Monte Carlo methods, one advantage of which is their ability to model multiple metrics of interest from a single catastrophe, over both time and space, in a natural and consistent way. For example, when considering tropical cyclone risk, the dependence between wind speeds, rainfall amounts and storm surge heights is captured by generating these from the same storm track model, which simulates the storm path and key storm parameters. Further, multiple linked components allow estimation, not only of the intensities of the physical phenomena, but also of any resulting impacts of interest (such as building damage, number of fatalities etc.), and these impacts may also be modelled probabilistically. Examples of this type of model, involving simulation and multiple linked components, include Lin et al. (2010) (hurricanes), Goda and Song (2016) (tsunami) Finney et al. (2011) (wildfire) and Falter et al. (2016) (flood).
The natural catastrophe models used by the insurance industry (known as catastrophe models) are of this type, consisting of many components and sub-components, which can be very different from each other in their nature, and computational expense. Their principal purpose is to estimate the expected insured loss and selected quantiles of the loss over the following year on any given portfolio. These models involve many sources of uncertainty. Firstly, there is an inherent randomness in the frequency and severity of extreme weather or earthquake events from year to year, which is modelled via the statistical components. This natural randomness, or aleatoric uncertainty, means that any statistics that are estimated from a finite number of simulations are themselves uncertain and subject to random variation. Other sources of uncertainty include the limited nature of, and uncertainties within, the historical data against which the models are calibrated, incomplete knowledge of the science behind the physical components, the known but practically necessary approximations in the model and the uncertainties involved in the choice of statistical distributions and model input parameters. We focus here on the source of uncertainty that is most readily controlled: the uncertainty in the key statistics of interest due to the finite number of simulations within the model. Having a sound understanding of this uncertainty has become increasingly important with the recent advent of cloud-based computing, and the consequent increase in the use of simulation in the models, replacing many of the necessary analytical approximations of the past.
Catastrophe models are run numerous times by multiple users, with different portfolios as input—each run involving a specific set of insurance exposures and financial contract terms. The variances of the loss estimates produced by the model, calculated from all the simulations, depend on the model design, and the specific configuration of any model runs including, in particular, the number of simulations of each component. Ensuring an appropriate balance between the precision of estimates produced by the model, against run-times is therefore an important part of the development process. In addition to estimating the total variance of the estimates that is due to simulation uncertainty, consideration of this balance also requires an understanding of how the variance is broken down between the various model components—for example, how much of the uncertainty in the mean annual loss estimate from the model is due to the simulation of the hazard, and how much to the simulation of the building damage, given the hazard. This understanding has multiple benefits. Firstly at the development stage, such an analysis can highlight deficiencies in the model, identifying areas to target to reduce the uncertainty. At this stage it can also inform the model’s design, including the default numbers of simulations to use, and the level of flexibility to be offered within the model to change these defaults. At the operational stage, such an analysis can be used to provide information and guidance to users to help them to determine how many samples of each statistical component in the model they should run, given the particular features of the analysis in question. Features that will vary between analyses include the nature and size of the portfolio of interest, the statistics of interest, the user’s computational and data storage resources, the time constraints for the analysis, and the user’s view as to acceptable precision.
The motivation for our analysis is to develop a framework to investigate the variance components of the estimators of the mean annual loss, and the quantiles of the annual loss. The framework needs to be easy to implement and general enough to be readily applied to a range of catastrophe models, whose statistical components could differ. We apply this framework here to a development version of a European flood modelFootnote 1. We used an artificial portfolio that approximated the total industry (national-level) market exposures, using typical contract structures. The analysis was carried out for this whole portfolio, and for a very large number of possible subsets of the portfolio, to understand how the split between components varied with key drivers, such as the size and nature of the portfolio.
We followed an analysis of variance (ANOVA) approach, which is a statistical tool for partitioning the total variance between factors, each of which may be assumed to have all possible values represented within the dataset (“fixed effects”), or only a random sample from a larger population (“random effects”), the latter being appropriate for this analysis [see for example Chapter 13 of Montgomery (2013)]. ANOVA analyses have been popular in recent years within the climate community. Yip et al. (2011), for example, used a fixed effects ANOVA to partition the uncertainty in climate model ensembles. Northrop and Chandler (2014) and Geinitz et al. (2015) use a Bayesian version of ANOVA for similar analyses, which allows factors to be considered as both fixed and random in a coherent way. Applications of ANOVA in the field of hydrology have included Osuch et al. (2016) and Bosshard et al. (2013).
Our analysis was inspired by these, but differs from them in that we calculate variance components for raw data values first, and then use these to derive variance components of statistics of the data values, rather than using summary statistics in the ANOVAs themselves. Our data values here are simulated annual loss estimates, and, as discussed, we are interested in the variance components of the estimated mean annual loss, and annual loss quantiles. The calculations for the mean annual loss follow from a random effects ANOVA on the annual losses in a fairly straightforward way. However, no existing literature was found that exactly addressed our requirement for quantiles. Analytical methods for estimating the standard errors of quantile estimators using asymptotic approximations exist for independent data (Bahadur 1966), and have been extended by various authors to scenarios where the data are dependent (e.g. Olsson and Rootzén 1996; Assaad and Choudhary 2013 considered quantile estimation for repeated measurements). However, difficulties arise in the required estimation of the density function. In cases where analytical methods are difficult to apply, bootstrapping is a natural alternative. However, problems with bootstrapping for random effects models are well documented (Brennan et al. 1987; McCullagh 2000; Field and Welsh 2007). Our proposed method combines a bootstrap estimate of the total variance with an asymptotic approximation for the variance components using an ANOVA approach, obviating the need to estimate the density directly.
In the next section we will briefly describe the nature and structure of the natural catastrophe models that are used within the insurance industry. In Sect. 3 we will highlight features of the particular model on which our analysis is based in more detail, focusing on the components with a stochastic element. Section 4 describes the statistical methodology used to partition the variance in the estimates of the average annual loss and quantiles between these components, with some results presented in Sect. 5. Finally, in Sect. 6, we present some conclusions, including thoughts on how our ideas could be of use for other natural catastrophe models.
2 The nature of insurance catastrophe models
Natural catastrophe models are used by the insurance industry, government bodies, and other interested parties to estimate the risk from extreme events such as floods, tropical cyclones, windstorms and earthquakes. The models are developed in multi-disciplinary teams by both commercial and public enterprises, with those involved including, amongst others, meteorologists, hydrologists, engineers, statisticians and actuaries. See Grossi and Kunreuther (2005) for a comprehensive analysis of the history, structure and applications of catastrophe models. The Florida Public Hurricane Loss Model is an example of a publicly available catastrophe model (Powell et al. 2005; Chen et al. 2009).
The models provide input into the whole range of insurance functions, including pricing, portfolio management and the determination of capital requirements. The latest generation of models (described here) simulate losses ground-up from the smallest risk unit (building, risk covered and peril), with the hazard defined at an appropriately fine spatial resolution, dependent on the peril. A peril in this context is a natural phenomenon that generates insurance loss. Perils for a tropical cyclone model, for example, include associated inland and coastal flood, in addition to the principal peril, wind. Hazard refers to the loss inducing characteristic, for example the maximum wind speed or flood depth for each event, at each of a set of grid points. The risks covered might, for example, include buildings and contents damage and business interruption. Losses can be aggregated up to any required level of spatial resolution, over the risks and perils covered, up to the total portfolio level.
The most important and computer-intensive component of the catastrophe model simulates events over the required spatial domain over tens of thousands of possible versions of the following year. This component typically involves many sub-components, with physical as well as statistical routines, and its creation can take several months to run, depending on the model. Once derived, therefore, the catalogue of simulated years is fixed in the model, where it is stored in a database, along with the event details and corresponding hazard values, to be accessed when the model is run. Events in different simulation years are independent of each other (since they represent individual realisations of the possible experience over 1 year), but they are typically dependent within years, allowing features such as temporal clustering of events or time-related insurance contract clauses to be allowed for.
The appropriate number of simulation years to include in the model must therefore be decided at the development stage, and once fixed, this determines the optimal convergence of the estimated statistics that can be achieved in the software: the user can reduce the number used in order to get a quicker estimate, but they cannot increase it. The uncertainty in the modelled losses and related statistics, that pertains to the frequency and nature of the events is called primary uncertainty.
In addition to the catalogue of simulated years, the models comprise a number of components which depend on the specific details of the portfolios, and which must therefore be run within the software. Some of these components involve further simulation. Any uncertainty in the modelled losses that pertains to these other statistical components is called secondary uncertainty. The nature of these other components will depend on the specific model, but all models have a vulnerability component. This contains a set of vulnerability functions, which determine the distribution of the proportion of a risk item that is damaged, given a hazard severity and the risk characteristics. When combined with an insurer’s exposure (property details and contract terms), and a financial module, the distribution of losses due to the peril can be estimated over the following year. As well as the mean loss for the year (referred to as the average annual loss or AAL), the other important statistics are the quantiles. These are referred to as “return levels” with, for example, the 200 year return level equivalent to the 99.5% quantile. Extreme quantiles are of particular interest for capital requirements, whereas those with low return periods are used by insurers for validating the catastrophe models. Although the main products from the model are the estimated statistics, users may also be interested in examining individual years and events, for validation “what if” scenarios, or to compare to real time catastrophes.
The statistics of interest may be calculated from several financial perspectives: for example, losses before any adjustments, or after allowing for deductibles and limits in the insurance contracts, or after the application of any basic reinsurance treaties (referred to as ground-up, gross and net pre-cat respectively).
3 High level description of example model and components
The Europe Inland Flood model, which is the example catastrophe model used here, includes flood events across thirteen countries, with a hazard event set providing flood depths on a high resolution grid. This hazard set is driven by a stochastic precipitation model. The modelled precipitation is fed into a hydrological model, which determines the resulting river flow volumes and flood depths for all potentially loss-causing events, assuming an undefended river network.
In addition to the simulated hazard, the Europe Inland Flood model involves three further stochastic components, which deal with flood defences, exposure locations and building vulnerability. As discussed in the previous section, these are incorporated within the software itself, and so there is scope to vary the number of samples used for each of these at run-time.
While some flood defences are permanent structures, designed to protect against a flood with a specified return period, many are temporary or offer an unknown level of protection. In addition, defence levels change over time, with the ageing of existing structures, and implementation of new initiatives, and so any information sources on defences involve some uncertainty. Defence levels are therefore modelled as stochastic variables and re-sampled within each simulation year, with a mean protection level for each sub-catchment based on known data and random variation around that mean. Another stochastic component is required to model the exact locations of buildings, if only low resolution exposure information is available. This is very important for flood hazard, where the risk is highly localised. For example, only the total insured value and number of buildings at a postal code sector resolution may be known. In that case, the risks are randomly allocated to the high-resolution hazard cells within the aggregate locations, using the multinomial distribution, based on a set of exposure weights. The exposure location sampling here reflects the inherent uncertainty in the precise location of the buildings. As for the defences, the exposure locations are re-sampled within every simulation year.
The final stochastic component is the vulnerability component, which reflects the uncertainty in a building’s characteristics and its response to a given level of hazard, and is applied to each affected building, for each event, given the sampled defence levels and locations. It involves sampling a damage ratio from a statistical distribution, whose parameters reflect the hazard level, building location and assumed building characteristics.
Re-sampling from the defence level and exposure location distributions independently multiple times for each simulated year, and from the damage ratio distribution multiple times for each building for each combination of hazard, defences and exposure locations, improves the accuracy of the average annual loss and quantiles, but adds to the computational cost. The question of interest is to understand to what extent each of these components contributes to the variance of the estimate, and therefore how valuable these additional samples are for any particular analysis and input portfolio.
4 Statistical methodology
4.1 Average annual loss
We start by considering the simulation uncertainty of the average annual loss, and assume that exposure is known only at an aggregate postcode sector level. It is useful to write the equation for the annual loss for some specific portfolio as the statistical representation:
\(L_{ijkm}\) here is the annual loss in simulated year i (for \(i = 1, \ldots I\)), with defence level sample j (\(j = 1,\ldots J\)), exposure location sample k (\(k = 1,\ldots K\)), and vulnerability sample m (\(m = 1,\ldots M\)). The parameter \(\mu\) represents the average annual loss, and \(\alpha _i\), \(\beta _{ij}\), \(\gamma _{ik}\), \(\delta _{ijk}\) and \(\varepsilon _{ijkm}\) are all mutually independent random variables with zero mean. Specifically, \(\alpha _i\) represents the random difference from the average loss due to the incidence and severity of the hazard simulated within year i. The two variables \(\beta _{ij}\) and \(\gamma _{ik}\) represent the random differences from the within-year average, due to the sampled defence levels and exposure locations within that simulation year. Note that these effects are nested within each simulation year i.e the defence levels and exposure locations are re-sampled within each simulation year. An interaction term between exposure and defences is also required, since the impact of the defence levels within a simulation year depends on where the exposure is placed in that simulation year, and this is represented by the variable \(\delta _{ijk}\). Finally \(\varepsilon _{ijkm}\) represents the random difference due to residual variability, which for our model is the variability due to the uncertainty in the vulnerability of buildings hit by the simulated events in year i, given defence levels j and exposure locations k.
Since the random components are all independent, the variance of \(L_{ijkm}\) is given by the sum of the variances of the individual components. We start by estimating the variance components of the annual loss, using the standard statistical method of analysis of variance (ANOVA), noting that the statistical representation defined in Eq. (1) is effectively a random effects model, also known as a multi-level or variance components model (Montgomery 2013). The ANOVA approach uses the method of moments to equate a set of statistics with their expectations under the model. We define the following parameters:
-
\(\sigma _h^2\) as the variance of \(\alpha _i\), i.e. the variance due to primary uncertainty,
-
\(\sigma _d^2\), \(\sigma _{x}^2\), \(\sigma _{xd}^2\) and \(\sigma _{v}^2\) as the variances due to the uncertainty in defence levels, exposure locations, the defences-exposure interaction and vulnerability respectively (the secondary uncertainties).
Table 1 gives the calculations required for the estimation of the components (a bar denotes averaging, and the dots indicate which terms have been averaged over). The Mean Squares (\(m.s._{C}\) where C denotes the component in question) are not shown in the table, but are given by the Sum of Squares divided by the degrees of freedom. Unbiased estimators for the parameters are given by:
In practice, the variances of the random components in our model are not constant—for example the uncertainty in the vulnerability will tend to be higher at lower hazard levels. However, we can fit the model as if the variances were constant, using Table 1 and Eqs. (2) to (6), as described, noting that our parameters are then effectively a shorthand for the expressions, given below, where the annual loss, L, has been expressed as a function of hazard, defence levels, exposure location and vulnerability \(\left({\rm i.e.}\,L = g(H, D, X, V)\right)\):
The parameter in Eq. (7), for example, which is represented by \(\sigma ^2_v\), should be interpreted as follows: we first calculate the variance in losses due to the stochastic vulnerability component, given each particular combination of hazard, exposure and defences, and then calculate the average of this conditional variance over all the possible combinations.
To show that the statistics in Table 1 are indeed estimating the expectations in Eqs. (7–10), we would follow a standard ANOVA proof (see Montgomery 2013 for example), but express each of the random variables \(\alpha ,\, \beta,\, \gamma,\, \delta\) and \(\varepsilon\) as a difference between two conditional expectations. For example, we would express \(\alpha\) as \(E_{D, X, V|H}( L | H) - E_{H, D, X, V}(L)\), and \(\beta\) as \(E_{X, V| H, D}( L | H, D) - E_{D, X, V | H}(L | H)\). The variance of \(\alpha\), would follow immediately, given the second term is a constant, giving the expression for \(\sigma ^2_h\) in Eq. (10). The other variances may be calculated by using the law of total variance, with the law of iterated expectations allowing simplification of the resulting expressions.
Having estimated the variance components of the annual loss, we can now estimate the variance of the estimator of the average annual loss, which is given by:
The nested structure in the model means that the losses \(L_{ijkm}\) are not independent— \(L_{ijkm}\) and \(L_{ij^{\prime}k^{\prime}m^{\prime}}\) share the same simulated events, for example. Calculating the variance of a sum of dependent random variables requires the covariance structure. Returning to the model of Eq. (1), this is given by:
where \({\mathbbm {1}}(x)\) is the indicator function, such that \({\mathbbm {1}}(x) = 1\) if x is true, and 0 otherwise.
Allowing for this covariance structure, the variance of the AAL estimator can be shown to be given by:
The precision of the estimator can thus be varied by changing any or all of I, J, K and M. The impact depends both on the relative size of the variance component of the annual loss (which will depend on the portfolio being analysed), and on the position of that component within the nested structure. This must be balanced against the computational cost of additional samples of each component. Adding additional simulation years clearly has the most impact since I appears in the denominator of all the terms, but as already discussed, is highly computationally onerous, and can no longer be increased once development of the model has been finalised.
4.2 Losses with selected return periods
In this section, we consider return levels i.e. the loss values which are expected to occur once every N years for selected values of N or the \(1-1/N\) quantiles of the annual loss distribution. Both the distributions of the total loss in a year and the maximum event loss (i.e. the maximum loss from a single event in a year) are of interest to insurers, but we focus here on the total annual loss. (The methodology would be the same in either case).
Define the empirical distribution function \({\hat{F}}(l)\) by:
where \({\mathbbm {1}}(x)\) is the indicator function as before. Define also the estimator of the pth quantile as \({\hat{L}}_p = {\hat{F}}^{-1}(p)= \inf \{l: {\hat{F}}(l) \ge p\}\) i.e. we estimate the quantiles from the ordered annual losses, across all the samples. Then, provided certain regularity conditions are met (most importantly that F is continuously differentiable in a neighbourhood of \(l_p\), with first derivative f, see Olsson and Rootzén (1996) for conditions and a proof for a one-way random effects model), it can be shown that:
The variance of the estimator, \({\hat{L}}_p\), can thus be approximated by \(\sqrt{\text {Var}({\hat{F}}(l_p))/f(l_p)^2}\), the term in the denominator, with \(l_p\) replaced by its estimator \({\hat{l}}_p\). In the case where the random variables are independent, Var\(({\hat{F}}(l_p)) = p(1-p)/n\), with n the sample size. The variance of the Bernoulli random variable, \({\mathbbm {1}}(L_{ijkm} \le l_p )\), is equal to \(p(1-p)\). However, our interest is in variance components, and for this purpose it is useful to re-express it instead as a summation of component terms by conditioning and using the general law of total variance, in the same way as for the annual loss in Eqs. (2–6). We write:
where \(\tau ^2_{p_h}\), for example is the component due to the variation in the hazard between simulated years (specifically \(\text {Var}_{H} \{\text {E}_{D, V, X | H}({\mathbbm {1}}(L_{ijkm} \le l_p ) | H)\}\)), and the other components are due to the variations in the other sampled factors, conditioned as appropriate given the nested structure.
Comparing Eq. (14) with Eq. (11), the similarity is clear. Instead of averaging the annual losses \(L_{ijkm}\) to estimate the average annual loss, we average the indicator random variables \({\mathbbm {1}}(L_{ijkm} \le l_p )\) to estimate the distribution function, \(F(l_p)\). The latter is equal to p by definition, but the point here is not to carry out this calculation, but to provide an insight into how the variance components of the quantile estimates might be calculated, given different numbers of samples. The similarity between Eqs. (14) and (11) suggests using the same ANOVA approach to estimate the variance components of \({\mathbbm {1}}(L_{ijkm}\le l_p )\), replacing the annual loss in the equations in Table 1 with an indicator of 0 or 1, depending on whether the loss in that year/sample is greater or smaller than the estimated quantile of interest (noting that this requires a separate set of indicators and calculations for each required quantile).
Once we have estimated all the \(\tau _p^2\) components using the ANOVA, these results can be used to estimate the variance of \({\hat{F}}(L_p)\) with different numbers of samples in the same way as we use the variance components of the annual loss to estimate the variance of the AAL. Here, as for the AAL (see Eq. 12) we need to allow for the dependencies between the samples. This gives:
So finally, an approximate variance of the quantile estimator with I, J, K and M numbers of the different samples, is given by:
This equation requires an estimate of the density function, \(f(\hat{l}_p)\). This could be estimated as the gradient of the empirical CDF using a differencing method or by using kernel density estimation or an alternative smoothing method. We found this extremely difficult to do accurately, however, even with a large number of observations. The difficulty related to finding an automated method for selecting the required smoothing parameter, that worked well across all required quantiles and spatial resolutions. Given this difficulty, we estimated the total variance using the bootstrap method. This estimate was then used in combination with Eq. (18), obviating the need to estimate the density function directly.
Bootstrapping could not be used in isolation as a method for estimating the variance components, since it is impossible to maintain all the required elements of the random effects model within the resamples without using a prohibitively large number of samples of each of the factors: namely the dependence structure due to the nested model, the randomness of the effects (i.e. the fact that they are just samples of the populations, rather than spanning the whole population), and the balanced design [see for example Field and Welsh (2007) for a discussion of different bootstrap sampling schemes for the one-way scenario and the biases involved with different schemes]. However, bootstrapping can be used to estimate the total variance assuming I simulation years, if we ensure that there is no dependence by having just a single sample of each of the secondary uncertainty factors (\(J=K=M=1\)). The experimental design is detailed in the next section, but note that, for the estimation of the numerator of Eq. (18), the ANOVA analysis will require \(J, K, M > 1\). In summary, the steps involved here are:
-
Design an appropriate computer experiment for the ANOVA and use it to estimate the variance components of \({\hat{F}}({\hat{l}}_p)\) for each required p. The sum of the components will be \(p(1-p)\).
-
Carry out a simple bootstrap (with no nested structure) to estimate the total variance of each quantile estimator. Substitute this variance into Eq. (18) with I the number of samples used, and \(J=K=M=1\) in order to estimate \(f({\hat{l}}_p)\) at each estimated quantile value.
-
Use the equation with the estimated \(\tau _p\) and densities, with different values of I, J, K, M, to examine the impact on the precision of the quantile estimates of adding additional samples.
A limitation that remains is the fact that the asymptotic variance equation is not appropriate for non-smooth functions, but the loss density function may have discontinuities at high levels of resolution (for example because of flood defences) or for certain financial perspectives. However, in practice, the return levels are of most interest at lower levels of resolution and for the gross financial perspective, where this is not an issue. In any cases where there is a lack of smoothness, an estimate of the total standard error is nevertheless available via the bootstrap.
4.3 Computer experiment
In order to estimate the variance components using the methods described in Section 4, we set up a structured computer experiment. A set of hazard events over 50,000 simulated years was pre-computed and loaded into the catastrophe model software engine. Within the engine, the defence levels, exposure location and vulnerability samples are all controlled by random seeds (with a seed for each component), so that running the software again with the same seeds gives the same results. In order to create the balanced design, the engine was run several times with different seeds, and the results were then merged together. For our analysis, we used four combinations of two exposure location samples and two defence samples, with two vulnerability samples within each of these i.e. \(I = 50,000, J = K = M = 2\). Taking two exposure samples, for example, means that within each year, we sample from the multinomial distribution parametrised by our exposure weights twice, giving two slightly different sets of assumed building locations.
The 50, 100, 200 and 500 year return levels were estimated by ordering the 400,000 annual losses in descending order, and taking the 8000th, 4000th, 2000th and 800th of these respectively. For the bootstrap to estimate the total variance of the quantile estimates, we sampled 50,000 annual losses randomly with replacement from the 400,000 and repeated 1000 times.
5 Results
In this section we investigate the variance components of the average annual loss and return level estimators for a specific set of input portfolios. All the figures and plots have been based on the methodology described, with sample numbers as in Sect. 4.3. We have then calculated variance components for a single sample by setting \(I=50,000\) and \(J = K = M = 1\) in Eqs. (13) and (18). This permits assessment of the benefit of reducing the secondary uncertainty by increasing the numbers of these samples. Total standard errors for the estimates with this set-up were also calculated (these are not shown in the plots). All losses are on a gross of reinsurance basis.
The results are of interest at different levels of resolution, depending on the purpose of the analysis, and here we consider country, CRESTA and postal code sector (subsequently referred to as just postal code). CRESTA (Catastrophe Risk Evaluating and Standardizing Target Accumulations) is a standard system, widely used in the reinsurance industry, which splits the world into natural hazard risk zones. As an example of the scale, the UK, excluding Northern Ireland, consists of 120 such zones. We also consider three distinct lines of business: residential, commercial and industrial. A representative industry exposure data set has been used for each country, assuming that the exposure is known at a postal code resolution.
The purpose of this analysis is to examine the variance components of the AAL and selected quantiles over many different example “portfolios” of different size, nature and spatial domain, where each such portfolio includes the set of exposures that fall within the specified spatial domain, for the line of business being considered. For example, when considering the CRESTA resolution, we have 360 such portfolios within the UK, one for each CRESTA zone and line of business. The country level portfolios are representative of the kind of analysis that users would run for capital requirement purposes. The smaller portfolios (CRESTA and postal code level) are of interest for underwriting, pricing and exposure management.
Proportion of the variance of the AAL due to primary uncertainty, by line of business, at different levels of resolution: Country, CRESTA and Postal Code. Each data point represents a result from a single portfolio (with of the order of 10, 500 and 30,000 points at these resolutions respectively, for each line of business)
Figure 1 shows the proportion of the variance of the average annual loss that is due to primary uncertainty (i.e. frequency and nature of hazard). The proportion reduces, and shows increasing variability across portfolios, with increasing resolution, and is highest for residential business, and lowest for industrial. These results indicate that there is little benefit, in terms of improving convergence, in sampling any of the secondary components more than once if an expected loss is required for a large diversified portfolio, similar to the country resolution. This is because, even though the uncertainty in these factors for an individual event and building can be very high, summing over numerous events and buildings smooths out these individual effects. Standard errors of the AAL estimates at this resolution are around 1–3% for a large country-wide portfolio. In the UK for example, the simulations included over 200,000 events (over 4 per year on average) and over 20 million insured buildings, with a standard error of 1.1%, across all lines of business. Meaningful improvements could only be achieved by increasing the total number of simulated years, but this would arguably constitute spurious accuracy, given the other sources of uncertainty discussed in Sect. 1.
What if we require an expected loss for a much smaller exposure? There is clearly a high variability in the variance components at postal code resolution. This leads to a very wide range of standard errors if the secondary uncertainty components are only sampled once. Only for residential business is primary uncertainty still dominant, with a typical standard error of around 5%, whereas errors are around 8–10% for commercial and industrial, but with some locations with smaller errors, and others where the errors are significantly larger.
Which of the secondary components is the most important, and what drives the results? The ANOVA and related analysis led to further insights here, which we briefly summarise. Most of the variance in the average annual loss estimate for industrial business at postal code resolution is due to uncertainty in building vulnerability. The difference compared with residential business is mainly due to the greater concentration of the exposure in the industrial and commercial lines of business (i.e. fewer buildings for the same sum insured), so the diversification benefit is reduced. Exposure location uncertainty can also lead to a high error in postal codes with a small number of buildings to be allocated across many hazard cells, particularly where relatively uniform exposure weights are combined with a high hazard gradient. The average annual loss may be well-converged even for a single building, however, if it is in a high flood risk location, where the events are not too dissimilar, since each simulation year involves sampling from the secondary uncertainty distributions.
The component proportions depend on localised differences in hazard and defences, but a typical split for each line of business at postal code resolution is shown in Table 2 (“typical” here, being taken as the rounded median proportion across all the postal code level portfolios). The proportion of the variance of the AAL due to uncertainty in defence levels and the exact exposure location generally represent the smallest contributions. However, both of these contributions to the AAL uncertainty can be much higher for some postal codes. The 95% quantile of the defence level contribution to AAL uncertainty across postal codes is around 30% for residential business, 20% for commercial and 15% for industrial, whereas the 95% quantile of the exposure location component is around 20% for commercial and industrial lines, and only 7% for residential.
We have considered the variance components and standard errors of the average annual loss estimator. Next we consider the split between primary and secondary uncertainty for the return level estimators. Figure 2 shows these for Country and CRESTA resolution, for 50, 100, 200 and 500 year return levels, by line of business. The proportion of the variance due to primary uncertainty tends to be fairly similar for return levels of 50–200 years, although typically reducing slightly with return period, but significantly lower at 500 years. Differences between the lines of business are much less marked than for the AAL.
Proportion of the variance of selected return levels due to primary uncertainty at different levels of resolution (Country, CRESTA), by line of business. Each data point represents a result from a single portfolio (with of the order of 500 and 30,000 points at these resolutions respectively, for each line of business)
As for the AAL, variance components of the return levels depend on localised features of the hazard and defences, but of the secondary components, vulnerability is again by far the most important, with an increasing proportion with increasing return period. The uncertainty due to exposure locations, which is generally very low, similarly increases with increasing return period. The proportion of the total variance that is due to defence level uncertainty tends to be highest at a return period of around 50, and then reduces with increasing return period.
Intuitively, we might expect the total standard error (expressed as a percentage of the estimator) to increase with increasing return period, but this is not necessarily the case. Equation (18) indicates that the total absolute standard error of the estimator of the pth quantile, assuming \(J=K=M=1\), is proportional to the standard deviation of \({\mathbbm {1}}(L_{ijkm} \le l_p )\),
and inversely proportional to the density of events, \(f(l_p)\). The standard deviation of \({\mathbbm {1}}(L_{ijkm} \le l_p )\), which is equal to \(\sqrt{p(1-p)}\), is maximised at 0.5, and reduces in the tails. The density typically also reduces in the upper tail as the return period increases. When the standard error is expressed as a percentage of the estimator, another factor is that this itself is increasing with the return period. The reduction in the density usually dominates these effects, leading to higher errors and at countrywide resolution, it is almost always true that the standard errors do increase with increasing return period. Standard errors are typically around 2–3% for the 50 year loss, rising to 3–5% for the 500 year loss, for a large country-wide portfolio.
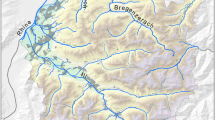
However, at higher resolutions, local features are no longer averaged out to the same extent, and this can lead to density functions and distribution curves that do not follow this typical pattern. For example, a region with defences built to withstand a 100-year event will tend to have a higher standard error for the 100 year loss (when expressed as a percentage of that loss), than at higher return periods. The defences have a gearing effect on the losses, particularly if it is assumed that they either do not fail or fail completely, with a large difference in losses either side of the defence level leading to a high standard error. Examples showing the standard errors of return levels for two UK CRESTAs are shown in the Appendix. For each of these we show a map with a set of assumed mean defence levels (these are example values, but at realistic levels), followed by an Exceedance Probability (EP) curve, and a plot of the standard error as a percentage of the estimator, against the return period. The first example is the region around Crewe in Cheshire in the north-west of England. The River Weaver flows from the south to the north, where it is joined by its tributary, the River Dane. In this CRESTA, the level of flood risk is relatively low in the main exposure areas, with correspondingly limited defences. Here, the standard errors are below 2% up to 100 years, increasing thereafter with increasing return period. The second, contrasting example, is the Bath CRESTA in the south-west of England, where the River Avon flows directly through the high exposure city of Bath itself. Extensive flood defence improvements were carried out in the 1970s after severe flooding in the 1960s, with additional improvements currently in progress (Environment Agency and Bath and North East Somerset Council 2014). Here, a defence level assumed at 150 years in our model in the area of high exposure has led to a spike in the standard error around the 150 year loss, with a peak error of around 9%.
Note that we are talking here about the impact of the defences themselves, and not the uncertainty in the defences, and most of this error is attributable to primary uncertainty, and hence not reducible with additional samples of the secondary uncertainty components. In locations where the uncertainty in the level of defences is high, the standard error of the AAL will be increased accordingly, but the gearing effect of the defences will be smoothed out over return periods, so the standard error at the mean defence level will be lower than if the defences were known for certain to be at this level.
6 Conclusion
In this paper we have demonstrated how the ANOVA model can be used to quantify the components of simulation uncertainty in a natural catastrophe model. We started with an analysis of the variation in the annual loss using a random effects representation and standard techniques. The variance component estimates were then used to determine how the standard error of the average annual loss would change, with different numbers of samples of each of the stochastic components in the model.
In addition to the average annual loss, selected quantiles of the loss distribution are also highly important for insurers and re-insurers, with the 200 year return level of particular interest for solvency calculations. In order to derive the variance components of quantiles, we first extended the approach to the empirical cumulative distribution function at quantiles of interest. Using an asymptotic result to relate the variance of quantiles to that of the empirical CDF, in combination with a bootstrap estimate of the total variance, we obtained the variance components of the quantiles themselves, as required.
These analyses allowed us to address the main question that had motivated the research: to consider the impact of using different number of samples of each of the stochastic components in the Europe Inland Flood model, for different portfolio types. In summary, our results showed that for reserving/capital requirements when large portfolios are considered, there is no need to take more than one sample for any of the secondary uncertainty components. This would allow estimation of the average annual loss, quantiles of the annual loss distribution, and the total variance of annual losses, but not of the variance components, for which at least two samples would be required. For underwriting purposes, which involve small exposures, additional vulnerability samples are highly important in almost all cases, whereas the exposure and defence components are important in selected cases only, depending on location. The detailed analysis, including the sample portfolio results for different lines of business and at the different levels of resolution, has been used to provide guidance to users, and to help decide which variance metrics should be included as output from the model. Each user of the model can then make their own decision as to the appropriate number of samples to use (within the flexibility offered), based on their particular portfolio, analysis, time constraints and computer set-up. The output from the model will include standard errors of the statistics, and (if at least two samples of secondary uncertainty components are used) an indication of how these errors would change with different numbers of samples.
In addition to addressing this question, the analysis proved extremely useful at improving our understanding of both our model, and the nature and uncertainties in the risk being modelled. In particular, it indicated which components of the system contribute most to the total uncertainty, for different portfolios and metrics. At the model development stage, this helped to identify areas to investigate, where that uncertainty might productively be reduced, or code written more efficiently. A summary of the process followed is given in the flowchart in Fig. 3 of the Appendix.
The framework that we have developed is flexible, and may readily be applied to other studies and models that use simulation with multiple stochastic components. It is particularly useful for large scale studies, where hazard simulation is highly computer-intensive, and where the ultimate question of interest relates to the impacts of the hazard. Hazard impacts may be varied, and may be of interest, not just at a global level, but also for subsets of the domain. While the development of this type of model has been limited in the past, due to its high computational requirements, this is no longer the case, and models are increasing in both their complexity, and in their use of simulations. Understanding and minimising the simulation uncertainty involved in such complex systems is therefore an important research topic. The additional information about simulation uncertainty also supports the move away from the historical black-box models towards the increased transparency required by today’s model users and government regulators.
An important aspect of the analysis here has been the requirement to consider thousands of possible subsets of the total exposure, in order to understand how results vary by spatial location, and size of portfolio. For the Europe Inland Flood model, for example, calculations were required for over 1500 CRESTA/line of business combinations, and over 100,000 postal code/line of business combinations. Therefore a pragmatic approach was important, and issues were addressed with this in mind. As an example, splitting a variance into a large number of components using what is effectively a “method of moments” approach can occasionally give nonsensical results, for examples negative estimates of variance components. This would ideally be dealt with by re-fitting models excluding the negative factor or factors. However, in practice such an approach would require iteration and would result in multiple different models. It was not considered viable or necessary here, at least for the investigation stage, with any such components set to zero, and others adjusted to retain the total.
Notes
The RMS Europe Inland Flood HD Models, development version.
References
Assaad HI, Choudhary PK (2013) L-statistics for repeated measurements data with application to trimmed means, quantiles and tolerance intervals. J Nonparametric Stat 25(2):499–521
Bahadur RR (1966) A note on quantiles in large samples. Annals Math Stat 37(3):577–580
Bosshard T, Carambia M, Goergen K, Kotlarski S, Krahe P, Zappa M, Schär C (2013) Quantifying uncertainty sources in an ensemble of hydrological climate-impact projections. Water Resour Res 49:15231536
Brennan RL, Harris DJ, Hanson BA (1987) The bootstrap and other procedures for examining the variability of estimated variance components in testing contexts (ACT Research Report 87–7). Technical report, ACT Inc, Iowa City, IA
Castillo E (1988) Extreme value theory in engineering. Academic Pres, New York
Chen S-C, Chen M, Zhao N, Hamid S, Chatterjee K, Armella M (2009) Florida public hurricane loss model: research in multi-disciplinary system integration assisting governemnt policy making. Gov Inf Q 26(2):285–294
Environment Agency and Bath & North East Somerset Council (2014) Bath quays waterside public consultation: April 2014. http://www.bathnes.gov.uk/sites/default/files/bath_quays_waterside_consultation.pdf. Accessed Jan 6 2016
Falter D, Dung N, Vorogushyn S, Schrter K, Hundecha Y, Kreibich H, Apel H, Theisselmann F, Merz B (2016) Continuous, large-scale simulation model for flood risk assessments: proof-of-concept. J Flood Risk Manag 9(1):3–21
Fawcett L, Walshaw D (2016) Sea-surge and wind speed extremes: optimal estimation strategies for planners and engineers. Stoch Environ Res Risk Assess 30(2):463–480
Field CA, Welsh AH (2007) Bootstrapping clustered data. J R Stat Soc Ser B 69(3):369–390
Finney MA, McHugh CW, Grenfell IC, Riley KL, Short KC (2011) A simulation of probabilistic wildfire risk components for the continental United States. Stochast Environ Res Risk Assess 25(7):973–1000
Geinitz S, Furrer R, Sain SR (2015) Bayesian multilevel analysis of variance for relative comparison across sources of global climate model variability. Int J Climatol 35:433–443
Goda K, Song J (2016) Uncertainty modeling and visualization for tsunami hazard and risk mapping: a case study for the 2011 Tohoku earthquake. Stochast Environ Res Risk Assess 30(8):2271–2285
Grossi P, Kunreuther H (eds) (2005) Catastrophe modelling: a new approach to managing Risk. Springer, Boston
Lin N, Emanuel KA, Smith JA, Vanmarcke E (2010) Risk assessment of hurricane storm surge for New York city. J Geophys Res Atmos 115. doi:10.1029/2009JD013630
McCullagh P (2000) Re-sampling and exchangeable arrays. Bernoulli 6:285–301
Montgomery DC (2013) Design and analysis of experiments. John Wiley and Sons Inc, Singapore
Northrop PJ, Chandler RE (2014) Quantifying sources of uncertainty in projections of future climate. J Clim 27:8793–8808
Olsson J, Rootzén H (1996) Quantile estimation from repeated measurements. J Am Stat Assoc 91(436):1560–1565
Osuch M, Lawrence D, Meresa HK, Napiorkowski JJ, Romanowicz RJ (2016) Projected changes in flood indices in selected catchments in Poland in the 21st century. Stochastic Environmental Research and Risk Assessment, pp 1–23
Powell M, Soukup G, Morisseau-Leroy N, Landsea C, Cocke S, Axe L, Gulati S (2005) State of Florida hurricane loss projection model: atmospheric science component. J Wind Eng Ind Aerodyn 93(8):651–674
Randell D, Turnbull K, Ewans K, Jonathan P (2016) Bayesian inference for nonstationary marginal extremes. Environmetrics 27(7):439–450 env.2403
Yip S, Ferro AT, Stephenson DB, Hawkins E (2011) A simple, coherent framework for partitioning uncertainty in climate predictions. J Clim 24:4634–4643
Acknowledgements
We would like to thank Bronislava Sigal and Paul Northrop for helpful comments, and the RMS Flood Model team for sharing their model with us, and supporting our analysis.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Flowchart of model development process
See Fig. 3.
1.2 Impact of defences on standard errors of return levels
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kaczmarska, J., Jewson, S. & Bellone, E. Quantifying the sources of simulation uncertainty in natural catastrophe models. Stoch Environ Res Risk Assess 32, 591–605 (2018). https://doi.org/10.1007/s00477-017-1393-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-017-1393-0