Abstract
Key message
Structural characteristics of tree crowns obtained by TLidar scanning can be used for estimating the course of the stem diameter growth in the past.
Abstract
To improve human well-being through sustainable management of ecosystems, particular attention is given to the structures, functions, and services of forest trees and stands. The classical timber provision has become only one of many other forest ecosystem services. At the same time, the methods of ecosystem observation, analysis, and modelling have enormously improved. Here, we fathomed the information potential of the tree crown structure. Our overarching hypothesis was that the crown structure reflects essential characteristics of the tree ring pattern. The empirical part of this study was based on sample trees from the combined spacing-thinning trial in Norway spruce (Picea abies [L.] Karst.) Fürstenfeldbruck 612 in Southern Germany. First, we showed that the external characteristics of tree crowns and the internal stem structure are functionally linked. Second, we derived metrics for the tree ring pattern and crown shape, and found especially close relationships between the level and bending of the growth curve and the size and stereometric shape of the crown. Third, we investigated how the derived statistical relationships between tree ring pattern and crown structure can be applied to derive the course of tree growth from the crown structure. We showed how measures such as size and variability of the crown could be used to estimate the course of diameter growth. Finally, we showed that the revealed link could be used to assess past and future growth and life expectancy of trees. These findings can be used to monitor the stress defence potential, resistance, and resilience of trees.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The structures, functions, and services of forest trees and stands are getting more particularised attention. They are essential for improving human well-being by a more sustainable management of ecosystems. The classical timber or biomass provision has become only one amongst many other providing, regulating, cultural, or supporting forest ecosystem services (Burkhard et al. 2010; De Groot et al. 2010). At the same time, the methods of ecosystem observation, analysis, and modelling, which are the precondition for forestry value creation, have enormously improved (Bravo et al. 2019; de Araujo Barbosa et al. 2015; Romijn et al. 2015). Classical methods of crown structure measurement were destructive and very laborious. For this purpose, the trees were felled, dissected, and re-erected in sections to measure the position, length, and angle of the branches of the section in an upright position (Seifert 2003).
However, technical advances, such as remote sensing of trees using TLidar, now allow fast, non-destructive, accurate, and detailed measurements of the crown structure (Jacobs et al. 2021; Uzquiano et al. 2021; Cattaneo et al. 2020; Barbeito et al. 2017; Liu et al. 2017; Bayer et al. 2013). So far, detailed remote-sensing measurements of the present crown structure have hardly been used to infer the past course of stem growth (but see Maltamo et al. 2022).
Similar to the tree ring pattern, the crown structure (e.g., whorl frequency, branch length, crown profile) contains information about the tree’s development in the past (Oldeman 1990; Assmann 1970, pp 87–88; Pretzsch 2021a). Certainly, crown shapes are species-specific (Pretzsch et al. 2015); however, wide and long crowns with paraboloidal shapes may have been associated with open growth in the past. This may go along with continuously and sigmoidally increasing stem diameter growth with increasing age. Layered crowns, structured in tiers, may indicate repeated periods of suppression, whereas, within the stem, the normally sigmoidal course of diameter growth is interrupted by periods of low growth (Oliver and Larson 1996). The relationship between crown structure and past external influences has already been used to characterise the competitive constellation (Assmann 1970, pp 87–88), and social class (Kraft 1884) of trees, browsing (Kupferschmid et al. 2013), groundwater lowering (Pretzsch and Kölbel 1988), N-deposition and fertilisation (Pretzsch 1985), acid rain (Roloff 2001; Oldeman 1990), and climate change-induced growth trends (Röhle 1987).
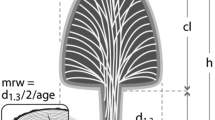
Figure 1 visualises how the crown shape may be related to the tree ring pattern of Norway spruce (Picea abies [L.] Karst.). A tree ring pattern with (a) regular wide rings may result in a uniform crown shape, whereas (b) an irregular crown profile may reflect irregular ring width. Stem growth courses (c) with wide rings in the juvenile phase and then continuously decreasing ring width can result in a paraboloidal crown shape well known from open-grown trees. Trees that initially exhibit low growth and later accelerated growth may develop a neiloidal crown shape (Fig. 1d). These are four basic relationships in a continuum of various interrelations between tree ring and crown patterns, determined mainly by internal genetical traits and external environmental factors.
Hypothesis on the relationship between tree ring development of the stem at 1.30 m (below) and crown structure (above) of Norway spruce visualised by four basic patterns. Depending on whether the tree ring width is a steady or regular, b irregular, c decreasing, or d increasing with progressing tree age, the crown shapes may be regular, irregular, paraboidal, or neiloidal, respectively
Some stand models that derived the stand growth from the three-dimensional development of individual trees (Mitchell 1975, p. 7 and p. 19, Pfreundt 1988, p. 15) established a link between stem growth and crown expansion. They used the predicted crown, tree, and stand structure to model stand structure, light absorption, and tree growth. Thus, those models also suppose a close link between stem and crown growth. However, they used it for 3D simulation, while in this study, we tried to harness it to deduce internal stem properties from external crown characteristics.
Our overarching hypothesis was that the external characteristics of tree crowns and the internal stem structure are functionally linked and that statistical relationships reflect this. The crown structure reflects essential attributes of the tree ring pattern. The hypotheses in detail are:
H I: Crown shape and tree ring pattern can be linked and modelled by a set of general allometric relationships.
H II: Metrics of crown structure and metrics of tree ring patterns are statistically correlated.
H III: The course of stem growth can be deduced from the crown characteristics measured by TLidar scanning.
Finally, we show that the revealed link between external characteristics of tree crowns and the internal stem structure can be used to assess past and future tree growth and life expectancy, as well as stability and other aspects of wood quality. Furthermore, we argue that these findings can be used to monitor trees' stress defence potential, resistance, and resilience.
Materials and methods
Rationale for the combination of simulation approach and empirical proof of concept
We combined a simulation with an empirical modelling approach to gain insights into the relationships between crown structure and tree ring pattern. We started with a simulation study based on simplified allometric relationships between crown structure and stem growth. We used a set of stem growth curves and simple allometric relationships for simulation of crown development and explored the relationships between stem growth and simulated crown structure. A collection of metrics was used to characterise both crown structure and course of stem growth. The statistical analyses revealed a close link between size and the shape of the upper crown part and the tree ring pattern.
Based on the insights of the simulation study, we analogously characterised the crowns and tree ring patterns of measured sample trees. We further analysed the statistical relationships between the external and internal structural aspects. The resulting functions allowed the estimation of tree growth based on selected crown traits. For the study, we extensively measured the crowns of 78 mature Norway spruce sample trees by TLidar and analysed their stem growth based on increment cores. To cover a broad range of crown sizes and shapes, we used the long-term spacing and thinning experiment Fürstenfeldbruck 612 (FFB 612), introduced in the following section. The trial was 47 years old, while the 78 selected N. spruce trees were 4 years older, i.e., 51 years old, at the sampling time. A sampling of cores (“Increment coring and tree ring analyses”) and TLidar scanning of all crowns (“TLidar scanning and information extraction”) resulted in a dataset with a high potential for information on crown-stem relationships. Due to the substantial variation in initial spacing and thinning, the included trees represented a broad spectrum of crown shapes and courses of stem diameter growth, reaching from development under solitary conditions to maximum stand density.
Simulation study
We started with a simulation study based on 100 generated stem growth curves to fathom the principal relationship between stem growth and crown structure. The stem growth curves and three basic allometric relationships were used to simulate the crown development over 50 years. A set of metrics characterised the stem growth curves and the simulated crowns; the correlations between these sets of metrics revealed insights into the links between growth and structure, valid for the subsequent empirical study.
To implement this approach, we first derived an allometric relationship based on the tree data from FFB 612. In detail, we parameterised allometric functions for estimating tree height, h, height to the crown base, hcb, and crown radius, crad, depending on stem diameter and tree age. All three relationships were modelled by the double-logarithmic relationship between crown characteristics, stem diameter, d, and tree age, age. The models were fitted to the data available from the repeated surveys of the long-term experiment, FFB 612 (see “Empirical study”),
Second, we generated the stem growth patterns of 100 trees (Supplementary Fig. 1) within the size and parameter range of the 78 sample trees from FFB 612. The generation was based on diameter values for ages 10, 25, and 50 (d10, d25, d50). We fitted a simple curve of the type \(\mathrm{ln}\left(y\right)={a}_{0}+{a}_{1}\times \mathrm{ln}\left(d\right)+{a}_{2}\times \mathrm{ln}\left(\mathrm{age}\right)+{a}_{3}\times \mathrm{ln}\left(d\right)\times \mathrm{ln}\left(\mathrm{age}\right)\) to those values and received the model curves shown in Supplementary Fig. 1. Based on the 5-year-diameter increment derived from these curves and the models 1–3, we estimated the three-dimensional extension of the crown, as exemplified in Fig. 2. The crown shapes resulting from 50 years simulation runs were characterised using the metrics introduced in “From measurement to metrics”. Pearson correlations between stem growth and crown shape metrics provided insights into the relationship between stem and crown dynamics.
Figure 2 visualises the relationship between the stem diameter growth of a tree (Fig. 2a) and the resulting crown structure (Fig. 2b). Both the stem diameter growth and crown development are shown in 5 years steps. The crown structure was derived from models 1–3. To better represent the development of the crown shape, the crown radius in Fig. 2 and the crown diagrams were doubled compared to the actual lateral crown extension. The tree’s age significantly contributed to the prediction of tree height, height to crown base and crown radius (models 1–3). This coincides with the other studies suggesting age as an additional predictor for stem and crown size development (Genet et al. 2011).
Empirical study
Combined spacing-thinning trial in Norway spruce in Fürstenfeldbruck 612 as an empirical basis
The experiment FFB 612 belongs to a series of long-term experiments initiated by the International Union of Forest Research Organizations (IUFRO) across Europe (Krutzsch 1974). Here, we report only the essential characteristics of FFB 612; for further information, see Schmied et al. (2022) or Pretzsch (2006). FFB 612 was established in 1974 with 4-years-old saplings. The experiment is located 40 km west of Munich, Bavaria, Germany, at 11.05°E longitude and 48.14°N latitude at an elevation of 550 m a.s.l. Over the past 30 years (1991–2020), the mean annual temperature was 8.8 °C (14.7 °C in the growing season), and the annual precipitation was 932 mm (575 mm in the growing season). The stand stocks on Lessivé soils on a Loess substrate. The growing conditions for N. spruce are excellent, represented by dominant heights at age 100 above 40 m (Assmann and Franz 1963). The experimental plots include 21 plots with different initial density and spacing (1 m × 1 m, 1.25 m × 2 m, 1.6 m × 2.5 m, 2.5 m × 4 m, 5 m × 5 m) and thinning regimes (no thinning, moderate, strong, and very strong thinning). To cover trees with a broad range of competitive status at present and development in the past, we sampled systematically 78 trees. We tested trees from unthinned and thinned plots at three different initial spacing levels (2.5 m × 1.6 m; 4 m × 2.5 m; 5 m × 5 m; see Table 1). The trees were equally distributed over plots with three initial densities (2.5 m × 1.6 m; 4 m × 2.5 m; 5 m × 5 m) and two thinning modes (unthinned, thinned).
Increment coring and tree ring analyses
For this study, we sampled 78 N. spruce trees in December 2020, using a 5 mm increment borer (Haglöf, Sweden). Each tree was cored twice at breast height (dbh, 1.3 m) from the northern and eastern cardinal direction to minimise influences of reaction wood. Overall, 156 cores were extracted and subsequently air-dried, glued onto a wooden slide, and sanded with increasingly finer grit sandpaper (120–400 grit). Standard dendrochronological techniques were applied to obtain annual ring widths (Speer 2010). We used the Lintab series 5 measuring table and the software Tsap-Win (both from Rinntech Heidelberg, Germany) to measure tree rings to the nearest of 0.01 mm. We relied on pointer years with distinctive narrow or wide rings common to most tree rings (Schweingruber et al. 1990) to check for cross-dating accuracy (Stokes and Smiley 1996). The drought years 2003, 2015, and 2018 were particularly helpful, as the trees developed exceedingly narrow growth rings in these years. After measuring, cross-dating accuracy was verified statistically. This involved detrending all tree-ring series with a 30 years spline to remove low-frequency variance, and then averaging them to a master dating series. Subsequently, all detrended series were individually tested against the master series while removing the component associated with the series under consideration. The series was split into small segments and correlated with the corresponding segments of the master series. By shifting the segments of the respective series in different directions, potentially better fits characterised by higher correlations could be determined, thus revealing potential measurement errors. The statistical cross-dating was performed using the programme Cofecha (Holmes 1983).
All trees had the same age (51 years at the end of 2020). However, due to the different initial spacing (4–25.0 m2 growing area per plant), thinning, and resulting local stand density (226–1644 trees ha−1), the stem and crown sizes varied considerably (Table 1). The stem diameter, for example, ranged between 14.0 and 55.7 cm, and the crown diameter was between 2.7 and 5.9 m. The mean annual diameter growth varied between 2.5 and 13.0 mm year−1. Table 1 shows that our sample also covered a broad range of different courses of diameter growth. The wide variation of internal stem growth and external crown size was a precondition for analysing the relationship between these two aspects of tree growth and structure.
Figure 3 shows the substantial variation of different levels and shapes of the stem diameter development (a) and annual stem growth (b) on FFB 612. Furthermore, our sample comprised trees that grew permanently slow or fast, i.e., those that always stayed at the lower or upper border of the set of curves. In addition, trees that changed their growth pattern from slow to fast-growing or the other way round were also present in our dataset.
Stem diameter development and annual stem diameter growth of the 78 trees of the combined spacing-thinning trial Fürstenfeldbruck 612. a Development of the stem diameter until 2020 (year of the increment coring). b Annual stem diameter growth until 2020. Note that in a few cases, the coring did not access the pith (see curves starting between 1990 and 2000)
TLidar scanning and information extraction
The RIEGL VZ-400i (RIEGL 2019) laser measurement system was used with a laser pulse repetition rate of 1200 kHz. We set the horizontal angular resolution to 0.04°, which, in our practical experience, achieved a reasonable trade-off between scan-time (45 s per scan) and the risk of disturbances due to tree movement caused by wind. One horizontal 360° scan was performed for each scan position with a 100° vertical field of view. For the scanning campaign, multiple scans were taken consecutively around the plots in the form of a grid with a repeated pattern of one scan approximately every 7 m.
The automatic registration, filtering, and multi-station adjustment (MSA) used to refine the overall registration was performed using the RiSCAN PRO version 2.10.1 software (http://www.riegl.com/products/software-packages/riscan-pro/). The point cloud was reduced using an octree to enable fast point-cloud processing without accuracy loss (Elseberg et al. 2013). After tree detection, the isolation of each tree was performed using a preprocessing algorithm in R (R Core Team 2021), which is based on the density-based spatial clustering algorithm with noise (dbscan) function (Ester et al. 1996), obtained from the dbscan package (Hahsler and Piekenbrock 2019). Multiple scanning positions provide many distributed point clouds with low overlapping from different viewing angles. By applying dbscan, the entire point cloud was classified into clusters. Each cluster was individually queried, which stem base cluster was closest in the distance and whether this distance was close enough to be classified as associated points (see, e.g., Jacobs et al. (2020, 2021, 2022), Uzquiano et al. (2021), and Alvites et al. (2021) for previous uses of this function for tree detection and isolation). After this step, each tree was visually checked for completeness. If necessary, unrecognised tree parts were added manually, and artefacts that appeared to be unrelated to our target trees were removed using the software RiSCAN PRO.
The total tree height was calculated by subtracting the isolated tree’s Z-axis minimum and maximum points. The point cloud was used to acquire the crown bases to determine the crown length. After that, the crowns were separated into 5 cm height classes, and each height class was subdivided into polar coordinate categories to calculate various crown expansion metrics visualised in Supplementary Fig. 2. Of particular interest were amongst others the maximum crown expansion and the respective height, the crown diameters in different heights, and the stem shape and stem diameters in different tree heights. An algorithm based on the dbscan function (Ester et al. 1996) isolated the stem. Therefore, measuring the basal area at crown base height was also possible. The stem of the specific height class was used as the centre for calculating the maximum extent of the crown. Distances were computed using the point distance functions from the VoxR package (Lecigne et al. 2014).
From measurement to metrics
Metrics for characterising the course of stem growth
We used a set of measures and metrics to analyse the relationship between the present crown structure and the present and past stem growth in terms of the tree ring pattern. The following six variables characterised the course of the stem diameter growth.
dc represents the current stem diameter.
dm is the tree’s stem diameter at half of its present age.
rdmdc is the ratio \(\mathrm{rdmdc}=\mathrm{dm}/\mathrm{dc}\) and reflects whether the diameter increased proportionally with age (rdmdc = 0.5), more slowly and delayed (rdmdc < 0.5), or fast and overproportionally (rdmdc > 0.5).
meanid represents the mean diameter growth rate and is the ratio between current stem diameter and current age; \(\mathrm{meanid}=\mathrm{dc}/\mathrm{age}\).
sdid based on the annual tree diameter growth, we calculated the standard deviation (sd) as a measure of the smoothness of the growth course.
cvid denotes the coefficient of variation of the annual diameter growth and represents a standardised measure of the smoothness or oscillation of the diameter development.
Table 2 shows the stem growth characteristics of the 78 sample trees. All measures vary broadly due to the site’s different spacing and thinning strategies.
Figure 4 shows the metrics rdmdc and cvid for characterising the course of the stem diameter development using three selected Norway spruces (plot 19/tree number 10, plot 21/tree number 8, and plot 13/tree number 13) as an example. Their rdmdc values indicate a nearly proportional (\(\mathrm{rdmdc}\cong 0.5\)), overproportional (\(\mathrm{rdmdc}=0.74\)), and strongly overproportional (\(\mathrm{rdmdc}=0.85\)) diameter development at half of the present tree age. The coefficient of variation of the annual stem diameter growth, cvid, was low (\(\mathrm{cvid}=0.28\)) in the case of the tree no. 19/10, average (\(\mathrm{cvid}=0.64\)) for tree no. 21/8, and high (\(\mathrm{cvid}=0.90\)) in the case of tree no. 13/13.
Visualisation of the metrics a ratio of diameter development at half of the present tree age and current tree diameter, rdmdc, and b coefficient of variation of the annual diameter growth, cvid, for characterising the course of the stem diameter development of three selected Norway spruces (solid line: plot 19/tree number 10, dashed line: plot 21/tree number 8, and dotted line: plot 13/tree number 13) on the combing spacing and thinning trial Fürstenfeldbruck 612. Shown is the development of (a) the stem diameter and (b) the annual stem diameter growth over age. The vertical line represents half of the present tree age
Metrics for crown structure
The TLidar-based measurements of the crowns provided the following stem and crown measures:
h, hcb, and cl tree height, h, the height of the crown base, hcb, and crown length, cl, as determined by \(\mathrm{cl}=h-\mathrm{hcb}\). The height of the crown base, hcb, was defined as the stem height of the starting point of the lowest primary branch. The lowest primary branch was manually determined in the point clouds by selecting the first branch without needles.
dcb stem diameter at the height of the crown base.
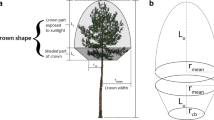
maxcrad and hmaxcrad maximum crown radius, maxcrad, and height of the maximum crown radius, hmaxcrad. For quantification, the crown was divided into 5 cm height classes; the points in each height class were split into 12 polar coordinate categories to detect the widest crown extension. This resulted in crown radii for all height classes and polar coordinate directions. The largest crown radius was chosen as maxcrad, and the mean height of the respective calls was hmaxcrad.
th top-heaviness, ratio between the maxcrad value and the distance between the position of the maxcrad and the tip of the tree (\(h-\mathrm{hmaxcrad}\)).
cratio crown ratio, the ratio between the length of the crown and the tree height.
sdcrad and cvcrad represent the standard deviation and coefficient of variation of the maximum crown radii in the 5 cm height classes along the stem axis.
Figure 5 shows selected crown metrics and how they reflect the crown structure. The metrics of maximum crown radius, crown top-heaviness, crown ratio, and standard deviation of crown radius were especially suitable for estimating the stem growth curve. The corresponding figure shows crowns with low, medium, and high values (left to right) for these four metrics. Here we report only the crown metrics we finally used for the evaluation, plus a few more to show the extraction of variables from TLidar crown scans. Indeed, the derived metrics of the different shaped crowns, scanned with TLidar, were more specific than the corresponding metrics used for the simplified concentric crowns of the simulation study.
Statistical evaluation and models
The pairwise correlation analyses between the metrics for stem growth and crown structure showed that the maximum crown radius, top-heaviness, crown ratio, and standard deviation of the crown radii along the crown firmly determined the course of stem growth. Therefore, we fitted models of the type \(\mathrm{ln}\left(y\right)={a}_{0}+{a}_{1}\times \mathrm{ln}({x}_{1})+{a}_{2}\times \mathrm{ln}\left({x}_{2}\right)\) to the data of the measured 78 trees. In detail, we parameterised
The TLidar scanning and subsequent point-cloud analysis yielded crown metrics and their relationship with stem growth metrics. The stem growth may be estimated as follows:
(i) The models 4–6 enabled the estimation of the variables d, rdmdc, and cvid, which were used to describe the individual tree’s stem diameter growth. For this purpose, we assumed that the curve has its origin at breast height age zero and diameter zero (0, 0), that the curve passes through \(\mathrm{dm}=\mathrm{rdmdc}\times \mathrm{dc}\) at \(\mathrm{age}/2\) (\(\mathrm{age}/2\), dm), and through present age and diameter (age, dc).
(ii) We fitted the standard stem diameter growth model \(\mathrm{ln}\left(d\right)={a}_{0}+{a}_{1}\times \mathrm{ln}(\mathrm{age})+{a}_{2}\times {(\mathrm{ln}(\mathrm{age}))}^{2}\) to the three points and arrived at a smooth diameter growth curve. The coefficients \({a}_{0}\), \({a}_{1}\), and \({a}_{2}\) can be derived from the value pairs (0, 0), (age/2, dm), and (age, dc).
(iii) The first derivation of the latter function, i.e., the diameter growth, is.
\(\mathrm{id}={\mathrm{exp}(a}_{0}+{a}_{1}\times \mathrm{ln}\left(\mathrm{age}\right)+{a}_{2}\times {(\mathrm{ln}(\mathrm{age}))}^{2}\times ({a}_{1}/\mathrm{age}+(2\times {a}_{2}\times \mathrm{ln}(\mathrm{age}))/\mathrm{age})\).
To add random variation accounting for growth oscillation, the smooth curve was furthermore superimposed by a variation estimated via model 6.
(vi) By accumulating and numerically integrating id + standard deviation, we obtained a first estimation and reconstruction of the course of stem growth based on the TLidar scans of the crown structure.
Finally, the empirical study provided equations and an algorithm to derive the stem growth curve of an individual tree based on its specific crown characteristics. All fitted models were subjected to the usual visual residual diagnostics. The residuals were plotted against the fitted values for all models to check for variance homogeneity. Likewise, the normality of errors was verified using quantile–quantile diagrams (Q–Q plots) of the residuals. For all calculations, we used the statistical software R 4.1.0 (R Core Team 2021) and the libraries nlme (Pinheiro et al. 2017) and lme4 (Bates et al. 2014).
Proof of concept
Results of the simulation study
Allometric relationships for linkage of stem diameter and crown development
Table 3 shows that the considered predictors and their interactions had significant effects on the crown variables (p < 0.05). We used the relationships to predict the crown growth and structure depending on the stem diameter (see “Simulation study”). Figure 6 shows how stem diameter and tree age modified the tree height, height to the crown base, and crown radius. Trees with larger diameters were also taller, with the height-to-diameter ratio shifting in favour of height with increasing age (Fig. 6a, model 1). A similar trend can be seen for the modelled crown ratio instead of tree height (Fig. 6c, model 3). On the other hand, crown base height decreased with increasing diameter, and the differences were more pronounced for older trees (Fig. 6b, model 2). Overall, significant interactions between predictor variables and tree age negatively affected all dependent variables (see Table 3, negative effect −).
Visualisation of the observed (points) and modelled (curves) allometric relationships between tree crown characteristics and tree diameter, d, and tree age, age, on the long-term experiments of Fürstenfeldbruck 612 in Norway spruce. Shown are the relationships for a tree height, h, b height to crown base, hcb, and c crown radius, crad, at tree age 20–50. The statistical characteristics of the fitted curves are provided in Table 3
Exemplified simulation results
In the upper row of Figs. 4, 7 (tree numbers 60, 13, 68, and 72) out of the 100 simulated stem diameter growth curves are presented (see Supplementary Fig. 1 for a complete overview). The inscriptions in the graph show some main growth characteristics (dc, rdmdc, and cvid) derived from the respective curves. The current stem diameter, dc, and the rdmdc and cvid values decrease from left to right (Fig. 7, a–g).
Stem diameter developments and simulated 5 years crown expansion until age 50 are shown for four trees, with crown width, crown length, and top-heaviness decreasing from left to right. The stem growth curve in (a) was used to simulate the crown development shown in (b); (c) and (d), (e) and (f), and (g) and (h) are related analogously. The inscriptions reflect some main characteristics of the stem growth (d, rdmdc, cvid) and crown (maxcrad, th, cratio), respectively
Each hull of the crown graphs reflects a 5-years-increment in size. The lower row of Fig. 7 visualises the respective crown developments until age 50, i.e., the crown in Fig. 7b was simulated based on the growth curve shown in Fig. 7a. The crown in Fig. 7d was simulated based on the growth shown in Fig. 7c, etc.
The presented crown shapes and metrics in the lower row reflect that the crowns become slimmer, shorter, and shift from top-heavy to bottom-heavy from left to right (Fig. 7, b–d–f–h). Beyond this visualisation of the simulation results for four trees, we used all 100 trees to correlate growth curve with crown shape metrics to reveal general relationships between stem growth characteristics and crown structure.
Correlations between stem growth and crown characteristics.
Essential information on the relationships between stem growth characteristics and crown structure is shown in the framed box in the bottom left of Fig. 8. In the following, we only comment on correlation coefficients higher than 0.30, which were significant at least at the level of \(p<0.05\). All significant correlations were positive.
Correlations between various metrics for stem growth (d, rdmdc, cvid) and present tree crown structure (cratio, th, cvcrad). Correlations are displayed by Pearson correlation coefficients on the left and corresponding visuals on the right. The ovals’ shape and direction indicate the strength (wide ovals = low, narrow ovals = strong correlation), respectively, the direction of the correlation (downward = negative, upward = positive correlation)
The present stem diameter, d, was closely correlated with the crown ratio, cratio, the top-heaviness, th, and the coefficient of variation of the crown radius, cvcrad. The relative diameter at half-time, rdmdc, was significantly correlated with th and cvcrad. Finally, the coefficient of variation of the annual stem diameter growth, cvid, was strongly positively correlated with the top-heaviness of the crown, th. In essence, these correlations show that the stem diameter growth strongly impacts the size and shape of the crown, even if we apply simple allometric relationships. The findings suggested further empirical studies, as presented in the next section.
The 3 \(\times\) 3 correlation coefficients in the framed box (Fig. 8, bottom left) reflect the most meaningful relationships between stem growth and crown structure characteristics. Correlations between stem growth characteristics (see correlation matrix top-left) and relationships between crown characteristics (see correlation matrix bottom right) are of less interest, as they are addressed more frequently in the literature.
Exemplified variable extraction based on TLidar
Figure 9 shows examples of the scans for nine of the 78 sample trees and the resulting metrics for top-heaviness, th, crown ratio, cratio, and standard deviation of the crown radius along the stem axis, sdcrad. The upper row (a–c) shows crowns with different top-heaviness and crown fullness (Assmann 1970, p. 112) but similar cratio and sdcrad values. In the second row (d–f), crowns with decreasing crown ratios are shown, whereas the other characteristics are kept constant. In the lower row (g–i), the sdcrad values decrease from left to right, i.e., the variation of the crown radii along the stem axis is high in the case of (g) and decreases from (g) to (i).
These and other metrics were used for deriving the subsequent relationships between crown structure and growth. Only a subset was later used to model the relationship between stem growth and crown structure. Table 4 gives an overview of all derived crown metrics.
Based on the total tree height and the height to crown base from the TLidar scanning, we calculated each tree’s crown length and crown ratio. The variation of total tree height reflects that we sampled predominant and subdominant trees. The wide range of height to crown base (1.85–12.95 m) and of the respective crown lengths and crown ratios indicate that we covered trees growing under both extraordinarily dense and wide-open conditions. The height to crown base is large on the dense and low on the wide-open plots, which explains the wide range of the stem diameter at the crown base (11.1–49.9 cm). The profile of the crown is reflected by the maximum crown radius, the distance from the tip to the height of the maximum crown radius, and especially by the ratio between both values; the latter reflects the top-heaviness and ranges from bottom-heavy to top-heavy crowns (0.21–0.58). The crown radii at 25, 50, and 75% of the crown length from above varied strongly, with the most substantial variation in the lower part of the crown (0.89–5.72 m). The coefficient of variation of the crown radii along the stem axis can be low for slim crowns and exceptionally high for bell-bottomed crowns.
It was suggested to select the crown characteristics maximum crown radius, maxcrad, top-heaviness, th, and standard deviation of the crown radius along the stem axis, sdcrad, as they showed significant correlations with the internal growth characteristics current stem diameter, half-time stem diameter, and coefficient of variation of stem diameter growth (cf. Figure 8). Table 5 shows the results of the regression analyses for fitting models 4–6 to the metrics of the sampled trees. All regression coefficients and models were significant, at least at the level of \(p<0.05\).
The corresponding visualisation is presented in Fig. 10. The crown radius increased with increasing diameter, while with increasing height, the relationship between crown radius and stem diameter shifted in favour of the latter (Fig. 10a, model 4). Figure 10b (model 5) reveals that trees with a high top-heaviness had strong growth early on, resulting in high values of the half-time stem diameter. However, larger crown expansions (cr) were associated with smaller half-time stem diameters. Furthermore, high variations in annual growth were linked to low standard deviations of the crown radius, shown in Fig. 10c (model 6). In addition, the further the greatest extension of the crown (top-heaviness) was at the top of the stem, the greater was the variation in annual growth and crown radius (see also positive effect + in Table 5).
Relationships between crown structure and stem growth characteristics of the examined 78 Norway spruces on the long-term experiments Fürstenfeldbruck 612. a current stem diameter, d, depending on the maximum crown radius, maxcrad, and tree height, h. b relative diameter at half-time since stand establishment, rdmdc, depending on top-heaviness, th, and crown ratio, cratio. c coefficient of variation of the annual stem diameter growth depending on th and the standard deviation of the crown radii, sdcrad. See Table 5 for statistical characteristics of the shown curves
Deriving the course of stem growth from crown structure characteristics
Figure 11 shows, by the example of four trees, how their stem growth may be reproduced based on the metrics of the crown structure and their relationship with the metrics of the stem growth. Based on the metrics extracted from the TLidar scans, we first estimated dc, rdmdc, and cvid of the respective trees based on Eqs. 4–6. Then, the diameter at half of the present age (\(dc\times rdmdc\)), the current diameter, and the individual age were used to parameterise the double-logarithmic relationship, \(\mathrm{ln}\left(d\right)={a}_{1}+{a}_{2}\times \mathrm{ln}\left(\mathrm{age}\right)+{a}_{3}\times {(ln(\mathrm{age}))}^{2}\), between stem diameter and tree age. Figure 11 (a and b) shows stem diameter developments derived from the crown structure and respective metrics indicated in the heading and inscription of Fig. 11. The corresponding reconstruction for the annual stem diameter progression is presented in the two figures below (Fig. 11 c and d). The smooth growth curves from Fig. 11 (a and b), estimated based on dc and dm, were superimposed by the standard deviation modelled by a standard normal, Gaussian distribution with \(\mathrm{sd}=\mathrm{cvid}\times \mathrm{mean}(\mathrm{id})\). Mean of id and cvid were derived from crown structure metrics using Eqs. 4–6. The rnom (0, std)-simulated deviations from mean id were added to the smooth components of the curves, and thus, the annual stem diameter curves were derived based on crown sizes and shapes obtained from TLidar scans.
Examples of reproducing the curves of a and b stem diameter development and c and d respective annual stem diameter growth curves based on the crown metrics maxcrad, h, th, cratio, and sdcrad derived from TLidar scans on Norway spruce. Long-term stem diameter development (a and b) was reconstructed without considering annual growth variation (see models 4 and 5). Contrary, for the respective annual stem diameter growth, annual growth variation was accounted for by including the estimated variables sdcrad and th (see equation model 6)
Discussion
Deriving stem growth from tree crown structure
The basic hypothesis that stem growth and crown structure are linked, so that the crown structure, similar to tree ring pattern, reflects the present state of a tree and its individual development in the past was analysed by a simulation study and tested empirically. The simulation study yielded high correlations between stem growth and crown structure metrics. Analogous to the stem shape, the crown structure finally emerges mainly from the annual accumulation of branch growth. The simulation resulted in crown shapes that are relatively simple compared with the crowns measured by TLidar. The observed and scanned crowns, for instance, also reflect the crown's acclimation to a specific neighbourhood and losses of parts of the crown due to competition or mechanical abrasion (crown shyness). However, the simulation study has shown that even simple allometric relationships can produce realistic crown structures and reveal close correlations between the crown and stem growth metrics; the results suggested the potential for more detailed empirical analyses. By modelling crown dynamics based on stem growth (Fig. 7), we have established the first version of a simulation platform that can be further improved in many ways. However, it demonstrates how stem growth can be revealed and modelled based on crown shapes scanned with TLidar.
The empirical findings corroborated the simulation-based relationships based on 78 trees analysed in terms of stem diameter growth and crown structure. The scans of the crowns allowed a much more detailed characterisation and quantification of the crowns. The crowns were no longer abstracted as concentric bodies, and the scans also detected concave parts of the crowns caused by plasticity or branch losses.
We selected the three crown characteristics maximum crown radius, maxcrad, top-heaviness, th, and standard deviation of the crown radius along the stem axis, sdcrad, as they showed significant correlations with the characteristics of current stem diameter, dc, the ratio of half-time stem diameter and current stem diameter, rdmdc, and the coefficient of variation of stem diameter growth, cvid.
This study used three relationships to estimate stem growth depending on crown characteristics. The first relationship (\(d=f(\mathrm{maxcrad}, h)\)) has been widely used in other studies to estimate the present stem diameter from extracted crown characteristics based on remote sensing of the crown (e.g., Liang et al. 2016; Heurich and Thoma 2008; Yao et al. 2012). However, this relationship has not been used to reconstruct past stem growth. The second relationship (\(\mathrm{rdmdc}=f(\mathrm{th},\mathrm{cratio})\)), for instance, may reflect that for trees with top-heavy crowns, stem growth has been high in the past and is stagnating at present (allometrically old state). Slim crowns with low top-heaviness may indicate low growth in the past and high growth at present (allometrically juvenile state). The third relationship (\(\mathrm{cvid}=f(\mathrm{sdcrad},\mathrm{th})\)) may suggest that widely extending crowns, such as those of solitary trees in open stands, enable a constant growth rate. In contrast, trees which are closely restricted by neighbours and have slim crowns may be more prone to an oscillation of stem growth depending on any changes in locale density caused by natural dropout or thinning of neighbouring trees. Our main objective was to demonstrate the potential of this approach as a first method for linking stem growth and crown structure. Further analyses may use more or other metrics, additional information about stand density or local competition.
Based on theoretical allometric considerations referring to Enquist (2002), Niklas (1994), and West et al. (1999), and a sample of trees analysed for both tree ring pattern and crown structure, our study showed how a quantitative relationship between the two could be derived. Further developments in TLidar scanning and variable extraction will underpin the revealed relationship and extend them to other tree sizes, tree ages, treatment effects, and tree species.
Explanation of the functional and structural relationships
The tree crown and stem growth at breast height are functionally linked in the following way. The vessels within the stem provide water and nutrient transport pipes into the crown (Grote and Pretzsch 2002; Mäkelä 1997; Valentine 1985). The other way round, the crown acquires light and carbon for stem growth. Due to this structural and functional relationship, the crown has been often used to estimate the current tree size and growth (Hemery et al. 2005; Kalliovirta and Tokola 2005; Attiwill 1966) and the stem for estimating crown properties (Pretzsch et al. 2015; Bechtold 2003).
Most studies to date have used the traditional methods to measure crown length, width, or transparency, such as calliper, hypsometer, crown mirror, or crown window (Hussein et al. 2000). Examples are studies on the relationship between crown size and actual stem size (Kato et al. 2009; Popescu et al. 2003), crown characteristics and current tree growth (Guerra-Hernández et al. 2017; Dobbertin 2005), or between crown properties and wood quality (Pretzsch and Rais 2016). Crown characteristics were also used for a qualitative assessment of the past growth and social status of trees (Kraft 1884), silvicultural treatment (Oliver and Larson 1996; Pretzsch and Spellmann 1994), damages in the past (Dobbertin 2005; Roloff 2001; Röhle 1987), or genetical traits (Kräuter 1965). Relationships between the crown shape and the course of stem growth and their determination by genetics have been analysed for Scots pine (Kräuter 1965), but yielded no clarity (Hertel and Kohlstock 1994) and are still open for debate (Wenk et al. 1990, p. 41).
We introduced a new approach enabled by modern remote sensing techniques of crowns. Compared with classical methods, further developed crown measurement by photogrammetric methods (Klemmt and Tauber 2008) or TLidar (Jacobs et al. 2022, 2020, Barbeito et al. 2017, Bayer et al. 2013, Bayer and Pretzsch 2017, Klemmt et al. 2010, Seifert et al. 2010) can provide much more detailed information about stem shape and taper, crown transparency, crown profile, surface roughness, or asymmetry.
More detailed measurements of the crown morphology may reveal the different tree histories and explain the differences in the present stem growth. Tree morphology may represent a structural memory embedded in the stem, crown, and root and affect the trees' functioning and growth (Ogle et al. 2014; Pretzsch 2021b). It may affect, amongst others, light interception, hydraulic conduction, or water and nutrient uptake (Pretzsch 2021b).
It is well known and modelled how the stem shape results from the annually accumulated layers of wood created by the near-surface meristem along the stem circumference (Schneider 2018; Prodan 1965; Pressler 1865). Depending upon the relative growth partitioning along the stem, the shape can become cylindrical, paraboloidal, or neiloidal (Prodan 1965). Analogously and simultaneously to the stem volume, the crown volume expands in annual layers by the leading shoot of the stem and the branch growth, resulting in cylindrical to neiloidal shapes. The tree crown also contains potential information for deciphering the tree's past development analogously to dendrochronology (Dwyer et al. 1995). Whereas the stem volume development is well described and modelled (Schneider 2018), the crown development is less explored. The relationship between the annual accumulation processes, the expansion of the 3D stem, and the crown body has been used for 3D modelling (Sloboda and Pfreundt 1989; Pfreundt 1988; Mitchell 1975), but hardly for assessment and retracement of a tree’s growth dynamics.
Possibilities and limits of the proposed approach
Crown measurements by remote sensing are becoming standard for tree inventory in forests (Calders et al. 2018; Liang et al. 2016; Ke and Quackenbush 2011) and urban areas (Liu et al. 2017; Alonzo et al. 2014). Such inventories provide crown characteristics, and the methods developed in this study might be used to derive stem growth and internal stem structural characteristics based on crown characteristics. Any link between the crown and the tree ring pattern paves the way to an indication of, amongst others, wood quality (Pont et al. 2012; Pretzsch and Rais 2016), tree stability (Côté et al. 2011), and tree age and size (Zhen et al. 2016). Crown characteristics may also reveal disturbance and treatment history (Wu et al. 2018) of trees, e.g., information about the individual tree growth and any disturbances at present and in the past (Jacobs et al. 2022; Lo and Lin 2012; Henning and Radtke 2006). In addition, crown characteristics may provide information about the heart and sapwood portion (Saito et al. 2015), the age and life expectancy (Lüdeker et al. 1999), and the vitality, stress resistance, and resilience of trees (Jacobs et al. 2022; Wu et al. 2018).
We simplified the tree crown structure in many aspects for the simulation study. For instance, horizontal branches were assumed, whereas from the tip to the foot of the tree, the branch direction may change from upward to horizontal and downward (Seifert 2003). We assumed that the crown is concentric and has a convex hull, whereas crowns used to be more plastic and have concave parts (Pretzsch 2014). We also neglected mechanical abrasion of lower branches by crown shyness (Fish et al. 2006). However, despite all those simplifications, the simulation study showed a clear relationship between the absolute size and the shape of the crown and the course of the stem diameter growth. The close relationships, even under such simplified conditions, are promising. We suggest further empirical analyses that specifically address the size and shape of the upper crown based on TLidar data and the relationship with the course of stem growth quantified by increment coring or stem analyses.
The empirical study was based only on 78 Norway spruces, one site, and one tree development stage. The shown relationships between crown structure and stem growth may vary, amongst others things, with site conditions, provenance, and tree age. Any generalisation would require further sampling. However, connections between crown structure and stem growth may be even stronger for morphologically more plastic tree species and heterogeneously structured or mixed stands.
We selected only a few relatively simple metrics for describing stem diameter growth and crown structure. We used classical correlation and regression analyses to link stem growth and crown structure. The set of variables may be extended with more detailed information about stem growth (e.g., proportions of early and latewood, wood density, the occurrence of compression wood, and sapwood/heartwood proportion) and also more detailed information of crown structure (e.g., crown transparency, whole structure, leaf area, stem shape). For linking both datasets, advanced methods such as neural networks (Abdullahi et al. 2017; Corne et al. 2004), deep machine learning (Zhou and Feng 2019), or other approaches of artificial intelligence (Proto et al. 2020; McRoberts et al. 1991) may yield even better results.
The same crown structure may result from different tree histories and be associated with different stem growth curves. By including information about the inside of the crown (e.g., fractal dimension, transparency, and leaf area density) and about the scanned stand structure (e.g., local density, vertical layering, and crown intersection) into the analysis, it would be possible to distinguish whether a given crown shape resulted from mechanical abrasion, competition for light, border tree status, etc. Stem growth reconstruction and prediction may be further improved by adding information about the inside of the crown or stand structural characteristics (Seidel et al. 2019).
Conclusion
Although biological views and ecophysiological theory suggest a close link between stem and crown development, the proposed quantitative link is novel. Based on both simulations and TLidar and tree ring measurements, we revealed promising relationships between tree ring pattern and crown structure by the example of mature Norway spruce in monospecific stands. In this way, the introduced approach may improve the knowledge of relationships between structure and growth, which is still scarce for monospecific stands and even poorer for mixed-species stands.
That tree growth can be derived from the crown structure and vice versa may improve monitoring, inventory, understanding, and modelling of tree structure and function. We successfully developed the methods under the difficult scanning conditions in closed conifer stands; thus, trees growing under solitary conditions, in urban areas, or horticulture may be measured and modelled even easier. The next step may be the extension of the database on tree rings and respective crown patterns and the generalisation of the approach across tree species and growing conditions.
Author contribution statement
HP and SA initiated the project. SA, MJ, and GS gathered the data. HP, MJ, and SA evaluated the data. HP and TH wrote the manuscript. SA, MJ, and SG revised the manuscript.
Change history
24 May 2022
A Correction to this paper has been published: https://doi.org/10.1007/s00468-022-02308-x
References
Abdullahi S, Schardt M, Pretzsch H (2017) An unsupervised two-stage clustering approach for forest structure classification based on X-band InSAR data—a case study in complex temperate forest stands. Int J Appl Earth Obs Geoinf 57:36–48
Alonzo M, Bookhagen B, Roberts DA (2014) Urban tree species mapping using hyperspectral and lidar data fusion. Remote Sens Environ 148:70–83
Alvites C, Santopuoli G, Maesano M, Chirici G, Moresi FV, Tognetti R, Marchetti M, Lasserre B (2021) Unsupervised algorithms to detect single trees in a mixed-species and multilayered Mediterranean forest using LiDAR data. Can J for Res 51:1766–1780. https://doi.org/10.1139/cjfr-2020-0510
Assmann E (1970) The principles of forest yield study. Pergamon Press, Oxford, p 506
Assmann E, Franz F (1963) Vorläufige Fichten-Ertragstafel für Bayern. Institut für Ertragskunde der Forstlichen Forschungsanstalt München, Germany. 104 p
Attiwill PM (1966) A method for estimating crown weight in Eucalyptus, and some implications of relationships between crown weight and stem diameter. Ecology 47(5):795–804
Barbeito I, Dassot M, Bayer D, Collet C, Drössler L, Löf M, Pretzsch H (2017) Terrestrial laser scanning reveals differences in crown structure of Fagus sylvatica in mixed vs. pure European forests. For Ecol Manag 405:381–390
Bates D, Mächler M, Bolker B, Walker S (2014) (2015) lme4: linear mixed-effects models using Eigen and S4. R Packag Version 1:1–7
Bayer D, Pretzsch H (2017) Reactions to gap emergence: Norway spruce increases growth while European beech features horizontal space occupation–evidence by repeated 3D TLS measurements. Silva Fenn. https://doi.org/10.14214/sf.7748
Bayer D, Seifert S, Pretzsch H (2013) Structural crown properties of Norway spruce (Picea abies [L.] Karst) and European beech (Fagus sylvatica [L.]) in mixed versus pure stands revealed by terrestrial laser scanning. Trees 27(4):1035–1047
Bechtold WA (2003) Crown-diameter prediction models for 87 species of stand-grown trees in the eastern United States. South J Appl For 27(4):269–278
Bravo F, Fabrika M, Ammer C, Barreiro S, Bielak K, Coll L, Fonseca T, Kangur A, Löf M, Merganičová K, Pach M, Pretzsch H, Stojanović D, Schuler L, Peric S, Rötzer T, del Río M, Dodan M, Bravo-Oviedo A (2019) Modelling approaches for mixed forests dynamics prognosis. Res Gaps Opp For Syst. https://doi.org/10.5424/fs/2019281-14342
Burkhard B, Petrosillo I, Costanza R (2010) Ecosystem services–bridging ecology, economy and social sciences. Ecol Complex 7(3):257
Calders K, Origo N, Burt A, Disney M, Nightingale J, Raumonen P, Lewis P (2018) Realistic forest stand reconstruction from terrestrial LiDAR for radiative transfer modelling. Remote Sens 10(6):933
Cattaneo N, Schneider R, Bravo F, Bravo-Oviedo A (2020) Inter-specific competition of tree congeners induces changes in crown architecture in Mediterranean pine mixtures. For Ecol Manag 476:118471. https://doi.org/10.1016/j.foreco.2020.118471
Corne SA, Carver SJ, Kunin WE, Lennon JJ, van Hees WWV (2004) Predicting forest attributes in southeast Alaska using artificial neural networks. For Sci 50(2):259–276
Côté JF, Fournier RA, Egli R (2011) An architectural model of trees to estimate forest structural attributes using terrestrial LiDAR. Environ Model Softw 26(6):761–777
de Araujo Barbosa CC, Atkinson PM, Dearing JA (2015) Remote sensing of ecosystem services: a systematic review. Ecol Ind 52:430–443
De Groot RS, Alkemade R, Braat L, Hein L, Willemen L (2010) Challenges in integrating the concept of ecosystem services and values in landscape planning, management and decision making. Ecol Complex 7(3):260–272
Dobbertin M (2005) Tree growth as indicator of tree vitality and of tree reaction to environmental stress: a review. Eur J For Res 124(4):319–333
Dwyer JP, Cutter BE, Wetteroff JJ (1995) A dendrochronological study of black and scarlet oak decline in the Missouri Ozarks. For Ecol Manag 75(1–3):69–75
Elseberg J, Borrmann D, Nüchter A (2013) One billion points in the cloud—an octree for efficient processing of 3D laser scans. ISPRS J Photogramm Remote Sens 76:76–88. https://doi.org/10.1016/j.isprsjprs.2012.10.004
Enquist BJ (2002) Universal scaling in tree and vascular plant allometry: towards a general quantitative theory linking plant form and function from cells to ecosystems. Tree Physiol 22(15–16):1045–1064
Ester M, Kriegel H-P, Sander J, Xu X (1996) A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, E. Simoudis, J. Han, and U. Fayyad, Eds. AAAI Press, 226–231
Fish H, Lieffers VJ, Silins U, Hall RJ (2006) Crown shyness in lodgepole pine stands of varying stand height, density, and site index in the upper foothills of Alberta. Can J for Res 36(9):2104–2111
Genet A, Wernsdörfer H, Jonard M, Pretzsch H, Rauch M, Ponette Q, Saint-André L (2011) Ontogeny partly explains the apparent heterogeneity of published biomass equations for Fagus sylvatica in central Europe. For Ecol Manag 261(7):1188–1202
Grote R, Pretzsch H (2002) A model for individual tree development based on physiological processes. Plant Biol 4(02):167–180
Guerra-Hernández J, González-Ferreiro E, Monleón VJ, Faias SP, Tomé M, Díaz-Varela RA (2017) Use of multi-temporal UAV-derived imagery for estimating individual tree growth in Pinus pinea stands. Forests 8(8):300
Hahsler M, Piekenbrock M (2019) dbscan: density based clustering of applications with noise (DBSCAN) and Related Algorithms. (R package version 1.1-4.)
Hemery GE, Savill PS, Pryor SN (2005) Applications of the crown diameter–stem diameter relationship for different species of broadleaved trees. For Ecol Manag 215(1–3):285–294
Henning JG, Radtke PJ (2006) Detailed stem measurements of standing trees from ground-based scanning lidar. For Sci 52(1):67–80
Hertel H, Kohlstock N (1994) Different genetic structures of two morphological types of Scots pine (Pinus sylvestris L.). Silvae Genet 43(5):268–271
Heurich M, Thoma F (2008) Estimation of forestry stand parameters using laser scanning data in temperate, structurally rich natural European beech (Fagus sylvatica) and Norway spruce (Picea abies) forests. Forestry (Lond) 81:645–661. https://doi.org/10.1093/forestry/cpn038
Holmes R (1983) Computer-Assisted Quality Control in Tree-Ring Dating and Measurement. Tree-Ring Bulletin 43:69–78
Hussein KA, von Gadow K, Albert M (2000) The Crown window—a simple device for measuring tree crowns. Forstwissenschaftliches Centralblatt Vereinigt Mit Tharandter Forstliches Jahrbuch 119(1–6):43–50
Jacobs M, Rais A, Pretzsch H (2020) Analysis of stand density effects on the stem form of Norway spruce trees and volume miscalculation by traditional form factor equations using terrestrial laser scanning (TLS). Can J for Res 50(1):51–64. https://doi.org/10.1139/cjfr-2019-0121
Jacobs M, Rais A, Pretzsch H (2021) How drought stress becomes visible upon detecting tree shape using terrestrial laser scanning (TLS). For Ecol Manag 489:118975. https://doi.org/10.1016/j.foreco.2021.118975
Jacobs M, Hilmers T, Leroy BML, Lemme H, Kienlein S, Müller J, Weisser W, Pretzsch H (2022) Assessment of defoliation and subsequent growth losses caused by Lymantria dispar using terrestrial laser scanning (TLS). Trees. https://doi.org/10.1007/s00468-021-02255-z
Kalliovirta J, Tokola T (2005) Functions for estimating stem diameter and tree age using tree height, crown width and existing stand database information. Silva Fenn 39(2):227–248
Kato A, Moskal LM, Schiess P, Swanson ME, Calhoun D, Stuetzle W (2009) Capturing tree crown formation through implicit surface reconstruction using airborne lidar data. Remote Sens Environ 113(6):1148–1162
Ke Y, Quackenbush LJ (2011) A review of methods for automatic individual tree-crown detection and delineation from passive remote sensing. Int J Remote Sens 32(17):4725–4747
Klemmt HJ, Tauber R (2008) Automatisierte Ermittlung forstinventurrelevanter Parameter aus 3D-Laserscanning-Daten sowie aus 2D-DendroScandaten – Eine vergleichende Feldstudie. In: DVFFA – Sektion Ertragskunde, Jahrestagung 2008, Trippstadt, 5.-8. Mai 2008, pp 169–179
Klemmt H-J, Seifert T, Seifert S, Kunneke A (2010) Assessment of branchiness in a Pinus pinaster plantation by terrestrial laser scanner data as a link between exterior and interior wood properties. Presented at the Silvilaser 2010, September 14–17, Freiburg, Germany
Kraft G (1884) Beiträge zur Lehre von den Durchforstungen, Schlagstellungen und Lichtungshieben. Klindworth´s Verlag, Hannover, 147 p
Kräuter G (1965) Die Behandlung von Kiefernjungbeständen auf der Grundlage von biologischen und dynamischen Merkmalen der Einzelstämme, Tagungsbericht der Deutschen Akademie der Laundwirtschaftswissenschaften, Berlin, 75:337–342
Krutzsch P (1974) The IUFRO 1964/68 provenance test with Norway Spruce (Picea abies (L.) Karst.). Silvae Genet 23(1):58–62
Kupferschmid AD, Zimmermann S, Bugmann H (2013) Browsing regime and growth response of naturally regenerated Abies alba saplings along light gradients. For Ecol Manag 310:393–404
Lecigne B, Delagrange S, Messier C (2014) VoxR: metrics extraction of trees from T-LiDAR data. (R package version 0.5.1.)
Liang X, Kankare V, Hyyppä J, Wang Y, Kukko A, Haggrén H, Vastaranta M (2016) Terrestrial laser scanning in forest inventories. ISPRS J Photogramm Remote Sens 115:63–77
Liu L, Coops NC, Aven NW, Pang Y (2017) Mapping urban tree species using integrated airborne hyperspectral and LiDAR remote sensing data. Remote Sens Environ 200:170–182
Lo CS, Lin C (2012) Growth-competition-based stem diameter and volume modeling for tree-level forest inventory using airborne LiDAR data. IEEE Trans Geosci Remote Sens 51(4):2216–2226
Lüdeker W, Dahn HG, Günther KP, Schulz H (1999) Laser-induced fluorescence—a method to detect the vitality of Scots pines. Remote Sens Environ 68(3):225–236
Mäkelä A (1997) A carbon balance model of growth and self-pruning in trees based on structural relationships. For Sci 43(1):7–24
Maltamo PM, Vartiainen MP, Packalen PP, Korhonen DL (2022) Estimation of periodic annual increment of tree ring widths by airborne laser scanning. Can J for Res. https://doi.org/10.1139/cjfr-2021-0267
McRoberts RE, Schmoldt DL, Rauscher HM (1991) Enhancing the scientific process with artificial intelligence: forest science applications. AI Applications 5(2):5–26
Mitchell KJ (1975) Dynamics and simulated yield of Douglas-fir. For Sci Monogr 17:39
Niklas KJ (1994) Plant allometry. Univ Chicago Press, Chicago
Ogle K, Barber JJ, Barron-Gafford GA, Bentley LP, Young JM, Huxman TE, Loik ME, Tissue DT (2014) Quantifying ecological memory in plant and ecosystem processes. Ecol Lett 18:221–235
Oldeman RA (1990) Forests: elements of silviology. Springer, Berlin, p 624
Oliver CD, Larson BC (1996) Forest stand dynamics, Updated. Wiley
Pfreundt J (1988) Modellierung der Räumlichen Verteilung von Strahlung, Photosynthesekapazität und Produktion in einem Fichtenbestand und ihrer Beziehung zur Bestandesstruktur. Berichte Forschungszentrum Waldökosysteme/Waldsterben Göttingen, Reihe A, Band 39, pp 163
Pinheiro J, Bates D, DebRoy S, Sarkar D, R Core Team (2021) nlme: Linear and Nonlinear Mixed Effects Models. R package version 3. pp 1–53
Pont D, Watt MS, Adams T, Marshall H, Lee J, Crawley D, Watt PJ (2012) Modelling variation in Pinus radiata stem velocity from area- and crown- based LiDAR metrics. In N. Coops, & M. Wulder (Eds.), SilviLaser 2012 Vancouver, Canada: Silvilaser 2012 Organizing Committee
Popescu SC, Wynne RH, Nelson RF (2003) Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can J Remote Sens 29(5):564–577
Pressler M (1865) Das Gesetz der Stammformbildung. Verlag Arnold, Leipzig, p 153
Pretzsch H (1989) Untersuchungen an kronengeschädigten Kiefern in Nordost-Bayern. Teil I: Krankheitsbild Und Wuchsverhalten. Forstarchiv 60(2):62–69
Pretzsch H (2006) Von der Standflächeneffizienz der Bäume zur Dichte-Zuwachs-Beziehung des Bestandes. Beitrag zur Integration von Baum-und Bestandesebene. Allgemeine Forst-und Jagdzeitung, 177(10), 188–199
Pretzsch H (2014) Canopy space filling and tree crown morphology in mixed-species stands compared with monocultures. For Ecol Manag 327:251–264
Pretzsch H (2021a) Tree growth as affected by stem and crown structure. Trees 35:947–960
Pretzsch H (2021) Trees grow modulated by the ecological memory of their past growth. Consequences for monitoring, modelling, and silvicultural treatment. For Ecolo Manag 487:118982
Pretzsch H, Kölbel M (1988) Einfluß von Grundwasserabsenkungen auf das Wuchsverhalten der Kiefernbestände im Gebiet des Nürnberger Hafens – Ergebnisse ertragskundlicher Untersuchungen auf der Weiserfächenreihe Nürnberg 317. Forstarchiv 59(3):89–96
Pretzsch H, Rais A (2016) Wood quality in complex forests versus even-aged monocultures: review and perspectives. Wood Sci Technol 50(4):845–880
Pretzsch H, Spellmann H (1994) Leistung und struktur des douglasien-durchforstungsversuchs lonau 135. Forst Und Holz 49(3):64–69
Pretzsch H, Biber P, Uhl E, Dahlhausen J, Rötzer T, Caldentey J, Pauleit S (2015) Crown size and growing space requirement of common tree species in urban centres, parks, and forests. Urban For Urban Green 14(3):466–479
Prodan M (1965) Holzmeßlehre. JD Sauerländer’s Verlag, Frankfurt am Main, p 644
Proto AR, Sperandio G, Costa C, Maesano M, Antonucci F, Macrì G, Zimbalatti G (2020) A three-step neural network artificial intelligence modeling approach for time, productivity and costs prediction: a case study in Italian forestry. Croat J For Eng 41(1):35–47
R Core Team (2021) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria
RIEGL (2019) RIEGL_VZ-400i_Datasheet_2019-11-22.indd 2019. Available online under http://www.riegl.com/uploads/tx_pxpriegldownloads/RIEGL_VZ-400i_Datasheet_2019-11-22.pdf. Accessed 8 Jan 2022
Röhle H (1987) Entwicklung von Vitalität, Zuwachs und Biomassenstruktur der Fichte in verschiedenen bayerischen Untersuchungsgebieten unter dem Einfluß der neuartigen Walderkrankungen. Frank
Roloff A (2001) Baumkronen: Verständnis und praktische Bedeutung eines komplexen Naturphänomens. Ulmer
Romijn E, Lantican CB, Herold M, Lindquist E, Ochieng R, Wijaya A, Verchot L (2015) Assessing change in national forest monitoring capacities of 99 tropical countries. For Ecol Manag 352:109–123
Saito T, Yamamoto K, Komatsu M, Matsuda H, Yunohara S, Komatsu H, Kumagai TO (2015) Using airborne LiDAR to determine total sapwood area for estimating stand transpiration in plantations. Hydrol Process 29(24):5071–5087
Schmied G, Hilmers T, Uhl E, Pretzsch H (2022) The past matters: previous management strategies modulate current growth and drought responses of Norway spruce (Picea abies H. Karst). Forests 13(2):243. https://doi.org/10.3390/f13020243
Schneider R (2018) Understanding the factors influencing stem form with modelling tools. Progress in Botany 80:295–316
Schweingruber H, Eckstein D, Serre-Bachet F, Bräker OU (1990) Identification, presentation and interpretation of event years and pointer years in dendrochronology. Dendrochronologia 8:9–38
Seidel D, Ehbrecht M, Dorji Y, Jambay J, Ammer C, Annighöfer P (2019) Identifying architectural characteristics that determine tree structural complexity. Trees 33(3):911–919
Seifert T (2003) Integration von Holzqualität und Holzsortierung in behandlungssensitive Waldwachstumsmodelle (Doctoral dissertation, Technische Universität München)
Seifert T, Klemmt H, Seifert S, Kunneke A, Wessels B (2010) Integrating terrestrial laser scanning based inventory with sawing simulation, in: Developments in Precision Forestry Since 2006, Proceedings of the International Precision Forestry Symposium, Stellenbosch University, Stellenbosch, South Africa, 1–3 March 2010; Ackerman PA, Ham H, Lu C (eds)., Department of Forest and Wood Science: Stellenbosch, South Africa
Sloboda B, Pfreundt J (1989) Baum- und Bestandeswachstum. Ein systemanalytischer, räumlicher Ansatz mit Versuchsplanungskonsequenzen für die Durchforstung und Einzelbaumentwicklung, Proc Dt Verb Forstl Forschungsanst, Sek Ertragskd, in Attendorn, pp 17/1–17/25
Speer J (2010) Fundamentals of tree-ring research. University of Arizona press, Tucson
Stokes M, Smiley T (1996) An introduction to tree-ring dating. University of Arizona Press, Tucson
Uzquiano S, Barbeito I, San Martín R, Ehbrecht M, Seidel D, Bravo F (2021) Quantifying crown morphology of mixed pine-oak forests using terrestrial laser scanning. Remote Sens 13(23):4955. https://doi.org/10.3390/rs13234955
Valentine HT (1985) Tree-growth models: derivations employing the pipe-model theory. J Theor Biol 117(4):579–585
Wenk G, Antanaitis V, Šmelko Š (1990) Waldertragslehre. VEB Deutscher Landwirtschaftsverlag, Berlin, p 448
West GB, Brown JH, Enquist BJ (1999) A general model for the structure and allometry of plant vascular systems. Nature 400(6745):664–667
Wu J, Yao W, Polewski P (2018) Mapping individual tree species and vitality along urban road corridors with LiDAR and imaging sensors: point density versus view perspective. Remote Sens 10(9):1403
Yao W, Krzystek P, Heurich M (2012) Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens Environ 123:368–380. https://doi.org/10.1016/j.rse.2012.03.027
Zhen Z, Quackenbush LJ, Zhang L (2016) Trends in automatic individual tree crown detection and delineation—evolution of LiDAR data. Remote Sens 8(4):333
Zhou ZH, Feng J (2019) Deep forest. Natl Sci Rev 6(1):74–86
Acknowledgements
The publication is part of the CARE4C project that has received funding from the European Union’s HORIZON 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 778322. The study was funded through the 2017–2018 Belmont Forum and BiodivERsA joint call for research proposals, under the BiodivScen ERA-Net COFUND programme, with the national funding organisation German Science Foundation (grant #16LC1805B). The publication is also part of the ASFORCLIC project that has received funding from the European Unions's Horizon 2020 research and innovation programme under grant agreement No 952314. The authors also wish to thank the German Science Foundation (Deutsche Forschungsgesellschaft) for funding the project “Structure and dynamics of mixed-species stands of Scots pine and European beech compared with monospecific stands; analysis along an ecological gradient through Europe” (# DFG PR 292/15-1). We would also like to thank the Bavarian State Ministry for Nutrition, Agriculture, and Forestry for the permanent support of the project W007, “Long-term experimental plots for forest growth and yield research” (# 7831-22209-2013). Thanks also go to anonymous reviewers for their constructive criticism.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Communicated by Lüttge.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pretzsch, H., Ahmed, S., Jacobs, M. et al. Linking crown structure with tree ring pattern: methodological considerations and proof of concept. Trees 36, 1349–1367 (2022). https://doi.org/10.1007/s00468-022-02297-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00468-022-02297-x