An energy-efficient GMRES–multigrid solver for space-time finite element computation of dynamic poroelasticity

Abstract

We present and analyze computationally Geometric MultiGrid (GMG) preconditioning techniques for Generalized Minimal RESidual (GMRES) iterations to space-time finite element methods (STFEMs) for a coupled hyperbolic–parabolic system modeling, for instance, flow in deformable porous media. By using a discontinuous temporal test basis, a time marching scheme is obtained. Higher order approximations that offer the potential to inherit most of the rich structure of solutions to the continuous problem on computationally feasible grids increase the block partitioning dimension of the algebraic systems, comprised of generalized saddle point blocks. Our V-cycle GMG preconditioner uses a local Vanka-type smoother. Its action is defined in an exact mathematical way. Due to nonlocal coupling mechanisms of 348 unknowns, the smoother is applied on patches of elements. This ensures damping of higher order error frequencies. By numerical experiments of increasing complexity, the efficiency of the solver for STFEMs of different polynomial order is illustrated and confirmed. Its parallel scalability is analyzed. Beyond this study of classical performance engineering, the solver’s energy efficiency is investigated as an additional and emerging dimension in the design and tuning of algorithms on the hardware.

1 Introduction

1.1 Mathematical model

We present and investigate numerically a geometric multigrid preconditioning technique, based on a local Vanka-type smoother, for solving by GMRES iterations the linear systems that arise from space-time finite element discretizations of the coupled hyperbolic–parabolic system of dynamic poroelasticity

$$\begin{aligned}&\rho \partial _t^2 \varvec{u} - \nabla \cdot (\varvec{C} \varvec{\varepsilon }(\varvec{u})) + \alpha \varvec{\nabla }p = \rho \varvec{f}\,, \quad \text {in } \; \Omega \times (0,T]\,, \end{aligned}$$

(1.1a)

$$\begin{aligned}&c_0\partial _t p + \alpha \nabla \cdot \partial _t \varvec{u} - \nabla \cdot (\varvec{K} \nabla p) = g\,, \quad \text {in } \; \Omega \times (0,T]\,, \end{aligned}$$

(1.1b)

$$\begin{aligned}&\varvec{u} (0) = \varvec{u}_0\,, \quad \partial _t \varvec{u} (0) = \varvec{u}_1\,, \nonumber \\&p(0) = p_0\,, \quad \text {in } \; \Omega \times \{0\} \,, \end{aligned}$$

(1.1c)

$$\begin{aligned}&\varvec{u} = \varvec{u}_D\,, \quad \text {on } \; \Gamma _{\varvec{u}}^{D} \times (0,T]\,, \end{aligned}$$

(1.1d)

$$\begin{aligned}&-(\varvec{C}\varvec{\varepsilon }(\varvec{u}) - \alpha p\varvec{E}) \varvec{n} = \varvec{t}_N\,, \quad \text {on } \; \Gamma _{\varvec{u}}^{{N}} \times (0,T]\,, \end{aligned}$$

(1.1e)

$$\begin{aligned}&p = p_D\,, \quad \text {on } \; \Gamma _p^{{D}} \times (0,T]\,, \end{aligned}$$

(1.1f)

$$\begin{aligned}&- \varvec{K} \nabla p \cdot \varvec{n} = p_N\,, \quad \text {on } \; \Gamma _p^{{N}} \times (0,T]\,. \end{aligned}$$

(1.1g)

In (1.1), $\Omega \subset \mathbb {R}^d$, with $d\in \{2,3\}$, is an open bounded Lipschitz domain with outer unit normal vector $\varvec{n}$ to the boundary $\partial \Omega$ and $T>0$ is the final time point. We let $\partial \Omega = \overline{\Gamma _{\varvec{u}}^{D}} \cup \overline{\Gamma _{\varvec{u}}^{N}}$ and $\partial \Omega = \overline{\Gamma _{p}^{D}}\cup \overline{\Gamma _{p}^{N}}$ with (open) portions $\Gamma _{\varvec{u}}^{D}$ and $\Gamma _{p}^{D}$ of non-zero measure. Important applications of the model (1.1), that is studied as a prototype system, arise in poroelasticity; cf. [66] and [16,17,18]. In poroelasticity, Eq. (1.1) are referred to as the dynamic Biot model. The system (1.1) is used to describe flow of a slightly compressible viscous fluid through a deformable porous matrix. The small deformations of the matrix are described by the Navier equations of linear elasticity, and the diffusive fluid flow is described by Duhamel’s equation. The unknowns are the effective solid phase displacement $\varvec{u}$ and the effective fluid pressure p. The quantity $\varvec{\varepsilon }(\varvec{u}):= (\nabla \varvec{u} + (\nabla \varvec{u})^\top )/2$ denotes the symmetrized gradient or strain tensor and $\varvec{E}\in \mathbb {R}^{d,d}$ is the identity matrix. Further, $\rho$ is the effective mass density, $\varvec{C}$ is Gassmann’s fourth order effective elasticity tensor, $\alpha$ is Biot’s pressure-storage coupling tensor, $c_0$ is the specific storage coefficient and $\varvec{K}$ is the permeability field. For brevity, the positive quantities $\rho >0$, $\alpha >0$ and $c_0 >0$ as well as the tensors $\varvec{C}$ and $\varvec{K}$ are assumed to be constant in space and time. The tensors $\varvec{C}$ and $\varvec{K}$ are assumed to be symmetric and positive definite,

$$\begin{aligned}&\exists k_0>0 \; \forall \varvec{\xi }= \varvec{\xi }^\top \in \mathbb {R}^{d,d}:\nonumber \\&\quad \sum _{i,j,k,l=1}^d \xi _{ij} C_{ijkl} \xi _{kl} \ge k_0 \sum _{j,k=1}^d |\xi _{jk}|^2\,, \end{aligned}$$

(1.2a)

$$\begin{aligned}&\exists k_1>0 \; \forall \varvec{\xi }\in \mathbb {R}^d: \nonumber \\&\quad \sum _{i,j,=1}^d \xi _{i} K_{ij} \xi _{j} \ge k_1 \sum _{i=1}^d |\xi _{i}|^2\,. \end{aligned}$$

(1.2b)

Well-posedness of (1.1) is ensured; cf., e.g. [43, 64, 67]. This can be shown by different mathematical techniques, by semigroup methods [43, Thm. 2.2], Rothe’s method and compactness arguments [67, Thm. 4.18 and Cor. 4.33] and Picard’s theorem [64, Thm. 6.2.1]. In these works, boundary conditions different to the ones in (1.1d) to (1.1g) are partly used. System (1.1) is studied as a prototype poromechanical model. In order to enhance physical realism, generalizations of the model (1.1) have been developed and investigated in, e.g. [19, 23, 58]. We note that the system (1.1) is also formally equivalent to the classical coupled thermoelasticity system which describes the flow of heat through an elastic structure; cf. [22, 43, 52].

1.2 Space-time finite element and multigrid techniques

The coupled hyperbolic–parabolic structure of the system (1.1) of partial differential equations adds a facet of complexity onto its numerical simulation. A natural and promising approach for the numerical approximation of coupled systems is obtained by STFEMs that are based on an uniform treatment of the space and time discretization by variational techniques. STFEMs enable the discretization of even complex coupling terms that involve combinations of temporal and spatial derivatives as in (1.1b). Moreover, STFEMs offer the natural construction of higher order schemes that achieve accurate results on computationally feasible grids with a minimum of numerical costs. Time discretizations of higher regularity can be designed by combining variational and collocation techniques; cf., e.g. [6]. Finally, space-time adaptivity based on a-posteriori error control by duality concepts and multi-rate in time approaches become feasible; cf., e.g. [9, 10, 21, 70].

STFEMs have been constructed in different ways. Holistic space-time methods on completely unstructured space-times meshes have been proposed and analyzed; cf., e.g. [51, 69] and the references therein. They aim at exploiting efficiently the enormous compute power of modern massively parallel high performance architectures. Time-parallel time-integrations methods like PARAREAL [32] are closely related to these methods. A further class of STFEMs is based on time-marching schemes that are constructed by the choice of a discontinuous temporal test basis, usage of a tensor product space-time mesh and discretization of the resulting problems in the spatial variables; cf., e.g. [1, 3, 40, 41] and the references therein. Such methods offer high flexibility for the finite element discretization of the temporal and spatial variables. The existing technology of iterative linear solver can be reused or adapted to the resulting linear systems that are built from blocks mimicing lower order time discretizations; cf. (4.6) and (4.7). Combinations of either approaches also exist. Therein, tensor product space-time meshes are used, but all time steps are assembled in a global system matrix and computed fully coupled without any sequential progressing; cf., e.g. [27, 33]. Within the classes of schemes, their members can differ by the application of continuous and discontinuous finite element techniques. For second-order hyperbolic problems further approaches are addressed in [12, 29, 74].

STFEMs lead to large linear systems of equations. Their solution demands for highly efficient and robust iterative solvers, in particular if three space variables are involved. Different Algebraic Multigrid (AMG) and GMG methods have been considered and investigated for the solution of STFEM algebraic systems, either in holistic or time marching form. Also, multigrid methods have been used as preconditioners for Krylov subspace iterations, like GMRES, to enhance their robustness. For the application of multigrid techniques in the STFEM context we refer, for instance, to [3, 27, 31, 33, 39, 40, 42, 51, 59, 63, 70,71,72,73]. In [33, 59], block Jacobi smoothing factors and two-grid convergence factors for arbitrary order discontinuous Galerkin time discretizations of a holistic approach are investigated for parabolic problems by using exponential local Fourier mode analysis. Instead of an adaptive coarsening as proposed in [33, 39], a space-time multigrid method, using an adaptive smoothing strategy in combination with standard coarsening in both temporal and spatial domains, was proposed and investigated by local Fourier analysis for the heat equation in [31]. Therein, the multigrid method is robust for both first-order Euler and second-order Crank-Nicolson temporal discretization schemes. In general, GMG techniques are widely used and employed in many variants. Flow and saddle point problems are prominent applications; cf. [28, 47, 77]. Massively parallel implementations of GMG methods on modern architectures show excellent scalability properties and their high efficiency has been recognized in [34, 35, 54]. Analyses of GMG methods (cf., e.g. [28, 38, 55]) have been done in particular for linear systems in saddle point form, arising from mixed discretizations of the Stokes problem.

Fig. 1

Space-time mesh for a piecewise linear ($k=1$) discontinuous Galerkin time discretization and a Lagrange basis w.r.t. the $k+1$ Gauss–Radau quadrature points of $I_n$

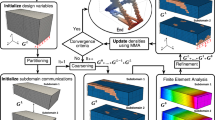
In this work, we use discontinuous Galerkin time discretization [75] with arbitrary polynomial order $k\in \mathbb {N}$ (for short dG(k)), recasted as a time marching scheme. Time interpolation on each subinterval $I_n=(t_{n-1},t_n]$ of the time mesh ${\mathcal {M}}_\tau := \{I_1,\ldots , I_N\}$, is done in terms of a Lagrangian basis with respect to the Gauss–Radau quadrature points of $I_n$; cf. Fig. 1. For the space discretization, inf-sup stable pairs of finite element spaces are applied. Alternative approaches are presented, for instance, in [37, 48]. Dirichlet boundary conditions are implemented in weak form. Two discrete systems differing by the treatment of the term $\nabla \cdot \partial _t \varvec{u}$ in (1.1b) are proposed. Well-posedness of the discrete problems is proved for arbitrary polynomial order in space and time. On each subinterval $I_n$, this discretization leads to a linear system of equations with a $(k+1)\times (k+1)$ block matrix (cf. (4.6)), where each of the blocks $\varvec{A}_{ab}$, for $a,b=1,\ldots , k+1$, exhibits the structure

$$\begin{aligned} \varvec{A}_{a,b} = \begin{pmatrix} \varvec{A} &{} \varvec{B}^\top \\ - \varvec{B} &{} \varvec{C} \end{pmatrix} \end{aligned}$$

(1.3)

with suitably defined submatrices $\varvec{A}$, $\varvec{B}$ and $\varvec{C}$ in (1.3) and $\varvec{A}$ itself being of the form in (1.3) again. We note that $\varvec{A}_{a,b}$ has a generalized saddle point form and is positive stable under certain conditions; cf. [14]. The block structure (1.3) of dG(k) time discretizations imposes an facet of complexity on the iterative solution of the systems. For the solver we propose and analyze numerically GMRES iterations that are preconditioned by a V-cycle GMG method. To the best of our knowledge, theoretical analyses of GMG methods for SFFEM block partitioned systems are still missing in the literature.

GMG methods exploit different mesh levels of the underlying problem in order to reduce different frequencies of the error by employing a relatively cheap smoother on each grid level. Different iterative methods have been proposed in the literature as smoothing procedure; cf. [28] and the references therein. They range from low-cost methods like Richardson, Jacobi, and SOR applied to the normal equation of the linear system to collective smoothers, that are based on the solution of small local problems. Here, we use a Vanka-type smoother [47, 55, 80] of the family of collective methods. Numerical computations have shown that an elementwise application of the Vanka smoother fails to reduce the high frequencies of the error on the multigrid levels. The reason for this comes through interelement couplings of spatial degrees of freedom of the scalar variable p in (1.1). As a remedy, we propose the application of the Vanka-type smoother on cell patches that are linked to the grid nodes and built from four neighbored cells in two dimensions and eight neighbored elements in three dimensions, with appropriate adaptations for grid nodes close to or on the domain’s boundary. Further, an averaging of the patchwise upates and relaxation strategy in the smoothing steps are employed. Then an efficient damping of frequencies in the error on the multigrid hierarchy is obtained. This Vanka-type smoother is presented in an mathematically exact way and its performance properties are investigated by numerical experiments of increasing complexity. Our numerical experiments confirm that GMRES iterations that are preconditioned by the proposed GMG method converge at a desired rate that is (nearly) independent of the mesh sizes in space and time; cf. also [3, 4].

1.3 Energy efficiency

In the past, performance engineering and hardware engineering for large scale simulations of physical phenomena have been eclipsed by the longing for ever more performance where faster seemed to be the only paradigm. ”Classical” performance engineering has been applied to enhance, firstly, the efficiency of the current method on the target hardware or to find numerical alternatives that might better fit to the hardware in use and/or, secondly, to develop other numerical methods can be found to improve the numerical efficiency. Tuning both simultaneously is called hardware-oriented numerics in the literature; cf. [78, 79]. Since recently, a growing awareness of energy consumption in computational science, particularly, in extreme scale computing with a view to exascale computing has raised; cf., e.g. [62]. It has been observed that as a consequence of decades of performance-centric hardware development there is a huge gap between pure performance and energy efficiency. An analysis of our algorithm’s parallel scaling and energy consumption properties by performance models exceeds the scope of this work and would overburden it. However, since energy consumption of application codes on the available hardware is of growing awareness and a key for future improvements, we study the energy consumption and parallel scaling properties of our algorithm and its implementation by three-dimensional numerical experiments. The development of a proper model that quantifies performance and energy efficiency in some appropriate metric and can be used for a code optimization still deserves research and is left as a work for the future.

1.4 Outline of the work

This work is organized as follows. In Sect. 2 we introduce our notation. In Sect. 3 the space-time finite element approximation of arbitrary order of (1.1) is derived and well-posedness of the fully discrete problem is proved. Our GMRES–GMG solver is introduced in Sect. 4. In Sect. 5 our performed numerical computations for analyzing the performance properties of the overall approach are presented. In Sect. 6 we end with a summary and conclusions. In the appendix, supplementary results are summarized.

2 Basic notation

In this work, standard notation is used. We denote by $H^1(\Omega )$ the Sobolev space of $L^2(\Omega )$ functions with first-order weak derivatives in $L^2(\Omega )$. Further, $H^{-1}(\Omega )$ is the dual space of $H^1_{0}(\Omega )$, with the standard modification if the Dirichlet condition is prescribed on a part $\Gamma ^D\subset \Gamma$ of the boundary $\partial \Omega$ only; cf. (1.1). The latter is not explicitly borne out by the notation of $H^{-1}(\Omega )$. It is always clear from the context. For vector-valued functions we write those spaces bold. By $\langle \cdot , \cdot \rangle _S$ we denote the $L^2(S)$ inner product for a domain S. For $S=\Omega$, we simply write $\langle \cdot , \cdot \rangle$. For the norms of the Sobolev spaces the notation is

$$\begin{aligned} \Vert \cdot \Vert := \Vert \cdot \Vert _{L^2}\,,\qquad \Vert \cdot \Vert _1 := \Vert \cdot \Vert _{H^1}\,. \end{aligned}$$

For short, we put

$$\begin{aligned} Q:=L^2(\Omega )\quad \text {and} \quad \varvec{V}:= \left( H^1(\Omega )\right) ^d. \end{aligned}$$

For a Banach space B, we let $L^2(0,T;B)$ be the Bochner space of B-valued functions, equipped with its natural norm. For a subinterval $J\subseteq [0,T]$, we will use the notation $L^2(J;B)$ for the corresponding Bochner space. In what follows, the constant c is generic and indepedent of the size of the space and time meshes.

For the time discretization, we decompose the time interval $I:=(0,T]$ into N subintervals $I_n=(t_{n-1},t_n]$, $n=1,\ldots ,N$, where $0=t_0<t_1< \cdots< t_{N-1} < t_N = T$ such that $I=\bigcup _{n=1}^N I_n$. We put $\tau := \max _{n=1,\ldots , N} \tau _n$ with $\tau _n = t_n-t_{n-1}$. Further, the set ${\mathcal {M}}_\tau := \{I_1,\ldots , I_N\}$ of time intervals is called the time mesh. For a Banach space B and any $k\in \mathbb {N}_0$, we let

$$\begin{aligned} {\mathbb {P}}_k(I_n;B):= & {} \bigg \{w_\tau : \, I_n \rightarrow B, \; \nonumber \\{} & {} \quad w_\tau (t) = \sum _{j=0}^k W^j t^j \; \forall t\in I_n, \; W^j \in B\; \forall j \bigg \}.\nonumber \\ \end{aligned}$$

(2.1)

For $k\in \mathbb {N}_0$ we define the space of piecewise polynomial functions in time with values in B by

$$\begin{aligned} Y_\tau ^{k} (B):= & {} \left\{ w_\tau : {\overline{I}} \rightarrow B \mid w_\tau {}_{|I_n} \in {\mathbb {P}}_{k}(I_n;B)\; \right. \nonumber \\{} & {} \left. \forall I_n\in {\mathcal {M}}_\tau ,\, w_\tau (0)\in B \right\} \subset L^2(I;B). \end{aligned}$$

(2.2)

For any function $w: {\overline{I}}\rightarrow B$ that is piecewise sufficiently smooth with respect to the time mesh ${\mathcal {M}}_{\tau }$, for instance for $w\in Y^k_\tau (B)$, we define the right-hand sided and left-hand sided limit at a mesh point $t_n$ by

$$\begin{aligned} w^+(t_n):= & {} \lim _{t\rightarrow t_n+0} w(t),\quad \text {for}\; n<N, \text {and}\nonumber \\ w^-(t_n):= & {} \lim _{t\rightarrow t_n-0} w(t),\quad \text {for}\; n>0. \end{aligned}$$

(2.3)

For the integration in time of a discontinuous Galerkin approach it is natural to use the right-sided $(k+1)$-point Gauss–Radau quadrature formula. On the subinterval $I_n$, it reads as

$$\begin{aligned} Q_n(w):= \frac{\tau _n}{2}\sum _{\mu =1}^{k+1} {\hat{\omega }}_ \mu ^{{\text {GR}}} w(t_{n,\mu }^{{\text {GR}}} ) \approx \int _{I_n} w(t) \,\textrm{d}t, \end{aligned}$$

(2.4)

where $t_{n,\mu }^{{\text {GR}}}=T_n({\hat{t}}_{\mu }^{{\text {GR}}})$, for $\mu = 1,\ldots ,k+1$, are the Gauss–Radau quadrature points on $I_n$ and $\hat{\omega }_\mu ^{{\text {GR}}}$ the corresponding weights. Here, $T_n({\hat{t}}):=(t_{n-1}+t_n)/2 + (\tau _n/2){\hat{t}}$ is the affine transformation from ${\hat{I}} = [-1,1]$ to $I_n$ and ${\hat{t}}_{\mu }^{{\text {GR}}}$ are the Gauss–Radau quadrature points on ${\hat{I}}$. Formula (2.4) is exact for all polynomials $w\in {\mathbb {P}}_{2k} (I_n;\mathbb {R})$. In particular, there holds that $t_{n,k+1}^{{\text {GR}}}=t_n$.

For the space discretization, let $\{{\mathcal {T}}_l\}_{l=0}^{L}$ be the decomposition on every multigrid level of $\Omega$ into (open) quadrilaterals or hexahedrals, with ${\mathcal {T}}_l = \{K_i\mid i=1,\ldots , N^{\text {el}}_l\}$, for $l=0,\ldots ,L$. These element types are chosen for our implementation (cf. Sect. 5) that is based on the deal.II library [7]. The finest partition is ${\mathcal {T}}_h={\mathcal {T}}_L$. We assume that all the partitions $\{{\mathcal {T}}_l\}_{l=0}^{L}$ are quasi-uniform with characteristic mesh size $h_l$ and $h_l=\gamma h_{l-1}$, $\gamma \in (0,1)$ and $h_0 = {\mathcal {O}}(1)$. On the actual mesh level, the finite element spaces used for approximating the unknowns $\varvec{u}$ and p of (1.1) are of the form ($l\in \{0,\ldots ,L\}$)

$$\begin{aligned} \varvec{V}_{h_l}^l&:= \{\varvec{v}_h \in \varvec{V} \cap C({\overline{\Omega }} )^d:\; \nonumber \\&\qquad \; \varvec{v}_{h}{}_{|K}\in {\varvec{V}(K)} \;\; \text {for all}\; K \in {\mathcal {T}}_l\}\,, \end{aligned}$$

(2.5a)

$$\begin{aligned} Q_{h_l}^{l,\text {cont}}&:= \{\varvec{q}_h \in Q\cap C({\overline{\Omega }} ) :\; \nonumber \\&\qquad \; \varvec{q}_{h}{}_{|K}\in {Q(K)} \;\; \text {for all}\; K \in {\mathcal {T}}_l\}\,, \end{aligned}$$

(2.5b)

$$\begin{aligned} Q_{h_l}^{l,\text {disc}}&:= \{\varvec{q}_h \in Q\; : \; \varvec{q}_{h}{}_{|K}\in {Q(K)} \;\; \text {for all}\; K \in {\mathcal {T}}_l\}\,. \end{aligned}$$

(2.5c)

By an abuse of notation, we skip the index l of the mesh level when it is clear from the context and put

$$\begin{aligned}{} & {} \varvec{V}_h:= \varvec{V}_h^l \quad \nonumber \\{} & {} Q_h:= Q_h^l \;\; \text {with} \;\; Q_h^l\in \{Q_h^{l,\text {cont}}, Q_h^{l,\text {disc}}\}. \end{aligned}$$

(2.6)

For the local spaces $\varvec{V}(K)$ and Q(K) we employ mapped versions of the pairs ${\mathbb {Q}}_r^d/{\mathbb {Q}}_{r-1}$ and $\mathbb Q_r^d/{\mathbb {P}}_{r-1}^{{\text {disc}}}$, for $r\ge 2$. The pair $\mathbb Q_r^d/{\mathbb {Q}}_{r-1}$ with a (globally) continuous approximation of the scalar variable p in $Q_h^{l,\text {cont}}$ is the well-known Taylor–Hood family of finite element spaces. The pair $\mathbb Q_r^d/{\mathbb {P}}_{r-1}^{{\text {disc}}}$ comprises a discontinuous approximation of p in the broken polynomial space $Q_h^{l,\text {disc}}$. For the Navier–Stokes equations, the multigrid method has shown to work best for higher-order finite element spaces with discontinuous discrete pressure; cf. [46] and [3]. For a further discussion of mapped and unmapped versions of the pair $\mathbb Q_r^d/{\mathbb {P}}_{r-1}^{{\text {disc}}}$ we refer to [44, Subsec. 3.6.4]. For an analysis of stability properties of (spatial) discretizations for the quasi-static Biot system we refer to, e.g. [61]. Both choices of the local finite element spaces, $\mathbb Q_r^d/{\mathbb {Q}}_{r-1}$ and ${\mathbb {Q}}_r^d/{\mathbb {P}}_{r-1}^{{\text {disc}}}$, satisfy under some restrictions (cf. [82]) the inf–sup stability condition,

$$\begin{aligned} \inf _{q_h \in Q_h\backslash \{0\}} \sup _{\varvec{v}_h\in \varvec{V}_h\backslash \{\varvec{0}\}} \dfrac{b(\varvec{v}_h,q_h)}{\Vert \varvec{v}_h \Vert _1 \, \Vert q_h\Vert } \ge \beta > 0, \end{aligned}$$

(2.7)

for some constant $\beta$ independent of h; cf. [44, 57]. In [8, 56] optimal interpolation error estimates for mapped finite elements on quadrilaterals and hexahedra are studied. It turned out that the optimality is given for special families of triangulations. In two and three dimensions, families of meshes, which are obtained by a regular uniform refinement of an initial coarse grid, are among these special families. Such a regular refinement that is natural for the construction of the multigrid hierarchy is used in our computations. Thus, for $\varvec{v}\in \varvec{H}^{r+1}(\Omega )$ and $q\in H^r(\Omega )$ there exist approximations $i_h \varvec{v} \in \varvec{V}_h$ and $j_h q \in Q_h$ such that, with some generic constant $c>0$ independent of h,

$$\begin{aligned}&\Vert \varvec{v} - i_h \varvec{v} \Vert + h \Vert \nabla (\varvec{v}-i_h \varvec{v})\Vert \le c h^{r+1}, \end{aligned}$$

(2.8a)

$$\begin{aligned}&\qquad \qquad \qquad \quad \qquad \Vert q - j_h q\Vert \le c h^r. \end{aligned}$$

(2.8b)

3 Space-time finite element approximation

For the discretization we rewrite (1.1) as a first-order in time system by introducing the new variable $\varvec{v}:= \partial _t \varvec{u}$. Then, we recover (1.1a) and (1.1b) as

$$\begin{aligned}&\partial _t \varvec{u} - \varvec{v} = \varvec{0}, \end{aligned}$$

(3.1a)

$$\begin{aligned}&\rho \partial _t \varvec{v} - \nabla \cdot (\varvec{C} \varvec{\varepsilon }(\varvec{u})) + \alpha \varvec{\nabla }p = \rho \varvec{f}\,, \end{aligned}$$

(3.1b)

$$\begin{aligned}&c_0\partial _t p + \alpha \nabla \cdot \varvec{v} - \nabla \cdot (\varvec{K} \varvec{\nabla }p) = g \end{aligned}$$

(3.1c)

along with the initial and boundary conditions (1.1c) to (1.1g). For the approximation of (3.1) we use a monolithic approach to capture efficiently the dynamics of (3.1) and avoid additional consistency errors. An iterative coupling scheme for (3.1) is proposed, for instance, in [19]. We employ discontinuous Galerkin methods (cf. [75]) for the discretization of the time variable and inf-sup stable pairs of finite elements (cf. Sect. 2) for the approximation of the space variables in (3.1). The derivation of the discrete scheme, presented below in Problem B.1, is standard and not explicitly presented here. It follows the lines of [11], where continuous in time Galerkin methods are applied to (1.1), and [3, 4, 41, 42], where discontinuous in time Galerkin methods are used to discretize the Navier–Stokes system. In contrast to [11], Dirichlet boundary conditions are implemented here by Nitsche’s method [15, 30, 60]. This yields a strong link between two different families of inf-stable finite element pairs for the space discretization. The main reason for using Nitsche’s method here comes through our more general software framework. Nitsche’s method captures problems on evolving domains solved on fixed computational background grids (cf. [5]). We note that Nitsche’s method does not perturb the convergence behavior of the space-time discretization; cf. Sect. 5.

For the discrete scheme we need further notation. On the multigrid level l with decomposition ${\mathcal {T}}_l$, for $\varvec{w}_h, \varvec{\chi }_h\in \varvec{V}_h$ and $q_h, \psi _h \in Q_h$ we define

$$\begin{aligned} A_\gamma (\varvec{w}_{h},\varvec{\chi }_h)&:= \langle \varvec{C} \varvec{\varepsilon }(\varvec{w}_h),\varvec{\varepsilon }(\varvec{\chi }_h)\rangle \nonumber \\&\quad -\langle \varvec{C}\varvec{\varepsilon }(\varvec{w}_h) \varvec{n}, \varvec{\chi }_h\rangle _{\Gamma ^D_{\varvec{u}}}+ a_\gamma (\varvec{w}_{h},\varvec{\chi }_h)\,, \end{aligned}$$

(3.2a)

$$\begin{aligned} C (\varvec{\chi }_{h},q_h)&:= -\alpha \langle \nabla \cdot \varvec{\chi }_h, q_h\rangle + \alpha \langle \varvec{\chi }_h \cdot \varvec{n} , q_h \rangle _{\Gamma ^D_{\varvec{u}}} \,, \end{aligned}$$

(3.2b)

$$\begin{aligned} B_\gamma (q_{h},\psi _h)&:= \left\{ \begin{array}{@{}lllll}\langle \varvec{K} \nabla q_h, \nabla \psi _h \rangle \\ - \langle \varvec{K} \nabla q_h \cdot \varvec{n}, \psi _h \rangle _{\Gamma _p^D} + b_\gamma (q_h,\psi _h)\,,\\ \text {for}\;\; Q_h = Q_h^{l,\text {cont}}\!\!\!,\\ \begin{array}{@{}l} \displaystyle \sum _{K\in \mathcal T_l}\langle \varvec{K} \nabla q_h, \nabla \psi _h \rangle _{K}\\ - \displaystyle \sum _{F\in \mathcal F_h} \big (\langle \{\hspace{-2.77771pt}\{\varvec{K} \nabla q_h \}\hspace{-2.77771pt}\}\cdot \varvec{n}, \{\hspace{-2.77771pt}\{\psi _h \}\hspace{-2.77771pt}\}\rangle _{F} \\ \displaystyle \quad + \langle \{\hspace{-2.77771pt}\{q_h\}\hspace{-2.77771pt}\}, \{\hspace{-2.77771pt}\{\varvec{K} \nabla \psi _h \}\hspace{-2.77771pt}\}\cdot \varvec{n} \rangle _{F}\big )\\ + \displaystyle \sum _{F\in \mathcal F_h} \frac{\gamma }{h_F} \langle \{\hspace{-2.77771pt}\{q_h \}\hspace{-2.77771pt}\}, \{\hspace{-2.77771pt}\{\psi _h\}\hspace{-2.77771pt}\}\rangle _F\,, \end{array} \\ \text {for}\;\; Q_h = Q_h^{l,\text {disc}}\!\!\!,\\ \end{array}\right. \end{aligned}$$

(3.2c)

where, for $\varvec{w} \in \varvec{H}^{1/2}(\Gamma ^D_{\varvec{u}})$ and $q\in H^{1/2}(\Gamma ^D_{p})$,

$$\begin{aligned} a_\gamma (\varvec{w} ,\varvec{\chi }_h)&:= - \langle \varvec{w}, \varvec{C}\varvec{\varepsilon }(\varvec{\chi }_h) \varvec{n} \rangle _{\Gamma ^D_{\varvec{u}}} + \frac{\gamma _a}{h_F} \langle \varvec{w}, \varvec{\chi }_h \rangle _{\Gamma ^D_{\varvec{u}}}\,, \end{aligned}$$

(3.3a)

$$\begin{aligned} b_\gamma (q, \psi _h)&:= - \langle q, \varvec{K} \nabla \psi _h \cdot \varvec{n}\rangle _{\Gamma _p^D} + \frac{\gamma _b}{h_F} \langle q, \psi _h \rangle _{\Gamma ^D_{p}} \,. \end{aligned}$$

(3.3b)

The second of the options in (3.2c) amounts to a symmetric interior penalty discontinuous Galerkin discretization of the scalar variable p; cf., e.g. [26, Sec. 4.2]. As usual, the average $\{\hspace{-2.77771pt}\{\cdot \}\hspace{-2.77771pt}\}$ and jump $\{\hspace{-2.77771pt}\{\cdot \}\hspace{-2.77771pt}\}$ of a function $w\in L^2(\Omega )$ on an interior face F between two elements $K^+$ and $K^-$, such that $F=\partial K^+ \cap \partial K^-$, are

$$\begin{aligned} \{\hspace{-2.77771pt}\{w \}\hspace{-2.77771pt}\}:= \frac{1}{2} (w^{+}+ w^{-})\quad \text {and} \quad \{\hspace{-2.77771pt}\{w \}\hspace{-2.77771pt}\}: = w^{+} - w^{-}. \end{aligned}$$

For boundary faces $F \subset \partial K \cap \partial \Omega$, we set $\{\hspace{-2.77771pt}\{w\}\hspace{-2.77771pt}\}:= w_{|K}$ and $\{\hspace{-2.77771pt}\{w \}\hspace{-2.77771pt}\}:= w_{|K}$. The set of all faces (interior and boundary faces) on the multigrid level ${\mathcal {T}}_l$ is denoted by ${\mathcal {F}}_h$. In the second of the options in (3.2c), the parameter $\gamma$ of the last term has to be chosen sufficiently large, such that discrete coercivity on $Q_h$ of $B_\gamma$ is preserved. The local length $h_F$ is chosen as $h_F = \{\hspace{-2.77771pt}\{h_F \}\hspace{-2.77771pt}\}:= \frac{1}{2} (|K^+|_d + |K^-|_d)$ with Hausdorff measure $|\cdot |_d$; cf. [26, p. 125]. For boundary faces we set $h_F:= |K|_d$. In (3.3), the quantities $\gamma _a$ and $\gamma _b$ are the algorithmic parameters of the stabilization terms in the Nitsche formulation. To ensure well-posedness of the discrete systems the parameters $\gamma _a$ and $\gamma _b$ have to be chosen sufficiently large; cf. Appendix A. Based on our numerical experiments we choose the algorithmic parameter $\gamma$, $\gamma _a$ and $\gamma _b$ in (3.2c) and (3.3) as

$$\begin{aligned} \gamma _a&= 5\cdot 10^4 \cdot r \cdot (r+1) \quad \text {and}\\ \gamma&= \gamma _b = \frac{1}{2} \cdot r \cdot (r-1)\,, \end{aligned}$$

where r is the polynomial degree of the finite element space (2.5a) for the displacement variable.

Finally, for given $\varvec{f} \in \varvec{H}^{-1}(\Omega )$, $\varvec{u}_D \in \varvec{H}^{1/2}(\Gamma ^D_{\varvec{u}})$, $\varvec{t}_N \in \varvec{H}^{-1/2}(\Gamma ^N_{\varvec{u}})$ and $g\in H^{-1}(\Omega )$, $p_D \in H^{1/2}(\Gamma ^D_{p})$, $p_N\in H^{-1/2}(\Gamma ^N_{p})$ for $Q_h = Q_h^{l,\text {cont}}$, and properly fitted assumptions about the data for $Q_h = Q_h^{l,\text {disc}}$, we put

$$\begin{aligned} F_\gamma (\varvec{\chi }_h)&:= \langle \varvec{f} , \varvec{\chi }_h\rangle - \langle \varvec{t}_N,\varvec{\chi }_h \rangle _{\Gamma ^N_{\varvec{u}}} + a_\gamma (\varvec{u}_D ,\varvec{\chi }_h)\,, \end{aligned}$$

(3.4a)

$$\begin{aligned} G_\gamma (\psi _h)&:= \left\{ \begin{array}{@{}lllll} \displaystyle \langle g,\psi _h \rangle - \alpha \langle \varvec{v}_D \cdot \varvec{n} , \psi _h \rangle _{\Gamma ^D_{\varvec{u}}}\\ - \langle p_N, \psi _h\rangle _{\Gamma ^N_p} + b_\gamma (p_D, \psi _h)\,,\\ \text {for}\;\; Q_h = Q_h^{l,\text {cont}}\!\!,\\ \begin{array}{@{}l} \displaystyle \langle g,\psi _h \rangle - \sum _{F\in {\mathcal {F}}_h^{D,\varvec{u}}} \alpha \langle \varvec{v}_D \cdot \varvec{n} , \psi _h \rangle _{F}\\ - \displaystyle \sum _{F\in {\mathcal {F}}_h^{D,p}}\langle p_D, \{\hspace{-2.77771pt}\{\varvec{K} \nabla \psi _h \}\hspace{-2.77771pt}\}\cdot \varvec{n} \rangle _{F}\\ \displaystyle \; + \sum _{F\in {\mathcal {F}}_h^{D,p}} \frac{\gamma }{h} \langle p_D, \{\hspace{-2.77771pt}\{\psi _h\}\hspace{-2.77771pt}\}\rangle _F\\ - \displaystyle \sum _{F\subset \mathcal F_h^{N,p}} \langle p_N, \{\hspace{-2.77771pt}\{\psi _h \}\hspace{-2.77771pt}\}\rangle _F\,, \end{array}\\ \text {for}\;\; Q_h = Q_h^{l,\text {disc}}\!\!. \end{array}\right. \end{aligned}$$

(3.4b)

In the second of the options in (3.4b), we denote by ${\mathcal {F}}_h^{D,p}\subset {\mathcal {F}}_h$ and $\mathcal F_h^{N,p}\subset {\mathcal {F}}_h$ the set of all element faces on the boundary parts $\Gamma _p^D$ and $\Gamma _p^N$, respectively; cf. (1.1). The second of the terms on the right-hand side of (3.4b), with $\varvec{v}_D = \partial _t \varvec{u}_D$, is added to ensure consistency of the form (3.2b) in the fully discrete formulation (3.5c) of (1.1b), i.e., that the discrete equation (3.5c) is satisfied by the continuous solution to (1.1).

We use a temporal test basis that is supported on the subintervals $I_n$; cf., e.g. [3, 41]. Then, a time marching process is obtained. In that, we assume that the trajectories $\varvec{u}_{ \tau ,h}$, $\varvec{v}_{ \tau ,h}$ and $p_{ \tau ,h}$ have been computed before for all $t\in [0,t_{n-1}]$, starting with approximations $\varvec{u}_{\tau ,h}(t_0):=\varvec{u}_{0,h}$, $\varvec{v}_{\tau ,h}(t_0):=\varvec{u}_{1,h}$ and $p_{\tau ,h}(t_0):= p_{0,h}$ of the initial values $\varvec{u}_0$, $\varvec{v}_0$ and $p_{0,h}$. Then, we consider solving the following local problem on $I_n$.

Problem 3.1

(Numerically integrated $I_n$-problem) For given $\varvec{u}_{h}^{n-1}:= \varvec{u}_{\tau ,h}(t_{n-1})\in \varvec{V}_h$, $\varvec{v}_{h}^{n-1}:=$ $\varvec{v}_{\tau ,h}(t_{n-1})\in \varvec{V}_h$, and $p_{h}^{n-1}:= p_{\tau ,h}(t_{n-1}) \in Q_h$ with $\varvec{u}_{\tau ,h}(t_0):=\varvec{u}_{0,h}$, $\varvec{v}_{\tau ,h}(t_0):=\varvec{u}_{1,h}$ and $p_{\tau ,h}(t_0):= p_{0,h}$, find $(\varvec{u}_{\tau ,h},\varvec{v}_{\tau ,h},p_{\tau ,h}) \in {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;Q_h)$ such that

$$\begin{aligned}&\begin{aligned}&Q_n \big (\langle \partial _t \varvec{u}_{\tau ,h} , \varvec{\phi }_{\tau ,h} \rangle - \langle \varvec{v}_{\tau ,h} , \varvec{\phi }_{\tau ,h} \rangle \big ) \\&\quad + \langle \varvec{u}^+_{\tau ,h}(t_{n-1}), \varvec{\phi }_{\tau ,h}^+(t_{n-1})\rangle = \langle \varvec{u}_{h}^{n-1}, \varvec{\phi }_{\tau ,h}^+(t_{n-1})\rangle \,, \end{aligned} \end{aligned}$$

(3.5a)

$$\begin{aligned}&\begin{aligned}&Q_n \Big (\langle \rho \partial _t \varvec{v}_{\tau ,h} , \varvec{\chi }_{\tau ,h} \rangle + A_\gamma (\varvec{u}_{\tau ,h}, \varvec{\chi }_{\tau ,h} ) + C(\varvec{\chi }_{\tau ,h},p_{\tau ,h})\Big ) \\&\quad + \langle \rho \varvec{v}^+_{\tau ,h}(t_{n-1}), \varvec{\chi }_{\tau ,h}^+(t_{n-1})\rangle \\&= Q_n \Big (F_\gamma (\varvec{\chi }_{\tau ,h})\Big ) + \langle \rho \varvec{v}_{h}^{n-1}, \chi _{\tau ,h}^+(t_{n-1})\rangle \,,\\ \end{aligned} \end{aligned}$$

(3.5b)

$$\begin{aligned}&\begin{aligned}&Q_n \Big (\langle c_0 \partial _t p_{\tau ,h},\psi _{\tau ,h} \rangle - C(\varvec{v}_{\tau ,h},\psi _{\tau ,h})+ B_\gamma (p_{\tau ,h}, \psi _{\tau ,h})\Big ) \\&\quad + \langle c_0 p^+_{\tau ,h}(t_{n-1}), \psi _{\tau ,h}^+(t_{n-1})\rangle \\&= Q_n \Big ( G_\gamma (\psi _{\tau ,h})\Big ) + \langle c_0 p_{h}^{n-1}, \psi _{\tau ,h}^+(t_{n-1})\rangle \end{aligned} \end{aligned}$$

(3.5c)

for all $(\varvec{\phi }_{\tau ,h},\varvec{\chi }_{\tau ,h},\psi _{\tau ,h})\in {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;Q_h)$.

The trajectories defined by Problem 3.1, for $n = 1,\ldots ,N$, satisfy that $\varvec{u}_{\tau ,h},\varvec{v}_{\tau ,h}\in Y_\tau ^k(\varvec{V}_h)$ and $p_{\tau ,h}\in Y_\tau ^k(Q_h)$. The quadrature formulas on the left hand-side of (3.5) can be rewritten by time integrals since the Gauss–Radau formula (2.4) is exact for all polynomials $w\in P_{2k}(I_n;\mathbb {R})$. Well-posedness of Problem 3.1 is ensured.

Lemma 3.2

(Existence and uniqueness of solutions to Problem 3.1) Problem 3.1 admits a unique solution.

Proof

We prove Lem. 3.2 for $Q_h=Q_h^{l,\text {cont}}$ only, thus assuming the first of the options in (3.2c) and (3.4b). For $Q_h=Q_h^{l,\text {disc}}$, the proof can be done similarly by using, in addition, standard techniques of error analysis for discontinuous Galerkin methods; cf., e.g. [26, Sec. 4]. Since Problem (3.5) is finite-dimensional, it suffices to prove uniqueness of the solution. Existence of the solution then follows directly from its uniqueness. Let now $(\varvec{u}^{(1)}_{\tau ,h},\varvec{v}^{(1)}_{\tau ,h},p^{(1)}_{\tau ,h}) \in {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;Q_h)$ and $(\varvec{u}^{(2)}_{\tau ,h},\varvec{v}^{(2)}_{\tau ,h},p^{(2)}_{\tau ,h}) \in {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;Q_h)$ denote two triples of solutions to (3.5a). Their differences $(\varvec{u}_{\tau ,h},\varvec{v}_{\tau ,h},p_{\tau ,h}) =(\varvec{u}^{(1)}_{\tau ,h},\varvec{v}^{(1)}_{\tau ,h},p^{(1)}_{\tau ,h}) -(\varvec{u}^{(2)}_{\tau ,h},\varvec{v}^{(2)}_{\tau ,h},p^{(2)}_{\tau ,h})$ then satisfy the equations

$$\begin{aligned}&Q_n \big (\langle \partial _t \varvec{u}_{\tau ,h} , \varvec{\phi }_{\tau ,h} \rangle - \langle \varvec{v}_{\tau ,h} , \varvec{\phi }_{\tau ,h} \rangle \big ) \nonumber \\&\quad + \langle \varvec{u}^+_{\tau ,h}(t_{n-1}), \varvec{\phi }_{\tau ,h}^+(t_{n-1})\rangle = 0\,, \end{aligned}$$

(3.6a)

$$\begin{aligned}&Q_n \Big (\langle \rho \partial _t \varvec{v}_{\tau ,h} , \varvec{\chi }_{\tau ,h} \rangle + A_\gamma (\varvec{u}_{\tau ,h}, \varvec{\chi }_{\tau ,h} ) + C(\varvec{\chi }_{\tau ,h},p_{\tau ,h})\Big ) \nonumber \\&\quad + \langle \rho \varvec{v}^+_{\tau ,h}(t_{n-1}), \varvec{\chi }_{\tau ,h}^+(t_{n-1})\rangle = 0 \,, \end{aligned}$$

(3.6b)

$$\begin{aligned}&Q_n \Big (\langle c_0 \partial _t p_{\tau ,h},\psi _{\tau ,h} \rangle - C(\varvec{v}_{\tau ,h},\psi _{\tau ,h})+ B_\gamma (p_{\tau ,h}, \psi _{\tau ,h})\Big ) \nonumber \\&\quad + \langle c_0 p^+_{\tau ,h}(t_{n-1}), \psi _{\tau ,h}^+(t_{n-1})\rangle = 0 \end{aligned}$$

(3.6c)

for all $(\varvec{\phi }_{\tau ,h},\varvec{\chi }_{\tau ,h},\psi _{\tau ,h})\in {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;Q_h)$. We let $\varvec{A}_\gamma : \varvec{V}_h \mapsto \varvec{V}_h$ be the discrete operator that is defined, for $\varvec{w}_h \in \varvec{V}_h$ and all $\varvec{\phi }_h\in \varvec{V}_h$, by

$$\begin{aligned} \langle \varvec{A}_\gamma \varvec{w}_h, \varvec{\phi }_h \rangle = A_\gamma (\varvec{w}_h,\varvec{\phi }_h). \end{aligned}$$

(3.7)

In (3.6) we choose $\varvec{\phi }_{\tau ,h}=\varvec{A}_\gamma \varvec{u}_{\tau ,h}$, $\varvec{\chi }_{\tau ,h}=\varvec{v}_{\tau ,h}$ and $\psi _{\tau ,h}=p_{\tau ,h}$. Adding the resulting equations yields that

$$\begin{aligned} \begin{aligned}&Q_n \big (\langle \partial _t \varvec{u}_{\tau ,h}, \varvec{A}_\gamma \varvec{u}_{\tau ,h} \rangle + \langle \rho \partial _t \varvec{v}_{\tau ,h}, \varvec{v}_{\tau ,h} \rangle \\&\quad + \langle c_0 \partial _t p_{\tau ,h}, p_{\tau ,h} \rangle + B_\gamma (p_{\tau ,h},p_{\tau ,h}) \big ) \\&\quad + \langle \varvec{u}^+_{\tau ,h}(t_{n-1}), \varvec{A}_\gamma u_{\tau ,h}^+(t_{n-1})\rangle \\&\quad + \langle \rho \varvec{v}^+_{\tau ,h}(t_{n-1}), \varvec{v}_{\tau ,h}^+(t_{n-1})\rangle \\&\quad + \langle c_0 p^+_{\tau ,h}(t_{n-1}), p_{\tau ,h}^+(t_{n-1})\rangle = 0. \end{aligned} \end{aligned}$$

(3.8)

Recalling the exactness of the Gauss–Radau formula (2.4) for $w\in {\mathbb {P}}_{2k}(I_n;\mathbb {R})$, Eq. (3.8) yields that

$$\begin{aligned} \begin{aligned}&\frac{1}{2} \int _{t_{n-1}}^{t_n} \frac{d}{dt} \big ( \langle \varvec{A}_\gamma \varvec{u}_{\tau ,h}, \varvec{u}_{\tau ,h} \rangle + \langle \rho \varvec{v}_{\tau ,h}, \varvec{v}_{\tau ,h} \rangle \\&\quad + \langle c_0 p_{\tau ,h}, p_{\tau ,h} \rangle \big ) \,\textrm{d}t + Q_n\big (B_\gamma (p_{\tau ,h},p_{\tau ,h}) \big ) \\&\quad + \langle \varvec{u}^+_{\tau ,h}(t_{n-1}), \varvec{A}_\gamma u_{\tau ,h}^+(t_{n-1})\rangle \\&\quad + \langle \rho \varvec{v}^+_{\tau ,h}(t_{n-1}), \varvec{v}_{\tau ,h}^+(t_{n-1})\rangle \\&\quad + \langle c_0 p^+_{\tau ,h}(t_{n-1}), p_{\tau ,h}^+(t_{n-1})\rangle = 0. \end{aligned} \end{aligned}$$

Using (3.7), this shows that

$$\begin{aligned}{} & {} A_\gamma (\varvec{u}_{\tau ,h}(t_n), \varvec{u}_{\tau ,h}(t_n)) + \langle \rho \varvec{v}_{\tau ,h} (t_n), \varvec{v}_{\tau ,h}(t_n) \rangle \nonumber \\{} & {} \quad + \langle c_0 p_{\tau ,h}(t_n), p_{\tau ,h}(t_n)\rangle + 2 Q_n \big (B_\gamma (p_{\tau ,h},p_{\tau ,h}) \big ) \nonumber \\{} & {} \quad + A_\gamma (\varvec{u}^+_{\tau ,h}(t_{n-1}), \varvec{u}_{\tau ,h}^+(t_{n-1})) \nonumber \\{} & {} \quad + \langle \rho \varvec{v}^+_{\tau ,h}(t_{n-1}), \varvec{v}_{\tau ,h}^+(t_{n-1})\rangle \nonumber \\{} & {} \quad + \langle c_0 p^+_{\tau ,h}(t_{n-1}), p_{\tau ,h}^+(t_{n-1})\rangle = 0. \end{aligned}$$

(3.9)

From (3.9) along with the discrete coercivity properties (A.3) of $A_\gamma$ and (A.5) of $B_\gamma$ we directly deduce that

$$\begin{aligned} \varvec{u}_{\tau ,h}(t_n)= & {} \varvec{u}_{\tau ,h}^+(t_{n-1})=\varvec{0}, \nonumber \\ \varvec{v}_{\tau ,h}(t_n)= & {} \varvec{v}_{\tau ,h}^+(t_{n-1})=\varvec{0}, \nonumber \\ p_{\tau ,h}(t_n)= & {} p_{\tau ,h}^+(t_{n-1})= 0, \end{aligned}$$

(3.10)

as well as

$$\begin{aligned} p_{\tau ,h}\big (t_{n,\mu }^{\text {GR}}\big ) = 0, \quad \text {for}\;\; \mu = 1,\ldots , k+1. \end{aligned}$$

(3.11)

In (3.11) we recall that $t_{n,k+1}^{\text {GR}}=t_n$. Relation (3.11) implies that $p_{\tau ,h}\equiv 0$ on $I_n$. For $k=0$, the uniqueness of $\varvec{u}_{\tau ,h}$ and $\varvec{v}_{\tau ,h}$ is already proved by (3.10).

From now, let $k\ge 1$. To prove that $\varvec{u}_{\tau ,h}\equiv \varvec{0}$ and $\varvec{v}_{\tau ,h}\equiv \varvec{0}$, by (3.10) it is sufficient to show that $\varvec{u}_{\tau ,h}(t_{n,\mu }^{\text {G}})=\varvec{0}$ and $\varvec{v}_{\tau ,h}(t_{n,\mu }^{\text {G}}) = \varvec{0}$, for $\mu = 1,\ldots , k$, where $t_{n,\mu }^{\text {G}}$, for $\mu = 1,\ldots , k$, are the nodes of the k-point Gauss quadrature formula on $I_n$ that is exact for all polynomials in ${\mathbb {P}}_{2k-1}(I_n;\mathbb {R})$. This is done now. Recalling (3.10), we conclude from (3.6a) by a suitable choice of test functions that

$$\begin{aligned}{} & {} \partial _t \varvec{u}_{\tau ,h}(t_{n,\mu }^{\text {GR}})=\varvec{v}_{\tau ,h}(t_{n,\mu }^{\text {GR}}), \text { for} \;\; \mu = 1,\ldots , k. \end{aligned}$$

(3.12)

Next, choosing $\chi _{\tau ,h}=\varvec{v}_{\tau ,h}$ in (3.6b) and recalling (3.12) imply that

$$\begin{aligned}{} & {} Q_n \Big (\langle \rho \partial _t \varvec{v}_{\tau ,h}, \varvec{v}_{\tau ,h} \rangle + A_\gamma (\varvec{u}_{\tau ,h}, \partial _t \varvec{u}_{\tau ,h} ) \Big )= 0 \end{aligned}$$

(3.13)

By the exactness of the Gauss–Radau formula (2.4) for all $w\in {\mathbb {P}}_{2k}(I_n;\mathbb {R})$ we have from (3.13) that

$$\begin{aligned}{} & {} \int _{t_{n-1}}^{t_n} \langle \rho \partial _t \varvec{v}_{\tau ,h}, \varvec{v}_{\tau ,h} \rangle \,\textrm{d}t \nonumber \\{} & {} + \frac{1}{2} \int _{t_{n-1}}^{t_n} \frac{d}{dt} A_\gamma (\varvec{u}_{\tau ,h}, \varvec{u}_{\tau ,h} ) \,\textrm{d}t = 0. \end{aligned}$$

(3.14)

The second of the terms in (3.14) vanishes by (3.10). The stability result of [49, Lem. 2.1] then implies that

$$\begin{aligned} \varvec{v}_{\tau ,h}(t_{n,\mu }^{\text {G}}) = \varvec{0}, \quad \text {for} \;\; \mu = 1,\ldots , k. \end{aligned}$$

(3.15)

From (3.15) along with (3.10) we then deduce that $\varvec{v}_{\tau ,h}\equiv \varvec{0}$ on $I_n$. Choosing the test function $\varvec{\phi }_{\tau ,h}=\varvec{u}_{\tau _h}$ in (3.6), using $\varvec{v}_{\tau ,h}\equiv \varvec{0}$ and applying the stability result [49, Lem. 2.1], it follows that

$$\begin{aligned} \varvec{u}_{\tau ,h}(t_{n,\mu }^{\text {G}}) = \varvec{0}, \quad \text {for} \;\; \mu = 1,\ldots , k. \end{aligned}$$

(3.16)

From (3.16) along with (3.10) we then have that $\varvec{u}_{\tau ,h}\equiv \varvec{0}$ on $I_n$. Thus uniqueness of solutions to (3.5) and, thereby, well-posedness of Problem 3.1 is thus ensured.

In Appendix B an alternative formulation for the system (3.6) is still presented. It is based on using the time derivative $\partial _t \varvec{u}_{\tau ,h}$ of the primal variable $\varvec{u}_{\tau ,h}$ instead of the auxiliary variable $\varvec{v}_{\tau ,h}$ in (3.5c). In this case, an additional surface integral has to be included; cf. Eq. (B.1c).

4 Algebraic solver by geometric multigrid preconditioned GMRES iterations

On the algebraic level, the variational problem (3.5) leads to linear systems of equations with complex block structure, in particular if higher order (piecewise) polynomial degrees k for the approximation of the temporal variable are involved. This demands for a robust and efficient linear solver, in particular in the three-dimensional case $\Omega \subset \mathbb {R}^3$. For solving (3.5) we consider using flexible GMRES iterations [65] that are preconditioned by a V-cycle geometric multigrid method (GMG) based on a local Vanka smoother. In [4], the GMG preconditioned GMRES solver is further embedded in a Newton iteration for solving space-time finite element discretizations of the Navier–Stokes system. Thus, nonlinear extensions of the prototype model (1.1) become feasible as well by our approach. For non-smooth nonlinearities, fixed point iterations, like the L-scheme [50], can be used instead of Newton’s method.

To derive the algebraic form of (3.5), the discrete functions $\varvec{u}_{\tau ,h}$, $\varvec{v}_{\tau ,h}$ and $p_{\tau ,h}$ are represented in a Lagrangian basis $\{\chi _{n,m}\}_{m=1}^{k+1}\subset {\mathbb {P}}_k(I_n;\mathbb {R})$ with respect to the $(k+1)$ Gauss–Radau quadrature points of $I_n$, such that

$$\begin{aligned} \varvec{u}_{\tau ,h}{}_{|I_n}(\varvec{x},t)&= \sum _{m=1}^{k+1} \varvec{u}_{n,m}(\varvec{x}) \chi _{n,m}(t)\,, \end{aligned}$$

(4.1a)

$$\begin{aligned} \varvec{v}_{\tau ,h}{}_{|I_n}(\varvec{x},t)&= \sum _{m=1}^{k+1} \varvec{v}_{n,m}(\varvec{x}) \chi _{n,m}(t)\,, \end{aligned}$$

(4.1b)

$$\begin{aligned} p_{\tau ,h}{}_{|I_n}(\varvec{x},t)&= \sum _{m=1}^{k+1} p_{n,m}(\varvec{x}) \chi _{n,m}(t)\,. \end{aligned}$$

(4.1c)

The resulting coefficient functions $(\varvec{u}_{n,m},\varvec{v}_{n,m},p_{n,m})\in \varvec{V}_h\times \varvec{V}_h\times Q_h$, for $m=1,\ldots ,k+1$, are developed in terms of the finite element basis of $\varvec{V}_h$ and $Q_h$, respectively. Letting $\varvec{V}_h= {\text {span}}\{\varvec{\psi }_1,\ldots ,\varvec{\psi }_R \}$ and $Q_h={\text {span}}\{\xi _1,\ldots ,\xi _S \}$, we get that

$$\begin{aligned} \varvec{u}_{n,m}(\varvec{x}) =&\sum _{r=1}^R u^{(r)}_{n,m} \varvec{\psi }_r(\varvec{x}), \end{aligned}$$

(4.2a)

$$\begin{aligned} \varvec{v}_{n,m}(\varvec{x}) =&\sum _{r=1}^R v^{(r)}_{n,m} \varvec{\psi }_r(\varvec{x}), \end{aligned}$$

(4.2b)

$$\begin{aligned} p_{n,m}(\varvec{x}) =&\sum _{s=1}^S p^{(s)}_{n,m}\, \xi _s(\varvec{x}). \end{aligned}$$

(4.2c)

For the coefficients of the expansions in (4.2a) we define the subvectors

$$\begin{aligned} \varvec{U}_{n,m}&= \big (u^{(1)}_{n,m},\ldots ,u^{(R)}_{n,m} \big )^\top \,, \;\; \varvec{V}_{n,m}= \big (v^{(1)}_{n,m},\ldots ,v^{(R)}_{n,m} \big )^\top , \end{aligned}$$

(4.3a)

$$\begin{aligned} \varvec{P}_{n,m}&= \big (p^{(1)}_{n,m},\ldots ,p^{(S)}_{n,m} \big )^\top \,, \quad \text {for}\;\; m=1,\ldots ,k+1\,, \end{aligned}$$

(4.3b)

of the degrees of freedom for all Gauss–Radau quadrature points and the global solution vector on $I_n$ by

$$\begin{aligned} \varvec{X}_n^\top= & {} \big ((\varvec{V}_{n,1})^\top ,(\varvec{U}_{n,1})^\top ,(\varvec{P}_{n,1})^\top ,\ldots , \nonumber \\{} & {} (\varvec{V}_{n,k+1})^\top ,(\varvec{U}_{n,k+1})^\top ,(\varvec{P}_{n,k+1})^\top \big ). \end{aligned}$$

(4.4)

We note that $\varvec{X}_n$ comprises the (spatial) degrees of freedom for all $(k+1)$ Gauss–Radau nodes, representing the Lagrange interpolation points in time, of the subinterval $I_n$. The approximations at these time points will be computed simultaneously. Substituting (4.1) and (4.2a) into (3.5) and choosing in (3.5) the test basis $\{\chi _{n,m}\varvec{\psi }_r,\chi _{n,m}\varvec{\psi }_r,\chi _{n,m}\xi _s\}$, for $m=1,\ldots ,k+1$, $r=1,\ldots , R$ and $s=1,\ldots ,S$, built from the trial basis in (4.1) and (4.2a), we obtain the following algebraic system.

Problem 4.1

(Algebraic $I_n$-problem) For the vector $\varvec{X}_n$, defined in (4.4) along with (4.3), of the coefficients of the expansions (4.2a) solve

$$\begin{aligned} \varvec{A}_n \varvec{X}_n = \varvec{F}_n, \end{aligned}$$

(4.5)

where the matrix $\varvec{A}_n$ exhibits the $(k+1)\times (k+1)$ block structure

$$\begin{aligned} \varvec{A}_n = \big (\varvec{A}_{a,b}\big )_{a,b=1}^{k+1} \end{aligned}$$

(4.6)

with block submatrices $\varvec{A}_{a,b}$, for $a,b=1,\ldots ,k+1$, defined by

$$\begin{aligned} \varvec{A}_{a,b} = \left( \begin{array}{@{}ccc@{}} - \varvec{M}^{0,\varvec{V}_h}_{{a}, {b}} &{} \varvec{M}^{1,\varvec{V}_h}_{{a},{b}} &{} \varvec{0} \\ \varvec{M}^{1,\varvec{V}_h}_{{a},{b}} &{} \varvec{S}_{{a},{b}} + \varvec{N}^{A}_{{a},{b}} &{} \varvec{C}^\top _{{a},{b}} \\ \varvec{0} &{} - \varvec{C}_{{a},{b}} &{} \varvec{M}^{1,Q_h}_{a,b} + \varvec{B}_{a,b} + \varvec{N}^B_{a,b} \end{array}\right) .\nonumber \\ \end{aligned}$$

(4.7)

For the choice $Q_h^l=Q_h^{l,\text {cont}}$ in (2.6), the explicit representation of the submatrices in (4.7) reads as

$$\begin{aligned} \begin{aligned} \big (\varvec{M}^{1,\varvec{V}_h}_{{a},{b}}\big )_{i,j}&:= Q_n\big (\langle \rho \partial _t \chi _{n,b} \varvec{\psi }_{j}, \chi _{n,a} \varvec{\psi }_{i} \rangle \big ) \\&\quad + \langle \rho \chi _{n,b}(t_{n-1}^+) \varvec{\psi }_{j}, \chi _{n,a}(t_{n-1}^+) \varvec{\psi }_{i} \rangle , \\ \big (\varvec{M}^{0,\varvec{V}_h}_{{a},{b}}\big )_{i,j}&:= Q_n \big (\langle \rho \chi _{n,b} \varvec{\psi }_{j}, \chi _{n,a} \varvec{\psi }_{i} \rangle \big ), \\ \big (\varvec{S}_{{a},{b}}\big )_{i,j}&: = Q_n \big (\langle \varvec{C} \varvec{\varepsilon }(\chi _{n,b}\varvec{\psi }_{j}), \varvec{\varepsilon }(\chi _{n,a} \varvec{\psi }_{i}) \rangle \\&\quad + \langle \varvec{C} \varvec{\varepsilon }(\chi _{n,b}\varvec{\psi }_{j}) \varvec{n}, \chi _{n,a} \varvec{\psi }_{i} \rangle _{\Gamma ^D_{\varvec{u}}} \big ), \\ \big (\varvec{N}^{A}_{{a},b}\big )_{i,j}&:= Q_n \big (a_\gamma (\chi _{n,b} \varvec{\psi }_{i},\chi _{n,a} \varvec{\psi }_{i})\big ) \end{aligned} \end{aligned}$$

as well as

$$\begin{aligned} \big (\varvec{C}_{{a},{b}}\big )_{r,j}&:= Q_n \big (-\alpha \langle \nabla \cdot (\chi _{n,b} \varvec{\psi }_{j}), \chi _{n,a} \xi _r \rangle \\&\quad +\alpha \langle \chi _{n,b} \varvec{\psi }_{j} \cdot \varvec{n} , \chi _{n,a} \xi _r \rangle _{\Gamma ^D_{\varvec{u}}}\big )\,,\\ \big (\varvec{M}^{1,Q_h}_{{a},{b}}\big )_{r,s}&:= Q_n\big (\langle c_0 \partial _t \chi _{n,b} \xi _s, \chi _{n,a} \xi _r \rangle \big ) \\&\quad +\langle c_0 \chi _{n,b}(t_{n-1}^+) \xi _{s}, \chi _{n,a}(t_{n-1}^+) \xi _{r} \rangle \big ) \end{aligned}$$

and

$$\begin{aligned} \big (\varvec{B}_{{a},{b}}\big )_{r,s}&:= Q_n \big (\langle \varvec{K} \nabla (\chi _{n,b}\xi _{s}), \nabla (\chi _{n,a} \xi _{r}) \rangle \\&\quad - \langle \varvec{K} \nabla (\chi _{n,b}\varvec{\xi }_{s}) \cdot \varvec{n} , \chi _{n,a} \xi _{r} \rangle _{\Gamma ^D_{p}} \big )\,, \\ \big (\varvec{N}^B_{{a},{b}}\big )_{r,s}&:= Q_n \big (b_\gamma (\chi _{n,b} \xi _{s},\chi _{n,a} \xi _{r})\big )\,, \end{aligned}$$

with $a_\gamma (\cdot ,\cdot )$ and $b_\gamma (\cdot ,\cdot )$ being defined in (3.3), for $i,j=1,\ldots , R$ and $r,s=1,\ldots , S$. The vector $\varvec{F}_n$ in (4.5) is defined similarly, according to (3.5) along with (3.4). Its definition is skipped here for brevity. We note that (3.1a) is still multiplied by $\rho >0$ for the definition of the first row in (4.7). Multiplying the first block row in (4.7) by $(-1)$ and recalling the symmetry of $\varvec{M}^{1,\varvec{V}_h}_{{a},{b}}$, for $a,b=1,\ldots k$, the upper left $2\times 2$ block subsystem in (4.7) itself admits the structure of the matrix (1.3). This might be exploited in future theorectical analyses of the solver or an improvement of the GMRES iterations (cf. [14, 36]), but is beyond the scope of the current work. For the family of finite element pairs with $Q_h^l=Q_h^{l,\text {disc}}$ in (2.6), the definition of $B_{a,b}$ has to be adjusted to the second of the options in (3.2c). Further, the contribution $\varvec{N}^B_{a,b}$ has to be omitted.

Increasing values of the piecewise polynomial degree in time k enhance the complexity of the block structure of the system matrix $\varvec{A}_n$ in (4.6) along with (4.7). They impose an additional facet of challenge on the construction of efficient block preconditioners for (4.5). We solve the linear system (4.5) for the unknown $\varvec{X}_n$ on the subinterval $I_n$ by flexible GMRES iterations [65] that are preconditioned by a V-cycle geometric multigrid (GMG) algorithm [76]. The ingredients of the GMRES–GMG approach are summarized in Alg. 4.1.

In our computational studies of Sect. 5, the standard choice is $J_{\max }=4$ and the parallel direct solver is SuperLU_DIST [53]. For the restriction and prolongation operators the deal.II classes MultiGrid and MGTransferPrebuilt are used. For the deal.II finite element library we refer to [7]. For details of the parallel implementation by the message passing interface (MPI) protocol of our GMG approach we also refer to [3].

The choice of the smoothing operator in the GMG method is extremely diverse; cf., e.g. [28, 47] for a further discussion. We use a collective smoother of Vanka type that is based on the solution of small local problems. Compared to the Navier–Stokes system [3], the dynamic Biot problem (1.1) requires adaptations in the construction of the local Vanka smoother. In inf-sup stable discretizations of the Navier–Stokes equations by the ${\mathbb {Q}}_r^d/{\mathbb {P}}_{r-1}^{\text {disc}}$, $r\ge 2$, family of finite element spaces no coupling between the pressure degrees of freedom is involved due to the discontinuous approximation of the pressure variable. This feature leads to excellent performance properties of the Vanka smoother [3]. In contrast to this, the discretization (3.5c) of (1.1b) by $\mathbb P_{r-1}^{\text {disc}}$, $r\ge 2$, elements involves a coupling between degrees of freedom of the scalar variable p due to the presence of the face integrals over the average and jump in the second of the options in (3.2c) for the definition of the bilinear form $B_\gamma$. This coupling reduces the smoothing properties of elementwise Vanka operator. For the ${\mathbb {Q}}_{r-1}$, $r\ge 2$, family of elements for the scalar variable p, leading to the first of the options in (3.2c), the coupling of degrees of freedom of p by its continuous in space approximation and the loss of smoothing properties arise likewise. As a remedy, for both families of inf-sup stable approximation in (3.5) the local Vanka smoother is computed on overlapping patches of adjacent elements. In addition, an averaging of the patchwise updates is done after the Vanka smoother has been applied on all of them.

To construct the patchwise Vanka, we let on the mesh partition ${\mathcal {T}}_l$, for $l=1,\ldots , L$, of the multigrid hierarchy the linear system, to be solved, be represented by

$$\begin{aligned} \varvec{A}_l \varvec{d}_l = \varvec{b}_l, \quad \text {for } \;\; l=1,\ldots , L. \end{aligned}$$

(4.8)

To each grid node $\xi _l^m$, for $m = 1\,,\ldots \,, M_l$, where $M_l$ denotes the total number of grid nodes on the mesh partition ${\mathcal {T}}_l$, we built a patch of adjacent elements such that

$$\begin{aligned} P_l^m:= \bigcup \{ K \in {\mathcal {T}}_l \mid \xi _l^m \in {\overline{K}} \}, \quad \text {for} \;\;m=1,\ldots , M_l. \end{aligned}$$

(4.9)

In two space dimensions $P_l^m$ is built from four elements, if $\xi _l^m \not \in \partial \Omega$. In three space dimensions, $P_l^m$ has eight elements, if $\xi _l^m \not \in \partial \Omega$. If $\xi _l^m \in \partial \Omega$, patches of less elements are obtained. On ${\mathcal {T}}_l$, let $Z_l$ denote the index set of all global degrees of freedom with cardinality $C_l$,

$$\begin{aligned} C_l:= {\text {card}}(Z_l). \end{aligned}$$

Let $Z_l(P_l^m)$ denote the subset of $Z_l$ all global degrees of freedom linked to the patch $P_l^m$, i.e. degrees of freedom of $\varvec{u}_{\tau ,h}$, $\varvec{v}_{\tau ,h}$ and $p_{\tau ,h}$ for the $(k+1)$ Gauss–Radau time points of $I_n$. The cardinality of $Z_l(P_l^m)$ is denoted by $C_l^m$,

$$\begin{aligned} C_l^m: = {\text {card}}(Z_l(P_m^l)), \quad \text {for} \;\; m=1,\ldots , M_l. \end{aligned}$$

Further, we denote the index set of all local degrees of freedom on $P_l^m$ by ${\hat{Z}}_l(P_m^l):=\{0,\ldots ,C_l^m-1\}$. For the notation, we note that the set ${\hat{Z}}_l(P_m^l)$ depends on the cardinality of the patch $P_l^m$. For a given patch $P_l^m$ and a local degree of freedom with number ${\hat{\mu }} \in {\hat{Z}}_l(P_m^l)$ let the mapping

$$\begin{aligned}{} & {} {\text {dof}}:{\mathcal {T}}_l\times {\hat{Z}}_l(P_m^l) \rightarrow Z_l,\nonumber \\{} & {} \qquad \mu = \textrm{dof}(P_l^m,{\hat{\mu }})\in Z_l(P_l^m), \end{aligned}$$

(4.10)

yield the uniquely defined global number $\mu \in Z_l$. Finally, we put $R = {\text {dim}}\, \varvec{V}_h$ and $S = {\text {dim}}\, Q_h$.

We are now in a position to define the local Vanka operator for the patch $P_l^m$ in an exact mathematical way; cf., e.g. [3, 40, 45, 80].

Definition 4.2

(Patchwise Vanka smoother) For a patch $P_l^m$, for $m\in \{1,\ldots ,M_l\}$, let the $P_l^m$-local restriction operator $\varvec{R}_K:\mathbb {R}^{(k+1)\cdot (2R+S)} \rightarrow \mathbb {R}^{C_l^m}$ be defined by

$$\begin{aligned}{} & {} (\varvec{R}_{P_l^m} \varvec{d})[{\hat{\mu }}] = \varvec{d}[{\text {dof}}(P_l^m,{\hat{\mu }})], \nonumber \\{} & {} \quad \text {for} \;\; {\hat{\mu }} \in {\hat{Z}}_l(P_l^m), \end{aligned}$$

(4.11)

and, for the system matrix $\varvec{A}$ of (4.8), the patch system matrix $\varvec{A}_{P_l^m}\in \mathbb {R}^{C_l^m,C_l^m}$ by

$$\begin{aligned}{} & {} \varvec{A}_{P_l^m}[\hat{\nu }][\hat{\mu }]:= \varvec{A}_l[{\text {dof}}(P_l^m,{\hat{\nu }})][{\text {dof}}(P_l^m,{\hat{\mu }})],\nonumber \\{} & {} \text {for}\;\; {\hat{\nu }},{\hat{\mu }} \in {\hat{Z}}_l(P_l^m). \end{aligned}$$

(4.12)

The local Vanka operator $\varvec{S}_{P_l^m}: \mathbb {R}^{(k+1) \, \cdot \, (2R+S)} \rightarrow \mathbb {R}^{C^l_m}$ is defined by

$$\begin{aligned} \varvec{S}_{P_l^m}(\varvec{d}) = \varvec{R}_ {P_l^m} \varvec{d} + \omega \, \varvec{A}_{P_l^m}^{-1} \, \varvec{R}_{P_l^m} \, (\varvec{b}_l-\varvec{A}_l \varvec{d}), \end{aligned}$$

(4.13)

with some underrelaxation factor $\omega >0$.

In the numerical experiments of Sect. 5 we choose $\omega = 0.7$. The $P_l^m$-local restriction operator (4.11) assigns to a global defect vector $\varvec{d}\in \mathbb {R}^{(k+1)\cdot (2R+S)}$ the local block vector $\varvec{R}_K \varvec{d}\in \mathbb {R}^{C_l^m}$ that contains all components of $\varvec{d}$ that are associated with all degrees of freedom (for all $(k+1)$ Gauss–Radau points of $I_n$) belonging to the patch $P_l^m$. For the computation of the inverse $(\varvec{A}_{P_l^m})^{-1}$ in (4.13) we use LAPACK routines. The application of the smoother for (4.8) on the mesh partition ${\mathcal {T}}_l$ is summarized in Algorithm 4.2.

In line 1 of Alg. 4.2 the defect and solution vector is pre-initialized with $\varvec{0}$. In line 4 the loop over all $J_{\max }$ smoothing steps starts. In line 4 and 5 the counter vector $\varvec{p}$ for the number of updates of the degrees of freedom and the auxiliary vector $\varvec{z}$ are initialized with $\varvec{0}$. In line 7 the loop over all patches $P_l^m$, for $m=1,\ldots ,M$, starts. In line 8 the local Vanka smoother is applied on patch $P_l^m$ to the current iterate $\varvec{d}$ of the defect vector and the image is stored in the local patch vector $\varvec{y}$. In line 10 the local vector $\varvec{y}$ is assigned to an auxiliary global vector $\varvec{z}$ by the $P_l^m$-dependent extension operator $\varvec{E}_{P_l^m}:\mathbb {R}^{C_l^m} \rightarrow \mathbb {R}^{(k+1)\cdot (2R+S)}$,

$$\begin{aligned} (\varvec{E}_{P_l^m} \varvec{y})[\mu ] = \left\{ \begin{array}{@{}ll} y[{{\hat{\mu }}}], &{} \text {if}\; \exists {\hat{\mu }} \in {\hat{Z}}_l(P_l^m):\; \mu = {\text {dof}}(K,{\hat{\mu }}), \\ 0, &{} \text {if}\; \mu \not \in Z_l(P_l^m).\end{array} \right. \end{aligned}$$

In line 11 the components of the counter $\varvec{p}$ are incremented for the (global) indices associated with the degrees of freedom of the patch $P_l^m$ processed in the loop. Finally, in line 15 the arithmetic mean of the local (patchwise) updates $\varvec{z}$ is assigned to the update of the global defect vector $\varvec{d}$.

Regarding the performance of Alg. 4.2 and the overall GMRES–GMG approach we note the following.

Remark 4.3

• Averaging of the patchwise updates implemented in line 10 and 15 of Alg. 4.2, that is used instead of overwriting successively the (global) degrees of freedom within the patch loop starting in line 7, is essential and ensures the convergence and efficiency of the local Vanka smoother and, thereby, the desired performance of the overall GMRES–GMG linear solver. Without the averaging operation we encountered convergence problems of the GMRES–GMG solver for the experiments of Sect. 5.

• Likewise, the application of the Vanka smoother on the patches (4.9), instead of using an elementwise Vanka smoother on the element K, ensures its smoothing properties. The latter would lead to systems (4.13) of smaller dimension, however fails to smoothen errors. This is expected to be due coupling of the degrees of freedom of the scalar variable p in the spatial discretizations used here.

5 Numerical studies

In this section we study numerically the proposed space-time finite element and GMRES–GMG solver approach with respect to its computational and energy efficiency. Firstly, we demonstrate the accuracy of solutions in terms of convergence rates for a prescribed solution. Secondly, we analyze the convergence of the discretization for goal quantities of physical interest and the robustness of the GMRES–GMG solver in a two-dimensional test setting that is of interest in practice, for instance, in geomechanics for elucidating suburface flow dynamics or in biomedical engineering for ultrasonic studies of bone or other calcified tissues to diagnose a variety of skeletal disorders. Finally, the investigations are extended to a challenging three-dimensional test case. Here a soft material with application in brain poromechanics [25] is used. The parallel scaling properties of our implementation are also investigated. Beyond these studies of classical performance engineering, the energy efficiency of the approach is considered further.

Table 1 $L^2(L^2)$ and $L^\infty (L^2)$ errors and experimental orders of convergence (EOC) for (5.1) with temporal polynomial degree $k=2$ and spatial degree $r=3$ for local spaces ${\mathbb {Q}}_r^2/{\mathbb {P}}_{r-1}^{\text {disc}}$

Table 2 $L^2(L^2)$ and $L^\infty (L^2)$ errors and experimental orders of convergence (EOC) with temporal polynomial degree $k=3$ and spatial degree $r=4$ for local spaces ${\mathbb {Q}}_r^2/{\mathbb {P}}_{r-1}^{\text {disc}}$

The implementation of the numerical scheme and the GMRES–GMG solver was done in an in-house high-performance frontend solver for the deal.II library [7]. For details of the parallel implementation of the geometric multigrid solver we refer to [3]. In all numerical experiments, the stopping criterion for the GMRES iterations is an absolute residual smaller than 1e-8. The computations were performed on a Linux cluster with 571 nodes, each of them with 2 CPUs and 36 cores per CPU. The CPUs are Intel Xeon Platinum 8360Y with a base frequency of 2.4 GHz, a maximum turbo frequency of 3.5 GHz and a level 3 cache of 54 MB. Each node has 252 GB of main memory.

Table 3 $L^2(L^2)$ and $l^\infty (L^2)$ errors and experimental orders of convergence (EOC) for (5.3) with temporal polynomial degree $k=2$ and spatial degree $r=5$ for local spaces ${\mathbb {Q}}_r^2/{\mathbb {Q}}_{r-1}$, showing superconvergence of order $2k+1$ in the discrete time nodes $t_n$, i.e., w.r.t. the norm $\Vert \cdot \Vert _{l^\infty (L^2)}$ defined in (5.2)

5.1 Accuracy of the discretization: experimental order of convergence

We study (1.1) for $\Omega =(0,1)^2$ and $I=(1,2]$ and the prescribed solution

$$\begin{aligned}{} & {} {\varvec{u}}({\varvec{x}}, t) = \phi ({\varvec{x}}, t) {\varvec{E}}_2 \;\; \nonumber \\{} & {} \text {and}\;\;p({\varvec{x}}, t) = \phi ({\varvec{x}}, t) \;\; \nonumber \\{} & {} \text {with}\;\; \phi ({\varvec{x}}, t) = \sin (\omega _1 t^2) \sin (\omega _2 x_1) \sin (\omega _2 x_2) \end{aligned}$$

(5.1)

and $\omega _1=\omega _2 = \pi$. We put $\rho =1.0$, $\alpha =0.9$, $c_0=0.01$ and ${\varvec{K}}={\varvec{E}}_2$ with the identity $\varvec{E}_2\in \mathbb {R}^{2,2}$. For the fourth order elasticity tensor ${\varvec{C}}$, isotropic material properties with Young’s modulus $E=100$ and Poisson’s ratio $\nu =0.35$, corresponding to the Lamé parameters $\lambda = 86.4$ and $\mu = 37.0$, are chosen. For an experiment with larger values of $\lambda$ and $\mu$ we refer to Table 10 in the appendix. In our experiments, the norm of $L^\infty (I;L^2)$ is approximated by computing the function’s maximum value in the Gauss quadrature nodes $t_{n,m}$ of $I_n$, i.e.,

$$\begin{aligned}{} & {} \Vert w\Vert _{L^\infty (I;L^2)} \approx \max \{ \Vert w_{|I_n}(t_{n,m})\Vert \mid m=1,\ldots ,M,\\{} & {} n=1,\ldots ,N\}, \quad \text {with}\;\; M=100. \end{aligned}$$

We study the space-time convergence behavior of the scheme (3.5). For this, the domain $\Omega$ is decomposed into a sequence of successively refined meshes of quadrilateral finite elements. The spatial and temporal mesh sizes are halved in each of the refinement steps. The step sizes of the coarsest space and time mesh are $h_0=1/(2\sqrt{2})$ and $\tau _0=0.1$. We choose the polynomial degree $k=2$ and $r=3$, such that discrete solutions $\varvec{u}_{\tau ,h}, \varvec{v}_{\tau }\in Y_\tau ^2(\varvec{V}_h)$, $p_{\tau ,h}\in Y_\tau ^2(Q_h)$ with local spaces ${\mathbb {Q}}_3^2/ P_2^{\text {disc}}$ are obtained, as well as $k=3$ and $r=4$ with $\varvec{u}_{\tau ,h}, \varvec{v}_{\tau }\in Y_\tau ^3(\varvec{V}_h)$ and $p_{\tau ,h}\in Y_\tau ^3(Q_h)$ and local spaces ${\mathbb {Q}}_4^2/{\mathbb {P}}_3^{\text {disc}}$; cf. (2.2), (2.5) and (2.6). The calculated errors and corresponding experimental orders of convergence are summarized in Tables 1 and 2, respectively. The error is measured in the quantities associated with the energy of the system (1.1); cf. [43, p. 15] and [11]. Tables 1 and 2 nicely confirm the optimal rates of convergence with respect to the polynomial degrees in space and time of the overall approach. A notable difference in the convergence behavior between the pairs ${\mathbb {Q}}_r^2/{\mathbb {P}}_{r-1}^{\text {disc}}$ and ${\mathbb {Q}}_r^2/{\mathbb {Q}}_{r-1}$ of local spaces for the discretization of the spatial variables is not observed. For completeness, we summarize in Appendix C the convergence results obtained for the pair ${\mathbb {Q}}_r^2/{\mathbb {Q}}_{r-1}$ of spaces of the Taylor–Hood family. A minor superiority of the pair ${\mathbb {Q}}_r^2/{\mathbb {P}}_{r-1}^{\text {disc}}$ over the pair ${\mathbb {Q}}_r^2/{\mathbb {Q}}_{r-1}$ is only seen in the approximation of the scalar variable p. The coincidence of the convergence results also holds for the application of Problem B.1 instead of Problem 3.1. The two discrete problems differ from each other by the discretization of the term $\alpha \nabla \cdot \partial _t \varvec{u}$ in (1.1b).

Next, we show numerically that the time discretization is even superconvergent of order $2k+1$ in the discrete time nodes $t_n$, for $n=1,\ldots , N$. For this, we introduce the time mesh dependent norm

$$\begin{aligned} \Vert w\Vert _{l^\infty (L^2)}:= \max \{ \Vert w(t_n)\Vert \mid n=1,\ldots , N\}. \end{aligned}$$

(5.2)

We prescribe the solution

$$\begin{aligned}{} & {} {\varvec{u}}({\varvec{x}}, t) = \begin{pmatrix} -2 (x-1)^2 x^2 (y-1) y (2 y-1) \sin (\omega _1 t) \\ 2 (x-1) x (2 x-1) (y-1)^2 y^2 \sin (\omega _1 t) \end{pmatrix}, \nonumber \\{} & {} p({\varvec{x}}, t) = -2 (x-1)^2 x^2 (y-1) y (2 y-1) \sin (\omega _2 t) \end{aligned}$$

(5.3)

with $\omega _1=40\cdot \pi$ and $\omega _2 = 10\cdot \pi$. We put $\rho =1.0$, $\alpha =0.9$, $c_0=0.01$ and ${\varvec{K}}={\varvec{E}}_2$ with the identity $\varvec{E}_2\in \mathbb {R}^{2,2}$. For the elasticity tensor ${\varvec{C}}$, isotropic material properties with Young’s modulus $E=100$ and Poisson’s ratio $\nu =0.35$ are used. For the local spaces we choose the pair ${\mathbb {Q}}_5^2/{\mathbb {Q}}_{4}$ such that, for any $t\in [0,T]$, the solution (5.3) belongs to the discrete spaces $\varvec{V}_h$ and $Q_h$, respectively, and its spatial approximation is exact. This simplification is done here since we aim to study the convergence of the temporal discretization only. In the experiment, we choose $k=2$ such that discrete solutions $\varvec{u}_{\tau ,h}, \varvec{v}_{\tau }\in Y_\tau ^2(\varvec{V}_h)$ and $p_{\tau ,h}\in X_\tau ^2(Q_h)$ are obtained. We use a spatial mesh that consists of 16 cells with $h=1/(2\sqrt{2})$ and set $\tau _0=0.02$. The calculated errors and corresponding experimental orders of convergence are summarized in Table 3. Superconvergence of order $2k+1$ in the discrete time nodes is clearly observed in the second of the arrays in Table 3.

5.2 Computational efficiency: accuracy of goal quantities and convergence of the GMRES–GMG solver in a 2d test case

For a two-dimensional test problem we study the potential of the proposed approach to compute reliably and efficiently goal quantities of physical interest. We also document the performance properties of the GMRES-GMG solver of Sect. 4 for the applied space-time finite element methods. Even though the test setting is still of academic nature, it is related to problems of practical interest in civil engineering (subsurface dynamics) or biomedical engineering (cf. [81]). In the numerical investigations a stiff material is assumed whereas in Sect. 5.3 a softer material will be studied. This is done for the sake of considering also a range of materials.

Beyond the boundary conditions (1.1d) and (1.1e), we also apply (homogeneous) directional (or componentwise) boundary conditions for $\varvec{u}$ on some part $\Gamma ^d_{\varvec{u}}\subset \partial \Omega$. The directional boundary conditions read as

$$\begin{aligned}{} & {} \varvec{u} \cdot \varvec{n} = 0 \qquad \text {and} \qquad (\varvec{\sigma }(\varvec{u})\varvec{n}) \cdot \varvec{t}_i = 0, \nonumber \\{} & {} \quad \text {for}\;\; i=1,\ldots , d-1, \quad \text {on}\;\; \Gamma ^d_{\varvec{u}} \times (0,T], \end{aligned}$$

(5.4)

for the stress tensor $\varvec{\sigma }(\varvec{u}) = \varvec{C} \varvec{\varepsilon }(\varvec{u})$ and the unit basis vectors $\varvec{t}_i$, for $i=1,\ldots ,d-1$, of the tangent space at $\varvec{x} \in \Gamma ^d_{\varvec{u}}$. In the definition of $A_\gamma$ in (3.2a) and (3.3a), the conditions (5.4) still need to be implemented properly. By the second of the conditions in (5.4) we get for the second of the terms on the right-hand of (3.2a) that

$$\begin{aligned}{} & {} \langle \varvec{C} \varepsilon (\varvec{u}_{\tau ,h})\varvec{n}, \varvec{\chi }_{\tau ,h} \rangle _{\Gamma _{\varvec{u}}^l} \nonumber \\{} & {} = \langle \varvec{C} \varepsilon (\varvec{u}_{\tau ,h}) \varvec{n} \cdot \varvec{n},\varvec{n} \cdot \varvec{\chi }_{\tau ,h} \rangle _{\Gamma _{\varvec{u}}^d}. \end{aligned}$$

(5.5)

For the boundary part ${\Gamma ^d_{\varvec{u}}}$ we then put, similarly to (3.3a),

$$\begin{aligned}{} & {} a^d_\gamma (\varvec{w},\varvec{\chi }_{h}):= - \langle \varvec{w}\cdot \varvec{n}, \varvec{C} \varepsilon (\varvec{\chi }_{h}) \varvec{n} \cdot \varvec{n}\rangle _{{\Gamma ^d_{\varvec{u}}}} \\{} & {} \quad + \gamma _a\, h^{-1} \langle \varvec{w}\cdot \varvec{n}, \varvec{\chi }_h \cdot \varvec{n} \rangle _{\Gamma ^d_{\varvec{u}}}, \end{aligned}$$

while leaving $a_\gamma$ unmodified for the part ${\Gamma ^D_{\varvec{u}}}$ where Dirichlet boundary conditions are prescribed for $\varvec{u}$. In its entirety, we thus have that $a_\gamma (\cdot ,\cdot ):= a_\gamma ^D (\cdot ,\cdot )+a_\gamma ^d (\cdot ,\cdot )$ with $a_\gamma ^D (\cdot ,\cdot )$ being defined by the right-hand side of (3.3a). By the arguments of Appendix A, the coercivity of the resulting form $A_\gamma$ is still ensured.

Fig. 2

Goal quantity $G_{\varvec{u}}$ of (5.7) for a sequence of successively refined meshes (left) and different polynomial orders of the STFEM on a fixed mesh (right)

Table 4 Maximum and minmum of the goal quantities (5.7) in the subinterval $t\;\in \;[3.5,4.5]$ of the simulation time $t\;\in \;[0,4.5]$ for different space-time mesh refinements and approximation orders

For our experiments, we consider the rectangular domain $\Omega =(0,0.5)\times (0,1)\subset \mathbb {R}^2$ with boundary segments $\Gamma _{\varvec{u}}^d=\{0\}\times (0,1)\;\bigcup \;\{0.5\}\times (0,1)$ and $\Gamma _{\varvec{u}}^N=(0,0.5)\times \{0\}\;\bigcup \; (0,0.5)\times \{1\}$. On the lower and upper part $\Gamma ^N_{\varvec{u}}$ of the boundary we impose in the boundary condition (1.1e) the traction force

$$\begin{aligned}{} & {} \varvec{t}_N = \begin{pmatrix} 0 \\ s(t)\cdot 16x\cdot (x-0.5)\cdot \sin (8\pi t) \end{pmatrix} \nonumber \\{} & {} \text {with} \quad s(t):={\left\{ \begin{array}{ll} 0.5-0.5\cos (4\pi t^2),&{} \text {for } t<0.5, \\ 1,&{} \text {else}, \end{array}\right. } \end{aligned}$$

(5.6)

which amounts to applying a simultaneous compression or decompression force at the upper and lower boundary. For the scalar variable p we prescribe a homogeneous Dirichlet boundary condition (1.1f) on the lower and upper part $\Gamma _{p}^N=(0,0.5)\times \{0\}\;\bigcup \; (0,0.5)\times \{1\}$ of $\partial \Omega$ and a homogeneous Neumann boundary condition (1.1g) else. We put $\rho =1.0$, $\alpha =0.9$, $c_0=0.01$ and ${\varvec{K}}={\varvec{E}}_2$ with the identity $\varvec{E}_2\in \mathbb {R}^{2,2}$. For the elasticity tensor ${\varvec{C}}$, isotropic material properties with Young’s modulus $E=20000$ and Poisson’s ratio $\nu =0.3$; cf. [81]. The final simulation time is $T=4.5$. As goal quantities of this problem, we measure the magnitude of the displacement variable in normal direction as well as the pressure on a cross section plane $\Gamma _m$, given by

$$\begin{aligned} G_{\varvec{u}}= & {} \int _{\Gamma _m} \varvec{u} \cdot \varvec{n} \, \,\textrm{d}o, \qquad \nonumber \\ G_{p}= & {} \int _{\Gamma _m} p \, \,\textrm{d}o, \qquad \text {for}\;\; \Gamma _m:= (0,0.5)\times \{0.25\}. \end{aligned}$$

(5.7)

We set the step sizes of the coarsest space-time mesh to $h_0=0.125$ and $\tau _0=0.2$. Further mesh levels are obtained by a successive refinement by a factor of two such that $h_i=h_0\cdot 2^{-i}$ and $\tau _i=\tau _0\cdot 2^{-1}$ for $i\in \mathbb {N}$.

In Fig. 2 and Table 4 we illustrate the space-time convergence of the goal quantities and their maximum and minimum value in the final part $t\in [3.5,4.5]$ of the simulation time $t \in [0,4.5]$. Various polynomial orders of the discretization in space and time are used. For brevity, only $G_{\varvec{u}}$ is visualized in Fig. 2. Convergence of the goal quantity is clearly observed even though the differences are not strong in this two dimensional test case. In particular, in Table 4 we observe a dominating temporal discretization error and the gain in accuracy by higher order time discretization. Furthermore, in Table 5 we summarize the average number of GMRES iterations per time step needed to solve the resulting linear system of equations. Since the GMG method with a single V-cyle is used as preconditioner and not as a system solver itself, the average number of GMRES iterations and the wall clock time are considered to be a reasonable measure for the performance of the GMRES–GMG solver. The robustness of the GMRES–GMG solver with respect to the refinement of the space-time mesh and the polynomial degrees in space and time is confirmed. In Table 6 we compare the contribution of asssembling and solving to the wall clock time. Further, the impact of the number of pre- and post-smoothing steps $J_{\max }$ in Alg. 4.2 on the performance of the GMRES–GMG solver is analyzed. The results show increasing wall clock time for higher numbers of smoothing steps. The relatively high computational costs of the GMRES–GMG suggests further performance tuning of the smoother. Nevertheless, the robustness of the GMG preconditioned GMRES iterations in Table 5 underline their potential as efficient black box solver for higher order STFEMs with complex block structures. In our numerical experiments, including the three-dimensional case (cf. Sect. 5.3) and further tests not documented here, we found that choosing $J_{\max }=4$ or $J_{\max }=5$ usually leads to a robust performance.

Table 5 Average number of performed GMG preconditioned GMRES iterations per time step

Table 6 Wall clock Time (WT) accumulated over all time steps and Percentage (P) of total wall clock time for $\mathbb {Q}_3 /\mathbb {P}_2$ space and dG(2) time discretization on mesh $(h_4,\tau _4)$ for different numbers of patchwise Vanka smoothing steps $J_{\max }$; cf. Alg. 4.2

5.3 Computational efficiency: accuracy of goal quantities and convergence of the GMRES–GMG solver in a 3d test case

In this section we extend the numerical studies of the previous section to three space dimensions. For the geometry, we consider the pipe socket that is visualized in Fig. 3a. The pipe has a diameter of $d = 2$ and consists in the $x_1-x_3$ plane of three parts: a quarter annulus with $L_0 = \frac{\pi }{2}$, an upper part, with $L_1 = L_0$ and a lower part with $L_2 = \frac{L_0}{2}$. In contrast to Sect.. 5.2, a soft material of brain poromechanics is now chosen; cf. [25]. We put $\rho =10^3$ [kg/m$^3$], $\alpha =0.49$ [–], $c_0=10^{-6}$ [m$^2$/N] and ${\varvec{K}}= k_0 {\varvec{E}}_3$, with $k_0=1.0$ [m$^2$/Pa] and the identity matrix $\varvec{E}_3\in \mathbb {R}^{3,3}$. For the elasticity tensor ${\varvec{C}}$, isotropic material properties with the Lamé parameter $\lambda =505$ [Pa] and $\mu =216$ [Pa], corresponding to Young’s modulus $E=583.3$ [Pa] and Poisson’s ratio $\nu = 0.35$ [–], are used. The geometry is supposed to mimic brain tissue or some section of an artery with neglecting the blood flow inside. On the curved surface area the directional boundary conditions (5.4) are prescribed. At the top and right outlet of the pipe socket a homogeneous Dirichlet condition for the pressure variable is used. For the displacement variable the traction force of (1.1e) is defined at the top ($x_1 = L_1$) outlet by

$$\begin{aligned} \varvec{t}_N = \left( s(t) \sin (2 \pi t) \left( \sqrt{x_2^2+(x_3-2)^2}-1\right) , 0, 0 \right) ^\top \end{aligned}$$

with s(t) being defined in (5.6), and at the right ($x_3 = L_2$) outlet by

$$\begin{aligned} \varvec{t}_N = \left( 0, 0, s(t) \sin (2 \pi t) \left( \sqrt{(x_1-2)^2+x_2^2}-1\right) \right) ^\top . \end{aligned}$$

We measure the benchmark quantities defined in (5.7) on the cross section plane $\Gamma _m: \left( \varvec{x} - \varvec{p}_m\right) \cdot \varvec{n}_m = 0$, with $\varvec{p}_m = \left( \frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}\right) ^\top$ and $\varvec{n}_m = \left( \frac{\sqrt{3}}{2}, 0, - \frac{1}{\sqrt{2}}\right) ^\top$; cf. Fig. 3a.

We put $I=(0, T]$ with $T = 7$ and set the time step size of the temporal discretization to $\tau = \frac{0.02}{(ref_n-3)}$, where $ref_n$ is the number of spatial refinement levels of the spatial grid, cf. Table 7. The spatial polynomial degree is fixed to $r = 1$ for all simulations (cf. Sect. 2). The calculated profile for $t=T$ of the modulus of the vectorial variable $\varvec{u}$ and the scalar variable p are illustrated in Fig. 3. In Table 7 we summarize characteristic quantities and results of our simulations for various spatial and temporal resolutions and different temporal polynomial degrees of the STFEMs. In Fig. 4 we visualize the computed benchmark quantities (5.7) of some of the simulations over the temporal axis. The benchmark quantities on each refinement level are within the same range for temporal discretizations with polynomial degree $k=1$ and $k=2$, but for $k = 1$ oscillations on $ref_4$ and $ref_5$ are observed, which is not the case for $k = 2$ or $k = 1$ when using a finer time step size ($ref_n = 6$). This indicates the superiority of higher order discretization schemes in the time domain.

Table 7 summarizes the results of our numerical convergence study for the goal quantities. The final row of Table 7 contains the results of the finest simulation that we could run on our hardware. Table 7 and Fig. 4 show that the solution (i.e., the goal quantities) is nearly fully converged. The final column of Table 7 summarizes the convergence statistics of the proposed GMRES–GMG solver. In terms of the average number of iterations per time step the solver is (almost) grid independent. This underlines its capability and robustness for solving efficiently the complex systems arising from space-time finite element discretizations of the considered coupled hyperbolic–parabolic system.

Fig. 3

Problem setting and profile of the solution at time $t = T$

Fig. 4

Goal quantities $G_{\varvec{u}}$ and $G_{p}$ of (5.7) for different discretizations (spatial mesh resolution and polynomial degrees)

5.4 Parallel scaling and energy efficiency

Here, we study briefly the parallel scaling and energy efficiency of our solver. By studying energy consumption, we’d like to draw attention to this emerging dimension in the tuning of algorithms. Energy efficiency broadens the classical hardware-oriented numerics that is applied to enhance the performance of the current method on the target hardware and/or to find other numerical methods to improve the numerical efficiency. For the longer term, energy and power consumption needs to be mapped into a rigorous performance model. Here, we restrict ourselves to illustrate numerically the parallel scaling and energy consumption properties of our implementation that uses Message Passing Interface(MPI) libraries and multi threading parallelism.

Table 7 Computed goal quantities (5.7) for different temporal and spatial approximations

We perform a strong scaling benchmark for the test problem of Sect. 5.3 with $k = 1$, $r = 3$ and ref$_3$ = 3, with 20996620 degrees of freedom in each subinterval $I_n$ on the fine level ${\mathcal {T}}_L$ and 45788 on ${\mathcal {T}}_1$. Throughout, we assign 36 MPI processes to each of the nodes used for the computations and vary the number n of nodes from $n=40$ to $n=200$. For the evaluation of the parallel scaling properties, we compute the parallel speedup of the code (cf. [2]) that is approximated by

$$\begin{aligned} S = \frac{t_{\text {wall}}(n=n_{\min })}{t_{\text {wall}}(n)}, \end{aligned}$$

(5.8)

where $t_{\text {wall}}(n)$ denotes the wall time of the simulation of fixed size on n compute nodes and $t_{\text {wall}}(n=n_{\min })$ is the wall time of the simulation on the minimum number of nodes involved in the scaling experiment. Secondly, we compute similarly the energy ratio by means of

$$\begin{aligned} R = \frac{E(n)}{E(n=n_{\min })}, \end{aligned}$$

(5.9)

where E(n) measures the total energy consumption of the simulation on n nodes. The energy consumption is determined by the Linux cluster workload manager slurm [68]. The energy consumption data is collected from hardware sensors using Intel’s Running Average Power Limit (RAPL) mechanism. It measures the energy consumption of the processor and memory. On our system, the sampling interval of energy consumption is determined by the value of 30 s. Figure 5 illustrates the results of the performance test. For $n=160$ and $n=200$, the parallel scaling properties deteriorate. The reason for this is that due to the fixed problem size of the scaling test with 20996620 degrees of freedom the local problem size on each of the nodes is reduced for an increasing number of nodes such that the processor load decreases and communication increases. However, the (global) problem size is limited by the minimum number $n=40$ of nodes involved in the experiment and the memory (RAM) available on each of these nodes.

Fig. 5

Results of the strong scaling and energy consumption benchmark

To quantify and evaluate the productivity or resource costs of the algorithm and its implementation, we use a simple model for the $\text {Productivity }P = \frac{\text {Output }O}{\text {Input } I}$; cf. [24]. In an economic sense, all outputs should be the desired ones. Therefore, we use the reciprocal of the wall time $t_{\text {wall}}$ as the output $O = \frac{1}{t_{\text {wall}}}$, such that a decrease in $t_{\text {wall}}$ represents an increase of the (abstract) output. As the input I we use the total energy consumption E of the simulation. We scale the result by multiplying P with the constant factor $E(n_{\min }) \cdot t_{\text {wall}}(n_{\min })$ such that the computation with $n = n_{\min }$ has a productivity of $P=1.0$:

$$\begin{aligned} P = \frac{\frac{1}{t_{\text {wall}}(n)}}{E(n)} \cdot E(n_{\min }) \cdot t_{\text {wall}}(n_{\min }) = \frac{S}{R}, \end{aligned}$$

(5.10)

with S and R being defined in (5.8) and (5.9), respectively. The resulting productivity curve of our computations is presented in Fig. 6. In our simulations, the one on 120 compute nodes is the most productive one, that is, the ratio of output (low wall-time) to input (energy) is best. The quadratic interpolation predicts an even slightly increased productivity for 107 nodes ($P = 1.09$). The characteristic quantities of our performance study are also summarized in Table 8.

6 Summary and outlook

In this work we presented and analyzed families of space-time finite element discretizations of the coupled hyperbolic–parabolic system (1.1) modeling, for instance, poroelasticity. The time discretization uses the discontinuous Galerkin method. The space discretization is based on inf-sup stable pairs of finite element spaces with continuous and discontinuous approximation of the scalar variable p. Well-posedness of the discrete problems is proved. For efficiently solving the arising algebraic systems with complex block structure in the case of increasing polynomial degrees of the time discretization a geometric multigrid preconditioner with a local Vanka smoother on patches of finite elements is proposed and studied. The overall approach is evaluated numerically. A convergence proof for our GMG methods to dynamic poroelasticity remains as a work for the future. Parallel scaling and energy consumption is also investigated. Multi-field formulations [12] of (1.1) with an explicit approximation of the stress tensor $\varvec{\sigma }= \varvec{C} \varvec{\varepsilon }$ and the flux vector $\varvec{q}=-\varvec{K} \nabla p$ might be advantageous for applications of (1.1) in that their prediction are of interest; cf. [12, 29]. The design of tailored iterative solvers for suitable space-finite element approximations of such systems becomes even more challenging due to the increasing complexity of the system’s block structure. The feasibility of Vanka-type smoothers needs to reconsidered. Such type of approaches remain as a work for the future.

Fig. 6

Piecewise quadratic interpolation of the productivity function (5.10)

Table 8 Computed quantities of the scaling and performance benchmark

Appendices

Appendix

Discrete coercivity

Here, we prove the discrete coercivity of the bilinear form $A_\gamma$ defined in (3.2a) along with (3.3a). For this we introduce the mesh- and parameter-dependent norm

$$\begin{aligned}{} & {} \Vert \varvec{v}_h \Vert _{h,{\widetilde{\gamma }}_a}:= \Big (\Vert \varepsilon (\varvec{v}_h) \Vert ^2 + {\widetilde{\gamma }}_a \, h^{-1}\Vert \varvec{v}_h \Vert _{\Gamma ^D_{\varvec{u}}}^2\Big )^{1/2}, \quad \text {for}\;\; \varvec{v}_h \in \varvec{V}_h,\nonumber \\ \end{aligned}$$

(A.1)

with some parameter ${\widetilde{\gamma }}_a> 0$. Its choice is addressed below. The norm property of (A.1) is ensured by a variant of Korn’s inequality; cf. [20, Eq. (1.19)]. We recall the well-known inverse inequality (cf. [75, p. 28])

$$\begin{aligned} \Vert \varvec{\varepsilon }(\varvec{v}_h) \varvec{n} \Vert _{\Gamma ^D_{\varvec{u}}} \le c h^{-1/2} \Vert \varvec{\varepsilon }(\varvec{v}_h) \Vert , \quad \text {for}\;\; \varvec{v}_h \in \varvec{V}_h. \end{aligned}$$

(A.2)

From (3.2a) along with (3.3a), it follows by the positive definiteness (1.2a) of $\varvec{C}$, the inequality of Cauchy–Young with a sufficiently small constant $\delta >0$ and the trace inequality (A.2) that, for all $\varvec{v}_h \in \varvec{V}_h$,

$$\begin{aligned} A_\gamma ( \varvec{v}_h, \varvec{v}_h)&= \langle \varvec{C} \varvec{\varepsilon }(\varvec{v}_h),\varvec{\varepsilon }(\varvec{v}_h)\rangle - \langle \varvec{C}\varvec{\varepsilon }(\varvec{v}_h) \varvec{n}, \varvec{v}_h\rangle _{\Gamma ^D_{\varvec{u}}} \\&\quad - \langle \varvec{v}_h, \varvec{C}\varvec{\varepsilon }(\varvec{v}_h) \varvec{n} \rangle _{\Gamma ^D_{\varvec{u}}} + \gamma _a \,h^{-1} \langle \varvec{v}_h, \varvec{v}_h \rangle _{\Gamma ^D_{\varvec{u}}}\\&\ge c \Vert \varvec{\varepsilon }(\varvec{v}_h) \Vert ^2 - c \Vert \varvec{\varepsilon }(\varvec{v}_h) \varvec{n} \Vert _{\Gamma ^D_{\varvec{u}}} \Vert \varvec{v}_h\Vert _{\Gamma ^D_{\varvec{u}}}\\ {}&\quad + \gamma _a \,h^{-1} \Vert \varvec{v}_h \Vert ^2_{\Gamma ^D_{\varvec{u}}}\\&\ge c \Vert \varvec{\varepsilon }(\varvec{v}_h) \Vert ^2 - c \delta \, h \Vert \varvec{\varepsilon }(\varvec{v}_h) \varvec{n} \Vert ^2_{\Gamma ^D_{\varvec{u}}}\\&\quad - c \delta ^{-1} h^{-1}\Vert \varvec{v}_h\Vert ^2_{\Gamma ^D_{\varvec{u}}} + \gamma _a \,h^{-1} \Vert \varvec{v}_h \Vert ^2_{\Gamma ^D_{\varvec{u}}}\\&\ge c \Vert \varvec{\varepsilon }(\varvec{v}_h) \Vert ^2 - c \delta \Vert \varvec{\varepsilon }(\varvec{v}_h) \Vert ^2 \\&\quad - c \delta ^{-1} h^{-1}\Vert \varvec{v}_h\Vert ^2_{\Gamma ^D_{\varvec{u}}} + \gamma _a \,h^{-1} \Vert \varvec{v}_h \Vert ^2_{\Gamma ^D_{\varvec{u}}}\\&= c\Big ( \Vert \varvec{\varepsilon }(\varvec{v}_h) \Vert ^2 + {\widetilde{\gamma }}_a \,h^{-1} \Vert \varvec{v}_h \Vert ^2_{\Gamma ^D_{\varvec{u}}}\Big )\,, \end{aligned}$$

with some constant ${\widetilde{\gamma }}_a >0$ for a sufficiently large choice of the algorithmic parameter $\gamma _a$ in (3.3a), such that ${\widetilde{\gamma }}_a:=\gamma _a -c\delta ^{-1}>0$. Thus, there holds for some constant $c>0$ that

$$\begin{aligned} A_\gamma ( \varvec{v}_h, \varvec{v}_h) \ge c \Vert \varvec{v}_h \Vert _{h,{\widetilde{\gamma }}_a}, \quad \text {for all}\;\; \varvec{v}_h \in \varvec{V}_h. \end{aligned}$$

(A.3)

Secondly, we prove the discrete coercivity of the bilinear form $B_\gamma$ defined in (3.2c) along with (3.3b). For brevity, we study the case $Q_h= Q_h^{l,\text {cont}}$ only, such that $Q_h\subset H^1(\Omega )$ is satisfied. The case $Q_h= Q_h^{l,\text {disc}}$ can be captured similarly. We introduce the mesh- and parameter-dependent norm

$$\begin{aligned}{} & {} \Vert q_h \Vert _{h,{\widetilde{\gamma }}_b}:= \Big (\Vert \nabla q_h \Vert ^2 + {\widetilde{\gamma }}_b \, h^{-1}\Vert q_h \Vert _{\Gamma ^D_{p}}^2\Big )^{1/2},\\{} & {} \quad \text {for}\;\; q_h \in Q_h\subset H^1(\Omega ), \end{aligned}$$

with some parameter ${\widetilde{\gamma }}_b> 0$, where $Q_h=Q_h^{l,\text {cont}}$; cf. (2.5). Further, we recall the well-known inverse inequality

$$\begin{aligned} \Vert \nabla q_h \cdot \varvec{n} \Vert _{\Gamma ^D_{p}} \le c h^{-1/2} \Vert \nabla q_h \Vert , \quad \text {for}\;\; q_h \in Q_h. \end{aligned}$$

(A.4)

From (3.2c) along with (3.3b), it follows by the positive definiteness (1.2b) of $\varvec{K}$, the inequality of Cauchy–Young with a sufficiently small constant $\delta >0$ and the trace inequality (A.4) that, for all $q_h \in Q_h$,

$$\begin{aligned}&B_\gamma ( q_h, q_h) = \langle \varvec{K} \nabla q_h ,\nabla q_h \rangle - \langle \varvec{K}\varvec{\nabla }q_h \cdot \varvec{n}, q_h\rangle _{\Gamma ^D_{p}} \\&\quad - \langle q_h, \varvec{K}\nabla q_h \cdot \varvec{n} \rangle _{\Gamma ^D_{p}} + \gamma _b \,h^{-1} \langle q_h, q_h \rangle _{\Gamma ^D_{p}}\\&\ge c \Vert \nabla q_h) \Vert ^2 - c \Vert \nabla q_h \cdot \varvec{n} \Vert _{\Gamma ^D_{p}} \Vert q_h\Vert _{\Gamma ^D_{p}}+ \gamma _b \,h^{-1} \Vert q_h \Vert ^2_{\Gamma ^D_{p}}\\&\ge c \Vert \nabla q_h \Vert ^2 - c \delta \, h \Vert \nabla q_h \cdot \varvec{n} \Vert ^2_{\Gamma ^D_{p}} - c \delta ^{-1} h^{-1}\Vert q_h\Vert ^2_{\Gamma ^D_{p}}\\&\quad + \gamma _b \,h^{-1} \Vert q_h \Vert ^2_{\Gamma ^D_{p}}\\&\ge c \Vert \nabla q_h \Vert ^2 - c \delta \Vert \nabla q_h \Vert ^2 - c \delta ^{-1} h^{-1}\Vert \varvec{v}_h\Vert ^2_{\Gamma ^D_{p}}\\&\quad + \gamma _b \,h^{-1} \Vert q_h \Vert ^2_{\Gamma ^D_{p}}\\&= c\Big ( \Vert \nabla q_h \Vert ^2 + {\widetilde{\gamma }}_b \,h^{-1} \Vert q_h \Vert ^2_{\Gamma ^D_{p}}\Big )\,, \end{aligned}$$

with some constant ${\widetilde{\gamma }}_b >0$ for a sufficiently large choice of the algorithmic parameter $\gamma _b$ in (3.3b), such that ${\widetilde{\gamma }}_b:=\gamma _a -c\delta ^{-1}>0$. Thus, there holds for some constant $c>0$ that

$$\begin{aligned} B_\gamma ( q_h, q_h) \ge c \Vert q_h \Vert _{h,{\widetilde{\gamma }}_b}, \quad \text {for all}\;\; q_h \in Q_h. \end{aligned}$$

(A.5)

Alternative formulation of the fully discrete problem

Here, we present an alternative formulation for the fully discrete system to (1.1). The difference to Problem 3.1 comes through using $\partial _t \varvec{u}_{\tau ,h}$ instead of $\varvec{v}_{\tau ,h}$ in (3.5c) by means of (3.1a) and (3.5a), respectively. However, this modification requires the inclusion of an additional boundary integral in the resulting equation (B.1c). This non-obvious adaptation results from the proof of well-posedness of the discrete problem. The following problem is thus considered.

Problem B.1

(Numerically integrated $I_n$-problem with $\partial _t \varvec{u}_{\tau ,h}$) For given $\varvec{u}_{h}^{n-1}:= \varvec{u}_{\tau ,h}(t_{n-1})\in \varvec{V}_h$, $\varvec{v}_{h}^{n-1}:= \varvec{v}_{\tau ,h}(t_{n-1})\in \varvec{V}_h$, and $p_{h}^{n-1}:= p_{\tau ,h}(t_{n-1}) \in Q_h$ with $\varvec{u}_{\tau ,h}(t_0):=\varvec{u}_{0,h}$, $\varvec{v}_{\tau ,h}(t_0):=\varvec{u}_{1,h}$ and $p_{\tau ,h}(t_0):= p_{0,h}$, find $(\varvec{u}_{\tau ,h},\varvec{v}_{\tau ,h},p_{\tau ,h}) \in {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;Q_h)$ such that

$$\begin{aligned}&Q_n \big (\langle \partial _t \varvec{u}_{\tau ,h} , \varvec{\phi }_{\tau ,h} \rangle - \langle \varvec{v}_{\tau ,h} , \varvec{\phi }_{\tau ,h} \rangle \big ) \nonumber \\&\quad + \langle \varvec{u}^+_{\tau ,h}(t_{n-1}), \varvec{\phi }_{\tau ,h}^+(t_{n-1})\rangle = \langle \varvec{u}_{h}^{n-1}, \varvec{\phi }_{\tau ,h}^+(t_{n-1})\rangle \, \nonumber \\\end{aligned}$$

(B.1a)

$$\begin{aligned}&Q_n \Big (\langle \rho \partial _t \varvec{v}_{\tau ,h} , \varvec{\chi }_{\tau ,h} \rangle + A_\gamma (\varvec{u}_{\tau ,h}, \varvec{\chi }_{\tau ,h} ) \nonumber \\&\quad + C(\varvec{\chi }_{\tau ,h},p_{\tau ,h})\Big ) + \langle \rho \varvec{v}^+_{\tau ,h}(t_{n-1}), \varvec{\chi }_{\tau ,h}^+(t_{n-1})\rangle \nonumber \\&= Q_n \Big (F_\gamma (\varvec{\chi }_{\tau ,h})\Big ) + \langle \rho \varvec{v}_{h}^{n-1}, \varvec{\chi }_{\tau ,h}^+(t_{n-1})\rangle \,, \end{aligned}$$

(B.1b)

$$\begin{aligned}&Q_n \Big (\langle c_0 \partial _t p_{\tau ,h},\psi _{\tau ,h} \rangle - C(\partial _t \varvec{u}_{\tau ,h},\psi _{\tau ,h})+ B_\gamma (p_{\tau ,h}, \psi _{\tau ,h})\Big )\nonumber \\&\quad + \langle c_0 p^+_{\tau ,h}(t_{n-1}) +\alpha \nabla \cdot \varvec{u}^+_{\tau ,h}(t_{n-1}), \psi _{\tau ,h}^+(t_{n-1})\rangle \nonumber \\&\quad - \alpha \langle \varvec{u}^+_{\tau ,h}(t_{n-1}) \cdot \varvec{n} ,\psi _{\tau ,h}^+(t_{n-1}) \rangle _{\Gamma ^D_{\varvec{u}}} \nonumber \\&= Q_n \Big ( G_\gamma (\psi _{\tau ,h})\Big ) + \langle c_0 p_{h}^{n-1} + \alpha \nabla \cdot \varvec{u}_{h}^{n-1}, \psi _{\tau ,h}^+(t_{n-1})\rangle \nonumber \\&\quad - \alpha \langle \varvec{u}_D(t_{n-1}) \cdot \varvec{n} ,\psi _{\tau ,h}^+(t_{n-1}) \rangle _{\Gamma ^D_{\varvec{u}}} \end{aligned}$$

(B.1c)

for all $(\varvec{\phi }_{\tau ,h},\varvec{\chi }_{\tau ,h},\psi _{\tau ,h})\in {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;\varvec{V}_h) \times {\mathbb {P}}_k (I_n;Q_h)$.

Lemma B.2

(Existence and uniqueness of solutions to Problem B.1) Problem B.1 admits a unique solution.

Proof

The proof follows basically the lines of the proof of Lem. 3.2 and is kept short. Only differences to Lem. 3.2 are depicted. For the differences $(\varvec{u}_{\tau ,h},\varvec{v}_{\tau ,h},p_{\tau ,h})$ of two triples satisfying (B.1) and the test functions $\varvec{\phi }_{\tau ,h}= A_\gamma \varvec{u}_{\tau ,h}$, $\varvec{\chi }_{\tau ,h}=\varvec{v}_{\tau ,h}$ and $\psi _{\tau ,h}=p_{\tau }$ there holds that

$$\begin{aligned} \begin{aligned}&\frac{1}{2} \int _{t_{n-1}}^{t_n} \frac{d}{dt} \big ( A_\gamma (\varvec{u}_{\tau ,h}, \varvec{u}_{\tau ,h}) \\&\quad + \langle \rho \varvec{v}_{\tau ,h}, \varvec{v}_{\tau ,h} \rangle + \langle c_0 p_{\tau ,h}, p_{\tau ,h} \rangle \big ) \,\textrm{d}t + Q_n\big (B_\gamma (p_{\tau ,h},p_{\tau ,h}) \big ) \\&\quad + Q_n\big (C_\gamma (\varvec{v}_{\tau ,h} - \partial _t \varvec{u}_{\tau ,h},p_{\tau ,h}) \big )\\&\quad + \alpha \langle \nabla \cdot \varvec{u}^+_{\tau ,h}(t_{n-1}), p_{\tau ,h}^+(t_{n-1})\rangle \\&\quad { - \alpha \langle \varvec{u}^+_{\tau ,h}(t_{n-1}) \cdot \varvec{n},p_{\tau ,h}^+(t_{n-1}) \rangle _{\Gamma ^D_{\varvec{u}}}}\\&\quad + A_\gamma (\varvec{u}^+_{\tau ,h}(t_{n-1}), u_{\tau ,h}^+(t_{n-1})) + \langle \rho \varvec{v}^+_{\tau ,h}(t_{n-1}), \chi _{\tau ,h}^+(t_{n-1})\rangle \\&\quad + \langle c_0 p^+_{\tau ,h}(t_{n-1}), p_{\tau ,h}^+(t_{n-1})\rangle = 0 . \end{aligned} \end{aligned}$$

(B.2)

Now, let $l\in \{1,\ldots ,k+1\}$ be arbitrary but fixed and $\varvec{\phi }_{\tau ,h}\in {\mathbb {P}}_{k}(I_n;\varvec{V}_{h})$ be chosen as

$$\begin{aligned}{} & {} \varvec{\phi }_{\tau ,h}(t):= \xi _{n,l}(t) \varvec{\phi }_h \quad \text {with} \\{} & {} \xi _{n,l}(t):= \left( \prod _{\begin{array}{c} i=1 \\ i \ne l \end{array}}^{k+1}\big (t-t_{n,i}^{\text {GR}}\big )\right) \left( \prod _{\begin{array}{c} i=1 \\ i \ne l \end{array}}^{k+1}\big (t_{n,l}^{\text {GR}} -t_{n,i}^{\text {GR}}\big )\right) ^{-1} \\ {}{} & {} \in {\mathbb {P}}_{k}(I_n;\mathbb {R}), \;\; \varvec{\phi }_h \in \varvec{V}_h, \end{aligned}$$

and the Gauss–Radau quadrature nodes $t_{n,\mu }^{\text{ G }R}$, for $\mu = 1,\ldots , k+1$; cf. (2.4). By the exactness of the Gauss–Radau quadrature formula (2.4) for all polynomials in ${\mathbb {P}}_{2k}(I_n;\mathbb {R})$ we deduce from (B.1a) that

$$\begin{aligned} 0&= \frac{\tau _n}{2}\sum _{\mu =1}^{k+1} {\hat{\omega }}_\mu ^{\text {GR}}(\langle \partial _t \varvec{u}_{\tau ,h}(t_{n,\mu }^{\text {GR}}), \varvec{\phi }_{\tau ,h}(t_{n,\mu }^{\text {GR}}) \rangle \\&\quad - \langle \varvec{v}_{\tau ,h}(t_{n,\mu }^{\text {GR}}), \varvec{\phi }_{\tau ,h}(t_{n,\mu }^{\text {GR}}) \rangle ) \\&\quad + \langle \varvec{u}^+_{\tau ,h}(t_{n-1}), \varvec{\phi }_{\tau ,h}^+(t_{n-1})\rangle \\&= \frac{\tau _n}{2}{\hat{\omega }}_l^{\text {GR}} \langle \partial _t \varvec{u}_{\tau ,h}(t_{n,l}^{\text {GR}}) - \varvec{v}_{\tau ,h}(t_{n,l}^{\text {GR}}), \varvec{\phi }_h \rangle \\&\quad + \langle \varvec{u}^+_{\tau ,h}(t_{n-1}), \xi ^+_{n,l}(t_{n-1}) \varvec{\phi }_h \rangle \,. \end{aligned}$$

Thus, we have that ($l=1,\ldots , k+1$)

$$\begin{aligned}&\varvec{v}_{\tau ,h}(t_{n,l}^{\text {GR}}) - \partial _t \varvec{u}_{\tau ,h}(t_{n,l}^{\text{ GR }}) = c_{n,l} \, \varvec{u}^+_{\tau ,h}(t_{n-1})\nonumber \\&\text {with}\;\; c_{n,l} = 2 \tau _n^{-1}\, \left( {\hat{\omega }}_l^{\text {GR}}\right) ^{-1}\, \xi ^+_{n,l}(t_{n-1}). \end{aligned}$$

(B.3)

Table 9 $L^2(L^2)$ and $L^\infty (L^2)$ errors and experimental orders of convergence (EOC) with temporal polynomial degree $k=3$ and spatial degree $r=4$ for local spaces ${\mathbb {Q}}_r^2/{\mathbb {Q}}_{r-1}$

Table 10 $L^2(L^2)$ and $L^\infty (L^2)$ errors and experimental orders of convergence (EOC) with temporal polynomial degree $k=2$ and spatial degree $r=3$ for local spaces ${\mathbb {Q}}_r^2/{\mathbb {P}}_{r-1}^{\text {disc}}$ for Young’s modulus $E=10000$ and Poisson’s ratio $\nu =0.35$, corresponding to the Lamé parameters $\lambda = 8642$ and $\mu = 3704$

Substituting (B.3) into the third term on the left-hand side of (B.2), we get that

$$\begin{aligned}&Q_n\big (C_\gamma (\varvec{v}_{\tau ,h} - \partial _t \varvec{u}_{\tau ,h},p_{\tau ,h}) \big )\nonumber \\&= \sum _{\mu =1}^{k+1} C_\gamma (\varvec{u}_{\tau ,h}^+(t_{n-1}),\xi ^+_{n,\mu }(t_{n-1}) p_{\tau ,h}(t_{n,\mu }^{\text {GR}}) ) \nonumber \\&= C_\gamma (\varvec{u}_{\tau ,h}^+(t_{n-1}), p_{\tau ,h}^+(t_{n-1}))\nonumber \\&= - \alpha \langle \nabla \cdot \varvec{u}_{\tau ,h}^+(t_{n-1}), p_{\tau ,h}^+(t_{n-1})\rangle \nonumber \\&\quad + \alpha \langle \varvec{u}_{\tau ,h}^+(t_{n-1}) \cdot \varvec{n} , p_{\tau ,h}^+(t_{n-1}) \rangle _{\Gamma ^D_{\varvec{u}}} \,. \end{aligned}$$

(B.4)

Combining (B.2) with (B.4) then implies that

$$\begin{aligned} \begin{aligned}&A_\gamma (\varvec{u}_{\tau ,h}(t_n), \varvec{u}_{\tau ,h}(t_n)) + \langle \rho \varvec{v}_{\tau ,h} (t_n), \varvec{v}_{\tau ,h}(t_n) \rangle \\&\quad + \langle c_0 p_{\tau ,h}(t_n), p_{\tau ,h}(t_n)\rangle + 2 Q_n \big (B_\gamma (p_{\tau ,h},p_{\tau ,h}) \big ) \\&\quad + A_\gamma (\varvec{u}^+_{\tau ,h}(t_{n-1}), \varvec{u}_{\tau ,h}^+(t_{n-1})) + \langle \rho \varvec{v}^+_{\tau ,h}(t_{n-1}), \chi _{\tau ,h}^+(t_{n-1})\rangle \\&\quad + \langle c_0 p^+_{\tau ,h}(t_{n-1}), p_{\tau ,h}^+(t_{n-1})\rangle = 0 . \end{aligned}\nonumber \\ \end{aligned}$$

(B.5)

From (B.5) along with the discrete coercivity properties (A.3) and (A.5) we deduce that

$$\begin{aligned} \varvec{u}_{\tau ,h}(t_n)= & {} \varvec{u}_{\tau ,h}^+(t_{n-1})=\varvec{0}, \\ \varvec{v}_{\tau ,h}(t_n)= & {} \varvec{v}_{\tau ,h}^+(t_{n-1})=\varvec{0}, \\ p_{\tau ,h}(t_n)= & {} p_{\tau ,h}^+(t_{n-1})= 0 \end{aligned}$$

as well as

$$\begin{aligned} p_{\tau ,h}\big (t_{n,\mu }^{\text {GR}}\big ) = 0 , \quad \text {for}\;\; \mu = 1,\ldots , k+1. \end{aligned}$$

The rest then follows as in the proof of Lem. 3.2.

Additional numerical experiments

Here, we present some additional results of our numerical experiments. Table 9 shows the results of the convergence study introduced in Subsec. 5.1 for the solution (5.1) of (1.1). For the computations of Table 9 the Taylor-Hood pair of finite element spaces ${\mathbb {Q}}_r^2/{\mathbb {Q}}_{r-1}$, with $r=4$, is used instead of the pair ${\mathbb {Q}}_r^2/{\mathbb {P}}_{r-1}^{\text {disc}}$ chosen for the results of Table 2. For the pressure approximation marginally smaller errors are observed. In Table 10 the computed errors of the approximation of (5.1) for larger values of the Lamé parameters $\lambda$ and $\mu$ in the elasticity tensor $\varvec{C}$ are summarized. No significant increase of the errors is observed, indicating the independence of the error constant on the magnitude of $\varvec{C}$.