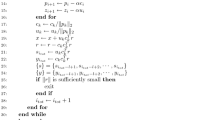1 Introduction

Topology optimization techniques provide the optimal material distribution with prescribed mechanical properties from scratch, i.e., without making any assumptions about the design configuration. Accordingly, these powerful techniques apply to several applications (Deaton and Grandhi 2014). We adopt a density-based topology optimization approach to evaluate the proposed geometric multigrid (GMG) method to accelerate it using adaptive mesh refinement (AMR) techniques. In particular, we adopt the Solid Isotropic Material with Penalization (SIMP) method (Zhou and Rozvany 1991). This method models the material properties interpolating between empty and solid by linking the elastic modulus of elemental stiffness and the design variables. Such an approach allows us to use optimization approaches based on the gradient. A key advantage of SIMP formulation is that it uses the same mesh during the topology optimization. This fact facilitates the concurrent implementation of the parallel stages of the method. We can affirm that SIMP formulation is the most attractive and implemented approach in commercial software, presumably due to its simpleness concerning other formulations.

The number of optimization variables is crucial in the topology optimization process. We usually obtain more accurate results using finite element analysis (FEA) with more refined meshes. A more precise structural response also provides more accurate evaluations of the objective function. Using more refined meshes also permits us to capture more details in the optimization, increasing the performance of the final design. However, high-resolution models require solving a high system of equations whose resolution is a considerable computational challenge (Venkataraman and Haftka 2004). Another problem in density-based topology optimization is the mechanical penalization of the modulus of elasticity of finite elements. The weak phase mimicking void material prevents the singularity of the stiffness matrix but induces errors in the FEA (Allaire et al. 2004). Besides, the system of equations becomes more and more badly conditioned as the discretization size tends to zero (Dambrine and Kateb 2010), which can be a high obstacle in the optimization problem.

We can improve the efficiency of the SIMP method using different strategies. We refer to the rescaling of the system of equations to reduce the condition number (Wang et al. 2007), the approximate reanalysis in some topology optimization iterations (Amir et al. 2009; Long et al. 2019), the use of low-accurate approximations of the solution of the system response (Amir et al. 2010), the efficient preconditioning for calculating the system response (Amir et al. 2014), and the reduction of the degrees of freedom (DoFs) of the system response (Zheng et al. 2020) using a gray-scale suppression method (Groenwold and Etman 2009). Multiresolution schemes decoupling analysis and design discretization are also rewarding. These methods use a coarse mesh for analyzing and a fine mesh for optimizing (Nguyen et al. 2010; Liu et al. 2018b). However, there is a dependency between the design variables and the finite elements used to estimate the system response, limiting the type and order of such finite elements depending on the design variable resolution (Gupta et al. 2020).

We also can improve computing performance using high-performance computing (HPC) techniques for addressing large-scale problems. We can mention the acceleration of the computationally intensive stages of the SIMP method using multi-core (Borrvall and Petersson 2001; Vemaganti and Lawrence 2005; Liu et al. 2019; Zhang et al. 2021) and many-core (Martínez-Frutos et al. 2015; Martínez-Frutos and Herrero-Peréz 2016; Martínez-Frutos and Herrero-Pérez 2017; Herrero-Pérez and Martínez-Castejón 2021) computing techniques. Recently, Liu et al. (2022) also use multi-core computing techniques to address and accelerate large-scale structural topology optimization using the level set method (LSM), including unstructured meshes (Lin et al. 2022).

We also can reduce the computing burden and increase the accuracy of system response using AMR techniques (Vogel and Junker 2021). These methods increase and decrease the tessellation size in the regions of interest. They use an error estimator for determining such areas of interest, roughening less important areas or refining them to reduce the error in the areas of interest. It is possible to use AMR techniques considering error estimators based on the system response estimation and the variables used for the topology optimization (Wang et al. 2014). The resolution of the system of equations of elasticity provides the accuracy of the system response, and the number of design variables permits us to capture more details in the final design. One can use error estimators to enhance the approximation of a concerning measure in topology optimization, e.g., the stress estimation in stress-constrained topology optimization using AMR (Salazar de Troya and Tortorelli 2018, 2020). Another option is refining the interface in topology optimization for a better interface definition (Nana et al. 2016). In our case, increasing the accuracy of the system response for calculating compliance does not modify the final design significantly. Thus, we adopt a coarsening strategy of the weak material based on the design variables of the density-based topology optimization approach to increase the computing performance.

We generally regard multigrid methods as the most suitable and efficient technique to solve large equation systems (Peetz and Elbanna 2021). We usually employ these methods for preconditioning a Krylov subspace solver (Li et al. 2021) in topology optimization problems. Aage et al. (2015) propose the GMG preconditioning for a generalized minimal residual (GMRES) iterative solver to address large-scale density-based topology optimization problems (Aage et al. 2017). They use the DMDA interface of PETSc (Balay et al. 2022) for parallel refining and coarsening the Cartesian hierarchical grids needed by the GMG V-cycle. Liu et al. (2018a) restrict the calculation of the system response to a narrow band around solid regions in an adaptive SIMP approach. The authors adopt a parallel matrix-free instance of a GMG method for preconditioning a Krylov subspace solver using shared memory. The matrix-free implementation permits them to omit the on-the-fly calculation on large void regions, improving the computing performance significantly.

We can find in the literature some works using parallel GMG methods coupled with AMR techniques to solve variable-coefficient elliptic partial differential equations (PDEs) efficiently. The early work of Sampath and Biros (2010) proposes a parallel global coarsening and refinement algorithm for constructing balanced coarse octrees, transferring the information among successive multigrid levels in parallel using PETSc (Balay et al. 2022) with MPI standard. They use such functionalities to implement a parallel GMG method for solving elliptic PDEs using finite elements on octree-based discretizations. The recent work of Clevenger et al. (2021) presents a parallel implementation of an adaptive GMG method used for preconditioning Krylov subspace solvers. The proposal is not constrained to quadtree or octree meshes performing the GMG cycle on adaptively refined meshes. The implementation is available as part of the deal II finite element library (Arndt et al. 2021). The parallel instance showed relevant computational advantages for three-dimensional elasticity problems compared to algebraic multigrid (AMG) solvers. To the best of the authors’ knowledge, adaptive GMG methods have not been previously used to address topology optimization using non-conforming meshes, where we can find relevant difficulties, such as the contrast between void/solid material, which can deteriorate the convergence severely.

We use the SIMP method with dynamic parallel AMR techniques to evaluate the performance of the adaptive parallel GMG preconditioner. This GMG method operates on the non-conforming hierarchical meshes of the GMG cycle scheme for preconditioning Krylov space solvers. The adaptive topology optimization method used for evaluating the adaptive GMG method provides an analogous design to the one obtained on a uniform conforming mesh with a lower computing cost (Baiges et al. 2019). The GMG method operating on the non-conforming hierarchical meshes permits us to evaluate the objective function on a dynamically coarsened mesh efficiently, improving the convergence of the Krylov space solver by providing extra geometric information. We have to remark that the analysis using finite elements is the more expensive stage of the SIMP process. Following (Herrero-Pérez et al. 2022), we use a fine mesh to regularize the design variables, compute the sensitivities, and optimize. On the other hand, we use a dynamically coarse mesh for the FEA (Zave and Rheinboldt 1979) using local criteria based on the values of the density field. This strategy achieves significant computational improvements in the approach used to evaluate the adaptive GMG preconditioner, especially configuring a small target volume because the density field is highly composed of void material after a few topology optimization iterations.

The adaptive GMG method roughs and refines the hierarchical non-conforming meshes from and to the coarsest level of the mesh hierarchy for each topology optimization iteration. This strategy permits us to reintroduce coarsened areas in previous topology optimization iterations. We also have to recalculate the restriction and interpolation operators for grid transferring between the non-conforming meshes of the GMG cycle scheme (setup stage) at all topology optimization iterations. The restriction and interpolation operators are the same for all the topology optimization iterations using conforming multiscale grids in the SIMP method. Thus, we have to find a trade-off between the performance improvement reducing the DoFs of the system response and the cost of recalculating the setup stage of the GMG method at each topology optimization iteration. We use the adaptive GMG method for preconditioning a parallel conjugate gradient method for calculating the structural response on the dynamically coarsened mesh. Finally, we evaluate the strong and weak scaling of the proposal for different three-dimensional problems.

We structure the remainder of the paper as follows. Section 2 describes the distributed density-based framework used to evaluate the parallel and adaptive GMG method for preconditioning Krylov subspace solvers. It also reviews the theoretical background of the SIMP method, introduces the AMR approach, and details the distributed implementation of the Krylov subspace solver. Section 3 presents the adaptive GMG approach using mesh transfer operators between the hierarchical non-conforming meshes in the GMG cycle scheme. Section 4 shows the experiments testing the efficiency and scalability of the adaptive GMG method for preconditioning the Krylov solver in the adaptive SIMP approach. Finally, Sect. 5 presents the conclusion of the proposed adaptive and parallel GMG implementation for improving the computing performance of the system response in adaptive topology optimization.

2 Parallel adaptive approach

2.1 Problem formulation

The SIMP method relaxes the solid/void topology optimization problem by modeling the material properties interpolating between empty and solid, characterizing composite materials (Bendsøe and Sigmund 1999). This approach links the elastic modulus of elemental stiffness and the continuous design variables \(\rho\), modeling the void material as \(\rho =0\) and the solid one with \(\rho =1\). We use structural compliance in the formulation of the optimization problem as follows

$$\begin{aligned} \min _{\varvec{\rho }}\ {}{} & {} {f}\Big ({\varvec{\bar{\tilde{\rho }}}}\Big ) = \textbf{F}^{\textrm{T}}{} \textbf{U} =\textbf{U}^{\textrm{T}}{} \textbf{K}{} \textbf{U} = \sum _e \mathbf{u_e}^{\textrm{T}}{} \mathbf{k_e}{} \mathbf{u_e} \nonumber \\ \text{s. t.:}\ {}{} & {} \textbf{K}{} \textbf{U}=\textbf{F} \nonumber \\ {:}\ {}{} & {} E\Big (\bar{\tilde{\rho }}_e\Big )={E}_{\text{min}}+\bar{\tilde{\rho }}_e^{p}\left( {E}_{0}-{E}_{\text{min}} \right) \nonumber \\ {:}\ {}{} & {} \dfrac{\sum _e \bar{\tilde{\rho }}_e v_e}{V_T} - V^* \le 0, \ {\rho (x)} \in [0,1], \end{aligned}$$
(1)

where f is the objective function, \(\textbf{K}\) is the global stiffness matrix, \(\textbf{U}\) and \(\textbf{F}\) are the displacement and force vectors, \(E(\bar{\tilde{\rho }}_e)\) is the artificial elastic modulus of an element, \(\textbf{E}_{0}\) and \(\textbf{E}_{\text{min}}>0\) are the elastic modulus for solid and void material, respectively, \(V_T\) is the total volume without material penalization, and \(V^*\) is the objective target volume. Lower-case symbols represent the element-wise quantities, \(v_e\) is the volume of each element e, and \(k_e=E(\bar{\tilde{\rho }}_e)\mathbf{k_e^0}\) is the element stiffness matrix, being \(\mathbf{k_e^0}\) the element stiffness matrix with \(\textbf{E}_{0}\) elastic modulus.

The topology optimization problem formulated as compliance minimization is ill-posed. We impose a length scale constraint by filtering the design field \(\rho (x)\) into \(\tilde{\rho }(x)\) to obtain a well-posed problem, proving Bourdin (2001) the existence of solutions in this setting. We adopt the conic filter introduced by Bruns and Tortorelli (2001) for regularizing the density field by the mean of a convolution operator. In particular, we perform the convolution product of the filter F and density \(\rho\) functions as follows

$$\begin{aligned} \tilde{\rho }(x) = (F *\rho )(x) = \int F(x-x')\rho (x') \text{d}x' \end{aligned}$$
(2)
$$\begin{aligned} \int _{B_R} F(x) \text{d}x = 1 \end{aligned}$$
(3)

where \(B_R\) denotes the open ball of radius \(R>0\), and the filter function satisfies \(F \ge 0\) \(\forall\) x \(\in\) \(B_R\). The filter requires that the volume is the same for the filtered and unfiltered field, and thus the volume constraint can be imposed on the latter (Lazarov and Sigmund 2011). We usually replace the expression (2) by

$$\begin{aligned} \tilde{\rho }_e = \dfrac{\displaystyle \sum _{i \in N_e} w(\textbf{x}_i) v_i \rho _i}{\displaystyle \sum _{i \in N_e} w(\textbf{x}_i) v_i} \end{aligned}$$
(4)

where \({\tilde{\varvec{\rho }}}\) represents the filtered design field, \(N_e\) is the neighborhood set of elements lying within the radius R, and \(w(\cdot )\) is the weighting function \(w(\mathbf{x_i})\) \(=\) \(R-\Vert \mathbf{x_i}-\mathbf{x_e}\Vert\), where \(\textbf{x}_i\) is the centroid coordinate of the element e, and \(\mathbf{x_e}\) is the centroid coordinate of the neighborhood set of elements lying within the radius R respecting to \(\textbf{x}_i\).

We use the volume-preserving Heaviside filter proposed by Xu et al. (2010) to prevent blurred boundaries in the material interface projecting to full or empty \(\bar{\tilde{\rho }}(x)\) the regularized design variables \(\tilde{\rho }(x)\). This filter combines the original Heaviside filter (Guest et al. 2004) and the modified Heaviside filter proposed by Sigmund (2007). It projects the regularized design variables \({\tilde{\varvec{\rho }}}\) above the threshold \(\eta\) to solid and below the \(\eta\) value to empty. We use the threshold function

$$\begin{aligned} \bar{\tilde{\rho }}_e = \dfrac{\tanh(\beta \eta ) + \tanh(\beta (\tilde{\rho }_e-\eta ))}{\tanh(\beta \eta ) + \tanh(\beta (1-\eta ))}, \end{aligned}$$
(5)

where the \(\beta\) parameter controls the smoothing operator (Wang et al. 2011). We obtain a similar design using \(\eta = 0\) to the Heaviside step filter proposed by Guest et al. (2004), ensuring a minimum length scale on the solid material distribution. If we use \(\eta = 1\), we generate a design similar to the one obtained using the modified Heaviside filter suggested by Sigmund (2007), providing a minimum length scale on the empty design.

We calculate the sensitivity of (1) to the design variable \(\rho\) using the chain rule as follows

$$\begin{aligned} \dfrac{\partial f\Big (\bar{\tilde{\rho }}\Big ) }{\partial {\rho }_i} = \displaystyle \dfrac{\partial f\Big (\bar{\tilde{\rho }}\Big ) }{\partial \bar{\tilde{\rho }}_e} \dfrac{\partial \bar{\tilde{\rho }}_e}{\partial {\tilde{\rho }}_e} \dfrac{\partial \tilde{\rho }_e }{\partial {\rho }_i}, \end{aligned}$$
(6)

obtaining the different terms as

$$\begin{aligned} \dfrac{\partial f\Big (\bar{\tilde{\rho }}\Big ) }{\partial \bar{\tilde{\rho }}_e}= & {} \mathbf{u_e}^{\textrm{T}} \mathbf{k_e} \dfrac{\partial \mathbf{u_e}}{\partial \bar{\tilde{\rho }}_i} = -\mathbf{u_e}^{\textrm{T}} \mathbf{k_e} \mathbf{k_e^{-1}} \dfrac{\partial \mathbf{k_e}}{\partial \bar{\tilde{\rho }}}{} \mathbf{u_e} \nonumber \\= & {} -\mathbf{u_e}^\textrm{T}p{\bar{\tilde{\rho }}}^{p-1}_e\left( {E}_{0}-{E}_{\text{min}}\right) \mathbf{k_e^0}{} \textbf{u} \end{aligned}$$
(7)
$$\begin{aligned} \dfrac{\partial \bar{\tilde{\rho }}_e}{\partial {\tilde{\rho }}_e}= & {} \dfrac{\beta (\text{sech}(\beta (\tilde{\rho }_e-\eta )))^2}{\tanh(\beta \eta ) + \tanh(\beta (1-\eta ))} \end{aligned}$$
(8)
$$\begin{aligned} \dfrac{\partial \tilde{\rho }_e }{\partial {\rho }_i}= & {} \dfrac{w(\textbf{x}_i) v_i}{\displaystyle \sum _{i \in N_e} w(\textbf{x}_i) v_i} \end{aligned}$$
(9)

where we use the element-wise relationship of the expression \(\dfrac{\partial \textbf{U}}{\partial \bar{\tilde{\rho }}} = -\textbf{K}^{-1} \dfrac{\partial \textbf{K}}{\partial \bar{\tilde{\rho }}} \textbf{U}\) obtained by deriving the expression \(\textbf{K}(\bar{\tilde{\varvec{\rho }}}) \textbf{U}(\bar{\tilde{\varvec{\rho }}}) = \textbf{F}\) from the regularized and projected physical design field \(\bar{\tilde{\varvec{\rho }}}\).

We use the Method of Moving Asymptotes (MMA) suggested by Svanberg (1987) as the optimization approach for its parallel scalability (Aage and Lazarov 2013). This optimization approach addresses inequality-constrained optimization problems, as formulated in (1), solving a set of convex subproblems rather than resolving the non-linear one.

2.2 Adaptivity

We use the approach proposed by Červený et al. (2019) for calculating the system response on non-conforming meshes. Non-conforming meshes are meshes containing at least one hanging node. Hanging nodes are vertices inside an edge or a face for 2D and 3D cases, respectively. We refer to master entities as the ones containing other slave entities. The AMR approach decouples the adaptivity and the equation governing the system’s behavior by removing constrained degrees of freedom (DOFs). This method requires solving a linear system of equations similar to (1), whose solution approximates \(\mathbf{U_h}\). Assuming that slave entities have hanging nodes with independent DOFs of their master DOFs in non-conforming meshes, we can restore the conformity in the interfaces containing hanging nodes restricting slave DOFs by interpolating the finite element functions of their masters.

We can obtain the solution \({\widehat{\textbf{U}}_h}\) in the non-conforming mesh as

$$\begin{aligned} {\widehat{\textbf{U}}_h} = \mathbf{P_c} \mathbf{U_h} = \begin{pmatrix} \mathbf{U_h} \\ \mathbf{W_h} \end{pmatrix} \quad \text {with} \ \mathbf{P_c} = \begin{pmatrix} \textbf{I} \\ \textbf{W} \end{pmatrix}, \end{aligned}$$
(10)

where \(\mathbf{U_h} \in \mathbb {R}^{d}\), \(\mathbf{W_h} \in \mathbb {R}^{\widehat{d}-d}\) with \(\widehat{d}\) > d represents all slave DOFs that we can evaluate by the linear interpolation \(\mathbf{W_h}\) \(=\) \(\textbf{W}\) \(\mathbf{U_h}\) using the interpolation operator \(\textbf{W}\), \(\textbf{I}\) is the identity matrix, and \(\mathbf{P_c}\) is the conforming prolongation matrix.

We can assemble the stiffness matrix \({\widehat{\textbf{K}}}\) and load vector \({\widehat{\textbf{F}}}\) obviating the hanging nodes in the non-conforming mesh. Solving the linear system \({\widehat{\textbf{K}}} {\widehat{\textbf{U}}_h} = {\widehat{\textbf{F}}}\), we obtain a non-conforming solution where the slave DOFs are not restricted. We can then interpolate \({\widehat{\textbf{U}}_h}\) using the conforming prolongation matrix \(\mathbf{P_c}\) to calculate the solution \(\mathbf{U_h}\). We refer to the work of Červený et al. (2019) and the implementation of the AMR method using the Mfem (Anderson et al. 2021) and Hypre (Hypre 2021) libraries for the details of the construction of the \(\mathbf{P_c}\) operator.

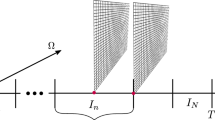
The adaptive topology optimization approach generates a set of consistent nested non-conforming meshes tessellating the domain \({\varvec{\Omega }}\) into the \(l=\{0,\dots ,L\}\) mesh levels with \(\{G^l_i\}_{i=1}^{n^l_e}\) the mesh of \(n^l_e\) elements for the level l and \(\Omega = \cup _i^{n^0_e} G^0_i = \dots = \cup _i^{n^L_e} G^L_i\). The hierarchical meshes satisfy \(G^L \subset \dots \subset G^0\), where \(G^0\) is the coarse mesh, and \(G^L\) is the fine one.

The AMR technique requires some criteria to find the regions on which to perform the coarsening and refinement operations. We choose the regions with weak material as regions of interest because they contribute meaningfully to the ill-conditioning of the system of equations to solve but little to the precision of the objective function estimation. For these reasons, coarsening these void material regions can increase computing performance meaningfully (Wang et al. 2014). Following (Herrero-Pérez et al. 2022), we use the following criteria

$$\begin{aligned} \varepsilon _e^{l-1} = \dfrac{ \displaystyle \int _{g_e^l} \bar{\tilde{\rho }}_e^l \text{{d}}\Omega }{ \displaystyle \int _{g_e^l} \text{{d}}\Omega } = \dfrac{ \displaystyle \sum _{g_e^l} \bar{\tilde{\rho }}_e^l v_e^l}{ \displaystyle \sum _{g_e^l} v_e^l}, \end{aligned}$$
(11)

where \(g_e^l = \{G^l_{k_c}\}_{k_c \in G^{l-1}_e}\) with \(k_c\) the child elements of the parent element \(G^{l-1}_e\), \(v_e^l\) is the elemental volume at the level l, and \(\varepsilon _e^{l-1}\) is the criteria to find the regions of interest for coarsening the children elements at the level l. We use the threshold \(\varepsilon _e^{l-1} \le \displaystyle \sum ^{g_e^l} {E}_{\text{min}} + \varepsilon\) with \(\varepsilon\) a threshold to find regions of elements with weak material properties for coarsening \(g_e^l\) child elements to their parent and \(\varepsilon _e^l \le {E}_{\text{min}} + \varepsilon\) for refining them again.

2.3 Parallel strategy

Fig. 1
figure 1

Flowchart of the parallel topology optimization using adaptivity for evaluating the adaptive GMG preconditioner

Full size image

Parallel computing approaches divide complex problems into smaller subproblems by distributing their computation across distributed computational resources. The efficiency of such distributed calculations depends on the communications needed between subdomains and the workload of each one, which can be optimized using efficient partitioning techniques. In this work, we choose a non-overlapping subdomain strategy to address the topology optimization problem using distributed resources.

Figure 1 shows the flowchart of the distributed memory implementation of the adaptive density-based topology optimization. First, we divide the problem into several non-overlapping subdomains for computing the recursive stages of the topology optimization method. We partition the domain minimizing the number of interface elements to reduce the data exchange between processes. We generate a dual graph from the mesh using nodes as elements and arcs as the shared entities between elements. We then use a multilevel k-way approach (Karypis and Kumar 1998) to tessellate such a representation minimizing the connectivity graph and enforcing the contiguous partitioning. We use the parallel version of the metis library (Karypis and Schloegel 2013) for graph partitioning with multilevel algorithms using MPI standards.

We then initialize the communications needed by distributed operations: the mesh transfer operators and the information required for regularizing the design field. We solve the elasticity equations in the non-conforming coarse mesh \(G^0\) following the criterion detailed in Eq. (11) to improve the performance. Since we use dynamic AMR techniques to obtain such a coarse mesh \(G^0\), we generate the nested hierarchical non-conforming meshes needed by the GMG cycle at each topology optimization iteration. This fact also requires calculating the mesh transfer operators from \(G^0\) to the coarse conforming mesh \(D^0\) defining the problem. We detail this procedure in Sect. 3.

Finally, we project the resulting displacement field to the fine mesh \(G^L\), calculating the sensitivities and updating the design variables in such a fine mesh. We have to remark that this strategy ensures a similar evolution of the functional to the conventional scheme evaluating the objective function on the uniform mesh \(G^L\). Besides, the design update in the fine mesh permits us to reintroduce elements coarsened previously.

2.4 Parallel solving using distributed memory

Let us consider the following linear equation system

$$\begin{aligned} \textbf{A} \mathbf{U_h} = \textbf{B}, \end{aligned}$$
(12)

where \(\textbf{A} = \mathbf{P_c^T} {\widehat{\textbf{K}}} \mathbf{P_c} \in \mathbb {R}^{n_u \times n_u}\) is the coefficient matrix, \(\textbf{B} = \mathbf{P_c^T} {\widehat{\textbf{F}}} \in \mathbb {R}^{n_u \times 1}\) is the right-hand side vector, \(\mathbf{U_h} \in \mathbb {R}^{n_u \times 1}\) is the solution vector, and \(n_u\) is the number of unknowns. We adopt a distributed representation of the coefficient matrix and vectors to evaluate the objective function of the expression (1) using multi-core computing architectures. Let’s assume that the matrix of coefficients \(\textbf{A}\) utilizing the parallel version of compressed sparse row (ParCSR) format (Falgout et al. 2006) is distributed across \(p = \{1,\dots ,n_p\}\) processes, with \(n_p\) the number of computing processes. We use the functionalities provided by the Hypre library (Hypre 2021) for manipulating and operating with matrices of coefficients and vectors using the ParCSR format with the standardized and portable MPI framework for communications.

We adopt a conjugate gradient solver using the ParCSR format as the Krylov subspace method for solving the expression (12). We commonly use multigrid approaches in structural mechanics problems as efficient preconditioners of iterative methods to obtain the system response of the elasticity system of equations. We propose preconditioning the distributed Krylov subspace method using the GMG method operating on the non-conforming meshes used by the adaptive density-based topology optimization scheme.

figure a

Algorithm 1 details the pidgin code of the iterative solver preconditioned by the V-cycle using the GMG method. The method needs the maximum number of iterations \({\text {max}}_{\text {it}}\), the tolerance \({\text {tol}}_{\text {abs}}\), the coefficient matrix \(\textbf{A}\), the right-hand side \(\textbf{B}\), the initial seed \(\mathbf{U_h^0}\) for the recursive method, the number of pre-smoothing \(\mu _1\) and post-smoothing \(\mu _2\) steps in the recursive cycle of the multigrid method, and the maximum number of grid levels L for performing the V-cycles of the GMG preconditioner. We configure the maximum number of grid levels L for coarsening the weak material in the adaptive topology optimization approach as the number of hierarchical mesh levels for the cycles of the adaptive GMG preconditioner operating on non-conforming meshes. The recursive solver provides an approximate solution \(\mathbf{U_h}\) of (12) with a residual \(||{{\varvec{\beta }}_{\text{nom}}}||_2\) after it iterations.

2.5 Parallel regularization

Fig. 2
figure 2

Parallel conic filter implementation that only uses communications between adjacent subdomains

Full size image

The density filter (Bourdin 2001) regularizes the dependency of design variables as the weighted average of the convolution operator of (2). The convolution operator requires the value of the design variables surrounding finite elements at a shorter distance than the radius of the open ball \(B_R\) defined in (3). We also can refer to the convolution operator as the conic filter. We have to remark that the resulting search in the non-conforming coarse grid \({G^0}\) is different during the iterations of the adaptive topology optimization, which requires updating the communications needed by the density filter, increasing the computational cost meaningfully. We only search the neighbor elements in the initialization of the adaptive topology optimization because we apply the parallel regularization to the fine mesh \(G^L\). We also should notice that the distributed memory parallel implementation of the conic filter uses communications intensively by sharing the design fields between computing processes. This data exchange increases as we increment the radius R defined in (3) for regularizing the design variable field.

Figure 2 shows an example of the communications needed for sharing the design fields close to the subdomain border in the distributed memory parallel implementation of the conic filter. We depict the shared information for filtering two design variables, showing data in the same memory space using gray circles and remote information using empty ones. We use arrows to indicate sharing information between subdomains to calculate the expression (4). We minimize the communications needed by compiling all the information required by the design variables in a preprocessing stage. This information gathering is crucial to achieving an efficient distributed memory instance of the conic filter.

We store the information needed for regularizing each design variable using hash tables. These hash tables include the following data by design variable: element indexes in the same subdomain within the radius R defined in (3), element indexes in a different subdomain inside such a radius R, and the Euclidean distance to the design variables inside the radius R. We can then employ point-to-point connections linking the computing processors during the regularization. The use of point-to-point communications facilitates scalability. Gathering the information for parallel regularization increases the efficiency at the cost of increasing the memory requirements to cache hash tables.

Alternatively, we could use a diffusion–reaction partial differential equation (PDE) to regularize the design variables. In particular, a Helmholtz-type PDE with homogeneous Neumann boundary conditions (Lazarov and Sigmund 2011). This approach requires determining the relationship between the length scale PDE parameter and the radius R of the conic filter. We have to remark that the geometric complexity increases as R \(\rightarrow\) 0 (Salazar de Troya and Tortorelli 2018), requiring a small length scale parameter in the PDE, which can induce fluctuations in the resulting design. When this problem appears, it is hard maintaining the filtered design variables in the range [0, 1]. We can solve the PDE using similar parallel iterative techniques to those used for solving the elasticity system of equations in Sect. 2.4. Therefore it is a scalable approach. However, we require tolerances of a higher order of magnitude to the elastic modulus \(E_{\text{min}}\) for void material to keep the robustness of the dynamic AMR approach based on the thresholding of design variables presented in Sect. 2.2. Such tolerances for the iterative solver can increase the computational cost meaningfully. For these reasons, we consider that the regularization using a PDE is a more suitable option for relatively large R values.

2.6 Parallel density update and sensitivity calculation

The parallel computation of the sensitivities of (6) applying the chain rule is straightforward in the different non-overlapped subdomains taking the results of the distributed calculations presented above. In particular, Eq. (7) uses the local elemental stiffness, the design variable, and the resulting displacement field of the corresponding finite element calculated following the techniques mentioned in Sect. 2.4. Equation (8) only requires the design field to project it to a manufacturable design. Finally, the expression corresponding to Eq. (9) needs the design field and the area/volume of the elements within the radius R of the regularization operation. We can obtain such data from the information stored in the hash tables mentioned in Sect. 2.5.

For the density update in the optimization loop, we follow the parallel implementation of the Method of Moving Asymptotes (MMA) proposed by Aage and Lazarov (2013). This implementation has already shown excellent scaling properties because it operates using the design variables of the non-overlapped subdomains independently. In particular, such an implementation consists of formulating the MMA optimization problem as several MMA subproblems in terms of Lagrange multipliers alone. Such subproblems are almost embarrassingly parallel, and we solve them using an interior point method.

3 Adaptive geometric multigrid preconditioner

Fig. 3
figure 3

V-cycle used by the adaptive parallel GMG preconditioner operating on non-conforming hierarchical meshes

Full size image

Multigrid methods use a multiscale grid scheme to address the problems. They are very efficient for solving problems exhibiting multiple scales of behavior. These methods eliminate the “smooth errors” \(\textbf{s}\) by relaxation and coarse grid correction. In particular, they remove the “smooth error” by smoothing and calculating the residual on a coarse mesh and then correcting it by prolonging the error to the fine-grid approximation. The preconditioning of Krylov subspace solvers using multigrid methods is quite common for addressing structural mechanics problems. The basis is that the prolongation operator will unlikely be optimal, making it less efficient for some error components. In these cases, the convergence of the multigrid approach deteriorates even though practically all error components reduce rapidly. An iterative method to remove such error components is usually easier than enhancing the prolongation operator.

We can broadly classify the multigrid approaches into two groups (Stüben 2001): GMG and AMG methods. The former uses geometric information to define the grid transfer operators (Hülsemann et al. 2006). The latter only uses the coefficient matrix information of the linear system of equations, permitting its usage as a “black-box” function. These solvers contain the setup and solving phases. The setup phase generates the transfer operators, while the solving one computes the cycle over the multiscale grids to eliminate the corresponding error components. We have to remark that the generation of the grid transfer operators is difficult to calculate in parallel. On the other hand, the solving stage performs matrix–vector and vector–vector product operations, which we can compute in parallel.

We propose an adaptive and parallel GMG implementation for preconditioning the iterative method used for solving the elasticity system efficiently in the iterations of the adaptive topology optimization scheme. We increase the preconditioner performance operating between the non-conforming hierarchical meshes. The adaptive GMG preconditioner uses an \(\omega\)-Jacobi relaxation as smoother for simplicity. We have to remark that the performance of these methods deteriorates by increasing the contrast in material properties (Briggs et al. 2000). We attribute this fact to the coarsening across discontinuities which affects the coarse grid correction (Sampath and Biros 2010). Nevertheless, GMG methods preconditioning Krylov solvers show high convergence rates for topology optimization problems using a sufficiently strong smoothing operator (Amir et al. 2014).

figure b

The adaptive GMG preconditioner operates from the coarse non-conforming mesh \(G^{0}\) shown in Fig. 1. Since we can modify this coarse non-conforming mesh \(G^{0}\) at each iteration of the adaptive topology optimization scheme, we have to calculate the setup stage for the adaptive GMG preconditioner at all the topology optimization iterations. We have to remark that this is not needed if we operate with multiscale conforming meshes. In this case, we keep the mesh transfer operators between hierarchical meshes during the topology optimization.

Algorithm 2 details the setup phase for the adaptive GMG approach. This phase needs the nested non-conforming hierarchical meshes \(\mathbf{D^l}\) with \(D^L \subset D^{L-1} \subset \dots \subset D^0\) obtained from \(D^L\) = \(G^{0}\) with \(\Omega = \cup _i D^L_i = \dots = \cup _i D^0_i = \cup _i G^0_i\), where \(G^0\) is the coarse mesh of the adaptive SIMP approach using the error estimator of (11) for coarsening the weak material. It also requires the tree refinement \(\mathbf{D^l_{tr}}\) storing the relationship between elements of the nested consistent hierarchical meshes, the essentials or Dirichlet boundary conditions \(\mathbf{ess^l}\) at the mesh levels, and the number of mesh levels L for the adaptive GMG cycle.

Figure 3 shows an example of a consistent nested non-conforming multiscale mesh hierarchy \(\mathbf{D^l}\) from \(D^L\) = \(G^{0}\) to the coarse mesh \(D^0\) for preconditioning using the adaptive and parallel GMG method. We can observe that the coarse mesh \(D^0\) is a conforming mesh with all the elements coarsened up to the maximum number of mesh levels L defined in the adaptive topology optimization scheme presented in Sect. 2. We assemble the coefficient matrices of elasticity \(\{ A_0, \dots , A_L \}\) in the different mesh levels of the consistent nested non-conforming multiscale mesh hierarchy \(\mathbf{D^l}\), considering the essentials or Dirichlet boundary conditions \(\mathbf{ess^l}\) when assembling the matrices of coefficients of elasticity at the l levels. We use such matrices of coefficients to define the smoothers \(\{ S_{0}, \dots , S_{L} \}\) for each mesh level. In our case, we use a distributed conjugate gradient solver \(S_0\) for solving the system of equations \(\mathbf{s_0} = \mathbf{A_0^{-1}} \mathbf{r_0}\) in the coarse mesh and an \(\omega\)-Jacobi relaxation as smoother in the \(\{ 1, \dots , L \}\) mesh levels for simplicity. Finally, we use the non-conforming multiscale mesh hierarchy \(\mathbf{D^l}\) and the tree refinement \(\mathbf{D^l_{tr}}\) for constructing the mesh transfer operators, \(\{ P_1, R_1, \dots , P_L, R_L \}\), between the non-conforming meshes. The tree refinement \(\mathbf{D^l_{tr}}\) stores the information for coarsening and refining the non-conforming meshes and for computing the relationship between children and parent elements between adjacent levels \(g_e^l\) used by the criteria of (11). It does this by restoring the parent element and eliminating the child elements forming it at the different mesh levels of the adaptive GMG preconditioner.

A key feature for supporting the parallelization scheme presented in Sect. 2 is that we assemble the coefficient matrices of elasticity with essentials in all the mesh levels using the ParCSR format (Falgout et al. 2006) described in Sect. 2.4. In particular, we use the distributed functionalities provided by the Hypre library (Hypre 2021) for supporting the distributed matrix–matrix and matrix–vector operations. We also use the ParCSR format to define the smoother operators \(\{ S_{1}, \dots , S_{L} \}\) and the distributed conjugate gradient solver to approximate \(S_0\). We then calculate the interpolator operator \(\{ P_1, \dots , P_L \}\) for prolonging from the coarse mesh \({l-1}\) to the finest one l. We use the non-conforming mesh hierarchy \(\mathbf{D^l}\) and the tree refinement \(\mathbf{D^l_{tr}}\) to construct consistent prolongation operators \(P_l\) between the hierarchical mesh levels. Finally, we calculate the restriction operator as the transpose of the interpolation operator \(R_l\) = \(P_l^T\).

figure c

Algorithm 3 shows the pseudo-code of the solving stage of the adaptive GMG method for preconditioning the distributed conjugate gradient solver presented in Algorithm 1. The solving consists of a V-cycle used to eliminate the residual error of Eq. (12). It does this by smoothing or solving the residual on the coarse mesh and then prolonging the error back, correcting it in the fine mesh approximation. The mesh transfer, smoothing, and solving stages use the ParCSR format for implementing the parallelization scheme of the adaptive SIMP method. The restriction and interpolation operators perform the mesh transferring between the non-conforming meshes of the GMG cycle scheme, as depicted in Fig. 3. The V-cycle applies \(\mu _1\) smoothing operations approximating the solution \(s_l\) at level l and calculates the residual \(r_l\) for the relaxed approximate solution \(s_l\). We adopt an \(\omega\)-Jacobi relaxation as smoother for simplicity, which only requires a dumping factor \(\omega\) and the inverse of the diagonal of the assembled coefficient matrix in the corresponding mesh level \(diag(\mathbf{A_l})^{-1}\). We restrict the residual recursively to the coarse mesh and solve the linear system if we reach the coarsest level \(l=0\). We prolongate the solution \(s_l\) from the coarse mesh to the fine one by applying \(\mu _2\) smoothing operations to the approximate solution.

The distributed conjugate gradient algorithm presented in Sect. 2.4 using the adaptive GMG V-cycle for preconditioning calculates the system response of \(\mathbf{U_h}\) efficiently using parallel computing with distributed memory systems. We can then use Eq. (10) to approximate the system response \({\widehat{\textbf{U}}_h}\) in the non-conforming meshes.

4 Numerical experiments

We evaluate the proposed parallel adaptive GMG preconditioner for solving the elasticity system penalized with the design variables using the adaptive density-based topology optimization scheme presented above. We test the preconditioning efficiency using topology optimization on a uniform conforming mesh as the reference. The solution of this reference allows us to check that we obtain a similar evolution of the objective function using the adaptive approach, validating that the proposal is feasible. We also evaluate the strong and weak scaling in 3D problems, testing the results for large-scale problems with limited computing resources.

We detail the cumulative timing for the whole SIMP process, the wall-clock time per iteration, and the iterations required by the iterative solver to converge. The cumulative timing aims to show the computing benefits of the proposal. The timing per iteration indicates when we achieve the performance improvement. Finally, the number of iterations of the iterative solver shows the computational benefits of the adaptive GMG preconditioner in the solver. We use two computers connected through a 10 Gbps Ethernet for running the experiments. These computing nodes incorporate two E5-2687W v4 CPUs and 256 GB of RAM. The CPUs include 12 cores working at 3.0 GHz, running up to 24 processes in parallel per computing node.

Table 1 Geometry and optimization parameter settings used in the numerical experiments
Full size table

We present two three-dimensional topology optimization experiments: a cantilever and a round arch. The former is a broadly used benchmark in the literature, which we use to evaluate the feasibility, performance, and scalability of the proposed GMG preconditioner to increase the computing performance of the adaptive topology optimization approach. The latter shows that the GMG instance is not constrained to a fixed pattern, such as the stencil computations used in octree-based methods. We solve large-scale topology optimization experiments using both models, evaluating the performance using the adaptive topology optimization approach with the adaptive GMG for preconditioning the iterative solver.

We specify the geometry and optimization settings in Table 1 to report reproducible benchmarks. We configure the tolerance \(\text{tol}_{\text{abs}}=10^{-6}\) for the iterative solver detailed in Algorithm 1. The power-law interpolation function of (1) uses the elastic modulus of solid \({E}_{0}=1\) and void \({E}_{\text{min}}=10^{-9}\) material and the penalization power \(p=3\). We use a radius R of approximately two times the maximum edge of elements to regularize the density field using Eq. (4). We thus tune the magnitude of the radius R depending on the discretization of the model.

We have to remark that small regularization distances R permit us to obtain more details in the optimized design. However, it increases the contrast in material properties, which deteriorates the performance of the GMG preconditioning (Briggs et al. 2000). For this reason, we use a damping factor \(\omega\) = 0.25 to ensure convergence in all the experiments using an \(\omega\)-Jacobi relaxation as smoother (Martínez-Frutos et al. 2017). We use the same number of pre and post-smoothing steps \(\mu _1 = \mu _2 = 4\). We use the value \(\eta =0.5\) for the projection of Eq. (5), following a heuristic continuation strategy for the \(\beta\) parameter. In particular, we initialize \(\beta =1.0\), doubling each 15 optimization steps from the iteration \(it=60\) until the \(\beta =16.0\) value. The experiments also use the system response of the previous optimization step as the seed of the iterative solver. This strategy accelerates the convergence of the iterative method in density-based topology optimization problems (Herrero-Pérez and Martínez-Castejón 2021).

4.1 Cantilever

Fig. 4
figure 4

Cantilever experiment: a geometric configuration and boundary conditions, b symmetry simplifications, and c tessellation and partitioning into eight subdomains

Full size image

We optimize a 3D beam by fixing all the DOFs on one side and applying a uniform load on the lower edge of the other side. Figure 4a depicts the geometric configuration and boundary conditions, detailing the setting parameters indicated in Table 1. Figure 4b specifies the symmetric simplifications applied to the finite element model, including the boundary conditions. Figure 4c depicts a coarse mesh tessellated into many subdomains using the parallel version of the metis library for graph partitioning, which we configure for minimizing sharing elements and balancing the number of finite elements per subdomain. We also parameterize the tessellation of the model using the div variable.

Fig. 5
figure 5

Strong scaling of topology optimization of cantilever experiment using a mesh of 96 \(\times\) 48 \(\times\) 192 elements: a scaled compliance, b the number of elements, and c, d cumulative wall-clock time with different computing resources

Full size image

Figure 5 shows the strong scaling experiments with the tessellation parameter \(div=96\), giving rise to a Cartesian grid of 96 \(\times\) 48 \(\times\) 192 (\(H \times W \times L\)) elements. This tessellation generates a model with 884,736 finite elements and 2,751,987 unknowns. We solve the same topology optimization problem with different computing resources from one computing core up to 48 computing cores in two computing nodes. We use a radius of R = 2/96 for regularizing, corresponding to the size of two edge elements. The GMG preconditioner for the reference conforming implementation uses four grid levels in the V-cycle of Algorithm 3 from the mesh \(D^4\) with 96 \(\times\) 48 \(\times\) 192 finite elements to the mesh \(D^0\) with 6 \(\times\) 3 \(\times\) 12 finite elements. On the other hand, the proposed adaptive GMG preconditioner also uses four grid levels to perform the V-cycle from the coarse mesh dynamically \(D^4=G^0\) using the adaptive density-based topology optimization scheme based on void material thresholding presented above. We limit the coarsening of the elements to the level \(L=0\), which generates a grid level \(D^0\) similar to the one with the uniform conforming fine mesh of 6 \(\times\) 3 \(\times\) 12 finite elements.

Fig. 6
figure 6

Weak scaling for the topology optimization of the cantilever experiment using 48 cores and two computing nodes for meshes of 96 \(\times\) 48 \(\times\) 192 (884,736 elements), 128 \(\times\) 64 \(\times\) 256 (2,097,152 elements), and 192 \(\times\) 96 \(\times\) 384 (7,077,888 elements): a cumulative wall-clock time and b wall-clock time per iteration

Full size image

Figure 5a shows the compliance evolution along the optimization using and neglecting the adaptive approach, i.e., using the adaptive topology optimization scheme with the proposed adaptive GMG preconditioning and ignoring AMR techniques. We can observe a similar evolution of the objective function using and ignoring the adaptive topology optimization approach. The progression of the objective function is also the same using different computational resources.

Figure 5b shows the number of finite elements employed for the analysis along the optimization. We can observe that the number of finite elements used for the topology optimization is the same for experiments using the adaptive scheme. The initial iterations of the topology optimization with the adaptive topology optimization scheme use a similar number of finite elements as the optimization neglecting AMR techniques. We observe a reduction of the number of finite elements, almost nine times smaller, using four grid levels \(L=4\) for coarsening weak material regions. The number of finite elements using the adaptive scheme quickly decreases until the optimization captures the shape of the design. Then, it maintains a stable number of finite elements to extract such details. We have to remark that the number of finite elements in the topology optimization iterations 105 and 120 increases, which corresponds to the reintroduction of finite elements to the design by the continuation strategy for the \(\beta\) parameter of Eq. (5).

Fig. 7
figure 7

(Top) The adaptive mesh for the last topology optimization iteration and (bottom) the design showing the system response for different tessellations

Full size image

Figure 5c and d show the cumulative wall-clock time for the topology optimization using and neglecting the adaptive scheme with different computing resources. We can observe a significant reduction in the wall-clock time using both approaches as increasing the computing resources. Besides, the adaptive method shows a performance increment concerning the scheme ignoring the adaptive methodology used as the reference. However, this performance increment decreases as we increase the computational resources. We can observe a speedup of almost 2.5\(\times\) using one computing core, whereas the speedup is around 1.07\(\times\) for six computing cores. We attribute this performance decrement to the small size of the subdomains as we increase the number of computing cores. The coarsening of weak material regions does not reduce the problem size meaningfully in small subdomains. Another relevant factor is the intensive use of communications between subdomains, which also can deteriorate the computing performance.

We also have to remark that we have to calculate the setup stage of the adaptive GMG preconditioner operating between non-conforming meshes for every topology optimization iteration of the adaptive topology optimization approach. On the other hand, the GMG preconditioner implementation that neglects the adaptive scheme uses the same grid transfer operators during the topology optimization process on a conforming mesh. Nevertheless, we observe that the adaptive proposal scales performing the topology optimization from 8 h 36\(^\prime\) using one computing core to 56\(^\prime\) using 48 computing cores with two computing nodes.

Figure 6 shows the weak scaling experiment for the cantilever model using 48 cores and two computational nodes with \(div=\{96,128,192\}\). These tessellations give rise to meshes of 884,736, 2,097,152, and 7,077,888 elements and finite element models with 2,751,987, 6,464,835, and 21,622,755 unknowns, respectively. We solve such topology optimization problems using a regularizing radius of approximately two times the edge of the uniform elements, which correspond to R = \(\{\)2/96,2/128,2/192\(\}\), respectively. The GMG and adaptive GMG preconditioning use the grid levels L = \(\{\)4,5,5\(\}\) in the V-cycle of Algorithm 3, limiting the coarsening of elements to the level \(L=0\) generating a coarse grid level \(D^0\) of 6 \(\times\) 3 \(\times\) 12, 4 \(\times\) 2 \(\times\) 8, and 6 \(\times\) 3 \(\times\) 12 finite elements, respectively.

Figure 6a shows the cumulative wall-clock time of the weak scaling experiment for the cantilever model. We can observe the long time spent initializing the large model of 7,077,888 finite elements. We use such time to store the required information in the hash tables for the distributed filtering described in Sect. 2.5. The results show a computing performance increment of the adaptive approach by increasing the model size with the same computing resources. We attribute such a performance increment to the larger size of the subdomains, which permits us to coarse the weak material regions. We also attribute such a performance increment to the number of multiscale mesh levels, which affect the performance meaningfully. The problem size limits the number of hierarchical mesh levels in the cycle of the GMG preconditioner. The topology optimization problems of 2,097,152 and 7,077,888 finite elements using adaptivity show a similar speedup of 1.5\(\times\). The reference for calculating the acceleration is the instance neglecting adaptivity. These larger models use \(L=5\) grid levels for the V-cycle of Algorithm 3 with two computing nodes. However, the smaller finite element model of 884,736 finite elements using \(L=4\) multiscale grid levels, previously shown in the strong scaling experiment, presents a poor acceleration.

Fig. 8
figure 8

The cantilever experiment with a mesh of 192 \(\times\) 96 \(\times\) 384 (7,077,888 elements) using 48 cores (two computing nodes): a scaled compliance, b the number of finite elements for solving, c cumulative wall-clock time, d wall-clock time for solving per topology optimization iteration, e the iterations of the conjugate gradient solver per topology optimization iteration, and f the percentage of time for the different phases of the optimization

Full size image

Figure 6b shows the timing per iteration of the conjugate gradient solver presented in Algorithm 1. Such timing includes the setup and solving stages of the GMG and adaptive GMG preconditioners. We can observe that the computing performance increases beginning the optimization for obtaining the optimum shape. We reduce the number of finite elements in such iterations meaningfully by coarsening the mesh following the weak material estimator of Eq. (11). However, the computing performance increment reduces when the topology optimization approach captures the shape details in the last iterations of topology optimization.

Figure 7 shows the final designs of the cantilever experiment for \(div=\{96,128,192\}\) and the adaptive coarse meshes \(G^0\) of the last topology optimization iteration to obtain them. We can observe the coarsening of four levels \(L=4\) for the experiment with the coarse mesh of 96 \(\times\) 48 \(\times\) 192 elements and the coarsening of five levels \(L=5\) for the experiments with the finer meshes of 128 \(\times\) 64 \(\times\) 256 and 192 \(\times\) 96 \(\times\) 384 finite elements. However, we have noticed that the coarsening of the higher model does not reach the mesh level \(L=0\) to capture the details of the topology optimization. We can observe that the experiment using \(div=\{96\}\) for tessellating the domain obtains truss-like designs. On the other hand, topology optimizations using the fine tessellations with \(div=\{128,192\}\) generate shell-like structures with variable thicknesses as final designs (Sigmund et al. 2016).

Figure 8 shows the details of the large-scale cantilever experiment with \(div=\{192\}\) using the two computing nodes connected with the 10 Gigabit Ethernet network. Figure 8a shows the evolution of compliance (objective function) during the topology optimization using and neglecting the adaptive scheme. We can observe that the sequence of the objective function is similar for both approaches since we optimize in the fine mesh \(G^L\). This approach permits us to reintroduce finite elements coarsened previously in the final design. Figure 8b shows the number of finite elements for solving. We can observe that the number of finite elements reduces seven times in the adaptive approach after some iterations of the topology optimization. We also can notice the increment of elements in the topology optimization iteration 110 due to the continuation strategy for the \(\beta\) parameter in the projection of Eq. (5). Figure 8c shows the cumulative wall-clock time for all the stages of the topology optimization. We observe a speedup of 1.4\(\times\) adopting the adaptive approach concerning the efficient reference method neglecting the AMR techniques.

Figure 8d shows the wall-clock time per topology optimization iteration for solving using and neglecting the adaptive approach. The wall-clock time includes the setup and solving stages of GMG and adaptive GMG for preconditioning the conjugate gradient method presented in Algorithm 1. We can observe a relevant performance increment as we reduce the number of elements used for assembling the system of equations. We obtain accelerations of up to 10\(\times\) in the first iterations of the topology optimization, decreasing such a speedup as we advance in the optimization. Figure 8e shows the number of iterations to converge the distributed conjugate gradient solver using and neglecting the adaptive approach per topology optimization iteration. We can observe an increment in the solver iterations performed by the adaptive approach concerning the method ignoring the AMR techniques. However, the computational cost is significantly lower since we perform the operations in the reduced system of equations.

Fig. 9
figure 9

The round arch experiment: a geometric configuration, b symmetry simplifications, and c mesh parameterization and partitioning into several subdomains

Full size image

Figure 8f shows the wall-clock time percentage for the different stages of the cantilever experiment with \(div=\{192\}\) using the two computing nodes connected with the 10 Gigabit Ethernet network. We depict these percentages using concentric doughnut charts, showing the outer ring the topology optimization results neglecting the AMR techniques and the inner one the topology optimization results using the proposed adaptive approach with the adaptive GMG preconditioning. We can observe a significant reduction in the percentage of the wall-clock time for the assembly and solving stages using adaptive techniques. The wall-clock time percentage for calculating the sensitivities and updating the design variables using MMA also increases using adaptive techniques. We perform these tasks on the same fine mesh, and thus the wall-clock time percentage reduces due to the reduction of the total time for the topology optimization iteration. Finally, we can observe that the wall-clock time percentage for coarsening and refinement using the adaptive approach is relevant. Coarsening and refinement stages take more than 37% of the wall-clock time, whereas the solving and assembling calculations take more than 56% of the wall-clock time. Therefore, it is of the utmost importance to make up for reducing the size of the equation system for estimating the system response. We can do this by tuning the maximum number of levels L for grid roughening and refining using adaptive techniques.

4.2 Round arch

We optimize a 3D semicircular beam arc in the round arch experiment. We fix all the DOFs on both sides of the beam, applying a uniform load in the arc center along the top edge in the direction perpendicular to the arc plane. This experiment shows that the proposed GMG preconditioner does not depend on any pattern computation constraint, such as stencil pattern computations used in hierarchical Cartesian grid methods like octree approaches. Figure 9a shows the geometry and boundary conditions indicating in Table 1 the settings to configure the optimization problem. These configuration parameters include the volume fraction \(V^*\), the tolerance of the distributed conjugate solver \({\text {tol}}_{\text {abs}}\), and the elastic module for weak material \(E_{\text{min}}\). Figure 9b shows the symmetric simplification used for the topology optimization, including the boundary conditions. Figure 9c depicts a coarse mesh partitioned into many subdomains using the parallel version of the metis library. As in the cantilever experiment, we tessellate the domain into balanced subdomains enforcing the contiguous partitions. We also show the parameterization of the tessellation with the div and \(div_a\) variables.

Fig. 10
figure 10

The round arch experiment using a mesh of 128 \(\times\) 128 \(\times\) 800 (13,107,200 elements) with 48 cores (two computing nodes): a the number of finite elements for solving, b cumulative wall-clock time, c wall-clock time per topology iteration, d the percentage of time for the phases of the topology optimization, and e the refinement detail of design variables and final design showing the displacement field

Full size image

Figure 10 shows the details of the large-scale round arch experiment with div = 128 and \(div_a\) = 800 using the two computing nodes connected through the 10 Gbps Ethernet network. This tessellation gives rise to a mesh of 128 \(\times\) 128 \(\times\) 800 (\(H \times W \times \frac{\pi R_a}{2}\)) with 13,107,200 finite elements and 39,988,323 unknowns. We solve this large-scale topology optimization problem using a radius R for regularization of approximately two times the edge of the finite elements, which corresponds to R  =  (\(\pi \cdot R_a\))/800. The GMG and adaptive GMG preconditioning use five grid levels L = 5 in the V-cycle of Algorithm 3, generating a coarse mesh level \(D^0\) of 4 \(\times\) 4 \(\times\) 25 elements.

Figure 10a shows the number of finite elements for solving using and neglecting the adaptive scheme. We can observe that the number of finite elements reduces more than thirteen times in the adaptive approach after some iterations of the topology optimization. We also notice the increment of elements in the topology optimization iterations 105 and 120 due to the continuation strategy for the \(\beta\) parameter in the projection of design variables. Figure 10b shows the cumulative wall-clock time for all the stages of the topology optimization. We observe a speedup of 1.75\(\times\) for the 200 topology optimization iterations of the adaptive approach concerning the efficient reference method neglecting the AMR techniques. We have to remark that the slopes of the cumulative wall-clock time indicate an increasing speedup as we perform more topology optimization iterations.

Figure 10c shows the wall-clock time per topology optimization iteration for solving using and neglecting the adaptive approach. The wall-clock time includes the setup and solving stages of GMG and adaptive GMG for preconditioning the conjugate gradient method presented in Algorithm 1. We can observe a relevant computing performance increment as we reduce the number of elements used for assembling the system of equations. We obtain accelerations of up to 6\(\times\) in the first iterations of the topology optimization, decreasing such a speedup as we advance in the optimization up to 2\(\times\) in the last iterations capturing the shape details.

Figure 10d shows the percentage of wall-clock time for the round arch topology optimization stages. We depict the information using the same format as Fig. 8f. The outer ring presents the results neglecting the adaptive approach, and the inner one shows the results using the proposed adaptive scheme with the adaptive GMG preconditioner operating between non-conforming meshes. The assembly and solving stages take 98% of the wall-clock time for the method ignoring the adaptive techniques. We reduce these calculation percentages using the adaptive scheme, taking 8% of the wall-clock time for assembling and 48% for solving. We observe an increment in the wall-clock time percentage for calculating the sensitivities and updating the design variables using MMA in the adaptive approach. This increment is because we perform these tasks on the same fine mesh using and neglecting adaptive techniques. However, the total time for the topology optimization iterations using the adaptive approach is significantly lower. Finally, we can observe that the wall-clock time percentage for coarsening and refinement using the adaptive scheme is relevant, taking more than 34% of the wall-clock time.

Figure 10e shows the final design of the round arch experiment and the adaptive coarse mesh \(G^0\) of the last topology optimization iteration to obtain it. We can observe that the topology optimization problem using a fine tessellation with almost 40 million unknowns generates final designs with similar shell-like structures with variable thicknesses (Sigmund et al. 2016).

5 Conclusion

We present a parallel and adaptive GMG implementation for preconditioning the iterative method for solving elasticity systems from adaptive topology optimization problems using non-Cartesian meshes. The resolution of the system of equations of elasticity penalized with the design variables is still the computational bottleneck of topology optimization approaches using adaptivity. We aim to increase the computing performance of the solver by operating on the non-conforming hierarchical meshes of the GMG cycle scheme. We use the geometric information for constructing the mesh transferring operators between the non-conforming hierarchical meshes.

We use an efficient adaptive instance of the SIMP method to evaluate the proposed adaptive GMG preconditioner method. This implementation combines parallel computing and dynamic adaptivity based on the thresholding of design variables, providing an efficient approach to address large-scale topology optimization problems. We use a topology optimization implementation without adaptivity as the reference. We use it to test the improvement in computing efficiency using the adaptive approach with the proposed adaptive GMG preconditioner. The experimental results show the computational advantages of the proposed adaptive GMG scheme for adaptive topology optimization approaches.

We evaluate the strong scaling of the proposal by solving a problem varying the number of computing threads using distributed memory. The proposed adaptive scheme shows good scalability using subdomains with significant size. We observe a speedup increment as increasing the number of topology optimization iterations. We also test the weak scaling by solving topology optimization problems with different problem sizes using two computing nodes. We observe good scalability as incrementing the size of the system of equations keeping the computational resources. We also notice a high computational cost using several refinement levels for coarsening and refinement operations. Thus, we should choose a suitable number of refinement levels to improve the computing efficiency.