1 Introduction

Cardiovascular diseases are the leading cause of mortality worldwide, representing an estimated 45% of all deaths in Europe alone [1]. Biomechanical factors are known to influence the inception and development of cardiovascular pathologies [2], such as atherosclerosis [3, 4] and aneurysms [5, 6]. The accrual of microdamage and the onset of vascular tissue failure are of particular importance, with their influence on clinical treatment and management strategies becoming increasingly evident. Nevertheless, there remains a pronounced deficit in the knowledge and understanding regarding specific microstructural damage and failure mechanisms, and how this ultimately manifests at the macroscale.

Much of this information has been gleaned from the study of bone, where intrinsic and extrinsic mechanisms are known to contribute toward its fracture toughness [7,8,9,10]. Additionally, skin has been seen to exhibit mostly intrinsic toughening processes, where crack propagation is described by crack blunting, accompanied by interfibrillar sliding, fibril straightening, fibrillar reorientation, and elastic stretching [11, 12]. However, such mechanisms undoubtedly emanate from the extracellular matrix (ECM) architecture and the underlying structure-function relationships that govern the mechanical functionality of the tissue in question. Furthermore, with only a limited number of load cases, such as dissection [13,14,15] and penetration [16, 17], having been investigated towards identifying crack tip mechanisms in vascular tissue, there is evidently still much more to discern concerning influential mechanisms in the healthy, and significantly, the diseased arterial wall.

The complexity and inherent challenges associated with the experimental investigation of failure have prompted the pursuance of computational methods to model damage [18,19,20,21,22,23,24] and fracture [25,26,27,28,29,30,31] in soft biological tissues. The computational modelling of fracture, in particular, constitutes an indispensable tool not only to predict the failure of cracking structures but also to shed insights into fracture processes. Various continuum-oriented methods have been proposed to tackle large deformation non-linear fracture mechanical problems and, specifically, regularise the non-polar continuum by introducing a length-scale associated with the damage mechanism of consequence [32,33,34,35,36]. This gives rise to mesh-independent results but at the cost of requiring an extensively refined mesh within the fracture process zone that invariably necessitates lengthy simulation times, which then prevents the analysis of most clinically relevant problems.

An alternate means of modelling material failure is to instead characterise the fracture surface discontinuously. Embedded formulations such as the embedded finite element method (EFEM) [37], the extended finite element method (XFEM) [38], and the partition of unity finite element method (PUFEM) [39], allow for a cohesive zone to be inserted directly within the element. A traction separation law (TSL) consequently defines the materials’ inelastic failure properties and determines the opening of the fracture surface. Approaches of this kind are particularly well-suited to clearly-defined problems where for example there is a single crack and no branching. However, fracture mechanical concepts alone cannot fully quantify soft tissue rupture that exhibits a distinct toughening mechanism [40, 41]. In the context of computational modelling using embedded discontinuities, the continuum material should therefore ideally consider the development of damage. The inclusion of such behaviour would then necessitate a crack initialisation criteria that accounts for the occurrence of material instabilities and localisation in the continuum [42, 43].

In our present work, we use the PUFEM, previously employed to model arterial dissection [25], to numerically investigate the fracture mechanical properties of the arterial wall. The computational framework provides a discrete representation of a discontinuity by enhancing the nodal degrees of freedom, giving rise to a two-field variational formulation with embedded strong discontinuities. The utilised crack tracking algorithm is detailed extensively elsewhere [44]. All constitutive descriptions are taken from our previous study that concerns collagen-related damage in soft biological tissues [45]. The continuous material model is microstructurally motivated and incorporates an interfibrillar failure mechanism that brings about collagen fiber damage. A transversely isotropic cohesive material is defined whereby a phenomenological TSL provides a surface-based description of fracture, with parameters derived from a bottom-up approach that qualitatively replicates a single-element mixed-mode fracture representation (detailed in [45]). A novel crack initialisation criterion and associated definition of the normal to the fracture surface is introduced, indicating the instance of numerical material instability and the subsequent placement of a discontinuity.

To effectively demonstrate the robustness and versatility of the computational modelling framework, we simulate the uniaxial tensile rupture and symmetry-constrained compact tension (symconCT) testing of the healthy porcine aorta. The latter is an experimental setup that results in the stable propagation of fracture at loading along either the circumferential or axial directions [46].

Fig. 1
figure 1

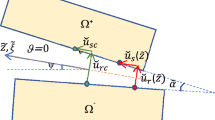
Discontinuous kinematics representing the reference configuration \(\Omega _{0}=\Omega _{0+}\cup \partial \Omega _\textrm{0d}\cup \Omega _{0-}\), and the current configuration \(\Omega =\Omega _{+}\cup \partial \Omega _\textrm{d}\cup \Omega _{-}\), of a body separated by a strong discontinuity: the related deformation gradients are \({\textbf {F}}_{\textrm{e}}={\textbf { I}}+\textrm{Grad}{\textbf {u}}_{\textrm{c}}+\textrm{Grad}{\textbf {u}}_{\textrm{e}}\), \({\textbf {F}}_{\textrm{d}}={\textbf { I}}+\textrm{Grad}{\textbf {u}}_{\textrm{c}}+{\textbf {u}}_{\textrm{e}}\otimes {\textbf {N}}/2\) and \({\textbf {F}}_{\textrm{c}}={\textbf { I}}+\textrm{Grad}{\textbf {u}}_{\textrm{c}}\)

Full size image

2 Continuum mechanical framework

In this section, we introduce the fundamental continuum mechanical features associated with the numerical implementation of the PUFEM. The kinematics of strong discontinuities and preliminary information concerning the continuum stress and cohesive traction responses are therefore detailed. A derivation of the spatial variational formulation is additionally presented.

2.1 Kinematics

We consider the reference configuration of a body to contain an embedded discontinuity \(\partial \Omega _{0\textrm{d}}\), that separates the body into the subdomains \(\Omega _{0+}\) and \(\Omega _{0-}\), see Fig. 1. A deformation \(\chi (\textbf{X})\) then maps \(\Omega _{0+}\) and \(\Omega _{0-}\) into the spatial configurations \(\Omega _{+}\) and \(\Omega _{-}\), with \(\textbf{X}\) denoting the referential position of a material point. The kinematics of the separation is represented by means of a strong discontinuity in the displacement field \(\textbf{u}=\textbf{u}_{\textrm{c}}(\textbf{X})+\mathcal {H}(\textbf{X})\textbf{u}_{\textrm{e}}(\textbf{X})\), where the Heavside function, \(\mathcal {H}(\textbf{X})\), holds a value of 0 for \(\textbf{X}\in \Omega _{0-}\) and a value of 1 for \(\textbf{X}\in \Omega _{0+}\) [47]. The additive decomposition of \(\textbf{u}\) ultimately introduces the smooth displacement fields \(\textbf{u}_{\textrm{c}}\) and \(\textbf{u}_{\textrm{e}}\), which characterise the compatible and enhanced displacements, respectively.

Following the definition of the displacement field, the deformation gradient, \({\textbf {F}}({\textbf {X}})={\textbf { I}}+\textrm{Grad}{\textbf {u}}({\textbf {X}})\), of the body is defined as

$$\begin{aligned} {\textbf {F}}({\textbf {X}})&={\textbf { I}}+\textrm{Grad}{\textbf {u}}_{\textrm{c}}({\textbf {X}})+\mathcal {H}(\textbf{X}) \textrm{Grad}{\textbf {u}}_{\textrm{e}}({\textbf {X}})\nonumber \\&\quad +\delta _{\textrm{d}}({\textbf {X}}) {\textbf {u}}_{\textrm{e}}({\textbf {X}})\otimes {\textbf {N}}({\textbf {X}}_{\textrm{d}})\;, \end{aligned}$$
(1)

where \(\textbf{I}\) is the identity tensor and \(\textrm{Grad}(\bullet )=\partial (\bullet )/\textbf{X}\) is the material gradient operator. The Dirac-delta function, \(\delta _\textrm{d}\), holds a value of 0 in \(\textbf{X}\in \Omega _{0-} \cup \Omega _{0+}\) and a value of \(\infty \) at \(\textbf{X}\in \partial \Omega _{0\,\textrm{d}}\). The relation \(\textrm{Grad}\mathcal {H}(\textbf{X})=\delta _\textrm{d}\textbf{N}(\textbf{X}_\textrm{d})\) is applied, with \(\textbf{N}(\textbf{X}_\textrm{d})\) being the unit normal vector defining the orientation of the discontinuity at an arbitrary point \(\textbf{X}_\textrm{d}\in \Omega _{0\textrm{d}}\).

A constitutive representation for the separation of a material body necessitates the assumption of a fictitious discontinuity \(\partial \Omega _\textrm{d}\), which is a bijective mapping of \(\partial \Omega _\textrm{0d}\) into the current configuration by means of the average deformation gradient

$$\begin{aligned} {\textbf {F}}_{\textrm{d}}({\textbf {X}}_{\textrm{d}})\!=\!{\textbf { I}}+\textrm{Grad}\bigg ({\textbf {u}}_{\textrm{c}} +\frac{1}{2}{\textbf {u}}_{\textrm{e}}\bigg )\!=\!{\textbf { I}}+\textrm{Grad}{\textbf {u}}_{\textrm{c}}\!+\!\frac{1}{2}{\textbf {u}}_{\textrm{e}}\otimes {\textbf {N}}\;. \end{aligned}$$
(2)

The factor 1/2 enforces that \(\partial \Omega _\textrm{d}\) is the middle between the two surfaces defining the crack [48]. The related unit normal vector of the fictitious discontinuity \(\partial \Omega _\textrm{d}\) is then found through the weighted push-forward operation of the covariant vector \(\textbf{N}\)

$$\begin{aligned} {\textbf {n}}= \frac{{\textbf {N}}{{\textbf {F}}_{\textrm{d}}}^{-1}}{|{\textbf {N}}{{\textbf {F}}_{\textrm{d}}}^{-1}|}\;. \end{aligned}$$
(3)

We note that the constrained (incompressible) deformation of the continuous material, and so the determination of \(\bar{{\varvec{\sigma }}}\) and \(\bar{\mathbbm {c}}\) in the subsequent section, requires the multiplicative decomposition of the deformation into volume-changing and volume-preserving parts [49]. As such, the modified-deformation gradient \(\bar{{\textbf {F}}}={J}^{-1/3}{{\textbf {F}}}\), with the Jacobian \(J=\textrm{det}\textbf{F}\), is introduced, completing the kinematic description.

2.2 Continuum response

The continuum response is determined subject to a classical uncoupled formulation [50], in order that incompressibility, a focal feature of soft biological tissues, is enforced. The Helmholtz free energy is therefore \(\Psi =\bar{\Psi }+U\), with \(\bar{\Psi }\) denoting a purely isochoric contribution and \(U={K{(\textrm{ln}J)}^2}/2\), with K being the bulk modulus, denoting a purely volumetric contribution. Consequently, the Cauchy stress and the associated spatial stiffness are given by

$$\begin{aligned} {\varvec{\sigma }}=\bar{{\varvec{\sigma }}}+{\varvec{\sigma }}_\textrm{vol}\;,\;\;\;\;\;\mathbbm {c} =\bar{\mathbbm {c}}+\mathbbm {c}_\textrm{vol}\;, \end{aligned}$$
(4)

where \(\bar{{\varvec{\sigma }}}\) and \(\bar{\mathbbm {c}}\) are constitutive isochoric contributions, whose full derivation is detailed in Sect. 3.1. The volumetric contributions are defined subject to

$$\begin{aligned} {\varvec{\sigma }}_\textrm{vol}=p{\textbf { I}}\;,\;\;\;\;\;\mathbbm {c}_\textrm{vol} =\tilde{p}{\textbf { I}}\otimes {\textbf { I}}-2p\mathbb {I}\;, \end{aligned}$$
(5)

where \(p=\textrm{d}U/\textrm{d}J\), is the hydrostatic pressure which acts as a Lagrangian multiplier, set to enforce incompressibility. For simplicity, we also use the scalar function \(\tilde{p}=p+{J}\partial p/\partial J\), and \(\mathbb {I}\) is the fourth-order identity tensor.

2.3 Cohesive traction response

The coalescence of underlying soft tissue failure mechanisms is lumped into a representative discrete surface [51]. The cohesive response assumes the existence of a transversely isotropic potential per unit undeformed area, \(\partial {\Omega }_{0d}\), of the discontinuity,

$$\begin{aligned} \psi =\psi ({\textbf {u}},{\textbf {n}},\delta )\;. \end{aligned}$$
(6)

As such, the cohesive zone properties depend upon; the gap displacement, \({\textbf {u}}={\textbf {u}}_{\textrm{e}}(\textbf{X}_\textrm{d})\), the current normal of the discontinuity, \({\textbf {n}}\), and the scalar internal damage variable \(\delta \in \{0,\infty \}\) that records the state of damage. The cohesive potential has to obey objectivity requirements, i.e. \(\psi =\psi ({\textbf {u}},{\textbf {n}},\delta )=\psi ({\textbf {Q}}{\textbf {u}},{{\textbf {Q}}}^\mathrm {-T}{\textbf {n}},\delta )\), where \({\textbf {Q}}\) is an arbitrary proper orthogonal tensor.

The damage surface \(\phi ({\textbf {u}},\delta )\) is introduced, and the Karush–Kuhn–Tucker loading and unloading conditions, \(\dot{\delta }\ge 0\), \(\phi \le 0\), \(\dot{\delta }\phi =0\), and the consistency condition, \(\dot{\delta }\dot{\phi }=0\), have to be satisfied.

In accordance with the Coleman–Noll procedure [52], the referential first Piola–Kirchoff traction vector, \(\textbf{T}\), and the internal dissipation, \(\mathcal {D}_\textrm{int}\), are provided by

$$\begin{aligned} \textbf{T}=\frac{\partial \psi }{\partial {\textbf {u}}},\;\;\;\;\;\;\mathcal {D}_\textrm{int}=-\frac{\partial \psi }{\partial \delta }\dot{\delta }\ge 0\;. \end{aligned}$$
(7)

Furthermore, to ensure a consistent linearisation within the PUFEM, we introduce the stiffness tensors

$$\begin{aligned} \textbf{C}_\textbf{u}=\frac{\partial \textbf{T}}{\partial {\textbf {u}}},\;\;\;\;\;\; \textbf{C}_\textbf{n}=\frac{\partial \textbf{T}}{\partial {\textbf {n}}},\;\;\;\;\;\; \textbf{C}_{\delta }=\frac{\partial \textbf{T}}{\partial \delta }, \end{aligned}$$
(8)

that describe the stiffness of the cohesive zone with respect to all the dependent variables.

2.4 Variational formulation

Beginning from the standard single-field variational principle, \(\int _{\Omega _{0}}\textrm{Grad}\delta \textbf{u}:\textbf{P}(\textbf{F})\textrm{d}V-\delta {\Pi }^\textrm{ext}(\delta {\textbf {u}})=0\), where \(\textrm{d}V\), \(\textbf{P}(\textbf{F})\) and \(\delta \textbf{u}\) denote the referential volume element, the first Piola–Kirchoff stress tensor and the admissible variation of the displacement field, respectively; the variational foundation for the PUFEM formulation may be derived [53]. Given the additive decomposition of the displacement field \(\delta \textbf{u}=\delta \textbf{u}_\textrm{c}+\mathcal {H}\delta \textbf{u}_\textrm{e}\), application of a push-forward operation leads to the two variational statements

$$\begin{aligned} {\left. \begin{array}{l} \int \limits _{\Omega _{-}}\textrm{sym}(\mathrm {grad_c}\delta {\textbf {u}}_\textrm{c}): {\varvec{\sigma }}_\textrm{c}\textrm{d}v\\ + \int \limits _{\Omega _{+}}\textrm{sym}(\mathrm {grad_e} \delta {\textbf {u}}_\textrm{c}):{\varvec{\sigma }}_\textrm{e} \textrm{d}v -\delta {\Pi }_\textrm{c}^\textrm{ext}(\delta {\textbf {u}}_\textrm{c}) = 0,\\ \int \limits _{\Omega _{+}}\textrm{sym}(\mathrm {grad_e}\delta {\textbf {u}}_\textrm{e}):{\varvec{\sigma }}_\textrm{e}\textrm{d}v\\ +\int \limits _{\partial \Omega _\textrm{d}}{\textbf {t}}\cdot \delta {\textbf {u}}_\textrm{e}\textrm{d}s -\delta {\Pi }_\textrm{e}^\textrm{ext}(\delta {\textbf {u}}_\textrm{e})= 0,\\ \end{array} \right\} } \end{aligned}$$
(9)

where \(\textrm{d}v\) is the spatial volume element in the current configuration and \(\textrm{d}s\) is the surface element on the fictitious discontinuity \(\partial \Omega _\textrm{d}\). The quantities \({\varvec{\sigma }}_\textrm{c}=J_\textrm{c}^{-1}\textbf{P}(\textbf{F}_\textrm{c})\textbf{F}_\textrm{c}^{\textrm{T}}\) and \({\varvec{\sigma }}_\textrm{e}=J_\textrm{e}^{-1}\textbf{P}(\textbf{F}_\textrm{e})\textbf{F}_\textrm{e}^{\textrm{T}}\) are the compatible and enhanced Cauchy stress tensors, whilst \(\textbf{t}=\textbf{T}\textrm{d}S/\textrm{d}s\) is the Cauchy traction vector acting on \(\partial \Omega _\textrm{d}\). The virtual energies \(\delta {\Pi }_\textrm{c}^\textrm{ext}\) and \(\delta {\Pi }_\textrm{e}^\textrm{ext}\) refer to the referential domains \(\Omega _{0-}\) and \(\Omega _{0+}\), respectively. Finally, \(\textrm{sym}(\bullet )=((\bullet )+{(\bullet )}^\textrm{T})/2\) gives the symmetric part of \((\bullet )\), whilst \(\textrm{grad}_\textrm{c}(\bullet )=\textrm{Grad}(\bullet )\textbf{F}_\textrm{c}^{-1}\) and \(\textrm{grad}_\textrm{e}(\bullet )=\textrm{Grad}(\bullet )\textbf{F}_\textrm{e}^{-1}\) are spatial gradient operators.

The consistent linearisation of Eq. (9) is extensively detailed in [39] and the outcome with respect to the finite element implementation is later elaborated upon in Sect. 4.1.

Fig. 2
figure 2

a A collagen fiber is composed of multiple CFPG-complexes, themselves consisting of collagen fibrils and a PG-dominated interfibrillar matrix that connects adjacent fibrils. PGs are made up of a GAG duplex and are attached to fibrils via a protein core, b following supraphysiological deformations interfibrillar failure occurs in the PG-rich matrix, leading to collagen fibril pull-out

Full size image

3 Constitutive descriptions

Here we outline the fundamental aspects concerning the motivation and mathematical necessities for the continuum microstructural damage model and the transversely isotropic cohesive zone model. We also establish the criteria governing crack initialisation and the orientation of the fracture surface.

3.1 Continuum microstructural damage model

The key features of the continuum microstructural damage model, first introduced in [45], are henceforth summarised to provide a generalised overview. Further details are provided in the appendices for the interested reader, which are taken directly from the original publication.

3.1.1 Histomechanical assumptions

We consider vascular tissue as a fiber-reinforced material at finite deformations, whereby collagen fibers with varying orientations are embedded in an isotropic ground substance. Each fiber is comprised of numerous CFPG-complexes, mechanical sub-units containing undulated collagen fibrils adjacently adjoined by a proteoglycan-rich interfibrillar matrix, see Fig. 2a. In the event that soft tissue is exposed to tension, fibrils begin to straighten and carry load. Two time-dependent proteoglycan (PG) deformations are considered: (i) their ability to slide when the CFPG-complex is exposed to heightened stresses, reducing the stress back down towards a homeostatic target stress, and (ii) their capacity to recover back towards a referential minimal energy state at low stresses [54]. Finally, it is assumed that interfibrillar failure will occur at some limiting PG deformation, see Fig. 2b, leading to the cessation of the CFPG-complexes load-carrying ability. Furthermore, this process is postulated as being stress-dependent; upon exposure to excessive supraphysiological stress, there is assumed to be a significant decline in the structural integrity of the interfibrillar material.

3.1.2 Collagen associated kinematics

Collagen fiber are assumed to have a referential orientation, in \(\Omega _{0}\), defined by the unit vector \(\textbf{M}\). An orientation density function \(\rho (\textbf{M})\) then defines the referential alignment distribution of collagen fibers. If we consider an affine deformation, then the spatial orientation of a fiber, in \(\Omega \), is \(\textbf{m}=\overline{\textbf{F}}\textbf{M}\), and \(\lambda =|\textbf{m}|\) denotes its stretch.

The ith CFPG complex within a fiber is therefore subjected to the one-dimensional stretch \(\lambda \), which can be multiplicatively decomposed into three parts, see Figure 2 in [45]. Firstly, the straightening stretch \(\lambda _{\textrm{st} \, i}\), maps the CFPG-complex from \(\Omega \) into \(\Omega _{\textrm{st}\,i}\), and acts to straighten the initially undulated fibril, where \(\lambda _{\textrm{st} \, i}\) is drawn from the probability density function \(f_{\lambda _{\textrm{st}}}(\lambda _{\textrm{st}})\). A triangular distribution is used for convenience, yet the model remains general and is equally applicable to any probability density function.

Secondly, the interfibrillar deformation \(\lambda _{\textrm{pg}\,i}\), maps the CFPG-complex from \(\Omega _{\textrm{st}\,i}\), into \(\Omega _{\textrm{pg}\,i}\), and represents the collective deformation of all PGs within the CFPG complex. However, if the threshold PG deformation \(\lambda _{\mathrm{pg\,fail}}\), is surpassed, then interfibrillar failure occurs and the CFPG complex alternatively maps into the other intermediate configuration, \(\Omega _{\mathrm {pg\, fail}\,i}\). Finally, the elastic fibril deformation \(\lambda _{\textrm{f} \, i}\), maps the CFPG -complex into \(\Omega \), such that

$$\begin{aligned} \lambda = \lambda _{\textrm{f}\,i} \overline{\lambda }_i\;;\;\overline{\lambda }_i=\lambda _{\textrm{pg}\,i}\lambda _{\textrm{st}\,i}\;\;\hbox {(no summation)}\;, \end{aligned}$$
(10)

encapsulates the multiplicative kinematics of the ith CFPG-complex belonging to a collagen fiber with the referential orientation \(\textbf{M}\).

3.1.3 CFPG-complex constitutive properties

A CFPG-complex is considered linear elastic in a first Piola–Kirchoff stress vs stretch setting, and so

$$\begin{aligned} P_{\textrm{f}\,i}= {\left\{ \begin{array}{ll} k_\textrm{f}\left( \dfrac{\lambda }{\overline{\lambda }_i}-1\right) \;; &{} \lambda >\overline{\lambda }_i\\ 0\;; &{} \text {otherwise}\;,\\ \end{array}\right. } \end{aligned}$$
(11)

defines the 1D stress of the ith CFPG-complex, where \(k_\textrm{f}\) is a stiffness parameter i.e., the fibrils stiffness. The corresponding referential stiffness of the CFPG-complex is then defined as

$$\begin{aligned} {C}_{\textrm{f}\,i} = 2 \frac{\partial {S}_{\textrm{f}\,i}}{ \partial \lambda ^2} = {\left\{ \begin{array}{ll} \dfrac{k_\textrm{f}}{\lambda ^{3}}\;; &{} \lambda >\overline{\lambda }_i\\ 0\;; &{} \text {otherwise},\\ \end{array} \right. } \end{aligned}$$
(12)

where with the assumption of incompressibility, \({S}_{\textrm{f}\,i}={P}_{\textrm{f}\,i}/\lambda \) denotes the second Piola–Kirchhoff stress.

Following on from the discussion of the different interfibrillar PG deformations in Sect. 3.1.1, \(\lambda _{\textrm{pg}\,i}\) evolves subject to

$$\begin{aligned} \frac{\partial \lambda _{\textrm{pg}\,i}}{\partial t}= {\left\{ \begin{array}{ll} \dfrac{P_{\textrm{f}\,i}/P_0-1}{\eta _{\textrm{slid}}}\;; &{} P_{\textrm{f}\,i} \ge P_0 \\ \dfrac{1-\lambda _{\textrm{pg}\,i}}{\eta _{\textrm{rec}}}\;; &{} P_{\textrm{f}\,i}<P_0\\ \end{array}\right. } \end{aligned}$$
(13)

where \(P_0\), is the desired homeostatic CFPG-complex stress and \(\eta _{\textrm{slid}}\), and \(\eta _{\textrm{rec}}\), are the rate parameters that govern the aforementioned mechanisms.

Lastly, the limiting interfibrillar PG deformation, \(\lambda _{\mathrm{pg\,fail}}\), likewise eluded to in Sect. 3.1.1, is defined by

$$\begin{aligned} \lambda _{\mathrm{pg\,fail}} = \frac{\alpha }{P_0}(P_{\textrm{f}}-P_0)+\beta , \end{aligned}$$
(14)

where \(\alpha \) and \(\beta \) are phenomenological damage-related parameters that determine the dependence of interfibrillar failure on the stress of a CFPG-complex, and additionally, as per Eq. (13), the rate of interfibrillar PG deformation. Specifically, \(\alpha \) determines the impact of the stress state when the CFPG-complex is stressed beyond \(P_0\), whilst \(\beta \) is independent of the stress.

3.1.4 Collagen fiber properties

The relation Eq. (13) results in a highly non-linear development of \(\lambda _{\mathrm{pg\,i}}\). Expressly, the imposition that only straightened fibrils are permitted to slide necessitates a discrete implementation of the model. As such, when determining the overall collagen fiber properties, a finite number \(n_\textrm{f}\) of CFPG-complexes are considered. Inverse transform sampling is used to generate a straightening stretch \(\lambda _{\textrm{st}\,i}\) for the ith CFPG-complex, with relevant equations pertaining to a triangular distribution provided in “Appendix A”.

We present here a general summary of the integral method for collagen fiber stress and stiffness determination. Upon inspection of Eq. (12), we observe that the referential stiffness of a CFPG-complex is solely dependent upon the overall stretch \(\lambda \), of the fiber. As such, the referential stiffness of a collagen fiber is found through the referential stiffness of a single CFPG-complex \(C_\textrm{f}\), multiplied by the proportion of those CFPG-complexes that are engaged in load-bearing, which we term \(p_\textrm{rec}\in \{0,1\}\). To identify said proportion, we linearly interpolate the cumulative density with respect to the squared fiber stretch, over the \(n_\textrm{f}\) discrete CFPG-complexes.

It is also necessary to compute the collagen fiber damage variable \(\delta \in \{0,1\}\), which represents the proportion of those CFPG-complexes that have failed based on the limiting interfibrillar deformation expressed by Eq. (14). It should be noted that this differs from the damage variable used in the cohesive traction response. The determination of \(\delta \) is detailed in “Appendix B”. The contribution of failed CFPG-complexes is then neglected from the overall fiber stiffness, and the referential collagen fiber stiffness reads, generally, as

$$\begin{aligned} C = \textrm{max}\Bigl \{0,{C}_{\textrm{f}}(p_{rec}-\delta )\Bigl \}\;. \end{aligned}$$
(15)

The corresponding second Piola–Kirchoff stress is then ascertained through the integration of the stiffness with respect to the squared fiber stretch, across all those CFPG-complexes in tension. It is defined by the general expression

$$\begin{aligned} S = \int _{{\bar{\lambda }_{\textrm{d}}}^2}^{ {\lambda }^2}C\textrm{d}\lambda ^2\;, \end{aligned}$$
(16)

where the lower bound, \(\bar{\lambda }_{\textrm{d}}\), is a function of \(\delta \), i.e., the bounds of integration will alter based on the proportion of failed CFPG-complexes. The dependency of C and S upon the loading history, and as such, the development of internal variables such as \(\lambda _{\mathrm{pg\,i}}\) and \(\delta \), leads to an expansive set of piecewise analytical expressions that are additionally detailed in “Appendix B”.

Finally, the Piola transform, i.e., the push-forward operation into the spatial configuration, determines the corresponding Cauchy stress \(\sigma =\lambda ^2S\), with incompressible fiber deformation having been assumed.

3.1.5 Macroscopic collagen contribution

In line with the theory of fibrous tissues [55], the total collagenous stress is found by integration of the fiber stress over the solid angle \(\omega \), i.e., by a spherical integration over the unit sphere, and thus is given by the relation

$$\begin{aligned} {\bar{{\varvec{\sigma }}}}_\textrm{coll} = \int _{\omega }^{}\rho ({\textbf {M}})\frac{\sigma (\lambda ({\textbf {M}}))}{\lambda ^{2}}\textrm{dev}({\textbf {m}}\otimes {\textbf {m}})d\omega \;. \end{aligned}$$
(17)

There is precedent for the use of the Bingham distribution to define the referential collagen fiber orientation density in the computational modelling of vascular tissue [56, 57]. The orientation density function \(\rho ({\textbf {M}})\), was therefore defined according to

$$\begin{aligned} \rho \bigl ({\textbf {M}}(\phi ,\theta )\bigl ) = \frac{1}{2c}\textrm{exp}[\kappa _{1}{(\cos \phi \cos \theta )}^2+\kappa _{2}{(\cos \phi \sin \theta )}^2]\;, \end{aligned}$$
(18)

with \(\phi \), and \(\theta \), denoting the azimuthal and elevation angles, respectively. With specific regard to the morphology of the arterial wall, values of \(\phi \!=\!\theta \!=\!0\) relate to the circumferential direction, values of \(\phi \!=\!\pi /2\) and \(\theta \!=\!0\) relate to the axial (longitudinal) direction, whilst \(\theta \!=\!\pi /2\) relates to the out-of-plane radial direction. Additionally, the parameters \(\kappa _1\), and \(\kappa _2\), determine the shape of the distribution, whilst c, is a normalisation parameter.

3.1.6 Non-collagenous contribution

The isotropic ground substance, consisting of non-collagenous material, is described by the (classical) Neo-Hookean strain energy density function

$$\begin{aligned} \psi _\textrm{nH}=\mu (\bar{I_{1}}-3)/2\;, \end{aligned}$$
(19)

where \(\mu \) denotes the referential shear stiffness and \(\overline{I_{1}}=\textrm{tr}\overline{{\textbf {b}}}\) is the modified first invariant, with \(\overline{{\textbf {b}}}=\overline{{\textbf {F}}}\overline{{\textbf {F}}}{}^\textrm{T}\) being the modified left Cauchy–Green tensor. The relation \(\overline{{\varvec{\sigma }}}_\textrm{nH}=\mu \textrm{dev}(\overline{{\textbf {b}}})\), then provides the deviatoric contribution of the Cauchy stress.

3.1.7 Overall soft tissue properties

The additive decomposition of the Cauchy stress, by means of the rule of mixtures, gives the total deviatoric stress as

$$\begin{aligned} \overline{{\varvec{\sigma }}}=\overline{{\varvec{\sigma }}}_\textrm{coll}+\overline{{\varvec{\sigma }}}_\textrm{nH}\;, \end{aligned}$$
(20)

The total stress for load-bearing soft-biological tissue is then obtained through the further addition of the isochoric stress \({\varvec{\sigma }}_\textrm{vol}\), as per the treatment discussed in Sect. 2.2.

3.2 Transversely isotropic cohesive zone model

In order to particularize the transversely isotropic cohesive model introduced in Sect. 2.3, we restrict our attention to the cohesive potential of the form \(\psi =\psi ({\textbf {u}}\otimes {\textbf {u}},{\textbf {n}}\otimes {\textbf {n}},\delta )\). Through application of the theory of invariants, with \(i_1, \ldots ,i_5\) denoting deformation dependent variables [58], the potential may be alternatively expressed as \(\psi =\psi (i_1,i_2,i_3,i_4,i_5,\delta )\), which following particularization reads

$$\begin{aligned} \psi =\psi (i_1,i_4,\delta ) = \dfrac{\kappa (\delta )}{2}\left[ i_1+(1-\beta )i_4)\right] \;, \end{aligned}$$
(21)

with \(i_{1}={\textbf { I}}:({\textbf {u}}\otimes {\textbf {u}})\), and \(i_{4}=({\textbf {u}}\otimes {\textbf {u}}):({\textbf {n}}\otimes {\textbf {n}})\), defining the invariants used in this constitutive description. The expression

$$\begin{aligned} \kappa = \dfrac{T_0}{\delta }\Bigg [a\, \textrm{exp}\bigg (-{b}{\Big (\dfrac{\delta }{\alpha }\Big )}^{c}\bigg )+(1-a)\, \textrm{exp}\bigg (-{d}{\Big (\dfrac{\delta }{\alpha }\Big )}^{e}\bigg )\Bigg ]\;, \end{aligned}$$
(22)

describes the evolution of the interface stiffness under normal loading (mode I) along with the accumulation of damage \(\delta \). The non-dimensional parameters a, b, c, d,  and e define the shape of the traction separation law as motivated by the response of the continuum damage model introduced in Sect. 3.1.

The parameter \({T_0}\) is the respective peak normal traction, and the parameter \(\alpha \) normalizes the displacement and is defined by

$$\begin{aligned} \alpha = \dfrac{G}{T_0\zeta }\;, \end{aligned}$$
(23)

with G denoting the respective mode I fracture energy. The energy needed to form a unit of undeformed fracture surface, whilst \(\zeta \) is the numerical approximation of the integral \(\int _{0}^{\infty } \big (a\cdot exp(-bx^c) + (1-a)\cdot exp(-dx^e)\big ) \,\textrm{d}x\).

In addition, the normal and shear responses at the interface are coupled by the parameter \(\beta \). It represents the ratio between the elastic stiffness and peak traction in the normal and shear directions, such that \(\beta \kappa \) and \(\beta T_0\) yield the interfaces’ shear stiffness and the peak shear traction, respectively. As with the parameters \(a,\ldots ,e\), also \(\kappa \) is motivated by the response of the continuum damage model introduced in Sect. 3.1.

Towards finalising the constitutive description, the development of the state of interface damage needs to be specified. The damage surface \(\phi ({\textbf {u}},\delta )=|{\textbf {u}}|-\delta \), and the expression

$$\begin{aligned} \dot{\delta }=\frac{|{\textbf {u}}|-\delta }{\eta _\textrm{cz}}\;, \end{aligned}$$
(24)

therefore determine the evolution of the internal scalar damage variable \(\delta \) (given that \(\phi >0\)). Here, the rate constant \(\eta _\textrm{cz}\) specifies how fast damage in the cohesive zone is able to develop. Interface damage is linked to volume deformation, and the time needed for interstitial fluid to flow into the failure domain thus determines the time scale set by \(\eta _\textrm{cz}\).

Figure 3 displays the normal and shear traction responses of the proposed cohesive zone model, with the accumulation of interface damage for \(\eta _\textrm{cz}\) being much smaller than the loading rate applied to the interface for the provided example.

Fig. 3
figure 3

Demonstration of the normal (blue) and shear (red) traction responses of the proposed transversely isotopic cohesive zone model with the accumulation of interface damage \(\delta =|{\textbf {u}}|\), where \(\theta _\textrm{n}=\textrm{tan}^{-1}(\kappa )\) and \(\theta _\textrm{s}=\textrm{tan}^{-1}(\beta \kappa )\) for illustrative purposes. (Color figure online)

Full size image

The first Piola–Kirchoff traction vector is determined through Eq. (7)\(_1\), and so is defined as

$$\begin{aligned} \textbf{T}=\kappa \textbf{u}_\textrm{n}+\beta \kappa \textbf{u}_\textrm{s}\;, \end{aligned}$$
(25)

where \({\textbf {u}}_\textrm{n}=({\textbf {u}}\cdot {\textbf {n}}){\textbf {n}}\) and \({\textbf {u}}_\textrm{s}= {\textbf {u}}-{\textbf {u}}_\textrm{n}\) denote the normal and shear displacement at the interface, respectively. The stiffnesses associated with the cohesive zone model are found through the application of Eq. (8) to Eq. (25), leading to

$$\begin{aligned} {\left. \begin{array}{l} \textbf{C}_\textbf{u}=\kappa (1-\beta )\textbf{n}\otimes \textbf{n}+\beta \kappa {\textbf { I}}\\ \textbf{C}_\textbf{n}=\kappa (1-\beta )\textbf{n}\otimes \textbf{u}\\ \textbf{C}_\delta =\gamma ({\textbf {u}}_\textrm{n}+\beta {\textbf {u}}_\textrm{s}) \end{array} \right\} } \end{aligned}$$
(26)

where the term \(\gamma =\partial \kappa /\partial \delta \) is obtained by appropriate treatment of Eq. (22).

Finally, the internal dissipation, following Eq. (7)\(_2\) reads

$$\begin{aligned} \mathcal {D}_\textrm{int}=-\frac{1}{2}\frac{\partial \kappa }{\partial \delta }\dot{\delta }(i_1+(1-\beta )i_4)>0\;, \end{aligned}$$
(27)

and imposes a constraint on the model parameters to be used in the traction separation law. Notably, the proposed approach of defining the interface properties through the stiffness factor \(\kappa \) naturally accounts for mixed-mode conditions at the interface.

3.3 Cohesive zone initialisation

The nature of the crack initialisation criteria in approaches utilising embedded strong discontinuities is critical because it determines the evolution of the fracture surface and thus crack propagation in the failed material. As the continuum microstructural model in the presented framework incorporates an internal damage mechanism and no associated method of regularisation, the initialisation of the cohesive zone must employ a bifurcation analysis and account for the emergence of material instability.

To this end, following the sufficient development of collagen fiber damage, the first Piola–Kirchhoff-related elasticity tensor

$$\begin{aligned} \mathcal {A}_{IjKl}=J\textbf{F}_{iI}^{-1}\textbf{F}_{kK}^{-1}\mathbbm {c}_{ijkl}\;, \end{aligned}$$
(28)

becomes non-positive definite, and localization in the non-polar continuum leads to material instability [42, 43]. This therefore marks the state of deformation and the point in space \({\textbf {X}}\) in which the cohesive zone model is introduced. In contrast to the description of the bulk material, the incompressibility of tissue within the fracture process zone is not enforced. Given the transversely isotropic nature of our cohesive zone description, it is necessary to determine whether a normal or shear deformation initialises the localization. We, therefore, consider the eigenvalue problem

$$\begin{aligned} (\mathcal {A}-\lambda \textbf{I}): \textbf{v}={\textbf {0}}\;, \end{aligned}$$
(29)

and use the first negative (lowest) eigenvalue \(\lambda _i;i=1,\ldots ,9\) [59] to inform the crack initialisation criteria. In the event that the lowest eigenvalue falls in the range \(1\le i\le 3\), the interface begins at the peak normal traction \(T_0\), whilst for \(4\le i\le 9\), shear failure triggers the fracture and the cohesive zone model begins at the peak shear traction \(\beta T_0\).

It is also necessary to define the referential normal vector \({\textbf {N}}\) of the discontinuity upon the activation of the cohesive zone model. Our symconCT experiments [46] showed fracture propagation along directions that were in between the maximum principal stress direction and the weakest material direction. Therefore, the condition

$$\begin{aligned} \widetilde{{\textbf {n}}} = w_\sigma {\textbf {n}}_\sigma + w_\textrm{cf}{\textbf {n}}_\textrm{cf}\;, \end{aligned}$$
(30)

with the weights \(w_\sigma =w_\textrm{cf}=0.5\), was used to set the normal to the interface. Here, \({\textbf {n}}_\sigma \) is a principal stress direction, the push forward of \({\textbf {N}}_\sigma \), which relates to the eigenvector \({\textbf {v}}_i\) associated with the lowest eigenvalue. Its determination subject to the solution of Eq. 29 is detailed later in Sect. 4.2.3. The vector \({\textbf {n}}_\textrm{cf}\) denotes the direction along which the in-plane orientation density of collagen fibers is lowest according to Eq. 18, i.e., the deformed axial direction. Both vectors refer to the point of loss of positive definiteness of \(\mathcal {A}\) in the deformed configuration \(\Omega \), and so the pull-back and normalization operation

$$\begin{aligned} {\textbf {N}}= \frac{\widetilde{{\textbf {n}}} {\textbf {F}}}{|\widetilde{{\textbf {n}}} {\textbf {F}}|}\;, \end{aligned}$$
(31)

provides the orientation of the discontinuity in the reference configuration \(\Omega _0\). Application of Cauchy’s stress theorem to the first Piola–Kirchoff stress of the continuum, \(\textbf{P}=J{\varvec{\sigma }}\textbf{F}^{-T}\), then provides the the peak normal traction \(T_0\).

4 Finite element implementation

This section details the key aspects of the framework’s finite element implementation. A brief elaboration of the PUFEM formulation’s cornerstone features is followed by a discussion of the specifics for the numerical implementation of the continuum microstructural damage model and the transversely isotropic cohesive zone model.

4.1 Overview of PUFEM formulation implementation

The computational framework is implemented in the multi-purpose finite element analysis program FEAP [60], using an in-house code. Within the PUFEM, the standard polynomial interpolation functions are enriched by the Heavside function to attain good local approximations for the underlying problem. The displacement field \(\underline{\textbf{u}}\) is therefore expressed as

$$\begin{aligned} \underline{\textbf{u}}=\sum _{i=I}^{n_\textrm{elem}}N^{I}\underline{{\textbf {u}}}_{Ic} +\mathcal {H}\sum _{i=I}^{n_\textrm{elem}}N^{I}\underline{{\textbf {u}}}_{Ie}\;, \end{aligned}$$
(32)

with \(N^{I}\) representing the standard interpolation functions, where I is an index running between 1 and \(n_\textrm{elem}\), the total number of nodes per element. Furthermore, the regular and enhanced nodal displacements are denoted by \(\underline{{\textbf {u}}}_{Ic}\) and \(\underline{{\textbf {u}}}_{Ie}\), respectively.

With the use of the displacement field in Eq. (32), further treatment of the variational statements provided in Eq. (9) leads to a linearised set of equations for a single finite element

$$\begin{aligned} \begin{bmatrix}\underline{\textbf{K}}_{\textbf{u}_\textrm{c}\textbf{u}_\textrm{c}} &{}\underline{\textbf{K}}_{\textbf{u}_\textrm{c}\textbf{u}_\textrm{e}}\\ \underline{\textbf{K}}_{\textbf{u}_\textrm{e}\textbf{u}_\textrm{c}} &{}\underline{\textbf{K}}_{\textbf{u}_\textrm{e}\textbf{u}_\textrm{e}}\\ \end{bmatrix}_{i-1}^{e}\begin{bmatrix}\Delta \underline{{\textbf {u}}}_{\textrm{c}}\\ \Delta \underline{{\textbf {u}}}_{\textrm{e}}\end{bmatrix}_{i}^{e}=\begin{bmatrix} \underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{c}}}^{\;\textrm{ext}}\\ \underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{e}}}^{\;\textrm{ext}} \end{bmatrix}_{i-1}^{e} -\begin{bmatrix}\underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{c}}}^{\;\textrm{int}}\\ \underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{e}}}^{\;\textrm{int}}\end{bmatrix}_{i-1}^{e}\;. \end{aligned}$$
(33)

The indices i and \(i-1\) relate to the iteration steps of the global Newton iteration procedure, whilst \(\Delta \underline{{\textbf {u}}}_{\textrm{c}}\) and \(\Delta \underline{{\textbf {u}}}_{\textrm{e}}\) are increments in the compatible and enhanced displacements, respectively.

The vectors \(\underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{c}}}^{\;\textrm{ext}}\), \(\underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{e}}}^{\;\textrm{ext}}\) and \(\underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{c}}}^{\;\textrm{int}}\), \(\underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{e}}}^{\;\textrm{int}}\) are the nodal force vectors due to external and internal loading. With the subscripts \({(\bullet )}_{\textbf{u}_\textrm{c}}\) and \({(\bullet )}_{\textbf{u}_\textrm{e}}\) denoting an association with compatible and enhanced degrees of freedom, respectively. The stiffness matrices \(\underline{\textbf{K}}_{\textbf{u}_\textrm{c}\textbf{u}_\textrm{c}}\), \(\underline{\textbf{K}}_{\textbf{u}_\textrm{c}\textbf{u}_\textrm{e}}\), \(\underline{\textbf{K}}_{\textbf{u}_\textrm{e}{\textbf {u}}_\textrm{c}}\) and \(\underline{\textbf{K}}_{\textbf{u}_\textrm{e}\textbf{u}_\textrm{e}}\) emerge from the consistent linearisation of the internal loading vectors with respect to the compatible and enhanced displacements. For details concerning the construction of the nodal force vectors and stiffness matrices, based on the output quantities from the continuum (Sect. 3.1) and discontinuous (Sect. 3.2) constitutive descriptions, see [39].

The solution of the linearised system (33) is often termed a monolithic approach. In the case of fracture mechanical problems however, a staggered approach is frequently utilised as it oftentimes presents as a more robust option. In this case, the system may alternatively be split into the two subsystems

$$\begin{aligned}{}[\underline{\textbf{K}}_{\textbf{u}_\textrm{c}\textbf{u}_\textrm{c}}]_{i-1}^{e} [\Delta \underline{{\textbf {u}}}_{\textrm{c}}]_{i}^{e}=[\underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{c}}}^{\;\textrm{ext}}]_{i-1}^{e} -[\underline{{\textbf {f}}}_{\;\textbf{u}_{\textrm{c}}}^{\;\textrm{int}}]_{i-1}^{e}\;;\end{aligned}$$
(34)
$$\begin{aligned} _{i-1}^{e} [\Delta \underline{{\textbf {u}}}_{\textrm{e}}]_{i}^{e}=[\underline{{\textbf {f}}}_{\; \textbf{u}_{\textrm{e}}}^{\;\textrm{ext}}]_{i-1}^{e}-[\underline{{\textbf {f}}}_{\; \textbf{u}_{\textrm{e}}}^{\;\textrm{int}}]_{i-1}^{e}\;. \end{aligned}$$
(35)

that are solved separately, one after the other. As such the contributions from \(\underline{\textbf{K}}_{\textbf{u}_\textrm{c}\textbf{u}_\textrm{e}}\) and \(\underline{\textbf{K}}_{\textbf{u}_\textrm{e}\textbf{u}_\textrm{c}}\) are neglected, resulting in the increments \(\Delta \underline{{\textbf {u}}}_{\textrm{c}}\) and \(\Delta \underline{{\textbf {u}}}_{\textrm{e}}\) being independent from one another.

A critical feature of numerical approaches that use embedded strong discontinuities, such as the PUFEM, is the usage of an effective method for the tracking of 3D crack surfaces. This work uses a two-step algorithm, first introduced in [44]. Here, the discontinuity normal \({\textbf {N}}\), defined in Sect. 3.3, serves as a trial state, which is then corrected to meet the the morphology (geometry) of the already existent crack. The method employs non-local smoothing to circumvent topological difficulties, thus providing a closed crack surface.

4.2 Numerical implementation of the continuum microstructural damage model

The finite element implementation of the continuum microstructural damage model requires the numerical treatment of some of those relations established in Sect. 3.1. Furthermore, Sequential details concerning the full numerical implementation of the continuum microstructural damage model are provided in Table 1. It conveys the ordering and usage of the various equations used to compute the overall soft-tissue stress and stiffness.

Table 1 Numerical implementation of the continuum damage model, detailing the determination of the Cauchy stress and the spatial stiffness at the Gauss point level of a partition of unity finite element
Full size table

4.2.1 Temporal update of the proteoglycan stretch

A first-order accurate backward Euler discretization of Eq. (13) informs the evolution of the interfibrillar PG deformation based on the stress-state of a CFPG-complex. The ith collective PG stretch is initialized as \(\lambda _{\textrm{pg}\,i\,0}\leftarrow 1.0\), after which it evolves subject to

$$\begin{aligned} \lambda _{{\textrm{pg}\,i\,N}}= {\left\{ \begin{array}{ll} \lambda _{\textrm{pg}\,i\,N-1} + \dfrac{\Delta t}{\eta _{\textrm{slid}}} (P_{\textrm{f}\,i}/P_0-1)\;; &{} P_{\textrm{f}\,i}> P_0 \\ \lambda _{\textrm{pg}\,i\,N-1} + \dfrac{\Delta t}{\eta _\textrm{rec}}(1-\lambda _{\textrm{pg}\,i\,N-1})\;; &{} P_{\textrm{f}\,i} \le P_0,\\ \end{array}\right. } \end{aligned}$$
(36)

where the subscripts \({(\bullet )}_{N}\) and \({(\bullet )}_{N-1}\) relate to the current and previous time points, respectively. Here, \(\Delta t =t_{\textrm{N}}-t_{\mathrm {N-1}}\) denotes the size of the time step and the updated \(\lambda _{\textrm{pg}\,i\, N}\) is stored in the history \(\mathcal {H}^{\textrm{con}}_{i+1\,N} \leftarrow \lambda _{\textrm{pg}\,i\, N}\) and serves as input for the next iteration.

4.2.2 Macroscopic collagen contribution—numerical integration

The determination of the macroscopic collagen contribution occurring at a Gauss point of a finite element, according to Eq. (17), requires the spherical integration of the collagen fiber response over the unit sphere. Spherical t-designs [61]

$$\begin{aligned} \int _{\omega }^{}(\bullet )\textrm{d}\omega \approx \bigg (\frac{4\pi }{l_\textrm{int}}\bigg )\sum _{j=1}^{l_\textrm{int}}(\bullet )_{j}\;, \end{aligned}$$
(37)

have been used to numerically perform said integration and calculate the 3D collagen-related stress, where \(l_\textrm{int}\) denotes the total number of spherical integration points.

4.2.3 Cessation of damage development in localised finite elements

Upon the initiation of a localisation in the continuum bulk material, arising from the significant accrual of collagen fiber damage, fracture formation begins, and all subsequent irreversible deformations are henceforth to be entirely represented by the cohesive traction model. Accordingly, once an eigenvalue \(\lambda _i\) of \(\mathcal {A}\) becomes negative, any further development of damage in the continuum model for the localised element is prevented, ultimately forcing the accumulation of damage in the cohesive zone and thus the propagation of the fracture surface. All algorithmic details concerning the identification and specification of localization are listed in Table 2.

Table 2 Algorithm for identification and specification of localization conditions at the Gauss-point level of a finite element
Full size table

However, in limited circumstances, there may also exist finite elements whose Gauss points meet the aforementioned localisation criterion, but they are not located ahead of the crack tip, and therefore the problem inhibits the initialisation of the cohesive zone model—the crack-tracking algorithm only permits the placement of cohesive zones in those elements situated at the crack tip. Therefore, to prevent the formation of a localised deformation, the further development of damage in the continuum model is also prevented in these elements.

4.3 Numerical implementation of the transversely isotropic cohesive zone model

The cohesive model is implemented in a user material routine, where the input data consists of the gap displacement \({\textbf {u}}({\textbf {x}}_{\textrm{d}}^{l})\) and normal vector \({\textbf {n}}({\textbf {x}}_{\textrm{d}}^{l})\) at the current time point. Additionally, the peak traction \({\textbf {T}}_0\) as well as the damage variable \(\delta ({\textbf {x}}_{\textrm{d}}^{l})\) from the previous time point are available, with \({\textbf {x}}_{\textrm{d}}^{l}\) denoting the spatial coordinate of the lth integration point of the discontinuity.

The backward Euler discretization of Eq. (24) yields the iteration \(\delta _N=(\delta _{N-1}+|{\textbf {u}}|\xi _N)/(1+\xi _N)\) with \(\xi _N=\Delta t/\eta _\textrm{cz}\) for the damage variable, where \(\delta _{N-1}\) and \(\Delta t\) denote the damage state at the previous time point and the time increment, respectively. The stiffness factor \(\kappa \) may then be computed by virtue of Eq. (22), and the model’s cohesive traction vector \({\textbf {T}}\) and the stiffness quantities \(\textbf{C}_\textbf{u}, \textbf{C}_\textbf{n}, \textbf{C}_{\delta }\) determined according to Eqs. (25, 26), respectively. The detailed algorithm is listed in Table 3.

Table 3 Numerical implementation of the transversely isotropic cohesive zone model, detailing the determination of the traction vector and associated stiffness entities at the Gauss integration point level of a PUFEM element
Full size table

In order to prevent the occurrence of an infinite scalar elastic stiffness \(\kappa \) that would result in the case of \(\delta =0\), as per Eq. (22), the damage variable is initialised with a value of \(1/\epsilon \), where \(\epsilon \) is an arbitrarily large number. The elastic stiffness-based implementation ensures the compatibility of the traction field in the cohesive zone with the stress field in the continuum (bulk) material.

Table 4 Material and structural parameters representing the medial layer of the porcine aorta
Full size table

5 Application of framework to numerical examples

In order to demonstrate the ability of the proposed constitutive formulation to study soft-tissue failure, we investigate fracture in the medial layer of the aortic vessel wall. The tissue is described by the set of parameters listed in Table 4, which represents porcine aortic wall tissue previously tested in our lab, with the cohesive zone model parameters numerically derived directly from the softening behaviour of the continuum via the bottom-up approach laid out in [45].

We first apply the discussed computational framework to the simulation of the uniaxial tensile testing of a notched specimen loaded along the arterial wall’s axial direction until rupture. We then move our attention to the simulation of the symconCT fracture test [46], an experimental setup conceived such that a more controlled fracture may take place, and in doing so, microstructural failure and damage mechanisms be more readily investigated. The quasi-static monolithic solution of the system (33) was computed, and all simulations were carried out on a DELL Precision 7560 Notepad with an i9 Intel processor. The fracture is forced to initiate in the middle of the notch and then propagates according to the method described previously.

5.1 Uniaxial tensile rupture test

A \(30\times 24~\times 1.0~\)mm\(^3\) sized patch of tissue was discretised into 560 linear tetrahedral elements, see Fig. 4 (left). As the prescribed traction separation law properties result in a cohesive length of approximately 2 mm, the model represents an overly coarse discretisation of the geometry, with the primary aim of evaluating the numerical robustness and capability of the PUFEM model. Dirichlet boundary conditions were applied perpendicular to the notch, in the axial direction, at the two outer edges, and a displacement rate of 10.0 mm s\(^{-1}\) was prescribed. The monolithic solution of the system (33) was computed and differing magnitudes of load increment were investigated. The resulting impact on the mechanical response is demonstrated in Fig. 4 (right).

Fig. 4
figure 4

Results for the uniaxial rupture test. A monotonically increasing axial displacement was applied at a rate of 10.0 \(\textrm{ms}^{-1}\), (left) coarse discretisation of the tissue sample, (right) influence of the displacement increment on the mechanical response, with convergence realised at sufficiently small increments

Full size image

The large element size paired with the small cohesive length yields a somewhat scattered force response, which did not pose any issues concerning numerical stability. As the first principal stress direction and the direction of the least in-plane collagen fiber coincide for this problem, the fracture propagates along a straight line from the notch towards the opposite edge of the specimen.

5.2 Symmetry-constrained compact tension test

The same 3D domain used in Sect. 5.1 was subsequently discretized into approximately 11k linear tetrahedral elements and then tightly linked to two rigid bodies, mimicking the clamps of the symconCT ex-vivo tissue test. As in the symconCT laboratory experiment, the specimen was first pre-stretched, undergoing an initial loading sequence where the distance between the hinge points of the clamps was increased. Subsequently, during the primary loading phase, these points were kept fixed in space, and the displacement of the loading points were increased at a rate of 3 \(\mathrm {mm/min}\).

Tissue fracture was studied for the loading of the tissue specimen in both the axial and circumferential directions. Whilst the specimen in the case of axial loading was completely fractured following 123 load steps, when exposed to loading in the circumferential direction, the crack ran into the clamps (rigid body) after 85 loading steps. With the computer system used, the simulation of this problem took approximately 20 and 15 min, respectively. Figure 5 displays a contour plot of the von Mises stress for the axial loading case approximately halfway through the fractured symconCT test, whilst Fig. 6 (left) and (right) compare the simulated load–displacement curves and the alternate fracture paths resulting for specimens loaded in the axial and circumferential directions, respectively.

Fig. 5
figure 5

von Mises stress contour plot for the sample loaded in the axial direction once the crack has propagated approximately halfway through the length of the specimen. A stress concentration ahead of the crack tip is clearly visible, as is the significant decline in stress for those PUFEM elements that have localised and a cohesive zone is present

Full size image
Fig. 6
figure 6

Results for symconCT testing, demonstrating the impact of sample orientation relative to loading direction and notch placement, (left) the mechanical response following the pre-stretching of the specimen, with red and blue denoting loading in the axial and circumferential directions, respectively, (right) the associated fracture paths, also displaying the facets formed when a discontinuity presents in a PUFEM element. Fracture paths are shown in the unloaded reference configuration. (Color figure online)

Full size image

6 Conclusion

The failure of vascular tissue, occurring from traumatic injury or the presentation of disease, is an issue of undoubted clinical relevance. For instance, the rupture or ulceration of the fibrous cap that characterises atherosclerotic lesions exposes flowing blood to highly thrombogenic plaque contents and the potential incidence of an acute thromboembolic event. Likewise, the rupture of abdominal aortic aneurysms (AAA) carries a demonstrable risk of mortality due to internal bleeding. However, the underlying structure-function relationships that govern both normal and pathological mechanical functionality, and ultimately the fracture properties of vascular tissue, are as yet unknown. To date, limited efforts have been taken to divulge the histo-mechanical mechanisms associated with damage development and rupture of the arterial wall, whether it be experimentally or computationally. The biomechanical simulation of fracture in load-bearing soft biological tissues, in particular, represents a uniquely challenging endeavour from a numerical standpoint.

The present study combines non-linear continuum mechanical and discontinuous cohesive zone frameworks within a robust and efficient PUFEM formulation that can effectively characterise 3D crack propagation. The continuum model incorporates time-dependent interfibrillar damage phenomena, motivated by the microstructural architecture of the collagenous ECM, whilst the response of the (phenomenological) transversely isotropic cohesive zone model is drawn directly from that of the continuum model. Significantly, the outlined traction separation law can effectively characterise mixed-mode fracture. Shear loading may influence failure processes in soft biological tissues, so it is imperative that such features are incorporated when seeking to model rupture and its associated processes. Given our cohesive description, the parameter \(\beta \) determines the coupling between normal and shear loading at the interface. As indicated by the single finite element response at softening, a constant \(\beta \) has been used. It implies that the structures that support normal and shear load transitioning in the failure process zone diminish homogeneously with the accumulation of damage \(\delta \).

To the best of the authors’ knowledge, this is the first instance in which a 3D finite-strain continuum damage formulation has been coupled with an embedded representation of the fracture surface. Namely, when the development of collagen fiber damage in the continuum material gives rise to a localised deformation, a discontinuous cohesive zone is embedded within the finite element of interest and all further evolution of damage in the continuum material is halted. All subsequent irreversible deformations are thus occupied by the cohesive zone, leading to the separation of the crack face in the PUFEM element. The localisation criteria, and specifically the definition of the normal to the fracture surface, is of paramount importance to numerical simulations that employ embedded discontinuities. A myriad of contributing factors likely influence the formation of fracture in load-bearing soft biological tissues. For instance, the orientation of the discontinuity may be a function of the stress state, the rate of stress, and the material’s microstructural organisation, with the true origin and impact of such considerations difficult to fully establish. Equation (30) may therefore be seen as the first attempt to address this problem, and the amassment of experimental data from individual tissues would likely result in more adequate definitions.

The discussed computational framework was able to qualitatively capture fracture mechanical behaviour for the explored representative numerical examples, with stable failure propagation negating the need for the introduction of inertial effects through transient solution methods. The application of the model to the uniaxial tensile rupture test aptly showcased its versatility, with the reliable simulation of tissue failure for a course mesh size and relatively large load increments. The simulation of the symconCT example well-replicated the general experimental observations for samples loaded in the axial direction, with the successful demonstration of a centralised crack trajectory and the stable/controlled decline of the force following the inception of fracture. Furthermore, as our framework is generic, it is likely that fracture in tissue types other than the vascular wall could also be analyzed.

However, in the case of samples loaded in the circumferential direction, disagreement between the simulation and experimental observations was evident. Whilst the numerical simulation could effectively reproduce the initial orientation of the crack (a consequence of the initialised normal definition), it was unable to recreate the ‘zig-zag’ pattern witnessed experimentally, see [46]. From a histological and microstructural perspective, this may stem from the repeated branching of the crack and the subsequent arrest of the remaining mother crack due to unknown failure mechanisms. The numerical formulation, as it currently stands, is limited to the presence of a single cohesive zone within a given PUFEM element, and so cannot suitably mimic the postulated phenomena. It is also worth noting that in the case of the symconCT testing of aneurysmatic aorta specimens loaded in the circumferential direction, the crack frequently propagates into the clamps, see Fig. 7. This observation stems from our ongoing experimental study concerning human thoracic aortas and matches with the PUFEM simulations predicted in this work. The diseased human aorta is particularly fibrous, histology that then promotes fracture in between collagen fibers.

Fig. 7
figure 7

Symmetry-constrained compact tension (symconCT) test of the aneurysmatic thoracic human aorta loaded along the circumferential direction. The experimentally provoked fracture path matches that predicted by the PUFEM method, as shown in Fig. 6

Full size image

Many of the recent modelling strategies used to characterise fracture in soft biological tissues have focussed on the phase field method [15, 28, 34]. It can handle topologically complex fractures, such as branching and intersecting cracks, without the need to explicitly trace the fracture surface, circumventing many of the numerical complexities of crack tracking. However, it does not allow full access to the constitutive description of fracture, and it is therefore not necessarily ideal with respect to designing and validating fracture laws. Additionally, the explicit integration of physical aspects, such as nonlinearities and the time dependencies associated with fracture processes, are not well understood.