1 Introduction

The modeling for the description and prediction of processes in nature often leads to partial differential equations. Solving these field equations can be done analytically in only very few cases, so that in practice numerical solution methods are frequently used. Variational methods such as the Galerkin method have proven to be very effective and are widely used in various fields in industry and research. After choosing a suitable solution space, which is the subject of ongoing research, a system of equations must generally be set up and solved to obtain an approximate solution. These two parts usually represent the largest computational effort and therefore, in addition to the choice of the variational method and the solution space, also offer the greatest potential for a reduction in computational time.

To set up the necessary system of equations, an integration over the simulated area is required. Analytical integration can become difficult or even infeasible for complex geometries or nonlinear equations, leading to numerical integration through weighted evaluations of the integrand, known as quadrature. To achieve quasi-optimal accuracy with the Galerkin method, as expected by Cea’s lemma [1], the quadrature scheme has also to be suitably accurate. In the case of the isoparametric finite element method (FEM), for example, one integration point per element is sufficient for a piecewise linear approach to evaluate the static tangent stiffness matrix accurately. A piecewise quadratic approach may improve convergence but typically requires an increased number of function evaluations, as discussed in [2]. An overview and literature on numerical integration methods can be found in [3, 4].

Especially in the case of complex constitutive laws, under-integration or even selective integration is often used in engineering to save computational time or to prevent locking, cf. [5]. The rank deficiency of the tangent matrix that occurs with complete underintegration is accompanied by a loss of stability and has to be treated by additional stabilization techniques [6]. These can be purely mathematically motivated, containing a case-dependent fitting parameter, but also physically motivated stabilizations without the need of tuning parameters are employed, see e.g. [7, 8].

The construction of a suitable stabilization is a tightrope walk between different goals to be achieved. On the one hand, it is the task of the stabilization to eliminate unphysical zero- or low-energy modes. On the other hand, the stabilization should not in turn lead to locking phenomena. In addition, objectivity, variational consistency and an applicability to nonlinear problems should be ensured. In most cases, it is not possible to completely satisfy all objectives, so a good compromise has to be found. The strategies and interpretations of the stabilization that have been developed include the isolation of hourglass modes [9], the use of mixed approaches [10] in combination with Taylor series expansions [11, 12], Taylor expansion of stress measures [13] and the decomposition of the deformation gradient into a homogeneous and inhomogeneous part [14, 15]. Most of these approaches are restricted to bi- and trilinear elements.

Another approach is to define the stabilization in such a way that it repairs the integration error due to under-integration. In [16], this has been pursued for bilinear finite elements involving a single integration point with a constant Jacobian and material tangent. Moutsanidis et al. [17] further extends this approach to reduced-integration for second-order finite elements, iso-geometric analysis and meshfree methods. The recovery of exact integration can again lead to locking phenomena, but these often become tolerable for higher order approaches, which is why in the present article a one-point integration approach is derived that is applicable to polynomial approaches of arbitrary order.

Further on, an alternative integration method based on series expansions and additional spatial derivatives of the integrand is proposed that can be used for polygonal element shapes and nonlinear material behavior. The fundamental idea is to achieve arbitrary order polynomial integration accuracy by evaluating higher order derivatives. Through the series expansions, the displacement-dependent quantities can be extracted from the integrals, replacing integration with the calculation of geometric moments in preprocessing. The procedure can be effectively combined with automatic differentiation and expression optimization, as further demonstrated in the use of the software AceGen [18] throughout this article.

In the following section, the moment integration scheme is introduced, starting with linear elasticity in small deformations. The procedure is then continued for finite deformations and nonlinear material behavior. In order to allow an efficient implementation, a geometric-material-nonlinearity integration split is presented that allows to capture the full geometric nonlinearity of the solution space while considering only a linear material behavior in the elements tangent space. As an excellent application of the integration scheme, the usage within the virtual element method (VEM) is illustrated further. Therefore, Sect. 3 introduces the VEM, where an alternative perspective was adopted in order to demonstrate its relationship to techniques in other discretization methods, such as variationally consistent meshfree methods. Section 4 is used for the detailed numerical analysis of the integration scheme. A conclusion is given in Sect. 5.

2 Moment integration in Galerkin methods

This section introduces a moment integration method for weak forms based on Taylor series expansion of stresses and its conjugate virtual and actual kinematic measures, inspired by the stabilization technique used in [19, 20]. The first subsection shows how to apply the procedure to the virtual work for linear elasticity, arising in the weak form of the linear momentum balance equation, and considers polynomial displacement approximations. The second subsection explores the extension to nonlinear equations and presents the idea of an integration split of geometric and material nonlinearities. The third subsection illustrates how to utilize the automatic differentiation package AceGen to obtain the derivatives.

2.1 Linear elasticity, small deformations

Beginning with linear elasticity and small deformations, we consider the integral of virtual work over a finite element occupying region \(\Omega _0^e\):

$$\begin{aligned} \int _{\Omega _0^e} \varvec{\sigma }: \delta \varvec{\varepsilon } \, d\Omega _0^e, \end{aligned}$$
(1)

Instead of choosing a suitable Gauss quadrature scheme for the considered ansatz, a single reference point in the element is chosen and Taylor series expansions of the product terms are performed. For the stresses, the first order expansion with respect to the strains yields:

$$\begin{aligned} \varvec{\sigma } = \overline{\varvec{\sigma }} + \overline{\varvec{\sigma }_{,\varvec{\varepsilon }}}: \Delta \varvec{\varepsilon } \end{aligned}$$
(2)

where \(\Delta \varvec{\varepsilon } = \varvec{\varepsilon } - \overline{\varvec{\varepsilon }}\) and \(\varvec{\sigma }_{,\varvec{\varepsilon }}\) denotes the material tangent. The further notation employs a subscript comma followed by the tensor to represent partial derivatives. Additionally, a constant value with respect to the argument of the Taylor series expansion is denoted by an overline. With linear elastic material behavior, i.e. \(\varvec{\sigma } = \mathbb {C}:\varvec{\varepsilon } = \overline{\varvec{\sigma }_{,\varvec{\varepsilon }}}:\varvec{\varepsilon }\), the virtual work yields

$$\begin{aligned} \int _{\Omega _0^e} \varvec{\sigma } : \delta \varvec{\varepsilon } \, d\Omega _0^e = \int _{\Omega _0^e} \left( \overline{\varvec{\sigma }_{,\varvec{\varepsilon }}}:\varvec{\varepsilon }\right) : \delta \varvec{\varepsilon } \, d\Omega _0^e \end{aligned}$$
(3)

In the case of a polynomial approximation for the primary variables (here displacements), the strain is also polynomial. Therefore, the virtual and actual strain can be described by a Taylor series expansion with respect to the position:

$$\begin{aligned} (\delta )\varvec{\varepsilon } = \overline{(\delta )\varvec{\varepsilon }} + \overline{(\delta )\varvec{\varepsilon },_{\textbf{X}}} \cdot \Delta \textbf{X} \, (+\, \cdots ). \end{aligned}$$
(4)

For the sake of clarity, a second order approximation is followed. However, an extension to arbitrary polynomial approximations is possible in an analogous way. Re-substituting into the virtual work and transforming into index notation such that constant terms are moved outside the integral results in

$$\begin{aligned}&\int _{\Omega _0^e} \varvec{\sigma }: \delta \varvec{\varepsilon } \ d\Omega _0^e\nonumber \\&\quad = \int _{\Omega _0^e} \left[ \overline{\varvec{\sigma }_{,\varvec{\varepsilon }}}: \left( \overline{\varvec{\varepsilon }} + \overline{\varvec{\varepsilon },_{\textbf{X}}} \cdot \Delta \textbf{X}\right) \right] :\left( \overline{\delta \varvec{\varepsilon }} + \overline{\delta \varvec{\varepsilon },_{\textbf{X}}} \cdot \Delta \textbf{X}\right) \, d\Omega _0^e \nonumber \\&\quad = \overline{\sigma _{,\varepsilon }}_{abcd}\overline{\varepsilon }_{cd} \overline{\delta \varepsilon }_{ab} \int _{\Omega _0^e} 1 \, d\Omega _0^e\nonumber \\&\qquad + \overline{\sigma _{,\varepsilon }}_{abcd}\overline{\varepsilon _{,X}}_{cde}\overline{\delta \varepsilon }_{ab} \int _{\Omega _0^e} \Delta X_e \ d\Omega _0^e\nonumber \\&\qquad + \overline{\sigma _{,\varepsilon }}_{abcd}\overline{\varepsilon }_{cd}\overline{\delta \varepsilon _{,X}}_{abe} \int _{\Omega _0^e} \Delta X_e \, d\Omega _0^e\nonumber \\&\qquad + \overline{\sigma _{,\varepsilon }}_{abcd}\overline{\varepsilon _{,X}}_{cde}\overline{\delta \varepsilon _{,X}}_{abf}\int _{\Omega _0^e} \Delta X_e \Delta X_f \, d\Omega _0^e \end{aligned}$$
(5)

The integral expressions are volume moments and can be viewed as integration weights. As they do not depend on the displacements, they can be calculated as part of the preprocessing. In this sense, the effort of integration can be accomplished offline, and in the analysis phase only evaluations at a reference point per element are required. The calculation of volume moments can be done either analytically or using Gauss quadrature. High-order quadrature methods on triangles can be found in [21]. For general polygons, the integral can also be shifted to the boundary where it can be integrated analytically as shown in Sect. 3.3 for straight edges. It should be noted that curved edges, pores, and other complex geometries can also be easily captured by the integration. In these cases, however, an appropriate ansatz space must be chosen to ensure continuity and completeness for optimal convergence.

Remark

In the case of linear elasticity under small deformations, the volume moments arise from the product of the strain tensor and its virtual counterpart. For a polynomial ansatz of degree n, volume moments of degree \(2(n-1)\) appear. The position of the integration point and hence the evaluation of the constant terms \(\overline{(\, )}\) can be chosen arbitrarily (it could even lie outside the element) since the integral of virtual work is calculated exactly. Thereby, the reference position must be taken into account when calculating the volume moments. When nonlinear material behavior is considered, as in the next subsection, the reference position gets relevant.

2.2 Finite deformations

To extend the method to the nonlinear regime, one could proceed as in the stabilization approach presented in [20] (subsection 6.3.2) and choose the first Piola–Kirchhoff stress tensor \(\textbf{P}=\Psi _{,\textbf{F}}\) and the deformation gradient tensor \(\textbf{F}\) as conjugate variables. However, this approach has the disadvantage that even for linear elastic material behavior, such as the St. Venant material model, an exact Taylor series expansion of \(\textbf{P}\) with respect to \(\textbf{F}\) requires an eighth order tensor, although it exhibits some symmetries. A more efficient approach is to use the right Cauchy–Green tensor \(\textbf{C}=\textbf{F}^T\cdot \textbf{F}\) and its conjugate stress measure \(\Psi _{,\textbf{C}}\) as kinematic variables. This has the advantage that both \(\textbf{C}\) and \(\Psi _{,\textbf{C}}\) are symmetric. Furthermore, it enables a clean separation between geometric and material nonlinearities. This is illustrated by considering the St. Venant model, which can be described by the following strain energy function:

$$\begin{aligned} \Psi ^{SV} = \frac{\lambda }{2} {\text {tr}}\left( \textbf{E}\right) ^2 + \mu {\text {tr}}\left( \textbf{E}^2\right) . \end{aligned}$$
(6)

Here, \(\lambda \) and \(\mu \) denote the two Lame constants, and \(\textbf{E}=\frac{1}{2} \left( \textbf{C}-\textbf{I}\right) \) is referred to as the Green–Lagrange strain tensor. The corresponding stress measure and material tangent can be computed as follows

$$\begin{aligned} \Psi ^{SV}_{,\textbf{C}}&= \frac{1}{2}\left( \lambda {\text {tr}} \left( \textbf{E}\right) \textbf{I} + 2 \mu \textbf{E}\right) = \frac{1}{2}\textbf{S} \end{aligned}$$
(7)
$$\begin{aligned} \Psi ^{SV}_{,\textbf{C}^2}&= \frac{1}{4}\left( \lambda \textbf{I}\otimes \textbf{I} + 2 \mu \mathbb {I}\right) = \frac{1}{4} \mathbb {C}, \end{aligned}$$
(8)

where \(\textbf{S}\) represents the second Piola–Kirchhoff stress tensor, \(\mathbb {C}\) denotes the tangent modulus with respect to the reference configuration, and \(\mathbb {I}\) symbolizes the fourth order identity tensor.

The St. Venant material model is special in that \(\Psi ^{SV}_{,\textbf{C}^2}\) is constant and thus the stress measure \(\Psi ^{SV}_{,\textbf{C}}\) is linear in \(\textbf{C}\). Therefore, the stress within a domain can be described using a Taylor series expansion with respect to \(\textbf{C}\) or \(\textbf{E}\), and the expansion can be truncated after the linear term without loss of accuracy. Hence, we now use \(\textbf{C}\) as the kinematic measure in our integration approach, and obtain the expression for the virtual work in the domain \(\Omega _0^e\) as

$$\begin{aligned} \int _{\Omega _0^e}\delta \Psi \, d\Omega _0^e = \int _{\Omega _0^e} \Psi _{,\textbf{C}}: \delta \textbf{C} \, d\Omega _0^e. \end{aligned}$$
(9)

The Taylor series expansion of the stress measure \(\Psi _{,\textbf{C}}\) is then expressed as

$$\begin{aligned} \Psi _{,\textbf{C}} = \overline{\Psi _{,\textbf{C}}} + \overline{\Psi _{,\textbf{C}^2}}: \Delta \textbf{C} + \left( \sum _{i=2}^{\infty }\frac{1}{i!} \overline{\Psi _{,\textbf{C}^{(i+1)}}}: \Delta \textbf{C}^{\otimes i}\right) , \end{aligned}$$
(10)

where we first consider only the linear part. The approach for the (virtual) right Cauchy–Green tensor is exact for a polynomial displacement ansatz of degree n when truncated to degree \(2\left( n-1\right) \). For instance, for a simplex-shaped second order finite element, this yields:

$$\begin{aligned} (\delta )\textbf{C}&= \overline{(\delta )\textbf{C}} + \overline{(\delta )\textbf{C}_{,\textbf{X}}} \cdot \Delta \textbf{X} + \frac{1}{2} \overline{(\delta )\textbf{C}_{,\textbf{X}^2}}: \Delta \textbf{X}^{\otimes 2} \nonumber \\&\quad + \left( \sum _{i=3}^{\infty }\frac{1}{i!} \overline{(\delta )\textbf{C}_{,\textbf{X}^i}}: \Delta \textbf{X}^{\otimes i}\right) . \end{aligned}$$
(11)

As mentioned in the previous subsection, the series expansion of the kinematic measure can now be substituted into the stress expression, as well as the virtual strain measure into the expression for the virtual work. Thus, the only non-constant values remaining in the integral are geometric quantities of the initial configuration and again result in volume moments. After some rearrangement, neglecting higher order terms, we obtain:

$$\begin{aligned} \int _{\Omega _0^e}\delta \Psi \ d\Omega _0^e = \sum _{i=0}^{4(n-1)} \frac{1}{i!} \overline{\delta \Psi _{,\textbf{X}^{i}}} \bullet \textbf{M}_i \end{aligned}$$
(12)

with the scalar product \(\bullet \) and the i-th order moment tensors

$$\begin{aligned} \textbf{M}_i = \int _{\Omega _0^e} \textbf{X}^{\otimes i} \, d\Omega _0^e. \end{aligned}$$
(13)

The abbreviations \(\delta \Psi _{,\textbf{X}^{i}}\) can be interpreted as the spatial derivative of the virtual strain energy evaluated at a reference integration point. In the considered example, they are composed as follows:

$$\begin{aligned} {\delta \Psi }&= {\Psi _{,C}}_{ab}\ {\delta C_{ab}}\nonumber \\ {\delta \Psi _{,X}}_e&= {\Psi _{,C^2}}_{abcd} {C_{,X}}_{cde}{\delta C}_{ab} + {\Psi _{,C}}_{ab} {\delta C_{,X}}_{abe}\nonumber \\ {\delta \Psi _{,X^2}}_{ef}&= {\Psi _{,C^2}}_{abcd} \left( {C_{,X^2}}_{cdef}{\delta C_{ab}} + 2 {C_{,X}}_{cde}{\delta C_{,X}}_{abf}\right) \nonumber \\&\quad + {\Psi _{,C}}_{ab} {\delta C_{,X^2}}_{abef}\nonumber \\ {\delta \Psi _{,X^3}}_{efg}&= 3{\Psi _{,C^2}}_{abcd}\left( {C_{,X^2}}_{cdef} {\delta C_{,X}}_{abg}\right. \nonumber \\&\quad \left. + {C_{,X}}_{cde} {\delta C_{,X^2}}_{abfg} \right) \nonumber \\ {\delta \Psi _{,X^4}}_{efgh}&= 6{\Psi _{,C^2}}_{abcd} {C_{,X^2}}_{cdef} {\delta C_{,X^2}}_{abgh}, \end{aligned}$$
(14)

where the overline is omitted for convenience while it is actually present for all measures, indicating the evaluation at the single integration point.

So far, the integration of the virtual work within the element is exact for the example of the second order approach in combination with the material model of St. Venant. Let us consider now, a nonlinear and non-polynomial strain energy function, such as the following neo-Hookean model according to [22],

$$\begin{aligned} \Psi ^{NH} = \frac{\mu }{2} \left( {\text {Tr}}\textbf{C} -3 - 2 \ln {J}\right) + \frac{\lambda }{4} \left( J^2 - 1 - 2 \ln {J}\right) \end{aligned}$$
(15)

with the determinant of the deformation gradient J. An exact integration using polynomial approximations is only feasible with an infinite number of terms, which is not practical. Even classical Gauss quadrature cannot fulfill this requirement. However, the Taylor series approach presented above provides the opportunity to selectively integrate the material and geometric nonlinearities with different levels of accuracy. To ensure stability, i.e., to avoid rank deficiency of the stiffness matrix, full geometric nonlinearity should be considered. This is achieved by including the complete basis functions of the Cauchy–Green tensor in the series expansion. Otherwise, for non-simplex elements or virtual elements (Sect. 3), all terms that ensure consistency must be included, and additional stabilization has to be used.

The considered material nonlinearity can be adjusted adaptively in the Taylor series expansion of the stress measure (10). From a stability point of view, at least the linear term is necessary, but often it is also sufficient. It should be noted that highly nonlinear material behavior could also be treated in this way, as the linear dependence is only formed in the material tangent space. The obvious advantage is that the evaluation of potentially computationally intensive evolution equations only needs to be performed once per element, while still retaining the benefits of a higher-order geometric approximation space. This becomes particularly interesting when a whole boundary value problem needs to be evaluated for each integration point, as is frequently done in the context of a multiscale approach, or the shape of an element requires a large number of Gauss points.

It should be noted, however, that in the example of plasticity, an element is only fully captured as either plastic or elastic. However, it is also possible to divide the integration domain into several parts per element, determine the volume moments separately for each part and evaluate the material equations accordingly. The division and number of integration domains could be chosen arbitrarily and, if necessary, adjusted during the simulation. Potential history variables would then have to be interpolated with a smoothing procedure. Furthermore, it should be noted that in the case of nonlinear material behavior, the position of the integration point is no longer negligible and can determine whether an element is captured, for example, as plastic or elastic. It is advantageous to place the integration point at the centroid of an element or an integration cell, as in this case, the first-order volume moment also disappears.

2.3 Automatic differentiation

The use of the Taylor series expansion of the stress tensor can quickly become complex and unwieldy for more complex material models, especially when considering a consistent linearization for the assembly of the stiffness matrix. Therefore, it is advisable to use software that allows for automatic differentiation (AD) and expression optimization. For the examples presented in Sect. 4 of this article, the packages AceGen and AceFEM were utilized. The expression optimization recognizes symmetries and optimizes the code accordingly, allowing for efficient generation of element routines. For instance, the fourth order tensor \(\Psi _{,\textbf{X}^4}\) (required for second-order approximations with nonlinear kinematic description) consists in two dimensions of 16 components, of which only five are independent. If full material nonlinearity was considered, the situation gets even severe and a manual implementation is not sensible anymore, as tensors up to order 10 have to be computed, analogous to Eq. (14). This strongly emphasizes the importance of AD and expression optimization for moment integration schemes.

To further improve efficiency in the automatic generation of element routines using AceGen, it is advantageous to start with a potential or pseudo potential, cf. [18]. The virtual work can be replaced by the strain energy, resulting in the residual being obtained from the derivative with respect to the actual unknowns (see also Sect. 3) while freezing potential history variables. The strain energy can then be integrated in a similar way as in Eq. (12) by

$$\begin{aligned} \int _{\Omega _0^e} \Psi \ d\Omega _0^e = \sum _{i=0}^{4(n-1)} \frac{1}{i!} \overline{\Psi _{,\textbf{X}^{i}}} \bullet \textbf{M}_i. \end{aligned}$$
(16)

The spatial derivatives of the strain energy can be calculated using AD:

$$\begin{aligned} \frac{{\hat{\delta }}^i \Psi }{{\hat{\delta }} \textbf{X}^i} = \Psi _{,\textbf{X}^i}, \end{aligned}$$
(17)

Thereby, \(\hat{\delta }\) denotes the AD operator. Prior to this, the strain energy has to be defined as a function of \(\textbf{X}\). This is ensured through the chain rule and an appropriate kinematic measure (here \(\textbf{C}\)). If the computational derivative is defined without special rules as in Eq. (17), all occurring terms are considered, as is done implicitly with Gauss quadrature. Separate consideration of geometric and material nonlinearities is possible through the additional specification of exception rules. Often, it is sufficient to consider material nonlinearity of first order, but an adaptive approach could also be pursued. In the example of the second order displacement approach, for a hyperelastic material model, the material nonlinearity of first order can be taken into account as follows:

$$\begin{aligned} \frac{{\hat{\delta }} \Psi }{{\hat{\delta }} \textbf{X}}&= \Psi _{,\textbf{X}}\Big \vert _{\frac{D \Psi }{D \textbf{C}}=\widehat{D_\textbf{C}\Psi }} \end{aligned}$$
(18)
$$\begin{aligned} \frac{{\hat{\delta }}^2 \Psi }{{\hat{\delta }} \textbf{X}^2}&= {\left( \frac{{\hat{\delta }} \Psi }{{\hat{\delta }} \textbf{X}}\right) }_{,\textbf{X}}\Bigg \vert _{\frac{\widehat{D_\textbf{C}\Psi }}{D \textbf{C}}=\widehat{D_{\textbf{C}^2}\Psi }} \end{aligned}$$
(19)
$$\begin{aligned} \frac{{\hat{\delta }}^3 \Psi }{{\hat{\delta }} \textbf{X}^3}&= {\left( \frac{{\hat{\delta }}^2 \Psi }{{\hat{\delta }} \textbf{X}^2}\right) }_{,\textbf{X}}\Bigg \vert _{\frac{\widehat{D_\textbf{C}\Psi }}{D \textbf{C}}=\widehat{D_{\textbf{C}^2}\Psi },\,\frac{\widehat{D_{\textbf{C}^2}\Psi }}{D \textbf{C}}=\textbf{0}} \end{aligned}$$
(20)
$$\begin{aligned} \frac{{\hat{\delta }}^4 \Psi }{{\hat{\delta }} \textbf{X}^4}&= {\left( \frac{{\hat{\delta }}^3 \Psi }{{\hat{\delta }} \textbf{X}^3}\right) }_{,\textbf{X}}\Bigg \vert _{\frac{\widehat{D_\textbf{C}\Psi }}{D \textbf{C}}=\widehat{D_{\textbf{C}^2}\Psi },\,\frac{\widehat{D_{\textbf{C}^2}\Psi }}{D \textbf{C}}=\textbf{0}}, \end{aligned}$$
(21)

where quantities marked with \(\widehat{\left( \,\,\,\right) }\) denote auxiliary variables that were defined priorly as

$$\begin{aligned} \widehat{D_{\textbf{C}}\Psi } = \Psi _{,\textbf{C}} \quad \text {and}\quad \widehat{D_{\textbf{C}^2}\Psi } = \Psi _{,\textbf{C}^2}. \end{aligned}$$
(22)

Note that as an exceptional rule, the material nonlinearity in the tangent space has been set to zero from second order onwards.

The integration of the strain energy within AceGen for the examples of Sect. 4 is performed using the code block shown in Fig. 1. Thereby, intSplit is a bool that specifies whether an integration split of material and geometrical nonlinearities should be performed. Further, ox represents the order of the polynomial integration accuracy, om represents the order of material nonlinearity, and C is the kinematic intermediate variable that depends on both the displacements \(\textbf{u}\) and the position relative to the reference integration point \(\textbf{X}\) via the shape functions. Details on how to compute the moments \(\textbf{M}_i\) will be discussed in Sect. 3.3.

Fig. 1
figure 1

Symbolic definition of moment integration of the strain energy in AceGen, taking into account the material nonlinearity om and the polynomial integration accuracy ox

Full size image

3 Application to second order virtual elements

If the moment integration from the previous section is used for bi- or tripolynomial elements, the required integration order increases rapidly and becomes inefficient. For example, moments up to degree eight are already required for the geometrically complete integration of a trilinear element in hyperelastic material models. While the highest polynomial degree in the basis is relevant for the complete integration, the convergence rate is, however, limited by the completeness of the basis set. A possible workaround for this problem is to under-integrate up to the polynomial degree required for convergence and to add stabilization in order to prevent a rank deficiency of the stiffness matrix.

This approach is used in the VEM in a very general way (see [23]). Thereby, the word virtual results from the fact that the generally implicit shape functions are to be evaluated only at the well-defined boundary and need not to be computed in the interior. Due to the evaluation at the boundary, the elements can in principle be of quite general shape (cf. [24]), so that also polygonal or polyhedron-shaped elements with curved boundaries are possible. This favors a wide range of applications, for example in the discretization of microstructures [25] or discrete particles [26] with single elements. As already mentioned, the approximation (here for the displacements) is thereby decomposed into two parts:

$$\begin{aligned} \textbf{u}_h = \textbf{u}_\pi + \textbf{u}_s \quad \text {with}\quad \textbf{u}_s = \textbf{u}_h - \textbf{u}_\pi . \end{aligned}$$
(23)

The first part, the projection \(\textbf{u}_\pi \), is usually a polynomial complete up to order k, which ensures the exactness and convergence, that are limited by the specification of the shape functions on the element edges. The remaining part \(\textbf{u}_s\) is mostly evaluated at the nodes only and is used for stabilization. By assuming that the strain energy of both parts can be modeled separately, it results on the region \(\Omega _0^e\) of the element e to be

$$\begin{aligned} \mathcal {G}_h^e = \mathcal {G}_\pi ^e + \mathcal {G}_s^e \end{aligned}$$
(24)

with the projection part

$$\begin{aligned} \mathcal {G}_\pi ^e = \int _{\Omega _0^e} \Psi \left( \textbf{u}_\pi \right) \,d\Omega _0^e \end{aligned}$$
(25)

and the stabilization part

$$\begin{aligned} \mathcal {G}_s^e = \frac{\gamma ^e}{2}\sum _I^{n_{nod}^e} \textbf{u}_s^2 \left( \textbf{X}_I\right) . \end{aligned}$$
(26)

To calculate the stabilization parameter \(\gamma ^e\), the approach from [27] is followed in the remainder of this paper:

$$\begin{aligned} \gamma ^e = \frac{\beta }{2} \mathbb {I} \bullet \Psi _{,\textbf{C}^2} \end{aligned}$$
(27)

where \(\beta \) equals 0.5 for Q2S meshes, 1 for Voronoi tessellations and \(\mathbb {I}\) denotes the fourth order unity tensor. The contribution of the element e to the global residual vector and stiffness matrix are then obtained as usual from

$$\begin{aligned} \textbf{R}^e = \mathcal {G}^e_{h,\textbf{u}^e} \quad \text {and}\quad \textbf{K}^e = \textbf{R}^e_{,\textbf{u}^e} \end{aligned}$$
(28)

3.1 Conditions of variational consistency

As already mentioned, the shape functions are assumed to be unknown or rather the solution of a boundary value problem within the element. The calculation of the projection must therefore refer to the known values at the boundary. Further, it should ensure consistency and thus be able to approximate the polynomial of degree k exactly. A simple least-squares regression is, however, not useful, since the use in the Galerkin method also requires a \(C^0\) continuity detected by the integration. Despite the fact that the virtual shape functions are defined in such a way that they have a global \(C^0\) continuity, this does not apply to the projection, which is therefore subject to additional conditions.

These additional integration constraints [28] (later called variational consistency constraints) ensure the fulfilment of the patch test and optimal convergence. The extension to polynomial approaches of arbitrary order (cf. [29]) has been used mainly in the context of meshfree methods, but is very similar to the projections in VEM and was developed around the same time. An overview in the context of meshfree methods can also be found in [20, 30]. The study of these conditions can reveal in a rather simple manner how the projections have to be defined. Therefore, a short introduction based on the Poisson equation is given in the following:

$$\begin{aligned} \Delta \theta + f = 0. \end{aligned}$$
(29)

The weak form is obtained by multiplication with a test function, partial integration and application of the Gauss theorem to obtain

$$\begin{aligned} \int _{\Omega _0} \theta _{,\textbf{X}}\cdot \delta \theta _{,\textbf{X}} - f \delta \theta \,d\Omega _0 = \int _{\partial \Omega _0} \theta _{,\textbf{X}} \cdot \textbf{n}_0 \delta \theta \,d\partial \Omega _0 \end{aligned}$$
(30)

Inserting the Galerkin ansatz for the test function \(\delta \theta = \sum _{I} \delta \theta _I \phi _I\) and differentiation with respect to \(\delta \theta _I\) gives the residual of node I. With the strong form \(f=-\Delta \theta \) this yields

$$\begin{aligned} \int _{\Omega _0} \theta _{,\textbf{X}}\cdot {\phi _I}_{,\textbf{X}} + \Delta \theta \phi _I \,d\Omega _0 = \int _{\partial \Omega _0} \theta _{,\textbf{X}}\cdot \textbf{n}_0 \phi _I \,d\partial \Omega _0 \end{aligned}$$
(31)

The conditions for variational consistency are obtained by first performing a Taylor series expansion of the primary variable up to the desired order (here \(k=2\)) and applying this to the source term, as well as the trial function:

$$\begin{aligned}&\int _{\Omega _0} \overline{\theta _{,\textbf{X}}} \cdot {\phi _I}_{,\textbf{X}} + \Delta \textbf{X} \otimes {\phi _I}_{,\textbf{X}}: \overline{\theta _{,\textbf{X}^{2}}} + \phi _I {\text {Tr}} \overline{\theta _{,\textbf{X}^{2}}} \,d\Omega _0\nonumber \\&\quad = \int _{\partial \Omega _0} \phi _I\left( \overline{\theta _{,\textbf{X}}}\cdot \textbf{n}_0 + \Delta \textbf{X}\otimes \textbf{n}_0: \overline{\theta _{,\textbf{X}^2}} \right) \,d\partial \Omega _0. \end{aligned}$$
(32)

In order to exactly reproduce arbitrary 2nd order polynomials, we then differentiate with respect to the constants \(\overline{\theta _{,\textbf{X}}}\) and \(\left( \overline{\theta _{,XX}},\overline{\theta _{,YY}},\overline{\theta _{,XY}}\right) \) and get the constraints for the test function integration

$$\begin{aligned}&\int _{\Omega _0} {\phi _I}_{,\textbf{X}} \,d\Omega _0 = \int _{\partial \Omega _0} \phi _I \textbf{n}_0 \,d\partial \Omega _0 \end{aligned}$$
(33)
$$\begin{aligned}&\int _{\Omega _0} \left( {\phi _I}_{,\textbf{X}}\otimes \Delta \textbf{X}\right) _{\text {sym}} + \phi _I \textbf{I} \,d\Omega _0\nonumber \\&\quad =\int _{\partial \Omega _0} \phi _I\left( \textbf{n}_0\otimes \Delta \textbf{X}\right) _{\text {sym}}\,d\partial \Omega _0 \end{aligned}$$
(34)

The first equation is necessary to fulfill the first order patch test, the second equation additionally for the second order patch test. Thereby, the surface integral has to vanish for shape functions that are zero on the boundary.

Remark

It should be noted that the conditions for variational consistency of the shape functions depend on the differential equation they are used in. Hence, above constraints derived using the Poisson equation are not sufficient to satisfy the second order patch test for linear elasticity. However, the constraints resulting from the virtual work principle can be derived in the same way. Instead of Eq. (34), then (cf. [29]) the very similar, but on the off-diagonal entries not equivalent condition appears:

$$\begin{aligned} \int _{\Omega _0} {\phi _I}_{,\textbf{X}}\otimes \Delta \textbf{X} + \phi _I \textbf{I} \,d\Omega _0 =\int _{\partial \Omega _0} \phi _I \textbf{n}_0\otimes \Delta \textbf{X}\,d\partial \Omega _0. \end{aligned}$$
(35)

3.2 Construction of projection

Provided the surface integrals are evaluated exactly, the conditions for variational consistency are equivalent to the requirement that the virtual work \(\varvec{\sigma }:\delta \varvec{\varepsilon }\) has to be integrated accurately for arbitrary second order displacement fields. In other words, in the case of the patch test, the virtual work must be completely captured by the projection, so that it can be derived from the orthogonality

$$\begin{aligned} \int _{\Omega _0^e} \varvec{\sigma }: \left( \varvec{\varepsilon }_\pi - \varvec{\varepsilon }_h\right) \,d\Omega _0^e = 0 \end{aligned}$$
(36)

for corresponding stress fields. The same projection can also be calculated by minimization of an error functional, where a suitable error norm has to be chosen in each case. Using this approach, a projection for the Poisson equation and subsequently the equations of linear elasticity is derived in the following. Moreover, the projection is applied directly to the shape functions, so that projected shape functions are calculated. The projection of the respective physical field is then obtained using the classical approach, such as \(\theta = \sum _{I} \theta _I {\phi _\pi }_I\). Here \(\Theta _I\) are the nodal unknowns and \({\phi _\pi }_I\) are the projected shape functions or rather the shape functions of the projection.

3.2.1 Poisson equation

If we consider a second-order ansatz (\(k=2\)) and assume that the shape functions in the interior of each element each satisfy Laplace’s equation, the projection of these onto a polynomial of degree two can then be represented as

$$\begin{aligned} \phi _\pi = \phi _{\pi _0} + \textbf{a}_\pi \cdot \textbf{p}, \end{aligned}$$
(37)

where \(\phi _{\pi _0}\) and \(\textbf{a}_\pi \) are coefficients and \(\textbf{p}\) is the centroid-relative, full set of polynomial monomials of degree one to two. A variationally consistent projection results from minimizing the scaled \(L^2\) error

$$\begin{aligned} \frac{1}{2} \int _{\Omega _0^e} \left( \phi _\pi -\phi _h\right) ^2 d\Omega _0^e \rightarrow \min _{\left\{ \phi _{\pi _0},\, \textbf{a}_\pi \right\} }. \end{aligned}$$
(38)

Differentiation results in the following:

$$\begin{aligned} \phi _{\pi _0}:0&=\int _{\Omega _0^e} \left( \phi _\pi -\phi _h\right) d\Omega _0^e \end{aligned}$$
(39)
$$\begin{aligned} \text {and}\quad \textbf{a}_{\pi }:\textbf{0}&=\int _{\Omega _0^e} \left( \phi _\pi -\phi _h\right) \textbf{p}\,d\Omega _0^e. \end{aligned}$$
(40)

The first equation yields by inserting the approach of Eq. (37) and reformulation

$$\begin{aligned} \int _{\Omega _0^e}\phi _{\pi _0}+\textbf{a}_\pi \cdot \textbf{p}\, d\Omega _0^e = \int _{\Omega _0^e}\phi _h\, d\Omega _0^e:= m_0^e. \end{aligned}$$
(41)

The right part denotes the moment of the shape function \(m_0^e\), which is approximated later on and is also called virtual moment. The gradient of the second part (Eq. (40)) is calculated as

$$\begin{aligned} \textbf{0} = \int _{\Omega _0^e} \textbf{p}\otimes \left( {\phi _{\pi }}_{,\textbf{X}}-{\phi _h}_{,\textbf{X}}\right) + \left( \phi _\pi -\phi _h\right) \textbf{p}_{,\textbf{x}}\,d\Omega _0^e \end{aligned}$$
(42)

where the later part is included in the original equation and thus is zero. A linear combination of the above equations that is equivalent to minimizing an \(H^1\)-error with respect to \(\textbf{a}_\pi \) yields

$$\begin{aligned} \textbf{0} = \int _{\Omega _0^e} \left( {\phi _{\pi }}_{,\textbf{X}}-{\phi _h}_{,\textbf{X}}\right) \cdot \textbf{p}_{,\textbf{X}} \,d\Omega _0^e \end{aligned}$$
(43)

Shifting the projection part to the left side, inserting the projection ansatz, using integration by parts and utilizing Gauß’ theorem leads to

$$\begin{aligned} \textbf{a}_\pi \cdot \int _{\Omega _0^e} \textbf{p}_{,\textbf{X}} \cdot {\textbf{p}_{,\textbf{X}}}^T \,d\Omega _0^e&= \int _{\Omega _0^e} {\phi _h}_{,\textbf{x}} \cdot {\textbf{p}_{,\textbf{X}}}^T \,d\Omega _0^e\end{aligned}$$
(44)
$$\begin{aligned}&= \int _{\partial \Omega _0^e} \phi _h \textbf{n}_0^e \cdot {\textbf{p}_{,\textbf{X}}}^T \,d\partial \Omega _0^e\nonumber \\&\quad - \int _{\Omega _0^e} \phi _h \Delta \textbf{p} \,d\Omega _0^e, \end{aligned}$$
(45)

where \(\textbf{n}_0^e\) stands for the normal on the surface of the element. In the case of a second order approach, the Laplacian of the monomials is constant, which allows the right integral to be identified as a scaled virtual moment. In the classical VEM, an additional unknown is introduced at the element level for this purpose. In the serendipity approaches, see for example [31,32,33], the virtual moment is approximated so that in the case of \(k=2\) no additional degrees of freedom are needed at the element level:

$$\begin{aligned} m_0^e \approx \int _{\Omega _0^e} \phi _c d\Omega _0^e. \end{aligned}$$
(46)

The function \(\phi _c\) can thereby be determined via a nodally integrated second-order least squares approach:

$$\begin{aligned} \phi _c= \textbf{a}_c \cdot \tilde{\textbf{p}}, \end{aligned}$$
(47)

with the complete basis (including 1) of second order polynomials \(\tilde{\textbf{p}}\). The coefficients then result from the minimization:

$$\begin{aligned} \textbf{a}_c= & {} \arg \min \left\{ \frac{1}{2} \sum _{I=1}^{n_{nod}^e} \left( \phi _c\left( \textbf{X}_I\right) -\phi _I\right) ^2 \right\} \nonumber \\= & {} \left( \sum _{I=1}^{n_{nod}^e} \tilde{\textbf{p}}_I \phi _I\right) \cdot \left( \sum _{I=1}^{n_{nod}^e} \tilde{\textbf{p}}_I\otimes \tilde{\textbf{p}}_I\right) ^{-1} . \end{aligned}$$
(48)

With this, the coefficients of the projected shape functions can now also be computed. By including the virtual moment, they are determined as

$$\begin{aligned} \textbf{a}_\pi&= \left( \int _{\partial \Omega _0^e} \phi \textbf{n}_0^e \cdot {\textbf{p}_{,\textbf{X}}}^T \,d\partial \Omega _0^e - \Delta \textbf{p} m_0 \right) \nonumber \\&\quad \cdot \left( \int _{\Omega _0^e} \textbf{p}_{,\textbf{X}} \cdot {\textbf{p}_{,\textbf{X}}}^T \,d\Omega _0^e\right) ^{-1} \end{aligned}$$
(49)
$$\begin{aligned} \text {and}\quad \phi _{\pi _0}&= \frac{1}{\Vert \Omega _0^e\Vert }\left( m_0-\textbf{a}_\pi \cdot \int _{\Omega _0^e} \textbf{p}\,d\Omega _0^e\right) , \end{aligned}$$
(50)

where \(\Vert \Omega _0^e\Vert \) denotes the volume of the element. The surface integral in Eq. (49) has a third order polynomial argument and can be computed either analytically or using a 3-point Gauß-Lobatto quadrature.

3.2.2 Balance of linear momentum

If the projected functions calculated in the previous subsection are used to solve the equations of linear elasticity, it turns out that they satisfy the first order patch test, but not the second order patch test, and in general do not guarantee optimal convergence. This is due to the fact that the conditions for variational consistency are not the same from the second order upwards. For linear quasistatic problems, it would be sufficient to perform a projection of the strain tensor, analogous to Eq. (36) (cf. [34]). Volume loads and dynamic terms can then be considered via separate projections. Here, however, once again the approach to apply the projection to the full shape functions (not just their derivatives) will be pursued.

Interior-optimal shape functions (in the sense that each of their linear combinations exactly satisfies the interior differential equation) cannot generally be represented by a scalar function in the case of linear elasticity, but require a tensor-valued representation:

$$\begin{aligned} \textbf{u}_\pi = \sum _{I=1}^{n_{nod}^e} {\varvec{\phi }_I}_\pi \cdot \textbf{u}_I, \end{aligned}$$
(51)

where \(\varvec{\phi }_{I\,\pi }\) is a tensor of second order. To calculate the projected shape functions, we first use a strain projector and then compute an \(L^2\) projection that results in the same strain projection. For the second order formulation, a linear strain field has to be considered. Thus, we may obtain the projected strain field of a shape function with the first order ansatz as

$$\begin{aligned} \varvec{\varepsilon }_\pi = \left( \mathbf {u_\pi }_{,\textbf{X}}\right) _{\text {sym}} = \textbf{a}_{\varvec{\varepsilon }_\pi } \cdot \left( \begin{array}{c} 1 \\ X \\ Y \end{array}\right) \end{aligned}$$
(52)

and calculate the 9 independent coefficients \(\textbf{a}_{\varvec{\varepsilon }_\pi }\) by minimizing

$$\begin{aligned} \frac{1}{2} \int _{\Omega _0^e} \Delta \varvec{\varepsilon }:\Delta \varvec{\varepsilon } \,d\Omega _0^e \rightarrow \min _{\textbf{a}_{\varvec{\varepsilon }_\pi }} \end{aligned}$$
(53)

with \(\Delta \varvec{\varepsilon } = \varvec{\varepsilon }_\pi - \varvec{\varepsilon }_h\). Following the procedure of least squares, the coefficients are the root of

$$\begin{aligned} \textbf{0} = \int _{\Omega _0^e} \left( \varvec{\varepsilon }_\pi - \varvec{\varepsilon }_h\right) : {\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }} \,d\Omega _0^e:= \textbf{Q}_{\varvec{\varepsilon }_\pi }. \end{aligned}$$
(54)

The integral of the left part can easily be computed via moment integration, since the argument is a second order polynomial:

$$\begin{aligned} \int _{\Omega _0^e} \varvec{\varepsilon }_\pi :{\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }} \,d\Omega _0^e = \sum _{i=0}^{2} \frac{1}{i!} \overline{\left( \varvec{\varepsilon }_\pi :{\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }}\right) _{,\textbf{X}^{i}}} \bullet \textbf{M}_i^e, \end{aligned}$$
(55)

where the overline denotes evaluations at the centroid. As the actual shape functions in the interior of an element shall not be computed, the integral of the right part has be transformed into a surface integral:

$$\begin{aligned}&\int _{\Omega _0^e} \varvec{\varepsilon }_h:{\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }} \,d\Omega _0^e = \int _{\Omega _0^e} {\textbf{u}_h}_{,\textbf{X}}:{\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }} \,d\Omega _0^e \nonumber \\&\quad = \int _{\Omega _0^e} \left( \textbf{u}_h\otimes {\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }}\right) _{,\textbf{X}} - \textbf{u}_h \cdot {\text {Div}}\left( {\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }}\right) \,d\Omega _0^e \nonumber \\&\quad = \int _{\partial \Omega _0^e} \left( \textbf{u}_h\otimes \textbf{n}_0^e\right) :{\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }} \, d\partial \Omega _0^e - \textbf{m}_{\textbf{u}}^e \cdot {\text {Div}}\left( {\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }}\right) . \end{aligned}$$
(56)

Thereby first the fact was used that the double contraction of a symmetrical tensor with an antisymmetrical yields zero. Then partial integration can be used and the volume integral is transformed into a surface integral, where a serendipity projection is performed on both entries of \(\int _{\Omega _0^e} \textbf{u}_h\,d\Omega _0^e\). The virtual moment of the displacement vector \(\textbf{m}_{\textbf{u}}^e\) can be computed analogous to Eqs. (46) to (48). Note that the divergence operates one the first or second index of \({\varvec{\varepsilon }_\pi }_{,\textbf{a}_{\varvec{\varepsilon }_\pi }}\). Having computed both integrals, we can obtain the projected strain field of Eq. (52) by performing one Newton step on (54):

$$\begin{aligned} \varvec{\varepsilon }_\pi = -\left[ \overline{\left( \frac{\partial \textbf{Q}_{\varvec{\varepsilon }_\pi }}{\partial \textbf{a}_{\varvec{\varepsilon }_\pi }}\right) }^{-1}\cdot \overline{\textbf{Q}_{\varvec{\varepsilon }_\pi }}\right] \cdot \left( \begin{array}{c} 1 \\ X \\ Y \end{array}\right) . \end{aligned}$$
(57)

As mentioned before, for dynamic analyses or the application of volume forces, the strain projection is not sufficient and the full projection of the shape functions is required. But they are not uniquely determined by \(\varvec{\varepsilon }_\pi \). To achieve uniqueness, the information about the constant part and the antisymmetric part of the shape function gradient is still needed. This can be included by an \(L_2\) minimization.

Therefore, we use a Taylor series expansion and compare the coefficients. In total, 12 equations are needed to uniquely determine the projection of the displacement field. The symmetric gradient of the shape function vector already includes nine components. Two additional equations come via the \(L^2\) minimization as in (38) for each component of the displacement field. The last equation may be obtained from the \(L_2\) minimization of the antisymmetric part of the shape function gradient, such that a full set of equations uniquely identifying the coefficients states

$$\begin{aligned} \overline{\left( {\textbf{u}_\pi }_{,\textbf{X}}\right) _{\text {sym}}}&= \overline{\varvec{\varepsilon }_\pi } \end{aligned}$$
(58)
$$\begin{aligned} \overline{{\left( {\textbf{u}_\pi }_{,\textbf{X}}\right) _{\text {sym}}}_{,\textbf{X}}}&= \overline{{\varvec{\varepsilon }_\pi }_{,\textbf{X}}} \end{aligned}$$
(59)
$$\begin{aligned} \int _{\Omega _0^e} \textbf{u}_\pi \,d\Omega _0^e&= \textbf{m}_{\textbf{u}}^e \end{aligned}$$
(60)
$$\begin{aligned} \overline{\left( {\textbf{u}_\pi }_{,\textbf{X}}\right) _{\text {asym}}}&= \frac{1}{2\left\| \Omega _0^e\right\| }\int _{\Omega _0^e}\textbf{u}_h\cdot \left( \begin{array}{c} {n_0^e}_Y \\ -{n_0^e}_X \end{array}\right) \,d\Omega _0^e. \end{aligned}$$
(61)

Finally, the projected shape functions can be easily obtained by differentiation with respect to the nodal displacements:

$$\begin{aligned} {\varvec{\phi }_I}_\pi = \frac{\partial \textbf{u}_\pi }{\partial \mathbf {u_I}}. \end{aligned}$$
(62)
Fig. 2
figure 2

Mathematica command for symbolic evaluation of the contribution of a straight surface segment to polynomial moments, here exemplarily \(\textbf{p}=\left( 1,x,y,x y^5\right) \). The variables \(\left\{ x1,y1\right\} \) and \(\left\{ x2,y2\right\} \) respectively stand for the position vectors (relative to the element’s centroid) of the nodes bounding the line element. nx denotes the fraction of the surface segment in the x direction

Full size image

3.3 Calculation of integration moments on polygons

The calculation of the monomial moments may e.g. be done either with triangulation and Gaussian quadrature or analytically (which was used for this article). Therefore, the volume integral can be shifted to an integral over the surface, similar as in [35]. Let us consider the integral of a polynomial monomial \(p=p\left( x,y\right) \) over \(\Omega _0^e\). We may integrate the monomial with respect to one of the coordinates, e.g. x, and name it P. Thus, \(p=P_{,x}\) and we compute the integral as the first component of

$$\begin{aligned} \int _{\Omega _0^e} \left( \begin{array}{c} p \\ \dots \end{array}\right) \,d\Omega _0^e = \int _{\Omega _0^e} {\text {Grad}} P \,d\Omega _0^e = \int _{\partial \Omega _0^e} P \textbf{n}_0^e \,d\partial \Omega _0^e \end{aligned}$$
(63)

Considering a polygonal region \(\Omega _0^e\), the integral formula over one line segment of \(\partial \Omega _0^e\) can be easily generated via Mathematica as exemplarily stated in Fig. 2. Once computed the monomial moments with respect to the centroid of the polygon, the integral of a polynomial can be easily be obtained from a Taylor series expansions as e.g. in Eq. (55).

Fig. 3
figure 3

On the left: Voronoi discretization for the patch test with free nodes (black), Dirichlet nodes (blue) and Neumann nodes (red). On the right: Exemplary deformed configuration of the second order patch test with the projection of Sect. 3.2.1 (color figure online)

Full size image

Alternatively, a quadrature rule can also be applied to evaluate the surface integrals. If the shape functions are included and the order is below \(2(k+1)-3\) (here \(k=2\)), the Gauss–Lobatto quadrature may be used, whereby only nodal evaluations are necessary and the edge nodes can be summed up.

3.4 Treatment of volume forces and tractions

One possibility to variationally consistently apply volume loads \(\overline{\textbf{b}}\) is to capture them in the consistency part of the weak form, see for example [36]. For this purpose, the potential from Eq. (25) has to be extended:

$$\begin{aligned} \mathcal {G}_\pi ^e = \int _{\Omega _0^e} \Psi \left( \textbf{u}_\pi \right) - \overline{\textbf{b}} \cdot \textbf{u}_\pi \,d\Omega _0^e - \int _{\partial \Omega _0 \cap \partial \Omega _0^e} \textbf{t} \cdot \textbf{u}_h \,d\partial \Omega _0^e \end{aligned}$$
(64)

For this, in the case \(k=2\), in the displacement projection, at least the constant monomial (as in Eq. (61)) must be included in the minimization of the \(L^2\) error. Thus, the constant source term necessary to satisfy the second-order patch test can be accurately accounted for. The surface loads \(\textbf{t}\) act on the boundary and can therefore be considered directly via the known polynomial shape functions.

For the sake of diversification, a different approach will be followed within the scope of this article: Direct application to the nodes. The necessary weights for this, such as the effective nodal surfaces normals, can be determined, for example, via the conditions for variational consistency, cf. [37, 38]. Another possibility is to define pseudo strain energy functions and evaluate the global residual vector in certain configurations. The nodal residuals then serve as nodal load applicants. This has the advantage that volume loads can be incorporated in the same manner. In addition, the implementation effort is marginal when using AD software, since only the definition of the strain energy has to be replaced in comparison to the mechanical analysis. For the calculation of the effective nodal surfaces, the trace of the deformation gradient can be used as pseudo strain energy.

$$\begin{aligned} \Psi ^{SL} = {\text {Tr}} \textbf{F}, \end{aligned}$$
(65)

where the surface normals result as nodal residuals, evaluated in the undeformed configuration (as in Eq. (28)):

$$\begin{aligned} \textbf{n}_{0\,I} = \mathcal {G}^{SL}_{\pi ,\textbf{u}_I}. \end{aligned}$$
(66)

Similarly, nodal volume load applicants can be calculated using the pseudo strain energy

$$\begin{aligned} \Psi ^{VL} = \frac{1}{2}\varvec{\varepsilon }:\varvec{\varepsilon } \end{aligned}$$
(67)

The residual vector now has to be evaluated in the deformed configuration

$$\begin{aligned} \textbf{u}_I = \frac{1}{2} \left( \begin{array}{c} X_I^2 \\ Y_I^2 \end{array}\right) . \end{aligned}$$
(68)

Again, the weighting factors result as

$$\begin{aligned} \textbf{v}_{\overline{\textbf{b}}\,I} = \mathcal {G}^{VL}_{\pi ,\textbf{u}_I} \end{aligned}$$
(69)

The application of the surface and volume loads can then simply be added to the strain energy part of Eqs. (25) and (26):

$$\begin{aligned} \mathcal {G} = \mathcal {G}_{\pi } + \mathcal {G}_{s} - \sum _{I}^{n_{nod}} \left[ \textbf{u}_I \cdot \textbf{P}_I \cdot \textbf{n}_{0\,I}+ \sum _d^{n_{dim}} u_{I\,d} \overline{b}_{I\,d} v_{\overline{\textbf{b}}\,I\,d} \right] . \end{aligned}$$
(70)

Note that corner nodes require separate treatment if the load application is different on both sides of the node. Since the nodal load applicants are effective quantities, the surfaces of the neighbored line segments are aggregated. The individual surfaces can be decomposed by projections of the effective surface vector in the direction of the adjacent surface unit normals.

4 Numerical examples

The following section contains five examples demonstrating moment integration in FEM and VEM. In the first part, the fulfillment of the patch test and the convergence rates within linear elasticity are examined. Subsequently, three classical examples in the field of hyperelasticity are given.

4.1 Linear elasticity patch test

With the patch test, the fulfillment of the conditions of variational consistency can be verified numerically in a simple way, since the conditions have also emerged from the requirement that the patch test is to be fulfilled. In this example the region \(\left\{ X\times Y\right\} \in \left\{ \left[ -1,1\right] \times \left[ -1,1\right] \right\} \) is discretized and the error to a polynomial solution is calculated. The integration of the errors was done with moment integration, including spatial derivatives up to order \(k^2\) with \(k=2\). In the patch test of first and second order, respectively, the used analytical solution is

$$\begin{aligned} \textbf{u}&= \left( \begin{array}{c} 0.1 X + 0.3 Y \\ 0.2 X + 0.4 Y \end{array}\right) \quad \text {or rather}\nonumber \\ \textbf{u}&= \left( \begin{array}{c} 0.12 X + 0.14 Y + 0.16 X^2 + 0.18 XY + 0.2 Y^2 \\ 0.11 X + 0.13 Y + 0.15 X^2 + 0.1 XY + 0.21 Y^2 \end{array}\right) \end{aligned}$$
(71)

For the latter, a source term is additionally necessary, which results from the strong form of linear elasticity:

$$\begin{aligned} \overline{\textbf{b}} = -\left( \begin{array}{c} 0.42 \lambda + 1.14 \mu \\ 0.6 \lambda + 1.32 \mu \end{array}\right) , \end{aligned}$$
(72)

where the Lamé constants are calculated from the Young’s modulus \(E=1\) and the Poisson’s ratio \(\nu =0.3\). The imposition of the boundary conditions is shown in Fig. 3. While the black points represent free nodes, the blue points refer to the Dirichlet boundary and the red points to the Neumann boundary. Additionally, the exemplary deformation in the case of the second order patch test is shown. Table 1 lists the errors in the \(L^2\) and \(H^1\) norm for the two projections from Sects. 3.2.1 and 3.2.2. It can be easily seen that the conditions for variational consistency of the Poisson equation from the second order on are no longer sufficient to guarantee accuracy in the weak form of the linear momentum preservation. Using the projection of Sect. 3.2.2, the patch test is satisfied up to machine precision.

Table 1 Error norms in \(L^2\) and \(H^1\) for the linear and quadratic patch tests with different projections
Full size table
Fig. 4
figure 4

Exemplary deformed configuration of the manufactured solution with a Voronoi discretization

Full size image
Fig. 5
figure 5

Plot of the \(L^2\) (left) and \(H^1\) (right) error for the manufactured solution with different element topologies and formulations. The mean convergence rate is plotted next to the abbreviations in the legends

Full size image

4.2 Convergence study

In the second example, a manufactured solution (cf. [39]) is used to investigate whether the expected convergence rates are achieved. For this, at the boundary of the domain \(\left\{ X\times Y\right\} \in \left\{ \left[ -1,1\right] \times \left[ -1,1\right] \right\} \) the displacement is imposed, corresponding to

$$\begin{aligned} \textbf{u} = \left( \begin{array}{c} \sin {\frac{\pi }{2}X} \cos {\frac{\pi }{2}Y} \\ \cos {\frac{\pi }{2}X} \sin {\frac{\pi }{2}Y} \end{array}\right) . \end{aligned}$$
(73)

A volume load is applied to all interior nodes in accordance with the strong form of linear elasticity:

$$\begin{aligned} \overline{\textbf{b}} = -\frac{E \left( 1-\nu \right) \pi ^2}{2\left( {2\nu ^2+\nu -1}\right) } \left( \begin{array}{c} \sin {\frac{\pi }{2}X} \cos {\frac{\pi }{2}Y} \\ \cos {\frac{\pi }{2}X} \sin {\frac{\pi }{2}Y} \end{array}\right) . \end{aligned}$$
(74)

As material parameters \(E=1\) and \(\nu = 0.3\) are used. The error in the \(L^2\) and \(H^1\) norm is calculated under continuous mesh refinement. Figure 4 shows an example of the deformed configuration for a Voronoi discretization with \(\left( 2N\right) ^2\) and \(N=3\) elements. The errors and the corresponding average convergence rate are plotted for different discretizations in Fig. 5. The abbreviation V2 stands for a second-order Voronoi mesh. The tessellation was regularized with an initially random seed point distribution using three Lloyd iterations. Furthermore, the abbreviation Q2S stands for an eight-node element and T2 for a six-node element. In addition, a one-point moment-integrated (MI) triangular third-order finite element was included. All formulations or element shapes show optimal convergence properties, only the virtual element with Laplace projection (LP, see Sect. 3.2.1) shows a disturbed convergence rate.

Fig. 6
figure 6

On the left: Deformed configuration of the thin beam problem. On the right: Convergence of the vertical displacement of the free end for different formulations and element topologies

Full size image

4.3 Cantilever with end load

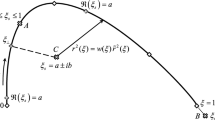
The further numerical examples consider finite deformations and a nonlinear material behavior corresponding to (15). First, a thin beam with a length of 1000 and a height of 1 is considered. At the left end the beam is clamped and at the right end it is loaded with a line load of \(10^{-6}\) in the (vertical) negative y-direction. Plane strain conditions with material parameters \(E=1\) and \(\nu = 0.49\) is considered. An exemplary deformed shape of the beam is shown in Fig. 6.

For discretization, one element is used along the y-direction. In the longitudinal direction, a refinement with \(2^{N-1}\) elements is performed. The resulting vertical displacement at the free end of the beam is plotted on the right side of Fig. 6 for different formulations. While a classical Gaussian quadrature was used for numerical integration for the FEM, the virtual elements were integrated by moment quadrature with linearized material behavior using a geometric material nonlinearity integration split. It is evident that despite the linearization in each element, the VEM solution with T2 elements is almost exactly above the FEM solution. Thus, moment integration can be used effectively even if large differences in stress occur within one element, as is the case with a discretization into two triangular elements. As such, bending stresses predominate in the left-hand region, while tensile stresses predominate in the right-hand region due to the large deformation. The locking to be observed is inherent to the displacement-based formulations without further treatment, as expected.

Finite elements with additional consistent components, as the FEM Q2 and FEM Q2S formulations, show in this specific example a slightly softer behavior. This is assumed to be because only the full polynomials to degree two are considered in the projection, and thus the VEM formulations have the same consistent basis set as the T2 FEM-Elements. Choosing a higher order moment integration scheme or using Gaussian quadrature does not affect this.

Fig. 7
figure 7

On the left: Geometry, boundary conditions and material parameters of the Cook’s membrane problem. On the right: Exemplary deformed configuration of a VEM Voronoi discretization with colored vertical displacement

Full size image
Fig. 8
figure 8

Convergence behavior of the vertical displacement of the upper right edge of Cook’s membrane for various element topologies with VEM and FEM. On the left, values are plotted over the element division, while on the right over the logarithmic scaled computational time of the analysis phase

Full size image

4.4 Cook’s membrane problem

The next example examined is Cook’s membrane problem, see e.g. [40]. The geometry of the problem, as well as the boundary conditions, material parameters and an example deformed state are shown in Fig. 7. Various virtual and finite element topologies were subject to refinement. The generated meshes contain \(2^N\) elements (the triangular ones twice as many). To ensure a mostly regular Voronoi discretization, 50 Lloyd iterations were performed with an initially random seed point distribution. All virtual elements were integrated using one-point moment quadrature with linear material behavior in the material tangent space per element, and the finite elements were integrated using Gaussian quadrature. For comparison, Voronoi-shaped VEM elements with triangulation and Gaussian integration (abbreviation GI) are also shown. The Load application was performed in one step and an average of 7 Newton iterations.

Table 2 Average computing times for the assembly of the global residual vector and stiffness matrix for one Newton iteration, devided by the number of elements
Full size table
Fig. 9
figure 9

On the left: Geometry, boundary conditions and material parameters of the punch problem. On the right: Deformed configuration in case of a random Voronoi discretization with the integration scheme X4. Blue coloring denotes nodes on the Dirichlet boundary, while the red nodes are on a combined Dirichlet/Neumann boundary (color figure online)

Full size image
Fig. 10
figure 10

Convergence of the vertical displacement of the upper left and upper right nodes with increasing mesh division for different moment integration schemes

Full size image

To compare the formulations, Fig. 8 plots the vertical displacement of the upper right corner against the element division and the computation time of the analysis phase (assembling time plus linear solver time). All calculations were performed on a desktop computer with intel core i7-7700. Due to the different integration, the VEM T2 and FEM T2 formulations are not identical and a deviation is observed for very coarse discretization. Nevertheless, the VEM, especially with the Voronoi discretization, shows very good convergence behavior in this example.

The average times required to assemble the residual vector and tangent matrix per element and iteration are listed in Table 2. Although for neo-Hooke’s material behavior, the moment integrated VEM elements on the T2 topology require about three times the assembling time as a Gaussian integrated FEM element, the factor is only about 1.8 for the Q2S topology.

Comparing triangulation with Gauss quadrature and moment integration using Voronoi cell-formed VEM elements shows a clear advantage of moment integration. Considering the computational effort for node-based stabilization and integration of the projection part separately, it is found that in the case of moment integration, the computational time of the stabilization part is predominant. In fact, the assembly time for the classical one-point underintegration increases to the fourth-order moment integration by only about 42 percent. If a combined element routine (stabilization plus projection) is generated by means of AceGen, the average evaluation time results to about \(11.18\,\upmu s\) compared to the Gaussian integration with \(24.58\, \upmu s\).

4.5 Punch test

Finally, the punch test is consulted as in the [32] The geometry, boundary conditions, material parameters and an exemplary deformed configuration are shown in Fig. 9. The nodes with Dirichlet boundary condition are highlighted in blue. The nodes colored red are subjected to a line load and are additionally constrained in the x-direction.

In a convergence study, the vertical displacement in the two upper vertices is analyzed. The calculated displacements are plotted in Fig. 10. Biquadratic finite elements integrated by Gaussian quadrature are used as reference. The VEM discretizations consist of randomly generated Voronoi cells without further Lloyd iterations. To ensure an element corner at the edge of the load application, the Voronoi mesh was generated on the left half of the domain and mirrored to the right. Three different moment integration schemes are compared as well as triangulation and Gaussian quadrature. The integration with geometric-material nonlinearity split with linear material behavior per element in the tangent space is given the abbreviation M1X4. For the X4 and X8 integration schemes, full material nonlinearity was included, i.e., without a differentiation exception. The fourth and eighth degrees were used as the highest derivative order, respectively.

It can be observed that due to the very large deformation, the assumption of material behavior linearly varying within an element can lead to a loss of accuracy with coarse discretization. Capturing the full material nonlinearity can address this inaccuracy, and the spatial derivative up to degree four can be considered sufficient. The additional cost of the X4 scheme is very small due to the efficient code generation by AceGen and is only a few percent. For the derivatives included up to degree eight, the assembly time doubles. Furthermore, oscillations are seen in the graph for the coarse discretizations, which is due to the random generation of the Voronoi cells. After sufficient refinement, the solution quickly converges to the reference solution.

5 Conclusion

The present article has presented an integration scheme alternative to the Gaussian quadrature of the weak form in Galerkin methods. By the additional evaluation of higher order derivatives, the number of integration points can be reduced to one without a loss of stability or disturbing the convergence rate. Thus, the integration method is particularly relevant in all those areas where either many integration points are needed or each individual integration point is very expensive. Its effective use was therefore demonstrated using a second-order VEM formulation where the assembly time for Voronoi cell shaped elements can be approximately halved compared to Gaussian quadrature in case of neo-Hooke’s material behavior.

The numerical examples presented show that in many cases it is sufficient to assume a linearly varying material behavior in each element. This considerably shortens the expressions for the spatial derivatives of the strain energy, which also allows a manual use, i.e. without AD software. If the accuracy is no longer sufficient for coarse discretizations and very large deformations, higher nonlinearities have to be considered. It is then advisable to switch directly to full nonlinearity, which, however, only makes sense when using AD.

For further development, particularly interesting areas are, on the one hand, the use in curvilinear elements, where often a large number of integration points is used. Moreover, the use in inelastic problems should be investigated, where it is necessary to consider the plastic yielding in the construction of the material tangent space. Last but not least, the use in macro elements in computational homogenization could offer a promising possibility to significantly reduce the number of micro problems to be solved.