A virtual element formulation for general element shapes

Abstract

The virtual element method is a lively field of research, in which considerable progress has been made during the last decade and applied to many problems in physics and engineering. The method allows ansatz function of arbitrary polynomial degree. However, one of the prerequisite of the formulation is that the element edges have to be straight. In the literature there are several new formulations that introduce curved element edges. These virtual elements allow for specific geometrical forms of the course of the curve at the edges. In this contribution a new methodology is proposed that allows to use general mappings for virtual elements which can model arbitrary geometries.

1 Introduction

The many different approaches to the approximate solution of problems involving partial differential equations include finite difference schemes, finite elements, finite volume techniques, boundary elements, and particle methods. Within the finite element method there have been various significant developments, including for example classical isoparametric mapping, see e.g. Hughes [15] and Zienkiewicz and Taylor [35], but also isogeometric schemes, see Cottrell et al. [10].

Research continues to be motivated by the goal of developing stable, efficient and robust discretization schemes for finite deformation applications in solid mechanics. Within this line also the virtual element technology is further refined and applied to nonlinear problems in mechanics, see e.g. Beirão da Veiga et al. [6], Chi et al. [9], Wriggers et al. [34], Artioli et al. [3], De Bellis et al. [11], Wriggers and Hudobivnik [33], Aldakheel et al. [1], Hussein et al. [17] and De Bellis et al. [12]. So far the assumptions—even for higher order virtual elements—contain the restriction to straight edges of the elements that are directly defined in the physical space, see e.g. Beirão da Veiga et al. [5]. This makes the definition of virtual elements having a general geometric shape more complicated which is due to the fact that mappings like the isoparametric map for finite elements or NURBS type maps in isogeometric analysis are not easily applicable. New formulations that introduce curved element edges allow specific geometrical forms of the course of the curve at the edges were discussed in Beirão da Veiga et al. [7], Artioli et al. [4] and Aldakheel et al. [2].

This paper introduces a possibility to employ general mappings also within the virtual element formulation. The idea is to map a virtual element, defined at a reference configuration, to a general shape in the initial (physical) configuration. With such a map general shapes of virtual elements can be created in the initial configuration while preserving the straight edges in the reference configuration. This type of mapping was investigated for shell problems in e.g. Pimenta and Campello [27], but so far has not been used in two- and three-dimensional solid mechanics and within the virtual element methodology.

The method is developed for hyperelastic materials undergoing finite strains. However it can as well be applied for small strain cases as for material nonlinearities such as plasticity. Here we use the neo-Hookean strain energy as a model. The mapping from the reference to the initial configuration is performed either with an isoparametric map based on a quadratic ansatz for the geometry or a Bezier type map using NURBS: Both formulations perform extremely well in a series of benchmark tests involving regular and Voronoi meshes.

After presenting the governing equations for nonlinear elasticity in Sect. 2. Section 3 is devoted to the general mapping procedure, followed by the formulation of a low order virtual element method in Sect. 4 that takes into account the general mapping. A number of numerical examples are presented and discussed in Sect. 5, and in Sect. 6 some concluding remarks are presented.

2 Governing equations for finite elasticity

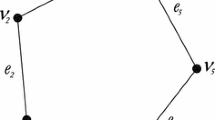
Consider an elastic body that occupies the bounded domain $\Omega _0 \subset {\mathbb {R}}^2$. The body $\Omega _0$ has a boundary $\Gamma$ which comprises non-overlapping sections $\Gamma _{D}$ and $\Gamma _{N}$ such that $\Gamma _{D} \cup \Gamma _{N} = \Gamma$ (Fig. 1).

The position $\varvec{x}$ of a material point initially at $\varvec{X}$ is given by the motion

$$\begin{aligned} \varvec{x} = \varvec{\varphi }(\varvec{X},t) = \varvec{X} + \varvec{u}(\varvec{X},t) \end{aligned}$$

(1)

where $\varvec{u}$ is the displacement field that depends generally on the time t. We also define the deformation gradient $\varvec{F}$ by

$$\begin{aligned} \varvec{F}(\varvec{u}) = \varvec{1}+\text{ Grad }\,\varvec{u}(\varvec{X},t), \end{aligned}$$

(2)

the gradient being evaluated with respect to $\varvec{X}$. The body satisfies for the static case, on $\Omega _0$ the equation of equilibrium

$$\begin{aligned} \text{ Div }\,\varvec{P} + \bar{\varvec{f}}= \varvec{0}, \end{aligned}$$

(3)

with the body force $\bar{\varvec{f}}$ and the first Piola–Kirchhoff stress $\varvec{P}$. The Dirichlet and Neumann boundary conditions are respectively

$$\begin{aligned}&\varvec{u} = \bar{\varvec{u}} \quad \text{ on }\ \Gamma _{D}, \end{aligned}$$

(4)

$$\begin{aligned}&\varvec{P}\varvec{N} = \bar{\varvec{t}}\quad \text{ on }\ \Gamma _{N}, \end{aligned}$$

(5)

with $\varvec{N}$ the outward unit normal vector, $\bar{\varvec{u}}$ the prescribed displacement, and $\bar{\varvec{t}}$ the prescribed surface traction $\text{ on }\ \Gamma _N$.

Fig. 1

Solid with boundary conditions

By introducing a strain energy function $\varPsi (\varvec{u})$ for elastic problems the first Piola–Kirchhoff stresses follow from

$$\begin{aligned} \varvec{P}(\varvec{u})=\frac{\partial \varPsi (\varvec{u})}{\partial \varvec{F} }. \end{aligned}$$

(6)

For a homogeneous compressible isotropic hyperelastic material we adopt the neo-Hookean strain energy function for the two-dimensional case

$$\begin{aligned} \varPsi (\varvec{u} )= & {} \frac{\lambda }{4}(J(\varvec{u} )^2-1-2\ln J(\varvec{u} )) \nonumber \\&+\, \frac{\mu }{2} (\text{ tr } \,\varvec{C}(\varvec{u} ) -2 -2 \ln J(\varvec{u} )) \end{aligned}$$

(7)

in which $\lambda$ and $\mu$ are the Lamé constants. This strain energy is known as Neo-Hookean model. The right Cauchy-Green tensor $\varvec{C}(\varvec{u} )$ is defined as $\varvec{C}= { \varvec{F}}^T \varvec{F}$ and the Jacobian $J(\varvec{u} )$ of the deformation is given as $J= \det \varvec{F} >0$.

In case of a hyperelastic material the development of a virtual element can start from the potential energy function directly instead of using the weak form, see e.g. Wriggers et al. [34]. In that case the potential energy can be written with (7) as

$$\begin{aligned} U(\varvec{u}) = \int \limits _{\Omega _0} \left[ \varPsi (\varvec{u}) - \bar{\varvec{f}}\cdot \varvec{u}\ \right] \ d\Omega - \int \limits _{\Gamma _N} \bar{\varvec{t}}\cdot \varvec{u} \ d\Gamma \end{aligned}$$

(8)

3 General mapping

The idea for the construction of general shaped virtual elements is to use a function that maps the coordinates $\varvec{X}_r$ of a virtual element from a reference configuration $\Omega _r$ to the coordinates $\varvec{X}_0$ of the initial configuration $\Omega _0$, see Fig. 2. The deformation is then given by the vector $\varvec{x}$ which describes the current configuration $\Omega _d$ that a solid assumes under loading.

Fig. 2

Configurations of a solid including map to initial configuration

The mapping from the reference to the initial configuration can be defined in an arbitrary way using either an isoparametric map or e.g. NURBS functions. For isoparametric maps we can use shape function $N_I$ that describe a polynomial basis in the reference configuration. The map is given by

$$\begin{aligned} \varvec{X}_0(X_r,Y_r) = \sum _{I=1}^{n_{iso} } N_I(X_r,Y_r) \varvec{X}_I^0 \end{aligned}$$

(9)

In this paper we use a quadratic function for the isoparametric map, explicit expressions for the ansatz functions can be found in e.g. Hughes [15], Wriggers [32] and Onate [25]. The coordinates of the reference configuration are here selected as $(X_r,Y_r) \in \left[ -1,1 \right] \times \left[ -1,1 \right]$.¹

A more general mapping that includes also mapping onto domains that cannot be exactly defined by polynomials is provided by NURBS, see e.g. Farin [13] and Piegl and Tiller [26]. These Non-Uniform Rational B-Splines are obtained for a two-dimensional map by a projection of a B-spline quantity from three-dimensional space which allows exact constructions of geometrical objects such as circles and ellipses. The NURBS projection maps from a parameter space $\Omega _r$ with $0\le \eta ^1\le 1$ and $0\le \eta ^2\le 1$ to the initial configuration $\Omega _0$ follows as

$$\begin{aligned} \varvec{X}_0(\eta ^1,\eta ^2) = \sum _{I=0}^{m} \sum _{J=0}^{n} R_{IJ}(\eta ^1,\eta ^2) \varvec{P}_{IJ}^0 \end{aligned}$$

(10)

where $\varvec{P}_{IJ}^0$ are the control points that define the domain in the initial configuration. The functions $R_{IJ}(\eta ^1,\eta ^2)$ are the rational B-spline basis functions. They are explicitly given by

$$\begin{aligned} R_{IJ}(\eta ^1,\eta ^2) = \frac{w_{IJ} N^1_I(\eta ^1) N^2_J(\eta ^2)}{\sum _{I=0}^{m } \sum _{J=0}^{n } w_{IJ} N^1_I(\eta ^1) N^2_J(\eta ^2)} \end{aligned}$$

(11)

with the weights $w_{IJ}$. For more details related to the order of the B-spline basic functions we refer to Piegl and Tiller [26], Hughes et al. [16] and Cottrell et al. [10]. The latter used this parametrization to develop the discretization technique known as isogemetrical analysis. We note that the NURBS functions can also be linearly mapped to $(X_r,Y_r) \in \left[ X_{min},X_{max} \right]$$\times$$\left[ Y_{min},Y_{max} \right]$. Thus we will write the mapping for both, isoparametric and NURBS, mapping as being a function of the coordinates $\varvec{X}_r=(X_r,Y_r)$.

According to Fig. 2 the deformation gradient in (2) can be computed via

$$\begin{aligned} \varvec{F} = \varvec{F}_u \, \varvec{F}_0 \end{aligned}$$

(12)

with

$$\begin{aligned} \varvec{F}_0 = \text{ Grad } \, \varvec{X}_0 \end{aligned}$$

(13)

following from the mapping functions (9) and (10). The Jacobian of this mapping is given by $J_0= \det \, \varvec{F}_0$. Furthermore the volume element in the initial configuration is connected to a volume element in the reference configuration by $d\Omega _0 = J_0\, d\Omega _r$. Depending on the used mapping we either have to differentiate in (13) with respect to $(X_r,Y_r)$ or $(\eta ^1,\eta ^2)$.

The deformation gradient $\varvec{F}_u$ that describes the deformation from the initial to the current configuration yields

$$\begin{aligned} \varvec{F}_u = \varvec{F} \, \varvec{F}_0^{-1}. \end{aligned}$$

(14)

Fig. 3

VEM element and boundary discretization in $\Omega _r$

Based on these general kinematical quantities we can compute the right Cauchy Green tensor in terms of the deformation gradient $\varvec{F}_u$ as

$$\begin{aligned} \varvec{C}_u = \varvec{F}_u^T \varvec{F}_u = \varvec{F}_0^{-T} \varvec{F}^T \varvec{F} \varvec{F}_0^{-1}. \end{aligned}$$

(15)

Now the potential (8) can be reformulated using (15)

$$\begin{aligned} U(\varvec{u}) = \int \limits _{\Omega _r} \left[ \varPsi (\varvec{\varvec{C}_u}) - \bar{\varvec{f}} \cdot \varvec{u}\ \right] \ J_0 \, d\Omega _r - \int \limits _{\Gamma _{N\,r}} \bar{\varvec{t}}\cdot \varvec{u} \ \Gamma _0\, d\Gamma \end{aligned}$$

(16)

where in the general three-dimensional case

$$\begin{aligned} \Gamma _0= \Vert \varvec{X}_{0,X_r} \times \varvec{X}_{0,Y_r}\Vert \end{aligned}$$

(17)

is the mapping of the area elements of the reference to the initial configuration, either with respect to the coordinates of the isoparametric or the NURBS mapping, respectively. Furthermore, the Jacobian J describing the volume change in the strain energy (7) is given by $J_u= J \,J_0^{-1}$.

In the two-dimensional case one can compute the gradient of the mapping from the reference to the initial configuration directly from the isoparametric or the NURBS map as

$$\begin{aligned} \varvec{F}_0^{iso}= & {} \sum _{I=1}^{n_{iso}} \left[ \begin{array}{cc} N_{I ,x} \,X_I^0 &{}\quad N_{I ,y} \,X_I^0 \\ N_{I ,x} \,Y_I^0 &{}\quad N_{I ,y} \,Y_I^0 \end{array}\right] \quad \text{ or }\nonumber \\ \varvec{F}_0^{N}= & {} \sum _{I=0}^{m} \sum _{J=0}^{n} \left[ \begin{array}{cc} R_{I J,\eta ^1} \,P_{xIJ}^0 &{} R_{I J,\eta ^2} \,P_{xIJ}^0 \\ R_{I J,\eta ^1} \,P_{yIJ}^0 &{} R_{I J,\eta ^2} \,P_{yIJ}^0 \end{array} \right] . \end{aligned}$$

(18)

The differentiations in (18) have to be performed with respect to the reference coordinates. Note that the computation of the derivatives of the rational B-splines is more involved due to the definition of the B-spline in (11).

Note that description of a solid may require more than one reference configurations. In this case it is possible to combine several configurations to model the solid which will be shown in the numerical example section.

4 Formulation of the virtual element method

The main idea of the virtual element method (VEM) is a projection of the deformation onto a specific ansatz space. In classical analysis using virtual elements a domain $\Omega$ is partitioned into non-overlapping polygonal elements which need not be convex. Here we extend this possibility by mapping the polygons into other geometrical objects using a nonlinear map as discussed in the last section. In this contribution we restrict ourselves to two dimensional solids and to a low-order approach using linear ansatz functions. Due to the construction of the mappings the developed methodology works without any changes for higher order ansatz spaces of virtual elements.

The construction of a low order virtual element is based on a linear ansatz space $\varvec{u}_h$, see e.g. Beirão da Veiga et al. [5], that has unknown displacements $\varvec{u}_k$ at the vertices k of the polygon, a linear ansatz for the displacement field $\varvec{u}_h$ at the edges of the polygon and the property that $\text{ Div }(\nabla \varvec{u}_h)=0$. The polygonal elements can have arbitrary number of vertices where $n_V$ is the total number. Furthermore, the element shape is restricted to straight edges, see Fig. 3, in the reference configuration $\Omega _r^e$.

Fig. 4

VEM element and boundary discretization in $\Omega _0$ and $\Omega _r$ using surface coordinate $\xi$

4.1 Ansatz functions

Generally the virtual element method relies on the split of the ansatz space for the displacement field $\varvec{u}_h$ into a part $\varvec{u}_\pi$ and a remainder

$$\begin{aligned} \varvec{u}_h = \varvec{u}_\pi + ( \varvec{u}_h - \varvec{u}_\pi ) \end{aligned}$$

(19)

Classically the projection $\varvec{u}_\pi$ is defined at element level by a function which is directly formulated in the coordinates that describe the real geometry of the domain. Hence the ansatz for a linear polynomial function yields for the two dimensional case in the initial configuration

$$\begin{aligned} \varvec{u}_\pi = {\mathbf {H}}^{2d} \,{\mathbf {a}} = \left[ \begin{array}{cccccccccccc} 1 &{}\quad 0 &{}\quad X_0 &{}\quad 0 &{}\quad Y_0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad X_0 &{}\quad 0 &{}\quad Y_0 \end{array} \right] \, \left\{ \begin{matrix} a_1 \\ a_2 \\ \ldots \\ a_{6} \end{matrix} \right\} \end{aligned}$$

(20)

4.2 Computation of the projection

There exist several methods to obtain the parameters $a_{i}$ in terms of the unknown nodal values of a virtual element $\Omega ^e$ as depicted in Fig. 3. Here we use a Galerkin projection of the gradients to project $\varvec{u}_\pi$ onto the ansatz $\varvec{u}_h$. Since this formulation does not rely on the mechanical weak form it leads to the same projection for linear and nonlinear elasticity problems. The Galerkin projection of the gradient $\nabla \varvec{u}_\pi$ is carried out in the initial configuration $\Omega _0^e$ of the virtual element. It can be formulated as

$$\begin{aligned} \int \limits _{\Omega _0^e} \left( \nabla _0 \varvec{u}_h -\nabla _0 \varvec{u}_\pi \right) \cdot \nabla _0 \varvec{N}_\pi \ d \Omega _0 =0. \end{aligned}$$

(21)

Here the index “0” in $\nabla$ refers to the differentiation with respect to the initial coordinates $\varvec{X}_0$. $\varvec{N}_\pi$ is the vector containing a weighting polynomial that has the same order as $\varvec{u}_\pi$. For the chosen linear ansatz the gradient $\nabla _0 \varvec{N}_\pi$ is constant when we select $\varvec{N}_\pi =\{ 1,X_0, Y_0 \}$. Thus we can write (21) as

$$\begin{aligned} \int \limits _{\Omega _0^e} \nabla _0 \varvec{u}_\pi \ d \Omega _0 = \int \limits _{\Omega _0^e} \nabla _0 \varvec{u}_h \ d \Omega _0 . \end{aligned}$$

(22)

Since $\nabla _0 \varvec{u}_\pi$ is constant in $\Omega _0^e$ for the linear ansatz in (20) we can write for the left side of the integral above as

$$\begin{aligned} \int \limits _{\Omega _0^e} \nabla _0 \varvec{u}_\pi \ d \Omega _0 = \Omega _0^e\, \nabla _0 \varvec{u}_\pi . \end{aligned}$$

(23)

Using now the Gauss theorem the second integral in (22) can be transformed to a boundary integral

$$\begin{aligned} \int \limits _{\Omega _0^e} \nabla _0 \varvec{u}_h \ d \Omega _0 = \int \limits _{\Gamma _0^e} \varvec{u}_h \otimes \varvec{N}_0 \ d \Gamma _0 \end{aligned}$$

(24)

with $\varvec{N}_0$ being the outward normal to the element area $\Omega _0$ in the initial configuration.

The integral on the right hand side in (24) can be transformed to the reference domain directly. The question is how to compute the normal vector $\varvec{N}_0$ at an edge $\gamma \in \Gamma _0$ where $\gamma$ stands for an edge between two vertices and $\Gamma _0$ is the entire boundary of the virtual element. Two different possibilities are available for the transformation:

• We can introduce along an edge $\gamma$ the coordinate $\xi$, see Fig. 4. The normal vector $\varvec{N}_0$ can then be discretized directly using the map (think of convective coordinates)

  $$\begin{aligned} \varvec{N}_0 = \frac{\varvec{X}_{0,\xi }^\gamma \times \varvec{E}_3 }{ \Vert \varvec{X}_{0,\xi }^\gamma \Vert } = \frac{1}{ \Vert \varvec{X}_{0,\xi } ^\gamma \Vert }\left\{ \begin{matrix} - Y_{0,\xi } \\ X_{0,\xi } \end{matrix} \right\} \end{aligned}$$

  (25)

  Where the edge $\gamma _0$ is defined through the reference configuration by

  $$\begin{aligned} \varvec{X}_r^\gamma = \frac{1}{2}(1-\xi )\, \varvec{X}_k + \frac{1}{2}(1+\xi ) \,\varvec{X}_{k+1} \end{aligned}$$

  (26)

  which yields the coordinate at the edge $\varvec{X}_0(\varvec{X}(\xi ))$ as a function of $\xi$. Now we define a linear ansatz for $\varvec{u}_h$ at the edge $\gamma _0$ as

  $$\begin{aligned} \varvec{u}_h(\xi ) = \frac{1}{2}(1-\xi )\, \varvec{u}_k + \frac{1}{2}(1+\xi ) \,\varvec{u}_{k+1} . \end{aligned}$$

  (27)

  With $d \Gamma _0^\gamma = \Vert \varvec{X}_{0,\xi }^\gamma \Vert \,d \xi$ we can write the integral as a sum over all $n_\gamma$ edges $\gamma \in \Gamma _0$ of the virtual element

  $$\begin{aligned} \int \limits _{\Omega _0^e} \nabla _0 \varvec{u}_h \ d \Omega _0= & {} \sum _{\gamma =1}^{n_\gamma } \int \limits _{\xi } \varvec{u}_h(\xi ) \otimes \varvec{N} _0(\xi ) \Vert \varvec{X}_{0,\xi }^\gamma \Vert \ d \xi \nonumber \\= & {} \sum _{\gamma =1}^{n_\gamma }\int \limits _{\xi } \varvec{u}_h(\xi ) \otimes \left\{ \begin{matrix} - Y_{0,\xi } \\ X_{0,\xi } \end{matrix} \right\} ^\gamma \ d \xi \end{aligned}$$

  (28)

  Note that the coordinate $\xi$ is related to a line in $\Omega _r$ that is straight, see right side in Fig. 4. For a specific map $\varvec{X}_0$ the integration of the right hand side in (28) follows by using an integration rule, e.g. Gauss integration,

  $$\begin{aligned}&\sum _{\gamma =1}^{n_\gamma }\int \limits _{\xi } \varvec{u}_h(\xi ) \otimes \left\{ \begin{matrix} - Y_{0,\xi } \\ X_{0,\xi } \end{matrix} \right\} ^\gamma \!\! d \xi \nonumber \\&\quad = \sum _{\gamma =1}^{n_\gamma } \sum _{g=1}^{n_g} w_g \left[ \varvec{u}_k \otimes \left\{ \begin{matrix} - Y_{0,\xi }(\xi _g) \\ X_{0,\xi }(\xi _g) \end{matrix} \right\} ^\gamma \right] \end{aligned}$$

  (29)

  where $w_g$ are the weights and $\xi _g$ the integration points with respect to the reference configuration. This integration holds for isoparametric and NURBS mappings. The integration order in (29) depends on the mapping function, e.g for a quadratic isoparametric map the integrand in (29) is represented by a second order polynomial, thus a two point Gauss integration is sufficient. But for a Bezier type mapping the number of Gauss points has to be increased.

• Another way to integrated the right hand side in (24) is to use Nanson’s formula. Then the integral can be transferred to the reference configuration by

  $$\begin{aligned} \int \limits _{\Gamma _0^e} \varvec{u}_h \otimes \varvec{N}_0 \ d \Gamma _0 = \sum _{\gamma =1}^{n_\gamma } \int \limits _{\gamma _r} \varvec{u}_h \otimes \varvec{F}_0^{-T} \, \varvec{N}_r^\gamma \,\det \varvec{F}_0 \ d \gamma _r \end{aligned}$$

  (30)

  where now $\varvec{N}_r$ is the normal related to the straight edges of the virtual element in the reference configuration. The inverse of this gradient is given for the isoparametric map in the two-dimensional case simply by

  $$\begin{aligned} \varvec{F}_0^{-T} = \frac{1}{\det \varvec{F}_0 } \sum _{I=1}^{n_{iso}} \left[ \begin{array}{cc} N_{I ,y} \,Y_I^0 &{}\quad -N_{I ,x} \,X_I^0 \\ -N_{I ,y} \,Y_I^0 &{}\quad N_{I ,x} \,X_I^0 \end{array} \right] \end{aligned}$$

  (31)

  with $\{ X_I^0,Y_I^0\} =\varvec{X}_0$. By defining

  $$\begin{aligned} \varvec{G}_0^T = \varvec{F}_0^{-T} \, \det \varvec{F}_0 = \sum _{I=1}^{n_{iso}}\, \left[ \begin{array}{cc} N_{I ,y} \,Y_I^0 &{}\quad -N_{I ,x}\,X_I^0 \\ -N_{I ,y}\,Y_I^0 &{}\quad N_{I ,x} \,X_I^0 \end{array} \right] \end{aligned}$$

  (32)

  the integral in (30) yields

  $$\begin{aligned} \int \limits _{\Gamma _0^e} \varvec{u}_h \otimes \varvec{N}_0 \ d \Gamma _0 = \sum _{\gamma =1}^{n_\gamma } \int \limits _{\gamma _r} \varvec{u}_h \otimes \varvec{G}_0^T \, \varvec{N}_r^\gamma \ d \gamma _r \end{aligned}$$

  (33)

One can combine (23) and (33) to finally obtain the projection of the gradient

$$\begin{aligned} \nabla _0 \varvec{u}_\pi = \frac{1}{\Omega _0} \sum _{\gamma =1}^{n_\gamma } \int \limits _{\gamma _r} \varvec{u}_h \otimes \varvec{G}_0^T \, \varvec{N}_r^\gamma \ d \gamma _r , \end{aligned}$$

(34)

or use (23) and (28) which yields the alternative form

$$\begin{aligned} \nabla _0 \varvec{u}_\pi = \frac{1}{\Omega _0} \sum _{\gamma =1}^{n_\gamma } \int \limits _{\xi } \varvec{u}_h(\xi ) \otimes \left\{ \begin{matrix} - Y_{0,\xi } \\ X_{0,\xi } \end{matrix} \right\} ^\gamma \! d \xi . \end{aligned}$$

(35)

In (34) and (35) the area $\Omega _0$ in the initial configuration is computed using the reference configuration of the virtual element. The integral can be evaluated over the edges using partial integration and Gauss integration

$$\begin{aligned} \Omega _0&=\int \limits _{\Omega _r} J_0\,d \Omega _r = \frac{1}{2} \sum _{\gamma =1}^{n_\gamma } \int \limits _{\gamma _r} \varvec{X}_r \cdot [\varvec{G} _0^T \varvec{N}_r^\gamma ] d \gamma _r\end{aligned}$$

(36)

$$\begin{aligned}&= \frac{1}{2}\sum _{\gamma =1}^{n_{\gamma }}\sum _{g=1}^{n_g} l^\gamma _r\, w_g \varvec{X}_r(\xi _g)\cdot \left[ \varvec{G}_0^T (\xi _g) \varvec{N} _r^\gamma (\xi _g)\right] . \end{aligned}$$

(37)

All quantities are related to the reference configuration, see Fig. 4. These are the coordinates $\varvec{X}_r$, the normal $\varvec{N}_r^\gamma$ at edge $\gamma$, the Gauss points $\xi _g$ and associated weights $w_g$ and the length of an edge $l^\gamma _r$. Note that also the first formulation leading to (35) can be applied to compute $\Omega _0$.

Finally the projection in (34) can be evaluated by inserting ansatz (27) into this equation. Again Gauss integration is employed

$$\begin{aligned} \nabla _0 \varvec{u}_\pi = \frac{1}{\Omega _0}\sum _{\gamma =1}^{n_{\gamma }}\sum _{g=1}^{n_g} l_r^\gamma \,w_g \varvec{u}_h(\xi _g)\otimes \left[ \varvec{G}_0^T (\xi _g) \varvec{N}_r^\gamma (\xi _g)\right] \end{aligned}$$

(38)

which yields the parameters $a_3$ to $a_6$ in (20) that now depend on the displacements $\varvec{u}_k$ at the vertices k of a virtual element. Again (35) can also be used to compute the projected gradient.

In the projection in (38) only the gradient plays a role. This allows to compute the parameters $a_3$ to $a_6$ of (20) directly. Hence the constant parts of the ansatz disappear. Thus the parameters $a_{1}$ and $a_{2}$, related to the constant parts, have to be obtained in a different way. Here the average displacement of the virtual element in the initial configuration along the edge $\Gamma _0$ is used. The equivalence

$$\begin{aligned} \frac{1}{\Gamma ^e} \int \limits _{\Gamma _0^e} \varvec{u}_\pi \ d\Gamma _0 = \frac{1}{\Gamma _e} \int \limits _{\Gamma _0^e} \varvec{u}_h\ d\Gamma _0 \end{aligned}$$

(39)

includes the parameters $a_{1}$ and $a_{2}$ and from (39) all parameters in (20) can be computed. A simplified expression follows, if the integrals are evaluated by the Gauss–Lobatto rule. In that case the nodal values of $\varvec{u}_\pi$ and $\varvec{u}_h$ appear in a sum over all vertices. This leads to

$$\begin{aligned} \frac{1}{n_v} \sum _{k=1}^{n_v} \varvec{u}_\pi ( \varvec{X}_{0\,k} ) = \frac{1}{n_v} \sum _{k=1}^{n_v} \varvec{u}_k \end{aligned}$$

(40)

Ansatz (20) can now be inserted into (40) and evaluated at $\varvec{X}_{0\,k} = \sum _{I=1}^{n_{iso}} N_I(X_{r k}, Y_{r k}) \varvec{X}^{0}_I$ for the left hand side, while on the right hand side only the nodal values of $\varvec{u}_h$ have to be used. This finally leads to two equations for the parameters $a_{1}$ and $a_{2}$.

4.3 Construction of the virtual element

In this contribution a linear ansatz is employed for the discretization using virtual elements. Thus the gradient of the displacement field is approximated by a constant part as a result of the projection in the last section. A construction of a virtual element which is based only on this projection would lead to a rank deficient element once the number of vertices is greater than 3. Thus the formulation has to be stabilized, as in the case of the classical one-point integrated elements developed by Flanagan and Belytschko [14], Belytschko and Bindeman [8], Reese et al. [30], Reese and Wriggers [29], Reese [28], Mueller-Hoeppe et al. [24], Korelc et al. [21] and Krysl [22], to mention some key contributions.

The formulation is provided here for finite deformation formulations. The potential U is a split into a constant part of the deformation gradient and an associated stabilization term. In this contribution we employ the hyperelastic potential function (16) as basis for the virtual element. By summing up all element contributions for the $n_e$ virtual elements that discretize a domain $\Omega _0$ one obtains

(41)

In the following we will first discuss the formulation of the consistency part $U_c^e(\varvec{u}_\pi )$ that stems from the projection, see last section. Furthermore, a possibility for the stabilization $U_{stab}^e$ of the virtual element method will be considered.

4.3.1 Constant part due to projection

The consistency part in the potential (41) can be evaluated by inserting the results obtained in the last section. This yields with respect to the initial configuration for a virtual element $\Omega _0^e$

$$\begin{aligned} U_c^e(\varvec{u}_\pi ) = \int \limits _{\Omega _0^e} \left[ \varPsi (\varvec{C}_u ) - \bar{\varvec{f}}\cdot \varvec{u}_\pi \ \right] \ d\Omega _0 - \int \limits _{{\Gamma }_0^e} \bar{\varvec{t}}\cdot \varvec{u}_\pi \ d\Gamma _0. \end{aligned}$$

(42)

Due to the fact that we are able to compute the projection of the gradient $\nabla _0 \varvec{u}_\pi$ in the initial configuration directly in (38) we obtain the deformation gradient describing the map from the initial to the current configuration as

$$\begin{aligned} \varvec{F}_u = \varvec{1} + \nabla _0 \varvec{u}_\pi \end{aligned}$$

(43)

which is constant. Note that here also (35) could have been inserted for $\nabla _0 \varvec{u}_\pi$ which leads to exactly the same results. Now the right Cauchy-Green tensor is given by

$$\begin{aligned} \varvec{C}_u = \varvec{F}_u^T \varvec{F}_u \end{aligned}$$

(44)

which is also constant within the virtual element $\Omega _e$ but depends in a nonlinear fashion on the nodal displacements.

The strain energy of the hyperelastic material

$$\begin{aligned} \varPsi (\varvec{u}_\pi )= \frac{\lambda }{4}[\,J_u^2-1-2\ln J_u \,] + \frac{\mu }{2} [\,\text{ tr } \,\varvec{C_u} -2 -2 \ln J_u\,] \end{aligned}$$

(45)

can now be computed in terms of the projected deformation measures which are the right Cauchy-Green tensor $\varvec{C}_u$ and the Jacobian $J_u$. The latter is given by

$$\begin{aligned} J_u= \det \varvec{F}_u = \det (\varvec{1} + \nabla _0 \varvec{u}_\pi ) . \end{aligned}$$

(46)

Hence all quantities in (45) depend only the projection $\nabla _0 \varvec{u}_\pi$.

The first integral in (42) can easily be computed since $\varPsi (\varvec{C}_u )$ is constant in $(X_0,Y_0)$ and $\Omega _0^e$ known from (37). The two loading terms have to be transformed for evaluation to the reference configuration, see also (28),

$$\begin{aligned} U_c^e(\varvec{u}_\pi )= & {} \Omega _0^e \, \varPsi (\varvec{C}_u ) - \int \limits _{\Omega _r^e} \bar{\varvec{f}}\cdot \varvec{u}_\pi \,\det \varvec{F}_0 \ d\Omega _r\nonumber \\&- \sum _{\gamma =1}^{n_\gamma }\int \limits _{\xi } \bar{\varvec{t}}_\gamma \cdot \varvec{u}_\pi \, \Vert \varvec{X}_{0,\xi }^\gamma \Vert \,d \xi . \end{aligned}$$

(47)

where $\gamma$ denotes the edges of the virtual element that are loaded by surface traction $\bar{\varvec{t}}_\gamma$.

Fig. 5

Internal triangular mesh

Once the integration over the reference coordinate is finalized, the derivations of the potential (47) with respect to the $n_V$ unknown nodal displacements at the vertices of the virtual element $\varvec{u}_e= \{ \varvec{u}_1,\varvec{u}_2,\ldots ,\varvec{u}_{n_V}\}$ can be carried out. This approach exploits the fact that $\nabla _0 \varvec{u}_\pi$ depends directly on the nodal displacements, see (35) and (38), and the displacements $\varvec{u}_\pi$ are linked via (20) and (40) to the nodal displacements as well.

All derivations, leading to the residual vector $\varvec{R}_e^c$ and the tangent matrix $\varvec{K}_{Te}^c$ , were performed with the symbolic tool AceGen, see Korelc and Wriggers [20]. This yields for (47)

$$\begin{aligned} \varvec{R}_e^c =\frac{\partial U_c^e(\nabla _0 \varvec{u}_\pi (\varvec{u}_e),\varvec{u}_\pi (\varvec{u}_e) ) }{\partial \varvec{u}_e} \quad \text{ and }\quad \varvec{K}_{Te}^c =\frac{\partial \varvec{R}_e^c(\varvec{u}_e) }{\partial \varvec{u}_e} \end{aligned}$$

(48)

where $\varvec{u}_e$ are the nodal displacements of the virtual element $\Omega _e$ at the vertices.

4.3.2 Stabilization techniques for nonlinear virtual elements

In the literature on virtual element technologies basically two different stabilization techniques were discussed that work well for classical solid mechanics problems. The first stabilization is directly based on the degrees of freedom. It introduces a point wise error measure between the nodal values $\varvec{u}_k$ and the approximation function $\varvec{u}_\pi$ evaluated at the vertices $\varvec{X}_k$, see e.g. Beirão da Veiga et al. [5], Beirão da Veiga et al. [6] and Chi et al. [9].

Here we use the stabilization approach developed in Wriggers et al. [34] for virtual elements. The essence of the approach is to introduce a new, positive definite strain energy $\hat{\varPsi }$ and to define the stabilization contribution to the strain energy by

$$\begin{aligned} U_{stab} (\varvec{u}_h -\varvec{u}_\pi ) = \hat{U}( \varvec{u}_h) - \hat{U}(\varvec{u}_\pi ). \end{aligned}$$

(49)

Such a stabilization was also used in Krysl [22] for stabilized mean strain formulations of finite elements. The second term on the right side ensures the consistency of the total potential energy, which is now given by

$$\begin{aligned} U (\varvec{u}_h) \simeq U_c (\varvec{u}_\pi ) + {\hat{U}} (\varvec{u}_h) - {\hat{U}} (\varvec{u}_\pi ). \end{aligned}$$

(50)

Actually $\hat{U}$ can be selected differently from the strain energy that describes the constitutive behavior of the solid, see e.g. Wriggers et al. [34], since it is only for stabilization. Note that ${\hat{U}} (\varvec{u}_h) - {\hat{U}} (\varvec{u}_\pi )$ disappears for element sizes $\Omega _0^e \rightarrow 0$. In this paper we use the same energy $\varPsi$ as in the consistency part $U_c$, however with different Lamé parameters $\hat{\lambda }$ and $\hat{\mu }$. The stabilization energy follows then by assembly over all virtual elements

(51)

The computation of the consistency part $U_c(\varvec{u}_\pi )$ was already discussed above. The last part of the potential energy ${\hat{U}} (\varvec{u}_\pi )$ depends also on $\varvec{u}_\pi$, thus it can be evaluated as the consistency part, see Sec. 4.3.1.

The question is now how to compute the stabilization term ${\hat{U}} (\varvec{u}_h)$ since $\varvec{u}_h$ is not known within the virtual element. The idea is to use an internal triangular mesh. This inscribed triangular finite element mesh, see Fig. 5, consists of $n_{int}$ linear three-noded triangles that are connected to the nodes of the virtual element. Hence this internal mesh does not creat new nodal unknowns. The ansatz functions for the triangles are then assumed to approximate $\varvec{u}_h$ in (19).

For this discretization of the potential ${\hat{U}}^e (\varvec{u}_h)$ within a virtual element $\Omega _0^e$ one has to add all contributions of the internal triangles $\Omega _m^i$

$$\begin{aligned} \hat{U}^e(\varvec{u}_h)= & {} \sum _{m=1}^{n_\mathrm{int}} \int \limits _{\Omega _{0 m}^i} \left[ \frac{\hat{\lambda }}{4}[\,J_m^2-1-2\ln J_m \,]\right. \nonumber \\&+\left. \frac{\hat{\mu }}{2} [\,\text{ tr } \,\varvec{C_m} -2 -2 \ln J_m\,] \right] \, d\Omega _0, \end{aligned}$$

(52)

which can be directly formulated with respect to the initial configuration $\Omega _{0 m}$.

To fulfill the condition that ${\hat{U}} (\varvec{u}_h) - {\hat{U}} (\varvec{u}_\pi ) \rightarrow 0$ for small virtual elements $\Omega _0^e \rightarrow 0$ one has to compute the potential $\bar{U}(\varvec{u}_\pi )$ using the area related to the triangular elements $\Omega ^e_{OT} = \sum _{m=1}^{n_\mathrm{int}} \Omega _{0 m}^i$ which leads to

$$\begin{aligned} \bar{U}(\varvec{u}_\pi ) = \Omega ^e_{OT} \,\hat{\varPsi } (\varvec{C}_u). \end{aligned}$$

(53)

Due to the straight edges of the inscribed triangular mesh, see Fig. 5, this slightly differs from the way the element area is computed in the consistency part in (47). However such approximation can be admitted since (53) is only the stabilization energy which approaches zero for fine meshes, see above.

All further derivations leading to the residual vector $\varvec{R}_e^s$ and the tangent matrix $\varvec{K}_{Te}^s$ were performed in the same manner as in (48) with the symbolic tool AceGen, see Korelc and Wriggers [20]. This yields for (49)

$$\begin{aligned} \varvec{R}_e^s =\frac{\partial U_{stab}(\varvec{u}_e) }{\partial \varvec{u}_e} \quad \text{ and }\quad \varvec{K}_{Te}^s =\frac{\partial \varvec{R}_e^s(\varvec{u}_e) }{\partial \varvec{u}_e}. \end{aligned}$$

(54)

Thus the final residual and tangent matrix of the virtual element are given by the sum of expressions (48) and (54): $\varvec{R}_e =\varvec{R}_e^c +\varvec{R}_e^s$ and $\varvec{K}_{Te}=\varvec{K}_{Te}^c+\varvec{K}_{Te}^s$.

The values of the Lamé parameters in the strain energy (52) have to be selected in a proper way. Krysl [23] suggested for cuboid finite elements a procedure that is based on a comparison of the bending energy of a thick beam and the bending energy of the finite element. This yields Lamé parameters $\hat{\lambda }$ and $\hat{\mu }$ that enhance the bending behavior of the element. Since this procedure is not directly applicable to arbitrary virtual elements we suggest a simple and computationally efficient way to compute the parameters from the basic geometric data of the virtual element in the initial configuration $\Omega _0^e$, see Fig. 6. The procedure was described in detail in Wriggers et al. [34] and will not be reported here. We just state the final results. The Young’s modulus is corrected by

$$\begin{aligned} \hat{E} = \frac{\beta }{1+\beta } \,E= \phi \,E \end{aligned}$$

(55)

while the Poisson ratio $\hat{\nu }$ is kept constant as $\hat{\nu } = 0.3$ since the Poisson ratio does not influence the convergence behavior of the element and avoids locking in the stabilization term for incompressible problems. The factor $\beta$ depends on the height to length ratio of the brick element. For a virtual element with arbitrary shape this ratio can be approximated by using the inner and outer radii, $R_i^2,R_a^2$ respectively, see Fig. 6, to obtain

$$\begin{aligned} \beta = 2 \sqrt{2} \,(1+\nu ) \frac{ R_i^2}{R_a^2-R_i^2}. \end{aligned}$$

(56)

The inner radius is computed by using the distance from the geometrical centre to the convex hull of the virtual element while the outer radius is defined by the maximum distance of nodes related to the virtual element. Another way to obtain $\beta$ can be found in van Huyssteen and Reddy [31] which is based on employing ellipses instead of the circles in Fig. 6. Once the corrected Young’s modulus and Poisson ratio are determined the Lamé parameters follow from

$$\begin{aligned} \hat{\lambda } = \frac{\hat{E} \,\hat{\nu } }{(1+\hat{\nu })(1-2 \hat{\nu })}\quad \hat{\mu } = \frac{\hat{E}}{2(1+\hat{\nu })} \end{aligned}$$

(57)

Fig. 6

Inner and outer radius of a virtual element

Remark

From (55) the Lamé parameters can be written as $\hat{\lambda } = \phi \,\lambda$ and $\hat{\mu } = \phi \,\mu$, and with that also the strain energy as $\hat{\varPsi }= \phi \,\varPsi$. This means that we can re-write the strain energy parts in (41) for a virtual element $\Omega _0^e$ with (47) and (53) as

$$\begin{aligned} U_s^e (\varvec{u}_h) = (\Omega _0^e - \phi \,\Omega _{0T}^e) \varPsi (\varvec{C}_u) + \phi \, {U}^e (\varvec{u}_h) . \end{aligned}$$

(58)

where ${U}^e (\varvec{u}_h)$ is the stabilization energy from (52) computed for the Lamé parameters $\lambda$ and $\mu$. Observe that for $\phi =0$ only the energy related to the consistency part acts which would lead to a singular element. On the other hand for $\phi =\Omega _0^e\,/\,\Omega _{0T}^e$ the consistency part disappears and a pure finite element formulation based on the internal triangles is left over. In Wriggers et al. [34] it was shown that the latter case does not have the same good solution behavior as a virtual element with a factor $\phi$ computed from (55).

Fig. 7

Ellipsoidal plate, a Set-up of the problem, b–e structured and Voronoi meshes

5 Numerical examples

In this section we compare the new mapping procedure for virtual element discretizations with existing formulations. The main goal is to show that this formulation blends perfectly into the idea of virtual elements and produces the same results for higher order isoparametric or NURBS mappings. The examples are subjected to loads that lead to finite deformation strain states. For an efficient solution all numerical simulations of the nonlinear problems have to be performed by using a Newton–Raphson algorithm with load stepping when necessary. Due to the fact that all formulations are linearized in a consistent manner, using AceGen, see Korelc [18], quadratic convergence is achieved. All geometric and constitutive data in the examples are given in consistent units.

In all examples either NURBS (denoted by a MB) or isoparametric functions (denoted by a MN) were used for the map from the reference to the initial configuration. Simulations were conducted with different virtual elements using the software AceFEM, see Korelc [19] and Korelc and Wriggers [20]:

• VEM-N4: virtual elements with four nodes and linear ansatz,

• VEM-N8: virtual elements with eight nodes and linear ansatz,

• VEM-VO: virtual elements within a Voronoi mesh with arbitrary number of nodes

The results of these discretizations were compared with linear Q1 and quadratic Q2 quadrilateral finite elements.

5.1 Squeezing of an ellipse

The solid structure shown in Fig. 7 is subjected to a traction load $\bar{t}_y=-300$ at the top. The ellipse is defined by its principal axes $R_x=3$ and $R_y=2$. The Lamé parameters, that govern the hyperelastic response of the solid, are given as $\lambda =71.0719$ and $\mu =36.6128$. The bottom part of the ellipse is flat, see Fig. 7a. It has the length $L=\sqrt{2} R_x$ and is fixed in y-direction. The left corner at the bottom is additionally fixed in x-direction. The total height of the ellipse is $H=(1+\frac{1}{2}\sqrt{2})R_y$.

In Fig. 7b, c the structured and Voronoi meshes are shown, respectively, with respect to the initial configuration $\Omega _0$. The associated meshes in the reference configuration $\Omega _r$ are displayed in Fig. 7d, e.

The von Mises stress distribution is depicted in Fig. 8 for a relatively coarse mesh of $8 \times 12$ elements. The discretizations in Fig. 8a, d show results that were computed with a standard finite element and virtual element discretization without mapping. The results depicted in Fig. 8b, c, e, f were obtained with the new mapping techniques from reference to initial configuration using either the isoparametric (M0) map or the NURBS (MB) approach. The results are almost equal for the standard virtual element formulation with 8 node elements (d) and the approach using M0 or MB mapping in (b) and (e) which shows that the mapping formulation works correctly. Here we do not expect much improvement of the results since there is for the linear ansatz only a small difference between the curved geometry and the straight edge approach of the classical virtual element scheme.

Fig. 8

Von Mises stress in the ellipsoidal structure for different formulations

5.2 Square plate with a hole

A plate with a hole, is depicted in Fig. 9, is subjected to an extension. The plate in Fig. 9a has a height of $H=2$, a width of $L=2$. The radius of the internal hole is $R=0.5$. The displacement is fixed at the bottom in y-direction. In the mid of the plate, at $x=\frac{L}{2}$ the displacement in x-direction was fixed. This example was considered in De Bellis et al. [12].

Fig. 9

Plate with a hole, a set-up of the problem, b–e structured and Voronoi meshes

A prescribed displacement $\bar{u}_y=1.5 \,H$ is applied at the top of the plate. The Lamé parameters, that govern the hyperelastic response of the solid, are given as $\lambda =71.0719$ and $\mu =36.6128$. In Fig. 9b, c the structured and Voronoi meshes are shown, respectively, with respect to the initial configuration. In Fig. 9d, e the associated meshes in the reference configuration are depicted. As well a quadratic isoparametric map as a NURBS map were employed to map the structure from the reference to the initial configuration. Note that here a combination of 8 mappings was used to model the problem. The different mappings were tied together in a suitable way such that the displacement constraints related to the boundary value problem were enforced correctly.

Fig. 10

Von Mises stress in a plate with a hole for different formulations

In Fig. 10 the von Mises stress is depicted for different discretizations and mappings at the deformed configuration. It is clearly visible that the new scheme leads to results that cannot be distinguished from existing virtual element formulations, see Wriggers et al. [34], and a finite element solution using quadrilateral elements with quadratic shape functions.

In order to compare the different approaches a convergence study was performed for the displacement component $u_x$ at the point ($x=L$, $y=\frac{H}{2}$) and the total force $R_y$, needed to obtain the resulting deformation state. Both results are depicted in Fig. 11 where a range from 30 to 9600 elements was used. Since there is no analytical solution available for this finite strain example an overkill solution based on the quadratic finite element with a mesh of around 0.5 Mio. element is used in this convergence study as reference solution for the displacement component $u_{x,ref}$ and the total reaction $R_{y,ref}$.

Fig. 11

Plate with a hole, convergence study

As expected the solution with the quadratic finite element Q2 is superior. However it seems that the virtual element based on the NURBS mapping performs slightly better than the other formulations, especially for the Voronoi discretization. All virtual element formulations yield a better response than the Q1 finite element.

5.3 Bending of a C-profile

In the last example a C-profil is considered, see Fig. 12. On the right side the web of the profile is cut. The geometrical data are $H=3$, $L=1$ and $R=0.5$. The profile is subjected at its flanges to a traction load $\bar{t}_x = 2$ in opposite directions, see Fig. 12a which varies from 0 to 2 in magnitude. The Lamé constitutive parameters of the hyperelastic strain energy function are $\lambda =71.0719$ and $\mu =36.6128$. The profile is fixed in the middle of the left web at $y=\frac{H}{2}$. As in the previous example, the total mesh of the boundary value problem is obtained by using 10 mappings from different reference configurations, shown in Fig. 12d, e. These generate the initial configuration $\Omega _0$ in Fig. 12b, c for the isoparametric and NURBS map.

Fig. 12

C-profile, Set-up of the problem, structured and Voronoi meshes

Due to the loading the C-profil bends and at the largest load level it assumes the deformed state that is depicted in Fig. 13. Again the results are plotted for different discretizations. The von Mises stresses are displayed in Fig. 13a for a finite element solution using Q2 finite element quadrilaterals and in (b) for a regular mesh with virtual elements that have 8 nodes. Furthermore, Fig. 13 includes results for the new mapping procedure. In (c) and (e) are the results for the isoparametric mapping for regular and Voronoi meshes, respectively, while (d) and (f) relate to the solutions obtained with the NURBS mapping. All discretizations produce basically the same answers.

Fig. 13

Von Mises stress in the C-profile, different formulations

Difference can be seen in the convergence study that is shown in Fig. 14. A solution based on quadratic finite elements with a very fine discretization of about 0.65 Mio. elements is used as a reference since analytical solutions are not available.

Fig. 14

C-profile, convergence study

All discretization schemes produce the same load displacement curve, see the left part of Fig. 14. Differences occur in the convergence of the displacement $u_y$ that is measured at the point ($x=L,y=H-L$). All formulations converge. Again the virtual element formulation using a Voronoi discretizations depicts good coarse mesh accuracy.

6 Summary and conclusions

In this contribution a virtual element method for finite strain elasticity was derived. The key novel feature is a general mapping which allows to deviate from the assumption of straight edges of virtual elements. It was shown that general mappings like the isoparametric map and the NURBS approach, related to computer aided design, can be introduced to model exact geometries of complex structures with virtual elements. The formulation is simple and has been presented for both isoparametric and NURBS maps. It seems that the projected formulation is better in the case of Voronoi meshes when compared to solutions obtained with standard virtual elements using Voronoi meshes. For the special case of structured meshes the difference is very small. Here the virtual element solutions are basically reproduced in an exact manner.

The method proposed here is amenable to extensions of various kinds: for example to higher-order VEM formulations, like serendipity elements, to problems in three dimensions, and to other nonlinear problems such as those involving inelastic material behavior. First results indicate that the same mapping procedure can be employed for virtual elements with higher order ansatz functions.