Unstructured surface mesh smoothing method based on deep reinforcement learning

Abstract

In numerical simulations such as computational fluid dynamics simulations or finite element analyses, mesh quality affects simulation accuracy directly and significantly. Smoothing is one of the most widely adopted methods to improve unstructured mesh quality in mesh generation practices. Compared with the optimization-based smoothing method, heuristic smoothing methods are efficient but yield lower mesh quality. The balance between smoothing efficiency and mesh quality has been pursued in previous studies. In this paper, we propose a new smoothing method that combines the advantages of the heuristic Laplacian method and the optimization-based method based on the deep reinforcement learning method under the Deep Deterministic Policy Gradient framework. Within the framework, the actor artificial neural network predicts the optimal position of each interior free node with its surrounding ring nodes. At the same time, a critic-network is established and takes the mesh quality as input and outputs the reward of the action taken by the actor-network. Training of the networks will maximize the cumulative long-term reward, which ends up maximizing the mesh quality. Training and validation of the proposed method are presented both on 2-dimensional triangular meshes and 3-dimensional surface meshes, which demonstrates the efficiency and mesh quality of the proposed method. Finally, numerical simulations on perturbed meshes and smoothed meshes are carried out and compared which prove the influence of mesh quality on the simulation accuracy.

1 Introduction

Unstructured mesh is popular in numerical simulations such as computational fluid dynamics (CFD) simulations due to its flexibility and ease of generation [1, 2]. In finite element analyses (FEA), the unstructured triangular mesh is also widely used and studied [3]. However, the quality of unstructured meshes remains a major concern in its applications since mesh quality affects simulation accuracy directly and significantly [4,5,6]. Initial mesh elements generated by automatic mesh generators often have poor quality and the mesh optimization process is indispensable [7].

Topological optimization and smoothing are the two most widely used methods to improve unstructured mesh quality in mesh generation practices. Topological optimization methods such as the Delaunay edge/face swap [8, 9] improve mesh quality by swapping the diagonal of quadrilaterals in which the Delaunay criterion is violated. Only triangular and tetrahedral meshes can be optimized by the Delaunay edge/face swap and the mesh quality cannot be maximized because node positions are not changed. Node inserting/deleting and local mesh reconstruction are other types of topological optimization methods [10,11,12]. These methods are effective in extreme cases such as the valence of an interior mesh node being too large or small.

Unlike topological optimization, smoothing methods move the interior nodes to their optimal position iteratively while keeping the topology unchanged. The smoothing methods can improve mesh quality substantially because node position displacement can be relatively large and can be applied in most cases for all interior nodes.

Smoothing methods mainly include optimization-based smoothing methods and heuristic smoothing methods. Compared with optimization-based smoothing methods, heuristic smoothing methods are more efficient but yield lower mesh quality. The balance between smoothing efficiency and mesh quality has been pursued in previous studies.

The Laplacian smoothing method [13] is one of the heuristic methods that move each interior node iteratively to the arithmetic averaging center of its surrounding neighbor nodes. Due to its extremely high efficiency and satisfactory mesh quality, the Laplacian method is widely adopted in mesh generation practices. But the Laplacian smoothing method may result in some low-quality or even invalid elements as well as deformation and shrinkage in smoothing 3D surface meshes [14]. Improvements have been proposed to avoid these problems and other heuristic methods have been developed. For example, Zhou [15] proposed the angle-based smoothing method which iteratively moves the interior free nodes to adjust the angles of adjacent elements of the free node. It turned out that the angle-based method generates higher quality mesh than the Laplacian method. Vartziotis [14, 16, 17] developed the geometric element transformation method (GETMe) that transforms poor-quality elements into regular ones and moves all nodes of an element simultaneously thus improving overall quality, which is different from other node-moving methods.

On the other hand, the optimization-based method [18,19,20] defines local or global objective functions such as inverse shape quality, skewness, etc., and minimizes the objective function by iterative methods such as the conjugate gradient solver or the Newton solver and eventually increases mesh quality after iterations. This method generally generates meshes with the highest quality at the highest computational cost.

Recently, due to its good generalization of nonlinear relations, artificial neural networks (ANN) are widely studied and applied to multi-disciplines such as solving PDEs [21, 22] and surrogate modeling [23, 24], computational mechanics [25,26,27,28,29], mesh adaptation [30,31,32] and mesh generation [33,34,35,36,37,38]. Application of ANN methods in computation-intensive fields can improve efficiency significantly while maintaining reasonable accuracy. The ANN-based mesh smoothing method (NN-Smoothing) proposed by Guo [38] predicts the optimal node positions by an ANN, which was trained by samples extracted from optimization-based smoothing meshes. The NN-Smoothing method imitates the optimization-based smoothing method in generating high-quality meshes while maintaining the high efficiency of the Laplacian method. In this method, the training samples are generated, optimized, and normalized by cumbersome manual work. In addition, seven separate neural networks are trained to handle input with different dimensions.

To eliminate the manual work of preprocessing training samples, and unify the networks into a single network capable of dealing with different input dimensions. This paper proposes a new smoothing method that combines the advantages of the heuristic Laplacian method and the optimization-based method based on the deep reinforcement learning (DRL) method under the Deep Deterministic Policy Gradient (DDPG) [39] framework. Within the DDPG framework, the actor-network predicts the optimal position of each interior free node with its surrounding ring nodes. At the same time, a critic-network is established and takes the mesh quality as input and outputs the reward of the action taken by the actor-network. Training of the networks will maximize the cumulative long-term reward, which ends up maximizing the mesh quality.

This paper is organized as follows: in Sect. 2, we briefly review popular mesh quality optimization methods including topological optimization methods and smoothing methods. The mesh smoothing based on deep reinforcement learning is illustrated in Sect. 3. Training algorithms and hyperparameters are studied in Sect. 4. Training, validations, and comparison between different methods on 2-dimensional and 3-dimensional surface meshes will be presented in Sects. 5 and 6. Numerical simulations on smoothed meshes and perturbed meshes are carried out and results are compared in Sect. 7. Finally, conclusions and possible future work of the method are proposed in Sect. 8.

2 Brief review of unstructured mesh quality optimization methods

Mesh quality is so important to CFD and FEA numerical simulations that mesh quality optimization is almost indispensable, either integrated into the mesh generation process or carried out afterward. Topological optimization and smoothing are two major types of mesh quality optimization methods.

The Delaunay edge swap [8, 9] is one type of topological optimization that swaps the diagonal of a quadrilateral which violates the Delaunay criterion. As Fig. 1 shows, point D lies in the circumcircle of $\Delta ABC$, which violates the Delaunay criterion. Point B also has the same problem. Therefore, an edge swap is performed in quadrilateral ABCD which diagonal AC is replaced by BD. After the edge swap, the thin triangle $\Delta ADC$ is eliminated thus improving mesh quality.

Fig. 1

Delaunay edge swap [8, 9]

The Laplacian smoothing method [13] calculates the optimal free node positions (v^*) by arithmetic averaging of its surrounding ring nodes (v₁-v₅), which can be expressed as Eq. (1). The smoothing process for a single free node and its surrounding cells is shown in Fig. 2.

$$ x^{ * } = \frac{1}{N}\sum\limits_{i = 1}^{N} {x_{i} } ,y^{ * } = \frac{1}{N}\sum\limits_{i = 1}^{N} {y_{i} } $$

(1)

Fig. 2

Laplacian smoothing

The angle-based smoothing method [15] tries to optimize the included angle of neighboring cells which share the same free node by moving the node. As shown in Fig. 3, the free node, v, is moved to v^* to make the included angles $\alpha_{1}$, $\alpha_{2}$ to be equal.

Fig. 3

Angle-based smoothing [15]

Smoothing based on the geometric element transformation method (GETMe) [14, 16, 17] improves the regularity and quality of each element by a two-step regularizing element transformation. Different from other smoothing methods which move one node each time, the GETMe moves all nodes of an element simultaneously. Figure 4 shows the clockwise and counterclockwise two-step transformation of a triangular element.

Fig. 4

Triangle geometric transformation using θ = 20 of GETMe smoothing [14]

Optimization-based method [18,19,20] improves mesh quality by minimizing an objective function that is defined by certain mesh quality metrics, such as inverse aspect ratio, inverse included angle, inverse shape quality, etc. Linear solvers such as conjugate gradient or Newton solver are adopted to iteratively find the minimum objective function value (Fig. 5).

Fig. 5

Optimization-based smoothing method

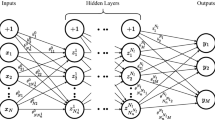
The neural network-based smoothing (NN-Smoothing) [38] predicts the optimal node positions with its surrounding ring nodes like the Laplacian smoothing by a fully connected artificial neural network as Fig. 6 shows. By training with samples extracted from mesh optimized by optimization-based method, the NN-Smoothing method imitates the optimization-based method in mesh quality while keeping high efficiency.

Fig. 6

Neural network-based smoothing method [38]

3 Deep reinforcement learning-based smoothing

3.1 Deep reinforcement learning framework

Deep learning based on artificial neural networks is capable of generalizing any nonlinear relation. Reinforcement learning is good at observing and exploring the environment and providing guidance to complete a certain task. Deep reinforcement learning (DRL) combines the strengths of both generalization and exploration.

Typical DRL algorithm procedures are shown in Fig. 7. The goal of reinforcement learning is to train an agent to complete a task within an unknown environment. The agent receives observations and a reward from the environment and sends actions to the environment. The reward is a measure of how successful an action is to complete the task goal. The policy is a mapping that selects actions based on the observations from the environment, which could be a function approximator with tunable parameters, such as a deep neural network. The learning algorithm continuously updates the policy parameters based on the actions, observations, and rewards. The goal of the learning algorithm is to find an optimal policy that maximizes the cumulative reward received during the task.

Fig. 7

Schematic graph of DRL

DRL algorithms can be categorized into policy-based and value-based models. Policy-based methods determine the action according to a probability and can output continuous actions, such as the policy gradient method, while value-based methods choose the action with the largest value, which only works in discrete action space, such as Deep Q-Network.

In this paper, a new unstructured mesh smoothing method based on DRL (DRL-Smoothing) is proposed. We implement the policy-based Deep Deterministic Policy Gradient (DDPG) DRL method [39] which works well in continuous action space to deal with continuous node coordinates. The DDPG agent can explore the environment and find the optimal strategy to complete the mesh smoothing task. Details of the DRL-Smoothing method will be discussed in the next subsection.

3.2 DRL-based mesh smoothing

To complete the mesh smoothing task, we define the environment, state, action, reward, and policy in the DDPG algorithm as follows.

Environment includes the mesh and the dynamics of the mesh.

Mesh: including all mesh nodes and cell topology information.

Dynamics of the mesh: including mesh nodes relocation and updating functions.

State:

The current free node v and its surrounding ring nodes (v₁–v₅) as Fig. 6a shows.

The interior free nodes are selected and smoothed one by one in the order of storage in one training episode. And the ring nodes (v1–v2–v3–v4–v5) are constructed in a clockwise/counter-clockwise way as shown in Fig. 6a. To eliminate the impact of the absolute location of the nodes and increase generalizability, normalization is applied to the coordinates of the ring nodes to transform the ring polygon into a unit-length box [38] as shown in Fig. 8.

Fig. 8

State normalization process [38]

Action:

Predicted the optimal free node position v* as Fig. 6a shows.

Having the prior knowledge that the Laplacian smoothing could improve mesh quality, we incorporate the knowledge by defining the node position as a summation of the Laplacian smoothing node position with the action vector $\left( {a_{x} ,a_{y} } \right)$, which can be expressed as:

$$ \begin{gathered} x^{new} = x^{ * } + a_{x} \hfill \\ y^{new} = y^{ * } + a_{y} \hfill \\ \end{gathered} $$

(2)

where $\left( {x^{ * } ,y^{ * } } \right)$ are node positions calculated by the Laplacian smoothing method in Eq. (1).

Reward:

Weighted mesh quality metrics.

The minimum equiangular skewness ($Q_{\min }$) and the average equiangular skewness ($Q_{avg}$) are weighted to construct the reward function R as shown in Eq. (3).

$$ R = \lambda Q_{\min } + \left( {1 - \lambda } \right)Q_{avg} $$

(3)

The equiangular skewness quality ($Q$) is defined as follows:

$$ Q_{i} = 1.0 - \max \left( {\frac{{\theta_{e} - \theta_{\min } }}{{\theta_{e} }},\frac{{\theta_{\max } - \theta_{e} }}{{180 - \theta_{e} }}} \right) $$

(4)

where $\theta_{e} = 60^{ \circ }$ for triangles, $\theta_{e} = 90^{ \circ }$ for quadrilaterals, $\theta_{\min }$ and $\theta_{\max }$ are the minimum and maximum included angles for a single cell. The range of $Q$ is from 0 to 1.0. When skewness quality $Q = 1.0$, the quality is the best and the corresponding reward should be the largest. When skewness quality $Q = 0.0$, the quality is the worst and the reward is the smallest. The influence of the weighted coefficient $\lambda$ will be discussed in Sect. 4.2.

In 2-dimensional meshes, when the intersection check failed or the predicted node locates outside its surrounding polygon composed of its ring nodes, a penalty of − 1 is given to the reinforcement learning agent. The geometrical intersection check of 2 line segments is simple and will not be illustrated in this paper.

In the DDPG agent, a critic-network is established to process the reward signal and provide guidance to the training of the actor-network. The critic-network consists of a state path, an action path, and a concatenation common path. As Fig. 9 shows, the state path is a 3-layer fully connected (FC) network, with 64, 16, and 8 neurons in each hidden layer. The action path is a 1-layer FC network with 8 neurons. The concatenation path also has 1 FC layer, with 4 neurons. ReLU activation functions are added with each fully connected layer.

Fig. 9

Critic neural network of the DDPG agent

Policy

The actor artificial neural network predicts the optimal node positions according to its ring nodes. The actor-network is also called the policy network, which is represented by a fully connected multilayer perceptron in this paper as shown in Fig. 10.

Fig. 10

Actor neural network of the DDPG agent

Previous work [38] established 7 neural networks with different input dimensions and trained each network separately to solve the problem of variance of the number of ring nodes. Meanwhile, training samples and neural networks need to be established and trained separately for triangular grids and quadrilateral grids.

In this paper, we fix the input dimension for the actor-network, only considering a maximum of 8 surrounding ring nodes. If the number of ring nodes is larger than 8, we use the Laplacian smoothing for these nodes. Zero-padding is adopted when the number of ring nodes is less than 8. Thus, the input dimension is fixed at 16. The influence of the input dimension of the actor-network and zero-padding strategy will be discussed in Sect. 4.2. We use 2 fully connected hidden layers, with 32 and 16 neurons in each layer. The output layer consists of 2 neurons that output the action vector (a_x, a_y), optimized node coordinates can be obtained by Eq. (2). ReLU activation functions are added with each hidden layer to improve nonlinear generalization, which is shown as follows:

$$ \sigma \left( x \right) = \left\{ {\begin{array}{*{20}c} {0,x < 0} \\ {x,x \ge 0} \\ \end{array} } \right. $$

(5)

3.3 Three-dimensional surface mesh smoothing based on the DRL method

Traditional surface mesh smoothing methods project the free nodes to the geometry after the relocation of every node, which is very inefficient. The DRL-Smoothing method can be applied to 3-dimensional (3D) surface mesh with minor modifications and only one projection is required.

Like the 2D mesh smoothing, we adopt the same DDPG framework and extend the state definition, normalization (Fig. 8), and action definition Eq. (2) to 3D situations. Specifically, a 3D triangle is normalized so that it can be fit into a unit bounding box, and 3D actions are defined by directly extending Eq. (2) to 3D. For the actor-network, we use 3 fully connected hidden layers, with 32, 16 and 16 neurons in each layer.

4 Training algorithm and hyperparameters

4.1 Training algorithm

As an actor-critic agent, the DDPG agent maintains four artificial neural networks: online actor $\mu \left( S \right)$, online critic $Q\left( {S,A} \right)$, target actor $\mu^{\prime}\left( S \right)$, and target critic $Q^{\prime}\left( {S,A} \right)$.

The actor-network takes observation S and outputs the corresponding action that maximizes the long-term reward. The critic-network takes observation S and action A as inputs and outputs the corresponding expectation of the long-term reward.

The online networks are used and updated in real time, while the target networks are periodically updated based on the parameters of the latest online networks to improve stability. The detailed training algorithm of the DDPG agent is as follows [39].

The general training procedure is depicted in the flowchart as shown in Fig. 11.

Fig. 11

General training procedure of the DRL-Smoothing method

4.2 Training hyperparameters

In the DDPG algorithm, the update smooth factor $\tau = 10^{ - 3}$, the random experience minibatch size is M = 64, the experience buffer size is R = $10^{6}$, and the discount factor $\gamma = 0.99$. The Ornstein Uhlenbeck noise model is adopted to encourage exploration.

We adopt the Adam optimizer with a learning rate = 10^–4 for the actor-network, and a learning rate = $5 \times 10^{ - 3}$ for the critic-network to improve learning results. $L_{2}$ regularization with factor = 10^–3 is adopted to avoid overfitting.

To get better training convergence and accumulative reward, we consider the influence of the weighted coefficient $\lambda$, dimension of the neuron network, input dimension of the actor-network, activation function, and padding strategy. In this section, we generate a triangular mesh with the node valence equal to 6 for all nodes and perturb the nodes' coordinates randomly to establish the training mesh and validation mesh. The initial mesh, the perturbed training mesh, and the perturbed validation mesh are depicted in Fig. 12, and information on the mesh is listed in Table 1.

• (1) Reward weighted coefficient $\lambda$

Fig. 12

Training and validation mesh for hyperparameters study

Table 1 Information of the perturbed training and validation mesh

To determine the weighted coefficient $\lambda$ in Eq. (3), we fix the input dimension of the actor-network to be 12 to adapt to the node valence (V = 6) of the training mesh. We use 2 hidden layers with 32 and 16 neurons in each layer, and the ReLU activation function is added to each hidden layer. Padding and Laplacian smoothing is not adopted in this case. We choose 5 different values for $\lambda$ and compare the training results. Figure 13 compares the normalized episode reward convergence history. In this figure, the rewards are normalized by the converged reward to ensure the rewards are comparable for different weighted coefficients. The figure shows that the reward convergence history is slightly affected by $\lambda$.

To determine the best pre-trained model and its corresponding $\lambda$, we validate the pre-trained models with different $\lambda$ and smooth the validation mesh for 5 iterations. Table 2 shows the mesh quality after smoothing. The data shows that the mesh quality improves significantly after smoothing for all cases. When $\lambda =1.0$, the reward is equal to the minimum skewness quality, and the smoothed mesh has the highest minimum quality and highest average quality. Therefore, we choose $\lambda =1.0$ in this paper hereafter.

• (2) Dimensions of actor-network.

Fig. 13

Episode reward convergence history of different reward weighted coefficient $\lambda$

Table 2 Validation results when weighted coefficient $\lambda$ varies

The dimension of the neural network affects the generalization and accuracy of the network. Overfitting and underfitting are two common problems in training neural networks. A large and deep neural network has good accuracy but it is hard to converge and more likely to be overfitting, while a small network may lead to underfitting problems. To train the best neural network, the dimension of the network is one of the important hyperparameters which should be carefully dealt with.

In this paper, the input of the actor-network is the 2-dimensional coordinates of the ring nodes, a fully connected multilayer perceptron (MLP) is suitable for modeling since the amount of sample data is moderate.

The optimal dimension of neural networks is always determined by continuous experiments. It is recommended to start with a small value such as 1–5 layers and 1–100 neurons, and then slowly add more layers and neurons if underfitting, and reduce the number of layers and neurons if overfitting. In addition, we can also consider introducing batch normalization, dropout, regularization, and other methods to reduce overfitting in the actual process.

To determine the best dimension of the actor-network, we train and validate the neural networks with different neural network dimensions on the training and validation mesh shown in Fig. 12.

We compared 8 cases with different dimensions as Table 3 shows. In these cases, we fix the input dimension of the actor-network to be 12 to adapt to the node valence (V = 6) of the training mesh and choose the ReLU activation function. We change the number of hidden layers and the number of neurons in each layer. We train different actor-network and compare episode reward and mesh quality of validation smoothed mesh. In Table 3, ‘[4, 4, 4, 4]’ means there are 4 hidden layers with 4 neurons for each layer. ‘[32, 8, 4]’ means there are 3 hidden layers with 32, 8, and 4 neurons respectively.

Table 3 Training episode reward and the mesh quality for validation smoothed mesh

Figure 14 shows the convergence history of episode reward. Table 3 shows the training reward when episode = 1000 and the mesh quality for validation smoothed mesh.

Fig. 14

Training reward convergence history for different network dimensions

In Case 1 and Case 2, we add more hidden layers from 1 to 4 layers, and only when we reach 4 hidden layers, the neural network has a better training and validation performance. In Case 3, we increase the number of neurons in the single hidden layer from 4 to 8, 16, 32, 64, and up to 128 to achieve better performance. From these analyses, we can conclude that adding more hidden layers or adding more neurons will improve training and validation performance.

Therefore, we add more layers and more neurons to the actor-network. In Case 4—Case 8, we achieve converged results with both 2 hidden layers and 3 hidden layers. Table 3 shows the episode reward and the mesh quality for Case 4—Case 8 are very close. However, the convergence histories differ significantly. Among all the results, Case 5 and Case 8 have the best convergence performance. Given that Case 5 is less computationally intensive, we use 2 hidden layers with 32 and 16 neurons for each layer like Case 5 in this paper.

• (3) Input dimension N and padding strategy.

For triangular mesh, the optimum valence of each interior free node is 6. For quadrilateral mesh, the optimum valence is 4. A valence that is larger or smaller than the optimum value may cause bad mesh quality. In complex meshes, the node valences are varying for different nodes, previous work [39] used 7 separate neural networks with different input dimensions.

In this paper, we use a single network with fixed input dimension 2*N (for 2D mesh). For free nodes that have more than N ring nodes, i.e., the node valence V > N, we adopt the Laplacian smoothing instead. For free nodes that have less than N ring nodes, i.e., the node valence V < N, we adopt a padding strategy to keep the input dimension fixed. Laplacian smoothing and padding will be automatically switched according to the number of ring nodes.

Zeroes are added if the actual number of ring nodes (node valence V) is less than N. Then, the padding dimension is D = 2(N–V) for 2-dimensional cases.

We train different actor-networks with different input dimensions when N varies from 6 to 10. For the training mesh in this section, the node valence is V = 6, therefore, the padding dimension D increases from 0 to 8 accordingly. Figure 15 compares the episode reward convergence history. It shows that the converged rewards are close for different padding dimensions but the robustness of the training process decreases when the padding dimension increases.

Fig. 15

Episode reward convergence history of actor-network with different input dimensions

After training, we validate the actor-network with the validation mesh as shown in Fig. 12c. Table 4 shows the skewness quality of the mesh smoothed by the actor-network with different input dimensions. As the table shows, when the padding dimension D < 4, the actor-network performance is not affected by the padding dimension, and the smoothed mesh has the highest quality when N = 8. When padding dimension D > 4, it may cause side effects to the performance of the actor-network and the quality of the smoothed mesh degrades.

Table 4 Validation results when the actor-network input dimension varies

For most 2D and 3D surface meshes, the node valence rarely exceeds 8. Therefore, the input size of the actor-network is fixed at 16 for 2D meshes and 24 for 3D meshes respectively. Zero-padding and Laplacian smoothing is switched automatically according to the node valence.

• (4) Activation functions.

The activation function is important for nonlinear fitting and plays an important role in the performance of the neural network. The ReLU function is widely adopted and can help to eliminate the gradient disappearance problem and solve the convergence problem of deep networks. Besides, compared with sigmoid and tanh, ReLU abandons complex calculations and increases the speed of operations.

As for this paper, different activation functions can also be adopted and tested, such as leakyReLU, tanh, and ELU as shown in Fig. 16.

Fig. 16

Four types of activation functions considered in this paper

For the training and validation mesh shown in Fig. 12, we train the neural networks with 4 different activation functions. The actor-network consists of 2 hidden layers with 32 and 16 neurons respectively. Figure 17 shows the convergence history of different activation functions. Table 5 shows the training episode reward and the mesh quality for validation smoothed mesh.

Fig. 17

Training reward convergence history for different activation functions

Table 5 Training episode reward and the mesh quality for validation smoothed mesh

The data shows that we can always get converged results with 4 activation functions. Table 5 shows the difference in episode reward and mesh quality is very small. Meanwhile, the difference in convergence histories is relatively more obvious. In terms of computation cost and convergence, ReLU has the best performance. Therefore, we choose ReLU as the activation function in this paper.

5 Training and validation cases on 2-dimensional meshes

5.1 Training cases

We train the DDPG agent with a perturbed mesh in a rectangular domain. The perturbed mesh (as shown in Fig. 18b) is generated by randomly perturbing the interior nodes of an initial regular triangular mesh (as shown in Fig. 18a). The information of the initial regular mesh and perturbed training mesh is illustrated in Table 6.

Fig. 18

Mesh before and after training

Table 6 Information of the initial regular mesh and training mesh

The smoothed mesh after training is shown in Fig. 18c which clearly shows that the smoothed mesh recovers regularity. Since only one smoothing iteration is conducted during the training episode, the smoothed mesh is still worse than the initial regular mesh.

The episode reward convergence history in Fig. 19 shows that the training converged within 700 episodes.

Fig. 19

Episode reward convergence history of the training process

Table 7 compares the mesh quality of the mesh optimized by DDPG training and by the Laplacian smoothing method. Three smoothing iterations are carried out for this comparison. It shows that mesh skewness quality increases after training. The DDPG training results are better than Laplacian smoothing for minimum skewness quality $\left( {Q_{\min } } \right)$ while the average quality $(Q_{{{\text{avg}}}} )$ is almost equivalent. This demonstrates the effectiveness of the DDPG training procedure.

Table 7 Comparison of mesh quality of DDPG training results and the Laplacian smoothing

5.2 Validation cases

To validate the pre-trained policy network, we adopt five cases to further analyze the performance of the DRL-Smoothing method. The first case is referenced from Ref. [38], which can represent common FEA simulation meshes. The other cases represent a 2D cylinder, a 2D NACA0012 airfoil, and a 2D 30P30N three-element airfoil which is commonly used in CFD simulations. The number of free nodes and mesh quality of the initial validation meshes are shown in Table 8. The minimum equiangular skewness quality of the 4 initial meshes is smaller than 0.25, a common criterion to judge the usability of the mesh, which indicates the bad quality of the initial meshes.

Table 8 Information of the initial validation meshes

The validation process only uses the actor-network, so the procedure is very simple and direct, as Fig. 20 shows. Both in the training and validation process, the free nodes are selected one by one according to the data storage order of mesh node coordinates.

Fig. 20

Validation procedure of the pre-trained actor neural network

Six mesh quality optimization methods introduced in Sect. 2, including the Laplacian smoothing, the angle-based smoothing, the GETMe, the NN-Smoothing, the optimization-based method, and the DRL-Smoothing proposed in this paper are compared in terms of quality and efficiency. All the methods are implemented in ${\text{C}}{+}{+}$ programming language to make sure the time cost is comparable. We used the optimization-based smoothing method in the mesquite mesh quality improvement toolkit [20]. The objective function of the optimization-based smoothing method is the ${L}_{1}$ norm of the aspect ratio gamma quality metric. Since multi-iterations are required to optimize the initial mesh, we run the cases from 1 to 10 iterations and check the mesh quality.

Figures 21, 22, 23 and 24 show the initial mesh and mesh smoothed by the DRL-Smoothing method for three iterations of the four validation cases respectively. All the validation meshes are more complex than the training mesh, which proves the robustness and extensibility of the pre-trained policy network.

Fig. 21

Validation case 1 for the DRL-Smoothing method

Fig. 22

Validation case 2 for the DRL-Smoothing method

Fig. 23

Validation case 3 for the DRL-Smoothing method

Fig. 24

Validation case 4 for the DRL-Smoothing method

Figure 25 shows the comparison of mesh quality for the six methods when smooth iteration increases from 1 to 10.

Fig. 25

Mesh quality comparison of different smoothing methods with iterations increase from 1 to 10

We can see from Fig. 25 that the mesh quality reaches the maximum values when smooth iteration increases to around 4. If more iterations were run, the mesh quality keeps the same and even degrade in some cases. Since the objective function of the optimization-based method is the L₁ norm of mesh quality, it has higher average quality than other methods.

As shown in Table 9, when smooth iteration is around 4, the DRL-Smoothing method generally outputs higher-quality meshes in all cases compared with the Laplacian smoothing, the angle-based smoothing, and the GETMe smoothing. In general, the performance of the DRL-Smoothing is similar to the NN-Smoothing method. Except in case 3, the DRL-Smoothing method is inferior slightly to the NN-Smoothing in minimum skewness but the average skewness is almost equivalent to the NN-Smoothing method. This indicates that the actor-network may require further training on different meshes to increase its generalizability.

Table 9 Comparison of mesh quality of different smoothing methods when iteration = 4 for different cases

Since the time cost of every smoothing iteration is very small, to calculate the time cost more accurately and consider the efficiency of the above smoothing methods, we run 100 and 1000 iterations of smoothing for each method with case 4 and count the time cost, which is listed in Table 10. In the meantime, we also calculate and compare the mesh quality after 4 and 100 smoothing iterations and the results are listed in the table. The data shows that mesh quality degrades when the number of smoothing iterations is too large for all methods. Even for the optimization-based method, the minimum skewness also degrades when iteration = 100.

Table 10 Comparison of time cost of different smoothing methods

The data shows time cost increases proportionally when smooth iteration increases. The Laplacian method is the most efficient, while the optimization-based method is the least efficient. The Laplacian method is 10 × faster than angle-based smoothing, 50 × faster than NN-Smoothing, DRL-Smoothing, and GETMe, and nearly 500 × faster than the optimization-based method.

The DRL-Smoothing is as efficient as the NN-Smoothing and both methods are slightly more efficient than the GETMe method. The NN-Smoothing uses seven separate neural networks to deal with different numbers of ring nodes, while the DRL-Smoothing method uses only one actor-network. The efficiency of the NN-Smoothing and DRL-Smoothing methods mainly depends on the dimensions of the neural network which is chosen to be the same as Ref. [38] in this paper.

6 Training and validation cases on 3-dimensional surface meshes

6.1 Training cases

We generate a 3-dimensional triangular surface mesh for a sphere as shown in Fig. 26a and perturb the nodes to get the training mesh as shown in Fig. 26b. The mesh after 3 DRL smoothing iterations is shown in Fig. 26c. The result indicates that the regularity and quality of the smoothed mesh improve significantly. The mesh information and quality are listed in Table 11.

Fig. 26

3D triangular surface mesh for DRL training

Table 11 Information of the initial regular mesh, perturbed training mesh, and smoothed mesh

6.2 Validation cases

We adopt 4 three-dimensional surface meshes to validate the DRL-smoothing method. The geometries are downloaded from the digital shape workbench v5.0 AIM@SHAPE [40] which represents some commonly used 3D visualization models.

Figures 27, 28, 29 and 30 show the initial perturbed mesh and the smoothed mesh after 4 smoothing and projection iterations. Table 12 shows the mesh quality of the initial meshes and the smoothed meshes. The results show that the mesh smoothness and mesh quality of the surface meshes improve significantly, which demonstrates the extensibility of the DRL-Smoothing.

Fig. 27

Validation case 1 for the DRL-Smoothing method on the 3D surface mesh

Fig. 28

Validation case 2 for the DRL-Smoothing method on the 3D surface mesh

Fig. 29

Validation case 3 for the DRL-Smoothing method on the 3D surface mesh

Fig. 30

Validation case 4 for the DRL-Smoothing method on the 3D surface mesh

Table 12 Mesh quality of the initial meshes and the smoothed meshes

Note that the 3D surface mesh smoothing examples are only used to demonstrate the extensibility of the DRL-Smoothing method. The DRL-Smoothing cannot accurately preserve the geometrical features of the 3D shape, such as sharp corners.

7 Numerical simulations with smoothed meshes

In this section, we adopt three typical numerical simulation cases in computational fluid dynamics, i.e., subsonic flow past the NACA0012 airfoil, transonic flow past the RAE2822 airfoil, and subsonic flow past the 30P30N three-element airfoil, and validate the numerical results with wind tunnel experiment data, to demonstrate the usability and effectiveness of the meshes optimized by the novel DRL-based mesh smoothing method.

The freestream conditions and mesh parameters of the three cases are listed in Table 13. The growth rate of the boundary layer anisotropic quadrilateral mesh is 1.2. To simulate the boundary layer more accurately, the normal initial grid spacing on the wall is determined so that the y⁺ is approximately equal to 2.

Table 13 Freestream conditions and mesh parameters of the three cases

Figure 31 shows the meshes optimized with our DRL-based smoothing method. Table 14 shows the maximum skewness and average skewness of the 6 meshes which indicates that the regularity and quality improve significantly after smoothing.

Fig. 31

Perturbed mesh and corresponding smoothed mesh of the three airfoil simulation cases

Table 14 Mesh quality of the perturbed meshes and the smoothed meshes

Numerical simulations are carried out by using the in-house code HyperFLOW [41, 42] developed by the author’s team. The simulations are based on second-order finite volume discretization of the Reynolds Averaged Navier–Stokes (RANS) equation. Inviscid fluxes are discretized with Roe’s flux difference method and viscous interface gradients are calculated by the difference of face normal variables [43]. Cell gradient is reconstructed by the cell-based Green-Gauss method and the Spalart–Allmaras one equation model is adopted to consider turbulence.

Figure 32 compares the numerical results on the smoothed mesh and the perturbed mesh of the lift and drag coefficients with experimental data of the NACA0012 airfoil. The differences in the lift curves near the stall attack angles indicate that the perturbed mesh may lead to an inaccurate prediction of the stall. Besides, the drag polar curves show that numerical results on the perturbed mesh over-predict drag significantly.

Fig. 32

Aerodynamic coefficients of NACA0012 under different angles of attack

Figure 33 compares the pressure coefficient (Cp) distribution and Mach contours on the smoothed mesh and the perturbed mesh of the RAE2822 airfoil. The Cp distribution on the upper surface of the airfoil shows a clear difference between the perturbed mesh and the smoothed mesh. And the isolines in the Mach contours are smoother for the smoothed mesh, indicating better flow resolution on the smoothed mesh.

Fig. 33

Pressure coefficient distribution and Mach contour of RAE2822 simulation with perturbed and smoothed meshes

Table 15 compares the force coefficients of CFD numerical results with experimental data. The lift and drag data show that numerical results on the smoothed mesh are closer to experimental data. Numerical results on perturbed mesh over-estimate the drag coefficient but underestimate the lift coefficient.

Table 15 Comparison of force coefficients between simulation and experiment

Figure 34 compares the pressure coefficient (Cp) distribution of the smoothed mesh and the perturbed mesh of the 30P30N airfoil. In the sub-figures, the flap, the slat, and the main wing are compared separately. The sub-figures show that the CFD results agree well with experimental data in general, and there are slight differences between the perturbed mesh and the smoothed mesh. Like the RAE2822 airfoil case, Mach contours in Fig. 35 show that isolines are smoother for smoothed mesh which is closer to the real physical phenomena.

Fig. 34

Pressure coefficient distribution of 30P30N simulation with perturbed and smoothed meshes

Fig. 35

Mach contour of 30P30N simulation with perturbed and smoothed meshes

8 Conclusions and future work

In this paper, a new unstructured mesh smoothing method based on Deep Reinforcement Learning (DRL-Smoothing) is proposed. The framework of DDPG is adopted and adapted to complete the mesh smoothing task. Different from previous work training separate neural networks by labeled data samples, this paper establishes and trains a single unified actor-network with fixed input dimensions by semi-supervised reinforcement learning. The DRL-Smoothing method predicts each interior free node position in the Laplacian smoothing manner, but the training of the actor-network maximizes the long-term reward thus maximizing mesh quality. Therefore, the DRL-Smoothing method can output high-quality mesh while maintaining high efficiency.

Training and validation results on a simple rectangular domain case show that the pre-trained policy network can be extended to more complex problems, such as 2D cylinder, 2D NACA0012 airfoil, and 2D 30P30N three-element airfoil mesh optimization. Quality comparisons of the six mesh smoothing methods show that the DRL-Smoothing method generally ranks top among the six methods. It outperforms the Laplacian method and the angle-based method in all cases while having similar performance to the NN-Smoothing method in the last two validation cases. Time cost tests show that the proposed DRL-Smoothing method is as efficient as the NN-Smoothing method and both methods are slightly more efficient than the GETMe smoothing method. Training and validation on 3D surface mesh prove the extensibility of the DRL-Smoothing method. Numerical simulations on 2D perturbed meshes and smoothed meshes are carried out and compared which proves the influence of mesh quality on the simulation accuracy.

Compared with the previous NN-Smoothing method, the DRL-Smoothing can achieve similar efficiency and quality performance and reduce the complexity of coding and repetitive manual work of preparing training samples.

Future work could be extending the current method to quadrilateral mesh and 3D volume mesh smoothing. Including mesh nodes further away from the current node may reduce the number of iterations required to smooth the mesh, and better smoothing performance may also be obtained. Further investigation is required to verify this. Meanwhile, a more effective and robust actor-network could be trained by using more complicated training meshes and fine-tuning the hyperparameters of the DRL framework. Investigating the combination of the r-adaptivity [44] and machine learning methods in mesh optimization is also worthwhile.

The source code, pre-trained model, the training data, and the validation data can be accessed at github repository(https://github.com/nianhuawong/DRL_Smoothing).