1 Introduction

In the last several decades, research and applications of unstructured grids in Computational Fluid Dynamics (CFD) numerical simulations had drawn much attention. Unstructured grids offer great flexibility in the treatment of complex geometries, and solution dependent grid adaptivity on unstructured grids can be easily implemented. Despite its advantages, unstructured grids also meet some challenges in improving computational efficiency and obtaining accurate unstructured finite-volume (FV) discretization schemes. Nowadays, nominally second-order accurate unstructured FV schemes are widely applied in industrial CFD applications. However, the actual numerical accuracy of unstructured FV schemes had long been a hot topic for CFD researchers.

Pioneering work had been done on mathematical and numerical accuracy study of cell-vertex schemes due to Jameson et al. [1] and Ni [2]. Relationship between the convergence of truncation error and convergence of discretization error had been studied and clarified that the solution error could be second-order even though the local truncation error is first order [3, 4]. Preliminary investigation on the influence of mesh types on solution accuracy had also been conducted [5] which proved that triangular schemes can perform as well as quadrilateral schemes under appropriate conditions. Ever since Barth and Jespersen [6] proposed the limited form of piecewise linear reconstruction, the upwind schemes based on gradient reconstruction became perhaps the most popular unstructured second-order FV schemes. For these upwind schemes, the first-order accurate gradient is necessary to achieve second-order accurate discretization. The accuracy of gradient reconstruction and gradient accuracy effects on the accuracy of FV schemes became key factors in analyzing the accuracy of FV numerical solution.

Generally, there are mainly two types of gradient reconstruction methods which can be readily implemented on unstructured second-order FV discretization of inviscid and viscous fluxes. One is the gradient reconstruction based on the Green-Gauss theorem (the GG methods); the other is based on the least-squares approach (the LSQ methods). Performances of these two types of reconstruction techniques on unstructured meshes are affected by a number of factors, such as mesh type, mesh quality, mesh regularity, formulation, etc.

On one hand, the comparison of these two types of gradient reconstruction methods was illustrated in earlier papers [7,8,9,10]. Valuable experiences were acquired such as these two types of methods produce similar results on regular quadrilateral and triangular meshes [7]; the GG method with either simple averaging or inverse distance weighted face averaging is inconsistent on irregular grids and fails to achieve the first-order accuracy and thus should not be preferred [8]; the LSQ methods are at least first-order accurate on arbitrary meshes [9], but accuracy deterioration occurs on highly stretched grids in the presence of surface curvature [10]. However, despite former analyses and comparisons, no definitive “best” gradient reconstruction method has emerged [8] and the fundamental reason for the accuracy degradation was not revealed comprehensively.

On the other hand, the relationship between mesh characteristics and gradient or solution accuracy were investigated [11,12,13,14,15,16]. Through studying gradient reconstruction methods on grids with a high aspect ratio, it was found that accuracy degradation occurs for solutions that vary predominately in the direction of large mesh spacing [11]. Apart from aspect ratio effects, other grid effects such as mesh stretching, curvature, skewness, and non-planar faces in 3D grids are also important parameters affecting gradient or solution accuracy. Previous studies had tried to identify schemes that yield the lowest level of solution error while maintaining stability over a wide range of mesh characteristics [14, 15]. Unfortunately, however, the relationship between mesh characteristics and solution accuracy are complicated [16] and are far from clear.

Meanwhile, preliminary but successful attempts in creating accurate and robust reconstruction of the gradient and eventually improving solution accuracy had been made [8, 17].

The focus of this study is analyzing gradient reconstruction methods both mathematically and numerically for cell-centered FV schemes, evaluating the gradient effects on solution accuracy of inviscid flow simulations. Cell-vertex schemes, while differing from cell-centered schemes in formulation details, can be analyzed in the same fashion; and they have been considered in previous works [12, 13, 15]. In this paper, the conditions to ensure at least first-order accurate gradient reconstruction are derived mathematically. Then, verifications are performed on typical isotropic grid stencils by analyzing the relationship between discretization error of gradient reconstruction and discretization error of the face midpoint value approximation of a given analytic function. Numerical accuracy of gradient reconstruction is examined with grid convergence study on typical isotropic grids such as quadrilateral grids, triangular grids, perturbed grids, skewed grids and grids over a cylinder with curve boundary. Since previous studies reported that poor gradient reconstruction accuracy does not necessarily imply large discretization error [13], solution errors have to be quantified to determine the impact of gradient accuracy. Quantification of solution errors require an exact solution and will be accomplished using the Method of Manufactured Solutions (MMS) [18]. Before the MMS method was adopted, validation of the method was performed by comparing results with an exact solution case, the 2D inviscid isentropic vortex. Grid convergence studies are carried out to determine the order of accuracy and the absolute magnitude of solution errors. Traditional mesh refinement instead of downscaling tests [19,20,21,22] is employed for grid convergence study since consistent refinement is easily carried out on currently considered isotropic grids. All the schemes are implemented within a second-order cell-centered finite volume CFD solver, HyperFLOW [23, 24].

This paper is organized as follows: in section II, we briefly introduce the second-order FV discretization schemes. A comprehensive description and mathematical analysis of gradient reconstruction methods are followed in section III. Mathematical gradient accuracy analyses are confirmed numerically in section IV. Next, we present principles of the method of manufactured solutions in section V and validate this method with an exact solution case. Finally, in section VI, gradient accuracy effects on solution accuracy of inviscid flows are investigated with a Euler manufactured solution.

2 Finite volume discretization schemes

In this paper, the discretization of the conservation law is implemented in an integral form [25]:

$$ \frac{\partial }{\partial t}\underset{\Omega}{\int}\mathbf{W}d\Omega +\underset{\mathrm{\partial \Omega }}{\oint}\left({\mathbf{F}}_{\mathrm{c}}-{\mathbf{F}}_{\mathrm{v}}\right) dS=\underset{\Omega}{\int}\mathbf{Q}d\Omega $$
(1)

where W, Fc, Fv, Q are the conservative variables, the convective flux vector, the viscous flux vector, and the source term respectively. Eq. (1) is simplified to the Euler equations where no viscous term and source term exists (Fv = 0, Q = 0) for inviscid problems considered in this paper.

2.1 Spatial discretization

The convective flux is discretized with the well-known Roe’s flux-difference splitting scheme [26] as follows:

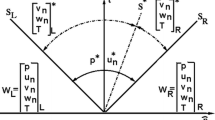
$$ {\left({\mathbf{F}}_{\mathrm{c}}\right)}_{\mathrm{ij}}=\frac{1}{2}\left[{\mathbf{F}}_{\mathrm{c}}\left({\mathbf{W}}_{\mathrm{R}}\right)+{\mathbf{F}}_{\mathrm{c}}\left({\mathbf{W}}_{\mathrm{L}}\right)-\left|{\overline{\mathbf{A}}}_{\mathrm{R}\mathrm{oe}}\right|\left({\mathbf{W}}_{\mathrm{R}}-{\mathbf{W}}_{\mathrm{L}}\right)\right] $$
(2)

where (Fc)ij is the convective flux through the interface of the neighboring control volume i and j, Fc(WL) and Fc(WR) are convective fluxes evaluated with the face left state WL and the face right state WR, respectively. The way to obtain face left and right states is called ‘solution reconstruction’ which will be discussed below. \( \left|{\overline{\mathbf{A}}}_{\mathrm{Roe}}\right| \) denotes the so-called Roe’s averaged matrix which is identical to the convective flux Jacobian. Anyway, other Riemann solvers for the convective flux can be adopted here, such as Lax-Friedrichs, Steger-Warming, van Leer, HLLC, AUSM series schemes, and so on. No matter which Riemann solver is adopted to calculate the convective flux, the face states on the left and right sides of an interface, the primitive variables UL and UR in most cases (as shown in Fig. 1), should be reconstructed firstly. For simplicity, we will denote any one of the primitive variables as U in the following context.

Fig. 1
figure 1

Solution reconstruction of a control volume face

Full size image

2.2 Solution reconstruction

Roe’s flux-difference splitting scheme, as well as other Riemann solvers, requires flow states to be reconstructed on the left and the right sides of an interface of neighboring control volumes, as sketched in Fig. 1.

If we assume that the solution is constant in each cell, a constant reconstruction is obtained which leads to first-order spatial discretization.

$$ {\displaystyle \begin{array}{l}{U}_L={U}_i\\ {}{U}_R={U}_j\end{array}} $$
(3)

where UL and UR are primitive variables at the left and right sides of a control volume interface. A second-order spatial discretization can be obtained by assuming a linear distribution of flow variables in each cell. With this assumption, the left and the right states are reconstructed through a piecewise linear interpolation as Eq. (4) [6]. Since low speed flows without discontinuity (such as shock wave) are currently studied, no limiter function is considered here.

$$ {\displaystyle \begin{array}{l}{U}_L={U}_i+{\left(\nabla U\right)}_i\cdotp {\mathbf{r}}_{\mathrm{L}}\\ {}{U}_R={U}_j+{\left(\nabla U\right)}_j\cdotp {\mathbf{r}}_{\mathrm{R}}\end{array}} $$
(4)

where (∇U)i is the gradient at cell center i, and rL represents the vector from the left cell center of i to the face midpoint, and rR represents the vector from the right cell center of j to the face midpoint.

At least first-order accurate gradient reconstruction is often required in Eq. (4) to achieve second-order accurate spatial discretization. Generally, there are mainly two types of gradient reconstruction methods which can be readily implemented in unstructured second-order finite volume discretization. One is the gradient reconstruction based on the Green-Gauss theorem (the GG methods); the other is based on the least-squares approach (the LSQ methods). These two types of methods are introduced and analyzed in the following section.

3 Gradient reconstruction methods

3.1 Green-gauss theorem based gradient reconstruction

The first type of gradient reconstruction methods is based on the Green-Gauss theorem expressed in Eq. (5).

$$ \underset{V}{\int}\nabla UdV=\underset{\partial V}{\oint }U\mathbf{n} dS $$
(5)

where U stands for any one of the primitive variables or any scalar variable, n is the surface unit normal vector. Firstly, we would like to derive the discretized form of Eq. (5).

With the linear distribution assumption of flow variables in each cell, the gradient will be constant within cells; we simplify the left-hand side of Eq. (5) as follows:

$$ {\left(\underset{V}{\int}\nabla UdV\right)}_i={\left(\nabla U\right)}_i{V}_i $$
(6)

where Vi is the volume of the control volume, (∇U)i is the gradient at cell center i. Combining Eq. (5) with Eq. (6), and introducing the Taylor-series expansion, we derive the discretized gradient of cell i as follows:

$$ {\displaystyle \begin{array}{l}{\left(\nabla U\right)}_i=\frac{1}{V_i}{\left(\underset{\partial V}{\oint }U\mathbf{n} dS\right)}_i\\ {}=\frac{1}{V_i}\sum \limits_{j=1}^{N_F}\left(\underset{\partial {V}_j}{\int}\left({U}_{ij}+\frac{\partial U}{\partial x}\left|{}_{ij}\right.\left(x-{x}_{ij}\right)+\frac{\partial U}{\partial y}\left|{}_{ij}\right.\left(y-{y}_{ij}\right)+\frac{\partial U}{\partial z}\left|{}_{ij}\right.\left(z-{z}_{ij}\right)\right){\mathbf{n}}_{ij} dS\right)\\ {}=\frac{1}{V_i}\sum \limits_{j=1}^{N_F}{U}_{ij}{\mathbf{n}}_{ij}\varDelta {S}_{ij}+\frac{1}{V_i}\sum \limits_{j=1}^{N_F}\left(\underset{\partial {V}_j}{\int}\left(\frac{\partial U}{\partial x}\left|{}_{ij}\right.\left(x-{x}_{ij}\right)+\frac{\partial U}{\partial y}\left|{}_{ij}\right.\left(y-{y}_{ij}\right)+\frac{\partial U}{\partial z}\left|{}_{ij}\right.\left(z-{z}_{ij}\right)\right){\mathbf{n}}_{ij} dS\right)\end{array}} $$
(7)

in which NF is the number of faces of the control volume, nijΔSij is the area vector of face j of cell i.

In Eq. (7), we once again use the assumption that U varies linearly within each cell so that the second and higher-order derivatives in the Taylor expansion can be neglected. Besides, Uij is the value at any point on face j up to now, if we introduce the midpoint quadrature which requires Uij to be the value at the midpoint (centroid) of face j, we obtain:

$$ {\left(\nabla U\right)}_i=\frac{1}{V_i}\sum \limits_{j=1}^{N_F}{U}_{ij}{\mathbf{n}}_{ij}\varDelta {S}_{ij} $$
(8)

Here, we would like to emphasize in Eq. (8) that Uij is the value at the midpoint of face j, and at the current stage, the gradient of cell i is represented exactly by Eq. (8) under the linear distribution assumption. Examining Eq. (8) more carefully, we found that potential errors of gradient reconstruction by Eq. (8) can only be introduced by the approximation of face midpoint value Uij.

How does the face midpoint value approximation influence the gradient accuracy? This question is answered by the following mathematical analysis. These derivations focus on the order of magnitude of gradient reconstruction error and face midpoint approximation error.

To find the necessary condition to obtain first-order gradient reconstruction of cell i, we need:

$$ {\left(\nabla U\right)}_{i\_ numerical}=\frac{1}{V_i}\sum \limits_{j=1}^{N_F}{U}_{ij}{\mathbf{n}}_{ij}\varDelta {S}_{ij}={\left(\nabla U\right)}_{i\_ exact}+O(h) $$
(9)

where O(h) is the order of magnitude of the mesh size. As mentioned earlier, the only contributor to gradient error is the approximation of face midpoint value. Here we assume the face midpoint value approximation to be expressed as follows:

$$ {U}_{ij}={\hat{U}}_{ij}+{a}_{ij}+{b}_{ij}O(h)+{c}_{ij}O\left({h}^2\right) $$
(10)

where \( {\hat{U}}_{ij} \) is the exact value at the face midpoint, aij, bij, cij are constant coefficients. Substituting Eq. (10) into Eq. (9), we obtain:

$$ {\displaystyle \begin{array}{l}{\left(\nabla U\right)}_{i\_ numerical}=\frac{1}{V_i}\sum \limits_{j=1}^{N_F}\left({\hat{U}}_{ij}+{a}_{ij}+{b}_{ij}O(h)+{c}_{ij}O\left({h}^2\right)\right){\mathbf{n}}_{ij}\varDelta {S}_{ij}\\ {}\kern9em =\frac{1}{V_i}\sum \limits_{j=1}^{N_F}{\hat{U}}_{ij}{\mathbf{n}}_{ij}\varDelta {S}_{ij}+\frac{1}{V_i}\sum \limits_{j=1}^{N_F}\left({a}_{ij}+{b}_{ij}O(h)\right){\mathbf{n}}_{ij}\varDelta {S}_{ij}+\frac{1}{V_i}\sum \limits_{j=1}^{N_F}\left({c}_{ij}O\left({h}^2\right)\right){\mathbf{n}}_{ij}\varDelta {S}_{ij}\end{array}} $$
(11)

if \( \sum \limits_{j=1}^{N_F}\left({a}_{ij}+{b}_{ij}O(h)\right){\mathbf{n}}_{ij}\varDelta {S}_{ij}\ne 0 \), and \( \sum \limits_{j=1}^{N_F}\left({c}_{ij}O\left({h}^2\right)\right){\mathbf{n}}_{ij}\varDelta {S}_{ij}\ne 0 \), we have:

$$ {\displaystyle \begin{array}{l}{\left(\nabla U\right)}_{i\_ numerical}={\left(\nabla U\right)}_{i\_ exact}+\frac{\left({a}_{ij}O(1)+{b}_{ij}O(h)\right)O\left({h}^2\right)}{O\left({h}^3\right)}+{c}_{ij}\frac{O\left({h}^2\right)O\left({h}^2\right)}{O\left({h}^3\right)}\\ {}\kern10em ={\left(\nabla U\right)}_{i\_ exact}+{a}_{ij}O\left({h}^{-1}\right)+{b}_{ij}O(1)+{c}_{ij}O(h)\end{array}} $$
(12)

On one hand, we notice that when \( \sum \limits_{j=1}^{N_F}\left({a}_{ij}+{b}_{ij}O(h)\right){\mathbf{n}}_{ij}\varDelta {S}_{ij}=0 \), in other words, the summation (integral) of first-and-lower-order terms in the approximation of face midpoint value counterbalances each other, gradient reconstruction achieves at least first-order accuracy.

On the other hand, we can see from Eq. (12) that in order to achieve at least first-order accurate gradient, constant coefficients aij, bij must be zero, which means the approximation of face midpoint value, i.e. Eq. (10), must be second-order accurate.

Consequently, if no counterbalance occurs for the first-and-lower-order terms, second-order accurate approximation of face midpoint value is necessary to achieve at least first-order gradient reconstruction.

As a supplement, we also prove that second-order accurate approximation of face midpoint value is sufficient to produce first-order accurate gradient.

Assuming that the second-order accurate approximation of the face midpoint value can be written as:

$$ {U}_{ij}={\hat{U}}_{ij}+O\left({h}^2\right) $$
(13)

Substituting Eq. (13) into Eq. (8), we get:

$$ {\displaystyle \begin{array}{l}{\left(\nabla U\right)}_{i\_ numerical}=\frac{1}{V_i}\sum \limits_{j=1}^{N_F}\left({\hat{U}}_{ij}+O\left({h}^2\right)\right){\mathbf{n}}_{ij}\varDelta {S}_{ij}\\ {}\kern9em =\frac{1}{V_i}\sum \limits_{j=1}^{N_F}{\hat{U}}_{ij}{\mathbf{n}}_{ij}\varDelta {S}_{ij}+\frac{1}{V_i}\sum \limits_{j=1}^{N_F}\left(O\left({h}^2\right)\right){\mathbf{n}}_{ij}\varDelta {S}_{ij}\\ {}\kern9em ={\left(\nabla U\right)}_{i\_ exact}+\frac{O\left({h}^2\right)O\left({h}^2\right)}{O\left({h}^3\right)}\\ {}\kern9em ={\left(\nabla U\right)}_{i\_ exact}+O(h)\end{array}} $$
(14)

Therefore, in terms of GG gradient reconstruction methods, we conclude that when the summation of first-and-lower-order terms in the integral process does not counterbalance each other, second-order accurate approximation of face midpoint value is the necessary and sufficient condition for at least first-order accurate gradient reconstruction.

According to the approach for face midpoint value approximation, the GG methods can be categorized into:

  1. (a)

    cell-based GG methods (GG-Cell), using the simple average value of face neighboring cells as face midpoint value;

  2. (b)

    nodal-based GG methods (GG-Node), using the simple average value of node surrounding cells as face nodal value;

  3. (c)

    GG methods based on least-squares face interpolation (GG-LSQ), using LSQ interpolation to calculate face midpoint value;

  4. (d)

    GG methods based on weighted tri-linear face interpolation (GG-WTLI), using weighted tri-linear interpolation to calculate face midpoint value.

Readers may refer to Appendix 1 for details. Of course, other approaches [11,12,13, 27] can be adopted which are not included in this paper.

Whether these methods guarantee second-order face midpoint value approximation on arbitrary grids is essential in determining the order of accuracy of gradient reconstruction. Here we tabulate the properties in Table 1 and their verifications are left in later sections.

Table 1 Properties of the order of accuracy of gradient reconstruction and face midpoint value approximation on arbitrary grids
Full size table

3.2 Least-squares approach based gradient reconstruction

The second type of gradient reconstruction methods is based on the least-squares (LSQ) approach. Applying the Taylor series expansion, we have:

$$ {U}_j={U}_i+{\left(\nabla U\right)}_i\cdot {\mathbf{r}}_{ij}+h.o.t. $$
(15)

where Ui is the variable at the center of cell i, and rij is the vector from cell center i to cell center j. If second-and-higher-order terms are neglected, Eq. (15) becomes

$$ {\left(\nabla U\right)}_i\cdot {\mathbf{r}}_{ij}={U}_j-{U}_i $$
(16)

Applying Eq. (16) to certain stencil cells, for instance, basic stencils consisting of immediate neighboring cells of cell i as shown in Fig. 2, or extended stencils consisting of all neighboring cells sharing cell vertexes, as shown in Fig. 3, or other augment stencils [28], we obtain:

$$ \left[\begin{array}{ccc}{\theta}_1\Delta {x}_{i1}& {\theta}_1\Delta {y}_{i1}& {\theta}_1\Delta {z}_{i1}\\ {}{\theta}_2\Delta {x}_{i2}& {\theta}_2\Delta {y}_{i2}& {\theta}_2\Delta {z}_{i2}\\ {}\vdots & \vdots & \vdots \\ {}{\theta}_j\Delta {x}_{ij}& {\theta}_j\Delta {y}_{ij}& {\theta}_j\Delta {z}_{ij}\\ {}\vdots & \vdots & \vdots \\ {}{\theta}_N\Delta {x}_{iN}& {\theta}_N\Delta {y}_{iN}& {\theta}_N\Delta {z}_{iN}\end{array}\right]\left[\begin{array}{l}\frac{\partial U}{\partial x}\\ {}\frac{\partial U}{\partial y}\\ {}\frac{\partial U}{\partial z}\end{array}\right]=\left[\begin{array}{l}{\theta}_1\left({U}_1-{U}_i\right)\\ {}{\theta}_2\left({U}_2-{U}_i\right)\\ {}\vdots \\ {}{\theta}_j\left({U}_j-{U}_i\right)\\ {}\vdots \\ {}{\theta}_N\left({U}_N-{U}_i\right)\end{array}\right] $$
(17)

where Δxij, Δyij, Δzij are the components of vector rij, N denotes the number of stencil cells, and θj is weight coefficient for each component equation, which is usually defined as the reciprocal of the distance between cell center i and cell center j. Eq. (17) has less number of unknowns than the number of equations and could be solved with a least-squares approach.

Fig. 2
figure 2

LSQ basic stencils [8] (cell 0–6)

Full size image
Fig. 3
figure 3

LSQ extended stencils [8] (cell 0–10)

Full size image

The accuracy order of the least-squares approach can be easily determined. Since the numerical gradient is reconstructed by retaining only the linear terms as Eq. (18).

$$ {U}_j={U}_i+{\left(\nabla U\right)}_{i\_ numerical}\cdot {\mathbf{r}}_{ij} $$
(18)

The exact expression is the Taylor series expansion as follows:

$$ {U}_j={U}_i+{\left(\nabla U\right)}_{i\_ exact}\cdot {\mathbf{r}}_{ij}+O\left({\left|{\mathbf{r}}_{ij}\right|}^2\right) $$
(19)

Combining Eq. (18) and Eq. (19), we have:

$$ {\left(\nabla U\right)}_{i\_ numerical}={\left(\nabla U\right)}_{i\_ exact}+O\left(\left|{\mathbf{r}}_{ij}\right|\right) $$
(20)

Therefore, Eq. (16) achieves first-order gradient reconstruction on arbitrary unstructured meshes regardless of mesh type and quality.

In the current study, both weighted and un-weighted LSQ with basic and extended stencils are considered. These methods will be denoted as LSQ-basic, WLSQ-basic, and WLSQ-extended in the following context.

4 Gradient accuracy analysis

4.1 Discretization error analysis

In this section, we will confirm the aforementioned relationship between the face midpoint value approximation and the gradient accuracy, and present a relatively fast and easy approach to determine the actual order of accuracy of gradient reconstruction methods.

All the analyses in this section are to determine the discretization errors of both gradient reconstruction and the face midpoint value approximation of the analytic function f(x, y) = sin x + sin y + cos xy by GG-Cell and LSQ method with basic stencils (LSQ-basic). More details about these two methods are supplemented in Appendix 1.

4.1.1 Flat mesh

First, we consider an isotropic regular quadrilateral grid (quads.) stencils with aspect ratio AR = 1 as shown in Fig. 4. The stencil only involves 5 points, i.e., point 0 – point 4; the coordinates of those points are readily determined and will not be listed below.

Fig. 4
figure 4

Flat mesh stencils

Full size image

Exact face midpoint value and exact gradient at cell center 0 can be obtained by substituting the coordinates into the function f(x, y) and gradient ∇f respectively. The discretized face midpoint values are approximated as the average value of neighboring cell values for the GG-Cell method. The discretized gradients are reconstructed by the GG-Cell method and the LSQ method with basic stencils. Discretization errors are quantified by the difference between the discretized value and the exact value. Here, we directly present the discretization errors of both face midpoint value approximation and gradient reconstruction as follows.

In Table 2, both GG-Cell and LSQ-basic reconstructed gradients achieve second-order accuracy and the absolute values of discretization error are identical. Special attention should be focused on the second-order accurate GG-Cell method; it is obvious in this case that the second-order terms in the face midpoint value approximation will counterbalance each other in the discretized integral process which results in higher-than-first-order accurate GG gradient reconstruction. And the LSQ-basic method achieves second-order accuracy because it is equivalent to the central difference on Cartesian grids [29].

Table 2 Discretization errors of gradient reconstruction and face midpoint value approximation (quads.)
Full size table

Following the analysis on regular quadrilateral grids, regular triangular grids (reg. tri.) and regular double-split triangular grids (reg. double-split tri.) can be considered in a similar way. Grid stencils are sketched in Figs. 5 and 6. Brief results on discretization errors of gradient reconstruction and face midpoint value approximation are shown in Table 3. Detailed results on discretization errors are provided in Appendix 2.

Fig. 5
figure 5

Regular triangular grid stencils (AR = 1; reg. tri.)

Full size image
Fig. 6
figure 6

Regular double-split triangular grid stencils (AR = 1; reg. double-split tri.)

Full size image
Table 3 Discretization errors of gradient reconstruction and face midpoint value approximation
Full size table

With reference to Table 3 and Table 8 in Appendix 2, it can be noted that on regular triangular grids, both GG-Cell and LSQ-basic reconstructed gradients achieve the first-order accuracy. However, on regular double split triangular grids, the GG-Cell method degrades to 0th order (O(1)) because the accuracy of face midpoint value approximation on two faces (face BC and face AC) degrades to first-order and no counterbalance occurs under this circumstance. This conclusion is different from those reported in previous works, for example, in Ref. [7], Green-Gauss method and least-squares gradient reconstruction were considered to produce similar results on regular meshes, and in Ref. [16], Green-Gauss methods were recognized insensitive to mesh regularity [16].

Further study on this problem shows that the accuracy degradation of GG-Cell method closely relates to mesh topology. If the face midpoint does not bisect the segment connecting the centers of two neighboring cells (as shown in Fig. 6), second-order accurate approximation of face midpoint value will be not achieved, and thus first-order gradient accuracy will not be maintained, as listed in Table 3.

Accuracy degradation was also predicted by Mavriplis [10] when the segments connecting neighboring cell centers do not bisect the shared mesh edge. Sozer et.al [8] confirmed that the Green-Gauss approach with either simple or IDW face averaging is 0th order accurate by numerical gradient accuracy tests. In this paper, a similar phenomenon of accuracy degradation is observed, and furthermore, the fundamental reason is located on the accuracy of face midpoint value approximation. However, we will show next on curved meshes that the conclusion by Mavriplis is not complete enough and there exists at least one special case that does not comply with his statement but can still be explained by the theory proposed in this paper.

4.1.2 Meshes on the curved surface (curved mesh)

For typical isotropic grids on curved surfaces, the accuracy of face midpoint value approximation and gradient reconstruction methods are analyzed with the stencil sketched in Fig. 7.

Fig. 7
figure 7

Quadrilateral grids on a curved surface

Full size image

Firstly, following the definition of Diskin et al. [11], curvature induced mesh deformation is characterized by parameter Γ:

$$ \Gamma =\frac{\left|{y}_1-{y}_0\right|}{\left|{y}_3-{y}_0\right|}=\frac{R-R\cos {h}_{\theta }}{2{h}_r}\approx \frac{Rh_{\theta}^2}{2{h}_r}= AR\frac{h_{\theta }}{2} $$
(21)

where yi is the y coordinate of point i in the Cartesian coordinate system, R is the radius at cell center 0, hθ and hr are mesh size in the circumferential direction and the radial direction. AR = Rhθ/hr is the grid aspect ratio, for isotropic grids considered in this paper, AR~O(1). We can see that when Γ → 0, point 0 and point 1 lie on the horizontal line, thus no curvature exists. On the contrary, when Γ increases, the curvature induced mesh deformation increases as well. Particularly, when we refine the grids at a specified AR, Γ decreases with hθ diminishing, and the curvature induced mesh deformation can be ignored when the mesh is refined to a certain scale.

Coordinates of the stencil points are determined as follows in Table 4:

Table 4 Coordinates of stencil points in Fig. 8
Full size table

in which r is the stretching ratio of the grids, for the isotropic grids considered in the paper, r = 1.

The gradient of function f(x, y) = sin x + sin y + cos xy at cell 0 is reconstructed by GG-Cell and LSQ-basic gradient reconstruction methods with AR = 1. The discretization errors are shown in Table 5.

Table 5 Discretization errors of gradient reconstruction and face midpoint value approximation
Full size table

From Table 5, face midpoint value approximations of face AB and face CD are first-order accurate which is not sufficient to produce first-order accurate gradient, however, we can still obtain the first-order gradient on isotropic quadrilateral grids on a curved surface. The reason is that the first-order terms counterbalance each other under this condition which can be seen from the discretization errors of face AB and face CD. Besides, Γ becomes a significant parameter in determining the true order of accuracy of gradient reconstruction methods. Second-order accurate gradient reconstruction can be obtained if Γ is so small that the first-order term O(Γhθ) is even smaller than the second-order term \( O\left({h}_{\theta}^2\right) \) and thus it can be ignored during the evaluation of the order of accuracy. This conclusion will be validated in the next sub-section via numerical tests on curved quadrilateral meshes.

4.2 Numerical tests of gradient reconstruction

In order to verify the accuracy analysis of the gradient reconstruction methods, numerical tests on typical 2D isotropic grids are performed.

4.2.1 Grids and the approach of grid convergence study

Sketches of 9 typical grids are listed below in Fig. 8.

  1. (a)

    regular quadrilateral grids (quads.);

  2. (b)

    regular triangular grids (reg. tri.) derived from the regular quadrilateral grids by splitting the diagonal of each quadrangle in the same direction;

  3. (c)

    skewed regular quadrilateral grids (skewed quads.);

  4. (d)

    skewed regular triangular grids (skewed reg. tri.);

  5. (e)

    perturbed quadrilateral grids (perturbed quads.) with grid nodes shifting from their initial location by a random but limited fraction of local mesh size. Specifically, grid node perturbation in this paper is defined as rh/4, where r ∈ [−1, 1] is a random number and h is the local mesh size [11,12,13];

  6. (f)

    random triangular grids (rand. tri.) derived from randomly splitting the diagonal of the regular quadrilateral grids (left diagonal and right diagonal appear with equal probability);

  7. (g)

    regular double-split triangular grids (reg. double-split tri.) derived from regular quadrilateral grids by double splitting the diagonal of each quadrangle in the same direction, i.e., splitting in the left and right diagonal respectively;

  8. (h)

    isotropic quadrilateral grids on a curved surface (curved quads.);

  9. (i)

    isotropic regular triangular grids on a curved surface (curved tri.);

Fig. 8
figure 8

Typical 2D isotropic grids. a Regular quadrilateral grids. b Regular triangular grids. c Skewed quadrilateral grids. d Skewed regular triangular grids. e Perturbed quadrilateral grids. f Random triangular grids. g Regular double-split triangular grids. h Isotropic quadrilateral grids on curved surface. i Isotropic regular triangular grids on curved surface

Full size image

Grid convergence studies are carried out on a series of consistently refined grids. Instead of shrinking the domain [19], mesh size is halved in a fixed domain by doubling the number of grid points on the boundary edges. The order of accuracy of gradient reconstruction is obtained asymptotically with the decrease of the mesh size. Here the mesh size is defined as [15]

$$ h={\left(\frac{V_{total}}{n_{dof}}\right)}^{\frac{1}{d}} $$
(22)

where Vtotal is the total volume of all cells in the domain, ndof is the number of degrees of freedom in the mesh, for cell-centered schemes, ndof is set to the number of cells, and d denotes the spatial dimension.

The flow function for gradient numerical tests is chosen to be a scalar manufactured solution [15] with 8 constant coefficients ϕ0, ϕx, ϕy, ϕxy, αϕx, αϕy, αϕxy, L:

$$ \phi \left(x,y\right)={\phi}_0+{\phi}_x\sin \left(\frac{\alpha_{\phi x}\pi x}{L}\right)+{\phi}_y\sin \left(\frac{\alpha_{\phi y}\pi y}{L}\right)+{\phi}_{xy}\cos \left(\frac{\alpha_{\phi x y}\pi x y}{L^2}\right) $$
(23)

Discretization errors are quantified by the difference between the exact gradient and the discretized one. The L1 norms, as shown in Eq. (24), of discretization error are calculated and plotted as a function of mesh size to study the convergence of discretization error. Here, the L2 and L∞ norms, as shown in Eqs. (25) and (26), can also be adopted since they have the same performance on self-similar grids and will not lead to essentially different results on currently considered grids which are generally self-similar. So only L1 norms are listed in the following context.

$$ {L}_1=\frac{\sum \limits_{i=1}^N\left|{f}_i-{f}_{\mathrm{i}, exact}\right|}{N} $$
(24)
$$ {L}_2={\left(\frac{\sum \limits_{i=1}^N{\left|{f}_i-{f}_{\mathrm{i}, exact}\right|}^2}{N}\right)}^{1/2} $$
(25)
$$ {L}_{\infty }=\max \left|{f}_i-{f}_{\mathrm{i}, exact}\right| $$
(26)

The order of accuracy (OOA) p can be determined by comparing discretization errors between two consistently refined grids (E1 and E2) as:

$$ p=\frac{\ln \left(\frac{E_2}{E_1}\right)}{\ln \left(\frac{h_2}{h_1}\right)} $$
(27)

4.2.2 Numerical results

Figure 9 illustrates the grid convergence performance of x-direction gradient discretization error (L1 norm) for different meshes with different gradient reconstruction methods. Overall agreement is observed between mathematical analyses and numerical tests.

Fig. 9
figure 9

Convergence of x-direction gradient of different grids and different reconstruction methods. a Regular quadrilateral grids. b Regular triangular grids. c skewed quadrilateral grids. d skewed regular triangular grids. e Perturbed quadrilateral grids. f Random triangular grids. g Regular double-split triangular grids

Full size image

Numerical results in Fig. 9a-d show that all gradient reconstruction methods produce at least first-order gradient on regular quadrilateral grids and regular triangular grids and their skewed counterparts. Mesh skewness does not cause degradation of the order of accuracy since skewness alone does not lead to violation of the face midpoint value condition. However, it doesn’t necessarily imply that mesh skewness does not influence gradient or solution accuracy. Skewness, in fact, was demonstrated a key factor deteriorating the solution accuracy of inviscid flow simulation by the authors [30].

Figure 9e-g show that the GG-Cell gradient reconstruction method degrades to 0th order on perturbed quadrilateral grids, random triangular grids, and regular double split triangular grids. This confirms the analysis for the GG-Cell method in the previous section that accuracy degradation occurs when the face midpoint does not bisect the segment connecting the neighboring cells which are the cases on these three types of grids.

Besides, GG-Node gradient reconstruction method also suffers from accuracy degradation on random triangular grids and perturbed quadrilateral grids as shown in Fig. 9e and f. However, other GG methods that ensure second-order accurate face midpoint value approximation, such as GG-LSQ, GG-WTLI, maintain at least first-order gradient accuracy on all tested isotropic grids.

Meanwhile, as shown in Fig. 10h, gradient accuracy of GG-Cell method reaches second order on isotropic quadrilateral grids on a curved surface which is consistent with previous analysis on the curved mesh. And all methods produce at least first-order gradient on curved quadrilateral grids and curved triangular grids. This confirms that other parameters such as curvature induced mesh deformation also play an important role in determining the actual order of accuracy of gradient reconstruction. And the condition whether the face midpoint bisects the segment connecting the neighboring cells, as bisection fails on the curved mesh, is not necessary for GG-Cell methods to be at least first-order accurate.

Fig. 10
figure 10

Convergence of x-direction gradient of different grids and different reconstruction methods. h Isotropic quadrilateral grids on a curved surface. i Isotropic regular triangular grids on a curved surface

Full size image

These results verify the previous conclusion that the fundamental reason of accuracy degradation of GG methods is not achieving second-order accurate face midpoint value approximation.

Numerical tests of gradient reconstruction methods based on least-squares approach indicate that these methods are at least first-order accurate on all tested isotropic grids regardless of mesh type, mesh perturbation, surface curvature, and skewness.

In terms of absolute magnitude of gradient discretization error and comparison of these gradient reconstruction methods, WLSQ method with extended stencil exhibits the lowest level of error on all tested grids except isotropic quadrilateral grids on curved surface, while other methods exhibit erratic behaviors and it is hard to identify the best method for all grids which, in fact, is not the goal of the current study.

5 Method of manufactured solutions

In order to quantify solution errors, we need an exact solution for the governing equations. Common exact solutions for real physical flows are either too difficult to obtain, or if exist, they are often solutions of the simplified equations and do not exercise all terms in the complete equations.

Therefore, except for simple exact solutions, a more powerful tool, the Method of Manufactured Solutions (MMS) [18, 31], is adopted in this paper. In a general procedure of MMS, non-trivial but analytic solutions are manufactured without being concerned about its physical realism since accuracy analysis is a purely mathematical exercise, and the analytic solutions should be complex enough to exercise all terms in the governing equations being tested.

Instead of solving the original partial differential equation (PDE), we solve the equations added with an analytic source term. Considering an analytic solution Qm, and substituting the solution into the governing PDE, then we can obtain an analytic source term Sm. It is obvious that the analytic solution Qm is the exact solution of the modified equation, i.e., the original equation added with an analytic source term, as shown in Eq. (28). Solving the modified equation, we can get the discretized numerical solution. Thus the solution errors can be quantified by comparing the exact manufactured solution and the numerical solution.

$$ \frac{\partial \mathbf{Q}}{\partial t}+\nabla \cdotp {\mathbf{F}}_c-\nabla \cdotp {\mathbf{F}}_v={\mathbf{S}}_m $$
(28)

In dealing with the analytic source term, two major approaches were presented in previous work. Katz [15] reported second-order accurate source term discretization, while Roache [18] suggested symbolic manipulation of the source term. In this paper, we adopt the symbolic manipulation to obtain the exact expression of the source term. Dirichlet boundary conditions are implemented.

5.1 Euler manufactured solution

Quantification of discretization error is accomplished by a vector Euler manufactured solution [15] for two-dimensional (2D) cases, and the manufactured solution Qm has the following components:

$$ {\displaystyle \begin{array}{l}\rho \left(x,y\right)={\rho}_0+{\rho}_x\sin \left(\frac{\alpha_{\rho x}\pi x}{L}\right)+{\rho}_y\sin \left(\frac{\alpha_{\rho y}\pi y}{L}\right)+{\rho}_{xy}\cos \left(\frac{\alpha_{\rho x y}\pi x y}{L^2}\right)\\ {}u\left(x,y\right)={u}_0+{u}_x\sin \left(\frac{\alpha_{ux}\pi x}{L}\right)+{u}_y\sin \left(\frac{\alpha_{uy}\pi y}{L}\right)+{u}_{xy}\cos \left(\frac{\alpha_{ux y}\pi x y}{L^2}\right)\\ {}v\left(x,y\right)={v}_0+{v}_x\sin \left(\frac{\alpha_{vx}\pi x}{L}\right)+{v}_y\sin \left(\frac{\alpha_{vy}\pi y}{L}\right)+{v}_{xy}\cos \left(\frac{\alpha_{vx y}\pi x y}{L^2}\right)\\ {}P\left(x,y\right)={P}_0+{P}_x\sin \left(\frac{\alpha_{Px}\pi x}{L}\right)+{P}_y\sin \left(\frac{\alpha_{Py}\pi y}{L}\right)+{P}_{xy}\cos \left(\frac{\alpha_{Px y}\pi x y}{L^2}\right)\end{array}} $$
(29)

in which ρ0, ρx, ρy, ρxy, αρx, αρy, αρxy, L and corresponding parameters in other component equations are constant coefficients. Analytic source terms are derived by Mathematica symbol manipulation. Modified Euler equation (added with an analytic source term) is solved to determine the discretized solutions. Initial density contours are plotted in Fig. 11.

Fig. 11
figure 11

Density contour of Euler manufactured solutions on different geometries. a Euler manufactured solution on flat geometry. b Euler manufactured solution on curved geometry. c Euler manufactured solution on skewed geometry

Full size image

5.2 Validation of MMS procedures

Validation of MMS procedures is performed by comparing the order of accuracy (OOA) obtained by the MMS procedure and an exact solution case. The exact solution adopted in this paper is a 2D inviscid isentropic vortex. Exact initial conditions are specified according to Ref. [8, 32] as

$$ {\displaystyle \begin{array}{l}u=-\frac{\varepsilon }{2\pi}\left(y-{y}_0\right){e}^{0.5\left(1-{r}^2\right)}\\ {}v=\frac{\varepsilon }{2\pi}\left(x-{x}_0\right){e}^{0.5\left(1-{r}^2\right)}\\ {}T=1-\frac{\left(\gamma -1\right){\varepsilon}^2}{8{\gamma \pi}^2}{e}^{\left(1-{r}^2\right)}\\ {}\rho ={T}^{\frac{1}{\gamma -1}},p={\rho}^{\gamma },S=p/{\rho}^{\gamma }=1\end{array}} $$
(30)

where \( r=\sqrt{{\left(x-{x}_0\right)}^2+{\left(y-{y}_0\right)}^2} \), the vortex strength is taken as ε = 5.0, and the vortex core is located at (x0, y0) = (0,  0). Eq. (30) is an exact solution for Euler equations thus can be adopted to verify and validate the MMS procedures. Initial density contour of a 2D inviscid vortex is plotted in Fig. 12.

Fig. 12
figure 12

Density contour of a 2D inviscid isentropic vortex

Full size image

Grid convergence studies on 4 types of grids, i.e., grids (a), (b), (e) and (f) in Fig. 8, are performed with same discretization scheme, and the OOA of the numerical solution is determined. Table 6 shows the L1 error and the OOA obtained by the inviscid vortex and by the MMS procedure with a Euler manufactured solution. It demonstrates that the Euler MMS procedure obtains the same OOA as the exact solution case.

Table 6 Validation of the MMS procedure
Full size table

6 Effects on the accuracy of inviscid flow simulation

Previous sections examined the accuracy of various gradient reconstruction methods, identified accuracy degradation for certain methods and verified former mathematical conclusions. However, poor gradient reconstruction accuracy does not necessarily imply large discretization error for the governing equations [10, 13]. The gradient accuracy and the FV discretization accuracy was thought to be unrelated. In this section, the effects of gradient accuracy on simulation of inviscid flows are considered. Solution errors are quantified by the validated Euler MMS procedure.

Results of grid convergence studies on grids (a)-(i) as shown in Fig. 8 are listed respectively in Fig. 13. It shows the convergence of L1 norm of density discretization error of the Euler MMS tests with different gradient reconstruction methods, in which ‘1st order’ implies the numerical schemes adopting a constant reconstruction (i.e., Eq. (3)), and ‘1st order ref.’ and ‘2nd order ref.’ are 1st order and 2nd order reference lines.

Fig. 13
figure 13

Convergence of density discretization error on different grids with different reconstruction methods. a Regular quadrilateral grids. b Regular triangular grids. c Skewed quadrilateral grids. d Skewed regular triangular grids. e Perturbed quadrilateral grids. f Random triangular grids. g Regular double-split triangular grids. h Isotropic quadrilateral grids on a curved surface. i Isotropic regular triangular grids on a curved surface

Full size image

Figure 13a-d show that FV schemes on grids (a)-(d) are second-order for all gradient reconstruction methods and the solution accuracy (absolute value of density discretization error) are nearly the same even though the gradient reconstructions have different accuracy as shown in Fig. 9a-d.

Figure 13e-g indicate that the schemes employing GG-Cell gradient reconstruction method degrade to first-order on grids (e)-(g) (perturbed quadrilateral grids, random triangular grids, and regular double-split triangular grids). The schemes employing GG-Node method also suffer from accuracy deterioration on these grids except regular double-split triangular grids. It proves that first-order accurate gradient reconstruction is necessary to maintain second-order FV schemes. These results clearly show that 0th order GG methods will lead to first-order FV schemes and generate a much higher level of absolute error.

In Fig. 13e-g, we also notice that even though gradient reconstruction of GG methods degrades to 0th order and the corresponding FV schemes degrade to 1st order, these schemes still yield a lower level of absolute error than the pure first-order FV scheme with a constant reconstruction. In other words, 0th order gradient reconstruction is still better than constant reconstruction.

Figure 13h-i show that all FV schemes on curved quadrilateral grids and curved triangular grids are second-order which confirms again the conclusion that first-order gradient reconstruction is necessary to yield second-order FV discretization.

Besides, FV discretization employing LSQ methods (LSQ-basic, WLSQ-basic, and WLSQ-extended) is always second-order accurate since LSQ gradient reconstruction is always at least first-order on arbitrary unstructured grids. Meanwhile, we also notice again that when gradient reconstruction achieves the first-order accuracy as shown in Fig. 9, the absolute error of gradient reconstruction does not directly imply the absolute error of numerical solution accuracy.

Although not considered in this paper, the computational efficiency of these schemes differs very much from each other. Preliminary studies on the complexity and efficiency of FV schemes were reported in previous studies [12, 13], and we will further study these issues in future work.

7 Conclusions and future work

Gradient reconstruction based on the Green-Gauss theorem (the GG methods) and the least-squares approaches (the LSQ methods) are analyzed both mathematically and numerically. Mathematical derivations reveal that, for gradient reconstruction based on the Green-Gauss theorem (the GG methods), if the summation of first-and-lower-order terms does not counterbalance in the discretized integral process, which rarely occurs, second-order accurate approximation of face midpoint value is necessary to produce at least first-order accurate gradient. However, gradient reconstruction methods based on the least-squares approach (LSQ methods) are at least first-order on arbitrary unstructured grids. These conclusions are verified by discretization error analysis on typical grid stencils and numerical accuracy tests on various types of isotropic grids.

If the face midpoint value condition is not satisfied, GG methods, such as GG-Cell and GG-Node method on irregular or perturbed mesh, will degrade to 0th order. Numerical tests indicated that on all tested isotropic grids, LSQ methods maintain at least first-order accurate gradient reconstruction.

In terms of gradient accuracy effects on the accuracy of inviscid flow simulation, it demonstrates that first-order accurate gradient is necessary to yield second-order FV discretization. The GG methods that produce the 0th order gradient should not be preferred in terms of simulation accuracy for practical flow simulations since they yield first-order FV discretization and generate much higher solution error. While second-order FV discretizations are ensured for all LSQ methods on all types of grids.

For gradient methods that yield the first-order gradient, which is sufficient for second-order FV schemes, it demonstrates that the gradient accuracy does not directly imply the numerical solution accuracy.

Previous work reported that GG methods may be more robust than LSQ methods on anisotropic grids on the curved surface [10, 11, 26, 27]. Future work will focus on the performance of gradient reconstruction methods on anisotropic and stretched grids with high aspect ratio and surface curvature for viscous flow simulations. Attempts on possible modifications of GG methods according to the face midpoint value condition will be carried out to improve the gradient and solution accuracy. While for the LSQ methods, improving robustness on high aspect ratio grids with surface curvature is worthful work.