Numerical experiment based on non-linear micropolar finite element to study micro-rotations generated by the non-symmetric Maxwell stress tensor

Abstract

The main aim of the present work is to investigate the role of the Maxwell stress tensor in the study of active materials. Despite the importance of this tensor in modeling mechatronic devices used in sophisticated applications, its non–symmetry still generates controversies in the literature, probably because classical continuum mechanics assumes a symmetric Cauchy stress, although the sum of Cauchy and Maxwell stresses is non–symmetric. In the framework of generalised continuum mechanics–a more advanced formalism than the classical one–, each material point has an associated microstructure so that the micro–rotations of the electric/magnetic dipoles present in real active materials may be simulated. To this end, a modified total stress formulation, including an angular momentum balance, is developed and implemented into a finite element research code using a complex–step formulation. It is concluded that generalised mechanics allows for incorporating both symmetric and non–symmetric contributions of the Maxwell tensor. Consequently, the rotations generated by the electromagnetic field may be analysed. The influence of the complete Maxwell tensor in a magnetostrictive actuator is studied by several magneto–mechanical numerical experiments of a Terfenol–D rod encircled by air, and several conclusions are highlighted.

1 Introduction

Active materials, such as piezoelectrics and piezomagnetics, are used in mechatronic devices due to their inherent ability to combine mechanical and electromagnetic fields by two separate couplings: the first can be modelled by constitutive equations–obtained from thermodynamic potentials–, and the second by electromagnetic body forces, commonly incorporated into the linear momentum balance by the Maxwell Stress Tensor (MST).

Physically, the origin of these couplings comes from two separate interactions, see [27, 31]:

• Short–range forces (local effects) due to interatomic interactions among material points inside the body that generate both forces and couples.

• Long–range forces (non–local effects) that emerge from the interactions between material points and external fields.

The short–range forces, see [37, 39], are closely related with the piezoelectric/piezomagnetic constitutive equations, some reported in [15]. As mentioned, the contribution of these forces to the linear momentum balance is often obtained from thermodynamic potentials, see [10, 13].

The long–range forces are commonly expressed as the divergence of the MST for an amenable implementation in numerical approaches such as the Finite Element (FE) method. However, the MST is non–symmetric in transversely isotropic materials such as piezoelectrics and piezomagnetics [25, 34, 37]. This lack of symmetry has generated a comprehensive discussion in the literature since Noether’s theorem [21] states that the angular momentum must be conserved, and non–symmetric stress tensors do not automatically fulfil this condition. For this reason, [31] reported that the non–symmetric MST does not have physical meaning since it is caused by the transformation of the electromagnetic long–range body forces into the short–range divergence of the MST.

Despite the importance of the MST in modelling mechatronic devices (for instance, for vibrations and noise control), it should be considered in many research works, for example, in [29, 32]. This is due to two main difficulties:

$\rhd$:

the non–linearity

$\rhd$:

the possible non–symmetry

The first difficulty is nowadays easily overcome by non–linear algorithms and sophisticated computer codes. But the second remains unsolved since the proper solution is not clear from a theoretical point of view, even if it is essential since the MST skew–symmetric part can generate electromagnetic torques as argued in [6, 14].

On this ground, two main approaches based on Classical Continuum Mechanics (CCM) may be found in the literature to model active materials considering the MST:

• (i) Analytically, [1, 2, 19, 37] introduce a symmetric total stress tensor as the sum of two non–symmetric tensors: a Cauchy–like stress tensor and the MST itself. FE models using this total stress are reported in [11, 22, 28, 30, 38].

• (ii) The numerical approach from [25] allows us to calculate electromagnetic torques and forces with a nodal force method. The torques are expanded into non–local (long–range) and local (short–range) terms, the latter due to the MST non–symmetric part.

Although the controversy on the MST non–symmetry was partially clarified through physical arguments in [19, 37], the main novelty of the present work is to establish the CCM limitations (including the use of the MST itself) to model active materials. For this purpose, a Generalised Continuum Mechanics (GCM) approach based on the Micropolar Mechanics (MM) theory is developed; see [17] for a general description of MM. Roughly, this theory extends CCM assuming that each material point in the continuum is associated with a micro–rigid body and, consequently, three micro–rotations are incorporated to the FE degrees of freedom (dofs).

Based on MM, in the current work both linear and angular momentum balances are stated, concluding that the MST holds a skew–symmetric part. Furthermore, the electromagnetic torque generated by this non–symmetry may only be studied with MM since, in the framework of CCM, each material point lays in the position of its centre of mass [24]. Then the point only transmits linear momentum to neighbours, not micro–rotations. As demonstrated in [19, 37], the absence of rotation implies that the MST must be symmetric for basic CCM.

Finally, and for completeness, a numerical study based on the FE method is developed to obtain some conclusions on the influence of the MST using MM. In particular, a mini–magnetostrictive actuator made out of the transversely isotropic Terfenol–D material is simulated. Four numerical experiments are developed, demonstrating that the micro–rotations can be of the macro order for magnetic fields of normal levels. Also, regardless of intensity, not all magnetic fields can produce rotations.

Dynamic effects are not considered in the present work for simplicity, and for the FE formulation, only the magneto–mechanical coupling is considered.

For clarity, index notation is used throughout the present work. Non-symmetric tensors are denoted by $(\cdot )_{ij}$, with their symmetric and skew–symmetric parts denoted by $(\cdot )_{(ij)}$ and $(\cdot )_{[ij]}$, respectively. In addition, the alternating third–order and identity second–order tensors are denoted by $e_{ijk}$ and $\delta _{ij}$. Finally, the Einstein summation convention is used throughout the document.

2 Balance equations

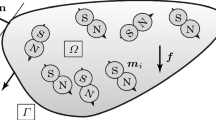
Consider a domain $\varOmega =\varOmega _{_{EM}} \cup \varOmega _{_M} \cup \varOmega _{_O}$ and its boundary $\varGamma$, containing electromagnetic $\varOmega _{_{EM}}$, mechanical $\varOmega _{_M}$ and other $\varOmega _{_O}$ matter, as shown in Fig.  1. The present section states the balances of linear and angular momentum considering electromagnetic forces $f_i^{EM} \in \varOmega _{_{EM}}$, mechanical forces represented by traction $t_i$ and couple stress $m_i$ vectors so that $\{t_i,m_i\}\in \varOmega _{_M}$. Other body forces $f_i\in \varOmega _{_{O}}$ are included for completeness due to long–range effects such as gravitation.

Fig. 1

Domain $\varOmega =\varOmega _{_{EM}}\cup \varOmega _{_M}\cup \varOmega _{_O}$ with boundary $\varGamma$ and outward normal $n_i$. The domain is under electromagnetic $f_i^{EM}$, mechanical traction $t_i$, couple stress vector $m_i$, and other body forces $f_i$

As introduced before, MM considers that each material point has an associated microstructure mathematically represented by a trihedron at each material point C. Consequently, the microstructure is modelled as a rigid body adding three micro–rotations $\theta _i$ to the three classical macro–displacements $u_i$.

For the most general case, the electromagnetic forces $f_i^{EM}$ are composed of:

• Long–range forces from electromagnetic source: free electric charge density $\rho _q^f$ and free electric current $j_i^f$.

• Short–range forces due to polarisation $P_i$ and magnetisation $M_i$ vectors related to the material media.

The vectors $t_i$ and $m_i$ exclusively represent short–range forces. The former is the classical traction related to a generic stress tensor $\sigma _{ij}$ by the Cauchy relation of (1) top. The latter is due to the microstructure, and it is related to the couple stress tensor $\tau _{ij}$ of (1) bottom, also by a Cauchy–like relation:

$$\begin{aligned} \begin{array}{lcr} t_i = \sigma _{ji}~n_j, \\ \\ m_i = \tau _{ji}~n_j. \end{array} \end{aligned}$$

(1)

Notice that both $\sigma _{ij}$ and $\tau _{ij}$ are a priori non–symmetric tensors.

2.1 Electromagnetic forces

Continuum Electrodynamics is founded on a set of four empirical laws called Maxwell equations [28] expressed as:

$$\begin{aligned} \begin{array}{lllllll} D_{i,i}=\rho _q^f, \\ \\ B_{i,i}=0, \\ \\ \displaystyle \big (E_je_{ijk}\big )_{,i}+\displaystyle \frac{\partial B_k}{\partial t}=0, \\ \\ \big (H_je_{ijk}\big )_{,i} - \displaystyle \frac{\partial D_k}{\partial t} - j_k^f=0, \end{array} \end{aligned}$$

(2)

where $E_i$, $D_i$, $H_i$, and $B_i$ denote electric field, electric displacement, magnetic field, and magnetic induction, respectively. In addition, t denotes time and $\partial$ partial derivative. The electromagnetic constitutive equations that relate $P_i$ and $M_i$ vectors are defined as:

$$\begin{aligned} \begin{array}{lcr} D_i=P_i+\epsilon _0E_i, \\ \\ B_i=\mu _0\big (H_i + M_i \big ), \end{array} \end{aligned}$$

(3)

where $\epsilon _0$ and $\mu _0$ are the vacuum permittivity and permeability, respectively.

The balance of linear electromagnetic momentum is obtained from Poynting’s theorem [28] and in quasi–static regime is expressed as:

$$\begin{aligned} f_i^{EM} = \sigma _{ji,j}^{EM}, \end{aligned}$$

(4)

where $\sigma _{ji}^{EM}$ is the mathematical symbol for the MST. There exist at least four expressions [9] for $f_i^{EM}$ or $\sigma _{ji}^{EM}$, but the present work uses:

$$\begin{aligned} \sigma _{ji}^{EM} = D_jE_i+B_jH_i - \left( \displaystyle \frac{D_kD_k}{\epsilon _0}+ \displaystyle \frac{B_kB_k}{\mu _0} \right) \displaystyle \frac{\delta _{ji}}{2}, \end{aligned}$$

(5)

According to [39] the previous expression satisfies the electromagnetic boundary conditions and may be obtained from a thermodynamic formulation as in [10] or from energy-momentum considerations as in [8].

Since any tensor may uniquely be decomposed into symmetric and skew–symmetric parts, the MST is split into both by introducing (3) into (5) to give:

$$\begin{aligned} \begin{array}{lll} \varvec{ \sigma }_{(ij)}^{EM} = &{}\displaystyle \frac{P_jE_i + P_iE_j}{2} + \frac{\mu _0}{2}\big (M_jH_i+M_iH_j\big )~+ \\ \\ &{}\displaystyle \epsilon _0E_iE_j+\mu _0H_iH_j- \left( \displaystyle \frac{D_kD_k}{\epsilon _0}+ \displaystyle \frac{B_kB_k}{\mu _0} \right) \displaystyle \frac{\delta _{ij}}{2}, \\ \\ \displaystyle \varvec{ \sigma }_{[ji]}^{EM} = &{}\displaystyle \frac{P_jE_i - P_iE_j}{2}+ \frac{\mu _0}{2}\big (M_jH_i-M_iH_j\big ), \end{array} \end{aligned}$$

(6)

where the second contribution represents the tensor form of the classical electromagnetic torque.

According to [23], applying the divergence theorem to the total MST allows to transform the long–range forces $f_i^{EM}$ into short–range ones by:

$$\begin{aligned} t_i^{EM} = \sigma _{ji}^{EM}~n_j, \end{aligned}$$

(7)

where $t_i^{EM}$ denotes the Maxwell traction vector.

2.2 Total linear momentum balance

From Noether’s theorem, the linear momentum must be conserved since the Lagrangian (function of movement) must be independent of the origin. Considering both mechanical and electromagnetic forces, the balance of linear momentum establishes the relationship between long–range and short–range forces by:

$$\begin{aligned} \int _{\varGamma }\left( t_i+t_i^{EM}\right) { \ {d}\varGamma }+\int _{\varOmega }f_i{ \ {d}\varOmega }=0, \end{aligned}$$

(8)

Applying the divergence theorem to the previous first integral, taking into account (1) top and (7), the local form of (8) becomes:

$$\begin{aligned} \big (\sigma _{ji}+\sigma ^{EM}_{ji}\big )_{,j}+f_i=0. \end{aligned}$$

(9)

2.3 Total angular momentum balance

Also, from Noether’s theorem, the angular momentum must be explicitly conserved since the Lagrangian function must be independent of the measurement angle. Depending on the material constitution, the MST skew–symmetric part may be:

$\rhd$:

$\varvec{ \sigma }_{[ij]}^{EM}=0$, then the angular momentum balance is automatic stated.

$\rhd$:

$\varvec{ \sigma }_{[ij]}^{EM}\ne 0$, then the angular momentum balance must be explicitly guaranteed in the formulation.

With $x_i$ denoting the position vector that locates each material point, for the second case and applying the definition of angular momentum, the second balance reads:

$$\begin{aligned} \displaystyle \int _{\varGamma }\left[ e_{ijk}x_i\left( t_j+t_j^{EM}\right) + m_k\right] { \ {d}\varGamma }+ \int _{\varOmega }e_{ijk}x_i f_j{ \ {d}\varOmega }=0. \end{aligned}$$

(10)

Again, the divergence theorem may be applied to the first term on the left-hand side of (10). Taking into account (1) bottom and (9), the balance of angular momentum in local form reads:

$$\begin{aligned} \begin{array}{l} \tau _{ji,j} + e_{ijk}\big (\sigma _{jk} + \sigma _{jk}^{EM}\big ) = 0. \end{array} \end{aligned}$$

(11)

3 On the symmetry of the Maxwell tensor

Based on the equations of the previous section, the main objectives are now: i) to analyse the CCM limitations to study the MST skew–symmetric part, ii) to formulate a new approach based on MM to include the MST skew–symmetric part. To address i), a revision of the different approaches for the MST is conducted.

3.1 Classical continuum mechanics approaches

In the CCM framework, the couple stress tensor and the micro–rotations are absent: $\tau _{ji} = \theta _i = 0$. In this context, at least three approaches exist to study the MST in the literature. The most important approaches are listed to highlight the absence of rotations.

3.1.1 Rinaldi

This approach was developed in [31] and is grounded on the lack of physical meaning in the mixture of long– and short–range forces. Specifically, even though the long–range force $f_i^{EM}$ (called maxwellian in the reference) may be mathematically expressed as a short–range force $t_i^{EM}$ related with $\sigma _{ji}^{EM}$, as in (7), the reference argues that (7) is not unique but “arbitrary to within an additive divergence–less tensor”. In this context, [20] also discusses the wrong “conceptual replacement” since $t_i^{EM}$ has no physical sense “unless it is integrated over a closed surface”.

Rinaldi concludes that the short–range forces must exclusively come from the classical and symmetric Cauchy stress tensor $\sigma _{(ij)}^{C}$. Consequently, the linear (9) and angular (11) balances simplify to:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \sigma _{(ij),j}^C+ f_i^{EM} + f_i=0, \\ \\ e_{ijk}\sigma _{(jk)}^C=0 \quad \Rightarrow \qquad \sigma _{(ij)}^{C}=\sigma _{(ji)}^{C}, \end{array} \right. \end{aligned}$$

(12)

Finally, Rinaldi remarks that $f_i^{EM}$ can only be replaced by $\sigma _{ji,j}^{EM}$ if the electromagnetic torque is added to (12) bottom.

3.1.2 Eringen

This approach reported in [4] modifies the balance of linear electromagnetic momentum (4) by splitting $f_i^{EM}$ as the sum of long–range Lorentz $f_i^L$ and of short–range ponderomotive $f_i^{PM}$ forces:

$$\begin{aligned} f_i^{EM} = f_i^{L}+f_i^{PM} = \sigma _{(ij),j}^{EM} +\sigma _{[ji],j}^{EM} . \end{aligned}$$

(13)

Also, Eringen argues that $f_i^{PM}$ only generates angular momentum, and therefore, it is not included in the linear momentum (9):

$$\begin{aligned} \big (\sigma _{(ji)}^C+\sigma ^{EM}_{(ji)}\big )_{,j}+f_i=0. \end{aligned}$$

(14)

3.1.3 Total stress

This approach is the most published: [1, 2, 19, 37]. It is grounded in the definition of a symmetric total stress $\sigma _{(ij)}^T$ as the sum of a non–symmetric and Cauchy–like tensor $\sigma _{ij}$ plus the MST tensor:

$$\begin{aligned} \sigma ^T_{(ij)}=\underbrace{\sigma _{(ij)}^C-\sigma _{[ij]}^{EM}}_{\sigma _{ij}}+\underbrace{\sigma _{(ij)}^{EM}+\sigma _{[ij]}^{EM}}_{\sigma _{ij}^{EM}}=\sigma _{(ij)}^C+\sigma _{(ij)}^{EM}. \end{aligned}$$

(15)

As argued in [1], this $\sigma _{(ij)}^T$ includes both long–range (electromagnetic) and short–range (mechanical) forces and satisfies boundary conditions. Along that line, the reference criticised Rinaldi’s approach for not considering proper boundary conditions. Still within CCM, the linear (9) and angular (11) balances become:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \sigma _{(ij),j}^T+f_i=\Big (\sigma _{(ij)}^C+\sigma _{(ij)}^{EM}\Big )_{,j}+f_i = 0, \\ \\ e_{ijk}\sigma _{(jk)}^T=0 \quad \Rightarrow \qquad {\sigma _{[ij]}^{C} = -\sigma _{[ij]}^{EM}}, \end{array} \right. \end{aligned}$$

(16)

This approach results in the same set of equations as (13) of Eringen from the previous subsection.

3.2 Micropolar mechanics

As commented, CCM represents each material point only by its centre of mass. A more sophisticated formalism such as MM can better describe the electric and magnetic dipole rotations at the micro–continuum scale.

Fig. 2

Polarisable body composed of electric dipoles $p_i^e$ defined by two electric charges $q^+$, $q^-$ represented by rigid bodies (zoom): stretching and rotation of $p_i^e$ under electric field

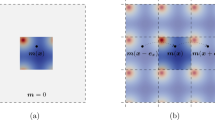
Consider the polarisable medium shown in Fig. 2 (the same arguments hold for magnetisable media) composed of electric dipoles $q_i$, defined by two electric charges $q^+$, $q^-$. As observed in the zoom and argued in [7], $q_i$ will stretch and rotate an angle $\theta _i$ upon application of an electric field. CCM captures the stretch, but a GCM approach such as MM must be used to study the rotation. Under this approach, the balances of linear and angular momentum read:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \Big (\sigma _{(ij)}^C+\sigma _{[ji]}^C+\sigma _{ji}^{EM}\Big )_{,j}+f_i = 0, \\ \\ \tau _{ji,j}+e_{ijk}\Big (\sigma ^C_{[jk]}+\sigma ^{EM}_{[jk]}\Big ) = 0, \end{array} \right. \end{aligned}$$

(17)

where $\sigma _{[ji]}^C$ may be considered null in a first approximation, see Sect. 4. Notice that with this nullity and according to [18], $\sigma ^{EM}_{[jk]}$ is closely related to a parameter called coupling number, which depends on the microstructure (intrinsic lattice size scale) of each material.

In conclusion, the current MM approach has several advantages, allowing to:

• sum the symmetric Cauchy $\sigma _{(ij)}^C$ to the non–symmetric Maxwell $\sigma _{ji}^{EM}$, since the angular momentum balance is fulfilled by the additional (17) bottom.

• use the classical constitutive equations of piezoelectrics and/or piezomagnetics (see Sect. 4) since they are expressed using only the symmetric part $\sigma _{(ij)}^C$.

• calculate the rotation of the electric/magnetic dipoles, and from it, the generated electromagnetic torque $\tau _{ji}$, relevant for mechatronic devices.

• recover the standard total stress method if the microstructure is not considered and $\tau _{ji}=0$.

4 Magnetostrictive governing equations

This section particularises the MM governing equations for the magnetostrictive problem used in the numerical experiments of Sect. 6. Seven dofs are considered: three macro–displacements $u_i$, three micro–rotations $\theta _i$, and the scalar magnetic potential $\varphi$.

The governing equations comprise balance (linear and angular) momenta, compatibility equations, boundary conditions, and material constitution. For the sake of clarity, this section summarises all equations.

4.1 Balance equations

The balance equations for the MM approach given in (17) are rewritten here without the separation into symmetric and skew-symmetric contributions. In addition, the magnetic field is balanced by the Gauss law, the second of (2) to obtain:

$$\begin{aligned} \begin{array}{l} \sigma _{ji,j}+f_i = 0, \\[3mm] \tau _{ji,j}-2\sigma _i^\times = 0, \\ B_{i,i}=0 \end{array} \end{aligned}$$

(18)

Assuming $\sigma _{[ji]}^C=0$, the tensor $\sigma _{ji}$ without the electric field and the new pseudo-vector $\sigma _i^\times$ read:

$$\begin{aligned} \begin{array}{lllll} \displaystyle \sigma _{ji}=\sigma _{(ij)}^C+B_jH_i- \displaystyle \frac{B_kB_k}{2\mu _0}\delta _{ji}, \\ \displaystyle \sigma _i^\times =-\frac{1}{2}e_{ijk}\sigma _{jk}, \end{array} \end{aligned}$$

(19)

where the latter may be expressed in matrix form as:

$$\begin{aligned} \{\sigma _i^\times \}=\frac{1}{2} \begin{Bmatrix} B_3H_2-B_2H_3 \\ B_1H_3-B_3H_1 \\ B_2H_1-B_1H_2 \end{Bmatrix}. \end{aligned}$$

(20)

4.2 Compatibility equations

Again, two compatibility equations must be considered due to the existence of mechanical and magnetic fields. For the former, the strain measures–energetically conjugated to $\sigma _{ji}$ and $\tau _{ji}$ from the first and second (18)–may be obtained from the additive decomposition of motion shown in Fig. 3. Then, the total deformation process may be mathematically represented by the gradient of macro–displacements $u_{j,i}$ composed of:

• I A mechanical deformation given by $\gamma _{ji}$.

• II A pure rotation of the microstructure given by the skew–symmetric tensor $\varTheta _{ji}=-e_{jik}\theta _k$.

Fig. 3

Micropolar mechanics deformation process, combining mechanical deformations and dipole micro–rotations, as in Fig. 2

Unlike the CCM model, for which there is only one strain measure, in the MM framework and as in some beam theories, there are two deformation measures:

$$\begin{aligned} \gamma _{ji} = u_{j,i}-e_{ijk}\theta _k, \qquad \chi _{ji}=\theta _{j,i}, \end{aligned}$$

(21)

where $\chi _{ji}$ is the gradient of micro–rotations. As observed, the CCM strain measure is recovered without micro–rotations.

The magnetic compatibility equation may be obtained by applying Helmholtz’s theorem to the last Maxwell law (2) without electric terms to get:

$$\begin{aligned} \displaystyle \big (H_je_{ijk}\big )_{,i} =0 \quad \Rightarrow \qquad H_i=-\varphi _{,i } \end{aligned}$$

(22)

4.3 Material constitution

The piezomagnetic constitutive equations used in the numerical experiments of Sect. 6 are presented as a set of four equations:

$$\begin{aligned} \begin{array}{llll} \sigma _{(ij)}^C=C_{ijkl}u_{k,l}-e^\varphi _{ijk}H_k, &{}&{}&{} \quad \sigma _{[ij]}^C=-\bar{C}_{ijkl}e_{klm}\theta _m, \\ \\ B_i=e^\varphi _{ijk}u_{j,k}+\mu _{ij}H_j, &{}&{}&{} \quad \tau _{ij}=C_{ijkl}^*\chi _{kl}, \end{array} \end{aligned}$$

(23)

where $C_{ijkl}$, $e^\varphi _{ijk}$, $\mu _{ij}$ and $C_{ijkl}^*$ are the elastic fourth–order tensor, piezomagnetic third–order tensor, magnetic permeability second–order tensor and micro–elastic fourth–order tensor, respectively. Furthermore, a new fourth–order tensor denoted by $\bar{C}_{ijkl}$ depends on the coupling number, see [18], assumed to be zero in the present work for simplicity.

Table 1 Tensorial notation with double indices $(\cdot )_{ij}$ and equivalent Voigt notation with single indices $(\cdot )_{I}$

Assuming the nine–component Voigt notation of Table 1 and considering that the material is magnetised along the $x_3$ direction as shown in Fig. 5, these constitutive tensors may be expressed in matrix forms as in the Appendix 1. For $C^*_{ijkl}$, the two micromechanical material coefficients $l_t$ and $l_b$ are the twisting and bending characteristic lengths; see [17].

4.4 Boundary conditions

For this coupled formulation, Dirichlet (essential) $\varGamma _D$ and Neumann (natural) $\varGamma _N$ boundary conditions are split into mechanical $(\varGamma _D^{u}, \varGamma _N^{u})$ and magnetic $(\varGamma _D^{\varphi }, \varGamma _N^{\varphi })$, satisfying:

$$\begin{aligned} \begin{array}{llllllllll} \varGamma _D^{u}\cup \varGamma _N^{u} &{}=&{}\varGamma \;&{}; &{}&{}\qquad \quad \varGamma _D^{u}\cap \varGamma _N^{u} &{}=&{} \emptyset &{}; \\ \varGamma _D^\varphi \cup \varGamma _N^\varphi &{}=&{}\varGamma \;&{}; &{}&{}\qquad \quad \varGamma _D^\varphi \cap \varGamma _N^\varphi &{}=&{} \emptyset &{}; \\ \end{array} \end{aligned}$$

Denoting by $\bar{u}_i$ and $\bar{\varphi }$ the prescribed displacements and scalar magnetic potential; and by $\bar{t}^C$ the prescribed Cauchy traction, both boundary conditions may be expressed as:

$$\begin{aligned} \begin{array}{lllll} \qquad \text{ Dirichlet }: &{} \qquad u_i=\bar{u}_i, &{} \qquad \varphi =\bar{\varphi }. \\ \qquad \text{ Neumann }:\qquad &{} \qquad t_in_i = \bar{t}^C, &{} \qquad B_in_i = 0. \end{array} \end{aligned}$$

(24)

Notice that there are no natural boundary conditions for the MST since they emerge from the body forces; see (4).

5 Finite element formulation

This section briefly describes the Finite Element (FE) formulation conducted to implement the theoretical MM formulation reported in Sect. 4. In particular, a three-dimensional, non–linear, and displacement–based FE equation set is developed. There are no geometrical non–linearities since small strain is considered, but the MST introduces material non–linearities that quadratically depend on the magnetic field, as shown in (20) top. For this reason, the FE formulation has two peculiarities:

$\rhd$:

It is based on three residuals: linear and angular momentum balances plus magnetic Gauss law, to be explicitly defined in (28).

$\rhd$:

A complex–step formulation with a perturbation parameter $h_n$ is conducted, as explained in [12, 16, 35].

5.1 Weak forms

To obtain the weak forms, the balance equations (18) are multiplied by test functions $\delta u_i,\delta \theta _i,\delta \varphi$ of the dofs and integrated over the whole domain $\varOmega$:

$$\begin{aligned} \begin{array}{lllll} \displaystyle \int _\varOmega \delta u_i~\big (\sigma _{ji,j}+f_i \big )~\text{ d }\varOmega =0, \\ \\ \displaystyle \int _\varOmega \delta \theta _i~\big (\tau _{ji,j}-2\sigma _i^\times \big )~\text{ d }\varOmega =0, \\ \\ \displaystyle \int _\varOmega \delta \varphi ~B_{i,i}~\text{ d }\varOmega = 0. \end{array} \end{aligned}$$

(25)

Applying the divergence theorem to the first term on the left-hand side of each (25), the final weak forms become:

$$\begin{aligned} \begin{array}{llll} \displaystyle -\!\int _\varOmega \delta u_{i,j}\sigma _{ji}~\text{ d }\varOmega +\int _\varGamma \delta u_it_i~\text{ d }\varGamma +\int _\varOmega \delta u_if_i~\text{ d }\varOmega =0, \\ \\ \displaystyle -\!\int _\varOmega \delta \theta _{i,j}\tau _{ji}~\text{ d }\varOmega +\int _\varGamma \delta \theta _i m_i~\text{ d }\varGamma -\int _\varOmega \delta \theta _i2\sigma _i^\times ~\text{ d }\varOmega =0, \\ \\ \displaystyle -\!\int _\varOmega \delta \varphi _{,i} B_i~\text{ d }\varOmega = 0. \end{array} \end{aligned}$$

(26)

5.2 Discretisations and residuals

In the present FE formulation, eight–noded elements with standard Lagrange functions $\mathcal {N}^a$ at node a are used for the discretisation. In particular, the dofs and their test functions may be expressed by an isoparametric formulation as:

$$\begin{aligned} \begin{array}{lllllll} u_i\approx \mathcal {N}_i^a\mathcal {I}(\bar{u}_i^a) ,&{}&{} \theta _i\approx \mathcal {N}_i^a\mathcal {I}(\bar{\theta }_i^a) ,&{}&{} \varphi \approx \mathcal {N}_i^a\mathcal {I}(\bar{\varphi }_i^a), \\ \\ \delta u_i\approx \mathcal {N}_i^a\mathcal {I}(\delta \bar{u}_i^a) ,&{}&{} \delta \theta _i\approx \mathcal {N}_i^a\mathcal {I}(\delta \bar{\theta }_i^a) ,&{}&{} \delta \varphi _i\approx \mathcal {N}_i^a\mathcal {I}(\delta \bar{\varphi }_i^a), \end{array} \end{aligned}$$

(27)

where $\mathcal {I}$ denotes a complex number. The residuals at each node a are obtained by introducing the discretisations of (27) in the weak forms of (26) to give:

$$\begin{aligned} \begin{array}{llll} R_{u_i}^a &{}= &{}\displaystyle -\!\! \int _{\varOmega _{e}} \! \mathcal {B}_{iJ}^a\sigma _{J}~\text{ d }\varOmega _e +\! \int _{\varOmega _e} \! \mathcal {N}^af_i~\text{ d }\varOmega _e \displaystyle +\! \int _{\varGamma _e} \! \mathcal {N}^at_i~\text{ d }\varGamma _e, \\ \\ R_{\theta _i}^a &{}=&{} \displaystyle -\!\! \int _{\varOmega _{e}} \! \mathcal {B}_{iJ}^a\tau _{J} \text{ d }\varOmega _e -\! \int _{\varOmega _e}\! \mathcal {N}^a2\sigma _i^\times \text{ d }\varOmega _e \! \displaystyle +\!\! \int _{\varGamma _e}\mathcal {N}^a m_i \text{ d }\varGamma _e, \\ \\ R_{\varphi }^a &{}= &{}\displaystyle -\!\! \int _{\varOmega _e}\! \mathcal {B}_i^a B_i~\text{ d }\varOmega _e, \end{array} \end{aligned}$$

(28)

where the uppercase subscripts refer to Voigt’s notation of Table 1 and the matrices $\mathcal {B}_{iJ}$ and $\mathcal {B}_i$ at each local node a are:

$$\begin{aligned}{}[\mathcal {B}^a_{Ji}]= \begin{bmatrix} \mathcal {N}_{,1}^a &{} 0 &{} 0 \\ 0 &{} \mathcal {N}_{,2}^a &{} 0 \\ 0 &{} 0 &{} \mathcal {N}_{,3}^a \\ \mathcal {N}_{,2}^a &{} 0 &{} 0 \\ 0 &{} \mathcal {N}_{,1}^a &{} 0 \\ 0 &{} \mathcal {N}_{,3}^a &{} 0 \\ 0 &{} 0 &{} \mathcal {N}_{,2}^a \\ 0 &{} 0 &{} \mathcal {N}_{,1}^a \\ \mathcal {N}_{,3}^a &{} 0 &{} 0 \end{bmatrix} , \qquad \{\mathcal {B}^a_{i}\}= \begin{Bmatrix} \mathcal {N}_{,1}^a \\ \mathcal {N}_{,2}^a \\ \mathcal {N}_{,3}^a \end{Bmatrix}. \end{aligned}$$

(29)

5.3 Tangent matrices

The complex–step method easily allows for computing the multi–coupled tangent matrices. These matrices are the derivatives of the residuals $R^a(u_b)$ for node a in terms of a generic nodal unknown $u_b$. Then, writing a Taylor series expansion about $u_b$ in terms of an imaginary change of each dependent variable at node n, one may write:

$$\begin{aligned} \begin{array}{llll} \displaystyle R^a(u_b + i \, \delta _{bn} h_n) = R^a(u_b) + \dfrac{\partial R^a}{\partial u_n} \, (i \, h_n)~+\\ \\ \dfrac{1}{2!} \dfrac{\partial ^2 R^a}{\partial u_n^2} \, (i \, h_n)^2 + \dfrac{1}{3!} \dfrac{\partial ^3 R^a}{\partial u_n^3} \, (i \, h_n)^3 + \cdots , \end{array} \end{aligned}$$

(30)

which upon collecting terms, yields:

$$\begin{aligned} \begin{array}{llll} \displaystyle R^a(u_b + i \, \delta _{bn} h_n) = \left[ R^a(u_b) - \dfrac{1}{2!} \dfrac{\partial ^2 R^a}{\partial u_n^2} h_n^2 \right] ~+\\ \\ i \, \left[ \dfrac{\partial R^a}{\partial u_n} \, h_n - \dfrac{1}{3!} \dfrac{\partial R^a}{\partial u_n^3} \, h_n^3 \right] + \cdots , \end{array} \end{aligned}$$

(31)

For cases where the higher derivatives are well behaved and using small values $h_n = 10^{-40}$, all residuals and tangent matrices are computed to full numerical accuracy from:

$$\begin{aligned} \begin{array}{llll} \displaystyle R^a &{} \approx \Re \big [R^a(u_b + i \, \delta _{bn} \, h_n) \big ], \\ \\ \dfrac{\partial R^a}{\partial u_n} &{}\approx \dfrac{1}{h_n} \, \Im \big [R^a(u_b + i \, \delta _{bn} \, h_n) \big ]. \end{array} \end{aligned}$$

(32)

This formulation is implemented into the research code FEAP [36] by using one of its dummy elements; the present numerical code without micro–rotations is tested against solutions of the total MST formulation developed in [26] obtaining perfect agreement. Notice that the multi–coupled tangent matrix is non–symmetric due to the inclusion of the MST and, consequently, the FEAP command UTAN must be used to invert the tangent matrix.

6 Numerical experiments

This section presents four numerical experiments to study the influence of the skew–symmetric part of the MST on the magneto–mechanical response in a magnetostrictive material under magnetic fields. For this purpose and as in [26], a magnetostrictive rod of length 6 [mm] and diameter 2 [mm] is simulated. The rod is made out of the alloy Terfenol–D, with properties listed in Table 2; the order of magnitude for $l_b,~l_t$ is taken from [3] for the crystal grains of many magnetic materials.

This alloy presents transversely isotropic planes $x_1$–$x_2$ since the magnetisation $M_3$ is along the $x_3$ axis, see the Fig. 4; therefore, the planes containing $x_3$ are anisotropic.

The skew–symmetric MST plays an essential role in activating the rotations as long as two conditions are met:

• The magnetic field $H_i$ interacts with an anisotropic plane, not with the transversely isotropic plane.

• The field is oblique to this anisotropic plane.

The idea is to prescribe an $H_i$ that activates the skew–symmetric term $\sigma _i^\times$ of (20), generating couple stresses $\tau _{ji}$ and therefore micro–rotations $\theta _i$. These rotations are closely related to the existence of the microstructure, introduced in the FE model by the $l_b$ and $l_t$ scale parameters in the third tensor of the Appendix 1.

Table 2 Terfenol–D material properties at $|\textbf{H}|$ = 100 [kA/m] from [33]: $C_{ij}$ stiffness, $e^\varphi _{ij}$ piezo-magnetic coupling, $\mu _{ij}$ magnetic permeability and $l_b=l_t$ micromechanical characteristic lengths

Fig. 4

Finite element mesh of the Terfenol–D rod (left) for all numerical experiments; finite element mesh of air (right) for numerical experiments 1 to 3

For all numerical experiments, the rod geometry is discretised by a FE mesh composed of 3,840 eight–noded elements, including 6,300 nodal points with seven dofs, as shown in Fig. 4 left. The mechanical dofs $u_i$ and $\theta _i$ are fixed at the rod bottom, the rest are free. Since the present is a displacement–based FE formulation, no tractions are prescribed due to the absence of mechanical forces or pressures.

To prescribe nonuniform magnetic fields for the first three experiments with the FE method, a discretised air domain with dimensions $3\!\times \!3\!\times \!6$ [mm] wraps the Terfenol–D rod: the additional mesh of 2,560 elements and 4,200 nodes is represented in Fig. 4 right. The vacuum permeability of air is $\mu _0$ = 1.256$\times 10^{-6}$ [N/A$^2$], and its mechanical dofs from the coupled FE of Sect. 5 are deactivated so that only one FE type is used though the analyses for both materials.

Table 3 For Fig. 4 left, definition of external faces by constant coordinates in [mm], and prescribed magnetic potential $\varphi$ in [A] for three numerical experiments

In Table 3, the magnetic boundary conditions for the cases in the next subsections are listed; if no prescription is applied, the word “free” is indicated.

6.1 Magnetic field in transversely isotropic planes

The quadrupole magnetic field reported in [5] is chosen for the first three experiments. In the laboratory, the quadrupole is created by four magnets arranged so that $\textbf{H}$ varies with the radial distance in planes $x_1$–$x_2$, but the field is constant along the $x_3$ axis. The magnetic potential boundary conditions are sketched in Fig. 5 left and listed in Table 3, producing a field that curves from one vertical side to the contiguous one (centre figure): then, $H_1 \approx H_ 2$ and $H_3$ = 0. The field is almost axisymmetric, as seen in the figure of the right for $\textbf{H}$ (smoothed through the whole mesh by the SPSVERBa1 software). But the critical domain is the Terfenol–D rod, where the field is uniform.

The maximum generated $\textbf{H}$ is 22 [kA/m], a value that could be obtained by a commercial magneto cell under an electric intensity of only 5 [A].

Fig. 5

Quadrupole magnetic field. Boundary conditions of magnetic scalar potential $\varphi$ in [A] applied to external vertical sides (left); direction of the magnetic field lines (centre); contour plot of the resulting magnetic field module in [A/m] (right). External dimensions $3\!\times \!3\!\times \!6$ [mm]

Figure 6 shows the resulting contour plots for the three micro–rotations $\theta _i$ generated inside the rod. As observed in the figure and expected, the micro–rotations are strictly zero in the air (green level) since its mechanical rigidity is null. The order of magnitude inside the Terfenol–D is $10^{-13}$ [rad], not zero but almost numerical noise. This result is logical since under the quadrupole the magnetic field is contained in the transversely isotropic planes $x_1$–$x_2$, and no rotations are activated as it will be demonstrated in (36).

Fig. 6

Terfenol–D rod wrapped by air under the nonuniform magnetic field of Fig. 5. Contour plots of micro–rotations in radians generated by the skew–symmetric part of the Maxwell stress tensor

The main shortcoming of the present MM formulation is the necessary CPU time: Table 4 shows the calculation times of three models for the current numerical experiment. The first row is for CCM without Maxwell stress tensor (CCM–w/o), the second for CCM with total Maxwell stress (CCM–w), and the third for the present GCM.

All simulations are executed in a dual–core Intel Core i5-2500T running at 2.3 [GHz]. For the first two models, the FE element developed in [26] was used with the mesh of Fig. 4.

Table 4 Calculation time (with respect to CCM–w/o) to solve the numerical experiment of Fig. 5 with three models. Number of Newton–Raphson iterations and converged residual norm for each experiment

As observed, the CPU time is substantially higher for MM, mainly because the three micro–rotations are extra nodal unknowns. The dofs are the same for the CCM–w/o and CCM–w models; however, the CPU time differs due to the non–linearity of the MST, which requires one more Newton–Raphson iteration. In this context, SPSVERBa1 calculates for all models the value:

$$\begin{aligned} val=\displaystyle \frac{||\varvec{\mathcal {R} }^{k+1}||}{||\varvec{\mathcal {R} }^0||}\le tol, \end{aligned}$$

(33)

The residuals’ superscripts $k+1$ and 0 refer to the current and the first iterations, respectively. The solution is reached when val is lower than the computer–dependent tolerance $tol=10^{-16}$.

6.2 Symmetric magnetic field in anisotropic planes

With the previous mesh, the micro–rotations are now studied with the boundary conditions of Fig. 7 left and of Table 3. Now $\textbf{H}$ varies in the vertical planes but not in the horizontal ones. In this way, the magnetic field curves from $\varphi$ = 0 [A] to all planes but primarily to the vertical ones crossing the anisotropic planes as in the centre figure.

Fig. 7

Modified quadrupole magnetic field. Boundary conditions of magnetic scalar potential $\varphi$ in [A] applied to external sides (left); direction of the magnetic field lines (centre); contour plot of the resulting magnetic field module in [A/m] (right). External dimensions $3\!\times \!3\!\times \!6$ [mm]

In Fig. 8, the resulting rotations are plotted. The micro–rotation $\theta _3$ is again only numerical noise (almost zero) since the only magnetic field to produce this component would be in the isotropic plane $x_1$–$x_2$ (of the Sect. 6.1 type), but as mentioned and demonstrated in Sect. 6.4, these fields do not create micro–rotations. The other two components are six or seven orders of magnitude higher than those of Sect. 6.1, thanks to the prevalence of the $H_3$ component; $H_1$ is also high but only at the edges of $x_1$ constant. The value of $\theta _2$ is almost three times larger than that of $\theta _1$ due to the magnetic field concentration on some of the edges.

Fig. 8

Terfenol–D rod wrapped by air under a nonuniform magnetic field of Fig. 7. Contour plots of micro–rotations in radians generated by the skew–symmetric part of the Maxwell stress tensor. In the central figure, only the solid is represented

In any case, the micro–rotations are still much smaller than expected for an $\textbf{H}$ partially applied in an anisotropic plane. There are two reasons for these low values: i) the perpendicularity of $\textbf{H}$ to the planes $x_1$–$x_2$ in some zones of the rod, and ii) the symmetry of this field that partially cancels $\theta _1$ and $\theta _2$ since the field concentrations at edges of the plane $x_1$ = 1.5 equilibrates the effect of the other concentrations at $x_1$ = $-$1.5, see the Fig. 7 right.

Fig. 9

Modified quadrupole magnetic field. Boundary conditions of magnetic scalar potential $\varphi$ in [A] applied to external sides (left); direction of the magnetic field lines (centre); contour plot of the resulting magnetic field module in [A/m] (right). External dimensions $3\!\times \!3\!\times \!6$ [mm]

6.3 Nonsymmetric magnetic field in anisotropic planes

Again, with the quadrupole set, the micro–rotations are partially activated in this experiment. In Fig. 9 left, the boundary conditions are changed so that $\textbf{H}$ varies in the vertical planes but now without vertical symmetry. With the prescribed boundary conditions of Table 3, the magnetic field curves from the $\varphi = \!-10$ [A] face towards all others in the whole domain.

Fig. 10

Terfenol–D rod wrapped by air under a nonuniform magnetic field of Fig. 9. Contour plots of micro–rotations in radians generated by the skew–symmetric part of the Maxwell stress tensor. In the central figure, only the solid is represented

In Fig. 10, the three rotations are represented: $\theta _1$ is still not activated, but $\theta _2$ is already a measurable 0.01$^\circ$, and again $\theta _3$ is practically zero. The reason for $\theta _2 > \theta _1$ is that most of the magnetic field curves in the $x_2$–constant vertical plane to the external face. In addition, the micro–rotation concentrates close to the face under $\varphi = \!-10$ [A] for the same reason, and any other rotation does not cancel it.

In the central figure of the highest component $\theta _2$, only the Terfenol–D part of the mesh has been represented to appreciate that the micro–rotation of the solid is uniform in horizontal planes and non–linear to fulfil the zero boundary condition at the rod base plus the free movement at the top. Although appreciable, these micro– rotations are still small since the magnetic field is primarily parallel (not oblique) to the vertical anisotropic planes in the central part of the rod.

Figure 11 presents two distributions: the left one relates the intensity of the magnetic potential up to a value of -50 [A] (achievable with commercial magnets) against the maximum $\theta _2$ of Fig. 10 centre in absolute value. The trend is approximately quadratic, producing a substantial 25 increase in rotations for only five in magnetic potential.

As commented before, the micro–rotations depend on the micro–scale parameters $l_b = l_t$. For this reason and to study their influence on $\theta _2$, the right Fig. 11 plots the order of magnitude of the maximum micro–rotation versus the order of magnitude of $l_b$. These rotations range from a non–physical 10$^5$ for very low $l_b$ to an almost zero 10$^{-10}$ [rad] for very high $l_b$; the real values given in [3] range from 10$^{-4}$ to 10$^{-6}$.

Fig. 11

For experiment of Fig. 9: left: absolute value of maximum micro–rotation in plane $x_1$–$x_3$ versus prescribed magnetic potential; right: exponent of 10 for micro–rotation versus same exponent for microstructure scale parameter

To understand the linearity of the result, consider the equations that govern the macro–mechanical bending of a beam:

$$\begin{aligned} \displaystyle \left. \begin{array}{lll} \displaystyle \frac{\partial M_b}{\partial x} = m _b \\ \displaystyle M_b = EI~\frac{\partial \phi }{\partial x} \end{array} \right\} \quad \Rightarrow \qquad \phi = \frac{m_b}{2EI}~x^2, \end{aligned}$$

(34)

with $M_b$, $m_b$, E, I, and $\phi$ denoting bending moment, moment source, Young modulus, second moment of area, and cross–section rotation in any plane, respectively. The integration of $\phi$ does not conserve constants due to the “cantilever”–type boundary conditions of Fig. 4.

For the current MM analogy, m is closely related to the skew–symmetric part of the MST and I to the bending scale length $l_b$, which can be interpreted as the inertia of the micro–continuum. Consequently, the maximum of the three rotations from Fig. 7 (right) inversely depends on $l_b$ as in (34), that is, the lower its value, the higher the micro–rotations and the relationship is linear.

6.4 Uniform oblique magnetic field in anisotropic planes

The objective of the last numerical experiment is to analyse the influence of a completely oblique magnetic field on the generation of substantial micro–rotations. The importance of this study is that, for real materials, the initial magnetisation direction $M_3$ of the grains can rotate a different amount under the presence of a variable $\textbf{H}$, provoking the domain switch phenomena and changing the macroscopic response of magnetostrictives.

Fig. 12

Left: Applied magnetic field $\bar{H}$ function of the angle $\alpha$. The $M_3$ vector denotes the magnetisation direction of the Terfenol–D rod. Right: Maximum micro–rotation in absolute value in plane $x_2$–$x_3$ versus $\alpha$

As observed in the left Fig. 12, the numerical experiment considers the Terfenol–D rod magnetised along $x_3$ under the action of an oblique and constant magnetic field function of the variable angle $\alpha$. A vertical $H_3$ = 22 [kA/m] is first considered; to study the effect of different directions of the magnetic field in the plane $x_2$–$x_3$, a rotation with a variable angle $\alpha$ is calculated:

$$\begin{aligned} \begin{Bmatrix} \bar{H}_1 \\ \bar{H}_2 \\ \bar{H}_3 \end{Bmatrix} = \begin{bmatrix} 1 &{}&{} 0&{}&{} 0 \\ 0 &{}&{}\cos \alpha &{}&{} -\sin \alpha \\ 0 &{}&{} \sin \alpha &{}&{} \cos \alpha \end{bmatrix} \begin{Bmatrix} 0 \\ 0 \\ H_3 \end{Bmatrix}, \end{aligned}$$

(35)

Fig. 13

Contour plots of micro–rotation $\theta _1$ (left), couple stress $\tau _{31}$ (middle) and contribution of skew-symmetric MST from (38) (right) all for angle $\alpha =45^\circ$ of Fig. 12 left. Deformed meshes magnified by a factor of 50,000

Although the present FE is not mixed and, therefore, first derivatives cannot directly be prescribed, thanks to the fully nonlinear formulation, the calculated $\bar{H}_1$, $\bar{H}_2$, $\bar{H}_3$ are introduced in the SPSVERBa1 input as Neumann boundary conditions. Then, they can be automatically assigned to the nodal values of the magnetic field during the first iteration.

Figure 12 right plots the calculated maximum micro–rotation inside the rod in absolute value versus $\alpha$. As observed, the micro–rotations are null for both $\alpha = 0^\circ$ and $\alpha = 90^\circ$ since the applied magnetic field is parallel (almost as in Sect. 6.2) and perpendicular (as in Sect. 6.1) to $M_3$. Increasing $\alpha$ from zero, the micro–rotations increase to a maximum of 0.0665 [rad] for $\alpha =45^\circ$.

The explanation of this distribution can be found in the second (18), which can be expanded to:

$$\begin{aligned} \left\{ {\begin{array}{c} \tau _{11,1} + \tau _{21,2} + \tau _{31,3} \\ \tau _{12,1} + \tau _{22,2} + \tau _{32,3} \\ \tau _{13,1} + \tau _{23,2} + \tau _{33,3} \end{array} } \right\} + \left\{ {\begin{array}{c} B_2\bar{H}_3 - B_3\bar{H}_2 \\ B_3\bar{H}_1 - B_1\bar{H}_3 \\ B_1\bar{H}_2 - B_2\bar{H}_1 \end{array} } \right\} = \left\{ {\begin{array}{c} 0 \\ 0 \\ 0 \end{array} } \right\} , \end{aligned}$$

(36)

where the diagonal entries $\tau _{ii}$ can be regarded as MM torsional moments and the off–diagonal $\tau _{ij}$ as MM bending moments. Consider first that $B_i$ is approximately proportional to $H_i$ ($u_{j,k}$ is very small); then the second and third entries of the second vector at the left–hand side of (36) are zero (in this experiment $\forall \alpha \rightarrow \bar{H}_1$ = 0 and therefore $B_1 \approx$ 0). Since from Table 2$\mu _{22} = \mu _{11} = 2.68\mu _{33}$, the non–zero components $\bar{H}_3$ and $\bar{H}_2$ of Fig. 12 contribute to the first entry as:

$$\begin{aligned} B_2\bar{H}_3 - B_3\bar{H}_2 \approx -4230~\sin \alpha \cos \alpha \end{aligned}$$

(37)

The right–hand side previous equation is maximum at $\alpha = 45^\circ$ and zero at $\alpha = 0^\circ$ or $90^\circ$ (vertical or horizontal $\bar{H}$ respectively), values that explain the maximum and minimums of Fig. 12 right. These two values also explain the nullity of the micro–rotations of Fig. 6 and, in part, the low values of Fig. 9, since for these angles, the second vector of the (36) right–hand side is nil. In these two experiments, the three equations give the trivial solution $\tau _{ji} = 0$, and without source, all micro–rotations are zero.

The discussion of (36) is qualitative but not quantitative: the difficulty lies in finding the distribution of the rotations inside the Terfenol–D rod, for which the present numerical method is necessary. Figure 13 shows FE contour plots (deformed mesh with zoom $\times$50,000) generated with the boundary conditions of Fig. 12. In the left figure, a non–linear distribution is observed due to the clamped fixation of the rod at the bottom end. The same non–linearity is observed for the $\tau _{31}$ component of the couple stress in the central figure, with a non–negligible reaction of 9.1 [N$\cdot$m] at the fixed end; the deformed mesh shows a global bending of the rod, a shape that cannot be produced with, for instance, the CCM model.

To quantify the influence of the MST skew-symmetric part, the Fig. 13 right shows a ratio between the Frobenius norm of $\sigma ^{EM}_{[ji]}$ and that of $\sigma ^{EM}_{ji}$:

$$\begin{aligned} \displaystyle N=\frac{\sqrt{\text{ trace }\Big (\sigma ^{EM}_{[ij]}\sigma ^{EM}_{[ji]}}\Big )}{\sqrt{\text{ trace }\Big (\sigma ^{EM}_{ij}\sigma ^{EM}_{ji}}\Big )}. \end{aligned}$$

(38)

The figure shows that the ratio is approximately constant since the applied magnetic field is also constant in the bar. The MST skew–symmetric part is significant given that it generates about 6% of the total.

One interesting outcome of the present study is that the mentioned “domain switching” phenomena could be explained with the micro–rotations and the influence of the magnetic dipoles’ rotation on the magnetic material properties. These investigations will be studied in future work.

7 Concluding remarks

The present article has presented a theoretical and numerical formulation based on the finite element method to investigate the influence of the non–symmetry of the Maxwell stress tensor. This tensor contains a skew–symmetric contribution necessary for the study of rotations in non–isotropic materials; physically, these local rotations arise from the conservation of angular momentum.

In the framework of classical continuum mechanics, the total stress tensor formulation allows for calculating displacements of the center of mass at each material point but does not calculate rotations. On the contrary, extended formulations such as the current generalised continuum mechanics take into account the skew–symmetric part of the Maxwell tensor, which generates local rotations and couple stresses.

Numerically, a three-dimensional finite element formulation with seven degrees of freedom (three displacements, three micro–rotations, and the magnetic scalar potential) using a complex–step approach for the tangent matrices has been formulated and implemented in the research finite element code FEAP.

Four numerical experiments have been studied to extract the following consequences:

• The skew–symmetric part of the Maxwell stress tensor generates both micro–rotations and couple stresses that depend on i) scale parameters (microsize–dependency) closely related with the internal structure of the magnetic materials and ii) orientation of the prescribed magnetic field.

• In the classical continuum mechanics framework, the scale parameters of i) are null and, therefore, there are no micro–rotations.

• The dependency of ii) could explain the highly non–linear domain switching mechanisms in magnetostrictive/electrostrictive materials since the rotations of the internal grains change the magnetisation/polarisation of materials.

• For a magnetic field of 22 [kA/m] and for Terfenol–D material, the order of magnitude of these micro–rotations is up to 0.066 radians and its corresponding couple stress $-9$ [N$\cdot$m].

In summary, the skew–symmetric part of the Maxwell tensor is a relevant 6% of the total. Therefore this part should be considered in modern and sophisticated electro–magneto–mechanical devices.

A constitutive matrices

This appendix reports the matrix forms of the constitutive equations used in the present work.

$$\begin{aligned}{}[C_{ijkl}] = \begin{bmatrix} C_{11}&{} C_{12} &{} C_{13} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ C_{12} &{}C_{11}&{} C_{13} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ C_{13} &{} C_{13} &{} C_{33} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} C_{66} &{} C_{66} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} C_{66} &{} C_{66} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{}0 &{} C_{44} &{} C_{44} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} C_{44} &{} C_{44} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} C_{44} &{} C_{44} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} C_{44} &{} C_{44} \end{bmatrix}, \end{aligned}$$

$$\begin{aligned}{}[e^\varphi _{ijk}]= \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} e_{15}^\varphi &{} e_{15}^\varphi &{} 0 &{} 0 \\ e_{31}^\varphi &{} e_{31}^\varphi &{} e_{33}^\varphi &{}0 &{} 0 &{} 0&{} 0 &{} e_{15}^\varphi &{} e_{15}^\varphi \end{bmatrix}, \end{aligned}$$

$$\begin{aligned}{}[\mu _{ij}] = \begin{bmatrix} \mu _{11} &{} 0 &{} 0 \\ 0 &{} \mu _{11} &{} 0 \\ 0 &{} 0 &{} \mu _{33} \end{bmatrix}, \end{aligned}$$

$$\begin{aligned}{}[C^*_{ijkl}] = \begin{bmatrix} C_{11}^*&{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{}C_{11}^*&{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} C_{33}^* &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} C_{66}^* &{}0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} C_{66}^* &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{}0 &{} C_{44}^* &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} C_{44}^* &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} C_{44}^* &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} C_{44}^* \end{bmatrix}, \end{aligned}$$

with $C_{11}^*=C_{44}l_t^2$, $C_{33}^*=C_{66}l_t^2$, $C_{66}^*=C_{66}l_b^2$ and $C_{44}^*=C_{44}l_b^2$.