Abstract
Fracture of materials with rate-dependent mechanical behaviour, e.g. polymers, is a highly complex process. For an adequate modelling, the coupling between rate-dependent stiffness, dissipative mechanisms present in the bulk material and crack driving force has to be accounted for in an appropriate manner. In addition, the resistance against crack propagation can depend on rate of deformation. In this contribution, an energetic phase-field model of rate-dependent fracture at finite deformation is presented. For the deformation of the bulk material, a formulation of finite viscoelasticity is adopted with strain energy densities of Ogden type assumed. The unified formulation allows to study different expressions for the fracture driving force. Furthermore, a possibly rate-dependent toughness is incorporated. The model is calibrated using experimental results from the literature for an elastomer and predictions are qualitatively and quantitatively validated against experimental data. Predictive capabilities of the model are studied for monotonic loads as well as creep fracture. Symmetrical and asymmetrical crack patterns are discussed and the influence of a dissipative fracture driving force contribution is analysed. It is shown that, different from ductile fracture of metals, such a driving force is not required for an adequate simulation of experimentally observable crack paths and is not favourable for the description of failure in viscoelastic rubbery polymers. Furthermore, the influence of a rate-dependent toughness is discussed by means of a numerical study. From a phenomenological point of view, it is demonstrated that rate-dependency of resistance against crack propagation can be an essential ingredient for the model when specific effects such as rate-dependent brittle-to-ductile transitions shall be described.
Similar content being viewed by others
1 Introduction
The mechanical behaviour of many engineering materials depends on rate of deformation. For example, the response of polymers can be much more stiff or brittle when the loading rate is increased, see [1, 2]. The same applies for natural materials such as cheese [3] or confections [4]. In order to reduce experimental effort for design and testing of engineering products as well as for the optimisation of production processes of foods, the computational modelling and simulation of crack phenomena in rate-dependent materials is of increasing interest.
For the modelling of crack phenomena, the phase-field approach to fracture has become a well-established concept. Different from classical finite element approaches (FE), it enables to simulate crack growth without the need for remeshing. Furthermore, complex crack patterns that are not a priori known can be simulated in a straightforward manner, which especially makes the concept attractive compared to alternative approaches such as Cohesive zone elements [5] or the Extended-finite-element-method (X-FEM) [6]. The phase-field fracture approach goes back to the variational formulation of brittle fracture of Francfort and Marigo [7], who recast the Griffith criterion [8] for crack propagation into a variational setting. Bourdin et al. [9, 10] introduced a diffuse crack representation by means of the phase-field variable, which continuously varies from the intact to the fully broken material state. In other words, cracks are no longer seen as sharp discontinuities, but approximated over a finite length scale \({\ell _\text {c}}\). Making use of this smeared crack representation, a regularisation of the pseudo-energy functional is carried out. One key feature of this fundamental work of Bourdin is the \(\Gamma \)-convergence of the regularised functional against the sharp discontinuity model when the length scale \({\ell _\text {c}}\) tends to zero, i.e. \({\ell _\text {c}}\rightarrow 0\).
Based upon the diffuse crack representation introduced in [9], numerous models of fracture have been proposed. Not for all of these models, an underlaying pseudo-energy functional can be provided, from which the governing differential equations can be derived by means of variational arguments. Moreover, even if, \(\Gamma \)-convergence for \({\ell _\text {c}}\rightarrow 0\) is not necessarily preserved. Nevertheless, these models, which are based on the smeared description of crack topology, are typically referred to as phase-field models of fracture. Furthermore, although a lack of \(\Gamma \)-convergence is undesirable from a theoretical point of view, many of these models enable to take several possibly complex influencing factors into account, e.g. fatigue effects [11,12,13] or concentration of hydrostatic stress [14, 15], and have proven of value. Models of brittle fracture that include several advancements with respect to the fundamental work [9] have been proposed within both the infinitesimal strain regime [16,17,18,19,20] as well as for finite deformation [21,22,23]. Very recently, the phase-field approach to fracture also is combined with machine learning and data-driven approaches [24,25,26,27,28]. Furthermore, fracture phase-field modelling has been advanced towards elasto-plastic materials, see [29] for an overview on several approaches within the infinitesimal strain setting. For the performance of these ductile fracture models, the description of interaction between inelastic dissipative mechanisms and crack growth has revealed crucial. In particular, in the absence of an adequate coupling, crack patterns that are experimentally observed in metals, for instance, can not be reproduced, see e.g. [30, Fig. 14]. Different manners of introducing such a coupling are proposed, including non-energetic ductile fracture driving forces based on accumulated plastic strain [31, 32], and an enhanced degradation function which, in addition to the phase-field variable, depends on plastic deformation and results in a distinct plastic contribution to the fracture driving force [30, 33]. Furthermore, instead of a fracture driving force related to inelastic mechanisms, degradation of fracture toughness depending on equivalent plastic strain is introduced [34]. Several other phase-field models of ductile fracture are based upon a pseudo-energy functional in which both elastically stored energy and a plastic quantity, which is referred to as plastic work or plastic energy, are assumed to degrade upon fracture. Depending on the specific formulation, the plastic contribution to free energy actually corresponds to hardening terms [35, 36] or accumulated plastic dissipation [37,38,39].
More recently, the approach is combined with rate-dependent models for the deformation of the bulk material. A first phase-field fracture model for viscoelastic solids is proposed by Schänzel [32], where a non-energetic fracture driving force based on a generalised principal stress criterion is adopted. Alternative driving forces based on energetic or thermodynamic arguments are introduced by Shen et al. [40] as well as Liu et al. [41] within the kinematically linear regime and by Loew et al. [42, 43] within the linear viscoelasticity framework [44] at finite deformation. In these models, a viscous dissipative contribution is incorporated into the degraded free energy and thus enters fracture driving force. Different from the aforementioned models, only equilibrium and over-stress parts of the strain energy density are assumed to promote crack propagation by Yin and Kaliske [45], who combined the phase-field approach to fracture with a model of finite viscoelasticity [46]. Recently, similar formulations are adopted by Brighenti et al. [47] based on statistical mechanics-based equations for the response of the bulk material, and in [48] where the rate- and temperature-dependent behaviour of polymer nanocomposites is investigated. In some of these models based on either non-energetic or energetically motivated driving forces [32, 42], the viscosity assumed for the evolution of phase-field that originally is solely numerically motivated, cf. [17, 18], is understood as a material parameter and identified from experimental data. In the recent work of Dammaß et al. [49, 50], a unified energetic phase-field model for fracture of viscoelastic solids has been presented in the kinematically linear regime. Depending on the specific choice of the degradation functions and model parameters, respectively, the modelling approaches of [40, 42, 43] or [45, 47] are retained as limiting cases of the present model and by means of representative numerical studies, the coupling between viscous effects and fracture is analysed.
Compared to the rate-dependent behaviour of the bulk material, less efforts have been devoted to the study of strain rate-dependent resistance against fracture. Miehe et al. [31] suggested a phenomenological ansatz for the rate-dependent toughness in order to investigate the brittle-to-ductile fracture mode transition observed in the Kalthoff–Winkler experiment, i.e. for shear-loaded metals. Yin et al. [51] assumed the toughness of a linear elastic material to depend on rate of deformation. In their formulation, dissipation due to crack formation is incorporated into the free energy so that additional stress contributions are obtained from the rate-dependent fracture toughness. In these two models [31, 51], rate-independent models for the deformation of the bulk are considered. To the best of the authors’ knowledge, so far, there are no phase-field models that consider both a rate-dependent toughness and a model of rate-dependent deformation of the bulk.
In the present contribution, a thermodynamically consistent phase-field model of fracture of materials with rate-dependent behaviour is presented. For this purpose, the previously introduced pseudo-energy functional [50], which consists of the free energy that includes a contribution related to viscous dissipative mechanisms, and the fracture contribution is advanced towards the finite viscoelasticity setting of Reese and Govindjee [46]. Depending on the specific choice of the model parameters, the modelling approaches of [40, 42, 43] or [45, 47] can be retained as limiting cases. Based on experimental data for an Ethylene Propylene Diene Monomer (EPDM) rubber from the literature [42], the model parameters for the response of the bulk and the fracture behaviour are identified and model predictions are qualitatively and quantitatively verified on experimental results. In doing so, two assumptions for the fracture driving force, i.e. whether there shall be a contribution related to viscous dissipation or not, are investigated. With the aim of studying the possible influence of such a driving force component on the crack path, an asymmetrical setup is studied in addition to the symmetrical ones considered in recent publications, e.g. [42, 45]. Furthermore, based on experimental evidence on strain rate-dependent fracture toughness, cf. [3, 52, 53], and motivated from a phenomenological point of view, a rate-dependent resistance against fracture is introduced. A numerical study on the coupling between rate-dependent resistance against crack propagation and viscoelastic bulk response is then performed. An overview on the structure of the proposed unified model is given in Fig. 1.
The paper proceeds as follows. In Sect. 2, the proposed phase-field model of fracture in rate-dependent materials at finite deformation is presented and its thermodynamic consistency is proven. Subsequently, in Sect. 3, algorithmic aspects are addressed. In Sect. 4, the model parameterization is described and various numerical examples serve for validation and analysis of the model. A short summary and an outlook regarding the future work is given in Sect. 5. In the Appendix, information on the tangent for the local Newton iteration and the global material tangent is given.
Within this paper, italic symbols are used for scalar quantities (d, \(\varPsi \)) and bold italic symbols for vectors (\(\varvec{u}\)). For Second-order tensors, bold non-italic letters (\(\textbf{T}\), \(\varvec{\uptau }\)) are used, whereas fourth-order tensors are written in Blackboard bold (\(\mathbb {C}\)).
2 Phase-field formulation
In this section, the phase-field model of fracture in materials with rate-dependent behaviour is presented. At first, the general energetic formulation of fracture in viscoelastic materials derived in [50] is extended to the finite deformation setting. Subsequently, the specific constitutive assumptions are outlined and the rate-dependent fracture toughness is introduced. Finally, governing equations are provided and thermodynamic consistency is proven.
2.1 Pseudo-energy functional
Diffuse crack representation Motivated by the fundamental work of Bourdin [9], cracks are described in a diffuse manner by means of the fracture phase-field variable
which continuously varies from the intact (\(d=0\)) to the fully broken (\(d=1\)) material state. Figure 2 illustrates the concept of diffuse crack representation. Using this variable, following Miehe et al. [17], a functional
can be defined,Footnote 1 in which the length scale parameter \({\ell _\text {c}}\) controls the characteristic width of the diffuse crack. The Nabla operator with respect to the reference coordinate is given by
with \(\varvec{e}_K\) denoting K-th basis vector of the Cartesian reference coordinate frame. This functional \(\gamma _{\ell _\text {c}}\) can be understood as a crack surface density, which has been discussed in [16, 17, 31, 56] based on geometrical arguments. With this functional at hand, the density of rate of dissipation due to crack evolution is defined as
which refers to a volume element of the reference or undeformed configuration \(\varOmega _0\subset \mathbb {R}^N\) of the N-dimensional domain under consideration. The parameter \({\mathcal {G}}_\text {c}>0\) quantifies the resistance of the material against fracture. This definition of \({\dot{\varPhi }}^\textrm{fr}\) is conceptionally similar to the hypothesis of Griffith [8] who assumed the increase of dissipation due to crack growth, which is referred to as surface energy, to be proportional to the increment of crack surface. As a consequence, in analogy to the proportionality constant of classical fracture mechanics, \({\mathcal {G}}_\text {c}\) is referred to as fracture toughness in this work, which is line with e.g. [34, 51, 57]. Nevertheless, it has to be noted that in the context of the proposed model and other approaches that do not guarantee \(\Gamma \)-convergence, \({\mathcal {G}}_\text {c}\) in general does not exactly correspond to the toughness or critical energy release rate according to the sharp crack description, which correlates with stress intensity factors of classical fracture mechanics. Instead, \({\mathcal {G}}_\text {c}\) rather has to be seen as a measure of resistance against fracture that is valid within the diffuse framework. Classically, \({\mathcal {G}}_\text {c}\) is assumed to be a constant, so that the density of dissipation due to crack evolution, which can be referred to as density of fracture-pseudo energy, can be written as
However, \({\mathcal {G}}_\text {c}\) can explicitly depend on the position in space in heterogeneous materials [58, 59]. Furthermore, in the recent literature on phase-field modelling of fracture, \({\mathcal {G}}_\text {c}\) is assumed to change during fatigue life, see e.g. [12], or due to plastic deformation [34, 60]. In these cases, the fracture-pseudo energy can not be assumed to be proportional to \(\gamma _{\ell _\text {c}}\). Instead, in order to determine \(\varPhi ^\textrm{fr}\), the process history has to be accounted for. In the following, the phase-field framework is set up for which \({\mathcal {G}}_\text {c}=\text {const}.\) is assumed, first. Subsequently, the model is extended to account for a fracture toughness that depends on rate of deformation in Sect. 2.4.
Pseudo-energy functional For a domain \(\varOmega _0\) affected by cracks that are represented by means of the phase-field variable d, the pseudo-energy functional
can be defined,Footnote 2 which consists of the stored free energy \(\varPi ^\textrm{sd}_{\ell _\text {c}}\), with its density with respect to the reference configuration denoted by \(\varPsi \), and the fracture pseudo-energy \(\varPi ^\textrm{fr}_{\ell _\text {c}}\) with its density given by \(\varPhi ^\textrm{fr}\), which can be assumed to remain apparently stored within the material.
In the phase-field setting, the decrease of free energy due to fracture is expressed by means of the degradation function
which has to fulfil the conditions
By means of g(d), the degraded reference free energy density can be written as
with the virtually undamaged density of free energy, i.e. the amount of free energy that would be stored in the material in the absence of damage, denoted by \(\psi \).
Generalisation for inelastic material response Following the previous work [50] and similar to phase-field fracture models for elasto-plastic materials, the free energy density
is assumed to be additively decomposed into two essential ingredients.Footnote 3 Naturally, the first one is the effectively stored strain energy \(\varPsi ^\text {st}\). In addition, in order to adequately account for the coupling between inelastic deformation and fracture mechanisms, a free energy contribution \(\varPsi ^\text {vi}\) related to accumulated viscous dissipation is assumed. Contributions similar to \(\varPsi ^\text {vi}\) are also considered in other recent phase-field models of fracture in viscoelastic materials [40, 42]. Furthermore, analogue terms are widely spread in modelling of failure in elasto-plastic materials [36,37,38,39, 61], where a free energy contribution related to inelastic deformation, which is degraded in case of crack growth can be essential for the description of ductile fracture, cf. [29, 30].Footnote 4 In \(\varPsi ^\text {vi}\), in order to keep the formulation as general as possible, the parameter \(\beta _\text {vi}\in [0,1]\) is introduced as a weight, cf. [39] and [40] or [37, 38] for analogous assumptions. This constant \(\beta _\text {vi}\) is conceptionally similar to the Taylor–Quinney parameter widely spread in the modelling of plasticity [62], which quantifies the amount of plastic work that remains stored in the material. For a rigorous motivation and interpretation of \(\varPsi ^\text {vi}\) from a physical point of view, and a numerical investigation in the kinematically linear regime, the reader is referred to [50].
The specific definitions of \(\psi ^\text {st}\) and \(\psi ^\text {vi}\) considered in this work are given in Sect. 2.2.Footnote 5 For the two contributions to the free energy, any degradation functions \(g_\text {st}\) and \(g_\text {vi}\) satisfying the conditions (8) can be considered, which, in general, do not have to coincide. In the literature, different approaches have been taken, e.g. quartic and cubic expressions [63, 64], a sinusoidal ansatz [34, 45], and parametric functions that include additional parameters, which can be fitted to the behaviour of a specific material [20, 64,65,66]. Within the scope of this publication, \( g_\text {st}(d)\equiv g_\text {vi}(d)\equiv g(d)\) is assumed. Furthermore, the frequently adopted [9, 17, 35, 40] quadratic function
in which a small residual k is included in order to enhance numerical stability, is considered.
2.2 Viscoelastic bulk response
2.2.1 Kinematics
The displacement of a material point with the coordinate \(\varvec{X} \in \varOmega _0\) in the reference configuration is denoted by
wherein
is the motion function, which can be assumed to be bijective and continuous in space and time. The deformation gradient \(\textbf{F}\) and its determinant J are then given by
For the rate-dependent deformation behaviour of the material, the approach of Reese and Govindjee [46] is pursued and a generalised Maxwell model is adopted as shown in Fig. 3.Footnote 6
In the non-equilibrium, or over-stress branch, deformation is assumed to consist of an elastic and an inelastic viscous portion, and the deformation gradient is multiplicatively decomposed into
accordingly. Furthermore, following Flory [67], a decomposition of the deformation gradient into volumetric and isochoric parts is applied. For the equilibrium branch, the split is given by
wherein \({\textbf{I}}\) designates the second-order unit tensor and \(\overline{\textbf{F}}\) is the isochoric portion of the deformation gradient. For the the non-equilibrium branch, \({\textbf{F}^\textrm{el}}\) and \({\textbf{F}^\textrm{vi}}\) are decomposed separately. Considering, for example, the elastic portion of deformation, its isochoric part is given by
wherein \({J^\textrm{el}}= \det \, {\textbf{F}^\textrm{el}}\). For the specific definition of the material model, the positive definite left and right Cauchy-Green deformation tensors, \(\textbf{b}= \textbf{F}\cdot \textbf{F}^\top \) and \(\textbf{C}= \textbf{F}^\top \cdot \textbf{F}\), as well as their elastic counterparts \({\textbf{b}}^\textrm{el}= {\textbf{F}^\textrm{el}}\cdot {{\textbf{F}^\textrm{el}}}^\top \) and \({\tilde{\textbf{C}}}^\textrm{el}= {{\textbf{F}^\textrm{el}}}^\top \cdot {{\textbf{F}^\textrm{el}}}\), are used, respectively. It has to be noted that \({\tilde{\textbf{C}}}^\textrm{el}\) does not refer to the reference configuration, but to a fictitious intermediate configuration defined by \({\textbf{F}^\textrm{vi}}\). The tilde symbol \({\tilde{\circ }}\) is introduced to mark quantities which refer to this inelastic intermediate configuration. Isotropy of the material is assumed and the constitutive equations are specified in terms of principal stretches \(\lambda _\alpha \) and \({\lambda _{\beta }^\textrm{el}}\), which are obtained from the spectral decompositions
in which \(N_\lambda \in \{1, 2, 3\}\) and \({N^\textrm{el}_\lambda }\in \{1, 2, 3 \}\) are the number of pair-wise different principal stretches \(\lambda _\alpha \) and elastic principal stretches \({\lambda _{\beta }^\textrm{el}}\), respectively. The second-order projection tensors, or eigenvalue-base tensors, are obtained from
with the Kronecker delta \(\delta _{\varrho \sigma }\) given by
and equivalent relations for \(\textbf{P}_\alpha \), \({\textbf{p}_{\beta }^\textrm{el}}\) and \({\tilde{\textbf{P}}_{\beta }^\textrm{el}}\) [68, 69].Footnote 7
2.2.2 Specification of free energy densities
Strain energy The strain energy density is additively decomposed into an equilibrium and over-stress part. Accordingly, for the virtually undamaged quantity \(\psi ^\text {st}\),
is defined, wherein \(\textbf{C}\) and \({\textbf{F}^\textrm{vi}}\) form the set of independent thermodynamic state variables considered here, in addition to the phase-field variable d. Each contribution splits further into a volumetric portion \({}^\textrm{vol}\psi ^\text {st,eq}\) and \({}^\textrm{vol}\psi ^\text {st,ov}\), and an isochoric part \({}^\textrm{iso}\psi ^\text {st,eq}\) and \({}^\textrm{iso}\psi ^\text {st,ov}\), respectively. A compressible Ogden model [70] is assumed for both the equilibrium and non-equilibrium branches and the respective strain energy density contributions are defined to
wherein \({\bar{\lambda }}_\varrho = J^{-1/3} \, \lambda _\varrho \) and \({{\bar{\lambda }}^\textrm{el}_{\sigma }} = {J^\textrm{el}}^{-1/3} \, {\lambda _{\sigma }^\textrm{el}}\) are the isochoric total and elastic principal stretches following from (16) and (17). Their algebraic multiplicity is given by \(\nu _\varrho \in \{1, 2, 3\}\) and \({\nu }^\textrm{el}_{\sigma } \in \{1, 2, 3\}\), respectively. Furthermore, the compression moduli are denoted by \(\kappa ^\textrm{eq}>0\) and \(\kappa ^\textrm{ov}>0\), and \(N_\textrm{O}^\textrm{eq}\), \(\alpha ^\textrm{eq}_{p}\), \(\mu ^\textrm{eq}_{p}> 0\), as well as \(N_\textrm{O}^\textrm{ov}\), \(\alpha ^\textrm{ov}_{p}\), \(\mu ^\textrm{ov}_{p}>0\) are parameters of the Ogden models. From these constants, the initial shear moduli and the according Poisson’s ratios can be defined. For example, for the equilibrium branch, they read
and similar relations hold for the non-equilibrium branch.
Viscous contribution The degraded free energy contribution \(\varPsi ^\text {vi}\) related to inelastic mechanisms is designed such that a certain portion of accumulated viscous dissipation can enter the phase-field fracture driving force. Before defining the respective virtually undamaged quantity \(\psi ^\text {vi}\) in the finite viscoelasticity framework, the simple setting of a uniaxial deformation in the kinematically linear regime is considered for motivational purpose. Then, in the absence of damage, viscous dissipation in a material described by means of the generalised Maxwell model takes the form
in which \({\dot{\varepsilon }^\textrm{vi}}\) is the rate of inelastic deformation and \(\eta \) designates the viscosity of the material. In order to generalise \({D}^\textrm{vi,1D}\), the tensor
is introduced as a measure of the rate of inelastic deformation in the finite viscoelasticity setting, wherein
is the Lie derivative of \({\textbf{b}}^\textrm{el}\). Furthermore, a fully symmetric, positive definite, isotropic fourth-order tensor

is defined, in which \(\mathbb {I}^\text {D}\),
is the fully symmetric fourth-order deviator projection tensor. Therein,  are viscosities with respect to the isochoric and volumetric portion of deformation, respectively. The virtually undamaged free energy density contribution related to viscous mechanisms is then defined to
are viscosities with respect to the isochoric and volumetric portion of deformation, respectively. The virtually undamaged free energy density contribution related to viscous mechanisms is then defined to
which is positive and monotonically increasing in time.
Remark on the measure of rate of inelastic deformation The definition of \({\textbf{d}}^\textrm{vi}\) (26) can be written in an alternative form, which may be more intuitive. For this purpose, the inelastic velocity gradient
is introduced. It refers to the intermediate configuration defined by \({\textbf{F}^\textrm{vi}}\). The counterpart of \({\tilde{\textbf{l}}{}^\textrm{vi}}\) transformed to the current configuration reads
Assuming that there is no inelastic spin, i.e. \({\tilde{\textbf{l}}{}^\textrm{vi}}= {\tilde{\textbf{d}}^\textrm{vi}}\) with \({\tilde{\textbf{d}}^\textrm{vi}}= {{\,\textrm{sym}\,}}{\tilde{\textbf{l}}{}^\textrm{vi}}\) denoting the rate of inelastic deformation with respect to the viscous intermediate configuration, (27)1 can be rewritten as
and
holds, from which, together with the transformation rule (32), the definition of \({\textbf{d}}^\textrm{vi}\) as an Eulerian measure of rate of inelastic deformation becomes clear. For more details, the reader is referred to [71], where similar kinematic relations are derived in the context of plasticity.
2.3 Evolution of phase-field
The equation governing the evolution of the fracture phase-field variable is deduced from the pseudo-energy functional \(\varPi _{\ell _\text {c}}\) by means of the variational derivative

wherein \({\eta _\text {f}}\) is introduced as a kinetic fracture parameter in order to avoid discontinuity of the field variables in time and for numerical purposes, i.e. for enhancing the stability of the solution scheme, cf. [35, 72] and \(\varvec{N}\) denotes the outward-pointing unit normal vector on \(\partial \varOmega _0\). For the simulations presented in Sect. 4, \({\eta _\text {f}}\) is chosen such small that its influence on the simulation results vanishes which is verified by means of a comparative study of different values.Footnote 8
Inserting the definitions made in the previous sections into \(\varPi _{\ell _\text {c}}\), the evolution equation (35)1 takes the form
from which it becomes clear that, depending on the specific choice of \(\beta _\text {vi}\), fracture is driven by stored strain energy and the free energy contribution related to a portion of accumulated viscous dissipation. It has to be noted that in the present form (36), the evolution equation enables the phase-field variable to decrease, i.e. crack healing is not prohibited. Therefore, a modification is adopted which overcomes this issue, see Sect. 3.1.
2.4 Rate-dependent fracture toughness
For various materials, in addition to or instead of the deformation behaviour of the bulk material, the resistance against fracture has been reported to depend on rate of deformation. For instance, in elastomers, at low rates of deformation, chain entanglements can be resolved, which is not the case at high rates of deformation. Therefore, the number of chemical bonds that are broken when a crack propagates can be assumed to rise with rate of deformation and the fracture toughness increases accordingly, cf. [2, 73] for a more detailed discussion and experimental results. Furthermore, for several natural materials and foods, where the underlaying microscopic mechanisms can be more complex, a rate-dependency of \({\mathcal {G}}_\text {c}\) has been reported [3, 52, 53].Footnote 9 Therefore, as an extension of the phase-field equation (36) that has been derived for \({\mathcal {G}}_\text {c}=\text {const}.\), the fracture toughness is considered to depend on deformation rate in what follows, which enables a maximum of flexibility in modelling rate-dependent fracture processes. For this purpose,

is introduced as a scalar measure of the rate of deformation \(\textbf{d}\), which is given by

Furthermore, in line with [74], the sigmoid-shaped function

is adopted, here, see Fig. 4. The phase-field evolution equation is than, similar to the suggestions made in [32, 75], for instance, extended in non-variational manner. For the case of \({\mathcal {G}}_\text {c}(\textbf{d})\), it is rewritten toFootnote 10

In Sect. 4.3, for different parameters \({\mathcal {G}}_\text {c}^1\), \({\mathcal {G}}_\text {c}^2\), c, \(r_\text {ref}\), coupling between rate-dependent deformation and toughness is analysed.
Fracture pseudo-energy and rate-dependent toughness If fracture toughness is a function of rate of deformation and thus implicitly depends on time, density of fracture pseudo-energy \(\varPhi ^\textrm{fr}\) no longer is proportional to the crack surface density functional \(\gamma _{\ell _\text {c}}\) as it is the case for \({\mathcal {G}}_\text {c}=\text {const}.\) Instead, \(\varPhi ^\textrm{fr}\) has to be determined by explicitly integrating \({\dot{\varPhi }}^\textrm{fr}\) according to (4) over the process history, i.e.

In addition, it is noted that, different from e.g. [51], in the proposed model, rate-dependency of fracture toughness does not affect the density of free energy \(\varPsi \), since dissipation due to crack growth is not supposed to enter \(\varPsi \). Accordingly, no additional stress terms arise from rate-dependent toughness, see the evaluation of the dissipation inequality below in Sect. 2.5.
2.5 Stress tensor, viscous evolution and thermodynamic consistency
Under isothermal conditions, the second law of thermodynamics can be stated by means of the density of dissipation power \(\dot{D}\) as
cf. [76], with \(\textbf{T}\) denoting the second Piola–Kirchhoff stress tensor. For \(\varPsi = \varPsi (\textbf{C}, {\textbf{F}^\textrm{vi}}, d)\), this inequality can be rewritten to
wherein the contributions to dissipation power density due to fracture, \({\dot{D}}^\textrm{fr}\), and viscous effects, \({\dot{D}}^\textrm{vi}\), can be identified. The standard argument that \(\dot{D}\ge 0\) shall hold for arbitrary processes leads to the definition of stress

with the virtually undamaged equilibrium and over-stress tensors denoted by  and
and  , respectively, and the residual inequalities
, respectively, and the residual inequalities

Stress tensor Inserting the definitions of \(\psi ^\text {st,eq}\) and \(\psi ^\text {st,ov}\), Eqs. (23) and (24), into (44), the contributions to the second Piola–Kirchhoff stress tensor take the form


Residual inequalities As both \(\psi ^\text {st}\) and \(\psi ^\text {vi}\) are positive, \(\beta _\text {vi}\in [0,1]\), and due to (8)\(_3\), the condition \({\dot{D}}^\textrm{fr}\ge 0\) reduces to \(\dot{d} \ge 0\), i.e. irreversibility of fracture. The fulfilment of this demand will be addressed in Sect. 3.1.
Due to (7), \({\dot{D}}^\textrm{vi}\ge 0\) reduces to
Making use of the relations outlined in Sect. 2.2, after some lengthy manipulations, the first term can be rewritten as

wherein

is the virtually undamaged Kirchhoff over-stress. For a more detailed derivation see also [46]. Then (48) takes the form

from which, in line with [46], the equation governing viscous evolution

is defined. By reason of \(\beta _\text {vi}\in [0,1]\), the quadratic form obtained from inserting (52) into (51) is compatible with the second law of thermodynamics.
3 Algorithmic aspects
3.1 Irreversibility of fracture
In order to guarantee the irreversibility of fracture, the history variable approach of Miehe et al. [17] is pursued. For this purpose, the phase-field equation (40) is rewritten to
wherein the history variable
comprises the maximum of fracture driving force which has occurred. By means of \({\mathcal {H}}\), crack healing effects are prevented.Footnote 11 If such a history variable was not considered, these unphysical phenomena could arise from either an increase in fracture toughness \({\mathcal {G}}_\text {c}(\textbf{d})\) or a decrease in virtually undamaged free energy \(\psi \). With the modified form of the phase-field evolution (53) at hand, the governing equations of the model are summarised in Table 1 considering the total Lagrangian approach.
As an alternative to the history variable approach, in line with [18, 77], Dirichlet boundary conditions can be applied to the phase-field on all nodes
where the phase-field variable has reached a critical value \(d_\textrm{crit}\):
For the setups analysed in Sect. 4, the two strategies have been compared, exemplary, and no relevant differences could be noticed.
3.2 Viscous evolution
For the integration of viscous evolution equation (52), an operator split scheme of predictor–corrector type is adopted as proposed in [46]. Within the scope of this well-established approach, the evolution of elastic deformation in the over-stress branch of the generalised Maxwell element
is split into the contributions from change in total deformation, which is considered in the predictor step, and viscous evolution, which is accounted for in the inelastic corrector. For the predictor step, viscous deformation \({\textbf{F}^\textrm{vi}}\) or \({{\textbf{C}}^\textrm{vi}}\) is frozen, giving a trial state of elastic deformation at time step \(t_n\) to
Subsequently, within the corrector step, (57) is evaluated for the total deformation assumed to be constant, i.e. \(\textbf{l}= \textbf{0}\), which, with evolution equation (52) and kinematic relations (26) and (27) can then be written as

Due to isotropy, the principal directions of \({\textbf{b}}^\textrm{el}\), \({\textbf{b}}^\textrm{el}_\textrm{tr}\) and  coincide, which makes the evaluation of (59) in terms of elastic principal stretches \({\lambda _{\beta }^\textrm{el}}\) attractive. For the viscosity tensor \(\mathbb {V}\) defined according to (28), this leads to
coincide, which makes the evaluation of (59) in terms of elastic principal stretches \({\lambda _{\beta }^\textrm{el}}\) attractive. For the viscosity tensor \(\mathbb {V}\) defined according to (28), this leads to

wherein  denote the principal components of the over stress deviator
denote the principal components of the over stress deviator  . Within the scope of the FE framework, differential equation (60) is integrated in an approximate manner by means of an exponential mapping ansatz and rewritten in terms of logarithmic elastic principal stretches \({\varepsilon _{\beta }^\textrm{el}}= \ln {\lambda _{\beta }^\textrm{el}}\) as
. Within the scope of the FE framework, differential equation (60) is integrated in an approximate manner by means of an exponential mapping ansatz and rewritten in terms of logarithmic elastic principal stretches \({\varepsilon _{\beta }^\textrm{el}}= \ln {\lambda _{\beta }^\textrm{el}}\) as

Generally, \({\varepsilon _{\beta }^\textrm{el}}\) are determined from an iterative solution of the system of non-linear algebraic equations \(r_\beta = 0\) with \(\beta \in [1,N] \subset {\mathbb {N}}\). However, in case of two-dimensional plane stress setups as considered in Sect. 4, in addition to these three equations, it has to be ensured that the out of plane stresses vanishes, i.e.  must hold. In these cases, in addition to \({\varepsilon _{\beta }^\textrm{el}}\), the out of plane stretch \(\lambda _3\) has to be determined from the system of equations
must hold. In these cases, in addition to \({\varepsilon _{\beta }^\textrm{el}}\), the out of plane stretch \(\lambda _3\) has to be determined from the system of equations

Regardless of whether a plane stress state is considered or not, the respective system of equations (61) or (62) is solved by means of a local Newton iteration scheme at each quadrature point. In the following, the procedure is briefly described for the case that a plane stress state has to be guaranteed. With the vector of unknowns then written as
and the local tangent matrix
the linearisation of (62) around \({}^j x_\sigma \) is given as

For the specification of the derivatives \(\partial {w_\varrho }/\partial {x_\sigma }\), the reader is referred to Appendix A. Based on the linearisation, the Newton procedure is carried out as summarised in Algorithm box 1. For this, at each increment \(t_n\), the iteration scheme is initialised by means of

with

Within the iterative solution procedure, special attention has to be paid to \(_\textrm{tr}{\varepsilon _{3}^\textrm{el}}\) as it needs to be updated after each local iteration j according to

due to the change of \(\varepsilon _3 = \ln \lambda _3\).

3.3 Weak forms of the governing equations
For the derivation of the weak forms of mechanical equilibrium and phase-field equation, the test function spaces
and
are defined. Therein, \({\mathbb {H}}^1(\varOmega _0)\) is the Sobolev space of square integrable functions possessing square integrable derivatives in \(\varOmega _0\), and \(\partial \varOmega _{0 \, u_j}\) denotes the parts of the boundary where the j-component of the displacement vector \(\varvec{u}\) is prescribed. Then, (a) and (b) from Table 1 are multiplied by
and \(\delta c\in \mathbb {W}_c\), respectively. Integration by parts and making use of the divergence theorem yields
wherein \(\hat{\varvec{p}}\) denotes the Piola traction vector with its components \({\hat{p}}_j\) prescribed on \(\partial \varOmega _0{\setminus } \partial \varOmega _{0 \, u_j}\), and
Time discrete forms are obtained by approximating the respective rates using an Euler backward scheme. For spatial discretization, Galerkin’s method is applied. Then, the discretized equations are implemented into a standard finite element framework. The coupled problem is solved by means of a staggered approach, i.e. the mechanical equilibrium and the phase-field equation are solved in sequential manner. Multiple iterations of this decoupled solution scheme are performed until a staggered convergence criterion is fulfilled, which is based on the update of the nodal degrees of freedom. Furthermore, adaptive control of the time step size is employed based on a heuristic scheme. For this, depending on the number of global Newton iterations as well as on the number of staggered loops, the time step is either lowered or increased. In addition, if the convergence criteria are not met after a certain number of Newton iterations or staggered loops, respectively, a cut back to the last converged increment is performed and the time step size is lowered, accordingly. Information on the material tangent that is required for the iterative solution of (72) is given in Appendix B.
4 Representative simulations
In this section, several numerical examples are presented in order to analyse the characteristics of the present model and to demonstrate its flexibility in describing different responses. Furthermore, the comparison of numerical predictions to experimental results of Loew et al. [42] serves for validation of its predictive capabilities.
Stress response of the bulk material under homogeneous uniaxial tension—experimental data [42] versus present model for three different stretch rates \({\dot{\lambda }}\)
4.1 Parameter identification from experimental data
Within this publication, the viscoelastic behaviour of EPDM rubber is considered that has been experimentally analysed in [42].
Bulk response At first, the parameters describing the deformation of the bulk material are determined. For this purpose, the averaged stress-stretch curves from [42, Fig. 6] are considered as depicted in Fig. 5. For three different rates of deformation, these curves have been identified from uniaxial tension tests with dumbbell specimens. A homogeneous uniaxial stress state is assumed and damage is not taken into account, here. Furthermore, as no information on deformation in transversal direction is available, \(\nu ^\textrm{eq}=\nu ^\textrm{ov}=0.48\) is set in order to account for the high resistance against volumetric deformation that is typically observed for rubber. For isochoric and volumetric deformation, an identical relaxation time

is assumed. The Ogden parameters \(\mu ^\textrm{eq}_{p}, \alpha ^\textrm{eq}_{p}, \mu ^\textrm{ov}_{p}, \alpha ^\textrm{ov}_{p}\) as well as \(\tau \) are then identified by means of minimising the deviation between experimental data and model prediction. In doing so, following [70, p. 305], it is demanded that the constants satisfy the requirements
for any p and similar constraints for the non-equilibrium branch. To this end, in Matlab R2020b, the GlobalSearch strategy together with the fmincon algorithm for constrained optimisation problems is employed.Footnote 12 For an adequate approximation of the material behaviour, two Ogden exponents have revealed necessary for both the equilibrium and over-stress branch, respectively, i.e. \(N_\textrm{O}^\textrm{eq}=N_\textrm{O}^\textrm{ov}=2\).Footnote 13 The parameters obtained are summarised in Table 2. From Fig. 5 it becomes clear that the finite viscoelasticity formulation together with the Ogden approach allows for a very good approximation of the experimental results over the entire range of stretch \(\lambda \in [1,2.5]\) that has been experimentally investigated. Furthermore, the present model enables to capture the rate-dependent response in a more reliable manner then the linear viscoelasticity model based on the Yeoh-type strain energy density [42].Footnote 14
Identification of the fracture parameters With the calibrated bulk deformation model at hand, the fracture phase-field is parameterized from SENT experiments, i.e. specimens with a single pre-existing notch under tension. These experiments have been conducted at two rates of prescribed displacement [42]. The according specimen geometry is depicted in Fig. 6.
For the numerically motivated kinetic fracture parameter and the residual stiffness, the values \({\eta _\text {f}}=10^{-4}\,{\hbox {Ns/mm}^{2}}\) and \(k=10^{-10}\), respectively, are chosen. In a convergence study, these values have revealed sufficiently small so that the influence of \({\eta _\text {f}}\) and k on the simulation results vanishes. For all the simulations presented in this paper, the pre-existing cuts within the specimens are modelled geometrically by means of notches.Footnote 15
SENT—experimental data [42] versus model for approaches A (\(\beta _\text {vi}=0\)) and B (\(\beta _\text {vi}=1\))
SENT—evolution of the energetic quantities for \(\dot{\bar{u}} = {25}\,{\hbox {mm} \, \hbox {min}^{-1}}\) and the model approaches A (\(\beta _\text {vi}=0\)) and B (\(\beta _\text {vi}=1\)). Work of external forces \(W^\textrm{ext}\) (grey), pseudo-energy functional \(\varPi _{{\ell _\text {c}}} = \varPi ^\textrm{sd}_{\ell _\text {c}}+ \varPi ^\textrm{fr}_{\ell _\text {c}}\) (blue), stored free energy \(\varPi ^\textrm{sd}_{\ell _\text {c}}\) (orange), fracture pseudo-energy \(\varPi ^\textrm{fr}_{\ell _\text {c}}\) (green), and the portion of viscous energy that does not enter the fracture driving force \(\int \limits _{ \varOmega _0} D^\textrm{vi} \; \textrm{d} V\) (red). For approach B (\(\beta _\text {vi}=1\)), the curves for \(W^\textrm{ext}\) and \(\varPi _{{\ell _\text {c}}}\) coincide. (Color figure online)
The length scale parameter \({\ell _\text {c}}\) is set to \({\ell _\text {c}}={0.275}{\hbox {mm}}\), which is identical to [42]. In order to enable a step-by-step analysis of the model, a constant fracture toughness is assumed, here, and \({\mathcal {G}}_\text {c}(\textbf{d})\) according to (39) is investigated in Sect. 4.3. Furthermore, with the aim of performing a thorough analysis of viscous fracture driving force contribution in Sect. 4.2, the two limiting cases \(\beta _\text {vi}= 0\) (approach A) and \(\beta _\text {vi}=1\) (approach B) are considered. Under these two assumptions, the respective values of \({\mathcal {G}}_\text {c}\) are identified from experimental data. For this purpose, regarding the critical deformation in SENT for the two rates experimentally investigated, deviation between simulation and mean values from the experiments is minimised by means of a gradient-free approach. Since the specimens are of low thickness, plane stress conditions are assumed and two-dimensional simulations are performed, here. Due to symmetry, only one half of the SENT specimen is considered. The mesh consists of quadratic triangular elements and is refined along the crack path. h-convergence is verified. The optimal simulation results are compared to the range of experimental data in Fig. 7 and the parameters of the fracture model are summarised in Table 3. Furthermore, the evolution of the relevant energetic quantities during the SENT is shown in Fig. 8, for which the lower displacement rate \(\dot{{\bar{u}}} = {25}\,{\hbox {mm/min}}\) is considered exemplary. For both \(\beta _\text {vi}=0\) with optimal \({\mathcal {G}}_\text {c}= {10.7}\,{\hbox {N/mm}}\), and \(\beta _\text {vi}=1\) with optimal \({\mathcal {G}}_\text {c}= {12.0}\,{\hbox {N/mm}}\), good agreement between simulation and experiment can be stated. With \(\beta _\text {vi}=1\), a marginally better approximation is obtained for this setup. However, in both cases, the critical force is slightly overestimated.Footnote 16 Furthermore, especially for the higher rate \(\dot{{\bar{u}}} = {200}\,{\hbox {mm/min}}\), the simulated F–u curves do not completely reproduce the smooth decrease experimentally observed in the post-critical stage preceding complete failure. Instead, the critical point is followed by a sudden drop of reaction force that, interestingly, does not come along with complete failure yet. It corresponds to crack initiation at the tip of the pre-existing notch, see Fig. 9, and is succeeded by a smoother decrease of force for which crack propagation through the specimen involves a slight increase of external load before, finally, it comes to complete failure.Footnote 17 To the best of the author’s knowledge, such a phenomenon does not arise in hyperelastic models, whereas it also has been reported for linear viscoelasticity [42, 50]. The effect is the more pronounced the lower \(\dot{{\bar{u}}}\). Apparently, it is provoked by the rate-dependent behaviour of the bulk material that involves an increase of effective stiffness as well as the effective load bearing capacity of the material when, locally in the vicinity of the crack, rate of deformation suddenly raises up due to the initiation of fracture. From an energetic point of view, as it can be seen from Fig. 8, the initiation of the phase-field crack at the critical point comes along with a sudden drop of free energy \(\varPi ^\textrm{sd}\) stored within the specimen and the fracture pseudo-energy \(\varPi ^\textrm{fr}\) raises, accordingly. In the post-critical range, when the crack propagates through the specimen, \(\varPi ^\textrm{fr}\) continues to increase, whereas \(\varPi ^\textrm{sd}\) does also raise directly after the critical force level, yet starts to decrease when the displacement load \({\bar{u}}\) approaches its maximum value. This behaviour is immaterial of the assumption made for \(\beta _\text {vi}\), i.e. for the portion of viscous dissipation entering the fracture driving force. For a rigorous analysis within the small strain context, the reader is referred to the previous work [50].
SENT—crack propagation through the specimen for \(\dot{{\bar{u}}}={200}\,{\hbox {mm/min}}\) and \(\beta _\text {vi}=0\) (approach A). The corresponding force–displacement curve is depicted in Fig. 7. Qualitatively similar results are obtained for approach B and other \(\dot{{\bar{u}}}\)
4.2 Model validation and analysis of viscous driving force
For further model validation and analysis, double notched specimens under tension (DENT) with varying length of the pre-existing notch z are considered as depicted in Fig. 10.
DENT—setup for model validation and analysis. For comparison of model prediction with experimental data from [42], symmetrical specimens are considered, i.e. \(m={75/2}\,{\hbox {mm}}\)
At first, a symmetrical specimen geometry is considered, i.e. \(m={75/2}\,{\hbox {mm}}\). The predictions of the model parameterized in the previous Sect. are compared to experimental data from [42] for \( z \in \{9, 5\} \, \textrm{mm}\) and a constant rate \(\dot{{\bar{u}}}={75}\,{\hbox {mm/min}}\) in Fig. 11. For both approaches A and B, model predictions fit the experimental results well, which is also true for \( z \in \{7, 3\} \, \textrm{mm}\) (not depicted). The good agreement demonstrates the predictive capability of the present model and the suitability of the parameter identification from experiments with homogeneous and single-notched specimens.
With the aim of more thoroughly analysing the rate-dependency of responses and elaborating on the driving force contributions, additional simulations are performed for \(z= {7}\,{\hbox {mm}}\) and various rates \(\dot{{\bar{u}}} \in [12.5, 400] \, \,{\hbox {mm/min}}\). The numerical predictions for the two approaches \(\beta _\text {vi}=0\) and \(\beta _\text {vi}=1\) are compared in Fig. 12.
Regardless of the approach for the driving force, for high displacement rates, the responses converge against an upper elastic limit for which there is almost no viscous dissipation until failure. For very low \(\dot{{\bar{u}}} \), the responses of the structure likewise approach a lower elastic limiting case where over-stresses do approximately vanish during entire simulation. In between, for intermediate displacement rates, the critical displacement level diminishes with \(\dot{{\bar{u}}}\) for both approaches A and B. In contrast, regarding the rate-dependency of critical force level, the model predictions do significantly differ depending on whether a viscous fracture driving force contribution is assumed or not. On the one hand, critical force monotonically increases with rate when there is no such contribution, i.e. \(\beta _\text {vi}=0\) (A). On the other hand, for \(\beta _\text {vi}=1\) (B), critical force becomes minimal for intermediate \(\dot{{\bar{u}}}\), for which the greatest critical values of \(\varPsi ^\text {vi}\) are observed, see Fig. 13. Although no experimentally-determined force–displacement curves are available, it can be stated that the former is in agreement with experimental observations [42], whereas the latter contradicts experimental experience. At least when modelling fracture of elastomeric materials under monotonic loading, in some cases, fracture driving force contribution associated to accumulated viscous dissipation can thus lead to erroneous model predictions. In other words, modelling approach A has revealed more plausible, which, in a sense, is different from plasticity, where a fracture driving force related to inelastic mechanisms has revealed advantageous [30, 39]. Interestingly, such an observation has not been made in the previous study within the small strain framework [50], where a less pronounced influence of viscous effects on crack propagation has been observed. This can probably be attributed to the fact that the present formulation enables to describe larger deviations away from thermodynamic equilibrium, resulting in considerably greater viscous contributions to fracture driving force.
As it has been comprehensively described in [50], it essentially is the change of effective stiffness and the amount of dissipation until failure that lead to the change of critical force and displacement level with rate of external load. While the amount of fracture driving force necessary for crack growth remains constant, the fracture driving force available for a constant level of deformation can change with rate. On the one hand, effective stiffness of the viscoelastic material monotonically increases with increasing rate of deformation. For a certain external displacement \({\bar{u}}\) prescribed, the density of strain energy raises with \(\dot{{\bar{u}}}\), accordingly. On the other hand, in case of monotonic loads, the amount of viscous dissipation and thus, in case of \(\beta _\text {vi}>0\), the level of \(\varPsi ^\text {vi}\) at failure becomes maximal for intermediate rates.
Although viscous fracture driving force contribution has revealed not advantageous for describing failure of elastomers under monotonic loads, it might be suitable for other classes of materials, e.g. thermoplastics, and especially for the modelling of fatigue fracture, e.g. with \(0 < \beta _\text {vi}\ll 1\). In composites and thermoplastic materials, for instance, viscous dissipation and self-heating mechanisms can have an important influence on fatigue life, cf. [80].Footnote 18 Furthermore, the viscous dissipative fracture driving force contribution may also be more suitable for materials that show some fluid-like properties, so that similar to plasticity, inelastic permanent deformations play a more important role.
Crack patterns in asymmetrical specimens In addition to the symmetrical specimens, simulation results are presented in the following for an asymmetrical DENT geometry as depicted in Fig. 10 with \(m={27.5}\,{\hbox {mm}}\) and \(z={9}\,{\hbox {mm}}\). Since for ductile fracture of metals, where instead of viscoelasticity another class of dissipative materials is involved, the choice of fracture driving force revealed crucial the appropriate numerical description of asymmetrical crack patterns, cf. [30], simulations are performed for both approaches A and B. The corresponding force–displacement curves are depicted in Fig. 14. The overall rate-dependency of the specimen response is identical to what has been described above for the symmetrical geometry. In particular, for \(\beta _\text {vi}=1\), the numerically predicted critical force becomes minimal for an intermediate rate of external displacement, which does hardly coincide with what would be observed in experiments. In Fig. 15, the final crack patterns are compared for \(\dot{{\bar{u}}}={200}\,{\hbox {mm/min}}\). In order to ease comparison, the phase-field is shown with respect to the reference domain \(\varOmega _0\). For both fracture driving forces A and B, the crack pattern predicted for the viscoelastic material is essential different from what is typically observed when metals fail in a ductile manner. Instead of a single crack that connects the two pre-existing notches, two cracks independently propagate through the specimen. At a certain length, one of the two stops to propagate, resulting in an asymmetrical final crack pattern, see Fig. 16. Regardless of \(\beta _\text {vi}\) and \(\dot{{\bar{u}}}\), qualitatively identical crack paths are predicted.Footnote 19 However, depending on \(\beta _\text {vi}\), slight differences concerning the final length of the shorter crack can be stated especially for intermediate rates. Interestingly, when critical force is reached, the two cracks suddenly propagate over a finite width, which comes along with a significant abrupt drop of force. For intermediate and higher rates, similar to SENT geometry, a slight increase of external displacement \({\bar{u}}\) is necessary to make one of the cracks propagate further, resulting in a less heavy slope of the force–displacement curve before it finally comes to catastrophic failure. For these higher rates, in the simulations there is a stage that can be seen as a kind of stick–slip-like crack propagation, where the crack tip suddenly advances over a finite distance and then arrests over and over again. Alternatively, this stick–slip behaviour can also be seen as a series of subsequent initiations of small cracks.Footnote 20
These effects also lead to a non-smooth F–u curve in the post-critical range. Interestingly, for very small \(\dot{{\bar{u}}}\), such a behaviour is not simulated. In the literature on dynamic crack growth, comparable phenomena have been reported, cf. e.g. [83]. However, it has to be noted that regarding this particular aspect, the predictive capabilities of the present model are somewhat limited, as inertia effects are not taken into account.
Asymmetrical DENT—final crack patterns in the reference configuration \(\varOmega _0\) for approaches A and B and \(\dot{\bar{u}} = {200}\,{\hbox {mm/min}}\). For the EPDM rubber considered, no experimental results are available for this setup. Nevertheless, the crack paths resemble experimental observations made for other viscoelastic materials such as the hydroxyl-terminated polybutadiene (HTPB)-based solid propellant investigated in [82]
Asymmetrical DENT—phase-field crack initiation and propagation through the specimen for \(\dot{{\bar{u}}}={200}\,{\hbox {mm/min}}\) and \(\beta _\text {vi}=0\) (approach A). The corresponding force–displacement curve is depicted in Fig. 14. Qualitatively similar results are obtained for approach B and other \(\dot{{\bar{u}}}\)
For the EPDM rubber for which the model has been parameterized here, no experimental results are available for crack propagation in asymmetrical specimens. Nevertheless, the crack patterns simulated with the present model are in excellent agreement with what has been observed in experiments for other viscoelastic materials, see e.g. [82]. It is obvious that, when specimen geometries are similar, these crack patterns in viscoelastic materials can differ from the ones that form in elasto-plastic ones, since the inelastic mechanisms are essentially different. For example, there typically is no zone of inelastic localisation in viscoelastic materials whereas localisation of plastic deformation can play an important role when it comes to ductile fracture of metals.
Creep fracture In addition to fracture under monotonically increasing loads, a qualitative analysis of creep fracture is performed by means of one representative example. For this purpose, the symmetrical DENT geometry with \(z={7}\,{\hbox {mm}}\) is revisited. Instead of \({\bar{u}}\), a traction force \({\overline{F}}\) is applied that linearly increases with time until a certain value \({\overline{F}}_\textrm{max}\) is reached and is hold constant, subsequently. For two different values of \({\overline{F}}_\textrm{max}\), boundary conditions and model predictions are depicted in Fig. 17 for both approaches A and B. It can be stated that, generally, creep fracture can be captured regardless of the value of the assumption made on fracture driving force.Footnote 21 In case of \(\beta _\text {vi}>0\), failure can occur for lower \({\overline{F}}_\textrm{max}\) and after a shorter amount of creep time than for \(\beta _\text {vi}=0\). Furthermore, if a fracture driving force contribution from viscous dissipation is assumed, it can also depend on the rate \(\dot{{\overline{F}}}\) if creep fracture is predicted, since viscous dissipation vanishes for very small \(\dot{{\overline{F}}}\), see [50] for a discussion in the small strain context.
4.3 Investigation of rate-dependent fracture toughness
In the foregoing section and the previous work [50], it is demonstrated that within the scope of an energetic phase-field fracture approach, a rate-dependent material model for the bulk induces a certain relationship between critical load and rate of deformation when \({\mathcal {G}}_\text {c}\) is constant. Therefore, in addition to experimental indication [2, 3, 52, 53, 73], there also is a clear motivation for assuming a rate-dependent toughness from a phenomenological point of view. Assuming \({\mathcal {G}}_\text {c}\) to be a function of effective rate of deformation \(r = \Vert \textbf{d}\Vert _\textrm{F}\) enables more flexibility in describing the rate-dependent failure of varied materials. In what follows, this is demonstrated by means of numerical studies considering both an increase and a decrease of \({\mathcal {G}}_\text {c}\) with r. For this purpose, the symmetrical DENT setup with \(z={7}\,{\hbox {mm}}\) and \(\beta _\text {vi}=0\) is revisited. For \({\mathcal {G}}_\text {c}\), the sigmoid-shaped function (39) is assumed with \({\mathcal {G}}_\text {c}^1={10.7}\,{\hbox {N/mm}}\) and \(\beta _\text {vi}=0\) as parameterized for EPDM whereas the responses for different \({\mathcal {G}}_\text {c}^2>{\mathcal {G}}_\text {c}^1\) as well as \({\mathcal {G}}_\text {c}^2< {\mathcal {G}}_\text {c}^1\) are investigated. Apart from that, the parameters are identical to the ones listed previously.
The case of \({\mathcal {G}}_\text {c}\) increasing with rate of deformation is investigated first. As a representative example, the specimen response is depicted in Fig. 18 for \({\mathcal {G}}_\text {c}^2= 2 \, {\mathcal {G}}_\text {c}^1\), \(r_\text {ref}={2}\,{s^{-1}}\), \(c=10/r_\text {ref}\). For this specific choice of \(r_\text {ref}\), before it comes to crack propagation, the effective rates of deformation r satisfy \(r \ll r_\text {ref}\) within the entire domain for all \(\dot{{\bar{u}}} \lesssim {300}\,{\hbox {mm/min}}\). Through comparison of Figs. 18 and 12, it becomes clear that for these smaller rates, the pre-critical range of the specimen response is identical to the case where \({\mathcal {G}}_\text {c}= {\mathcal {G}}_\text {c}^1= \text {const}.\) In particular, effective stiffness and critical force raise with rate \(\dot{{\bar{u}}}\), whereas critical deformation decreases. When the critical point is reached and crack propagation starts, effective rate of deformation r suddenly raises up within the material, resulting in an increase of \({\mathcal {G}}_\text {c}\left( r(\textbf{d}) \right) \). Accordingly, in the post-critical range of the F–u curves, a slightly less sharp slope can be observed with respect to \({\mathcal {G}}_\text {c}= \text {const}.\) However, this effect is not very pronounced compared to the effects arising from the rate-dependent toughness when pre-critical rate of deformation r becomes close to the threshold value \(r_\text {ref}\).Footnote 22 In that case, deformation at failure begins to raise with rate similar to stiffness and critical force. Experimentally, similar effects can be observed for some natural materials, see e.g. [84] for an overview, as well as viscoelastic silicone elastomer based model systems [85].
For the discussion of \({\mathcal {G}}_\text {c}\) decreasing with r, \({\mathcal {G}}_\text {c}^2={\mathcal {G}}_\text {c}^1/4\), \(r_\text {ref}={2}\,{s^{-1}}\), \(c=5/r_\text {ref}\), are considered, exemplary. From the force–displacement curve depicted in Fig. 19 it appears that for \(\dot{{\bar{u}}} \ll {300}\,{\hbox {mm/min}}\), the responses do again coincide with the case \({\mathcal {G}}_\text {c}= {\mathcal {G}}_\text {c}^1= \text {const}.\) Naturally, the initiation of the phase-field crack at the notch tips is immediately followed by complete failure, since in this moment, the sudden increase in rate of deformation comes along with a drop of toughness. Nevertheless, for the DENT geometry, similar behaviour is obtained as simulation result for \({\mathcal {G}}_\text {c}=\text {const}.\), which is in agreement with experiments. For high rates \(\dot{{\bar{u}}} \ge {400}\,{\hbox {mm/min}}\), where \( r \gtrsim r_\text {ref}\) also holds in pre-critical range, the decrease of deformation of failure that stems from the rate-dependent stiffness of the viscoelastic material is further intensified by the rate-dependent fracture toughness. In addition, the critical force does no longer raise up with \(\dot{{\bar{u}}}\) yet also decreases. For sugar-based confections [86], a similar characteristic behaviour has been observed very recently. For high displacement rates, these materials fail in a brittle manner, i.e. at small deformation as well as low external force, whereas at low rates, they can undergo large deformation.Footnote 23
5 Conclusion and outlook
For the simulation of fracture of materials with rate-dependent behaviour, a flexible phase-field model is presented. To this end, the theory of finite viscoelasticity [46] is adopted for the deformation of the bulk material. The phase-field model is formulated such that, depending on the choice for the parameters, a portion of viscous dissipation can enter the fracture driving force. Moreover, in addition to the viscoelastic model of the bulk material, a fracture toughness function that depends on rate of deformation can be considered.
In order to analyse the coupling between different rate effects, a gradual analysis of the model is performed. The model of finite viscoelasticity is parameterized for an EPDM rubber based upon stress-deformation curves from the literature. Ogden-type strain energy densities are considered for both the equilibrium and over-stress parts of the response and very good agreement of the model with experimental data is obtained. Assuming a constant fracture toughness for the EPDM rubber, two limiting cases are studied regarding the fracture driving force and the respective values of toughness are identified from experimentally-determined SENT force–displacement curves. In doing so, either entire viscous dissipation or only effectively stored strain energy is assumed to enter the fracture driving force, respectively. In the absence of a driving force contribution related to viscous dissipative mechanisms, very good agreement between model predictions and experiments can be stated for different setups. In this case, plausible results are obtained over a broad range of rates of external load and deformation, respectively. On the contrary, if viscous dissipation is assumed to enter fracture driving force, erroneous model predictions can arise, here. In this case, agreement with experimental data is obtained for some specific rates, only. Accordingly, different from e.g. phase-field modelling of ductile fracture in metals, a distinct fracture driving force contribution related to inelastic dissipative mechanisms as proposed in [42, 43] or [40] has revealed not favourable for viscoelastic materials, in particular not for rubbery polymers. Furthermore, comparing the crack paths predicted in asymmetrical DENT specimens, it is demonstrated that such a driving force contribution is not necessary in order to predict non-symmetric crack patterns in an appropriate manner.
By means of a numerical study, it is demonstrated that a rate-dependent fracture toughness can significantly increase the capability of the phase-field model in capturing varied experimentally-observable responses. In particular, it seems suitable to describe rate-dependent brittle-to-ductile fracture mode transitions. In contrast, in case of a constant toughness, the rate-dependent model of bulk deformation induces a certain rate-dependency of critical stress and deformation, which does not coincide with experimental evidence for some specific materials. At least from a phenomenological point of view, rate-dependent fracture toughness thus seems to be an essential tool for modelling of rate-dependent fracture phenomena. While this contribution clearly demonstrates the potential of a rate-dependent fracture toughness within the proposed model, a quantitative description of rate-dependent brittle-to-ductile fracture mode transitions is beyond its scope. A thorough experimental analysis of these effects in materials with rate-dependent deformation behaviour, e.g. caramel-based confections [86], as well as a quantitative description based upon the framework presented in this contribution are the subject of current work.
Notes
For sake of brevity, terms arising from external loads are omitted in (6) and what follows.
Note that different from [39, 61] and in line with e.g. [17, 36], dissipation due to evolution of crack surface is not assumed to contribute to the free energy \(\varPsi \), yet included as a distinct contribution \(\varPhi \) or \(\varPi ^\textrm{fr}_{\ell _\text {c}}\), respectively, into the pseudo-energy functional \(\varPi _{\ell _\text {c}}\).
It has to be noted that there are alternative concepts for the phase-field modelling of ductile failure, also. For example, a degradation function g which, in addition to the fracture phase-field, depends on a measure of plastic deformation [30, 33], and a fracture toughness that diminishes with accumulated inelastic strain [34], have been proposed.
\(\psi ^\text {st}\) and \(\psi ^\text {vi}\) can be understood as virtually undamaged densities of free energy with respect to a volume element in the reference configuration, i.e. the respective free energy which would be stored in such a reference volume element in the absence of damage.
Herein, without loss of generality, only one non-equilibrium branch is considered, which is sufficient for the material investigated in Sect. 4. The extension to multiple non-equilibrium branches can be done in a straightforward manner, though.
If there are three pair-wise different principal stretches, i.e. \(N_\lambda =3\) or \({N^\textrm{el}_\lambda }=3\), the projection tensors can also be represented by means of the eigenvectors in a straightforward manner, e.g. \(\textbf{p}_\alpha =\varvec{n}_\alpha \otimes \varvec{n}_\alpha \) with \(\varvec{n}_\alpha \) denoting the \(\alpha \)-th eigenvector of \(\textbf{b}\).
In several other models, e.g. [42, 56], \({\eta _\text {f}}\) is assigned a finite value and thus considered as an additional material parameter. On the one hand, such a direct coupling of rate effects into the evolution of phase-field by means of \(\dot{d}\) can enable more modelling flexibility especially regarding the post-critical stage of a response. On the other hand, when it comes to damage, incorporation of a finite \({\eta _\text {f}}\) is equivalent to assuming a pseudo-viscous dissipation in addition to proper viscous effects and fracture dissipation. However, for fracture dissipation, according to the fundamental modelling hypothesis (4), the fracture toughness \({\mathcal {G}}_\text {c}\) is assumed to be the essential parameter. Therefore, a toughness depending on rate of deformation is presumed to be more consistent from an energetic point of view if a direct coupling of rate-effects into phase-field evolution is necessary. Furthermore, a finite \({\eta _\text {f}}\) would also incorporate some redundant information which should rather be taken into account by the viscoelastic model for deformation.
It has to be noted that, unlike here, in some publications dealing with fracture of inelastic materials, \({\mathcal {G}}_\text {c}\) is not only regarded as a measure of dissipation directly coming along with breaking of bonds but also comprises dissipative mechanisms of the bulk material.
Similar to unloading, in principle, an increase in \({\mathcal {G}}_\text {c}(\textbf{d})\) could lead to unphysical crack healing In Sect. 3.1, a modification is presented that enables to overcome this issue.
With this definition of \({\mathcal {H}}\), in the absence of gradients, i.e. \(\nabla _{\varvec{X}}d = \varvec{0}\), it can be discussed that \(\dot{d} \ge 0\) holds, cf. [16]. For the heterogeneous case, there is strong numerical evidence that \(\dot{d} \ge 0\) is also fulfilled.
A proof of uniqueness of the parameters identified, i.e. a global minimum of discrepancy between model and experiment, can not be provided. Nevertheless, GlobalSearch involves minimisation for a huge number of different start values in order to obviate local minima.
An increase of the number of Ogden branches to \(N_\textrm{O}^\textrm{eq}=N_\textrm{O}^\textrm{ov}=3\) did not lead to a perceptibly better approximation.
It has to be noted that the rate-dependency perceptible in Fig. 5 is not too pronounced. Accordingly, it could be worth investigating a broader range of stretch rates, since the rate-dependent behaviour of EPDM rubber can play a crucial role when it comes to failure, e.g. in case of creep fracture. Furthermore, additional experiments such as relaxation or creep tests could allow for differentiating between equilibrium and non-equilibrium contributions to stress in a significantly more accurate manner. However, within this contribution, we proceed with the experimental results available in the literature.
Alternatively, pre-existing cuts can be described using initial conditions for the phase-field variable or the fracture driving force, respectively. For the setups under consideration, the two approaches have been compared, exemplary. In general, no significant differences have been stated. However, in case of the non-geometrical modelling, for some setups a small additional kink has been observed in the pre-critical range of the F–u curves, which is not in agreement with experimental evidence.
Exemplary, in addition to the simulations presented in Fig. 7, the so-called AT-1 model has also been investigated, for which a slightly different expression for the crack surface density \(\gamma _{\ell _\text {c}}\) has been adopted, cf. e.g. [54]. However, in this case, the approximation of experimental data has revealed worse compared to the AT-2 approach considered here. In particular, for the AT-1 model, a more brittle response is predicted for the SENT, which is not in agreement with experimental evidence.
A straightforward way for tuning the model such that it would better reproduce this specific experimental observation could be defining a finite
 , which leads to a smooth decrease of post-critical F–u curve instead of a sudden jump, see e.g. [56, Fig. 9] However, as outlined in Sect. 2.3, this approach has some important drawbacks which is why it is not pursued here. For a more expressive investigation, it may be eligible to thoroughly elaborate on crack initiation mechanisms. For example, cavitation or void formation are often observed in rubbery polymers, see e.g. [78], and modified fracture phase-field models that explicitly take these mechanisms into account have recently been proposed in [15, 79], wherein hyperelasticity is assumed for the bulk.
, which leads to a smooth decrease of post-critical F–u curve instead of a sudden jump, see e.g. [56, Fig. 9] However, as outlined in Sect. 2.3, this approach has some important drawbacks which is why it is not pursued here. For a more expressive investigation, it may be eligible to thoroughly elaborate on crack initiation mechanisms. For example, cavitation or void formation are often observed in rubbery polymers, see e.g. [78], and modified fracture phase-field models that explicitly take these mechanisms into account have recently been proposed in [15, 79], wherein hyperelasticity is assumed for the bulk.For example, in the phase-field fatigue fracture model [81], which is applied to a rubbery polymer, a fatigue fracture driving force is introduced that also incorporates viscous dissipation. However, similar to [42], a model of linear viscoelasticity at finite deformation is used which does not allow for separation of accumulated viscous dissipation and non-equilibrium part of stored strain energy. As a consequence, entire viscous dissipation is also included in the quasi-static fracture driving force contribution.
For all the simulations performed, it is always the right crack tip which stops propagating at a certain length. It is deemed likely that this is due to the non-symmetric mesh that has been used for all the computations.
It is worth mentioning that it has been verified by means of a comparative study for different \({\eta _\text {f}}\) that this stick–slip phenomenon seems not to be induced by the viscous regularisation of crack growth.
For the specific setup considered here, no experimental results are available. Nevertheless, from [42], it can be reasoned that for both the lower and the higher value of \({\overline{F}}_\textrm{max}\) considered here, creep fracture would have to be expected in an experiment which is not captured in case of approach A. However, this deviation is assumed to essentially arise from the lack of non-monotonic experimental data for parameterization of the viscoelastic bulk deformation model. Since the model could solely be calibrated from monotonic experiments, an uncertainty of the prediction in case of creep loads can not be avoided.
It has to be noted that, when crack propagation takes place, quantitative predictive capability regarding the rate of deformation is somewhat limited for present formulation, since inertia effects are not taken into account.
A publication on experimental and numerical investigation of this brittle-to-ductile fracture mode transition is in preparation.
For the implementation of the local Newton iteration, no case-by-case analysis needs to be made accounting for whether there are multiple principal stretches and elastic principal stretches or not. Accordingly, the derivatives are given here with \(N_\lambda ={N^\textrm{el}_\lambda }=3\) assumed. If algebraic multiplicities \(\nu _\lambda ,{\nu }^\textrm{el}_{\sigma }>1\) were explicitly considered, identical values for the derivatives would be obtained.
It is assumed that an appropriate orthonormalization method is used in case of multiple principal stretches.
References
Grellmann W, Seidler S, Altstädt V (eds) (2015) 3rd edn. Hanser, München
Gent AN (2012) Engineering with rubber: how to design rubber components, 3rd edn. Carl Hanser Verlag, München. https://doi.org/10.3139/9783446428713
Goh S, Charalambides M, Williams J (2005) On the mechanics of wire cutting of cheese. Eng Fract Mech 72(6):931. https://doi.org/10.1016/j.engfracmech.2004.07.015
van Vliet T, Luyten H, Walstra P (2005) Time dependent fracture behaviour of food. In: Food colloids and polymers. Elsevier, Amsterdam, pp 175–190. https://doi.org/10.1533/9781845698270.175
Ortiz M, Pandolfi A (1999) Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int J Numer Methods Eng 44(9):1267. https://doi.org/10.1002/(SICI)1097-0207(19990330)44:9<1267::AID-NME486>3.0.CO;2-7
Moës N, Dolbow JE, Sukumar N (2017) Extended finite element methods. In: Stein E, de Borst R, Hughes TJR (eds) Encyclopedia of computational mechanics, 2nd edn. Wiley, Chichester, pp 1–21. https://doi.org/10.1002/9781119176817.ecm2111
Francfort G, Marigo JJ (1998) Revisiting brittle fracture as an energy minimization problem. J Mech Phys Solids 46(8):1319. https://doi.org/10.1016/S0022-5096(98)00034-9
Griffith AA (1921) The phenomena of rupture and flow in solids. Philos Trans R Soc A Math Phys Eng Sci 221(582–593):163. https://doi.org/10.1098/rsta.1921.0006
Bourdin B, Francfort G, Marigo JJ (2000) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48(4):797. https://doi.org/10.1016/S0022-5096(99)00028-9
Bourdin B, Francfort GA, Marigo JJ (2008) The variational approach to fracture. J Elast 91(1–3):5. https://doi.org/10.1007/s10659-007-9107-3
Carrara P, Ambati M, Alessi R, De Lorenzis L (2020) A framework to model the fatigue behavior of brittle materials based on a variational phase-field approach. Comput Methods Appl Mech Eng 361:112731. https://doi.org/10.1016/j.cma.2019.112731
Seiler M, Linse T, Hantschke P, Kästner M (2020) An efficient phase-field model for fatigue fracture in ductile materials. Eng Fract Mech 224:106807. https://doi.org/10.1016/j.engfracmech.2019.106807
Schreiber C, Kuhn C, Müller R, Zohdi T (2020) A phase field modeling approach of cyclic fatigue crack growth. Int J Fract 225(1):89. https://doi.org/10.1007/s10704-020-00468-w
Kumar A, Francfort GA, Lopez-Pamies O (2018) Fracture and healing of elastomers: a phase-transition theory and numerical implementation. J Mech Phys Solids 112:523. https://doi.org/10.1016/j.jmps.2018.01.003
Kumar A, Lopez-Pamies O (2021) The poker-chip experiments of Gent and Lindley (1959) explained. J Mech Phys Solids 150:104359. https://doi.org/10.1016/j.jmps.2021.104359
Miehe C, Hofacker M, Welschinger F (2010) A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits. Comput Methods Appl Mech Eng 199(45–48):2765. https://doi.org/10.1016/j.cma.2010.04.011
Miehe C, Welschinger F, Hofacker M (2010) Thermodynamically consistent phase-field models of fracture: variational principles and multi-field FE implementations. Int J Numer Methods Eng 83(10):1273. https://doi.org/10.1002/nme.2861
Kuhn C, Müller R (2010) A continuum phase field model for fracture. Eng Fract Mech 77(18):3625. https://doi.org/10.1016/j.engfracmech.2010.08.009
Amor H, Marigo JJ, Maurini C (2009) Regularized formulation of the variational brittle fracture with unilateral contact: numerical experiments. J Mech Phys Solids 57(8):1209. https://doi.org/10.1016/j.jmps.2009.04.011
Steinke C, Kaliske M (2019) A phase-field crack model based on directional stress decomposition. Comput Mech 63(5):1019. https://doi.org/10.1007/s00466-018-1635-0
Weinberg K, Hesch C (2017) A high-order finite deformation phase-field approach to fracture. Contin Mech Thermodyn 29(4):935. https://doi.org/10.1007/s00161-015-0440-7
Mang K, Fehse A, Kröger NH, Wick T (2021) A mixed phase-field fracture model for crack propagation in punctured EPDM strips. Theor Appl Fract Mech 115:103076. https://doi.org/10.1016/j.tafmec.2021.103076
Swamynathan S, Jobst S, Kienle D, Keip MA (2022) Phase-field modeling of fracture in strain-hardening elastomers: variational formulation, multiaxial experiments and validation. Eng Fract Mech 265:108303. https://doi.org/10.1016/j.engfracmech.2022.108303
Goswami S, Anitescu C, Rabczuk T (2020) Adaptive fourth-order phase field analysis using deep energy minimization. Theor Appl Fract Mech 107:102527. https://doi.org/10.1016/j.tafmec.2020.102527
Feng Y, Wang Q, Wu D, Luo Z, Chen X, Zhang T, Gao W (2021) Machine learning aided phase field method for fracture mechanics. Int J Eng Sci 169:103587. https://doi.org/10.1016/j.ijengsci.2021.103587
Aldakheel F, Satari R, Wriggers P (2021) Feed-forward neural networks for failure mechanics problems. Appl Sci 11(14):6483. https://doi.org/10.3390/app11146483
Carrara P, De Lorenzis L, Stainier L, Ortiz M (2020) Data-driven fracture mechanics. Comput Methods Appl Mech Eng 372:113390. https://doi.org/10.1016/j.cma.2020.113390
Carrara P, Ortiz M, De Lorenzis L (2021) Data-driven rate-dependent fracture mechanics. J Mech Phys Solids 155:104559. https://doi.org/10.1016/j.jmps.2021.104559
Alessi R, Marigo JJ, Maurini C, Vidoli S (2018) Coupling damage and plasticity for a phase-field regularisation of brittle, cohesive and ductile fracture: one-dimensional examples. Int J Mech Sci 149:559. https://doi.org/10.1016/j.ijmecsci.2017.05.047
Ambati M, Gerasimov T, De Lorenzis L (2015) Phase-field modeling of ductile fracture. Comput Mech 55(5):1017. https://doi.org/10.1007/s00466-015-1151-4
Miehe C, Hofacker M, Schänzel LM, Aldakheel F (2015) Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic–plastic solids. Comput Methods Appl Mech Eng 294:486. https://doi.org/10.1016/j.cma.2014.11.017
Schänzel LM (2015) Phase field modeling of fracture in rubbery and glassy polymers at finite thermo-viscoelastic deformations. Ph.D. thesis, Universität Stuttgart, Stuttgart
Ambati M, Kruse R, De Lorenzis L (2016) A phase-field model for ductile fracture at finite strains and its experimental verification. Comput Mech 57(1):149. https://doi.org/10.1007/s00466-015-1225-3
Yin B, Kaliske M (2020) Fracture simulation of viscoelastic polymers by the phase-field method. Comput Methods Appl Mech Eng 366:113068. https://doi.org/10.1016/j.cma.2020.113068
Kuhn C, Müller R (2016) A discussion of fracture mechanisms in heterogeneous materials by means of configurational forces in a phase field fracture model. Comput Methods Appl Mech Eng 312:95. https://doi.org/10.1016/j.cma.2016.04.027
Miehe C, Aldakheel F, Raina A (2016) Phase field modeling of ductile fracture at finite strains: a variational gradient-extended plasticity-damage theory. Int J Plast 84:1. https://doi.org/10.1016/j.ijplas.2016.04.011
Arriaga M, Waisman H (2017) Combined stability analysis of phase-field dynamic fracture and shear band localization. Int J Plast 96:81. https://doi.org/10.1016/j.ijplas.2017.04.018
McAuliffe C, Waisman H (2015) A unified model for metal failure capturing shear banding and fracture. Int J Plast 65:131. https://doi.org/10.1016/j.ijplas.2014.08.016
Borden MJ, Hughes TJ, Landis CM, Anvari A, Lee IJ (2016) A phase-field formulation for fracture in ductile materials: finite deformation balance law derivation, plastic degradation, and stress triaxiality effects. Comput Methods Appl Mech Eng 312:130. https://doi.org/10.1016/j.cma.2016.09.005
Shen F, Kang G, Lam YC, Liu Y, Zhou K (2019) Thermo-elastic-viscoplastic-damage model for self-heating and mechanical behavior of thermoplastic polymers. Int J Plast 121:227. https://doi.org/10.1016/j.ijplas.2019.06.003
Liu Z, Roggel J, Juhre D (2018) Phase-field modelling of fracture in viscoelastic solids. Procedia Struct Integr 13:781. https://doi.org/10.1016/j.prostr.2018.12.129
Loew PJ, Peters B, Beex LA (2019) Rate-dependent phase-field damage modeling of rubber and its experimental parameter identification. J Mech Phys Solids 127:266. https://doi.org/10.1016/j.jmps.2019.03.022
Loew PJ, Peters B, Beex LA (2020) Fatigue phase-field damage modeling of rubber using viscous dissipation: crack nucleation and propagation. Mech Mater 142:103282. https://doi.org/10.1016/j.mechmat.2019.103282
Holzapfel G (1996) On large strain viscoelasticity: continuum formulation and finite element applications to elastomeric structures. Int J Numer Methods Eng 39:3903
Yin B, Kaliske M (2020) Fracture simulation of viscoelastic polymers by the phase-field method. Comput Mech 65:293. https://doi.org/10.1007/s00466-019-01769-1
Reese S, Govindjee S (1998) A theory of finite viscoelasticity and numerical aspects. Int J Solids Struct 35(26–27):3455. https://doi.org/10.1016/S0020-7683(97)00217-5
Brighenti R, Rabczuk T, Zhuang X (2021) Phase field approach for simulating failure of viscoelastic elastomers. Eur J Mech A Solids 85:104092. https://doi.org/10.1016/j.euromechsol.2020.104092
Arash B, Exner W, Rolfes R (2021) A finite deformation phase-field fracture model for the thermo-viscoelastic analysis of polymer nanocomposites. Comput Methods Appl Mech Eng 381:113821. https://doi.org/10.1016/j.cma.2021.113821
Dammaß F, Ambati M, Kästner M (2021) Phase-field modelling and simulation of fracture in viscoelastic materials. PAMM 21(1):e202100108. https://doi.org/10.1002/pamm.202100108
Dammaß F, Ambati M, Kästner M (2021) A unified phase-field model of fracture in viscoelastic materials. Contin Mech Thermodyn 33(4):1907. https://doi.org/10.1007/s00161-021-01013-3
Yin B, Steinke C, Kaliske M (2020) Formulation and implementation of strain rate-dependent fracture toughness in context of the phase-field method. Int J Numer Methods Eng 121(2):233. https://doi.org/10.1002/nme.6207
Gamonpilas C, Charalambides MN, Williams JG (2009) Determination of large deformation and fracture behaviour of starch gels from conventional and wire cutting experiments. J Mater Sci 44(18):4976. https://doi.org/10.1007/s10853-009-3760-9
Forte AE, D’Amico F, Charalambides MN, Dini D, Williams JG (2015) Modelling and experimental characterisation of the rate dependent fracture properties of gelatine gels. Food Hydrocolloids 46:180. https://doi.org/10.1016/j.foodhyd.2014.12.028
Tanné E, Li T, Bourdin B, Marigo JJ, Maurini C (2018) Crack nucleation in variational phase-field models of brittle fracture. J Mech Phys Solids 110:80. https://doi.org/10.1016/j.jmps.2017.09.006
Ambrosio L, Tortorelli VM (1990) Approximation of functional depending on jumps by elliptic functional via T-convergence. Commun Pure Appl Math 43(8):999. https://doi.org/10.1002/cpa.3160430805
Miehe C, Schänzel LM (2014) Phase field modeling of fracture in rubbery polymers. Part I: finite elasticity coupled with brittle failure. J Mech Phys Solids 65:93. https://doi.org/10.1016/j.jmps.2013.06.007
Hansen-Dörr AC, Dammaß F, de Borst R, Kästner M (2020) Phase-field modeling of crack branching and deflection in heterogeneous media. Eng Fract Mech 232:107004. https://doi.org/10.1016/j.engfracmech.2020.107004
Hansen-Dörr AC, de Borst R, Hennig P, Kästner M (2019) Phase-field modelling of interface failure in brittle materials. Comput Methods Appl Mech Eng 346:25. https://doi.org/10.1016/j.cma.2018.11.020
Hansen-Dörr AC, Brummund J, Kästner M (2020) Phase-field modeling of fracture in heterogeneous materials: jump conditions, convergence and crack propagation. Arch Appl Mech. https://doi.org/10.1007/s00419-020-01759-3
Han J, Matsubara S, Moriguchi S, Kaliske M, Terada K (2021) Crack phase-field model equipped with plastic driving force and degrading fracture toughness for ductile fracture simulation. Comput Mech. https://doi.org/10.1007/s00466-021-02087-1
Kuhn C, Noll T, Müller R (2016) On phase field modeling of ductile fracture. GAMM-Mitteilungen 39(1):35. https://doi.org/10.1002/gamm.201610003
Taylor GI, Quinney H (1934) The latent energy remaining in a metal after cold working. Proc R Soc Lond Ser A Contain Pap Math Phys Charact 143(849):307. https://doi.org/10.1098/rspa.1934.0004
Kuhn C, Schlüter A, Müller R (2015) On degradation functions in phase field fracture models. Comput Mater Sci 108:374. https://doi.org/10.1016/j.commatsci.2015.05.034
Borden MJ, Verhoosel CV, Scott MA, Hughes TJ, Landis CM (2012) A phase-field description of dynamic brittle fracture. Comput Methods Appl Mech Eng 217–220:77. https://doi.org/10.1016/j.cma.2012.01.008
Wu JY (2017) A unified phase-field theory for the mechanics of damage and quasi-brittle failure. J Mech Phys Solids 103:72. https://doi.org/10.1016/j.jmps.2017.03.015
Sargado JM, Keilegavlen E, Berre I, Nordbotten JM (2018) High-accuracy phase-field models for brittle fracture based on a new family of degradation functions. J Mech Phys Solids 111:458. https://doi.org/10.1016/j.jmps.2017.10.015
Flory PJ (1961) Thermodynamic relations for high elastic materials. Trans Faraday Soc 57:829. https://doi.org/10.1039/tf9615700829
Miehe C (1993) Computation of isotropic tensor functions. Commun Numer Methods Eng 9(11):889. https://doi.org/10.1002/cnm.1640091105
Miehe C (1998) Comparison of two algorithms for the computation of fourth-order isotropic tensor functions. Comput Struct 66(1):37. https://doi.org/10.1016/S0045-7949(97)00073-4
Ogden RW (1997) Non-linear elastic deformations. Courier Corporation, Chelmsford
Wriggers P (2008) Nonlinear finite element methods. Springer, Berlin
Gurtin ME (1996) Generalized Ginzburg-Landau and Cahn-Hilliard equations based on a microforce balance. Physica D 92(3–4):178. https://doi.org/10.1016/0167-2789(95)00173-5
Gent AN, Lai SM (1994) Interfacial bonding, energy dissipation, and adhesion. J Polym Sci Part B Polym Phys 32(8):1543. https://doi.org/10.1002/polb.1994.090320826
Miehe C, Schänzel LM, Ulmer H (2015) Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput Methods Appl Mech Eng 294:449. https://doi.org/10.1016/j.cma.2014.11.016
Bilgen C, Weinberg K (2019) On the crack-driving force of phase-field models in linearized and finite elasticity. Comput Methods Appl Mech Eng 353:348. https://doi.org/10.1016/j.cma.2019.05.009
Coleman BD, Noll W (1963) The thermodynamics of elastic materials with heat conduction and viscosity. Arch Ration Mech Anal 13(1):167. https://doi.org/10.1007/BF01262690
Kuhn C (2013) Numerical and analytical investigation of a phase field model for fracture. Ph.D. thesis, TU Kaiserslautern
Euchler E (2020) Charakterisierung des Deformations- und Versagensverhaltens von Elastomeren unter querdehnungsbehinderter Zugbelastung. Ph.D. thesis, TU Dresden
Kumar A, Lopez-Pamies O (2020) The phase-field approach to self-healable fracture of elastomers: a model accounting for fracture nucleation at large, with application to a class of conspicuous experiments. Theor Appl Fract Mech 107:102550. https://doi.org/10.1016/j.tafmec.2020.102550
Mortazavian S, Fatemi A (2015) Fatigue behavior and modeling of short fiber reinforced polymer composites: a literature review. Int J Fatigue 70:297. https://doi.org/10.1016/j.ijfatigue.2014.10.005
Loew PJ, Poh LH, Peters B, Beex LA (2020) Accelerating fatigue simulations of a phase-field damage model for rubber. Comput Methods Appl Mech Eng 370:113247. https://doi.org/10.1016/j.cma.2020.113247
Han B, Ju Y, Zhou C (2012) Simulation of crack propagation in HTPB propellant using cohesive zone model. Eng Fail Anal 26:304. https://doi.org/10.1016/j.engfailanal.2012.05.025
Hageman T, de Borst R (2021) Stick-slip like behavior in shear fracture propagation including the effect of fluid flow. Int J Numer Anal Methods Geomech 45(7):965. https://doi.org/10.1002/nag.3186
Schuldt S (2018) Analysis of rate-dependent deformation and fracture phenomena during cutting of viscoelastic. Ph.D. thesis, TU Dresden
Boisly M, Schuldt S, Kästner M, Schneider Y, Rohm H (2016) Experimental characterisation and numerical modelling of cutting processes in viscoelastic solids. J Food Eng 191:1. https://doi.org/10.1016/j.jfoodeng.2016.06.019
Schab D, Zahn S, Rohm H (2021) Development of a caramel-based viscoelastic reference material for cutting tests at different rates. Materials 14(14):3798. https://doi.org/10.3390/ma14143798
Holzapfel GA (2000) Nonlinear solid mechanics: a continuum approach for engineering, 1st edn. Wiley, Chichester
Kalina K (2020) Mehrskalige Modellierung und Finite-Elemente-Simulation magnetorheologischer Elastomere. Ph.D. thesis, TU Dresden
Acknowledgements
Support for this research was provided by the German Research Foundation (DFG) under grant KA 3309/9-1. The authors gratefully acknowledge Jörg Brummund for the fruitful discussions. The computations were performed on a HPC cluster at the Centre for Information Services and High Performance Computing (ZIH) at TU Dresden. The authors thank the ZIH for allocation of computational time. In Fig. 15, the image of the experimental result from [82] is reprinted with permission from Elsevier.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There is no conflict of interest to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
1.1 A Tangent for the local Newton iteration
For the iterative solution of the viscous evolution equation (61) in the corrector step, the derivatives

withFootnote 24


are required. For the plane stress case, in addition, the derivatives


have to be evaluated.
B Material tangent
The consistent Lagrangian material tangent

is determined in order to enable the iterative solution of the weak form of balance of mechanical equilibrium (72). In line with e.g. [87], the derivation of the tangent is performed assuming \(N_\lambda ={N^\textrm{el}_\lambda }=3\) and the case of identical principal stretches or elastic principal stretches is then a posteriori addressed by means of L’Hôpital’s rule. The equilibrium part of the virtually undamaged tangent is given by

wherein \(\varvec{N}_\varrho \) denote the orthonormal eigenvectors of \(\textbf{C}\),Footnote 25 see e.g. [68, 69] or [88] for a derivation of the derivatives of principle stretches and projection tensors. Into this expression (83), for the specific model under consideration,

can be inserted. In case of multiple principal stretches, i.e. \(\exists \beta \ne \alpha : \lambda _\beta = \lambda _\alpha \), the second term in (83) can be evaluated making use of L’Hôpital’s rule [87]

Following [46], for the derivation of  , a virtually undamaged over-stress tensor
, a virtually undamaged over-stress tensor

is introduced with reference to the intermediate configuration defined by the viscous deformation gradient of the previous time step  , i.e. based on the decomposition of the deformation gradient at increment n into
, i.e. based on the decomposition of the deformation gradient at increment n into

With
the over-stress part of the virtually undamaged material tangent then can be written as

wherein the Einstein summation convention applies for double indices. From this, the over-stress tangent in terms of the intermediate configuration described by  can be defined to
can be defined to

In analogy to (83), this contribution to the material tangent is given by

wherein \(\breve{\varvec{N}}_{\varrho }\) denote the orthonormal eigenvectors of \({\breve{\textbf{C}}}^\textrm{el}_\textrm{tr}\) and  are the eigenvalues of
are the eigenvalues of  . The first term in (91) can be rewritten making use of
. The first term in (91) can be rewritten making use of

Furthermore, for the derivatives with respect to the trial stretch quantities, use of
which holds if the local Newton iteration has converged towards zero, is made. This assumption leads to
which is given by (76) and further specified in Appendix A. Accordingly, the derivative  in (92) can be expressed as
in (92) can be expressed as

with

and the two contributions in (96) specified by (77) and (78). In case of multiple elastic principal stretches, i.e. \(\exists \beta \ne \alpha : {\lambda _{\beta }^\textrm{el}} = {\lambda _{\alpha }^\textrm{el}}\), for the treatment of the second term in (91), the same procedure applies as outlined above for the case of multiple principal stretches. In particular, L’Hôpital’s rule reads

with the respective derivatives given by (92).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dammaß, F., Kalina, K.A., Ambati, M. et al. Phase-field modelling and analysis of rate-dependent fracture phenomena at finite deformation. Comput Mech 72, 859–883 (2023). https://doi.org/10.1007/s00466-023-02310-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-023-02310-1


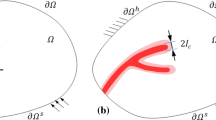



















 , which leads to a smooth decrease of post-critical F–u curve instead of a sudden jump, see e.g. [
, which leads to a smooth decrease of post-critical F–u curve instead of a sudden jump, see e.g. [