Abstract
In this contribution, a variational diffuse modeling framework for cracks in heterogeneous media is presented. A static order parameter smoothly bridges the discontinuity at material interfaces, while an evolving phase-field captures the regularized crack. The key novelty is the combination of a strain energy split with a partial rank-I relaxation in the vicinity of the diffuse interface. The former is necessary to account for physically meaningful crack kinematics like crack closure, the latter ensures the mechanical jump conditions throughout the diffuse region. The model is verified by a convergence study, where a circular bi-material disc with and without a crack is subjected to radial loads. For the uncracked case, analytical solutions are taken as reference. In a second step, the model is applied to crack propagation, where a meaningful influence on crack branching is observed, that underlines the necessity of a reasonable homogenization scheme. The presented model is particularly relevant for the combination of any variational strain energy split in the fracture phase-field model with a diffuse modeling approach for material heterogeneities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Modern engineering simulation challenges comprise the prediction of failure, which is one of the most severe mechanism affecting the bearing capacity. The phase-field method for the simulation of crack growth proved to be a powerful tool because it incorporates crack nucleation and arrest, as well as branching and merging of cracks [1,2,3]. Based on the variational approach to brittle fracture [4], it regularizes the underlying energy functional [5] and approximates the crack by an auxiliary scalar field, which is referred to as crack phase-field. The phase-field smoothly bridges the intact and fully broken state by introducing a length scale \({\ell _\text {c}}\). The approach is consistent with the energetic cracking criterion introduced by Griffith [6]. The phase-field method for crack modeling allows for fixed meshes where the element edges do not have to be aligned with the crack path, i.e., remeshing is avoided when the crack changes its direction or branches.
The approach for a non-conforming description can be extended to a more general setting, where all discontinuities within a heterogeneous structure are captured in such a way. Cumbersome preprocessing such as manual identification of heterogeneities and meshing can be skipped or at least simplified if the structure is for example obtained from direct imaging [7,8,9]. Prominent representatives are the extended finite element method [10,11,12] or the finite cell method [13, 14]. The latter is among the category of fictitious domain methods, where the geometry is fully embedded within a larger domain [15,16,17].
Another way to incorporate material heterogeneities is closely related to the phase-field model for cracks. A (multi)phase-field, which introduces a diffuse region \(\varGamma ^{\ell _\text {i}}\), with a characterizing width length scale \({\ell _\text {i}}\), along the formerly sharp interface \(\varGamma ^\text {i}\), marks the individual subdomains, and offers a broad range of applications in the field of thermodynamics, chemistry and mechanics [18,19,20]. The individual phase-field parameters are often referred to as order parameters. Far away from the interface, the properties of the constituents are recovered. Within the diffuse region, additional assumptions such as the treatment of strong discontinuities of the stress or strain are required, which will be highlighted in the following.
In classical homogenization theory, the Voigt and Reuss limits play a major role. Transferring the corresponding assumptions of a constant strain or a constant stress within multiple constituents to the diffuse interface region implies, that either the strain or stress does not exhibit a jump and the corresponding quantities are equal for each phase. It can be shown, that these assumptions converge towards the sharp interface limit [18]. However, better approaches exist, which account for the stress and strain discontinuity across the interface simultaneously [17, 21,22,23]. The improvement manifests itself in better convergence rates and the fact, that the kinematics of an energy driven, moving interface are captured correctly [24]. The improved homogenization scheme is often referred to as partial rank-I relaxation, which will become apparent in the remainder of the paper, and yields a pointwise fulfillment of the equilibrium and compatibility within the diffuse region.
We presented a modeling framework [25], where a crack phase-field and a static order parameter were used to simulate crack branching and deflection in heterogeneous media. Besides a qualitatively and quantitatively good agreement with analytical predictions from linear elastic fracture mechanics [26], we observed inconsistencies of the modeling results when comparing the diffuse interface approach to a sharp interface simulation. We presumed, that the Voigt–Taylor homogenization approach, which was incorporated in the diffuse region, biased the crack phase-field driving force in a way, that a straight crack instead of a deflection at the interface was favored. As discussed above, the homogenization scheme significantly influences the energetic driving force of the phase transition.
This work extends our diffuse modeling framework [25] in a way, that a partial rank-I relaxation is incorporated within the diffuse interface region. The key novelty of the present paper is the variationally consistent combination of the aforementioned homogenization approach with an additive strain energy decomposition, which is necessary to account for physically meaningful crack behavior such as the tension compression asymmetry. It will be shown, that the novel scheme is superior to the classical Voigt–Taylor assumption.
The paper is structured as follows. Section 2 provides a variational formulation of the modeling approach. Subsequently in Sect. 3, a convergence study and crack propagation simulations provide an insight into the functionality and advantages of the model. Final conclusions summarize the paper in Sect. 4. Additional information concerning technical details are provided in “Appendices A–D”.
2 Phase-field model for cracks and diffuse heterogeneities
2.1 Phase-field modeling of cracks
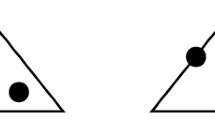
The investigations presented in this contribution build on a fully diffuse framework for crack propagation simulations in heterogeneous materials. The crack is described following the phase-field approach. Suppose, a one-dimensional rod \(x\in (-\infty ,\infty )\) of infinite length is cracked at \(x=0\). The sharp crack location can be fixed using the Dirac distribution, cf. Figure 1a. In contrast to a sharp crack, the phase-field approach introduces an additional scalar field
with a characteristic length \({\ell _\text {c}}\), cf. Figure 1b, where \(c=1\) and \(c=0\) resemble intact and fully broken material, respectively. Consequently, a three-dimensional generalization for the corresponding surface energy of the crack [3, 27]

can be derived, which is a measure for the energy required to form the corresponding crack surface. The fracture toughness \({\mathcal {G}}_\text {c}\) stems from the energetic cracking criterion by Griffith [6]. In other words, the crack surface has been regularized [5]. In case of a homogeneous fracture toughness, Eq. (1) is obtained by rewriting Eq. (2) for the one-dimensional case and subsequent minimization of the functional, subject to the boundary conditions \(c(0)=0\) and \(c'(x\rightarrow \pm \infty )=0\). For a heterogeneous fracture toughness, phase-field profiles different from Eq. (1) are obtained, cf. [25] for more detailed considerations. In Fig. 2a on the left, a phase-field crack \(\varGamma ^{\ell _\text {c}}\) is depicted, which possibly interacts with the interface between the two subdomains \(\varOmega _1\) and \(\varOmega _2\). Next, the diffuse representation of these subdomains is outlined.
The diffuse modeling approach is exemplarily depicted in a, where a heterogeneity is embedded in a regular mesh. The dashed interface mid-surface is described by the level-set \(d(\varvec{x})\equiv 0\) of the signed distance function. The sharp interface \(\varGamma ^\text {i}\) is smoothed by a hyperbolic tangent transition b, and becomes a diffuse region \(\varGamma ^{\ell _\text {i}}\)
2.2 Diffuse modeling of elastic heterogeneities
In the present work, two linear elastic domains \(\varOmega _i\) with \(i=1,2\) are considered. A static order parameter \(p\in [0,1]\) describes for every material point whether it belongs to the one \(\varOmega _1\) or other \(\varOmega _2\) subdomain, and introduces a smooth transition in the vicinity of the former sharp interface \(\varGamma ^\text {i}\), cf. Figure 2a. The transition width is controlled by the interface length scale \({\ell _\text {i}}\). The order parameter does not change in time and is a priori known, e.g., derived from a direct imaging technique. Finally, the motion is described by the displacement \(\varvec{u}\in \mathbb {R}^3\). The elastic energy density of each domain corresponds to

where
is a quadratic degradation function to account for previously introduced phase-field cracks. Various other degradation functions are proposed in [28, 29], including multiple functions for isotropic and anisotropic contributions [30] and compared for example in [31, 32]. The residual stiffness \(\eta \ll 1\) prevents numerical problems for fully degraded material \(c=0\). Furthermore, only the positive part  of the strain energy density is degraded to account for the tension compression asymmetry of cracks. Note, that positive does not refer to the sign of the strain energy density but to a one-dimensional analogy, where only positive stresses are degraded. A correct and physically meaningful, yet simple and efficient, splitting of the strain energy has been subject of discussion of several publications, cf. for example [27, 28, 33,34,35,36,37,38]. In case of large deformation kinematics, similar approaches can be found [39,40,41,42,43]. In this contribution, the so-called tensile split [27, Section 3.3]
of the strain energy density is degraded to account for the tension compression asymmetry of cracks. Note, that positive does not refer to the sign of the strain energy density but to a one-dimensional analogy, where only positive stresses are degraded. A correct and physically meaningful, yet simple and efficient, splitting of the strain energy has been subject of discussion of several publications, cf. for example [27, 28, 33,34,35,36,37,38]. In case of large deformation kinematics, similar approaches can be found [39,40,41,42,43]. In this contribution, the so-called tensile split [27, Section 3.3]

with the Lamé constants \(\overset{i}{\lambda },\overset{i}{\mu }\) and Macaulay brackets \(\langle \bullet \rangle _\pm =\tfrac{1}{2}(\bullet \pm \vert \bullet \vert )\) is adopted. For further information on the strains \(\overset{i}{\varvec{\varepsilon }}_\pm \), please refer to the cited section. It is noted that the diffuse interface model is not restricted to the tensile split, but can be applied to any decomposition of type (3).
The diffuse interface region with \(p\in (0,1)\) in the vicinity of the formerly sharp interface \(\varGamma ^\text {i}\) is referred to as \(\varGamma ^{\ell _\text {i}}\). The order parameter p, which recovers the values \(p=0\) for \(\varOmega _1\) and \(p=1\) for \(\varOmega _2\) far away from the interface, cf. Figure 2a, varies according to
which corresponds to a three-dimensional generalization of the one-dimensional solution of the Modica–Mortola functional [44], cf. Figure 2b. The signed distance \(d(\varvec{x})\) measures the shortest distance from any point in \(\varOmega _1\cup \varOmega _2\) to the interface mid-surface in the direction of the interface normal \(\varvec{n}^{\text {i}}=\nabla p / \vert \nabla p \vert \), cf. Figure 2a on the right. In this contribution, the signed distance \(d(\varvec{x})\), and thus \(p(\varvec{x})\) are a priori known. Within the diffuse region, the elastic energy density is defined as

which also holds for the individual phases, because one or the other contribution vanishes for \(p=0\) or \(p=1\). The approach of interpolating the individual constituents is a widespread approach, cf. for example [18,19,20,21, 24]. An alternative representation

can be obtained by inserting Eq. (3) into (7). The individual dependencies on \(\overset{i}{\varvec{\varepsilon }}\) are omitted above for the sake of readability. Analogously to Eq. (7), an interpolation
of the individual strains is assumed in the diffuse region. Together with the strain jump  , the independent variables for the strain energy density are now changed from \(\lbrace \overset{1}{\varvec{\varepsilon }},\overset{2}{\varvec{\varepsilon }} \rbrace \) to
, the independent variables for the strain energy density are now changed from \(\lbrace \overset{1}{\varvec{\varepsilon }},\overset{2}{\varvec{\varepsilon }} \rbrace \) to  with the relations
with the relations


which is more convenient in view of the presented model. The strain is obtained from the displacement \(\varvec{u}\) by
whereas different homogenization assumptions for  are discussed in Sect. 2.4. The next section combines the energy contributions from the phase-field crack and the linear elastic deformation, and derives the coupled field problem.
are discussed in Sect. 2.4. The next section combines the energy contributions from the phase-field crack and the linear elastic deformation, and derives the coupled field problem.
2.3 Global incremental potential and governing differential equations
Starting from the findings and definitions of the previous section, the internal energy density

is presented, which is used in the following derivations of the governing differential equations. It contains bulk material and crack phase-field contributions, \(\psi ^\text {el}\) and \(\psi ^\text {c}\), respectively. The global incremental potential

is defined according to [45, Equation (90)]. The index n refers to the previous, converged time increment, whereas quantities without the index are related to the current \((n+1)^\text {th}\) increment. The time increment is denoted by \(\tau =t_{n+1}-t_n\). It is noted that a first order Euler backward time integration scheme is employed for the rate \(\dot{c}\) of the crack phase-field, which enters the dissipation potential \(\varPhi (\dot{c})=\frac{\eta _\text {f}}{2}\dot{c}^2\). Here, \(\eta _{\text {f}}\ge 0\) is a kinetic parameter, often referred to as viscosity, which is of purely numerical nature in this contribution. Its choice is discussed in Sect. 3. The incorporation of \(\dot{c}\) can be understood as a viscous regularization, which makes it possible to use a monolithic solution approach. Various other approaches and their implications can be found in literature, see e.g., [2, 46]. The vector \(\bar{\varvec{t}}\) denotes given external tractions on Neumann boundaries \(\partial \varOmega _{\varvec{t}}\). The strain jump, which enters \(\psi \), is determined within a local minimization procedure, cf. Section 2.4, and is therefore known which is indicated by the star  . Hence, \(\varvec{u}\) and c are obtained by the global minimization principle
. Hence, \(\varvec{u}\) and c are obtained by the global minimization principle
with admissible sets
The first constraint in \({\mathcal {C}}\) is only relevant for the initial crack along \(\varGamma ^\text {c}_0\). Afterwards, the second condition, also known as fracture-like irreversibility constraint [3, 47], suffices, where \(c_\text {th}\ll 1\) is a small, positive threshold value. Previous investigations [25] confirmed, that setting \(c_\text {th}=0.03\) does not impact the crack path, while ensuring irreversibility. A discussion on different irreversibility constraints can be found in [47]. Subsequently, the Euler–Lagrange equations
can be derived, subject to Neumann boundary conditions
where \(\varvec{n}^{\text {b}}\) denotes the outward normal vector along the corresponding boundary. Equation (4) has been used in Eq. (19). The thermodynamically consistent relation for the Cauchy stress tensor is defined by

It is noted that the chain rule has been used together with Eqs. (10) and (11). The next section is dedicated to the determination of the strain jump  which enters the incremental potential (14). The validity of Eq. (22) is demonstrated in “Appendix A”.
which enters the incremental potential (14). The validity of Eq. (22) is demonstrated in “Appendix A”.
2.4 Homogenization assumptions within the diffuse interface region
In this section, two different approaches from the homogenization theory are examined to determine the unknown strain jump  , which enters the incremental potential (14) as
, which enters the incremental potential (14) as  . In particular, the Voigt–Taylor approach and a partial rank-I relaxation are introduced. In contrast to existing works [20], the combination of an additive strain energy decomposition and the above approaches is presented. This work incorporates the tensile split by Miehe [27] but is not limited to it.
. In particular, the Voigt–Taylor approach and a partial rank-I relaxation are introduced. In contrast to existing works [20], the combination of an additive strain energy decomposition and the above approaches is presented. This work incorporates the tensile split by Miehe [27] but is not limited to it.
Voigt–Taylor approach In classical homogenization theory, the Voigt–Taylor approach assumes equal strains in every constituent, i.e.,
From that, the strain jump  follows, which is inserted in the incremental potential above. In other words, the Voigt–Taylor approach is automatically implemented in any diffuse modeling framework similar to this one, if the strain jump is not treated by some means or other.
follows, which is inserted in the incremental potential above. In other words, the Voigt–Taylor approach is automatically implemented in any diffuse modeling framework similar to this one, if the strain jump is not treated by some means or other.
Different from the assumption of equal strains in the constituents, the Reuss–Sachs approach assumes equal stresses. It is, however, not investigated in this contribution, because there are various other publications doing so [21, 22, 24]. The two approaches yield upper and lower energetic barriers for the energy, respectively, cf. [21, Equation (55)] or [24, Equation (62)].
Partial rank-I relaxation The previous approaches do not include any information about the interface but only interpolate between the bulk energies, cf. Equation (7). In contrast, the partial rank-I relaxation correctly incorporates all mechanical jump conditions by means of the strain jump, which can be expressed by the Hadamard condition [48, Equation (2.2.9)]

without loss of generality,Footnote 1 and the stress jump \(\llbracket \varvec{\sigma } \rrbracket ^\top \cdot \varvec{n}^{\text {i}}={\varvec{0}}\). The former is stated here for a symmetric tensor \(\varvec{\varepsilon }\). The vector \(\varvec{a}\) is the strain jump amplitude and \(\varvec{n}^{\text {i}}= \nabla p /\vert \nabla p \vert \) the interface normal. The latter is fulfilled as follows: In order to calculate \(\varvec{a}\), a pointwise minimization procedure [21, Equation (50)]

with the associated necessary condition

is pursued, which is a relaxation of  with respect to \(\varvec{a}\) [24]. The stresses
with respect to \(\varvec{a}\) [24]. The stresses  are calculated according to Eq. (22). For the cases \(p=0\) or \(p=1\), which indicate bulk material away from the diffuse interface region, the condition is fulfilled and the jump \(\llbracket \varvec{\varepsilon }\rrbracket ={\varvec{0}}\) either way. For \(p\in (0,1)\), the expression in the curly braces has to be zero, which is similar to the aforementioned stress jump condition at sharp interfaces. Here, a pointwise enforcement throughout the whole diffuse interface region is required. In absence of a crack, \(g(1)=1\), the analytical solution for linear elastic material according to [24, Equation (42)] is recovered because the additive strain energy decomposition is unnecessary. The same is valid for \(g(c)<1\) if there is no strain energy decomposition at all, cf. [20], because g(c) does not exhibit any jump across the interface. In this contribution, the key novelty lies in the incorporation of any (variational) additive decomposition of the strain energy into a degraded and persistent part. The nonlinearity of the spectral decomposition for the tensile split requires a local Newton–Raphson scheme to solve for \(\varvec{a}\) as soon as a crack emerges within the diffuse interface region. In the context of an elasto-plastic multiphase-field model, Schneider et al. [19] had to solve a very similar Eq. (26) because of the nonlinearity due to plasticity. The local Newton–Raphson scheme is presented in “Appendix B”.
are calculated according to Eq. (22). For the cases \(p=0\) or \(p=1\), which indicate bulk material away from the diffuse interface region, the condition is fulfilled and the jump \(\llbracket \varvec{\varepsilon }\rrbracket ={\varvec{0}}\) either way. For \(p\in (0,1)\), the expression in the curly braces has to be zero, which is similar to the aforementioned stress jump condition at sharp interfaces. Here, a pointwise enforcement throughout the whole diffuse interface region is required. In absence of a crack, \(g(1)=1\), the analytical solution for linear elastic material according to [24, Equation (42)] is recovered because the additive strain energy decomposition is unnecessary. The same is valid for \(g(c)<1\) if there is no strain energy decomposition at all, cf. [20], because g(c) does not exhibit any jump across the interface. In this contribution, the key novelty lies in the incorporation of any (variational) additive decomposition of the strain energy into a degraded and persistent part. The nonlinearity of the spectral decomposition for the tensile split requires a local Newton–Raphson scheme to solve for \(\varvec{a}\) as soon as a crack emerges within the diffuse interface region. In the context of an elasto-plastic multiphase-field model, Schneider et al. [19] had to solve a very similar Eq. (26) because of the nonlinearity due to plasticity. The local Newton–Raphson scheme is presented in “Appendix B”.
2.5 Numerical implementation
The weak form including consistent linearization for the global Newton–Raphson scheme can be found in “Appendix C”. The spatial discretization is carried out using locally refined Truncated Hierarchical non-uniform rational B-splines [49] (NURBS) with quadratic shape functions in Sect. 3.1 and linear shape functions in Sect. 3.2. An adaptive refinement strategy is pursued, which allows for efficient computations with a high resolution of the steep gradient in regions where the crack develops and propagates. Additionally, the mesh is prerefined along the interface \(\varGamma ^{\ell _\text {i}}\) to resolve the diffuse transition for p sufficiently. Spatial convergence with respect to the crack length scale \({\ell _\text {c}}\) is ensured by choosing the finest element level in a way, that the characteristic element size is at least three times smaller than \({\ell _\text {c}}\), cf. Figure 3. All simulations are carried out using a MATLAB-based in-house finite element code.
Setup for two-dimensional convergence study: Top left the circular domain with a circular inclusion is depicted. A radial displacement is applied to the outer boundary. For the simulation, only the dashed square region is considered and depicted top right. Two studies, without and with the crack of length 2e, are conducted. The associated meshes are presented in the bottom row. Only the upmost refinement level of the NURBS meshes is shown
3 Numerical examples
3.1 Convergence study
For verification of the implementation, the convergence of the presented modeling approach with respect to the sharp interface solution is tested. For this purpose, a quarter of a circular bi-material disc is subjected to a radial displacement \(u_\text {R}=r_2/1000\), cf. Figure 3. In the study, the simulated domain is reduced to a square. The geometry parameters are given as \(r_1={3}~\mathrm{mm}\), \(r_2={15}~\mathrm{mm}\) and \(a={8}~\mathrm{mm}\). Plane strain is assumed. The signed distance for Eq. (6) reads
Symmetry boundary conditions are applied along \(\partial \varOmega _\text {left}\) and \(\partial \varOmega _\text {bottom}\). Along \(\partial \varOmega _\text {top}\) and \(\partial \varOmega _\text {right}\), a traction \(\bar{\varvec{t}}\) is applied, cf. Eq. (73) in “Appendix D”. Two error norms, the well known energy norm
and total error in energy
are defined, where the index \((\bullet )_\text {ex}\) stands for the exact solution and \(\vert \bullet \vert \) stands for the absolute value. The subscript ‘loc’ for the energy norm \(e_\text {loc}\) refers to the fact, that the error is calculated locally before integration. For the case without a crack, the analytical solution, cf. “Appendix D”, is used for \((\bullet )_\text {ex}\), and the denominator in \(e_\text {tot}\) is replaced by the analytical expression (69). For the cracked case, an overkill solution with a sharp interface serves as ‘exact’ solution. The overkill solution is calculated on a much finer mesh. The evaluation of the energy norm \(e_\text {loc}\) is not possible because of differing integration point locations.
Investigation without a crack At first, the model is tested for the linear-elastic case in the absence of a crack. The material parameters are set to \(\nu _1=\nu _2=\nu =0.3\), \(E_2={100}~{\mathrm{GPa}}\), \({\ell _\text {c}}={50}~\upmu {\mathrm{m}}\) and a very high value \({\mathcal {G}}_\text {c}=10^{5}~\hbox {kN mm}^{-1}\) to prevent any crack formation or propagation. The viscosity \(\eta _{\text {f}}\) is set to zero. Two cases \(E_1/E_2=\lbrace 2,20\rbrace \) allow to study the influence of the intensity of the elastic dissimilarity. The coarsest element level of the mesh is depicted in Fig. 3 on the bottom left. An \(h{\ell _\text {i}}\)-refinement study is undertaken, where the interface length scale and the mesh size are reduced simultaneously, i.e., more refinement levels are added along the arc with radius \(r_1\). The ratio \({\ell _\text {i}}/h\approx 2.7\) is kept constant.
The results of the convergence study are depicted in Fig. 4. In general, it can be seen, that the partial rank-I scheme exhibits the same or better convergence rates and error levels than the Voigt–Taylor approach with respect to the analytical sharp interface solution. Furthermore, the obtained results are consistent with literature, compare Fig. 4a to [17, Figure 8b], or Fig. 4b to [24, Figure 5b]. Additionally, the Voigt–Taylor approach reacts more sensitive to a more intense elastic dissimilarity which can be seen when comparing the left and right plots in Fig. 4a and b. This is also reported in [18].
The local (a) and total (b) error in energy for the convergence investigation in the absence of a crack are presented. First, the partial rank-I scheme exhibits the same or better convergence rates and error levels. Second, the Voigt–Taylor approach reacts more sensitive to a change in the elastic dissimilarity, which can be seen from a comparison between the left and the right plot in a and b
The total error in energy \(e_\text {tot}\) for the convergence investigation with a crack across the interface is presented for various residual stiffnesses (a)–(c). The residual stiffness does not have an influence on the convergence behavior. Furthermore, the convergence rates and error levels are similar to the case without a crack
Investigation with a crack across the interface Next, a phase-field crack along \(\varGamma ^\text {c}_0\) with \(e={0.5}~\mathrm{mm}\) is introduced as shown in Fig. 3, with the corresponding finite element mesh on the bottom right. The mesh is prerefined to the finest level along the crack to rule out any inaccuracies due to approximation errors of the phase-field. It serves as coarsest refinement level and is gradually refined along the interface for the \(h{\ell _\text {i}}\)-convergence study. All parameters and the boundary conditions are chosen similar to the previous investigation, except that only results for \(E_1/E_2=2\) are considered for the sake of brevity. It is noted that the traction \(\bar{\varvec{t}}\) does not reproduce the analytical solution as before, nor does it lead to a circumferentially constant radial displacement \(u_\text {R}\), which is why an overkill solution is used as reference. For the overkill solution, the NURBS mesh has to account for the physical \(C^0\)-continuity of the displacement along the arc \(r_1\). Additionally, the crack boundary condition along \(\varGamma ^\text {c}_0\) has to be set. This is why the finite element mesh is different from the mesh of the previous convergence study. Convergence of the overkill solution has been verified.
The results for three different values of the residual stiffness \(\eta \), cf. Eq. (4), are depicted in Fig. 5. All plots are identical, i.e., the residual stiffness does not influence the convergence, which is expected. However, for crack propagation simulations, a zero value most probably leads to numerical problems. Furthermore, the obtained results are more or less identical to the intact case, cf. Fig. 5 to the left plot in Fig. 4b: Convergence rate and error level are matching.
The two convergence studies suggest the successful verification of the implemented method and validation by means of literature results. The major question whether any impacts on propagating cracks can be observed is answered in the next section.
The general setup for the crack branching study is sketched on the left. The diffuse interface is schematically depicted by the grey hatched region. The material parameters are assigned according to the functions depicted on the right, using values of \(E_1\), \(E_2\), \(\hat{{\mathcal {G}}}_\text {c}^\text {i}\) and \({\mathcal {G}}_\text {c}^\text {b}\). The initial phase-field crack is depicted by \(\varGamma ^{\ell _\text {c}}_0\). Dirichlet boundary conditions are applied for the displacement along the bold marked side edges \(\partial \varOmega _{u,\text {s}}\) whereas homogeneous Neumann boundary conditions are applied on \(\partial \varOmega \setminus \partial \varOmega _{u,\text {s}}\). (color figure online)
In a, the NURBS mesh is depicted. The red square marks the location of the contours in b–d. In total, seven hierarchical levels are used. The simulation results for \(\alpha =-0.5\) and \({\mathcal {G}}_\text {c}^\text {b}/\hat{{\mathcal {G}}}_\text {c}^\text {i}=23\) are depicted in b–d. For these three plots, the two black lines mark the interface midline with \(d\equiv 0\). Shortly after meeting the interface, branching is predicted by the sharp reference solution. In case of a diffuse interface, the partial rank-I relaxation predicts the same phenomenon, while the Voigt–Taylor approach fails. The visibility of elements with \(c<0.1\) is turned of which is why the contour legend stops at 0.1. (Color figure online)
3.2 Crack branching at interfaces
Besides the improved convergence of the presented model with respect to the sharp interface solution it is of great interest whether any impacts on crack propagation at diffuse interfaces are recognized. Hansen-Dörr et al. [25] thoroughly investigated many different setups, where a crack approaches a possibly inclined interface and, depending on the ratio of the elastic moduli on both sides of the interface and the ratio of the bulk material and interface fracture toughnesses, decides to branch or to go straight into the adjacent bulk material. A comparison to analytical results from He and Hutchinson [26] and to a sharp interface reference revealed inaccuracies of the Voigt–Taylor approach, which was used therein. This section demonstrates, that the presented model extension to a partial rank-I relaxation yields the same critical deflection ratios as the sharp interface reference, while the Voigt–Taylor gives different results.
The setup for this study, which is similar to [25], is depicted in Fig. 6. The corresponding NURBS mesh is shown in Fig. 7a. A square domain with an initial phase-field crack \(\varGamma ^{\ell _\text {c}}_0\) is subjected to a horizontal displacement load. For this purpose, the concept of the so-called surfing boundary condition [50] is exploited, which proved to be very suitable for quantification purposes [50, 51]. The key idea of this approach is to introduce a point with the time dependent position \(\bar{\varvec{x}}\), which is moving along the y-axis
A displacement of hyperbolic tangent-like shape is applied on the side edges \(\partial \varOmega _{u, \text {s}}\),
with respect to the moving point, assuming \(u_\text {ref} = {7.5}~{\upmu \mathrm{m}}\), \(d={0.5}~\mathrm{mm}\), \(v={0.3}~\hbox { mm s}^{-1}\) and \({\bar{y}}_0={-4}~{\mathrm{mm}}\). Similar parameters proved to be suitable in previous studies [25]. Homogeneous Neumann boundary conditions are considered along the top and bottom edges. A horizontal interface, implied by the grey hatched bar in Fig. 6, divides the domain in two halves. The fracture toughness of the interface is different from the bulk material. This is accounted for by locally reducing the fracture toughness according to a Gaussian-like distribution
cf. Figure 6 blue plot in the middle. Far away from the interface, the bulk material fracture toughness \({\mathcal {G}}_\text {c}^\text {b}={2.7}\hbox {N mm}^{-1}\) is recovered. Along the interface, a potential crack is supposed to propagate for a critical energy release rate equal to \({\mathcal {G}}_\text {c}^\text {i}\). However, the crack experiences a bulk material influence due to the interaction of both length scales \({\ell _\text {i}}\) and \({\ell _\text {c}}\) [25], and tends to propagate at critical energy release rates, which are higher compared to the minimum of the function in Eq. (32). Hence, a compensated interface fracture toughness \(\hat{{\mathcal {G}}}_\text {c}^\text {i}\) is specified in a way, that a crack propagates along the interface midline at the true interface fracture toughness \({\mathcal {G}}_\text {c}^\text {i}\), i.e., \(\hat{{\mathcal {G}}}_\text {c}^\text {i}<{\mathcal {G}}_\text {c}^\text {i}\). For more details on the compensation procedure, the reader is referred to [25, 52, 53]. The ratio of the elastic moduli with \(E_1={210}{\hbox { GPa}}\) varies, while the Poisson ratio \(\nu =0.3\) is kept constant, i.e., the interpolation in Eq. (7) directly translates into a hyperbolic tangent function for \(E_1\) and \(E_2\), cf. orange line in Fig. 6 on the right. For the sharp interface reference solution, the elastic moduli vary according to the purple step function. The elastic dissimilarity is described with the first Dundurs’ parameter [54]
Following the study of Hansen-Dörr et al. [25], the length scale parameters are set to \({\ell _\text {i}}={18.75}~{\upmu \mathrm{m}}\) and \({\ell _\text {c}}={15}~{\mathrm{mm}}\), while the viscosity and the residual stiffness take the values \(\eta _{\text {f}}={10^{-5}}~\hbox {kN s} \upmu \mathrm{m}^{-2}\) and \(\eta =10^{-5}\), respectively.
A parameter study with \(\alpha =\lbrace -0.5,-0.25,0.25,0.5 \rbrace \) and different ratios \({\mathcal {G}}_\text {c}^\text {b}/{\mathcal {G}}_\text {c}^\text {i}\) is conducted, and the results for the sharp interface and the diffuse interface description using the Voigt–Taylor approach or partial rank-I relaxation are compared with respect to the crack behavior at the interface: Fixing \(\alpha \), the tendency of the crack to branch is higher for larger ratios \({\mathcal {G}}_\text {c}^\text {b}/{\mathcal {G}}_\text {c}^\text {i}\). The NURBS mesh is adaptively refined according to the crack path. All elements, where the phase-field fell below a value of \(c=0.5\), are marked for refinement [49]. For the sake of brevity, only the results where the two homogenization approaches yielded different crack phenomena at the interface are presented.
Figure 7b–d present the crack patterns shortly after the crack met the interface, with \(\alpha =-0.5\) and \({\mathcal {G}}_\text {c}^\text {b}/{\mathcal {G}}_\text {c}^\text {i}=8\), i.e., \({\mathcal {G}}_\text {c}^\text {b}/\hat{{\mathcal {G}}}_\text {c}^\text {i}=23\). For better interpretation, the elements with \(c<0.1\) are made invisible. It can be seen, that the sharp interface solution and the diffuse interface approach with a partial rank-I relaxation predict a branching of the crack. On the contrary, the Voigt–Taylor approach yields a straight crack with no such tendency. Even setting \({\mathcal {G}}_\text {c}^\text {b}/{\mathcal {G}}_\text {c}^\text {i}=10\), i.e., \({\mathcal {G}}_\text {c}^\text {b}/\hat{{\mathcal {G}}}_\text {c}^\text {i}=30.3\), did not change this fact. This is in line with the presumption of Hansen-Dörr et al. [25], who also observed such deviations. For further loading, all cracks started to propagate further in y-direction, while the two crack branches for the sharp interface and the diffuse partial rank-I relaxation arrested. For \(\alpha =-0.25\) and \({\mathcal {G}}_\text {c}^\text {b}/{\mathcal {G}}_\text {c}^\text {i}=5.5\), i.e., \({\mathcal {G}}_\text {c}^\text {b}/\hat{{\mathcal {G}}}_\text {c}^\text {i}=12\), a similar behavior is observed. For \(\alpha =\lbrace 0.25,0.5 \rbrace \), the three approaches always yield the same outcome. On the one hand this could imply an increased sensitivity of the crack behavior towards the homogenization scheme for negative \(\alpha \) values. On the other hand, only discrete values of \({\mathcal {G}}_\text {c}^\text {b}/{\mathcal {G}}_\text {c}^\text {i}\) are investigated and it is possible, that only those were picked from the infinite amount of possible ratios, where the results are identical. This is, why future model investigations will include a deeper and also three-dimensional analysis of the phenomena reported above. To conclude with, it was shown, that the present model extension meaningfully influences the crack behavior and yields closer results to the sharp interface solution.
4 Conclusions
In this contribution, a variational diffuse modeling approach was presented. Heterogeneities were described by an order parameter which is obtained from the signed distance function and a hyperbolic tangent, and smoothly bridges material discontinuities. The mechanical boundary value problem is monolithically coupled to a phase-field model for cracks.
Due to the diffuse transition between two materials, the mechanical jump conditions are not necessarily fulfilled for a general case. Instead, without taking any measures, the Voigt–Taylor homogenization approach is implemented within the diffuse region, which states equal strains in both phases. As shown above, this fails to reproduce several crack patterns compared to the sharp interface. A remedy to this issue is the partial rank-I relaxation, which was extended to account for a strain energy density decomposition. The decomposition is in general necessary for physically meaningful crack behavior like closure. The partial rank-I relaxation yields a point-wise fulfillment of the mechanical jump conditions and was successfully validated by means of convergence investigations. The presented scheme includes a local Newton–Raphson loop, which is the main drawback of the approach: Although, the local algorithm always converged without any problems, it is more time consuming than avoiding it by employing the Voigt–Taylor approach. A final study of a crack propagating towards an interface demonstrated, that the partial rank-I relaxation does not only improve the convergence of the global energy, but also influences the crack growth locally towards the sharp interface solution since it alters the crack driving force directly. The Voigt–Taylor approach did not achieve this for the given length scale of the interface, which is in line with observations from literature, and underlines the necessity to fulfill the mechanical jump conditions.
Change history
26 February 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00419-020-01788-y
Notes
The Hadamard condition holds for a continuous deformation field and is also referred to as kinematical compatibility condition. A proof is provided in [48, Sect. 2.1.6]. Because of the regularized description of the crack, the displacement field is always continuous. Thus, the condition also holds when a crack meets the interface.
References
Bourdin, B., Francfort, G.A., Marigo, J.-J.: The variational approach to fracture. J. Elast. 91(1–3), 5–148 (2008)
Miehe, C., Hofacker, M., Welschinger, F.: A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 199(45–48), 2765–2778 (2010)
Kuhn, C., Müller, R.: A continuum phase field model for fracture. Eng. Fract. Mech. 77(18), 3625–3634 (2010)
Francfort, G.A., Marigo, J.-J.: Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 46(8), 1319–1342 (1998)
Bourdin, B., Francfort, G.A., Marigo, J.-J.: Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 48(4), 797–826 (2000)
Griffith, A.A.: The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 221(582–593), 163–198 (1921)
Nguyen, T.T., Yvonnet, J., Zhu, Q.-Z., Bornert, M., Chateau, C.: A phase field method to simulate crack nucleation and propagation in strongly heterogeneous materials from direct imaging of their microstructure. Eng. Fract. Mech. 139, 18–39 (2015)
Nguyen, T.T., Yvonnet, J., Zhu, Q.-Z., Bornert, M., Chateau, C.: A phase-field method for computational modeling of interfacial damage interacting with crack propagation in realistic microstructures obtained by microtomography. Comput. Methods Appl. Mech. Eng. 312, 567–595 (2016)
Nguyen, L., Stoter, S., Baum, T., Kirschke, J., Ruess, M., Yosibash, Z., Schillinger, D.: Phase-field boundary conditions for the voxel finite cell method: surface-free stress analysis of CT-based bone structures: phase-field boundary conditions for the voxel finite cell method. Int. J. Numer. Methods Biomed. Eng. 33(12), e2880 (2017)
Sukumar, N., Chopp, D.L., Moës, N., Belytschko, T.: Modeling holes and inclusions by level sets in the extended finite-element method. Comput. Methods Appl. Mech. Eng. 190(46–47), 6183–6200 (2001)
Belytschko, T., Gracie, R., Ventura, G.: A review of extended/generalized finite element methods for material modeling. Modell. Simul. Mater. Sci. Eng. 17(4), 043001 (2009)
Fries, T.-P., Belytschko, T.: The extended/generalized finite element method: an overview of the method and its applications. Int. J. Numer. Methods Eng. 84, 253–304 (2010)
Parvizian, J., Düster, A., Rank, E.: Finite cell method: h- and p-extension for embedded domain problems in solid mechanics. Comput. Mech. 41(1), 121–133 (2007)
Düster, A., Parvizian, J., Yang, Z., Rank, E.: The finite cell method for three-dimensional problems of solid mechanics. Comput. Methods Appl. Mech. Eng. 197(45–48), 3768–3782 (2008)
Hansbo, A., Hansbo, P.: An unfitted finite element method, based on Nitsches method, for elliptic interface problems. Comput. Methods Appl. Mech. Eng. 191(47–48), 5537–5552 (2002)
Schillinger, D., Rank, E.: An unfitted hp-adaptive finite element method based on hierarchical B-splines for interface problems of complex geometry. Comput. Methods Appl. Mech. Eng. 200(47–48), 3358–3380 (2011)
Hennig, P., Maier, R., Peterseim, D., Schillinger, D., Verfürth, B., Kästner, M.: A diffuse modeling approach for embedded interfaces in linear elasticity. GAMM-Mitteilungen 43, e202000001 (2019)
Steinbach, I., Apel, M.: Multi phase field model for solid state transformation with elastic strain. Physica D 217(2), 153–160 (2006)
Schneider, D., Schmid, S., Selzer, M., Böhlke, T., Nestler, B.: Small strain elasto-plastic multiphase-field model. Comput. Mech. 55(1), 27–35 (2015)
Schneider, D., Schoof, E., Huang, Y., Selzer, M., Nestler, B.: Phase-field modeling of crack propagation in multiphase systems. Comput. Methods Appl. Mech. Eng. 312, 186–195 (2016)
Mosler, J., Shchyglo, O., Hojjat, H.M.: A novel homogenization method for phase field approaches based on partial rank-one relaxation. J. Mech. Phys. Solids 68, 251–266 (2014)
Schneider, D., Tschukin, O., Choudhury, A., Selzer, M., Böhlke, T., Nestler, B.: Phase-field elasticity model based on mechanical jump conditions. Comput. Mech. 55(5), 887–901 (2015)
Herrmann, C., Schoof, E., Schneider, D., Schwab, F., Reiter, A., Selzer, M., Nestler, B.: Multiphase-field model of small strain elasto-plasticity according to the mechanical jump conditions. Comput. Mech. 62(6), 1399–1412 (2018)
Kiefer, B., Furlan, T., Mosler, J.: A numerical convergence study regarding homogenization assumptions in phase field modeling. Int. J. Numer. Methods Eng. 112(9), 1097–1128 (2017)
Hansen-Dörr, A.C., Dammaß, F., de Borst, R., Kästner, M.: Phase-field modeling of crack branching and deflection in heterogeneous media. Eng. Fract. Mech. 232, 107004 (2020)
He, M.-Y., Hutchinson, J.W.: Crack deflection at an interface between dissimilar elastic materials. Int. J. Solids Struct. 25(9), 1053–1067 (1989)
Miehe, C., Welschinger, F., Hofacker, M.: Thermodynamically consistent phase-field models of fracture: variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 83(10), 1273–1311 (2010)
Steinke, C., Kaliske, M.: A phase-field crack model based on directional stress decomposition. Comput. Mech. 63, 1019–1046 (2018)
Pillai, U., Triantafyllou, S., Essa, Y., de la Escalera, F.M.: An anisotropic cohesive phase field model to model quasi-brittle fractures in thin fibre-reinforced composites. Compos. Struct. p. 112635 (July 2020)
Mandal, T.K., Nguyen, V.P., Wu, J.-Y.: A length scale insensitive anisotropic phase field fracture model for hyperelastic composites. Int. J. Mech. Sci. p. 105941 (July 2020)
Kuhn, C., Schlüter, A., Müller, R.: On degradation functions in phase field fracture models. Comput. Mater. Sci. 108, 374–384 (2015)
Strobl, M., Seelig, T.: Restrictions in phase field modeling of brittle fracture. PAMM 18(1), e201800157 (2018)
Amor, H., Marigo, J.-J., Maurini, C.: Regularized formulation of the variational brittle fracture with unilateral contact: numerical experiments. J. Mech. Phys. Solids 57(8), 1209–1229 (2009)
Freddi, F., Royer-Carfagni, G.: Regularized variational theories of fracture: a unified approach. J. Mech. Phys. Solids 58(8), 1154–1174 (2010)
Strobl, M., Seelig, T.: On constitutive assumptions in phase field approaches to brittle fracture. Proc. Struct. Integr. 2, 3705–3712 (2016)
Bryant, E.C., Sun, W.C.: A mixed-mode phase field fracture model in anisotropic rocks with consistent kinematics. Comput. Methods Appl. Mech. Eng. 342, 561–584 (2018)
Meng, F., Yan, J., Thomas, W.: A Phase-Field Description for Mixed-mode Fracture Propagation. Institutionelles Repositorium der Leibniz Universität Hannover, Hannover (2019)
Nguyen, T.T., Yvonnet, J., Waldmann, D., He, QC: Implementation of a new strain split to model unilateral contact within the phase field method. Int. J. Numer. Methods Eng. p. 6463 (June 2020)
Borden, M.J.: Isogeometric analysis of phase-field models for dynamic brittle and ductile fracture. Ph.D. Thesis (2012)
Hesch, C., Gil, A.J., Ortigosa, R., Dittmann, M., Bilgen, C., Betsch, P., Franke, M., Janz, A., Weinberg, K.: A framework for polyconvex large strain phase-field methods to fracture. Comput. Methods Appl. Mech. Eng. 317, 649–683 (2017)
Storm, J., Supriatna, D., Kaliske, M.: On the analysis of crackclosure behaviour using the phasefield method together with the novel concept of representative crack elements. PAMM 19(1), e201900314 (2019)
Tang, S., Zhang, G., Guo, T.F., Guo, X., Liu, W.K.: Phase field modeling of fracture in nonlinearly elastic solids via energy decomposition. Comput. Methods Appl. Mech. Eng. 347, 477–494 (2019)
Tarafder, P., Dan, S., Ghosh, S.: Finite deformation cohesive zone phase field model for crack propagation in multi-phase microstructures. Comput. Mech. 66, 723–743 (2020)
Modica, L., Mortola, S.: Un esempio di gamma-convergenza. Bollettino della Unione Matematica Italiana B 14, 258–299 (1977)
Miehe, C.: A multi-field incremental variational framework for gradient-extended standard dissipative solids. J. Mech. Phys. Solids 59(4), 898–923 (2011)
Gerasimov, T., De Lorenzis, L.: A line search assisted monolithic approach for phase-field computing of brittle fracture. Comput. Methods Appl. Mech. Eng. 312, 276–303 (2016)
Linse, T., Hennig, P., Kästner, M., de Borst, R.: A convergence study of phase-field models for brittle fracture. Eng. Fract. Mech. 184, 307–318 (2017)
Ilhavý, M.: The Mechanics and Thermodynamics of Continuous Media. Springer, Berlin (1997)
Hennig, P., Müller, S., Kästner, M.: Bézier extraction and adaptive refinement of truncated hierarchical NURBS. Comput. Methods Appl. Mech. Eng. 305, 316–339 (2016)
Hossain, M.Z., Hsueh, C.-J., Bourdin, B., Bhattacharya, K.: Effective toughness of heterogeneous media. J. Mech. Phys. Solids 71, 15–32 (2014)
Kuhn, C., Müller, R.: A discussion of fracture mechanisms in heterogeneous materials by means of configurational forces in a phase field fracture model. Comput. Methods Appl. Mech. Eng. 312, 95–116 (2016)
Hansen-Dörr, A.C., de Borst, R., Hennig, P., Kästner, M.: Phase-field modelling of interface failure in brittle materials. Comput. Methods Appl. Mech. Eng. 346, 25–42 (2019)
Hansen-Dörr, A.C., Hennig, P., Kästner, M., Weinberg, K.: A numerical analysis of the fracture toughness in phase-field modelling of adhesive fracture. PAMM 17(1), 249–250 (2017)
Dundurs, J.: Discussion: edge-bonded dissimilar orthogonal elastic wedges under normal and shear loading. J. Appl. Mech. 36(3), 650–652 (1969)
Acknowledgements
The authors gratefully acknowledge support by the Deutsche Forschungsgemeinschaft in the Priority Program 1748 Reliable simulation techniques in solid mechanics. Development of non-standard discretization methods, mechanical and mathematical analysis under the Project KA3309/3-2. The computations were performed on a HPC-Cluster at the Center for Information Services and High-Performance Computing (ZIH) at TU Dresden. The authors thank the ZIH for allocations of computational time.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Stress–strain relationship
In this section, the validity of Eq. (22) is demonstrated. For better readability of the tensor products, the index notation is used where appropriate. Differentiation of Eq. (7) with respect to the strain yields

where  and
and  correspond to the stresses in the individual phases. Subsequently, the strains of phase 1 and 2 are differentiated with respect to the interpolated strain using Eqs. (10), (11) and (24), and one obtains
correspond to the stresses in the individual phases. Subsequently, the strains of phase 1 and 2 are differentiated with respect to the interpolated strain using Eqs. (10), (11) and (24), and one obtains
where \(\delta _{ij}\) denotes the Kronecker symbol. Inserting Eqs. (35) and (36) into Eq. (34) yields

In case of the Voigt–Taylor approach,  and the derivatives of
and the derivatives of  vanish. For the partial rank-I relaxation,
vanish. For the partial rank-I relaxation,  depends on the strain state \(\varvec{\varepsilon }\), cf. Appendix B, which is why the chain rule is applied. The corresponding derivative
depends on the strain state \(\varvec{\varepsilon }\), cf. Appendix B, which is why the chain rule is applied. The corresponding derivative
is obtained by exploiting Eq. (24). Hence, the last summand in Eq. (37) vanishes, because Eq. (26) holds. This has been confirmed in combination with the local Newton–Raphson scheme B, which yielded deviations from zero in the order of \(10^{-20}{}\). Finally,

is obtained, which is equal to Eq. (22).
Appendix B: Local Newton–Raphson scheme for the strain jump
A local Newton–Raphson scheme is employed in order to determine the strain jump amplitude \(\varvec{a}\), for which

holds, cf. Equation (26). For this purpose, the local residual

of the ith local iteration is defined. Index notation is used for better readability of the tensor products. It is noted that the stresses of the individual phases comprise the degraded and persistent stress contributions. A first order Taylor series expansion of the local residual with respect to a variation of the strain jump amplitude yields

The incremental increase of the strain jump amplitude

can be obtained by rearrangement. The local tangent reads

The specific choice of the strain energy split influences the stress tangents \(\overset{i}{{\mathfrak {C}}}_{lmoh}\) of the individual phases. Hence, the scheme can be applied to any split, which fits in the present model.
For the consistent linearization in Appendix C, the derivative \(\partial a_o/\partial \varepsilon _{lm}\) is needed. It is obtained, by implicitly differentiating the converged local residual
with respect to the strain. Together with Eqs. (35) and (36) and some rearrangement,
is obtained, which finally gives
Appendix C: Weak form and consistent linearization
The weak form of the coupled differential Eqs. (18) and (19) reads
where \(\delta \varvec{\varepsilon }=\frac{1}{2}(\nabla \delta \varvec{u}+(\nabla \delta \varvec{u})^\top )=\nabla _\text {s}\delta \varvec{u}\), \(\delta \varvec{u}\) and \(\delta c\) denote the variations of the strain, the displacement and the phase-field. The total domain is subsequently divided into \(n_\text {el}\) finite elements for which, the primary field variables and corresponding variations are approximated by
with shape functions \(N^\alpha \), where \(\alpha \) is the global node number, and the corresponding nodal value \((\bullet )^\alpha \). The weak form (48) has to hold for arbitrary variations \(\delta \varvec{u}\) and \(\delta c\), which is why the residuals
of the ith iteration and \((n+1)\)th time step are defined. All variables with no time index refer to time step \(n+1\). A first order Taylor series expansion of the residuals with respect to a variation of the primary field variables gives


In order to determine the incremental increase of the displacement and the phase-field for the \((n+1)\)th time step, the system of equations
is solved for the global node number \(n_\text {nd}\) in every iteration i. It is noted that the global stiffness matrix is symmetric due to the variational structure of the problem. The four submatrices are given as
with the derivatives
and

Please refer to Eqs. (37), (38), (44) and (47) for the evaluation of the two above equations. For better readability of the tensor products, the index notation is used. It is noted that the evaluation of \(\partial ^2 a_o/\partial \varepsilon _{lm}\partial \varepsilon _{ij}\) is not necessary, because the stress jump condition is pointwise fulfilled for \(p\in (0,1)\).
Appendix D: Boundary condition and reference energy for convergence investigation
A circular disc according to Fig. 3 is considered. In a general setting, the inner and outer part have different elastic properties, i.e., \(E_1, \nu _1\) and \(E_2, \nu _2\), respectively. For the plane strain setting, auxiliary material parameters are defined as
The radial and tangential strain components are given as
The three integration constants read
The radial and tangential stress components are obtained from
for \(i=1\) if \(r\le r_1\), and \(i=2\) if \(r> r_1\). The strain energy within the simulated domain in Fig. 3 can be calculated analytically
for the square domain of unit thickness, and is used as reference for the convergence investigation of the total energy for the case without a crack. The stress components in Cartesian coordinates read
with the angle \(\varphi =\arctan (y/x)\) and radius \(r=\sqrt{x^2+y^2}\). The traction \(\bar{\varvec{t}}\) along \(\partial \varOmega _\text {top}\) and \(\partial \varOmega _\text {right}\) for the convergence investigation with and without a crack is obtained from
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hansen-Dörr, A.C., Brummund, J. & Kästner, M. Phase-field modeling of fracture in heterogeneous materials: jump conditions, convergence and crack propagation. Arch Appl Mech 91, 579–596 (2021). https://doi.org/10.1007/s00419-020-01759-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-020-01759-3