Abstract
Neural networks (NN) have been studied and used widely in the field of computational mechanics, especially to approximate material behavior. One of their disadvantages is the large amount of data needed for the training process. In this paper, a new approach to enhance NN training with physical knowledge using constraint optimization techniques is presented. Specific constraints for hyperelastic materials are introduced, which include energy conservation, normalization and material symmetries. We show, that the introduced enhancements lead to better learning behavior with respect to well known issues like a small number of training samples or noisy data. The NN is used as a material law within a finite element analysis and its convergence behavior is discussed with regard to the newly introduced training enhancements. The feasibility of NNs trained with physical constraints is shown for data based on real world experiments. We show, that the enhanced training outperforms state-of-the-art techniques with respect to stability and convergence behavior within FE simulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The quasi-static motion of an isothermal deformable solid can be described with a set of three basic equations: equilibrium of forces, definition of kinematics and constitutive relations. The former is deeply rooted in physical balance principles. The description of motion is at maximum a question of the desired accuracy. Constitutive or material laws on the other hand, as a link between the kinetic and kinematic quantities, are far more vague in their descriptions. Phenomenological material models - which are the only ones considered throughout this paper - are based on qualitative real world observations and quantitative experimental results. Usually, a mathematical model is defined based on physical principles the material has to fulfill, like elasticity, see e.g. [14]. The free model parameters are then fitted to experimental data. A good material model should have as few parameters as possible, which can be determined by experiment, but as many as necessary to represent arbitrary deformation behavior [37]. The idea to replace the process of model function definition and parameter identification with an artificial neural network (NN) started in the early 1990s, as [9] modeled the behavior of concrete in a plain stress state with an incremental approach, even considering cyclic loading. From this point on, a lot of progress has been made in the field of artificial neural networks, their use as material models and the field of computational mechanics itself. The following is a subjective selection of publications, without claim of completeness. In [23] an incrementally defined NN material model was implemented in a finite element code, while the corresponding material tangent was approximated by finite differences. An analytic tangent was later introduced in [13]. NN material models were for example applied to reinforced concrete [41], composites [24] or human bones [12]. The data from which the NN is trained can either come from real world experimental data or from numerical experiments using homogenization techniques. The latter applies to most publications currently available. Furthermore, NN material models are very well suited to be embedded in uncertainty modeling, as they can easily be parameterized and are fast to compute in comparison to e.g. numerical homogenization techniques. For example, in [7] a recurrent NN is used to model time dependent material behavior based on fuzzy data, whereas in [2, 3] stochastic data from random representative volume elements is used.
NN material models have some great advantages. They use the experimental data - from the real worls or numerical homogenization - directly, without the need of defining a specific function. Through analytic differentiation, the corresponding material tangent, which is needed in the framework of a Newton iteration scheme, can always be computed in the same way. It is therefore independent of the material one wants to approximate. Furthermore, as universal function approximators [6], it is theoretically possible to use them on any material, as long as it can be defined as a continuous function. On the other hand, there are some serious disadvantages. NN training usually requires a lot of data, which raises the question on how to generate or gather it feasibly. Even if trained well, they are referred to as black box functions. Their free parameters are large in number and cannot be physically interpreted afterwards. In addition, the NN function as a material model is not restricted to physical boundaries, like objectivity, material symmetries, growth conditions, energy conservation, etc. The advantage of no longer having to define a model is therefore countered by the disadvantage of no longer being able to take physical restrictions into account that are well known and have been used for decades. Considering prior knowledge is therefore a subject of research nearly as long as NN development itself. A subjectively good overview is given in [16]. In [1], they introduce ”hints”, which is a penalty approach by considering constraints as additional training patterns - virtually the application-free basis of this paper. The Lagrange multiplier method was investigated in [29], with sobering results. Other approaches use application-related NN architectures, like the promising deep material networks from [25]. Through reference configuration rotation, isotropy can be indirectly considered as additional training samples, see e.g. [35], whereas material objectivity can be considered by rotation of the current configuration, see e.g. [23, 44].
In this paper, the consideration of physical constraints in the NN training process with application to a hyperelastic NN material model is shown. Through the introduction of constraints, the above listed disadvantages of sample size, physical material properties, etc. are weakened down to a point, were the NN material concept is feasible to use. This includes comprehensive discussions of the numerical implementation, studies on NN and constraints’ settings and the application to the well known data for vulcanized rubber from [39]. The highlights can be summarized as follows:
-
Recap on how to generally enforce constraints in NN training based on constraint optimization techniques,
-
Definition and implementation of specific constraints for hyperelastic materials,
-
Investigations on the training behavior with respect to physical error measures, sample sizes and noisy data,
-
Investigations on the numerical behavior within finite element calculations,
-
Application to real world data to show the practicability of the used approach.
More precisely, the novelties of this paper are the introduction of constrained neural network training to material modeling and the definition of specific hyperelastic material constraints.
The paper is organized as follows. In Sect. 2, the NN training under general constraints is described. The hyperelastic material specific constraints are given in Sect. 3, as well as their impact on the training process with respect to representative error measures within a parameter study. Numerical implementation is shown in Sect. 4. In Sect. 5, the method is applied to experimental data [39].
2 NN training as a constrained optimization problem
A feedforward NN is a function
with the \(n_i\)- dimensional input vector \(\mathbf {x}\) and the \(n_o\)- dimensional output vector \(\mathbf {z}^{NN}\). The free parameters, called weights, are collected in the \(n_w\)- dimensional vector \(\mathbf {w}\). The NN used for all calculations in this paper is the multilayer perceptron (MLP) described in Appendix A.
2.1 Conventional NN training and notation
Given a set of P training samples
the goal of the training process is to determine a suitable set of free parameters \(\hat{\mathbf {w}}\), so that the NN provides a good approximation
of their input and output behavior. The NN should also generalize, thus providing a good approximation for points \(\mathbf {x}\) not included in the set of training samples. The sample points could be given e.g. by experiments, or arbitrarily generated in the sample space \(\varOmega \subset \mathbb {R}^{n_i}\). By defining an error function
considering deviation from the training data in a mean square sense, the determination of the weights \(\hat{\mathbf {w}}\) can be defined as the search for the solution of the following nonlinear optimization problem:
with the global minimum \(\mathbf {w}_{min}\) fulfilling the condition
There are lots of first and second order methods known for solving the optimization problem (5) in the literature. They all need at least the gradient of the error function with respect to the weights
which can be calculated by backpropagation [34, 45]. In practical application, one is often satisfied with a solution \(\hat{\mathbf {w}}>\mathbf {w}_{min}\), leading to a sufficient approximation, which depends on defined tolerances.
2.2 Conventional NN regularization
When training a NN there are lots of difficulties to face, which are direct consequences of the large number of free parameters and the nonlinearity of the error function. With regularization techniques it is in general possible to reduce overfitting and the influence of noisy data. In the following, two well known representatives are shown to emphasize the difference to the constraint training approach. It is only a short recap. More in depth discussions can be found in [10].
2.2.1 Early stopping using a test set
During NN training, one usually splits the set of given samples into a training subset and a test subset: \(T=T^{\text {trn}}\cup T^{\text {tst}}\) with sample sizes \(P^{\text {trn}}\) and \(P^{\text {tst}}\) respectively. The NN only sees the training set \(T^{\text {trn}}\), while the test set is used to check whether the NN is overfitting with respect to the training data or is globally approximating well. This behavior is principally depicted in Fig. 1. This is usually a problem for ill-posed problems, e.g. with an insufficient number of samples or spatially not well represented input spaces as in the example of Sect. 2.4. The method of early stopping breaks the training process at epoch \(t^{\text {min}}\) , if the test set error
is minimal. In practical application it is not always clear when to stop training. In contrast to the concept of constraint optimization, the early stopping method does not modify the training algorithm and does not add information to the training process.
2.2.2 L2-regularization
Adding the squared norm of the weights vector to the error function is called L2- or Tikhonov-regularization in NN training:
It pulls the solution of the optimization problem to smaller values for \(\mathbf {w}\), leading to smaller curvature and therefore preventing overfitting up to a point. The scalar factor \(\varepsilon ^{L2}\) controls the desired smoothness of the NN response surface. In practical application, the specification of this regularization factor is problem dependent and therefore no straight forward task. In contrast to the concept of constraint optimization, the Tikhonov regularization does not add information in an expert knowledge sense to the optimization process.
Similar to the L2-regularization, general constraint optimization can also work with an extension to the error function. The advantage will be the possibility to add expert knowledge to the training process, which can be used to enhance NN performance, while keeping or even improving the benefits of classical regularization. It should be noted, that the following methods are well known and have proven themselves in other applications. Therefore, the mathematical theory is shrunken to the needed minimum to follow the motivation behind this approach.
2.3 Considering constraints by error term extension
In general, the optimization problem (5) can be extended by \(n_{eq}\) equality and \(n_{ie}\) inequality constraints, leading to the following constraint optimization problem:
where ‘s.t.’ means ‘subjected to’. Its solution \(\mathbf {w}_{min}^{C}\) fulfills the condition
There are lots of methods in the literature related to constrained optimization for solving problems like (10), see e.g. [8, 19]. For differentiable error and constraint functions, a suitable one is an appropriate extension to the error function
leading to an unconstrained optimization problem
which has the same solution \(\mathbf {w}_{min}^{C}\) and is therefore equivalent to the constrained optimization problem defined in (10). The big advantage is the possibility to use the same optimization algorithms as for (5). Accordingly, the calculation of the corresponding gradient is needed:
2.3.1 Indirect enforcement with constraint samples
In NN training one has to distinguish between the network input variables \(\mathbf {x}\) and the function parameters, the weights \(\mathbf {w}\). While the approximation condition (3) is defined in terms of the network input and output variables, the optimization problem (5) is done with respect to the weights. Because of the non-linearity of the NN, the least squares condition cannot be transformed in an explicit solution for the function parameters - contrary to linear least squares approximations - and must therefore be solved numerically. The constraints behave mostly the same. The definition of the constraint functions \(h_i(\mathbf {w})\) and \(g_j(\mathbf {w})\) solely in terms of the weights \(\mathbf {w}\) is in general not possible, because the desired constraints may be defined in terms of the network output or even its derivatives. In contrast to the definition in (10), the constraint functions can take the following forms:
Similar to the training samples, they have to be enforced on a set of discrete sample points \(\mathbf {x}_k\in \varOmega ^C,k=1,...,P^C\), with \(P^C\) being the total number of constraint samples. These constraint sample points could be the original training sample points, but in general they are independent.
In the following, only equality constraints will be taken into account. The treatment of inequality constraints is possible but needs consideration of additional numerical methods which would make it difficult to focus on the papers essentials.
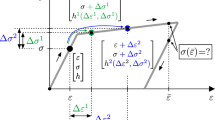
Penalty method (left) and exact penalty method (right) for optimization problem (18): unconstrained error function and extended error functions for various penalty parameters, including corresponding minima
2.3.2 The classical penalty method
The penalty method (PM) defines the error function extension for \(n_{eq}\) equality constraints with a mean squared error term. Therefore, the additional error term writes
with the corresponding gradient
The gradient of the constraint function \(\nabla h_i(\mathbf {x}_k)\) is problem dependent. The simplicity of its implementation is usually contrasted by the handling of the scalar penalty factor \(\varepsilon \), which controls the hardness of penalization. Mathematically, the constraints are only fulfilled exactly for \(\varepsilon \rightarrow \infty \), which is only approximately possible from a numerical point of view. This behavior is illustrated with the analytic optimization problem from [28]:
with the single exact solution \(w^C_{min}=1\). The minimum value
to the equivalent unconstrained penalty error function
is illustrated in Fig. 2. As can be seen graphically and analytically, only for \(\varepsilon \rightarrow \infty \) the exact solution is found. Consequently, there is always a trade-off between exactness and calculability. The problem gets worse if more constraints are involved and the solution is not only dependent on the absolute values but also on their ratios.
2.3.3 The exact penalty method
There are some methods known for imposing constraints mathematically exact without the need of a scalar factor going to infinity. The member which will be examined here is the type of so called exact penalty functions (EP). It can be shown, that they reach exactness in the constraints for a finite value of the penalty parameter. The L1-penalty function used here writes
with its corresponding gradient
The disadvantage of these functions is their gradient not being defined at \(h_i=0\). It will be approximated with help of the signum-function:
Still, the gradient at \(h_i=0\) is not continuous, which could cause numerical problems for the optimization process. Applied to the exemplary optimization problem (18), the unconstrained exact penalty error function writes
with the derivative approximation
As can be seen in Fig. 2, a penalty factor \(\varepsilon = 2\) is already large enough for leading to the exact solution.
2.3.4 Discussion of exactness for NN training
In NN training, one can distinguish between different kinds of errors regarding the NN approximation behavior with respect to the ideal or exact function. A brief and good discussion can be found in [36]. In the context of constrained NN training the ”representation error” is important to mention. It is the theoretical error obtained with optimal weights \(\mathbf {w}_{\text {min}}\) for the particular network topology chosen, having theoretically infinitely many training samples. If the topology is to restrictive, meaning not enough free parameters \(\mathbf {w}\) for the NN to reproduce the needed functional behavior, the NN can never reach a perfect approximation. Keeping this in mind, the expression ”exact” in terms of constrained training is only to be understood as an ”exact within the scope of possibilities” for the current topology.
2.4 The sinc function as an example
Before the method is applied to hyperelastic materials, with its own issues and solutions, the concepts’ advantages are shown on an illustrative example. Therefore, the two dimensional sinc function
which is shown in Fig. 3, will be approximated by the MLP from Appendix A. It consists of two hidden layers with ten neurons each, named [2-10-10-1], resulting in \(n_w=151\) free weights to be determined by the training process. For this example no input or output transformations are used. To make things difficult, sampling will only be done on the x- and y-axis, with 15 equidistantly distributed sample points per axis, leading to \(P=29\) training samples in total. They are depicted in Fig. 4. A Quasi Newton method with a Wolfe condition line search strategy [46, 47] is used to solve the minimization problems (5) and (13). We enforce the function’s radial symmetry by defining the single constraint
It is motivated by the dot product between the sinc functions’ gradient and the tangent vector to concentric circles around the origin, illustrated in Fig. 3. Using the classical penalty approach, the additional term to the error function is
with the corresponding gradient
The calculation of the gradient terms of network derivatives, \(\nabla z^{NN}_{,y}(\mathbf {x}_k,\mathbf {w})\) and \(\nabla z^{NN}_{,x}(\mathbf {x}_k,\mathbf {w})\), is done with a modified backpropagation method described in Appendix B. The training results after \(10\,000\) epochs are shown in Fig. 4, with and without constraints. Besides: the same initial weights are used in both cases. Using \(P^C=300\) randomly distributed constraint samples with \(\varepsilon =1\), the impact of enforcing the radial symmetry is clearly visible: it adds information as expert knowledge to the regions not sampled appropriately, preventing overfitting and leading to good approximation results. For comparison: the early stopping concept of Sect. 2.2.1 and the L2-regularization of Sect. 2.2.2 only reduce the amplitude of the chaotic response surface. In the following section, specific constraints for hyperelastic material modeling are introduced.
3 Material constraints for hyperelasticity
3.1 Hyperelastic material behavior
An isothermal material model is referred to as hyperelastic, if a scalar strain-energy density function \(\varPsi \) exists, whose partial derivative defines the constitutive model
with \(\mathbf {E}\) and \(\mathbf {S}\) beeing the Green-Lagrangian strain tensor and its work conjugate Second Piola-Kirchhoff stress tensor. Taking advantage of their symmetry, they can be written in vector notation:
In the following, no explicit distinction is made between the symbols of tensors and their vector notation. A hyperelastic material is by definition energy conserving, meaning the entire energy stored during deformation can be regained after unloading. Usually, there are four additional requirements for strain-energy density functions when dealing with large deformations:
with the volume ratio J being the determinant of the deformation gradient. For more detailed descriptions, see e.g. [14, 31]. In this paper, only the normalization condition (32) is addressed directly. At the \(\mathbf {E},\mathbf {S}\)-level, the conditions (33)–(35) are difficult to enforce, leaving it at this point up to future research. For numerical implementation in the context of an incremental Newton scheme, the material tangent
is needed, which is a forth order tensor. Matching the definitions of (31), its matrix notation is:
The existence of a strain-energy density function \(\varPsi (\mathbf {E})\) and the major symmetry of the material tangent, meaning
are equivalent [14]. This relation can be used to enforce hyperelastic material behavior. Four more notes on the choice of \(\mathbf {E}\) and \(\mathbf {S}\) as strain and stress measures: (a) all methods are applicable to anisotropic elastic materials without any limitation, (b) further transformations of the constraints due to the use of strain eigenvalues are not needed and therefore do not complicate their introduction, (c) they are defined solely with respect to the reference configuration, leading automatically to an objective constitutive equation, (d) the use of their vector form is based on their tensor symmetry. Therefore, one could interpret the restriction of the NN output being the six independent stress variables as a symmetry constraint, which is enforced exactly here.
3.2 Four constraints for hyperelastic materials
For material modeling the NN input vector is split into two parts:
with the six strain components in \(\mathbf {E}\) and \(n_a\) additional material parameters \(a_1,...,a_{n_a}\). The latter could be anything, from material parameters like Young’s modulus over volume proportions to testing humidity or temperature. The NN output vector will only contain the six stress components: \(\mathbf {z}^{NN}=\mathbf {S}^{NN}\). Usually, the input and output spaces are transformed to a normalized training space:
This accelerates convergence, see e.g. [22]. In the context of this paper, only linear and independent transformations are considered, meaning:
Common transformations seek for example unit variance of the input and output space or fixed boundaries between \(-1\) and 1. Therefore, not the physical but the transformed training sample error
is extended with properly transformed constraint terms:
Mind, that this error term \(\hat{E}^C(\mathbf {w})\) is optimized eventually and that we omit the hat for \(\bar{E}(\mathbf {w})\) for better readability. In the following, four material constraints are presented. The derivation follows always the same scheme: (1) definition of the physical restriction and (2) suitable transformation to the training space.
3.2.1 Zero stress constraint
The normalization condition (32) can be treated as a special set of additional training samples. With definition of the \(n_a\)-dimensional subset \(\varOmega _a\subset \varOmega \) regarding the parameters \(\mathbf {a}\), with \(\varOmega \) being the sample space defined in Sect. 2.1, one can generate a set
of \(P^{C0}\) artificial training samples. For simplicity, we define
The \(n_{eq}=n_{\text {strain}}=6\) equality constraints per constraint sample \(\mathbf {x}_k^0\) are
Keeping in mind the output vector transformation (42), the constraints transform to
with their gradients
Continuing in the transformed space, with the classical penalty approach the additional error term is
For the exact penalty approach, the additional error term in the transformed space is
The corresponding gradients are defined analogously to their introductions in Sects. 2.3.2 and 2.3.3.
3.2.2 Energy conservation constraint
As mentioned in Sect. 3.1 the existence of a strain-energy density function, and therefore the energy conserving material behavior, is equivalent to the material tangents major symmetry. This condition is fulfilled if all 15 off-diagonal pairs have zero difference: \(C_{ji}-C_{ij}=0\). Therefore, the \(n_{eq}=15\) equality constraints per constraint sample \(\mathbf {x}_k\) are
In this case, the sample space for the constraint is the entire training sample space: \(\mathbf {x}_k\in \varOmega , k=1,...,P^C\). The NN partial derivatives can be calculated with the forward loop described in Appendix B, Eqs. (97)–(102). The transformed version of constraint \(h_{ji}\) at sample \(\mathbf {x}_k\) is
with the gradient
The gradients of the NN partial derivatives \(\nabla (\partial \hat{z}_j/\hat{x}_i)\) and \(\nabla (\partial \hat{z}_i/\hat{x}_j)\) can be calculated with the modified backpropagation algorithm written in Appendix B.
It turns out, that a combination with the transformed training sample error (43) is not readily possible, since the latter is usually normalized in a unit range or variance kind of way. Keeping in mind common stress and strain magnitudes, of course depending on chosen units, the ratios \(s_z/s_x\) can take huge values, leading to unbalanced error term components. This implies poor convergence for the optimization process. Therefore, an additional normalization number
is introduced, which leads to satisfying results in numerical application. Continuing with the classical penalty approach the additional transformed error term is
For the exact penalty approach the formula writes
The corresponding gradients are defined analogously to their introductions in Sects. 2.3.2 and 2.3.3.
3.2.3 Material symmetry constraints for linear elasticity
The first two constraints are in any case mandatory for a hyperelastic material and should therefore always be considered. Material symmetries on the other hand can be used additionally if one has further information about the observed material, e.g. orthotropy or isotropy. For example, for the linear elastic isotropic case, the material tangent (37) takes the following form:
It has only three independent components left, which are dependent on two material constants, e.g. Young’s modulus E and Poisson’s ratio \(\nu \). It should be noted, that these kind of material symmetry conditions do not apply for the nonlinear elastic case. Furthermore, they can vary if the material is not described in its major axes. However, if linearity is assumed, the constraints can take two forms: setting a specific tangent component to zero,
or setting the difference of a specific component pair to zero:
which are already written in the transformed form. The number of equality constraint terms \(n_{eq}\) per constraint sample \(\mathbf {x}_k\) depends on the kind of material symmetry one wants to enforce in the NN training process. For the first form, the normalization number \(\alpha _{ji}^M\) is simply the ratio \(s_{zj}/s_{xi}\). The second one is defined similar to definition (55):
The respective gradients and penalty and exact penalty terms can be defined analogously to the tangent symmetry condition in Sect. 3.2.2.
3.2.4 Material isotropy constraint for nonlinear elasticity
The simple correlation between tangent components and material symmetry is not transferable to nonlinear elastic materials. Therefore, a more general approach with help of reference configuration rotations is presented. For visualization, see Fig. 5. Given a unit rotation vector \(\mathbf {n}\) and a rotation angle \(\theta \), one can define a rotation matrix with the well known Rodrigues’ formula
with the cross-product matrix form of \(\mathbf {n}\):

Subsequently, one can transform the strain and stress tensors from the coordinate system \(\mathbf {e}_i\) to the rotated one \(\mathbf {e}_i^{\text {*}}\):
By for example random generation of rotation matrices, one could now create artificial training samples to enrich the sample size, which has been done in e.g. [35]. This is surely not harmful to the training process, but restricted in the way information is added. We desire a material symmetry constraint, which adds information to all regions in the input domain, without the need of training samples in the first place. Assuming the existence of a strain-energy density function \(\varPsi ^{NN}(\mathbf {E})\), we demand zero tangential slope with respect to a rotation around the unit vector \(\mathbf {n}\):
with the matrix
Due to the symmetry of \(\mathbf {E}^\times \), one can define a vector form \(\mathbf {E}^{\times ,\text {v}}=\mathbf {n}^\text {v}\mathbf {E}\),with
Therefore, the vector form \(\mathbf {S}^{NN}\) can also be used, which simplifies numerical implementation. The single training constraint per constraint sample \(\mathbf {x}_k\) and rotation vector \(\mathbf {n}\) writes in the physical space
The transformed training space form is
with its gradient
Again, it is advisable to define an additional normalization number, for better numerical convergence behavior of the training process. With a similar approach as for the tangent symmetry constraint, we define
The corresponding error term extensions for one specific rotation vector \(\mathbf {n}\), using either the classical penalty approach or the exact one, are
and
The corresponding gradients are defined analogously to their introductions in Sects. 2.3.2 and 2.3.3. By defining the rotation vectors arbitrarily, isotropy is enforced. If the rotations are restricted to specific axes, one could enforce other forms of material symmetries.
3.3 Studies on constrained training performance
3.3.1 Description of study framework
In order to evaluate the effects of constrained NN training, the following strain-energy function for rubber-like solids
Influence of NN topology in terms of number of layers \(n_h\) and the number of weights \(n_w\) on the mean test error \(\bar{E}^{\text {tst}}\) and the mean skew symmetric tangent norm \(\bar{C}^{\text {skew}}\) taken from epoch \(t^\text {min}\). No constraints were activated. The number of training samples is constant with \(P^{\text {trn}}=10^5\). No noise is considered
Influence of constraint sample size \(P^C\) and the number of training samples \(P^{\text {trn}}\) on the mean test error \(\bar{E}^{\text {tst}}\) and the mean skew symmetric tangent norm \(\bar{C}^{\text {skew}}\) taken from epoch \(t^\text {min}\). Classical penalty method is used with \(\varepsilon =100\). The topology is constant [6-35-35-35-6]. No noise is considered
Influence of training sample size \(P^\text {trn}\) and the penalty factor \(\varepsilon \) on the mean test error \(\bar{E}^{\text {tst}}\) and the mean skew symmetric tangent norm \(\bar{C}^{\text {skew}}\) taken from epoch \(t^\text {min}\). Classical penalty method is used with \(P^\text {C}=1000\) constraint samples. The topology is constant [6-35-35-35-6]. No noise is considered. The dashed line is also for \(P^{\text {trn}}=1000\), but with 10 times more epochs of training
Influence of training sample size \(P^\text {trn}\) and the penalty factor \(\varepsilon \) on the mean test error \(\bar{E}^{\text {tst}}\) and the mean skew symmetric tangent norm \(\bar{C}^{\text {skew}}\) taken from epoch \(t^\text {min}\). Comparison between exact (EP) and classical penalty method (PM) with \(P^\text {C}=1000\) constraint samples. The topology is constant [6-35-35-35-6]. No noise is considered
Influence of constraint sample size \(P^C\) and the penalty factor \(\varepsilon \) on the mean test error \(\bar{E}^{\text {tst}}\) and the mean skew symmetric tangent norm \(\bar{C}^{\text {skew}}\) taken from epoch \(t^\text {min}\). Classical penalty method is used. The topology is constant [6-35-35-35-6]. \(P^\text {trn}=100\) training samples are used. No noise is considered
Influence of penalty factor \(\varepsilon \) and local noise in terms of the ratio \(s_\sigma \) between the local standard deviation and the noise-less stress components on the mean test error \(\bar{E}^{\text {tst}}\) and the mean skew symmetric tangent norm \(\bar{C}^{\text {skew}}\) taken from epoch \(t^\text {min}\). Classical penalty method is used. The topology is constant [6-35-35-35-6]. \(P^\text {trn}=100\) training samples and \(P^C=1000\) constraint samples are used
is used to generate artificial samples from an imaginary compressible material, with \(\lambda _i\) beeing the principal stretches, J the volume ratio, \(\varLambda \) Lamé’s first parameter and \(\mu _i\) and \(\alpha _i\) parameters related to the shear modulus. This form is taken from [30]. The material parameters are chosen academically as follows: \(n_r=2\), \(\mu _1=50\), \(\mu _2=-14\), \(\alpha _1=2\), \(\alpha _2=-2\), \(\varLambda =100\), motivated by [21]. Strain samples for training, testing and constraints are generated randomly and evenly distributed. Their components are restricted with \(E_{ii} \in [-0.3,1.5]\) and \(E_{ij}\in [-0.5,0.5]\) for \(i\ne j\), with the additional restriction \(J\in [0.75,1.5]\). This ensures physically reasonable stress values, sufficiently far away from the singularities of (74). The six study variables whose influences are under investigation are:
-
The number of training samples \(P^{\text {trn}}\),
-
The penalty parameter \(\varepsilon \),
-
The number of constraint samples \(P^C\),
-
The NN topology, defined by the number of weights \(n_w\) in \(n_h\) hidden layers and
-
The factor \(s_{\sigma }\) [%] for the local standard deviation \(\sigma _S=s_{\sigma }\cdot S_{ij}\) to simulate artificial noise.
The constraints of Sects. 3.2.1, 3.2.2 and 3.2.4 are applied to the training process. For the isotropy constraint 100 random rotation vectors are defined for each constraint sample. No bunch parameters \(\mathbf {a}\) are considered. Additionally to the test error \(E^{\text {tst}}\) from (8) taken at the early stopping epoch \(t^{\text {min}}\), the average Frobenius norm of the skew symmetric part of the material tangent, taken from the same epoch, is introduced as error measure:
Both error measures are evaluated at \(P^{\text {tst}}=1000\) equally distributed, randomly generated control samples. A Quasi Newton method with a Wolfe condition line search strategy [46, 47] is used to solve the minimization problems (5) and (13). The maximum number of epochs is 10 000. Due to the randomness of weight initialization and sampling, the error measures are averaged over \(n_{\text {av}}=10\) independent NN training processes, keeping the set of study variables constant:
The square root is taken to assure correct stress units. The evaluation of all error measures at the same training epoch \(t^{\text {min}}\) is due to the fact, that one would use the NN from this particular training state to get the best result.
3.3.2 Presentation and discussion
In the following, selected studies are shown, where some study variables are held constant, whereas two are varied. All error measures are plotted logarithmic. It will be seen, that the less data available and the more noise included, the greater is the effect of the constrained approach.
Topology in terms of depth and neurons, see Fig. 6
First of all, the range of possible NN topologies is investigated with a study depending on the number of layers \(n_h\) and the number of weights \(n_w\). The latter should be understood as a lower bound, because the number of neurons must be an integer. No constraints are activated and the number of training samples is large with \(P^{\text {trn}}=10^5\) in order to get an idea of the ”representation error” described in Sect. 2.3.4. The fact that ”deep networks with lots of weights” seems to be a good choice, gives an impression about the underlying nonlinearity of the material model in the \(\mathbf {E},\mathbf {S}\)-space.
Training and Constraint sample sizes, see Fig. 7
Next, the influence of the training and constraint sample sizes is under investigation. Both samples sets, \(P^{\text {trn}}\) and \(P^C\), show a convergence behavior with respect to their corresponding error terms, \(\bar{E}^{\text {tst}}\) and \(\bar{C}^{\text {skew}}\). The relative limits they approach depend on the relative magnitudes of the penalty factors, with \(\varepsilon ^{\text {trn}}=1\), and the spatial density of the respective samples. In the case of sparse training data, the positive effect of the constraints is greatest. However, if lots of data is available, the compromise in the minimization of data and constraint errors can lead to a higher test error \(\bar{E}^{\text {tst}}\), while still having advantages of the lower constraint error terms. In Sect. 5.2.2 this is discussed in terms of numerical stability.
Training sample size and penalty factor, see Fig. 8
Next, the influence of the penalty factor is under investigation with different amounts of training data available. One can observe that the higher the penalty factor, the better the constraint for symmetric tangent is fulfilled. This behavior is practically independent of the number of training samples and was to be expected by constraint optimization theory. The sample test error on the other hand shows a negative trend up from a specific penalty factor. This can also be expected by theory, but in addition can be very well due to the maximum number of epochs of \(10^4\). Therefore, the \(P^{trn}=1000\)-line is also shown for \(10^5\) epochs training time. This time, there is no strong test error increase for larger \(\varepsilon \). This indicates, that the classic disadvantage of the penalty approach, the choice of the penalty parameter for different error terms, is weakened for NN training. We believe this is due to the high dimension of the weight space and lots of equally valued local minima. However, training time increases.
Classical and exact penalty method, see Fig. 9
The same study as in Fig. 8 is done, but the classical penalty method (PM) is compared to the exact one (EP). There are several observations: the EP can in fact lead to better performance regarding the parameter \(\bar{C}^{\text {skew}}\), while keeping the \(\bar{E}^{\text {tst}}\) error low, as can bee seen in the range \(\varepsilon \in [10^{-4},10^{-2}]\), which is approximately the equivalent for the range \([10^{2},10^{4}]\) for the PM. On the other hand, up from \(\varepsilon =10^0\) the EP fails. This is because both constraints have a trivial solution: if all weights and therefore all stresses are constant zero. This leads to the conclusion, that it is possible to enforce constraints successfully with the exact penalty method but it is more sensitive to the penalty factor, which could lead to non reasonable results. Thus, we do not recommend this method at this point.
Constraint sample set and penalty factor, see Fig. 10
A convergence behavior of the constraint sample set can also be observed in Fig. 10. Additionally, one can see that this convergence behavior with respect to the constraints’ samples is independent of the penalty factor. This is convenient, because in practical terms the simple rule ”as many constraint samples as possible” holds.
Relative stress noise and penalty factor, see Fig. 11
Finally, the effect of noise on the training behavior is investigated. Therefore, every stress component \(S_{ij}\) will be multiplied with a noise term \(S_{ij}^{\text {noise}}=S_{ij}\cdot u\cdot s_{\sigma }\), with u being a standard normal distributed Gaussian random number and \(s_{\sigma }\) the weighting factor in \(\%\). The corresponding study is depicted in Fig. 11. In general, this kind of noise has only a weak effect on the test set error. This can be explained with the early stopping method, see Sect. 2.2.1: this regularization technique is already used in the scope of the parameter studies. What can be observed is, that if the penalty factor is chosen high enough, the noise has no effect at all on the training process, up to \(s_{\sigma }=32\%\), which approximately means a scattering range of the noise-free stress component itself.
3.4 Computational time with and without constraints
Due to the additional constraint terms in the error function and its gradient the computational time for the NN training is higher than the conventional one. This, of course, does not affect the computational time of the execution as a material model. For a brief overview it is convenient to compare the number of backward passes through the NN per sample. One single training sample needs one backward pass for the delta values of Eq. (94). The normalization constraint of Sect. 3.2.1 behaves similarly, as it can be considered as adding additional samples. The energy conservation constraint of Sect. 3.2.2 can be implemented efficiently in twelve backward passes per sample, which is the two variables \(\delta \) and \(\gamma \) from Eqs. (94) and (95) times the number of input strains. They can be defined not only in terms of one partial derivative, but for all output variables derivated after one single input variable. This is not shown in Appendix B but can be found in [4]. The isotropy constraint of Sect. 3.2.4 also needs only one backward pass per sample. This is independent of the number of rotation vectors, because the corresponding generalized delta values can be defined in terms of all vectors given, using the same idea as for the energy conservation constraint.
4 Implementation into a FE model
The implementation of the NN material into a FE model is briefly described in the following. The reader is referred to the wide range of literature for FE details, e.g. [17, 48]. Considering a three dimensional solid with volume V and arbitrary loading and boundary conditions, the principle of virtual work can be written in the following form:
We assume throughout this section only the vector forms of \(\mathbf {E}\) and \(\mathbf {S}\), as defined in (31). The virtual work of external loads \(\delta \pi _{ext}\) is assumed to be independent of the displacement field \(\mathbf {u}\) for the sake of simplicity. Displacement dependent loads, as used in the example of Sect. 5.2.1, would lead to additional contributions to the following linearization. In order to solve this nonlinear equation in a Newton iteration scheme the virtual work \(\delta \pi \) is linearized, leading to
being the linear equation to solve in each iteration step. In the context of the finite element method, the terms of residual \(\delta \pi \) and its linearization \(\varDelta \delta \pi \) are calculated on a subset \(V^e\subset V\), the volume of the finite element e, and then assembled later. They are discretized based on the element displacement field ansatz \(\mathbf {u}_e=\mathbf {N}\mathbf {v}_e\) with nodal displacements \(\mathbf {v}_e\), from which also the ansatz for the virtual and linearized strains follows respectively: \(\delta \mathbf {E}=\mathbf {B}\delta \mathbf {v}_e\) and \(\varDelta \mathbf {E}=\mathbf {B}\varDelta \mathbf {v}_e\). Without going too much into detail, both terms can be written on element level in the following way:
The element residual vector \(\mathbf {G}_e\) consists of the element load vector \(\mathbf {P}_e\) and the element vector of internal forces
The element tangential stiffness matrix \(\mathbf {K}_{Te}\) consists of a geometric part \(\mathbf {K}_{Ge}(\mathbf {S})\) depending on the current stress state and the material part
which follows from the linearization of the constitutive law
After assembling all quantities and assuming arbitrary but non-zero virtual displacements \(\delta \mathbf {v}\), this eventually leads to the system of linear equations
for the vector of unknown nodal displacement increments \(\varDelta \mathbf {v}\). The detailed definitions of \(\mathbf {N}\),\(\mathbf {B}\), etc., depend on the chosen element formulation. For more information about the shell and solid shell element used in the following examples, see e.g. [20, 42].
The by definition nonlinear NN material model can readily be implemented in the described finite element framework. The NN stresses \(\mathbf {S}^{NN}\) are part of the vector of internal forces \(\mathbf {F}_e^{NN}\) and the geometric tangential stiffness matrix \(\mathbf {K}_{Ge}^{NN}(\mathbf {S}^{NN})\). The NN material tangent \(\mathbf {C}^{NN}\) is part of the material tangential stiffness matrix \(\mathbf {K}_{Me}^{NN}\). It can be calculated with the forward loop described in Appendix A with Eqs. (97)–(101). This is independent of the material one wants to approximate. In the context of this paper, the NN and its derivative are added as a material model in an extended version of the general purpose finite element program FEAP [38].
5 Application to rubber-like material data
5.1 Training NN materials on Treloar’s data
5.1.1 Notes on training space and samples
In this section the feasibility of NN training with constraint optimization techniques applied to scarce data taken from Treloar [39] is shown. The data is directly taken from [37], who provided it in tabular form. The reader is referred to Appendix C for the full data set which is transformed from the given principal stretch and nominal stress pairs to the associated nearly incompressible \(\mathbf {E}\) and \(\mathbf {S}\) components. Particular attention should be paid to the described assumptions for the data transformation. Eventually, \(P=121\) sample pairs \(\{\mathbf {E},\mathbf {S}\}\) are available for the NN training process. In contrast to the studies in Sect. 3.3, the training samples are not evenly distributed in the whole training space, but given by the loading curves defined in the experimental setups. Thus, they form lower dimensional subspaces inside the whole six dimensional training space, leaving the space in between without information. This is the same problem as in the motivation example shown in Sect. 2.4. Furthermore, the majority of the space is physically not reasonable due to the material’s incompressibility. Due to the data transformation, the nearly incompressibility constraint is approximately \(J\in [0.95,1.45]\) in accordance to the training data from Appendix C. To summarize: the training space is highly non-convex and the noisy data is sparsely and not evenly distributed within it. As one can imagine, it is impossible to train a usable NN material model from this basis without proper regularization techniques.
5.1.2 Training different NN materials
In the following, three different training setups for corresponding NN materials are presented. Similar to the parameter study, a Quasi Newton method with a Wolfe condition line search strategy [46, 47] is used to solve the minimization problems (5) and (13). For reasons of comparability, all networks will have the same topology [6-60-60-60-6], with \(n_w=8\,106\) weights. This high number of weights is due to the highly non-convex training space in combination with the choice of \(\mathbf {S}\) and \(\mathbf {E}\), which can be expected from the behavior in Fig. 6. All samples created in the following, whether artificial training or constraint samples, meet the following restrictions regarding the strain space:
This matches the training data from Appendix C. The \(||\cdot ||\) denotes the vector norm, \(|\cdot |\) the absolute value. The training phase of the following three NN materials is terminated if the maximum number of \(10\,000\) epochs is reached. The NNs at epoch \(t^{\text {min}}\) are used for calculation. Therefore, 10% of the available samples are randomly taken as a test set within the early stopping strategy of Sect. 2.2.1.
As a state-of-the-art (SOTA) NN material, the first network NN\(_{\text {SOTA}}\) is trained without the introduced constraints. The training sample set is extended by rotating the given \(P=121\) samples randomly, see Eqs. (64), leading eventually to \(P=3000\) samples. They all meet the restrictions (86). At this point it should be mentioned, that even more artificial samples do not change the results of the following sections. In addition, L2-regularization from Sect. 2.2.2 is applied. The in our opinion best choice \(\varepsilon ^{L2}=0.001\) for this example was found by trial and error. The second NN material NN\(_{\text {CONS}}\) is trained with the three constraints of Sects. 3.2.1, 3.2.2 and 3.2.4. No additional training samples through reference configuration rotation are considered. They all share the same penalty factor \(\varepsilon = 1000\) within the classical penalty method. The tangent and material symmetry constraints share the same \(P^C=5000\) constraint samples, with 100 random rotation vectors for the latter. The samples are randomly generated in the strain space of \(\mathbf {E}\) with the restrictions (86). The third NN material NN\(_{\text {MIX}}\) is trained as a mix of both previous settings. The given \(P=121\) samples are artificially rotated, again, leading eventually to \(P=3000\) samples with restrictions (86). In addition, the three constraints are applied with \(\varepsilon = 10\) and \(P^C=5\,000\) within the classical penalty method. L2-regularization with \(\varepsilon ^{L2}=0.0001\) is applied, with the penalty factor being found by trial and error.
5.1.3 NN material performance on simple tests
The numerical solutions obtained from NN materials are compared to ones calculated with a reference Ogden material of the form (74), with the material parameters taken from [14], given in Table 1. Note that the Lamé parameter \(\varLambda =3.8\,MPa\) matches the nearly incompressible pseudo material from Appendix C with \(\nu _0=0.45\), which is under investigation here. The minimum requirement for a NN material trained from scarce data is to represent this particular data reliably. Therefore, we compare the three NN materials and the Ogden reference one with the original data in Fig. 12 for uniaxial and equibiaxial tension and compression as well as pure shear and simple shear, which for the data was transformed from the latter with \(J=1\). It should be noted, that the pure shear data was not directly transformed to the associated \(\mathbf {E}\),\(\mathbf {S}\) pairs and is not included in the training processes. If the data point is filled, the associated data was known to the NN from the training process. The calculations are done with one eight-node solid element by defining the boundary conditions and deformations as indicated by the deformation states in Fig. 12.
Discussion: without interpreting too much into the figures, one can state two conservative statements. First, the consideration of constrained optimization techniques does not affect the NN material’s ability to represent the given data reliably. This would be a strong argument against the method, if not true. And second, the pure shear behavior, which is not directly used as samples during training, can be approximated well with all three NNs, even with the NN\(_{\text {CONS}}\) to which not even rotated samples are known.
5.2 Numerical examples within FE simulations
Next, the NN materials are used within FE simulations for the inflation of a rubber balloon and the stretching of a thin sheet with a hole. Despite being simple in their descriptions, they both face some numerical subtleties like local stability points and global softening behavior. The NN results are again compared to the reference Ogden material. The balloon calculation is done with an eight node solid shell element with tri-linear shape functions, see e.g. [20]. It is extended with assumed natural strain and enhanced assumed strain (EAS) methods to improve the element behavior for example with respect to locking. The rubber sheet calculation is done with a quadrilateral shell element. The robust shell element formulation, which was originally published 2005 in [42], is based on Reissner-Mindlin theory and a three-field variational formulation. Later it was extended by independent thickness strains [21], which allow incorporation of arbitrary 3D constitutive equations, in our case the NN material model. The present version [11] is additionally capable of calculating the complicated three-dimensional stress state in layered structures, including elasto-plastic behavior. For the present calculation, two EAS parameters for membrane, bending and shear strains are used, respectively.
Rubber balloon: convergence behavior in terms of residual norm \(||\mathbf {G}||\) with respect to the Newton iteration step for the NN materials for load step six, see Fig. 14. Dashed lines are for calculations with the unsymmetric NN material tangent
5.2.1 Inflation of a rubber balloon
This classic example examines the inflation behavior of a spherical balloon under internal pressure and is discussed e.g. in [14]. With respect to the problem’s symmetry only one eighth of the balloon is considered with corresponding boundary conditions, see Fig. 13. The FE mesh consists of \(10\times 10\) solid shell elements, with one element in thickness direction. A regular FE mesh is obtained by the chosen discretization with a small hole at the top. The internal pressure load \(p_i\) is defined as a follower load at the inner surface to take into account the large increase of the inflated area with respect to the reference one. What makes the example interesting from an algorithmic point of view is the softening phenomenon, which can easily be seen in reality. A purely load controlled Newton’s method diverges at the limit point. Therefore, an arc length method with prescribed displacement of node 1 (see Fig. 13) is used. In addition, the example is numerically sensitive to stress disturbances. This challenges especially the NN material model. The inflation pressure \(p_i\) with respect to the circumferential stretch \(\lambda \) is shown in Fig. 14. The stretch can be calculated as ratio between inflated and initial radius. To highlight the effect of the \(C_T^{NN}\) symmetry constraint, we compare the convergence behavior of the Newton scheme for the NN materials near the limit point. The residual for the sixth load step is shown with respect to the iteration number in Fig. 15. In addition, the convergence behavior is shown for a formulation with a symmetrized tangent
which are the solid lines in Fig. 15. This is often used within FE formulations, saves time computing the element stiffness matrices, reduces required storage and allows the use of symmetric solvers.
Discussion: it turns out, that the inflating balloon example is very challenging for NN materials. Without constraints, we were not able to train a neural network purely with L2-regularization to overcome the limit point. The constraints do not guarantee a stable calculation for arbitrary stretches either, but they make it possible in the first place. More interesting is the Newton method convergence study, which is depicted in Fig. 15. It seems that the symmetrized tangent leads to a better convergence behavior, even for the state-of-the-art NN material. Furthermore, the NN materials trained with the energy conserving constraint of Sect. 3.2.2 converge considerably faster and one can barely distinguish the convergence behavior from that of the Ogden material. Moreover, since the behavior of NN materials trained with constraints hardly changes with the forced symmetrization, it can be assumed that their material tangents are already very symmetric from the start. On the other hand, the computation time for the material law at every Gauss integration point increases with the number of weights in the NN. However, this is independent of the constraints in the training phase.
5.2.2 Square sheet with a hole
In this numerical example, which was previously analyzed in e.g. [21, 32], a thin sheet of rubber with a central hole is subjected to a stretching load. With respect to the problem’s symmetry only one quarter of the sheet is considered with associated boundary conditions, which can be seen in Fig. 16. The FE mesh consists of \(16\times 16\) quadrilateral shell elements. The shell formulation is symmetric, thus needs the symmetrization (87) of the NN material tangent. The loading is done with a prescribed displacement \(u_x(L)=u\) at the right edge, leading to a corresponding reaction force 2F. Due to compression forces occurring perpendicular to the stretching direction, a stability problem can be observed at \((x,y)=(R,0)\). This leads to an out of plane buckling in z-direction. A constant perturbation load \(P=10^{-6}\,N\) is applied at the hole’s edge to follow the secondary equilibrium path which is characterized by a vertical displacement w normal to the plane, see Fig. 16. After the secondary path is entered, the load P is removed. It should be noted, that a switch to the secondary path at the bifurcation point is possible as well, see e.g. [43]. In Fig. 17 the load deflection curves with respect to the longitudinal displacement u and the vertical displacement w are shown for the different NN material models. The load at which the stability point occurs is of special interest. Therefore, in Fig. 18 this part of the load deflection curve is depicted in more detail.
Discussion: in this example it is interesting to note, that there is a relatively large variation of the bifurcation point at approximately \(F=1\,N\). Due to the compromise between data and constraint error minimization, this behavior can be expected. One should keep this behavior in mind when aiming for precise quantitative studies based on sparse data. However, talking again about the possibility of stable calculations it is apparent, that the NN materials with constraints allow a complete example calculation, while the state-of-the-art (SOTA) material fails at an earlier stage. Moreover, during the whole loading process, the load-deflection behavior is met very well and the variation is smaller compared to the bifurcation point. In our opinion the major message from both numerical examples is, that even with the original 121 samples alone, it is possible to train a numerically stable NN material and use it within complex finite element calculations. It should be noted, that a NN material trained only with the 121 samples and a L2-regularization is hardly able to run a single successful load step, which is because of the overfitting phenomenon described in Sect. 2.2.1.
6 Conclusions
In this paper, a new approach for considering physical knowledge for the training of NN material models is presented. After a short recapitulation of constraint optimization basics, the approach is motivated by an analytical example. Afterwards, specific constraints for hyperelastic materials are introduced and discussed in a comprehensive parameter study. Following a short overview of their implementation in a finite element scheme, the constrained training approach is applied to a pseudo material based on Treloar’s well known data of vulcanized rubber. The advantages of enhancing NN training with physically motivated constraints are highlighted and shown by numerical examples.
One of the major problems that has always accompanied the NN material topic is how to get the large amount of data that is needed to train a NN sufficiently. Despite challenging boundary conditions we showed that it is possible to train NN materials from scarce real world data and use them within complicated finite element computations. This represents an essential innovation compared to most publications, which have to generate a large amount of analytical or artificial data for their studies. The consideration of constraints during the NN training process is applicable on every NN architecture based on optimization strategies. It is not limited to elasticity or the explicit material formulation used here. It can be used on data based on real world or numerical experiments, e.g. from numerical homogenization. Whenever the amount of available data is limited, this approach seems to be an excellent way to add information to the training process. The only drawback is the data error being not weighted as much as without constraints. This is in our opinion no concern. We argue that one wants a NN material law which is computable in the first place and does not perfectly represent the given data.
As we have emphasized in Sect. 3.1, the choice for \(\mathbf {E}\) and \(\mathbf {S}\) as strain and stress measures and not, as usual for isotropic materials, the principal stretches and stresses was for the sake of introduction and the easy transfer to anisotropic materials. This, of course, makes NN training much more difficult due to the additional three input and output dimensions, which leads to far more degrees of freedom needed. Additionally, inelastic or anisotropic materials need other constraints, which can be formulated in the same way as the ones introduced here. Further developments may deal with some of this concerns. After all, we think the NN material approach is a promising way of generating a material model relatively quick, without the need of finding an analytical function.
References
Abu-Mostafa YS (1990) Learning from hints in neural networks. J Complex 6(2):192–198
Balokas G, Czichon S, Rolfes R (2018) Neural network assisted multiscale analysis for the elastic properties prediction of 3d braided composites under uncertainty. Compos Struct 183:550–562
Bessa M, Bostanabad R, Liu Z, Hu A, Apley DW, Brinson C, Chen W, Liu WK (2017) A framework for data-driven analysis of materials under uncertainty: countering the curse of dimensionality. Comput Methods Appl Mech Eng 320:633–667
Bishop C (1993) Curvature-driven smoothing: a learning algorithm for feedforward networks. IEEE Trans Neural Netw 4(5):882–884
Blatz PJ, Ko WL (1962) Application of finite elastic theory to the deformation of rubbery materials. Trans Soc Rheol 6(1):223–252
Cybenko G (1989) Approximation by superpositions of a sigmoidal function. Math Control Signals Syst 2(4):303–314
Freitag S, Graf W, Kaliske M (2013) A material description based on recurrent neural networks for fuzzy data and its application within the finite element method. Comput Struct 124:29–37
Geiger C, Kanzow C (2002) Theorie und Numerik restringierter Optimierungsaufgaben. Springer, Berlin Heidelberg
Ghaboussi J, Garrett JH, Wu X (1991) Knowledge-based modeling of material behavior with neural networks. J Eng Mech 117(1):132–153
Goodfellow I, Bengio Y, Courville A (2016) Deep learning. MIT Press, London
Gruttmann F, Wagner W (2020) An advanced shell model for the analysis of geometrical and material nonlinear shells. Comput Mech 66(6):1353–1376
Hambli R, Katerchi H, Benhamou CL (2010) Multiscale methodology for bone remodelling simulation using coupled finite element and neural network computation. Biomech Model Mechanobiol 10(1):133–145
Hashash YMA, Jung S, Ghaboussi J (2004) Numerical implementation of a neural network based material model in finite element analysis. Int J Numer Methods Eng 59(7):989–1005
Holzapfel GA (2000) Nonlinear solid mechanics. Wiley, New Jersey
Horgan CO, Murphy JG (2009) Simple shearing of incompressible and slightly compressible isotropic nonlinearly elastic materials. J Elast 98(2):205–221
Hu BG, Qu HB, Wang Y, Yang SH (2009) A generalized-constraint neural network model: associating partially known relationships for nonlinear regressions. Inf Sci 179(12):1929–1943
Ibrahimbegovic A (2010) Nonlinear solid mechanics. Springer, Netherlands
Jones DF, Treloar LRG (1975) The properties of rubber in pure homogeneous strain. J Phys D Appl Phys 8(11):1285–1304
Jorge Nocedal SW (2006) Numerical optimization. Springer, Berlin
Klinkel S, Gruttmann F, Wagner W (1999) A continuum based three-dimensional shell element for laminated structures. Comput Struct 71(1):43–62
Klinkel S, Gruttmann F, Wagner W (2008) A mixed shell formulation accounting for thickness strains and finite strain 3d material models. Int J Numer Methods Eng 74(6):945–970
LeCun YA, Bottou L, Orr GB, Müller KR (2012) Efficient BackProp. Springer, Berlin Heidelberg, pp 9–48
Lefik M, Schrefler B (2003) Artificial neural network as an incremental non-linear constitutive model for a finite element code. Comput Methods Appl Mech Eng 192(28–30):3265–3283
Lefik M, Boso D, Schrefler B (2009) Artificial neural networks in numerical modelling of composites. Comput Methods Appl Mech Eng 198(21–26):1785–1804
Liu Z, Wu C, Koishi M (2019) A deep material network for multiscale topology learning and accelerated nonlinear modeling of heterogeneous materials. Comput Methods Appl Mech Eng 345:1138–1168
MATLAB (2019) version 9.6.0 (R2019a). The MathWorks Inc., Natick, Massachusetts
Moreira D, Nunes L (2013) Comparison of simple and pure shear for an incompressible isotropic hyperelastic material under large deformation. Polym Test 32(2):240–248
Murray W, Wright MH, Gill PE (1982) Practical optimization. Academic Press Inc., London
Márquez-Neila P, Salzmann M, Fua P (2017) Imposing hard constraints on deep networks: promises and limitations
Ogden RW (1972) Large deformation isotropic elasticity: on the correlation of theory and experiment for compressible rubberlike solids. Proc R Soc Lond A Math Phys Sci 328(1575):567–583
Ogden RW (1997) Non-linear elastic deformations. Dover Publications, Mineola
Parisch H (1986) Efficient non-linear finite element shell formulation involving large strains. Eng Comput 3(2):121–128
Rivlin RS (1948) Large elastic deformations of isotropic materials IV. further developments of the general theory. Philos Trans R Soc Lond Seri A Math Phys Sci 241(835):379–397
Rumelhart DE, McClelland JL (1987) Learning internal representations by error propagation. MIT Press, London, pp 318–362
Shin H, Pande GN (2002) Enhancement of data for training neural network based constitutive models for geomaterials. CRC Press, London, pp 141–146
van der Smagt PP (1994) Minimisation methods for training feedforward neural networks. Neural Netw 7(1):1–11
Steinmann P, Hossain M, Possart G (2012) Hyperelastic models for rubber-like materials: consistent tangent operators and suitability for treloar’s data. Arch Appl Mech 82(9):1183–1217
Taylor RL (2021) FEAP - finite element analysis program. http://projects.ce.berkeley.edu/feap/
Treloar LRG (1944) Stress-strain data for vulcanized rubber under various types of deformation. Rubber Chem Technol 17(4):813–825
Treloar LRG (2005) Phys Rubber Elast. Oxford University Press, Oxford
Unger JF, Könke C (2009) Neural networks as material models within a multiscale approach. Comput Struct 87(19–20):1177–1186
Wagner W, Gruttmann F (2005) A robust non-linear mixed hybrid quadrilateral shell element. Int J Numer Methods Eng 64(5):635–666
Wagner W, Wriggers P (1988) A simple method for the calculation of postcritical branches. Eng Comput 5(2):103–109
Wang K, Sun W (2018) A multiscale multi-permeability poroplasticity model linked by recursive homogenizations and deep learning. Comput Methods Appl Mech Eng 334:337–380
Werbos PJ (1982) Applications of advances in nonlinear sensitivity analysis. In: Drenick RF, Kozin F (eds) System modeling and optimization. Springer, Berlin, pp 762–770
Wolfe P (1969) Convergence conditions for ascent methods. SIAM Rev 11(2):226–235
Wolfe P (1971) Convergence conditions for ascent methods. II: some corrections. SIAM Rev 13(2):185–188
Wriggers P (2010) Nonlinear finite element methods. Springer, Berlin Heidelberg
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Dedicated to Professor Walter Wunderlich on the occasion of his \(90^{\text {th}}\) birthday.
Appendices
A Multilayer perceptron topology and definitions
The class of feed forward NN used in this paper’s studies is a fully connected multilayer perceptron (MLP). Its topology and used terminologies are shown in Fig. 19. It consists of one input layer \(L=0\), several hidden layers \(L=1,...,n_h\) and an output layer \(L=n_h+1\). To avoid confusion regarding variables, the layer number is added in square brackets as superscript. A specific MLP topology is labeled with its neuron quantities summarized in square brackets: [\(n_{i}\) - \(n_1\) - ... - \(n_{n_h}\) - \(n_o\)]. Input and output transformations are considered as defined in Eqs. (41) and (42). Neurons are named after their output values \(y^{[L]}_m=g(s^{[L]}_m)\), with g(s) denoting the activation function depending on the weighted sum of the previous layer outputs
The activation threshold is defined with bias neurons giving the constant output \(y_0\equiv -1\). The weights are defined with the ’receiving’ neuron index as first subscript, in front of the index of the ’giving’ neuron. For easy formula reading: the layer indices are defined as l(eft), m(id), r(ight). With this definitions in mind, a complete forward calculation of the MLP mapping (1) takes the following steps.
-
1.
Input variable transformation: \(\mathbf {x}\mapsto \hat{\mathbf {x}}\).
-
2.
First hidden layer \(L=1\):
$$\begin{aligned} y_m^{[1]}=g\bigg (\sum \limits _{i=0}^{n_i}w_{mi}^{[1]}\cdot \hat{x}_i\bigg )~,~~ m=1,...,n_1. \end{aligned}$$(89) -
3.
Remaining sequential hidden layers \(L=1,...,n_h\):
$$\begin{aligned} y_m^{[L]}=g\bigg (\sum \limits _{l=0}^{n_{L-1}}w_{ml}^{[L]}\cdot y_{l}^{[L-1]}\bigg )~,~~ m=1,...,n_L. \end{aligned}$$(90) -
4.
Output layer \(L=n_h+1\):
$$\begin{aligned} y_j^{[n_h+1]}=g_{\text {out}}\bigg (\sum \limits _{l=0}^{n_{n_h}}w_{jl}^{[n_h+1]}\cdot y_{l}^{[n_h]}\bigg )=\hat{z}_j,~~ j=1,...,n_o. \end{aligned}$$(91) -
5.
Output variable back transformation: \(\hat{\mathbf {z}}\mapsto \mathbf {z}^{NN}\).
Within this paper the hyperbolic tangent is used as activation function g(s) for the hidden layers, whereas the identity function is applied at the output layer as \(g_{\text {out}}(s)\). Input and output transformations seek unit variance for each component. The training process for the described MLP, including all constraint related methods, are programmed in Matlab [26].
B Backpropagation for derivative components
The backpropagation algorithm shown here is a slight modification of the work of e.g. [4], where it is used for curvature smoothing. Considering the transformations (41) and (42), the partial derivatives transform as follows:
In the following, the partial derivative of this transformed input output derivative \(\partial \hat{z}_j/\partial \hat{x}_i\) with respect to an arbitrary weight \(w_{ml}^{[L]}\) is derived. It is part of the whole gradient \(\nabla (\partial z^{NN}_j\) / \(\partial x_i)\), which may be needed in constraint NN training. Its neuronal neighborhood is depicted in Fig. 20. Using the independence of \(\mathbf {w}\) and \(\mathbf {x}\) to change order of derivative and the chain rule combined with the definition of the weighted sum (88), the partial derivative can be transformed:
By defining the variables
and making use of the product rule, the partial derivatives can be calculated with the following formula:
The neuron outputs \(y_l^{[L-1]}\) depend on the current input vector \(\mathbf {x}\) and are calculated with the forward propagation (89)–(91) written in Appendix A. Simultaneously, the variables \(\partial y_{l}^{[L-1]}/\partial \hat{x}_i\) can be determined in the same forward pass by adding the following steps respectively.
-
2.
First hidden layer \(L=1\):
$$\begin{aligned}&\frac{\partial y_{m}^{[1]}}{\partial \hat{x}_i}=g'(s_m^{[1]})\bigg (\frac{\partial s_m^{[1]}}{\partial \hat{x}_i}\bigg ),\quad m=1,...,n_1~~, \end{aligned}$$(97)$$\begin{aligned}&\text {with}\quad \frac{\partial s_m^{[1]}}{\partial \hat{x}_i}=w_{mi}^{[1]}~~. \end{aligned}$$(98) -
3.
Remaining sequential hidden layers \(L=2,...,n_h\):
$$\begin{aligned}&\frac{\partial y_{m}^{[L]}}{\partial \hat{x}_i}=g'(s_m^{[L]})\bigg (\frac{\partial s_m^{[L]}}{\partial \hat{x}_i}\bigg )\quad m=1,...,n_L~~, \end{aligned}$$(99)$$\begin{aligned}&\text {with}\quad \frac{\partial s_m^{[L]}}{\partial \hat{x}_i}=\sum \limits _{l=1}^{n_{L-1}}w_{ml}^{[L]}\bigg (\frac{\partial y_{l}^{[L-1]}}{\partial \hat{x}_i}\bigg )~~. \end{aligned}$$(100) -
4.
Output layer \(L=n_h+1\):
$$\begin{aligned}&\frac{\partial y_{j}^{[n_h+1]}}{\partial \hat{x}_i}=g_{\text {out}}'(s_j^{[n_h+1]})\bigg (\frac{\partial s_j^{[n_h+1]}}{\partial \hat{x}_i}\bigg )=\frac{\partial \hat{z}_{j}}{\partial \hat{x}_i}~~,\nonumber \\&\quad ~~ j=1,...,n_o~~, \end{aligned}$$(101)$$\begin{aligned}&\text {with}\quad \frac{\partial s_j^{[n_h+1]}}{\partial \hat{x}_i}=\sum \limits _{l=1}^{n_{n_h}}w_{jl}^{[n_h+1]}\bigg (\frac{\partial y_{l}^{[n_h]}}{\partial \hat{x}_i}\bigg ). \end{aligned}$$(102)
In contrast, the variables \(\delta _{jm}^{[L]}\) and \(\gamma _{jim}^{[L]}\) must be determined with a backpropagation algorithm beginning at the output neurons. Starting with the \(\delta \)-values: the partial derivatives of the transformed network output with respect to the weighted sums will be rewritten with aid of the chain rule, considering the sum \(s_m^{[L]}\) influencing all weighted sums in the following Layer \(L+1\).
The involved neurons and weights are shown in Fig. 20. This transformation is the same as in the classical backpropagation of error algorithm. Finally, the recursive formula for the \(\delta \)-values is
with the initial values at the output neurons easily derivable from its definition (94):
The recursive formula for the \(\gamma \)-values can be derived in the same way, eventually leading to
where in addition to the \(\gamma \)- and \(\delta \)-values from the following layer \(L+1\) also the partial derivatives of the weighted sums with respect to the transformed input is needed, which are calculated in the forward pass, see Eqs. (98), (100) and (102). The initial values for the recursive process can be derived from the \(\gamma \)-value definition (95):
In summary, the procedure to calculate the gradient with respect to the weights of a partial derivative of a network output to one of its inputs \(\nabla \partial z_j/\partial x_i\) is as follows:
-
1.
Transformation of the current (constraint) node: \(\mathbf {x}\mapsto \hat{\mathbf {x}}\).
-
2.
Forward calculation for the neuron outputs \(y^{[L]}_m\) and the derivatives \(\partial y^{[L]}_m/\partial \hat{x}_i\) and \(\partial s^{[L]}_m/\partial \hat{x}_i\) with Eqs. (89)–(91) and (97)–(102).
-
3.
Backward calculation for variables \(\delta _{jm}^{[L]}\) and \(\gamma _{jim}^{[L]}\). Starting from (105) and (107), they can be calculated with (104) and (106).
-
4.
Every gradient component can be calculated with (96) and (92).
C Data for rubber-like materials from [39]
The data for the incompressible rubber material used within the numerical examples in Sect. 5 was first given by [39]. A documentation of this data in tabulated form for uniaxial and equibiaxial tension as well as pure shear in P and \(\lambda \) can be found in [37], with P being the nominal stress and \(\lambda \) the only independent stretch. All following transformations to the Second Piola-Kirchhoff stress tensor \(\mathbf {S}\) and the Green-Lagrangian strain tensor \(\mathbf {E}\) are based on their data. The incompressibility constraint \(\det {\mathbf {F}}=J=1\) leads to ambiguous stress states for a given strain state, e.g. different stresses for equivalent strains under uniaxial tension and biaxial compression, because information about the hydrostatic pressure is missing. Therefore, the authors assumed nearly incompressible material behavior for the data transformation. This is specified in the following sections regarding the different deformation modes. It should be noted, that especially this assumption leads to the NN material not representing the given material, but a pseudo compressible material, based on Treloar’s data. In our opinion, this is not an issue regarding the paper’s actual goal.
1.1 Uniaxial tension/compression (UT/UC)
For uniaxial tension, let \(\lambda _1^{\text {UT}} = \lambda ^{\text {UT}}\) be defined as the stretch in the elongated direction, leaving one unknown stretch since \(\lambda _2^{\text {UT}} = \lambda _3^{\text {UT}}\). Following an approach proposed by [5] for compressible rubber materials at finite strains, we assume that the dilatation J of the specimen can be expressed in terms of a constant parameter \(\nu \le 0.5\), which leads for \(\nu =0.5\) to incompressible material behavior. In case of linear elasticity, this parameter would correspond to the Poisson’s ratio \(\nu _0\). As suggested in [5] for uniaxial deformation, the dilatation is assumed to be
which, considering \(J = \lambda _1\lambda _2\lambda _3\), results in \(\lambda _2^{\text {UT}}=\lambda _3^{\text {UT}}=(\lambda ^{\text {UT}})^{-\nu }\). Under this assumption the deformation gradient for uniaxial tension \(\mathbf {F}^{\text {UT}}\) has the form
Hence, given the definition of the Green-Lagrangian strain tensor \(\mathbf {E} = 0{.}5(\mathbf {F}^T \mathbf {F} - \mathbf {1})\), its non-zero diagonal elements \(E_{11}^\text {UT}\) and \(E_{22}^\text {UT}=E_{33}^\text {UT}\) can readily be calculated. Furthermore, the relationship \(\mathbf {S} = \mathbf {F}^{-1} \mathbf {P}\), with \(\mathbf {P}\) beeing the First Piola-Kirchhoff stress tensor, leads to the following transformation of the only non-zero nominal stress component \(P_{11}^{\text {UT}}\) to the Second Piola-Kirchhoff stress:
The nonlinear stress response in the compression case can not be approximated appropriately with only tension data at hand. Therefore, the data from the equibiaxial tension (ET) specimen of the next section will be transformed into equivalent uniaxial compressive (UC) data, by firstly assuming \(\lambda _{2}^{\text {UC}} = \lambda _{3}^{\text {UC}} = \lambda ^{\text {ET}}\) at the same state of inner work. It should be mentioned, that due to the nearly incompressibility assumption, this transformation is only valid approximately. This results with assumption (108) for \(\lambda ^{\text {UC}}\) in
The strain components of \(\mathbf {E}^{\text {UC}}\) can be calculated afterwards. For the corresponding stresses, we assume equal incremental work in both cases for the non-zero stress components, see also [40]:
The equivalent nominal compressive stress can subsequently be expressed as
The transformed non-zero training data entries of \(\mathbf {E}\) and \(\mathbf {S}\) for the uniaxial tension and compression case and a value \(\nu = 0.45 \) are given in Table 2. We have restricted the data for UT/UC to \(\lambda ^{\text {UC/UT}} \in \left[ 0.84, 3.01\right] \).
1.2 Equibiaxial tension/compression (ET/EC)
In this test, the specimen is stretched in two orthogonal directions with corresponding stretches \(\lambda _1^{\text {ET}} = \lambda _2^{\text {ET}} = \lambda ^{\text {ET}}\). As suggested in [5] for equibiaxial tension, the dilatation is assumed to be
The remaining stretch is therefore \(\lambda _3^{\text {ET}} = (\lambda ^{\text {ET}})^{-2\nu /(1-\nu )}\). With the resulting deformation gradient for biaxial tension \(\mathbf {F}^{\text {ET}}\), the non-zero diagonal elements \(E_{11}^\text {ET}=E_{22}^\text {ET}\) and \(E_{33}^\text {ET}\) of the Green Lagrangian Strain tensor can be obtained. The two non-zero stresses are given by
Once again, the data can be further enhanced by transforming the UT data to equivalent equibiaxial compression (EC) data. Using a similar approach as in Eq. (112). Equation (114) for \(\lambda ^{\text {EC}}\) leads with the assumption \(\lambda _3^{\text {EC}}=\lambda ^{\text {UT}}\) to
Assuming incremental work equivalence leads to
All transformed non-zero entries of \(\mathbf {E}\) and \(\mathbf {S}\) for the equibiaxial tension and compression case and \(\nu = 0.45\) are given in Table 3, with the stretches beeing restricted to \(\lambda ^{\text {EC/ET}} \in \left[ 0.95, 2.49 \right] \).
1.3 Pure and simple shear (PS/SS)
At this point, we consciously accept an inconsistency: for the pure shear data, we must assume perfect incompressibility with \(J=1\). This contradicts our assumptions from the nearly incompressible uni- and equibiaxial samples, but allows the transformation to simple shear in the first place. In our eyes, this is not a serious issue for the sake of NN training, but should be noted at this point. Continuing, for the pure shear test, a thin sheet of rubber with its height being much larger than its width, is clamped along the edges normal to the direction of the applied tensile force. The associated stretch in the elongated direction is defined as \(\lambda _1 = \lambda ^{\text {PS}}\). For the incompressible case \(J=1\), the stretch in thickness direction is given by \(\lambda _3^{\text {PS}} = 1/\lambda ^{\text {PS}}\) and given the definition of pure shear \(\lambda _2^{\text {PS}} = 1\). This kind of experimental setup does not contain any information about the shear stress strain relationship, e.g. \(S_{\text {12}}\) and \(E_{\text {12}}\). This makes a transformation from pure to simple shear necessary. We follow the assumption made by Jones and Treloar [18] that ”simple shear differs from pure shear only by a rotation”. The deformation of simple shear is discussed for a specimen subjected to shear in the 1-2-Plane. The deformation gradient is given by
with \(\gamma \) being the amount of shear. The relationship between \(\gamma \) and the principal stretches \(\lambda \) can be obtained by solving the eigenvalue problem of the simple shear case
for the corresponding first principal stretch \(\lambda ^{\text {SS}}\). By following the assumption quoted above, which is \(\lambda ^{\text {SS}}=\lambda ^{\text {PS}}\), we eventually get
as a relation between the kinematic quantities of the desired simple shear and the given pure shear. For more information, see [31]. Hence, the deformation gradient for simple shear can be obtained by inserting Eq. (120) into Eq. (118). The non-zero elements \(E_{12}^\text {SS}\) and \(E_{22}^\text {SS}\) of the Green Lagrangian Strain tensor follow straightforwardly. For the transformation of the nominal pure stress \(P_{11}^{\text {PS}}\) of the experimental setup into equivalent simple shear components, Treloar [40] assumed that the only work done in simple shear is due to the Cauchy stress \(\sigma _{21}^{\text {SS}}=\sigma _{12}^{\text {SS}}\) on the amount of shear \(\gamma \), which leads to the equivalence of incremental work for both deformation cases:
With Eq. (120) follows eventually
To obtain the remaining non-zero entries of the Cauchy stress tensor \(\varvec{\sigma }\), a zero normal traction formulation is used, which assumes that the normal component of the traction on the inclined faces on a cube subjected to simple shear deformation as defined by Eq. (118) is zero [15, 33]. For simplicity, we assume that the pseudo data’s strain energy density function does not depend on the second Cauchy-Green strain invariant, leaving only one independent stress \(\sigma _{12}^{\text {SS}}\) which is obtained by Eq. (122). The remaining Cauchy stresses are then given by:
For more information, see e.g. [15]. Respectively, the Second-Piola Kirchhoff stress tensor for simple shear can be calculated by the relation \(\mathbf {S} = J\mathbf {F}^{-1} \varvec{\sigma }\mathbf {F}^{-T}\) with \(J=1\) since simple shear is characterized by an isochoric deformation.
It is known, that the assumptions made by Treloar and Jones concerning the equivalence of incremental work for pure and simple shear do not hold for large deformations, which is why the transformation of the data is only done for principal shear stretches up to \(\lambda ^{\text {PS}} \approx 1.3\) in accordance with the observations made by [27]. This leaves only four remaining sample points which can be enhanced by adding negative shear deformations which are given in Table 4, neglecting \(S_{11} \approx 0\). It should be noted, that the calculation of \(\sigma _{ii}^{\text {SS}}\) is based on the zero traction assumption, which is highly controversial. Therefore, the corresponding \(S_{ii}^{\text {SS}}\) values do not follow directly from Treloars experiments and thus are based on further assumptions.
1.4 Additional enhancements and editing related to the data
The data for uni- and equibiaxial tension and compression are tripled by exchanging the direction of the principal stretches. The data for simple shear can be rearranged six times, first by exchanging the plain of shear and second by exchanging the shear direction, e.g. 1-3 and 3-1 shear in the 1-3 plane. This leads eventually to \(P=121\) sample points, with one stress free sample, 33 for uniaxial tension and compression, 39 for equibiaxial tension and compression and 48 for simple shear. All samples lie approximately in the following boundaries regarding the volume ratio: \(J\in [0.95,1.45]\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Weber, P., Geiger, J. & Wagner, W. Constrained neural network training and its application to hyperelastic material modeling. Comput Mech 68, 1179–1204 (2021). https://doi.org/10.1007/s00466-021-02064-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-021-02064-8