Aorta zero-stress state modeling with T-spline discretization

Abstract

The image-based arterial geometries used in patient-specific arterial fluid–structure interaction (FSI) computations, such as aorta FSI computations, do not come from the zero-stress state (ZSS) of the artery. We propose a method for estimating the ZSS required in the computations. Our estimate is based on T-spline discretization of the arterial wall and is in the form of integration-point-based ZSS (IPBZSS). The method has two main components. (1) An iterative method, which starts with a calculated initial guess, is used for computing the IPBZSS such that when a given pressure load is applied, the image-based target shape is matched. (2) A method, which is based on the shell model of the artery, is used for calculating the initial guess. The T-spline discretization enables dealing with complex arterial geometries, such as an aorta model with branches, while retaining the desirable features of isogeometric discretization. With higher-order basis functions of the isogeometric discretization, we may be able to achieve a similar level of accuracy as with the linear basis functions, but using larger-size and much fewer elements. In addition, the higher-order basis functions allow representation of more complex shapes within an element. The IPBZSS is a convenient representation of the ZSS because with isogeometric discretization, especially with T-spline discretization, specifying conditions at integration points is more straightforward than imposing conditions on control points. Calculating the initial guess based on the shell model of the artery results in a more realistic initial guess. To show how the new ZSS estimation method performs, we first present 3D test computations with a Y-shaped tube. Then we show a 3D computation where the target geometry is coming from medical image of a human aorta, and we include the branches in our model.

Introduction

The patient-specific arterial fluid–structure interaction (FSI) computations reported in [1,2,3,4] were among the earliest of its kind. The core method in these computations was the early version of the Deforming-Spatial-Domain/Stabilized Space–Time (DSD/SST) method [5, 6], which is now called the “ST-SUPS.” The acronym “SUPS” indicates the stabilization components, the Streamline-Upwind/Petrov–Galerkin (SUPG) [7] and Pressure-Stabilizing/Petrov–Galerkin (PSPG) [5] stabilizations.

The ST computations have been only a small part of the large number of cardiovascular fluid mechanics and FSI computations seen in the last 15 years (see, for example, [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]), with the Arbitrary Lagrangian–Eulerian (ALE) method [30] having the largest share in the computations reported. Still, a large number of computations with the ST methods were also reported in the last 15 years. In the first 8 years of that period the ST computations were for FSI of abdominal aorta [31], carotid artery [31] and cerebral aneurysms [32,33,34,35,36,37,38]. In the last 7 years, the ST computations focused on even more challenging aspects of cardiovascular fluid mechanics and FSI, including comparative studies of cerebral aneurysms [39, 40], stent treatment of cerebral aneurysms [41,42,43,44,45], heart valve flow computation [46,47,48,49,50,51], aorta flow analysis [51,52,53,54], and coronary arterial dynamics [55]. The large number of computational challenges encountered were addressed by the advances in core methods for moving boundaries and interfaces (MBI) and FSI (see, for example, [20, 21, 40, 46, 47, 49, 50, 56,57,58,59,60,61,62,63,64] and references therein) and in special methods targeting cardiovascular MBI and FSI (see, for example, [20, 38, 44, 45, 48,49,50,51, 54, 65] and references therein).

A challenge very specific to patient-specific arterial FSI computations, such as patient-specific aorta FSI computations, is how to use the image-based arterial geometry. The image-based geometry does not come from the zero-stress state (ZSS) of the artery. Special methods targeting cardiovascular MBI and FSI include those designed to account for that. The attempt to find a ZSS for the artery in the FSI computation was first made in a 2007 conference paper [66], where the concept of estimated zero-pressure (EZP) arterial geometry was introduced. The method introduced in [66] for calculating an EZP geometry was also included in a 2008 journal paper on ST arterial FSI methods [32], as “a rudimentary technique” for addressing the issue. It was pointed out in [32, 66] that quite often the image-based geometries were used as arterial geometries corresponding to zero blood pressure, and that it would be more realistic to use the image-based geometry as the arterial geometry corresponding to the time-averaged value of the blood pressure. Given the arterial geometry at the time-averaged pressure value, an estimated arterial geometry corresponding to zero blood pressure needed to be built. Special methods developed to address the issue include the newer EZP versions [20, 34, 37, 38, 65] and the prestress technique introduced in [16], which was refined in[18] and presented also in [20, 65].

We introduced in [67] a method for estimation of the element-based ZSS (EBZSS) in the context of finite element discretization of the arterial wall. The method has three main components. (1) An iterative method, which starts with a calculated initial guess, is used for computing the EBZSS such that when a given pressure load is applied, the image-based target shape is matched. (2) A method for straight-tube segments is used for computing the EBZSS so that we match the given diameter and longitudinal stretch in the target configuration and the “opening angle.” (3) An element-based mapping between the artery and straight-tube is extracted from the mapping between the artery and straight-tube segments. This provides the mapping from the arterial configuration to the straight-tube configuration, and from the estimated EBZSS of the straight-tube configuration back to the arterial configuration, to be used as the initial guess for the iterative method that matches the image-based target shape. Test computations with the method were also presented in [67] for straight-tube configurations with single and three layers, and for a curved-tube configuration with single layer. The method was used also in [55] in coronary arterial dynamics computations with medical-image-based time-dependent anatomical models.

In [68], we introduced the version of the EBZSS estimation method with isogeometric wall discretization, using NURBS basis functions. With isogeometric discretization, we can obtain the element-based mapping directly, instead of extracting it from the mapping between the artery and straight-tube segments. That is because all we need for the element-based mapping, including the curvatures, can be obtained within an element. With NURBS basis functions, we may be able to achieve a similar level of accuracy as with the linear basis functions, but using larger-size and much fewer elements, and the NURBS basis functions allow representation of more complex shapes within an element. The 2D test computations with straight-tube configurations presented in [68] showed how the EBZSS estimation method with NURBS discretization works. In [69], which is an expanded, journal version of [68], we also showed how the method can be used in a 3D computation where the target geometry is coming from medical image of a human aorta.

In this article we are introducing a new method for estimating the ZSS. The estimate is based on T-spline discretization of the arterial wall and is in the form of integration-point-based ZSS (IPBZSS). The method has two main components. (1) An iterative method, which starts with a calculated initial guess, is used for computing the IPBZSS such that when a given pressure load is applied, the image-based target shape is matched. (2) A method, which is based on the shell model of the artery, is used for calculating the initial guess. The T-spline discretization enables dealing with complex arterial geometries, such as an aorta model with branches, while retaining the desirable features of isogeometric discretization. The IPBZSS is a convenient representation of the ZSS because with isogeometric discretization, especially with T-spline discretization, specifying conditions at integration points is more straightforward than imposing conditions on control points. Calculating the initial guess based on the shell model of the artery results in a more realistic initial guess. To show how the new method for estimating the ZSS performs, we first present 3D test computations with a Y-shaped tube. Then we show a 3D computation where the target geometry is coming from medical image of a human aorta, and we include the branches in our model.

In Sect. 2, we describe the Element-Based Total Lagrangian (EBTL) method, including the EBZSS and IPBZSS concepts. How the initial guess is calculated based on the shell model of the artery is described in Sect. 3. The numerical examples are given in Sect. 4, and the concluding remarks in Sect. 5.

EBTL method

In this section we provide an overview of the EBTL method [67], including the EBZSS concept, and describe the IPBZSS concept and the conversion between the two ZSS.

Let $\varOmega _0\subset \mathbb {R}^{n_{\mathrm {sd}}}$ be the material domain of a structure in the ZSS, where ${n_{\mathrm {sd}}}$ is the number of space dimensions, and let $\varGamma _0$ be its boundary. Let $\varOmega _t\subset \mathbb {R}^{n_{\mathrm {sd}}}$, $t \in (0,T)$, be the material domain of the structure in the deformed state, and let $\varGamma _{t}$ be its boundary. The structural mechanics equations based on the total Lagrangian formulation can be written as

$$\begin{aligned}&\int _{\varOmega _0} \mathbf {w}\cdot \rho _0\frac{\mathrm {d}^2 \mathbf {y}}{\mathrm {d}t^2}~\mathrm {d}\varOmega + \int _{\varOmega _0} \delta \mathbf {E}: \mathbf {S}~\mathrm {d}\varOmega - \int _{\varOmega _0} \mathbf {w}\cdot \rho _0\mathbf {f}~\mathrm {d}\varOmega \nonumber \\&\quad = \int _{\left( \varGamma _t\right) _\mathrm {h}} \mathbf {w}\cdot \mathbf {h}~\mathrm {d}\varGamma . \end{aligned}$$

(1)

Here, $\mathbf {y}$ is the displacement, $\mathbf {w}$ is the virtual displacement, $\delta \mathbf {E}$ is the variation of the Green–Lagrange strain tensor, $\mathbf {S}$ is the second Piola–Kirchhoff stress tensor, $\rho _0$ is the mass density in the ZSS, $\mathbf {f}$ is the body force per unit mass, and $\mathbf {h}$ is the external stress vector applied on the subset $\left( \varGamma _t\right) _\mathrm {h}$ of the boundary $\varGamma _{t}$.

EBZSS

In the EBTL method the ZSS is defined with a set of positions $\mathbf {X}_0^e$ for each element e. Positions of nodes from different elements mapping to the same node in the mesh do not have to be the same. In the reference state, $\mathbf {X}_\mathrm {REF}$, all elements are connected by nodes, and we measure the displacement $\mathbf {y}$ from that connected state. The implementation of the method is simple. The deformation gradient tensor $\mathbf {F}$ is evaluated for each element:

$$\begin{aligned} \mathbf {F}^e&\equiv \frac{\partial \mathbf {x}}{\partial \mathbf {X}_0^e}, \end{aligned}$$

(2)

$$\begin{aligned}&= \frac{\partial \left( \mathbf {X}_\mathrm {REF}+ \mathbf {y}\right) }{\partial \mathbf {X}_0^e}, \end{aligned}$$

(3)

where $\mathbf {x}$ is the position in the deformed configuration. The deformation gradient tensors for different elements are on different states, but the terms in Eq. (1), including the second term, do not depend on the orientation. Therefore the rest of the process is the same as it is in the total Lagrangian formulation.

IPBZSS

The key idea behind the EBZSS method was that, due to the objectivity, all the quantities seen in Eq. (1) can be computed with any orientation of the ZSS. We can extend the way we see $\mathbf {X}_0^e$ to integration-point counterpart of $\mathbf {X}_0^e$. As we did with the EBZSS, we work with the reference domain. With the reference Jacobian

$$\begin{aligned} J_\mathrm {REF}&= \det \left( \frac{\partial \mathbf {X}_\mathrm {REF}}{\partial \mathbf {X}_0}\right) , \end{aligned}$$

(4)

Eq. (1) can be rearranged as

$$\begin{aligned}&\int _{\varOmega _{\mathrm {REF}}} \mathbf {w}\cdot \rho _0\frac{\mathrm {d}^2 \mathbf {y}}{\mathrm {d}t^2}~J_\mathrm {REF}^{-1} \mathrm {d}\varOmega + \int _{\varOmega _{\mathrm {REF}}} \delta \mathbf {E}: \mathbf {S}~J_\mathrm {REF}^{-1} \mathrm {d}\varOmega \nonumber \\&\quad - \int _{\varOmega _{\mathrm {REF}}} \mathbf {w}\cdot \rho _0\mathbf {f}~J_\mathrm {REF}^{-1} \mathrm {d}\varOmega = \int _{\left( \varGamma _t\right) _\mathrm {h}} \mathbf {w}\cdot \mathbf {h}~\mathrm {d}\varGamma . \end{aligned}$$

(5)

In our implementation, we use the natural coordinates, with covariant basis vectors

$$\begin{aligned} \mathbf {g}_I&= \frac{\partial \mathbf {x}}{\partial \xi ^I}, \end{aligned}$$

(6)

$$\begin{aligned} \mathbf {G}_I&= \frac{\partial \mathbf {X}}{\partial \xi ^I}, \end{aligned}$$

(7)

where $\xi ^I$ is the parametric coordinate, and $I = 1, \ldots , {n_{\mathrm {pd}}}$, with ${n_{\mathrm {pd}}}$ being the number of parametric dimensions. The contravariant basis vectors can be calculated with the metric tensor components as

$$\begin{aligned} \mathbf {g}^I&= g^{IJ} \mathbf {g}_J , \end{aligned}$$

(8)

$$\begin{aligned} \mathbf {G}^I&= G^{IJ} \mathbf {G}_J , \end{aligned}$$

(9)

where

$$\begin{aligned} g_{IJ}&= \mathbf {g}_I \cdot \mathbf {g}_J, \end{aligned}$$

(10)

$$\begin{aligned} G_{IJ}&= \mathbf {G}_I \cdot \mathbf {G}_J, \end{aligned}$$

(11)

$$\begin{aligned} \left[ g^{IJ} \right]&= \left[ g_{IJ} \right] ^{-1} , \end{aligned}$$

(12)

$$\begin{aligned} \left[ G^{IJ}\right]&= \left[ G_{IJ} \right] ^{-1} . \end{aligned}$$

(13)

With those vectors, we can express the deformation gradient tensor:

$$\begin{aligned} \mathbf {F}&= \mathbf {g}_I \mathbf {G}^I , \end{aligned}$$

(14)

and the Cauchy–Green deformation tensor:

$$\begin{aligned} \mathbf {C}&=\mathbf {F}^T\cdot \mathbf {F}\end{aligned}$$

(15)

$$\begin{aligned}&= \mathbf {G}^I \mathbf {g}_I \cdot \mathbf {g}_J \mathbf {G}^J \end{aligned}$$

(16)

$$\begin{aligned}&= g_{IJ} \mathbf {G}^I \mathbf {G}^J . \end{aligned}$$

(17)

The Jacobian, $J= \det \mathbf {F}$, can be expressed as

$$\begin{aligned} J^2&= \det \mathbf {C}. \end{aligned}$$

(18)

We can write $\det \mathbf {C}$ as

$$\begin{aligned} \det \mathbf {C}&= \frac{\det \left[ g_{IJ}\right] }{\det \left[ G_{IJ}\right] }, \end{aligned}$$

(19)

and from that we obtain

$$\begin{aligned} J&= \left( \frac{\det \left[ g_{IJ}\right] }{\det \left[ G_{IJ}\right] } \right) ^{\frac{1}{2}}. \end{aligned}$$

(20)

We define the covariant basis vectors corresponding to $\mathbf {X}_\mathrm {REF}$:

$$\begin{aligned} \left( \mathbf {G}_\mathrm {REF}\right) _I&= \frac{\partial \mathbf {X}_\mathrm {REF}}{\partial \xi ^I}, \end{aligned}$$

(21)

and the components of the metric tensor are

$$\begin{aligned} \left( G_\mathrm {REF}\right) _{IJ} = \left( \mathbf {G}_\mathrm {REF}\right) _I \cdot \left( \mathbf {G}_\mathrm {REF}\right) _J. \end{aligned}$$

(22)

In Eq. (20), we replace $\mathbf {g}_I$ and $\mathbf {g}_J$ with $\left( \mathbf {G}_\mathrm {REF}\right) _I$ and $\left( \mathbf {G}_\mathrm {REF}\right) _J$ and obtain an alternative to the expression given by Eq. (4):

$$\begin{aligned} J_\mathrm {REF}&= \left( \frac{\det \left[ \left( G_\mathrm {REF}\right) _{IJ}\right] }{\det \left[ G_{IJ}\right] } \right) ^{\frac{1}{2}} . \end{aligned}$$

(23)

The Green–Lagrange strain tensor,

$$\begin{aligned} \mathbf {E}&= \frac{1}{2}\left( \mathbf {C}- \mathbf {I}\right) , \end{aligned}$$

(24)

where $\mathbf {I}$ is the identity tensor, can be expressed with the contravariant basis vectors as

$$\begin{aligned} \mathbf {E}&= \frac{1}{2}\left( g_{IJ} - G_{IJ} \right) \mathbf {G}^I \mathbf {G}^J. \end{aligned}$$

(25)

The second Piola–Kirchhoff tensor can be expressed with the covariant basis vectors as

$$\begin{aligned} \mathbf {S}&= S^{IJ} \mathbf {G}_I \mathbf {G}_J, \end{aligned}$$

(26)

where $S^{IJ}$ can be expressed with the components of the metric tensors. Thus, the inner product $\delta \mathbf {E}: \mathbf {S}$, and all the other quantities, in the weak form given by Eq. (5) can be evaluated without actually using the basis vectors $\mathbf {G}_I$. This justifies using $\left( G_{IJ}\right) _k$ as the integration-point counterpart of $\mathbf {X}_0^e$, with $k=1, \ldots , n_\mathrm {int}$, where $n_\mathrm {int}$ is the number of integration points. Note that $G_{IJ}$ is symmetric, and therefore the IPBZSS representation will in 3D have $6{\times }n_\mathrm {int}$ parameters for each element.

EBZSS to IPBZSS

Converting the EBZSS representation to IPBZSS representation is straightforward. From given $\mathbf {X}_0^e$ we can calculate the covariant basis vectors at each integration point $\pmb {\xi }_k$:

$$\begin{aligned} \left( \mathbf {G}_I\right) _k&= \left. \frac{\partial \mathbf {X}_0^e}{\partial \xi ^I}\right| _{\pmb {\xi }=\pmb {\xi }_k}, \end{aligned}$$

(27)

and obtain the components of the metric tensor from Eq. (11).

IPBZSS to EBZSS

Converting the IPBZSS representation to EBZSS representation, which we might need for visualization purposes, will, in general, not be exact because the IPBZSS has more parameters than the EBZSS. Given $\left( G_{IJ}\right) _k$, we solve a steady-state element-based problem (with $\mathbf {f}=\mathbf {0}$ and $\mathbf {h}= \mathbf {0}$):

$$\begin{aligned} \int _{\varOmega ^e_{\mathrm {REF}}} \delta \mathbf {E}: \mathbf {S}~J_\mathrm {REF}^{-1} \mathrm {d}\varOmega = 0, \end{aligned}$$

(28)

and the solution to that, in the form $\mathbf {X}_\mathrm {REF} + \mathbf {y}$, will be the EBZSS representation. If the stress calculated from the solution is zero, then the conversion will be exact. We note that to obtain a steady-state solution, we need to preclude translation and rigid-body rotation by imposing 6 appropriate constraints. To do that we first select three control points: A, B and C. We set all three components of $\mathbf {y}_A$ to be zero and constrain $\mathbf {y}_B$ to be in the direction $(\mathbf {X}_\mathrm {REF})_B - (\mathbf {X}_\mathrm {REF})_A$. The last constraint is $\mathbf {y}_C$ to be on the plane defined by the vector $\left( (\mathbf {X}_\mathrm {REF})_B - (\mathbf {X}_\mathrm {REF})_A\right) \times \left( (\mathbf {X}_\mathrm {REF})_C - (\mathbf {X}_\mathrm {REF})_A\right)$.

An iterative method

Here we assume that we have a reasonably good initial guess for the IPBZSS (see Sect. 3). The iterative method below is used in calculating the IPBZSS that results in the target state associated with the given load. In the iterative method, we estimate $\mathbf {F}$ from the ith solution. We simply assume

$$\begin{aligned} \mathbf {F}^{i+1}&= \mathbf {F}^{i}, \end{aligned}$$

(29)

which means

$$\begin{aligned} \left( \mathbf {F}^{i+1}\right) ^{-1}&= \left( \mathbf {F}^{i}\right) ^{-1}. \end{aligned}$$

(30)

The inverse of the deformation gradient tensor from the ith solution can be written as

$$\begin{aligned} \left( \mathbf {F}^{i} \right) ^{-1}&= \left( \mathbf {G}_I\right) ^{i} \left( \mathbf {g}^I\right) ^{i} . \end{aligned}$$

(31)

Similarly, the inverse of the target deformation gradient tensor is

$$\begin{aligned} \left( \mathbf {F}^{i+1} \right) ^{-1}&= \left( \mathbf {G}_I\right) ^{i+1} \left( \mathbf {G}_\mathrm {REF}\right) ^I . \end{aligned}$$

(32)

Thus, we obtain the following equation:

$$\begin{aligned} \left( \mathbf {G}_K\right) ^{i+1} \left( \mathbf {G}_\mathrm {REF}\right) ^K&= \left( \mathbf {G}_K\right) ^{i} \left( \mathbf {g}^K\right) ^{i} . \end{aligned}$$

(33)

Inner-producting both sides of this equation from the right with the covariant basis vectors corresponding to $\mathbf {X}_\mathrm {REF}$, we obtain

$$\begin{aligned} \left( \mathbf {G}_K\right) ^{i+1} \left( \mathbf {G}_\mathrm {REF}\right) ^K \cdot \left( \mathbf {G}_\mathrm {REF}\right) _I&= \left( \mathbf {G}_K\right) ^{i} \left( \mathbf {g}^K\right) ^{i} \cdot \left( \mathbf {G}_\mathrm {REF}\right) _I , \end{aligned}$$

(34)

which results in

$$\begin{aligned} \left( \mathbf {G}_I\right) ^{i+1}&= \left( \mathbf {G}_K \right) ^{i} \left( \mathbf {g}^K \right) ^{i} \cdot \left( \mathbf {G}_\mathrm {REF}\right) _I . \end{aligned}$$

(35)

The components of the metric tensor are

$$\begin{aligned} \left( G_{IJ}\right) ^{i+1}&= \left( \left( \mathbf {G}_K\right) ^{i} \left( \mathbf {g}^K\right) ^{i} \cdot \left( \mathbf {G}_\mathrm {REF}\right) _I \right) \nonumber \\&\quad \cdot \left( \left( \mathbf {G}_L\right) ^{i} \left( \mathbf {g}^L\right) ^{i} \cdot \left( \mathbf {G}_\mathrm {REF}\right) _J \right) . \end{aligned}$$

(36)

Rearranging the terms, we obtain

$$\begin{aligned} \left( G_{IJ}\right) ^{i+1}&= \left( G_{KL}\right) ^{i} \left( \left( \mathbf {g}^K\right) ^{i} \cdot \left( \mathbf {G}_\mathrm {REF}\right) _I \right) \nonumber \\&\quad \times \left( \left( \mathbf {g}^L\right) ^{i} \cdot \left( \mathbf {G}_\mathrm {REF}\right) _J \right) . \end{aligned}$$

(37)

Thus, we update the components of the metric tensor without actually knowing the basis vectors $\mathbf {G}_I$.

Once we obtain the IPBZSS at the end of the iterations, we will have the option to convert it to EBZSS and use that in the subsequent $\mathbf {y}$ computations.

Initial guess based on the shell model of the artery

An analytical relationship between the ZS and reference states of straight-tube segments was given in [67]. The relationship was called “straight-tube ZSS template” in [69] and was extended to curved tubes. These were for the EBZSS. Here we directly build the IPBZSS instead of building the EBZSS first. This is simpler because with isogeometric discretization, especially with T-spline discretization, specifying conditions at integration points is far more straightforward than imposing conditions on control points.

We start with the artery inner surface, which is what the medical images show. Typically, we cannot discern the wall thickness from the medical image. Therefore we first build the inner-surface mesh with T-splines. Then we build a T-spline volume mesh by extruding the surface elements by an estimated thickness.

In our notation here, $\mathbf {x}$ will now imply $\mathbf {X}_\mathrm {REF}$, which is our “target” shape, and $\mathbf {X}$ will imply $\mathbf {X}_0$. We explain the method in the context of one element in the thickness direction. Extending the method to multiple elements is straightforward.

Inner-surface coordinates in the target state

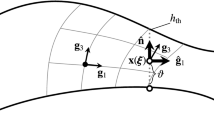
The coordinate system we have here is similar to the one used for the shell modeling in [70]. We note that the “midsurface” of the shell formulation has been shifted to the inner surface here, and $\overline{\bullet }$ indicates the inner surface. The basis vectors are

$$\begin{aligned} \overline{\mathbf {g}}_\alpha&= \frac{\partial \overline{\mathbf {x}}}{\partial \xi ^{\alpha }}, \end{aligned}$$

(38)

where $\alpha = 1, \ldots , {n_{\mathrm {sd}}}-1$, and the third direction is

$$\begin{aligned} \mathbf {n}&= \frac{ \overline{\mathbf {g}}_1 \times \overline{\mathbf {g}}_2 }{ \left\| \overline{\mathbf {g}}_1 \times \overline{\mathbf {g}}_2 \right\| } . \end{aligned}$$

(39)

The second fundamental form is defined as

$$\begin{aligned} \overline{b}_{\alpha \beta }&= \frac{\partial \overline{\mathbf {g}}_\alpha }{\partial \xi ^{\beta }} \cdot \mathbf {n}, \end{aligned}$$

(40)

and the curvature tensor is

$$\begin{aligned} \hat{\pmb {\kappa }}&= \underbrace{ - \overline{b}_{\alpha \beta } }_{\hat{\kappa }_{\alpha \beta }} \overline{\mathbf {g}}^{\alpha } \overline{\mathbf {g}}^{\beta } . \end{aligned}$$

(41)

Clearly, $\hat{\pmb {\kappa }}$ is symmetric.

For a given unit vector $\mathbf {t}$ on the surface, we obtain the curvature $\hat{\kappa }$ as

$$\begin{aligned} \hat{\kappa }&= \mathbf {t} \cdot \hat{\pmb {\kappa }}\cdot \mathbf {t} . \end{aligned}$$

(42)

If $\mathbf {t}$ is a principal direction,

$$\begin{aligned} \hat{\pmb {\kappa }}\cdot \mathbf {t}&= \hat{\kappa }\mathbf {t} , \end{aligned}$$

(43)

and $\hat{\kappa }$ is the corresponding principal curvature. The eigenvector can be expressed as

$$\begin{aligned} \mathbf {t}&= t^\beta \overline{\mathbf {g}}_{\beta }. \end{aligned}$$

(44)

Substituting this into Eq. (43) and inner-producting with $\overline{\mathbf {g}}^\alpha$, we obtain

$$\begin{aligned} \overline{g}_{\gamma \alpha } \left( \hat{\kappa }^\alpha _{\bullet \beta } - \hat{\kappa }\delta ^{\alpha }_{\beta } \right) t^{\beta }&=0, \end{aligned}$$

(45)

where the mixed components indicate

$$\begin{aligned} \hat{\pmb {\kappa }}&= \hat{\kappa }^\alpha _{\bullet \beta } \overline{\mathbf {g}}_\alpha \overline{\mathbf {g}}^\beta . \end{aligned}$$

(46)

Since the inverse of $\left[ \overline{g}_{\gamma \alpha }\right]$ exists,

$$\begin{aligned} \det \left[ \hat{\kappa }^\alpha _{\bullet \beta } - \hat{\kappa }\delta ^{\alpha }_{\beta } \right]&=0, \end{aligned}$$

(47)

$\hat{\kappa }$ is an eigenvalue of the matrix defined by the mixed components $\hat{\kappa }^\alpha _{\bullet \beta }$, and we will call the two eigenvalues $\hat{\kappa }_1$ and $\hat{\kappa }_2$. For $\hat{\kappa }_1 > \hat{\kappa }_2$ we obtain the corresponding eigenvectors:

$$\begin{aligned} \mathbf {t}_1&= \left( t_1\right) ^\beta \overline{\mathbf {g}}_\beta , \end{aligned}$$

(48)

$$\begin{aligned} \mathbf {t}_2&= \left( t_2\right) ^\beta \overline{\mathbf {g}}_\beta , \end{aligned}$$

(49)

where $\mathbf {t}_1$ and $\mathbf {t}_2$ are unit vectors. From Eq. (43), we write

$$\begin{aligned} \hat{\pmb {\kappa }}\cdot \mathbf {t}_1&= \hat{\kappa }_1\mathbf {t}_1 , \end{aligned}$$

(50)

$$\begin{aligned} \hat{\pmb {\kappa }}\cdot \mathbf {t}_2&= \hat{\kappa }_2 \mathbf {t}_2 . \end{aligned}$$

(51)

Since $\hat{\pmb {\kappa }}$ is symmetric,

$$\begin{aligned} \mathbf {t}_2 \cdot \hat{\pmb {\kappa }}\cdot \mathbf {t}_1&= \mathbf {t}_1 \cdot \hat{\pmb {\kappa }}\cdot \mathbf {t}_2 . \end{aligned}$$

(52)

Substituting Eqs. (50) and (51) into this, we obtain

$$\begin{aligned} \hat{\kappa }_1 \mathbf {t}_1 \cdot \mathbf {t}_2&= \hat{\kappa }_2 \mathbf {t}_1 \cdot \mathbf {t}_2. \end{aligned}$$

(53)

Thus, the two vectors are orthonormal, and we can express the curvature tensor as

$$\begin{aligned} \hat{\pmb {\kappa }}&= \hat{\kappa }_1 \mathbf {t}_1 \mathbf {t}_1 + \hat{\kappa }_2 \mathbf {t}_2 \mathbf {t}_2 . \end{aligned}$$

(54)

When $\hat{\kappa }_1 = \hat{\kappa }_2$, an arbitrary orthonormal set of $\mathbf {t}_1$ and $\mathbf {t}_2$ can be used in the above equation.

For more details on calculating the eigenvalues and eigenvectors, see Appendix A.

Inner-surface coordinates in the ZSS

Since the principal curvature directions $\mathbf {t}_1$ and $\mathbf {t}_2$ of the target shape are orthogonal to each other, we can build the ZSS shape using those directions. The basis vectors on the inner surface in the ZSS are

$$\begin{aligned} \overline{\mathbf {G}}_\alpha&= \frac{\partial \overline{\mathbf {X}}}{\partial \xi ^{\alpha }}, \end{aligned}$$

(55)

and the third direction is

$$\begin{aligned} \mathbf {N}&= \frac{ \overline{\mathbf {G}}_1 \times \overline{\mathbf {G}}_2 }{ \left\| \overline{\mathbf {G}}_1 \times \overline{\mathbf {G}}_2 \right\| } . \end{aligned}$$

(56)

The stretches corresponding to those directions will be $\hat{\lambda }_1$ and $\hat{\lambda }_2$. Then the ZSS basis vectors are calculated from

$$\begin{aligned} \hat{\lambda }_1 \mathbf {t}_1&= \mathbf {F} \cdot \mathbf {t}_1, \end{aligned}$$

(57)

$$\begin{aligned} \hat{\lambda }_2 \mathbf {t}_2&= \mathbf {F} \cdot \mathbf {t}_2. \end{aligned}$$

(58)

That is

$$\begin{aligned} \hat{\lambda }_1 \mathbf {F}^{-1} \cdot \mathbf {t}_1&= \mathbf {t}_1, \end{aligned}$$

(59)

$$\begin{aligned} \hat{\lambda }_2 \mathbf {F}^{-1} \cdot \mathbf {t}_2&= \mathbf {t}_2. \end{aligned}$$

(60)

Because the third direction is orthogonal to $\mathbf {t}_1$ and $\mathbf {t}_2$, we can reduce these equations to

$$\begin{aligned} \hat{\lambda }_1 \overline{\mathbf {G}}_\beta \overline{\mathbf {g}}^\beta \cdot \mathbf {t}_1&= \mathbf {t}_1, \end{aligned}$$

(61)

$$\begin{aligned} \hat{\lambda }_2 \overline{\mathbf {G}}_\beta \overline{\mathbf {g}}^\beta \cdot \mathbf {t}_2&= \mathbf {t}_2. \end{aligned}$$

(62)

Substituting Eqs. (48) and (49) into these, we get

$$\begin{aligned} \hat{\lambda }_1 \left( {t}_1\right) ^\alpha \overline{\mathbf {G}}_\alpha&= \left( {t}_1\right) ^\alpha \overline{\mathbf {g}}_\alpha , \end{aligned}$$

(63)

$$\begin{aligned} \hat{\lambda }_2 \left( {t}_2\right) ^\alpha \overline{\mathbf {G}}_\alpha&= \left( {t}_2\right) ^\alpha \overline{\mathbf {g}}_\alpha . \end{aligned}$$

(64)

This can also be written as

$$\begin{aligned} \begin{bmatrix} \hat{\lambda }_1&\quad 0 \\ 0&\quad \hat{\lambda }_2 \\ \end{bmatrix} \begin{bmatrix} \left( {t}_1\right) ^1&\quad \left( {t}_1\right) ^2 \\ \left( {t}_2\right) ^1&\quad \left( {t}_2\right) ^2 \\ \end{bmatrix} \begin{bmatrix} \overline{\mathbf {G}}_1 \\ \overline{\mathbf {G}}_2 \\ \end{bmatrix}&= \begin{bmatrix} \left( {t}_1\right) ^1&\quad \left( {t}_1\right) ^2 \\ \left( {t}_2\right) ^1&\quad \left( {t}_2\right) ^2 \\ \end{bmatrix} \begin{bmatrix} \overline{\mathbf {g}}_1 \\ \overline{\mathbf {g}}_2 \\ \end{bmatrix}, \end{aligned}$$

(65)

and from that we calculate the basis vectors as

$$\begin{aligned} \begin{bmatrix} \overline{\mathbf {G}}_1 \\ \overline{\mathbf {G}}_2 \\ \end{bmatrix}&= \begin{bmatrix} \left( {t}_1\right) ^1&\quad \left( {t}_1\right) ^2 \\ \left( {t}_2\right) ^1&\quad \left( {t}_2\right) ^2 \\ \end{bmatrix}^{-1} \begin{bmatrix} \frac{1}{\hat{\lambda }_1}&\quad 0 \\ 0&\quad \frac{1}{\hat{\lambda }_2} \\ \end{bmatrix} \begin{bmatrix} \left( {t}_1\right) ^1&\quad \left( {t}_1\right) ^2 \\ \left( {t}_2\right) ^1&\quad \left( {t}_2\right) ^2 \\ \end{bmatrix} \begin{bmatrix} \overline{\mathbf {g}}_1 \\ \overline{\mathbf {g}}_2 \\ \end{bmatrix}. \end{aligned}$$

(66)

Wall coordinates in the target state

The position in the target configuration is

$$\begin{aligned} \mathbf {x}&= \overline{\mathbf {x}} + \mathbf {n}\vartheta , \end{aligned}$$

(67)

where $0 \le \vartheta \le h_\mathrm {th}$, and $h_\mathrm {th}$ is the wall thickness in the target configuration. The basis vectors will vary along the thickness direction as

$$\begin{aligned} \mathbf {g}_\alpha&= \frac{\partial \mathbf {x}}{\partial \xi ^\alpha } \end{aligned}$$

(68)

$$\begin{aligned}&= \overline{\mathbf {g}}_\alpha + \frac{\partial \mathbf {n}}{\partial \xi ^\alpha } \vartheta \end{aligned}$$

(69)

$$\begin{aligned}&= \overline{\mathbf {g}}_\alpha - \overline{b}_{\alpha \gamma } \overline{\mathbf {g}}^\gamma \vartheta . \end{aligned}$$

(70)

The second and third lines are explained in Appendix 1. The third coordinate is mapped as

$$\begin{aligned} \vartheta&= \frac{1+\xi ^3}{2} h_\mathrm {th}, \end{aligned}$$

(71)

where $-1 \le \xi ^3 \le 1$. The basis vector in the third direction is constant as

$$\begin{aligned} \mathbf {g}_3&= \frac{ h_\mathrm {th}}{2} \mathbf {n}, \end{aligned}$$

(72)

and

$$\begin{aligned} \mathbf {g}^3&= \frac{2}{h_\mathrm {th}} \mathbf {n}. \end{aligned}$$

(73)

With that, the components of the metric tensor are

$$\begin{aligned} g_{\alpha \beta }&= \overline{g}_{\alpha \beta } - 2 \overline{b}_{\alpha \beta } \vartheta + \overline{b}_{\alpha \gamma } \overline{g}^{\gamma \delta } \overline{b}_{\beta \delta } \vartheta ^2, \end{aligned}$$

(74)

$$\begin{aligned} g_{3 \alpha }&= 0, \end{aligned}$$

(75)

$$\begin{aligned} g_{\alpha 3}&= 0, \end{aligned}$$

(76)

$$\begin{aligned} g_{33}&= \frac{h_\mathrm {th}^2}{4} . \end{aligned}$$

(77)

Wall coordinates in the ZSS

The position in the ZSS configuration is

$$\begin{aligned} \mathbf {X}&= \overline{\mathbf {X}} + \mathbf {N} \vartheta _0, \end{aligned}$$

(78)

where $0 \le \vartheta _0 \le \left( h_\mathrm {th}\right) _0$, and $\left( h_\mathrm {th}\right) _0$ is the wall thickness in the ZSS configuration. The basis vectors will vary along the thickness direction as

$$\begin{aligned} \mathbf {G}_\alpha&= \frac{\partial \mathbf {X}}{\partial \xi ^\alpha } \end{aligned}$$

(79)

$$\begin{aligned}&= \overline{\mathbf {G}}_\alpha + \frac{\partial \mathbf {N}}{\partial \xi ^\alpha } \vartheta _0 \end{aligned}$$

(80)

$$\begin{aligned}&= \overline{\mathbf {G}}_\alpha - \overline{B}_{\alpha \gamma } \overline{\mathbf {G}}^\gamma \vartheta _0 . \end{aligned}$$

(81)

The curvature tensor in the ZSS configuration is

$$\begin{aligned} \hat{\pmb {\kappa }}_0&= \left( \hat{\kappa }_0\right) _1 \mathbf {t}_1 \mathbf {t}_1 + \left( \hat{\kappa }_0\right) _2 \mathbf {t}_2 \mathbf {t}_2 . \end{aligned}$$

(82)

From that,

$$\begin{aligned} \overline{B}_{\alpha \beta }&= - \hat{\pmb {\kappa }}_0 : \overline{\mathbf {G}}_\alpha \overline{\mathbf {G}}_\beta \end{aligned}$$

(83)

$$\begin{aligned}&= - \left( \hat{\kappa }_0\right) _1 \left( \mathbf {t}_1 \cdot \overline{\mathbf {G}}_\alpha \right) \left( \mathbf {t}_1 \cdot \overline{\mathbf {G}}_\beta \right) \nonumber \\&\quad - \left( \hat{\kappa }_0\right) _2 \left( \mathbf {t}_2 \cdot \overline{\mathbf {G}}_\alpha \right) \left( \mathbf {t}_2 \cdot \overline{\mathbf {G}}_\beta \right) . \end{aligned}$$

(84)

Similar to what we had for $\mathbf {t}_1$ and $\mathbf {t}_2$,

$$\begin{aligned} \lambda _3 \mathbf {F}^{-1} \cdot \mathbf {n}&= \mathbf {n}, \end{aligned}$$

(85)

which becomes

$$\begin{aligned} \lambda _3 \mathbf {G}_3 \mathbf {g}^3 \cdot \mathbf {n}&= \mathbf {n}. \end{aligned}$$

(86)

We substitute Eq. (73) into this and obtain

$$\begin{aligned} \mathbf {G}_3 = \frac{h_\mathrm {th}}{2 \lambda _3} \mathbf {n}, \end{aligned}$$

(87)

and

$$\begin{aligned} \mathbf {G}^3 = \frac{2 \lambda _3}{h_\mathrm {th}} \mathbf {n}. \end{aligned}$$

(88)

Calculating the components of the ZSS metric tensor at each integration point

For an integration point $\pmb {\xi }$, we can obtain the components of the metric tensor as

$$\begin{aligned} G_{\alpha \beta }&= \overline{G}_{\alpha \beta } - 2 \overline{B}_{\alpha \beta } \vartheta _0 + \overline{B}_{\alpha \gamma } \overline{G}^{\gamma \delta } \overline{B}_{\beta \delta } \vartheta _0^2 , \end{aligned}$$

(89)

$$\begin{aligned} G_{3 \alpha }&= 0, \end{aligned}$$

(90)

$$\begin{aligned} G_{\alpha 3}&= 0, \end{aligned}$$

(91)

$$\begin{aligned} G_{33}&= \frac{h_\mathrm {th}^2}{4 \lambda _3^2} . \end{aligned}$$

(92)

The third coordinate can be obtained from

$$\begin{aligned} \vartheta _0&= \int _{-1}^{\xi ^3} \frac{h_\mathrm {th}}{2 \lambda _3} \mathrm {d}\xi ^3. \end{aligned}$$

(93)

Assuming incompressible material, $J=1$,

$$\begin{aligned} \lambda _3&= \frac{A_0}{A}, \end{aligned}$$

(94)

where

$$\begin{aligned} A^2&= \det \left[ g_{\alpha \beta }\right] , \end{aligned}$$

(95)

$$\begin{aligned} A^2_0&= \det \left[ G_{\alpha \beta }\right] . \end{aligned}$$

(96)

The components of the matrix tensors are given by Eqs. (74) and (89).

Design of the ZSS

The design parameters are the principal curvatures $\left( \hat{\kappa }_0\right) _1$ and $\left( \hat{\kappa }_0\right) _2$, and the stretches $\hat{\lambda }_1$ and $\hat{\lambda }_2$ for each principal curvature direction. Those parameters can be determined from $\hat{\kappa }_1$ and $\hat{\kappa }_2$ of the target configuration.

Fig. 1

Y-shaped tube. Target state. The end diameters are 20, 14 and 10 mm

Fig. 2

Y-shaped tube. Mesh made of cubic and quartic T-splines. Red circles represent the control points. The parts with the quartic T-splines, obtained by order elevation [72], are around the two extraordinary points, each connected to six edges. (Color figure online)

Fig. 3

Y-shaped tube. Wall thickness distribution

Fig. 4

Y-shaped tube. The IPBZSS initial guess, shown using the EBZSS representation

As proposed in [69], the two principal directions are seen as circumferential and longitudinal directions, and $\hat{\kappa }_1$ is in the circumferential direction, giving us

$$\begin{aligned} \left( \hat{\kappa }_0\right) _1 = \frac{2 \pi - \phi }{2 \pi } \hat{\kappa }_1. \end{aligned}$$

(97)

Here $\phi$ is the opening angle, which is seen after a longitudinal cut, based on artery experimental data [71]. The stretch in that direction, $\hat{\lambda }_1$, corresponds to $\lambda _\theta$ in [69] and that is determined from the 2D computations in [69]. We assume that in the longitudinal direction the ZSS configuration has zero curvature, $\left( \hat{\kappa }_0\right) _2 = 0$. The stretch in that direction, $\hat{\lambda }_2$, corresponds to $\lambda _z$ in [69]. If at an integration point $\hat{\kappa }_2 \approx \hat{\kappa }_1$, we set $\left( \hat{\kappa }_0\right) _2 = \left( \hat{\kappa }_0\right) _1$ and $\hat{\lambda }_2 = \hat{\lambda }_1$. That makes the assignment of the principal directions less consequential.

Fig. 5

Y-shaped tube. An element in the target state (top) and the corresponding IPBZSS initial guess, shown using the EBZSS representation (bottom)

Fig. 6

Y-shaped tube. Colored by $\Vert \mathbf {y}\Vert$ computed from the converged IPBZSS. (Color figure online)

Fig. 7

Y-shaped tube. The von Mises strain, from the IPBZSS initial guess (top) and from the converged IPBZSS (bottom)

Fig. 8

Y-shaped tube. The converged IPBZSS element corresponding to the element in Fig. 5, shown using the EBZSS representation

Numerical examples

In the numerical examples we use the Fung’s model [20, 38, 70] with $D_1 = 2.6447{\times }10^3~\mathrm {Pa}$, $D_2 = 8.365$, and the Poisson’s ratio $\nu = 0.45$. The energy-density function we use is in the form

$$\begin{aligned} \varphi _{\mathrm {FR}}\left( \mathbf {C}\right)&= D_1 \left( e^{D_2 \left( \mathrm {tr}J^{-\frac{2}{3}}\mathbf {C}- 3\right) } - 1\right) \nonumber \\&\quad + \frac{1}{2}\kappa \left( \frac{1}{2}\left( J^2-1\right) -\ln J\right) , \end{aligned}$$

(98)

where

$$\begin{aligned} \kappa&= \frac{4 D_1 D_2 \left( 1 + \nu \right) }{3 \left( 1 - 2 \nu \right) }. \end{aligned}$$

(99)

We assume the pressure associated with the target shape is 92 mm Hg.

Fig. 9

Y-shaped tube. Colored by $\Vert \mathbf {y}\Vert$ computed after converting the converged IPBZSS to EBZSS. (Color figure online)

Fig. 10

Y-shaped tube. The von Mises strain, obtained after converting the converged IPBZSS to EBZSS

The initial guess for the iterations is determined as described in Sect. 3, with $\phi = \frac{5}{2}\pi$ and $\hat{\lambda _2} = 1.05$. After the iterations, explained in Sect. 2.5, for comparison purposes, we convert the IPBZSS representation to EBZSS representation, with the method described in Sect. 2.4. With the EBZSS, we compute $\mathbf {y}$ again, and compare that to what we obtained directly from the IPBZSS.

Y-shaped tube

The target state of the Y-shaped tube is shown in Fig. 1. The end diameters of the tube are 20, 14 and 10 mm. Figure 2 shows the T-spline mesh. The mesh is based on a mixture of cubic and quartic T-splines. The wall thickness distribution is smooth, outcome of solving the Laplace’s equation over the inner surface, with Dirichlet boundary conditions at the tube ends, where the value specified is 0.1 times the end diameter. Figure 3 shows the thickness distribution. The volume mesh is built with one element (cubic Bézier element) in the thickness direction. The number of control points and elements are 5, 180 and 2, 592.

Since the IPBZSS cannot be visualized, we show it using the EBZSS representation. Figure 4 shows the initial guess for the IPBZSS. Figure 5 shows an element in the target state and the corresponding IPBZSS initial guess.

Fig. 11

Patient-specific aorta geometry. Target state, extracted from medical images

Fig. 12

Patient-specific aorta geometry. Mesh made of cubic and quartic T-splines. Red circles represent the control points. The parts with the quartic T-splines, obtained by order elevation [72], are around the eight extraordinary points. (Color figure online)

We iterate and obtain the converged IPBZSS. Figure 6 shows $\Vert \mathbf {y}\Vert$ computed from that. The maximum value of $\Vert \mathbf {y}\Vert$ is $1.279{\times }10^{-14}~\mathrm {mm}$. Figure 7 shows the von Mises strain, computed from the IPBZSS initial guess and from the converged IPBZSS. The converged IPBZSS element is shown in Fig. 8.

Remark 1

Figure 8 shows that the opening angle and the longitudinal stretch do not change much between the IPBZSS initial guess and the converted IPBZSS. However, the circumferential stretches are somewhat different. The initial guess for the circumferential stretch was based on the 2D computations reported in [69]. Alternatively, we can estimate the stretch by an analytical solution, similar to the one described in [70].

We also compute $\mathbf {y}$ after converting the converged IPBZSS to EBZSS. Figure 9 shows $\Vert \mathbf {y}\Vert$ computed that way. The maximum value of $\Vert \mathbf {y}\Vert$ is $1.626{\times }10^{-2}~\mathrm {mm}$. Figure 10 shows the von Mises strain. There is no visible difference between the strains obtained from the IPBZSS directly and after conversion to EBZSS.

Patient-specific aorta geometry

The target state of the patient-specific geometry is shown in Fig. 11. Figure 12 shows the T-spline mesh.

Fig. 13

Patient-specific aorta geometry. Wall thickness distribution

Fig. 14

Patient-specific aorta geometry. The IPBZSS initial guess, shown using the EBZSS representation

The wall thickness distribution is smooth, outcome of solving the Laplace’s equation over the inner surface, with Dirichlet boundary conditions at the tube ends, where the value specified is 0.08 times the end diameter. In some parts of the branched area the thickness exceeds the radius of curvature, and there we reduce the thickness to 0.8 times the radius of curvature. Figure 13 shows the thickness distribution.

The volume mesh is built again with one element (cubic Bézier element) in the thickness direction. The number of control points and elements are 9, 244 and 4, 360.

Figure 14 shows the initial guess for the IPBZSS. We again iterate and obtain the converged IPBZSS. Figure 15 shows $\Vert \mathbf {y}\Vert$ computed from that. The maximum value of $\Vert \mathbf {y}\Vert$ is $1.163{\times }10^{-13}~\mathrm {mm}$. Figure 16 shows the von Mises strain, computed from the IPBZSS initial guess and from the converged IPBZSS.

We again compute $\mathbf {y}$ after converting the converged IPBZSS to EBZSS. Figure 17 shows $\Vert \mathbf {y}\Vert$ computed that way. The maximum value of $\Vert \mathbf {y}\Vert$ is $1.057{\times }10^{-1}~\mathrm {mm}$. Figure 18 shows the von Mises strain. These results indicate that the EBZSS obtained by conversion from the IPBZSS is also a reasonable representation of the aorta ZSS.

Fig. 15

Patient-specific aorta geometry. Colored by $\Vert \mathbf {y}\Vert$ computed from the converged IPBZSS. (Color figure online)

Fig. 16

Patient-specific aorta geometry. The von Mises strain, from the IPBZSS initial guess (top) and from the converged IPBZSS (bottom)

Fig. 17

Patient-specific aorta geometry. Colored by $\Vert \mathbf {y}\Vert$ computed after converting the converged IPBZSS to EBZSS. (Color figure online)

Fig. 18

Patient-specific aorta geometry. The von Mises strain, obtained after converting the converged IPBZSS to EBZSS

Concluding remarks

We have introduced a new method for estimating the ZSS required in patient-specific arterial FSI computations, where the image-based arterial geometries do not come from the ZSS of the artery. The estimate is based on T-spline discretization of the arterial wall and is in the form of IPBZSS. The method has two main components. (1) An iterative method, which starts with a calculated initial guess, is used for computing the IPBZSS such that when a given pressure load is applied, the image-based target shape is matched. (2) A method, which is based on the shell model of the artery, is used for calculating the initial guess. The T-spline discretization enables dealing with complex arterial geometries, such as an aorta model with branches, while retaining the desirable features of isogeometric discretization. The desirable features of higher-order basis functions of isogeometric discretization include being able to achieve a similar level of accuracy as with the linear basis functions, but using larger-size and much fewer elements, and being able to represent more complex shapes within an element. The IPBZSS is a convenient representation of the ZSS because with isogeometric discretization, especially with T-spline discretization, specifying conditions at integration points is more straightforward than imposing conditions on control points. Calculating the initial guess based on the shell model of the artery results in a more realistic initial guess. To show how the new ZSS estimation method performs, we first presented 3D test computations with a Y-shaped tube. Then we presented a 3D computation where the target geometry was coming from medical image of a human aorta, and the model included the aorta branches.

Appendices

A Eigenvalues and eigenvectors of the curvature tensor

In calculating the eigenvalues from the quadratic equation

$$\begin{aligned} \hat{\kappa }^2 - \hat{\kappa }\mathrm {tr}\left[ \hat{\kappa }^\alpha _{\bullet \beta } \right] + \det \left[ \hat{\kappa }^\alpha _{\bullet \beta } \right] =0, \end{aligned}$$

(100)

we obtain

$$\begin{aligned} \hat{\kappa }&= \frac{ \mathrm {tr}\left[ \hat{\kappa }^\alpha _{\bullet \beta } \right] \pm \sqrt{ \mathrm {tr}^2 \left[ \hat{\kappa }^\alpha _{\bullet \beta } \right] -4 \det \left[ \hat{\kappa }^\alpha _{\bullet \beta } \right] } }{2}. \end{aligned}$$

(101)

This can also be written as

$$\begin{aligned} \hat{\kappa }_{l}&= \frac{ \mathrm {tr}\left[ \hat{\kappa }^\alpha _{\bullet \beta } \right] -(-1)^l \sqrt{ \mathrm {tr}^2 \left[ \hat{\kappa }^\alpha _{\bullet \beta } \right] -4 \det \left[ \hat{\kappa }^\alpha _{\bullet \beta } \right] } }{2}, \end{aligned}$$

(102)

with $l=1, 2$. In calculating the eigenvectors, we work with $\left( v_1\right) ^\alpha$ and $\left( v_2\right) ^\alpha$, the contravariant components of the non-normalized eigenvectors. The vectors are normalized with the scaling factors $\tau _1$ and $\tau _2$:

$$\begin{aligned} \left( t_l\right) ^\alpha&= \tau _l \left( v_l\right) ^\alpha . \end{aligned}$$

(103)

With that, we obtain the relationship

$$\begin{aligned} \left( \tau _l\right) ^2 \left( v_l\right) ^\alpha g_{\alpha \beta } \left( v_l\right) ^\beta&=1, \end{aligned}$$

(104)

which yields

$$\begin{aligned} \tau _l&= \left( \left( v_l\right) ^\alpha g_{\alpha \beta } \left( v_l\right) ^\beta \right) ^{-\frac{1}{2}} . \end{aligned}$$

(105)

Given $(v_1)^\alpha$, which we will explain later how to calculate, from Eqs. (103) and (105) we obtain

$$\begin{aligned} \left( t_1\right) ^{\alpha }&= \left( \left( v_1\right) ^\gamma g_{\gamma \delta } \left( v_1\right) ^\delta \right) ^{-\frac{1}{2}} \left( v_1\right) ^\alpha . \end{aligned}$$

(106)

We calculate $\mathbf {t}_2$ from the orthogonality between $\mathbf {t}_1$ and $\mathbf {t}_2$:

$$\begin{aligned} \mathbf {t}_1 \cdot \mathbf {t}_2 = 0. \end{aligned}$$

(107)

With the substitutions $\mathbf {t}_1 = \left( {t}_1\right) ^\alpha \overline{\mathbf {g}}_\alpha$ and $\mathbf {t}_2 = \left( {t}_2\right) _\beta \overline{\mathbf {g}}^\beta$, we obtain

$$\begin{aligned} \left( {t}_1\right) ^\alpha \left( {t}_2\right) _\alpha = 0. \end{aligned}$$

(108)

The expression

$$\begin{aligned} \left( v_2\right) _{\alpha }&= R_{\alpha \beta } \left( t_1\right) ^\beta , \end{aligned}$$

(109)

where

$$\begin{aligned} \left[ R_{\alpha \beta } \right]&= \begin{bmatrix} 0&1 \\ -1&0 \\ \end{bmatrix}, \end{aligned}$$

(110)

satisfies Eq. (108). To calculate $\tau _2$, we start from the covariant version of (105):

$$\begin{aligned} \tau _2&= \left( \left( v_2\right) _\alpha g^{\alpha \beta } \left( v_2\right) _\beta \right) ^{-\frac{1}{2}} . \end{aligned}$$

(111)

Substituting Eq. (109) into Eq. (111), we obtain

$$\begin{aligned} \left( \tau _2\right) ^{-2}&= R_{\alpha \gamma } \left( t_1\right) ^\gamma g^{\alpha \beta } R_{\beta \delta } \left( t_1\right) ^\delta . \end{aligned}$$

(112)

By expanding the matrices and rearranging, we obtain the relationship

$$\begin{aligned} R_{\alpha \gamma } g^{\alpha \beta } R_{\beta \delta }&= \det [g^{\gamma \delta }] \left[ g^{\gamma \delta } \right] ^{-1} \end{aligned}$$

(113)

$$\begin{aligned}&= {\det }^{-1}[g_{\gamma \delta }] g_{\gamma \delta }. \end{aligned}$$

(114)

Combining Eqs. (112) and (114), we obtain

$$\begin{aligned} \left( \tau _2\right) ^{-2}&= {\det }^{-1}[g_{\gamma \delta }] \underbrace{ g_{\gamma \delta } \left( t_1\right) ^\gamma \left( t_1\right) ^\delta }_{=1} , \end{aligned}$$

(115)

and then

$$\begin{aligned} \tau _2&= {\det }^{\frac{1}{2}}[g_{\gamma \delta }]. \end{aligned}$$

(116)

Using Eqs. (109) and (116) in the expression

$$\begin{aligned} \left( t_2\right) _\alpha&= \tau _2 \left( v_2\right) _\alpha , \end{aligned}$$

(117)

we obtain

$$\begin{aligned} \left( t_2\right) _{\alpha }&= {\det }^{\frac{1}{2}}\left[ g_{\gamma \delta }\right] R_{\alpha \beta } \left( t_1\right) ^\beta . \end{aligned}$$

(118)

Now we explain how to calculate $\left( v_1\right) ^{\alpha }$. From Eqs. (43) and (100), we write the equations that $\left( v_1\right) ^\alpha$ and $\hat{\kappa }_1$ satisfy:

$$\begin{aligned}&\left( \hat{\kappa }^1_{\bullet 1} - \hat{\kappa }_1\right) \left( v_1\right) ^1 + \hat{\kappa }^1_{\bullet 2} \left( v_1\right) ^2 = 0, \end{aligned}$$

(119)

$$\begin{aligned}&\hat{\kappa }^2_{\bullet 1} \left( v_1\right) ^1 + \left( \hat{\kappa }^2_{\bullet 2} - \hat{\kappa }_1\right) \left( v_1\right) ^2 = 0, \end{aligned}$$

(120)

$$\begin{aligned}&\left( \hat{\kappa }^1_{\bullet 1} - \hat{\kappa }_1 \right) \left( \hat{\kappa }^2_{\bullet 2} - \hat{\kappa }_1 \right) - \hat{\kappa }^2_{\bullet 1} \hat{\kappa }^1_{\bullet 2} =0. \end{aligned}$$

(121)

If $\hat{\kappa }^1_{\bullet 2}$ or $\hat{\kappa }_1 - \hat{\kappa }^1_{\bullet 1}$ is nonzero, we can write, from Eq. (119),

$$\begin{aligned} \left[ \left( v_1\right) ^\alpha \right]&= \begin{bmatrix} \hat{\kappa }^1_{\bullet 2} \\ \hat{\kappa }_1 - \hat{\kappa }^1_{\bullet 1} \\ \end{bmatrix}. \end{aligned}$$

(122)

If $\hat{\kappa }_1 - \hat{\kappa }^2_{\bullet 2}$ or $\hat{\kappa }^2_{\bullet 1}$ is nonzero, we can write, from Eq. (120),

$$\begin{aligned} \left[ \left( v_1\right) ^\alpha \right]&= \begin{bmatrix} \hat{\kappa }_1 - \hat{\kappa }^2_{\bullet 2} \\ \hat{\kappa }^2_{\bullet 1} \\ \end{bmatrix}. \end{aligned}$$

(123)

If both $\hat{\kappa }_1 - \hat{\kappa }^1_{\bullet 1}$ and $\hat{\kappa }^2_{\bullet 1}$ are zero, we can write,

$$\begin{aligned} \left[ \left( v_1\right) ^\alpha \right]&= \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix}. \end{aligned}$$

(124)

Taking into account the numerical stability issues related to dealing with very small numbers, we select one of these three equations in the order given below.

• 1. If $\left| \hat{\kappa }_1-\hat{\kappa }^1_{\bullet 1}\right| > \varepsilon \left| \hat{\kappa }^1_{\bullet 2} \right|$, where $\varepsilon = 10^{-6}$, then Eq. (122) is selected.

• 2. If $\left| \hat{\kappa }_1-\hat{\kappa }^1_{\bullet 1}\right| \le \varepsilon \left| \hat{\kappa }^1_{\bullet 2} \right|$ and if $\left| \hat{\kappa }^2_{\bullet 1} \right| > \varepsilon \left| \hat{\kappa }_1 - \hat{\kappa }^2_{\bullet 2} \right|$, then Eq. (123) is selected.

• 3. Otherwise Eq. (124) is selected.

B Derivative of the normal vector

Derivative of the normal vector with respect to $\xi ^\alpha$ can be obtained as follows:

$$\begin{aligned} \overline{\mathbf {n}}_{,\alpha }&= \frac{\partial }{\partial \xi ^\alpha }\left( \frac{\overline{\mathbf {g}}_1\times \overline{\mathbf {g}}_2}{\left( \overline{\mathbf {g}}_1\times \overline{\mathbf {g}}_2\right) \cdot \mathbf {n}} \right) \end{aligned}$$

(125)

$$\begin{aligned}&= \left( \mathbf {I}- \mathbf {n}\mathbf {n}\right) \cdot \frac{\overline{\mathbf {g}}_{1,\alpha }\times \overline{\mathbf {g}}_2 + \overline{\mathbf {g}}_1\times \overline{\mathbf {g}}_{2,\alpha }}{\left( \overline{\mathbf {g}}_1\times \overline{\mathbf {g}}_2\right) \cdot \mathbf {n}} \end{aligned}$$

(126)

$$\begin{aligned}&= \left( \mathbf {I}- \mathbf {n}\mathbf {n}\right) \cdot \frac{ \overline{\mathbf {g}}_{1,\alpha }\times \left( \mathbf {n}\times \overline{\mathbf {g}}^1\right) + \overline{\mathbf {g}}_{2,\alpha }\times \left( \mathbf {n}\times \overline{\mathbf {g}}^2\right) }{\left( \overline{\mathbf {g}}^1\times \overline{\mathbf {g}}^2\right) \cdot \mathbf {n}{\left( \overline{\mathbf {g}}_1\times \overline{\mathbf {g}}_2\right) \cdot \mathbf {n}}} \end{aligned}$$

(127)

$$\begin{aligned}&= \left( \mathbf {I}- \mathbf {n}\mathbf {n}\right) \cdot \left( \overline{\mathbf {g}}_{\beta ,\alpha }\times \left( \mathbf {n}\times \overline{\mathbf {g}}^\beta \right) \right) \end{aligned}$$

(128)

$$\begin{aligned}&= \left( \mathbf {I}- \mathbf {n}\mathbf {n}\right) \cdot \left( \left( \overline{\mathbf {g}}_{\beta ,\alpha } \cdot \overline{\mathbf {g}}^\beta \right) \mathbf {n}- \left( \overline{\mathbf {g}}_{\beta ,\alpha } \cdot \mathbf {n}\right) \overline{\mathbf {g}}^\beta \right) \end{aligned}$$

(129)

$$\begin{aligned}&= -\left( \overline{\mathbf {g}}_{\beta , \alpha } \cdot \mathbf {n}\right) \overline{\mathbf {g}}^{\beta } + \mathbf {n}\underbrace{\left( \mathbf {n}\cdot \overline{\mathbf {g}}^\beta \right) }_{=0} \left( \overline{\mathbf {g}}_{\beta , \alpha } \cdot \mathbf {n}\right) \end{aligned}$$

(130)

$$\begin{aligned}&= -\overline{\mathbf {g}}^{\beta } \overline{\mathbf {g}}_{\beta , \alpha } \cdot \mathbf {n}\end{aligned}$$

(131)

$$\begin{aligned}&= -\overline{\mathbf {g}}^{\beta } \overline{b}_{\alpha \beta }. \end{aligned}$$

(132)

In the derivation, we used the following relationships, which generally hold:

$$\begin{aligned}&\mathbf {g}_1 = \frac{\mathbf {g}^2 \times \mathbf {n}}{\left( \mathbf {g}^1\times \mathbf {g}^2\right) \cdot \mathbf {n}}, \end{aligned}$$

(133)

$$\begin{aligned}&\mathbf {g}_2 = \frac{\mathbf {n}\times \mathbf {g}^1}{\left( \mathbf {g}^1\times \mathbf {g}^2\right) \cdot \mathbf {n}}, \end{aligned}$$

(134)

$$\begin{aligned}&\left( \mathbf {g}^1 \times \mathbf {g}^2\right) \cdot \mathbf {n}= \left( \left( \mathbf {g}_1 \times \mathbf {g}_2\right) \cdot \mathbf {n}\right) ^{-1}. \end{aligned}$$

(135)