A two-scale approach for trabecular bone microstructure modeling based on computational homogenization procedure

Abstract

In this paper the numerical implementation of two-scale modelling of bone microstructure is presented. The study is a part of long-term project on bone remodelling which drives bone microstructure change based directly on trabeculae surface energy. The proposed approach is based on a first-order computational homogenization technique. The coincidence of macro- and micro-model kinematics is done with the use of uniform displacement and traction boundary conditions. The computational homogenization procedure is driven by a self-prepared manager which is coded in Python. The computation on real bone structure (a piece of female Wistar rat bone) is performed as well.

Introduction

Bone tissue is a heterogeneous material which can be classified into two basic types, cortical and cancellous. The cortical bone is dense and creates hard outer layer for cancellous bone which is geometrically complex three-dimensional structure, a mixture of trabeculae in a stochastic form of small beams, struts or rods and voids (see Fig. 1).

The shape and topology of the bone trabeculae are still changing [19] and the phenomenon is called bone remodelling. There are several phenomenological computational models of bone remodelling which can be used in numerical simulation [4, 7, 8, 10, 16, 20, 21, 24, 30]. However, they either base on simple isotropic material models and use a scalar function to modify a bone stiffness ignoring a directional character of the remodelling process [2, 4, 15, 20, 40] or although consider anisotropy properties of material, need complex nonlinear constitutive models. The progress in computing performance and parallel computations now allows for the bone remodelling simulation using the real complex geometry of the cancellous bone [27]. The analysis of real size bone requires a huge FE model [11, 25, 28, 29]. Therefore, the goal of the work presented in this paper is to develop an efficient and robust technique to model cancellous bone microstructure in the case of real size (whole bone) FE simulation of mechanical bone behavior for the purpose of bone remodelling. The technique should describe the global behavior of the bone providing information on surface energy of microstructure at the same time.

Fig. 1

The FE model of cancellous bone microstructure (fragment of Wistar rat bone, European Union grant QLRT-1999-02024, MIAB)

The size reduction of FE model in the case of material which is heterogeneous at a certain scale can be done using a homogenization approach [1, 13, 31, 32]. There are a few different, well-known methods of homogenization of a heterogeneous material. The simplest one bases on a rule of mixtures. In this case, the homogenized properties are calculated as an average over the particular properties of ingredients, which are weighed with their volume fractions. This approach can take into account only one microstructural characteristics. The other method assumes an effective medium approximation [9, 17, 26] which can be used only for structures which have regular and patterned geometry. In this method the equivalent material properties are calculated based on an analytical solution of a boundary value problem. Thus, it cannot take into consideration the non-regular microstructure of cancellous bone. The next homogenization method bases on the mathematical asymptotic homogenization theory [3]. It makes it possible to obtain both: a homogenized properties and local stress and strain values. However, this homogenization method can be used only in cases of very simple microscopic geometries. Today, a group of methods called unit cell [34] are very common for complex microstructure. The unit cell method helps to obtain the information on material state on a local microstructural level and simultaneously on homogenized global material properties. These macroscopic properties are calculated using closed-form phenomenological constitutive equations based on the averaged state (stress–strain) from the analysis of a representative cell of microstructure subjected to a corresponding load scheme. From the viewpoint of the problem discussed, the key weakness of the unit cell method is the requirement of a representative cell of microstructure. In the case of cancellous bone as microstructure it is impossible to define for each macro level material point corresponding representative volume element (RVE). This limitation is of course crucial in the same sense for all homogenization methods discussed above. To sum up, the typical homogenization methods cannot be used directly for simulation of cancellous bone microstructure.

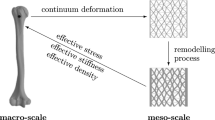
In the context of the discussed problem, the useful alternative for the classical homogenization methods can be a hierarchical approach [5, 14, 23]. This method bases on two-scale approaches and uses the micro- and the macro-scale to describe global bone characteristics. In the global scale, bone is modeled as a continuum material which is characterized by homogenized properties. In the micro scale the bone tissue is considered to be a representative cell of trabeculae of a cancellous bone. This representative cell is assumed to be periodic and has predefined geometric topology [5, 23].

The two-scale modelling approach proposed in this paper determines the macroscopic constitutive behavior based directly on detail geometry of cancellous bone microstructure.

Computational homogenization

The homogenization of heterogeneous materials with the use of multi-scale technique is a common method today [12, 22, 33, 35–37]. The main idea of this method, also called global-local analysis, bases on the direct calculation of the local macroscopic constitutive response from the corresponding microstructure boundary value problem. The foundation of the computational homogenization method is consistent with the other concepts of homogenization techniques. It can be described as a classical four-steps homogenization scheme proposed by Suquet [33]. In the first step, a microstructural RVE is defined. Its constitutive behaviour is assumed to be known. In the second step, microscopic boundary conditions from the macroscopic input variables are formulated and applied to the RVE (so-called macro-to-micro transition). The third step is the calculation of the homogenized macroscopic characteristics based on the analysis of the microstructural RVE (so called micro-to-macro transition). In the last step, the relation between the macroscopic characteristics and inputs is calculated.

The computational homogenization technique has a few crucial advantages. First of all, it does not require any explicitly formulated constitutive equations on a macro-scale level. The macroscopic constitutive behaviour is directly obtained from the corresponding micro-scale boundary value problem analysis [35]. The second advantage is the possibility of taking into consideration the evolution of the microstructure on the macroscopic level analysis and coupling this evolution with results of the macro-scale analysis. Last but not least, there is the advantage that this method can be still effectively used even if the requirement of RVE is not exactly fulfilled for all micro-scale levels analyses.

Basics

The basic scheme of the computational homogenization procedure is shown in Fig. 2. The macroscopic deformation gradient tensor ${{\varvec{F}}}_{M}$ is calculated for each integration point of the macro-scale finite element model (called further macro-model). Next, it is used to define the boundary conditions of the micro-scale model (called further micro-model) which corresponds to the particular integration points. This micro-model defines the microstructure boundary value problem and can be understood in the sense of the RVE. The macroscopic stress tensor ${{\varvec{P}}}_{M}$ is calculated based on the results from the micro-model as averaged stress field over the volume. The stress–deformation relationship at the macro-scale level (macro-model element) is defined as a local macroscopic stiffness tangent matrix. This equivalent matrix is derived directly from the microstructural stiffness. We assume that micro-model is linear, the strains are small and the bone material is elastic. Taking into account the above assumptions, the tangent stiffness matrix can be easily calculated.

Fig. 2

The scheme of the computational homogenization procedure

In the first step of the computational homogenization procedure a microstructural RVE has to be defined. In the approach the micro-model describes physical and geometrical properties of the microstructure and simultaneously defines RVE. The schematic description of RVE is shown in Fig. 3. The dimensions of RVE should be large enough to reproduce the microstructure heterogeneity in a proper way, on the other hand, they should be small enough to allow for reasonable times of calculations. Because of the non-continuous character of cancellous bones which contain a mixture of trabeculae and voids, it is impossible to define the appropriate corresponding RVE for each element of macro-model. The three cases of micro-model configuration can be distinguished: completely filled with bone material, completely empty and partially filled. The first two cases can be clearly treated as RVE while there is no certainty that the requirements of appropriate RVEs are met for the last case. However, we can still estimate the “homogenized” anisotropic behavior of the material on macro-scale level. Generally, the problem on the micro-scale level can be considered as a standard problem of the continuum solid mechanics. The field of deformation of the micro-model in a point described with the initial position vector $\vec {X}$ and the actual position vector is $\vec {x}$ defined by the microstructural deformation gradient tensor:

$$\begin{aligned} F_m =\nabla _{\mathrm{0m}} \vec {x}, \end{aligned}$$

(1)

where the gradient operator $\nabla _{\mathrm{0m}}$ is taken with respect to the reference microstructural configuration. The equilibrium conditions have to be fulfilled for the RVE:

$$\begin{aligned} \nabla _{\mathrm{0m}} P_m =\vec {0}, \end{aligned}$$

(2)

where the stress tensor ${{\varvec{P}}}_{m}$ is defined as the first Piola–Kirchhoff tensor for the reference domain $V_{0}$.

Fig. 3

Schematic description of the RVE; vertices represent transition nodes

In the second step, microscopic boundary conditions from the macroscopic input variables are formulated and applied to the RVE. This macro-to-micro transition is done by enforcement of the macroscopic gradient deformation tensor ${{\varvec{F}}}_{M}$ on the microstructural RVE. This averaging procedure can be used in a few different ways under different assumptions and criteria. There is a general requirement that they should fulfil the assumption of the so-called averaging theorems [18]. The averaging theorems assume that the coupling between micro- and macro-levels is done in an energetically consistent way. In the presented approach the macroscopic input variables are transferred to the microstructural RVE via the boundary conditions (Taylor/Voigt assumption). However, these assumptions are not fulfilled accurately if the appropriate RVE doesn’t exist. The displacement boundary conditions are prescribed in such a way that the position vector $\vec {x}_{m}$ of a point on the deformed micro-model boundary $\varGamma$ is defined as:

$$\begin{aligned} \vec {x}_{m} =F_{M} \vec {X}_{m}, \end{aligned}$$

(3)

where $\vec {X}_{m}$ is the position vector of a point on undeformed micro-model boundary $\varGamma _{0}$. This condition introduces a mapping of the RVE boundaries as a linear relationship.

The first averaging relation for the kinematic quantities is defined by the macroscopic gradient deformation tensor ${{\varvec{F}}}_{M}$ which is the volume average of the microstructural gradient deformation tensor ${{\varvec{F}}}_{m}$:

$$\begin{aligned} F_{M} =\frac{1}{V_{0}}\int \limits _{V_{0}} {F_{m}} dV_{0} =\frac{1}{V_{0}}\int \limits _{\varGamma _{0}} {\vec {x}} \vec {N}d\varGamma _{0} \,. \end{aligned}$$

(4)

Next, the averaging of stresses for the first Piola–Kirchhoff stress tensor can be defined in a similar way:

$$\begin{aligned} P_{M} =\frac{1}{V_{0}}\int \limits _{V_{0}} {P_{m}} dV_{0}\,. \end{aligned}$$

(5)

the macroscopic first Piola–Kirchhoff stress tensor ${{\varvec{P}}}_{M}$ can be written in the microstructural quantities with the use of the following expression:

$$\begin{aligned} P_{m} =\left( {\nabla _{\mathrm{0m}} \cdot P_{m}} \right) \vec {X}+P_{m} \cdot \left( {\nabla _{\mathrm{0m}} \vec {X}} \right) , \end{aligned}$$

(6)

If we take into account equilibrium condition (Eq. 2) and because of:

$$\begin{aligned} \nabla _{\mathrm{0m}} \vec {X}=I, \end{aligned}$$

(7)

the stress tensor ${{\varvec{P}}}_{M}$ (Eq. 6) can be transformed into:

$$\begin{aligned} P_{m} =\nabla _{\mathrm{0m}} \cdot \left( {P_{m} \vec {X}}\right) \,. \end{aligned}$$

(8)

Now, we can substitute (Eq. 8) into (Eq. 5):

$$\begin{aligned} P_{M} =\frac{1}{V_{0}}\int \limits _{V_{0}} {\nabla _{\mathrm{0m}}} \cdot \left( {P_{m} \vec {X}} \right) dV_{0} \end{aligned}$$

(9)

and obtain the following expression after using the Gauss–Ostrogradsky theorem and the first Piola–Kirchhoff stress vector definition $\vec {p}=\vec {N}\cdot P_{m}$ :

$$\begin{aligned} P_{M} =\frac{1}{V_{0}}\int \limits _{\varGamma _{0}} {\vec {N}} \cdot P_{m} \vec {X}\,d\varGamma _{0} =\frac{1}{V_{0}}\int \limits _{\varGamma _{0}} {\vec {p}} \vec {X}d\,\varGamma _{0}\,. \end{aligned}$$

(10)

The obtained Eq. (10) can be directly used to calculate averaging stresses on macro-scale level based on results of microstructural analysis.

Finally, the internal work of the microstructure is averaged as well. The average over the volume energy in the micro-model and macro-model should be the same:

$$\begin{aligned} \delta {W}_{0M} =\delta W_{0m} . \end{aligned}$$

(11)

This assumption is known as the Hill–Mandel condition [18].

The third step of computational homogenization procedure is micro-to-macro transition. In this step the homogenized macroscopic characteristics are calculated based on the micro-models analysis. It has been assumed that the micro-model is linear – the strains and deformations are small and the bone material is elastic. The stress–deformation relationship at the macro-scale level (macro-model element) is defined as a local equivalent stiffness matrix. This matrix is derived directly from the microstructural stiffness matrix. For each micro-model all the “internal” degrees of freedom $\vec {u}_{I}$ are eliminated except those which correspond to the degrees of freedom of nodes of the macro-model elements. These nodes are called transition nodes $\vec {u}_{T}$. Thus, on the macro-level the micro-models are represented by the stiffness (equivalent stiffness matrix) of these retained degrees of freedom. This equivalent stiffness matrix can be derived based on virtual work equation and Hill–Mandel condition (Eq. 11). The virtual work contribution of the selected element of the macro-model can be expressed as a virtual work of micro-model which corresponds to them. It can be written as follow:

$$\begin{aligned} \delta W_{0M}^{Elem}&= \left[ {\delta \vec {u}_T \delta \vec {u}_I} \right] \left( {\left[ { \begin{array}{c} \vec {P}_T \\ \vec {P}_I \\ \end{array}} \right] } \right. \nonumber \\&\left. -\left[ {{ \begin{array}{cc} {K_{mTT}} &{} \quad {K_{mTI}} \\ {K_{mIT}} &{} \quad {K_{mII}} \\ \end{array}}}\right] \left[ {\begin{array}{c} \vec {u}_T \\ \vec {u}_I \\ \end{array}}\right] \right) , \end{aligned}$$

(12)

where $\vec {P}_{T}$ and $\vec {P}_{I}$ are nodal forces which are applied to the micro-model based on the macro-scale response. They can be understood as macroscopic input variables. The stiffness matrix of the microstructure is defined as:

$$\begin{aligned} K_m =\left[ {{ \begin{array}{cc} {K_{mTT}} &{} \quad {K_{mTI}} \\ {K_{mIT}} &{} \quad {K_{mII}} \\ \end{array}}} \right] \, . \end{aligned}$$

(13)

Because the micro-model has to be in internal equilibrium and the internal degrees of freedom are eliminated on macro-level, the equation conjugated to $\delta \vec {u}_{I}$ in the contribution of the virtual work given above (Eq. 12) has to fulfill:

$$\begin{aligned} \vec {P}_I -K_{mIT} \vec {u}_T -K_{mII} \vec {u}_I =0 \end{aligned}$$

(14)

These equations can be rewritten to express $\vec {u}_{I}$ in the following format:

$$\begin{aligned} \vec {u}_{I} =K_{mII^{-1}} \left( {\vec {P}_I -K_{mIT} \vec {u}_T} \right) \end{aligned}$$

(15)

Now, the virtual work of micro-model can be written with the use of the transition constituents and (23) as follows:

$$\begin{aligned}&\vec {u}_T \left( {\left( {\vec {P}_T \!-\!K_{mIT} K_{II}^{-1} \vec {P}_I} \right) \!-\!\left( \! {K_{mTT} \!-\!K_{mTI} K_{mII}^{-1} K_{mIT}} \right) \vec {u}_T} \!\right) \nonumber \\&\delta W_{0M}^{Elem} =\delta , \end{aligned}$$

(16)

Finally, the equivalent stiffness matrix can be defined, based on the above equation, in the form:

$$\begin{aligned} K_{M} =K_{mTT} -K_{mTI} K_{mII}^{-1} K_{mIT}\,. \end{aligned}$$

(17)

In the last step the relation between the macroscopic characteristics and inputs is calculated. It has been done by using the finite element macro-model. Both, macro- and micro-models are discussed in the next section.

Models

In the presented approach the finite element method is used to realize computational homogenization procedure on macro- and micro-levels. Both macro- and micro-models are created in Abaqus/Standard code. In this section the macro- and micro-models are described.

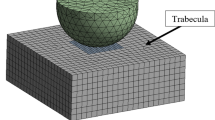
In the discussed method there are no restrictions for the macro-model geometry. The discrete geometry can be general and complex as it is needed. However, for each element of macro-model an individual micro-model has to be assigned (Fig. 4). Therefore, the one to one relation causes that the size of macro-model element determines the size of the micro-model in a direct way. Each node of macro-model is by definition the transition node (Fig. 4).

Fig. 4

The scheme of two-scale FE modelling of bone microstructure

Each micro-model represents the part of the microstructure of cancellous bone (Fig. 4). It simultaneously defines microstructure boundary value problem. From the viewpoint of homogenization procedure, the crucial parts of the micro-model are its boundaries. The micro-model boundaries are the same for all micro-models – hexagonal prisms (Fig. 4). The size and shape of these prisms are described directly by the size and shape of the associated macro-model element. The six faces of prisms are defined explicitly in the micro-model as a membrane-like finite element (MFE) with zero stiffness. The linear Lagrange polynomial functions are used to interpolate the field of displacement in these elements [41]. The six MFEs create the virtual box, the eight vertices of which coincidence with transition nodes (Fig. 4). The macro-to-micro transition is done with the use of the fully prescribed displacement boundary conditions (Eq. 3). The displacements of all nodes on the boundary are defined as:

$$\begin{aligned} \vec {u}_{B} =\left( {F_M -I} \right) \cdot \vec {X}_B, \quad B=1,\ldots , N_B, \end{aligned}$$

(18)

where $N_{B}$ is the number of boundary nodes. These boundary conditions (Eq. 18) are applied to the model by static condensation using the additional weight functions which describe spatial location of boundary nodes relative to the transition nodes. These functions couple each boundary node on a particular face of a virtual box with three closest vertices of this face [6]. The degrees of freedom of the coupled nodes are eliminated from the micro-model system of equations.

Benchmark problems

Because the developed two-scale modelling implementation is based on homogenization technique, the homogenization of a reference microstructure, i.e. one material, continuous cube, is done as a verification in the first place (test A1–A5). Next, this two-scale procedure is verified for bone-like discontinuous material (B6–D12). The proposed approach was implemented in Abaqus FEA code (Dassault Systèmes) driven by self-prepared manager codded in Python.

This reference microstructure is a cube of edge length equal to 10 mm. The structure is divided into 125,000 8-node linear continuum elements. The linear, isotropic material properties are assigned to the structures with Young’s modulus and Poisson’s ratio equal 20e9 Pa and 0.3, respectively. The mechanical parameters of the structures correspond to bone tissue mechanical characteristics [38]. For the reference microstructure, a macro-model and a set of micro-models have been created.

The discontinuity is generated by adding ten spherical holes. The coordinates of the centers and radiuses are randomly generated. The obtained test structures for the three layout of holes are shown in Fig. 5.

Additionally, different discretization levels of macro-model are checked for continuous (test A) and discontinuous (tests C) microstructure. Basic specification of all test models is presented in Table 1.

Fig. 5

Examples of the test specimens: a test set B, spherical holes-layout 1, b test set C, spherical holes-layout 2, c test set D, spherical holes-layout 3

The two-scale models are based directly on the mesh of the reference microstructure. The reference microstructure is divided into cubic elements of the same size. Each cubic element defines a micro-model and corresponds to exact one macro-model element. The micro-models, depending on discretization, consist of from 125,000 to none elements of reference microstructure.

Table 1 Tests models specification

Three load cases are checked: compression (L1), shear (L2) and torsion (L3) (Fig. 6). The boundary conditions are the same for all cases. All nodes of bottom face are fixed. The kinematic constraint is applied to all the nodes of the top face. This constraint couples the displacements of a set of nodes to the movement of a single node, called reference point [6]. The reference point is located 5mm above the centroid of the top face (coordinates: 5, 5, 15 mm). The concentrated force or moment is applied to the reference point for selected DOF. The other DOFs are fixed simultaneously. The following magnitudes of loads are defined: 1N for compression and shear and 1Nmm for torsion. The directions of loads are shown in Fig. 6. All analyses have been done using Abaqus FEA code.

Fig. 6

The load cases of example test structures: a L1—compression, b L2—shear and c L3—torsion

The scalar value of the internal energy is a convenient measure to compare the results obtained from FE analyses in the benchmark cases [18]. However, from the viewpoint of continuum mechanics and used numerical approach, the analyzed example problem is linear. In such a case, the strain energy is a linear function of a deformation gradient. Therefore percentage errors of the global deformation can be compared (Table 2). The results obtained for one-scale approach can be considered as reference, “exact” values. The difference between the solutions taken from two-scale and one-scale models can be considered as an error (the last columns in Table 2).

Table 2 Verification of homogenization—the global deformation of tested specimens for one-scale and two-scale analyses along with percentage error

The crucial aspect of the verification of the homogenization procedure is the mesh convergence evaluation done with the tests A1–A5 for completely filled cube and C7–C11 for porous microstructure. In both cases the mesh refinement reduces the mean error to 0.3 and 4.9 % for tests A5 and C11, respectively. However, the error below 10 % can be achieved already for the macro-model which has at least five elements per each edge of the cube (tests A3 and C9). The character of the mesh convergence curve and small values of the error for fine meshes enable us to conclude that global responses of the one-scale and two-scale models are comparable. It confirms that macro-to-micro and micro-to-macro transitions are done in a proper way and the error due to homogenization procedure in the case o f the two-scale model is acceptable.

The tests B, C and D illustrate the influence of material discontinuity which is a crucial aspect from the viewpoint of bone microstructure modelling. The results obtained are qualitatively the same and quantitatively almost the same (Table 2). Since these three tests can represent three stages of evolution of the cancellous bone microstructure, the verification clearly shows that the presented procedure can be used in the case of evaluating bone-like material.

Real case study: Wistar rat trabecular bone

The presented two-scale modelling procedure is examined for finite element modelling of a real bone. For this purpose the finite element model of a piece of female Wistar rat bone is prepared based on the data from European Union grant QLRT–1999–02024, (MIAB) [39]. The 4.8 mm pieces of bone of living rat were scanned with the use of the micro Computer Tomography (micro CT) method with resolution of $21.8\,\upmu \mathrm{m}$. The 2-dimensional images of micro CT slices after some graphical operations are directly used for building 3-dimensional tetrahedral finite element mesh (Fig. 7) [28]. The linear, isotropic material properties for bone tissue are used. The mechanical parameters of bone are defined as follows: the Young’s modulus equals 20e9 Pa and Poisson’s ratio equals 0.3 [40]. The two load cases are analyzed: compression (L1) and shear (L2). The concentration forces $\hbox {CF}_{\mathrm{X}}=1.0~\hbox {N}$ and $\hbox {CF}_{\mathrm{Z}} = -1.0~\hbox {N}$ are applied to the reference point of the kinematic constraint which is applied to all the nodes of the top face (Fig. 8). The other degrees of freedom of reference point are fixed. The boundary conditions are the same for both cases. All nodes of bottom face are fixed (Fig. 8). The finite element analyses of this bone model are carried out with the use of one-scale and two-scale approaches. The resulting one-scale FE model has up to 6.7379941e+7 elements and 3.6231480e+7 degrees of freedom. In the case of two-scale model the size of the problem is significantly smaller. The macro-model has 2.774e+3 elements and 5.964e+3 degrees of freedom. The number of micro-models is equal to numbers of macro-model elements. The largest micro-model has 9.6006e+4 elements and 5.5500e+4 degrees of freedom. The average size of micro-models is 4.3874e+4 elements and 2.7027e+4 degrees of freedom.

Fig. 7

The geometrical model of a piece of rat bone (data from European Union grant QLRT-1999-02024, MIAB)

Fig. 8

The load cases for rat bone analysis: a L1—compression, b L2—shear

In the case of one-scale model special computer resources for parallel finite element analysis are needed. The calculations of one-scale model of rat’s bone are carried out with the use of the home-made parallel finite element solver based on Message Passing Interface (MPI). The computations are run on 20 CPUs with the use of the Beowulf cluster (8 x CPUs, 16 GB RAM per node) developed in the Division of Machine Design Methods at Poznan University of Technology. The self-prepared tools are created for the parallel result visualization as well [27]. The total time of calculation of the one-scale model is 2.1289e4 seconds $({\sim }6~\hbox {h})$. The calculations of two-scale model are carried out with the use of PC workstation (8 $\times$ CPUs, 24 GB RAM). The total time of calculation is 4.147e3 s $({\sim }1~\hbox {h})$. Results for both approaches and load cases are compared. The global deformation is shown in Table 3.

Table 3 The global deformation of rat bone model in direction of applied load for one-scale and two-scale analyses

The results obtained for two-scale modelling are very close to results obtained with the use of one-scale approach. The relative errors of the global deformation are equal to 5.7 and 4.7 % for compression and shear, respectively. These errors values clearly correspond to the results of two-scale modelling verification presented in the previous section (Table 2). The displacement contour plots for both load cases are also in good agreement (Figs. 9, 10).

Fig. 9

The displacement contour plots for compression: a X–Z view, b X–Z section view, c section view

Fig. 10

The displacement contour plots for shear: a X–Z view, b X–Z section view, c section view

Conclusions

The paper deals with the concept of procedure which, using a two-scale modelling, allows for a fruitful analysis of bone considering its porous, non-homogenous, non-continuous, stochastic form. The global displacement (equivalently strain energy) comparison for test problems, as well as real rat bone geometry, show that proposed modelling approach can be used to simulate bone microstructure with satisfactory accuracy. It can be done not only in an efficient way but also with an acceptable calculation cost. The analysis of a piece of rat bone shows that presented two-scale approach makes it possible to reduce significantly the size of the problem from system of questions with more then 36 million unknowns to set of 2,774 systems of questions with no more then 27,000 unknowns each one. The solving of these set of systems of questions in the two-scale approach is perfectly linearly scalable. The two-scale model can be analyzed with the use of the regular PC workstation instead of the Beowulf cluster (8 CPUs vs 20 CPUs) and nonetheless the time of calculation is four times faster. Moreover, the two-scale technique makes it possible to calculate mechanical bone behavior for large models and to keep the detailed information about cancellous bone microstructure simultaneously. This technique opens a door to the effective simulations of bone remodelling on the level of particular trabeculae as a common practice in biomechanical studies.

The proposed approach has several general significant advantages as well. Firstly, there are no assumptions concerning micro-scale geometry. Secondly, the macroscopic behavior of other heterogeneous materials, not only bone-like, can be described without the explicitly formulated constitutive relations on the macro-scale level. Next, from the viewpoint of engineering application, any arbitrary non-linear and time dependent material behavior can be taken into consideration on the micro-scale level. At the same time this method can be used in the cases of complex loading paths, large deformations and large rotations on the macro-scale level. Next, the hierarchical approach significantly reduces the cost and time of calculation in the case of large models of complex structures. Finally, the averaged stress can be calculated to estimate stress level for homogenized material.

The disadvantage of the method should also be mentioned. In the fully coupled micro-macro technique the computational cost of all nested boundary value problems analyses can be very large. However, this problem can be successfully solved with the use of parallel computing. In the proposed approach the parallelization ratio is close to one.